Open Access Article
Open Access ArticleFirst-principle oligopeptide structural optimization with physical prior mean-driven Gaussian processes: a test of synergistic impacts of the kernel functional and coordinate system†
Yibo Chang,
Chong Teng and
Junwei Lucas Bao *
*
Department of Chemistry, Boston College, Chestnut Hill, Massachusetts 02467, USA. E-mail: lucas.bao@bc.edu
First published on 12th February 2025
Abstract
First-principle molecular structural determination is critical in many aspects of computational modeling, and yet, the precise determination of a local minimum for a large-sized organic molecule is time-consuming. The recently developed nonparametric model, the physical Gaussian Processes (GPs) with physics-informed prior mean function, has demonstrated its efficiency in exploring the potential-energy surfaces and molecular geometry optimizations. Two essential ingredients in physical GPs, the kernel functional and the coordinate systems, could impact the optimization efficiency, and yet the choice of which on the model performance has not yet been studied. In this work, we constructed a testing dataset consisting of 20 oligopeptides and performed a systematic investigation using various combinations of coordinates (structural descriptors) and kernel functionals to optimize these biologically interesting molecules to local minima at the density-functional tight-binding (DFTB) quantum mechanical level. We conclude that the combination of the kernel functional form and coordinate systems matter significantly in model performance as well as its robustness in locating local minima. For our testing set, the synergy between the periodic kernel and the non-redundant delocalized internal coordinates yields the best overall performance for physical GPs, significantly superior to other choices.
I. Introduction
Molecular structural optimization is one of the cornerstones in computational modeling of chemistry, materials, and chemical biology. One starts with a set of initial-guess structures, in which the atomic coordinates are built based on chemical knowledge, known bond lengths or angles, and the atomic hybridization states, and this set of initial structures undergoes geometry optimization to relax their electronic structure energies to reach local minima. In the case of finding a transition-state structure, the initial structure is relaxed to a first-order saddle point that connects the reactant with the product's local minimum structures. The energies and gradients at a non-stationary structure are commonly generated by quantum chemistry calculations on the fly, which are used to guide the search directions. This task of determining molecular structure is equivalent to a multidimensional optimization problem in computational science. In particular, the target function, E(x), is a function of all atomic coordinates, x, in the molecule. The local minimum on this potential energy surface (PES) corresponds to a structure of chemical interest.For small molecules, the computational cost associated with structural optimizations is manageable. Nevertheless, since the dimensionality quickly grows as the molecule becomes larger, the optimization itself becomes costly, in addition to the cost of computing energies and gradients. Therefore, biologically interesting small molecules, which are often too large from the perspective of molecular chemistry, are usually treated at a lower level of theory. One either does not optimize the structure to a local minimum and relies on dynamic sampling or docking to qualitatively explore the structural information, or one optimizes the structure with classical mechanics, i.e., classical force fields, to gain qualitative insights on structural features. Both approaches are indeed effective, especially when experimentally resolved structural information for similar systems is available for comparison. Nevertheless, due to the intrinsic limit and uncertainty in these methods, e.g., the inability of classical force fields to describe electron correlation-induced non-covalent interactions with high accuracy (or the interaction parameters for the system under study are missing), a fully quantum mechanical (QM) structural optimization may be preferred. To be more specific, if affordable, a first-principle determination (without system-dependent parameters) with a quantitatively reliable energy calculation would be beneficial to predicting structures at a higher resolution. Density-functional theory (DFT),1,2 including its semi-empirical approximation, the density-functional tight-binding (DFTB) theory,3–13 provides an excellent balance between computational cost and accuracy, in this context, for main-group chemistry and molecules. Although models like AlphaFold14–17 provide sophisticated direct predictions of dominant conformations for macromolecules such as proteins without relying on first-principles calculations or conventional geometry optimization, the relatively small and conformationally flexible oligopeptides and polypeptides are underrepresented in their training data. Consequently, first-principles structural determination, including the exploration of the entire ensemble of conformers accessible at around room temperature, remains critical. This approach not only complements predictive models like AlphaFold but is also crucial for achieving high-accuracy quantum chemistry modeling. Our work addresses this need by studying a new method to accelerate oligopeptide structure optimizations, enhancing the accuracy and efficiency of first-principles calculations for these challenging systems.
Even with computationally efficient quantum chemistry methods for calculating energies and forces, the optimization itself remains a computational bottleneck for higher-dimensional systems, such as polypeptides, macrocyclic peptides, and oligopeptides, which are important in biological chemistry and therapeutics. Structural predictions continue to attract the efforts of practitioners, including the application of advanced reinforcement machine learning techniques for small molecular geometry optimizations.18 We have recently developed an on-the-fly learning model, the physical prior mean-driven Gaussian Processes (GPs),19 to mitigate the high computational cost associated with geometry optimizations. A GP with a constant prior mean does not include prior physical approximation to the PES; nevertheless, such a model is still useful in local minimum search20–23 and PES exploration,24–28 albeit its efficiency and robustness could be further enhanced due to the criticalness of physicochemical information in structure search.29 GPs are a class of nonparametric models rooted in Bayesian probability, exploring functional space with a prior mean that characterizes the assumed probabilistic distribution a priori.30 In our model, the prior mean is chosen based on a lower-order approximation to the true PES, e.g., a simple classical force field,19 a semi-empirical molecular orbital theory, an adaptive set of computationally efficient models,31,32 or a previously learned PES.33 Without the need to pre-constructing an extensive dataset for training the PES to be explored, one directly starts the geometry optimization task on the GPs’ surrogate PES (SPES), and the surrogate posterior mean learns from the QM information (energies and gradients) on the fly and drives the optimizer to reach a local minimum, completing the GP-assisted ab initio molecular structure determination. This critical feature makes the model highly data-efficient and permits real-time learning and predictions.
Although nonparametric, the model performance of physical GPs is determined by three components primarily: the kernel functional, coordinate systems, and the physical prior mean function. We have previously studied the benefit of introducing physical prior mean function, which not only makes the model robust and efficient but, more importantly, the learned surrogate closely resembles the ground truth (true full QM PES) even for the underexplored region, permitting its future recycling in other tasks as well as meta-learning. The kernel functional k(xi,xj) is fundamental in GPs because it defines how the points (xi and xj) in the input space are covariant with one another, impacting the optimizer's robustness and generalization ability,34 and influencing the smoothness of the SPESs. When combined with molecular structural descriptors, namely, coordinate representation of the structure (xi, which is itself a function of atomic Cartesian coordinates), the kernel functional encodes physical knowledge a priori as well, controlling the model flexibility, complexity, and how sensitive it responds to the correlation between two structures on the same QM PES. We expect such an impact would become much more evident for molecules with more than 100 atoms, the optimization costs of which are no longer negligible. Given the unique importance of the definition of k(xi,xj), which includes the choice of the functional form of k and the structural descriptor x, in this work, we present a systematic study to explore how the efficiency of our physical GP optimizer is impacted by it for large-sized molecules, in particular, first-principle oligopeptide structural optimization.
We constructed a testing dataset consisting of 20 oligopeptides and implemented four commonly used kernels (including the squared exponential kernel, the twice differentiable Matern kernel, the rational quadratic kernel, and the periodic kernel) combined with three types of internal coordinates frequently used in computational chemistry (including the redundant internal coordinates, non-redundant internal coordinates, and the Coulombic coordinates). Note that it is well-known that atomic Cartesian coordinates themselves are not good coordinate choices for molecular geometry optimizations, even for small molecules, due to numerical inefficiency, breakdown of PES invariance to overall translation and rotation, and potentially unphysical changes in bond lengths and angles. Consequently, we did not test the optimization performance in Cartesian coordinates in this work.
II. Theory background overview
Gaussian processes (GPs) with physical prior mean
In physical GPs, the surrogate (SPES) is constructed as a weighted average of the kernel, the derivatives of the kernel, and a non-constant physically inspired prior mean function, μ(x), as,
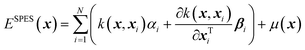 | (1) |
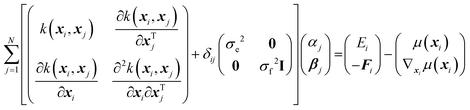 | (2) |
Kernel functional
The kernel functional defines the reproducing kernel Hilbert space according to Mercer's theorem, and consequently, the functional space that GPs search and the posterior sample path (i.e., when we condition the GP on the QM energies and forces, a single function drawn from the GP's distribution), influencing the posterior mean prediction (i.e., the SPES). In this work, we implemented the following four kernel functionals to explore their efficiency and effectiveness in GP optimization of large-sized molecules.(A) The squared exponential (SE) kernel (also known as the radial basis function (RBF) kernel):
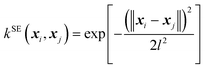 | (3) |
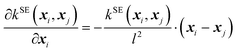 | (4) |
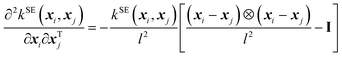 | (5) |
(B) The rational quadratic (RQ) kernel:
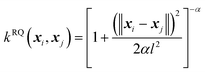 | (6) |
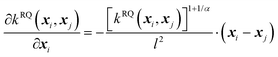 | (7) |
The RQ kernel is a generalization of the SE kernel, in particular, 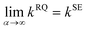 . In addition, it can be viewed as an average of the SE kernels over a distribution of the inverse squared length scales, l′ = l−2, i.e.,
. In addition, it can be viewed as an average of the SE kernels over a distribution of the inverse squared length scales, l′ = l−2, i.e., 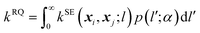 , where p(l′;α) is a gamma distribution of l′.38 Compared to the SE kernel, which is more suitable for a uniform smoothness of data, the RQ kernel is flexible in describing the changes in smoothness in the input space, accommodating non-stationary regions on the PES, and capable of capturing its local and global patterns.
, where p(l′;α) is a gamma distribution of l′.38 Compared to the SE kernel, which is more suitable for a uniform smoothness of data, the RQ kernel is flexible in describing the changes in smoothness in the input space, accommodating non-stationary regions on the PES, and capable of capturing its local and global patterns.
The second-order derivative of the RQ kernel is,
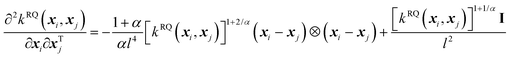 | (8) |
(C) The twice differentiable Matern (M) kernel:
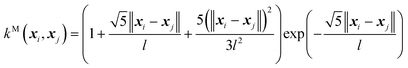 | (9) |
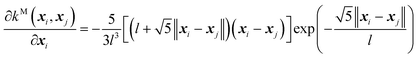 | (10) |
And, its second-order derivative is,
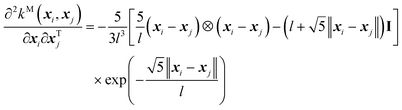 | (11) |
(D) The periodic (P) kernel:
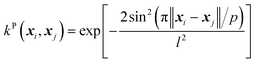 | (12) |
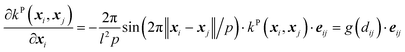 | (13) |
Its second-order derivative is,
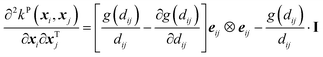 | (14) |
Coordinate systems
Cartesian coordinates are known to be inefficient in geometry optimization31,44,45 and are not suitable for large-sized local minimum search. Importantly, the Cartesian coordinates are not invariant with respect to the center-of-mass translation and overall rotation of the molecule. Curvilinear coordinates, on the other hand, represent the molecular structure with a non-linear combination of Cartesians, including a combination of bond length, valence angles, torsions, and out-of-plane improper torsions. These internal coordinates have been widely used in spectroscopy as well as first-principle geometry optimization. In our early work,31 we implemented various curvilinear coordinates along with their gradient transformations in GPs, and in this work, we focus on the following three:(1) The redundant internal coordinates,46–48 r, which contain more coordinates than the internal degrees of freedom (i.e., 3Natm − 6 for a non-linear molecule) and are generated by the transformation through Wilson's B matrix,49 δr = Bδx, where δx is the displacements in atomic Cartesian coordinates.
(2) The non-redundant delocalized internal coordinates,50 s, which contain precisely 3Natm − 6 coordinates for a non-linear molecule. They are constructed by combining the redundant internal coordinates via a linear transformation, s = UTr, where U is the transformation, consisting of the set of non-redundant eigenvectors of G = BTB with positive eigenvalues.
(3) The Coulombic coordinates,51,52 C, which contain Natm (Natm – 1)/2 unique interatomic distances. In particular, for a pair of atoms, i and j, Cij = 0.5Z2.4i when i = j, and Cij = ZiZj/||Ri – Rj|| when i ≠ j, where Zi is the nuclear charge of the atom i, and ||Ri – Rj|| is the interatomic separation.
Overview of the physical prior GP optimization
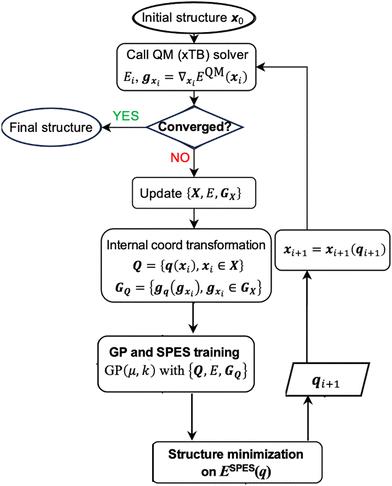
In first-principle molecular geometry optimization, the overall cost is determined by the expense of evaluating QM forces and energy at each iteration, as well as the total number of iterations required to reach the local minimum (defined by the convergence threshold using the QM gradients). The cost of QM force and energy evaluation at an intermediate structure is intrinsically dictated by the electronic structure method and the size of the molecule (i.e., the number of basis functions) and is therefore approximately invariant across iterations. Consequently, to evaluate the efficiency of the optimizer, our focus is on the number of iterations needed to achieve convergence, as the computational cost is proportional to this number.The workflow of the physical prior-mean GP optimization algorithm is depicted in Scheme 1. We first start with an initial guess structure x0, and at the initial cycle, we call the QM solver (an electronic-structure method) to compute the energy and gradient at this point. If the gradient is lower than the convergence threshold, then the structure is converged. This is not the case in initial rounds, and one proceeds to include the current structure and its energy as well as the force in the on-the-fly GP training. In internal coordinate representation, we need to perform the coordinate transformation to transform the Cartesian-coordinate gradients (gx) and Cartesian coordinates of the structure (x) to the corresponding representation in the chosen internal coordinates (gq and q). The details of this transformation in GP are reported in our prior work.31 Next, we perform the GP training based on the training set at the current optimization iteration, which includes all intermediate structures generated so far (i.e., Q = {q(xi)}). This training is based on the energy-and-force GP regression. We then search for a local minimum on the trained GP surrogate SPES, ESPES(q), which will be converted back to the Cartesian-coordinate structural representation. This updated structure will be subject to a QM calculation to evaluate its energy and gradient, and if this structure is not a true local minimum at the QM level, the iteration continues. Each time we generate a new intermediate structure, the GP training set (denoted as the set {Q,E,GQ}) is augmented to include its structure, QM energy, and QM gradient, and the GP SPES is updated based on the data accumulated.
III. Computational details
First-principle methods
All molecular structures are optimized to local minima quantum mechanically with the second-generation extended density-functional tight binding theory for geometries, vibrational frequencies, and non-covalent interactions (GFN2-xTB).7 This is a quantitatively highly reliable and computationally efficient electronic structure theory suitable for large systems. The prediction error in bond lengths is less than 6 pm, and in non-covalent interactions, less than 3 kcal mol−1 (for main-group uncharged systems).7 The target PESs in our physical GPs are thus the GFN2-xTB PESs. We utilize the implementation of GFN2-xTB in the xTB-python package (version 22.1).53 In our physical GPs, the non-constant prior mean function used in this work is the semi-empirical Austin Model 1 (AM1) theory,54 which is developed for quantitative descriptions of structures and energies around the local minima by introducing the modified neglect of differential overlap (MNDO) strategy in Hartree–Fock formalism with improved model parametrization. We implemented our GP optimizer to be interfaced with the Gaussian 16 C.01 program55 for the evaluation of the AM1 electronic structure prior mean function.Gaussian processes setting
The length scale hyperparameters in the kernel functionals are set to generic values. In particular, for the redundant internal and non-redundant delocalized internal coordinates, l = 1.8 bohr (∼1 Å), in which an angle coordinate is converted to a unit of length by using the corresponding arc length in a circle of 1 bohr radius. For the Coulombic coordinates, l = 10 Å−1, a generic value considering that the interatomic distance is on the order of 1 Å and the nuclear charge product is on the order of 10. The noise parameters σe2 = 4.0 × 10−6 eV and σf2 = 2.5 × 10−5 eV Å−1. The structure search on the surrogate (SPES) is performed by energy minimization using the limited-memory Broyden–Fletcher–Goldfarb–Shanno with bounds (L-BFGS-B) optimizer, in which the bond-length internal coordinates are confined to be no less than 0.6 Å. The GP optimization is converged if the maximum Cartesian-coordinate force on an atom, evaluated by GFN2-xTB, is lower than fQMmax = 0.05 eV Å−1, a reasonable threshold for large-sized molecules (with more than 100 atoms). The surrogate structure minimization convergence threshold on the SPES is set to 0.05fQMmax, in which fQMmax corresponds to the latest geometry in the GP optimization.Oligopeptide structure testing dataset
We have constructed a set of de novo oligopeptides to test the performance of using physical prior mean-driven GPs as a molecular structure optimizer in first-principle calculations. We have tabulated these 20 structures in the testing set in Table 1, detailing their components. Their initial geometries, the starting point for all the GP optimizer tests, are shown in Fig. 1 in ribbon diagrams, with all the atomic Cartesian coordinates (in Å) along with the full atomistic visualization provided in the ESI.† This set of test structures includes common amino acids and represents key secondary structures, such as the alpha helix, beta sheet, and cyclic structures (e.g., the ones that are stabilized by disulfide bonds). We first selected a set of readily available protein structures and truncated them into oligopeptides to facilitate full QM-level structural optimization. The structures were then modified to ensure they function as true testing systems without any pre-training. Moreover, these oligopeptides do not occur naturally (to date), in which some of the amino acid side chains are mutated, making them well-suited for theoretical structural predictions and testing.| ID | Chemical formula | Secondary structure encoded | Amino acid sequencea |
|---|---|---|---|
| a The amino acids are represented by their respective single-letter code. The code with a prime, e.g., R′, indicates an artificial modification, as explained in the text. | |||
| 1 | C21O11N10H34 | Alpha helix | GGGAGGGGGG |
| 2 | C27O13N11S2H45 | Beta sheet | GAGCSGCGAGG |
| 3 | C36O17N15H59 | Alpha helix | GPGEGGSAGR′GGS′ |
| 4 | C27O12N9S2H45 | Alpha helix; cyclic | C′SSAAAAAC′ |
| 5 | C29O16N13H47 | Alpha helix | GSAGGGSGDGGG |
| 6 | C26O13N14H42 | Beta sheet | GGGGGGGGGGGGG′ |
| 7 | C31O16N13SH47 | Beta sheet | G′GCGNGGPGGGG |
| 8 | C31O16N13H47 | Alpha helix | PGGDGGGGGGNG |
| 9 | C38O20N18H60 | Beta sheet | GQGGGGGGSGGGGGGGG |
| 10 | C32O12N9S2H43 | Cyclic | G′GPC′NGGYC′′ |
| 11 | C30O16N13H47 | Alpha helix | GGGGAGDGQGGG |
| 12 | C32O14N11H45 | Linear | F′GEGGAGGGG′ |
| 13 | C33O15N12S2H48 | Alpha helix; cyclic | C′′GGPGGPGGGC′G |
| 14 | C27O15N13H43 | Alpha helix | GGGGGGGGGGGSG |
| 15 | C33O15N15H53 | Beta sheet | GGGGGPGGGGGTGG′ |
| 16 | C29O16N13H45 | Beta sheet | GGANGDGGGGGG |
| 17 | C34O16N15S4H51 | Alpha helix; cyclic | C′GC′GGGGGGGC′GGGC′ |
| 18 | C36O18N17H55 | Beta sheet | G′GPGGGGGGGGGGGGG′′ |
| 19 | C35O19N17H55 | Alpha helix | GGGGGGGGGGGGGGSGG |
| 20 | C38O16N18H62 | Beta sheet; cyclic | K′GGGGGGG′K′GGGGGGG′ |
 | ||
| Fig. 1 The geometries of the 20 constructed oligopeptides in the testing set visualized using the ribbon model, in which the explicit atomistic arrangements are hidden. Notice that the heteroatoms are not represented in the ribbon model, so the cyclic oligopeptide structures 4, 10, 13, 17, and 20 are a bit obscured in atomic connectivity in this figure. The explicit all-atom ball-and-stick model of these structures is provided in the (ESI†). | ||
With the assistance of Gaussian16's built-in global MMX (GMMX) conformational search algorithm using the MMFF94 force field, one could pre-screen the peptide bond dihedral angles by searching within a subspace of the conformers (e.g., limiting to 100 structures) stochastically and generate a reasonably low-energy initial structure. Nevertheless, for the purpose of this work, i.e., testing the efficiency of the GP optimizers with various kernels and coordinates, we need not use the lowest-energy structures. In fact, it would be interesting to test if our method also works for higher energy structures (without any secondary structure). We created one such example (ID 12), for which its initial structure is linear.
In Table 1, the amino acid unit denoted with a prime, e.g., R′, indicates an ad hoc modification performed on the natural structure. For ID 3, the side chain in R (arginine) is truncated to –CH2NH2, and in S (serine), its C-terminus has a –CONH2 group instead of –COOH. For ID 4, both C's (cysteines) have their side chains forming a disulfide bridge (with a loss of H atoms), and the first C has its N-terminus defined as a –NHCOOH group, while the last C terminates the chain with an H atom instead of –COOH. For ID6, the G (glycine) has a –CONH2 group as the C-terminus instead of –COOH. For ID7, the N-terminus in G starts with a –NHCOOH group instead of –NH2. For ID10, the first G starts with a –CONH2 group as its N-terminus, and the first C has its side chain forming a disulfide bridge, while the second C (i.e., C′′) loses the H atom on –SH in the side chain, and this chain ends with an H atom. For ID12, the first F (phenylalanine) starts with a –NHCOOH group at the N-terminus, and the G ends with a –CONH2 group at the C-terminus. For ID13, the first C (i.e., C′′) starts with the –NHCOOH group at the N-terminus, and the –SH becomes a disulfide bridge, which is also the case for the second C. For ID15, the chain ends with a –CONH2 group in G at the C-terminus. For ID17, all C's form the disulfide bridges. For ID18, the first G starts with a –NHCOOH group at the N-terminus, while the second G (i.e., G′′) ends with a –CONH2 group at the C-terminus. For ID20, the side chain on K (lysine) connects with the C-terminus on G.
Structural comparison
We need to compare the structures predicted by GP optimizers, which differ in the kernel and coordinate representation, to ensure the same or similar structures were acquired. It is known that the optimized local minima may have slight discrepancies with different coordinate systems unless an extremely tight convergence threshold is applied. We define the reference structures as the QM-level local minima optimized with the non-redundant delocalized internal coordinates, s, by the physical prior-mean GPs using the RQ kernel for IDs 2–5 and 7–20, the P kernel for ID 1, and the SE kernel for ID 6.The root mean squared deviations (RMSDs in Å) in atomic Cartesian coordinates are calculated as a metric to assess the structural geometric differences. In particular, we used the Kabsch algorithm56 in our comparison, in which the structures are re-centered and re-orientated to minimize the RMSD via the quaternions. In addition, we included the “--reorder” flag to perform the atom order adjustment to make sure that the order of atoms (i.e., atomic indices) in the two structures under comparison is consistent.
Furthermore, we have calculated the QM energy differences of the optimized local minima compared to the corresponding reference structures. We found that among all structures optimized by GPs when r and s coordinates were used, the energy differences were within 0.03 eV on average, and the RMSDs were within 0.2 Å on average. In the case of C coordinates, a few systems converged to higher energy conformers compared to the reference structures.
To show the limitation in the AlphaFold 3 prediction for oligopeptide structures, we also use RMSDs to compare our first-principle GP-optimized reference structures with the AlphaFold structures. Note that because our testing structures include modified amino acids and AlphaFold only takes in the natural amino acid sequence as input, we have to calculate the RMSDs for the common set of atoms shared by both predictions. In addition, if the atomic connectivity is different in two structures (physical GPs vs. AlphaFold), we exclude the case in our comparison.
IV. Results and discussions
We have tabulated the number of iterations for converging the 20 oligopeptides with the GP optimizers in Table 2, along with each optimizer's averaged number of iterations for reaching the local minima and the standard deviations. We have applied a combination of the kernel functionals (including the SE, RQ, M, and P kernels) and the structural descriptor (i.e., the r, s, and C coordinates). The structural descriptor impacts the efficiency of the optimization significantly. In particular, the internal coordinates, including the r and s, have a much better performance than the C coordinates. Although the C coordinates are indeed invariant with respect to the overall translation and rotation of the molecule, the inverse interatomic distance, 1/Rij, for a pair of well-separated nuclei is not sensitive to the structure change. In addition, the redundancy included in C is too high as compared to the other two coordinate systems. In particular, the number of unique coordinates scales as ∼Natm2, which is unfavorable in such a high dimensional optimization task. Consequently, its performance in optimizing large-sized molecules, which have multiple large interatomic separations, is not optimal.| ID | kSE(xi,xj) | kRQ(xi,xj) | kM(xi,xj) | kP(xi,xj) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r | s | C | r | s | C | r | s | C | r | s | C | |
| a The entry labeled “Failed” indicates that an unphysical structure is generated during the optimization process (e.g., radical generation, broken bonds, etc.). For each column, the average number of iterations excludes any failed cases. The convergence threshold for all optimizers was set to the maximum atomic force (at QM level) being less than 0.05 eV Å−1. | ||||||||||||
| 1 | 372 | 374 | 307 | 74 | Failed | 81 | 230 | 231 | 477 | 61 | 55 | 94 |
| 2 | 195 | 211 | 1308 | 43 | 42 | 580 | 130 | 130 | 1442 | 39 | 28 | 351 |
| 3 | 516 | 515 | 947 | 93 | 56 | 316 | 289 | 290 | 1623 | 72 | 67 | 305 |
| 4 | 210 | 206 | 1193 | 44 | 43 | 375 | 130 | 129 | 1435 | 43 | 43 | 512 |
| 5 | 250 | 261 | 807 | 49 | 53 | 127 | 151 | 150 | 743 | 65 | 67 | 172 |
| 6 | 55 | 59 | 471 | Failed | Failed | 103 | 26 | 27 | 455 | Failed | Failed | 101 |
| 7 | 159 | 168 | 441 | 25 | 34 | 62 | 93 | 95 | 368 | 33 | 33 | 151 |
| 8 | 608 | 738 | 824 | 116 | 111 | 130 | 351 | 344 | 838 | 120 | 101 | 172 |
| 9 | 123 | 123 | 487 | 28 | 24 | 67 | 79 | 78 | 478 | 26 | 25 | 118 |
| 10 | 96 | 92 | 874 | 26 | 20 | 136 | 24 | 24 | 887 | 19 | 18 | 160 |
| 11 | 281 | 279 | 667 | 50 | 48 | 98 | 154 | 152 | 590 | 58 | 53 | 136 |
| 12 | 65 | 59 | 264 | 13 | 13 | 130 | 14 | 14 | 156 | 12 | 9 | 39 |
| 13 | 111 | 109 | 1319 | 23 | 23 | 191 | Failed | 329 | 1320 | 24 | 23 | 222 |
| 14 | 625 | 566 | 807 | 105 | 99 | 126 | 308 | 315 | 701 | 60 | 75 | 349 |
| 15 | 436 | Failed | 895 | 91 | 55 | 139 | 281 | 211 | 783 | 88 | 95 | 287 |
| 16 | 157 | 157 | 739 | 32 | 30 | 114 | 91 | 91 | 661 | 34 | 30 | 88 |
| 17 | 1301 | 1235 | Failed | 189 | 180 | Failed | Failed | 695 | Failed | Failed | Failed | 731 |
| 18 | 391 | Failed | 582 | 60 | 72 | 94 | 256 | 252 | 586 | 76 | 65 | 236 |
| 19 | 761 | 753 | 925 | 129 | 126 | 197 | 535 | 544 | 780 | 93 | 86 | 143 |
| 20 | 439 | 390 | 739 | 97 | 71 | 123 | 455 | 269 | 985 | Failed | Failed | 222 |
| Average | 357.6 | 349.7 | 768.2 | 67.7 | 61.1 | 167.8 | 199.8 | 218.5 | 805.7 | 54.3 | 51.4 | 229.5 |
| Std. | 302.0 | 310.7 | 303.1 | 45.7 | 43.4 | 127.5 | 149.2 | 173.5 | 398.4 | 29.5 | 28.1 | 163.3 |
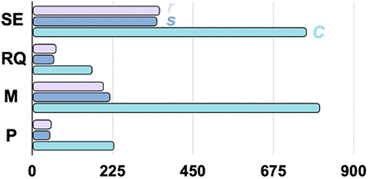
The synergistic effect of the kernel and coordinates is clear in our tests. In Fig. 2, we plot the average number of iterations, excluding the cases that failed to converge, in four kernel categories, each of which is subjected to three choices of the coordinate systems. The non-redundant delocalized internal coordinates, in general, show better performance than the other two coordinates for any kernel. For the Matern kernel, although r shows slightly better efficiency than s (199.8 vs. 218.5 iterations), since s only includes 3Natm – 6 coordinates, it greatly reduces the memory requirement for GP optimizations.
One of the approaches to introduce a physically motivated learning model is through the design of the kernel in GPs. Our observation is consistent with the physical insights brought by the kernel. Specifically, the RQ and M kernels improve the modeling of the smoothness of realistic PESs as compared to the SE kernel, which is infinite-order differentiable. This is consistent with our performance test, in which the SE kernel is less efficient compared to the RQ and M kernels in general, except that kSE(Ci,Cj) is slightly more efficient than kM(Ci,Cj). When comparing the RQ with the M kernel, we found that the M kernel is less efficient, particularly when combined with the C coordinates. Nevertheless, when combined with s, kM(si,sj) is very robust because it successfully converged all 20 structures without convergence issues.
Overall, using kP(si,sj) yields the best performance for our testing set, which, on average, only requires 51.4 iterations to reach convergence, which is a factor of ∼16 more efficient than kM(Ci,Cj). This observation shows the synergy between the periodic kernel and s. The periodic kernel includes critical physical insights in optimizing oligopeptides or any molecule with a large number of internal rotations (torsional degree of freedom). When combined with internal coordinates, which include the dihedral angles for torsions, the local periodicity of the torsional motion, essential for geometry optimization in our task, generates a periodic function (the torsional projected PES). If one encounters a convergence failure with the kP(si,sj)-driven GP optimizer, an advisable solution without resorting to pre-optimize the structure with a classical force field is to switch to the RQ kernel in s coordinates, which provides similar performance.
Furthermore, under the periodic kernel, the redundant coordinate (r) requires 54.3 iterations on average, and thus, it performs similarly to the s coordinate system. Nevertheless, from the computational memory requirement perspective, the number of coordinates involved in the optimization for the non-redundant coordinate s is much fewer than the redundant coordinate choice (>3Natm). Therefore, the s coordinate serves as a better choice than the r coordinates.
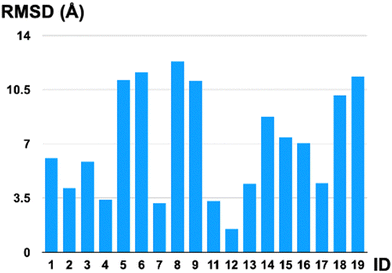
The final investigation we performed was to compare the first-principle structures optimized by the GP optimizer (in particular, the reference structure defined in the “Structural comparison” section) with the AlphaFold 3 predictions. These two approaches are fundamentally different in working principle, in which our physical GP method requires first-principle information and optimizes for local minima on the surrogate surfaces, while AlphaFold does not require detailed atomistic level energy calculations and aims for structural prediction for proteins. We have calculated the RMSDs in Å for all oligopeptides that have the same atomic connectivity predicted by these two models. Note that, in some cases (IDs 10 and 20), AlphaFold predicted completely different atomic connectivity compared to the first-principle optimized ones. The AlphaFold model uses the predicted template modeling (pTM) score to assess the prediction quality internally, indicating the overlap between the generated structure and the hypothetical true structure. All the predicted oligopeptides have a pTM score that falls within 0.02–0.03, drastically lower than the pTM = 0.5 threshold, indicating an internal diagnosis of highly unreliable predictions. The oligopeptide structures generated by AlphaFold tend to be linear and show no secondary structures (Fig. 3); thus, they are energetically unfavorable conformers compared to our GP-optimized ones at the QM level. The low pTM scores are consistent with our structural comparison in terms of the RMSDs, shown in Fig. 4, highlighting the qualitatively different predictions from AlphaFold compared to the QM-level optimized structures. Even for the intentionally created linear structure, ID 12, for which our GP optimizer has no trouble optimizing to a local minimum quantum mechanically, the AlphaFold prediction still deviates from the reference by 1.5 Å. (Note that the C–H bond is ∼1.1 Å and the C–C bond is ∼1.5 Å.) The QM method, GFN2-xTB, is capable of predicting highly accurate geometries, with an error of ∼6 pm in bond lengths, and consequently, its local minima serve as benchmark-level structures in this work. This discrepancy is understandable since AlphaFold is trained on macromolecular complexes (proteins) without on-the-fly first-principle guidance in structural search. Furthermore, the smaller yet more flexible polypeptides are underrepresented in its training.
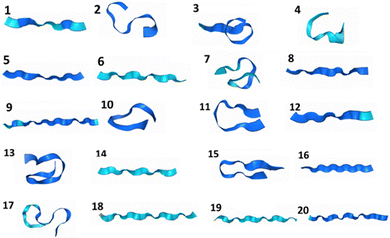 | ||
| Fig. 3 The predicted oligopeptide structures generated by AlphaFold 3 in the ribbon model representation. | ||
V. Conclusion
First-principle-level molecular structure optimization is an essential starting point for structure-based modeling and design. Large molecules with high degrees of freedom pose a challenge in the efficient search for local minima. We examined the usefulness of using a surrogate model-driven structure optimization for oligopeptides at the quantum mechanical level. In particular, we investigated the impact of the kernel functional choice and structural descriptor (including the redundant internal coordinates, the non-redundant delocalized internal coordinates, and the Coulombic coordinates) in physical prior mean-based GP optimizations. We concluded that for large torsionally flexible molecules, the periodic kernel, which approximates the physically periodic torsional potential energies, coupled with the delocalized internal coordinates, provides a highly efficient option for performing ab initio molecular geometry optimization with on-the-fly GP training and prediction.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. L. B. acknowledges the financial support provided by the Schiller Institute Grant for Exploratory Collaborative Scholarship (SIGECS) as well as, in part, the American Chemical Society Petroleum Research Fund (PRF no. 65744-DNI6). In addition, we thank the Boston College Linux Cluster Center for cluster computing resources.References
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- D. Porezag, Th Frauenheim, Th Köhler, G. Seifert and R. Kaschner, Construction of Tight-Binding-Like Potentials on the Basis of Density-Functional Theory: Application to Carbon, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957 CrossRef CAS PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner and M. Haugk, Th. Frauenheim, S. Suhai, and G. Seifert, Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- M. Gaus, Q. Cui and M. Elstner, DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB), J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS PubMed.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Semiempirical Quantum Mechanical Methods for Noncovalent Interactions for Chemical and Biochemical Applications, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- M. Gaus, A. Goez and M. Elstner, Parametrization and Benchmark of DFTB3 for Organic Molecules, J. Chem. Theory Comput., 2013, 9, 338–354 CrossRef CAS PubMed.
- M. Gaus, X. Lu, M. Elstner and Q. Cui, Parameterization of DFTB3/3OB for Sulfur and Phosphorus for Chemical and Biological Applications, J. Chem. Theory Comput., 2014, 10, 1518–1537 CrossRef CAS PubMed.
- M. Gaus, H. Jin, D. Demapan, A. S. Christensen, P. Goyal, M. Elstner and Q. Cui, DFTB3 Parametrization for Copper: The Importance of Orbital Angular Momentum Dependence of Hubbard Parameters, J. Chem. Theory Comput., 2015, 11, 4205–4219 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- M. Vujovic, M. Huynh, S. Steiner, P. Garcia-Fernandez, M. Elstner, Q. Cui and M. Gruden, Exploring the Applicability of Density Functional Tight Binding to Transition Metal Ions. Parameterization for Nickel with the Spin-Polarized DFTB3 Model, J. Comput. Chem., 2019, 40, 400–413 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended Tight-Binding Quantum Chemistry Methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly Accurate Protein Structure Prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- M. Varadi, S. Anyango, M. Deshpande, S. Nair, C. Natassia, G. Yordanova, D. Yuan, O. Stroe, G. Wood, A. Laydon, A. Žídek, T. Green, K. Tunyasuvunakool, S. Petersen, J. Jumper, E. Clancy, R. Green, A. Vora, M. Lutfi, M. Figurnov, A. Cowie, N. Hobbs, P. Kohli, G. Kleywegt, E. Birney, D. Hassabis and S. Velankar, AlphaFold Protein Structure Database: Massively Expanding the Structural Coverage of Protein-Sequence Space with High-Accuracy Models, Nucleic Acids Res., 2022, 50, D439–D444 CrossRef CAS PubMed.
- M. Baek, F. DiMaio, I. Anishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millán, H. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodrigues, A. A. van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Accurate Prediction of Protein Structures and Interactions Using a Three-Track Neural Network, Science, 2021, 373, 871–876 CrossRef CAS PubMed.
- J. Abramson, J. Adler, J. Dunger, R. Evans, T. Green, A. Pritzel, O. Ronneberger, L. Willmore, A. J. Ballard, J. Bambrick, S. W. Bodenstein, D. A. Evans, C.-C. Hung, M. O’Neill, D. Reiman, K. Tunyasuvunakool, Z. Wu, A. Žemgulytė, E. Arvaniti, C. Beattie, O. Bertolli, A. Bridgland, A. Cherepanov, M. Congreve, A. I. Cowen-Rivers, A. Cowie, M. Figurnov, F. B. Fuchs, H. Gladman, R. Jain, Y. A. Khan, C. M. R. Low, K. Perlin, A. Potapenko, P. Savy, S. Singh, A. Stecula, A. Thillaisundaram, C. Tong, S. Yakneen, E. D. Zhong, M. Zielinski, A. Žídek, V. Bapst, P. Kohli, M. Jaderberg, D. Hassabis and J. M. Jumper, Accurate Structure Prediction of Biomolecular Interactions with AlphaFold 3, Nature, 2024, 630, 493–500 CrossRef CAS PubMed . (With the online server accessible via https://alphafoldserver.com/about; accessed on Nov. 12, 2024.).
- K. Ahuja, W. H. Green and Y.-P. Li, Learning to Optimize Molecular Geometries Using Reinforcement Learning, J. Chem. Theory Comput., 2021, 17, 818–825 CrossRef CAS PubMed.
- C. Teng, Y. Wang, D. Huang, K. Martin, J.-B. Tristan and J. L. Bao, Dual-Level Training of Gaussian Processes with Physically Inspired Priors for Geometry Optimizations, J. Chem. Theory Comput., 2022, 18, 5739–5754 CrossRef CAS PubMed.
- A. Denzel and J. Kästner, Gaussian Process Regression for Geometry Optimization, J. Chem. Phys., 2018, 148, 094114 CrossRef.
- D. Born and J. Kästner, Geometry Optimization in Internal Coordinates Based on Gaussian Process Regression: Comparison of Two Approaches, J. Chem. Theory Comput., 2021, 17, 5955–5967 CrossRef CAS PubMed.
- G. Raggi, I. Fdez Galván, C. L. Ritterhoff, M. Vacher and R. Lindh, Restricted-Variance Molecular Geometry Optimization Based on Gradient-Enhanced Kriging, J. Chem. Theory Comput., 2020, 16, 3989–4001 CrossRef CAS PubMed.
- I. F. Galván, G. Raggi and R. Lindh, Restricted-Variance Constrained, Reaction Path, and Transition State Molecular Optimizations Using Gradient-Enhanced Kriging, J. Chem. Theory Comput., 2021, 17, 571–582 CrossRef PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian Process Regression for Materials and Molecules, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- R. Snyder, B. Kim, X. Pan, Y. Shao and J. Pu, Bridging Semiempirical and Ab Initio QM/MM Potentials by Gaussian Process Regression and Its Sparse Variants for Free Energy Simulation, J. Chem. Phys., 2023, 159, 054107 CrossRef CAS PubMed.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-Fly Active Learning of Interpretable Bayesian Force Fields for Atomistic Rare Events, npj Comput. Mater., 2020, 6, 20 CrossRef.
- B. Kolb, P. Marshall, B. Zhao, B. Jiang and H. Guo, Representing Global Reactive Potential Energy Surfaces Using Gaussian Processes, J. Phys. Chem. A, 2017, 121, 2552–2557 CrossRef CAS PubMed.
- B. Jiang, J. Li and H. Guo, High-Fidelity Potential Energy Surfaces for Gas-Phase and Gas-Surface Scattering Processes from Machine Learning, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS PubMed.
- Y.-C. Chang and Y.-P. Li, Integrating Chemical Information into Reinforcement Learning for Enhanced Molecular Geometry Optimization, J. Chem. Theory Comput., 2023, 19, 8598–8609 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- C. Teng, D. Huang and J. L. Bao, A Spur to Molecular Geometry Optimization: Gradient-Enhanced Universal Kriging with On-the-Fly Adaptive Ab Initio Prior Mean Functions in Curvilinear Coordinates, J. Chem. Phys., 2023, 158, 024112 CrossRef CAS PubMed.
- C. Teng, Y. Wang and J. L. Bao, Physical Prior Mean Function-Driven Gaussian Processes Search for Minimum-Energy Reaction Paths with a Climbing-Image Nudged Elastic Band: A General Method for Gas-Phase, Interfacial, and Bulk-Phase Reactions, J. Chem. Theory Comput., 2024, 20, 4308–4324 CrossRef CAS PubMed.
- C. Teng, D. Huang, E. Donahue and J. L. Bao, Exploring Torsional Conformer Space with Physical Prior Mean Function-Driven Meta-Gaussian Processes, J. Chem. Phys., 2023, 159, 214111 CrossRef CAS PubMed.
- M. G. Genton, Classes of Kernels for Machine Learning: A Statistics Perspective, J. Mach. Learn. Res., 2001, 2, 299–312 Search PubMed.
- S. Laue, M. Mitterreiter and J. Giesen, Computing Higher Order Derivatives of Matrix and Tensor Expressions, Adv. Neural Inf. Process. Syst., 2018, 31, 2750 Search PubMed.
- S. Laue, M. Mitterreiter and J. Giesen, A Simple and Efficient Tensor Calculus, Proc. Assoc. Adv. Artif. Intell., 2020, 34, 4527 Search PubMed.
- D. Huang, C. Teng, J. L. Bao and J.-B. Tristan, mad-GP: Automatic Differentiation of Gaussian Processes for Molecules and Materials, J. Math. Chem., 2022, 60, 969–1000 CrossRef CAS.
- M. L. Stein, Interpolation of Spatial Data, Springer-Verlag, New York, 1999 Search PubMed.
- J. Zheng, T. Yu, E. Papajak, I. M. Alecu, S. L. Mielke and D. G. Truhlar, Practical Methods for Including Torsional Anharmonicity in Thermochemical Calculations on Complex Molecules: The Internal-Coordinate Multi-Structural Approximation, Phys. Chem. Chem. Phys., 2011, 13, 10885–10907 RSC.
- J. Zheng and D. G. Truhlar, Quantum Thermochemistry: Multistructural Method with Torsional Anharmonicity Based on a Coupled Torsional Potential, J. Chem. Theory Comput., 2013, 9, 1356–1367 CrossRef CAS PubMed.
- J. L. Bao, L. Xing and D. G. Truhlar, Dual-Level Method for Estimating Multistructural Partition Functions with Torsional Anharmonicity, J. Chem. Theory Comput., 2017, 13, 2511–2522 CrossRef CAS PubMed.
- L. Simon-Carballido, J. L. Bao, T. V. Alves, R. Meana-Pañeda, D. G. Truhlar and A. Fernandez-Ramos, Anharmonicity of Coupled Torsions: The Extended Two-Dimensional Torsion Method and Its Use to Assess More Approximate Methods, J. Chem. Theory Comput., 2017, 13, 3478–3492 CrossRef CAS PubMed.
- J. Zheng, S. L. Mielke, J. L. Bao, R. Meana-Pañeda, K. L. Clarkson and D. G. Truhlar, MSTor: A Program for Calculating Partition Functions, Free Energies, Enthalpies, Entropies, and Heat Capacities of Complex Molecules Including Torsional Anharmonicity, Version 2017-B, 2017.
- H. B. Schlegel, Exploring Potential Energy Surfaces for Chemical Reactions: An Overview of Some Practical Methods, J. Comput. Chem., 2003, 24, 1514–1527 CrossRef CAS PubMed.
- M. von Arnim and R. Ahlrichs, Geometry Optimization in Generalized Natural Internal Coordinates, J. Chem. Phys., 1999, 111, 9183–9190 CrossRef CAS.
- G. Fogarasi, X. Zhou, P. W. Taylor and P. Pulay, The Calculation of Ab Initio Molecular Geometries: Efficient Optimization by Natural Internal Coordinates and Empirical Correction by Offset Forces, J. Am. Chem. Soc., 1992, 114, 8191–8201 CrossRef CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, Using Redundant Internal Coordinates to Optimize Equilibrium Geometries and Transition States, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- V. Bakken and T. Helgaker, The Efficient Optimization of Molecular Geometries Using Redundant Internal Coordinates, J. Chem. Phys., 2002, 117, 9160–9174 CrossRef CAS.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, McGraw-Hill, 1955 Search PubMed.
- J. Baker, A. Kessi and B. Delley, The Generation and Use of Delocalized Internal Coordinates in Geometry Optimization, J. Chem. Phys., 1996, 105, 192–212 CrossRef CAS.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. von Lilienfeld, Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- F. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Crystal Structure Representations for Machine Learning Models of Formation Energies, Int. J. Quantum Chem., 2015, 115, 1094–1101 CrossRef CAS.
- Python API for the Extended Tight Binding Program. (With online access to the open-source code: https://xtb-python.readthedocs.io/en/latest/; accessed on Jan. 28, 2025.).
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, AM1: A New General Purpose Quantum Mechanical Molecular Model, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01., Gaussian, Inc., 2016 Search PubMed.
- K. W. Kabsch, A Solution for the Best Rotation to Relate Two Sets of Vectors, Acta Crystallogr., 1976, A32, 922–923 CrossRef . (With online access to the open-source code: https://github.com/charnley/rmsd; accessed on Nov. 13, 2024.).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04378b |
| This journal is © the Owner Societies 2025 |