Carbonless DNA

Abstract

Carbonless DNA was designed by replacing all carbon atoms in the standard DNA building blocks with boron and nitrogen, ensuring isoelectronicity. Electronic structure quantum chemistry methods (DFT(ωB97XD)/aug-cc-pVDZ) were employed to study both the individual building blocks and the larger carbon-free DNA fragments. The reliability of the results was validated by comparing selected structures and binding energies using more accurate methods such as MP2, CCSD, and SAPT2+3(CCD)δ_MP2. Carbonless analogs of DNA components, including cytosine, thymine, guanine, adenine, and deoxyribose, were investigated, showing strong resemblance to the carbon-based versions in terms of spatial structure, polarity, and molecular interaction capabilities. Complementary base pairs of the carbonless analogs exhibited a similar number and length of hydrogen bonds as those found in their carbon-containing counterparts, with binding energies for A–T and G–C analogs remaining comparable. Carbonless DNA fragments containing two and six base pairs were studied, revealing double-helix structures analogous to natural DNA. Structural parameters such as fragment size, hydrogen bond lengths, and rise per base pair were consistent with those observed in unmodified DNA. Docking simulations with a 12 base pair fragment and netropsin as a ligand indicated a slight shift in binding preference for the carbonless DNA through the minor groove, with an approximate 25% increase in binding affinity compared to natural DNA.

---

1. Introduction

Deoxyribonucleic acid (DNA) is the fundamental molecule responsible for storing and transmitting genetic information in all known forms of life. Its structure, composed of four nucleotide bases, a deoxyribose sugar backbone, and phosphate groups, is inherently dependent on carbon atoms to form stable, complex organic frameworks. However, despite the centrality of carbon in terrestrial biochemistry, there has been increasing interest in exploring alternative biochemical structures that do not rely on this element, as the design and synthesis of carbon-free analogs of biomolecules offer an intriguing frontier in the fields of synthetic biology, materials science, and molecular engineering.^1–3

One of the most explored elements in this context is silicon, which shares similar chemical properties with carbon due to its position in the same group of the periodic table. This has led to investigations into the possibility of fully silicon-based biological systems where silicon replaces carbon in key structural roles. Previous studies have examined the potential of silanes (Si–H bonds) and siloxanes (Si–O bonds) to form stable, silicon-centered analogs of organic molecules,^4,5 though achieving silicon-based life forms has posed significant challenges. Notably, the concept of silicon-based amino acids, where carbon atoms are replaced by silicon, was once explored, highlighting the potential for alternative biochemistries.^6–8 While these systems have yet to reach the level of complexity or stability seen in carbon-based biology, they offer valuable insights into how the substitution of carbon with silicon could give rise to novel biochemical frameworks.

An alternative approach is to replace carbon atoms with elements that have one fewer valence electron (boron) or one more (nitrogen). This becomes possible through the use of so-called electronic transmutation, which is a concept introduced by Olson and Boldyrev⁹ who utilized the isoelectronic principle¹⁰ by proving that an element M with atomic number Z (i.e., _ZM) is expected to undergo a transmutation into _Z+1M via the acquisition of an extra electron. It was demonstrated^11–19 that the resulting species (having Z + 1 electrons) possesses the chemical bonding properties of the neighboring element _Z+1M as if it was put in the place of the transmuted element _ZM. Certainly, the same reasoning can be applied to transform the element _ZM into _Z−1M by withdrawing one electron from it. Returning to the idea of using boron and nitrogen atoms, earlier studies have shown that the B⁻ anion, being isoelectronic with the carbon atom, exhibits the same bonding pattern in simple compounds.^9,11,12 However, these studies relied on the use of ions, which essentially rendered their practical application in biological molecules nearly impossible (for example, the dianion (B₂H₆)²⁻ shows strong structural similarities to ethane, but for obvious reasons must be stabilized (neutralized) by the presence of two Li⁺ ions). Nevertheless, the concept of electronic transmutation to replace carbon atoms in a given molecule with boron and/or nitrogen atoms appears promising, provided the ionic character of the resulting systems is eliminated.

Another compelling reason to explore boron and nitrogen as substitutes for carbon lies in the well-established ability of these elements to form structures analogous to carbon-based frameworks.^20–23 For example, boron nitride nanotubes (BNNTs) are considered structural analogs to carbon nanotubes (CNTs), sharing similar cylindrical geometry, strength, and electrical properties.²⁴ However, BNNTs also exhibit unique characteristics, such as superior thermal stability and electrical insulation, which make them highly valuable in nanotechnology and materials science.^25,26 Beyond nanotubes, hexagonal boron nitride (h-BN), often referred to as “white graphene”, mirrors the layered structure of carbon-based graphene but possesses distinct chemical resistance and thermal conductivity properties.^27,28 These examples underscore the versatility of boron and nitrogen in mimicking the behavior of carbon in various nanostructures while introducing novel properties. This capability to replicate carbon-based architectures strengthens the rationale for investigating boron–nitrogen frameworks in biological systems like DNA, where such structural flexibility could open new avenues in the design of alternative molecular systems.

Bringing together the two preceding paragraphs raises the question – what underlies the stability of BN-based systems and their resemblance to analogous carbon structures, given that, as mentioned above, electronic transmutation of B and N atoms to C atoms requires the transformation of these atoms into B⁻ and N⁺ ions? The answer seems quite simple: the simultaneous presence of B⁻/N⁺ pairs in a compound creates the possibility of mimicking pairs of carbon atoms, while eliminating the issue of the resulting molecule's ionic character. In our view, this is precisely what explains the well-known stability of boron–nitrogen nanotubes and hexagonal boron-nitride “graphene”.

In this context, the concept of a carbon-free DNA system, in which the carbon atoms in DNA's building blocks are systematically replaced by boron and nitrogen atoms, presents an unexplored but theoretically plausible innovation. Such a substitution preserves the electronic structure of DNA through the creation of isoelectronic systems. Specifically, pairs of boron and nitrogen atoms can collectively provide the same number of electrons as pairs of carbon atoms, maintaining the necessary electronic and bonding configurations while altering, at least to some extent, the chemical properties of the molecule. The theoretical foundation for this substitution might be supported by ab initio calculations, which may demonstrate the feasibility of maintaining structural integrity and functionality despite the absence of carbon.

The rationale behind designing carbonless DNA is multi-faceted. First, from a research perspective, it expands our understanding of the possible chemical diversity of life and the potential for alternative biochemistries. Although life as we know it is carbon-based, the possibility of non-carbon-based genetic systems opens new avenues for exploring the limits of molecular biology and synthetic life forms. These investigations could yield insights into the adaptability of life's chemistry, with implications for the search for extraterrestrial life. For instance, understanding how genetic information can be stored and propagated in carbon-free systems might inform the search for life on planets or moons with environments where carbon-based life forms could not survive or thrive.

Moreover, carbonless DNA could have practical applications in materials science and nanotechnology. Boron and nitrogen-based frameworks exhibit unique chemical and physical properties compared to their carbon analogs, such as enhanced thermal stability, resistance to oxidation, and altered electronic characteristics.^29–31 These properties could make carbonless DNA a candidate for novel biomaterials or nanoscale devices that require high stability under extreme conditions. Such systems may also offer advantages in medical or biochemical applications, where the chemical inertness and biocompatibility of boron and nitrogen compounds are highly valued. For example, boron-based drugs are already in use for cancer therapy,^32–34 and integrating boron into genetic systems might provide novel pathways for targeted drug delivery or gene therapy.

From an evolutionary biology perspective, designing carbon-free DNA pushes the boundaries of what constitutes life. The ability to create stable genetic structures without carbon challenges the assumption that carbon is a universal building block of life.³⁵ By experimenting with these alternative biochemistries, scientists can better grasp the full spectrum of life's potential molecular foundations and their evolutionary adaptability in diverse environments. Additionally, carbonless DNA could provide models for developing synthetic life forms or protocells with tailored properties that do not rely on the constraints of carbon chemistry.

In summary, the synthesis and theoretical exploration of carbon-free DNA are not only scientifically novel but also hold broad implications for understanding biochemical possibilities beyond carbon. The implications for research, practical applications in materials science, and synthetic biology make the design of such systems a compelling field of study.

Therefore, in this contribution, we employ quantum chemistry methods to explore the possibility of designing a representative fragment of carbon-free DNA. This is achieved by substituting all carbon-containing DNA building blocks, specifically the four nucleotide bases and deoxyribose, with their carbonless equivalents, in which carbon atoms have been replaced by boron and nitrogen atoms. After justifying our selection of specific isomeric carbonless analogs, we discuss in detail the formation of complementary base pairs by the carbonless counterparts of nucleobases, followed by an examination of the structure of larger carbonless DNA fragments and their interaction with a selected ligand. We believe that this work contributes to an emerging area of molecular innovation, providing a foundation for future investigations into the design, synthesis, and potential uses of carbon-free biomolecules.

2. Methods

The stationary-point structures of cytosine (C), thymine (T), adenine (A), guanine (G), and D-2-deoxyribose (R), as well as their corresponding carbonless equivalents (denoted clC, clT, clA, clG, and clR, respectively) were obtained through density functional theory (DFT) using the ωB97XD long-range-corrected functional including empirical dispersion corrections³⁶ with the aug-cc-pVDZ valence basis set.^37,38

The equilibrium structures of the A–T and G–C complementary base pairs, along with their carbonless analogs clA–clT and clG–clC, were determined at four theoretical levels: (i) using the ωB97XD/aug-cc-pVDZ approach, (ii) applying the second-order Møller–Plesset perturbation method (MP2)^39–41 with the aug-cc-pVDZ basis set, (iii) utilizing the GFN0-xTB method,⁴² and (iv) using the GFN2-xTB method⁴³ (where both GFN0-xTB and GFN2-xTB are density functional based tight binding (DFTB) methods).

In all cases studied, the harmonic vibrational frequencies characterizing the stationary points were evaluated at the same theoretical level to ensure that the obtained structures correspond to true minima on the potential energy surface.

The base–base binding energies (BEs) for the A–T, G–C, clA–clT, and clG–clC systems were calculated at the following computational levels: (i) ωB97XD/aug-cc-pVDZ, (ii) MP2/aug-cc-pVDZ, (iii) CCSD/aug-cc-pVDZ//ωB97XD/aug-cc-pVDZ, (iv) SAPT2+3(CCD)δ_MP2/aug-cc-pVDZ//ωB97XD/aug-cc-pVDZ, (v) GFN0-xTB, and (vi) GFN2-xTB. Here, CCSD refers to the coupled cluster method with single and double substitutions,^44–47 while SAPT2+3(CCD)δ_MP2 represents the symmetry-adapted perturbation theory methodology as described below. The notation employed denotes the computational level used for determining the binding energy (before the symbol ‖) and the computational level used for obtaining the optimized structure (after the symbol ‖). In cases where energy and geometry were determined at the same theory level, we use notation without the ‖ symbol.

To elucidate the physical nature of the interactions between the bases comprising the studied complementary pairs, symmetry adapted perturbation theory (SAPT)⁴⁸ calculations were performed at the highest possible level, SAPT2+3(CCD)δ_MP2.^49–51 This level of SAPT includes second- and third-order terms in the perturbation expansion, along with coupled-cluster doubles (CCD) corrections for dispersion effects and δ_MP2 correction based on MP2 supermolecular interaction energy. The SAPT2+3(CCD)δ_MP2 method has been widely applied to characterize systems with various compositions and interaction types,^52–54 including DNA nucleobase pairs.⁵⁵ For comparative purposes, interaction energies calculated at other (less advanced) SAPT levels, i.e., SAPT2+3(CCD), SAPT2+3δ_MP2, SAPT2+3, SAPT2, SAPT0, and sSAPT0 are also reported. All SAPT calculations were carried out using the PSI4 computational package (1.9.1 release).⁵⁶

The ωB97XD/aug-cc-pVDZ electron densities of base pairs were subjected to quantum theory of atoms in molecules (QTAIM) analysis to determine the potential energy densities corresponding to bond critical points (BCPs) of intermolecular hydrogen bonds.⁵⁷ BCPs are transition states on the electron density surface, representing minima along the bond path and maxima in all other directions.⁵⁸ The energies of hydrogen bonds (E_H-bond) were calculated as the negative of half the potential energy densities (V(r)) at the corresponding BCPs, as suggested by Espinosa and coworkers.⁵⁹ The potential energy density, V(r), is defined as 0.25∇²ρ(r) − 2G(r), where G(r) is the Lagrangian kinetic energy density. The QTAIM analysis was conducted using the Multiwfn (Version 3.8(dev)) software.⁶⁰

The structures of the carbon-containing and carbonless DNA fragments comprising two base pairs (GA sequence denoted DNA(dimer) and clGclA sequence denoted clDNA(dimer)) were determined using the ωB97XD/aug-cc-pVDZ computational approach, allowing for full relaxation of all variables (i.e., no geometric parameters were constrained). The structures of the carbon-containing and carbonless DNA fragments comprising six base pairs (GATATC sequence denoted DNA(hexamer) and clGclAclTclAclTclC sequence denoted clDNA(hexamer)) were obtained through partial geometry optimizations at the ωB97XD/cc-pVDZ theory level. In this case, the geometric parameters of the terminal base pairs were “frozen” (to stabilize the helix), while the geometric variables of the four central base pairs were optimized. This approach was chosen because these fragments were artificially “cut” from a double helix, resulting in a lack of stabilization usually provided by neighboring helical segments in native DNA. Additionally, during the optimization of the DNA(hexamer) and clDNA(hexamer) structures, the negatively charged phosphate groups in the phosphate-deoxyribose backbone were neutralized by H⁺ cations.

To assess the binding potential of a carbonless DNA chain, docking simulations were carried out using the docking submodule of xTB. The submodule operates in three stages: (i) interaction site screening, (ii) genetic optimization using a rigid intermolecular force field (xTB-IFF), and (iii) geometry optimization using GFN2-xTB. Detailed information on the submodule's operation can be found in the work of Plett and Grimme.⁶¹ The equilibrium geometry of netropsin (which was chosen to play the ligand role) was optimized at the ωB97XD/aug-cc-pVDZ level and then used as the starting point. The structure of the CGCGATATCGCG B-DNA dodecamer (selected as the receptor) was generated using Chimera (version 1.17.3),⁶² while the structure of its carbonless counterpart was obtained using a script developed by the authors, based on the findings and assumptions described in the forthcoming parts of the manuscript.

The interaction energies between netropsin and the DNA fragments (i.e., segments consisting of netropsin and four DNA base pairs, crucial for netropsin binding) were calculated, accounting for basis set superposition error (BSSE), using the B3LYP-D3BJ^63–66/def2-SVP⁶⁷ level of theory implemented in ORCA (version 5.0.3).⁶⁸ The plots of the lowest energy structures of the complexes comprising netropsin with DNA(tetramer) and clDNA(tetramer) were generated using VMD software, version 1.9.4a53.⁶⁹

The molecular electrostatic potential (MEP) maps for GA DNA dimer and GATATC DNA hexamer and their carbonless counterparts were generated by projecting the electrostatic potential onto electron density isosurfaces (0.01 a.u.), as obtained from ωB97XD/cc-pVDZ calculations.

The bond orders were evaluated (using ωB97XD/aug-cc-pVDZ electron densities) by the natural bond orbital (NBO) analysis scheme^70–73 employing the NBO 7.0 software.⁷⁴

All remaining quantum chemical calculations, particularly those related to structure optimization and the determination of harmonic vibrational frequencies, were performed using the GAUSSIAN16 (Rev. C.01) program suite.⁷⁵

3. Results

3.1. Design of the carbonless DNA

We begin our discussion by explaining our motivations for the design of carbonless DNA, particularly by outlining the assumptions we adopted and providing a detailed description of the design and testing (verification) of the individual molecular fragments that comprise the target system.

3.1.1. Preliminary assumptions. Our concept for designing a carbonless DNA structure is based on replacing all carbon atoms with other atoms while maintaining the molecular structure's greatest possible resemblance to the original carbon-containing DNA. This resemblance is to be understood both in a molecular sense (spatial structure) and a physicochemical sense (properties such as polarity and interaction capabilities with other molecules). Therefore, constructing carbonless DNA as an isoelectronic system with an unmodified, carbon-containing DNA (having the same sequence of canonical nucleotide bases) appears to be a natural approach. To maintain control over the modifications, we decided to independently construct carbonless equivalents of all DNA components (e.g., cytosine (C), thymine (T), guanine (G), adenine (A), and deoxyribose (R)), verify their similarity to the original (unmodified) molecules, and then construct the carbonless DNA using these equivalents.

Adopting isoelectronicity as a sine qua non condition naturally limits the possibilities for designing carbonless DNA. However, even with this limitation, numerous potential options for realization remain. To simplify this process, we arbitrarily chose to replace any even number 2n of carbon atoms with n boron atoms and n nitrogen atoms. This procedure preserves both the number of atoms and the total number of electrons in the system. Nevertheless, since all DNA components (except for cytosine) contain an odd number (2n + 1) of carbon atoms, we had to add one hydrogen atom (when replacing 2n + 1 carbon atoms with n + 1 boron atoms and n nitrogen atoms) or remove one hydrogen atom (when replacing 2n + 1 carbon atoms with n boron atoms and n + 1 nitrogen atoms) to maintain isoelectronicity. In the case of specific DNA components containing an odd number of carbon atoms, for three of them (thymine, adenine, guanine), we applied the strategy of replacing 2n + 1 carbon atoms with n + 1 boron atoms and n nitrogen atoms, accompanied by the addition of one hydrogen atom, whereas for one component (2-deoxyribose), we opted to introduce n boron atoms, n + 1 nitrogen atoms, and remove one hydrogen atom. The strategic placement of a single hydrogen atom in the carbonless DNA model was guided by two key considerations. First, the choice of the specific site for hydrogen addition aimed to select the most stable isomer of the modified DNA component. Second, the placement avoided positions involved in the formation of intercomponent bonds within the DNA structure, ensuring that the fundamental architecture of the molecule remained unaltered. Nevertheless, it is important to note that the addition of this hydrogen atom plays a critical role in stabilizing the electronic structure of the carbonless DNA. By satisfying valency requirements at the selected site, the hydrogen atom prevents the formation of reactive radicals, thereby reducing the susceptibility of the molecule to hydrolytic or oxidative damage. As revealed by earlier studies, the substitution of specific atoms within DNA components was shown to significantly affect the stability and reactivity of the molecule by modulating the electronic environment and conformational preferences.⁷⁶ Additionally, it was observed that such modifications can reduce the formation of reactive intermediates, thereby minimizing molecular hotspots prone to undesired reactions.⁷⁷ These findings underscore the importance of precise atomic modifications in achieving a balance between reactivity control and structural stability.

Building on these insights, our approach incorporates the targeted addition of a hydrogen atom to mitigate potential hotspots of reactivity, ensuring a stable electronic environment for the carbonless DNA model. By carefully balancing chemical stability with functional preservation, this design contributes to advancing the understanding and application of carbonless nucleic acids in molecular research.

The specific design of the carbonless equivalents of cytosine, thymine, adenine, guanine, and deoxyribose are detailed in subsequent sections. However, it is important to note that the addition or removal of a single hydrogen atom in a given fragment was carried out at a site that is not involved in forming hydrogen bonds related to base pair formation, nor does it significantly impact the formation of covalent bonds connecting the fragment to the rest of the DNA. This approach aims to preserve the functional role of each fragment within the overall DNA structure.

3.1.2. Design of carbonless cytosine (clC). The isolated cytosine molecule (C₄H₅N₃O) contains an even number of carbon atoms (4), allowing their replacement with two boron atoms and two nitrogen atoms. This results in the carbonless equivalent B₂H₅N₅O, which is isoelectronic with cytosine. The procedure for replacing C atoms with B and N (i.e., the design of the carbonless equivalent of cytosine, clC) was carried out by retaining the nitrogen and oxygen atoms in their original positions within the cytosine molecule, while considering all possible isomers formed by replacing the four carbon atoms in the ring (positions 2, 4, 5, 6) with two boron atoms and two nitrogen atoms. This leads to 6 isomers, as shown in Fig. 1.

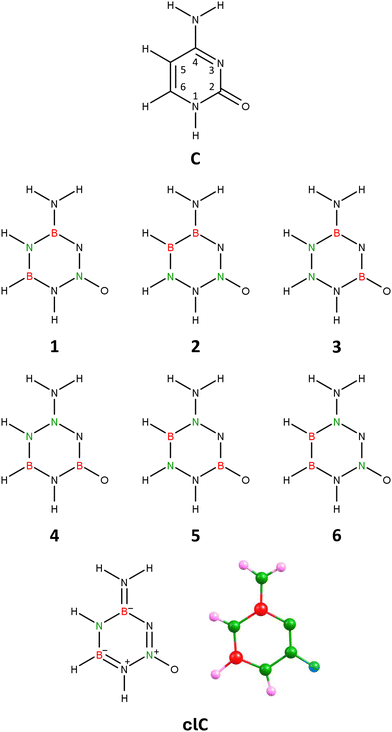Fig. 1 Cytosine (C), isomers 1–6 of carbonless cytosine, and the equilibrium structure of the chosen cytosine equivalent (isomer 1), clC.

Geometry optimization performed independently for each of these 6 isomers revealed that only one (labeled 1 in Fig. 1) preserves the planarity of the six-membered ring, while in the other cases (isomers 2–6), the resulting structures exhibit either a broken ring (isomer 3), a slightly deformed (non-planar) ring (isomers 4 and 6), or a severely deformed ring with deviations from planarity on the order of 20–30° (isomers 2 and 5), see Fig. S1 in ESI.† Additionally, our calculations showed that isomer 1 is the lowest energy isomer among all considered isomers, whereas the relative energies of isomers 2–6 exceed 30 kcal mol⁻¹.

Isomer 1 corresponds to a planar structure with C_s symmetry, similar to the unmodified cytosine molecule. The hydrogen atom attached to the nitrogen at position 1 of the ring is tilted towards the oxygen atom, forming an HNN bond angle of 109.07°. Notably, there is also a slight slant in the amino group, with its nitrogen forming an angle of 116.45° with the boron and nitrogen atoms at positions 4 and 5, respectively. The polarity of isomer 1 (|[small mu, Greek, vector]| = 4.711 D) is comparable to, though slightly less than, the polarity of the unmodified cytosine molecule (|[small mu, Greek, vector]| = 6.755 D, as calculated at the same theory level).

In light of these results, we conclude that isomer 1 of the B₂H₅N₅O molecule, whose geometric structure and bond orders (derived from NBO population analysis) are presented in Fig. 1, is a suitable carbonless equivalent of cytosine, which we will refer to as clC in this work.

3.1.3. Design of carbonless thymine (clT). Since the isolated thymine molecule (C₅H₆N₂O₂) contains an odd number of carbon atoms, replacing them with boron and nitrogen atoms requires the addition or removal of a hydrogen atom to create a carbonless thymine molecule (clT) that is isoelectronic with the unmodified thymine molecule (T). In this case, we decided to replace the five carbon atoms in thymine with three boron atoms and two nitrogen atoms, necessitating the addition of one hydrogen atom. An important decision was where to attach this additional hydrogen atom. It was impossible to attach hydrogen to a B or N atom replacing the methyl group carbon (as it would result in a pentavalent atom), and attaching hydrogen to any C or N atom in the ring would likely create a quasi-tetrahedral configuration, distorting the ring from planarity. Thus, the only feasible option was to attach the hydrogen atom to one of the two oxygen atoms in the structure. Given that one oxygen atom (attached to the ring at position 4, see Fig. 2) is involved in forming a hydrogen bond related to base pair formation in DNA, the only viable option was to attach the additional hydrogen atom to the oxygen atom connected to the ring at position 2.

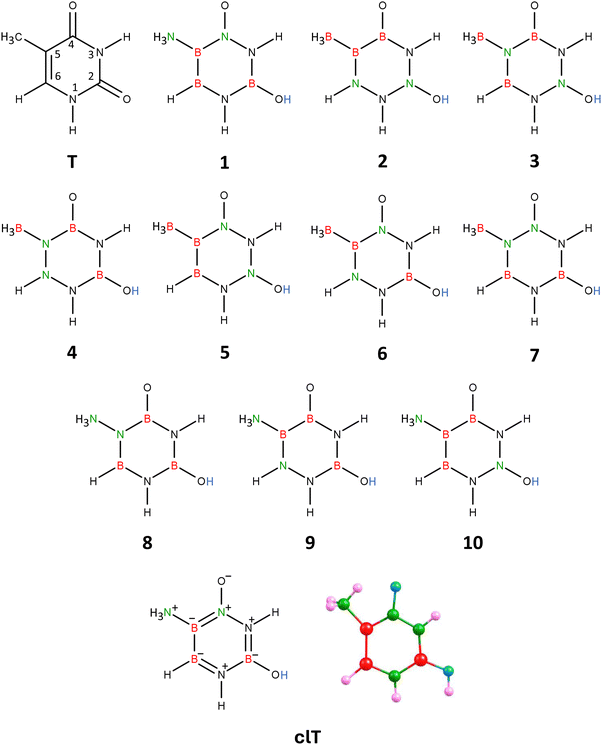Fig. 2 Thymine (T), isomers 1–10 of carbonless thymine, and the equilibrium structure of the chosen thymine equivalent (isomer 1), clT.

The resulting molecule, with the B₃H₇N₄O₂ formula, has 10 structural isomers (assuming the two nitrogen atoms in unmodified thymine remain at positions 1 and 3 in the ring). Geometry optimization of these 10 isomeric structures (labeled 1–10 in Fig. 2) revealed that only four of them (isomers labeled 1, 4, 6, and 7) maintain the planarity of the six-membered ring, whereas the others either have a broken ring (isomers 2 and 3) or a significantly deformed ring (isomers 5 and 8–10), see Fig. S2 in ESI.† Among the planar ring isomers, the lowest energy structure is isomer 1, while the energies of isomers 4, 6, and 7 are higher by 9–82 kcal mol⁻¹. Additionally, the polarity of isomers 4, 6, and 7 (manifested by their dipole moments |[small mu, Greek, vector]| spanning the 9.518–11.994 D range) is significantly higher than that of isomer 1 (4.343 D).

The equilibrium structure of isomer 1 of the B₃H₇N₄O₂ molecule exhibits C_s symmetry, with the symmetry plane encompassing all atoms except the two hydrogen atoms of the NH₃ group attached to the ring (see Fig. 2, which also shows the bond orders in 1, derived from NBO population analysis). The six-membered ring in isomer 1 forms an almost perfect hexagon, with deviations from the 120° valence bond angles not exceeding 6°. Furthermore, the polarity of isomer 1 (|[small mu, Greek, vector]| = 4.343 D) is very close to that of the unmodified thymine molecule (|[small mu, Greek, vector]| = 4.478 D, as calculated at the same theory level). Therefore, given that isomer 1 corresponds to the lowest energy structure and has similar polarity to thymine, we conclude that it is the appropriate carbonless equivalent of thymine, which we will refer to as clT (carbonless thymine) in this work.

3.1.4. Design of carbonless adenine (clA). The adenine molecule (C₅H₅N₅), despite being a purine nucleobase and consisting of two fused rings (pyrimidine and imidazole), contains the same number (five) of carbon atoms as thymine. Therefore, we applied an analogous procedure of replacing these carbon atoms with three boron atoms and two nitrogen atoms, while adding an additional hydrogen atom to make the resulting molecule isoelectronic with unmodified adenine. Regarding the position for attaching the additional hydrogen, only the heterocyclic nitrogen atoms in positions 3 and 7 were considered (see Fig. 3), because attaching hydrogen to the nitrogen in position 1 would disrupt the ability to form a complementary base pair, and attaching it to other ring positions would create an atom with four substituents, likely distorting the rings from planarity.

Fig. 3 Adenine (A), isomers 1–10 of carbonless adenine, and the equilibrium structure of the chosen adenine equivalent (isomer 1), clA.

Since there are 10 structural isomers of the B₃H₆N₇ molecule with a hydrogen atom attached at position 3, and 10 analogous isomers with a hydrogen atom attached at position 7, we performed geometry optimizations for all these 20 isomers. It turned out that the global minimum corresponds to one of the isomers with a hydrogen atom attached to the imidazole ring (position 7). In Fig. 3, we present only the isomers with a hydrogen atom in position 7 (see structures 1–10) because the structures with a hydrogen atom in position 3 (referred to in this section as 1′–10′, respectively) are analogous in terms of the arrangement of B and N atoms in the rings.

Geometry optimization for each structure showed that isomers 3, 6, 7, 8, 5′, and 9′ have significantly deformed rings, while the rings of isomers 2, 10, 2′, 4′, and 10′ are less deformed (with deviations from the 120° valence bond angles not exceeding 9°), see Fig. S3 in ESI.† The structures 1, 4, 5, 9, 1′, 3′, 6′, 7′, and 8′ possess planar rings, making them the only isomers suitable for consideration as the carbonless equivalent of adenine. Furthermore, we found that isomer 1 corresponds to the global minimum, while the relative energies of systems 2–10 and 1′–10′ span the 58–148 and 24–149 kcal mol⁻¹ range, respectively, indicating that isomer 1 is the most appropriate candidate.

Isomer 1 has a planar structure (C_s symmetry), encompassing both rings and the amino group. Due to the presence of three nitrogen atoms in positions 1, 2, and 3, the pyrimidine ring in isomer 1's structure does not correspond to a perfect hexagon. Aside from this difference, isomer 1 structurally resembles unmodified adenine. Its polarity, indicated by a dipole moment of 1.654 D, is also close to that of adenine (|[small mu, Greek, vector]| = 2.424 D, as predicted at the same theory level).

Therefore, we conclude that isomer 1, whose equilibrium structure and bond orders derived from NBO population analysis are shown in Fig. 3, is the appropriate carbonless equivalent of adenine, which we will refer to as clA (carbonless adenine) in this work.

3.1.5. Design of carbonless guanine (clG). The guanine molecule (C₅H₅N₅O), similarly to adenine, contains an odd number of five carbon atoms in its fused imidazole and pyrimidine rings (see Fig. 4). Therefore, we applied an analogous procedure to replace these five carbon atoms with three boron atoms and two nitrogen atoms, necessitating the addition of one hydrogen atom to ensure the designed molecule is isoelectronic with unmodified guanine. This additional hydrogen atom can only be placed at position 3 or 7 of the structure, as attaching it to the oxygen atom could disrupt the formation of a complementary base pair, and adding it to other ring positions would create an atom with four substituents, likely deforming the rings from planarity.

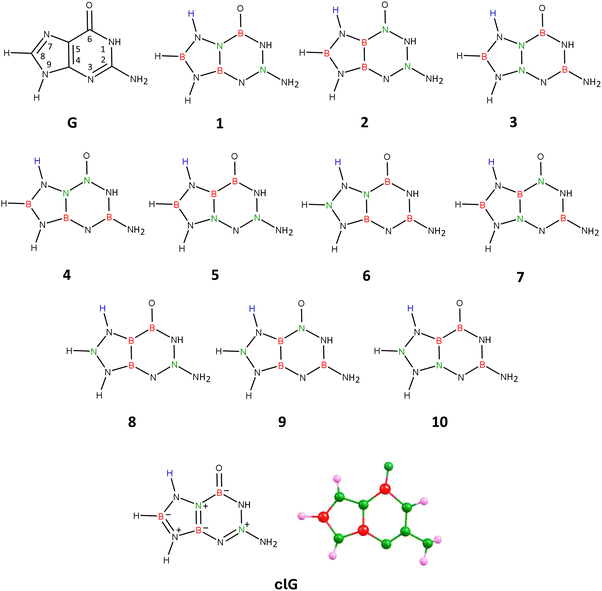Fig. 4 Guanine (G), isomers 1–10 of carbonless guanine, and the equilibrium structure of the chosen guanine equivalent (isomer 1), clG.

Attaching the hydrogen atom to either position 3 or 7 leads to 10 analogous isomers differing in the location of B and N atoms in the molecular structure, resulting in a total of 20 isomeric systems. Our calculations showed that the global minimum corresponds to one of the isomers with the hydrogen atom attached to the pyrimidine ring (position 3). However, this isomer exhibits excessively high polarity (|[small mu, Greek, vector]| = 11.990 D) compared to the unmodified guanine molecule (|[small mu, Greek, vector]| = 6.680 D, as calculated at the same theory level) and a different dipole moment vector orientation, and therefore cannot serve as a carbonless equivalent of G. Since the requirement of similar polarity for the carbonless equivalent must be met according to our assumption, we selected the isomer with the additional hydrogen atom attached at position 7 (i.e., to the imidazole ring), which features a planar structure of fused rings and polarity similar to the unmodified guanine molecule (see structure labeled 1 in Fig. 4).

Thus, in Fig. 4, we present the isomers with hydrogen attached at position 7 (see structures labeled 1–10). The analogous isomers with hydrogen connected to the pyrimidine ring (position 3) are not shown in the figure but have the same arrangement of B and N atoms in their structures (referred to in this discussion as structures 1′–10′).

Geometry optimizations performed for each of these 20 structures revealed that the rings in isomers 8, 5′, and 8′ are broken, while the rings in isomers 5, 9, 10, 1′, 2′, 3′, 7′, and 10′ are deformed from planarity. The rings in the remaining isomeric structures (i.e., 1, 2, 3, 4, 6, 7, 4′, 6′, and 9′) are planar, making these structures potential candidates for being the carbonless equivalent of guanine, see Fig. S4 in ESI.† It turned out, however, that among these listed isomers exhibiting a planar structure of fused rings, only the isomer labeled 1 in Fig. 4 shows similar polarity (|[small mu, Greek, vector]| = 7.823 D) to unmodified guanine and almost identical orientation and direction of the dipole moment vector. Isomer 1 exhibits, as mentioned, similarities to unmodified guanine, which include a planar structure of fused rings, a slight displacement of the oxygen atom towards the nitrogen atom at position 1, a non-planar (pyramidal) structure of the amino group attached to the pyrimidine ring at position 2, and most importantly, similar polarity and orientation of the dipole moment vector. According to NBO population analysis, the oxygen atom in isomer 1 is double-bonded to the nitrogen atom at position 6 (the bond orders of the remaining bonds are marked in Fig. 4). Due to these mentioned similarities to unmodified guanine, we determined that isomer 1 (see Fig. 4 for its equilibrium geometry) represents the appropriate carbonless equivalent of guanine, which we will refer to as clG in this work.

3.1.6. Design of carbonless D-2-deoxyribose (clR). In addition to the C, T, A, and G nucleobases, another carbon-containing building block of DNA is 2-deoxyribose (C₅H₁₀O₄). To find a carbonless equivalent of this molecule, we need to replace the five carbon atoms with boron and nitrogen atoms, similar to the procedure we used for C, T, A, and G. However, applying the exact same strategy (replacing five carbon atoms with three boron atoms and two nitrogen atoms and adding one hydrogen atom) would not be suitable for 2-deoxyribose, as it would result in a boron or nitrogen atom having five substituents in the resulting system. Additionally, adding hydrogen to the oxygen atom in the ring could significantly affect the structure and properties of the molecule. Moreover, attaching hydrogen to the oxygen atom of the terminal hydroxyl group is not feasible since, in the DNA structure, this atom is part of the phosphate group.

Therefore, we decided to replace five carbon atoms with two boron atoms and three nitrogen atoms while simultaneously removing one hydrogen atom. The resulting molecule, B₂H₉N₃O₄, is isoelectronic with 2-deoxyribose. We chose to remove the hydrogen atom attached at position 5 (see Fig. 5) to maintain the number of substituents on each ring atom.

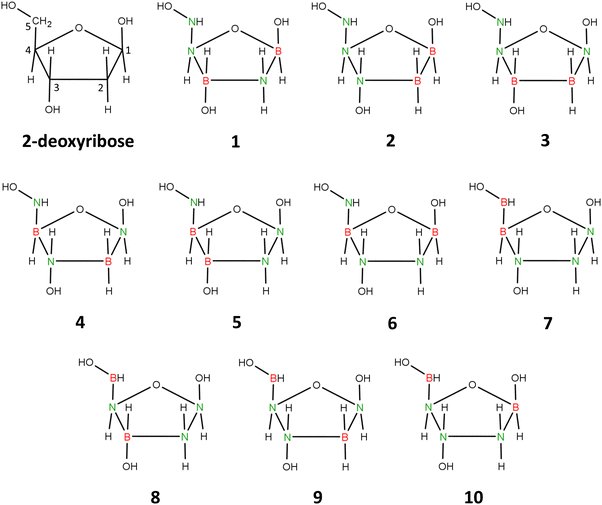Fig. 5 2-Deoxyribose and 1–10 isomers of its carbonless equivalent. Structure 1 corresponds to the most stable isomer chosen as carbonless deoxyribose equivalent (clR).

The described procedure results in 10 isomeric structures, presented in Fig. 5. Geometry optimizations performed for each of these structures revealed that the five-membered ring maintains its integrity only in the cases of isomers 1 and 4. In the other cases (isomers 2, 3, 5–10), the local energy minimum corresponds to structures with a broken ring. Additionally, we found that the global minimum corresponds to isomer 1, while the energies of isomers 2–10 are higher by 11–162 kcal mol⁻¹ compared to this isomer.

Isomer 1 exhibits a five-membered ring conformation analogous to that of unmodified deoxyribose, as seen in Fig. 6, resulting in a nearly identical arrangement of substituents attached to the ring. The only differences observed when comparing the equilibrium structures of deoxyribose and isomer 1 are in the slightly different orientations of the hydrogen atoms in the hydroxyl groups attached at positions 3 and 5 (see Fig. 5 for atom numbering). This is due to the relatively free rotation around the single bonds connecting the oxygen atoms to the atoms in these positions and should not affect the properties of the system. The polarity of isomer 1 (manifested by its dipole moment of 5.416 D) is also close to that of 2-deoxyribose (|[small mu, Greek, vector]| = 4.720 D).

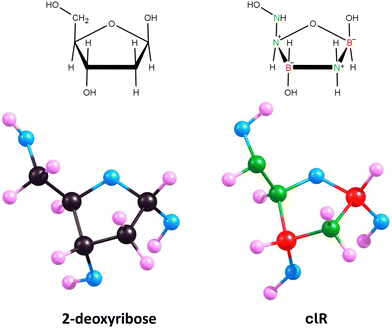Fig. 6 Equilibrium structures of 2-deoxyribose and its lowest energy carbonless equivalent (isomer 1, clR).

Therefore, we conclude that isomer 1 is an appropriate carbonless equivalent of deoxyribose (which we will refer to as clR in this work).

3.2. Properties of the carbonless DNA (clDNA)

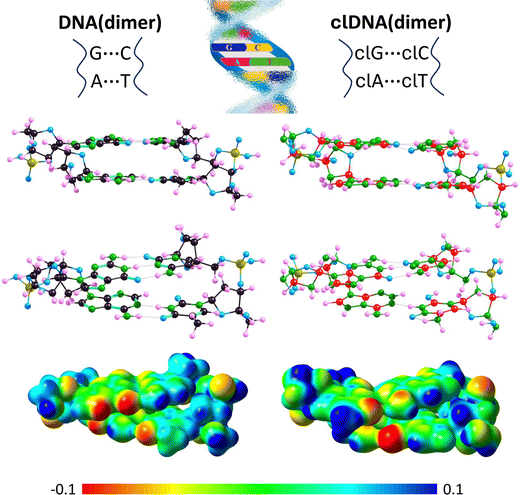
Having discussed carbonless equivalents of nucleobases and deoxyribose, we now move on to the examination of larger structures formed by these DNA building blocks. In this section, we will first explore the formation of complementary base pairs by carbonless equivalents of nucleobases and compare them with analogous complementary pairs formed by unmodified A, T, G, and C. Next, we will analyze the shortest possible DNA sequence formed by the previously described carbonless equivalents of nucleobases (clA, clT, clG, and clC), that is, a sequence containing only two pairs of complementary bases, comparing it with an analogous sequence formed by unmodified bases. Subsequently, we will discuss the helical structure of a selected DNA fragment, once again, formed by carbonless equivalents of DNA building blocks as well as their unmodified counterparts containing carbon atoms. Finally, we will address the interaction between the carbonless and carbon-containing DNA fragments with a selected ligand.

3.2.1. Base pair formation with carbonless nucleobase equivalents. One of the most crucial structural roles played by nucleobases within the DNA structure is the formation of complementary pairs. Therefore, it is essential to verify the ability of carbonless equivalents of DNA, namely clA, clT, clG, and clC (described in previous sections), to form analogous pairs. In order to achieve this, we determined the equilibrium structures of the clA–clT and clG–clC systems and compared them with the structures of the corresponding A–T and G–C systems. The calculations aimed to determine the molecular structures were performed at four different theoretical levels, specifically using the ωB97XD/aug-cc-pVDZ approach applied during the design of the carbonless equivalents, as well as using a reliable ab initio method, MP2 (with the same basis set, aug-cc-pVDZ), which partially accounts for electron correlation effects. Additionally, to assess whether simpler computational techniques under the density functional based tight binding (DFTB) methods provide relatively reasonable results in this case, we employed the GFN0-xTB and GFN2-xTB methods (as confirming the applicability of DFTB methods would enable the efficient study of even very large structures of this type due to the low computational cost of DFTB techniques). In comparing complementary base pairs formed by unmodified molecules and their carbonless counterparts, we focus on the overall structure of the system, the number and length of intermolecular hydrogen bonds, the energy of each of these hydrogen bonds, and the base–base binding energy.

The equilibrium structures of the A–T, G–C, clA–clT, and clG–clC pairs shown in Fig. 7 exhibit significant similarities between the carbonless systems and the systems containing carbon atoms. These similarities include the mutual orientation of the molecules in a given complementary pair, the planarity of all single and fused rings, and the number of intermolecular hydrogen bonds formed.

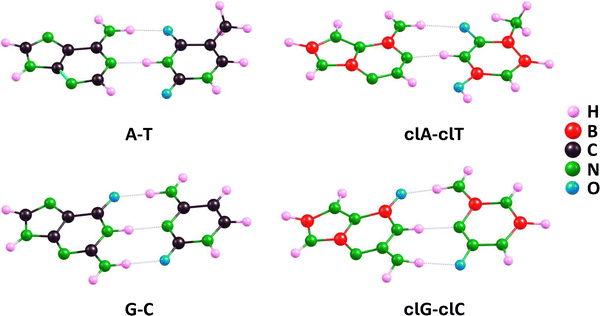Fig. 7 Equilibrium structures (determined at the ωB97XD/aug-cc-pVDZ theory level) of A–T and G–C complementary pairs and their clA–clT and clG–clC carbonless analogs.

A more detailed analysis of the mentioned intermolecular hydrogen bonds, however, reveals some minor differences. In relation to the clG–clC and G–C pairs, we found that three bonds in the clG–clC pair are very similar to those in the G–C pair (the maximum difference does not exceed 0.036 Å). In particular, the hydrogen bond involving the oxygen atom of the clC molecule, labeled as (clG)NH⋯O(clC) in Table 1, is longer than the corresponding bond in the G–C pair by 0.036 Å, the (clG)O⋯HN(clC) bond in clG–clC is shorter by 0.021 Å compared to its counterpart in G–C, whereas the (clG)NH⋯N(clC) bond in clG–clC and the analogous NH⋯N bond in G–C are nearly identical (differing by 0.003 Å), cf. ωB97XD results in Table 1. When comparing the clA–clT and A–T pairs, we found that the (clA)N⋯HN(clT) bond is longer than the (A)N⋯HN(T) bond by 0.038 Å, while the (clA)NH⋯O(clT) bond is longer than its counterpart in the A–T pair by 0.246 Å. Thus, we conclude that the lengths of hydrogen bonds in carbonless base pairs are comparable to or slightly longer than those in the corresponding unmodified base pairs, yet these differences are very small, except for one case of the hydrogen bond involving the oxygen atom in thymine (or its carbonless equivalent) where the difference is nearly 0.25 Å. The larger length of intermolecular hydrogen bonds in the complementary clA–clT and clG–clC pairs compared to the A–T and G–C pairs, respectively, indicates that the base–base binding energies may be slightly lower for the former pairs than for the latter, particularly concerning clA–clT vs. A–T.

Table 1 Lengths of hydrogen bonds (r in Å) predicted for unmodified A–T and G–C complementary base pairs and their carbonless counterparts clA–clT and clG–clC

Base pair	H-bond lengths
	ωB97XD^a	MP2^a	GFN2-xTB
a Structures obtained using the aug-cc-pVDZ basis set.
A–T	r[(A)NH⋯O(T)] = 1.889	r[(A)NH⋯O(T)] = 1.896	r[(A)NH⋯O(T)] = 1.789
	r[(A)N⋯HN(T)] = 1.773	r[(A)N⋯HN(T)] = 1.755	r[(A)N⋯HN(T)] = 1.623
clA–clT	r[(clA)NH⋯O(clT)] = 2.135	r[(clA)NH⋯O(clT)] = 2.114	r[(clA)NH⋯O(clT)] = 1.991
	r[(clA)N⋯HN(clT)] = 1.811	r[(clA)N⋯HN(clT)] = 1.783	r[(clA)N⋯HN(clT)] = 1.737
G–C	r[(G)O⋯HN(C)] = 1.726	r[(G)O⋯HN(C)] = 1.723	r[(G)O⋯HN(C)] = 1.637
	r[(G)NH⋯N(C)] = 1.875	r[(G)NH⋯N(C)] = 1.876	r[(G)NH⋯N(C)] = 1.781
	r[(G)NH⋯O(C)] = 1.872	r[(G)NH⋯O(C)] = 1.871	r[(G)NH⋯O(C)] = 1.778
clG–clC	r[(clG)O⋯HN(clC)] = 1.705	r[(clG)O⋯HN(clC)] = 1.707	r[(clG)O⋯HN(clC)] = 1.612
	r[(clG)NH⋯N(clC)] = 1.878	r[(clG)NH⋯N(clC)] = 1.837	r[(clG)NH⋯N(clC)] = 1.811
	r[(clG)NH⋯O(clC)] = 1.908	r[(clG)NH⋯O(clC)] = 1.935	r[(clG)NH⋯O(clC)] = 1.769

---

Indeed, the base–base binding energies (BEs) presented in Table 2 confirm these initial predictions made based on structural considerations. Specifically, the BE values obtained for G–C using DFT(ωB97XD), MP2, and CCSD methods are very similar to those determined for clG–clC (the differences do not exceed 0.5 kcal mol⁻¹). On the other hand, the binding energies predicted by these three methods for A–T are slightly (by about 2–3 kcal mol⁻¹) higher than the BE values obtained for clA–clT. Comparable BE values were obtained for the aforementioned base pairs using the symmetry-adapted perturbation theory (SAPT) methodology (in this case, in Table 2, we present the BE values as the interaction energies taken with the opposite sign derived from the energy decomposition analysis, details of which are discussed in the following paragraphs of this section).

Table 2 Base–base binding energies (BE in kcal mol⁻¹) predicted for unmodified A–T and G–C complementary base pairs and their carbonless counterparts clA–clT and clG–clC

Base pair	Binding energy
	ωB97XD^a	MP2^b	CCSD^c	BE(SAPT)^d	GFN0-xTB^e	GFN2-xTB^f
a ωB97XD/aug-cc-pVDZ results. b MP2/aug-cc-pVDZ results. c CCSD/aug-cc-pVDZ//ωB97XD/aug-cc-pVDZ results. d SAPT2+3(CCD)δMP2/aug-cc-pVDZ//ωB97XD/aug-cc-pVDZ results. e GFN0-xTB results. f GFN2-xTB results.
A–T	16.6	17.7	16.0	15.7	18.2	16.1
clA–clT	14.0	16.2	14.3	13.7	18.2	12.4
G–C	30.6	30.3	28.8	31.1	29.0	29.2
clG–clC	30.2	30.8	29.1	32.5	28.7	27.8

---

Furthermore, the application of the QTAIM model based on electron density distribution allowed us to determine the energy of individual hydrogen bonds in the studied nucleobase pairs (see the obtained values presented in Fig. 8).

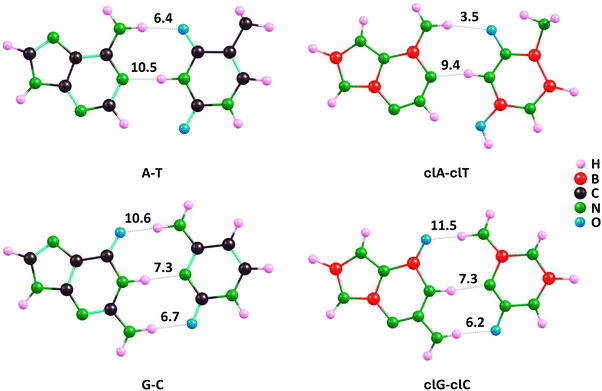Fig. 8 Hydrogen bond energies (in kcal mol⁻¹) determined for A–T and G–C complementary pairs and their clA–clT and clG–clC carbonless analogues using the QTAIM model.

The individual hydrogen bond energies (E_H-bond) for the A–T, G–C, clA–clT, and clG–clC systems predicted using the QTAIM model are consistent with the differences in H-bond lengths listed in Table 1. For the corresponding A–T and clA–clT pairs, the (A)NH⋯O(T) bond is stronger than the (clA)NH⋯O(clT) bond by 2.9 kcal mol⁻¹, which corresponds to the longer bond length in clA–clT by 0.246 Å. Similarly, the (A)N⋯HN(T) bond is stronger than the (clA)N⋯HN(clT) bond by 1.1 kcal mol⁻¹, reflecting the longer bond length in clA–clT by 0.038 Å, as shown in Fig. 8 and Table 1. The resulting difference in base–base binding energy (A–T vs. clA–clT) of 4 kcal mol⁻¹ is partially compensated by a stronger stabilizing interaction (resembling an additional hydrogen bond) in clA–clT between the hydrogen atom at position 2 of the clA pyrimidine ring and the oxygen atom in clT, compared to the unmodified A–T pair. According to the QTAIM model, this stabilization is stronger by 1.8 kcal mol⁻¹ in clA–clT compared to A–T (these E_H-bond values are not indicated in Fig. 8). Consequently, the QTAIM model predicts the overall base–base binding energy in A–T to be about 2 kcal mol⁻¹ higher than in clA–clT, aligning with the BE values determined by DFT(ωB97XD), MP2, and CCSD methods shown in Table 2.

Regarding the QTAIM-predicted E_H-bond values in G–C and clG–clC pairs, we found nearly identical energies for the (G)NH⋯N(C) and (clG)NH⋯N(clC) bonds (7.3 kcal mol⁻¹), consistent with the almost identical bond lengths (differing by 0.003 Å). Additionally, the (G)NH⋯O(C) bond energy is 0.5 kcal mol⁻¹ higher than that of (clG)NH⋯O(clC), while the (G)O⋯HN(C) bond energy is 0.9 kcal mol⁻¹ lower than that of (clG)O⋯HN(clC). This corresponds to the elongation (by 0.036 Å) of the first bond and the shortening (by 0.021 Å) of the second when transitioning from the unmodified to the carbonless base pairs (see Fig. 8 and Table 1). Consequently, the QTAIM model predictions lead to nearly identical (within 0.5 kcal mol⁻¹) base–base binding energies for G–C and clG–clC pairs, consistent with the BE values determined by ωB97XD, MP2, and CCSD methods presented in Table 2.

The SAPT2+(3)(CCD)δ_MP2/aug-cc-pVDZ interaction energies presented in Table 3 demonstrate that the SAPT-calculated interaction energies are consistent with those obtained using other methods (ωB97XD, MP2, CCSD or GFN2-xTB). The SAPT2+(3)(CCD)δ_MP2 interaction energy calculated for A–T is 2.01 kcal mol⁻¹ higher than that determined for clA–clT. In contrast, the interaction energy between the nucleobases in G–C is 1.46 kcal mol⁻¹ lower than that determined for clG–clC. Regarding individual contributions to the total interaction energies, it can be concluded that there are only slight differences between the regular and carbonless base pairs. Specifically, for the A–T/clA–clT pairs, all components of the total interaction energy, i.e., electrostatics, induction, dispersion, and exchange, are calculated to be higher for the A–T pair. Conversely, for the G–C/clG–clC pairs, the carbonless pair (clG–clC) exhibits stronger interactions across all contributions. The largest difference, 5.62 kcal mol⁻¹, is observed in the exchange interaction, indicating that the A–T pair experiences greater repulsion via this interaction compared to clA–clT. Interestingly, when the percentage contribution of each interaction to the total energy is considered, the intermolecular interactions within A–T/clA–clT as well as G–C/clG–clC pairs are very similar in nature. Overall, regardless of the complementary pair considered, the most significant attractive interactions are: electrostatics ≫ induction > dispersion.

Table 3 Total SAPT2+3(CCD)δ_MP2 interaction energy (in kcal mol⁻¹), individual contributions to that energy (in kcal mol⁻¹) as well as the corresponding percentage contributions

Base pair	SAPT2+3(CCD)δMP2	Electostatics	Induction	Dispersion	Exchange
A–T	−15.72	−29.46 (32.4%)	−12.79 (14.1%)	−11.03 (12.1%)	37.56 (41.3%)
clA–clT	−13.71	−25.74 (33.2%)	−9.42 (12.1%)	−10.48 (13.5%)	31.94 (41.2%)
G–C	−31.07	−45.99 (34.8%)	−21.57 (16.3%)	−14.12 (10.7%)	50.62 (38.3%)
clG–clC	−32.53	−47.39 (34.6%)	−22.99 (16.8%)	−14.30 (10.5%)	52.15 (38.1%)

---

Our results are in agreement with those obtained by Kumawat and Sherill, who found the interaction energies of A–T and G–C calculated at the SAPT2+(3)(CCD)δ_MP2/aug-cc-pVTZ level on B3LYP-D3(BJ)/aug-cc-pVDZ geometries to be −16.87 and −32.82 kcal mol⁻¹, respectively (the interaction energies obtained by us differ from those of Kumawat and Sherrill by 1.15 and 1.75 kcal mol⁻¹ for A–T and G–C respectively).⁵⁵

The values of SAPT interaction energies obtained at levels of theory lower than SAPT2+3(CCD)δ_MP2 are collected in Table 4. From this table, it can be concluded that: (i) SAPT2+3(CCD), SAPT2+3δ_MP2, and SAPT2, while being less computationally demanding, produce results that on average differ by no more than 1 kcal mol⁻¹ from SAPT2+3(CCD)δ_MP2; (ii) SAPT2+3δ_MP2 interaction energies are closer to SAPT2+3(CCD)δ_MP2 than to SAPT2+3(CCD), indicating that the δ_MP2 correction is more critical than the CCSD in studied case; (iii) SAPT2+3 calculations, with an average error of 1.36 kcal mol⁻¹, yield results of moderate quality for the systems considered; and (iv) SAPT0 and sSAPT0 proved unreliable for the studied systems.

Table 4 Interaction energies between components of base pairs calculated at different SAPT level (in kcal mol⁻¹)

Base pair	SAPT2+3(CCD)δMP2	SAPT2+3(CCD)	SAPT2+3δMP2	SAPT2+3	SAPT2	SAPT0	sSAPT0
A–T	−15.72	−16.79	−16.14	−17.21	−15.68	−19.61	−18.96
clA–clT	−13.71	−13.96	−14.22	−14.47	−13.40	−16.25	−15.79
G–C	−31.07	−32.29	−31.57	−32.78	−30.15	−37.56	−36.90
clG–clC	−32.53	−33.42	−33.10	−33.99	−31.43	−38.55	−37.83

---

It is also worth noting that the computational approach ωB97XD/aug-cc-pVDZ used to calculate the base–base binding energy proved to be reliable, as very similar BE values (within 2 kcal mol⁻¹) were obtained based on electronic energies refined with the CCSD method. Furthermore, the reliability of the DFT(ωB97XD) approach in determining structures (as well as in calculating binding energies) was confirmed by results obtained using the MP2 method with the same basis set (see Tables 1 and 2). Last but not least, it is noteworthy that even the simplified computational approaches GFN0-xTB and GFN2-xTB yield results in these cases that are consistent with the results of DFT(ωB97XD) and MP2, both in terms of structure (Table 1) and predicted binding energies (Table 2). Particularly notable are the results from the GFN0-xTB approach, which are close to the ωB97XD results (yet the difference in binding energies for A–T vs. clA–clT is not as well reproduced). This suggests the potential effectiveness of the GFN0-xTB and GFN2-xTB methods for larger structures containing A–T and G–C pairs as well as clA–clT and clG–clC pairs.

Summarizing the observations regarding the formation of complementary pairs by carbonless equivalents of nucleobases, we conclude that they form analogous structures to A–T and G–C, maintaining the planar arrangement of all rings and the number of intermolecular hydrogen bonds. However, in the clA–clT and clG–clC pairs, the hydrogen bonds are slightly longer compared to A–T and G–C, respectively, which results in lower base–base binding energies, particularly noticeable in the clA–clT pair. This may lead to slightly lower stability of the carbonless DNA structure compared to the corresponding unmodified DNA structure (which will be discussed in the following sections).

3.2.2. Structure of the carbonless DNA fragment containing two base pairs. The next step in our research involved comparing molecular systems containing two nucleobase pairs, which together represent a fragment of the DNA structure (referred to here as DNA(dimer)). The unmodified fragment, which contains carbon atoms, consists of complementary A–T and G–C base pairs linked by a phosphate-deoxyribose backbone. In contrast, the carbonless DNA fragment (referred to here as clDNA(dimer)) contains all of these building blocks in their previously discussed carbonless forms. Geometry optimization for both systems allowed for the relaxation of all variables (i.e., no geometric parameters were frozen).

Even a preliminary comparison of the resulting DNA(dimer) and clDNA(dimer) structures (shown in Fig. 9) reveals that they are very similar. Specifically, it can be concluded that (i) in both cases, the complementary bases are paired, (ii) the A–T and clA–clT pairs are linked by two hydrogen bonds, (iii) the G–C and clG–clC pairs are joined by three hydrogen bonds, (iv) the complementary base pairs A–T, G–C, clA–clT, and clG–clC form approximately planar structures, (v) the planes defined by A–T and G–C are roughly parallel, with the same orientation observed for clA–clT and clG–clC, and (vi) the phosphate-deoxyribose backbones exhibit a similar spatial orientation in both DNA(dimer) and clDNA(dimer). Since a detailed comparative analysis of the DNA(dimer) and clDNA(dimer) structures would be too extensive, we limit our focus here to the comparison of the hydrogen bond lengths between complementary bases (see Table 5), as these structural elements are the most susceptible to potential distortions and are expected to show the greatest differences between the carbon-containing system and its carbonless counterpart.

Fig. 9 Equilibrium structures (determined at the ωB97XD/aug-cc-pVDZ theory level) of DNA(dimer) containing A–T and G–C complementary pairs (left panel) and clDNA(dimer) containing clA–clT and clG–clC carbonless base pairs (right panel), each depicted in two views. The corresponding molecular electrostatic potential (MEP) maps calculated based on ωB97XD/aug-cc-pVDZ electron densities and plotted on the 0.01 a.u. isodensity surface are presented below. The values on the electrostatic potential scale are presented in atomic units (a.u.).

Table 5 Lengths of hydrogen bonds (r in Å) predicted at the ωB97XD/aug-cc-pVDZ level for unmodified A–T and G–C complementary base pairs forming DNA(dimer) and their carbonless counterparts clA–clT and clG–clC forming clDNA(dimer). Changes in bond length (in Å) compared to the corresponding isolated complementary base pair are given in parentheses (cf.Table 1)

DNA(dimer)	clDNA(dimer)
A–T	clA–clT
r[(A)NH⋯O(T)] = 1.990 (+0.101)	r[(clA)NH⋯O(clT)] = 2.213 (+0.078)
r[(A)N⋯HN(T)] = 1.730 (−0.043)	r[(clA)N⋯HN(clT)] = 1.780 (−0.031)

---

DNA(dimer)	clDNA(dimer)
G–C	clG–clC
r[(G)O⋯HN(C)] = 1.711 (−0.015)	r[(clG)O⋯HN(clC)] = 1.698 (−0.007)
r[(G)NH⋯N(C)] = 1.872 (−0.003)	r[(clG)NH⋯N(clC)] = 1.873 (−0.005)
r[(G)NH⋯O(C)] = 1.906 (+0.034)	r[(clG)NH⋯O(clC)] = 1.879 (−0.029)

---

It should be noted that the hydrogen bond lengths within each complementary pair change only slightly (in most cases by less than 0.05 Å) when incorporated into either DNA(dimer) or clDNA(dimer) and forming part of the dimer structure (cf.Tables 1 and 5, which list the hydrogen bond lengths in isolated base pairs and in those within DNA(dimer) or clDNA(dimer), respectively). The only significant change was observed for the (A)NH⋯O(T) bond (an increase of 0.101 Å) in DNA(dimer) and the corresponding (clA)NH⋯O(clT) bond (an increase of 0.078 Å) in clDNA(dimer). Since other corresponding changes also occur in the same direction (except for the (G)NH⋯O(C) and (clG)NH⋯O(clC) bonds, where the former shows a slight elongation and the latter a slight shortening), and given that these changes are generally minor, and that the hydrogen bond lengths in the isolated complementary pairs and their isolated carbonless counterparts were similar (see the preceding section), we conclude that the hydrogen bonds linking the A–T and G–C complementary pairs in DNA(dimer) are comparable in length to those in the clA–clT and clG–clC pairs in clDNA(dimer).

Regarding the electrostatic potential distribution around DNA(dimer) and clDNA(dimer), although similarities are evident, some differences can be observed, most notably in the region of the guanine imidazole ring and its carbonless equivalent. These differences are illustrated in Fig. 9, where molecular electrostatic potential maps are plotted.

Summarizing the observations regarding the formation of two stacked nucleobase pairs by carbonless equivalents of nucleobases and deoxyribose, we conclude that they form analogous structures to the corresponding systems built from unmodified bases and phosphate-deoxyribose backbone fragments, maintaining the planar arrangement of all rings and preserving the number of intermolecular hydrogen bonds of comparable lengths.

3.2.3. Structure of the carbonless DNA fragment containing six base pairs. After discussing small DNA fragments, such as systems consisting of two nucleobase pairs, we now proceed to compare larger systems – fragments of DNA containing six complementary base pairs (GATATC sequence), constructed from either standard (carbon-based) components or their carbonless analogs. We will refer to these systems as DNA(hexamer) and clDNA(hexamer), respectively. For fragments of this size, it is already possible to observe the helical structure characteristic of native DNA. Aiming to compare the structures of DNA(hexamer) and clDNA(hexamer), we performed partial geometry optimizations of these systems. Given that the fragments under study were artificially “cut” from a double helix and, as a result, lacked the stabilization provided by the neighboring helix segments in native DNA, we “froze” the geometric parameters of the terminal base pairs. In contrast, the geometric variables corresponding to the four central base pairs were optimized. This approach aimed to partially recreate the structural conditions of native DNA, with the hope that the optimized segment would mimic real interactions between the components of the system. Additionally, the negatively charged phosphate groups in the phosphate-deoxyribose backbone were neutralized by H⁺ cations in our computational model. Due to the large size of the studied structures, we were compelled to conduct the geometry optimizations of DNA(hexamer) and clDNA(hexamer) using a slightly smaller basis set (cc-pVDZ) compared to the aug-cc-pVDZ basis used for the smaller systems previously described.

The resulting structures of DNA(hexamer) and clDNA(hexamer), along with their molecular electrostatic potential (MEP) maps, are shown in Fig. 10. As can be easily observed, both structures are very similar, sharing comparable dimensions. The internal structure of both helices is also analogous, with individual base pairs being approximately parallel to one another (the largest deviations from planarity, visible in Fig. 10, were observed in both cases for the central base pairs of the helix). Moreover, the vertical distances between consecutive base pairs are comparable. Specifically, the distances between stacked complementary base pairs (measured as the distances between the centers of neighboring pyrimidine rings) range from 3.391 to 3.982 Å for DNA(hexamer) and from 3.117 to 3.858 Å for clDNA(hexamer), with the extreme values corresponding to analogous distances in DNA(hexamer) and clDNA(hexamer). As a result, the maximum difference in the distance between stacked carbon-based bases and their carbonless analogs does not exceed 0.18 Å. This suggests that the DNA(hexamer) and clDNA(hexamer) structures are similarly tightly coiled. It is also worth noting that, in a typical B-DNA helix, the rise per base pair (i.e., the distance between each base pair along the helical axis) is approximately 3.3–3.4 Å, indicating that our calculations reproduce the native DNA structure reasonably well.

Fig. 10 Structures of DNA(hexamer) containing A–T and G–C complementary pairs (left panel) and clDNA(hexamer) containing clA–clT and clG–clC carbonless base pairs (right panel) determined at the ωB97XD/cc-pVDZ theory level. The corresponding molecular electrostatic potential maps calculated based on ωB97XD/cc-pVDZ electron densities and plotted on the 0.01 a.u. isodensity surface are presented below. The values on the electrostatic potential scale are presented in atomic units (a.u.).

The twist angle values in DNA(hexamer) range from 32° to 38° (with an average value of 35°), which are very close to the typical values observed in B-DNA (∼36°). In contrast, the corresponding values in clDNA(hexamer) are slightly higher, ranging from 36° to 43° (with an average value of 39°). This suggests that the carbonless base pairs in clDNA may induce a tighter helical twist compared to canonical DNA, potentially affecting the overall helical structure and inter-base pair interactions, which could have implications for its stability and interaction with proteins or other biomolecules. As for the propeller angle values, the range in DNA(hexamer) is from 4° to 18° (with an average value of 10°), while in clDNA(hexamer), it spans from 3° to 12° (with an average value of 7°). Hence, these values are comparable to those observed in B-DNA, where typical values range from 10° to 20°, yet they remain in the lower end of this typical range.

The similarity in size and shape between the DNA(hexamer) and clDNA(hexamer) systems is also evident in the molecular electrostatic potential maps shown in Fig. 10. However, a comparison of these MEP maps also reveals certain differences in charge distribution between the two systems. Specifically, the terminal phosphate-deoxyribose backbone segment of one strand (visible in the upper right corner of the MEP map) shows a more pronounced absence of electron density in the clDNA(hexamer) case compared to DNA(hexamer). In contrast, within the complementary base pairs of DNA(hexamer), regions of negative MEP values, indicating an abundance of electron density, are more distinctly visible. Aside from these general observations, it is challenging to make more detailed interpretations of the electrostatic potential maps for these systems, primarily due to their complexity.

Summarizing the observations regarding the formation of a double helix fragment containing six pairs of carbonless equivalents of nucleobases and the carbonless analog of phosphate-deoxyribose backbones, we conclude that its structure (in terms of helix dimensions, twist and propeller angles, vertical distances between consecutive base pairs, i.e., the rise per base pair, and the lengths of individual hydrogen bonds) is very similar to the corresponding fragment of DNA constructed from carbon-containing structural elements.

3.2.4. Interactions of the carbonless DNA fragment with netropsin ligand. To assess the binding potential of a carbonless DNA chain, we conducted docking simulations for carbon-containing and carbonless DNA fragments (each comprising 12 base pairs) mimicking the receptor and arbitrarily chosen ligand that proceeded in three stages: initial interaction site screening, genetic optimization using a rigid intermolecular force field (xTB-IFF), and geometry optimization utilizing GFN2-xTB method. Netropsin, a polyamide antibiotic known for its preference for binding to DNA through the minor groove in its cationic form,^78–80 was selected as a representative ligand. The receptors in our analysis comprised the CGCGATATCGCG dodecamer of B-DNA and its carbonless counterpart. The choice of this sequence was guided by data from Coll and coworkers, who elucidated the crystal structure of netropsin interacting with this dodecamer via the minor groove. Their findings emphasized netropsin's preference for binding to AT-rich sites.⁸¹

The lowest energy isomers of the netropsin/DNA(dodecamer) and netropsin/clDNA(dodecamer) complexes, obtained from docking simulations, were subjected to further analysis. Segments consisting of netropsin and four base pairs (see Fig. 11, where these systems are depicted and labeled as netropsin/DNA(tetramer) and netropsin/clDNA(tetramer)), crucial for netropsin binding, were extracted from both the netropsin/DNA(dodecamer) and netropsin/clDNA(dodecamer) systems. Subsequently, the binding energies between netropsin and these isolated fragments (referred to as DNA(tetramer) and clDNA(tetramer)) were calculated, accounting for basis set superposition error. The results yielded binding energies of 50.0 kcal mol⁻¹ for the netropsin/DNA(tetramer) interaction and 67.3 kcal mol⁻¹ for netropsin/clDNA(tetramer). Although it might be tempting to conclude that carbonless DNA binds more strongly to netropsin (by approximately 25%) compared to unmodified DNA, the binding energies we determined must be approached with caution for several reasons. Firstly, our calculations did not account for solvent effects or the ionic strength of the medium. The former is significant for obvious reasons, while recent studies clearly indicate that the latter is also critically important. For instance, this has been demonstrated in studies of the interaction between metallacarborane o-cobaltabis(dicarbollide) ([COSAN]⁻) and DNA using a combination of microsecond-scale molecular dynamics and hybrid quantum mechanics/molecular mechanics simulations,⁸² as well as in studies of Nile Blue (NB) binding with calf thymus DNA through molecular modeling, spectroscopic, and thermodynamic techniques.⁸³ These studies show that both the DNA/[COSAN]⁻ interaction and the DNA/NB interaction are highly dependent on the ionic strength/salt concentration of the medium. Secondly, it should be noted that the binding energy we calculated for netropsin/DNA(tetramer) is likely significantly overestimated, as it is several times greater than the experimental value of 12.7 kcal mol⁻¹ reported by Breslauer and coworkers,⁸⁴ as well as the theoretically determined value of 13.2 kcal mol⁻¹ by Zhang et al.⁸⁵ This leads to the conclusion that our predicted binding energies for both netropsin/DNA(tetramer) and netropsin/clDNA(tetramer) are subject to significant errors (for the reasons outlined above). Therefore, we refrain from interpreting these binding energies and simply state that our results suggest that carbonless DNA likely interacts more strongly with polar and charged moieties (e.g., water, netropsin) compared to regular DNA. This could be attributed to the fact that the B–N bonds present in clDNA are polarized (due to being formed between different atoms), whereas the C–C bonds in DNA are not polarized (excluding the effects of substituents). Consequently, the accumulation of such highly polar structural motifs in specific regions, such as the minor groove, could result in stronger interactions with polar or charged ligands.

Fig. 11 The lowest energy structures of the complexes of netropsin with DNA(tetramer) and clDNA(tetramer).

4. Summary

In summary of our accomplishments described in this work, we conclude that:

(1) We set the goal of designing a carbonless DNA fragment and attempted to achieve this by replacing all carbon atoms with boron or nitrogen atoms, adopting isoelectronicity as a sine qua non condition.

(2) To accomplish this, we applied theoretical quantum chemistry methods, specifically the DFT method with the ωB97XD functional and the aug-cc-pVDZ basis set. For selected systems, we verified its reliability by comparing the obtained structures and binding energies with those derived from more accurate methods such as MP2 (for structural parameter comparisons), as well as CCSD and SAPT2+3(CCD)δ_MP2/aug-cc-pVDZ (for comparing binding energies in complementary pairs).

(3) We initiated our goal by independently constructing carbonless equivalents of all DNA components (e.g., cytosine, thymine, guanine, adenine, and deoxyribose), ensuring that they resembled the original carbon-containing DNA components (in terms of analogous spatial structure, polarity, and interaction capabilities with other molecules).

(4) After determining the structure of all DNA building block equivalents, we established the structure of carbonless analogs of complementary base pairs and compared them with unmodified (i.e., carbon-based) base pairs. We found that the number and length of the corresponding hydrogen bonds in these systems show remarkable similarity. Moreover, we found that the binding energies of the carbonless analogs of the base pairs are also very close to those in their respective carbon-based A–T and G–C pairs.

(5) We determined the structure of two carbonless DNA fragments containing two and six base pairs, respectively, and found that they form double-helix fragments, analogous to those formed by unmodified (i.e., carbon-based) DNA, as evidenced by the comparison of structural parameters such as the size and shape of these fragments, the length of individual hydrogen bonds, twist and propeller angles, and the rise per base pair (i.e., the distance between each base pair along the helical axis).

(6) Using docking simulations for carbon-containing and carbonless DNA fragments (each comprising 12 base pairs) mimicking the receptor and an arbitrarily chosen ligand (netropsin), we found that this example ligand exhibits a slightly different preference (in spatial/structural terms) for binding to carbonless DNA through the minor groove compared to unmodified DNA.

In conclusion, we assert that the design approach for carbonless DNA described here has proven to be effective. The structure of such DNA should display all structural similarities to carbon-based DNA, as well as analogous stability. However, we anticipate that it may interact somewhat differently with various ligands.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Foundation for Polish Science (FNP) (J. B.) and by the Polish Ministry of Science and Higher Education grant no. DS 531-T110-D844-24 (P. S.). The calculations have been carried out using resources provided by Wroclaw Centre for Networking and Supercomputing (https://wcss.pl) grants no. 455 (P. S.) and 560 (J. B.).

References

1. P. L. Luisi, The Emergence of Life, From Chemical Origins to Synthetic Biology, Cambridge University Press, 2010 DOI:10.1017/CBO9780511817540.
2. S. A. Benner, Life, the Universe and the Scientific Method, FfAME Press, 2009, ISBN-10: 0615267459.
3. S. H. Schneider and P. J. Boston, Scientists on GAIA, The MIT Press, 1993, ISBN: 9780262691604.
4. J. J. Petkowski, W. Bains and S. Seager, On the Potential of Silicon as a Building Block for Life, Life, 2020, 10, 84.
5. D. Darling and D. Schulze-Makuch, The Extraterrestrial Encyclopedia, Design Pub., Sarasota, FL, 1st edn, 2016.
6. B. Minkovich, I. Ruderfer, A. Kaushansky, D. Bravo-Zhivotovskii and Y. Apeloig, α-Sila-Dipeptides: Synthesis and Characterization, Angew. Chem., 2018, 130, 13445–13449.
7. M. Mortensen, R. Husmann, E. Veri and C. Bolm, Synthesis and Applications of Silicon-Containing α-Amino Acids, Chem. Soc. Rev., 2009, 38, 1002–1010.
8. M. Czapla, Silicon amino acids, Int. J. Quantum Chem., 2017, 118, e25488.
9. J. K. Olson and A. I. Boldyrev, Electronic transmutation: Boron acquiring an extra electron becomes ‘carbon’, Chem. Phys. Lett., 2012, 523, 83–86.
10. R. G. Gillis, Isoelectronic molecules: The effect of number of outer-shell electrons on structure, J. Chem. Educ., 1958, 35, 66–68.
11. E. D. Jemmis and E. G. Jayasree, Analogies between Boron and Carbon, Acc. Chem. Res., 2003, 36, 816–824.
12. A. N. Alexandrova, K. A. Birch and A. I. Boldyrev, Flattening the B₆H₆²⁻ Octahedron. Ab Initio Prediction of a New Family of Planar All-Boron Aromatic Molecules, J. Am. Chem. Soc., 2003, 125, 10786–10787.
13. J. T. Gish, I. A. Popov and A. I. Boldyrev, Homocatenation of Aluminum: Alkane-like Structures of Li₂Al₂H₆ and Li₃Al₃H₈, Chem. – Eur. J., 2015, 21, 5307–5310.
14. I. A. Popov, X. Zhang, B. W. Eichhorn and A. I. Boldyrev, Bowen, Aluminum chain in Li₂Al₃H₈⁻ as suggested by photoelectron spectroscopy and ab initio calculations, Phys. Chem. Chem. Phys., 2015, 17, 26079–26083.
15. X. Zhang, I. A. Popov, K. A. Lundell, H. Wang, C. Mu, W. Wang, H. Schöckel, A. I. Boldyrev and K. H. Bowen, Realization of an Al≡Al Triple Bond in the Gas-Phase Na₃Al₂⁻ Cluster via Double Electronic Transmutation, Angew. Chem., Int. Ed., 2018, 57, 14060–14064.
16. E. Osorio, J. K. Olson, W. Tiznado and A. I. Boldyrev, Analysis of Why Boron Avoids sp² Hybridization and Classical Structures in the B_nH_n+2 Series, Chem. – Eur. J., 2012, 18, 9677–9681.
17. X. Zhang, K. A. Lundell, J. K. Olson, K. H. Bowen and A. I. Boldyrev, Electronic Transmutation (ET): Chemically Turning One Element into Another, Chem. – Eur. J., 2018, 24, 9200–9210.
18. I. A. Popov and A. I. Boldyrev, Computational probing of all-boron Li_2nB_2nH_2n+2 polyenes, Comput. Theor. Chem., 2013, 1004, 5–11.
19. K. A. Lundell, J. K. Olson and A. I. Boldyrev, Exploring the limits of electronic transmutation: Ab initio study of Li_nBe_n (n = 3–5), Chem. Phys. Lett., 2020, 739, 136994.
20. Z. Zhang, E. S. Penev and B. I. Yakobson, Two-Dimensional Boron: Structures, Properties and Applications, Chem. Soc. Rev., 2017, 46, 6746–6763.
21. X. Chen, D. Tan and D.-T. Yang, Multiple-Boron–Nitrogen (Multi-BN) Doped π-Conjugated Systems for Optoelectronics, J. Mater. Chem. C, 2022, 10, 13499–13532.
22. G. Seifert, P. W. Fowler, D. Mitchell, D. Porezag and T. Frauenheim, Boron-nitrogen analogues of the fullerenes: electronic and structural properties, Chem. Phys. Lett., 1997, 268, 352–358.
23. G. Chen, L. N. Zakharov, M. E. Bowden, A. J. Karkamkar, S. M. Whittemore, E. B. Garner, III, T. C. Mikulas, D. A. Dixon, T. Autrey and S.-Y. Liu, Bis-BN Cyclohexane: A Remarkably Kinetically Stable Chemical Hydrogen Storage Material, J. Am. Chem. Soc., 2015, 137, 134–137.
24. S. V. Sawant, S. Banerjee, A. W. Patwardhan, J. B. Joshi and K. Dasgupta, Synthesis of Boron and Nitrogen Co-Doped Carbon Nanotubes and Their Application in Hydrogen Storage, Int. J. Hydrogen Energy, 2020, 45, 13406–13413.
25. A. L. Tiano, C. Park, J. W. Lee, H. H. Luong, L. J. Gibbons, S.-H. Chu, S. Applin, P. Gnoffo, S. Lowther, H. J. Kim, P. M. Danehy, J. A. Inman, S. B. Jones, J. H. Kang, G. Sauti, S. A. Thibeault, V. Yamakov, K. E. Wise, J. Su and C. C. Fay, Boron Nitride Nanotube: Synthesis and Applications, Proc. SPIE, 2014, 9060, 906006.
26. Y. Yue, X. Yang, K. Yang, K. Li, Z. Liu, F. Wang, R. Zhang, J. Huang, Z. Wang, L. Zhang and G. Xin, Highly Thermally Conductive Super-Aligned Boron Nitride Nanotube Films for Flexible Electronics Thermal Management, ACS Appl. Mater. Interfaces, 2024, 16, 33971–33980.
27. K. Harikrishnan, A. Hoque, R. Patel, V. P. Singh, U. K. Gaur and M. Sharma, Electronic, Electrical, and Optical Properties of Hexagonal Boron Nitride, in Hexagonal Boron Nitride, ed. K. Deshmukh, M. Pandey and C. M. Hussain, Micro and Nano Technologies, Elsevier, 2024, pp. 89–123.
28. P. E. Kosbe, Thermal Stability and Thermal Conductivity Studies of Hexagonal Boron Nitride, in Hexagonal Boron Nitride, ed. K. Deshmukh, M. Pandey and C. M. Hussain, Micro and Nano Technologies, Elsevier, 2024, pp. 153–178.
29. S. Roy, X. Zhang, A. B. Puthirath, A. Meiyazhagan, S. Bhattacharyya, M. M. Rahman, G. Babu, S. Susarla, S. K. Saju, M. K. Tran, L. M. Sassi, M. A. S. R. Saadi, J. Lai, O. Sahin, S. M. Sajadi, B. Dharmarajan, D. Salpekar, N. Chakingal, A. Baburaj, X. Shuai, A. Adumbumkulath, K. A. Miller, J. M. Gayle, A. Ajnsztajn, T. Prasankumar, V. V. J. Harikrishnan, V. Ojha, H. Kannan, A. Z. Khater, Z. Zhu, S. A. Iyengar, P. A. D. S. Autreto, E. F. Oliveira, G. Gao, A. G. Birdwell, M. R. Neupane, T. G. Ivanov, J. Taha-Tijerina, R. M. Yadav, S. Arepalli, R. Vajtai and P. M. Ajayan, Structure, Properties and Applications of Two-Dimensional Hexagonal Boron Nitride, Adv. Mater., 2021, 33, 2101589.
30. H. Zhang, Y. Liu, K. Sun, S. Li, J. Zhou, S. Liu, H. Wei, B. Liu, L. Xie, B. Li and J. Jiang, Applications and Theory Investigation of Two-Dimensional Boron Nitride Nanomaterials in Energy Catalysis and Storage, EnergyChem, 2023, 5, 100108.
31. M. Simanullang and L. Prost, Nanomaterials for On-Board Solid-State Hydrogen Storage Applications, Int. J. Hydrogen Energy, 2022, 47, 29808–29846.
32. S. L. Kraft, P. R. Gavin, C. E. DeHaan, C. W. Leathers, W. F. Bauer, D. L. Miller and R. V. Dorn, 3rd., Borocaptate Sodium: A Potential Boron Delivery Compound for Boron Neutron Capture Therapy Evaluated in Dogs with Spontaneous Intracranial Tumors, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 11973–11977.
33. M. A. Dymova, S. Y. Taskaev, V. A. Richter and E. V. Kuligina, Boron Neutron Capture Therapy: Current Status and Future Perspectives, Cancer Commun., 2020, 40, 406–421.
34. S. Kulkarni, D. Bhandary, Y. Singh, V. Monga and S. Thareja, Boron in Cancer Therapeutics: An Overview, Pharmacol. Ther., 2023, 251, 108548.
35. N. R. Pace, The universal nature of biochemistry, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 805–808.
36. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
37. T. H. Dunning, Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
38. R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806.
39. C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622.
40. M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506.
41. M. J. Frisch, M. Head-Gordon and J. A. Pople, A direct MP2 gradient method, Chem. Phys. Lett., 1990, 166, 275–280.
42. S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13, 1989–2009.
43. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB – An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671.
44. J. Čížek, On the Use of the Cluster Expansion and the Technique of Diagrams in Calculations of Correlation Effects in Atoms and Molecules, in Advances in Chemical Physics, ed. R. Lefebvre and C. Moser, John Wiley & Sons, Ltd., 1969, vol. 14, pp. 35–89.
45. G. D. Purvis III and R. J. Bartlett, A full coupled-cluster singles and doubles model – the inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918.
46. G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, An efficient reformulation of the closed-shell coupled cluster single and double excitation (CCSD) equations, J. Chem. Phys., 1988, 89, 7382–7387.
47. R. J. Bartlett and G. D. Purvis III, Many-body perturbation-theory, coupled-pair many-electron theory, and importance of quadruple excitations for correlation problem, Int. J. Quantum Chem., 1978, 14, 561–581.
48. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes, Chem. Rev., 1994, 94, 1887–1930.
49. E. G. Hohenstein and C. D. Sherrill, Density Fitting of Intramonomer Correlation Effects in Symmetry-Adapted Perturbation Theory, J. Chem. Phys., 2010, 133, 014101.
50. E. G. Hohenstein and C. D. Sherrill, Wavefunction Methods for Noncovalent Interactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 304–326.
51. R. M. Parrish, E. G. Hohenstein and C. D. Sherrill, Tractability Gains in Symmetry-Adapted Perturbation Theory Including Coupled Double Excitations: CCD+ST(CCD) Dispersion with Natural Orbital Truncations, J. Chem. Phys., 2013, 139, 174102.
52. J. Brzeski, Can H₂ Be Superacidic? A Computational Study of Triel-Bonded Brønsted Acids, J. Phys. Chem. A, 2024, 128, 5009–5020.
53. K. Kříž, P. J. van Maaren and D. van der Spoel, Impact of Combination Rules, Level of Theory, and Potential Function on the Modeling of Gas- and Condensed-Phase Properties of Noble Gases, J. Chem. Theory Comput., 2024, 20, 2362–2376.
54. J. G. Hill and A. C. Legon, Radial Potential Energy Functions of Linear Halogen-Bonded Complexes YX⋯ClF (YX = FB, OC, SC, N₂) and the Effects of Substituting X by Second-Row Analogues: Mulliken Inner and Outer Complexes, J. Phys. Chem. A, 2022, 126, 2511–2521.
55. R. L. Kumawat and C. D. Sherrill, High-Order Quantum-Mechanical Analysis of Hydrogen Bonding in Hachimoji and Natural DNA Base Pairs, J. Chem. Inf. Model., 2023, 63, 3150–3157.
56. D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, III, A. Y. Sokolov, K. Patkowski, A. E. DePrince, III, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, PSI4 1.4: Open-Source Software for High-Throughput Quantum Chemistry, J. Chem. Phys., 2020, 152, 184108.
57. R. F. W. Bader, A Quantum Theory of Molecular Structure and Its Applications, Chem. Rev., 1991, 91, 893–928.
58. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, Are Bond Critical Points Really Critical for Hydrogen Bonding?, J. Chem. Theory Comput., 2013, 9, 3263–3266.
59. E. Espinosa, E. Molins and C. Lecomte, Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities, Chem. Phys. Lett., 1998, 285, 170–173.
60. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592.
61. C. Plett and S. Grimme, Automated and Efficient Generation of General Molecular Aggregate Structures, Angew. Chem., Int. Ed., 2023, 62, e202214477.
62. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, UCSF Chimera – A Visualization System for Exploratory Research and Analysis, J. Comput. Chem., 2004, 25, 1605–1612.
63. A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
64. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
65. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
66. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
67. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
68. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA Quantum Chemistry Program Package, J. Chem. Phys., 2020, 152, 224108.
69. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.
70. J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102, 7211–7218.
71. A. E. Reed and F. Weinhold, Natural bond orbital analysis of near-Hartree–Fock water dimer, J. Chem. Phys., 1983, 78, 4066–4073.
72. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746.
73. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint, Chem. Rev., 1988, 88, 899–926.
74. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2018.
75. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
76. Y. E. R. Jeong, R. W. Kung, J. Bykowski, T. K. Deak and S. D. Wetmore, Effect of Guanine Adduct Size, Shape, and Linker Type on the Conformation of Adducted DNA: A DFT and Molecular Dynamics Study, J. Phys. Chem. B, 2023, 127, 9035–9049.
77. A. M. A. Abdelgawwad, A. Monari, I. Tuñón and A. Francés-Monerris, Spatial and Temporal Resolution of the Oxygen-Independent Photoinduced DNA Interstrand Cross-Linking by a Nitroimidazole Derivative, J. Chem. Inf. Model., 2022, 62, 3239–3252.
78. M. L. Kopka, C. Yoon, D. Goodsell, P. Pjura and R. E. Dickerson, The Molecular Origin of DNA-Drug Specificity in Netropsin and Distamycin, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 1376–1380.
79. J. Dolenc, R. Baron, C. Oostenbrink, J. Koller and W. F. van Gunsteren, Configurational Entropy Change of Netropsin and Distamycin upon DNA Minor-Groove Binding, Biophys. J., 2006, 91, 1460–1470.
80. A. Ciesielska, J. Brzeski, D. Zarzeczańska, M. Stasiuk, M. Makowski and S. Brzeska, Exploring the Interaction of Biologically Active Compounds with DNA through the Application of the SwitchSense Technique, UV-Vis Spectroscopy, and Computational Methods, Spectrochim. Acta, Part A, 2024, 316, 124313.
81. M. Coll, J. Aymami, G. A. Van der Marel, J. H. Van Boom, A. Rich and A. H. J. Wang, Molecular Structure of the Netropsin-d(CGCGATATCGCG) Complex: DNA Conformation in an Alternating AT Segment, Biochemistry, 1989, 28, 310–320.
82. D. Halder, A. M. A. Abdelgawwad and A. Francés-Monerris, Cobaltabis(dicarbollide) Interaction with DNA Resolved at the Atomic Scale, J. Med. Chem., 2024, 67, 18194–18203.
83. M. Mohammad, H. A. R. Gazi, K. Pandav, P. Pandya and M. M. Islam, Evidence for Dual Site Binding of Nile Blue A toward DNA: Spectroscopic, Thermodynamic, and Molecular Modeling Studies, ACS Omega, 2021, 6, 2613–2625.
84. L. A. Marky, K. S. Blumenfeld and K. J. Breslauer, Calorimetric and spectroscopic investigation of drug-DNA interactions. 1. The binding of netropsin to polyd(AT), Nucleic Acids Res., 1983, 11, 2857–2870.
85. H. Zhang, H. Gattuso, E. Dumont, W. Cai, A. Monari, C. Chipot and F. Dehez, Accurate Estimation of the Standard Binding Free Energy of Netropsin with DNA, Molecules, 2018, 23, 228.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04410j

---