First principles assessment of solvent induced cage effects on intramolecular hydrogen transfer in the free radical polymerization of acrylates†
Received
19th November 2024
, Accepted 12th February 2025
First published on 12th February 2025
Abstract
We investigate the rate constant of poly-butyl acrylate backbiting between 310 and 510 K using semi-empirical metadynamics in the gas phase, bulk and solution. The simulations in the condensed phase are performed through a hybrid quantum mechanics/molecular mechanics approach. The free energy landscape associated with the reactive events under vacuum and in the condensed phase is used to correct harmonic transition state theory (TST) rate constants. The Arrhenius parameters so determined are introduced in a semi-detailed mechanistic kinetic mechanism of butyl acrylate polymerization in bulk and in solution, allowing it to test how the butyl acrylate polymerization rate is affected by solvent-induced cage effects on backbiting. The results show that the backbiting rate constant is higher in the condensed phase than in the gas phase. In addition, a twofold increase is observed in xylene compared to the bulk. These results differ significantly from previous theoretical calculations, especially at high temperatures, aligning better with experimental rate measurements. The semi-detailed model, incorporating our calculated rate coefficients, is validated against monomer concentration profiles from bulk and solution polymerizations in various reactor configurations, demonstrating good agreement with experimental data. This study paves the way for developing detailed kinetic models in the condensed phase using a priori kinetic parameters derived from molecular simulations, thus widening their range of applicability beyond the one experimentally accessible.
I. Introduction
Butyl acrylate (BA) is among the most relevant acrylate monomers, being an important building block for the industrial production of coatings thanks to its film-forming properties and flexibility at low temperatures, which also makes it useful for the production of elastomers, plastics, and adhesives. Such materials are mainly used in the biomedical sector and packaging in general. The synthesis of homo- and co-polymers from BA is mainly carried out through free radical polymerization (FRP) in solution, in the presence or absence of an initiator. When an initiator is absent, the radical chain mechanism is initiated by raising the temperature, thus triggering thermal self-initiation. For these reasons, this monomer has been the subject of numerous experimental, theoretical and modelling studies, making it an ideal benchmark system for the development of novel theoretical methodologies devoted to the determination of kinetic rate parameters of radical chain mechanisms in the condensed phase. This topic is becoming increasingly relevant because of the need to design sustainable and efficient waste recycling technologies able to process the sheer amount of plastic waste produced by society. In this context thermochemical recycling offers a valid solution because it allows plastic waste to be transformed into energy vectors and valuable products. The study of radical chain kinetic mechanisms in the condensed phase presents numerous challenges to the current state-of-the-art experimental and theoretical methodologies. Knowledge of rate parameters of elementary reactions in the condensed phase (in solution or bulk) is key for formulating predictive kinetic mechanisms and to interpret the experimental observations. To this day, individual kinetic rate parameters of radical chain propagations, depropagations, as well as isomerizations (backbiting) can be experimentally obtained through pulsed laser polymerization coupled with size exclusion chromatography (PLP-SEC),1–6 semi-batch solution polymerization coupled with nuclear magnetic resonance (NMR)7 or by directly measuring the number of quaternary carbons, resulting from backbiting and successive monomer addition, by means of 13C NMR.8 The rate coefficients resulting from the first technique are gathered in the IUPAC database for standard monomers, which is typically considered as the gold standard for the validation of theoretical calculations due to their accuracy. In particular, the experimental studies employing the PLP-SEC technique provide the propagation, backbiting and β-scission rate coefficients for poly-butyl acrylate in bulk,2,5,6 whereas semi-batch experiments7 and NMR measurements of quaternary carbons (or branching levels) provide the same parameters in solution (mainly a mixture of ortho/meta/para-xylene). Fig. 1 shows a schematic representation of the main reaction pathways involved in the FRP of butyl acrylate taken from the literature.2,7,9 Once end-chain radicals (ECRs) are formed by thermal self-initiation (kti) or by reacting with an initiator radical, they most likely undergo propagation, forming a new ECR. Otherwise, they can either undergo termination (kt) by adding to another end-chain (or mid-chain) radical, forming a linear polymer chain (or branched chain) P, or backbiting (kbb). The latter pathway leads to mid-chain radicals, which create a competitive reaction pathway for monomer consumption and ultimately result in short polymer chains and branched polymer chains through β-scission (kβ) and tertiary propagation (ktp), respectively.
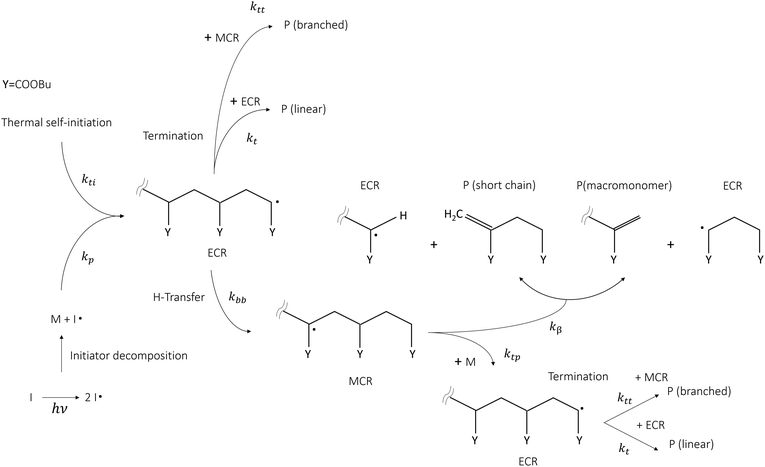 |
| | Fig. 1 Kinetic scheme summary of butyl acrylate's free radical polymerization mechanism in the presence and absence of an initiator (I). | |
Backbiting, together with chain-end propagations are the main reactions controlling the monomer conversion rate as was found in the seminal study of Nikitin and Hutchinson4 on the FRP of BA. As pointed out in ref. 2, 4 and 10, intramolecular hydrogen transfer, or backbiting, significantly affects the polymerization rate already at low temperatures (<300 K) and increases in relevance as temperature increases. This reaction governs the formation of mid-chain radicals (MCRs) from which secondary reactivity arises. Concerning polymerization processes, especially FRP technology, the secondary reactivity is undesired because it leads to low molecular weight polymers or branched chains caused by the addition of monomers to MCRs instead of ECRs. In contrast, thermochemical processes such as pyrolitic depolymerization, which are of interest in the context of recycling, are carried out under conditions that favor secondary reactivity because the presence of MCRs substantially reduces the energy required to break the polymer backbone, leading to β-scission instead of bond fission. While the propagation rate constant can be accessed directly from PLP-SEC experiments,2 the backbiting kinetic constant must be inferred indirectly through a detailed kinetic mechanism, potentially leading to error propagation. On the other end, DFT-based, static theoretical calculations have shown to significantly overestimate both the pre-exponential factor and activation energy of this reaction and neglect the effect of solvents.11–13
This work aims to establish a theoretical methodology to assess the interactions of solvents on intrinsic kinetic rate parameters from first principles. The theoretical methodology used in this work combines enhanced sampling, free energy calculations and transition state theory, as outlined in our previous work.14 Here we focus on the backbiting of poly-butyl acrylate in polar and nonpolar solvents because of its relevance in both polymerization8 and depolymerization processes.15,16 The intramolecular hydrogen transfer (backbiting) requires the folding of an ECR into a stable ring structure whose size depends on the chain length. It is known that six-membered rings are generally more stable than other types of ring structures.8,12,17 For this reason, this study focuses on the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 backbiting.
5 backbiting.
The solvent-dependent rate coefficients are validated, on the one hand, against PLP-SEC based elementary kinetic constant measurements2 and nuclear magnetic resonance (NMR) based measurements,8 while on the other, against concentration profiles from more conventional initiated feed-starved semi-batch polymerization7 and thermally self-initiated batch polymerization.9 The validation against concentration profiles in a chemical reactor requires knowledge of the detailed kinetic mechanism of BA polymerization, which has been widely studied in previous literature.3,4,7–9 The BA thermal self-initiation reaction, which is of paramount importance in this mechanism, has been theoretically investigated in the gas phase,18,19 however, estimates in solution have only been obtained through experiments.9,20 Therefore, a general consensus on the solvent-dependent thermal self-initiation reaction is still lacking. In this context, we believe that a theoretical approach aimed at determining kinetic rate parameters in solution would be beneficial also in interpreting the experiments, complementing parameter estimation from experimental measurements. Previous studies on BA free radical polymerization always considered β-scission and backbiting independent of the solvent. We have observed in our previous work14 through molecular simulations that not only does the β-scission dramatically change from the gas phase to the condensed phase, but different solvents can have a different impact on kinetic rate parameters. This study investigates the solvent effects on backbiting by applying the same theoretical framework used in our previous work on β-scission. By introducing the solvent-dependent rate parameters of backbiting (from this work) and β-scission (from the previous work14) in a mechanistic kinetic model of BA polymerization we want to assess whether kinetic rates calculated from first principles can be used to reproduce macroscopic monomer conversion in time and how the solvent-corrections implemented on BA secondary reactivity affect the overall polymerization rate.9
II. Methods
II.A. Simulation details
The intramolecular hydrogen transfer reactions in a vacuum and solvent were simulated using CP2K 9.1.21 We used the general Amber force field (GAFF)22 for the initial equilibration of a BA trimer ECR inside a cubic box with 180 solvent molecules for xylene and BA monomer and 2700 molecules for water, with periodic boundary conditions. Overall, the equilibration has been subdivided into a preliminary 100 ps run at constant pressure and temperature (NPT) to equilibrate the liquid density. Then, an additional 50 ps equilibration run at constant volume (NVT) was performed. The Nose–Hoover thermostat23,24 with a time constant of 50 fs is used to maintain a constant temperature throughout the equilibration runs. Long-range electrostatics is accounted for with the smooth particle mesh Ewald25 method with a real space cutoff of 10 Å. The molecular dynamics time step is 0.5 fs in all simulations. Reactive trajectories were simulated by adopting a QM/MM scheme where the ECR trimer undergoing intramolecular hydrogen transfer constitutes the QM region, whereas the solvent constitutes the MM region. The potential energy of the QM region is switched from GAFF to a tight-binding Hamiltonian, the GFN1 extended tight-biding26 (GFN1 xTB), because of its low computational cost. QM and MM regions are coupled using a Coulombic potential.27 Before the actual reactive trajectory, the QM/MM system is first thermalized in an NVT ensemble for 1 ps, which stabilizes the interactions between the QM and MM regions. For all the production reactive trajectories, we employed the Bussi–Donadio–Parrinello thermostat.28
II.B. Enhanced sampling technique: metadynamics
Reactive hydrogen transfer trajectories are sampled using metadynamics,29–31 a popular enhanced sampling technique based on the introduction of a repulsive bias potential acting on a low-dimensional set of collective coordinates describing relevant metastable states, often referred to as collective variables (CVs) space. In metadynamics, the bias potential is a time-dependent sum of Gaussian contributions, which are updated at discrete time intervals (t′). Applying this bias potential forces the exploration of the system configurational space, as projected on the selected set of CVs. The analytical expression of the bias potential accumulated up to time t in a standard metadynamics simulation, Vt(s), can be reconstructed as the sum of the individual Gaussian contributions:| |
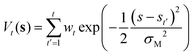 | (1) |
Where wt is the height of a Gaussian contribution, s indicates the CVs adopted to apply the bias, and σM is the width of the Gaussian contribution.
II.C. Free energy surface from MFI
The free energy landscape is recovered from metadynamics simulations through the mean force integration (MFI)32 algorithm implemented in the pyMFI package.33 This implementation of the MFI reconstructs an analytical expression of the mean thermodynamic force in the collective variables space ∇Ft(s) up to a given time t, where Ft(s) refers to the potential of mean force (PMF). As reported in ref. 32, the mean force has two components, namely the gradient with respect to s of the natural logarithm of the biased probability density pbt(s) and the gradient of the bias potential Vt(s) accumulated up to time t (see the Appendix in Section VI), as shown in eqn (2).| |
∇Ft(s) = −β−1∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pbt(s) − ∇Vt(s) pbt(s) − ∇Vt(s)
| (2) |
The biased probability density pbt(s) is reconstructed through kernel density estimation, in the time interval between each update of the bias potential Vt(s), by using multivariate Gaussian kernels centered in s, which is the vector of the selected CVs at time t, as reported in eqn (3). This allows us to derive an analytical expression for the derivative with respect to s.32| |
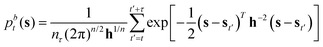 | (3) |
nτ is the number of values of each CV stored between each bias potential update. In our case, the CV values are saved every 10 steps, and a Gaussian bias is spawned every 90 steps; therefore, nτ equals 9. The bandwidths of the Gaussian kernels hi are set to 0.2, the same width as the Gaussians constructing the metadynamics bias potentials. Since the mean force does not require the estimate of any alignment constant between the free energy of ensembles of configurations generated under the effect of different bias potentials,32,34 this methodology allows merging multiple independent simulations into a single refined estimate of the average PMF. As a result, the convergence of the PMF estimate can be significantly accelerated because multiple short independent simulations can be used to compute and refine the PMF instead of relying on the convergence rate of a single, long simulation. The estimator of the average PMF 〈F(s)〉 across independent simulations can be determined using a bootstrap procedure as:| |
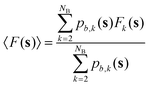 | (4) |
Eqn (4) shows that the mean thermodynamic force must be integrated at each k-th iteration of the bootstrap procedure. The total number of bootstrap operations NB used in this work is 500. The error is estimated through the bootstrap variance, as detailed in Section S1 of the ESI.†
The average marginal PMF along the CV space is obtained by integrating out the normalized probability density p(s) along all the orthogonal degrees of freedom as in eqn (5):
| |
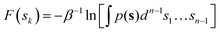 | (5) |
where the probability density
p(
s) is calculated as in
eqn (6):
| |
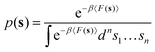 | (6) |
In eqn (6), 〈F(s)〉 indicates the bootstrap average of F(s) obtained via eqn (4).
II.D. QM/MM correction to the activation free-energy
Once the free energy profiles are determined at different temperatures, it is possible to decouple the enthalpic and entropic contributions along sk as the position-dependent intercept and the slope of least squares fit in that temperature range, respectively (see Section S1 of the ESI†). This decoupling allows us to use the configurational entropy contribution extracted from the QM/MM free energy surface to compute activation free energies at a higher level of theory and include zero-point energy contributions missed by the classical treatment of the QM/MM simulations.
The enthalpy of activation in vacuum ΔH≠ was calculated by optimizing the geometries and vibrational frequencies of snapshots taken from the metadynamics trajectory using the DFT functional ωB97XD/def2-TZVPP implemented in Gaussian 16 Rev. C02.35 The difference in electronic energy between reactants and transition states includes the zero-point vibrational energy (ZPE), which corresponds to the enthalpy of activation at 0 K, as in eqn (7).
| | |
ΔH≠ω97XD = (E≠ + ZPE≠) − (ER + ZPER)
| (7) |
This approach combines activation energy barriers obtained with an accurate DFT formulation with configurational entropies computed by direct sampling and an estimate of the reaction free energy profile under the influence of various solvents, as discussed in detail in Section III.B.
II.E. Kinetic modelling of BA polymerization
Batch and semi-batch experiments were modelled as ideal constant temperature reactors. The kinetic model of BA polymerization used in this work, which is adapted from previous literature,3,9 is coupled to the ideal reactor models yielding the system of differential equations for the batch and semi-batch reactors reported in eqn (8) and (9), respectively.| |
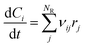 | (8) |
| |
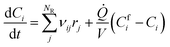 | (9) |
Where Ci is the molar concentration of species i inside the reactor, Cfi is the concentration of species i in the inlet flowrate of the semi-batch reactor, ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is the inlet volumetric flowrate in the semi-batch reactor, rij is the jth reaction rate involving species i, NR is the total number of reactions and νij is the stoichiometric coefficient of species i in the jth reaction. The resulting systems of ordinary differential equations (ODE) has been solved with the stiff ODE solver ode15s implemented in MATLAB 2024b. By defining the right hand side of eqn (8) and (9) as a generic function of the concentrations of species i and the vector of parameters k, the previous systems of differential equations can be generalized as in eqn (10)
is the inlet volumetric flowrate in the semi-batch reactor, rij is the jth reaction rate involving species i, NR is the total number of reactions and νij is the stoichiometric coefficient of species i in the jth reaction. The resulting systems of ordinary differential equations (ODE) has been solved with the stiff ODE solver ode15s implemented in MATLAB 2024b. By defining the right hand side of eqn (8) and (9) as a generic function of the concentrations of species i and the vector of parameters k, the previous systems of differential equations can be generalized as in eqn (10)| |
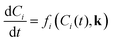 | (10) |
the local sensitivity coefficients can be written as the adjoint set of ordinary differential equations in eqn (12)| |
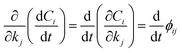 | (11) |
Therefore, we indicate with ϕij the local sensitivity coefficient of species i with respect to the parameter kj, which, in this work, stands for the kinetic rate parameter of the jth reaction involving the ith species.| |
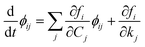 | (12) |
Once the adjoint system is solved for ϕij, the dimensionless local sensitivity coefficient is derived as in eqn (13).
| |
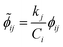 | (13) |
Then, the dimensionless integral sensitivity coefficient can be calculated by integrating the local dimensionless sensitivity coefficient over the reaction time τR.
| |
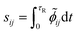 | (14) |
Since these integral coefficients can be arbitrarily large, it is useful to normalize these coefficients by the sum over the absolute values of all the integral contributions:
| |
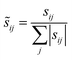 | (15) |
In this framework, we have considered 6 pseudo-species for the free radical polymerization of BA, namely the initiator I and its radical I*, the monomer M, the end-chain radicals R
e, the mid-chain radicals R
m, the polymer P and the solvent S. The chain dependence is neglected, in that each chain-dependent pseudo-species, namely R
e, R
m and P incorporate all possible chain lengths.
16 For instance, the end-chain radicals of each length are summed into the pseudo-species R
e as in
eqn (16).
| |
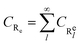 | (16) |
where
l stands for the chain length. The pseudo-species P includes dead polymer chains of every length, of every type,
i.e. linear and branched, as well as macromonomers that may arise from the β-scission.
III. Results and discussion
III.A. Dynamics of intramolecular hydrogen transfer
Reactive semi-empirical molecular dynamics simulations have been performed on a trimer model molecule, shown in Fig. 2, representative of a poly-butyl acrylate end-chain radical. Results from multiple, independent, metadynamics trajectories are merged through MFI to converge the PMF in the CV space given by the distance of the radical chain end carbon C5 and the hydrogen attached to C1 and the dihedral angle formed by the atoms C5–H–C1–C2, which are CV1 and CV2 in Fig. 3, respectively. CV2 is introduced as an orthogonal degree of freedom with respect to the distance of the forming bond (CV1) and is also biased to sample the ring conformation. Then, the two-dimensional, time-independent PMF is projected on a one-dimensional, effective reaction coordinate, namely CV1.
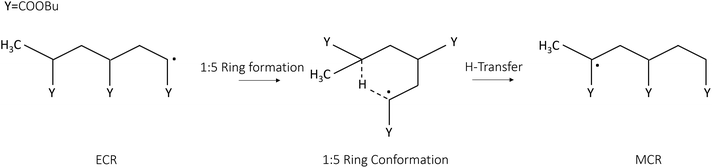 |
| | Fig. 2 Schematic representation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 intramolecular hydrogen transfer (backbiting) of the BA model trimer, which is the model system used to study the reactivity of the poly-butyl acrylate. This chemical reaction requires the formation of a stable ring structure, enabling the hydrogen abstraction between the ECR and the MCR carbons. 5 intramolecular hydrogen transfer (backbiting) of the BA model trimer, which is the model system used to study the reactivity of the poly-butyl acrylate. This chemical reaction requires the formation of a stable ring structure, enabling the hydrogen abstraction between the ECR and the MCR carbons. | |
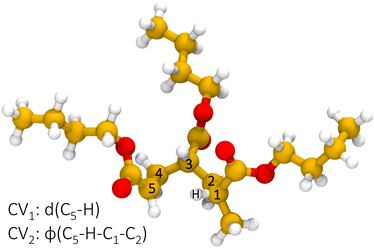 |
| | Fig. 3 Definition of the collective variables space for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 intramolecular hydrogen transfer. 5 intramolecular hydrogen transfer. | |
Fig. 4 shows the marginal PMF in the presence and absence of various solvents at 410 K, from which correction factors to activation energy barriers can be easily extrapolated. Overall, the results show that the various solvents reduce the free energy barrier of activation of the hydrogen transfer, which corresponds to the range of C5–H distances between 2.6 and 2.9 Bohrs, compared to the gas phase. The difference in activation-free energy barrier assessed from the PMF analysis is mainly related to the electrostatic interactions between the ECR and the solvent environment, contributing to the solvation free energy. In addition, among the solvents, xylene presents the largest effect on the reaction free energy landscape. For instance, the activation free energy barrier in xylene is 1 kcal mol−1 lower with respect to the cases in bulk and water (see Section S2 of the ESI† for the latter). This difference can be explained by considering the specific interactions occurring between the solvent and the ring structure precursor to the hydrogen transfer reaction. Fig. 4 also shows the equilibrium configurations that can be described by the C5–H distance and how these configurations are affected by the various solvents. Distances in the range 5–5.5 Bohrs represent the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring conformation, whereas 9–10 Bohrs represent the ECR's linear conformation and 2 Bohrs the MCR. As expected, the MCR is more stable than the ECR by ∼2 kcal mol−1 because tertiary carbon radicals are generally more stable than secondary carbon radicals. These equilibrium conformations are affected by the solvent in which the equilibrium C5–H distance associated with the 1
5 ring conformation, whereas 9–10 Bohrs represent the ECR's linear conformation and 2 Bohrs the MCR. As expected, the MCR is more stable than the ECR by ∼2 kcal mol−1 because tertiary carbon radicals are generally more stable than secondary carbon radicals. These equilibrium conformations are affected by the solvent in which the equilibrium C5–H distance associated with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure is approximately 0.5 Bohr lower compared to vacuum conditions. This indicates that the viscous forces between the reacting fragment and the solvent are producing a steric cage effect on the folded chain, which bolsters reactivity. Conversely, the ECR's linear conformation is more elongated in water (see Section S2 of the ESI†) compared to the other cases, which could be caused by hydrogen bonding stretching the polymer chains. On the other hand, the repulsive interactions between the aromatic rings of xylene and the BA carbonyl groups result in a tighter ring structure, which stands out from Fig. 4 where the free energy well associated with the ring state is wider in xylene compared to the bulk. This suggests that the radical carbon C5 and the hydrogen that is being transferred are kept closer in xylene, further facilitating the hydrogen transfer.
5 ring structure is approximately 0.5 Bohr lower compared to vacuum conditions. This indicates that the viscous forces between the reacting fragment and the solvent are producing a steric cage effect on the folded chain, which bolsters reactivity. Conversely, the ECR's linear conformation is more elongated in water (see Section S2 of the ESI†) compared to the other cases, which could be caused by hydrogen bonding stretching the polymer chains. On the other hand, the repulsive interactions between the aromatic rings of xylene and the BA carbonyl groups result in a tighter ring structure, which stands out from Fig. 4 where the free energy well associated with the ring state is wider in xylene compared to the bulk. This suggests that the radical carbon C5 and the hydrogen that is being transferred are kept closer in xylene, further facilitating the hydrogen transfer.
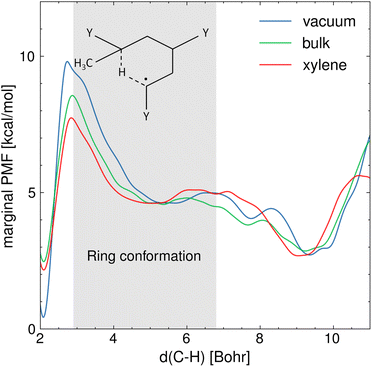 |
| | Fig. 4 Marginal PMF profiles [kcal mol−1], projected over the distance between the carbon radical (C5) and the hydrogen attached to C1 that is being transferred, in vacuum, in bulk and in xylene T = 410 K. The gray area indicates the interval of C5–H distances at which the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring conformation is found, which is the precursor state to the hydrogen transfer. 5 ring conformation is found, which is the precursor state to the hydrogen transfer. | |
III.B. Estimation of solvent-dependent hydrogen transfer kinetic parameters
Rate constants are calculated by combining harmonic transition state theory (TST) with statistical information that can be derived from the marginal PMF profiles. As shown in Fig. 2 and 4, this chemical reaction is characterized by the formation of the ring intermediate. The ring configuration results from the rotation of the linear ECR, therefore, the reactive flux should account for both the probability of forming the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure within the reactant ensemble of configurations and the consecutive hydrogen transfer, as was previously suggested by Yu et al.13 As regards the hydrogen transfer step, harmonic TST is applied considering the ground state (0 K) potential energy and vibrational frequencies of the reactive configurations found with the semi-empirical metadynamics sampling and introducing quantum mechanical corrections, namely the zero-point energy (ZPE) and Eckart tunneling. We chose as the reactant state the 1
5 ring structure within the reactant ensemble of configurations and the consecutive hydrogen transfer, as was previously suggested by Yu et al.13 As regards the hydrogen transfer step, harmonic TST is applied considering the ground state (0 K) potential energy and vibrational frequencies of the reactive configurations found with the semi-empirical metadynamics sampling and introducing quantum mechanical corrections, namely the zero-point energy (ZPE) and Eckart tunneling. We chose as the reactant state the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure (indicated here as r), which is known from previous studies to be the most stable precursor to BA intramolecular hydrogen transfer.12 In addition, by performing simulations at different temperatures, a fully coupled classical entropy of activation ΔS≠cl is estimated from the thermodynamic relationship in eqn (17).
5 ring structure (indicated here as r), which is known from previous studies to be the most stable precursor to BA intramolecular hydrogen transfer.12 In addition, by performing simulations at different temperatures, a fully coupled classical entropy of activation ΔS≠cl is estimated from the thermodynamic relationship in eqn (17).| |
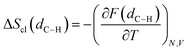 | (17) |
Fig. 5 shows the marginal entropic and enthalpic profiles and their standard deviation along the C5–H distance. It is shown that there is a positive classical entropy change of 0.007 ± 0.002 kcal mol−1 K−1 in the hydrogen transfer step. In contrast, the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring from the linear ECR configuration shows a negative entropy change of the same magnitude. Furthermore, it stands out that the enthalpy of activation estimated from the GFN1 xTB for the hydrogen transfer is 10.0 ± 0.4 kcal mol−1, and the enthalpy change associated with the rotation of the ECR leading to the 1
5 ring from the linear ECR configuration shows a negative entropy change of the same magnitude. Furthermore, it stands out that the enthalpy of activation estimated from the GFN1 xTB for the hydrogen transfer is 10.0 ± 0.4 kcal mol−1, and the enthalpy change associated with the rotation of the ECR leading to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring is 1.8 ± 0.4 kcal mol−1.
5 ring is 1.8 ± 0.4 kcal mol−1.
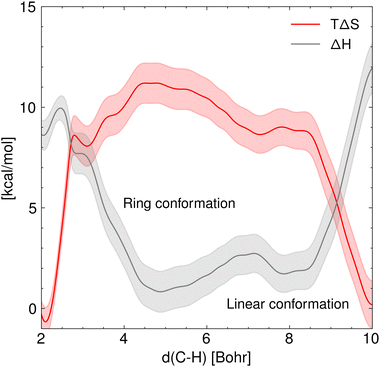 |
| | Fig. 5 Marginal entropy and enthalpy profiles [kcal mol−1] projected over the C5–H distance in vacuum along with their standard deviation at T = 410 K. This plot highlights the opposing trends of enthalpy and entropy involved in the hydrogen transfer reaction. | |
The effect of the solvent on the hydrogen transfer rate constant is introduced through correction factors, which are given by Boltzmann inversion of the difference in free energy barriers of activation (ΔΔF≠g→sol) between the gas phase and each solvent as in eqn (18).
| |
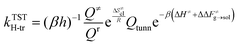 | (18) |
where
β = (
kBT)
−1 is the inverse of the thermal energy (where
kB is the Boltzmann constant and
T is the absolute temperature) and
h is the Planck constant.
Q≠ and
Qr are the molecular partition functions, divided into vibrational and rotational contributions, of the transition state and reactant configurations, respectively. The classical entropy of activation, estimated as in
eqn (17) complements the frequency factor determined by the quantum harmonic partition functions. This constitutes an alternative approach to hindered rotor partition function corrections. Notably, the correspondence between PMF and Helmholtz free energy has been tested through normal mode analysis. An imaginary frequency of 1599.5 cm
−1, associated with the full dimensional dividing surface, or transition state, has been found for the configuration extracted from the dynamic sampling, which corresponds to the relative maximum on the marginal free energy profile located at 2.6 Bohrs (
Fig. 4). The ring formation step is accounted for by the relative frequency (or classical probability) of finding the system in the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
5 ring conformation over the reactant ensemble of configurations. This correction factor, which we call
γr, arises naturally from the TST expression of the rate constant considering the probability of forming the reactive ring configuration (
r) within the reactant ensemble of configurations (
R). This probability is formally expressed as the ratio between partition functions, as shown in
eqn (19). The calculation of this probability is carried out by integrating the free energy profiles over the range of C
5–H distances equal to the maximum amplitude of a quantum harmonic oscillator (
eqn (21)) at temperature
T, centered on the equilibrium distance of the 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
5 ring state (
d0).
| |
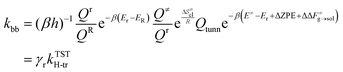 | (19) |
The calculation of γr, which is reported in eqn (20), is carried out by approximating the free energy well corresponding to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring equilibrium configuration with a quadratic potential.
5 ring equilibrium configuration with a quadratic potential.
| |
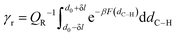 | (20) |
The partition function related to the reactant state QR is the integral of the probability density over the reactant ensemble of configurations, namely in the interval of C5–H distances between 2.6 Bohrs and infinite distance and acts as a normalization constant for the probability γr. The integration domain for γr, namely ±δl, corresponds to the maximum amplitude Amax of a quantum harmonic oscillator, which is determined by the internal energy of the quantum harmonic oscillator Uvib at a given temperature T and the average harmonic vibrational frequency ν of the normal modes that mostly impact the C5–H distance as in eqn (21).
| |
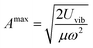 | (21) |
where
μ is the reduced mass of the C
5–H bond and
ω is the pulsation of the harmonic oscillator calculated as 2π
ν. The internal energy of the quantum harmonic oscillator
Uvib is calculated as in
eqn (22).
| |
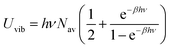 | (22) |
The value of ν found in this work is 400 cm−1. The final rate constant is evaluated by multiplying the relative probability of being in the ring structure within the reactant ensemble of configurations, γr, by the rate constant determined from harmonic TST, including Eckart tunneling and the classical entropy corrections, as previously shown in eqn (19).
Fig. 6 shows that accounting for the relative probability of being in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring state, which is the precursor to the hydrogen transfer transition state, for quantum tunneling effects and the free energy of solvation, the agreement between theory and experiments is significantly improved compared to our gas phase results as well as previous theoretical results.12,13 This allows us to derive intrinsic kinetic parameters of the intramolecular hydrogen transfer (or backbiting) from pure theory in a temperature range that is hardly accessible with state-of-the-art experimental techniques,2 without substantial loss in accuracy. In fact, our results in bulk match the experimental PLP-SEC rate measurements in the temperature range 303–323 K obtained in bulk by Vir et al.6 in terms of activation energy, 7.61 kcal mol−1 against 7.32 kcal mol−1, respectively, whereas a factor of 2 discrepancy is observed in the pre-exponent, which lies within the uncertainty of the method.14 Excellent agreement is instead found with the lower temperature (293–303 K) PLP-SEC measurements by Nikitin et al.2 Experiments above 323 K were performed in the study of Nikitin et al.,8 which provide estimates of the poly-BA backbiting rate constant in xylene solvent from direct measurements of branch points in the polymer chains (called branching levels) through nuclear magnetic resonance (NMR). While the activation energy derived from their Arrhenius fit (EA = 7.8 ± 0.1 kcal mol−1) matches our calculated value, their pre-exponential factor (A = (7.4 ± 1.5) × 107 s−1) is roughly twice as large as our estimates for both bulk and xylene. As regards the comparison with theoretical rate parameters from previous studies of Yu et al. and Cuccato et al., the higher the temperature, the larger the discrepancy with respect to our results in the gas phase, even though at 310 K, our results match the ones of Yu et al.13 Overall, our results show improved agreement with the experiments compared to the results from Cuccato et al. and Yu et al. In addition, our results show that the rate constant in the gas phase has an activation energy of 2 kcal mol−1 higher with respect to the case in xylene and 1.5 kcal mol−1 higher with respect to the case in bulk. A summary of the Arrhenius parameters calculated in the gas phase and in solution is reported in Table 1.
5 ring state, which is the precursor to the hydrogen transfer transition state, for quantum tunneling effects and the free energy of solvation, the agreement between theory and experiments is significantly improved compared to our gas phase results as well as previous theoretical results.12,13 This allows us to derive intrinsic kinetic parameters of the intramolecular hydrogen transfer (or backbiting) from pure theory in a temperature range that is hardly accessible with state-of-the-art experimental techniques,2 without substantial loss in accuracy. In fact, our results in bulk match the experimental PLP-SEC rate measurements in the temperature range 303–323 K obtained in bulk by Vir et al.6 in terms of activation energy, 7.61 kcal mol−1 against 7.32 kcal mol−1, respectively, whereas a factor of 2 discrepancy is observed in the pre-exponent, which lies within the uncertainty of the method.14 Excellent agreement is instead found with the lower temperature (293–303 K) PLP-SEC measurements by Nikitin et al.2 Experiments above 323 K were performed in the study of Nikitin et al.,8 which provide estimates of the poly-BA backbiting rate constant in xylene solvent from direct measurements of branch points in the polymer chains (called branching levels) through nuclear magnetic resonance (NMR). While the activation energy derived from their Arrhenius fit (EA = 7.8 ± 0.1 kcal mol−1) matches our calculated value, their pre-exponential factor (A = (7.4 ± 1.5) × 107 s−1) is roughly twice as large as our estimates for both bulk and xylene. As regards the comparison with theoretical rate parameters from previous studies of Yu et al. and Cuccato et al., the higher the temperature, the larger the discrepancy with respect to our results in the gas phase, even though at 310 K, our results match the ones of Yu et al.13 Overall, our results show improved agreement with the experiments compared to the results from Cuccato et al. and Yu et al. In addition, our results show that the rate constant in the gas phase has an activation energy of 2 kcal mol−1 higher with respect to the case in xylene and 1.5 kcal mol−1 higher with respect to the case in bulk. A summary of the Arrhenius parameters calculated in the gas phase and in solution is reported in Table 1.
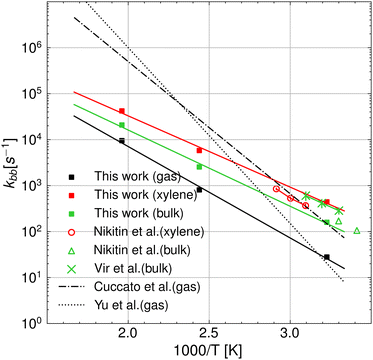 |
| | Fig. 6 Arrhenius plot of the backbiting rate constants in a vacuum and the various solvents, namely o-/m-/p-xylene, BA monomer, and water at T = 310, 410, and 510 K. The results from this work are compared with experiments2,6,8 and the theoretical predictions from ref. 12 and 13, which were obtained neglecting the presence of the solvent. | |
Table 1 Summary of the Arrhenius parameters of poly BA backbiting calculated with eqn (19). The probability γr at 410 K, which has been used to determine the Arrhenius coefficients, has been also reported
| Solvent |
γr (410 K) |
A [s−1] |
EA [kcal mol−1] |
| Gas |
6.0 × 10−3 |
6.70 × 107 |
9.100 |
| Bulk |
3.0 × 10−3 |
4.15 × 107 |
7.600 |
| Xylene |
3.7 × 10−3 |
3.36 × 107 |
7.091 |
III.C. Solvent effects on BA polymerization rate
The solvent-dependent kinetic rate coefficient of β-scission has been obtained by applying the solvent correction determined in ref. 14 to the Arrhenius parameters from Nikitin et al.3 and introduced into the kinetic model of BA polymerization detailed in Section II. In contrast, the solvent-corrected backbiting kinetic parameter reported in Table 2 is the result of first-principles calculations only (eqn (19)). Through kinetic modelling we aim at establishing whether the solvent-dependence derived from pure theory reflects the experimental trends of the BA polymerization rate in different solvents. To this end, the kinetic model has been compared with semi-batch experiments carried out in the work of Peck et al.7 and experiments performed by Mätzig et al.9 The former experiments involve BA polymerization in xylene solvent, in the presence of tert-butyl peroxyacetate (TBPA) initiator, whereas the latter consists of a thermally induced polymerization (without an initiator) in a batch reactor in various solvents. Fig. 7 shows the concentration profiles over time, resulting from the semi-batch simulations at 410 K, using the model in Table 2 (continuous lines), under three different monomer inlet flow rates, of the pseudo-species present in the mechanism, that is, the initiator (I), solvent (S), monomer (M), end-chain radical (Re), mid-chain radical (Rm) and polymer P. Because the comparison with experiments is carried out in terms of monomer conversion only, the kinetic model is rather simplified with respect to the models that can be found in the literature.3,9 For instance, the approach followed here does not allow us to distinguish the species chain length or between linear and branched polymer chains, as explained in the methods Section II. While the dependence of individual kinetic rate parameters on the chain length can be neglected, because of the dominant role of the local electronic structure, as extensively discussed in the literature,17,36,37 the overall polymerization rate may be affected by the local monomer concentration. Long chains exert a higher steric hindrance which can alter the concentration of monomer in the vicinity of the radical sites.38 Nevertheless, because in our modelling approach all chain lengths are lumped into pseudo-species, we neglect here the chain-length dependence and we focus on the overall monomer conversion as a function of temperature and solvent.
Table 2 Summary of the kinetic mechanism and corresponding Arrhenius parameters for BA polymerization. Here, two versions of the model are shown depending on the polymerization conditions. For radical polymerization in xylene solvent, solvent-specific correction factors to secondary reactivity are introduced. The solvent-dependent backbiting rate parameter is derived from eqn (19), while the β-scission coefficient in xylene is derived by applying the solvent correction from Serse et al.14 to the rate parameter in bulk from Nikitin et al.3 The Arrhenius pre-exponents followed by * have units of s−1
| No. |
Reaction name |
Reaction |
Solvent |
k (403 K) |
A [l mol−1 s−1] |
EA [kcal mol−1] |
Ref. |
| (I) |
TBPA initiator decomposition |
I → 2fI* |
Bulk |
|
6.78 × 1015* |
35.239 |
7 |
| (II) |
Initiator propagation |
M + I* → Re |
|
|
2.21 × 107 |
4.282 |
39 |
| (III) |
Thermal self-initiation |
M + M → 2Re |
Bulk |
|
1.03 × 107 |
28.947 |
9 |
| |
|
|
Xylene |
|
6.09 × 109 |
33.254 |
9, this work |
| (IV) |
Propagation |
Re + M → Re |
|
|
2.21 × 107 |
4.282 |
39 |
| (V) |
Chain transfer to monomer |
Re + M → Re + P |
|
|
2.90 × 105 |
7.799 |
40 |
| (VI) |
Tertiary propagation |
Rm + M → Re |
|
|
1.98 × 106 |
7.201 |
6 |
| (VII) |
Backbiting |
Re → Rm |
Bulk |
|
4.15 × 107* |
7.600 |
This work |
| |
|
|
Xylene |
|
3.36 × 107* |
7.091 |
This work |
| (VIII) |
β-Scission |
Rm → P + Re |
Bulk |
|
1.50 × 109* |
15.287 |
3 |
| |
|
|
Xylene |
|
7.45 × 108* |
18.301 |
3 and 14 |
| (IX) |
Termination |
Re + Re → P |
|
|
3.50 × 109 |
2.010 |
3 |
| (X) |
Termination |
Rm + Re → P |
|
|
4.50 × 108 |
3.349 |
3 |
| (XI) |
Termination |
Rm + Rm → P |
|
|
5.30 × 108 |
4.689 |
3 |
| (XII) |
Chain transfer to solvent |
Re + S → Re + P |
Xylene |
|
0.66 × 109 |
11.531 |
9 |
| (XIII) |
Chain transfer to solvent |
Rm + S → Re + P |
Xylene |
8.39 × 10−1 l mol−1 s−1 |
|
|
9 |
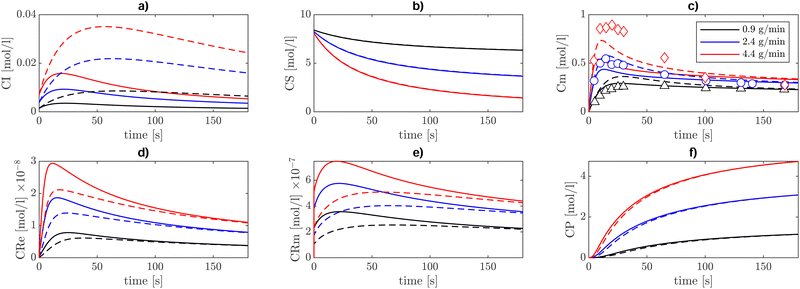 |
| | Fig. 7 Concentration profiles [mol l−1] of (a) initiator, (b) solvent, (c) monomer, (d) end chain radical, (e) mid-chain radicals, and (f) polymer. These profiles are obtained at T = 410 K in a semi-batch reactor setup, using three different monomer inlet flow rates, 0.9 g min−1 (black), 2.4 g min−1 (blue), and 4.4 g min−1 (red). The initial solvent (xylene) charge in the reactor is 194 g together with 0.014 g of the tert-butylperoxyacetate (TBPA) initiator. The comparison between experiments and model results is carried out on the monomer concentration. The continuous lines show the model results obtained with the initiator decomposition rate taken from ref. 7, whereas the dashed lines show the results with that rate parameter increased by five times. | |
The decreasing trend in monomer concentration over time is expected, as the monomer is consumed during polymerization. The rate of decrease is influenced by the monomer inlet flow rate, with higher flow rates leading to a slower decrease due to the continuous replenishment of the monomer. The tradeoff between inlet monomer flowrate and monomer consumption kinetics produces a peak in monomer concentration at the beginning of the semi-batch operation. As expected, lower inlet flowrates lead to a lower initial accumulation of monomer and a slightly lower consumption rate, whereas higher inlet flowrates result in a higher peak followed by a higher consumption rate. Model results with inlet monomer flowrates of 0.9 g min−1 and 2.4 g min−1 show an excellent agreement with the experiments both qualitatively and quantitatively. Conversely, a slight discrepancy between model predictions and experiments emerges for a monomer feed rate of 4.4 g min−1 in estimating the transient peak in concentration while the stationary concentration is correctly captured, which is in line with the findings of Peck et al.7 The source of this discrepancy could be related to the initiator kinetics (reaction I in Table 2), which is responsible for both the initial monomer accumulation, when the initiator radicals are yet to be formed, and its depletion after the peak when initiator radicals start to form. The monomer concentration profile is more sensitive to reaction I when the initiator concentration relative to monomer concentration is lower and the solvent feed rate is lower. It stands out from Table 3 that the case showing the largest discrepancy (monomer feed rate of 4.4 g min−1) corresponds to the lowest initiator to monomer ratio in the feed and without solvent reintroduction. To substantiate this observation, the sensitivity of monomer concentration profiles to the initiator decomposition (reaction I in Table 2) reaction rate has been tested by using a rate of initiator decomposition five times larger and keeping all the other rate coefficients of Table 2 unaltered. The results, reported with dashed lines in Fig. 7, show improved agreement in terms of the transient peak of monomer concentration, while preserving the steady state concentration values.
Table 3 Summary of inlet flowrates of monomer, solvent, and initiator in the semi-batch experiments
| nBuA flowrate [g min−1] |
Xylene flowrate [g min−1] |
TBPA [g min−1] |
| 0.9 |
2.3 |
0.125 |
| 2.4 |
1.1 |
0.028 |
| 4.4 |
0.0 |
0.034 |
The initiator concentration (CI) first increases until the rate of decomposition (2I → 2fI*) counterbalances its feed rate. Then, it decreases over time as it decomposes to generate radicals. In this work, the reverse reaction, namely the radical initiator recombination, is neglected. This approximation should hold since the initiator concentration always remains relatively low. The resulting initiator radical (I*) adds to the BA monomer and gets incorporated into the first ECR (Re) through the propagation reaction II shown in Table 2.
End-chain radicals are formed by propagations, namely reactions II, IV, V, and VI, by thermal self-initiation, namely reaction III, and by β-scission, reaction VIII.
Both ECR and MCR concentrations are understandably higher in the cases with a higher monomer feed rate and lower solvent feed rate. In solution polymerization, the solvent acts as a diluent, ensuring a slower but more controlled chain growth. The polymer concentration (CP), which here includes dead polymer chains of any length, steadily increases during the reaction time and higher monomer feed rates result in a higher final polymer concentration. However, within this framework, there is no indication of the morphology of the resulting polymer. Nevertheless, we can infer that branched chains should account for a relevant proportion of the final polymer because the concentration of MCRs is approximately ten times higher than ECRs (Fig. 7).
The experimental data on self-initiated polymerization by Mätzig et al.9 report the time derivative of monomer concentration, regarded as an overall polymerization rate, as a function of the instantaneous monomer concentration in the temperature range from 393.15 K to 413.15 K. This data was used in ref. 9 in conjunction with a detailed kinetic model to infer the solvent-dependent Arrhenius parameters of the thermal self-initiation and chain transfer to solvent. This analysis has been carried out for a number of solvents, including xylene. Kinetic Monte Carlo simulations performed in ref. 9 allowed the authors to validate their rate coefficients on SEC measurements of molar mass distributions and branching levels of the products. Fig. 8(a) shows how our model predictions in bulk and the experimental polymerization rates in bulk from Mätzig et al. are in excellent agreement. In addition, it stands out from Fig. 8(b) that our model prediction including the solvent corrections derived from theory for backbiting and β-scission correctly represents the variation in polymerization rate when xylene is used as the solvent by employing an activation energy of thermal self-initiation 0.5 kcal mol−1 lower than the one provided in ref. 9. Therefore, based on our theoretical calculations, we present the hypothesis that the increased polymerization rate observed in xylene could be partly caused by the solvent effects on secondary reactivity (i.e. β-scission and backbiting) and not exclusively on self-initiation. Fig. 8(c) and (d) show that the theoretical solvent corrections introduced in this work lead to different MCR to ECR molar ratios with respect to the one displayed by the kinetic Monte Carlo simulations with the detailed model of Mätzig et al. (dashed lines). While the impact of xylene solvent on that ratio is qualitatively and quantitatively similar to the detailed model results of Mätzig et al., the introduction of our calculated rate coefficients leads to a lower ratio in bulk compared to the detailed model.
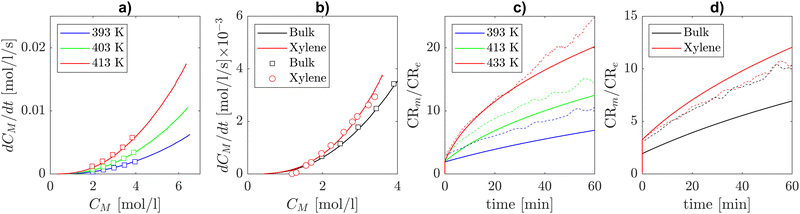 |
| | Fig. 8 Comparison between model predictions (lines) and experiments in bulk (squares) and in xylene (circles) of BA's global polymerization rate [mol l−1 s−1] against monomer concentration [mol l−1]. (a) BA's overall polymerization rate against instantaneous monomer concentration in bulk in the temperature range 393.15–413.15 K in bulk. (b) Overall BA polymerization rate in bulk and xylene solvent at T = 403.15 K. (c) Comparison between our model and the kMC simulations from Mätzig et al. in terms of MCR to ECR concentration in bulk at different temperatures. (d) Comparison between our model and the kMC simulations from Mätzig et al. in terms of MCR to ECR concentration in bulk and in xylene. | |
Sensitivity analyses performed in the batch and semi-batch reactors models show that, in both cases, the monomer concentration is influenced mainly by propagations (Re + M → Re) and intramolecular hydrogen transfer (Re → Rm), as shown in Fig. 9. This result is consistent with previous studies4 that emphasize the importance of backbiting in BA and other monomers polymerizations.41,42
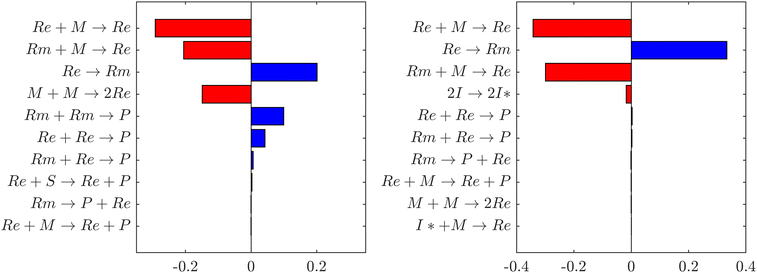 |
| | Fig. 9 Normalized time integral of dimensionless sensitivity coefficient of monomer (M) concentration with respect to the first nine most relevant reactions in the polymerization mechanism. The negative contributions (red) indicate that monomer is consumed faster than the base case, whereas positive contributions (blue) indicate a slower consumption. Left: sensitivity analysis performed in the batch thermal self-initiated polymerization in xylene solvent at 403 K. Right: sensitivity analysis in the semi-batch polymerization in xylene in the presence of TBPA initiator at 403 K. | |
The right panel of Fig. 9 shows sensitivity analysis of the monomer concentration with respect to the kinetic parameters of each reaction in the mechanism in the semi-batch reactor setup. It stands out that backbiting (Re → Rm) has the second largest contribution to monomer concentration variation over the reaction time from ref. 7 (3 hours), right after ECR propagation. The positive contribution of the backbiting rate coefficient to monomer concentration highlights the importance of the solvent correction. By incorporating this correction, which results in a lower activation energy (see Tables 1 and 2), the predicted polymerization rate accurately reflects experimental observations (Fig. 8). The left panel of Fig. 9 shows instead the sensitivity analysis on monomer concentration in the conditions of the thermal self-initiated batch polymerization in xylene solvent from ref. 9. It is shown that the thermal self-initiation rate is less sensitive than ECR propagation, tertiary propagation (Rm + M → Re + P), and backbiting (Re → Rm). This further supports our hypothesis that solvent effects on backbiting play a relevant role in the accurate modelling of polymerization rate in solution.
IV. Conclusions
In this study, we investigated the influence of solvent-induced cage effects on the intramolecular hydrogen transfer reaction in butyl acrylate radical polymerization using semi-empirical metadynamics in explicit solvent with a hybrid QM/MM approach. We have determined a theoretical methodology for computing solvent-dependent rate coefficients for the intramolecular hydrogen transfer reaction of poly-BA and incorporated them into a semi-detailed mechanistic kinetic model of BA polymerization based on previous literature.2,7,9 These solvent-dependent corrections can be derived from the projection of the time-independent PMF on the distance of the bond being formed, namely CV1 in Fig. 3, throughout the hydrogen transfer. The first correction that could be derived from the marginal PMF was the relative probability of forming the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure intermediate, which is preliminary to the hydrogen transfer reaction. This reaction emerged as a key factor in improving the agreement with the experiments compared to previous theoretical calculations,12,13 especially in terms of pre-exponential factor. The PMF profiles also provided solvation free energy corrections to the activation energy barrier, which had to be determined with the more accurate ωB97XD/def2-TZVPP in the gas phase, including the ZPE correction. Finally, PMF profiles at different temperatures were used to extrapolate a classical entropy of activation, which comes from the fully coupled and intrinsically anharmonic dynamics, complementing the frequency factor determined in the quantum harmonic TST framework. The insights gained from molecular-scale simulations are used to modify the existing kinetic mechanism of poly-butyl acrylate polymerization.2,7,9 The modified detailed kinetic model accurately predicted the experimental polymerization rates in bulk and xylene,20 supporting the validity of the solvent corrections on the backbiting and its subsequent impact on the overall polymerization kinetics. Our findings provide valuable insights in free radical polymerization processes in solution, focusing on the role of solvent-induced cage effects on backbiting. The theoretical methodology for calculating rate parameters of backbiting in vacuum and condensed phase developed here is generally applicable to other chemical processes. This approach extends beyond polymerization to investigate elementary reaction steps in solution, enabling the development of detailed mechanistic models that guide experimental interpretation and chemical reactor design.
5 ring structure intermediate, which is preliminary to the hydrogen transfer reaction. This reaction emerged as a key factor in improving the agreement with the experiments compared to previous theoretical calculations,12,13 especially in terms of pre-exponential factor. The PMF profiles also provided solvation free energy corrections to the activation energy barrier, which had to be determined with the more accurate ωB97XD/def2-TZVPP in the gas phase, including the ZPE correction. Finally, PMF profiles at different temperatures were used to extrapolate a classical entropy of activation, which comes from the fully coupled and intrinsically anharmonic dynamics, complementing the frequency factor determined in the quantum harmonic TST framework. The insights gained from molecular-scale simulations are used to modify the existing kinetic mechanism of poly-butyl acrylate polymerization.2,7,9 The modified detailed kinetic model accurately predicted the experimental polymerization rates in bulk and xylene,20 supporting the validity of the solvent corrections on the backbiting and its subsequent impact on the overall polymerization kinetics. Our findings provide valuable insights in free radical polymerization processes in solution, focusing on the role of solvent-induced cage effects on backbiting. The theoretical methodology for calculating rate parameters of backbiting in vacuum and condensed phase developed here is generally applicable to other chemical processes. This approach extends beyond polymerization to investigate elementary reaction steps in solution, enabling the development of detailed mechanistic models that guide experimental interpretation and chemical reactor design.
Data availability
All the data of this research are present in the main manuscript as well as in the ESI† within the journal.
Conflicts of interest
There are no conflicts to declare.
Appendices
Internal energy of a quantum harmonic oscillator
The energy partition function of a quantum harmonic oscillator can be written as follows:43| |
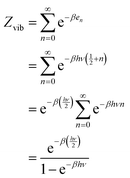 | (23) |
Let us consider an Avogadro number of quantum harmonic oscillators:
| |
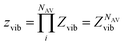 | (24) |
We define the vibrational temperature as follows:
The internal energy of a quantum harmonic oscillator is calculated as follows:
| |
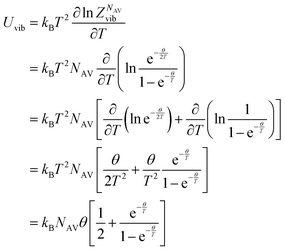 | (26) |
Where
kBNAV =
R is the universal gas constant.
Derivation of mean thermodynamic force w.r.t. the CVs
We can write the non-Boltzmann biased probability density in the collective variable space as follows:| |
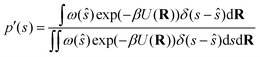 | (27) |
where ŝ ≡ s(R), R stands for the atomic coordinates and ω(ŝ) is a generic bias function. By exploiting the properties of Dirac's δ, it follows that| |
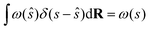 | (28) |
and therefore eqn (27) can be rewritten as follows:| |
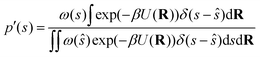 | (29) |
If we multiply and divide by the configurational integral in the unbiased ensemble Z0, it leads to the following expression:
| |
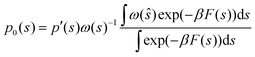 | (30) |
where we exploited the relationship between the potential of mean force
F(
s) and the configurational integral, neglecting the reference state. In metadynamics the bias function is
ω(
s) = exp(−
βV(
s)), where
V(
s) is a Gaussian-type repulsive potential.
| |
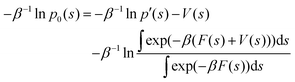 | (31) |
The LHS represents the potential of mean force (F(s)). In contrast, the mean thermodynamic force is represented by its gradient w.r.t. s as in eqn (32), assuming that the collective variables space is multi-dimensional (s).
| |
∇F(s) = −β−1∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p′(s) − ∇V(s) p′(s) − ∇V(s)
| (32) |
Eqn (32) shows that the mean force has two components, namely the gradient with respect to s of the natural logarithm of the biased probability density p′(s) and the gradient of the bias potential V(s), as reported in ref. 32.
Acknowledgements
The authors acknowledge the CINECA award HP10B98SC8 under the ISCRA initiative for the availability of high-performance computing resources and support. M. S. acknowledges funding from the ht-MATTER UKRI Frontier Research Guarantee Grant (EP/X033139/1).
References
- M. Buback, R. G. Gilbert, R. A. Hutchinson, B. Klumperman, F. D. Kuchta and B. G. Manders, et al., Critically evaluated rate coefficients for free-radical polymerization, 1. Propagation rate coefficient for styrene, Macromol. Chem. Phys., 1995, 196(10), 3267–3280 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/macp.1995.021961016.
- A. N. Nikitin, R. A. Hutchinson, M. Buback and P. Hesse, Determination of Intramolecular Chain Transfer and Midchain Radical Propagation Rate Coefficients for Butyl Acrylate by Pulsed Laser Polymerization, Macromolecules, 2007, 40(24), 8631–8641, DOI:10.1021/ma071413o.
- A. N. Nikitin and R. A. Hutchinson, Effect of Intramolecular Transfer to Polymer on Stationary Free Radical Polymerization of Alkyl Acrylates, 2, Macromol. Theory Simul., 2006, 15(2), 128–136 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/mats.200500063.
- A. N. Nikitin and R. A. Hutchinson, The Effect of Intramolecular Transfer to Polymer on Stationary Free Radical Polymerization of Alkyl Acrylates, Macromolecules, 2005, 38(5), 1581–1590, DOI:10.1021/ma048361c.
- A. B. Vir, Y. W. Marien, P. H. M. Van Steenberge, C. Barner-Kowollik, M. F. Reyniers and G. B. Marin, et al., Access to the β-scission rate coefficient in acrylate radical polymerization by careful scanning of pulse laser frequencies at elevated temperature, React. Chem. Eng., 2018, 3, 807–815 RSC . Available from: https://dx.doi.org/10.1039/C8RE00171E.
- A. B. Vir, Y. W. Marien, P. H. M. Van Steenberge, C. Barner-Kowollik, M. F. Reyniers and G. B. Marin, et al., From n-butyl acrylate Arrhenius parameters for backbiting and tertiary propagation to β-scission via stepwise pulsed laser polymerization, Polym. Chem., 2019, 10, 4116–4125 RSC . Available from: https://dx.doi.org/10.1039/C9PY00623K.
- A. N. F. Peck and R. A. Hutchinson, Secondary Reactions in the High-Temperature Free Radical Polymerization of Butyl Acrylate, Macromolecules, 2004, 37(16), 5944–5951, DOI:10.1021/ma049621t.
- A. N. Nikitin, R. A. Hutchinson, G. A. Kalfas, J. R. Richards and C. Bruni, The Effect of Intramolecular Transfer to Polymer on Stationary Free-Radical Polymerization of Alkyl Acrylates, 3 – Consideration of Solution Polymerization up to High Conversions, Macromol. Theory Simul., 2009, 18(4–5), 247–258 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/mats.200900009.
- J. Mätzig, M. Drache, G. Drache and S. Beuermann, Kinetic Monte Carlo Simulations as a Tool for Unraveling the Impact of Solvent and Temperature on Polymer Topology for Self-Initiated Butyl Acrylate Radical Polymerizations at High Temperatures, Macromol. Theory Simul., 2023, 32(4), 2300007 CrossRef . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/mats.202300007.
- R. X. E. Willemse, A. M. van Herk, E. Panchenko, T. Junkers and M. Buback, PLPESR Monitoring of Midchain Radicals in n-Butyl Acrylate Polymerization, Macromolecules, 2005, 38(12), 5098–5103 CrossRef CAS Available from: https://doi.org/10.1021/ma050198d.
- S. Hamzehlou, N. Ballard, Y. Reyes, A. Aguirre, J. M. Asua and J. R. Leiza, Analyzing the discrepancies in the activation energies of the backbiting and -scission reactions in the radical polymerization of n-butyl acrylate, Polym. Chem., 2016, 7, 2069–2077 RSC . Available from: https://dx.doi.org/10.1039/C5PY01990G.
- D. Cuccato, E. Mavroudakis, M. Dossi and D. Moscatelli, A Density Functional Theory Study of Secondary Reactions in n-Butyl Acrylate Free Radical Polymerization, Macromol. Theory Simul., 2013, 22(2), 127–135 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/mats.201200079.
- X. Yu and L. J. Broadbelt, Kinetic Study of 1,5-Hydrogen Transfer Reactions of Methyl Acrylate and Butyl Acrylate Using Quantum Chemistry, Macromol. Theory Simul., 2012, 21(7), 461–469 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/mats.201200005.
- F. Serse, A. Bjola, M. Salvalaglio and M. Pelucchi, Unveiling Solvent Effects on β-Scissions through Metadynamics and Mean Force Integration, J. Chem. Theory Comput., 2024, 20(14), 6253–6262, DOI:10.1021/acs.jctc.4c00383 . PMID:38959515.
- A. Locaspi, M. Ferri, F. Serse, M. Maestri and M. Pelucchi Chapter Two – Chemical kinetics of catalytic/noncatalytic pyrolysis and gasification of solid plastic wastes, in Towards Circular Economy: Closing the Loop with Chemical Recycling of Solid Plastic Waste, ed. D. Moscatelli and M. Pelucchi, Advances in Chemical Engineering, Academic Press, 2022, vol. 60, pp. 21–76. Available from: https://www.sciencedirect.com/science/article/pii/S0065237722000205 Search PubMed.
- A. Locaspi, M. Pelucchi, M. Mehl and T. Faravelli, Towards a lumped approach for solid plastic waste gasification: Polyethylene and polypropylene pyrolysis, Waste Manage., 2023, 156, 107–117 CrossRef CAS PubMed . Available from: https://www.sciencedirect.com/science/article/pii/S0956053X22005633.
- S. W. Benson Thermochemical Kinetics, John Wiley Sons, New York, 2nd edn, 1976 Search PubMed.
- S. Liu, S. Srinivasan, J. Tao, M. C. Grady, M. Soroush and A. M. Rappe, Modeling Spin-Forbidden Monomer Self-Initiation Reactions in Spontaneous Free-Radical Polymerization of Acrylates and Methacrylates, J. Phys. Chem. A, 2014, 118(40), 9310–9318, DOI:10.1021/jp503794j . PMID: 25188223.
- S. Srinivasan, M. W. Lee, M. C. Grady, M. Soroush and A. M. Rappe, Self-Initiation Mechanism in Spontaneous Thermal Polymerization of Ethyl and n-Butyl Acrylate: A Theoretical Study, J. Phys. Chem. A, 2010, 114(30), 7975–7983, DOI:10.1021/jp102772v . PMID: 20666544.
- J. Mätzig, M. Drache and S. Beuermann, Self-Initiated Butyl Acrylate Polymerizations in Bulk and in Solution Monitored By In-Line Techniques, Polymers, 2021, 13(12), 2021 CrossRef PubMed . Available from: https://www.mdpi.com/2073-4360/13/12/2021.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald and F. Stein, et al., CP2K: An electronic structure and molecular dynamics software package -Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103, DOI:10.1063/5.0007045.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, The General AMBER Force Field (GAFF) Can Accurately Predict Thermodynamic and Transport Properties of Many Ionic Liquids, J. Phys. Chem. B, 2015, 119(18), 5882–5895, DOI:10.1021/acs.jpcb.5b00689 . PMID: 25853313.
- S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52(2), 255–268, DOI:10.1080/00268978400101201.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519, DOI:10.1063/1.447334.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593, DOI:10.1063/1.470117.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009, DOI:10.1021/acs.jctc.7b00118 . PMID: 28418654.
- T. Laino, F. Mohamed, A. Laio and M. Parrinello, An Efficient Linear-Scaling Electrostatic Coupling for Treating Periodic Boundary Conditions in QM/MM Simulations, J. Chem. Theory Comput., 2006, 2(5), 1370–1378, DOI:10.1021/ct6001169 . PMID: 26626844.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101, DOI:10.1063/1.2408420.
- A. Barducci and M. Bonomi, Michele P. Metadynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 9(1), 826–843 Search PubMed.
- M. Bonomi, A. Barducci and M. Parrinello, Reconstructing the equilibrium Boltzmann distribution from well-tempered
metadynamics, J. Comput. Chem., 2009, 8(30), 1615–1621 CrossRef PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.100.020603.
- V. Marinova and M. Salvalaglio, Time-independent free energies from metadynamics via mean force integration, J. Chem. Phys., 2019, 151(16), 164115, DOI:10.1063/2F1.5123498.
- A. Bjola and M. Salvalaglio, Estimating Free-Energy Surfaces and Their Convergence from Multiple, Independent Static and History-Dependent Biased Molecular-Dynamics Simulations with Mean Force Integration, J. Chem. Theory Comput., 2024, 20(13), 5418–5427, DOI:10.1021/acs.jctc.4c00091 . PMID: 38913384.
- J. Kästner and W. Thiel, Bridging the gap between thermodynamic integration and umbrella sampling provides a novel analysis method:“Umbrella integration”, J. Chem. Phys., 2005, 123(14), 144104, DOI:10.1063/1.2052648.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al. Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- D. Moscatelli, M. Dossi, C. Cavallotti and G. Storti, Ab Initio Calculation of the Propagation Kinetics in Free Radical Polymerization: Chain Length and Penultimate Effects, Macromol. Symp., 2007, 259(1), 337–347 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/masy.200751338.
- S. W. Benson and J. H. Buss, Additivity Rules for the Estimation of Molecular Properties. Thermodynamic Properties, J. Chem. Phys., 1958, 29(3), 546–572, DOI:10.1063/1.1744539.
- H. Kattner and M. Buback, Propagation and Chain-Length-Dependent Termination Rate Coefficients Deduced from a Single SP–PLP–EPR Experiment, Macromolecules, 2016, 49(10), 3716–3722, DOI:10.1021/acs.macromol.6b00483.
- J. M. Asua, S. Beuermann, M. Buback, P. Castignolles, B. Charleux and R. G. Gilbert, et al., Critically Evaluated Rate Coefficients for Free-Radical Polymerization, 5, Macromol. Chem. Phys., 2004, 205(16), 2151–2160 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/macp.200400355.
- S. Maeder and R. G. Gilbert, Measurement of Transfer Constant for Butyl Acrylate Free-Radical Polymerization, Macromolecules, 1998, 31(14), 4410–4418, DOI:10.1021/ma9800515.
- D. Moscatelli, C. Cavallotti and M. Morbidelli, Prediction of Molecular Weight Distributions Based on ab Initio Calculations: Application to the High Temperature Styrene Polymerization, Macromolecules, 2006, 39(26), 9641–9653, DOI:10.1021/ma061291k.
- M. Dossi, G. Storti and D. Moscatelli, Relevance of backbiting and beta-scission reactions in the free radical polymerization of Acrylonitrile, Macromol. Symp., 2010, 289(1), 119–123 CrossRef CAS . Available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/masy.200900013.
- P. W. Atkins and J. De Paula Elements of Physical Chemistry, Oxford University Press, 2017. Available from: https://books.google.it/books?id=bCyhDQAAQBAJ Search PubMed.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Matteo Salvalaglio
*a,
Matteo Salvalaglio b and
Matteo Pelucchi
b and
Matteo Pelucchi *a
*a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 backbiting.
5 backbiting.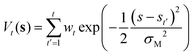
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pbt(s) − ∇Vt(s)
pbt(s) − ∇Vt(s)
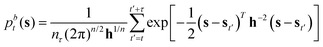
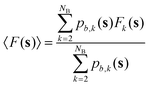
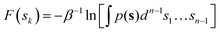
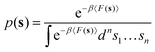
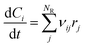
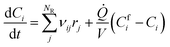
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is the inlet volumetric flowrate in the semi-batch reactor, rij is the jth reaction rate involving species i, NR is the total number of reactions and νij is the stoichiometric coefficient of species i in the jth reaction. The resulting systems of ordinary differential equations (ODE) has been solved with the stiff ODE solver ode15s implemented in MATLAB 2024b. By defining the right hand side of eqn (8) and (9) as a generic function of the concentrations of species i and the vector of parameters k, the previous systems of differential equations can be generalized as in eqn (10)
is the inlet volumetric flowrate in the semi-batch reactor, rij is the jth reaction rate involving species i, NR is the total number of reactions and νij is the stoichiometric coefficient of species i in the jth reaction. The resulting systems of ordinary differential equations (ODE) has been solved with the stiff ODE solver ode15s implemented in MATLAB 2024b. By defining the right hand side of eqn (8) and (9) as a generic function of the concentrations of species i and the vector of parameters k, the previous systems of differential equations can be generalized as in eqn (10)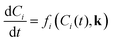
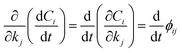
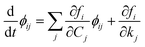
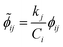
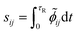
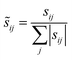
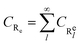
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring conformation, whereas 9–10 Bohrs represent the ECR's linear conformation and 2 Bohrs the MCR. As expected, the MCR is more stable than the ECR by ∼2 kcal mol−1 because tertiary carbon radicals are generally more stable than secondary carbon radicals. These equilibrium conformations are affected by the solvent in which the equilibrium C5–H distance associated with the 1
5 ring conformation, whereas 9–10 Bohrs represent the ECR's linear conformation and 2 Bohrs the MCR. As expected, the MCR is more stable than the ECR by ∼2 kcal mol−1 because tertiary carbon radicals are generally more stable than secondary carbon radicals. These equilibrium conformations are affected by the solvent in which the equilibrium C5–H distance associated with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure is approximately 0.5 Bohr lower compared to vacuum conditions. This indicates that the viscous forces between the reacting fragment and the solvent are producing a steric cage effect on the folded chain, which bolsters reactivity. Conversely, the ECR's linear conformation is more elongated in water (see Section S2 of the ESI†) compared to the other cases, which could be caused by hydrogen bonding stretching the polymer chains. On the other hand, the repulsive interactions between the aromatic rings of xylene and the BA carbonyl groups result in a tighter ring structure, which stands out from Fig. 4 where the free energy well associated with the ring state is wider in xylene compared to the bulk. This suggests that the radical carbon C5 and the hydrogen that is being transferred are kept closer in xylene, further facilitating the hydrogen transfer.
5 ring structure is approximately 0.5 Bohr lower compared to vacuum conditions. This indicates that the viscous forces between the reacting fragment and the solvent are producing a steric cage effect on the folded chain, which bolsters reactivity. Conversely, the ECR's linear conformation is more elongated in water (see Section S2 of the ESI†) compared to the other cases, which could be caused by hydrogen bonding stretching the polymer chains. On the other hand, the repulsive interactions between the aromatic rings of xylene and the BA carbonyl groups result in a tighter ring structure, which stands out from Fig. 4 where the free energy well associated with the ring state is wider in xylene compared to the bulk. This suggests that the radical carbon C5 and the hydrogen that is being transferred are kept closer in xylene, further facilitating the hydrogen transfer.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure within the reactant ensemble of configurations and the consecutive hydrogen transfer, as was previously suggested by Yu et al.13 As regards the hydrogen transfer step, harmonic TST is applied considering the ground state (0 K) potential energy and vibrational frequencies of the reactive configurations found with the semi-empirical metadynamics sampling and introducing quantum mechanical corrections, namely the zero-point energy (ZPE) and Eckart tunneling. We chose as the reactant state the 1
5 ring structure within the reactant ensemble of configurations and the consecutive hydrogen transfer, as was previously suggested by Yu et al.13 As regards the hydrogen transfer step, harmonic TST is applied considering the ground state (0 K) potential energy and vibrational frequencies of the reactive configurations found with the semi-empirical metadynamics sampling and introducing quantum mechanical corrections, namely the zero-point energy (ZPE) and Eckart tunneling. We chose as the reactant state the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure (indicated here as r), which is known from previous studies to be the most stable precursor to BA intramolecular hydrogen transfer.12 In addition, by performing simulations at different temperatures, a fully coupled classical entropy of activation ΔS≠cl is estimated from the thermodynamic relationship in eqn (17).
5 ring structure (indicated here as r), which is known from previous studies to be the most stable precursor to BA intramolecular hydrogen transfer.12 In addition, by performing simulations at different temperatures, a fully coupled classical entropy of activation ΔS≠cl is estimated from the thermodynamic relationship in eqn (17).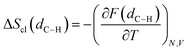
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring from the linear ECR configuration shows a negative entropy change of the same magnitude. Furthermore, it stands out that the enthalpy of activation estimated from the GFN1 xTB for the hydrogen transfer is 10.0 ± 0.4 kcal mol−1, and the enthalpy change associated with the rotation of the ECR leading to the 1
5 ring from the linear ECR configuration shows a negative entropy change of the same magnitude. Furthermore, it stands out that the enthalpy of activation estimated from the GFN1 xTB for the hydrogen transfer is 10.0 ± 0.4 kcal mol−1, and the enthalpy change associated with the rotation of the ECR leading to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring is 1.8 ± 0.4 kcal mol−1.
5 ring is 1.8 ± 0.4 kcal mol−1.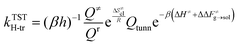
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring conformation over the reactant ensemble of configurations. This correction factor, which we call γr, arises naturally from the TST expression of the rate constant considering the probability of forming the reactive ring configuration (r) within the reactant ensemble of configurations (R). This probability is formally expressed as the ratio between partition functions, as shown in eqn (19). The calculation of this probability is carried out by integrating the free energy profiles over the range of C5–H distances equal to the maximum amplitude of a quantum harmonic oscillator (eqn (21)) at temperature T, centered on the equilibrium distance of the 1
5 ring conformation over the reactant ensemble of configurations. This correction factor, which we call γr, arises naturally from the TST expression of the rate constant considering the probability of forming the reactive ring configuration (r) within the reactant ensemble of configurations (R). This probability is formally expressed as the ratio between partition functions, as shown in eqn (19). The calculation of this probability is carried out by integrating the free energy profiles over the range of C5–H distances equal to the maximum amplitude of a quantum harmonic oscillator (eqn (21)) at temperature T, centered on the equilibrium distance of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring state (d0).
5 ring state (d0).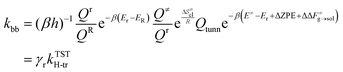
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring equilibrium configuration with a quadratic potential.
5 ring equilibrium configuration with a quadratic potential.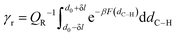
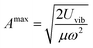
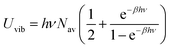
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring state, which is the precursor to the hydrogen transfer transition state, for quantum tunneling effects and the free energy of solvation, the agreement between theory and experiments is significantly improved compared to our gas phase results as well as previous theoretical results.12,13 This allows us to derive intrinsic kinetic parameters of the intramolecular hydrogen transfer (or backbiting) from pure theory in a temperature range that is hardly accessible with state-of-the-art experimental techniques,2 without substantial loss in accuracy. In fact, our results in bulk match the experimental PLP-SEC rate measurements in the temperature range 303–323 K obtained in bulk by Vir et al.6 in terms of activation energy, 7.61 kcal mol−1 against 7.32 kcal mol−1, respectively, whereas a factor of 2 discrepancy is observed in the pre-exponent, which lies within the uncertainty of the method.14 Excellent agreement is instead found with the lower temperature (293–303 K) PLP-SEC measurements by Nikitin et al.2 Experiments above 323 K were performed in the study of Nikitin et al.,8 which provide estimates of the poly-BA backbiting rate constant in xylene solvent from direct measurements of branch points in the polymer chains (called branching levels) through nuclear magnetic resonance (NMR). While the activation energy derived from their Arrhenius fit (EA = 7.8 ± 0.1 kcal mol−1) matches our calculated value, their pre-exponential factor (A = (7.4 ± 1.5) × 107 s−1) is roughly twice as large as our estimates for both bulk and xylene. As regards the comparison with theoretical rate parameters from previous studies of Yu et al. and Cuccato et al., the higher the temperature, the larger the discrepancy with respect to our results in the gas phase, even though at 310 K, our results match the ones of Yu et al.13 Overall, our results show improved agreement with the experiments compared to the results from Cuccato et al. and Yu et al. In addition, our results show that the rate constant in the gas phase has an activation energy of 2 kcal mol−1 higher with respect to the case in xylene and 1.5 kcal mol−1 higher with respect to the case in bulk. A summary of the Arrhenius parameters calculated in the gas phase and in solution is reported in Table 1.
5 ring state, which is the precursor to the hydrogen transfer transition state, for quantum tunneling effects and the free energy of solvation, the agreement between theory and experiments is significantly improved compared to our gas phase results as well as previous theoretical results.12,13 This allows us to derive intrinsic kinetic parameters of the intramolecular hydrogen transfer (or backbiting) from pure theory in a temperature range that is hardly accessible with state-of-the-art experimental techniques,2 without substantial loss in accuracy. In fact, our results in bulk match the experimental PLP-SEC rate measurements in the temperature range 303–323 K obtained in bulk by Vir et al.6 in terms of activation energy, 7.61 kcal mol−1 against 7.32 kcal mol−1, respectively, whereas a factor of 2 discrepancy is observed in the pre-exponent, which lies within the uncertainty of the method.14 Excellent agreement is instead found with the lower temperature (293–303 K) PLP-SEC measurements by Nikitin et al.2 Experiments above 323 K were performed in the study of Nikitin et al.,8 which provide estimates of the poly-BA backbiting rate constant in xylene solvent from direct measurements of branch points in the polymer chains (called branching levels) through nuclear magnetic resonance (NMR). While the activation energy derived from their Arrhenius fit (EA = 7.8 ± 0.1 kcal mol−1) matches our calculated value, their pre-exponential factor (A = (7.4 ± 1.5) × 107 s−1) is roughly twice as large as our estimates for both bulk and xylene. As regards the comparison with theoretical rate parameters from previous studies of Yu et al. and Cuccato et al., the higher the temperature, the larger the discrepancy with respect to our results in the gas phase, even though at 310 K, our results match the ones of Yu et al.13 Overall, our results show improved agreement with the experiments compared to the results from Cuccato et al. and Yu et al. In addition, our results show that the rate constant in the gas phase has an activation energy of 2 kcal mol−1 higher with respect to the case in xylene and 1.5 kcal mol−1 higher with respect to the case in bulk. A summary of the Arrhenius parameters calculated in the gas phase and in solution is reported in Table 1.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ring structure intermediate, which is preliminary to the hydrogen transfer reaction. This reaction emerged as a key factor in improving the agreement with the experiments compared to previous theoretical calculations,12,13 especially in terms of pre-exponential factor. The PMF profiles also provided solvation free energy corrections to the activation energy barrier, which had to be determined with the more accurate ωB97XD/def2-TZVPP in the gas phase, including the ZPE correction. Finally, PMF profiles at different temperatures were used to extrapolate a classical entropy of activation, which comes from the fully coupled and intrinsically anharmonic dynamics, complementing the frequency factor determined in the quantum harmonic TST framework. The insights gained from molecular-scale simulations are used to modify the existing kinetic mechanism of poly-butyl acrylate polymerization.2,7,9 The modified detailed kinetic model accurately predicted the experimental polymerization rates in bulk and xylene,20 supporting the validity of the solvent corrections on the backbiting and its subsequent impact on the overall polymerization kinetics. Our findings provide valuable insights in free radical polymerization processes in solution, focusing on the role of solvent-induced cage effects on backbiting. The theoretical methodology for calculating rate parameters of backbiting in vacuum and condensed phase developed here is generally applicable to other chemical processes. This approach extends beyond polymerization to investigate elementary reaction steps in solution, enabling the development of detailed mechanistic models that guide experimental interpretation and chemical reactor design.
5 ring structure intermediate, which is preliminary to the hydrogen transfer reaction. This reaction emerged as a key factor in improving the agreement with the experiments compared to previous theoretical calculations,12,13 especially in terms of pre-exponential factor. The PMF profiles also provided solvation free energy corrections to the activation energy barrier, which had to be determined with the more accurate ωB97XD/def2-TZVPP in the gas phase, including the ZPE correction. Finally, PMF profiles at different temperatures were used to extrapolate a classical entropy of activation, which comes from the fully coupled and intrinsically anharmonic dynamics, complementing the frequency factor determined in the quantum harmonic TST framework. The insights gained from molecular-scale simulations are used to modify the existing kinetic mechanism of poly-butyl acrylate polymerization.2,7,9 The modified detailed kinetic model accurately predicted the experimental polymerization rates in bulk and xylene,20 supporting the validity of the solvent corrections on the backbiting and its subsequent impact on the overall polymerization kinetics. Our findings provide valuable insights in free radical polymerization processes in solution, focusing on the role of solvent-induced cage effects on backbiting. The theoretical methodology for calculating rate parameters of backbiting in vacuum and condensed phase developed here is generally applicable to other chemical processes. This approach extends beyond polymerization to investigate elementary reaction steps in solution, enabling the development of detailed mechanistic models that guide experimental interpretation and chemical reactor design.
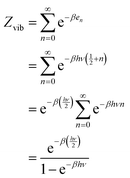
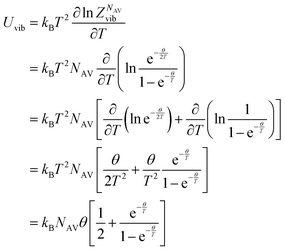
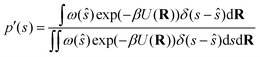
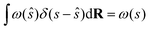
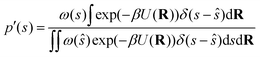
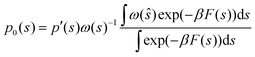
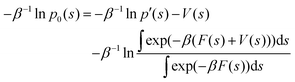
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p′(s) − ∇V(s)
p′(s) − ∇V(s)






