Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimizing cation–π force fields for molecular dynamics studies of competitive solvation in conjugated organosulfur polymers for lithium–sulfur batteries†
Diptesh
Gayen
 a,
Yannik
Schütze‡
a,
Yannik
Schütze‡
 b,
Sébastien
Groh
b,
Sébastien
Groh
 a and
Joachim
Dzubiella
a and
Joachim
Dzubiella
 *a
*a
aApplied Theoretical Physics – Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, 79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
bTheoretical Chemistry, Institute of Chemistry and Biochemistry, Freie Universität Berlin, 14195 Berlin, Germany
First published on 18th February 2025
Abstract
Lithium–sulfur (Li/S) batteries are emerging as a next-generation energy storage technology due to their high theoretical energy density and cost-effectiveness. π-Conjugated organosulfur polymers, such as poly(4-(thiophene-3-yl)benzenethiol) (PTBT), have shown promise in overcoming challenges such as the polysulfide shuttle effect by providing a conductive framework and enabling sulfur copolymerization. In these cathodes, cation–π interactions significantly influence Li+ diffusion and storage properties in π-conjugated cathodes, but classical OPLS-AA force fields fail to capture these effects. This study employs a bottom-up approach based on density functional theory (DFT) to optimize the nonbonded interaction parameters (OPLS-AA/corr.), particularly for the Li+–π interactions with the PTBT polymer. Following prior work, we used an ion-induced dipole potential to model the cation–π interactions. The impact of the solvent on the PTBT monomers was examined by computing the potential of mean force (PMF) between PTBT monomers and Li+ ions in both explicit and implicit solvents using the Boltzmann inversion of probability distributions close to room temperature. In the implicit solvent case, the magnitude of the binding free energy decreased with increasing dielectric constant, as the dominant electrostatics scaled with the dielectric constant. In contrast, in the explicit solvent case, considering the mixtures of organic solvent DME and DOL, the binding free energy shows minimal dependence on solvent composition due to the competing interaction of TBT and Li+ with the solvent molecules. However, increasing salt concentration decreases the binding free energy due to Debye–Hückel screening effects. In general, this work suggests that the optimized parameters can be widely used in the simulation of polymers in electrolytes for the Li/S battery to enhance the representation of cation–π interactions for a fixed charge force field.
1 Introduction
The lithium–sulfur (Li/S) battery is a promising electrochemical storage system due to its high theoretical energy density and cost-effectiveness.1,2 However, several challenges hinder its practical applications, including the electronic and ionic insulating nature of both sulfur and the discharge product lithium sulfide (Li2S), the formation and shuttling of dissolved lithium polysulfides species between the anode and the cathode, and complicated compositional and structural changes. To address these issues, the scientific community has proposed several strategies, including (i) developing novel cathodes,3 anodes, binders, and electrolytes; and (ii) advancing the understanding of Li/S redox chemistries.4,5 One promising approach involves the confinement of the polysulfides directly via the covalent bonding to the cathode host material. Due to its ability to (i) suppress the polysulfide effect and (ii) reduce the volumetric expansion/contraction during charge/discharge, conjugated organosulfur polymers are notable candidates for high-performance Li/S batteries.6Poly(4-(thiophene-3-yl)benzenethiol) (PTBT) is a flexible conjugated organosulfur-based polymer envisioned as a potential candidate to be used as a carbon-additive-free cathode in Li/S batteries.7–9 In PTBT, the polythiophene main chain forms a highly conducting framework. In contrast, the benzenethiol side chain facilitates copolymerization with sulfur chains, resulting in the crosslinked organosulfur polymer (S/PTBT). According to our previous study,8 among the two possible regioregularities – HH–TT and HT–HT (H: head, T: tail) – we considered the HT–HT regioregularity because it is predominantly found in the experimental studies, as also supported by the simulation results. The monomeric unit of PTBT, 4-(thiophene-3-yl)benzenethiol (TBT), consists of a benzenethiol group and a thiophene group. These structural features contribute to its electronic properties, as TBT contains a total five π-bonds: two from the thiophene group and three from the benzenethiol group. These π-bonds arise from the unhybridized p-orbitals on each carbon atom, which are parallel to each other and overlap side-by-side. This overlap creates a delocalized π-electron system above and below the plane of the rings. These π-electron systems can interact with the lithium ions from the electrolytes, through the non-bonded cation–π interactions.10,11
Recently, it was shown, using a combination of experimental techniques and numerical methods such as molecular dynamics (MD) and density functional theory (DFT) applied to equivalent polymer systems, that cation–π interactions can, in addition to being critical for the diffusion of Li+-ions, enhance the lithium storage property12 and facilitate lithium ions to stay into the polymer network.13 However, the cation–π interaction, an ion-induced dipole-type interaction,10 is not explicitly included in conventional non-polarizable fixed-charge force fields.14 Therefore, the binding energy of ions to aromatic molecules is usually underestimated in force-field approaches compared to DFT predictions.15–17 To overcome this issue, different routes were explored to introduce ion-induced dipole in classical force fields.14,17–22 For instance, Huang et al.22 employed an empirical approach to calculate cation–π interaction energies in proteins. In that approach, the interaction energy between a cation and a π-bonded molecule is represented by an empirical equation with six free parameters, which depend on two variables: the distance r and the orientation angle θ. Then, the free parameters are optimized based on the benchmark calculations from B3LYP/6-311+G(d,p) theory. In another study, for metal ions, Li et al.14 proposed to model the ion-induced dipole by enriching the force field functional form with an electrostatic ion-induced dipole −Cij4/rij4 term, where Cij4, which represents the interaction strength, is a fitting parameter for the interactions between specific sites i and j. Such a correction for the ion-induced dipole (ID) interaction leading to a Lennard-Jones plus a correction term (LJ-ID) accurately captures the binding energy obtained from DFT calculations. Following that study, for protein–ligand systems, Turupcu et al.15 corrected the force field for the cation–π interactions by using the LJ-ID. Differently, for protein–ligand systems, Liu et al.23 used the nonbonded FIX (NBFIX) feature of the CHARMM force field to capture the cation–π interaction. They selectively optimized the LJ parameters for specific atom pairs, while all other LJ parameters are obtained from standard combining rules. They referenced the quantum mechanical/molecular mechanics (QM/MM) potential energy of mean force data in an aqueous solution to refine the NBFIX parameters.
In our study, we used LJ-ID, similar to Li et al.,14 to capture the interaction strength of the binding energy profiles. Additionally, the van der Waals diameters for specific atom pairs were considered as free parameters, similar to Liu et al.,23 since the LJ-ID alone could not accurately capture the location of the minimum binding energy in the previous study.15 The consideration of van der Waals diameters is justified since the pairwise additive force fields with basic combination rules do not represent polarization, charge transfer, and covalent bonding effects.16,23–25 However, in contrast to the study by Liu et al.,23 we did not alter the interaction strength parameter ε of the LJ. Therefore, in addition to Cij4, the van der Waals diameters σij are considered as fitting parameters for the interactions between sites i and j to accurately capture both the strength and location of the minimum binding energy. For parameterization, we introduced a novel approach compared to previous studies, which were mostly limited to a specific one-dimensional bottom-up approach. Instead, a two-dimensional (2D) bottom-up approach is applied, where the 2D binding energy landscape between the molecules and Li+-ion is calculated in the gas phase using DFT, and used as a reference for the fitting of the force field needed in all-atom MD simulations. This binding energy landscape not only reveals the global minimum of the binding energy but also highlights potential pathways for ion hopping.
This study aims (i) to enrich the existing classical force field to accurately capture the cation–π interaction in the gas phase, and (ii) to examine the effects of the cation–π interaction in the solvated environment. With the optimized parameters in hand, we estimate the binding behavior of Li+ ions and TBT and TriTBT (an oligomer of three TBT molecules) systems in solutions and compare these results with those obtained in the gas phase. We consider two solvation models in the MD: the “implicit solvent model”, and the “explicit solvent model”. The implicit solvent model represents the solvent as a continuum through the dielectric constant, while the explicit solvent model includes discrete solvent molecules. For the solution, dioxolane (DOL) and dimethoxyethane (DME) are used as solvents, and lithium bis(trifluoromethane)sulfonimide (LiTFSI) is used as salt. LiTFSI contains Li+ cation and TFSI− anion.
This paper is organized as follows: in Section 2, we provide a detailed description of the methods, including the gas-phase density functional theory and molecular statics (MS) calculations setup, parameterization strategy, and verification procedure. This section also covers the implicit and explicit solvation models in classical MD and the procedures used to estimate the binding free energy in the solution environment. We then present and discuss the binding (free) energies and optimized parameters for benzene, benzenethiol, and thiophene in the gas phase, and “free TBT monomer”, and “PTBT constituent monomer” both in the gas phase and the solvated environments in Section 3. Finally, Section 4 contains our concluding remarks.
2 Methods
Density functional theory and molecular statics (MS) were performed to parametrize and validate the force field, and molecular dynamics was performed to simulate cation–π interactions in the solvated environment close to room temperature. GAMESS26 and LAMMPS27 were used for DFT, and MS and MD, respectively. In both MS and MD, force fields for TBT and TriTBT were taken from our previous studies.7,82.1 Gas phase: density functional theory and molecular statics
All reference binding energies for parameterization were calculated in the gas phase using DFT. The optimized geometries and binding energies of the systems were obtained using the B3LYP/6-311++G(d,p) level of theory with Grimm's dispersion corrections28 and with consideration of counterpoise correction for basis set superpositions errors (BSSE).29 The BSSE corrections were considered to ensure the accuracy of the calculated binding energies by accounting for artificial stabilization arising from basis set limitations. The B3LYP functional30 has been widely used for studying cation–π interactions due to its balance between accuracy and computational efficiency.18,31 Different exchange–correlation functions rescale the binding energy by 10–15%;32 however, the qualitative shape of the binding energy profiles is not altered by the choice of the exchange–correlation functional form.33 Therefore, we did not modify these functions to calculate the open parameters. Previous studies have demonstrated that higher-level exchange–correlation functions, such as ωB97X-D/6-311++G(d,p), produce results that are comparable to those obtained with B3LYP/6-311++G(d,p). However, B3LYP/6-311++G(d,p) is less computationally demanding,18,31 making it an ideal choice for calculating interaction energies for numerous configurations. Therefore, we opted to use the B3LYP/6-311++G(d,p) level of theory for all our calculations. The binding energy calculation procedure is discussed in the parameterization strategy and verification section.The gas phase simulations were performed in MS by considering a large simulation box without periodic boundary conditions. Due to the non-periodic boundaries, long-range interactions were considered by employing a high cutoff radius of approximately 5 nm for the Coulombic interactions. The cut-off radius for LJ interactions was set at 1 nm. Uncorrected (OPLS-AA) and corrected (OPLS-AA/corr.) force field parameters are provided in the ESI.† Energy minimization was carried out using a conjugate gradient algorithm. Relative energy and force of 10−4 and 10−4 kcal mol−1 Å−1, respectively, were used for the convergence criteria.
2.2 Parameterization strategy and verification
The modified total non-bonded interaction between a cation, i, and an atom from an aromatic molecule, j, is expressed as a sum of three terms given by: | (1) |
 | (2) |
For the parameterization of the potential, we fitted the binding energy landscape obtained from MS, ΔEMS(x,y,zmin) (see eqn (4)), with the reference binding energy obtained from DFT, ΔEDFT(x,y,zmin) (see eqn (3)), by tuning some of the interactions between carbon/sulfur from the aromatic molecule and Li+.
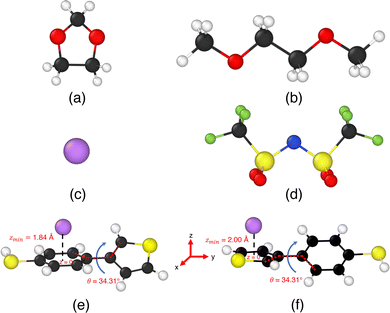
In particular, we treated the interaction between carbon atoms (CX, where X = CA/CW/CS – carbon atoms based on their bonding environments) and Li+, and between sulfur (S) atoms and Li+ as free parameters. Therefore, we optimized 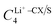 and σLi+–CX/S. For benzene and benzenethiol, we optimized “CA” atom type of carbon (see Fig. S1(a) for benzene and Fig. S1(b) for benzenethiol, ESI†). For thiophene, we optimized “CS”, “CW”, and “S” atom types (see Fig. S1(c), ESI†). For both the free-standing TBT monomer (“free TBT monomer”) and the TBT monomer as it exists within the PTBT polymer (“PTBT constituent monomer”) we optimized “CA”, “CS”, “CW”, and “S” atom types (see Fig. S1(d), ESI†).
and σLi+–CX/S. For benzene and benzenethiol, we optimized “CA” atom type of carbon (see Fig. S1(a) for benzene and Fig. S1(b) for benzenethiol, ESI†). For thiophene, we optimized “CS”, “CW”, and “S” atom types (see Fig. S1(c), ESI†). For both the free-standing TBT monomer (“free TBT monomer”) and the TBT monomer as it exists within the PTBT polymer (“PTBT constituent monomer”) we optimized “CA”, “CS”, “CW”, and “S” atom types (see Fig. S1(d), ESI†).
To calculate the binding energy profile in DFT, the aromatic molecule (mol) was first optimized and fixed in the z = 0 plane. Then, the single-point energy of the aromatic molecule, Emol(x,y,0), was calculated. Subsequently to optimize the aromatic molecule and Li+ complex, a single Li+ ion was positioned at various imaginary grid points across the x–y plane at a distance of z = 3 Å, while the aromatic molecule remained fixed in the z = 0 plane. The imaginary grid points were spaced at intervals of 0.1 Å, ensuring fine sampling. The scanning region covered the maximum width and breadth of the aromatic molecule, thus exploring the entire spatial extent of the molecule.
The Li+ ion was allowed to optimize its position along the z-coordinate only. At the optimized position, zmin, the single-point energy of the aromatic molecule and Li+ complex, ELi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol(x,y,zmin), was calculated. The binding energy landscape in DFT, ΔEDFT(x,y,zmin), is defined as follows,
mol(x,y,zmin), was calculated. The binding energy landscape in DFT, ΔEDFT(x,y,zmin), is defined as follows,
ΔEDFT(x,y,zmin) = ELi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol(x,y,zmin) − Emol(x,y,0) − ELi+(x,y,zmin), mol(x,y,zmin) − Emol(x,y,0) − ELi+(x,y,zmin), | (3) |
ΔEMS(x,y,zmin) = ELi+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol(x,y,zmin) − Emol(x,y,0), mol(x,y,zmin) − Emol(x,y,0), | (4) |
To obtain the free parameters, Cij4 and σij, we minimized the objective function L2 given by:
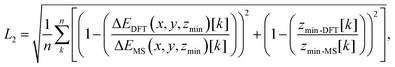 | (5) |
For the analysis of the effect of the choice of grid points used to fit the energy surface σij and Cij4, we employed two distinct sets of surrounding points around the energy minimum. In the first set (setup-A), we considered n = 9 points, consisting of the energy minimum and 8 surrounding grid points that were distributed symmetrically in its vicinity. In the second set (setup-B), we expanded the grid to include n = 25 points, comprising the energy minimum and 24 surrounding points.
The 2D binding energy landscapes were used to fit the potential. To validate the parameterization method, we calculated the binding energy profile along a path perpendicular to the molecular plane using the optimized parameters. This path is aligned along the z-direction and centered at (xmin,ymin), where xmin and ymin represent the position of the minimum binding energy in the x–y plane. The point (xmin,ymin) was determined from the 2D binding energy landscape. The distance z was systematically varied from z = 0 to z = 6 Å in increments of 0.1 Å. At each point along this path, the binding energy was calculated using DFT and MS. For the calculations in the MS framework, both corrected and uncorrected force fields were considered. For all the systems, we estimated the value of the binding energy, ΔE(zmin), by identifying the global minimum of the binding energy profile at zmin.
2.3 Simulations of the solution phase at room temperature
To analyze the effects of the DFT parameterization in the solution phase, we calculated the free energy profiles (as a function of radial distance) between groups of the oligomers and the Li+ ion in classical MD at T = 300 K. Specifically, we examined TBT and 2 TBTs in the implicit solvent model, and TBT and TriTBT in the explicit solvent model.The TBT monomer was chosen to investigate the free energy profiles in solution, from which the energetic part of the binding energy was directly compared to the binding energy obtained in the gas phase. In contrast, 2 TBTs were selected to determine whether any sandwiched structure forms and to assess whether cation–π interactions can prevent the formation of these structures, which might enhance the Li+ transport through the polymer network.13,34 Finally, TriTBT, a simple oligomer consisting of three TBT monomers, was chosen to apply the force field correction from the “PTBT constituent monomer”.
The non-bonded interactions were treated by a combination of LJ-ID and electrostatics potentials, with the electrostatics interactions being decomposed in short- and long-range contributions. The LJ-ID and the short-range Coulomb potentials were truncated at 1 and 0.8 nm, respectively. The long-range electrostatic interactions were evaluated with the particle–particle–particle–mesh (PPPM) method with a desired relative error in forces of 10−4 kcal (mol Å)−1. All bonds and angles were constructed with harmonic potentials, and the OPLS style was considered for dihedrals. The SHAKE algorithm was employed for all hydrogen bond constraints.
The implicit solvent model treats the solvent as a continuous, homogeneous, and isotropic medium characterized by a static dielectric constant, ε.35 Due to the clustering effect of Li+ and TFSI− ions36 (see Fig. S4, ESI†), our study focuses on varying the dielectric constant within two simplified systems: (Ii) a single TBT with one LiTFSI, and (IIi) 2 TBTs with one LiTFSI, where superscript i represents the implicit solvent environment. We examined three dielectric constants of 10.6, 6.0, and 8.0, representative of DME, DOL, and a mixture of DME and DOL37 (see Table 1). The force field for Li+ and TFSI− ions are based on Dang et al.38 and Lopes et al.,39 respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DOL (1
DOL (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)), and (c) ε = 6.0 (pure DOL). The superscript i represents the implicit solvent environment
1)), and (c) ε = 6.0 (pure DOL). The superscript i represents the implicit solvent environment
| System | Salt | TBT | Dielectric constant | |
|---|---|---|---|---|
| Li+ | TFSI− | ε | ||
| Ii a/b/c | 1 | 1 | 1 | 10.6/8.0/6.0 |
| IIi a/b/c | 1 | 1 | 2 | 10.6/8.0/6.0 |
Simulations were performed in the canonical ensemble where the temperature was maintained by a Langevin thermostat40 using a damping parameter of 100 fs. Since the origin of the correction term −Cij4/rij4 is electrostatics, hence, for our continuous, homogeneous, and isotropic dielectric medium, the correction term is scaled by the respective dielectric constant of the medium, ε.
| System | Salt | Solvent | Solvent composition | ||
|---|---|---|---|---|---|
| Li+ | TFSI− | DME | DOL | x | |
| C salt: 0.5 M | |||||
| Ie a | 25 | 25 | 500 | 0 | 0.00 |
| Ie b | 43 | 43 | 450 | 550 | 0.55 |
| Ie c | 20 | 20 | 0 | 500 | 1.00 |
| C salt: 1.0 M | |||||
| IIe a | 62 | 62 | 500 | 0 | 0.00 |
| IIe b | 99 | 99 | 450 | 550 | 0.55 |
| IIe c | 46 | 46 | 0 | 500 | 1.00 |
| C salt: 1.5 M | |||||
| IIIe a | 116 | 116 | 500 | 0 | 0.00 |
| IIIe b | 168 | 168 | 450 | 550 | 0.55 |
| IIIe c | 83 | 83 | 0 | 500 | 1.00 |
Force fields for DME, DOL, and LiTFSI, were taken from Park et al.,37 which accurately reproduce experimental values for density, the conductivity of the bulk electrolytes, and diffusion coefficients for Li+ and TFSI− across various electrolyte concentrations. In contrast to the implicit solvent model, the correction term Cij4 is not scaled by the dielectric constant as all solvent molecules are explicitly resolved.
The production simulations were performed in the NPT ensemble at constant pressure P and constant temperature T of 1 bar and 300 K, respectively, in a cubic box with periodic boundary conditions. The timestep was fixed at 2 fs. The temperature was maintained by a Berendsen thermostat with a time constant of 0.1 ps. The pressure was controlled by a Parrinello-Rahman barostat with a coupling constant of 0.5 ps.
2.4 Free energy in solution
For estimating the free energy in solution, we simulated the system at a finite temperature, thus accounting for both the internal energy and the entropic contributions. As a result, the calculated energy is referred to as the free energy rather than the binding energy, and its minimum is identified as the binding free energy.The overall free energy between the oligomers and the Li+ ion was determined without following any specific pathways. We instead performed an extensive sampling of the systems to obtain well-converged radial density profiles (RDPs), ρij(r), between the center of mass (COM) of oligomer i and ion j as a function of their distance r. To have a well-defined reference value of the free energy, the RDPs were normalized by the bulk density, ρ0, defining the dimensionless distribution function gij(r) = ρij(r)/ρ0. The bulk density was estimated from the density profile near the boundaries of the simulation box, where the profile converges and significant fluctuations are absent. The free energy, ΔFij(r), as a function of distance, also called the potential of mean force (PMF) along the radial direction, was then obtained using a standard Boltzmann inversion:
ΔFij(r) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(gij(r)). ln(gij(r)). | (6) |
A significantly negative ΔFij(r) close to the oligomer indicates the binding and adsorption of groups j to i. For large distances r, the PMF goes to zero because of the normalization. We then estimate the binding free energy, ΔF(rmin), by locating the global minimum of the PMF at the corresponding distance rmin.
3 Results and discussion
3.1 Binding energy profiles in the gas phase
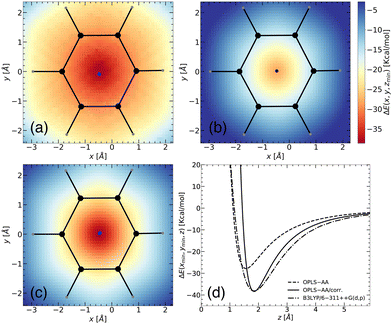
To validate the corrected OPLS/corr. force field, we first investigated the interaction between benzene and Li+ using B3LYP/6-311++G(d,p) (dash-dot line in Fig. 2(d)). Our calculations revealed a minimum binding energy of −38.12 kcal mol−1 at a distance of 1.84 Å. The finding is in agreement with previously reported studies, which have found values −36.12 kcal mol−1 at a distance 1.84 Å for B3LYP/6-311++G(d,p),41 −35.35 kcal mol−1 for B3LYP/6-31G++(d,p),42 −38.10 kcal mol−1 for B3LYP/6-31G(d,p),41 and −38.18 kcal mol−1 for ωB97X-D/6-311++G(d,p) at a distance 1.9 Å.15 An experimental binding energy of −38.30 kcal mol−1 further supports our finding.18 In contrast, with the OPLS-AA force field, the binding energy is −27.83 kcal mol−1 at a distance of 1.57 Å (dashed line in Fig. 2(d)). This comparison reveals a substantial difference of more than 10 kcal mol−1 energy and a shift of 0.27 Å in the binding distance. Using the optimized OPLS-AA/corr. parameters, as a prediction, we accurately captured the magnitude and location of the binding energy concerning the B3LYP/6-311++G(d,p) level. Furthermore, the long-range behavior of the binding energy profile along the specific path was also well captured, except for deviations of 1–2 kcal mol−1. However, for the short-range region, this prediction indicated an overly stiff potential. This deviation is reasonable since the model is parameterized using 2D binding energy landscapes, where each point corresponds to the minimum energy and the minimum distance between the conjugated molecule and the Li+ ion, rather than being based on a distance-dependent binding energy profile.
The quality of the fitting was tested by increasing the number of points (setup-A vs. setup-B). While setup-A leads to a minimum binding energy of −38.28 kcal mol−1 at 1.84 Å with L2 = 0.0043, a minimum binding energy of −38.67 kcal mol−1 at 1.84 Å with L2 = 0.0086 was obtained with setup-B. Though the fitting with setup-B captures the surrounding region more accurately, it deviated slightly from the minimum energy and L2. So setup-A was chosen to balance accuracy and computational efficiency. Detailed parameters for Cij4 and σij for both setups are reported in ESI† (see Table S1).
Similar to benzene, we observed significant binding energy discrepancies for benzenethiol (15 kcal mol−1) and thiophene (19 kcal mol−1) when comparing the OPLS-AA force field with the B3LYP/6-311++G(d,p) theory (see Table 3). As a result, we applied a similar correction approach for these molecules (see ESI,† Fig. S2(a)–(c) for thiophene and Fig. S3(a)–(c) for benzenethiol). For benzenethiol, ‘CA’ type carbons were used as a free parameter, excluding ‘SH’ since it lies outside the π-system, while for thiophene, ‘CW’, ‘CS’, and ‘S’ atoms were included as they are within the π-conjugation. The refined parameters and minimum binding energies of benzenethiol and thiophene are reported in Tables 3 and 4, respectively. In the case of benzenethiol, the binding energy is consistent with the calculated binding energy for benzene. In addition, both the minimum binding energy and its location obtained for thiophene align well with a previous study, which reported a binding energy of −37.34 kcal mol−1.43 Minimum binding energy and its location are summarized in Table 3.
| π-System | B3LYP/6-311++G(d,p) | OPLS-AA | OPLS-AA/corr. | |||
|---|---|---|---|---|---|---|
| ΔE(zmin) | z min | ΔE(zmin) | z min | ΔE(zmin) | z min | |
| Benzene | −38.12 | 1.84 | −27.83 | 1.57 | −38.28 | 1.84 |
| Thiophene | −36.15 | 1.94 | −18.87 | 1.72 | −35.95 | 1.94 |
| Benzenethiol | −37.92 | 1.86 | −22.14 | 1.64 | −38.00 | 1.86 |
| “Free TBT monomer” | ||||||
| Zone-1 | −41.13 | 1.84 | −29.63 | 1.55 | −41.58 | 1.86 |
| Zone-2 | −37.77 | 1.97 | −30.15 | 1.75 | −38.50 | 2.00 |
| Zone-3 | −39.82 | 2.00 | −34.93 | 1.62 | −39.46 | 2.01 |
| “PTBT constituent monomer” | ||||||
| Zone-1 | −41.66 | 1.82 | −26.54 | 1.55 | −42.42 | 1.81 |
| Zone-2 | −38.63 | 1.99 | −19.54 | 1.88 | −40.18 | 1.96 |
| Zone-3 | −42.68 | 2.00 | −14.94 | 2.04 | −42.41 | 1.98 |
| π-System | Type | Atom | C ij 4 | σ ij | L 2 |
|---|---|---|---|---|---|
| Benzene | |||||
| CA | Li+ | 104.69 | 2.69 | 0.0043 | |
| Thiophene | |||||
| CW | Li+ | 161.81 | 2.71 | 0.004 | |
| CS | Li+ | 161.81 | 2.71 | 0.004 | |
| S | Li+ | 190.24 | 2.76 | 0.004 | |
| Benzenethiol | |||||
| CA | Li+ | 139.92 | 2.70 | 0.001 | |
| “Free TBT monomer” | |||||
| CA | Li+ | 65.28 | 2.80 | 0.05 | |
| CW | Li+ | 68.09 | 2.87 | 0.05 | |
| CS | Li+ | 68.09 | 2.87 | 0.05 | |
| S | Li+ | 78.28 | 2.76 | 0.05 | |
| “PTBT constituent monomer” | |||||
| CA | Li+ | 59.78 | 2.67 | 0.02 | |
| CW | Li+ | 114.88 | 2.72 | 0.02 | |
| CS | Li+ | 114.88 | 2.72 | 0.02 | |
| S | Li+ | 110.26 | 2.65 | 0.02 | |
Overall, the optimized force field parameters successfully improved the accuracy of the binding energy profiles at the equilibrium distances, demonstrating the effectiveness of our approach in capturing the cation–π interactions. Given that our model performs well for small molecules, we aim to extend its application to larger molecules such as “free TBT monomer” and “PTBT constituent monomer”.
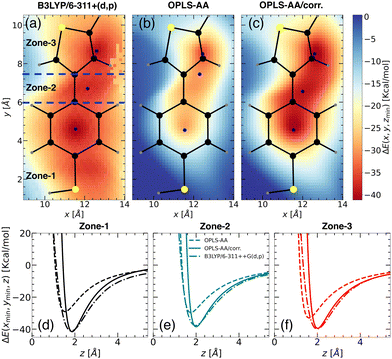
Upon closer look, we identified the local minimum in each region and inferred the presence of energy maximum between zone-1 and zone-2, as well as between zone-2 and zone-3, as depicted in Fig. 3(a). These maxima could represent pathways for Li+ ion hopping. Now comparing the DFT binding energy profile with that obtained from the OPLS-AA force field (see Fig. 3(b)), discrepancies emerged in order of 5–10 kcal mol−1. Compared to the binding energy surface obtained by DFT for which the lowest and highest minimum binding energies were found in zone-1 and zone-2, respectively, the OPLS-AA force field predicted the lowest and highest minimum binding energies in zone-3 and zone-1, respectively. A similar observation concerning the location of the minimum binding energies in each zone is valid as well. To rectify these disparities, we applied corrections to the σi–Li+ and 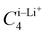 parameters, where i represents “CA,” “CW,” “CS,” and “S” atom types. The resulting parameters are reported in Table 4. Incorporating these corrections into the uncorrected force field produced an updated binding energy profile, OPLS-AA/corr., as illustrated in Fig. 3(c). As a result of the fitting procedure, the lowest and highest minimum binding energies are located in zone-1 and zone-2, respectively, in agreement with the DFT prediction. In addition, the location of the minimum binding energy in each zone along the z-axis is correctly captured by OPLS-AA/corr. Furthermore, the binding energy surface not only captures the minimum binding energy but also provides an accurate representation of the surrounding binding energy landscape. However, since only a few points (9 for each zone) around the minimum were considered for fitting the energy profile, we are unable to capture the profile away from the minima, as observed in Fig. 3(c).
parameters, where i represents “CA,” “CW,” “CS,” and “S” atom types. The resulting parameters are reported in Table 4. Incorporating these corrections into the uncorrected force field produced an updated binding energy profile, OPLS-AA/corr., as illustrated in Fig. 3(c). As a result of the fitting procedure, the lowest and highest minimum binding energies are located in zone-1 and zone-2, respectively, in agreement with the DFT prediction. In addition, the location of the minimum binding energy in each zone along the z-axis is correctly captured by OPLS-AA/corr. Furthermore, the binding energy surface not only captures the minimum binding energy but also provides an accurate representation of the surrounding binding energy landscape. However, since only a few points (9 for each zone) around the minimum were considered for fitting the energy profile, we are unable to capture the profile away from the minima, as observed in Fig. 3(c).
For a quantitative comparison and also for validation, we calculated the binding energy profiles perpendicular to the minimum energy plane for each TBT zone using the updated parameters (Fig. 3(d) and (e)), with results summarized in Table 3. Compared to individual systems, binding energies significantly increased in the TBT structure due to cooperative effects. Zone-1 shows an increase to −41.13 kcal mol−1, compared to −37.92 kcal mol−1 in the standalone benzenethiol (see Fig. 3(d)). Similarly, zone-3's binding energy rose to −37.77 kcal mol−1 from −36.15 kcal mol−1 in isolated thiophene (see Fig. 3(f)). This enhancement aligns with prior studies,32,45 where larger alkyl substituents or ring expansions were shown to increase binding energies due to enhanced dispersion and electrostatic interactions.
Although the validation of the binding energy with experimental data was performed for the benzene–Li+ complex, the individual binding affinities for TBT and its oligomer with Li+ are not currently available in the literature, which limits the validation of the force field with respect to experimental data. However, the corrected force field is validated by calculating the binding energy profiles – which were not included in the fitting database – with OPLS-AA/corr. parameters along a specific pathway and comparing those to their DFT counterparts.
Accurately simulating the binding behavior of PTBT polymer presented the challenge of accounting for various planes and orientations, that complicated a straightforward two-dimensional representation. To overcome this, the hydrogen atoms at the α-positions (2, 5) of the thiophene ring were replaced by methyl groups (–CH3), as described by Schütze et al. Consequently, we adopted a CH3–TBT–CH3 reference structure within our DFT framework. The CH3–TBT–CH3 structure, while maintaining neutrality, effectively mimics the adjacent aromatics carbons bonded to the thiophene, offering a more representative model of the PTBT polymer. However, for the molecular dynamics simulations, the force field parameters for such a system are unknown. Therefore, we have used the “PTBT constituent monomer” (see Fig. 4(b)), identified as a neutral unit in our previous study,7 as the system to compare with the CH3–TBT–CH3 reference system. Like TBT, the CH3–TBT–CH3 molecule is not a planar structure. First, we relaxed the molecule with B3LYP/6-311G++(d,p) level theory. In the relaxed structure, the benzenethiol molecule makes 46.82° angle with CH3–thiophene–CH3 molecule. Therefore, we placed the benzenethiol molecule in the x–y plane, with the CH3–thiophene–CH3 molecule oriented at a 46.82° angle relative to the x–y plane. In this orientation, the left CH3 group is away from the x–y plane, and the right CH3 group is towards the x–y plane.
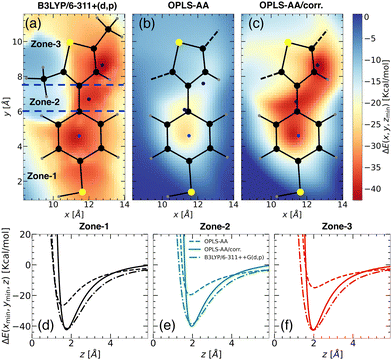 | ||
| Fig. 4 Binding energy landscapes of the “PTBT constituent monomer” and a Li+ ion calculated using (a) DFT profile with B3LYP/6-311++G(d,p) for CH3–TBT–CH3 molecule, (b) MS with OPLS-AA force field, and (c) MS with updated OPLS-AA/corr. force field. Similar to the “free TBT monomer” (refer to Fig. 3), the z-coordinate was minimized at different x, y points to determine the binding energy. The profiles are categorized into three zones: zone-1, zone-2, and zone-3 (see panel (a)), with color intensity representing the magnitude of the binding energy. Blue points indicate the locations of minimum energy. Predicted binding energy curves ΔE(xmin,ymin,z) for (d) zone-1, (e) zone-2, and (f) zone-3, are displayed for B3LYP/6-311++G(d,p) (dash-dot lines), OPLS-AA (dashed lines), and OPLS-AA/corr. (solid lines). | ||
Initially, we employed the B3LYP/6-311++G(d,p) functional form to calculate the 2D binding energy landscape for CH3–TBT–CH3, as depicted in Fig. 4(a). The overall binding energy profile is quite similar to that of the “free TBT monomer” (Fig. 3(a)), except for the region near the CH3. As the left CH3 molecule extends out of the x–y plane, it results in a positive binding energy due to the repulsion between the Li+ ion and hydrogen atoms from the CH3 group. However, this repulsion does not affect our parameterization calculation, as we considered only the points close to the minimum binding energy.
For the MS force field simulations, we calculated the energy profiles for the “PTBT constituent monomer”, using both OPLS-AA and OPLS-AA/corr. force fields. The energy profile for OPLS-AA (Fig. 4(b)) significantly differs from the DFT profile, especially in the zone-2 and zone-3 regions. Consequently, the binding energies in zone-2 and zone-3 decrease from −30.15 kcal mol−1 and −34.93 kcal mol−1 (as observed in “free TBT monomer”) to −19.54 kcal mol−1 and −14.94 kcal mol−1, respectively. This difference is due to the different charge distribution in zone-3.
Similar to the “free TBT monomer” case, we applied the corrections to the “CA”, “CW”, “CS” and “S” atom types as reported in Table 4. These corrections significantly improved the binding energy landscape, ensuring it closely resembles the DFT-derived binding energy landscape. The effectiveness of our approach is evident when comparing Fig. 4(a) with Fig. 4(c), showcasing a notable consistency between the two energy landscapes.
Fig. 4(d)–(f) illustrate the binding energy profiles along the axis perpendicular to the plane of the “PTBT constituent monomer” in different zones, comparing results from the OPLS-AA, OPLS-AA/corr., and B3LYP/6-311++G(d,p) methods. The “PTBT constituent monomer” is not completely planar, as the benzene and thiophene rings lie in different planes. For these calculations, the molecule was rotated such that the z = 0 plane aligns with the specific zone. In Fig. 4(d), the z-axis is perpendicular to the plane of the benzene ring for zone-1. In Fig. 4(e) and (f), the z-axis is perpendicular to the benzene ring in zone-2 and the thiophene ring in zone-3, respectively.
In each zone, the binding energies obtained using the OPLS-AA method deviate significantly from the reference B3LYP/6-311++G(d,p) method. The OPLS-AA/corr. method shows a significant improvement in aligning both the magnitude and location of the minimum energy points. These improvements highlight that with the parameterization method, we can not only capture the binding energy and its location for the small molecule, but we can also apply the parametrization strategy for complex molecules.
3.2 Free energy profiles in solvated environments
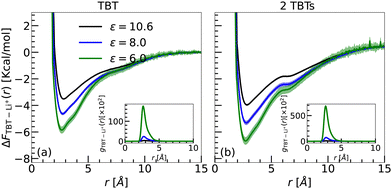
To investigate the cation–π interactions in solution, we employed two solvent models: implicit and explicit. Comprehensive details of the systems, computational setups, and methodologies are outlined in Sections 2.3.1 and 2.3.2.Sys. Ii a/b/c: one TBT with one LiTFSI salt. We examined the interaction between a single TBT molecule and one LiTFSI salt pair under three different dielectric constants, ε = 10.6, 8.0, and 6.0. The correction term, Cij4, is scaled with the dielectric constant. As a consequence, one would expect that the energetic contribution to the free energy between the Li+ ion and the TBT system is given by the binding energy calculated in the gas phase scaled by the dielectric constant.
To calculate the free energy between the TBT monomer and Li+, we first computed the RDPs between the COM of the TBT monomer and the Li+ ion (see inset of Fig. 5(a)). The RDPs provide insights into the spatial distribution of Li+ ions around the monomer's COM. For all dielectric constants, only the first coordination shell is visible in the RDPs. Beyond this point, the RDPs decrease with the distance and converge to a bulk value. The maximum of the first coordination shell is located between 2.66 Å to 2.81 Å. As the dielectric constant decreases, the location of the maximum shifts to shorter distances, indicating an increase in the interaction strength between the TBT monomer and Li+ ion. Furthermore, the magnitude of the first peak increases as the dielectric constant of the medium decreases, suggesting that the Li+ ion experiences stronger binding with the TBT monomer in a medium with lower dielectric constants.
The free energy profiles are shown in Fig. 5(a). The profiles exhibit a similar shape to the energy profiles obtained in the gas phase, as presented in Fig. 3 and 4. As summarized in Table 5, the global minimum of the free energy decreases with the lowering of the dielectric constant. Furthermore, since the binding free energy remains negative around the minimum, the ability of the Li+ ion to bind to TBT is conserved while scaling the correction terms of the interatomic potential by the dielectric constant.
| System | ΔF(rmin) | r min | ΔF(rmin) | r min | ΔF(rmin) | r min |
|---|---|---|---|---|---|---|
| ε = 10.6 (a) | ε = 8.0 (b) | ε = 6.0 (c) | ||||
| TBT(Ii) | −3.51 | 2.81 | −4.63 | 2.76 | −5.85 | 2.66 |
| 2 TBTs(IIi) | −3.95 | 2.86 | −5.31 | 2.86 | −6.67 | 2.86 |
We now argue that the free energies obtained in the implicit solvent are consistent with the 0 K binding energies calculated in the gas phase, provided the dielectric screening, as well as thermal (entropic) effects, are accounted for. Since the energetic contribution to the free energy in the solvated case is dominated by the electrostatic interactions, one can estimate the energetic contribution to the free energy by a simple electrostatic screening of the binding energy in the gas phase. For instance, considering ΔE ≈ −40 kcal mol−1 for TBT in the gas phase and ε = 6.0, the energetic contribution to the free energy in the implicit solvent is approximately ΔE/ε = −6.6 kcal mol−1. Furthermore, the translational entropy of a particle in a large (box) volume V is reduced by kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(v0/V) when particles move from V into a small volume v0. If one considers the rough order of v0 ≃ 1 nm3 as the volume of the first solvation shell, the entropic contribution to the binding free energy is reduced by approximately −1.9 kcal mol−1.
ln(v0/V) when particles move from V into a small volume v0. If one considers the rough order of v0 ≃ 1 nm3 as the volume of the first solvation shell, the entropic contribution to the binding free energy is reduced by approximately −1.9 kcal mol−1.
By combining the energetic contribution with the entropy loss, the binding free in the solution phase is about −4.7 kcal mol−1, which is in good agreement with the calculated value of ΔF = −5.8 kcal mol−1 obtained in the implicit solvent. The same reasoning can be applied for ε = 8.0 and ε = 10.6, resulting in binding free energies of −3.0 kcal mol−1 and −1.8 kcal mol−1 for ε = 8.0 and ε = 10.6, respectively, which compare well with the simulated value (ΔF = −4.6 kcal mol−1 and −3.5 kcal mol−1 for ε = 6.0 and ε = 8.0, respectively).
Sys. IIi a/b/c: two TBTs with one LiTFSI salt. We also investigated the effect of implicit solvation on the interaction between 2 TBTs and a single Li+ ion. Similar to system Ii a/b/c, we calculated the radial density profile between the COM of each TBT and the Li+ ion. The reported RDP is an average over the two individual RDPs calculated for the COMs of the two TBTs.
The RDPs, as shown in the inset of Fig. 5(b), closely resemble those obtained with the Sys. Ii setup (inset of Fig. 5(a)). The primary difference is an increased peak height of the first solvation shell in the Sys. IIi setup, indicating a stronger interaction. This enhancement suggests that the Li+ ion binds more strongly in the Sys. IIi setup, as it can simultaneously interact with both TBTs, thereby strengthening its binding ability compared to the Sys. Ii. Therefore the binding free energies per TBT monomer for Sys. IIi setup (2 TBT) are higher than the Sys. Ii setup (1 TBT) (Fig. 5(a)). Also, the minimum of the free energy decreases with decreasing the dielectric constant as summarized in Table 5. These results confirm that Li+–π interactions are stronger than the π–π interactions, causing Li+ ion to insert itself between the π–π bonds of benzene–benzene and thiophene–thiophene.13
In summary, the magnitude of the binding free energy in the implicit solvent is consistent with the magnitude of the binding energy in the gas phase considering the dielectric screening of the medium as well as entropic effects. Moreover, the magnitude of the binding free energy can be tuned by altering the dielectric constant of the medium, providing a means to control and tune the interaction strength between the TBT monomer and Li+ ion. However, a direct comparison of the predicted binding free energies for TBT and its oligomer in solution to the experiment is very difficult, because the latter is hard to measure. In the future, we plan to connect to well-controlled experiments, e.g., simple adsorption of the Li+ ions at the TBT or PTBT cathode – in a dilute polymer solution or dense electrodes44 – with which one could estimate the binding energies.
The distribution of the anion (TFSI−) around the TBT and 2 TBTs setup, shown in the ESI† (Fig. S7), is similar to that of Li+ but with lower magnitude. The peak in the anion distribution occurs at approximately 5 Å from the center of mass (COM) of TBT, further away than for Li+, indicating a weaker interaction in comparison to the cation–π interaction and the formation of a significant dipolar salt ion-pair structure.
Sys. Ie a/b/c, IIe a/b/c, and IIIe a/b/c: TBT and TriTBT in different solvent compositions with fixed salt concentration. The free energy profiles, ΔFTBT–Li+(r), between Li+ ions and TBT as well as the RDPs, gTBT–Li+(r), are given in Fig. 7(a) for a fixed salt concentration of 1.5 M (TBT – IIIe a/b/c) and varying solvent composition (see Fig. S5(a) and S6(a) of the ESI† for different salt concentration). The same information is plotted in Fig. 7(c) for the interaction between TriTBT and Li+ ions.
The analysis of the RDPs uncovered the presence of two binding sites located at approximately 2.52 Å and 3.03 Å relative to the TBT's COM. These binding sites are associated with the benzene and thiophene components of the TBT molecule as revealed by the gas-phase analysis. By integrating the RDPs up to the first solvation shell, the coordination number of Li+ ions binding to the TBT molecule increases with the solvent composition shift from pure DME to pure DOL (increasing x), as exemplified in Fig. 6. Such a trend is similar to what is already reported for the implicit solvent environment. The analysis of the MD trajectories further revealed that while the Li+ ions constantly switch between the binding sites, the presence of the first solvation shell prevents them from going away from the TBT molecule. Similarly, Li+ ions from the bulk cannot penetrate the first solvation layer of the solvent molecule and thus bind to the TBT molecule. As a consequence, there is a depletion of salt in the first solvation layer of solvent molecules corresponding to a high energy barrier for Li+ to escape from the vicinity of the TBT molecule. Notably, this energy barrier is modified by approximately 10% when the solvent composition shifts from pure DME to pure DOL. Away from the TBT molecule, the RDPs smoothly converge to a bulk value.
Finally, we report binding free energies from the global minima in Table 6. Unlike the binding free energy obtained for the implicit solvent that revealed a dependency on solvent composition, no significant variation in binding free energy with changes in solvent composition, independently of the salt concentration, was found for the explicit solvent. A part of this discrepancy may be attributed to the radial dependency of the dielectric constant relative to the TBT's center of mass (COM) in the explicit solvent, in contrast to the uniform dielectric constants assumed in the implicit model. The radial dependency arises from the complex interplay between TBT, Li+, and solvent molecules. As reported by Chanbum et al.,37 Li+ interacts more strongly with DME than with DOL, while our previous work7 shows that TBT interacts more strongly with DOL than with DME. This indicates a competition between TBT and Li+ for solvent interactions. However, a detailed quantification of the radial dielectric profile near TBT lies beyond the scope of this study and may be worth studying in future investigations.46
| System | ΔF(rmin) | r min | ΔF(rmin) | r min | ΔF(rmin) | r min |
|---|---|---|---|---|---|---|
| C salt | x = 0.00 (a) | x = 0.55 (b) | x = 1.00 (c) | |||
| TBT | ||||||
| 0.5 M (Ie) | −2.80 | 2.78 | −2.94 | 2.78 | −3.14 | 3.03 |
| 1.0 M (IIe) | −2.11 | 2.78 | −2.20 | 3.03 | −2.60 | 3.03 |
| 1.5 M (IIIe) | −1.85 | 3.03 | −1.91 | 3.03 | −2.30 | 3.03 |
| TriTBT | ||||||
| 0.5 M (Ie) | −2.62 | 2.52 | −2.53 | 3.02 | −3.35 | 2.78 |
| 1.0 M (IIe) | −2.01 | 2.52 | −2.22 | 2.52 | −2.26 | 3.54 |
| 1.5 M (IIIe) | −1.66 | 1.63 | −1.90 | 2.52 | −1.95 | 2.27 |
When considering TriTBT, although the binding free energy is independent of the solvent composition, and independently of the salt concentration, the free energy profiles have significant differences compared to the ones obtained for TBT. Assuming the binding energy surface in the solvated environment is the same as in the gas phase, a total of 18 binding sites (6 per TBT monomer) are possible for TriTBT, which can be reduced to 12 due to symmetry. The analysis of the RDPs for TriTBT revealed the presence of only 5–6 peaks distributed uniformly between 2 Å and 10 Å from the TriTBT's COM (see Fig. 7(c)). Additionally, due to the hopping of Li+ ions between different binding sites, the RDPs for TriTBT exhibit broader distributions compared to the TBT case. This hopping behavior results in a more distributed energy landscape. Although TriTBT also presents an energy barrier, it is lower than that observed for TBT. Specifically, the energy barrier is reduced for the pure DOL case (x = 1.00) (Fig. S6(b) and (d), ESI†), as already observed in TBT since the first solvation layer is less compact around the TriTBT than the one around TBT. Furthermore, the free energy profile up to the maximum barrier displays a step-like formation, allowing Li+ ions to jump from one binding site to another and eventually escape the energy barrier. This finding suggests that such a mechanism in a large polymer structure can facilitate Li+ ion transport, potentially enhancing battery performance.
In summary, for the explicit solvent system at a fixed salt concentration, no significant difference in binding free energy between Li+ and TBT/TriTBT is observed with varying solvent composition. This can be attributed to the competing interactions between TBT, Li+, and solvent molecules.7,37 However, compared to the implicit solvent model, a steep energy barrier is observed in the explicit solvent system, likely due to the competition between cation–π interactions and the solvation structure.
Sys. (Ie a, IIe a, IIIe a), (Ie b, IIe b, IIIe b), and (Ie c, IIe c, IIIe c): TBT and TriTBT in different salt concentrations with fixed solvent composition. To investigate the effect of varying salt concentration on the binding behavior of TBT and TriBT oligomers, we fixed the solvent composition at x = 0.55 (Ie b, IIe b, IIIe b) and analyzed the systems across three different salt concentration: 0.5, 1.0, and 1.5 M. First, we calculated the RDPs for TBT (see inset Fig. 7(b)) and TriTBT (see inset Fig. 7(d)) for three different salt concentrations: 0.5 M (dashed line), 1.0 M (solid line), and 1.5 M (dash-dotted line). For both cases, as the salt concentration increases, the height of the first maximum peak decreases. This reduction in peak height should be attributed to the increased electrostatic Debye–Hückel screening due to the higher concentration of Li+ ions. When more salt is added to the solution, the additional Li+ ions and corresponding anions create an ionic atmosphere that screens the electrostatic interactions between the Li+ ions and the conjugated π-system of the polymer. A similar trend was observed for x = 0.00 (see inset of Fig. S5(b) and (d), ESI†) and x = 1.00 (see inset of Fig. S6(b) and (d), ESI†).
The magnitude of the binding free energy decreases with increasing salt concentration, as shown in Fig. 7(b) for TBT and Fig. 7(d) for TriTBT. This indicates that, due to the screening effect, Li+ ions bind loosely to the oligomer as the salt concentration increases. For the TBT case, we found the lowest binding free energy to be −2.94 kcal mol−1 at a salt concentration of 0.5 M, while for the TriTBT case, it was −2.53 kcal mol−1.
Interestingly, in the case of x = 1.00 (DOL only) (see Fig. S6(b) and (d), ESI†), the energy barriers are significantly lower for all salt concentrations compared to other solvent compositions, in both TBT and TriTBT cases. This observation is consistent with a previous study, which showed that in pure DME and pure DOL solutions, Li+ ions bind more closely and strongly to DME than to DOL.37 As a result, in the presence of DOL, Li+ ions are pushed towards the oligomer, and due to cation–π interactions, they are strongly attracted towards the oligomer, leading to significantly lower energy barriers compared to other solvent compositions.
In summary, for the explicit solvent systems at a fixed solvent composition, the magnitude of the binding free energy decreases as the salt concentration increases, with a difference of 1–1.5 kcal mol−1 observed between 0.5 M and 1.5 M salt concentrations. Overall, these observations indicate that the binding and transport properties of Li+ ions in the TBT and TriTBT oligomer are influenced by both solvent compositions and salt concentrations, providing valuable insights for optimizing electrolyte compositions in battery applications.
4 Conclusions
Incorporating cation–π interactions into classical fixed-charge force fields has historically posed challenges.15,47,48 To address this, we adopted the methodologies of Li et al.14,49 for incorporating ion-induced dipole interactions into the LJ potential to model cation–π interactions, which we refer to as the LJ-ID potential. Using this approach, we optimized the free parameters of the induced dipole interactions through a unique bottom-up strategy. This process began with the calculation of the reference binding energy landscape using DFT theory. We then optimized the free parameters of the LJ-ID potential by comparing the MS simulation binding energies with DFT results.To verify our bottom-up parameterization method, we first applied it to simple systems, including benzene, thiophene, and benzenethiol. After successfully parameterizing the cation–π interactions for these systems, we extended our model to more complex systems, such as the “free TBT monomer” and the “PTBT constituent monomer”. With this bottom-up approach, we can parameterize not only the simple organic molecules but also polymer monomers. Additionally, this model seamlessly integrated with the fixed-charge OPLS-AA force field. However, the limitation of the optimized force field is that it might not be fully transferable to all configurations and geometries. As a fixed-charge non-polarizable force field, it is efficient and can be used for upscaling to larger systems. However, as the parameters are based on minimal energy conditions in the gas phase, inaccuracies may occur for dense and highly stressed polymers. For systems close to the benchmark, it is expected that the OPLS-AA/corr. force field will perform better than the uncorrected one.
To analyze the parametrization in the solution phase, we calculated the binding free energies of TBT and its oligomers with Li+ in both implicit and explicit solvent environments. For the implicit solvent model, the magnitude of the binding free energy decreases with increasing dielectric constant in both the single TBT and two TBT setups. This indicates that the binding free energy can be tuned by altering the dielectric constant of the medium. Such tunability allows for the adjustment of binding affinity based on the desired solvent environment, offering flexibility in optimizing interactions for battery applications.
Furthermore for a single TBT setup, with a simplistic model, we estimated the entropy loss due to the binding and calculated the binding free energy by considering the energetic contribution as the dielectric scaled binding energy in gas phase. The binding free energies from the simulation and calculated values were in good agreement. This agreement suggests that using this simplified model and knowledge of the binding energy in gas phase, we can estimate the binding free energy in the case of the implicit solvent model. Additionally, in the case of a simple system involving two TBT molecules and a single Li+ ion, we found out that the cation–π interaction hinders the π–π stacking, and therefore facilitates the formation of π–cation–π structures.
In the explicit solvent simulations, we investigated three solvent compositions and three salt concentrations for both TBT and TriTBT oligomers. At a fixed salt concentration, variations in solvent composition resulted in only minor changes in binding free energy, attributed to the competing interactions among TBT, Li+, and solvent molecules.7,37 In contrast, increasing the salt concentration consistently reduced the binding free energy, likely due to Debye–Hückel screening effects.
By incorporating the ion-induced dipole interaction through the −Cij4/rij4 term, we successfully capture cation–π interactions within a classical fixed-charge force field. To further optimize force fields, one of the modern solutions could involve creating a hybrid machine learning (ML) potential by coupling a traditional molecular mechanics (MM) force field with a ML potential – similar to the ML/MM method50,51 analogous to the QM/MM approach.52 In this scenario, the ML potential would numerically model the cation–π interaction for both short and the long ranges, rather than a predefined functional form, while the remaining interaction would be calculated using the traditional MM force field, such as OPLS-AA. Nevertheless, the advancement allows for accurate simulations of structure and transport in complex cathode systems, such as polymer networks (PTBT and S/PTBT) and electrolytes for Li/S battery materials. Of interest is also the electrode–electrolyte interface to better understand interfacial electrostatic, adsorption, and diffusion behavior.53,54 Furthermore, with the same electrolyte system, one may use the optimized force field for a covalent organic framework (COF) structure,55 which has a similar kind of molecular environment to that of the TBT molecule.56
Abbreviations
| Li/S | Lithium–sulfur |
| PTBT | Poly(4-(thiophene-3-yl)benzenethiol) |
| S/PTBT | PTBT polymer with sulfur chain |
| TBT | 4-(Thiophene-3-yl)benzenethiol |
| TriTBT | An oligomer with 3-TBT monomer |
| DOL | 1,3-Dioxolane |
| DME | 1,2-Dimethoxyethane |
| LiTFSI | Lithium bis(trifluoromethane)sulfonimide |
| DFT | Density functional theory |
| MD | Molecular dynamics |
| MS | Molecular statics |
| NPT | Isothermal–isobaric ensemble |
| LJ | 12-6 Lennard-Jones potential |
| LJ-ID | LJ-ion-induced dipole interactions |
| OPLS-AA | All-atom optimized potentials for liquid simulations |
| OPLS-AA/corr. | OPLS-AA with potential with correction |
| RDPs | Radial density profiles |
| PMF | Potential of mean force |
| B3LYP | Becke, 3-parameter, Lee–Yang–Parr |
| 6-311++G(d,p) | Triple-split valence basis set with diffuse and polarization functions |
| BSSE | Basis set superpositions errors |
| PPPM | Particle–particle–particle–mesh |
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support provided by the state of Baden-Württemberg through the bwHPC initiative via Grant No. INST 39/963-1 FUGG (bw-ForCluster NEMO). Additionally, we express our gratitude to the Deutsche Forschungsgemeinschaft (DFG) for funding this work as part of the Priority Programme “Polymer-based Batteries” (SPP 2248, Project No. 441211139).Notes and references
- H. Raza, S. Bai, J. Cheng, S. Majumder, H. Zhu, Q. Liu, G. Zheng, X. Li and G. Chen, Electrochem. Energy Rev., 2023, 6, 29 CrossRef CAS.
- A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2012, 46, 1125–1134 CrossRef PubMed.
- M. del Carmen Rojas, M. L. N. Lobos, M. L. Para, M. E. G. Quijón, O. Cámara, D. Barraco, E. L. Moyano and G. L. Luque, Biomass Bioenergy, 2021, 146, 105971 CrossRef.
- A. Manthiram, S. Chung and C. Zu, Adv. Mater., 2015, 27, 1980–2006 CrossRef CAS PubMed.
- D. Diddens and A. Heuer, ACS Macro Lett., 2013, 2, 322–326 CrossRef CAS PubMed.
- G. Hu, Z. Sun, C. Shi, R. Fang, J. Chen, P. Hou, C. Liu, H.-M. Cheng and F. Li, Adv. Mater., 2017, 29, 1603835 CrossRef PubMed.
- D. Gayen, Y. Schütze, S. Groh and J. Dzubiella, ACS Appl. Polym. Mater., 2023, 5, 4799–4810 CrossRef CAS.
- Y. Schütze, D. Gayen, K. Palczynski, R. de Oliveira Silva, Y. Lu, M. Tovar, P. Partovi-Azar, A. Bande and J. Dzubiella, ACS Nano, 2023, 17, 7889–7900 CrossRef PubMed.
- Y. Schütze, R. de Oliveira Silva, J. Ning, J. Rappich, Y. Lu, V. G. Ruiz, A. Bande and J. Dzubiella, Phys. Chem. Chem. Phys., 2021, 23, 26709–26720 RSC.
- A. S. Mahadevi and G. N. Sastry Lamoureux, Chem. Rev., 2012, 113, 2100–2138 CrossRef PubMed.
- R. Motoyoshi, S. Li, S. Tsuzuki, A. Ghosh, K. Ueno, K. Dokko and M. Watanabe, ACS Appl. Mater. Interfaces, 2022, 14, 45403–45413 CrossRef CAS PubMed.
- W. Wei, G. Chang, Y. Xu and L. Yang, J. Mater. Chem. A, 2018, 6, 18794–18798 RSC.
- L. Yang, Q. Li, Y. Wang, Y. Chen, X. Guo, Z. Wu, G. Chen, B. Zhong, W. Xiang and Y. Zhong, Ionics, 2020, 26, 5299–5318 CrossRef CAS.
- P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2014, 119, 883–895 CrossRef PubMed.
- A. Turupcu, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2020, 16, 7184–7194 CrossRef CAS PubMed.
- C. Chipot, B. Maigret, D. A. Pearlman and P. A. Kollman, J. Am. Chem. Soc., 1996, 118, 2998–3005 CrossRef CAS.
- J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 4177–4178 CrossRef CAS.
- J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS PubMed.
- H. Minoux and C. Chipot, J. Am. Chem. Soc., 1999, 121, 10366–10372 CrossRef CAS.
- K. Kumar, S. M. Woo, T. Siu, W. A. Cortopassi, F. Duarte and R. S. Paton, Chem. Sci., 2018, 9, 2655–2665 RSC.
- G. Kaminski and W. Jorgensen, J. Chem. Soc., Perkin Trans. 2, 1999, 2365–2375 RSC.
- Q. Du, S. Long, J. Meng and R. Huang, J. Comput. Chem., 2011, 33, 153–162 CrossRef PubMed.
- H. Liu, H. Fu, X. Shao, W. Cai and C. Chipot, J. Chem. Theory Comput., 2020, 16, 6397–6407 CrossRef CAS PubMed.
- E. A. Orabi, R. L. Davis and G. Lamoureux, J. Comput. Chem., 2019, 41, 472–481 CrossRef PubMed.
- S. Du, H. Fu, X. Shao, C. Chipot and W. Cai, J. Chem. Theory Comput., 2019, 15, 1841–1847 CrossRef CAS PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. K. Bhattacharyya, J. Phys. Chem. A, 2017, 121, 3287–3298 CrossRef CAS PubMed.
- A. S. Reddy and G. N. Sastry, J. Phys. Chem. A, 2005, 109, 8893–8903 CrossRef CAS PubMed.
- H. M. Khan, C. Grauffel, R. Broer, A. D. MacKerell, R. W. A. Havenith and N. Reuter, J. Chem. Theory Comput., 2016, 12, 5585–5595 CrossRef CAS PubMed.
- T. A. Pham, S. G. Mortuza, B. C. Wood, E. Y. Lau, T. Ogitsu, S. F. Buchsbaum, Z. S. Siwy, F. Fornasiero and E. Schwegler, J. Phys. Chem. C, 2016, 120, 7332–7338 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Chem. Rev., 1999, 99, 2161–2200 CrossRef CAS PubMed.
- N. Molinari, J. P. Mailoa and B. Kozinsky, Chem. Mater., 2018, 30, 6298–6306 CrossRef CAS.
- C. Park, M. Kanduč, R. Chudoba, A. Ronneburg, S. Risse, M. Ballauff and J. Dzubiella, J. Power Sources, 2018, 373, 70–78 CrossRef CAS.
- L. X. Dang, J. Chem. Phys., 1992, 96, 6970–6977 CrossRef CAS.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302–1322 CrossRef CAS.
- C. Garau, A. Frontera, D. Quiñonero, P. Ballester, A. Costa and P. M. Deyà, Chem. Phys. Lett., 2004, 392, 85–89 CrossRef CAS.
- Y. Mo, G. Subramanian, J. Gao and D. M. Ferguson, J. Am. Chem. Soc., 2002, 124, 4832–4837 CrossRef CAS PubMed.
- L. Chen, Y. Wang, H. Wang, Y. Yang and J. Li, Chem. Phys. Lett., 2021, 783, 139042 CrossRef CAS.
- J. Ning, H. Yu, S. Mei, Y. Schütze, S. Risse, N. Kardjilov, A. Hilger, I. Manke, A. Bande and V. G. Ruiz, et al. , ChemSusChem, 2022, 15, e202200434 CrossRef CAS PubMed.
- D. Vijay and G. N. Sastry, Phys. Chem. Chem. Phys., 2008, 10, 582–590 RSC.
- S. A. Hassan, F. Guarnieri and E. L. Mehler, J. Phys. Chem. B, 2000, 104, 6478–6489 CrossRef CAS.
- M. M. Ghahremanpour, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2022, 126, 5896–5907 CrossRef CAS PubMed.
- D. Moreno Martinez, D. Guillaumont and P. Guilbaud, J. Chem. Inf. Model., 2022, 62, 2432–2445 CrossRef CAS PubMed.
- P. Li and K. M. Merz, J. Chem. Theory Comput., 2013, 10, 289–297 CrossRef PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- M. Wen and E. B. Tadmor, Phys. Rev. B, 2019, 100, 195419 CrossRef CAS.
- E. Brunk and U. Rothlisberger, Chem. Rev., 2015, 115, 6217–6263 CrossRef CAS PubMed.
- R. Jorn, R. Kumar, D. P. Abraham and G. A. Voth, J. Phys. Chem. C, 2013, 117, 3747–3761 CrossRef CAS.
- G. D. Smith, O. Borodin, S. P. Russo, R. J. Rees and A. F. Hollenkamp, Phys. Chem. Chem. Phys., 2009, 11, 9884 RSC.
- T. Sun, J. Xie, W. Guo, D. Li and Q. Zhang, Adv. Energy Mater., 2020, 10, 1904199 CrossRef CAS.
- H. Liao, H. Ding, B. Li, X. Ai and C. Wang, J. Mater. Chem. A, 2014, 2, 8854–8858 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Sensitivity analysis and optimized parameters for benzene, thiophene, benzenethiol, TBT, and TriTBT, presented in Tables S1–S5, respectively. Additionally, Fig. S1 shows the atom types for benzene, benzenethiol, and thiophene. The 2D representations of binding energy for thiophene–Li+ and benzenethiol–Li+, calculated using DFT and MS with and without correction, are provided in Fig. S2 and S3. Fig. S4 depicts the clustering behavior of LiTFSI salt in implicit solvent for varying salt concentrations. Free energy profiles (ΔFTBT–Li+) for TBT and TriTBT at fixed salt concentrations and various solvent compositions for explicit solvent are shown in Fig. S5 and S6. Furthermore, the free energy profiles (ΔFTBT–TFSI−) for TBT and a two-TBT setup at three different dielectric constants are presented in Fig. S7. Finally, Fig. S8 illustrates the free energy profiles (ΔFTBT–TFSI−) for TBT and TriTBT at a fixed salt concentration of 1.5 M and a fixed solvent composition of 0.55. See DOI: https://doi.org/10.1039/d4cp04484c |
| ‡ Research Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie GmbH, 14109 Berlin, Germany. |
| This journal is © the Owner Societies 2025 |