Open Access Article
Open Access ArticleMagnetic quantum phase transition extension in strained P-doped graphene
Natalia
Cortés
 *a,
J.
Hernández-Tecorralco
b,
L.
Meza-Montes
*a,
J.
Hernández-Tecorralco
b,
L.
Meza-Montes
 c,
R.
de Coss
de and
Patricio
Vargas
c,
R.
de Coss
de and
Patricio
Vargas
 f
f
aInstituto de Alta Investigación, Universidad de Tarapacá, Casilla 7D, Arica, Chile. E-mail: natalia.cortesm@usm.cl
bInstituto de Física, Universidad Nacional Autónoma de México, Apartado Postal 20-364, Ciudad de México, C.P. 01000, Mexico
cInstituto de Física, Benemérita Universidad Autónoma de Puebla, Apartado Postal J-48, 72570, Puebla, Mexico
dDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados del IPN, Apartado Postal 73, Cordemex, 97310, Mérida, Yucatán, Mexico
eCentro Mesoamericano de Física Teórica, Universidad Autónoma de Chiapas, 29050 Chiapas, Mexico
fDepartamento de Física, Universidad Técnica Federico Santa María, 2390123 Valparaíso, Chile
First published on 7th February 2025
Abstract
We explore quantum-thermodynamic effects in a phosphorous (P)-doped graphene monolayer subjected to biaxial tensile strain. Introducing substitutional P atoms in the graphene lattice generates a tunable spin magnetic moment controlled by the strain control parameter ε. This leads to a magnetic quantum phase transition (MQPT) at zero temperature modulated by ε. The system transitions from a magnetic phase, characterized by an out-of-plane sp3 type hybridization of the P–carbon (P–C) bonds, to a non-magnetic phase when these bonds switch to in-plane sp2 hybridization. Employing a Fermi–Dirac statistical model, we calculate key thermodynamic quantities such as the electronic entropy Se and electronic specific heat Ce. At finite temperatures, we find a MQPT extension characterized by Se and Ce, where both display a distinctive Λ-shape profile as a function of ε. These thermodynamic quantities sharply increase up to ε = 5% in the magnetic regime, followed by a sudden drop at ε = 5.5%, transitioning to a linear dependence on ε in the nonmagnetic regime. This controllable magnetic-to-nonmagnetic switch offers potential applications in electronic nanodevices operating at finite temperatures.
I. Introduction
The transformation of one state of matter into another one driven by temperature T is typically characterized by a phase transition, where both states of matter (or phases) are separated by a boundary and touching at a critical T value. When a phase transition occurs in a magnetic material, the magnetic moment of the electrons plays the major role as T varies, i.e., the orientation of the electron spins changes due to thermal fluctuations induced by T. Depending on the magnetic properties of the material (iron, for example), one can observe a magnetic phase transition as a function of temperature, going from a magnetic state into a nonmagnetic state at a critical T value.1At the quantum level, the nature of phase transitions can be different as they manifest in a quantum critical region, where quantum and thermal fluctuations are equally important.2 This type of phase transition starts at absolute zero (T = 0 K) and can continue as T increases to some small finite value, as seen in a ferromagnetic phase diagram controlled by an applied magnetic field, for example.2 At T = 0 the state is denominated quantum phase transition (QPT),2 and the main feature of a QPT is the so-called quantum critical point (QCP), where thermal fluctuations are suppressed and quantum fluctuations are predominant in the system. The quantum fluctuations are driven by a nonthermal control parameter such as an applied magnetic field, the amount of charge carriers, pressure, or strain, among others.2,3
Graphene is a versatile material where magnetic, topological, or quantum phase transitions can appear, which are ruled by diverse control parameters.4–7 Pristine graphene is a nonmagnetic material, and some ways to induce magnetism in it are through defects,8 creating samples with defined edges,9 or by adding foreign atoms to their lattice.10 It has been shown that phosphorous (P) atoms are good candidates to produce magnetism in graphene by substitutional doping.11,12 Graphene also allows the application of strain at finite temperatures, where its two-dimensional (2D) hexagonal structure possesses exceptional mechanical properties, allowing large deformations without breaking.13 Uniaxial and biaxial strain are experimentally accessible techniques that can be applied to graphene systems by lattice deformations of its carbon (C) atoms. Strain can be useful as a tool for tuning graphene electronic properties14 and organic hexagonal shaped 2D systems.15 Strain can also serve as a way to assist self-assembly of adsorbed atoms on the graphene lattice,16 and can induce a QPT in magic-angle twisted bilayer graphene.5
Density functional theory (DFT) studies show that at T = 0 K, a P-impurity atom opens a gap in bulk graphene and induces a narrow band at the Fermi level (EF), generating magnetism through a large spin-polarized state with spin splitting of 267 meV.17 This magnetic state is associated with P–C out-of-plane bonds showing sp3-like hybridization in graphene real-space lattice. As tensile strain is applied on P-doped graphene, the sp3 electronic configuration remains up to a certain critical strain value, then the hybridization for the atoms changes to sp2 as strain increases, recovering the flat hexagonal lattice with combined P–C bonds in the constructed supercell. In this process, a magnetic quantum phase transition (MQPT) occurs from a magnetic state to a nonmagnetic state driven by the strain control parameter ε.17
One fundamental question may emerge from the abovementioned processes: what will happen with the predicted MQPT in P-doped graphene when temperature is turned on? To answer this question, we should know how the entropy can influence the MQPT at T above zero. We can access this thermodynamic quantity for electrons through the electronic entropy Se, and then obtain the electronic specific heat Ce, both by employing Fermi–Dirac statistics. These two thermodynamic–electronic quantities are directly linked to each other by temperature, so they only play a role at finite T. Experimental measurements of Se have allowed the acquisition of fundamental information about the accessible electronic states of different systems, such as quantum dots18 and magic angle twisted bilayer graphene.19,20 It was found that in graphene, doping can induce changes in Ce as a function of T,21 and edge states in zigzag graphene nanoribbons can improve Ce at low T.22 Only just a few years ago, it was possible to measure Ce in graphene monolayer by using ultrasensitive calorimetric techniques.23
In this work, we theoretically predict both thermodynamic quantities Se and Ce for strained P-doped graphene at finite temperatures. We find that Se and Ce are three orders of magnitude larger than strained pristine graphene. We show Se and Ce are the extensions of the MQPT at finite temperatures with a Λ-type line shape as a function of ε. We can observe the two characteristic magnetic (0% ≤ ε ≤ 5%), and nonmagnetic (5.5% ≤ ε ≤ 10%) regimes are still present in the phase diagram at finite T as compared to T = 0 phase diagram. We evaluate three different orders of magnitude for T and find that the Λ-type line shape is preserved. Interestingly, thermal fluctuations present in Se and Ce do not destroy the quantum critical region found at T = 0 phase diagram, instead it is preserved within the same ε values for Se and Ce at finite T.
II. DFT-thermodynamic model
To obtain the electronic and magnetic properties of strained pristine graphene and strained P-doped graphene (the latter labeled as P-graphene), we performed DFT calculations using a plane-wave and pseudopotential method, as implemented in the QUANTUM-ESPRESSO code.24,25 Valence electrons were represented by plane waves with a kinetic energy cutoff of 55 Ry (320 Ry for the charge density), while core electrons were replaced by ultrasoft pseudopotentials.26 We employ the generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE) parametrization27 for the exchange–correlation functional. A vacuum spacing of 15 Å was used to avoid interaction between periodic images along the z-direction. For all cases, atomic positions were relaxed until the internal forces were below 0.01 eV Å−1. Brillouin zone integrations were carried out with a 21 × 21 k-point grid28 using a Methfessel–Paxton scheme smearing29 with a width of 0.005 Ry for the constructed unit cells for strained pristine graphene and strained P-graphene.We simulated P substitutional impurities by replacing one C atom from a graphene layer considering a 5 × 5 graphene supercell. Our model consists of 49 C atoms and one P atom, corresponding to 2.0% of impurities concentration of P atoms.17 Biaxial tensile strain modulated by the control parameter ε is applied on the systems by increasing the lattice constant as a = (1 + ε)a0, where a0 is the unstrained graphene lattice constant, and ε takes values from 0% to 10% because the MQPT extension occurs around the middle of these strain values, as we will see below. Within these DFT calculations at zero temperature, the electronic density of states (DOS) is obtained for strained pristine graphene and strained P-graphene. The DOS, D, we use throughout the paper is the sum of spin up (↑) and spin down (↓), majority and minority components respectively, D(E, ε) = D↑ + D↓. The density of states depends on both the electronic state with energy eigenvalue E, and the control parameter ε applied on either strained graphene system.
Fig. 1 shows the DOS for strained pristine graphene with ε ranging from 0% to 7%. At zero energy [charge neutrality point (CNP)], D = 0 for each ε value, then D linearly increases with different slopes around CNP [up to D ≈ 0.1 states (eV cell)−1]. The two van Hove singularities around CNP are nonsymmetric as we use more than one single orbital for C atoms in our DFT calculations.
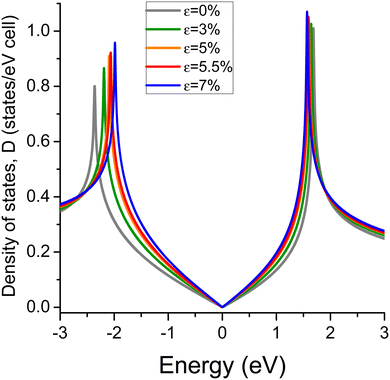 | ||
| Fig. 1 DOS for strained pristine graphene where ε = 0 represents the unstrained graphene monolayer. The unit cell for pristine graphene has two C atoms. All Fermi levels are set to zero energy. | ||
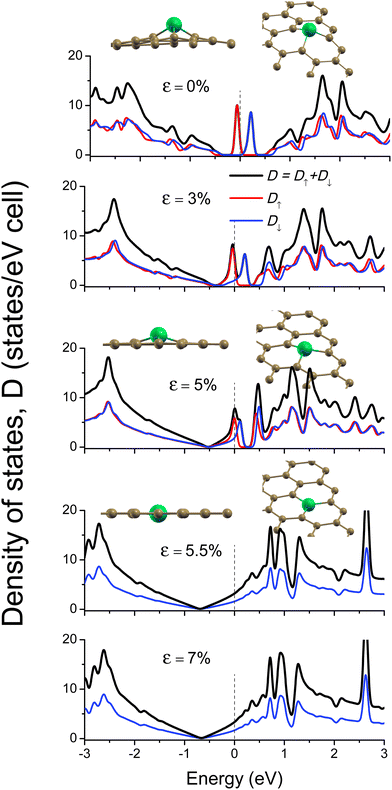
When a substitutional P impurity atom is added to the monolayer graphene, the behavior of the DOS drastically changes. In Fig. 2, we show D for strained P-graphene, including contributions of D↑ and D↓ with red and blue lines, respectively. At ε = 0% (top panel), two large spin-splitting peaks appear around EF (within the energy range −0.5 ≤ E ≤ 0.5 eV). Each peak corresponding to one type of spin density has contributions of the P-impurity and C atoms of graphene, generating a maximum spin magnetic moment (MS).30 As strain increases, the spin splitting between both spin densities reduces until they become identical at a critical value ε = 5.5%, indicating the change from a magnetic (D↑ ≠ D↓) to a nonmagnetic state (D↑ = D↓). When ε ≥ 5.5%, the C atoms of the graphene monolayer make room for the P impurity in the hexagonal plane, and the two peaks vanish and merge in the DOS. These latter types of DOS are responsible for the nonmagnetic regime. These changes in the DOS as ε increases are in connection with structural changes in the atomic lattice, as seen in the atomic arrangements shown above the DOS for ε = 0, 5, and 5.5% in Fig. 2. We will discuss these transitions in the next sections.
We anticipate these previous DOS calculations at T = 0 K do not significantly vary for moderate temperatures, as seen for example in strained organic 2D materials.15 Under this assumption, we can obtain Se and Ce at finite T through Fermi–Dirac statistics using the DOS at T = 0 K in the following way. From the constructed graphene supercell, we have that the total number of electrons is N = 201, in which N must be preserved for each system regardless of the T value. First, we can obtain the chemical potential μ(T) as a function of T for each ε value by inversion of
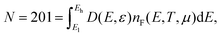 | (1) |
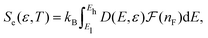 | (2) |
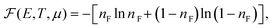 | (3) |
is approximated by a Lorentzian-like function
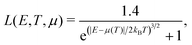 | (4) |
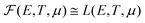 , see Fig. 3. Hence, we can use the L function in eqn (4), which plays the role of a filter around EF for each DOS, as it captures states of the DOS of width ≃4kBT. This approximation can be applied to other 2D materials because L is a generic function depending on the system's energy eigenvalues E, μ and T, as demonstrated for different quantum structures.31,32 Therefore, eqn (2) transforms as
, see Fig. 3. Hence, we can use the L function in eqn (4), which plays the role of a filter around EF for each DOS, as it captures states of the DOS of width ≃4kBT. This approximation can be applied to other 2D materials because L is a generic function depending on the system's energy eigenvalues E, μ and T, as demonstrated for different quantum structures.31,32 Therefore, eqn (2) transforms as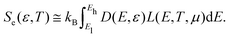 | (5) |
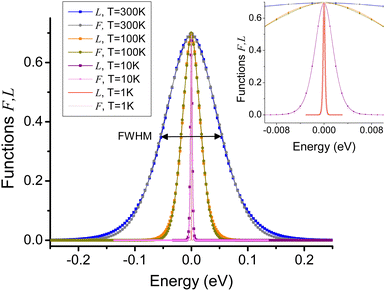 | ||
Fig. 3 Comparison plot between 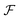 function in eqn (3) and L function in eqn (4) at μ = 0 and different temperatures as indicated. The black horizontal arrow indicates the full width at half maximum for the curves at T = 300 K, and the right inset presents a zoom area near zero energy, showing high agreement for both functions at all T we consider. function in eqn (3) and L function in eqn (4) at μ = 0 and different temperatures as indicated. The black horizontal arrow indicates the full width at half maximum for the curves at T = 300 K, and the right inset presents a zoom area near zero energy, showing high agreement for both functions at all T we consider. | ||
Through eqn (5), we calculate the electronic specific heat Ce as
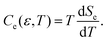 | (6) |
III. Finite-temperature results
Fig. 4 shows Se in left panels, and Ce in right panels for strained pristine graphene (top panels) and strained P-graphene (bottom panels). We emphasize that the thermodynamic quantities are calculated per unit cell in each case.33 When pristine graphene is biaxially strained, Se and Ce show similar behavior as seen in panels (a) and (b). Both quantities monotonically increase as T increases, but Ce increases faster than Se, and their lowest values occur for the unstrained case ε = 0, while the maxima are for ε = 7%. The inset in Fig. 4(a) shows that Se is a linear function of T up to T ≃ 20 K, and Ce is linear with T up to T ≃ 8 K as shown in the inset of Fig. 4(b). These monotonically thermodynamic responses for strained pristine graphene do not show significant variations as ε changes and T increases.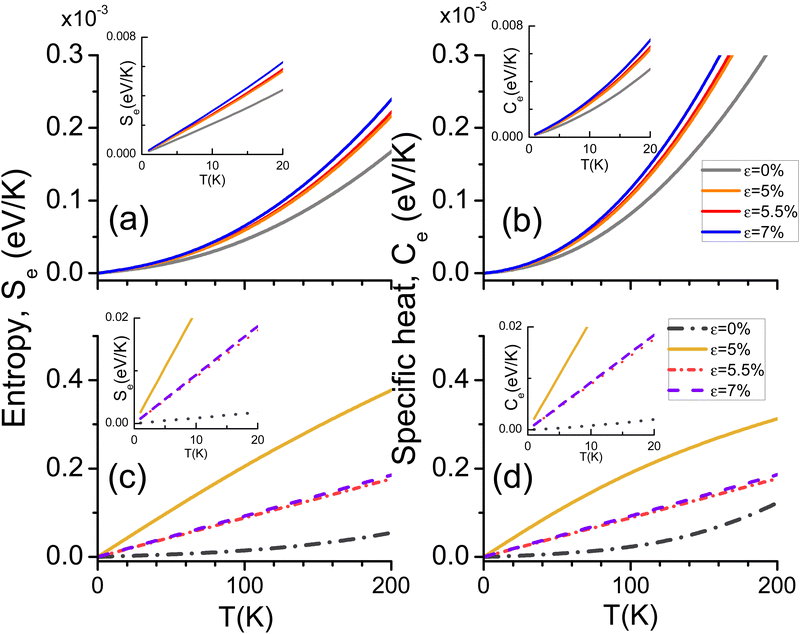 | ||
| Fig. 4 (a) and (c) Electronic entropy (Se) calculated through eqn (5); (b) and (d) electronic specific heat (Ce) from eqn (6), both per supercell. All quantities as a function of temperature T for different values of ε as indicated. Top panels (a) and (b): Strained pristine graphene, bottom panels (c) and (d): strained P-doped graphene. Insets show a zoom for each quantity with T going from 1 K to 20 K. Vertical scales in (a) and (b) and their respective insets times 10−3. Notice ε = 0% corresponds to unstrained graphene in each plot. | ||
However, Se and Ce substantially change their behavior for strained P-graphene, as shown in Fig. 4(c) and (d), respectively. Both quantities are three orders of magnitude larger than for strained pristine graphene due to the contribution of the P-impurity atom states. For P-graphene, the L function in eqn (4) captures more available states of each DOS as T increases, as one can infer from Fig. 2 in connection with Fig. 3. These captured states are mainly due to the spin-polarized peaks around EF for each strain value. The highest Se and Ce magnitudes occur for ε = 5% instead of ε = 7% as in the pristine case. For ε = 5%, the L function captures a maximum around EF, see the mid panel in Fig. 2, indicating the highest quantity of available electronic states occur at ε = 5%. When ε > 5%, Se and Ce linearly increase as T increases. For these strain values (ε > 5%), one can see from the DOS in Fig. 2 that the peak states are no longer distinguishable near EF, therefore the L function captures less available states and Se and Ce are lower than for ε = 5%. At T ≤ 20 K, Se and Ce show high similarity, linearly increasing with T as shown in insets of Fig. 4(c) and (d). The non monotonically behavior for Se and Ce as a function of T, and the sudden jump at ε = 5% for all T, indicates that a phase transition can be taking place in strained P-graphene at finite T.
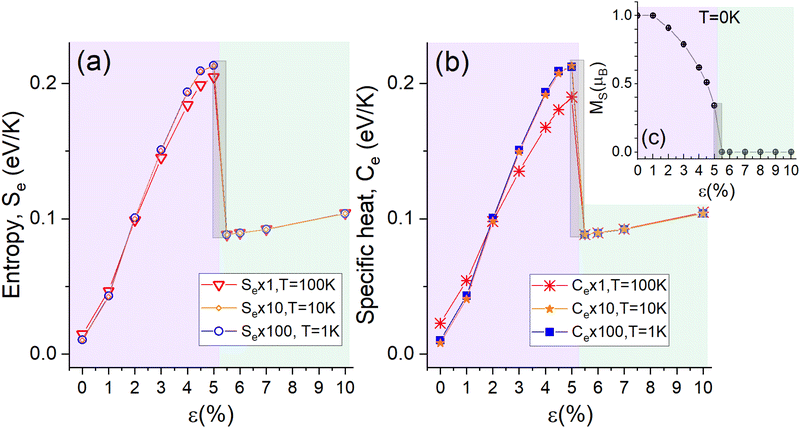
To get insight into that peculiar behavior for strained P-graphene, we present in Fig. 5, Se in panel (a), and Ce in panel (b), both as a function of ε and three different T values, T = 1 K, T = 10 K and T = 100 K. We choose the curve for T = 100 K [red triangles in panel (a) and red asterisk symbols in panel (b)] for the following description; however, the same applies as T decreases up to T = 1 K (with the exception of their numerical magnitudes). We also include results for the spin magnetic moment, MS, in panel (c), to highlight the MQPT at T = 0 K. All these results are particularly interesting due to several factors.
At finite temperatures, both Se and Ce exhibit a strikingly similar behavior. Their respective line shapes increase sharply with rising ε, reaching a peak value of ≈0.2 eV K−1 at ε = 5%. Beyond this point, both quantities suddenly drop at ε = 5.5%, with a magnitude of ≈0.1 eV K−1. For ε ≥ 5.5%, Se and Ce gradually increase with ε, displaying minor variations in their linear profiles as T rises. This overall behavior, characterized by a Λ-type line shape that remains largely consistent with changing T,34 suggests the presence of two distinct regimes when in comparison to the MQPT observed at T = 0, as depicted in Fig. 5, panel (c).
In Fig. 5(c), we show the MQPT with MS as a function of ε at T = 0,17 where we can identify two regimes, the first one is the magnetic phase, in the range 0% ≤ ε ≤ 5.5% (violet color area). In the second regime in the range 5.5% ≤ ε ≤ 10% (green color area), a nonmagnetic phase (MS = 0) is seen. This MQPT is closely related to the electronic configuration of the electron states that contribute to Se and Ce. When ε < 5.5%, the substitutional P impurity atom is positioned above the graphene plane because the P atom does not fit into the graphene hexagonal lattice. However, when ε ≥ 5.5%, the P impurity aligns within the same plane as graphene, transitioning from an sp3-like to an sp2 electronic configuration, see atomic structures in Fig. 2. This transition causes the spin-polarized state for the P atom to go to zero (MS = 0) as ε ≥ 5.5%, leading the system from a magnetic phase into a nonmagnetic one, and the MQPT is manifested in strained P-graphene at T = 0.
As Fig. 5 panels (a) and (b) show, Se and Ce increase for the same strain values when the magnetism goes down at T = 0, see violet regions in all panels of Fig. 5. In this regime, the strained P-graphene system increases the quantity of available electronic states as long as the P-atom induces magnetism up to ε = 5%. Then Se and Ce abruptly drop at ε = 5.5%. Since Se and Ce involve electronic states within a small energy range of width ≃4kBT, and very close to EF, the phenomenon of the transition between ε = 5% and ε = 5.5% is evident in the DOS shown in Fig. 2. The DOS around EF for ε = 5% is completely different compared to the DOS for ε = 5.5%. The first one shows a peak, and the latter a small curvature around EF; the DOS significantly decreases between these two strain values. This explains the abrupt drop for Se and Ce at ε = 5.5%.
Following the drop of Se and Ce (green zone in panels (a) and (b) of Fig. 5), both thermodynamic quantities show a linear behavior as ε increases, with no significant changes in their line profiles for the three different temperatures. Is in this regime where the magnetism vanishes as compared to the MQPT in panel (c). The MQPT extension is then observed as the Λ-type line profile in Se and Ce as a function of ε and T different from zero.
Notably, Se and Ce reveal a critical region for ε in the range 5% ≤ ε ≤ 5.5% (see shading gray rectangle in each plot), just when the system transitions from a magnetic phase to a nonmagnetic one (or vice versa) even at temperatures higher than zero. This critical region can tell us that there is a mixing of quantum and thermal fluctuations competing to lower the electronic entropy and specific heat to reach a stable state for the system. In other words, the thermodynamic quantities Se and Ce for T ≠ 0 may indicate quantum criticality within this region.2 We highlight that the thermodynamic quantities reported here are for temperatures up to T = 200 K. Although extending the analysis to higher temperatures is feasible, our focus is based on electronic specific heat experiments,23 which are done within this T range, capturing the behavior for moderate temperatures.
IV. Conclusions
Strained phosphorous-doped graphene exhibits emergent magnetism as long as a sp3-like hybridization of the P–C bonds takes place in the system. The applied strain control parameter ε, plays a critical role in modulating the sp3-like electronic configuration at absolute zero (T = 0 K), as well as influencing thermodynamic quantities such as the electronic entropy Se, and electronic specific heat Ce at finite temperatures T ≠ 0.At T = 0 K, the system undergoes a MQPT driven by ε, shifting from a magnetic state characterized by an sp3-type hybridization (0% ≤ ε ≤ 5%) to a nonmagnetic state with sp2 hybridization (5.5% ≤ ε ≤ 10%) where the phosphorus atom becomes coplanar with the graphene sheet. At non-zero temperatures, the behavior for Se and Ce when as a function of ε captures an extension of the MQPT, which presents a distinctive Λ-lineshape response that persists for temperatures around 100 K.
The quantities Se and Ce are particularly effective in distinguishing between the magnetic and nonmagnetic regimes at finite temperatures, corresponding to the same strain values where the MQPT is observed at T = 0. The transition between these two regimes defines a critical strain region, approximately in the range 5% ≤ ε ≤ 5.5%, where a competition between quantum and thermal fluctuations emerges. The Λ-type line shape identified here is crucial for understanding the accessible states near the Fermi level. This behavior could be experimentally probed via the thermodynamic responses of Se and Ce, providing insights into the on–off magnetism occurring at temperatures above zero in strained P-doped graphene.
Author contributions
N. C. and L. M.-M. started the discussions and first ideas. J. H.-T. made the DFT calculations. P. V. made the thermodynamic calculations. N. C. wrote the first version of the manuscript. N. C. and P. V. contributed to the core discussions and wrote the final version of the manuscript. All the authors participated and contributed to the analysis and discussions of the work and reviewed the manuscript.Data availability
The authors confirm that the data supporting the findings of this study are available within the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
N. C. acknowledges support from ANID Iniciación en Investigación Fondecyt Grant No. 11221088 and DGII-UTA, and the hospitality of Universidad Federico Santa María, Valparaíso, Chile. J. H.-T. acknowledges a postdoctoral fellowship from CONAHCyT-México. The authors thankfully acknowledge the computer resources, technical expertise, and support provided by the Laboratorio Nacional de Supercómputo del Sureste de México (LNS), a member of the CONACYT national laboratories, with project no. 202303063N. One of the authors (R. de Coss) is grateful for the hospitality of the Mesoamerican Centre for Theoretical Physics (MCTP), where part of this work was developed during a research visit. P. V. wishes to thank the Fondecyt grant project No. 1240582.References
- R. K. Pathria and P. D. Beale, Phase Transitions: Criticality, Universality And Scaling, in Statistical Mechanics, ed. R. K. Pathria and P. D. Beale, Academic Press, 4th edn, 2022, ch. 12, pp. 417–476, https://www.sciencedirect.com/science/article/pii/B978075062469550013X Search PubMed.
- S. Sachdev, Quantum phase transitions, Phys. World, 1999, 12(4), 33 CrossRef CAS.
- M. Klanjšek, A critical test of quantum criticality, Physics, 2014, 7, 74 CrossRef.
- P. Vancsó, I. Hagymási and L. Tapasztó, A magnetic phase-transition graphene transistor with tunable spin polarization, 2D Mater., 2017, 4(2), 024008 CrossRef.
- D. E. Parker, T. Soejima, J. Hauschild, M. P. Zaletel and N. Bultinck, Strain-induced quantum phase transitions in magic-angle graphene, Phys. Rev. Lett., 2021, 127(2), 027601 CrossRef CAS PubMed.
- L. Palma-Chilla, J. A. Lazzús and J. Flores, Entropy and Negative Specific Heat of Doped Graphene: Topological Phase Transitions and Nernst's Theorem Revisited, Entropy, 2024, 26(9), 771 CrossRef CAS PubMed.
- A. Huang, S. Ke, J. H. Guan, J. Li and W. K. Lou, Strain-induced topological phase transition in graphene nanoribbons, Phys. Rev. B, 2024, 109(4), 045408 CrossRef CAS.
- O. V. Yazyev and L. Helm, Defect-induced magnetism in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(12), 125408 CrossRef.
- G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth and P. Nemes-Incze, et al., Room-temperature magnetic order on zigzag edges of narrow graphene nanoribbons, Nature, 2014, 514(7524), 608–611 CrossRef CAS PubMed.
- J. Hernández-Tecorralco, L. Meza-Montes, M. Cifuentes-Quintal and R. de Coss, Understanding the sp magnetism in substitutional doped graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 105(22), 224425 CrossRef.
- L. Lin, L. Fu, K. Zhang, J. Chen, W. Zhang and S. Tang, et al., P-superdoped graphene: Synthesis and magnetic properties, ACS Appl. Mater. Interfaces, 2019, 11(42), 39062–39067 CrossRef CAS PubMed.
- R. Langer, P. Błoński, C. Hofer, P. Lazar, K. Mustonen and J. C. Meyer, et al., Tailoring electronic and magnetic properties of graphene by phosphorus doping, ACS Appl. Mater. Interfaces, 2020, 12(30), 34074–34085 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321(5887), 385–388 CrossRef CAS PubMed.
- V. M. Pereira, A. Castro Neto and N. Peres, Tight-binding approach to uniaxial strain in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(4), 045401 CrossRef.
- I. Alcón, R. Santiago, J. Ribas-Arino, M. Deumal, I. D. P. Moreira and S. T. Bromley, Controlling pairing of π-conjugated electrons in 2D covalent organic radical frameworks via in-plane strain, Nat. Commun., 2021, 12(1), 1705 CrossRef PubMed.
- C. Si, Z. Sun and F. Liu, Strain engineering of graphene: a review, Nanoscale, 2016, 8(6), 3207–3217 RSC.
- J. Hernández-Tecorralco, L. Meza-Montes, M. Cifuentes-Quintal and R. de Coss, Effects of biaxial strain on the impurity-induced magnetism in P-doped graphene and N-doped silicene: a first principles study, J. Phys.: Condens. Matter, 2020, 32(25), 255801 CrossRef PubMed.
- N. Hartman, C. Olsen, S. Lüscher, M. Samani, S. Fallahi and G. C. Gardner, et al., Direct entropy measurement in a mesoscopic quantum system, Nat. Phys., 2018, 14(11), 1083–1086 Search PubMed.
- A. Rozen, J. M. Park, U. Zondiner, Y. Cao, D. Rodan-Legrain and T. Taniguchi, et al., Entropic evidence for a Pomeranchuk effect in magic-angle graphene, Nature, 2021, 592(7853), 214–219 CrossRef CAS PubMed.
- Y. Saito, F. Yang, J. Ge, X. Liu, T. Taniguchi and K. Watanabe, et al., Isospin Pomeranchuk effect in twisted bilayer graphene, Nature, 2021, 592(7853), 220–224 CrossRef CAS PubMed.
- H. Mousavi and J. Khodadadi, Electronic heat capacity and conductivity of gapped graphene, Phys. E, 2013, 50, 11–16 CrossRef CAS.
- K. Yi, D. Kim and K. S. Park, Low-energy electronic states and heat capacities in graphene strips, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(11), 115410 CrossRef.
- M. A. Aamir, J. N. Moore, X. Lu, P. Seifert, D. Englund and K. C. Fong, et al., Ultrasensitive calorimetric measurements of the electronic heat capacity of graphene, Nano Lett., 2021, 21(12), 5330–5337 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car and C. Cavazzoni, et al., Quantum espresso: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli and M. Calandra, et al., Advanced capabilities for materials modelling with Quantum Espresso, J. Phys.: Condens. Matter, 2017, 29(46), 465901 CrossRef CAS PubMed.
- A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- M. Methfessel and A. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616 CrossRef CAS PubMed.
- Note that the ground state occurs at ε = 0% with MS = 1μB per supercell.
- N. Cortés, O. Negrete, F. J. Peña and P. Vargas, Gate-tunable charge carrier electrocaloric effect in trilayer graphene, Sci. Rep., 2021, 11(1), 1–13 CrossRef PubMed.
- N. Cortés, F. J. Peña, O. Negrete and P. Vargas, Proximity-induced spin-polarized magnetocaloric effect in transition metal dichalcogenides, Phys. Rev. B, 2022, 105(1), 014443 CrossRef.
- Since entropy and specific heat are extensive properties, they can be easily normalized using appropriate factors, such as per atom or in J (mol K)−1. In this study, we present the entropy and specific heat values on a per-unit-cell basis, reported in units of eV K−1.
- Interestingly, the specific heat as a function of T for a superconducting phase transition35 is similar to the line shape we find here for Se and Ce.
- R. Szczesniak, A. P. Durajski and M. W. Jarosik, Specific heat and thermodynamic critical field for calcium under the pressure at 120 GPa, Mod. Phys. Lett. B, 2012, 26(08), 1250050 CrossRef.
| This journal is © the Owner Societies 2025 |