Ultrathin liquid sheets: water gets in shape for VUV absorption

Abstract

We present absorption spectra of thin, free-flowing liquid sheets in the vacuum ultraviolet energy range using a gas-squeezed liquid jet. Compared to liquid flow cells, operation without transmission windows eliminates restrictions on the energy range. The temperature of the water sheet is estimated at 0 ± 3 °C, at the verge of the supercooled regime. By adjusting flow conditions in situ, we recorded absorption spectra at water sheet thicknesses ranging from 20 to 50 nm. We show that the absorption spectra of thin jets contain significant contributions from interference effects that need to be deconvoluted from spectral contributions due to the electronic structure. We employ a Fresnel propagation model to model the spectral changes and understand the impact of thickness variations and thin film interference. This opens the door for the investigation of solvation, interface, and similar effects by recording valence band spectra.

---

1. Introduction

Vacuum ultraviolet (VUV) light is ideally suited to investigate the valence transitions of molecular systems. VUV radiation induces and probes σ → σ* and n → σ* electronic transitions, as well as electronic excitation from occupied molecular orbitals to Rydberg orbitals. The spectral positions of these transitions can be correlated with the types of bonds present in the molecular system and how they interact with the surrounding environment. In contrast to UV-visible spectroscopy, which probes transitions from π orbitals, VUV absorption spectroscopy also probes σ electrons, which are highly dependent on the molecular structure and inter- and intramolecular interactions.

VUV absorption cross-sections are typically in the tens of megabarns (1 Mb = 10⁻¹⁸ cm⁻²). This implies that VUV radiation is completely absorbed within a millimeter in ambient gases and within a micrometer in the condensed phase. As a result, the sample, transport optics, and detection system must be in a vacuum environment, hence the name vacuum ultraviolet. Such constraints make recording transmission spectra of samples in the condensed phase challenging. Liquid-phase samples introduce another layer of complexity, as rapid evaporation in a vacuum environment increases the background pressure, leading to vapor contamination of the signal, and the ensuing evaporative cooling ultimately leads to the freezing of the sample.

Absorption cells transparent up to 10.5 eV have been developed to address these issues. Restricting the discussion to water measurements, lithium or magnesium fluoride windows transmit light up to approximately 10.5 eV and were used for absorption cells to record the highest resolution water vapor absorption spectrum up to 10.8 eV.¹ The peak absorption cross-section of gaseous water was measured to be approximately 20 Mb.^1,2 Reflectivity measurements of liquid water were performed by Kerr et al.³ and Ike-hata et al.⁴ in the energy range between 9.2 eV and 14.9 eV.^3,4 Optical constants were obtained by the Kramers–Kronig analysis, reporting peak absorption values at 8.30 and 8.37 eV, respectively. Most recently, Janik and Marin developed an absorption cell sealed with a variable thickness spacer encapsulated between two sapphire windows.⁵ This cell allows path lengths from hundreds of nanometers to hundreds of microns at high pressures and temperatures but constrains the photon energy range below 8.5 eV. By measuring the VUV absorption spectrum of sub- and supercritical liquid water as a function of temperature, they could nevertheless draw solid conclusions regarding the H-bonding structure.⁶ The absorption cross-section of room temperature liquid water at 8.46 eV was found to be 1600 M⁻¹ cm⁻¹, equivalent to 6 Mb. At such cross-sections, a transmission measurement is only feasible with a sample path length of less than several hundred nanometers.

In this study, we introduce an experimental setup for measuring VUV absorption spectra in the transmission geometry of free-flowing liquid samples. We present the unique features and implementation of this setup, based on a windowless, double-duty differentially pumped gas filter,^7,8 and gas-squeezed liquid jet setup.⁹ The experiment allows for the in situ generation and tuning of thin liquid sheets below 100 nanometers, as characterized using thin film interference in the visible spectrum. The capabilities of this setup allowed us to record absorption spectra for sheet thicknesses ranging from 20 to 50 nm from 7 to 13 eV. The combination of ultrathin liquid sheets and VUV radiation enables us to obtain previously elusive extinction coefficients directly.

Nanometer thin sheets approach a regime where bulk and interface spectral signatures may become comparable, allowing the investigation of interface effects. When comparing thin liquid sheets to aerosols of comparable droplet size, the latter is less defined in dimension, and because of their geometry, nanofocusing and shadowing artifacts impede the determination of extinction coefficients.¹⁰

We show in our data analysis that interference effects and thickness inhomogeneities must be considered explicitly to extract precise absorption coefficients. As the thickness of the film approaches tens of nanometers, it becomes commensurate with the probe wavelength, and interference effects become considerable. Such interference effects are inevitable when measuring absorption cross-sections directly in the vacuum ultraviolet, and careful assessment and correction are required to obtain accurate absolute absorption cross-sections. To do so, we employ a model based on Fresnel propagation equations to simulate the thin-film interference, considering the sheet thickness and optical properties derived using Kramers–Kronig integrals.

A full understanding of VUV propagation and absorption in liquid water enables us to identify potential biases in future measurements. Moreover, the presented setup is versatile, allowing us to study a wide range of solvents and solutes without the limitations imposed by transmission windows.

2. Methods

Here, we briefly summarize the setup and measurement approach. The ESI† gives a detailed account of the experiments and procedures.

2.1. Light source and beamline

The measurements were performed at the VUV beamline of the Swiss Light Source (SLS). VUV radiation from a bending magnet is collimated, dispersed in grazing incidence by a 150 lines per mm blazed grating and focused on the interaction region at the liquid sheet. The beamline offers a high flux of 10¹¹ photons s⁻¹ at the endstation at 10 eV photon energy, with a spectral resolution higher than E/ΔE = 10³. This is possible because three optical elements have been designed to accommodate the 4 mrad vertical divergence of the bending magnet synchrotron radiation at a large horizontal acceptance of 8 mrad.^7,11

The beamline monochromator allows scanning of the photon energy from 5 eV to more than 30 eV. A compact, differentially pumped gas filter is installed at the end of the beamline, maintaining ultrahigh vacuum in the transfer line towards the accelerator. In the middle section of the gas filter, a 10 cm long chamber is filled with 10 mbar of rare gas to suppress high-harmonic radiation from the grating. In the present experiments, a mixture of neon, argon, and krypton was used to ensure sufficient light extinction above 14 eV.^7,11 The maximum absorption cell pressure is set around 9 mbar, below the operating pressure of the rare gas absorption chamber.⁸

2.2. Free-flowing liquid sheet

For the free-flowing liquid jet, we employed a gas-squeezing nozzle capable of generating a thin sheet down to tens of nanometers.⁹ We used an adaption of the commercially available microfluidic nozzle system by Micronit.¹² Adjusting the liquid and gas flow rates allows the sheet thickness and size to be precisely and reproducibly controlled. Fig. 1a illustrates typical sheet dimensions under experimental conditions.

Fig. 1 (a) Water sheet comparison at different flow parameters. For a fixed liquid flow rate of 0.15 ml min⁻¹, the helium flow rate was varied between 120 and 160 sccm. (b) Liquid sheet with a He flow rate of 140 sccm illuminated with a 520 nm laser beam. Overlaid on the sheet images is a red ruler showing the thickness variation and the effective probe dimension (white circle). (c) The thin-film interference intensity profile (blue) was modeled using a Fresnel model (orange). The derived thickness profile (right Y axis) is represented in green.

Since absorption through the sheet is exponentially dependent on the thickness, maintaining short- and long-term stability during operation is critical. Short-term stability requires a consistent gas and liquid flow to prevent pulsation, or “breathing,” caused by pressure fluctuations. In the long term, chamber pressure changes or flash freezing of the jet may lead to instabilities or interruptions in the measurement. Freezing can occur if the liquid stream contacts a surface in the chamber before breaking up into droplets. Additionally, gas bubbles can form in the jet stream, which may act as a nucleation source, causing interruption of the flow. Minimizing bubble formation is achieved by degassing the sample before the experiment.

2.3. Sheet characterization and monitoring

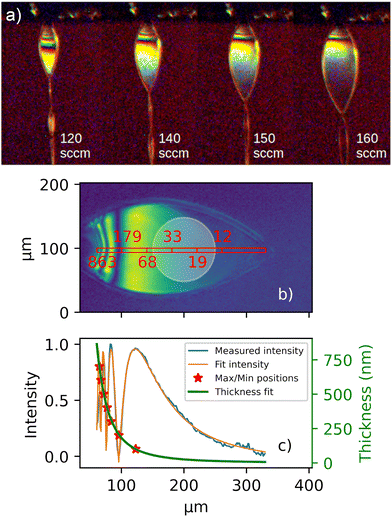
Characterization and continuous monitoring of the liquid sheet are essential to obtain reliable absorption spectra. A Navitar long-distance microscope with a 16 μm resolution and a field of view measuring 10 × 10 mm² was installed close to the experimental chamber with optical access to the interaction volume.

In Fig. 1a, examples of varying sheet thicknesses are shown. The water flow rate was kept constant at 0.15 ml min⁻¹, while the helium gas flow was adjusted from 120 sccm to 160 sccm. Elevated gas flow rates increased the size and decreased the thickness of the sheet simultaneously.

Using thin film interference, with either monochromatic or white light, allowed the estimation of the sheet thickness.^9,13 Fig. 1b illustrates a liquid sheet illuminated by a 520 nm light, enabling the direct anchoring of the fringe maxima and minima to a thickness determined by mλ increments. Utilizing these anchor points and the interference pattern recorded by the microscope, a profile of the liquid sheet thickness was obtained, showing a rapid decrease of the thickness near the nozzle and plateauing as the sheet propagates away from the nozzle, as shown in Fig. 1c. A model for the thickness profile was adapted from cylindrical impinging liquid jet systems,^14–16 following the relationship d(r) = K/(r − r₀)^m + c for sheets with varying thicknesses d. Here, r is the distance from the nozzle and K and c are constants depending on the viscosity of the liquid, nozzle dimension, helium flow rates, and the angle of the gas nozzles. Further, r₀ is a lateral offset in the image and m is an exponent factor of ≈2.6 for all conditions. A Fresnel model for thin film interference was used to fit and reproduce the recorded interference patterns taking into account the incident angle of light, index of refraction of water at low temperatures, and angular change due to variation in the thickness profile.

The reliability of thickness estimates diminishes for ultrathin sheets (<8 nm) due to the reduced signal intensity in these image regions, where the signal becomes obscured by the camera pixel noise. To monitor the stability of the sheet thickness, the positions of the interference fringes are tracked, providing a reliable method to assess the thickness of the sheet's thinnest part. Typically observed dimensions of the sheet were 150 μm in width and less than 100 nm in thickness, as shown in Fig. 1c.

2.4. Experimental chamber and detection system

The setup was based on a windowless absorption experiment for gaseous samples⁸ and integrated into a compact, differentially pumped vacuum system, depicted in Fig. S1 of the ESI.† The liquid sheet is housed in a central absorption vacuum chamber separated from the beamline gas filter and the detector chamber by two skimmers. An upstream chamber served as a mounting point for a 1 mm diameter entrance skimmer and was pressurized with approximately 15 mbar of helium. Opposite the entrance skimmer, the smaller detector skimmer was installed to shield the photodiode detector and act as an exit slit defining the photon energy and the probe area on the liquid sheet. The detector skimmer featured a 100 μm diameter aperture and the detector chamber, which was pressurized with 5 mbar of helium. This arrangement ensured a unidirectional helium flow from the gas filter and detector chambers toward the absorption chamber, preventing vapor migration from the interaction region toward the gas filter or detector.

A photodiode (OptoDiode SXUV100) was employed as the detector to measure the transmitted photon intensity. The photocurrent was read with a Keithley 6485 Picoammeter. The diode and skimmer were mounted on a three-axis manipulator, allowing alignment with the incoming beam and adjusting the distance between the skimmers. The distance between the skimmers during the operation was typically 2 mm, as depicted in Fig. 2.

Fig. 2 Close-up of the interaction region. The entrance skimmer towards the gas filter is seen on the left. On the right is the detector skimmer acting as an exit slit, defining the probe area as well as shielding the photodiode from contamination. The Micronit glass chip with the three channels and the produced liquid sheet can be seen in between.

Opposite the liquid sheet inlet, a liquid nitrogen-cooled trap was mounted to catch and store the liquid jet as well as a cryogenic pump condensing the vapor in the chamber. The detailed experimental procedure on how the jet is started and the overall system is aligned is described in the ESI.†

2.5. VUV transmission measurements

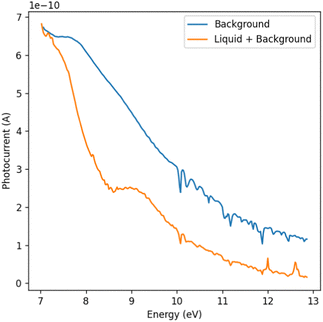
A series of absorption measurements were performed on pure water in the VUV energy range between 7 and 13 eV. The water used as the sample was purified by a Milli-Q simplicity system (18.2 MΩ cm at 25 °C).

The transmission measurements will always have liquid and vapor contributions. To isolate the absorption spectrum of the liquid sample, we referenced the transmission spectrum of the liquid sheet against the background. The background measurements were taken under operational conditions. The reference spectrum could be acquired without perturbation of the experimental environment through the rotation and slight translation of the liquid sheet relative to the beam. Fig. 3 illustrates the reference transmission spectrum and transmission through the water sheet. Notably, the overall transmission for vapor alone is higher, displaying distinct peaks consistent with the literature values for water vapor at and above 10 eV.¹⁷

Fig. 3 Photocurrent as a function of photon energy for the background, including vapor contributions (blue line) and a liquid water sheet (orange line). The discrete features above 10 eV in the background spectra that are also visible in the sheet spectra can be attributed to water vapor. The positive spikes in the liquid sheet data may stem from bubbles.

The data acquisition procedure considered the long- and short-term stability of the entire system. Reference measurements, with comparable statistics and energy steps as the sample data, were repeated several times for each dataset. The scans were conducted in steps of 20 meV covering a photon energy range from 7 to 13 eV with a dwell time of 3 seconds and three consecutive current readings. Multiple scans were performed within this energy range to acquire the absorption spectrum of liquid water.

Before averaging the scans, outliers were identified and removed. Occasional gas bubbles introduced sporadic spikes in the recorded data, which resulted in erratic transmission readings. These randomly appearing spikes were subsequently filtered out of the absorption spectrum. Furthermore, Kr absorption lines from the gas filter are sharp and may be sampled in the background scan and missed in the liquid measurement or vice versa. These lines were used to calibrate the energy of the beamline and removed from the spectra accordingly. Finally, the absorption spectra were calculated using the Lambert–Beer law and averaged.

For an error estimate, the 95% confidence intervals around the derived cross-section at each photon energy are shown in Fig. 4. The error increases towards higher photon energies, which can be attributed to two main reasons. The photocurrent dropped towards higher energies due to the changing photon flux and the sensitivity of the photodiode, and a lower photocurrent increases the error bar on the extinction measurement with the liquid sheet. Simultaneously, the absorption of the sample increases towards higher photon energies. These combined effects significantly lowered the signal on the photodiode, as shown in Fig. 3, leading to an increased uncertainty. Nonetheless, our experimental setup had the ability to adjust the thickness of the liquid sheet in situ. This feature allowed the identification of an optimal thickness to achieve the highest possible signal-to-noise ratio.

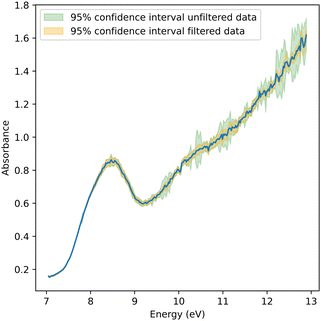Fig. 4 Absorption spectrum of pure water between 7 and 13 eV. Confidence intervals of both filtered and unfiltered data are shown in orange and green, respectively.

3. Results and discussion

The absorption spectrum of liquid water from 7 eV to 13 eV is shown in Fig. 4. The presented spectrum was derived from 15 scans collected in the manner described earlier. The most prominent peak at 8.52 eV was previously assigned to non-bonding electrons located at oxygen being promoted to a σ*-orbital.⁶ Comparing the spectral shape to that reported in the literature,^3,6 notable differences can be identified. First, the measured spectrum is blue-shifted relative to the one reported in the literature by ≈0.06 eV.⁶ Second, there is a shoulder at ≈7.9 eV. And third, there is a persistent offset below the absorption edge at 7 eV that is substantially higher than those reported earlier. Neither of these differences could be associated with water vapor contributions, given the significant spectral shift of the vapor spectrum of −0.85 eV for the à and +1.2 eV for the B̃ bands relative to the liquid spectrum. Using the same experimental chamber, pure vapor spectra were recorded without the jet, which have been reported elsewhere.⁸ All three effects, i.e., blueshift, shoulder, and offset, will be discussed in the context of jet temperature, geometry, and thin jet film interference effects.

The blueshift in the water absorption spectrum with decreasing temperature reflects the weakening of the hydrogen-bond (H-bond) network due to thermal energy. Hexagonal ice, for example, with a peak absorption at 8.65 eV, represents the maximum H-bonded state, while gas-phase water, at 7.45 eV, corresponds to the absence of H-bonds.^17,18 This 1.20-eV difference indicates the significant influence of H-bonds on water's electronic and vibrational states. On average, each H-bond contributes a 0.30 eV shift in energy. However, this simplification overlooks the bimodal distribution of H-bond strengths, which becomes more pronounced as fewer H-bonds remain at higher temperatures.¹⁹

Experimental findings show that water loses approximately 0.0065 H-bonds per degree Celsius.^6,20,21 At 23 °C, molecules average 3.4 H-bonds, while only 1.2 persist at 350 °C, reflecting substantial network disruption. Stronger H-bonds stabilize the OH bond, leading to lower vibrational energy states, whereas weaker H-bonds result in higher vibrational energy levels.⁶ Resonant inelastic X-ray scattering (RIXS) data reveal a clear relationship between H-bond strength and vibrational fine structure. As thermal energy weakens H-bonds, vibrational and electronic energy levels shift upward. This provides a detailed understanding of H-bond dynamics and their role in unique molecular behavior of water.¹⁹

Due to the rapid evaporative cooling of free-flowing water in a vacuum environment, the temperature of the sheet decreases with increasing distance from the nozzle.²² Marin et al.⁶ found that the temperature-dependent shape of the absorption peak can be described by a combination of four Gaussian curves in the 7.4–8.6 eV energy range,⁶ and reported fitting parameters from 23 °C to 350 °C. We extrapolated these parameters to lower temperatures to reproduce the absorption peak in Fig. 4 and its maximum at 8.52 eV to obtain the sheet temperature. Fig. 5 shows the extrapolated spectrum at 0 °C overlaid on the background-subtracted and scaled measured spectrum, showing excellent agreement. The calculated spectrum matches the peak of the spectrum at 8.5 eV and describes the shoulder at 7.9 eV. At energies below 7.4 eV, the agreement between the spectra is good after subtracting an absorption offset. We note already here that the offset can be attributed to thin film interference, which will be discussed below. Thus, the temperature of the sheet could be determined to be at the verge to the supercooled water regime at 0 ± 3 °C. This value represents the average temperature within the investigated focal volume, accounting for the spatial integration of thermal variations across the probed region.²²

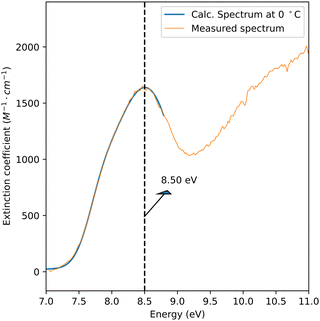Fig. 5 In blue, a calculated absorption spectrum of water at 0 °C is presented using extrapolated fitting parameters from the work of Marin et al.⁶ The calculated spectrum matches the measured spectrum of a sheet thickness of 41 nm after background subtraction and normalization.

To determine absolute absorption cross sections using the Lambert–Beer law, the optical path length, i.e. the sheet thickness and the measured extinction factor are required. A determination of the precise sheet thickness using spectral interferometry was not possible due to the uncertainty of the probe's position relative to the sheet height. We therefore anchored our results to the literature data^3,6 at 8.5 eV. Specifically, our data were normalized to the extrapolated cross-section at 0 °C, 1638 M⁻¹ cm⁻¹. Based on this, the sheet thickness was estimated using the Lambert–Beer law, which yielded a nominal sheet thickness of 41 nm.

In the following, we will focus the discussion on interference effects in the thin water films. Typical absorption cross-sections in the VUV are on the order of tens of Mb. This means that thin sheets of tens to hundreds of nanometers are required to study the absorption of liquid phase samples. For instance, measuring the absorption spectrum of liquid water up to 13 eV was only feasible at less than 100 nm sheet thickness. Such sample thicknesses are significantly shorter than the coherence length of the monochromatized VUV beam and even shorter than a wavelength at 8.5 eV (145 nm), leading to spectral interference effects that distort the measured transmission/absorption spectrum. An additional experimental complication for free-flowing jets is that the sheet thickness may not be uniform over the absorption area. In this work, the sheet thickness along the probed area was not uniform, varying from 10 to several hundred nanometers within the probed area, as illustrated in Fig. 1b. We note that these challenges are not unique to free-flowing liquid sheets; thin film interference artifacts also affect liquid flow cells, underlining the importance of their careful analysis.

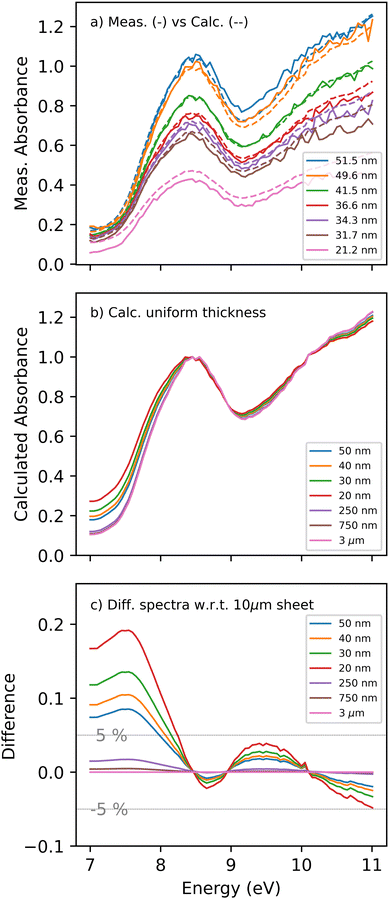
To investigate the impact of jet thickness variations and interference effects, a series of absorption spectra for various sheet thicknesses were recorded to elucidate the artifacts and their impact on the measured spectra. A combination of increasing the helium flow rate to decrease the sheet thickness and probing at the bottom of the sheet was used to record the spectra. Background and water spectra were collected at each condition, enabling the acquisition of the absorption spectrum presented in Fig. 6a. The legend indicates the average sheet thickness estimated using the previously reported absorption cross-section at the peak (≈8.5 eV).

Fig. 6 (a) Measured absorption spectra of various water sheet thicknesses between 20 and 50 nm are presented in solid curves. Calculated spectra for each thickness are presented in dashed lines. (b) Calculated absorption spectra of flat sheets at similar thicknesses are normalized to the peak to emphasize the thin film interference effects. (c) Difference spectra between flat sheets in (b) and 10 μm sheet, highlighting the expected spectral changes and extent of error. Two grey lines are drawn at the ±5% error threshold.

A dominant trend in the thickness dependent data is a spectral broadening for thinner sheets, where the shoulder intensity at 7.9 eV increases relative to the peak. In principle, the broadening could be rationalized by a shift in the absorption spectrum or spectral change around the peak from changing temperatures. As the sheet gets thinner, its width and length increase. This is expected to reduce the water temperature due to the increased surface area exposed to vacuum and enhanced evaporative cooling. According to the literature, temperature reduction results in a shift towards higher energies.⁶ However, the observed broadening/shift exhibits the opposite tendency, excluding temperature variation as the reason.

Other effects that can contribute to the spectral shape changes are interference and saturation phenomena. To investigate their impact in detail, we developed a model based on wavefront propagation through a thin film, where the Fresnel equations describe the absorption, reflection, and transmission of light at each sheet interface.²³ Depending on the sheet thickness, index of refraction, and probe wavelength, the reflections from each interface may interfere destructively or constructively, altering the total transmitted intensity observed by the detector as a function of wavelength or energy, respectively.

The propagation model uses the energy-dependent optical constants of water, specifically the complex index of refraction n(λ) = η(λ) + ik(λ), where both η and k are real values. η(λ) is the real part of the refractive index, defining the ratio of the speed of light in a vacuum to the phase velocity of light in the material. k(λ) represents the absorptive part of the refractive index, which corresponds to the light extinction coefficient due to absorption. The Kramers–Kronig relations, based on the theory of analytic complex functions, are used to calculate the wavelength-dependent refractive index solely from the wavelength-dependent absorption data.^24–28

As a starting point, we use the spectrum presented in Fig. 5, i.e., the experimental data corrected for the offset below the absorption edge. The absorption spectrum represents k(λ), which is then used with the Kramers–Kronig relation to calculate the refractive index η(λ). To solve Kramers–Kronig integrals, the measurements must cover a spectral window, including a transparent region. This is where k(λ) is negligible, and the refractive index equals the square root of the real part of the dielectric constant. Using this spectral region, the refractive index is shifted from 1 by a factor of n_offset. This region for water would have been at an energy <6 eV, which has not been covered in the measurements herein. Instead, the baseline refractive index was offset to match the literature values at low energies, and a dielectric constant of 1.784 was used based on the refractive index reported by Daimon and Masumura.²⁹ The estimated sheet thickness for that spectrum was only ≈40 nm. Therefore, it is not possible to calculate a distortion-free refractive index since spectral interference artifacts distort the underlying absorption spectrum. However, the calculated refractive index can still be employed to create similar trends observed in the data and understand the extent of the distortions expected.

To investigate thin-film interference effects for the transmission of VUV light through a sheet of water with a defined thickness, we employ a Fresnel model using the calculated complex index of refraction n(λ). The liquid sheet, being thinner than the probe wavelength, can be described as a thin film where the back reflections from the front and back interface coherently interfere. The sheet profile and probe footprint enable the transmittance calculation as depicted in Fig. 1b. For a specific beam position along the sheet, spectra were computed for each thickness in 1 μm increments along the jet propagation. Each spectrum was weighted by the integral beam footprint (100 μm diameter) along the jet propagation direction since the thickness variation is prominent along that axis. The spectra were then integrated to produce the final absorption spectrum.

The dashed curves in Fig. 6a represent the calculated spectra for the various sheet thicknesses. The calculated spectra fit the measured ones reasonably well and reproduce the experimentally observed trends. The peak amplitudes are well reproduced except for the 20 nm sheet, where a higher absorption is observed than predicted by the model. The discrepancy could be caused by the accidental inclusion of the bottom of the sheet, whereby the thick and opaque edges of the sheet are included in the detector's field of view. The model gives an error range for the approximated thicknesses: 51±²²⁰₂₂ nm and 21±⁶⁰₁₄ nm for the thickest and thinnest sheets reported. Despite the significant variation, the spectral shape for uniform sheets compared to thickness-varying sheets did not change drastically. As the thickest part of the sheet is still less than 220 nm, thin film interference is considerable throughout.

Considering the model's ability to describe the measurements qualitatively, we use it to disentangle the impact of the thin film interference from the thickness variation. The calculated spectra of a flat water sheet with increasing thicknesses are presented in Fig. 6(b). The spectra are normalized to the peak at ≈8.5 eV. Most importantly, the absorption shows a substantial change at lower energies between the thinnest and thickest sheets. Sheets thicker than 250 nm converge to similar baseline absorption at energies below 7.5 eV, indicating that thin film interference has to be considered for thinner sheets.

To illustrate the extent of the thin-film interference induced spectral changes, the spectrum of a 10 μm sheet is subtracted from the rest, and the difference spectrum is shown in Fig. 6c. For a 20 nm sheet, deviations in the apparent absorbance of up to 20% are observed. The primary difference is in the region from 7 to 8 eV, where the absorption cross-section is low enough to allow for strong back-reflections from the second interface. This agrees with the spectral broadening reported in the measured spectra through the increased apparent absorbance in the transparency region. The deviations due to the thin-film interference effects become smaller at higher energies due to the increasing absorption of water, yielding attenuated back reflection from the second interface. The most significant absorption/reflectivity change appears in the transparency region below 8 eV, where the back reflection from the transmitted beam is not absorbed in the water, and the thickness is small enough not to introduce a substantial phase shift. This will coherently and constructively interfere with the front-face reflection, amplifying the reflectivity of the water sheet and leading to the observed absorption baseline.

Returning to the water absorption spectrum presented in Fig. 4, it is evident that it is biased by thin film interference effects and thickness variations. The orange curve in Fig. 6c shows the extent of over- or under-estimation of the absorption cross-section. For energies below 8 eV, the reported spectrum would overestimate the absorption by up to 10%, while for higher energies, the discrepancy will be limited to 2.5% at its highest.

Similar considerations must be taken into account when approaching nanometric sample thicknesses and performing similar measurements in a liquid cell. Furthermore, the windows' index of refraction will impact such artifacts as it changes the reflectivity of the liquid–window interfaces. To extract absolute cross-sections with nanometric thin samples, the windows' index of refraction must be well characterized.

4. Conclusions

We have introduced an experiment for measuring vacuum ultraviolet (VUV) absorption spectra of free-flowing liquid jets that can overcome the current energy restriction of window absorption cells. Using transmission geometry, we report the first VUV absorption spectrum of liquid water up to 13 eV. Distinct spectral features in the absorption spectra can be attributed to thin-film interference effects in the liquid sheets with thicknesses in the range of tens to hundreds of nanometers. These interference effects are a common feature for free-flowing jets as well as absorption cells. They are carefully examined for the interpretation of the absorption spectra of liquids or solvation and interface effects across the valence bands.

Our findings underscore the interplay between thin-film interference and VUV absorption in liquid water, laying the groundwork for further explorations into solvation and interfacial phenomena at the nanometer scale. By providing a pathway to disentangle interference effects and intrinsic spectral features, these insights open the way for VUV studies of absorption in complex liquid systems and highlight the potential of ultrathin liquid sheets for advancing molecular spectroscopy in vacuum ultraviolet. These results demonstrate how a combined experimental and analytical approach can address fundamental challenges in VUV spectroscopy, offering a framework for absorption measurements in ultrathin liquid films.

Author contributions

A. A., A. B., and C. B. conceived the idea for the experiment. J. K., P. H., P. A., S. T., R. W., J. D. K., A. B., and A. A. designed and implemented the experimental setup. J. K., A. S., P. H., S. A., C. B., D. H., G. K., S. M., Z. S., K. S., J. D. K., A. B., and A. A. performed the experiment and discussed and interpreted the data. J. K., A. B., and A. A. analyzed the data and together with C. B. wrote the manuscript with support from all authors. All authors have approved the final version of the manuscript.

Data availability

The processed data used in this study are available in the Zenodo.org database under https://doi.org/10.5281/zenodo.14269809. This is in accordance with the Swiss National Science Foundation Guidance and FAIR data accessibility principles.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The measurements were carried out at the Swiss Light Source's VUV beamline located at the Paul Scherrer Institute in Villigen, Switzerland. The work is supported by an ERA-NET + EJP grant from the Swiss National Science Foundation. JDK and DJH were supported by the Linac Coherent Light Source (LCLS), U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515, and by the Department of Energy, Laboratory Directed Research and development program at SLAC National Accelerator Laboratory, under contract DE-AC02-76SF00515.

References

1. R. Mota, R. Parafita, A. Giuliani, M.-J. Hubin-Franskin, J. M. C. Lourenço, G. Garcia, S. V. Hoffmann, N. J. Mason, P. A. Ribeiro, M. Raposo and P. Limão-Vieira, Chem. Phys. Lett., 2005, 416, 152–159.
2. K. H. Tan, C. E. Brion, P. E. Van der Leeuw and M. J. van der Wiel, Chem. Phys., 1978, 29, 299–309.
3. G. Kerr, R. Hamm, M. Williams, R. Birkhoff and L. Painter, Phys. Rev. A, 1972, 5, 2523.
4. A. Ikehata, N. Higashi and Y. Ozaki, J. Chem. Phys., 2008, 129, 234510.
5. I. Janik and T. W. Marin, Rev. Sci. Instrum., 2015, 86, 015102.
6. T. W. Marin, I. Janik, D. M. Bartels and D. M. Chipman, Nat. Commun., 2017, 8, 15435.
7. M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610, 597–603.
8. A. Bodi, J. Knurr, P. Ascher, P. Hemberger, C. Bostedt and A. Al Haddad, J. Synchrotron Rad., 2024, 31, 1257–1263.
9. J. D. Koralek, J. B. Kim, P. Bruža, C. B. Curry, Z. Chen, H. A. Bechtel, A. A. Cordones, P. Sperling, S. Toleikis, J. F. Kern, S. P. Moeller, S. H. Glenzer and D. P. DePonte, Nat. Commun., 2018, 9, 1353.
10. R. Signorell, M. Goldmann, B. L. Yoder, A. Bodi, E. Chasovskikh, L. Lang and D. Luckhaus, Chem. Phys. Lett., 2016, 658, 1–6.
11. A. Bodi, P. Hemberger, T. Gerber and B. Sztáray, Rev. Sci. Instrum., 2012, 83, 083105.
12. Liquid NanoSheet Nozzles – Gas accelerated, https://micronit.com/sheet-nozzle-coated.html, Accessed: 2024-08-16.
13. S. Menzi, G. Knopp, A. A. Haddad, S. Augustin, C. Borca, D. Gashi, T. Huthwelker, D. James, J. Jin, G. Pamfilidis, K. Schnorr, Z. Sun, R. Wetter, Q. Zhang and C. Cirelli, Rev. Sci. Instrum., 2020, 91, 105109.
14. G. Taylor, Proc. R. Soc., Lond., Ser. A, 1960, 259, 1–17.
15. D. Hasson and R. E. Peck, AIChE J., 1964, 10, 752–754.
16. Y.-B. Shen and D. Poulikakos, J. Fluids Eng., 1998, 120, 482–487.
17. R. Mota, R. Parafita, A. Giuliani, M.-J. Hubin-Franskin, J. Lourenço, G. Garcia, S. Hoffmann, N. Mason, P. Ribeiro, M. Raposo and P. Limão-Vieira, Chem. Phys. Lett., 2005, 416, 152–159.
18. M. Seki, K. Kobayashi and J. Nakahara, J. Phys. Soc. Jpn., 1981, 50, 2643–2648.
19. V. Vaz da Cruz, F. Gelmukhanov, S. Eckert, M. Iannuzzi, E. Ertan, A. Pietzsch, R. C. Couto, J. Niskanen, M. Fondell and M. Dantz, et al., Nat. Commun., 2019, 10, 1013.
20. M. Chaplin, Water Structure and Science, 2022, https://water.lsbu.ac.uk/water/interfacial_water.html.
21. A. G. Kalinichev, Rev. Mineral. Geochem., 2001, 42, 83–129.
22. Y.-P. Chang, Z. Yin, T. Balciunas, H. J. Wörner and J.-P. Wolf, Struct. Dyn., 2022, 9, 014901.
23. S. J. Byrnes, arXiv preprint, arXiv:1603.02720, 2016.
24. F. Seitz, D. Turnbull and H. Ehrenreich, Solid state physics, Academic Press, 1968.
25. H. Phillip and E. Taft, Phys. Rev., 1964, 136, A1445.
26. F. C. Jahoda, Phys. Rev., 1957, 107, 1261.
27. J. S. Toll, Phys. Rev., 1956, 104, 1760.
28. L. Benatto, O. Mesquita, L. S. Roman, M. Koehler, R. B. Capaz and G. Candiotto, Comput. Phys. Commun., 2024, 298, 109100.
29. M. Daimon and A. Masumura, Appl. Opt., 2007, 46, 3811–3820.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04619f

---