Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of bijel formation dynamics during solvent transfer-induced phase separation using phase-field simulations†
Jesse M.
Steenhoff
 * and
Martin F.
Haase
* and
Martin F.
Haase
 *
*
Van 't Hoff Laboratory for Physical and Colloid Chemistry, Utrecht University, Utrecht, The Netherlands. E-mail: j.m.steenhoff@uu.nl; m.f.haase@uu.nl
First published on 14th February 2025
Abstract
Solvent transfer-induced phase separation (STrIPS) is a versatile and scalable method for the fabrication of bicontinuous interfacially jammed emulsion gels (bijels), a soft material with ample potential in membrane separation and energy storage. STrIPS, however, does not facilitate in situ observation of bijel formation, rendering it difficult to relate the phase separation process to the resulting bijel morphology. To address this issue, a phase-field (PF) model is presented that captures the principle components of STrIPS through relatively simple methods. Comparison with experimental results demonstrates that the PF model accurately describes STrIPS, reproducing morphological trends in a complex experimental system. Simultaneously, the model provides insight into the origin of such morphological features, relating the formation of the bijel structure in STrIPS to relatively slow dynamics of phase separation compared to solvent diffusion. Visualising phase separation during the entire STrIPS process, the PF model can therefore help elucidate the formation mechanisms underlying current STrIPS bijel morphologies, in addition to aiding the fabrication of novel ones.
1 Introduction
The stabilisation of emulsion droplets with solid particles has been a fixture in colloid science over the past few decades.1–4 More recently, this concept was extended to include bicontinuous emulsions, giving rise to the so-called bicontinuous interfacially jammed emulsion gel (bijel).5,6 Owing to its unique morphology, the bijel has ample potential for application in a wide variety of industrially relevant fields, such as membrane separation,7,8 coatings,9 energy storage10,11 and catalysis.12,13While multiple methods for the fabrication of bijels exist,6,14,15 solvent transfer-induced phase separation16 (STrIPS) offers unique advantages in terms of composition versatility17,18 and process scalability.19 During STrIPS, the removal of a solvent induces phase separation of a liquid precursor mixture additionally containing water, oil and interfacially active nanoparticles. The nanoparticles subsequently attach to the interface between the newly formed immiscible phases, eventually creating a jammed monolayer that kinetically arrests the structure and prevents further coarsening.
By employing a solvent to induce phase separation, the range of suitable precursor liquids, previously limited to only a few binary liquid pairs with select thermal properties,6,14,20,21 is greatly expanded. Simultaneously, the inclusion of the solvent enables the transition from a purely batch-based to a continuous synthesis process.
While STrIPS has these distinct advantages over other fabrication methods, it does not allow for facile in situ observation of bijel formation through conventional techniques (e.g. confocal microscopy). As such, current research often attempts to establish relationships between the initial state of the precursor mixture and the final bijel morphology, while the intermediate processes remain unclear. Recent work has partially addressed this issue through time-controlled solidification of a polymerisable oil,7,8 but this remains limited in scope due to the restrictive selection of suitable precursor components.
Instead, simulations can provide useful insights into bijel formation during the STrIPS process. Relating the properties of the precursor mixture's constituent components to the observed phase separation dynamics can help rationalise previously obtained experimental results, in addition to aiding the realisation of new, specifically tailored bijel morphologies.
Simulations have always been prevalent in research surrounding the bijel, being first discovered through numerical simulations by Stratford et al.5 prior to its experimental realisation by Herzig et al. two years later.6 Later work explored the influence of different liquid volume fractions,22 particle properties such as arbitrary size, shape or wettability23,24 and substrate wetting effects.25 While these simulations provided invaluable insights into the fundamentals of bijel formation, they are generally based on either the Lattice-Boltzmann (LB)5,22,24,26–28 or dissipative particle dynamics (DPD)29 methods, severely limiting the spatial and temporal scales over which simulations can be performed (micrometers over the course of milliseconds). For STrIPS these limitations are especially problematic, as the length and time scales of interest are set by the macroscopic molecular diffusion of the solvent (hundreds of micrometers over the course of seconds).
To simulate the formation of bijels on these larger scales, phase-field (PF) models are a promising alternative. Rather than the discrete LB or DPD methods, PF models work by solving partial differential equations of continuous fields that represent the different components of the system, with interactions that follow from mean-field approximations. In this manner, PF models can access time and length scales that are unfeasible for either LB or DPD. PF models have already found extensive employment in the simulation of phase separation processes, particularly related to the formation of polymeric membranes through phase inversion.30–34 Moreover, a combined PF/Brownian dynamics model has been used to investigate bijel formation in thin-film geometries.23,25,35 The explicit inclusion of particles and their interactions, however, still renders these types of simulations impractical for the large scales associated with the STrIPS process.
In this work, a PF model is introduced that captures the key characteristics of the STrIPS process while remaining computationally inexpensive. To this end, two distinct phase-field variables are evolved that together capture the physics of the oil/water/solvent system. In this model, the arrest of phase separation does not come about through the modelling of explicit particles. Rather, a local measure of the interfacial tension is continuously calculated and phase separation arrested when it exceeds a certain threshold value. In this way, the process of particles attaching to and jamming the formed interfaces is effectively replicated.
After the description of the underlying theory and subsequent model verification, the influence of different model parameters on the structure of the STrIPS bijel is investigated. The parameters controlling the relative dynamics of phase separation and solvent diffusion are found to be especially crucial and their role in the formation process is further elucidated. Finally, model results are compared with experimentally obtained STrIPS bijel morphologies, showing strong qualitative agreement. In particular, the potential of the PF model is demonstrated by readily capturing trends in the morphological features of the STrIPS bijel based on different experimental conditions.
2 Theory
The STrIPS process can be separated in three distinct components: solvent diffusion, phase separation and interfacial nanoparticle jamming. While the former two can be described via the same set of equations,30 it is simpler to treat them as separate processes. In this work, this is achieved by simultaneously evolving two different phase-fields, one which represents the oil/water mixture and one that represents the solvent. By making the oil/water interaction dependent on the value of the solvent field, the physics of the oil/water/solvent system can be replicated.2.1 Oil/water phase separation
In this work, the phase separation of the oil/water mixture is described in accordance with Cahn–Hilliard theory.36 Herein, the thermodynamic properties of the mixture can be derived from its free energy functional F, which in addition to the bulk free energy density f also contains gradient energy contributions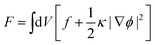 | (1) |
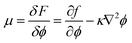 | (2) |
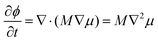 | (3) |
In this work, the oil/water mixture is treated as a simple regular solution with a free energy density given by
f = α(ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ)) ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ)) | (4) |
2.2 Solvent diffusion
Separated from the oil/water mixture, the phase-field of the solvent is evolved via Fick's second law of diffusion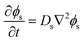 | (5) |
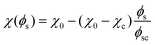 | (6) |
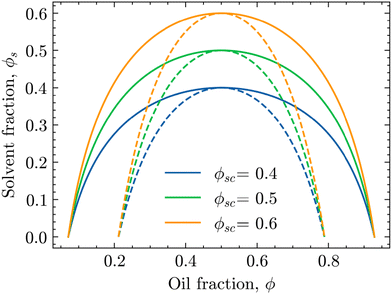 | ||
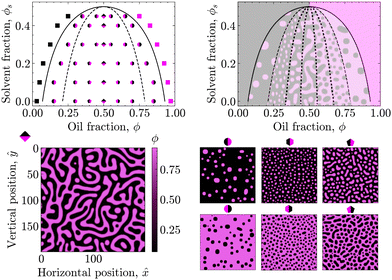
| Fig. 1 Phase diagrams of the oil/water mixture with respect to the solvent volume fraction ϕs for different values of ϕsc. The solid and dashed lines are the binodal and spinodal curves, respectively, calculated using eqn (4) and (6) for χ0 = 3.0. | ||
In these phase diagrams, the two-phase region is located under the calculated binodal curve (solid line). Choosing lower values of the critical solvent fraction ϕsc shrinks this region and shifts it down in the phase diagram. As such, the oil/water mixture stays homogeneous at lower solvent values, representing an increase in the solvent strength.
Closer observation of the phase diagram in Fig. 1 reveals one of the main considerations of modelling the diffusion of the solvent separately from the phase separation of the oil/water mixture. Namely, as these two processes are solely coupled through the interaction parameter χ(ϕs), there is no condition that enforces that ϕ + ϕs = 1. Consequently, this kind of coupling renders it difficult to physically interpret ϕs and ϕ as true fractions within the same system.
Rather, as a means to control the interaction parameter between the phase-separating species, the solvent fraction ϕs can be considered the STrIPS analogue of the absolute temperature T for the temperature induced phase separation of binary polymer mixtures.31,32 An alternative, perhaps more physical, interpretation is to treat ϕs as the solvent fraction of a composite oil/solvent component ϕ. While this interpretation was originally introduced for the PF modelling of non-solvent induced phase separation of ternary polymer solutions,34 a slightly different formulation of the relation between χ and ϕs in eqn (6) would also allow it to be applied here.
2.3 Nanoparticle interfacial jamming
In STrIPS, phase separation is eventually arrested due to the interfacial jamming of adsorbed nanoparticles. However, explicitly modelling nanoparticles is complex and computationally expensive, limiting the scale over which simulations can be performed. Instead, the influence of the nanoparticles can be implicitly included by taking into account the driving force of their interfacial adsorption: the interfacial tension σ. In STrIPS the diffusion of solvent and subsequent formation of interfaces due to phase separation is associated with an increase in the interfacial tension. If the interfacial tension exceeds a certain threshold σc, particles are irreversibly adsorbed to the interface and jamming occurs. For a planar 1D interface, the interfacial tension can be calculated in accordance with37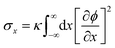 | (7) |
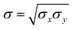 | (8) |
3 Methods
3.1 Nondimensionalisation
In the PF model, the governing equations of phase separation and solvent diffusion, respectively eqn (3) and (5), are numerically solved in a dimensionless form. To this end, the following dimensionless variables are introduced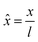 | (9) |
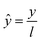 | (10) |
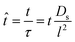 | (11) |
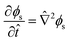 | (12) |
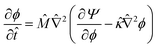 | (13) |
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) = Mα/Ds is the relative mobility of the oil/water mixture with respect to the solvent, whereas
= Mα/Ds is the relative mobility of the oil/water mixture with respect to the solvent, whereas ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = κ/(l2α) sets the relative energy penalty of creating compositional gradients, compared to the bulk free energy.
= κ/(l2α) sets the relative energy penalty of creating compositional gradients, compared to the bulk free energy.
3.2 Numerical implementation
The nondimensionalised eqn (12) and (13) were numerically solved via a finite difference method on a 2D 200 × 200 regular square lattice. Herein, space and time were discretised via central finite difference and forward Euler schemes, respectively. In order to solve eqn (12) and (13), both periodic and Neumann boundary conditions were employed, with the exact implementation varying between simulations.For the validation of the PF model in Section 4.1, periodic boundary conditions are applied at all edges of the simulation domain. In the remaining sections, dealing with multiple aspects of the STrIPS process, periodic boundary conditions were only applied at the left and right (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) edges of the simulation domain. To control the diffusion of solvent, Neumann boundary conditions were used at the top and bottom (ŷ) edges instead. More detailed descriptions of these Neumann boundary conditions, along with their interpretations for the investigated systems, are provided in the respective Results sections and Section S0 of the ESI.†
) edges of the simulation domain. To control the diffusion of solvent, Neumann boundary conditions were used at the top and bottom (ŷ) edges instead. More detailed descriptions of these Neumann boundary conditions, along with their interpretations for the investigated systems, are provided in the respective Results sections and Section S0 of the ESI.†
As eqn (13) requires compositional inhomogeneities to induce phase separation, all simulations were started by seeding the initial composition ϕ0 with random thermal noise, sampled uniformly from the [−0.01, 0.01] interval. Over the course of the resulting phase separation, the local interfacial tension σ was continuously calculated viaeqn (8). When σ exceeded the critical value σc, phase separation was arrested by multiplying the value of the local relative mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) with a factor 10−6. The simulations were terminated when σ ≥ σc for the entirety of the simulation domain.
with a factor 10−6. The simulations were terminated when σ ≥ σc for the entirety of the simulation domain.
These respective values of σc were based on profiles of the average interfacial tension σav, showing the evolution of σav over the course of the simulations. The profiles of σav, along with the corresponding values of σc and a list of the other simulation parameters used in this work, can be found in the ESI† (Section S1).
Finally, it is worth to specifically mention that for all simulations the lattice spacing was kept at Δ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = Δŷ = 1
= Δŷ = 1 ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) . For a total system length of L = 100 μm, a typical length scale for the STrIPS system, this entails a characteristic length of l = 0.5 μm. With Ds = 103 μm2 s−1 as a representative diffusion coefficient for a STrIPS solvent, this then gives a characteristic time of τ = 0.25 × 10−3 s.
. For a total system length of L = 100 μm, a typical length scale for the STrIPS system, this entails a characteristic length of l = 0.5 μm. With Ds = 103 μm2 s−1 as a representative diffusion coefficient for a STrIPS solvent, this then gives a characteristic time of τ = 0.25 × 10−3 s.
4 Results
4.1 Model validation: construction of the phase diagram
First, the phase diagram in Fig. 2 was constructed to validate the PF model with respect to the underlying theory. In particular, the spinodal (dashed) and binodal (solid) curves were calculated in accordance with eqn (4) and (6) for χ0 = 3.00 and ϕsc = 0.50 to qualitatively match the phase diagram of a typical STrIPS precursor mixture.18,38 These theoretical curves delineate different regions of the phase diagram with distinct phase separation dynamics. PF simulations were then conducted for initial compositions across these different regions and the subsequent phase separation behaviour compared to theoretical expectations.For initial compositions under the spinodal curve, the results of the PF model are in full agreement with theoretical expectations. Namely, in this region of the phase diagram the oil/water mixture should be thermodynamically unstable and undergo spontaneous phase separation due to minor thermal fluctuations in the composition. The PF model readily captures this behaviour, known as spinodal decomposition, by displaying spontaneous demixing for initial compositions seeded with some uniformly sampled random noise (see Section 3.2).
Considering that this spinodal decomposition effectively provides the template for the STrIPS bijel structure, the influence of the initial composition on the PF system morphology is further investigated. Around the symmetry axis of the phase diagram (ϕ = 0.50), the PF simulations yield the characteristic spinodal morphology of continuous, interwoven channels (rhombus markers). However, moving away from the symmetry axis these continuous channels start to break up, forming elongated droplets of a minority phase in a continuous majority phase (pentagon markers). Consequently, in order for the STrIPS process to yield bicontinuous structures it is imperative that phase separation occurs within the centre of the spinodal region.
In direct contrast, for initial compositions close to the spinodal curve the PF model yields dispersions of distinctively circular droplets of the minority phase in a continuous majority phase (hexagon markers). It must be stressed that these droplets are formed due to spinodal decomposition, rather than the more commonly associated process of nucleation and growth. This notion is further supported through comparison with the PF results for initial compositions located in between the binodal and spinodal curve, where nucleation and growth is the dominant phase separation mechanism.
Namely, for initial compositions between the spinodal and binodal curves, the PF model fails to phase separate and returns homogeneous systems. This is in line with theory, as these compositions lie within the metastable region of the phase diagram. Herein, the oil/water mixture is stable with respect to small fluctuations in the composition and spinodal decomposition does not occur. However, phase separation can still happen through the nucleation of regions with a sufficiently different composition, which subsequently grow and coalesce. Such nuclei are not naturally formed by the PF model, which includes only minor random compositional noise, but can be introduced manually.
By seeding an initial composition in the metastable region with circular nuclei of the opposite (with respect to the symmetry axis) binodal composition, the PF simulations show the growth of these droplets in a manner analogous to Ostwald ripening, with larger droplets growing at the expense of the smaller ones. The resulting morphology resembles polydisperse circular droplets suspended in a continuous phase (circular markers). Consequently, while the PF model lacks the ‘nucleation’ component required for phase separation via the nucleation and growth mechanism, it adheres to theory by capturing the 'growth' aspect of such nuclei in the metastable region of the phase diagram.
Finally, for initial compositions outside the binodal curve PF simulations consistently return homogeneous systems, even after the manual addition of compositional nuclei. This is in agreement with theory, as for compositions outside the binodal curve the oil/water mixture should be unconditionally stable.
To summarise, the results of the PF model are fully consistent with the presented theory, showcasing different mechanisms of phase separation in their expected regions of the phase diagram. Even though the PF model can only partially reproduce the process of nucleation and growth, it fully describes phase separation via spinodal decomposition. Considering that the structure of the bijel mainly originates from spinodal decomposition, the PF model is therefore suitable for simulating the formation of bijels via STrIPS, as is done in the following.
4.2 Simulation of STrIPS bijel formation
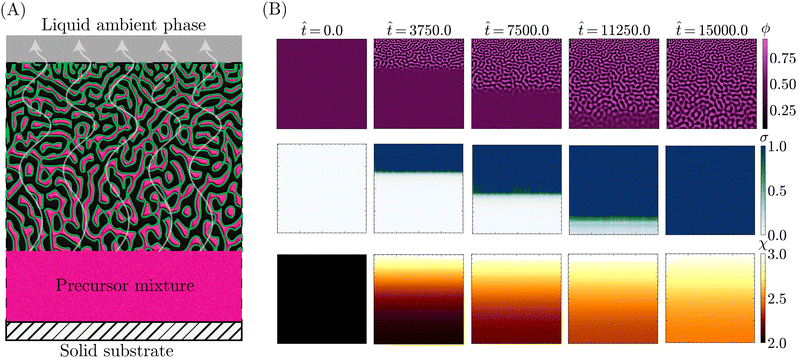
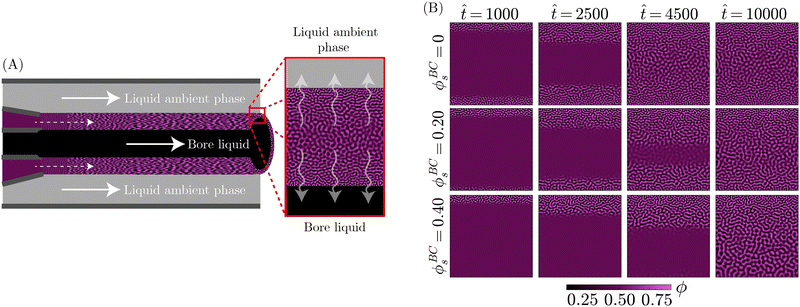
With the theoretical soundness of the model firmly established, the next step was to examine whether the simplified, core components distilled from the STrIPS process are sufficient to emulate bijel formation. Specifically, it was investigated whether the PF model, operating under these basic guidelines, could produce structures with characteristic morphological features of the STrIPS bijel. To this end, the PF simulations needed to replicate the experimental conditions of a suitable STrIPS synthesis method.Owing to its simple geometry and relative relevance for applications, the roll-to-roll fabrication of bijel films19 was chosen as the initial STrIPS model system. A schematic depiction of bijel formation in this system is shown in Fig. 3A. Here, the bijel precursor is deposited as a thin film on top of a solid substrate, which is immersed in a liquid ambient phase. The solid substrate blocks the diffusion of solvent from the bottom of the precursor film, causing phase separation to start only from the top interface with the ambient phase. As a result, bijel films formed in this manner display a characteristic trend in the average pore size: small pores at the top surface that progressively get larger closer to the solid substrate. This size gradient serves as an effective hallmark for the accuracy of the PF simulations, requiring the implementation of asymmetric diffusion to properly reflect the experimental conditions of the model system.
This asymmetric diffusion of solvent is readily incorporated into the PF model through different boundary conditions. Based on the schematic depiction of the model system in Fig. 3A, the simulation domain represents a 2D cross-section of the deposited precursor film, made to be infinitely wide via periodic boundary conditions at the left and right edges. Employing a Neumann boundary condition, solvent is allowed to diffuse across the top edge into the ambient liquid. Considering that the volume of the ambient phase is significantly larger than that of the precursor film, the solvent content of the ambient phase ϕBCs is treated as constant. At the same time, another Neumann boundary condition prevents solvent from crossing the bottom edge of the system, representing the presence of a solid substrate.
Consistent with the different interpretations of ϕ and ϕs in Section 2.2, exchange between the precursor and the ambient liquid is thus limited solely to the solvent fraction ϕs. This is further enforced by imposing Neumann boundary conditions on eqn (13) that close both the top and bottom system boundary to the direct transport of oil/water associated with phase separation. With these different boundary conditions, PF simulations were conducted that qualitatively matched the experimental conditions of the STrIPS roll-to-roll process, the results of which are depicted in Fig. 3B.
Specifically, the images in Fig. 3B illustrate the different stages of structure formation in the PF simulations of STrIPS. Phase separation is shown through the evolution of the oil fraction ϕ, along with the associated local interfacial tension σ. The diffusion of the solvent is represented by the oil/water interaction parameter χ. Mirroring the experimental procedure, the simulation starts (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 0) from a homogeneous precursor with a composition located at the critical point of the phase diagram. For the aforementioned STrIPS precursor parameters of χ0 = 3.0 and ϕsc = 0.50, this corresponds to an initial composition of ϕ0 = 0.50 ± 0.01 and ϕs = 0.50 (see Fig. 1). As a homogeneous mixture, the initial state has constant values for χ and σ, with notably σ = 0. This changes, however, as the difference in solvent content between the precursor mixture and the liquid ambient phase, which contains no solvent (ϕBCs = 0), causes the solvent to diffuse out of the precursor into the ambient phase.
= 0) from a homogeneous precursor with a composition located at the critical point of the phase diagram. For the aforementioned STrIPS precursor parameters of χ0 = 3.0 and ϕsc = 0.50, this corresponds to an initial composition of ϕ0 = 0.50 ± 0.01 and ϕs = 0.50 (see Fig. 1). As a homogeneous mixture, the initial state has constant values for χ and σ, with notably σ = 0. This changes, however, as the difference in solvent content between the precursor mixture and the liquid ambient phase, which contains no solvent (ϕBCs = 0), causes the solvent to diffuse out of the precursor into the ambient phase.
Namely, the diffusion of solvent shifts the composition in the adjacent region of the precursor mixture into the spinodal region. The corresponding increase in χ induces local phase separation (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 3750), with the resulting formation of interfaces giving rise to a non-zero value for σ. As the solvent continues to diffuse away, this front of phase separation and increasing interfacial tension progressively makes its way through the system (
= 3750), with the resulting formation of interfaces giving rise to a non-zero value for σ. As the solvent continues to diffuse away, this front of phase separation and increasing interfacial tension progressively makes its way through the system (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 7500). At a certain point, σ locally exceeds the set threshold value, here σc = 1.0, resulting in the arrest of phase separation in that region. Meanwhile, phase separation and structure coarsening continue in the deeper regions where the interfacial tension remains lower. Eventually, the solvent level will have been sufficiently depleted to induce phase separation over the entire system domain (
= 7500). At a certain point, σ locally exceeds the set threshold value, here σc = 1.0, resulting in the arrest of phase separation in that region. Meanwhile, phase separation and structure coarsening continue in the deeper regions where the interfacial tension remains lower. Eventually, the solvent level will have been sufficiently depleted to induce phase separation over the entire system domain (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 11
= 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250), with the evolution of the interfacial tension σ lagging somewhat behind. Finally, σ catches up and causes the complete arrest of phase separation and structure coarsening throughout the entire simulation domain (
250), with the evolution of the interfacial tension σ lagging somewhat behind. Finally, σ catches up and causes the complete arrest of phase separation and structure coarsening throughout the entire simulation domain (![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 15
= 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), after which the simulation is stopped.
000), after which the simulation is stopped.
These simulations evidently demonstrate that the PF model can capture the key components of the STrIPS process. Not only do they display progressive phase separation induced by the diffusion of solvent, they also indicate that the interfacial tension σ functions as an effective measure for arresting phase separation. The most obvious sign, however, is the fact that the resulting morphology bears a striking resemblance to the STrIPS bijel as expected for the roll-to-roll process.
Most notably, the final morphology in the top row of Fig. 3B has a distinct gradient in the pore size. Matching experimental results, the pores are smallest at the top edge of the system domain, at the interface with the ambient liquid. Deeper into the structure the pores get gradually larger, reaching a maximum at the bottom next to the solid substrate. As this characteristic morphological feature of the STrIPS bijel was reproduced by the PF model, its origin in simulations could help elucidate their appearance in experiments as well.
In the PF simulations, the pore size gradient results due to there being local differences in the solvent flux over the course of the simulation. Deeper in the structure, the solvent content remains higher, for longer, compared to the region adjacent to the ambient phase. Consequently, there is a longer period of time between the onset of phase separation and the interfacial tension reaching σc, arresting the structure. As the structure continues to coarsen in this period, this results in comparatively larger pores than near the surface. Notably, these observations support the proposed explanations of pore size gradients for experimental STrIPS bijels.8,19
While these findings highlight the potential of the PF model for simulating bijel formation via STrIPS, some major points require further discussion. In particular, the influence of the PF model parameters on the obtained morphology and how this physically relates to the STrIPS process. For example, the simulations in Fig. 3 were performed for ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) = 0.01 and
= 0.01 and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 0.50 in eqn (13). The values of these parameters and their respective interpretations proved to be crucial for the success of the PF model in simulating STrIPS. As such, they are discussed in detail in the next section.
= 0.50 in eqn (13). The values of these parameters and their respective interpretations proved to be crucial for the success of the PF model in simulating STrIPS. As such, they are discussed in detail in the next section.
4.3 The influence of ![[M with combining circumflex]](https://www.rsc.org/images/entities/h3_i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/h3_i_char_e109.gif)
The dynamics of phase separation and structure coarsening are crucial elements of the formation of bijels via STrIPS. In this PF model, these elements are represented through the relative oil/water mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and gradient energy coefficient
and gradient energy coefficient ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) in eqn (13). To gain further insight into the influence of these parameters on the formed morphology, STrIPS simulations as in Fig. 3 were performed with different combinations of
in eqn (13). To gain further insight into the influence of these parameters on the formed morphology, STrIPS simulations as in Fig. 3 were performed with different combinations of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) . In particular, somewhat low values of
. In particular, somewhat low values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) were expected to yield the characteristic spinodal morphology associated with the bijel.
were expected to yield the characteristic spinodal morphology associated with the bijel.
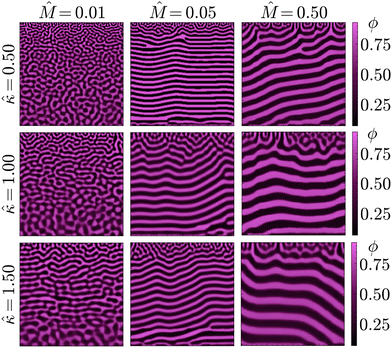
Namely, these low parameter values represent a system where solvent diffusion is fast compared to phase separation (![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) ) and the presence of compositional gradients is not severely penalised (
) and the presence of compositional gradients is not severely penalised (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) ). The former effectively imposes a ‘deep quench’ on the bijel precursor, bringing the composition deeper into the spinodal region prior to phase separation, whereas the latter reduces the influence of local composition inhomogeneities. Reflecting the STrIPS process, this combination should facilitate spinodal decomposition in an isotropic manner over the entire depth of the system.
). The former effectively imposes a ‘deep quench’ on the bijel precursor, bringing the composition deeper into the spinodal region prior to phase separation, whereas the latter reduces the influence of local composition inhomogeneities. Reflecting the STrIPS process, this combination should facilitate spinodal decomposition in an isotropic manner over the entire depth of the system.
This expectation is seemingly confirmed by the results of the PF model, shown in Fig. 4 for different combinations of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) . Lower values of
. Lower values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) result in the formation of structures visually similar to experimental STrIPS bijels, containing randomly oriented domains with a size gradient perpendicular to the surface. In contrast, higher values of
result in the formation of structures visually similar to experimental STrIPS bijels, containing randomly oriented domains with a size gradient perpendicular to the surface. In contrast, higher values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) seem to favour the formation of a more laminar morphology after phase separation, displaying alternating layers of both the oil- and water-rich phase parallel to the surface. Close to the interface with the ambient phase, however, these laminar structures contain a localised region with a notably different structure. This surface region displays a wider variety of domain orientations, appearing similar to the structures observed for lower
seem to favour the formation of a more laminar morphology after phase separation, displaying alternating layers of both the oil- and water-rich phase parallel to the surface. Close to the interface with the ambient phase, however, these laminar structures contain a localised region with a notably different structure. This surface region displays a wider variety of domain orientations, appearing similar to the structures observed for lower ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) . Overall, however, it can be concluded that low values of
. Overall, however, it can be concluded that low values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) yield isotropic bijel structures, whereas higher values induce the formation of laminar pores.
yield isotropic bijel structures, whereas higher values induce the formation of laminar pores.
As illustrated by simulations shown in Fig. 5, this observed morphological differences can be explained by progressive phase separation directed by a planar diffusion front. That is, phase separation sequentially occurring in distinct, adjacent regions of the simulation domain, following the sufficient depletion of solvent. In particular, it is the minimisation of the gradient energy associated with this mechanism of phase separation that causes the morphological differences. Namely, compositional differences between adjacent regions will induce the formation of a boundary layer in order to minimise the gradient energy. For a planar diffusion front, these boundary layers can give rise to the observed laminar structures. Whether this actually occurs, however, depends on the extent of progressive phase separation.
As it controls the relative dynamics of phase separation and solvent diffusion, this extent is mainly set by ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) . High values of
. High values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) reflect systems with relatively fast phase separation compared to solvent diffusion. In these systems, phase separation can keep up with the moving diffusion front, causing the edge of this diffusion front to effectively become an interface between the region undergoing phase separation and the adjacent region where it has yet to occur. Minimisation of gradient energies will then induce the formation of a planar boundary layer, matching the shape of the diffusion front (ESI,† S3). As the diffusion front progressively moves deeper into the structure, the associated phase separation continuously generates such planar boundary layers, which eventually coarsen into the laminar morphologies observed in Fig. 4 and 5.
reflect systems with relatively fast phase separation compared to solvent diffusion. In these systems, phase separation can keep up with the moving diffusion front, causing the edge of this diffusion front to effectively become an interface between the region undergoing phase separation and the adjacent region where it has yet to occur. Minimisation of gradient energies will then induce the formation of a planar boundary layer, matching the shape of the diffusion front (ESI,† S3). As the diffusion front progressively moves deeper into the structure, the associated phase separation continuously generates such planar boundary layers, which eventually coarsen into the laminar morphologies observed in Fig. 4 and 5.
In contrast, for low values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) the dynamics of phase separation are slow compared to the solvent diffusion. In such systems, phase separation can not keep up with the moving diffusion front, thereby lowering the influence of the associated interface and allowing for phase separation in a more isotropic manner. The same principle explains the existence of the differently structured surface regions observed for higher values of
the dynamics of phase separation are slow compared to the solvent diffusion. In such systems, phase separation can not keep up with the moving diffusion front, thereby lowering the influence of the associated interface and allowing for phase separation in a more isotropic manner. The same principle explains the existence of the differently structured surface regions observed for higher values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) . As these regions are directly adjacent to the ambient phase, phase separation can not keep up with the rapid depletion of solvent from this region. This rapid depletion of solvent causes the formation of a locally isotropic structure, which is then quickly arrested before considerable coarsening can take place.
. As these regions are directly adjacent to the ambient phase, phase separation can not keep up with the rapid depletion of solvent from this region. This rapid depletion of solvent causes the formation of a locally isotropic structure, which is then quickly arrested before considerable coarsening can take place.
The influence of ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) on the morphology is similar to
on the morphology is similar to ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) , albeit less pronounced. The value of
, albeit less pronounced. The value of ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) determines the relative energy penalty for gradients in the composition, thereby also setting the degree of influence a moving interface such as the diffusion front can exert over the system. For higher values of
determines the relative energy penalty for gradients in the composition, thereby also setting the degree of influence a moving interface such as the diffusion front can exert over the system. For higher values of ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) smaller compositional variations become more relevant, enhancing the ability of the diffusion front to direct phase separation. This is mainly noticeable at lower values of
smaller compositional variations become more relevant, enhancing the ability of the diffusion front to direct phase separation. This is mainly noticeable at lower values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) , such as in the left column of Fig. 4. Herein, the increase in
, such as in the left column of Fig. 4. Herein, the increase in ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) causes the formation of more laminar structures, mostly located in the central region of the structure. Both the regions located near the surface (top) and the solid support (bottom), however, display relatively isotropic features. This is because progressive phase separation is most prominent in the central region. As mentioned above, the surface region has a more isotropic structure due to the rapid depletion of solvent. For the region directly adjacent to the solid surface, the shape of solvent profile remains mostly flat over time (ESI,† S3). As such, phase separation occurs relatively simultaneously throughout this region and is therefore not significantly influenced by a moving diffusion front, also yielding a more isotropic morphology.
causes the formation of more laminar structures, mostly located in the central region of the structure. Both the regions located near the surface (top) and the solid support (bottom), however, display relatively isotropic features. This is because progressive phase separation is most prominent in the central region. As mentioned above, the surface region has a more isotropic structure due to the rapid depletion of solvent. For the region directly adjacent to the solid surface, the shape of solvent profile remains mostly flat over time (ESI,† S3). As such, phase separation occurs relatively simultaneously throughout this region and is therefore not significantly influenced by a moving diffusion front, also yielding a more isotropic morphology.
Concluding, the PF simulations revealed that the interplay between phase separation and structure coarsening, represented by the values of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) , plays a major role in acquiring isotropic bijels via STrIPS. In particular, it was found that isotropic bijel structures only occurred for fast solvent diffusion compared to phase separation, while different relative dynamics resulted in the formation of laminar pores.
, plays a major role in acquiring isotropic bijels via STrIPS. In particular, it was found that isotropic bijel structures only occurred for fast solvent diffusion compared to phase separation, while different relative dynamics resulted in the formation of laminar pores.
With these relations established, the final parameter in the PF model to be discussed is the critical interfacial tension σc. Similar to ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) , the value of σc has a distinct influence on the morphology and can be directly related to a physical property of the bijel system, as will be shown next.
, the value of σc has a distinct influence on the morphology and can be directly related to a physical property of the bijel system, as will be shown next.
4.4 The influence of σc
Owing to its considerable influence on the obtained morphology, the value of the critical interfacial tension σc warrants additional discussion. The relevance of σc, above which phase separation is arrested, can be readily made apparent by considering it as an effective stand-in for the nanoparticle size. Namely, in accordance with eqn (14), the attachment energy ΔG of a particle at a liquid–liquid interface scales with the interfacial tension σ times the square of the particle radius r239ΔG = −πr2σ(1 − |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|)2 θ|)2 | (14) |
Consequently, as an interface develops during phase separation, the increasing interfacial tension will irreversibly trap larger particles earlier than smaller ones. In other words, larger particles can cause interfacial jamming at lower interfacial tensions compared to smaller particles. This can be qualitatively reflected in the value of σc, with lower values corresponding to the presence of larger particles in the system. In this manner, the pore size can be controlled via σc, with lower values of σc resulting in smaller pores.
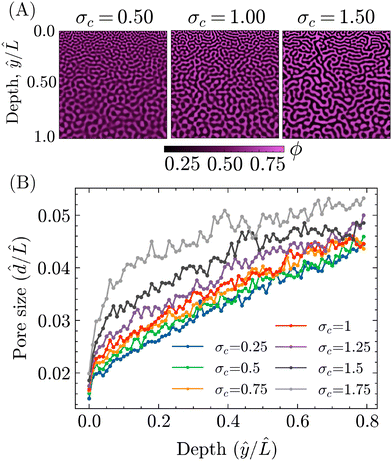
To investigate this potential effect of σc, PF simulations were carried out with different values of σc, while keeping the other parameters the same as for the STrIPS simulations in Fig. 3. Some representative examples of the resulting morphologies are shown in Fig. 6A, all displaying the characteristic STrIPS bijel structure with a distinct pore size gradient. While the pore sizes visually already seem to differ between them, the pore size profiles in Fig. 6B were calculated (ESI,† S4) to properly compare the different morphologies.
These profiles show the average pore size over the depth of the structure, both normalised with respect to the length of the simulation domain, for different values of σc. Corroborating previous results, they unambiguously demonstrate that the average pore size increases deeper into the structure, further away from the boundary with the ambient phase. Furthermore, the profiles also indicate that the value of σc does have a noticeable effect on the pore size. In line with expectations, lower values of σc translate to smaller average pore sizes over the entire depth of the structure. The strength of this effect, however, varies within the structure, being the most pronounced close to the surface and lessening deeper in.
This difference can be explained by considering that the surface region, being directly adjacent to the ambient phase, is depleted of solvent considerably faster compared to the rest of the system. Therefore, the quench of the composition into the spinodal region is faster and deeper, resulting in correspondingly fast dynamics of phase separation and a relatively steep increase in the interfacial tension. As such, equivalent changes in σc result in greater differences in the average pore size for the structure's surface compared to ‘slower’ regions deeper within. Regardless of this discrepancy, it can be concluded that σc can effectively be used to tune the particle size in the bijel system.
While these findings seem to align with the expected behaviour of σc in its qualitative relation to the particle size, there remain some key issues with directly transposing it to the experimental system. Most importantly, the PF model does not sufficiently take into account the explicit diffusion, attachment and subsequent jamming of particles.
For example, not only do smaller particles simply diffuse faster, the bijel structure is also not immediately arrested following the irreversible attachment of particles, as implied by the σc rationale in the PF simulation. Rather, structure coarsening continues until the decreasing interfacial area causes the jamming of an attached particle layer. Consequently, it is the liquid interfacial area available, in relation with the number of particles present, that sets the criterion for arresting phase separation. For example, when present in equivalent volumes, smaller particles require larger interfacial areas compared to larger particles, resulting in the stabilisation of smaller pores.15,40 Furthermore, the minimum dimensions of a particle-stabilised pore are dictated by the size of the particles. That is, particles can not stabilise pores with smaller dimensions than the particles themselves. Consequently, for large differences in particle size, the smaller particles are likely to yield structures with smaller pores compared to larger ones.
Even though its relation with the physical bijel might not be fully complete, the value of σc remains an effective tool for controlling the average pore size in PF simulations. With the role of this parameter elucidated, in addition to ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) , the next step was to directly compare PF simulations to experimental bijel systems. In particular, it is demonstrated that the PF model can match trends in bijel morphologies for different experimental conditions, providing a potential explanation behind their origin.
, the next step was to directly compare PF simulations to experimental bijel systems. In particular, it is demonstrated that the PF model can match trends in bijel morphologies for different experimental conditions, providing a potential explanation behind their origin.
4.5 Comparison with experimental results
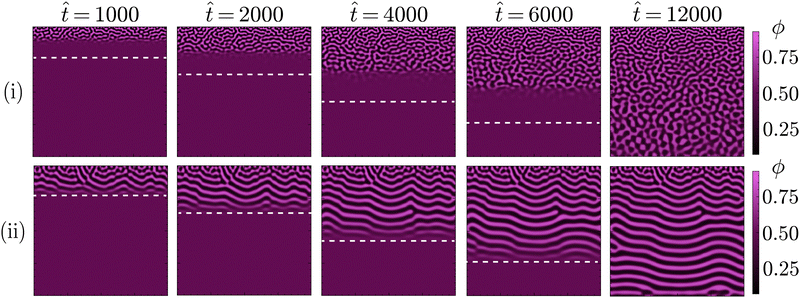
So far, the PF model has shown capable of replicating the core components of the STrIPS process, yielding structures with very similar morphological features to bijels. To further support this notion, in addition to demonstrating the potential of the PF model in rationalising experimental findings, PF simulations are directly compared to experimental morphologies of STrIPS bijels synthesised under different experimental conditions. As will be shown, the observed morphological trends can be readily explained by the PF model, providing further insight into the tailoring of the bijel structure for this experimental system.The experimental system in questions involves the formation of a bijel fibre containing a central borehole, which is filled with a liquid. While the experimental details of this system are described elsewhere,41 a schematic depiction of the PF model is shown in Fig. 7A. The principal feature of this specific bijel system is that the solvent can diffuse in two directions during STrIPS, both into the exterior ambient phase and into the liquid occupying the central bore. In experiments, it is found that this results in the formation of a two-sided pore size gradient: the pores are smallest next to the interfaces with both the interior bore liquid and the ambient phase, while they are largest near the centre of the bijel shell.
Additionally, the solvent content in the bore liquid can be varied. Experimentally, it was found that varying this solvent content shifts the position of the maximum pore size in the bijel shell, moving closer to the interface with the bore liquid for higher solvent contents. In order for simulations to assist in providing a possible explanation behind the origin of these morphological trends, the experimental system first had to be replicated in the PF model.
Fig. 7A shows a schematic depiction of the PF model used for this experimental system. A section of the precursor shell is represented by a square simulation domain, neglecting the influence of curvature on the diffusion of solvent. The top edge of the simulation domain represents the boundary between the bijel precursor and the exterior ambient phase, whereas the bottom edge represents the boundary with the interior bore channel. The exchange of solvent with both the liquid bore channel and the ambient phase was controlled through Neumann boundary conditions. In particular, the solvent content in the liquid bore channel was varied through ϕBCs, whilst for the ambient phase it was consistently kept at zero. Subsequently, PF simulations were performed with the same parameters as for the STrIPS simulations in Fig. 3, while the values of ϕBCs were varied.
The results of these simulations, shown in Fig. 7B, reveal that the diffusion of solvent into the ambient phase and liquid bore channel initiates phase separation at the top and bottom of the simulation domain, respectively. When there is no solvent present in the bore liquid (ϕBCs = 0), this phase separation continues in a symmetric fashion towards the centre of the system. As the solvent content in the centre remains higher over a longer period of time, prolonged coarsening of the structure results in larger pores. This process finally yields a morphology with a distinct two-sided pore size gradient, corroborating experimental observations.
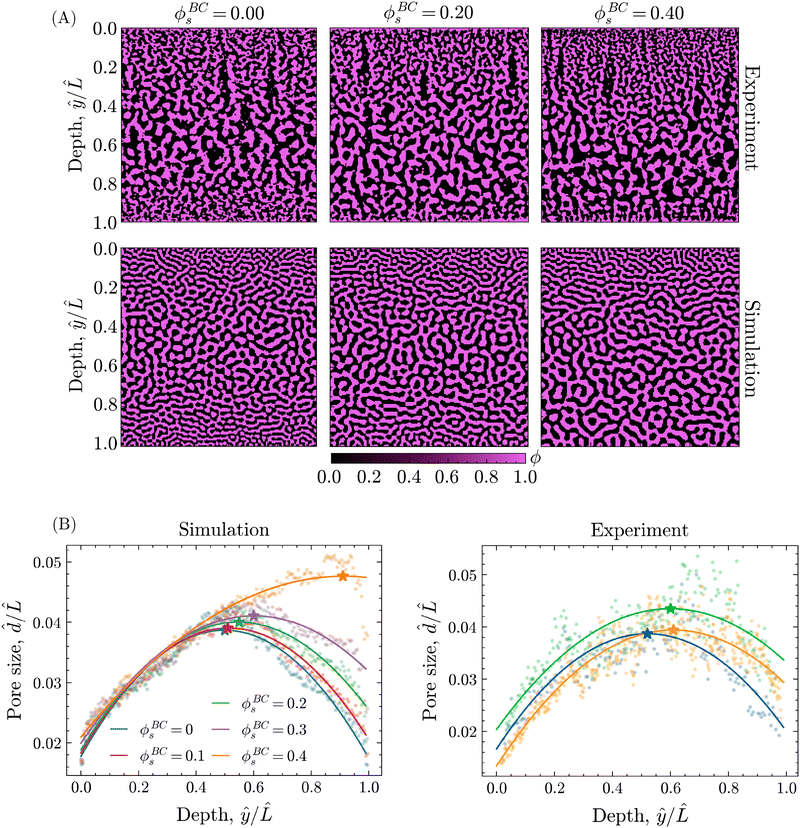
The introduction of solvent into the bore liquid, however, induces asymmetric phase separation that considerably changes the resulting morphology. In particular, higher solvent contents in the bore liquid lower the rate of solvent depletion in the adjacent precursor region, delaying the onset of phase separation. Additionally, this region maintains higher levels of solvent over a longer time, allowing for a greater extent of coarsening prior to the arrest of phase separation. Consequently, the pores closer to the bore channel become larger with increasing ϕBCs. An overview of the resulting structures for the different values of ϕBCs is shown in Fig. 8A, additionally containing the corresponding morphologies of experimental STrIPS bijels, acquired via confocal microscopy.
On first sight, the experimental and simulated morphologies of the STrIPS bijels already appear strikingly similar, indicating that the PF model accurately managed to replicate the experimental conditions of the STrIPS synthesis. To quantitatively substantiate this observation, pore size profiles were calculated for the different values of ϕBCs and subsequently fitted with a quadratic polynomial curve. In order to compare the pore size profiles between the simulations and the experimental images, the average pore size ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) and the depth within the structure ŷ were normalised with respect to the length
and the depth within the structure ŷ were normalised with respect to the length ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) , corresponding to the length of the simulation domain and confocal image, respectively. These profiles, shown in Fig. 8B, confirm the presence of a two-sided pore size gradient for both the PF simulations and the experimental bijel morphologies. Starting from either the top or the bottom boundary of the structure the pores are the smallest, which then increase in size deeper into the structure before reaching a maximum and subsequently decreasing again while approaching the opposite boundary. The depth where the pore size reaches its maximum, indicated by the star marker in the pore size profiles, appears to shift depending on the solvent fraction of the bore liquid.
, corresponding to the length of the simulation domain and confocal image, respectively. These profiles, shown in Fig. 8B, confirm the presence of a two-sided pore size gradient for both the PF simulations and the experimental bijel morphologies. Starting from either the top or the bottom boundary of the structure the pores are the smallest, which then increase in size deeper into the structure before reaching a maximum and subsequently decreasing again while approaching the opposite boundary. The depth where the pore size reaches its maximum, indicated by the star marker in the pore size profiles, appears to shift depending on the solvent fraction of the bore liquid.
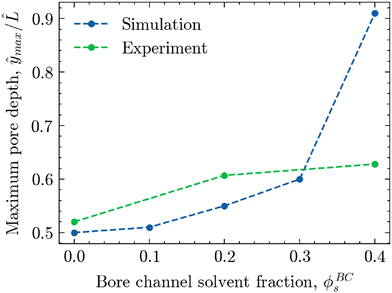
To better visualise this shift for both experimental and simulated morphologies, Fig. 9 shows the relative depth of maximum pore size ŷmax/![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) plotted against the solvent volume fraction within the bore liquid ϕBCs. As seen in the simulations of Fig. 7B, phase separation for ϕBCs = 0 is relatively symmetric due to the equal rates of solvent depletion to the ambient phase and bore channel. This results in an equally symmetric, parabolic pore size profile with a maximum located near the centre of the morphology, roughly around ŷ/
plotted against the solvent volume fraction within the bore liquid ϕBCs. As seen in the simulations of Fig. 7B, phase separation for ϕBCs = 0 is relatively symmetric due to the equal rates of solvent depletion to the ambient phase and bore channel. This results in an equally symmetric, parabolic pore size profile with a maximum located near the centre of the morphology, roughly around ŷ/![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) = 0.5. In contrast, increasing the solvent fraction in the bore liquid slows down the diffusion rate towards the bore channel relative to the ambient phase. As a result, phase separation in the region adjacent to the bore channel is arrested at a later stage, facilitating a greater extent of structure coarsening. Consequently, the average pore size on the side of the bore channel increases, shifting the maximum away from the centre towards the interface with the bore liquid, corresponding to an increase in ŷmax/
= 0.5. In contrast, increasing the solvent fraction in the bore liquid slows down the diffusion rate towards the bore channel relative to the ambient phase. As a result, phase separation in the region adjacent to the bore channel is arrested at a later stage, facilitating a greater extent of structure coarsening. Consequently, the average pore size on the side of the bore channel increases, shifting the maximum away from the centre towards the interface with the bore liquid, corresponding to an increase in ŷmax/![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) .
.
While this shift in the location of the maximum pore size as a function of ϕBCs is visible for both the experimental and simulated morphologies, it is distinctly more pronounced in the simulations. There, increasing the solvent content in the bore liquid up to ϕBCs = 0.40 nearly creates a linear pore size profile with a maximum very close to the boundary of the bore channel. For the experimental structures, however, the shift in the pore size maximum appears to flatten off somewhat, not exceeding ŷmax/![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) = 0.63 for ϕBCs = 0.40.
= 0.63 for ϕBCs = 0.40.
Likely, part of the discrepancy can be attributed to the fact that the solvent parameter ϕs in simulations simply does not directly translate to the actual solvent volume fraction as employed in experimental work. Additionally, there are other, underlying mechanisms at play during STrIPS that are currently not captured by the model. For example, the influx of both ambient and bore liquids or the preferential partitioning of solvents18 can disrupt the ideal diffusion behaviour as assumed by the model, causing deviation from the predicted pore size profiles.
In conclusion, there is a significant level of agreement between the simulated and experimental bijel morphologies, indicating that the PF model can accurately describe bijel formation via STrIPS in this complex experimental system. In this manner, the PF simulations allowed for the in situ observation of the STrIPS process, providing a potential explanation for the morphological trends found in the experimental bijels depending on the synthesis conditions.
5 Discussion
The results presented in this work demonstrate that the simple PF model can effectively capture the core mechanisms of the complex STrIPS process. Through these basic principles, the simulations readily produce structures with the characteristic features of STrIPS bijels. Consequently, the PF model allows for the observation and investigation of the entirety of the STrIPS process, not only the final structure. In this manner, the influence of critical parameters, such as the mobility![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) , on the final morphology could be directly associated with differences in the formation mechanism. Moreover, the PF simulations were used to rationalise the appearance of morphological trends in experimental STrIPS bijels.
, on the final morphology could be directly associated with differences in the formation mechanism. Moreover, the PF simulations were used to rationalise the appearance of morphological trends in experimental STrIPS bijels.
While these findings showcase the potential of the PF model, its current version remains limited in some aspects. Firstly, the approach of modelling phase separation and solvent diffusion through two separate phase-fields prevents direct comparison between the model solvent parameter ϕs and the experimental solvent volume fraction. Additionally, this method excludes multi-component interactions and by extension the associated effects that could be relevant for the STrIPS process, such as preferential solvent partitioning.18
Secondly, the PF model employs considerable simplifications by assuming constant values of the mobility M and a free energy density f given by a regular solution. While these are sufficient for describing the main principles underlying STrIPS, they need to be further extended to provide a more accurate representation. For example, composition-dependent mobilities can result in different coarsening kinetics for the formed structure.42 Additionally, a Flory–Huggins free energy density could better match the thermodynamics of the STrIPS precursor mixture while simultaneously including multi-component interactions.38 This extension of the current model to include full multi-component phase separation with composition-dependent mobilities will be the topic of future work.
Furthermore, the present version of the PF model only includes diffusive mass transport, neglecting convective transport via fluid flows. However, as is the case for polymeric membranes fabricated via phase inversion,30,33 it is likely that such hydrodynamic effects also play a role in determining the final morphology of the STrIPS bijel. Consequently, a full description of the STrIPS process requires the incorporation of hydrodynamics. While outside the scope of this current work, the coupling of hydrodynamics into the PF model has the additional benefit of expanding the selection of relevant system parameters that can be examined. For example, the influence of the component viscosity on the morphology of the STrIPS bijel, currently reflected only to a limited extent in the relative mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) , could be explicitly investigated.
, could be explicitly investigated.
Finally, while the interfacial jamming of nanoparticles during STrIPS is effectively replicated through the surface tension σ, there remain some issues with this approach (see Section 4.4). PF models, however, have additional options for the direct inclusion of the nanoparticles. For example, ongoing research involves describing the nanoparticles through their own continuous phase-field. In this manner, the interfacial activity and subsequent arrest of phase separation could be modelled while remaining computationally feasible on the spatial and temporal scales relevant to STrIPS.
6 Conclusions
In this work, a PF model is presented that captures the complex mechanism of bijel formation via STrIPS through relatively simple methods. This is achieved through the evolution of two distinct phase-fields, representing the oil/water mixture and the solvent, respectively. By making the oil/water interaction dependent on the solvent field, the physics of the oil/water/solvent system can be effectively replicated, showing phase separation behaviour consistent with the underlying theory. It is further demonstrated that the role of the nanoparticles in arresting phase separation can be reproduced by using the interfacial tension as a substitute measure.Through this PF model, it is then shown that morphologies with characteristic bijel features are obtained in systems with relatively slow dynamics of phase separation compared to solvent diffusion. In the model, such a system is represented by low values of the relative oil/water mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and gradient energy coefficient
and gradient energy coefficient ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) . Increasing these values, thus transitioning to a system with faster relative dynamics and a higher energy penalty for compositional gradients, instead results in the formation of laminar pores. These morphological differences are explained in the context of progressive phase separation directed by a planar diffusion front.
. Increasing these values, thus transitioning to a system with faster relative dynamics and a higher energy penalty for compositional gradients, instead results in the formation of laminar pores. These morphological differences are explained in the context of progressive phase separation directed by a planar diffusion front.
Finally, the PF model is applied to investigate the formation of STrIPS bijels by replicating the conditions of a complex experimental system. The resulting, simulated morphologies show strong qualitative agreement with the experimental bijel structures obtained from experiments. Moreover, the PF model could reproduce morphological trends found in the experimental system, while simultaneously providing a potential explanation for their origin. While some discrepancies remain, it is expected that these can be further remedied by extending the model to include full multi-component phase separation.
Overall, this work unambiguously demonstrates the potential of the PF model in the simulation of bijel formation via STrIPS, especially in conjunction with experimental work. By allowing effective in situ observation of the entire STrIPS process, the PF model can help clarify the formation mechanisms of current STrIPS bijel morphologies, as well as facilitate the synthesis of new ones.
Author contributions
Jesse Steenhoff: conceptualisation, methodology, software, investigation, formal analysis, data curation, visualisation, writing – original draft, writing – review & editing Martin Haase: conceptualisation, supervision, funding acquisition, writing – review & editing.Data availability
The code and datasets underlying the findings in this work are available on GitHub (https://github.com/JesseSteenhoff/A-simple-phase-field-model-of-bijel-formation-via-solvent-transfer-induced-phase-separation) and have been archived on Zenodo (https://doi.org/10.5281/zenodo.14755856). These include the Python scripts for the presented phase-field model and the pore size analysis. The datasets (both experimental and simulated) required for the reproduction of the pore size analysis are additionally provided.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is part of the project “Bijel templated membranes for molecular separations” (with project number 18632 of the research programme Vidi 2019), which is financed by the Dutch Research Council (NWO). The authors would like to acknowledge Mariska de Ruiter for providing the raw confocal microscopy data of the bijel structures with bore channels.References
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- Y. Yang, Z. Fang, X. Chen, W. Zhang, Y. Xie, Y. Chen, Z. Liu and W. Yuan, Front. Pharmacol., 2017, 8, 235054 Search PubMed.
- H. Zhao, Y. Yang, Y. Chen, J. Li, L. Wang and C. Li, Chem. Eng. Sci., 2022, 248, 117085 CrossRef CAS.
- J. Texter, Colloid Polym. Sci., 2022, 300, 587–592 CrossRef CAS.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS PubMed.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS PubMed.
- M. F. Haase, H. Jeon, N. Hough, J. H. Kim, K. J. Stebe and D. Lee, Nat. Commun., 2017, 8, 1234 CrossRef PubMed.
- H. Siegel, A. J. Sprockel, M. S. Schwenger, J. M. Steenhoff, I. Achterhuis, W. M. de Vos and M. F. Haase, ACS Appl. Mater. Interfaces, 2022, 14, 43195–43206 Search PubMed.
- T. Wang, R. A. Riggleman, D. Lee and K. J. Stebe, Mater. Horiz., 2023, 10, 1385–1391 RSC.
- J. A. Witt, D. R. Mumm and A. Mohraz, J. Mater. Chem. A, 2016, 4, 1000–1007 RSC.
- D. Cai, F. H. Richter, J. H. J. Thijssen, P. G. Bruce and P. S. Clegg, Mater. Horiz., 2018, 5, 499–505 Search PubMed.
- G. Di Vitantonio, T. Wang, M. F. Haase, K. J. Stebe and D. Lee, ACS Nano, 2019, 13, 26–31 CrossRef CAS PubMed.
- T. Park, G. H. Choi, D. Lee and P. J. Yoo, J. Membr. Sci., 2021, 634, 119386 CrossRef CAS.
- J. W. Tavacoli, J. H. J. Thijssen, A. B. Schofield and P. S. Clegg, Adv. Funct. Mater., 2011, 21, 2020–2027 CrossRef CAS.
- D. Cai, P. S. Clegg, T. Li, K. A. Rumble and J. W. Tavacoli, Soft Matter, 2017, 13, 4824–4829 RSC.
- M. F. Haase, K. J. Stebe and D. Lee, Adv. Mater., 2015, 27, 7065–7071 CrossRef CAS PubMed.
- S. P. Kharal and M. F. Haase, Small, 2022, 18, 2106826 Search PubMed.
- M. A. Khan, A. J. Sprockel, K. A. Macmillan, M. T. Alting, S. P. Kharal, S. Boakye-Ansah and M. F. Haase, Adv. Mater., 2022, 34, 2109547 CrossRef CAS PubMed.
- H. Siegel, M. de Ruiter, G. Athanasiou, C. M. Hesseling and M. F. Haase, Adv. Mater. Technol., 2024, 9, 2301525 CrossRef CAS.
- L. Bai, J. W. Fruehwirth, X. Cheng and C. W. Macosko, Soft Matter, 2015, 11, 5282–5293 RSC.
- D. Cai and P. S. Clegg, Chem. Commun., 2015, 51, 16984–16987 RSC.
- E. Kim, K. Stratford, R. Adhikari and M. E. Cates, Langmuir, 2008, 24, 6549–6556 Search PubMed.
- P. C. Millett and Y. U. Wang, J. Colloid Interface Sci., 2011, 353, 46–51 CrossRef CAS PubMed.
- F. Jansen and J. Harting, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046707 CrossRef PubMed.
- J. M. Carmack and P. C. Millett, J. Chem. Phys., 2015, 143, 154701 Search PubMed.
- E. Kim, K. Stratford and M. E. Cates, Langmuir, 2010, 26, 7928–7936 Search PubMed.
- A. S. Joshi and Y. Sun, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 066703 CrossRef PubMed.
- N. Karthikeyan and U. D. Schiller, Soft. Matter., 2024, 20, 8952–8967 Search PubMed.
- M. J. A. Hore and M. Laradji, J. Chem. Phys., 2007, 126, 244903 Search PubMed.
- B. Zhou and A. C. Powell, J. Membr. Sci., 2006, 268, 150–164 CrossRef CAS.
- Y. Mino, T. Ishigami, Y. Kagawa and H. Matsuyama, J. Membr. Sci., 2015, 483, 104–111 CrossRef CAS.
- G. Zhang, T. Yang, S. Yang and Y. Wang, Phys. Rev. E, 2017, 96, 032501 Search PubMed.
- D. R. Tree, T. Iwama, K. T. Delaney, J. Lee and G. H. Fredrickson, ACS Macro Lett., 2018, 7, 582–586 CrossRef CAS PubMed.
- M. R. Cervellere, X. Qian, D. M. Ford, C. Carbrello, S. Giglia and P. C. Millett, J. Membr. Sci., 2021, 619, 118779 CrossRef CAS.
- J. M. Carmack and P. C. Millett, Soft Matter, 2018, 14, 4344–4354 RSC.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- R. C. Desai and R. Kapral, in Free energy functional, Cambridge University Press, Cambridge, 2009, pp. 20–24 Search PubMed.
- H. Zhang, Y. Wu, F. Wang, F. Guo and B. Nestler, Langmuir, 2021, 37, 5275–5281 CrossRef CAS PubMed.
- B. P. Binks and T. S. Horozov, Colloidal Particles at Liquid Interfaces, Cambridge University Press, Cambridge, 2006 Search PubMed.
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138 RSC.
- R. de Ruiter, PhD thesis (Research UU/Graduation UU), Universiteit Utrecht, 2024.
- B. König, O. J. J. Ronsin and J. Harting, Phys. Chem. Chem. Phys., 2021, 23, 24823–24833 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04638b |
| This journal is © the Owner Societies 2025 |