Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy transfer booster: how a leaving group controls the excited state pathway within a caging BASHY–BODIPY dyad†
Yagmur
Aydogan-Sun‡
 a,
Maximiliane
Horz‡
a,
Maximiliane
Horz‡
 a,
Rebekka
Weber
b,
Myron
Heinz
a,
Markus
Braun
a,
Rebekka
Weber
b,
Myron
Heinz
a,
Markus
Braun
 a,
Alexander
Heckel
a,
Alexander
Heckel
 *b,
Irene
Burghardt
*b,
Irene
Burghardt
 *a and
Josef
Wachtveitl
*a and
Josef
Wachtveitl
 *a
*a
aInstitute for Physical and Theoretical Chemistry, Goethe-University Frankfurt, Max-von-Laue Str. 7, 60438 Frankfurt, Germany. E-mail: wveitl@theochem.uni-frankfurt.de; burghardt@chemie.uni-frankfurt.de
bInstitute for Organic Chemistry and Chemical Biology, Goethe-University Frankfurt, Max-von-Laue Str. 7, 60438 Frankfurt, Germany. E-mail: heckel@uni-frankfurt.de
First published on 14th February 2025
Abstract
Photocages are powerful tools for spatiotemporal control of molecule release or biological activity. However, many photocages are unsuitable for biological experiments since they are mostly activated by harmful ultraviolet (UV) light and often lack a sufficient optical readout. Thus, there is a high demand for near infrared (NIR) and/or two-photon activatable photocages with a characteristic readout. In this report, we will study a supramolecular, covalently linked energy-transfer dyad based on a BASHY fluorophore serving as a two-photon antenna for a poorly two-photon absorbing BODIPY photocage. The herein investigated systems, with and without a leaving group (LG), show different excitation energy transfer (EET) efficiencies and therefore differ in their fluorescence properties. To understand the molecular basis for these significant differences, detailed spectroscopic and theoretical analyses were employed from ultrafast transient absorption spectroscopy to excited-state electronic structure calculations and quantum dynamical modelling. The result of our comprehensive study reveals the pivotal role of the LG as an EET booster through specific pathway guidance. In contrast, without the LG, the EET efficiency is reduced and the excitation energy predominantly dissipates within the BASHY chromophore. The present study highlights that LGs can actively contribute to optimizing the properties of dyad based systems and offers new design principles for monitoring uncaging via an intrinsic fluorescence readout.
1 Introduction
In recent decades, photocages evolved to an indispensable element for spatiotemporal control of light-driven processes. As an integral part of their structure, photocages usually carry a “caged” molecular unit whose functionality is masked by the photocage. Upon light irradiation this molecular unit, often classified as the leaving group (LG), can be released from the photocage and its activity is restored. While the chromophore represents the light-responsive unit, the LG is typically designed to be the key functional component. Thus, many applications are possible with a single photocage by varying its LG for the desired experimental observation. The applications range from triggering biological activity1–3 or manipulating it via optogenetic approaches4,5 to medical applications such as drug release6,7 or photodynamic therapy.8,9Despite these promising applications, photocages are still far from clinical applications, since most of them are only efficiently activated by UV excitation which is harmful to biological tissue. Ideally, photocages would respond within the therapeutic window ranging from 650 to 950 nm, where the penetration into biological tissue is the most effective.10 However, activation in the red through 1-photon excitation is usually inefficient due to the increase of non-radiative transitions and the lack of energy needed for successful cleavage.11 Still, many advances were recently made in 1-photon NIR-activatable photocages.8,12,13 Another possibility for NIR activation is through 2-photon excitation which allows photorelease within the biological window while likely maintaining the uncaging efficiency of UV photocages. Unfortunately, most commonly used photocages inherently exhibit poor 2-photon absorption (2PA)14 and therefore high excitation intensities are needed due to the squared dependency of 2PA on intensity. On the one hand, this allows high spatial resolution, but on the other hand this approach makes the observation of 2-photon activated release challenging owing to the small excitation volume of a few femtoliters. So far, 2-photon uncaging is usually observed by 2-photon fluorescence microscopy and mainly on immobilized samples to avoid diffusion effects. For such experiments biological activity, induced by the LG, typically results in a change of fluorescence properties which is used as the optical readout.15–17
Nevertheless, the beneficial properties of 2PA outweigh these challenges and thus there is a high demand for photocages with efficient 2PA capabilities. There are three main strategies to improve 2PA of photocages. One strategy involves structural modifications on the chromophore such as extension of the π-system or attachment of push–pull groups.14,18 A downside of this strategy is, however, that it typically results in a significant loss of uncaging efficiency since further possible deactivation pathways are introduced. Another, less common strategy, involves refunctioning 2-photon fluorophores into photocages. The benefit of this strategy is that fluorophores are highly optimized molecules with a long-lived excited state, where fast deactivation channels are already eliminated.19,20 So far, this strategy is not straightforward and involves careful assessment of the structural features and a perfect positioning of the LG for a significant uncaging efficiency. The third strategy is based on cooperative dyad systems where the excitation and uncaging processes are separated onto two molecular units.21,22 The first unit acts as an antenna, mainly absorbing the excitation light and subsequently transferring it to the functional unit, in this case the photocage. Usually, the antenna is chosen to be a molecule with good 1-photon and 2-photon properties to yield a more efficient excitation process. The details of excitation energy transfer (EET) highly depend on the nature and length of the connecting linker between the two units. While conjugated and flexible linkers lead to supermolecular systems with new properties, non-conjugated and rigid linkers, preferably also in “meta”-connectivity allow a strong separation of the excitation energy localization and thus preservation of the respective chromophore properties. Therefore, this modular approach offers a variety of possibilities by slight adjustments of the linker design.
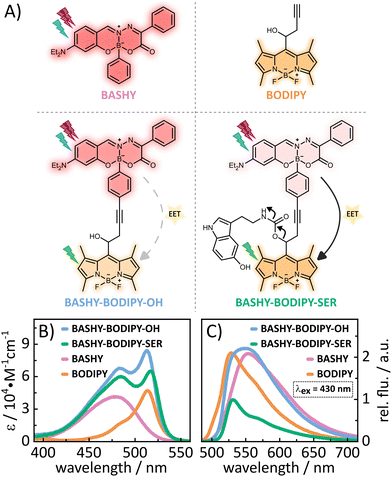
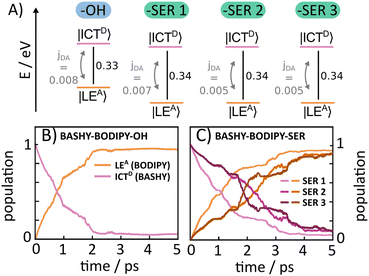
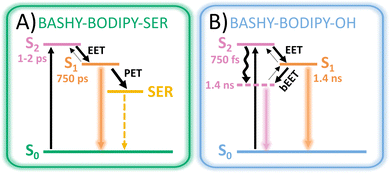
In this context, our aim is to enhance the 2PA properties of a photocage without extensive derivatization of its chromophore. To this end, we developed a dyad based on BASHY and BODIPY featuring an energy transfer between the two moieties (see Fig. 1A). While BODIPY is known to be an excellent fluorophore,23 since its discovery many decades ago, in recent years it has also evolved as an important photocage.24 Meanwhile, BASHY was introduced in 2016 in a collaborative work of the Pischel and Gois labs.25 Despite having similarly advantageous properties as BODIPY and even featuring intrinsically good 2PA for the basic chromophore,26BASHY still finds little usage by the majority of the community. In this work, we present two BASHY–BODIPY dyads, where BASHY serves as a 2P antenna for the poorly 2-photon absorbing BODIPY photocage. In both dyads, the two moieties are covalently bound through a rigid alkyne linker. The only difference between the two dyads is the mesomethyl position of BODIPY where one dyad (BASHY–BODIPY–SER) bears serotonin (SER) as a leaving group and the other one (BASHY–BODIPY–OH) carries a hydroxy group instead. Interestingly, while this seems to be a small difference at first sight, the leaving group has an impact not only on the fluorescence properties (see Fig. 1C), but also on the excited state dynamics and especially the energy transfer efficiency. Notably, this behavior was previously observed in another dyad with the same linker construction.27 In order to understand the cause of these remarkable differences, both dyads as well as the respective single chromophores BASHY and BODIPY were subjected to detailed spectroscopic and theoretical analyses. The structures of the investigated molecules are displayed in Fig. 1A and their syntheses are presented in the ESI.†
2 Results and discussion
2.1 Steady state properties
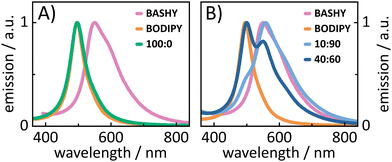
A lot of information about the electronic coupling and the EET efficiency within a dyad can be obtained from the stationary properties of the dyad and its individual chromophore units. Thus, in the following a detailed discussion of the absorption (Fig. 1B) and fluorescence (Fig. 1C) properties is provided. Regarding the steady state properties of the single chromophores, BODIPY shows a more redshifted absorption, while its fluorescence is more blueshifted compared to BASHY. This reflects a large difference in their Stokes shifts. While BODIPYs generally show small Stokes shifts, BASHYs tend to have a larger, highly solvent-dependent Stokes shift. In polar solvents such as DMSO, BASHYs display a strong intramolecular charge transfer (ICT) character in the excited state (see Fig. S17, ESI† and ref. 25). This ICT state can be stabilized by polar solvents, resulting in a redshift and a reduction in fluorescence efficiency. The absorption spectra of both dyads resemble the sum of the single chromophores' absorption spectra. This preservation of the respective building block properties indicates a localization of the excited states on either one or the other chromophore. Another important aspect of energy-transfer systems like dyads is their fluorescence spectra since the amount of fluorescence from either the donor or the acceptor state will indicate how efficient the EET is. The fluorescence spectra of the two dyads differ significantly, as can be seen in Fig. 1C. While BASHY–BODIPY–OH seems to show a mixed fluorescence from both states, the fluorescence in BASHY–BODIPY–SER completely results from the BODIPY state. Thus, the EET within BASHY–BODIPY–OH seems to be less efficient compared to BASHY–BODIPY–SER. The leaving group SER, as the only remarkable difference between both dyads, apparently facilitates the energy transfer. Given that SER is a relatively large leaving group, capable of forming a hydrogen bond with the fluorine atoms of BODIPY (see Fig. S2, ESI†), we initially hypothesized that this interaction might play a key role in the divergent EET efficiencies. However, our investigation of another dyad BASHY–BODIPY–AC, with acetic acid as the LG (see Fig. S18, ESI†), which exhibits similar EET efficiency to BASHY–BODIPY–SER, showed that the observed behavior cannot be solely attributed to the hydrogen bonding. Furthermore, the leaving group also appears to affect the fluorescence quantum yield, as shown for BASHY–BODIPY–SER in Table 1. While with 22%, BASHY–BODIPY–OH preserves the fluorescence quantum yield of the individual chromophores, the fluorescence quantum yield of BASHY–BODIPY–SER drops to 10%. Such a significant drop can be caused by a photoinduced electron transfer (PET) from the BODIPY to the LG.28 Another possibility is that the fluorescence becomes less efficient as other competing pathways like uncaging increase.| Molecule | ϕ f (%) | ε 484nm (cm−1 M−1) | ε 514nm (cm−1 M−1) |
|---|---|---|---|
| BASHY | 21 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 500 000 ± 500 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 100 700 ± 100 |
| BODIPY | 21 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 ± 120 240 ± 120 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 200 000 ± 200 |
| BASHY–BODIPY–OH | 22 | 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 400 300 ± 400 |
84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 400 000 ± 400 |
| BASHY–BODIPY–SER | 10 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 ± 900 300 ± 900 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 700 000 ± 700 |
In addition to the one-photon absorption properties, the 2P excitation spectra for all four molecules (see Fig. 2A) were recorded using 2-photon induced fluorescence in order to verify the improved 2P excitability of BODIPY within the dyads. All molecules show power squared dependence (see Fig. 2B) within the measured power range (see the ESI† for details of the experimental settings). In accordance with the literature,29BODIPY shows low 2PA over the whole measured wavelength range. The highest obtained value for BODIPY is 5 GM at 960 and 1030 nm. BASHY on the other hand is known to be a better 2P absorber and shows 2PA cross-sections of 25 GM at 920 nm and 20 GM at 970 nm, which are assigned to a vibrational feature and the maximum of the S1 transition. Notably, this vibrational feature aligns well with the one observed in the steady-state absorption spectrum with toluene (see Fig. S17, ESI†). In general, these values are in the range expected for the basic BASHY chromophore.30BASHY–BODIPY–OH shows 2PA cross-sections of 37 GM at 910 nm and 32 GM at 960 nm, while BASHY–BODIPY–SER exhibits slightly lower values of 35 GM at 910 nm and 30 GM at 960 nm. Thereby, they not only compensate the low 2PA cross-sections of BODIPY but even enhance the 2P excitability of BASHY. Small contributions of BODIPY to the 2PA of the dyads are noticeable at 960 and 1050 nm.
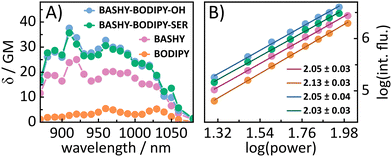 | ||
| Fig. 2 (A) 2P excitation spectra of the molecules in DMSO obtained by the 2P induced fluorescence method. (B) Power squared dependence of the 2P induced fluorescence. | ||
For a more detailed insight into the excited state properties, electronic structure calculations employing density functional theory (DFT) and its time-dependent extension (TD-DFT) as implemented in the Gaussian16 package were performed for the dyads and their molecular components BODIPY and BASHY.31 The ground state equilibrium structures of the single chromophores BASHY and BODIPY as well as of both dyads were obtained using the long-range corrected CAM-B3LYP functional32 and Ahlrich's def2-SVP double-zeta basis set.33,34 These geometries were confirmed to be minima via a subsequent harmonic vibrational analysis. Excited state properties, i.e., vertical excitation energies, oscillator strengths f, transition dipole moments and density differences were obtained within the adiabatic approximation employing the same functional and basis set combination. Solvent effects of DMSO were accounted for using the polarizable continuum model (PCM).35–37 Analysis of the state character was obtained via the TheoDORE tool where electron–hole maps are constructed from fragment-based transition densities.38–40
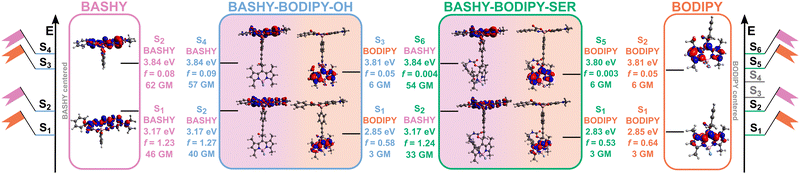
The excited state analysis of BASHY–BODIPY–OH and BASHY–BODIPY–SER is reported in Fig. 3 and Table 2. The state ordering is very similar between the two dyads with BASHY–BODIPY–OH displaying two one-photon bright states with excitation energies of 2.85 eV (435 nm) and 3.17 eV (391 nm), followed by two spectroscopically dark states at 3.81 eV (325 nm) and 3.84 eV (323 nm), while BASHY–BODIPY–SER features two bright states at 2.83 eV (438 nm) and 3.17 eV (391 nm), followed by four dark states at 3.19 eV (389 nm), 3.65 eV (340 nm), 3.80 eV (327 nm) and 3.84 eV (323 nm). Corresponding to the spectroscopic indications, the excited states are mostly localized on either of the two moieties, with the S1 state being localized on the BODIPY fragment and the S2 state on the donor BASHY moiety. While both excited states are localized on either moiety of the dyad, the first BASHY excitation is known to exhibit an ICT character on the BASHY fragment as previously observed by experimental and computational analyses.41–43 This ICT character is reflected in a shift of the density from the outer part of the big π-system and the diethylamine-substituent to the center of the BASHY scaffold, which is facilitated by the planarization of the benzyl-substituent with regard to the rest of the π-system upon photoexcitation (see Fig. S5, ESI†). A detailed partitioning for the ICT analysis based on the TheoDORE tool can be found in Fig. S7 in the ESI.†
| System | BASHY–BODIPY–OH | BASHY–BODIPY–SER | |
|---|---|---|---|
| S1 | Excitation energy (eV) | 2.85 | 2.85 |
| Oscillator strength f | 0.58 | 0.53 | |
| σ 2P (GM) | 3 | 3 | |
| Character (ICT number) | LEBODIPY (0.035) | LEBODIPY (0.038) | |
| S2 | Excitation energy (eV) | 3.17 | 3.17 |
| Oscillator strength f | 1.27 | 1.24 | |
| σ 2P (GM) | 40 | 33 | |
| Character (ICT number) | ICTBASHY (0.462) | ICTBASHY (0.469) | |
| S3 | Excitation energy (eV) | 3.81 | 3.19 |
| Oscillator strength f | 0.003 | 0.003 | |
| σ 2P (GM) | 6 | 0.06 | |
| Character (ICT number) | LEBODIPY (0.033) | ICT BODIPY (0.994) | |
| S4 | Excitation energy (eV) | 3.84 | 3.65 |
| Oscillator strength f | 0.09 | 0.0004 | |
| σ 2P (GM) | 57 | 0.4 | |
| Character (ICT number) | ICTBASHY (0.530) | ICT BODIPY (0.996) | |
| S5 | Excitation energy (eV) | 4.08 | 3.80 |
| Oscillator strength f | 0.08 | 0.003 | |
| σ 2P (GM) | 23 | 6 | |
| Character (ICT number) | ICT BASHY (0.244) | LEBODIPY (0.036) | |
| S6 | Excitation energy (eV) | 4.11 | 3.84 |
| Oscillator strength f | 0.05 | 0.004 | |
| σ 2P (GM) | 4 | 54 | |
| Character (ICT number) | LE BODIPY (0.045) | ICTBASHY (0.530) |
The description of BASHY in the dyad setup is in accordance with this established ICT character, indicated by an ICTBASHY label in Table 2. Corresponding to previous computational investigations, the ICT BASHY state is mainly described via a HOMO → LUMO transition,41,42 and further analysis of natural transition orbitals (NTOs) for the BASHY localized states can be found in Fig. S6 in the ESI.†
Following the first two excited states BASHY–BODIPY–SER exhibits two intermediate dark states at 3.19 eV (389 nm, f = 0.003) and 3.65 eV (340 nm, f = 0.0004) that are not present in BASHY–BODIPY–OH. These are localized on BODIPY and SER and display a strong ICT character. While they do not play any role in the initial excitation due to the negligible accessibility at the Franck–Condon (FC) geometry, they likely contribute to the uncaging following the energy transfer as discussed by various mechanistic studies.44,45 Accordingly, the S3 state of BASHY–BODIPY–OH corresponds to the S5 state of BASHY–BODIPY–SER which is again localized on the acceptor BODIPY fragment and the S4 state of BASHY–BODIPY–OH matches the S6 state of BASHY–BODIPY–SER and is another BASHY-centered state for both dyads. The respective excited states exhibit the same contributions of orbital transitions and in general display similar properties when compared to the molecular compounds of BASHY and BODIPY as can be seen in Fig. 3 and in the ESI† (Fig. S3 and S4). This is mainly a consequence of the non-conjugated and rigid alkyne linker placed between the two fragments that prevents strong electronic coupling or stacking interactions. Moreover, the orbital transitions involved in the lowest-lying singlet excitations of BODIPY and BASHY confirm the observed differences regarding the ICT character with BODIPY displaying locally excited (LE) states and BASHY featuring a stronger redistribution of electron density across the scaffold upon photoexcitation (see Fig. S3–S6 in the ESI†).
Complementary to the measurements, the 2PA cross-sections σ2P were computed employing a sum-over-states expression within a quadratic response scheme as implemented in DALTON using the CAM-B3LYP functional and def2-SVP basis set.46 The 2P activities of the respective states are indicated in Fig. 3 and confirm the accessibility of the dyads via 2P excitation. As demonstrated by the experimental measurements, there is a significant difference in the 2PA cross-sections of BODIPY and BASHY, which is reproduced by the simulated 2PA cross-sections. BODIPY exhibits a σ2P of 3 GM for the S1 state and 6 GM for the S2 state while the cross-sections of BASHY generally range from 40 GM to 60 GM. The 2P active states in the dyads correspond to the BASHY-centered states and upon introduction of the LG the cross-sections are slightly decreased. In general, the calculated and experimental 2PA values for the S1 transitions of BASHY and BODIPY and their corresponding match in the dyads (S1 and S2 state, respectively) show good agreement. It should be noted that in the 2PA experiments, we only measured within the range of the S1 transition of BASHY and BODIPY. However, our calculations suggest that the S2 transition of BASHY should exhibit higher 2-photon activity and approximately lie around 800 nm. Indeed, Pischel, Gois and their coworkers demonstrated in a previous publication that BASHY is highly 2-photon active in this wavelength region,30 further validating our calculations.
Considering the assignments above, the following picture of the photochemical response to the initial excitation emerges: upon irradiation with a UV/vis pulse the target state of the excitation is dependent on the wavelength as either the S2 state localized on the BASHY fragment or the S1 state on the BODIPY fragment is addressed. Upon irradiation with a NIR pump pulse, the dyad is directly excited to one of the BASHY-centered states, either the S2 state or the higher lying S4/S6 state, which possibly leads to an initial excitation into a superposition state. This excitation to higher lying singlet states is followed by internal conversion to the S2 state within the BASHY fragment and a subsequent EET to the BODIPY-centered S1 state. In general, these steps are not necessarily sequential and may exhibit temporal overlap, especially if the initial excitation is not strictly limited to one state.
2.2 fs-time-resolved dynamics
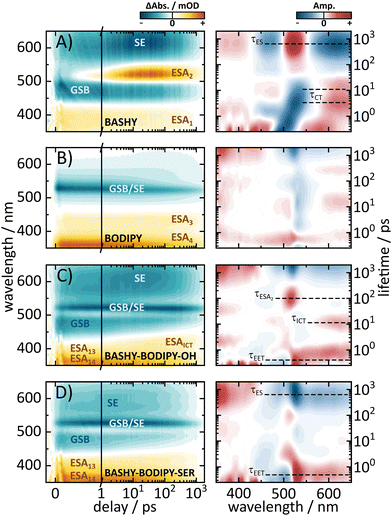
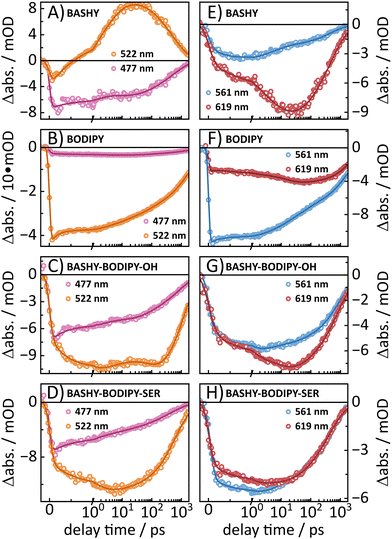
To gain further insight into the dynamics of the respective dyads, we performed ultrafast UV/vis transient absorption measurements to investigate the EET in a time-resolved manner. To ensure that we primarily address the energy-transfer from BASHY to BODIPY, an excitation wavelength of 420 nm was chosen, since the absorption of BODIPY for this wavelength is negligible. The obtained time-resolved maps as well as the lifetime density analyses of the dyads and the individual chromophores are shown in Fig. 4. While BASHY was also excited at 420 nm, the BODIPY map was measured with an excitation wavelength of 525 nm. Starting with BASHY, the single chromophore shows a negative band around 465 nm, assigned to its ground state bleaching (GSB) from the S1 state, which decays with an approximate lifetime of 800 ps. Similar to BASHY's GSB, the excited state around 370 nm (ESA1) is already populated within the IRF of the experiment. This indicates that ESA1 originates from the locally excited S1 state of BASHY. Furthermore, the lack of any spectral shift in ESA1 over time suggests that it is associated with the more localized, initial excited state rather than the charge-transfer state that forms later due to solvent stabilization. The most recognizable signatures of BASHY are ESA2 around 510 nm and its broad stimulated emission (SE) ranging from 500 nm to 650 nm and beyond. The initial SE from the locally excited S1 state is centered at 510 nm. Within the first 20 ps the SE shows a strong bathochromic shift, which can be described by two lifetimes. The first lifetime describes the rise of the SE and its initial shift within 500 fs, while the second lifetime around 3–4 ps describes the increase of the SE intensity in the red region. The SE shift lasts till 20–30 ps, which is visible from the extension of the second lifetime into a few tens of ps. These two lifetimes also contribute to the rise of ESA2 which presumably emerges due to the shift of the SE. The strong Stokes shift of the SE is characteristic for molecules with a strong ICT character like BASHY. It should be noted that the fluorescence maximum of BASHY in DMSO is located around 555 nm. However, in the transient maps, the strongest emission appears to be around 610 nm. This discrepancy is caused by the positive contribution of ESA2 on the short wavelength side of the SE which leads to compensation of the negative SE signal.In contrast to BASHY, BODIPY has only one negative band (GSB/SE) around 525 nm which is most likely a combined contribution of its GSB and SE due to its small Stokes shift. The GSB/SE appears to have a blueshift from 530 nm to 523 nm which can be attributed to a contribution of an underlying ESA since GSBs cannot exhibit any shift, while SEs only shift into the red. In the lifetime density map (LDM), this blueshift is represented by broadly distributed lifetimes around 530 nm, resulting in multi-exponential decay dynamics. Around 600 nm a slight shift of GSB/SE into the red (Fig. 4B) occurs which is likely a redshift of the SE component of GSB/SE. This shift is described with a positive amplitude of a 20 ps lifetime in the LDM. Within the observed time-frame, the ground state is not fully recovered yet, but additional time-correlated single photon counting (TCSPC) experiments revealed an excited-state lifetime of 2.1 ns (Fig. S20, ESI†). BODIPY also features two ESAs, which are termed ESA3 and ESA4. Both ESAs decay with the same lifetime as GSB/SE.
Overall, BODIPY and BASHY both show pronounced excited state features which are used in the following to distinguish their contributions within the dyads.
Similar to the steady state fluorescence measurements, BASHY–BODIPY–OH shows mixed signatures of BASHY and BODIPY. While the BODIPY GSB/SE rises in amplitude within a few femtoseconds, the BASHY GSB decays with the same time constant. This behavior can be attributed to an energy transfer from the BASHY to the BODIPY chromophore. According to the LDM (Fig. 4C, right), this energy transfer happens within 750 fs. Beyond the energy transfer, BASHY–BODIPY–OH shows complex dynamics around 522 nm, which is more visible when a single transient at 522 nm (Fig. 5C) is compared with the transient of ESA2 (Fig. 5A) in BASHY. After the initial EET in BASHY–BODIPY–OH, this transient shows a decay between 2 and 20 ps. On the same timescale a strong amplitude increase of ESA2 in BASHY occurs. Since ESA2 has a positive amplitude, it is assumed that an overlap with GSB/SE in BASHY–BODIPY–OH leads to an overall decrease of the negative amplitude causing the decay of the transient at this timescale. Then once more, GSB/SE shows an increase in its intensity until 120 ps, which is roughly described by a lifetime of 100 ps in the LDM (Fig. 4C, right). On approximately the same timescale, ESA2 in BASHY (Fig. 5A) starts to decay which in turn leads to an increase of the negative amplitude in BASHY–BODIPY–OH. Around 600 ps, the decay of GSB/SE develops, but similar to the BODIPY chromophore, the ground state is not fully recovered within the time-frame of the measurement. Also here, additional TCSPC experiments depicted an excited-state lifetime of 1.4 ns for BASHY–BODIPY–OH (Fig. S20, ESI†). Conveniently, this excited-state lifetime lies exactly in between the two parent chromophores BASHY (800 ps) and BODIPY (2.1 ns), which further confirms the bisected behavior. ESA13 and ESA14 closely resemble the ESAs of BODIPY while an underlying ESA1 contribution from the BASHY chromophore is highly likely. The most noticeable difference of BASHY–BODIPY–OH, compared to the parent chromophores, is a new ESAICT, which is more apparent at later delay times around 420 nm. The LDM shows that this ESAICT starts to shift at least from 520 nm downwards, as can be seen from the diagonal evolution of a positive amplitude trace starting at 520 nm. This large blue-shift of ESAICT fits well with the intramolecular charge-transfer stabilization of the BASHY chromophore, hence the name ESAICT. The initial position of ESAICT strongly overlaps with BODIPY's GSB/SE and BASHY's GSB, which is why it seems that both signatures shift towards each other once the underlying contribution of ESAICT vanishes. On later delay times, ESAICT leads to a partial compensation of BASHY's GSB on the blue side. Further evidence for the strong ICT stabilization of the BASHY chromophore within BASHY–BODIPY–OH is the quite significant shift of BASHY's SE with a lifetime of 10 ps. The shift of the SE is more apparent when transients of the SE at two different wavelengths are plotted together (Fig. 5G). Compared to the pure BASHY (Fig. 5E), BASHY–BODIPY–OH shows a similar evolution of the transients as can be seen by the amplitude increase of the 617 nm SE transient up to 20–30 ps. The dyad and the parent BASHY chromophore only differ in their excited state lifetimes and their relative ratio of the SE transients. The shifts of ESAICT and SE indicate that despite the fast EET, a significant amount of the population still dissipates within the BASHY chromophore.
Similar to BASHY–BODIPY–OH, BASHY–BODIPY–SER shows both GSB of BASHY and GSB/SE of BODIPY. The BODIPY GSB/SE signal increases until 2–3 ps, then remains constant until 10 ps, when it starts to decay (Fig. 5D). This constant regime indicates an equilibrium where the rate of energy transfer is equal to the decaying rate of the BODIPY moiety. The GSB signal of BASHY in BASHY–BODIPY–SER (Fig. 5D) on the other hand decays faster compared to the single BASHY chromophore (Fig. 5A). This signal pattern can be attributed to an EET as well. According to the LDM the energy transfer occurs mainly with a lifetime of 1–2 ps, which appears to be slightly slower than BASHY–BODIPY–OH (Fig. 4D right). After the energy transfer, BODIPY's GSB/SE appears to have a slight blue shift in BASHY–BODIPY–SER as well, which is described by a lifetime of 5–20 ps, where a positive amplitude is followed by a red shifted negative amplitude. At the end, both chromophore parts decay with a lifetime of 700–800 ps. Therefore, BASHY–BODIPY–SER has apparently a shorter excited state lifetime than BASHY–BODIPY–OH. This behavior, additionally to the fluorescence quantum yields, further supports the prior suggested quenching effect of the leaving group. As seen from the transients in Fig. 5H, BASHY–BODIPY–SER does not show any significant SE shift and thus, the 10 ps lifetime for the SE shift is missing in the LDM of BASHY–BODIPY–SER. As in the case of BASHY–BODIPY–OH, ESA13 and ESA14 also resemble the ESAs of BODIPY. But unlike BASHY–BODIPY–OH, there is no visible ESAICT in BASHY–BODIPY–SER. The missing ESAICT as well as the absence of a SE shift indicate that the excitation energy predominately remains within the BODIPY chromophore from where the majority of the dynamics take place.
To further investigate the differences between the two dyads, the possibility of a reverse energy transfer from BODIPY to BASHY was investigated. Due to the short distance between the two chromophores and the close proximity of the energetic levels, a reverse energy transfer is conceivable. For this purpose, additional transient absorption measurements of the two dyads at two other excitation wavelengths were conducted (Fig. S20, ESI†). Thereby, an excitation wavelength of 490 nm was used to address both chromophores equally, whereas 525 nm was used to mainly excite the BODIPY chromophore. As expected, by shifting the excitation wavelength towards increasing BODIPY absorption, the BODIPY dynamics are present with the initial excitation, without the need of an EET. The overall signal patterns are the same as for an excitation with 420 nm despite the more pronounced BODIPY contribution. For an excitation at 525 nm, the transient signatures in both BASHY–BODIPY–OH and BASHY–BODIPY–SER are dominated by the BODIPY chromophore. Yet a small BASHY population is present from the start, noticeable from the GSB at 485 nm in both dyads and the underlying ESA2 contribution in BASHY–BODIPY–OH, which is attributed to the residual BASHY absorbance at the excitation wavelength. Overall, these results further emphasize that the properties of the components are preserved and that the excitation energy is transferred predominantly via a relatively weak electronic coupling between the two chromophores.
2.3 Quantum dynamical EET analysis
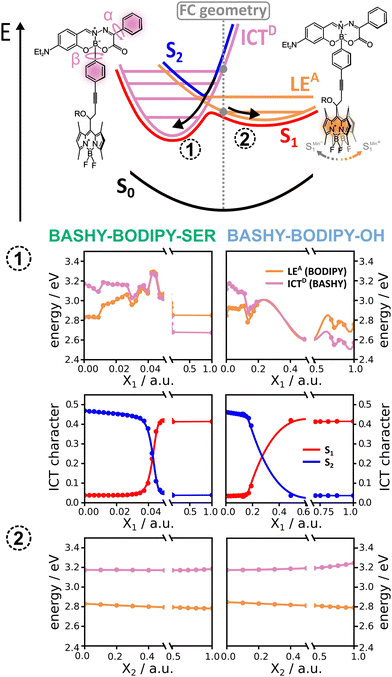
The dyad systems under study bear strong analogies to the rhodamine(RHO)–BODIPY dyad which was recently investigated by some of us.47 Due to the spatial extension of the donor and acceptor moieties and the ultrafast character of the EET dynamics, a computational treatment beyond the standard Förster theory is required.48 Therefore, our previous analysis combined the computation of electronic couplings by a transition density analysis with high-dimensional quantum dynamics in the full normal-mode space.47 Importantly, we found that the EET step, on a time scale around 100 fs, is of coherent character, and a superposition of donor and acceptor states persists on a picosecond scale. For the present BASHY–BODIPY systems, we choose a similar approach while anticipating that the EET time scale will be longer.Quantum dynamical simulations were performed for both dyads employing the multi-layer multiconfiguration time-dependent Hartree (ML-MCTDH) method49–51 in combination with a linear vibronic coupling (LVC) Hamiltonian52 and including the full set of normal modes (N = 264 for BASHY–BODIPY–OH and N = 339 for BASHY–BODIPY–SER). We focus on initial excitation to the BASHY-centered S2 state; excitation to higher-lying states would necessitate including internal conversion dynamics. The Hamiltonian comprises two diabatic fragment-based states i.e., the ICT state on the donor (BASHY) moiety, labeled |ICTD〉, and the locally excited state on the acceptor (BODIPY) moiety, labeled |LEA〉
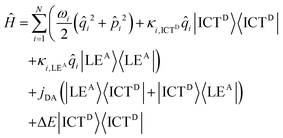 | (1) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) i is the position operator,
i is the position operator, 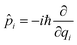 is the corresponding momentum operator and mass and frequency weighted coordinates are used. Furthermore, κi denote the vibronic couplings, jDA the electronic coupling constant and ΔE the electronic offset between donor and acceptor state. Due to the small electronic coupling between the fragments, the diabatic energy gap is approximated by the adiabatic gap between the S1 and S2 states from our supermolecular calculations. The strong localization of the excited states further suggests the use of fragment-based normal modes. This includes ND = 147 modes on the BASHY moiety and either NA = 117 (OH) or NA = 192 (SER) on the BODIPY fragment. The vibronic coupling constants are obtained as the projection of the gradient of the two excited states at the FC geometry onto the respective ground state normal modes.53 With the excited states showing strong localization, the vibronic couplings of a given state only contribute significantly in combination with the normal modes localized on the same fragment (Fig. S10–S13, ESI†). From the vibronic couplings, the reorganization energies
is the corresponding momentum operator and mass and frequency weighted coordinates are used. Furthermore, κi denote the vibronic couplings, jDA the electronic coupling constant and ΔE the electronic offset between donor and acceptor state. Due to the small electronic coupling between the fragments, the diabatic energy gap is approximated by the adiabatic gap between the S1 and S2 states from our supermolecular calculations. The strong localization of the excited states further suggests the use of fragment-based normal modes. This includes ND = 147 modes on the BASHY moiety and either NA = 117 (OH) or NA = 192 (SER) on the BODIPY fragment. The vibronic coupling constants are obtained as the projection of the gradient of the two excited states at the FC geometry onto the respective ground state normal modes.53 With the excited states showing strong localization, the vibronic couplings of a given state only contribute significantly in combination with the normal modes localized on the same fragment (Fig. S10–S13, ESI†). From the vibronic couplings, the reorganization energies 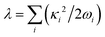 are obtained, yielding λD = 0.26 eV for the ICT state on the BASHY moiety and λA = 0.05 eV for the LE state on the BODIPY moiety.
are obtained, yielding λD = 0.26 eV for the ICT state on the BASHY moiety and λA = 0.05 eV for the LE state on the BODIPY moiety.
The electronic coupling jDA is obtained via the EET implementation in Gaussian16 including a solvent description.54 Transition densities are used to obtain exchange and overlap interaction terms alongside the Coulombic effect and solvent effects are introduced via the integral equation formalism (IEF) version of the PCM
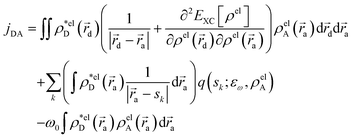 | (2) |
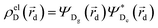 and
and 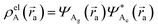 , where ΨDg, ΨDe, ΨAg and ΨAe are the donor and acceptor ground (g) and excited state (e) wavefunctions,
, where ΨDg, ΨDe, ΨAg and ΨAe are the donor and acceptor ground (g) and excited state (e) wavefunctions, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) a and
a and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) d are the electron coordinates on the respective fragment, EXC[ρel] is the exchange correlation functional, sk is the center of the discrete elements of the solvent cavity surface, εω the respective dielectric constant of the chosen solvent and q represents the point charges placed at the center of the solvent cavity elements.
d are the electron coordinates on the respective fragment, EXC[ρel] is the exchange correlation functional, sk is the center of the discrete elements of the solvent cavity surface, εω the respective dielectric constant of the chosen solvent and q represents the point charges placed at the center of the solvent cavity elements.
As the rotational potential around the linker axis is expected to exhibit low barriers due to the restrictive geometry of the bridged scaffold, a ground state relaxed potential energy surface (PES) scan was conducted (see Fig. S1, ESI†) in both cases. This revealed that the BASHY–BODIPY–OH dyad is freely rotatable, while the BASHY–BODIPY–SER dyad exhibits a slight preference for parallel-oriented structures. Since the different rotational conformations in the case of BASHY–BODIPY–SER can have some influence on the timescale of the EET, three different rotamers (–SER1, –SER2, –SER3) are considered for the subsequent quantum dynamical analysis (see Fig. S2, ESI†). The models for all different conformations were parameterized based on the ground state equilibrium geometries and normal mode analyses complemented by excited state gradients. Fig. 6A displays a summary of the electronic Hamiltonian for all four conformations highlighting the slight differences between the two dyads and the conformations while Fig. 6B and C show the time-evolving diabatic populations of the ICTD and LEA states for BASHY–BODIPY–OH (B) and BASHY–BODIPY–SER (C), respectively. In comparison to the very fast coherent transfer of the previously investigated RHO–BODIPY dyad,47 both systems, including BASHY as the donor moiety, feature a much slower process leading up to a timescale of 1–3 ps for the decay to the acceptor state rather than the 300 fs EET occurring in RHO–BODIPY–OH. The slight differences between the –OH and –SER based dyads can be reconciled with the slightly smaller ΔE and slightly higher coupling jDA displayed by BASHY–BODIPY–OH. A similar line of reasoning can be applied to –SER1. As the –SER2 and –SER3 conformations do not display any differences in terms of their electronic Hamiltonian, the small discrepancies between them can be attributed primarily to the variation in their vibronic couplings. Table 3 gives an overview of the electronic couplings jDA, the energy difference ΔE for the considered orientations, the respective torsional angle θ describing the rotation around the linker as well as the timescales of the population transfer represented by an approximate exponential decay rate. In contrast to the ultrafast, coherent EET step observed in ref. 47 for the RHO–BODIPY system, the BASHY–BODIPY dyads are closer to a quasi-kinetic regime where coherence builds up and decays transiently, while the overall decay appears irreversible (see Fig. S15, ESI†).
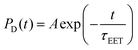
| Molecule | N vib | θ (°) | j DA (eV) | ΔE (eV) | τ EET (ps) |
|---|---|---|---|---|---|
| BASHY–BODIPY–OH | 264 | 17.5 | 0.008 | 0.33 | 1.2 |
| BASHY–BODIPY–SER1 | 339 | −10.4 | 0.007 | 0.34 | 1.7 |
| BASHY–BODIPY–SER2 | 339 | 169.2 | −0.005 | 0.34 | 3.1 |
| BASHY–BODIPY–SER3 | 339 | 266.7 | −0.005 | 0.34 | 3.1 |
The discrepancy between the dyads including RHO and BASHY can be attributed to the greater energy separation between the two states and the magnitude of the electronic coupling. Typical ratios for the BASHY–BODIPY system are jDA/ΔE ∼ 10−2, i.e. an order of magnitude smaller than in the RHO–BODIPY system, resulting in correspondingly larger transfer times. Despite the differences between the RHO and BASHY based dyads, the observed time scales extracted from the LVC description align well with the experimental results for the BASHY–BODIPY systems, as the timescales observed in the time-resolved spectroscopic measurements for BASHY–BODIPY–OH and BASHY–BODIPY–SER lie in the ps range as well.
2.4 Beyond the LVC description: potential energy surface scans
Despite the fact that the time scales of the energy transfer are adequately described by LVC dynamics, this description predicts a nearly complete EET for all BASHY–BODIPY dyads, contrary to the experimental observations where the transfer appears incomplete in the case of the –OH substituted dyad. The reason for the discrepancy most likely lies in the LVC approximation, which represents the potential energy surfaces within a shifted harmonic oscillator model, constructed around the FC geometry. This becomes manifested in a comparison of the theoretical reorganization energies obtained from the LVC parametrization with the experimental Stokes shift of the system. The reorganization energy of the BASHY fragment is obtained from the LVC model as λD = 0.25 eV, while λA is much smaller (see Section 2.3), such that the energy gap ΔE > λ throughout. In contrast, in the experimental steady-state spectrum of BASHY, the Stokes shift in DMSO measures approximately 0.4 eV. As the Stokes shift exceeds the initial energetic offset of around 0.3 eV between the S1 and S2 state, an interchange of the two states seems to occur during the measurement. The lower reorganization energy from the LVC parametrization cannot capture this so that the BASHY-centered state remains the higher lying state throughout. This may be one of the reasons why the LVC dynamics do not predict any difference between the dyad without and with LG, whereas the experimental steady-state and time-resolved experiments demonstrate a clear difference. The aforementioned disparity in the fluorescence properties of the dyad with and without the LG are evidenced in the previously investigated RHO based dyad as well. The markedly elevated fluorescence observed upon the cleavage of the leaving group enables its utilization, e.g., in 2P fluorescence microscopy.55To further analyze the difference from a theoretical viewpoint, rigid scans between the FC geometry and the optimized state geometries on the BASHY and BODIPY fragments were conducted. The scan coordinates X1 and X2 in Fig. 7 follow the gradient between the FC point and the respective LEA or ICTD state minimum, where one increment is normalized to the total displacement of atoms. Under the assumption that the step size between the scan points is reasonably small, following the gradient approximates the minimum energy pathway (MEP). The starting geometry (X = 0) is referring to the FC geometry, while the final geometries (X = 1) represent the optimized excited state geometries of the ICTD and LEA state, respectively (corresponding to pathway 1 vs. pathway 2). The scan reveals a reorganization energy for the ICTD state, as the difference between the energies at X1 = 0 and X1 = 1, of approximately 0.5 eV, which is in reasonable agreement with the experimental Stokes shift. The elevated reorganization energy may facilitate pathway 1, as illustrated in Fig. 7. However, one should keep in mind that the actual dynamics does not follow the MEP since vibrational relaxation is not expected to be immediate.
 | ||
| Fig. 7 Potential pathways within the BASHY–BODIPY dyads after initial photoexcitation. The PESs of the BASHY-centered state as well as the BODIPY-centered state are indicated via the pink and orange solid lines. Investigated pathways are flagged with the respective number in the schematic depiction of harmonic potentials above. Pathway 1 refers to the relaxation within the BASHY-centered ICT state that is initially excited. Potentials are obtained via a rigid scan following the gradient from the FC point to the S2 state minimum geometry. This is referred to as scanning coordinate X1. The evolution of the ICT character of the adiabatic S1 and S2 states is indicated in red and blue, respectively. For this analysis the BASHY–BODIPY dyads are divided into three sub-fragments of BASHY, the bridge and the BODIPY fragment. A more detailed definition of the ICT character as well as the exact partitioning of the BASHY fragment employed in the TheoDORE analysis can be found in the ESI.† Pathway 2 displays the relaxation to the S1 state minimum along the scanning coordinate X2. As the scanning coordinates of each panel correspond to the motion on the respective dyad moiety, these motions are included in the schematic depiction of potentials. | ||
A comparison of pathway 1 for the two dyads in Fig. 7 reveals that the crossing for BASHY–BODIPY–SER is situated closer to the FC point than that for BASHY–BODIPY–OH. Additionally, the slope of the PES for the dyad without leaving group (right hand side in Fig. 7) suggests a smooth transition towards the ICTD geometry. The PES for the dyad with leaving group (left hand side in Fig. 7), on the other hand, displays a shallower slope enabling a redirection to the BODIPY-centered state. Both are in agreement with experimental findings.
A projection of the effective X1 scanning coordinate onto molecular coordinates reveals two primary molecular movements, i.e., the dihedral rotations around the respective benzyl substituents, denoted α and β in Fig. 7. Here, α corresponds to the rotation of the α-keto acid benzyl substituent relative to the extended π-system, while β corresponds to the dihedral rotation around the benzyl-linker forming the connection to the BODIPY moiety. In BASHY–BODIPY–SER, these two rotations act in an almost strictly sequential way, where the planarization of α is dominant before reaching the crossing, and the β rotation dominates after passage of the crossing. In contrast, the α rotation is significantly slower in BASHY–BODIPY–OH and continues to evolve after the crossing, together with the β rotation. Additional details can be found in Fig. S9 of the ESI.†
While both states are termed localized states in the sense that they are strictly localized on either fragment, the intra-fragment ICT character of the BASHY-centered state can be analyzed as shown in Fig. 7. The S2 state (localized on BASHY) clearly shows an ICT character in the beginning, whereas the S1 state (localized on BODIPY) exhibits no ICT character. Along the scan, the ICT character of the two states gradually shifts and swaps in the vicinity of the crossing.
In addition to the LVC dynamics and the investigation of the excited state PESs, absorption and emission spectra are simulated to model the emission of the equilibrium formed in BASHY–BODIPY–OH. The vibronic absorption and emission spectra can be obtained via the corresponding autocorrelation function.48,56,57 The cross-section in the case of the absorption is computed employing the initial condition ψg(0) of the ground state, while for the emission cross-section, the initial condition ψe(0) is obtained via relaxation in the excited states. ψe(0) can involve a superposition of |LEA〉 and |ICTD〉 depending on the respective energy difference ΔE and the coupling strength jDA. The emission spectrum is then obtained as56
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 and 40
90 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 for the state population of |LEA〉
60 for the state population of |LEA〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ICTD〉, thus attesting to the incomplete EET in the case of an absent LG. As the ICT character of the BASHY fragment, as previously discussed, is less important in the case of BASHY–BODIPY–SER no relaxation of the |ICTD〉 state is assumed, yielding an emission spectrum resembling the isolated BODIPY fragment (see Fig. 8A). The obtained emission spectra in both cases are in good agreement with the experimental steady-state spectra, thus further corroborating the importance of the ICT character for BASHY–BODIPY–OH in comparison to BASHY–BODIPY–SER.
|ICTD〉, thus attesting to the incomplete EET in the case of an absent LG. As the ICT character of the BASHY fragment, as previously discussed, is less important in the case of BASHY–BODIPY–SER no relaxation of the |ICTD〉 state is assumed, yielding an emission spectrum resembling the isolated BODIPY fragment (see Fig. 8A). The obtained emission spectra in both cases are in good agreement with the experimental steady-state spectra, thus further corroborating the importance of the ICT character for BASHY–BODIPY–OH in comparison to BASHY–BODIPY–SER.
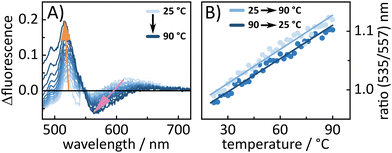
To further look into the behavior of BASHY–BODIPY–OH temperature-dependent fluorescence experiments were conducted for both dyads to examine whether the equilibrium between |ICTD〉 and |LEA〉 can be manipulated in favor of a transfer towards the BODIPY-centered state. In fact, for BASHY–BODIPY–OH, we clearly see that an increase in temperature leads to a shift towards a BODIPY-like fluorescence (Fig. 9A). This temperature-induced fluorescence change is reversible, when the temperature is decreased again (Fig. 9B), further validating the existence of an equilibrium between the |LEA〉 and |ICTD〉 state. The same experiment was repeated for BASHY–BODIPY–SER, however, the fluorescence shape did not show any significant change.
In contrast, BASHY–BODIPY–SER appears to decompose at elevated temperatures, resulting in an irreversible alteration of its photophysical properties, particularly its fluorescence (Fig. S22, ESI†). Thus, a comparison of the absorption spectra before and after the temperature excursion experiment revealed the decomposition of the caging dyad in the course of the experiment.
2.5 Effective Förster resonance energy transfer rates
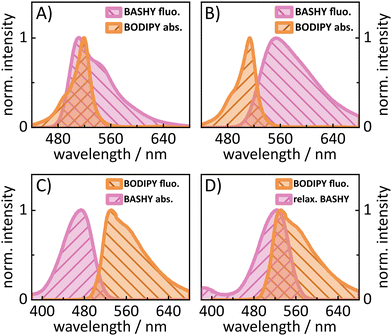
As previously shown the transient absorption measurements and subsequent lifetime density analysis reveal EET timescales of a few picoseconds for both dyads, aligning well with the calculated values from the quantum dynamical simulations. Due to the slow timescale of the quasi-kinetic EET (see Section 2.3), we will explore a more approximate, effective Förster resonance energy transfer (FRET) description in this section. Given the spatial extension of the chromophores and the center-of-mass separation between the chromophores of 1.19 nm, the accuracy of the FRET model and its parameters may be compromised as previously discussed in the literature.58–60 Due to these limitations, we will adopt a more phenomenological treatment of FRET to mainly evaluate whether the FRET model can account for the observed differences between the two dyads.FRET depends on many characteristic parameters such as chromophore distance, dipole orientation and spectral overlap. In the following, these parameters and their contributions to the FRET efficiencies will be briefly discussed. A more detailed explanation of the FRET theory and its parameters is given in the ESI.† The major difficulty in these calculations is how to distinguish between the two dyads, given that they are structurally almost identical despite the LG. For example, due to the similarity of the systems, the chromophore distance (1.19 nm) is identical and can be excluded as a reason for the divergent FRET efficiencies. Also, the quite rigid geometry, owing to the alkyne linker between the chromophore units, is similar in both dyads. The rigidity of the dyads makes a dynamic averaging of the orientation factor κ2, usually done for many biomolecular systems, unreasonable. Thus, for an accurate determination of κ2, the different rotamer conformations and their Boltzmann distribution (see the ESI† for more details) were examined, resulting in an average κ2 value of 0.48 for both dyads. Thus, the chromophore orientation is seemingly not responsible for the different energy transfer efficiencies. The overlap integral J, based on the overlap between the donor emission and the acceptor absorbance, would theoretically be the same for both dyads as well due to the identical chromophore units. However, the previously discussed steady state and transient absorption measurements showed significant differences in their emission behavior, which can in turn impact the EET. Specifically, BASHY–BODIPY–OH exhibits a pronounced ICT stabilization of its BASHY chromophore, while BASHY–BODIPY–SER shows no significant ICT relaxation. To consider these differences for the calculation of J, the fluorescence of BASHY in DMSO serves as a good approximation for BASHY–BODIPY–OH, while the fluorescence of BASHY in toluene is more appropriate for BASHY–BODIPY–SER, as it reflects BASHY's initial fluorescence without any ICT stabilization. As illustrated in the upper panel of Fig. 10, the presence or absence of the ICT relaxation significantly impacts the overlap integral. In the absence of an ICT stabilization of the BASHY chromophore (Fig. 10A), the overlap with BODIPY's absorbance is larger by almost one order of magnitude compared to the case with an ICT fluorescence of BASHY (Fig. 10B), as can be seen by the calculated values in Table 4. Even though the overlap integrals differ significantly, both cases result in nearly 100% FRET efficiencies, EFRET. This is due to the short distance (1.19 nm) between the centers of mass of the chromophores, which is way smaller than the calculated Förster radii R0 in Table 4. Since these results do not explain the observed difference between the two dyads, the possibility of a back-EET from BODIPY to BASHY was considered as well (see lower panel of Fig. 10C), as the short distance and significant overlap between the spectra makes it nearly as efficient as the forward-EET (compare Table 4). However, in contrast to the FRET efficiencies, the energy transfer rates kT differ significantly in their magnitudes and thus the equilibrium constant between forward- and back-EET will determine the directional preference of the EET, which will be discussed in the following for different scenarios. For BASHY–BODIPY–SER, using the ratio of the forward rate A and backward rate C, where no ICT stabilization of BASHY is involved, results in an equilibrium constant of 52, indicating a clear preference for the forward-EET in BASHY–BODIPY–SER. For BASHY–BODIPY–OH, considering the ICT stabilization by using the transfer rate of B for the forward-EET and the transfer rate of C for the backward-EET, leads to a significant drop of the equilibrium constant to 8. Comparing both scenarios, the equilibrium constant decreases as the ICT character of BASHY strengthens, meaning the forward-EET slows down. However, it does not fully align with the experimental data, which suggest at least a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 distribution, corresponding to an equilibrium constant of 1.
50 distribution, corresponding to an equilibrium constant of 1.
| Case | J | R 0 (nm) | E FRET (%) | τ D (ns) | k T (s−1) | τ FRET (ps) |
|---|---|---|---|---|---|---|
| Further details on the calculation of FRET rates are provided in the ESI. The transfer rates kT were determined using the donor lifetimes τD, which were all taken from TCSPC measurements, expect for case B, where the lifetime was within the timescale of our transient absorption setup. | ||||||
| A | 1.3815 | 4.65 | 99.9 | 2.4 | 1.512 | 0.7 |
| B | 2.4914 | 2.77 | 99.3 | 0.7 | 2.311 | 4.3 |
| C | 9.4513 | 2.36 | 98.4 | 2.1 | 2.910 | 34 |
| D | 3.2115 | 4.24 | 99.9 | 2.1 | 9.711 | 1.0 |
This discrepancy arises because steady-state spectra alone cannot fully account for the excited-state dynamics in the dyads. For instance, the reverse energy transfer is calculated using BASHY's steady state absorption without considering the relaxed potential energy surface, which would cause a stronger redshift in its absorption and likely a greater overlap integral with BODIPY's fluorescence. Therefore, the reverse energy transfer rate might be higher than anticipated. For this instance, a forth case (Fig. 10D) was introduced, where the steady-state absorption spectrum of BASHY (shown in Fig. 10C) was shifted by 40 nm to mimic the relaxed potential of BASHY. Indeed, this leads to a greater overlap integral of BODIPY's fluorescence and BASHY's absorption (see Table 4). Calculating the equilibrium constant now using the case (Fig. 10B) for the forward-EET and case (Fig. 10D) for the back-EET, leads to a value of 0.25, a clear preference for the back-EET by four times. These scenarios explain how the stronger ICT stabilization of the BASHY chromophore in BASHY–BODIPY–OH leads to an incomplete forward-EET. Furthermore, these results imply that the back-EET is preferred in the case of a relaxed BASHY potential, meaning that a direct BODIPY excitation will not lead to any significant population of BASHY. This additionally explains why a back-EET is not directly observable in a transient absorption measurement with a direct excitation of the BODIPY chromophore. A comparison of the calculated FRET lifetimes in Table 4 with the experimental results from the transient absorption measurements and the calculated values from the quantum dynamical analysis in Table 3 reveals that the FRET calculations fall within a reasonable range. In particular, the FRET calculations of the forward-EET lifetimes τFRET, which range from 0.7–4.3 ps, depending on the extent of the ICT stabilization, align well with the experimental and theoretical results of a few picoseconds. In contrast, the back-EET lifetime from BODIPY to an ICT-stabilized BASHY is calculated to be 1 ps, placing it into the same timescale as the forward-EET. This estimated temporal overlap of forward- and backward-EET makes a clear assignment of a reverse EET in the transient absorption spectra difficult. Despite using several approximations for the calculation of the FRET rates and lifetimes, these calculations are reasonable and in good agreement with the previous results. Additionally, the kinetic nature of the EET process within the dyads and its strong dependence on the ICT stabilization of the BASHY chromophore could be further confirmed.
2.6 Schematic models of excited-state pathways
Based on the experimental and theoretical results, two possible models (see Fig. 11) are outlined in order to visualize the special characteristics of the two dyads. After excitation of the BASHY chromophore, there are two possible pathways for the distribution of the excitation energy. It either remains within the excited BASHY chromophore and enables the solvent-guided relaxation due to the ICT character or an energy transfer to the BODIPY chromophore can take place. The latter is the dominant pathway in BASHY–BODIPY–SER, while in BASHY–BODIPY–OH both pathways are accessible to a certain degree.In BASHY–BODIPY–SER the EET (∼1–2 ps) from BASHY to BODIPY is the dominant pathway to an extent, in that no relaxation in the BASHY-centered state is noticeable. Since there is no significant lowering of the BASHY state, the back-EET (bEET) from BODIPY to BASHY is less likely as discussed within the perspective of a rate process. Thus, the main dynamics take place from BODIPY, where various relaxation processes are involved. Besides the fluorescence from BODIPY, PET to SER seems to be a dominant deactivation channel as noticeable by the reduced fluorescence quantum yield (∼10%) and the shortened excited state lifetime (∼750 ps). Uncaging as the most important process in a photocage will be discussed in the upcoming section.
In BASHY–BODIPY–OH on the other hand, the EET (∼750 fs) from BASHY to BODIPY strongly competes with the relaxation process within the BASHY chromophore. As the state ordering changes in the process of the relaxation of the ICT BASHY state, the transfer at some point will change direction as well. Coincidentally with the ICT relaxation, the bEET from BODIPY to the relaxed BASHY PES takes over, which also increases the BASHY population. Hence, the excitation energy is more likely to remain within the BASHY chromophore as the ICT relaxation plays a significant role. Since both chromophore states are possibly populated, the BASHY–BODIPY–OH dyad shows mixed dynamics, resulting in combined spectroscopic properties from both chromophore units. Hence, the excited-state lifetime (∼1.4 ns) lies in between the individual chromophores.
The equilibrium of the EET can be influenced by temperature as we have shown for BASHY–BODIPY–OH (Fig. 9). In addition to the temperature dependence, the PES landscape could also be influenced by solvent molecules as their proticity, polarity and viscosity cannot only affect the amount of ICT relaxation, but also its timescale and in turn the equilibrium directly. Indeed, steady-state spectra suggest a high solvent dependency even for BASHY–BODIPY–SER, where the EET efficiency is slightly reduced in a more polar solvent (MECN/water mixture) as notable from the significant increase in BASHY fluorescence (Fig. S18, ESI†).
2.7 Uncaging experiments
Finally, after extensive analysis of the energy transfer, the uncaging ability of the BASHY–BODIPY–SER dyad was investigated. Since for most photocages, it is assumed that the uncaging proceeds via formation of a cation followed by hydroxylation through a protic solvent,44 a DMSO/water (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture was used. The hydroxylation of the cation would result in BASHY–BODIPY–OH as the main photoproduct. As both dyads exhibit such distinct fluorescence spectra, it was assumed that the uncaging progress could be tracked by the changes in fluorescence. Therefore, fluorescence spectra were recorded after a certain time of illumination. As seen in (Fig. 12), BASHY–BODIPY–SER changes both in its absorption and fluorescence. The absorption changes (Fig. 12A) mainly result from the bleaching of the BODIPY photoproduct which is common for BODIPY photocages.44 However, there are no further photoproducts distinguishable from the absorption spectra.
1) mixture was used. The hydroxylation of the cation would result in BASHY–BODIPY–OH as the main photoproduct. As both dyads exhibit such distinct fluorescence spectra, it was assumed that the uncaging progress could be tracked by the changes in fluorescence. Therefore, fluorescence spectra were recorded after a certain time of illumination. As seen in (Fig. 12), BASHY–BODIPY–SER changes both in its absorption and fluorescence. The absorption changes (Fig. 12A) mainly result from the bleaching of the BODIPY photoproduct which is common for BODIPY photocages.44 However, there are no further photoproducts distinguishable from the absorption spectra.
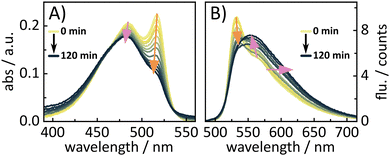 | ||
| Fig. 12 Illumination experiment of BASHY–BODIPY–SER to investigate the uncaging progress by changes in the (A) absorption and (B) fluorescence. | ||
As expected, the fluorescence spectra (Fig. 12B) show more significant changes during the illumination experiment. While the fluorescence of BODIPY at 532 nm decreases, the fluorescence of BASHY at 554 nm starts to increase and extends further into the red. To further validate these changes, the fluorescence quantum yields were recorded before and after the experiment since BASHY–BODIPY–SER has a lower fluorescence quantum yield than BASHY–BODIPY–OH. Indeed, the fluorescence efficiency also increases from 2.2% to 5.8%. It should be noted that the fluorescence quantum yields are significantly reduced in the DMSO/water mixture due to the stabilization of the ICT state. But the overall tendency of the lower fluorescence efficiency of BASHY–BODIPY–SER seems to be preserved in more polar solvents as well. Overall, the changes in fluorescence are useful to follow the uncaging progress, but they cannot be used to determine the uncaging quantum yield quantitatively. Therefore, illumination experiments were conducted in the IR to track the CO2 release from BASHY–BODIPY–SER. CO2 should be formed due to decarboxylation of the carbamate linker during the uncaging process. An uncaging quantum yield of 0.03% was determined from the CO2 release (Fig. S23, ESI†). Small changes of two peaks in the carbamate region were observed as well, but these peaks are covered by the strong solvent interactions nearby. These interactions led to a strong rise of solvent associated bands which in turn presumably masked many of the molecule's vibrations. Overall, the uncaging efficiency of the dyad certainly leaves space for further optimization by better photocage chromophores. For example a better BODIPY photocage with more rigid12 and/or halogenated substituents44 can lead to improved uncaging efficiencies as seen in our recent publication.27
3 Conclusion
In conclusion, we designed an intramolecular dyad based on a BASHY fluorophore and BODIPY photocage as an EET system that features greatly superior 2-photon excitability as compared with the BODIPY photocage by itself. Interestingly, it turned out that the leaving group is an active player in the EET process. Notably, we showed that the excited state PES landscape is sensitive to the addition of a LG, which highly boosts the EET compared to the dyad without LG. Thus, the leaving group can be used to control the energy transfer and in turn the fluorescence output.Since other leaving groups lead to a similar preference of the EET pathway, the present observations could lead to a new design concept. This concept allows a significant fluorescence read-out upon uncaging, which should make it attractive for microscopic applications, which usually rely on fluorescence quenchers as LGs to restore the fluorescence upon uncaging. Furthermore, we showed that an antenna with a strong ICT character can be exploited to control the EET efficiency by external factors such as temperature or solvent. This kind of system could be useful for dynamical applications where environment sensitivity is crucial.
At the molecular level, we have shown that the changes of the potential energy surface in the presence of the LG are subtle and non-local. These changes translate to differences in the approach towards the non-adiabatic crossing, along with differences in the participation of two dihedral angles in the minimum energy path. Both aspects shift the balance between the EET pathway and relaxation in the donor ICT state. Certain key vibrations likely have to be active to induce efficient vibrational relaxation in the donor state. These issues will be fully explored in follow-up work where the dynamics at the non-adiabatic crossing will be investigated.
Author contributions
Yagmur Aydogan-Sun: writing – original draft, data curation, investigation, methodology, visualization. Maximiliane Horz: writing – original draft, data curation, investigation, methodology, visualization. Rebekka Weber: investigation, resources, data curation, methodology. Myron Heinz: data curation. Markus Braun: validation. Alexander Heckel: supervision, funding acquisition, conceptualization. Irene Burghardt: supervision, writing – review and editing, supervison, funding acquisition, conceptualization. Josef Wachtveitl: supervision, writing – review and editing, supervison, funding acquisition, conceptualization.Data availability
Additional data supporting this article have been included as part of the ESI.† Furthermore, all raw and corrected data sets for this article are available at Goethe University Data Repository at https://doi.org/10.25716/gude.031v-j4fc.Conflicts of interest
There are no conflicts to declare.Acknowledgements
It is a great pleasure to dedicate this article to Christel Marian on the occasion of her 70th birthday. Furthermore, we gratefully acknowledge Deutsche Forschungsgemeinschaft (DFG) for the funding of our research training group “CLiC” (GRK 1986, Complex Light-Control). We express our sincere gratitude to the European Union for funding our TCSPC laser system through the European Regional Development Fund as part of the Union's response to the COVID-19 pandemic – REACT-EU, IWB-EFRE-Programm Hessen, #20008794.Notes and references
- P. Seyfried, L. Eiden, N. Grebenovsky, G. Mayer and A. Heckel, Angew. Chem., Int. Ed., 2017, 56, 359–363 Search PubMed.
- N. Klöcker, F. P. Weissenboeck, M. van Dülmen, P. Špaček, S. Hüwel and A. Rentmeister, Nat. Chem., 2022, 14, 905–913 CrossRef PubMed.
- V. Gatterdam, T. Stoess, C. Menge, A. Heckel and R. Tampé, Angew. Chem., Int. Ed., 2012, 51, 3960–3963 CrossRef CAS PubMed.
- C. Bier, D. Binder, D. Drobietz, A. Loeschcke, T. Drepper, K.-E. Jaeger and J. Pietruszka, Synthesis, 2016, 42–52 Search PubMed.
- S. B. Cambridge, D. Geissler, F. Calegari, K. Anastassiadis, M. T. Hasan, A. F. Stewart, W. B. Huttner, V. Hagen and T. Bonhoeffer, Nat. Methods, 2009, 6, 527–531 CrossRef CAS PubMed.
- L.-M. Herzig, I. Elamri, H. Schwalbe and J. Wachtveitl, Phys. Chem. Chem. Phys., 2017, 19, 14835–14844 Search PubMed.
- I. Elamri, C. Abdellaoui, J. K. Bains, K. F. Hohmann, S. L. Gande, E. Stirnal, J. Wachtveitl and H. Schwalbe, J. Am. Chem. Soc., 2021, 143, 10596–10603 Search PubMed.
- G. He, M. He, R. Wang, X. Li, H. Hu, D. Wang, Z. Wang, Y. Lu, N. Xu, J. Du, J. Fan, X. Peng and W. Sun, Angew. Chem., Int. Ed., 2023, 62, e202218768 Search PubMed.
- E. M. Digby, S. Ayan, P. Shrestha, E. J. Gehrmann, A. H. Winter and A. A. Beharry, J. Med. Chem., 2022, 65, 16679–16694 CrossRef CAS PubMed.
- A. M. Smith, M. C. Mancini and S. Nie, Nat. Nanotechnol., 2009, 4, 710–711 CrossRef CAS PubMed.
- R. Weinstain, T. Slanina, D. Kand and P. Klán, Chem. Rev., 2020, 120, 13135–13272 CrossRef CAS PubMed.
- P. Shrestha, K. C. Dissanayake, E. J. Gehrmann, C. S. Wijesooriya, A. Mukhopadhyay, E. A. Smith and A. H. Winter, J. Am. Chem. Soc., 2020, 142, 15505–15512 Search PubMed.
- A. Egyed, K. Németh, T. A. Molnár, M. Kállay, P. Kele and M. Bojtár, J. Am. Chem. Soc., 2023, 145, 4026–4034 Search PubMed.
- M. Klausen and M. Blanchard-Desce, J. Photochem. Photobiol., C, 2021, 48, 100423 CrossRef CAS.
- E. B. Brown, J. B. Shear, S. R. Adams, R. Y. Tsien and W. W. Webb, Biophys. J., 1999, 76, 489–499 CrossRef CAS PubMed.
- M. Matsuzaki, G. C. R. Ellis-Davies, T. Nemoto, Y. Miyashita, M. Iino and H. Kasai, Nat. Neurosci., 2001, 4, 1086–1092 CrossRef CAS PubMed.
- V. Nikolenko, K. E. Poskanzer and R. Yuste, Nat. Methods, 2007, 4, 943–950 CrossRef CAS PubMed.
- M. Pawlicki, H. Collins, R. Denning and H. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266 CrossRef CAS PubMed.
- G. Bassolino, C. Nançoz, Z. Thiel, E. Bois, E. Vauthey and P. Rivera-Fuentes, Chem. Sci., 2018, 9, 387–391 RSC.
- R. Klimek, M. Asido, V. Hermanns, S. Junek, J. Wachtveitl and A. Heckel, Chem. – Eur. J., 2022, 28, e202200647 CrossRef CAS PubMed.
- M. Klausen, V. Dubois, J.-B. Verlhac and M. Blanchard-Desce, ChemPlusChem, 2019, 84, 589–598 Search PubMed.
- C. A. Hammer, K. Falahati, A. Jakob, R. Klimek, I. Burghardt, A. Heckel and J. Wachtveitl, J. Phys. Chem. Lett., 2018, 9, 1448–1453 CrossRef CAS PubMed.
- G. Ulrich, R. Ziessel and A. Harriman, Angew. Chem., Int. Ed., 2008, 47, 1184–1201 CrossRef CAS PubMed.
- P. Shrestha, D. Kand, R. Weinstain and A. H. Winter, J. Am. Chem. Soc., 2023, 145, 17497–17514 Search PubMed.
- F. M. F. Santos, J. N. Rosa, N. R. Candeias, C. P. Carvalho, A. I. Matos, A. E. Ventura, H. F. Florindo, L. C. Silva, U. Pischel and P. M. P. Gois, Chem. – Eur. J., 2016, 22, 1631–1637 CrossRef CAS PubMed.
- M. M. Alcaide, F. M. F. Santos, V. F. Pais, J. I. Carvalho, D. Collado, E. Pérez-Inestrosa, J. F. Arteaga, F. Boscá, P. M. P. Gois and U. Pischel, J. Org. Chem., 2017, 82, 7151–7158 CrossRef CAS PubMed.
- R. Weber, K. Chok, S. Junek, C. Glaubitz and A. Heckel, Chem. – Eur. J., 2023, 29, e202300149 CrossRef CAS PubMed.
- T. Kobayashi, T. Komatsu, M. Kamiya, C. Campos, M. González-Gaitán, T. Terai, K. Hanaoka, T. Nagano and Y. Urano, J. Am. Chem. Soc., 2012, 134, 11153–11160 CrossRef CAS PubMed.
- C. Xu and W. W. Webb, J. Opt. Soc. Am. B, 1996, 13, 481 CrossRef CAS.
- F. M. F. Santos, Z. Domínguez, J. P. L. Fernandes, C. Parente Carvalho, D. Collado, E. Pérez-Inestrosa, M. V. Pinto, A. Fernandes, J. F. Arteaga, U. Pischel and P. M. P. Gois, Chem. – Eur. J., 2020, 26, 14064–14069 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245 CrossRef.
- J. L. Pascual-ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127–1138 CrossRef CAS.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- F. Plasser, THEODORE: A package for theoretical density, orbital relaxation, and exciton analysis, 2019, https://theodore-qc.sourceforge.net Search PubMed.
- J. Felicidade, F. M. F. Santos, J. F. Arteaga, P. Remón, R. Campos-González, H.-C. Nguyen, F. Nájera, F. Boscá, D. Y. W. Ng, P. M. P. Gois and U. Pischel, Chem. – Eur. J., 2023, 29, e202300579 CrossRef CAS PubMed.
- A. D. Laurent, B. Le Guennic and D. Jacquemin, Theor. Chem. Acc., 2016, 135, 173 Search PubMed.
- F. M. F. Santos, J. N. Rosa, N. R. Candeias, C. P. Carvalho, A. I. Matos, A. E. Ventura, H. F. Florindo, L. C. Silva, U. Pischel and P. M. P. Gois, Chem. – Eur. J., 2016, 22, 1631–1637 CrossRef CAS PubMed.
- T. Slanina, P. Shrestha, E. Palao, D. Kand, J. A. Peterson, A. S. Dutton, N. Rubinstein, R. Weinstain, A. H. Winter and P. Klán, J. Am. Chem. Soc., 2017, 139, 15168–15175 CrossRef CAS PubMed.
- M. Kawatani, M. Kamiya, H. Takahashi and Y. Urano, Bioorg. Med. Chem. Lett., 2018, 28, 1–5 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- M. Asido, C. Hamerla, R. Weber, M. Horz, M. S. Niraghatam, A. Heckel, I. Burghardt and J. Wachtveitl, Phys. Chem. Chem. Phys., 2022, 24, 1795–1802 RSC.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, John Wiley & Sons, Ltd, 3rd edn, 2011 Search PubMed.
- H. Wang, J. Phys. Chem. A, 2015, 119, 7951–7965 CrossRef CAS PubMed.
- M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- G. Worth, M. Beck, A. Jäckle and H.-D. Meyer, MCTDH Package, Version 8.5.5, Heidelberg University, 2016, https://www.mctdh.uni-hd.de Search PubMed.
- H. Köuppel, W. Domcke and L. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef.
- H. Tamura, R. Martinazzo, M. Ruckenbauer and I. Burghardt, J. Chem. Phys., 2012, 137, 22A540 CrossRef PubMed.
- M. F. Iozzi, B. Mennucci, J. Tomasi and R. Cammi, J. Chem. Phys., 2004, 120, 7029–7040 CrossRef CAS PubMed.
- R. Weber, S. Junek and A. Heckel, Chem. – Eur. J., 2023, 29, e202300997 CrossRef CAS PubMed.
- D. J. Tannor, Introduction to Quantum Mechanics: A Time-Dependent Perspective, University Science Books, USA, 1st edn, 2007 Search PubMed.
- S. Mukamel, S. Abe and R. Islampour, J. Phys. Chem., 1985, 89, 201–204 CrossRef CAS.
- D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599 CrossRef CAS PubMed.
- E. Yang, J. Wang, J. R. Diers, D. M. Niedzwiedzki, C. Kirmaier, D. F. Bocian, J. S. Lindsey and D. Holten, J. Phys. Chem. B, 2014, 118, 1630–1647 CrossRef CAS PubMed.
- J. F. Galindo, V. M. Freixas, S. Tretiak and S. Fernandez-Alberti, J. Phys. Chem. Lett., 2021, 12, 10394–10401 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04776a |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2025 |