Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting and interpreting EPR spectra of POPC lipid bilayers with transmembrane α-helical peptides from all-atom molecular dynamics simulations†
Andrea
Catte‡
 and
Vasily S.
Oganesyan
and
Vasily S.
Oganesyan
 *
*
School of Chemistry, Pharmacy and Pharmacology, University of East Anglia, Norwich, NR4 7TJ, UK. E-mail: v.oganesyan@uea.ac.uk
First published on 14th February 2025
Abstract
This study reports a large-scale all-atom MD simulation of POPC lipid bilayers in the presence of different concentrations of the transmembrane peptide acetyl-K2(LA)12K2-amide ((LA)12) and doped with 5-PC paramagnetic spin probes used in EPR studies. We apply a combined MD-EPR simulation methodology for the prediction of EPR spectra directly and completely from MD trajectories. This approach serves three major purposes. Firstly, comparing predicted EPR spectra with experimental ones, which are highly sensitive to motions, provides an ultimate test bed for the force fields currently employed for modeling lipid bilayer systems with embedded proteins or peptides. Secondly, simulations of EPR spectra directly from the atomistic MD models simplify the interpretation of the EPR line shapes and their changes induced by the presence of peptides in the lipid bilayer. These changes are directly linked to the dynamics and order of spin probes and POPC host molecules. Lastly and importantly, we demonstrate how the MD-EPR methodology can be employed to test the validity and limitations of the widely used approach for the estimation of the order parameter of lipids directly from the EPR experimental line shapes.
Introduction
Transmembrane peptides are integral components of cell membranes which contribute to the physical structure of the lipid bilayer, affecting membrane thickness, fluidity, and curvature, which are important for the membrane's integrity and the formation of lipid rafts.1–3 These peptides play an important role in various cellular functions such as signalling, transport of molecules and ions across membranes, and cell–cell communication.4,5 Peptide–lipid structures are not static and change on different timescales depending on the bilayer composition and the concentration of peptides.6–8 However, the behaviour of transmembrane peptides in cell membranes and their impact on membrane functionality is still poorly understood.Phospholipid bilayers composed of different types of lipids and with various lipid compositions have been extensively used as models for biological membranes including their complexes with transmembrane proteins and peptides.9–13 A range of spectroscopic techniques have been employed to study the structural organisation and dynamics of such systems.14–16 Among them continuous wave (CW) electron paramagnetic resonance (EPR) with paramagnetic spin probes was the first to provide information about mobility and ordering in lipid membranes.17–19 EPR can resolve molecular re-orientational dynamics of the introduced paramagnetic spin probes on a sub-nanosecond timescale.20,21 Hubbell and McConnell first used nitroxide spin probes such as 1-palmitoyl-2-stearoyl-(n-doxyl)-sn-glycero-3-phosphocholines (n-PC spin probes) with EPR to study fatty acid chains in bilayers.19 Subczynski and co-workers studied the organization and dynamics in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) membranes with the peptide acetyl-K2L24K2-amide (L24) and different n-PC spin probes.22 They also investigated the effects of the peptide acetyl-K2(LA)12K2-amide ((LA)12) on POPC membranes.6 In particular, EPR measurements detected a homogeneous membrane environment for these peptides, suggesting their good dispersion in the bilayer. The effects of (LA)12 on the phase transition in 1,2-dimyristoyl-sn-glycero-3-phosphatidylcholine (DMPC) membranes at different pH values were also monitored using EPR.23 The location of transmembrane peptides and proteins forming water channels was investigated by EPR with different nitroxide spin probes.24,25 Freed and co-workers used both multi-frequency CW EPR and 2D-ELDOR spectroscopies to study lipid–protein interactions in lipid bilayers.26–28 Recently, Steinhoff and co-workers used EPR with different spin probes to study the dynamics in lipid nanoparticles encased by maleic copolymers.29 EPR techniques combined with spin labelling are also employed in assessment of ion channel conformation and oligomerisation.30
By fitting of spectra using a rigid rod model for the rotation motions of the spin probes and careful line shape analysis, detailed information about ordering and motions of the lipids in the membrane can be obtained.31 Such an approach however relies on the use of simplified models for molecular movements (e.g. particle in an anisotropic potential) and does not reflect the complexity of the actual molecular environment of the spin probe and its impact on the motions of the probe. Moreover, with the use of multiple adjustable parameters the fitting and, therefore, interpretation of EPR line shapes in many cases might not be unique.20
At the same time, the last decade has seen radical improvement in the modelling of complex molecular and bio-molecular systems, including lipid bilayers, using molecular dynamics (MD) simulations performed at the fully atomistic level.32–34 MD simulation models are becoming more accurate allowing researchers to predict complex molecular phenomena using explicit atomistic structures. For example, MD at both all-atom and coarse-grained levels have been employed to model the action of antimicrobial peptides such as alamethicin, melittin, magainin-2, and crysophsin-3 in lipid membranes.35–38 Parametrisation of the force-field parameters for modelling the behaviour of phospholipids in model membranes is currently an area of considerable interest and development.39,40
Furthermore, novel theoretical and computational approaches have also been developed that allow prediction of motional EPR spectra from the generated MD trajectories by their direct propagation.20,41–44 The advantage of such approaches is twofold. Firstly, they allow detailed analysis of the motions of atoms (at picosecond snapshot resolution) and can greatly simplify the interpretation of experimental spectra, leading to unambiguous conclusions about molecular order and motions. Secondly, the MD-EPR simulation methodology serves as an ideal test bed for MD computational models thus facilitating their improvement. MD-EPR simulations have been successfully applied to various complex partially ordered systems such as spin labelled proteins,41,42,45–49 thermotropic21,50–53 and lyotropic54 liquid crystals, DNA fragments55 and also lipid bilayers.56,57
Here, we apply a combined MD-EPR simulation methodology to lipid bilayers containing transmembrane peptides. In particular, we report large scale all-atom MD simulations performed for different compositions of POPC with an α-helical peptide (LA)12 and doped with 5-PC spin probes. The resulting MD trajectories are used to predict EPR spectra and to compare structural organisation and dynamics of POPC host molecules and 5-PC probes in the absence and presence of (LA)12. Predictions from MD EPR spectra are compared with experimental ones available from the literature.
In this report we address the following points. Firstly, through a direct link with experiment, our MD-EPR approach serves as a test bed for the accuracy of the force fields currently employed in the MD modelling of such systems. Secondly, simulations of EPR directly from the atomistic MD model simplify interpretation of the changes observed in the EPR line shapes upon insertion of the peptides into the lipid bilayer. Thirdly, we use MD-EPR spectral predictions to test the validity and the limits of the widely used equation introduced by Hubbell and McConnell19 for the estimation of the order parameter from the EPR line shape. Given the structural and dynamical complexity of the lipid–peptide complexes formed in membranes, this kind of knowledge would be of particular importance in guiding future EPR applications with biological membranes and model lipid bilayers. Finally, by performing the MD analysis on the host POPC molecules, the relationship between the motions of the host and the probe is explored.
Computational methods
MD simulations
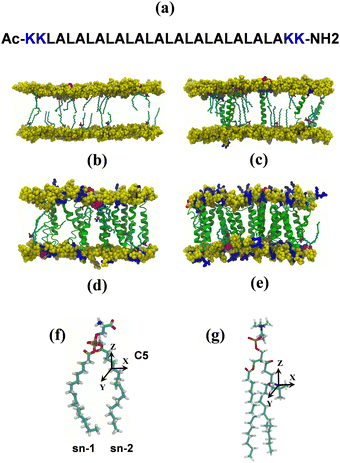
Initial structures of POPC lipid bilayers were generated with the CHARMM-GUI membrane builder,58–61 to create input files for all-atom MD simulations of lipid bilayers with different compositions. Significant system sizes allowed us to use multiple spin probes for enhanced sampling of their motions. Concatenated MD trajectories of relatively long lengths were used for prediction of the EPR line shapes. Both peptide free and bilayers with low concentrations of peptides were modelled with ca. 600 lipids and 6 spin probe molecules in each leaflet with simulation times of ca. 200 ns. The system with a high concentration of peptides, namely 10% mol, was modelled with the lower numbers of lipid (ca. 200) and spin probe molecules (three 5-PC in each leaflet) but simulated for a significantly longer time (525 ns). The Stockholm lipids (Slipids) and CHARMM36 force fields were used for lipids and peptides, respectively, and Gromacs version 4.5.562 was used for all simulations.The structure of the 5-PC spin probe is shown in Fig. 1g. Parametrisation of 5-PC has been described by us previously56 and details are provided in the ESI.† 5-PC spin probe molecules were inserted into each lipid bilayer in the presence and absence of transmembrane peptides by replacing an equivalent number of lipid molecules per leaflet in non-overlapping positions. All simulations had the concentration of the spin probe of 2% mol, corresponding to the common experimental condition.6,56 The insertion of (LA)12 peptides in each lipid bilayer involved the replacement of two lipid molecules (one per leaflet) per peptide. Each lipid bilayer was further solvated with 30 water molecules per lipid with an appropriate amount of Na+ and Cl− ions to reach a physiological ionic strength of 150 mM. The total number of atoms, including water and ions, was approximately 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 135
000 and 135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms for systems with and without transmembrane peptides (LA)12, respectively. Non-bonded van der Waals and electrostatics interactions were truncated using a cut-off distance of 12 Å. The PME treatment of long-range electrostatic interactions was employed. Temperature and pressure for all simulated lipid bilayers were stabilised at different temperatures and 1 atm using a Nosé–Hoover thermostat63 and a Parrinello–Rahman barostat,64 respectively. Calculations employed a time step of 1 fs with production carried out using an NPT ensemble. Analysis was performed with the utilities of Gromacs version 4.5.5 and with TCL scripts written for VMD versions 1.9.2 and 1.9.3.65 Images of all simulated structures were generated with VMD version 1.9.2.
000 atoms for systems with and without transmembrane peptides (LA)12, respectively. Non-bonded van der Waals and electrostatics interactions were truncated using a cut-off distance of 12 Å. The PME treatment of long-range electrostatic interactions was employed. Temperature and pressure for all simulated lipid bilayers were stabilised at different temperatures and 1 atm using a Nosé–Hoover thermostat63 and a Parrinello–Rahman barostat,64 respectively. Calculations employed a time step of 1 fs with production carried out using an NPT ensemble. Analysis was performed with the utilities of Gromacs version 4.5.5 and with TCL scripts written for VMD versions 1.9.2 and 1.9.3.65 Images of all simulated structures were generated with VMD version 1.9.2.
Rotational autocorrelation functions of molecular motions and calculation of effective rotational correlation times
The autocorrelation function of a selected vector![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) (e.g. z-magnetic axis of 5-PC spin probe discussed in the text) was calculated from MD trajectories according to the following expression:56,66
(e.g. z-magnetic axis of 5-PC spin probe discussed in the text) was calculated from MD trajectories according to the following expression:56,66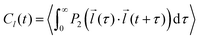 | (1) |
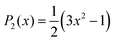 | (2) |
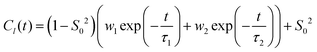 | (3) |
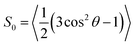 | (4) |
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) . Note that S02 = Cl(∞). The effective correlation time, τeff, represents the average of the individual motional contributions, each associated with a specific correlation time τi and a weight wi. The following relationship holds between τeff and τ1 and τ2:
. Note that S02 = Cl(∞). The effective correlation time, τeff, represents the average of the individual motional contributions, each associated with a specific correlation time τi and a weight wi. The following relationship holds between τeff and τ1 and τ2: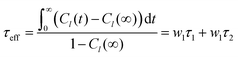 | (5) |
Prediction of EPR spectra directly from MD trajectories
A trajectory-based method that employs the numerical solution of the stochastic Liouville equation (SLE) in the Langevin form for the spin density matrix has been used for simulation of the EPR line shapes20,21,42,43,46 (see the ESI†). A program, developed and described previously by one of us, was employed.20,21,41 This methodology has been successfully applied to various complex molecular systems, including proteins, liquid crystals, lyotropic mesophases, DNA fragments and lipid membranes.21,41,54–56 In the program a single substantially long concatenated MD trajectory is used to calculate the variation in time of the averaged transverse magnetisation and, eventually, the EPR line shapes by taking one-sided Fourier transform of the transverse magnetisation.20,21 According to the properties of the Fourier transform to achieve a reasonable resolution in the EPR spectrum the following two conditions should be satisfied: T > 1/δω and δt < 1/Δω, where δω and δt are resolutions in the frequency and time domains, respectively, and Δω is the width of the spectrum in the frequency domain. To achieve a desired resolution of δB ∼ 0.1 Gauss (0.28 MHz between frequency points) a dynamical trajectory should be T > 600 ns. In the current work, relatively long concatenated MD trajectories (∼1200 ns) from multiple spin probes in the bilayer allowed the simulation of EPR spectra directly by propagation of the spin density matrix along the sampling time T without further approximations. At each time increment the propagation of the spin density matrix is achieved numerically in the Hilbert space using eigenvalues and eigenvectors of the spin-Hamiltonian21,42 (see the ESI† for details). A sufficient number of propagations from randomly selected initial points in the MD trajectory are generated and used for statistical averaging. Additional angular averaging is carried out in order to account for even distribution of lipid bilayers in the sample.The EPR spectral line shapes of nitroxide spin probes are determined entirely by the variation in time of two angles that define the orientation of the applied magnetic field to the principal axis of the nitroxide group. Therefore, the orientational history of the magnetic axes in the fixed frame of the simulation box is calculated and processed. The z axis of the nitroxide ring (coincident with the direction of the pz-orbital of N) is calculated from the cross-product of the unit vectors of the two N–C bonds of the ring (see Fig. 1).41 The x axis is calculated as a projection vector of the N–O bond on the nitroxide plane (defined by the C–N–C atoms) and the y axis is taken as a cross-product of the z and x vectors. The following principal values of the g and A hyperfine coupling tensors for the 5-PC spin probe have been employed: gxx = 2.0081; gyy = 2.0061; gzz = 2.0029; Axx = 5.9 G; Ayy = 5.9 G; Azz = 32.0 G, which are in agreement with the ones reported previously for this spin probe in bilayer systems.31,56 As reported by Subczynski and co-workers, for the 5-PC probe the hydrophobicity correction of the principal values of the hyperfine coupling tensor A due to the presence of (LA)12 in the bilayer is negligible (∼0.5 Gauss).6 Therefore, the same set of magnetic parameters was used in all simulations of the EPR spectra. The homogeneous line broadening parameter was 0.07 μs, corresponding to 0.8 Gauss, in all simulations.
Results and discussion
Impact of (LA)12 peptides on the structural organisation and motions of POPC and 5-PC molecules
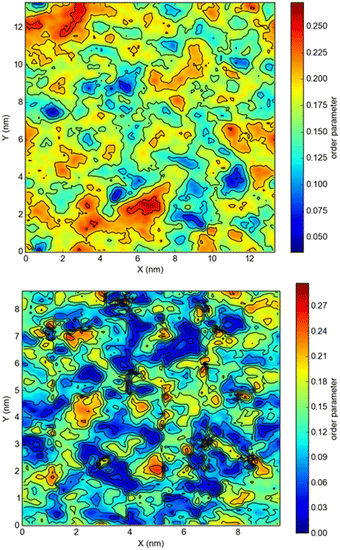
The snapshots from all-atom MD simulations of POPC lipid bilayers at 293 K doped with 5-PC spin probes and having (LA)12 concentrations ranging from 0% mol to 10% mol are shown in Fig. 1. The presence of the (LA)12 peptide affects the structural and dynamical properties of POPC lipids, such as the area per molecule, lateral diffusion, the order parameter profiles and the re-orientational rotational diffusion of both carbon chains. As can be seen in Table 1 the area per molecule of POPC and also 5-PC is progressively increased with the increased concentration of transmembrane (LA)12 peptides in the bilayer. In the absence of (LA)12 the POPC area per lipid is in good agreement with the previously reported experimental and computational values of 62.7 Å2 and 63.2 Å2, respectively, at 293 K.68 Order parameter profiles of POPC sn-1 and sn-2 acyl chains at different concentrations of (LA)12 are presented in Fig. 2. Again, the order parameters of POPC in the absence of (LA)12 peptides are in good agreement with those reported in the literature.68 The results of MD simulations show that the presence of (LA)12 induces a decrease of the order parameters of both acyl chains in POPC except, notably, in the system with 1% mol of (LA)12 when the opposite is observed. A slight decrease in area per lipid is also evident at 1% mol concentration of (LA)12. This can be explained as follows. At relatively low concentration the peptide tends to disarrange the acyl chains of POPC molecules in close proximity promoting higher packing of phospholipids in peptide free areas resulting in an increase in the order parameters averaged among all lipids. With the increasing concentration of (LA)12 the directly affected area is extended leading to an overall decrease in the order parameters of both sn-1 and sn-2 chains, as observed in Fig. 2. Notably, in the presence of transmembrane peptides the order of C–H bonds in the double bond region of the sn-2 acyl chain (carbons C10 and C11) is significantly increased for all concentrations of (LA)12. The effect of the peptides on the average order parameter of sn-1 and sn-2 POPC acyl for 1% and 10% mol of (LA)12 is illustrated in Fig. 3 with the help of a two-dimensional plot that also highlights the positions of both (LA)12 and 5-PC molecules in the system. The increased concentration of (LA)12 also leads to on average progressive reduction in the lateral diffusion rates of both POPC molecules and 5-PC spin probes as shown in Table 1.| [(LA)12] [% mol] | A POPC [Å2] | A 5-PC [Å2] | D POPC [10−8 cm2 s−1] | D 5-PC [10−8 cm2 s−1] | τ z POPC [ns] |
|---|---|---|---|---|---|
| 0 | 61.3 | 60.8 | 2.2 | 1.4 | 1.8 |
| 1 | 60.5 | 62.3 | 1.9 | 1.2 | 4.7 |
| 5 | 73.5 | 65.5 | 1.2 | 1.0 | 5.3 |
| 10 | 88.1 | 82.9 | 0.46 | 0.61 | 8.1 |
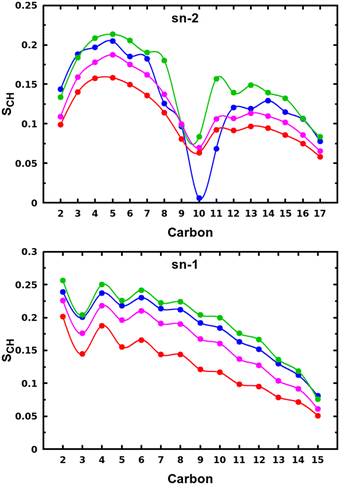 | ||
| Fig. 2 Order parameter profiles of sn-2 (top panel) and sn-1 (bottom panel) acyl chains of POPC lipid molecules for different concentrations of (LA)12 peptides are shown in blue, green, magenta, and red for 0%, 1%, 5% and 10% mol of (LA)12, respectively. Order parameter SCH is calculated according to eqn (4) for the vector defined by the C–H bond. | ||
Autocorrelation functions of the z magnetic axes of 5-PC at different concentrations of (LA)12 calculated from MD simulations using eqn (1) are shown in Fig. 4. They are fitted using eqn (3) which represents two contributions to the re-orientational dynamics of the 5-PC probe.
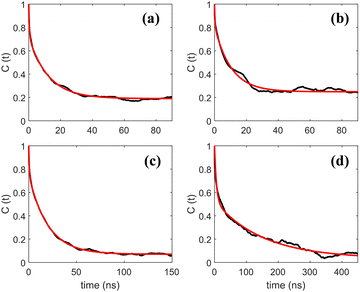 | ||
| Fig. 4 Autocorrelation functions of the z-magnetic axis of 5-PC doped in a POPC lipid bilayer with different concentrations of (LA)12 peptides at 293 K. Subpanels (a)–(d) correspond to 0%, 1%, 5% and 10% mol concentrations of (LA)12, respectively. Autocorrelation functions calculated from MD trajectories using eqn (1) and their bi-exponential fittings using eqn (3) are shown by black and red lines, respectively. | ||
The adjusted parameters associated with fast (local) and slow (global) motional contributions of 5-PC are summed up in Table 2 together with the values of effective correlation time calculated using eqn (5). Similarly, rotational correlation functions for the relevant molecular z-axis of POPC C atoms at position 5 in the sn-1 chain (see Fig. 1f), defined as the cross product between two adjacent C–H bonds, were calculated and fitted using eqn (3) (plots are presented in the ESI†). The effective rotational correlation times for the z axis of POPC lipids for different concentrations of (LA)12, calculated using eqn (5), are summarised in Table 1. Overall, the data show that the effective correlation times for both POPC and 5-PC progressively increase as the concentration of (LA)12 peptides rises.
| [(LA)12] [% mol] | τ L [ns] | w L | τ G [ns] | w G | τ eff [ns] | S 0 | S H–M | S L | S G |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.44 | 0.35 | 12.31 | 0.65 | 8.2 | 0.43 | 0.69 | 0.85 | 0.51 |
| 1 | 0.34 | 0.25 | 10.40 | 0.75 | 8.0 | 0.49 | 0.74 | 0.90 | 0.55 |
| 5 | 0.61 | 0.27 | 20.00 | 0.73 | 14.8 | 0.26 | 0.76 | 0.86 | 0.31 |
| 10 | 5.90 | 0.48 | 150.3 | 0.52 | 79.9 | 0.18 | 0.81 | 0.73 | 0.25 |
Comparison between predictions from MD and experimental EPR spectra
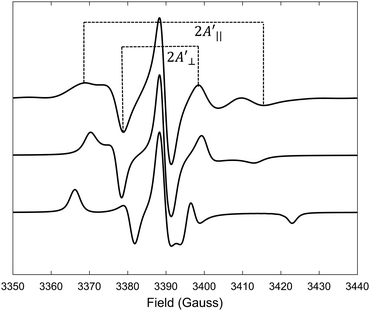
Predicted MD EPR spectra corresponding to four different concentrations of (LA)12 peptides are presented in Fig. 5 as red lines. They show excellent agreement with the experimental spectra available from the literature for 0% mol and 10% mol of (LA)12 in POPC,6 reproducing in both cases all the characteristic features in the line shapes, including the position of the outer and inner peaks. A subtle but noticeable difference between 0% mol and 10% mol cases is observed in both predicted and experimental spectra, with the differences in positions of the outer peaks indicated in Fig. 5 by vertical dotted lines. Generally, the EPR spectra of 5-PC in lipid bilayers are characterised by broad line shapes that are sensitive to the presence of transmembrane peptides.6,26 Such characteristic line shapes are associated with the restrained motion of the spin label in the oriented environment of the lipids.6,26,56 As one can see from Fig. 1, the nitroxide ring of the 5-PC probe lies approximately perpendicular to the acyl chain. The magnetic z-axis, corresponding to the principal value Azz of the hyperfine coupling tensor, is oriented perpendicular to the nitroxide ring with the averaged orientation along the membrane normal. The outer peak positions in the EPR spectra of the Iz = ±1 hyperfine coupling lines are sensitive to both the order and the dynamics of this axis.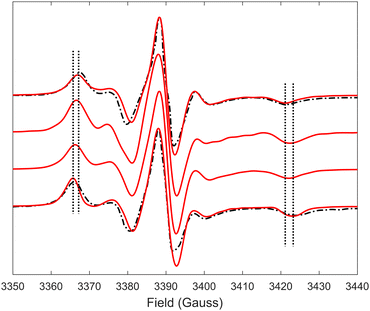 | ||
| Fig. 5 EPR spectra predicted from MD trajectories of 5-PC in POPC bilayers doped with different concentrations of (LA)12 peptides are shown by red lines. Predicted spectra from top to bottom correspond to 0%, 1%, 5% and 10% mol concentrations of (La)12, respectively. Experimental spectra for POPC without and in the presence of 10% mol of (LA)12, available from the literature and reproduced with permission from ref. 6, are shown by top and bottom dash-dotted black lines, respectively. All spectra were normalised to their maximal values. Vertical lines indicate the shifts in the positions of the outer peaks of the hyperfine coupling lines. | ||
In principle, the reduction in the rotational diffusion coefficient and the increase of the order parameter of the spin probe would both contribute to the broadening of the EPR line shape and the increase of 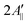 , the distance expressed in Gauss between the outer peaks in the EPR spectrum.18,19,24
, the distance expressed in Gauss between the outer peaks in the EPR spectrum.18,19,24
Upon addition of 10% mol of (LA)12 peptides the predicted EPR spectrum becomes slightly broader, in full agreement with the experimental data (see Fig. 5). In particular, our predictions have been able to adequately reproduce an increase of 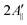 by ∼3 Gauss upon increasing the concentration of (LA)12 from 0% to 10% mol. The predicted spectra at 1% and 5% mol of (LA)12 confirm the gradual change in the EPR line shape upon increasing the concentration of the peptide. The bi-exponential fitting of the autocorrelation functions for the magnetic z-axis of 5-PC reveals that, in the presence of peptides, there is a dramatic approximately ten-fold increase in the correlation times for both fast and slow motional contributions (see Table 2). The effective correlation time of the z-axis of 5-PC increases from 8.2 ns in the peptide free bilayer to 79.9 ns in the 10% mol presence of (LA)12 peptides. Such a dramatic increase of rotational correlation time of the probe leads to the broadening of the EPR line shape. The opposite, however, is observed for the generalised order parameter of 5-PC which undergoes significant reduction in value from S0 = 0.43 in the peptide free bilayer to S0 = 0.18 at 10% mol of (LA)12, thus compensating for the broadening effect on the line shape by the slow motion. The predicted MD value of the order parameter of 5-PC at 10% mol of (LA)12 appears to be in strong disagreement with the previously reported estimations based on the approach by Hubbell and McConnell.6
by ∼3 Gauss upon increasing the concentration of (LA)12 from 0% to 10% mol. The predicted spectra at 1% and 5% mol of (LA)12 confirm the gradual change in the EPR line shape upon increasing the concentration of the peptide. The bi-exponential fitting of the autocorrelation functions for the magnetic z-axis of 5-PC reveals that, in the presence of peptides, there is a dramatic approximately ten-fold increase in the correlation times for both fast and slow motional contributions (see Table 2). The effective correlation time of the z-axis of 5-PC increases from 8.2 ns in the peptide free bilayer to 79.9 ns in the 10% mol presence of (LA)12 peptides. Such a dramatic increase of rotational correlation time of the probe leads to the broadening of the EPR line shape. The opposite, however, is observed for the generalised order parameter of 5-PC which undergoes significant reduction in value from S0 = 0.43 in the peptide free bilayer to S0 = 0.18 at 10% mol of (LA)12, thus compensating for the broadening effect on the line shape by the slow motion. The predicted MD value of the order parameter of 5-PC at 10% mol of (LA)12 appears to be in strong disagreement with the previously reported estimations based on the approach by Hubbell and McConnell.6
MD-EPR approach as a testbed for the Hubbell–McConnell equation used in the estimation of the order parameter
In their seminal paper Hubbell and McConnell19 have introduced an equation for the estimation of the order parameter of spin probes in lipid bilayers directly and conveniently from the experimental EPR spectrum. This equation has been highly successful in characterisation of the order of spin probes in the partially ordered environments.18,19,23 The authors have shown that the order parameter of the phospholipid spin probe, associated with the magnetic z-axis, in the partially ordered media can be estimated directly from the difference between the outer and inner peak positions in the EPR line shape using the following equation: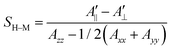 | (6) |
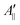 and
and 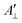 are the effective outer and inner hyperfine splitting, respectively, observed in the measured EPR spectrum, as indicated in Fig. 6. The derivation of eqn (6) assumes that Axx and Ayy are approximately equal to each other, which is normally the case for nitroxide based spin probes.18,19 The effective hyperfine splitting parameter
are the effective outer and inner hyperfine splitting, respectively, observed in the measured EPR spectrum, as indicated in Fig. 6. The derivation of eqn (6) assumes that Axx and Ayy are approximately equal to each other, which is normally the case for nitroxide based spin probes.18,19 The effective hyperfine splitting parameter 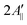 serves as a measure of nitroxide mobility with larger values corresponding to lower mobility.6,19,67
serves as a measure of nitroxide mobility with larger values corresponding to lower mobility.6,19,67
Naturally, atomistic MD simulations in conjunction with the MD-EPR prediction approach provide perfect grounds for testing the limits of the applicability of eqn (6).
Previous analysis of the EPR spectra of POPC doped with (LA)12 peptides6 using a similar approach has concluded that the order parameter of 5-PC was S0 = 0.65 and S0 = 0.75 in the cases of 0% and 10% mol concentration of (LA)12, respectively. As pointed above, these values are in clear disagreement with the ones obtained either directly from the MD trajectories using eqn (4) or by fitting the autocorrelation functions using eqn (3). Table 2 provides comparison between the order parameters estimated by eqn (6) and those calculated from MD data for all four predicted spectral line shapes. As one can see, the results indicate a systematic increase in the overestimation of the order parameter by eqn (6) upon increasing the concentration of (LA)12 in the POPC bilayer. At 10% mol (LA)12 the difference between the order parameter values becomes most prominent (0.18 from MD data vs. 0.81 obtained by using eqn (6)).
It is important to mention that eqn (6) was derived under the assumption of the partial averaging of the magnetic tensor components due to the fast motion of the spin probe (so-called fast motional limit). At the X-band (ca. 9.5 GHz) the hyperfine interaction dominates the time modulation of the spin-Hamiltonian, and the fast motional regime can be approximately defined by the following characteristic time:43τc < ħ/|Azz − A⊥| ∼ 2.2 ns. The effective correlation times for 5-PC presented in Table 2 clearly indicate that the dynamics of the spin probe is in the slow motional regime for all concentrations of (LA)12 and, therefore, eqn (6) is inadequate for the estimation of the order parameter.
In order to test the limits of applicability of the equation we have performed an additional MD simulation of the POPC bilayer with 1% mol (LA)12 at an elevated temperature of 330 K. The calculated effective correlation time of 5-PC at this temperature is 2.95 ns which is just outside the fast motional regime. The predicted spectrum is shown as the top line in Fig. 6.
The order parameter values calculated from MD and estimated by eqn (6) are 0.42 and 0.52, respectively. They are much closer to each other compared to all four previous cases. In addition, we have performed EPR spectral simulations in the fast motional regime using the dynamical trajectories generated from the Brownian dynamics (BD) simulation model for rotational diffusion of the spin probe in the presence of restoring axial potential.20,69 BD trajectories have been generated using a numerical solution of the Langevin equation for a simple model of the BD rotational diffusion of the molecule in the presence of axially symmetric ordering potential, U(θ(t)) = kT![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) (3
(3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t) − 1)/2, where θ(t) is the angle between the z-axis and the main axis of the potential using the numerical approach reported previously.43,69 The results for the cases with τc = 1 ns and
θ(t) − 1)/2, where θ(t) is the angle between the z-axis and the main axis of the potential using the numerical approach reported previously.43,69 The results for the cases with τc = 1 ns and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = 1 and τc = 0.2 ns and
= 1 and τc = 0.2 ns and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = 3, both at T = 295 K, are shown in Fig. 6 as middle and bottom lines, respectively. The order parameter calculated from MD using eqn (4) for the first and second cases are 0.40 and 0.79, respectively. They are in perfect agreement with the ones estimated from those predicted from BD spectra using eqn (6) which are 0.41 and 0.80, respectively. Our MD-EPR analysis thus concludes that eqn (6) indeed provides a very accurate and efficient way of estimating the order parameter of the nitroxide based spin probes in the oriented media directly from the spectra in the case of a fast motional regime. At the same time, this equation tends to significantly overestimate the order parameter when the fast motional condition is broken. Therefore, our results demonstrate that the application of eqn (6) should be made with extra care, particularly when it is difficult or impossible to conclude a priori whether the internal dynamics of the probe falls within the fast motional regime.
= 3, both at T = 295 K, are shown in Fig. 6 as middle and bottom lines, respectively. The order parameter calculated from MD using eqn (4) for the first and second cases are 0.40 and 0.79, respectively. They are in perfect agreement with the ones estimated from those predicted from BD spectra using eqn (6) which are 0.41 and 0.80, respectively. Our MD-EPR analysis thus concludes that eqn (6) indeed provides a very accurate and efficient way of estimating the order parameter of the nitroxide based spin probes in the oriented media directly from the spectra in the case of a fast motional regime. At the same time, this equation tends to significantly overestimate the order parameter when the fast motional condition is broken. Therefore, our results demonstrate that the application of eqn (6) should be made with extra care, particularly when it is difficult or impossible to conclude a priori whether the internal dynamics of the probe falls within the fast motional regime.
Local and global order parameters of the 5-PC spin probe from all-atom MD data
MD simulations provide an explicit picture of molecular motions with atomistic resolution of contributions arising from both local and global dynamics of host and probe molecules. Previously, for different aggregate states of lyotropic liquid crystals, we have demonstrated how the outputs of MD simulations can be combined with the so-called model-free (MF) approach66 in order to gain insight into the global and local motions of spin probes and their impact on the EPR line shapes.54According to the MF approach and assuming that the global and internal motions of the probe are independent from each other, the total rotational correlation function C(t) can be decomposed into the product of the correlation functions for the overall tumbling, CG(t), and the internal motion, CL(t).
| C(t) = CL(t)CG(t) | (7) |
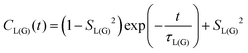 | (8) |
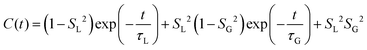 | (9) |
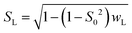 | (10a) |
| SG = S0/SL | (10b) |
It is instructive to examine how the rotational correlation times and order parameters of the carbon chains of POPC at position 5 in the sn-1 chain, where the nitroxide group attaches in 5-PC, and the spin probe itself, correlate with each other. Relevant correlation functions and their fitting using eqn (3) are presented in Fig. S1 of the ESI.† Similar to 5-PC, the effective correlation time of the relevant molecular z-axis of POPC C atoms at position 5 increases with the concentration of (LA)12, as shown in the last column of Table 1. Specifically, the correlation time for the z-axis of POPC changes from 1.8 ns to 8.1 ns as the concentration of (LA)12 increases from 0% mol to 10% mol. This approximately four-fold increase is less pronounced compared to the ca. ten-fold increase observed for the effective correlation time of the magnetic z-axis of 5-PC, which changes from 8.2 ns to 79.9 ns (see Table 2). The order parameters for POPC and 5-PC are affected similarly also. For POPC at the chain position 5, the order parameter decreases from approximately 0.22 to 0.16 for sn-1 and 0.20 to 0.15 for sn-2 (see Fig. 2). A more dramatic change is observed for 5-PC, where the order parameter decreases from 0.43 to 0.18 (see Table 2). This difference is likely due to local isomeric jumps in the carbon chain of POPC, which are responsible for the reorientation of C–H bonds, being less affected by the disentanglement of POPC molecules compared to the tumbling motions of the much larger nitroxide head group of the 5PC probe.
Our MD simulation results and analyses align with recent modelling and experimental reports on the influence of peptides on membrane dynamics, suggesting that transmembrane peptides can indeed slow down the dynamics of lipids in membranes, affecting both the lateral and re-orientational mobility of lipids. In particular, a decrease in the lateral diffusion of lipids has been observed in DMPC lipid bilayers with transferrin receptor peptides.8 A decrease in the average order parameters SCH has been reported for a wide range of lipid bilayers embedded with magainin antimicrobial peptides,70 POPC bilayers with amyloid beta peptides71 and antimicrobial and cell penetrating peptides.72 An increase in the average rotational correlation time of lipids has been observed in POPC:POPG and POPE:POPG lipid bilayers upon insertion of antimicrobial peptides73 and in DLPC, DMPC, and DPPC bilayers upon doping of KALP peptides.74 It has been suggested that such effects on host dynamics can influence the formation and maintenance of lipid domains.8
Conclusions
In summary, this study presents the results of extensive all-atom molecular dynamics (MD) simulations on POPC lipid bilayers, both with and without the transmembrane peptide (LA)12, using Slipids force fields for POPC and CHARMM force fields for the peptide. We provide the first prediction of EPR spectra of lipid bilayers with transmembrane peptides and spin labels directly from MD simulations. Our approach had two main objectives. First, by comparing predicted EPR spectra with experimental data, which are highly sensitive to the structure and dynamics of lipid bilayers, we tested the accuracy of current simulation models and force fields for lipid bilayer systems, including those with embedded proteins and peptides. Our results show excellent agreement with experimental data, confirming the reliability of the force fields employed. Second, the direct MD-EPR simulation approach allows for a detailed account of both local and global motions of the probes. Our findings indicate that the presence of the (LA)12 peptide causes significant disorder and disarrangement in the acyl chains of nearby POPC molecules. This disorder impacts the lateral and rotational diffusion of both phospholipids and probes. As the concentration of peptides in the bilayer increases, these effects become more pronounced. Concurrently, the order parameters for both host and probe molecules decrease, in contrast to previous interpretations of EPR data. Importantly, our MD-EPR approach enabled us to validate and numerically assess the limitations of the widely used eqn (6) for estimating the order parameter from measured EPR spectra. This validation is crucial due to the widespread use of eqn (6) in EPR studies of partially disordered systems such as lipid membranes. We demonstrate that eqn (6) provides accurate estimates for the order parameter of the probe under fast motional regime conditions, aligning perfectly with values derived from dynamical trajectories. However, when the spin probe's dynamics fall within the slow motional regime, which is not typically known a priori, the use of this equation results in an expected significant overestimation of the order parameter.Author contributions
AC and VSO: data curation, formal analysis, investigation and writing; VSO: conceptualization, methodology, funding acquisition, project administration and supervision.Data availability
Data supporting this article are available on Zenodo (DOI: https://doi.org/10.5281/zenodo.14531328).Conflicts of interest
There are no conflicts to declare.Acknowledgements
VSO gratefully acknowledges financial support of this work from EPSRC (grants EP/H020411/1 and EP/L001322/1). The authors wish to thank the Research Computing Service at the University of East Anglia for access to the High-Performance Computing Cluster (Ada).References
- J. H. Lorent, B. Diaz-Rohrer, X. Lin, K. Spring, A. A. Gorfe, K. R. Levental and I. Levental, Nat. Commun., 2017, 8, 1219 CrossRef PubMed.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374 CrossRef CAS PubMed.
- R. D. Usery, T. A. Enoki, S. P. Wickramasinghe, V. P. Nguyen, D. G. Ackerman, D. V. Greathouse, R. E. Koeppe, F. N. Barrera and G. W. Feigenson, Biophys. J., 2018, 114, 2152–2164 CrossRef CAS PubMed.
- J. Dinic, A. Riehl, J. Adler and I. Parmryd, Sci. Rep., 2015, 5, 10082 CrossRef CAS PubMed.
- J. Lin, A. Weiss and T. S. Finco, J. Biol. Chem., 1999, 274, 28861–28864 CrossRef CAS PubMed.
- W. Subczynski, M. Pasenkiewicz-Gierula, R. N. McElhaney, J. S. Hyde and A. Kusumi, Biochemistry, 2003, 42, 3939–3948 CrossRef CAS PubMed.
- E. G. Kelley, P. D. Butler and M. Nagao, Soft Matter, 2021, 17, 5671–5681 RSC.
- L. Ebersberger, T. Schindler, S. A. Kirsch, K. Pluhackova, A. Schambony, T. Seydel, R. A. Böckmann and T. Unruh, Front. Cell Dev. Biol., 2020, 8, 579388 CrossRef PubMed.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed.
- Y. H. M. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef CAS PubMed.
- P. S. Niemelä, M. S. Miettinen, L. Monticelli, H. Hammaren, P. Bjelkmar, T. Murtola, E. Lindahl and I. Vattulainen, J. Am. Chem. Soc., 2010, 132, 7574–7575 CrossRef PubMed.
- V. Corradi, B. I. Sejdiu, H. Mesa-Galloso, H. Abdizadeh, S. Y. Noskov, S. J. Marrink and D. P. Tieleman, Chem. Rev., 2019, 119, 5775–5848 CrossRef CAS PubMed.
- S. Park, I. Levental, R. W. Pastor and W. Im, J. Chem. Theory Comput., 2023, 19, 5303–5314 CrossRef CAS PubMed.
- E. Strandberg, S. Esteban-Martín, J. Salgado and A. S. Ulrich, Biophys. J., 2009, 96, 3223–3232 CrossRef CAS PubMed.
- A. Holt, R. B. M. Koehorst, T. Rutters-Meijneke, M. H. Gelb, D. T. S. Rijkers, M. A. Hemminga and J. A. Killian, Biophys. J., 2009, 97, 2258–2266 CrossRef CAS PubMed.
- A. Holt and J. A. Killian, Eur. Biophys. J., 2010, 39, 609–621 CrossRef CAS PubMed.
- Z. Guo, D. Cascio, K. Hideg and W. L. Hubbell, Protein Sci., 2008, 17, 228–239 CrossRef CAS PubMed.
- L. Berliner, Spin Labeling: The Next Millennium, Springer, 1998 Search PubMed.
- W. L. Hubbell and H. M. McConnell, J. Am. Chem. Soc., 1971, 93, 314–326 CrossRef CAS PubMed.
- V. Oganesyan, in SPR: Electron Paramagnetic Resonance, ed. B. Gilbert, V. Chechik and D. M. Murphy, Royal Society of Chemistry, London, 2015, vol. 24, pp. 32–61 Search PubMed.
- V. S. Oganesyan, Liq. Cryst., 2018, 45, 2139–2157 CrossRef CAS.
- W. Subczynski, R. N. A. H. Lewis, R. N. McElhaney, R. S. Hodges, J. S. Hyde and A. Kusumi, Biochemistry, 1998, 37, 3156–3164 CrossRef CAS PubMed.
- W. Subczynski, A. Wisniewska, A. Kusumi and R. N. McElhaney, Biochim. Biophys. Acta, 2005, 1720, 99–109 CrossRef CAS PubMed.
- D. Marsh, Eur. Biophys. J., 2010, 39, 513–525 CrossRef CAS PubMed.
- D. Marsh, D. Kurad and V. A. Livshits, Chem. Phys. Lipids, 2002, 116, 93–114 CrossRef CAS PubMed.
- B. Dzikovski, P. P. Borbat and J. H. Freed, J. Phys. Chem. B, 2011, 115, 176–185 CrossRef CAS PubMed.
- E. Georgieva, S. Xiao, P. P. Borbat, J. H. Freed and D. Eliezer, Biophys. J., 2014, 107, 1441–1452 CrossRef CAS PubMed.
- B. Dzikovski, P. P. Borbat and J. H. Freed, Biophys. J., 2004, 87, 3504–3517 CrossRef CAS PubMed.
- A. Colbasevici, N. Voskoboynikova, P. S. Orekhov, M. E. Bozdaganyan, M. G. Karlova, O. S. Sokolova, J. P. Klare, A. Y. Mulkidjanian, K. V. Shaitan and H.-J. Steinhoff, Biochim. Biophys. Acta, Biomembr., 2020, 1862, 183207 CrossRef CAS PubMed.
- C. Pliotas, Methods Enzymol., 2017, 594, 203–242 CAS.
- Y. Chiang, Y. Shimoyama, G. W. Feigenson and J. H. Freed, Biophys. J., 2004, 87, 2483–2496 CrossRef CAS PubMed.
- H. Ingólfsson, M. N. Melo, F. J. van Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. de Vries, D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 14554–14559 CrossRef PubMed.
- S. Marrink, A. H. de Vries and D. P. Tieleman, Biochim. Biophys. Acta, 2009, 1788, 149–168 CrossRef CAS PubMed.
- G. Shahane, W. Ding, M. Palaiokostas and M. Orsi, J. Mol. Model., 2019, 25, 76 CrossRef PubMed.
- A. Catte, M. R. Wilson, M. Walker and V. S. Oganesyan, Soft Matter, 2018, 14, 2796–2807 RSC.
- M. Mihajlovic and T. Lazaridis, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1485–1493 CrossRef CAS PubMed.
- D. Sengupta, H. Leontiadou, A. E. Mark and S.-J. Marrink, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 2308–2317 CrossRef CAS PubMed.
- H. Leontiadou, A. E. Mark and S. J. Marrink, J. Am. Chem. Soc., 2006, 128, 12156–12161 CrossRef CAS PubMed.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Phys. Chem. B, 2012, 116, 3164–3179 CrossRef PubMed.
- F. Grote and A. P. Lyubartsev, J. Phys. Chem. B, 2020, 124, 8784–8793 CrossRef CAS PubMed.
- V. Oganesyan, Phys. Chem. Chem. Phys., 2011, 13, 4724–4737 RSC.
- S. DeSensi, D. P. Rangel, A. H. Beth, T. P. Lybrand and E. J. Hustedt, Biophys. J., 2008, 94, 3798–3809 CrossRef CAS PubMed.
- H. Steinhoff and W. L. Hubbell, Biophys. J., 1996, 71, 2201–2212 CrossRef CAS PubMed.
- D. Sezer, J. H. Freed and B. Roux, J. Phys. Chem. B, 2008, 112, 5755–5767 CrossRef CAS PubMed.
- V. S. Oganesyan, F. Chami, G. F. White and A. J. Thomson, J. Magn. Reson., 2017, 274, 24–35 CrossRef CAS PubMed.
- D. Sezer, J. H. Freed and B. Roux, J. Am. Chem. Soc., 2009, 131, 2597–2605 CrossRef CAS PubMed.
- C. Beier and H.-J. Steinhoff, Biophys. J., 2006, 91, 2647–2664 CrossRef CAS PubMed.
- E. Kuprusevicius, G. White and V. S. Oganesyan, Faraday Discuss., 2011, 148, 283–298 RSC.
- P. D. Martin, B. Svensson, D. D. Thomas and S. Stoll, J. Phys. Chem. B, 2019, 123, 10131–10141 CrossRef CAS PubMed.
- V. Oganesyan, E. Kuprusevicius, H. Gopee, A. N. Cammidge and M. R. Wilson, Phys. Rev. Lett., 2009, 102, 1–1300 CrossRef PubMed.
- G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, ChemPhysChem, 2009, 10, 125–136 CrossRef CAS PubMed.
- F. Chami, M. R. Wilson and V. S. Oganesyan, Soft Matter, 2012, 8, 6823 RSC.
- E. Kuprusevicius, R. Edge, H. Gopee, A. N. Cammidge, E. J. L. McInnes, M. R. Wilson and V. S. Oganesyan, Chem. – Eur. J., 2010, 16, 11558–11562 CrossRef CAS PubMed.
- C. Prior and V. S. Oganesyan, Chem. – Eur. J., 2017, 23, 13192–13204 CrossRef CAS PubMed.
- C. Prior, L. Danilāne and V. S. Oganesyan, Phys. Chem. Chem. Phys., 2018, 20, 13461–13472 RSC.
- A. Catte, G. F. White, M. R. Wilson and V. S. Oganesyan, ChemPhysChem, 2018, 19, 2183–2193 CrossRef CAS PubMed.
- P. Håkansson, P. O. Westlund, E. Lindahl and O. Edholm, Phys. Chem. Chem. Phys., 2001, 3, 5311–5319 RSC.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- B. Brooks, C. L. Brooks III, A. D. MacKerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- E. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004 CrossRef CAS PubMed.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith and P. M. Kasson, Bioinformatics, 2009, 29, 845–854 CrossRef PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- M. Parrinello and A. J. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- G. Liparit and A. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef.
- J. H. Freed, in Spin labeling theory and applications, ed. L. J. Berliner, Academic Press, New York, 1976, pp. 53–132 Search PubMed.
- J. Jambeck and A. P. Lyubartsev, J. Chem. Theory Comput., 2012, 8, 2938–2948 CrossRef PubMed.
- H. Gopee, A. N. Cammidge and V. S. Oganesyan, Angew. Chem., Int. Ed., 2013, 52, 8917–8920 CrossRef CAS PubMed.
- N. Harmouche and B. Bechinger, Biophys. J., 2018, 115, 1033–1044 CrossRef CAS PubMed.
- G. Grasso, C. Lionello and F. Stojceski, J. Mol. Graphics Modell., 2020, 100, 107670 CrossRef CAS PubMed.
- A. Farrotti, G. Bocchinfuso, A. Palleschi, N. Rosato, E. S. Salnikov, N. Voievoda, B. Bechinger and L. Stella, Biochim. Biophys. Acta, Biomembr., 2015, 1848, 581–592 CrossRef CAS PubMed.
- D. Roversi, C. Troiano, E. Salnikov, L. Giordano, F. Riccitelli, M. De Zotti, B. Casciaro, M. R. Loffredo, Y. Park, F. Formaggio, M. L. Mangoni, B. Bechinger and L. Stella, Biophys. Chem., 2023, 300, 107060 CrossRef CAS PubMed.
- S. K. Kandasamy and R. G. Larson, Biophys. J., 2006, 90, 2326–2343 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04802d |
| ‡ Present address: Institute for the Chemistry of OrganoMetallic Compounds (ICCOM) Via Madonna del Piano 10, Sesto Fiorentino (FI) – 50019, Italy. |
| This journal is © the Owner Societies 2025 |