Exploring the influence of M-anion modifications on the physical properties of lead-free novel halide inorganic compounds Ba₃MCl₃ (M = N, P, As, Sb)

Abstract

This study investigates the effects of M-anion modifications on lead-free halide inorganic compounds, specifically Ba₃MCl₃ (M = N, P, As, Sb), using DFT and SCAPS-1D software. It focuses on analyzing their optical, electronic, and structural properties. The lattice parameters for Ba₃MCl₃ were found to be a = 6.14, 6.44, 6.51, and 6.69 Å, respectively, which is consistent with previous research. Initially, GGA with the PBE functional theory was used. The materials displayed semiconductor characteristics, with direct band gaps of 0.551 eV for Ba₃NCl₃, 0.927 eV for Ba₃PCl₃, 0.980 eV for Ba₃AsCl₃, and 0.996 eV for Ba₃SbCl₃. Optical characteristics such as absorption, loss function, dielectric function, electrical conductivity, reflectance, and refractive index were also examined. Additionally, the SCAPS-1D software was exploited to thoroughly estimate the efficiency of absorber-based PV cell structures Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃ with a CdS ETL layer at varying thicknesses, defect densities, and doping levels. QE and J–V characteristics were assessed, with maximum PCEs of 23.06%, 19.93%, 17.12%, and 15.71% for Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃, respectively. These computational findings offer valuable insights for developing efficient, lead-free, durable, and cost-effective solar cells based on Ba₃MCl₃ compounds.

---

1. Introduction

As the global population grows and industrialization progresses, the demand for energy continues to rise. To meet this demand sustainably, renewable energy sources are essential. The urgent issue revolves around the increasing need for advanced photovoltaic cells, optoelectronics, and electronic gadgets, especially as population growth intensifies energy shortages.^1–4 Organic–inorganic hybrid PSCs have made considerable development in the construction of devices and control elements because of their enhanced charge carrier mobility, minimal trap density, reduced exciton binding energy of excitons, excellent optical absorption, and prolonged charge carrier lifetime.^5–7 However, the volatility and thermal instability of organic cations limit their commercial use.^7–14 Creating more environmentally friendly PSCs requires the innovation of eco-friendly and non-toxic materials.^14–17 Lead-free perovskites are becoming more popular for their environmental benefits and potential use in electronic devices, especially halide double perovskites, which are ideal for solar and thermoelectric devices.^18–22 Reproducibility presents another challenge since the performance of PSCs can fluctuate greatly depending on the materials used and fabrication processes.^23–25 Scaling up production remains difficult as the creation of affordable, efficient, and high-capacity perovskite solar panels poses challenges. To address these issues, we focus on the A₃MX₃ group of inorganic compounds, known for their strong potential in solar energy capture.^26–30 Several researchers have conducted experimental studies on this inorganic compound from the A₃MX₃ group, publishing their findings in well-regarded journals. Their research emphasizes the unique structural, optical, and electronic properties of the compound. Additionally, these studies investigate its potential applications in diverse fields such as photovoltaics, optoelectronics, and semiconductor technology. The insights gained contribute to advancements in synthesis, characterization, and performance optimization, fostering further progress in materials science and technological innovation.^31–35 This article introduces a set of new cubic inorganic compounds, Ba₃MCl₃ (where M = Sb, As, P and N), belonging to the lead-free A₃MX₃ group. Studying the previously unexplored mechanical, optoelectronic, and thermodynamic properties of these materials has shown that they could be useful, particularly in optoelectronics and solar cell technology.

The current study employs first-principles computations using DFT^36,37 to investigate the various characteristics of this material. The SCF method was exploited to analyze the DOS, ECD, and band structure. The CASTEP method, based on DFT, was applied to examine the properties of Ba₃MCl₃ (M = N, P, As, and Sb).^38,39 Despite the lack of detailed theoretical work on the optical and electronic characteristics of these perovskite materials in the existing literature, its significant crystal features and practical applications prompted our investigation. We conducted a comprehensive analysis of its physical attributes using DFT simulations with the CASTEP code, comparing the results with similar compounds. Subsequently, investigations were conducted in hybrid PSCs using A₃MX₃ materials with a CdS ETL, focusing on the impact of layer thickness, doping levels, bulk defect density, QE and JV characteristics. Ultimately, the efficiency of all proposed devices under optimal conditions was evaluated. Although it is a set of novel inorganic compounds, Ba₃MCl₃ (M = Sb, As, P and N) exhibits promising properties, suggesting its suitability as an effective absorber and for optoelectronic applications due to its excellent electronic and optical characteristics. We anticipate that this study will significantly contribute to research on perovskite-based technologies in modern technology.

2. Experimental

2.1. Computational details

In this study, we conducted first-principles DFT^40,41 calculations utilizing the CASTEP method⁴² to explore the characteristics of Ba₃MCl₃ (M = Sb, As, P and N) perovskite cells. The Kohn–Sham equation⁴³ was employed to ascertain the crystal system. The process began with geometric optimization, followed by electronic property calculations employing ultrasoft pseudopotentials⁴⁴ and the BFGS⁴⁵ algorithm. GGA⁴⁶ and the PBE approach were utilized to improve our understanding of the characteristics of Ba₃MCl₃ perovskite cells (M = Sb, As, P and N). For this research, we set specific convergence standards, including an energy cutoff of 700 eV, a highest displacement of 0.0002 Å, a highest force of 0.05 eV per atom, a SCF tolerance of 1.0 × 10⁻⁶ eV per atom, and a highest energy of 2.0 × 10⁻⁵ eV per atom. For accurate computations, we applied a 7 × 7 × 7 k-point mesh based on the Monkhorst–Pack scheme⁴⁷ for sampling the BZ. The SCF method was exploited to compute the DOS and band structure, while also establishing parameters for the ECD. To examine the optical characteristics, we applied the linear feedback approach to measure how the dielectric function varies with frequency. Additionally, we computed the refractive index, the conductivity's real and imaginary segments, and the dielectric constant. Convergence checks were carried out to establish the chosen k-point mesh size and convergence criteria, ensuring both accuracy and computational efficiency. These computational approaches were carefully chosen to guarantee the precision and dependability of the results gained. In summary, this computational approach proposes an in-depth examination of the characteristics of Ba₃MCl₃ materials (M = Sb, As, P and N) and may serve as a valuable tool in the future.

2.2. Chemical reactions

However, the chemical reaction of this inorganic compound Ba₃MCl₃ is outlined below. The Ba₃NCl₃ inorganic compound consisting of barium (Ba), nitrogen (N), and chlorine (Cl), forms through a specific chemical reaction, as shown by eqn (1).⁴⁸

Ba₃N₂ + 3BaCl₂ → 2Ba₃NCl₃ (1)

On the other hand, the creation of the inorganic compound Ba₃PCl₃ is given below. This compound, composed of barium (Ba), phosphorus (P), and chlorine (Cl), is produced through a particular chemical reaction, as shown by eqn (2).

Ba₃P₂ + 3BaCl₂ → 2Ba₃PCl₃ (2)

Additionally, the synthesis of the inorganic compound Ba₃AsCl₃ is detailed below. This compound, which comprises barium (Ba), arsenic (As), and chlorine (Cl), is formed through a precise chemical reaction, as shown by eqn (3). The process involves the careful combination of these elements in exact proportions, leading to the creation of Ba₃AsCl₃.

Ba₃As₂ + 3BaCl₂ → 2Ba₃AsCl₃ (3)

The formation of the inorganic compound Ba₃SbCl₃ is described below. This compound, made up of barium (Ba), antimony (Sb), and chlorine (Cl), is produced through a specific chemical reaction. The procedure requires the precise mixing of these elements in the correct proportions, resulting in the synthesis of Ba₃SbCl₃ as shown by eqn (4).

Ba₃Sb₂ + 3BaCl₂ → 2Ba₃SbCl₃ (4)

3. Results and discussion

3.1. Structural study of Ba₃MCl₃ (M = N, P, As, and Sb)

Fig. 1(a) shows that the crystal structures of Ba₃MCl₃ (M = N, P, As, and Sb) belong to the cubic space group Pm3̄m (no. 221). Each structure comprises a unit cell containing 7 atoms. The Cl atoms hold the 3d Wyckoff site with relevant positions of (0, 0, 0.5) on the borders of one face, while the central position is occupied by the M atom (N, P, As, and Sb) at the 1b Wyckoff site with relevant positions of (0.5, 0.5, 0.5). Additionally, the Ba atoms at the 3c Wyckoff site are located near the vertices of a single cell, with relative positions of (0.5, 0.5, 0). Fig. 1(b) visually signifies the trajectory in k-space within the primary BZ. The electronic band arrangement of Ba₃MCl₃ is determined by the points of high symmetry (X–R–M–G–R) in the BZ, where the band diagram is replicated throughout the structure. The most optimized structures of Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃ yielded the computed lattice parameters of 6.14, 6.44, 6.51, and 6.69, respectively. The respective unit cell volumes of Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃ are 1563.6448 (a.u.)³, 1804.2245 (a.u.)³, 1863.6998 (a.u.)³, and 2022.6062 (a.u.)³.

Fig. 1 (a) Crystal structure of Ba₃MCl₃ (M = N, P, As, and Sb), (b) BZ path (X_R_M_G_R) and the distribution of electronic charges in (c) Ba₃NCl₃, (d) Ba₃PCl₃, (e) Ba₃AsCl₃ and (f) Ba₃SbCl₃.

3.2. Electron charge density

The type of bonding present among different atoms is elucidated by means of the arrangement of charge density. To understand the movement of the charge between atoms and discern the bonding within Ba₃MCl₃ (M = Sb, As, P and N), we evaluated the charge density. Fig. 1(c)–(f) illustrate the pattern of electrical charge density in Ba₃MCl₃ (M = Sb, As, P and N), respectively. The images feature a scale bar positioned on the left side that utilizes color representation to indicate the electron density's intensity. The cyan color corresponds to regions of high electron density, whereas the yellow color indicates areas with low electron density. In this case, the ECD is highest around the Cl ion and lowest around the Ba ion. Because an ionic bond develops when negative and positive charges are balanced at atomic locations, the absence of overlap between the Ba and Cl ions means an ionic bond. In contrast, the charge density is comparable between Cl and M ions (where M = N, P, As, and Sb), which is indicative of a covalent bond. Additionally, a notable difference in electron density between the Ba and M (N, P, As, and Sb) ions suggests an ionic bond connecting them.

3.3. Electronic study of Ba₃MCl₃ (M = N, P, As, and Sb)

The electrical band arrangement of a material is crucial for understanding its physical features such as charge transport behavior and optical characteristics. In the case of Ba₃MCl₃ (M = N, P, As, and Sb), its band structures are depicted in Fig. 2 along the BZ path X–R–M–G–R, by employing the PBE process. The analysis reveals band gaps of 0.551 eV, 0.927 eV, 0.980 eV, and 0.996 eV for Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃, respectively, using the GGA-PBE function at the G point, known for its accuracy.⁴⁹ Notably, different exchange–correlation (XC) functions may yield varying band-gap results.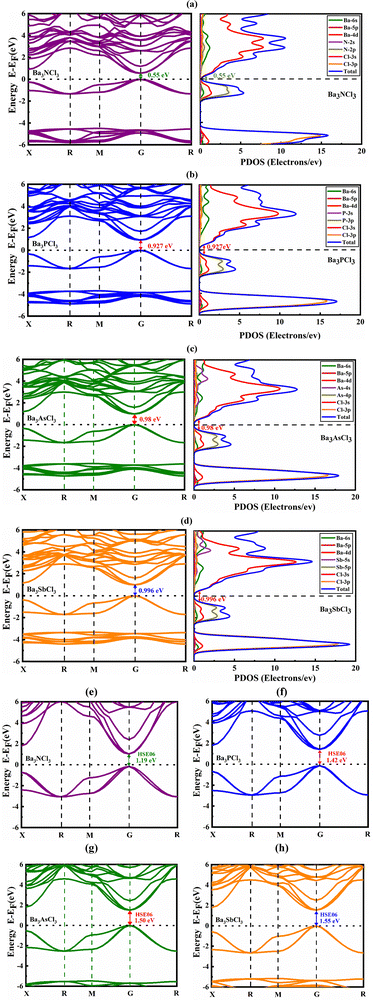

Fig. 2 Electronic band structures and inorganic cubic PDOS structures of (a) Ba₃NCl₃, (b) Ba₃PCl₃, (c) Ba₃AsCl₃, and (d) Ba₃SbCl₃ structures and (e)–(h) the band structures using the HSE06 function.

In this representation, the Fermi level (E_f) is denoted at 0 eV, while the energy stages vary from −6 to +6 eV. The upper lines in the band structure correspond to the CB, whereas those at the Fermi level signify the VB. This direct bandgap emerges from the intriguing alignment of the maximum VB energy state with the minimum CB energy state at the G symmetry point.⁵⁰

The narrow band gap of Ba₃MCl₃ (M = N, P, As, and Sb) allows efficient capture of visible light and reduces thermalization losses, improving its efficacy in converting light to electricity. Such materials exhibit elevated electron mobility and are proficient in light emission, making them desirable for electronic and optical devices.^51,52 A smaller band gap permits light absorption with lower energy levels, such as near-infrared wavelengths corresponding to 0.551 eV, 0.927 eV, 0.980 eV, and 0.996 eV band gaps. This analysis suggests the suitability of the material for optoelectronic devices, given its semiconducting nature, which is a crucial consideration for solar cell applications.

In Fig. 2(e)–(h), using the HSE06 functional, the materials Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃ were found to have direct bandgaps of approximately 1.19 eV, 1.42 eV, 1.50 eV, and 1.55 eV, respectively. These values were calculated using the HSE06 exchange–correlation functional. The band structure analysis, conducted along the trajectory in reciprocal space (X_R_M_G_R), corresponds to the cubic arrangement of Ba₃MCl₃ under the HSE06 functional.

Typically, PDOS analysis reveals the impact of several atoms and their locations on the band gap of Ba₃MCl₃ compounds. Fig. 2(a)–(d) illustrate the PDOS distribution for Ba₃MCl₃ structures (M = Sb, As, P and N) spanning the energy range from −6 to +6 eV. The states associated with the Ba and Sb, As, P and N atoms, which interact with Cl in Ba₃MCl₃ (M = Sb, As, P and N), are found to spread throughout the total energy spectrum without impacting the band gap. This proposal proposes that the bonding between Ba–Cl, N–Cl, P–Cl, As–Cl, and Sb–Cl is predominantly covalent in nature. Furthermore, in Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃, electron charge transfer occurs from Ba and N, P, As, and Sb to Cl, respectively, potentially resulting in substantial changes in atomic situations. Because of their separation from the Fermi level, the Ba²⁺ atoms have only a minimal influence on the determination of band edge conditions in this scenario. In our study of the cubic phase, we noted that the VB of Ba₃MCl₃ is mainly shaped by the Cl-3p orbital, whereas the CB is mainly determined by the Ba-4d orbital, with slight involvement from the N-2s, P-3s, As-4s and Sb-5s orbitals. The strong contribution from Cl-3p orbitals in the valence band indicates a significant ionic character in the bonding between Cl and Ba. The Ba-4d orbitals' involvement in the conduction band suggests that these states are important for electronic transitions and charge carrier transport. This combination of contributions from both orbitals plays a critical role in defining the material's bandgap and electronic structure.

3.4. Optical study of Ba₃MCl₃ (M = N, P, As, and Sb)

Various applications, including optical coatings, rectifiers, light absorbers, and devices converting light into electricity, are explored depending on their optical characteristics. When subjected to an external electromagnetic wave, a material's interaction with photons can reveal facts about its characteristics and potential applications relative to energy. An investigation of electronic conversions between bond types, occupied and unoccupied energy states, band arrangements, and internal structural properties of compounds is achieved by examination of their optical spectra.⁵³ Certain optical properties of a perovskite that vary with energy levels comprise energy loss function L(ω), reflectivity R(ω), optical conductivity σ(ω), refractive index N(ω), dielectric function ε(ω), and absorption coefficient α(ω). We compute and examine these optical features to explore how Ba₃MCl₃ (M = N, P, As, and Sb) reacts to incoming photons in this section.

Fig. 3(a)–(h) illustrate the spectra for the parameters mentioned above, spanning incident energies equal to 40 eV and an exclusively polarized electric field that has the crystal plane [1 0 0].⁵⁴ The complex dielectric constant, which changes with frequency or energy, is attained through the Kramers–Kronig transformation as follows:⁵⁵

ε(ω) = ε₁(ω) + iε₂(ω) (5)

Fig. 3 Energy-associated (a) absorption index, (b) loss function, (c) real, (d) imaginary component of conductivity, (e) real, (f) imaginary dielectric function, (g) real and (h) imaginary segment of refractive index of Ba₃MCl₃ (M = N, P, As, and Sb).

Furthermore, other optical properties were determined using the real portion ε₁(ω) and the imaginary portion iε₂(ω).

Fig. 3(a) illustrates the optical absorption coefficient of Ba₃MCl₃ (M = N, P, As, and Sb).⁵⁴ The optical absorption coefficient plays a vital role in evaluating a material's ability to absorb light, providing valuable insights into its suitability for efficient solar energy conversion.^56,57 The absorption coefficient spans from 5 to 25 eV, with the absorption being notably high, reaching its peak around 17 eV of photon energy for all materials. It starts at 0.7 eV and diminishes to zero after 25 eV, indicating a considerable photon energy absorption ranging from 0.7 to 25 eV. This proposes that Ba₃MCl₃ possesses a wider optical bandgap, resulting in significant photon absorption at high energies.

Fig. 3(b) depicts the loss function L(ω), which varies with energy or frequency. This component, typically imaginary, within the dielectric function mimics the way light is absorbed by a semiconductor. The peak is observed at a photon energy level of 23 eV for Ba₃NCl₃ and 21 eV for the other three materials, after which it returns to zero. This peak indicates the plasmon energy characteristic of the respective materials. The plasma oscillates at this exact energy due to the collective motions of charged particles. Note that significant decreases in the reflectivity and absorption coefficient coincide with the plasma energy.

Fig. 3(c) and (d) display the optical conductivity's real and imaginary parts for Ba₃MCl₃ (M = N, P, As, and Sb). The imaginary part of the photoconductivity initiates at 0.42 eV, while the real portion begins with approximately 0 eV for all materials, affirming the material's favorable photoconductivity characteristics. Furthermore, the real part drops to zero beyond 25 eV of photon energy, suggesting an improvement in the conductivity at upper energies.⁵⁸ This phenomenon could be attributed to the movement of electrons to elevated energy states, enabling their participation in electrical flow.

Fig. 3(e) and (f) depict the dielectric function's real ε₁(ω) and imaginary portion ε₂(ω) for Ba₃MCl₃ (M = Sb, As, P and N). These components are derived from the elements of the momentum matrix, considering all feasible conversions between the filled and empty electronic conditions.^59,60 The real segment of the dielectric function, ε₁(ω), corresponds to electrical polarization, while the imaginary component, ε₂(ω), relates to dielectric loss.^61,62 Notably, the real portion reaches zero at 9 eV photon energy for Ba₃NCl₃ and 17 eV for the other three materials and gradually approaches unity. In contrast, the imaginary part ε₂(ω) begins at zero and drops back to zero when the photon energy hits 25 eV. The dielectric constant of Ba₃MCl₃ indicates metallic properties depending on its band structure and electronic DOS, also showing semiconducting characteristics and high reflectivity.⁶¹

In Fig. 3(g) and (h), a complex factor, the refractive index, is depicted. It is also a function dependent on energy or frequency and can be formulated as:⁵⁵

N(ω) = n(ω) + ik(ω) (6)

where the extinction factor is indicated by k(ω), representing the imaginary portion of N(ω). The refractive index's imaginary portion (extinction factor) gauges the absorption of electromagnetic radiation by the materials, while the real part resolves the phase velocity in the materials.⁶³ It can be observed that the refractive index's real part demonstrates a greater value in the visible spectrum at low phonon-energy levels. Thus, the material under investigation demonstrates optical features appropriate for application in optoelectronic devices.⁶⁴

3.5. Design of devices and simulation techniques

The proposed photovoltaic cell structure, represented as Al/FTO/CdS/(Ba₃NCl₃/Ba₃PCl₃/Ba₃AsCl₃/Ba₃SbCl₃)/Au, includes devices labeled device-I (Ba₃NCl₃), II (Ba₃PCl₃), III (Ba₃AsCl₃), and IV (Ba₃SbCl₃). These devices have been simulated utilizing the SCAPS-1D software. The essential formulas were resolved to thoroughly analyze and predict the electrostatic potential formulas in steady-state situations, as well as the electron–hole continuity formulas for both structures.⁶⁵ The solar cell contains a p-type absorber layer (Ba₃NCl₃/Ba₃PCl₃/Ba₃AsCl₃/Ba₃SbCl₃), a highly n-doped ETL made of CdS and an FTO window stratum. The metal electrodes at the front and rear are aluminum (Al) and gold (Au), with WF of 4.2 eV (100) and 5.37 eV (110), respectively. The distinct alignment of the quasi-Fermi levels Fn and Fp under illumination provides evidence for the formation of electron and hole pairs inside the device. The electric fields and intrinsic potential at the absorber/ETL interface facilitate the separation of light-induced electron–hole pairs. The imitation data for the active materials FTO, CdS, Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃, and Ba₃SbCl₃, presented in Table 1, were derived from the established literature and the DFT calculations of this study, with the electron and hole paces set at 10⁷ cm s⁻¹.^66,67 The specifications for each of the four proposed PV devices at the absorber/ETL boundary are detailed in Table 2.

Table 1 Parameters set for the FTO, ETL, and absorber layer

Parameters	Ba3NCl3	Ba3PCl3	Ba3AsCl3	Ba3SbCl3	CdS	FTO
Thickness (nm)	1000	1000	1000	1000	50	50
Band gap, Eg (eV)	0.55	0.927	0.98	0.996	2.4	3.6
Electron affinity, χ (eV)	3.687	4.5	4.562	4.805	4.4	4.5
	6.606	3.206	5.602	5.48	9	10
CB effective density of states, NC (1 cm^−3)	6.78 × 10^18	7.728 × 10^18	7.94 × 10^18	9.347 × 10^18	1.8 × 10^19	2 × 10^18
VB effective density of states, NV (1 cm^−3)	1.007 × 10^19	1.09 × 10^19	1.136 × 10^19	1.2 × 10^19	2.4 × 10^18	1.8 × 10^19
Electron mobility, μn (cm^2 V^−1 s^−1)	60	70	65	45	100	100
Hole mobility, μh (cm^2 V^−1 s^−1)	55	60	45	40	25	20
N A (1 cm^−3)	1 × 10^16	1 × 10^16	1 × 10^16	1 × 10^16	0	0
N D (1 cm^−3)	0	0	0	0	1 × 10^15	1 × 10^18
Defect density, Nt (1 cm^−3)	1 × 10^12	1 × 10^12	1 × 10^12	1 × 10^12	1 × 10^12	1 × 10^12

---

Table 2 Input parameters of the interface of the Ba₃MCl₃ (M = N, P, As, and Sb) based solar cells

Parameters	Ba3NCl3/SnS2	Ba3PCl3/SnS2	Ba3AsCl3/SnS2	Ba3SbCl3/SnS2
Defect type	Neutral	Neutral	Neutral	Neutral
σ e (cm^2)	1 × 10^−19	1 × 10^−19	1 × 10^−19	1 × 10^−19
σ h (cm^2)	1 × 10^−19	1 × 10^−19	1 × 10^−19	1 × 10^−19
E r	0.6	0.6	0.6	0.6
Total defect density (cm^−1)	10^12	10^12	10^12	10^12

---

3.6. Optimization of absorber layer thickness and charge carrier concentration

Fig. 4(a) displays the impact of altering the absorber layer thickness at 100–2000 nm to achieve optimal outcomes in the suggested devices without altering other factors, as shown in the previous table. It was observed that both carrier generation and recombination speeds rise significantly with a thicker absorber layer. A thickening of the absorber layer led to an upsurge in the V_OC of the PSCs in every configuration. The maximum V_OC of 0.5 V was attained for device I. Similarly, improvements in V_OC were observed for device II (from 0.47 to 0.49 V), device III (from 0.42 to 0.49 V), and device IV (from 0.17 to 0.49 V). The J_SC also increased with the denser absorber layer, mainly because of improved absorption across the spectrum, with a focus on longer wavelengths. J_SC values rose from 32.61 to 54.45 mA cm⁻² in device I, 30.99 to 51.26 mA cm⁻² in device II, 29.32 to 47.78 mA cm⁻² in device III, and 28.79 to 47.19 mA cm⁻² in device IV. The rise in J_SC can be ascribed to the greater formation of electron and hole pairs from increased photon absorption in a thicker absorber. These changes in V_OC and J_SC are in line with findings described in previous studies.^68–70

Fig. 4 Influence of alteration of the absorber layer (Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃) (a) thickness and (b) acceptor density with PV factors of V_OC, J_SC, FF and PCE.

FF values improved from 79.64% to 80.05% for device II, from 76.03% to 79.19% for device III, and from 55.97% to 75.92% for device IV with increasing absorber thickness, but FF values improved from 81.37% to 84.39% for device I with decreasing absorber thickness. PSCs generally operate most efficiently once the absorber thickness corresponds to the charge carriers' diffusion length. Although thicker absorber layers result in higher photon absorption, they also lead to increased recombination rates. Thus, optimizing between these factors is essential for achieving high-efficiency PSCs.^71–73

Fig. 4(b) shows how electrical properties, such as J_SC, PCE, V_OC and FF, vary with acceptor doping density (N_A) ranging from 10¹⁰ to 10¹⁸ cm⁻³ for the absorbers Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃ in the proposed configuration. During optimization, the V_OC of the PSCs exhibited minimal variation up to an N_A of 10¹⁴ cm⁻³.⁷⁴ The maximum V_OC observed was 0.5 V for device I (mainly constant all the time), 0.54 V for device II, 0.58 V for device III and 0.54 V for device IV (which showed a relatively higher rate of change). The fill factor exhibited similar trends, with a noticeable 4–5% improvement, reaching nearly saturated values of 82.06%, 80.01%, 78.15%, and 74.49% for Ba₃NCl₃, Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃, respectively, at an N_A of 10¹⁶ cm⁻³, as shown in Table 3. This behavior aligns with previous reports.^75,76 However, when the acceptor density in the absorber layer was varied from 10¹⁰ to 10¹⁵ cm⁻³, the J_SC remained almost constant. Beyond 10¹⁵ cm⁻³, the J_SC marginally decreased for Ba₃PCl₃, Ba₃AsCl₃ and Ba₃SbCl₃. For Ba₃NCl₃, the J_SC remained unchanged up to 10¹⁸.

Table 3 Performance metrics of solar cells using the CdS ETL are evaluated against various absorbers

Parameters	Ba3NCl3	Ba3PCl3	Ba3AsCl3	Ba3SbCl3
V OC (V)	0.5	0.49	0.47	0.46
J SC (mA cm^−2)	53.97	50.78	46.76	45.55
FF (%)	82.06	80.01	78.15	74.49
PCE (%)	23.06	19.93	17.12	15.71

---

3.7. Impact of device thickness (I, II, III, and IV) and defect density

Fig. 5 displays the impact of the defect density (N_t) on the efficiency of PV cells by illustrating the alterations in both the thickness and the N_t of the Ba₃NCl₃ absorber layer, varying from 0.1 to 2.0 μm and from 10¹⁰ to 10¹⁸ cm⁻³, respectively. The solar cell outcome noticeably deteriorates when the N_t of Ba₃NCl₃ surpasses 10¹² cm⁻³.⁶⁸J_SC, V_OC, PCE and FF for Al/FTO/CdS/Ba₃NCl₃/Au structures drop from 57 to 32.6 mA cm⁻², from 0.63 to 0.14 V, from 31.6% to 3.1%, and from 85.6% to 40%, respectively. As shown in Fig. 5(a), a peak V_OC of 0.5 V is obtained if the N_t is kept underneath 10¹² cm⁻³ and the thickness remains less than 1 μm. In contrast, if the N_t goes beyond 10¹² cm⁻³, the V_OC decreases markedly to 0.16 V.

Fig. 5 Influence of variations in absorber thickness and defect density (device-I, Ba₃NCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

Fig. 5(b) and (c) indicate that to attain the highest values of J_SC and FF of 53.97 mA cm⁻² and 82.06%, respectively, the thickness should exceed 1 μm and the N_t should remain below 10¹² cm⁻³. Fig. 5(d) depicts that the highest conversion efficiency, exceeding 23.06%, is obtained once the thickness is within 0.1 to 2.0 μm and the N_t is up to 10¹² cm⁻³. Higher carrier recombination rates, caused by increased defects in the absorber layer, consequently reduce the cell's efficiency.^77–79 The optimal criteria for reaching a maximum PCE of 23.06% for device-I have been identified. This involves ensuring an absorber layer thickness of 1.0 μm for Ba₃NCl₃ with a N_t of 10¹² cm⁻³. With these parameters, the PV cell obtained a V_OC of 0.5 V, a J_SC of 53.97 mA cm⁻², and an FF of 82.06%.

For Al/FTO/CdS/Ba₃PCl₃/Au (device II) structures, increasing the defect density leads to a decline in J_SC, PCE, V_OC, and FF, while thickening the absorber layer improves these values. In particular, these parameters increase significantly with a thickness up to 1 μm, beyond which further increases produce only marginal improvements. In contrast, the values drop sharply as the N_t increases up to 10¹² cm⁻³, and any increase beyond this threshold results in a slight decline. Therefore, the optimal absorber layer thickness is 1 μm with a N_t of 10¹² cm⁻³. In these optimal circumstances, J_SC, V_OC, PCE, and FF reach values of 50.78 mA cm⁻², 0.49 V, 19.93%, and 80.01%, respectively. Fig. 6(a) shows that the highest V_OC of 0.49 V is gained with a thickness less than 1 μm and a N_t below 10¹² cm⁻³. However, exceeding this defect density threshold significantly reduces the V_OC to 0.27 V. Fig. 6(b) and (c) suggest that to achieve the highest J_SC and FF values of 50.78 mA cm⁻² and 80.01%, the thickness should exceed 1 μm and the N_t should remain below 10¹² cm⁻³. Fig. 6(d) specifies that maintaining a thickness between 0.1 and 2.0 μm and a N_t equal to 10¹² cm⁻³ yields the peak conversion efficiency, surpassing 19.93%.

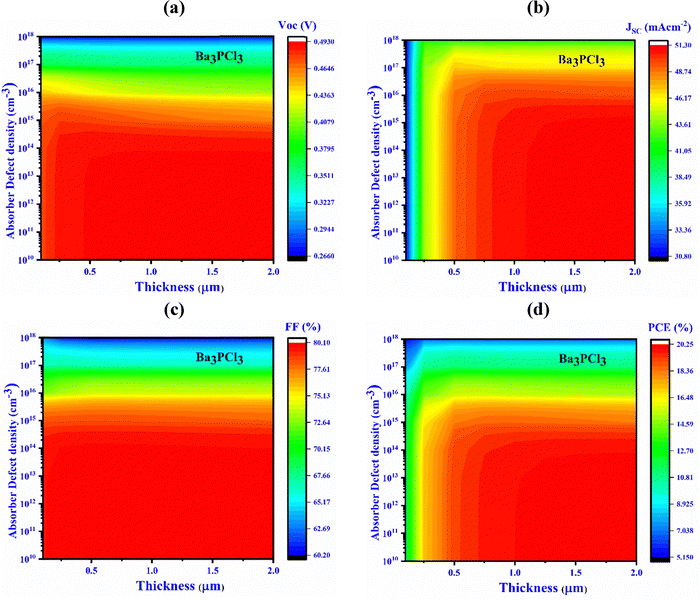Fig. 6 Influence of variations in absorber thickness and defect density (device II, Ba₃PCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

The FF, J_SC, PCE, and V_OC of the Al/FTO/CdS/Ba₃AsCl₃/Au (device III) structures decline significantly from 79.2% to 59%, 47.8 to 29.15 mA cm⁻², 18.4% to 5.3%, and 0.49 to 0.3 V, respectively. Fig. 7(a) shows that the peak V_OC of 0.47 V is reached when the N_t is underneath 10¹² cm⁻³ and the absorber layer thickness is under 1 μm. When N_t exceeds 10¹² cm⁻³, V_OC drops sharply to 0.31 V. Fig. 7(b) and (c) suggest that to obtain the highest values of J_SC and FF of 46.76 mA cm⁻² and 78.15%, the thickness needs to exceed 1 μm and the N_t should remain under 10¹² cm⁻³. As demonstrated in Fig. 7(d), maintaining a thickness among 0.1 and 2.0 μm and keeping the N_t equal to 10¹² cm⁻³ results in the optimal conversion efficiency, which exceeds 17.12%.

Fig. 7 Influence of variations in absorber thickness and defect density (device-III, Ba₃AsCl₃) on key PV performance parameters: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

In contrast, the performance metrics of the Al/FTO/CdS/Ba₃SbCl₃/Au (device IV) structures degrade as the PCE drops from 17.45% to 2.55%, the FF from 76% to 52.4%, the J_SC from 47.2 to 28.45 mA cm⁻², and the V_OC from 0.49 to 0.17 V. Fig. 8(a) shows that the peak V_OC of 0.46 V is reached once the N_t is below 10¹² cm⁻³ and the absorber layer thickness is below 1 μm. However, exceeding this N_t threshold significantly reduces the V_OC to 0.19 V. Fig. 8(b) and (c) suggest that to achieve the highest J_SC and FF values of 45.55 mA cm⁻² and 74.49%, the thickness should exceed 1 μm and the N_t should remain under 10¹² cm⁻³. Fig. 8(d) indicates that maintaining a thickness ranging from 0.1 to 2.0 μm and keeping the N_t equal to 10¹² cm⁻³ results in the optimal conversion efficiency, which exceeds 15.71%.

Fig. 8 Influence of variations in absorber thickness and defect density (device-IV, Ba₃SbCl₃) on key PV performance parameters: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

3.8. Impact of device thickness (I, II, III, and IV) and interface change in solar energy efficiency

Fig. 9 presents the influence of N_int on the outcome of photovoltaic cells, illustrating alterations in the N_int as well as the thickness of the Ba₃NCl₃ absorber layer. These parameters range from 10¹⁰ to 10¹⁸ cm⁻³ for defect density and 0.1 to 2.0 μm for thickness. The metrics for solar cell performance reduces significantly if the N_int in the Ba₃NCl₃ interface exceeds 10¹² cm⁻³. The J_SC, V_OC, PCE, and FF of Al/FTO/CdS/Ba₃NCl₃/Au structures reduce from 64.5 to 42 mA cm⁻², 0.57 V to 0.15 V, 24.9% to 2.4%, and 77% to 37.8%, respectively.

Fig. 9 Influence of variations in absorber thickness and defect interface density (device-I, Ba₃NCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

Fig. 9(a) shows that the peak V_OC of 0.5 V is gained while the absorber layer is 1 μm thick and the N_int is below 10¹² cm⁻³. However, exceeding this threshold of the N_int significantly reduces the V_OC to 0.16 V. Fig. 9(b) and (c) indicate that to achieve the peak J_SC of 53.97 mA cm⁻² and FF of 82.06%, the absorber thickness should be larger than 1 μm, and the N_int should remain below 10¹² cm⁻³. Fig. 9(d) depict that the highest conversion efficiency, surpassing 23.06%, occurs within a thickness ranging from 0.1 to 2.0 μm and when N_int is equal to 10¹² cm⁻³. The addition of high-defect states to the absorber layer boosts carrier recombination, causing a decline in total cell performance.^77–79 The best conditions for attaining the peak PCE of 23.06% for device I were identified, which includes a constant Ba₃NCl₃ absorber thickness of 1.0 μm and an N_int of 10¹² cm⁻³. A V_OC of 0.5 V, a J_SC of 53.97 mA cm⁻², and an FF of 82.06% were achieved by the solar cell in this case.

For Al/FTO/CdS/Ba₃PCl₃/Au (device II) structures, performance factors such as J_SC, PCE, V_OC, and FF are negatively impacted by a rise in interface defect density, while an upsurge in the absorber layer's thickness generally improves these values. Up to a thickness of 1 μm, these parameters increase significantly. However, beyond 1 μm, the improvements are marginal. Similarly, these values decrease significantly as the N_int rises up to 10¹² cm⁻³, but the reduction is more gradual once the N_int surpasses 10¹² cm⁻³. Therefore, the optimal thickness is 1 μm, and the ideal N_int is 10¹² cm⁻³. Under these conditions, the PCE is 19.93%, the FF is 80.01%, the J_SC is 50.78 mA cm⁻², and the V_OC is 0.49 V. As illustrated in Fig. 10(a), the peak V_OC of 0.49 V is gained with a thickness below 1 μm and a N_int under 10¹² cm⁻³. However, exceeding this interface defect density threshold significantly reduces the V_OC to 0.32 V. Fig. 10(b) and (c) indicate that to reach the greatest values of J_SC (50.78 mA cm⁻²) and FF (80.01%), the thickness should be superior to 1 μm and the N_int should not exceed 10¹² cm⁻³. According to Fig. 10(d), maintaining a thickness between 0.1 and 2.0 μm and an N_int equal to 10¹² cm⁻³ results in the optimal conversion efficiency, which exceeds 19.93%.

Fig. 10 Influence of variations in absorber thickness and defect interface density (device-II, Ba₃PCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

The J_SC, V_OC, PCE, and FF of Al/FTO/CdS/Ba₃AsCl₃/Au (device-III) structures decrease from 47.8 to 28.6 mA cm⁻², 0.49 to 0.38 V, 18.4 to 7.8%, and 79.2 to 72.44%, respectively. Fig. 11(a) shows that the peak V_OC of 0.47 V is gained if the thickness is below 1 μm and the N_int is under 10¹² cm⁻³. However, exceeding this interface defect density threshold significantly reduces the V_OC to 0.39 V. Fig. 11(b) and (c) show that the thickness needs to exceed 1 μm and the N_int should not exceed 10¹² cm⁻³ to attain the peak J_SC and FF values of 46.76 mA cm⁻² and 78.15%, respectively. Fig. 11(d) shows that a thickness ranging from 0.1 to 2.0 μm and a N_int equal to 10¹² cm⁻³ result in the maximum efficiency, exceeding 17.12%.

Fig. 11 Influence of variations in absorber thickness and defect interface density (device-III, Ba₃AsCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

The FF, J_SC, PCE, and V_OC of the Al/FTO/CdS/Ba₃SbCl₃/Au (device IV) structures decrease from 76 to 55.8%, 47.2 to 28.15 mA cm⁻², 17.45 to 2.6%, and 0.49 to 0.17 V, respectively. Fig. 12(a) shows that the highest V_OC of 0.46 V is reached if the thickness is below 1 μm and N_int is under 10¹² cm⁻³. Besides, when the N_int exceeds 10¹² cm⁻³, the V_OC noticeably falls into 0.19 V. Fig. 12(b) and (c) indicate that the thickness needs to exceed 1 μm and the N_int should not exceed 10¹² cm⁻³ to achieve the highest J_SC and FF values of 45.55 mA cm⁻² and 74.49%, respectively. Fig. 12(d) demonstrates that a thickness spanning from 0.1 to 2.0 μm and an N_int equal to 10¹² cm⁻³ result in the utmost efficiency, exceeding 15.71%.

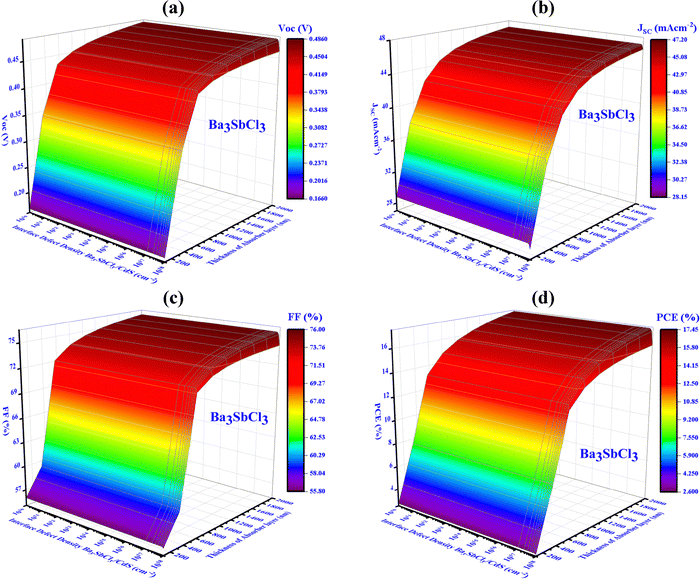Fig. 12 Influence of variations in absorber thickness and defect interface density (device-IV, Ba₃SbCl₃) on key PV performance factors: (a) V_OC, (b) J_SC, (c) FF, and (d) PCE.

As absorber thickness increases, more incident photons are absorbed due to the longer optical path, enhancing light absorption. However, beyond a certain point, further thickness results in only marginal gains, as absorption approaches saturation, consistent with the Beer–Lambert law.⁸⁰ While thicker layers generate more carriers, they also increase the transport distance, leading to higher recombination, particularly if the carrier diffusion length is shorter than the absorber thickness. This trade-off affects overall efficiency, where thinner layers underperform in photon absorption, and excessively thick layers suffer from recombination losses.⁸¹ The optimal thickness, around 1000 nm, strikes a balance between maximizing photon absorption and minimizing recombination. According to Shockley–Read–Hall recombination theory,⁸² this intermediate thickness offers the highest efficiency by reducing recombination losses while maintaining strong absorption.

3.9. Optimized J–V and QE characteristics

The J–V curves for the device, with optimal parameters (N_A of 10¹⁶ cm⁻³, N_int of 10¹² cm⁻², N_t of 10¹² cm⁻²) and absorber thicknesses between 100 and 2000 nm, are shown in Fig. 13(a). Analysis determined 1000 nm as the ideal absorber thickness, yielding values of (V_OC: 0.5 V, J_SC: 53.97 mA cm⁻², FF: 82.06%), (V_OC: 0.49 V, J_SC: 50.78 mA cm⁻², FF: 80.06%), (V_OC: 0.47 V, J_SC: 46.76 mA cm⁻², FF: 78.15%), and (V_OC: 0.46 V, J_SC: 45.55 mA cm⁻², FF: 74.49%) for devices I, II, III and IV, respectively, with CdS producing the highest PCE. Fig. 13(b) shows the QE curve for absorber thicknesses from 100 to 2000 nm, where QE, the fraction of photogenerated charge carriers per incident photon,^83–85 nearly reached saturation at 1000 nm, then rapidly dropped to zero at cutoff wavelengths of 1460, 1330, 1260, and 1240 nm for devices I, II, III and IV, respectively. The 1000-nm thickness was deemed ideal, as supported by the QE spectra and J–V characteristics.

Fig. 13 (a) J–V and (b) PSC QE curves for devices I, II, III, and IV.

4. Conclusions

This study examines the impact of M-anion modifications on lead-free halide inorganic compounds, specifically Ba₃MCl₃ (M = N, P, As, Sb), using DFT and SCAPS-1D software. The analysis begins with the use of GGA and PBE functional theory. Band structure and DOS analyses confirm the semiconductor properties of Ba₃MCl₃ compounds (M = N, P, As, Sb). Optical features such as absorption, dielectric function, electrical conductivity, loss function, reflectance, and refractive index, are explored. ECD mapping reveals the ionic bond nature of these compounds. For the perovskite solar cell, the SCAPS simulator was used to design the structure Al/FTO/CdS/(Ba₃NCl₃/Ba₃PCl₃/Ba₃AsCl₃/Ba₃SbCl₃)/Au. The simulation results show that Ba₃NCl₃ delivers the highest J_SC, V_OC, PCE, and FF values, with 53.97 mA cm⁻², 0.5 V, 23.06%, and 82.06%, respectively, outperforming other compounds under similar conditions. In contrast, Ba₃SbCl₃ exhibits the lowest output values, with J_SC of 45.55 mA cm⁻², V_OC of 0.46 V, PCE of 15.71%, and FF of 74.49%. These results indicate that Ba₃MCl₃ (M = N, P, As, Sb) compounds have promise for further research in optoelectronic applications.

List of abbreviations

J–V	Current density–voltage
N t	Defect density
PCE	Power conversion efficiency
ECD	Electron charge density
SCAPS	Solar cell capacitance simulator
J SC	Short circuit current density
QE	Quantum efficiency
VB	Valence band
V OC	Open circuit voltage
ETL	Electron transport layer
SCF	Self-consistent field
DFT	Density functional theory
N int	Interface defect density
BZ	Brillouin zone
FTO	Fluorine-doped tin oxide
PSC	Perovskite solar cell
FF	Fill factor
CB	Conduction band
HTL	Hole transport layer
WF	Work function
PV	Photovoltaic

Data availability

Data are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors have no conflicts of interest.

Acknowledgements

A. Irfan extends his appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Large Research Project under grant number RGP2/172/45.

References

1. S. Marimuthu, S. Pandiaraj, M. Muthuramamoorthy, K. E. Alzahrani, A. N. Alodhayb, S. Pitchaimuthu and A. N. Grace, Experimental and computational DFT, drift-diffusion studies of cobalt-based hybrid perovskite crystals as absorbers in perovskite solar cells, Phys. Chem. Chem. Phys., 2024, 26, 4262–4277.
2. C. Xing, Y. Lei, M. Liu, S. Wu, W. He and Z. Zheng, Environment-friendly Cu-based thin film solar cells: materials, devices and charge carrier dynamics, Phys. Chem. Chem. Phys., 2021, 23, 16469–16487.
3. C. Paduani and A. M. Rappe, Tuning the gap of lead-based halide perovskites by introducing superalkali species at the cationic sites of ABX₃-type structure, Phys. Chem. Chem. Phys., 2017, 19, 20619–20626.
4. D. Liu, H. Zeng, H. Peng and R. Sa, Computational study of the fundamental properties of Zr-based chalcogenide perovskites for optoelectronics, Phys. Chem. Chem. Phys., 2023, 25, 13755–13765.
5. Y.-C. Zhao, W.-K. Zhou, X. Zhou, K.-H. Liu, D.-P. Yu and Q. Zhao, Quantification of light-enhanced ionic transport in lead iodide perovskite thin films and its solar cell applications, Light: Sci. Appl., 2017, 6, e16243–e16243.
6. D. Luo, W. Yang, Z. Wang, A. Sadhanala, Q. Hu, R. Su, R. Shivanna, G. F. Trindade, J. F. Watts, Z. Xu, T. Liu, K. Chen, F. Ye, P. Wu, L. Zhao, J. Wu, Y. Tu, Y. Zhang, X. Yang, W. Zhang, R. H. Friend, Q. Gong, H. J. Snaith and R. Zhu, Enhanced photovoltage for inverted planar heterojunction perovskite solar cells, Science, 2018, 360, 1442–1446.
7. H. Bencherif and M. Khalid Hossain, Design and numerical investigation of efficient (FAPbI₃)_1−x(CsSnI₃)_x perovskite solar cell with optimized performances, Sol. Energy, 2022, 248, 137–148.
8. D. Nadhiya, A. Kala, P. Sasikumar, M. K. A. Mohammed, P. Thirunavukkarasu, M. Prabhaharan, C. Karnan, S. Albukhaty, M. S. Jabir, A. Syed, A. M. Elgorban and N. S. S. Zaghloul, Influence of Cu²⁺ substitution on the structural, optical, magnetic, and antibacterial behaviour of zinc ferrite nanoparticles, J. Saudi Chem. Soc., 2023, 27, 101696.
9. M. Mohammed, A. K. Al-Mousoi, S. M. Majeed, S. Singh, A. Kumar, R. Pandey, J. Madan, D. Ahmed and D. Dastan, Stable Hole-Transporting Material-Free Perovskite Solar Cells with Efficiency Exceeding 14% via the Introduction of a Malonic Acid Additive for a Perovskite Precursor, Energy Fuels, 2022, 36, 13187–13194.
10. J. Jiang, Z. Jin, J. Lei, Q. Wang, X. Zhang, J. Zhang, F. Gao and S. (Frank) Liu, ITIC surface modification to achieve synergistic electron transport layer enhancement for planar-type perovskite solar cells with efficiency exceeding 20%, J. Mater. Chem. A, 2017, 5, 9514–9522.
11. F. Meinardi, Q. A. Akkerman, F. Bruni, S. Park, M. Mauri, Z. Dang, L. Manna and S. Brovelli, Doped Halide Perovskite Nanocrystals for Reabsorption-Free Luminescent Solar Concentrators, ACS Energy Lett., 2017, 2, 2368–2377.
12. M. K. A. Mohammed, S. Singh, A. K. Al-Mousoi, R. Pandey, J. Madan, D. Dastan and G. Ravi, Improving the potential of ethyl acetate green anti-solvent to fabricate efficient and stable perovskite solar cells, RSC Adv., 2022, 12, 32611–32618.
13. L. Huxin, X. Liu, X. Gong, R. Zhou, X. Peng, Y. Ouyang, J. Zhuang, H. Li and H. Wang, Multifunctional Additive of Potassium Cinnamate Improve Crystallization and Passivate Defect for Perovskite Solar Cell with Efficiency Exceeding 22\%, Energy Technol., 2022, 10, 2200125.
14. M. K. Hossain, G. F. I. Toki, A. Kuddus, M. H. K. Rubel, M. M. Hossain, H. Bencherif, M. F. Rahman, M. R. Islam and M. Mushtaq, An extensive study on multiple ETL and HTL layers to design and simulation of high-performance lead-free CsSnCl₃-based perovskite solar cells, Sci. Rep., 2023, 13, 1–24.
15. Z. Shi, J. Guo, Y. Chen, Q. Li, Y. Pan, H. Zhang, Y. Xia and W. Huang, Lead-Free Organic–Inorganic Hybrid Perovskites for Photovoltaic Applications: Recent Advances and Perspectives, Adv. Mater., 2017, 29, 1605005.
16. X. Meng, Y. Wang, J. Lin, X. Liu, X. He, J. Barbaud, T. Wu, T. Noda, X. Yang and L. Han, Surface-Controlled Oriented Growth of FASnI₃ Crystals for Efficient Lead-free Perovskite Solar Cells, Joule, 2020, 4, 902–912.
17. G. Schileo and G. Grancini, Lead or no lead? Availability, toxicity, sustainability and environmental impact of lead-free perovskite solar cells, J. Mater. Chem. C, 2021, 9, 67–76.
18. N. Pandit, R. Singh, T. K. Joshi, A. Shukla, P. K. Kamlesh, A. Dubey, T. Kumar, M. S. Chauhan and A. S. Verma, Investigation of a potential photovoltaic absorber based on first principles spectroscopic screening of chalcogenide perovskites: CaZrX₃ (X = S, Se), J. Comput. Electron., 2024, 24, 11.
19. N. Pandit, R. Singh, P. K. Kamlesh, N. Kumar, P. Sharma, S. Kumari, T. Kumar, S. Al-Qaisi and A. S. Verma, Study of chalcogenide-based metal perovskites BaZrX₃ (X = S and Se): DFT insight into fundamental properties for sustainable energy generation using AMPS-1D, J. Comput. Electron., 2024, 23, 1014–1028.
20. N. Pandit, R. Singh, A. Kumar, T. K. Joshi, A. Shukla, U. Rani, P. K. Kamlesh, T. Kumar, Priyanka and A. S. Verma, Physical properties and power conversion efficiency of SrZrX₃ (X = S and Se) chalcogenide perovskite solar cell, Mod. Phys. Lett. B, 2024, 38, 2450345.
21. S. Kumari, U. Rani, M. Rani, R. Singh, P. K. Kamlesh, S. Kumari, T. Kumar and A. S. Verma, Computational investigation of the fundamental physical properties of lead-free halide double perovskite Rb₂NaCoX₆ (X = Cl, Br, and I) materials: potential prospects for sustainable energy, Mod. Phys. Lett. B, 2024, 38, 2450323.
22. N. Pandit, A. Dubey, T. K. Joshi, A. Shukla, U. Rani, P. K. Kamlesh, R. Gupta, T. Kumar, K. Kaur and A. S. Verma, Effect of anion (S²⁻ & Se²⁻) replacement on photovoltaic properties in transition metal (Ba-Barium) chalcogenide perovskites, Int. J. Mod. Phys. B, 2024, 2550059.
23. H. Park, R. Mall, F. H. Alharbi, S. Sanvito, N. Tabet, H. Bensmail and F. El-Mellouhi, Exploring new approaches towards the formability of mixed-ion perovskites by DFT and machine learning, Phys. Chem. Chem. Phys., 2019, 21, 1078–1088.
24. Y. Zhou and A. Gray-Weale, A numerical model for charge transport and energy conversion of perovskite solar cells, Phys. Chem. Chem. Phys., 2016, 18, 4476–4486.
25. Y.-Q. Zhao, Q.-R. Ma, B. Liu, Z.-L. Yu and M.-Q. Cai, Pressure-induced strong ferroelectric polarization in tetra-phase perovskite CsPbBr₃, Phys. Chem. Chem. Phys., 2018, 20, 14718–14724.
26. M. F. Rahman, M. M. Islam, M. R. Islam, A. Ghosh, M. A. Rahman, M. H. Rahman, M. A. I. Islam, M. A. Islam, H. Albalawi and Q. Mahmood, An investigation on strain-incited electronic and optical properties of novel inorganic cubic material Sr₃AsCl₃, J. Solid State Chem., 2023, 328, 124341.
27. M. F. Rahman, M. H. Rahman, M. R. Islam, M. K. Hossain, A. Ghosh, M. S. Islam, M. M. Islam, M. Harun-Or-Rashid, H. Albalawi and Q. Mahmood, The optical and electronic properties of inorganic halide perovskite Sr₃NCl₃ under applied biaxial strain, J. Mater. Sci., 2023, 58, 13100–13117.
28. M. F. Rahman, M. A. I. Islam, M. R. Islam, M. H. Ali, P. Barman, M. A. Rahman, M. Harun-Or-Rashid, M. Hasan and M. K. Hossain, Investigation of a novel inorganic cubic perovskite Ca₃PI₃ with unique strain-driven optical, electronic, and mechanical properties, Nano Select, 2023, 4, 632–645.
29. M. F. Rahman, M. A. Rahman, M. R. Islam, A. Ghosh, M. A. Bashar Shanto, M. Chowdhury, M. Al Ijajul Islam, M. H. Rahman, M. K. Hossain and M. A. Islam, Unraveling the strain-induced and spin-orbit coupling effect of novel inorganic halide perovskites of Ca₃AsI₃ using DFT, AIP Adv., 2023, 13, 085329.
30. A. Ghosh, M. F. Rahman, M. R. Islam, M. S. Islam, M. Amami, M. K. Hossain and A. B. Md Ismail, Inorganic novel cubic halide perovskite Sr₃AsI₃: strain-activated electronic and optical properties, Heliyon, 2023, 9, e19271.
31. C. Hadenfeldt and H. O. Vollert, Darstellung, thermisches Verhalten und Kristallstruktur des Calciumarsenidchlorids Ca₃AsCl₃, J. Inorg. Gen. Chem., 1982, 491, 113–118.
32. C. Hadenfeldt and H. Herdejürgen, Darstellung, kristallstruktur und thermisches verhalten der calciumphosphidchloride Ca_2−xP_1−xCl_1+x (0 ≤ x ≤ 0.18) und Ca₃PCl₃, J. Less-Common Met., 1986, 124, 93–103.
33. V. C. Hadenfeldt and W. Fester, Reindarstellung und thermische Stabilitat von Calcium-phosphid- und -arsenidiodiden: Ca, PI, Ca, AsI, Ca, PI und Ca, Asl, Anorg. Chem., 1982, 30, 25–30.
34. S. Andersson, Magnesium nitride fluorides, J. Solid State Chem., 1970, 1, 306–309.
35. C. Hadenfeldt and P. Schulz, Darstellung, Struktur und Temperaturabhängigkeit der Phasenbreite der Phase Ca_2−xAs_1−xBr_1+x und thermisches Verhalten der Verbindung Ca₃AsBr₃, J. Inorg. Gen. Chem., 1984, 518, 77–86.
36. D. A. Dixon, in Encyclopedia of Geochemistry, ed. W. M. White, Springer International Publishing, Cham, 2016, pp. 1–7.
37. M. H. K. Rubel, M. A. Hossain, M. K. Hossain, K. M. Hossain, A. A. Khatun, M. M. Rahaman, M. Ferdous Rahman, M. M. Hossain and J. Hossain, First-principles calculations to investigate structural, elastic, electronic, thermodynamic, and thermoelectric properties of CaPd₃B₄O₁₂ (B = Ti, V) perovskites, Results Phys., 2022, 42, 105977.
38. M. F. Rahman, M. N. H. Toki, M. R. Islam, P. Barman, S. Chowdhury, M. Rasheduzzaman and M. Z. Hasan, A computational study of electronic, optical, and mechanical properties of novel Ba₃SbI₃ perovskite using DFT, Opt. Quantum Electron., 2023, 56, 206.
39. M. Ferdous Rahman, P. Barman, M. Azizur Rahman, M. Mushtaq, M. Rasidul Islam, M. Atikur Rahman, M. Z. Sultan, A. R. Chaudhry and A. Irfan, Electronic, optical, thermophysical, and mechanical properties of lead-free Ba₃SbBr₃ perovskite, Polyhedron, 2024, 254, 116937.
40. Q. Wang, W. Yu, X. Fu, C. Qiao, C. Xia and Y. Jia, Electronic and magnetic properties of SnSe monolayers doped by Ga, In, As, and Sb: a first-principles study, Phys. Chem. Chem. Phys., 2016, 18, 8158–8164.
41. M. Faizan, J. Xie, G. Murtaza, C. Echeverría-Arrondo, T. Alshahrani, D. Bhamu, A. Laref, I. Seró and S. Khan, A first-principle study of the stability, electronic structure, and optical properties of halide double perovskite Rb₂Sn_1−xTe_xI₆ for solar cell applications, Phys. Chem. Chem. Phys., 2023, 23, 4646–4657.
42. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
43. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev. A: At., Mol., Opt. Phys., 1965, 140, 1133.
44. G. P. Francis and M. C. Payne, Finite basis set corrections to total energy pseudopotential calculations, J. Phys.: Condens. Matter, 1990, 2, 4395–4404.
45. T. H. Fischer and J. Almlöf, General methods for geometry and wave function optimization, J. Phys. Chem., 1992, 96, 9768–9774.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. H. J. Monkhorst and J. D. Pack, Special points for Brillonin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
48. M. H. Rahman, H. Full, M. A. Rahman, S. R. Al Ahmed, L. Ben Farhat, S. Ezzine and M. F. Rahman, ETL engineering in lead-free new Ca₃PBr₃ perovskite type structure of anti-perovskite derivative material for stable and effective photovoltaic solar cells, New J. Chem., 2025, 49, 3044–3066.
49. S. Bhattacharyya and A. K. Singh, Semiconductor–metal transition in semiconducting bilayer sheets of transition-metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 1–7.
50. W.-J. Yin, J.-H. Yang, J. Kang, Y. Yan and S.-H. Wei, Halide perovskite materials for solar cells: a theoretical review, J. Mater. Chem. A, 2015, 3, 8926–8942.
51. D.-Y. Chen, Y. Wu, L. Jin, Y. Li, X. Wang, J. Duan, J. Han, X. Li, Y.-Z. Long, X. Zhang, D. Chen and B. Teng, Superconducting properties in a candidate topological nodal line semimetal SnTaS₂ with a centrosymmetric crystal structure, Phys. Rev. B, 2019, 100, 64516.
52. M. Petrović, V. Chellappan and S. Ramakrishna, Perovskites: solar cells & engineering applications – materials and device developments, Sol. Energy, 2015, 122, 678–699.
53. M. A. Islam, M. Z. Rahaman and S. K. Sen, A comparative study of hydrostatic pressure treated environmentally friendly perovskites CsXBr₃ (X = Ge/Sn) for optoelectronic applications, AIP Adv., 2021, 11, 075109.
54. M. A. Islam, J. Islam, M. N. Islam, S. K. Sen and A. K. M. A. Hossain, Enhanced ductility and optoelectronic properties of environment-friendly CsGeCl₃ under pressure, AIP Adv., 2021, 11, 45014.
55. S. ur Rehman, F. K. Butt, Z. Tariq, F. Hayat, R. Gilani and F. Aleem, Pressure induced structural and optical properties of cubic phase SnSe: an investigation for the infrared/mid-infrared optoelectronic devices, J. Alloys Compd., 2017, 695, 194–201.
56. F. Ahmad, A. Lakhtakia and P. B. Monk, Double-absorber thin-film solar cell with 34% efficiency, Appl. Phys. Lett., 2020, 117, 33901.
57. D. Tsukahara, S. Yachi, H. Takeuchi, R. Takabe, W. Du, M. Baba, Y. Li, K. Toko, N. Usami and T. Suemasu, p-BaSi₂/n-Si heterojunction solar cells with conversion efficiency reaching 9.0%, Appl. Phys. Lett., 2016, 108, 152101.
58. G. Yu, C. H. Lee, A. J. Heeger and S.-W. Cheong, Photoconductivity and optical conductivity in lightly doped Nd₂CuO_4−δ, Phys. C, 1992, 203, 419–425.
59. M. A. Ali, N. Alam, S. Ali, S. A. Dar, A. Khan, G. Murtaza and A. Laref, A theoretical study of the structural, thermoelectric, and spin-orbit coupling influenced optoelectronic properties of CsTmCl₃ halide perovskite, Int. J. Quantum Chem., 2020, 120, 1–9.
60. M. A. Ali, R. Ullah, S. Murad, S. A. Dar, A. Khan, G. Murtaza and A. Laref, Insight into pressure tunable structural, electronic and optical properties of via DFT calculations, Eur. Phys. J. Plus, 2020, 135, 309.
61. X. Liu, B. Xie, C. Duan, Z. Wang, B. Fan, K. Zhang, B. Lin, F. J. M. Colberts, W. Ma, R. A. J. Janssen, F. Huang and Y. Cao, A high dielectric constant non-fullerene acceptor for efficient bulk-heterojunction organic solar cells, J. Mater. Chem. A, 2018, 6, 395–403.
62. S. Saha, T. P. Sinha and A. Mookerjee, Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8828–8834.
63. M. M. Rahaman, M. H. K. Rubel, M. A. Rashid, M. A. Alam, K. M. Hossain, M. I. Hossain, A. A. Khatun, M. M. Hossain, A. K. M. A. Islam, S. Kojima and N. Kumada, Mechanical, electronic, optical, and thermodynamic properties of orthorhonmbic LiCuBiO₄ crystal: a first-priciples study, J. Mater. Res. Technol., 2019, 8, 3783–3794,  DOI:10.1016/j.jmrt.2019.06.039.
64. M. Roknuzzaman, K. (Ken) Ostrikov, K. Chandula Wasalathilake, C. Yan, H. Wang and T. Tesfamichael, Insight into lead-free organic-inorganic hybrid perovskites for photovoltaics and optoelectronics: a first-principles study, Org. Electron., 2018, 59, 99–106.
65. M. Burgelman, P. Nollet and S. Degrave, Modelling polycrystalline semiconductor solar cells, Thin Solid Films, 2000, 361–362, 527–532.
66. M. A. Ghebouli, B. Ghebouli, R. Larbi, T. Chihi and M. Fatmi, Effect of buffer nature, absorber layer thickness and temperature on the performance of CISSe based solar cells, using SCAPS-1D simulation program, Optik, 2021, 241, 166203.
67. A. Kuddus, M. F. Rahman, S. Ahmmed, J. Hossain and A. B. M. Ismail, Role of facile synthesized V₂O₅ as hole transport layer for CdS/CdTe heterojunction solar cell: validation of simulation using experimental data, Superlattices Microstruct., 2019, 132, 106168.
68. U. Mandadapu, Simulation and Analysis of Lead based Perovskite Solar Cell using SCAPS-1D, Indian J. Sci. Technol., 2017, 10, 1–8.
69. L. Lin, L. Jiang, P. Li, B. Fan and Y. Qiu, A modeled perovskite solar cell structure with a Cu₂O hole-transporting layer enabling over 20% efficiency by low-cost low-temperature processing, J. Phys. Chem. Solids, 2019, 124, 205–211.
70. I. Alam, R. Mollick and M. A. Ashraf, Numerical simulation of Cs₂AgBiBr₆-based perovskite solar cell with ZnO nanorod and P3HT as the charge transport layers, Phys. B, 2021, 618, 413187.
71. A. Bag, R. Radhakrishnan, R. Nekovei and R. Jeyakumar, Effect of absorber layer, hole transport layer thicknesses, and its doping density on the performance of perovskite solar cells by device simulation, Sol. Energy, 2020, 196, 177–182.
72. D. E. Tareq, S. M. AbdulAlmohsin and H. H. Waried, Efficiency of TiO₂/Peroviskites/Cu₂O Solar Cells with Optimal Thickness at Varying of Environment Temperature, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 928, 072044.
73. D. Liu, M. K. Gangishetty and T. L. Kelly, Effect of CH₃NH₃PbI₃ thickness on device efficiency in planar heterojunction perovskite solar cells, J. Mater. Chem. A, 2014, 2, 19873–19881.
74. P. K. Patel, Device simulation of highly efficient eco-friendly CH₃NH₃SnI₃ perovskite solar cell, Sci. Rep., 2021, 11, 3082.
75. A. Tara, V. Bharti, S. Sharma and R. Gupta, Device simulation of FASnI₃ based perovskite solar cell with Zn(O_0.3, S_0.7) as electron transport layer using SCAPS-1D, Opt. Mater., 2021, 119, 111362.
76. K. D. Jayan and V. Sebastian, Comparative performance analysis of mixed halide perovskite solar cells with different transport layers and back metal contacts, Semicond. Sci. Technol., 2021, 36, 065010.
77. M. Samiul Islam, K. Sobayel, A. Al-Kahtani, M. A. Islam, G. Muhammad, N. Amin, M. Shahiduzzaman and M. Akhtaruzzaman, Defect Study and Modelling of SnX₃-Based Perovskite Solar Cells with SCAPS-1D, Nanomaterials, 2021, 11, 1218.
78. G. K. Gupta, A. Garg and A. Dixit, Electrical and impedance spectroscopy analysis of sol–gel derived spin coated Cu₂ZnSnS₄ solar cell, J. Appl. Phys., 2018, 123, 013101.
79. F. Ferdiansjah and K. Tirtakusuma Mularso, Analysis of Back Surface Field (BSF) Performance in P-Type And N-Type Monocrystalline Silicon Wafer, E3S Web Conf., 2018, 43, 01006.
80. M. A. Green, K. Emery, Y. Hishikawa, W. Warta and E. D. Dunlop, Solar cell efficiency tables (Version 45), Prog. Photovoltaics Res. Appl., 2015, 23, 1–9.
81. S. Rühle, Tabulated values of the Shockley–Queisser limit for single junction solar cells, Sol. Energy, 2016, 130, 139–147.
82. W. Shockley and W. T. Read, Statistics of the Recombinations of Holes and Electrons, Phys. Rev., 1952, 87, 835–842.
83. G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, Inorganic caesium lead iodide perovskite solar cells, J. Mater. Chem. A, 2015, 3, 19688–19695.
84. J. Hossain, M. M. A. Moon, B. K. Mondal and M. A. Halim, Design guidelines for a highly efficient high-purity germanium (HPGe)-based double-heterojunction solar cell, Opt. Laser Technol., 2021, 143, 107306.
85. M. M. A. Moon, M. H. Ali, M. F. Rahman, A. Kuddus, J. Hossain and A. B. M. Ismail, Investigation of thin-film p-BaSi₂/n-CdS heterostructure towards semiconducting silicide based high efficiency solar cell, Phys. Scr., 2020, 95, 035506.

---