 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Red blood cell Raman microscopy: modelling sub-cellular biochemistry†
Victor V. Volkov a,
Joanna Aizenberg
a,
Joanna Aizenberg b and
Carole C. Perry
b and
Carole C. Perry *a
*a
aInterdisciplinary Biomedical Research Centre, School of Science and Technology, Nottingham Trent University, Clifton Lane, Nottingham NG11 8NS, UK. E-mail: Carole.Perry@ntu.ac.uk
bJohn A. Paulson School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, Cambridge, MA 02138, USA
First published on 19th May 2025
Abstract
We develop a quantitative Raman microscopy approach to study erythrocyte biochemistry at the sub-cellular level. To model Raman microscopy images, we review theory of Raman tensors and derive expressions for Raman responses suitable to compute Raman micro-images accounting effects of radial and vertical deformations of cellular envelopes. In application to membrane components, we extend the approach to a “counted per rotation” fast imaging protocol: once having Raman tensors for a molecule, precomputed expressions of molecular distributions can be used to construct Raman images of the modelled membrane envelope and its Raman spectra under any polarisation setting instantly. Using the theory, we review sub-cellular distributions of oxy-, deoxy- and methaemoglobins, as measured in experiment, considering their role in oxygen transport and oxidative stress mechanisms in the cytosol and when next to a membrane. We discuss possible applications of the approach in membrane specific studies, and its potential for combination with phase-sensitive and confocal fluorescence microscopy for advancing health care diagnostics.
Introduction
One of the products of blood cell production – erythrocytes (or red blood cells, RBCs) provide oxygen transport,1–3 ensure that most of the CO2 is transported as bicarbonate,4 take part in the regulation of optimal blood flow,5,6 and affect vascular tension.7,8 Also, the cells play a role in immunity9 and antibacterial responses.10,11Counting RBC, as well as monitoring their shape and size are routinely used in health checkups as these properties provide valuable information on physiology. Typically, mature mammalian RBCs are flexible, oval biconcave discocytes in the size range of 2 to 6 μm.12 Departure from the regular shape may indicate anaemic tendencies,13 physiological perturbations,14,15 and neurodegenerative processes.16 Moreover, the composition of RBC membranes may provide information on general deficiencies,17,18 the presence of excess reactive-oxygen species,19 diabetes biochemistry20 and neurodegenerative processes.21,22
Since discovering that the size and shape of erythrocytes vary with environment,23–25 membrane biophysics,26 and biochemistry,27 modelling of equilibrium shapes and deviations from the same has attracted significant research.28–30 Understanding principles of structural integrity and plasticity in connection to the biochemistry of the membrane and cytoskeleton are of clear importance when supporting the main function of RBC – oxygen transport. Indeed, correlation of RBCs’ shape and haemoglobin content has been observed experimentally.31 For resolving cellular restructuring and subcellular biochemical reactivities, confocal Raman microscopy, due to its ultimate capacity of subwavelength spatial resolution and sensitivity to molecular structure, has the potential to quantify spatial gradients of characteristic chemical species in different RBC compartments with time. Also, using specific excitation wavelengths, the Raman signal may be tuned to enhance spectral response from specific molecular systems.32 At the same time as controlling polarisation settings for excitation and emission radiation, one may sample signal from sub-sets of molecular orientations in space.33
Characterization of RBC sub-cellular molecular distributions has attracted considerable attention. Early fluorescence studies suggested possible haemoglobin association with membranes.34 The reported binding was assigned to interactions with the inner segment of a band 3 protein complex,35 and with glycophorin and phospholipid specific sites.36 Dynamics of haemoglobin form distribution within an envelope in dependence on chemistry and physiology of the local environment is an open research frontier. From this perspective, sensitive to electronic pre-resonance and controlled by the polarisation of the radiation field, spontaneous Raman, with its linear response to concentration can be helpful to develop quantitative analysis of molecules, their presence and orientation that could aid high throughput diagnostics in biomedical and industrial applications.
Previously, we derived theory for nonlinear Infrared/Raman signals from molecules at the surface of micro-spheroids accounting possible incomplete orientation averaging.37 Also, we reported resonant Raman microscopy of RBC supported by density functional theory (DFT) predictions to anticipate differences in sub-cellular biochemistry for healthy and unhealthy cells.38 In this contribution, we further develop quantitative methods for the application of Raman microscopy to single RBCs. To do this, first, we describe the theory of Raman responses showing their suitability for modelling sub-cellular molecular distributions using quantum chemistry predictions for Raman tensors of several molecules present in RBCs. Second, using insight from multivariate analysis on spectra detected at different RBC sites and on the shapes of Raman microscopy images reconstructed at different Raman frequencies, we develop and test a method to describe sub-cellular molecular distributions. Following this, for experimental data collected on cells, we model and compare relative presences of oxy, deoxy and met forms of haemoglobin in the central region of a cell, in the toroidal cavity, and next to the membrane. This we conduct for both, an ideal symmetric cell and for a deformed one. We describe the introduction of adjustable deformation to better match the experimental observations. Such an approach can be extended to tune deformations according to the results of phase sensitive microscopy.39 Using the results of our modelling, we discuss the role of membranes in organizing haemoglobin distributions to support oxygen transport and to maintain redox balance regulating autoxidation next to the cellular envelope.
Recognizing the role of membranes in RBC biochemistry we develop a theory of imaging the membrane contribution. This is particularly important since identification of membrane contributions is a well-known challenge in RBC Raman experiments, unless employing SERS nanoparticles40 or researching cellular ghosts.41 Our theory predicts experimental polarisation settings that can be used to distinguish the contribution of membrane of a RBC. Furthermore, we present a “counts per rotation” eigen-image method to speed up computing Raman microscopy images of a modelled membrane structure and its Raman spectra for any polarisation setting, for a molecule of interest whose Raman tensors are known. Our results offer a systematic approach for the use of Raman image analysis in health support: ESI† offer introductory data sets and a Mathematica notebook for Raman microscopy image sorting using a convolutional neural net architecture pioneered by Yann LeCun et al.,42 but adapted to three classes of oxy-, deoxy- and methaemoglobin subcellular distributions.
Materials and methods
Raman microscopy experiment
Human haemoglobin was acquired from Sigma-Aldrich (CAS no. 9008-02-0) as lyophilized powder. Preparation of different haemoglobin forms was according to the protocol provided by the company. Raman microscopy studies of single human red blood cells were performed as described previously.38 Red blood cells deposited on an unprotected gold mirror (PFSQ05-03-M03 Thorlabs Ltd, Ely, United Kingdom) were scanned using a DXR microscope station from Thermo Fisher Scientific (Madison, Wisconsin, USA) equipped with a 100× microscopy objective, numerical aperture 0.8. Estimation of a cell's height was approximated by bright field images of the substrate and the cells surface at the top. For Raman microscopy of RBC, we used excitation radiation at 532 and 780 nm with excitation power of 1 mW, as determined not to damage a cell, not to alter chemical composition at a site of sampling regardless of a number of measurements under the adopted focusing and timing conditions. To collect reliable data without damaging, during resonant and non-resonant Raman experiments, data sampling time at a selected site was 30 seconds and 1 minute, respectively. Spectral resolution was 2 cm−1 according to the limit of the microscope operated with a 25 μm confocal aperture. Raman activities at different sites of the selected cells were sampled with a spatial resolution of 1 μm in both directions of the imaging plane. For a selected cell, we collected representative maps taking a cut across approximately at the middle of the cell height.According the results of our recent studies,38 excitation at 532 nm is close to the intense optical absorption of oxyhaemoglobin at 541 nm (molar extinction coefficient 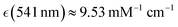 ) which we ascribed to oxyhaem biradical transitions 17-20, proximal to the prominent absorption band of deoxyhaemoglobin at 554 nm
) which we ascribed to oxyhaem biradical transitions 17-20, proximal to the prominent absorption band of deoxyhaemoglobin at 554 nm 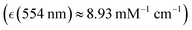 we assigned to deoxyhaem transition 14, and near the weak transitions of methaemoglobin at 498 nm
we assigned to deoxyhaem transition 14, and near the weak transitions of methaemoglobin at 498 nm 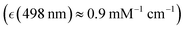 and 539 nm
and 539 nm 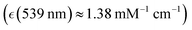 which we assigned to methaem transition sets 33-31 and 30-27, respectively: for details see ESI† of ref. 38. Since using comparable spectral detuning, we may expect similar effective pre-resonant enhancements of Raman. In the case of excitation at 780 nm, the discussed experimental spectra in this spectral region present very weak optical absorption of oxyhaemoglobin (assigned to 6th transition of oxyhaem biradical), of deoxyhaemoglobin (we may consider to be due to 4th transition of deoxyhaem), and optical transparency for methaemoglobin, though theory suggests that the 7th transition of methaem may have a weak optical absorption there.38 Since there is very weak optical absorption, overall, we may expect the non-resonant Raman contribution to dominate in microscopy measurements using excitation at 780 nm.
which we assigned to methaem transition sets 33-31 and 30-27, respectively: for details see ESI† of ref. 38. Since using comparable spectral detuning, we may expect similar effective pre-resonant enhancements of Raman. In the case of excitation at 780 nm, the discussed experimental spectra in this spectral region present very weak optical absorption of oxyhaemoglobin (assigned to 6th transition of oxyhaem biradical), of deoxyhaemoglobin (we may consider to be due to 4th transition of deoxyhaem), and optical transparency for methaemoglobin, though theory suggests that the 7th transition of methaem may have a weak optical absorption there.38 Since there is very weak optical absorption, overall, we may expect the non-resonant Raman contribution to dominate in microscopy measurements using excitation at 780 nm.
Spectra sampled at different sites, i, were analysed to extract amplitudes of Raman activities, Aω,i, at frequencies of interest, ω, which were used in reconstructions of microscopically resolved Raman images, as we describe in the further, fourth sub-section. Evaluation of Raman amplitudes was according to both, (i) direct measure of intensity of a resonance compared to intensity at a nearby suitable spectral region, where we did not expect the resonance to contribute and (ii) fitting the spectra with a suitable set of Gaussian and Lorentzian line-shapes.
DFT studies
Details of DFT studies of haem centres were reported previously.38 The initial structures of the Fe–porphyrin complex in the deoxy and oxy-forms (with top and bottom histidine ligands) are according to 2HHB43 and 1GZX44 X-ray crystal structure entries as reported in the Structural Bioinformatics Protein Data Bank.To model phospholipid contribution in images of RBC membrane envelopes we computed properties of 1,2-bis(O-decanoyl)-sn-glyceryl-3-phosphorylcholine. DFT structural optimizations and normal modes were conducted using the B3LYP functional45 within the Gaussian 09 program package46 with 6-311++g(d,p) basis set for hydrogen, carbon, nitrogen and oxygen atoms; and LANL2DZ (and SDS) basis sets for the iron ion.47
Modelling of the RBC cellular envelope
The common theory of membrane vesicle shape is according to a curvature model for a two-dimensional surface in three-dimensional Euclidean space that exhibits purely elastic behaviour according to its mean and Gaussian curvatures, as well as two material constants (splay and saddle-splay) associated with the bending rigidity of the membrane.48,49 Consistently, recent efforts to model erythrocyte profiles search for a stationary shape for a Euler–Lagrange equation by the Helfrich curvature energy functional. This may be achieved either by minimizing membrane bending energy50 to express a suitable set of parametric equations,28 or by finding an equilibrium shape solution under uniform hydrostatic pressure.30 In this contribution, we test both approaches to model equilibrium RBC profiles.To compute Raman images specific to RBC volume and membrane, we subdivided the computed cellular surface and volume into a finite number of (surface and volume) elements sufficient to model smooth images and suitable for book-keeping (of position, volume value, and surface geometry of each element). In the following, we refer to this as surface and volume discretization. Approaching this, first, we grid the computed equilibrium profile with a set of vertices. The suggested grid should demonstrate a certain regularity. For this, two factors are considered. First is the variance of curvature: suggested steps confirm that change of angles between every next normal (at the centres of every neighbouring span between a pair of vertices) would not be larger than 7.5°. Second, in the spatial region of small curvature (as next to the centre of the envelope), the grid step would be about 130 nm, to provide reasonable oversampling dimensions of the computed profile (considering wavelength of optical radiation). The green contour in Fig. 1A demonstrates an example of a grid according to the described criteria.
 | ||
| Fig. 1 Model for RBC volume subdivision (discretization). Panel A: Green contour presents equilibrium shape solution under uniform hydrostatic pressure according to ref. 30, blue dotted line contour shows the central region elliptic profile, orange dotted line contour is an interpolation between the blue and green contours by their contributions according to the radial distance. Panel B: Tetragonal subdivision of the internal space of the equilibrium solution shape (for convenience expanded vertically) using vertices of the contours as shown in panel A. Panel C: Increasing fines of discretization via suggesting 38 interpolating layers between the central ellipse and the external profile. Panel D: Centres of unit volumes between tetragons of two vertical slices rotated by 37.5° and 45° about the Z axis. ESI† includes an archive with Mathematica Examples to include a code (Fig1_Fig2_making.zip) to compute some of the panels. | ||
Then, accounting both, the radial symmetry of an “ideal shape” RBC and bilateral symmetry of the computed contour, we suggest an elliptical profile with ratio 6 at the central region of the modelled section: see the dash boxed blue dotted line and its expansion in Fig. 1A. The long axis of the blue dotted line ellipse is about 5 times smaller than the maximal radial distance for the computed equilibrium profile by the green dotted line in Fig. 1A: also, see the star marks for the radial numerical values. We grid the ellipse having the same number of vertices and accounting its curvature as for the equilibrium profile.
Having vertices of the central ellipse and of the equilibrium profile as internal and external structural references, respectively, we may interpolate any intermediate profile at a desired distance from the centre scaling contributions of the central ellipse and of the external equilibrium profile: for example, see orange dotted line in Fig. 1A. Following this, we may connect neighbouring vertices to form tetragonal units (Fig. 1B). Next, we increase the number of interpolated layers to improve resolution of characterization of the space under the profile in dependence on curvature, and according to the set of vertices within a vertical slice, as shown in Fig. 1C. Having the constructed set of vertices, we may apply a series of rotation transformations about the Z axis to span the three-dimensional space of an ideal RBC model with a desired number of radially oriented equilibrium shape discretized, as we describe. Here, we prepare 48 rotations with step of 7.5°. A set of 4 vertices of the same tetragons but belonging to two neighbouring vertical slices provides a discrete volume unit suitable for book-keeping. We describe the centre of a selected discrete volume unit taking the mean of its eight vertices. Next, we compute its volume using a convex Hull algorithm, as implemented in Wolfram Mathematica. Fig. 1D presents centres of unit volumes between tetragons of two vertical slices rotated by 37.5° and 45° about the Z axis. Consistently, in respect to a membrane model, using pairs of vertices, which belong to the rotated neighbouring equilibrium profiles, we may find areas of discrete surface units, their centres and directions of normals to each surface unit. After this conduct a Euler transformation on the whole set of vertices to orient the discretized model RBC envelope as we would wish. Knowing or assuming concentration and surface densities, we can use projections of the unit centres onto the XY plane: their volumes and surface areas with directions of the normals (to the surface units) are used to scale the Raman contributions (into the image) to integrate modelled Raman images specific to volume and membrane of the oriented discretized RBC envelope, correspondingly.
In respect to modelling of Raman images specific to volume content (solvated haemoglobin proteins, for example), we anticipate possible special roles of the toroidal cavity and of the central region since they have slightly different distribution of haemoglobins,38 and the peculiarity of the RBC shape. At the same time, a particular sub-population of haemoglobins in the space next to the membrane is plausible due to their reported distinctive biochemistry.51 Accordingly, we may suggest three types of haemoglobin sub-cellular concentration distribution models: the first describes possible preferences to occupy the central region of RBC, the second type of distribution would address association with membrane, and the third would account the possible role of the toroidal cavity: see dotted densities in Fig. 2A–C, respectively. The degree of fading for the presented dotted density is proportional to considered concentration models. Specifically, for the central contribution, as shown in Fig. 2A, we may suggest a decay of concentration by exp[−k2/200], where k is the number of a vertex along the line connecting the same index vertices of different layers (see blue colour numbering along the blue line in Fig. 1B) counted from the centre to the surface. Considering a 0.13 micron distance between the layers along the radial direction starting from the central ellipse, the modelled concentration decreases 50% and 95% at 2.2 and 4 micron, from the centre along the chosen direction, respectively: see Fig. 2A.
 | ||
| Fig. 2 Haemoglobin heterogeneous distribution models: with exponential preferences to reside at the centre (A), with exponential preference to associate with the membrane (B), and in the toroidal cavity by normal distribution exp[−((y − y0)2/wy2 + z2/wz2)] according to the dimensions of the equilibrium solution shape (C). Panels Cib–Cic show transverse and longitudinal amplitude (concentration) slices across distributions shown as 2D (panels Cia) and 3D (panels Cid) presentations of the toroidal cavity model realizations according to maximum position along the y axis: y0, and widths along the y and z axes: wy and wz, respectively, as indicated. For details, see the main text. ESI† includes an archive with Mathematica Examples to include a code (Fig1_Fig2_making.zip) to compute some of the panels. | ||
In the case of membrane association, as shown in Fig. 2B, we may suggest a decay of concentration by exp[−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/50], where
2/50], where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the number of a vertex along the line connecting the same index vertices of different layers (see red colour numbering along the red line in Fig. 1B) counted from the surface toward the centre. For the same 0.13 micron distance between the discretization layers, the exponent rules the concentration to decrease 50% and 95% at distances 0.63 and 2 micron from the surface, along the radial direction, respectively: see Fig. 2B.
is the number of a vertex along the line connecting the same index vertices of different layers (see red colour numbering along the red line in Fig. 1B) counted from the surface toward the centre. For the same 0.13 micron distance between the discretization layers, the exponent rules the concentration to decrease 50% and 95% at distances 0.63 and 2 micron from the surface, along the radial direction, respectively: see Fig. 2B.
In the case of modelling of molecular preferences (in principle, any molecule) to occupy the toroidal cavity of RBC, we tested several distributions by exp[−((yi,j − y0)2/wy2 + zi,j2/wz2)]: here, y0 describes the position of the distribution maximum along the Y axis; wy and wz set the widths in respect to the y and z directions (considering Fig. 1A); while {yi,j, zi,j} are the coordinates of a vertex by i and j indices of a layer number and of a vertex along layers, respectively: see Fig. 1A. Specifically, Fig. 2C1a and C1d show 2D and 3D presentations of concentration distributions within the equilibrium solution shape when, {y0 = 2.9, wy = 1.0, wz = 0.3}. Correspondingly, Fig. 2C1b and C1c demonstrate concentration slices selected along the z direction at y = 2.9, and along the y direction at z = 0, respectively. To demonstrate sensitivity of the model to its parameters, in Fig. 2C2a–C2d we present a broader distribution and its characteristic slices setting wy = 1.2, wz = 0.7. Additionally, to compare with Fig. 2C1a–C1d, in Fig. 2C3a–C3d, we present a distribution with a shifted maximum according to y0 = 3.0. Since the adopted approach depends on the space gridding, we develop these figures to demonstrate how a selected model may be tested to be sensitive (to a 0.1 micron change in parameter settings) according to the adopted fines of the gridded space. Sensitivity to parameters becomes obvious upon fitting experimental data. If not sufficient, we have to increase the number of interpolating layers, as shown in Fig. 1C. ESI† includes an archive with Mathematica codes to show how to compute the suggested modal contributions.
In this study, we vary decays, widths and maxima positions for the described distribution functions to superimpose the modelled sub-cellular distributions to reproduce RBC images reconstructed at different Raman resonances, as well as differences of normalized Raman images, which we ascribed to different forms of haem.38 To follow this approach, we must manage two additional tasks. First, when we wish to reproduce the Raman image specific to volume of an RBC (which is of micron dimensions), we must take into account that the Raman signal is stimulated along the path of light propagating through the cell. Such a path is different according to which part of the RBC the light field propagates through and depends on the orientation of the RBC in respect to the field direction. Second, to model images as in experiment, we must account for local deformations in respect to both, thickness and radial distance from the centre of a cell. This approach allows quantitative tuning according to experimental imaging using phase sensitive techniques.39
To deal with the first issue, for a selected orientation (by Euler rotation transformation on the set of modelled RBC vortices) of a modelled envelope, we determine the position of the highest (in Z direction) vertex of the envelope. From that point we step up by the distance corresponding to the used wavelength of light to set up the initial sampling plane. In this plane we define {x, y} sampling positions, where the exciting field propagates (along the Z axis) according to the setting of the Raman microscopy experiment. For a selected {x, y} sampling position in the initial sampling plane, we compute distances to every centre of the discretized sub-volumes of the RBC model. For every centre, which is located at distances shorter than 1 micron (from the selected {x, y} sampling position) we store: the distance to the selected {x, y} sampling position, the coordinates of the centre, the value of the sub-volume, and the amplitude factor. Here, the amplitude factor is according to concentration by an adopted model: centre, membrane, or toroid.
Next, for each of the sorted centres (with its discretized sub-volume), we express Raman amplitude taking the product of (i) the Gaussian function (with the full width at half maximum of the excitation wavelength) for the distance to the centre, (ii) volume of the unit, (iii) the amplitude factor and (iv) square of Raman susceptibility (see the following section of the article). Here, the value of the Gaussian function on the distance between the selected {x, y} sampling position and a unit-centre accounts for distance attenuation according to the wavelength dependent coherent envelope excited in space; while the amplitude factor is according to the model (centre, membrane, or toroid). Next, we sum the Raman amplitudes for the sorted units to assign a value to the selected {x, y} sampling position in the initial sampling plane. Then, we move to another sampling position till we characterize all the points in the initial sampling plane. To integrate a Raman image, we analyse a series of sampling planes downward along the Z direction (for example, 0.15 micron separated) to compute Raman amplitudes according to the {x, y} positions in each of the sampling planes. The distance between the planes (for example, 0.15 micron) is according to a discretion we wish to adopt to resolve the modelled envelope according to the curvature of the surface. The lowest plane is at the distance of the used wavelength of light lower than the lowest (in the Z direction) vertex of the modelled envelope. In the case of a symmetric envelope about the Z direction, we may sample half of the structure.
To address the second issue, we take advantage of cellular symmetry to alter the protocol for modelling of the RBC cellular envelope suggesting a modulating function: we vary radial distances for vertices in a vertical slice (these are y distances for the set as shown in Fig. 1C) in dependence of ϕ angle for the slice rotation. Specifically, the modulating function may be expressed as a sum of Gaussian like line-shapes  in the ϕ angular space of rotation in the xy plane about the Z axis. Rotated to a selected angle ϕ, y distances for the vertices in a vertical slice would decrease or increase by positive or negative ai amplitude of an ith component when in the angular range of ϕi by the corresponding width factor, wi. An analogous function may be elaborated to modulate z distances for vertices in a vertical slice, as shown in Fig. 1C.
in the ϕ angular space of rotation in the xy plane about the Z axis. Rotated to a selected angle ϕ, y distances for the vertices in a vertical slice would decrease or increase by positive or negative ai amplitude of an ith component when in the angular range of ϕi by the corresponding width factor, wi. An analogous function may be elaborated to modulate z distances for vertices in a vertical slice, as shown in Fig. 1C.
Raman intensity
We may express Raman susceptibilities by their dependence on the polarisation conditions of an experiment and on variances of Euler angles of molecular orientation as
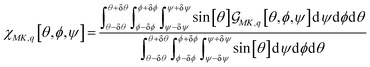 | (1) |
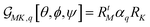 . Here, RtM = (RMx, RMy, RMz) is the row M-index vector (respecting the M polarisation direction for the detection) of the transposed Euler rotation matrix R about the M axis; as well as RK = (RKx, RKy, RKz) is the column K-index vector (according to the K polarisation direction for the excitation) of the Euler rotation matrix R about the K axis. αq is Raman tensor specific to a normal mode q.
. Here, RtM = (RMx, RMy, RMz) is the row M-index vector (respecting the M polarisation direction for the detection) of the transposed Euler rotation matrix R about the M axis; as well as RK = (RKx, RKy, RKz) is the column K-index vector (according to the K polarisation direction for the excitation) of the Euler rotation matrix R about the K axis. αq is Raman tensor specific to a normal mode q.
Prior to application of eqn (1), we have to account for two facts. First, results of Euler rotations are specific to “initial” orientation. Second, using DFT we compute αq,SO Raman tensor for a normal mode (q) of a molecule in its standard orientation (SO): by the eigenvectors of the molecular inertia tensor. To use eqn (1), we have to find a preliminary Euler rotation set R0 = {θ0, ϕ0, ψ0} to reorient the molecule from SO into such initial orientation, that effects of the angles {θ, ϕ, ψ} in eqn (1) would describe an orientational distribution we wish to model. Once we have a preliminary angular set, we have to redefine the Raman tensor αq = Rt0αq,SOR0 to enter eqn (1), as well.
Often, when at a locally flat interface, if we sample an ensemble of molecules with a preference to orient one of their structural directions (within the molecular frame) along the normal to the interface plane, we may adopt a symmetric top representation simplifying expressions of molecular derived properties (dipole moments or Raman tensors) upon integration over the angle of rotation about that molecular direction.
For example, in the case of a phospholipid in a membrane, we may suggest a preparatory R0 angular set to reorient the molecule from its standard orientation (according to the centre of mass and the eigenvectors of the inertia tensor) into such, that its hydrocarbon chains are parallel to the Z laboratory axis and perpendicular to the X and Y laboratory axes, which are parallel to the membrane surface: see Fig. S1 in the ESI.† Considering that a phospholipid molecule in the membrane is free to rotate about its long axis (parallel to the hydrocarbon chains), to describe the response of such molecules we may adopt ψ-rotation averaging about the long axis. Correspondingly, integrating eqn (1) over the ψ angle on the interval [0, 2π], for a selected normal mode, q, we derive four orientation distribution functions 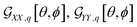 and
and 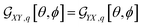 :
:
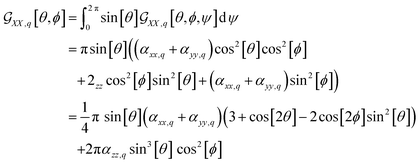 | (2) |
 | (3) |
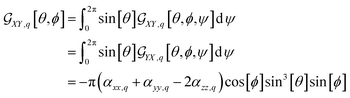 | (4) |
In the case of microscopic structures larger than the wavelength of the probing light (that we may consider a membrane area within the waist of exciting radiation to be flat), we may use θ and ϕ angles to describe orientation of the local normal (at a site area under focused excitation) in respect to the Z laboratory axis: for details see ref. 37. When we model a micro-structure, we know θ and ϕ angles at any site on its surface. Accordingly, using eqn (2)–(4), we can compute the orientation distribution functions at a selected site i to express Raman susceptibility at the site normalizing the corresponding response functions as:
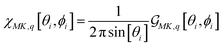 | (5) |
For the sake of universality, let us address limits of the equations. Specifically, suggesting integral limits for ϕ ∈ {0, 2π} we may derive equations to describe the response of symmetric top molecules at a flat interface (e.g. Langmuir–Blodgett), when the long axes of molecules take any orientation within a conical opening (about the Z laboratory axis) according to a θ angle suggested range: 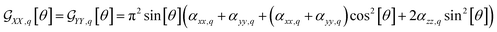 .
.
Furthermore, here, if we integrate the orientational distribution functions over the full range for θ and ϕ angle, we receive expressions specific to the isotropic limit: eqn (2) and (3) become equal to (αxx,q + αyy,q + αzz,q)/3, and eqn (4) averages to zero. As a result, we may compute the corresponding susceptibility as:
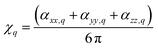 | (6) |
Raman microscopy images
In this study we present three types of Raman activity microscopy images (RAM): images reconstructed using Raman amplitudes of a selected resonance detected in experimental scans using confocal microscopy; theoretical images of haemoglobin haem centres distributed in cellular volume; computed images of membrane envelopes. In all cases, we follow the protocol according to
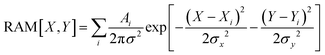 | (7) |
In the case of experimental RAM, Ai is the amplitude of the Stokes Raman signal of a selected resonance detected at the sampling site. When we compute images of haemoglobin haem distributed in cellular volume,
| Aq,i = αχq2Nq,i | (8) |
| Aq,i = αχMK,q2[θi, ϕi]Nq,i. | (9) |
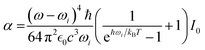 | (10) |
 , speed of light c, and occupation by Boltzmann factor.52–54
, speed of light c, and occupation by Boltzmann factor.52–54
Counted per rotation (CPR) eigen-image protocol
For the theoretical limit we adopt, it is possible to establish a fast (instantaneous) protocol to image a microscopic structure under a selected orientation and polarisation setting for a given Raman tensor. Let us consider computing a Raman image of a membrane structure taking a space convolution in the laboratory XY imaging plane (by eqn (7)) according to χXX,q[θi, ϕi] for every i site of a computed membrane envelope under a selected orientation. According to eqn (8) and (9), we have square contributions of the orientation distribution function by eqn (2). Specifically, expanding the square of we receive three terms: the first is proportional to (αxx,q + αyy,q)2, the second to be scaled by the product 2(αxx,q + αyy,q)αzz,q, and the third is proportional to αzz,q2. Each of the terms has own trigonometric part. For example, for the second term, this is sin6[θ]cos4[ϕ]. The scaling factors are by the diagonal elements of a Raman tensor expressed according to the “initial” alignment of a molecule, as we describe earlier. Consequently, a variance of Raman amplitude in space is by the trigonometric parts, which account orientation of the local normal to the membrane surface at any ith site expressed via the θi and ϕi angles (in respect to the Z laboratory axis).
we receive three terms: the first is proportional to (αxx,q + αyy,q)2, the second to be scaled by the product 2(αxx,q + αyy,q)αzz,q, and the third is proportional to αzz,q2. Each of the terms has own trigonometric part. For example, for the second term, this is sin6[θ]cos4[ϕ]. The scaling factors are by the diagonal elements of a Raman tensor expressed according to the “initial” alignment of a molecule, as we describe earlier. Consequently, a variance of Raman amplitude in space is by the trigonometric parts, which account orientation of the local normal to the membrane surface at any ith site expressed via the θi and ϕi angles (in respect to the Z laboratory axis).
Next, instead of operating on all the three terms together while under their scaling factors, we use eqn (7) to map each of the three terms separately, and each map is scaled by 1. Following this, we may use the corresponding elements of a αq Raman tensor to scale each of the three convolved image maps to sum them to receive the intended image specific to χXX,q. Since scaling of the contributing maps is according to the diagonal elements of αq Raman tensor, we call such maps “eigen-images”. To model images specific to χYY,q and χYX,q we need another 3 and 1 eigen-images, according to the number of squared terms of  and
and  functions, respectively.
functions, respectively.
Having a full set (of seven) eigen-images for a modelled envelope under a specified orientation, first, we can compute a Raman image of any other normal mode q for any desired polarisation setting (YY(SS), XX(PP) or YX(SP)), instantly. To do this we take a corresponding superposition of eigen-images scaled by the corresponding (αxx,q + αyy,q)2, αzz,q2 etc. numerical values, which are the diagonal elements of Raman tensor. Second, the same eigen images can be used to simulate Raman images of the envelope for normal modes of any other molecule or their superposition (we refer to the described example of a haemoglobin tetramer associated with a membrane), as long as the described effective symmetric top model is adequate in description of organisation in respect of the membrane. Third, having a set of Raman tensors for all normal modes, for a selected polarization, we may express (instantly) a set of images specific to the normal modes. Then, for each image we may take a sum of intensities in the image plane. Such integral intensities in dependence of the normal mode frequencies would describe a “macroscopic” Raman spectrum specific to three-dimensional variance of the modelled envelope, its orientation in space, and selected polarisation setting. If we change orientation of the modelled envelope in space, then, to re-evaluate properties, we would need to compute a new set of seven eigen-images. Hence, here, we introduce a counted per rotation (CPR) eigen-image method in quantitative modelling of Raman microscopy images of computed envelope microstructures. The ESI† includes an archive with Mathematica Examples to include a code (CPR_Eigens_Examples.zip) to show how to compute selected CPR eigen-images.
Processing and analysis of spectra and images
We process spectra (to subtract background), reconstruct images, conduct principal component analysis and Raman microscopy image sorting using Wolfram Mathematica (version 12.1.1.0). The adopted image sorting approach employs convolutional neural net architecture developed by Yann LeCun et al.42 edited to train and sort Raman images specific to three classes of sub-cellular distributions of: oxy, deoxy and met haemoglobins.Results
Images at selected Raman and principal components
First, we address the effect of excitation wavelength: how this may help a better discussion of sub-cellular biochemistry. In Fig. 3 (upper panels) we present representative-average Raman spectra of single RBC detected using excitation wavelengths at 780 and 532 nm. Trying to factor different contributions in the spectra detected in single cells, in the lower panels of Fig. 3 we show experimental spectra of oxy, deoxy and met-haemoglobins in aqueous solution. | ||
| Fig. 3 Raman spectra of a single red blood cell (RBC), and of aqueous solutions of oxygenated haemoglobin (oxyHb), deoxygenated Hb (deoxyHb) and metHb, as indicated, measured using excitation radiation at 780 nm and 532 nm as shown in the left and right panels, respectively. Left set: Black stars next to the Raman spectrum of deoxyHb (excited using 780 nm) indicate spectral regions, where dithionate contribution overwhelms; red stars next to spectra of RBC spectra indicate resonances used to reconstruct microscopy resolved images as shown in the upper row in Fig. 4. Right set: Red, blue and magenta stars indicate resonances we consider to be specific to Raman scattering of oxy, deoxy and methaems of Hb excited using 532 nm radiation. | ||
Detected using the corresponding excitation wavelengths. Considering spectra for Hb protein aqueous solutions detected using 780 nm radiation (lower three spectra in the left set in Fig. 3), we may note that shapes of Raman scattering bands of oxyHb in spectral regions 960–1005 cm−1, 1200–1300 cm−1 and 1500–1700 cm−1 most closely resemble spectral line-shapes detected in the same spectral regions for the single RBC using the same radiation (upper spectrum in the left set in Fig. 3). The spectrum of deoxyHb disagrees with Raman of RBC in the spectral region 1200–1300 cm−1. Line-shape of the metHb band at 1600 cm−1 does not agree with the line-shape of Raman scattering in the same spectral region as detected in single RBC. If we explore Raman signatures of haems as stimulated using 532 nm radiation (lower three spectra in the right set in Fig. 3), we may also note that the oxyhaem spectrum (red colour spectrum in the right set in Fig. 3) resembles most closely the spectrum of the single RBC using the same radiation (upper spectrum in the right set in Fig. 3): this is more obvious if we account the fine structure of resonances in the spectral region 1500–1700 cm−1. In result, we may suggest that, overall, the oxyhaemoglobin contribution dominates in the single cell spectra detected using excitation either at 780 or 532 nm. This is consistent with the experimental condition where the single cell is exposed to air.
It is interesting to note that experimental spectra detected using 780 nm excitation demonstrate a relatively strong and narrow Raman resonance at 1003 cm−1, which is specific to phenylalanine. At the same time, Raman spectra detected using 532 nm excitation reveal rather weak and relatively broad Raman activity in the same frequency range. For that reason, we ascribe the weak Raman at ca. 1001 cm−1 (right side in Fig. 3) to the haem, predominantly. This agrees with the assignments given in previous studies,55,56 and corresponds to theoretical results we reported recently.38 Next, comparing spectra of oxy- and deoxyhaemoglobin with those detected using 780 nm excitation, we account Raman signals at 1230 and 1540 cm−1 as more specific to the protein hosting the two haem forms, respectively, rather than to the two forms of the haem. This agrees with results of previous studies on RBC Raman stimulated under 780 nm.32,57
Raman spectrum of methaemoglobin under 780 nm excitation does not suggest usefully distinct resonances. Furthermore, its Raman scattering at about 1550 cm−1 may overlap with the signature of deoxyHb at about 1540 cm−1. Such complication may compromise a discussion unless contribution of the met form is negligible. Accounting for these considerations, using three frequencies (1003, 1230 and 1540 cm−1 as a red star marked in the left top spectrum in Fig. 3), we reconstruct Raman microscopy images specific to protein phenylalanine, oxy- and deoxyhaemoglobins: see Fig. 4A–C, respectively. To complement these, in Fig. 4D–F, we present Raman microscopy images reconstructed using Raman scattering at 1360, 1556 and 1636 cm−1 stimulated under 532 nm excitation: see magenta, left blue and red star indications in the right-side spectra in Fig. 3. In the previous contribution, we assigned these resonances (stimulated using 532 nm) to met, deoxy and oxy forms of the haem, respectively: a reader may explore the detailed account of the computed normal modes in the ESI of ref. 38 and their review in the main text of ref. 38. Here, comparing the results of Raman experiment using different excitations, we review which of the possible assignments could be more helpful to follow RBC biochemistry at a sub-cellular level.
 | ||
| Fig. 4 Panels A–C: Raman microscopy images of RBC reconstructed at 1003 (protein phenylalanine), 1230 (oxyHb) and 1540 cm−1 (deoxyHb), respectively, (see red stars in the upper left panel in Fig. 3) in experiment using 780 nm excitation radiation. Panels D–F: Raman microscopy images of RBC reconstructed using scattering at 1360 (methaem), 1556 (deoxyhaem) and 1636 cm−1 (oxyhaem) stimulated under 532 nm radiation: see magenta, left blue and red star in the upper right panel in Fig. 3. To simplify comparative presentation of spatial distributions, we normalize intensities of the images are normalized by their maximal values. | ||
To compare Raman images under the two excitations, we must address possible limits for such an evaluation. First, the images detected using 780 nm excitation are less resolved spatially. On one hand, this arises from (i) less tight focusing radiation at 780 nm than in the case when using 532 nm (since the longer wavelength, but the same focusing conditions); (ii) sampling emission from broader coherent envelopes, what is accounted for upon convolution; and (iii) possible internal content redistribution due to a time-delay, since the confocal scan using 780 nm wavelength is taken after the scan using 532 nm radiation (priority is given to the resonant Raman experiment). At the same time, the lower resolution of images detected using 780 nm (than is the case when using 532 nm) may indicate the different nature of the normal modes to contribute, as well. The latter would agree with our conclusion that the two wavelengths stimulate responses of different normal modes. For example, as we discussed earlier, the obvious 1003 cm−1 Raman of phenylalanine under 780 nm excitation suggests a dominant contribution of the haemoglobin protein, which hosts the haem. In the case where we sample more the hosting protein cavity rather than the haem, Raman modes are expected to vary according to structural heterogeneity of the protein. Here it is interesting to note that distribution of phenylalanine (Fig. 4A) does not correlate exactly with distribution of oxyhaemoglobin (Fig. 4B). This suggests that Raman under 780 nm excitation is sensitive to protein structural variance. Accounting differences of excitation and sampling conditions when using the two wavelengths, as well as the differences of nature of the contributing normal modes, we may note, that the spatial distributions of oxyHb (Fig. 4B) and of the oxy form of haem (Fig. 4F) are comparable, and according to the dominance of the toroidal cavity content. At the same time, the deoxy (Fig. 4C and E) and met form (Fig. 4D) are distributed less uniformly, along the circle of the toroidal cavity.
Overall, sensitive to haem states, Raman images in experiments using 532 nm excitation are more promising for quantitative analysis. In the previous contribution we gave a tentative indication on certain aspects of sub-cellular biochemistry.38 To do this we used differences of normalized Raman images ascribed to different states of haem rather than methods of multivariate analysis, which may be limited due to dynamics of the cellular envelope and the content,38 and may mislead as spectral degeneracies for some vibrations affect the whole spectral manifold upon its factoring. Here, searching for quantitative assessments, first, in Fig. 5 we present results of principal component analysis in respect to spectral variances. Specifically, considering the radial symmetry of an ideal RBC shape, in Fig. 5A we introduce radial distance from the cell centre as a sample attribute. To visualise this, we blend red and blue colours. Having spectra sampled at different positions, we find eigenvalues for principal components (Fig. 5B) to compare loadings of the two main components (Fig. 5E) with a typical experimental reading (Fig. 5D) and explore the relative distribution of the eigenvalues for the detected set of spectra in the score plot (Fig. 5C). The score plot indicates that the spectra sampled in the central cell region account more intense scattering at 1590 and 1639 cm−1, and less intense Raman at 747, 1128, 1300 and 1540 cm−1 that all correlate with the loadings of the first component, as shown in Fig. 5E. Such PCA anticipated tendencies for signatures at 1540 and 1639 cm−1 are consistent with the assignments to reduced and oxidized forms and their spatial distributions with those we developed previously assisted with DFT and conducting image reconstructions according to intensity of detected Raman resonances.38
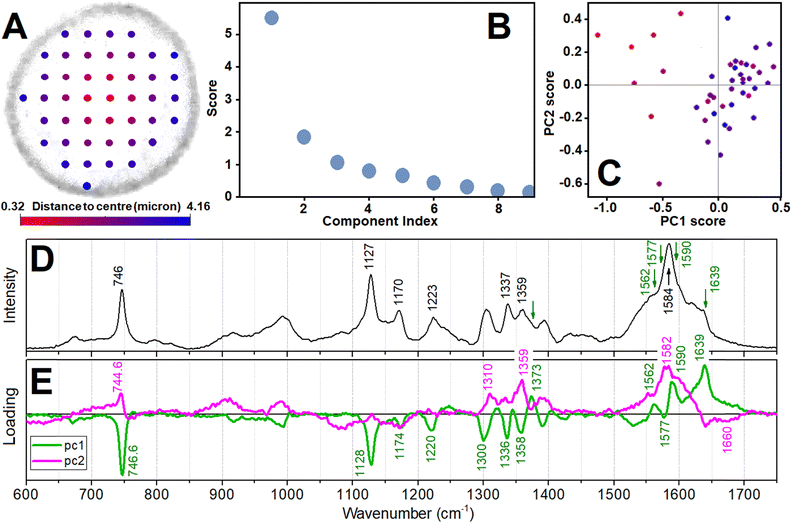 | ||
| Fig. 5 Principal component analysis in respect to spectral variance detected for a resonant Raman experiment. Panel A: Attributing data to radial distance from the centre (colour blend from red to blue) as a mesh of selected acquisition points to overlap with the low contrast outer contour of the RBC of the cell. This mesh is for the cell, which we image in Fig. 4D–F. Panel B: Eigenvalues (or scores) of principal components. Panel C: Score plot for the first and second principal component. Panel D: Raman spectrum from an arbitrary sampling position. Panel E: Spectra of the first and second principal components. ESI† includes an archive with Mathematica Examples to include a code (PCA_spectra_Example.zip) to compute some panels. | ||
Next, in Fig. 6 we present results of principal component analysis in respect to image variances. Here, we conduct component analysis correlating spatial variabilities of Raman images reconstructed at frequencies of the thirteen most intense Raman resonances in the fingerprint spectral range. Fig. 6A1 and B1 present example images reconstructed at 1556 and 1636 cm−1, respectively. First, all images are normalized on the sums of their intensities. Then, they are “whitened” subtracting the mean image from each of them: Fig. 6A2 and B2 present whitened images at 1554 and 1636 cm−1. Third, we flatten each whitened image by setting its data rows (one after another) as a one-dimensional sequence of intensity values to a vector. Consequently, we express covariance matrix (Fig. 6C) and eigenvalues (Fig. 6D) of the principal components: Fig. 6E and F present images of the two main components folded back from the one-dimensional vector space into two-dimension image space. Consequently, in Fig. 6G we show the score plot for the two main principal components. It is interesting, that images at 1584 and 1636 cm−1 (which one may consider to be specific to oxyhaem38) occupy a different quarter about the first component than images at 1554 and 1620 cm−1 (which can be ascribed to deoxyhaem38). At the same time, the first principal component (Fig. 6E) draws attention to the role of the cell central region, toroidal cavity and membrane.
 | ||
| Fig. 6 Principal component analysis in respect to image variance. Panels A1 and A2: Image reconstructed using Raman scattering at 1554 cm−1 (in Fig. 4E) and its “whitening” by subtraction of mean of the image set. Panels B1 and B2: Image reconstructed using Raman scattering at 1636 cm−1 (in Fig. 4E) and its “whitening” by subtraction of mean of the image set. Panel C: Covariance matrix for the vectors of the images selected for analysis: vector for an image is by setting rows of the image (one after another) as one-dimensional sequence of intensity values. Panel D: Eigenvalues (scores) of principal components of the image set. Panels E and F: First and second principal component images. Panel G: Score plot for the first and second principal component of the image set with indication of Raman frequencies. | ||
Symmetric shape intracellular distribution models
To approach sub-cellular biochemistry, we need numerical modelling of Raman images. First, we compute a representative radially averaged slice across a Raman RBC image, see black circled line Fig. 7A. Then, using the cell contours according to the bright field microscopy image, we model the correspondent radius of cellular envelopes28,30 to compute Raman images of the volume content according to model distributions as we described in the Material and methods. The simplest picture may assume that haemoglobins are evenly distributed in the internal volume of the cell. A selected slice of a computed image (black line in Fig. 7A) demonstrates inconsistency of this model with experimental distribution (open circle line in Fig. 7A): the model overestimates haemoglobin presence in the centre and underestimates at the edges of the RBC. The former mismatch is significant and cannot be amended unless the computed membrane profile to construct the envelope28,30 should include a dramatic thinning of the cell at its centre. This, however, would contradict experimental observations.39,58 | ||
| Fig. 7 Panel A: Representative radially averaged slice across RBC Raman image at 1636 cm−1 (open circles) and computed profile assuming that a haemoglobin form is evenly distributed in modelled RBC volume (black solid line). Panel B: Slices of image computed for the membrane associated shell model (see Fig. 2B) by concentration according to exp[−j2/3] (green line S3) and exp[−j2/50] (olive line S50), where j is the number of a vertex along the line connecting the same index vertices of different layers counted from the surface toward the centre. Blue line (labelled with M) presents a slice from image modelled considering haemoglobins tightly bound to membrane with the axis of its central cavity to be perpendicular to the membrane surface according to CPR eigen-image protocol. Panel C: Slices of image computed for the central ellipsoid model (see Fig. 2A) by the decay of concentration by exp[−j2/100] (dark cyan), exp[−j2/200] (magenta), and exp[−j2/300] (blue), where j is the number of a vertex along the line connecting the same index vertices of different layers counted from the centre to surface. Panel D: Slices of image computed employing toroidal models, as described in Fig. 2C, C1–C3 and in the Materials and methods. | ||
Starting from the modelled structure of RBC, in Fig. 7 we present slices selected from Raman images computed according to three modes of haemoglobin inhomogeneous distributions: (i) under different forms of association next to or with the membrane (panel B), (ii) with preferences to occupy the cellular centre (panel C), and to dominate in the toroidal cavity of RBC (panel D): details of the models are in Materials and methods. Searching for criteria to find a plausible combination of haemoglobin sub-cellular distributions, beside the representative radially averaged slice across Raman RBC image (black circled line, Fig. 7A), also, we take representative radially averaged slices across the difference of normalized Raman images (as introduced in ref. 38) reconstructed at 1610 and 1636 cm−1: see black circled line Fig. 8B1–B3.
Following this, in Fig. 8A1 we show the best conceivable fit (red line) of the radial averaged representative slice of the experimental image (open circles) combining scaled slices from images computed assuming a uniform distribution of haemoglobin (black line U0, as in Fig. 7A), membrane tight associated haemoglobins (green line S3 by exp[−j2/3], as in Fig. 7B) and a toroidal contribution (orange line T4). Confirming that a reasonable fit is possible, next, we use these components to model the slice from the difference of experimental images: red line and black circles in Fig. 8B1. The observed mismatch suggests that the assumed dominant role of the evenly distributed haemoglobins (see comparison Fig. 7A) cannot be justified even if we try to amend it admitting contributions of the next to membrane and toroidal populations. In general, dismissing the idea that haemoglobins may tend to distribute within an RBC envelope may be in an accord with the very peculiar shape of the cell type. However, we do this according to numerical analysis. Further, in Fig. 8A2 and B2, we test haemoglobin distributions with three types of tendency: to associate with the membrane tightly (green line S3), to prefer occupying the toroid cavity (purple line, model T4b) and to reside in the central ellipsoid region while protruding into the toroid cavity (blue line, model C300). As we can see in Fig. 6B2, the mismatch between the difference slices improves. Following this, in Fig. 8A3 and B3 we present results, when we reduce the protrusion of the central ellipsoid population into the toroid cavity (magenta line, model C200) and add a population of haemoglobins, which are loosely associated with the membrane (dark yellow line, model S50).
Modelling deformations
Having a tentative agreement for representative radially averaged slices across Raman and Raman difference images, we may proceed to better tune the corresponding experimental images introducing radial and vertical deformations for the modelled envelope. To define the radial deformation, using the cell contour in the bright field image, we may anticipate an average radius of the cell and extract departure of the distance from the centre to the contour edge from the average radius in dependence on ϕ-angle of the 2Pi space of the cell contour considering the centre of the cellular envelope coincides with {0, 0, 0} of the laboratory frame, and the plane of the envelope is parallel to the XY laboratory plane. Then, we may fit the ϕ-angle dependence of the distance from {0, 0, 0} to the edge of the contour with a suitable set of Gaussian line-shapes. We do the same to deform the slice (as shown in Fig. 1C) vertically in dependence on the ϕ angle of its rotation. To suggest the vertical scaling as a function of ϕ angle, at a first approach, we may sample Raman amplitude variance along a circular line at about the toroid maximum. ESI† includes an archive with Mathematica codes to demonstrate how we introduce deformation fitting.In Fig. 9C and D we present graphical images for selected layers of a symmetric (not deformed) envelope to compute Raman and Raman difference images (Fig. 9E and F) using intra-cellular distribution models, as we describe in Fig. 8A3 and B3. Comparatively, adopting the described deformations, in Fig. 9G and H we present graphical images for selected layers of a deformed envelope to compute Raman and Raman difference images (Fig. 9I and H) in the best resemblance to the experimentally defined corresponding images (Fig. 9A and B). The approach allows developing a platform to model various types of deformation systematically. Furthermore, there is a capacity to account deformations if anticipated using quantitative phase imaging.39
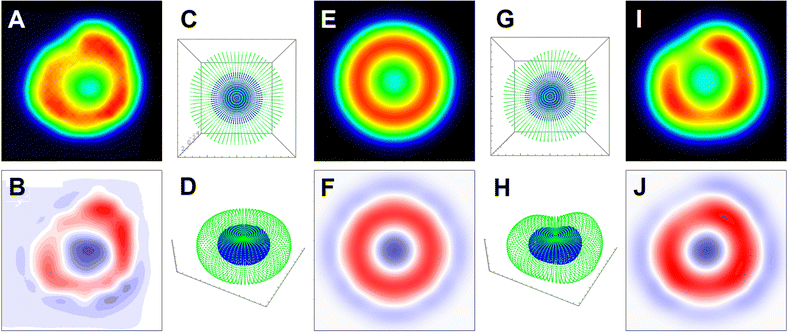 | ||
| Fig. 9 (A) RBC Raman image reconstructed at 1636 cm−1 (same as in Fig. 4F). (B) Difference of normalized Raman image at 1610 cm−1 (see Fig. 4D) minus normalized Raman image at 1636 cm−1. (C) and (D) Top and side view of external (green) and of an intermediate (blue) layer of vertices according to equilibrium shape solution under uniform hydrostatic pressure.30 (E) and (F) Modelling of images as shown in A and B using the symmetric envelope as depicted in C and D, and according to subcellular haemoglobin distributions as shown in Fig. 8A3 and B3. (G) and (H) Top and side view of external (green) and of an intermediate (blue) layer of vertices according to equilibrium shape, as in (C) and (D), under radial and vertical deformations to reproduce nonuniform intensity patterns shown in images in A and B. (I) and (J) Modelling of images as shown in A and B using the deformed envelope as described in (G) and (H). ESI† includes an archive with a Mathematica examples to include a code (Volume_3D_Shell_Tor_Cntre_Examples.zip) to compute distributions to model image as shown in panel (I). | ||
Having developed a theoretical approach to classify and sort sub-cellular spatial contributions from different haemoglobins we may describe the cell main function status quantitatively. Using both, the computed amplitudes specific to normal modes of the three haem forms, and experimental spectra for the corresponding haemoglobins, we anticipate the cell studied to contain about 7% of met, 50% of deoxy and 44% oxy form. The anticipated level for the oxy-form (in respect to deoxy form) is lower than typically expected. Often or commonly, methaemoglobinemia is considered to be a life threat when concentration of the met-form is 10%, or higher.59,60 In result, we may conclude that this particular cell is hypoxic but contains levels of met-haemoglobin below that thought to be a life threat.
CPR eigen-imaging: membrane component
Modelling the deoxy-oxy difference slice (black open circles in Fig. 8B3) suggests a larger presence of the oxy form near the membrane and in the centre of the cell with the negative signature indicated by the blue star mark in Fig. 8B3 being according to the exp[−j2/3] tight surface attraction model. In contrast, deoxy-Hb shows a slightly higher population in the toroidal cavity. Trying to fit better the difference data in Fig. 8B3, we introduce a positive contribution of the exp[−j2/50] component, which describes a weak surface attraction. Here, it is interesting to note that, contrary to oxy-Hb, the met from does not anticorrelate with the deoxy-Hb when next to the membrane. This we may conclude according to the blue open rhombus line in Fig. 8B3: the line presents a radially averaged slice across experimental deoxy-met Raman difference image. When approaching the surface, the line falls to zero while positive: at the membrane, the two haemoglobin forms tend to be equally co-present though deoxy form dominates slightly.Since the result indicates that the RBC envelope membrane plays a significant role in subcellular dynamics for different haemoglobin distributions, ideally it is desirable to plan an experiment where the membrane contribution may be specified. Here it is important to stress that to describe experimental Raman images of RBC we reflect the possible role of the membrane in subcellular organization with two exponential distributions to decrease concentration of a certain Hb-form by exponential laws in dependence on distance from the surface. The correspondent computed distributions (green and dark yellow lines in Fig. 7B) indicate the maxima of such populations to be slightly shifted deeper into the volume in dependence on the adopted exponential constant. Here it is interesting to see what such a distribution would look like if we assume haemoglobin molecules attach to the membrane. This requires modelling of Raman images with molecules at the interface under incomplete orientation averaging.
Following the CPR eigen imaging protocol (see Materials and methods) for the response functions of an effective symmetric top limit (eqn (2)–(4)) in Fig. 10A we present 6 eigen-images (we omit SPxyz image as it rather similar to SSxyz). Furthermore, in Fig. 10 (panels C, D, F, and G) we show sums of the eigen images to build YY (or SS), XX (or PP), YX (or SP) polarisation specific and unpolarised Raman images of a membrane to account phospholipid and attached haemoglobin tetramers (with the axes along their cavity perpendicular to the surface).
 | ||
| Fig. 10 Panel A: CPR eigen images for a symmetric envelope under flat orientation. Panel B: DFT isotropic, as in solution, pre-resonant Raman spectrum of phospholipid (blue line); theoretic SP and PP polarised pre-resonant Raman spectra according to anisotropic distribution of phospholipids in symmetric undeformed RBC envelope under flat (θ = 0°) and tilted (θ = 45°) orientation by black and red line, respectively. Panel C and D: Pre-resonant Raman microscopy images of symmetric undeformed RBC envelope under flat (θ = 0°) and tilted (θ = 45°), respectively, using CPR protocol for mode 122: see black star label in panel (B). Panel E: DFT isotropic, as in solution, Raman spectrum of deoxyHb (blue line); SP and pre-resonant Raman spectra according to anisotropic distribution of deoxyHb tetramers in symmetric undeformed RBC envelope under flat orientation and SP and PP polarisations (black and red line, respectively). Panel F and G: Pre-resonant Raman microscopy images of undeformed and deformed RBC model envelope, respectively, under flat (θ = 0°) while using CPR protocol for mode 250: see blue star mark in panel. ESI† includes an archive with Mathematica Examples to include a code (CPR_Eigens_Examples.zip) to show how to compute some of the eigen-images. | ||
Comparing isotropic spectra and polarisation specific spectra of molecules under incomplete orientation averaging within the membrane of the computed envelope, and according to the tilt of the envelope, Fig. 10 (panels B and E) demonstrates the resolving sensitivity of Raman microscopy if assisted with adequate theory. Fig. 10C and D show how much the intensity pattern may change in dependence on the tilt. At the same time, comparing images in the panels, we may see how the envelope of deformation may smear the symmetric image patterns computed for different polarisation settings.
It is instructive here to pay attention to the CPR eigen-images in Fig. 10A. Considering terms in the response functions, one may note that diagonal entries of a Raman tensor (after rotation to account molecular orientation in respect to the laboratory frame) would contribute differently. If αxx,q + αyy,q is larger than αzz,q, PPx,y and SSx,y would become the main contributions under PP and SS polarisation setting, respectively: see eqn (2) and (3). Their expressions may be smeared when we sum-up with the PPxyz and SSxyz eigen-image, which are the cross-terms due to squaring the Raman susceptibility, as in eqn (8) and (9). However, a Raman image detected or computed under a selected polarisation would be revealing. For example, the pp image in Fig. 10C (since it is similar to PPx,y), the CPR eigen-image in Fig. 10A instructs that αxx,q + αyy,q for the normal modes q = 122 of the phospholipid (transformed to match the initial geometry: long axis along Z laboratory axis) is larger than αzz,q and the role of the cross-term PPxyz CPR eigen image is negligible. Here, there are several take-home messages. First, in an unpolarized experiment, the membrane contribution into an image is according to the sum of the presented images under polarized settings. In the case of a symmetric undeformed envelope, the ring pattern (see the sum image in Fig. 10, panel B) is symmetric. The Blue M line in Fig. 7B and 8A4 presents a horizontal slice from such an image, that can be used further to discuss the role of the membrane. Second, in experiments under SS or PP polarisation settings, the contribution of haemoglobin in volume should overwhelm the membrane contribution. Taking a difference between such measurements would secure a clean detection of the membrane contribution. The SP polarisation setting should secure a clean detection of the membrane contribution, unless molecules in the main volume are not under complete orientation averaging: for example, as for the formation of hemozoin crystals.61
We now consider a slice from a membrane specific unpolarized image computing using the Raman tensor of haemoglobin to model Raman difference images according to those obtained in experiment. In Fig. 8B4 we demonstrate that such a profile may replace the contribution of tightly associated membrane haemoglobins (green line S3 in Fig. 8B). Even though this model is competitive with that in Fig. 8A3–B3, we disregard it since it requires more than 6% of haemoglobin to be bound to membrane while fluorescence quenching studies suggested that under physiological pH, only about 3% of the intracellular haemoglobin would bind to membranes.34 This means that using conventional Raman microscopy, it should be difficult to distinguish the membrane contribution. Indeed, experimentally, RBC membrane microscopy required either SERS application,39 or working with RBC ghosts.40 As mentioned earlier, in this contribution, we provide a theoretical background that shows that polarisation Raman microscopy may assist distinguishing contributions of Raman signals from the main volume and from the membrane. Therefore, while explaining differences of resonant RBC images reconstructed at 1636 cm−1 and at 1556 cm−1, we suggest that the oxy form slightly dominates near the membrane and in the centre, while deoxy-Hb shows a slightly higher population in the toroidal cavity.
Discussion
Quantitative analysis of RBC Raman microscopy provides several practical outcomes. Having reasonable agreement between theory derived data and that established by experiment it is possible to generate insights on subcellular biochemistry. According to the theory predictions, experimental approaches for analysis may be proposed as well as practical implications in the biomedical field.First, let us review our outcomes from the perspective of RBC biochemistry as reported so far. Specifically, early fluorescence studies suggested that haemoglobin binding to membranes displays two binding mechanisms: the majority of haemoglobin molecules follow a low affinity binding with an equilibrium dissociation constant Kd = 1.6 × 10−6 M, while a small portion exhibits a high affinity binding process with Kd about 1.2 × 10−8 M.34 The high-affinity sites for haemoglobin binding to the cytoplasmic surface of the red cell membrane are localized to the inner segment of a band 3 protein complex,35 while the lower affinity sites were thought to involve glycophorin and phospholipids.36 Later, dynamics of haemoglobin interactions with band 3 proteins was reviewed to suggest a first association constant of 1.54 ± 0.25 × 107 M−1 for binding of a first Hb tetramer, and a second intrinsic constant of 5.48 ± 0.22 × 106 M−1 for binding of a second Hb tetramer.51
In recent decades, significant research efforts have been made to review the introductory description of binding dynamics constants from the perspective of the redox biochemistry of haemoglobin. While the equilibrium between oxy-Hb and deoxy-Hb provides the main RBC function (to carry and release oxygen), such processes as autooxidation of oxy-Hb, oxidation and reduction of met-Hb affects oxidative stress inflammation and vascular tone.62
The main source of RBC metHb is due to spontaneous autooxidation of oxyHb (into metHb) to generate superoxide radical anion O2−˙.59,63 Another pathway concerns exposure to oxidizing agents,64 such as naturally present H2O2 and nitric oxide: in fact, a direct reaction of H2O2 with Fe(II)-haemoglobin undergoes a Fenton pathway reaction producing the highly reactive hydroxyl radical.65 Consistently, hydroxyl radicals were reported in sickle erythrocytes.60 Additionally, commonly administered nitroglycerin, benzocaine, dapsone, and phenazopyridine may bring life-threatening drug-induced methaemoglobinemia.35,66
As one of compensations, cytochrome b5 and cytochrome-b5 reductase are reported to convert metHb into deoxyHb.62 Our modelling of Raman microscopy images suggests that, on average, enrichment or depletion of metHb follows the distribution of deoxyHb. This corresponds with the perspective that cytochrome b5/cytochrome-b5 reductase dominates in the cytosol.67 This supports the findings in our previous contribution where we suggested that local, non-uniform slight dominance of metHb may indicate the spatial regions where the reducing enzyme system is failing.38
Beside the cytoplasmic reactivities, redox biochemistry of haemoglobin concerns interactions with membranes: ultrafiltration suggested that deoxyHb binds to membranes with eightfold greater affinity than oxyHb.68 Furthermore, using crystallography, Walder et al.69 specified that each band 3 dimer may interact with two haemoglobin tetramers, and that a binding site extends deep (about 18 Å) into the central cavity between the β chains, along the dyad symmetry axis of a haemoglobin tetramer. This cavity is inaccessible upon Hb oxygenation.70,71 To complement the crystallography data, a series of experiments using genetically engineered mice with mutations in the deoxyHb binding domain of band 3 suggested that binding of deoxyHb to band 3 may be an important molecular switch to regulate various subcellular events.72 For example, the authors proposed that deoxyHb would sterically displace ankyrins from band 3 to increased deformability and mobility, and would trigger discharge of ATP through pannexin-1 to promote generation of NO,73 therefore, causing vasodilation.
A different perspective has been put forward by Rifkind et al.:74 that partially oxygenated haemoglobin tetramers (due to their distinct conformation) may dominate in interactions with band 3 protein complexes,75 and may increase the rate of autoxidation of oxygenated haemoglobin producing superoxide,76 hence facilitating the release of the superoxide from the erythrocyte without being scavenged by erythrocyte antioxidant enzymes where oxidative processes taking place on the surface of the membrane are not neutralized by the cellular antioxidant systems.77–79
Second, our modeling of the results of conventional unpolarized Raman microscopy, indicate that the technique does not have the resolving capacity to distinguish the membrane contribution. Nonetheless, the modelling protocol developed is sensitive enough to anticipate distributions of different haemoglobins within different subcellular spatial regions, and when next to membranes. In particular, using the approach established it is possible to distinguish a slight dominance of oxyHb when next to a membrane by the S3 distribution (see the blue star mark in Fig. 8B3). The compartment next to membrane is first to receive oxygen from the surroundings, particularly, when a cell is hypoxic. At the same time, previous studies indicate that deoxyHb and tetramers with deoxy contribution would be attracted from cytosol to bind to the membrane tightly72 therefore diminishing reduced proteins in the compartment next to the membrane.
Third, our quantitative evaluation of the studied cell (with about 7% met, 50% deoxy and 44% oxy form of haemoglobin) suggests that it is hypoxic but with the methaemoglobin level below critical levels. If the approach is expanded further, it may be used to report if drug-induced methaemoglobinemia is present in intensive care and upon surgery, whenever anaesthetics such as dapsone, nitrates (e.g., nitroglycerin), and metoclopramide are used.64,66 In this respect, we note that the approach may be further supported by deep learning training to account variations in molecular distributions, shape and orientation. In the ESI,† an introductory image dataset and Mathematica notebook (CNN_toSort_RBC_Raman_images.zip) developed for Raman microscopy image sorting using convolutional neural net architecture developed by Yann LeCun et al.42 is provided; edited to sort for three classes of haemoglobins (oxy, deoxy and met), for a very limited sampling space. The network is tuned to demonstrate reasonable accuracy (of about 0.8) to show that AI assisted Raman microscopy has the potential to aid intensive care and health support.
Conclusions
Here, we focus on quantitative analysis of Raman microscopy experimental data for a red blood cell, as reported earlier.38 Specifically, first, we review the reported Raman microscopy assignments using methods of multivariate analysis and address the application of deep learning approaches to assist Raman image classification to support decision making in intensive care and in health support.Next, to simulate Raman images of a discocyte, we adopt an equilibrium membrane profile computed according to parametric solution of a General Curvature Hamiltonian,28,30 and introduce a deformation protocol to affect radial and vertical dimensions according to the bright image, cell contour and Raman intensity. The developed approach does have capacity to accommodate local membrane deformations if anticipated using quantitative phase imaging into Raman image modelling.58
Using the developed theory and DFT computed molecular tensors, we test Raman microscopy results for haemoglobin and phospholipids modelling molecular distributions in the main cellular volume, next to the cell membrane, and in the cell membrane. Comparing to the experimental data, we suggest different modes of haemoglobin intra-cellular distributions and discuss the slight dominance of oxyHb in the regions next to the membrane of a hypoxic cell. This we consider to be due to both, ambient oxygen transport through the membrane and the higher affinity of deoxyHb to bind to the membrane according to the range of sub-cellular antioxidant mechanisms.59,64,65,74–79
Third, for the case of membrane contributions, we suggest Raman response functions (written for incomplete orientation averaging of effective symmetric top molecular system) to define an instantaneous (any polarisation) Raman microscopy image reconstruction protocol using “counts per rotation” eigen-images, precomputed for a desired envelope under a specified orientation. According to the theory of response functions and modelling outcomes, we discuss the role of polarisation settings which would facilitate detection of Raman properties specific to the membrane.
Our results suggest that modelling of Raman microscopy resolved haemoglobin distributions in correlation with confocal fluorescence (sampling the cellular skeleton), assisted with phase-sensitive measures and AI supported image analysis sorting is the next methodology frontier to map and understand RBC subcellular biochemistry.
Author contributions
Victor V. Volkov: investigation, methodology, software, theoretical studies, analysis, writing. Joanna Aizenberg: facilities for theoretical studies, review. Carole Perry: funding acquisition, theoretical studies, analysis, writing.Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI† and associated Mathematica workbooks.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Harvard University, for continued access to the Odyssey/Cannon cluster supported by the Faculty of Arts and Sciences division, Research Computing Group at Harvard University. Dr Michael Aizenberg is thanked for his insightful reading of versions of the manuscript. VVV and CCP are grateful to AFOSR FA9550-20-1-0206 and FA9550-24-1-0274 funds. Since 2021, VVV is a self-funded researcher living in Russia on savings collected during the USA Air Force Research program at Nottingham Trent University, 2016–2020.References
- F. L. Hünefeld, Der Chemismus in der thierischen Organisation, F. A. Brockhaus, Leipzig, 1840 Search PubMed.
- F. Hoppe-Seyler, Über die oxydation in lebendem blute, Med-chem Untersuch Lab, 1866, vol. 1, pp. 133–140 Search PubMed.
- M. F. Perutz, M. G. Rossmann, A. F. Cullis, H. Muirhead, G. Will and A. C. T. North, Structure of haemoglobin: a three-dimensional Fourier synthesis at 5.5-A. resolution, obtained by X-ray analysis, Nature, 1960, 185, 416–422 CrossRef CAS PubMed.
- N. U. Meldrum and F. J. W. Roughton, Carbonic anhydrase. Its preparation and properties, J. Physiol., 1933, 80, 113–142 CrossRef CAS PubMed.
- J. Wan, W. D. Ristenpart and H. A. Stone, Dynamics of shear-induced ATP release from RBCs, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16432–16437 CrossRef CAS PubMed.
- D. L. Diesen, D. T. Hess and J. S. Stamler, Hypoxic vasodilation by RBCs: evidence for an s-nitrosothiol-based signal, Circ. Res., 2008, 103, 545–553 CrossRef CAS PubMed.
- P. Kleinbongard, R. Schutz and T. Rassaf, et al., RBCs express a functional endothelial nitric oxide synthase, Blood, 2006, 107, 2943–2951 CrossRef CAS PubMed.
- P. Ulker, L. Sati, C. Celik-Ozenci, H. J. Meiselman and O. K. Baskurt, Mechanical stimulation of nitric oxide synthesizing mechanisms in RBC, Biorheology, 2009, 46, 121–132 CAS.
- G. A. Benavides, G. L. Squadrito, R. W. Mills, H. D. Patel, T. S. Isbell, R. P. Patel, V. M. Darley-Usmar, J. E. Doeller and D. W. Kraus, Hydrogen sulfide mediates the vasoactivity of garlic, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17977–17982 CrossRef CAS PubMed.
- K. Shobana, RBCs do more than just carry oxygen; new findings by NUS team show they aggressively attack bacteria too, The Straits Times, Yong Ann Nee, Biological Sciences, NUS, 1 September 2007 Search PubMed.
- N. Jiang, N. S. Tan, B. Ho and J. L. Ding, Respiratory protein-generated reactive oxygen species as an antimicrobial strategy, Nat. Immunol., 2007, 8, 1114–1122 CrossRef CAS PubMed.
- G. Gulliver, On the size and shape of red corpuscles of the blood of vertebrates, with drawings of them to a uniform scale, and extended and revised tables of measurements, Proc. Zool. Soc. London, 1875, 474–495 Search PubMed.
- M. Leach and B. J. Bain, Haematology: from the image to the diagnosis, John Wiley & Sons Ltd, 2022 Search PubMed.
- M. Gedde and W. H. Huestis, Membrane potential and human RBC shape, Biophys. J., 1997, 72, 1220–1233 CrossRef CAS PubMed.
- J. L. Sebastian, S. Muñoz, M. Sancho and J. M. Miranda, Modeling the internal field distribution in human RBC exposed to MW radiation, Bioelectrochemistry, 2004, 64, 39–45 CrossRef CAS PubMed.
- J. Lan, J. Liu, Z. Zhao, R. Xue, N. Zhang, P. Zhang, P. Zhao, F. Zheng and X. Sun, The peripheral blood of Aβ binding RBC as a biomarker for diagnosis of Alzheimer's disease, Age Ageing, 2015, 44, 458–464 CrossRef PubMed.
- S. C. Sidenstein, E. D'Este, M. J. Böhm, J. G. Danzl, V. N. Belov and S. W. Hell, Multicolour Multilevel STED nanoscopy of Actin/Spectrin Organization at Synapses, Sci. Rep., 2016, 6, 26725 CrossRef CAS PubMed.
- H. Shimo, S. N. V. Arjunan, H. Machiyama, T. Nishino, M. Suematsu, H. Fujita, M. Tomita and K. Takahashi, Particle Simulation of Oxidation Induced Band 3 Clustering in Human Erythrocytes, PLoS Comput. Biol., 2015, 11, e1004210 CrossRef PubMed.
- L. Jiang, C.-H. He, H.-Y. Chen, C.-Y. Xi, E. K. Fodjo, Z.-R. Zhou, R.-C. Qian, D.-W. Li and M. E. Hafez, In Situ Monitoring of Hydrogen Peroxide Released from Living Cells Using a ZIF-8-Based Surface-Enhanced Raman Scattering Sensor, Anal. Chem., 2021, 93, 12609–12616 CrossRef CAS PubMed.
- G. Maulucci, E. Cordelli, A. Rizzi, F. De Leva, M. Papi and G. Ciasca, et al., Phase separation of the plasma membrane in human red blood cells as a potential tool for diagnosis and progression monitoring of type 1 diabetes mellitus, PLoS One, 2017, 12, e0184109 CrossRef PubMed.
- M. Aoun, P. A. Corsetto, G. Nugue, G. Montorfano, E. Ciusani, D. Crouzier, P. Hogarth, A. Gregory, S. Hayflick, G. Zorzi, A. M. Rizzo and V. Tiranti, Changes in Red Blood Cell membrane lipid composition: a new perspective into the pathogenesis of PKAN, Mol. Genet. Metab., 2017, 121, 180–189 CrossRef CAS PubMed.
- J. P. Blass, I. Hanin, L. Barclay, U. Kopp and M. J. Reding, Red Blood Cell Abnormalities in Alzheimer Disease, J. Am. Geriatr. Soc., 1985, 33, 401–405 CrossRef CAS PubMed.
- M. Gedde, E. Yang and W. H. Huestis, Shape response of human RBC to altered cell pH, Blood, 1995, 86, 1595–1599 CrossRef CAS PubMed.
- R. Glaser, Does the transmembrane potential or the intracellular pH control the shape of human RBC?, Biophys. J., 1998, 75, 569–570 CrossRef CAS PubMed.
- S. M. Recktenwald, K. Graessel, F. M. Maurer, T. John, S. Gekle and C. Wagner, Red blood cell shape transitions and dynamics in time-dependent capillary flows, Biophys. J., 2022, 121, 23–36 CrossRef CAS PubMed.
- P. Wong, A basis of echinocytosis and stomatocytosis in the disc-sphere transformations of the erythrocyte, J. Theor. Biol., 1999, 196, 343–361 CrossRef CAS PubMed.
- N. S. Gov and S. A. Safran, Red Blood Cell Membrane Fluctuations and Shape Controlled by ATP-Induced Cytoskeletal Defects, Biophys. J., 2005, 88, 1859–1874 CrossRef CAS PubMed.
- P. W. Kuchel, Parametric-Equation Representation of Biconcave Erythrocytes, Bull. Math. Biol., 1999, 61, 209–220 CrossRef CAS PubMed.
- S. Muñoz, J. L. Sebastian, M. Sancho and G. Alvarez, Modeling Human Erythrocyte Shape and Size Abnormalities, arXiv, 2005, preprint, arXiv:q-bio/0507024v1 DOI:10.48550/arXiv.q-bio/0507024.
- P. A. Djondjorova, V. M. Vassileva and I. M. Mladenov, Analytic description and explicit parametrization of the equilibrium shapes of elastic rings and tubes under uniform hydrostatic pressure, Int. J. Mech. Sci., 2011, 53, 355–364 CrossRef.
- K. Shou, M. Sarter, N. R. de Souza, L. de Campo, A. E. Whitten, P. W. Kuchel, C. J. Garvey and A. M. Stadler, Effect of red blood cell shape changes on haemoglobin interactions and dynamics: a neutron scattering study, R. Soc. Open. Sci., 2020, 7, 201507 CrossRef CAS PubMed.
- B. R. Wood, P. Caspers, G. J. Puppels, S. Pandiancherri and D. McNaughton, Resonance Raman spectroscopy of red blood cells using near-infrared laser excitation, Anal. Bioanal. Chem., 2007, 387, 1691–1703 CrossRef CAS PubMed.
- T. G. Spiro and T. C. Strekas, Resonance Raman Spectra of Hemoglobin and Cytochrome c: Inverse Polarization and Vibronic Scattering, Proc. Natl. Acad. Sci. U. S. A., 1972, 69, 2622–2626 CrossRef CAS PubMed.
- N. Shaklai, J. Yguerabide and H. M. Ranney, Interaction of Hemoglobin with Red Blood Cell Membranes as Shown by a Fluorescent Chromophore, Biochem., 1977, 16, 5585–5592 CrossRef CAS PubMed.
- J. M. Salhany, K. A. Cordes and E. D. Gaines, Light-scattering measurements of hemoglobin binding to the erythrocyte membrane. Evidence for transmembrane effects related to a disulfonic stilbene binding to band 3, Biochemistry, 1980, 19, 1447–1454 CrossRef CAS PubMed.
- P. B. Rauenbuehler, K. A. Cordes and J. M. Salhany, Identification of the hemoglobin binding sites on the inner surface of the erythrocyte membrane, Biochim. Biophys. Acta, 1982, 692, 361–370 CrossRef CAS PubMed.
- V. Volkov and C. C. Perry, Modeling of Infrared–Visible Sum Frequency Generation Microscopy Images of a Giant Liposome, Microsc. Microanal., 2016, 22, 1128–1145 CrossRef CAS PubMed.
- V. V. Volkov, J. McMaster, J. Aizenberg and C. C. Perry, Mapping blood biochemistry by Raman spectroscopy at the cellular level, Chem. Sci., 2022, 13, 133–140 RSC.
- H. Park, S. Lee, M. Ji, K. Kim, Y. Son, S. Jang and Y. Park, Measuring cell surface area and deformability of individual human red blood cells over blood storage using quantitative phase imaging, Sci. Rep., 2016, 6, 34257 CrossRef CAS PubMed.
- G. Zito, G. Rusciano, G. Pesce, A. Dochshanov and A. Sasso, Surface-Enhanced Raman Imaging of Cell Membrane by Highly Homogeneous and Isotropic Silver Nanostructure, Nanoscale, 2015, 7, 8593–8606 RSC.
- C. Ghanashyam, S. Shetty, S. Bharati, S. Chidangil and A. Bankapur, Optical Trapping and Micro-Raman Spectroscopy of Functional Red Blood Cells Using Vortex Beam for Cell Membrane Studies, Anal. Chem., 2021, 93, 5484–5493 CrossRef PubMed.
- Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, Gradient-Based Learning Applied to Document Recognition, Proc. IEEE, 1998, 86, 2278–2324 CrossRef.
- G. Fermi, M. F. Perutz, B. Shaanan and R. Fourme, The crystal structure of human deoxyhaemoglobin at 1.74 A resolution, J. Mol. Biol., 1984, 175, 159–174 CrossRef CAS PubMed.
- M. Paoli, R. Liddington, J. Tame, A. Wilkinson and G. Dodson, Crystal Structure of T State Haemoglobin with Oxygen Bound at All Four Haems, J. Mol. Biol., 1996, 256, 775–792 CrossRef CAS PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behaviour, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09, revision B.01, 2010 Search PubMed.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations – potentials for the transition-metal atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- P. B. Canham, The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell, J. Theor. Biol., 1970, 26, 61–81 CrossRef CAS PubMed.
- W. Helfrich, Elastic properties of lipid bilayers: theory and possible experiments, Z. Naturforsch., C, 1973, 28, 693–703 CrossRef CAS PubMed.
- S. Svetina and B. Zeks, Membrane bending energy and shape determination of phospholipid vesicles and red blood cells, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS PubMed.
- A. A. Demehin, O. O. Abugo, R. Jayakumar, J. R. Lakowicz and J. M. Rifkind, Binding of Hemoglobin to Red Cell Membranes with Eosin-5-maleimide-Labeled Band 3: Analysis of Centrifugation and Fluorescence Lifetime Data, Biochemistry, 2002, 41, 8630–8637 CrossRef CAS PubMed.
- J. D. Jackson, Classical electrodynamics, Wiley, 1999 Search PubMed.
- G. Placzek, The Rayleigh and Raman Scattering, Akademische Verlagsgesellschaft VI, Leipzig, 1934, pp. 205–374 Search PubMed.
- D. A. Long, The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules, John Wiley & Sons Ltd, 2002 Search PubMed.
- M. Abe, T. Kitagawa and K. Kyogoku, Resonance Raman spectra of octaethylporphyrinato-Ni(II) and meso-deuterated and 15N substituted derivatives. II. A normal coordinate analysis, J. Chem. Phys., 1978, 69, 4526–4534 CrossRef CAS.
- S. Choi, T. G. Spiro, K. C. Langry, K. M. Smith, D. L. Budd and G. N. La Mar, Structural Correlations and Vinyl Influences in Resonance Raman Spectra of Protoheme Complexes and Proteins, J. Am. Chem. Soc., 1982, 104, 4345–4351 CrossRef CAS.
- A. Chowdhury and R. Dasgupta, Effects of acute hypoxic exposure on oxygen affinity of human red blood cells, Appl. Opt., 2017, 56, 439–445 CrossRef CAS PubMed.
- F. S. Ruggeri, C. Marcott, S. Dinarelli, G. Longo, M. Girasole, G. Dietler and T. P. J. Knowles, Identification of Oxidative Stress in Red Blood Cells with Nanoscale Chemical Resolution by Infrared Nanospectroscopy, Int. J. Mol. Sci., 2018, 19, 2582 CrossRef PubMed.
- H.-S. Hsieh and E. Jaffé, The metabolism of methemoglobin in human erythrocytes. The Red Blood Cell, Academic Press, New York, NY, USA, 1975, pp. 799–824 Search PubMed.
- R. P. Hebbel, Auto-oxidation and a membrane-associated ‘Fenton reagent’: a possible explanation for development of membrane lesions in sickle erythrocytes, Clin. Haematol., 1985, 14, 129–140 CrossRef CAS PubMed.
- J. W. Kang, N. Lue, C.-R. Kong, I. Barman, N. C. Dingari, S. J. Goldfless, J. C. Niles, R. R. Dasari and M. S. Feld, Combined confocal Raman and quantitative phase microscopy system for biomedical diagnosis, Biomed. Opt. Exp., 2011, 2, 2484–2492 CrossRef PubMed.
- M. T. Bozza and V. Jeney, Pro-inflammatory Actions of Heme and Other Hemoglobin-Derived DAMPs, Front. Immunol., 2020, 11, 1323 CrossRef CAS PubMed.
- C. C. Winterbourn, B. M. McGrath and R. W. Carrell, Reactions involving superoxide and normal and unstable haemoglobins, Biochem. J., 1976, 155, 493–502 CrossRef CAS PubMed.
- R. O. Wright, W. J. Lewander and A. D. Woolf, Methemoglobinemia: Etiology, Pharmacology, and Clinical Management, Ann. Emerg. Med., 1999, 34, 646–656 CrossRef CAS PubMed.
- S. M. Sadrzadeh, E. Graf, S. S. Panter, P. E. Hallaway and J. W. Eaton, Hemoglobin. a biologic Fenton reagent, J. Biol. Chem., 1984, 259, 14354–14356 CrossRef CAS.
- S. Riaz, P. Kudaravalli and S. A. Saleem, D. Heisig. Methemoglobinemia: A Life-threatening Complication of Topical Pharyngeal Anesthetics, Cureus, 2020, 12, e7900 Search PubMed.
- E. R. Jaffe and D. E. Hultquist, Cytochrome b5 reductase deficiency and enzymopenic hereditary methemoglobinemia, The Metabolic and Molecular Basis of Inherited Disease, McGraw-Hill, New York, 7th edn, 1995, pp. 2267–2280 Search PubMed.
- A. Tsuneshige, K. Imai and I. Tyuma, The binding of hemoglobin to red cell membrane lowers its oxygen affinity, J. Biochem., 1987, 101, 695–704 CrossRef CAS PubMed.
- J. A. Walder, R. Chatterjee, T. L. Steck, P. S. Low, G. F. Musso, E. T. Kaiser, P. H. Rogers and A. Arnone, The Interaction of Hemoglobin with the Cytoplasmic Domain of Band 3 of the Human Erythrocyte Membrane, J. Biol. Chem., 1984, 259, 10238–10246 CrossRef CAS PubMed.
- M. F. Perutz, Stereochemistry of cooperative effects in haemoglobin, Nature, 1970, 228, 726–739 CrossRef CAS PubMed.
- G. Chetrite and R. Cassoly, Affinity of hemoglobin for the cytoplasmic fragment of human erythrocyte membrane band 3. Equilibrium measurements at physiological pH using matrix-bound proteins: the effects of ionic strength, deoxygenation and of 2,3-diphosphoglycerate, J. Mol. Biol., 1985, 185, 639–644 CrossRef CAS PubMed.
- H. Chu, M. M. McKenna, N. A. Krump, S. Zheng, L. Mendelsohn, S. L. Thein, L. J. Garrett, D. M. Bodine and P. S. Low, Reversible binding of hemoglobin to band 3 constitutes the molecular switch that mediates O2 regulation of erythrocyte properties, Blood, 2016, 128, 2708–2716 CrossRef CAS PubMed.
- M. L. Ellsworth, C. G. Ellis, D. Goldman, A. H. Stephenson, H. H. Dietrich and R. S. Sprague, Erythrocytes: oxygen sensors and modulators of vascular tone, Physiology, 2009, 24, 107–116 CrossRef CAS PubMed.
- J. M. Rifkind, J. G. Mohanty, E. Nagababu, M. T. Salgado and Z. Cao, Potential Modulation of Vascular Function by Nitric Oxide and Reactive Oxygen Species Released From Erythrocytes, Front. Physiol., 2018, 9, 690 CrossRef PubMed.
- Z. Cao, J. B. Bell, J. G. Mohanty, E. Nagababu and J. M. Rifkind, Nitrite enhances RBC hypoxic ATP synthesis and the release of ATP into the vasculature: a new mechanism for nitrite-induced vasodilation, Am. J. Physiol.: Heart Circ. Physiol., 2009, 297, H1494–H1503 CrossRef CAS PubMed.
- O. O. Abugo and J. M. Rifkind, Oxidation of hemoglobin and the enhancement produced by nitroblue tetrazolium, J. Biol. Chem., 1994, 269, 24845–24853 CrossRef CAS PubMed.
- J. M. Rifkind, L. Zhang, J. M. Heim and A. Levy, The role of hemoglobin in generating oxyradicals, Basic Life Sci., 1988, 49, 157–162 CAS.
- J. M. Rifkind, L. Zhang, A. Levy and P. T. Manoharan, The hypoxic stress on erythrocytes associated with superoxide formation, Free Radical Res. Commun., 1991, 12–13, 645–652 CrossRef CAS PubMed.
- A. A. Demehin, O. O. Abugo and J. M. Rifkind, The reduction of nitroblue tetrazolium by red blood cells: a measure of red cell membrane antioxidant capacity and hemoglobin-membrane binding sites, Free Radical Res., 2001, 34, 605–620 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00236b |
| This journal is © the Owner Societies 2025 |

