Reposition pathways of GTP in orthoflavivirus NS5-methyltransferase revealed by enhanced molecular dynamics simulations

Abstract

The NS5-methyltransferase (MTase) domain is highly conserved in the orthoflavivirus genus. This enzyme catalyzes the methylation of the 5′-RNA cap and its adjacent nucleotide, responsible for viral RNA capping that is crucial for the survival and replication of the virus. The catalytic mechanism of this enzymatic domain is yet to be understood. In particular, the experimentally determined cap-binding site on the MTase is outside the catalytic site putatively responsible for N⁷-methylation. Herein we employ GTP as a model of the 5′-RNA cap to investigate the process of repositioning of the cap from the GTP-binding pocket to the putative catalytic center. To overcome the computational challenge in sampling transitions, we deploy a two-step approach in which extensive Gaussian-accelerated molecular dynamics are performed to explore transition paths followed by a path-based umbrella sampling for determining the free energy change during the transition. We find that the GTP substrate interacts with conserved residues along the pathways from the crystallographic pocket to near the methyl donor S-adenosyl-L-methionine (SAM). Interestingly, our observation is in accordance with experimental mutagenesis studies on the N⁷-MTase reaction. Through an energy decomposition analysis along the pathway, we further find that residues E149, R57, H110 and R84 contribute to the placement of the GTP substrate. The complex relationship between MTase global conformational changes and the GTP repositioning process has been revealed which could be relevant to the functional mechanism of this enzyme. This work provides the rationale behind residue contribution and substrate requirement of orthoflavivirus MTase activities and provides invaluable insights for the rational design of MTase-targeted inhibitors.

---

Introduction

The orthoflavivirus genus (formerly named flavivirus)¹ is represented by major mosquito-borne pathogens.² Well-known species under the genus include Zika virus (ZIKV), Dengue virus (DENV), Japanese encephalitis virus (JEV), yellow fever virus (YEFV), West Nile virus (WNV), and Omsk hemorrhagic fever virus (OHFV). The genome of orthoflavivirus expresses three structural proteins and seven non-structural proteins, among which, the NS5 protein in orthoflavivirus is essential for viral replication.³ This protein contains two functional domains: the RNA-dependent RNA-polymerase (RdRp) domain and the methyltransferase (MTase) domain (Fig. 1A). The highly conserved MTase domain (Fig. S1, ESI†)^4–6 is responsible for two essential reactions that transfer methyl groups to methylate the N⁷-position of the guanine of the 5′-GTP cap and to the 2′-O-position of the adjacent nucleotide, respectively. Both methylation reactions were catalyzed within the same active site of the MTase domain that uses S-adenosyl-L-methionine (SAM) as the methyl donor (Fig. 1B).^7–9 Structural and functional studies^3,7–17 revealed multiple structural features of the active site in the MTase domain, including a K-D-K-E catalytic tetrad, a SAM-binding pocket, a GTP-binding pocket that can bind a guanosine triphosphate (GTP) or the GTP part of a 7-methylguanosine triphosphate (m⁷GTP) cap, and an RNA-binding site (Fig. 1A, top).

Fig. 1 Structure and function of orthoflavivirus NS5-MTase. (A) Top: ZIKV MTase–GTP–SAH ternary complex highlighting the catalytic tetrad (green), GTP-pocket (pink), SAM-pocket (yellow), RNA-binding site (slate), and conserved residue E149 (cyan); middle and bottom: ZIKV full-length NS5 and DENV NS5–SLA complex showing the arrangement of the MTase–RdRp domain and the binding site of RNA-5′–SLA, highlighting MTase (gray), RdRp (yellow), and RNA in the DENV complex (dark green), within the MTase domain the GTP-pocket (pink) and RNA-binding site (slate). Rearrangement of the MTase–RdRp interface may occur upon RNA binding and the orientation varies among different orthoflavivirus species. (B) Reactions of cap methylation catalyzed by orthoflavivirus MTase, assuming the order of MTase reactions to be similar to that in eukaryotes. (C) Chemical structures of cap-analogues GTP/m⁷GTP and the MTase cofactor SAM.

Experimental structures of orthoflavivirus MTase revealed the binding position of GTP distant from the methyl donor SAM (Fig. 1A). This structural information suggests that either the RNA 5′-cap or SAM must reposition for the N⁷-MTase reaction. With the high affinity of SAM in orthoflavivirus MTase compared to 5′-capped RNA,¹⁸ it is more likely that the RNA cap repositions itself to be in proximity to the methyl donor SAM. Further evidence from mutagenesis has located the catalytic site for the N⁷-MTase reaction. Early work by Dong et al. revealed the contribution of active site residues in WNV MTase.⁸ D146 and the K61-D146-K182-E218 tetrad are responsible for catalyzing the N⁷-MTase reaction and 2′-O-MTase reaction, respectively. Non-catalytic residues with major contributions to the MTase activity (i.e. mutation to alanine led to less than twenty percent activities) were also identified: R37, R57, and W87 are crucial for both MTase reactions; E149, R84 and the aromatic ring of F24 are important for the N⁷-MTase activity. Experimental researchers have also reported that the RNA 5′-stem loop A (SLA) structure is required for the N⁷-MTase activty⁷ and the effect of MTase mutation around the active site on GTP binding.¹⁰ These studies identified contributions of residues that do not interact with GTP in the crystallographic structure. However, detailed energetic contributions by residues outside the GTP-binding pocket remain elusive.

Various experimental studies attempted to sample the binding mode of capped RNA to capture the modes of interactions relevant to the MTase reactions of orthoflavivirus MTase. These studies have provided preliminary insights into the need for a transition process for the MTase-substrate system to proceed from the crystallographic GTP-pocket to the site of the N⁷-MTase reaction.¹⁵ MTase–RNA binding assays of WNV and DENV have been reported by Milani¹¹ and Henderson,¹² which identified residues responsible for the binding of RNA and the 5′-cap between the GTP-pocket and the putative N⁷-MTase site proximal to the SAM-pocket. The key residues and binding mode of NS5(MTase)–SLA interaction were later proposed by Bujalowski¹³ and Choi¹⁴ with the updated experimental structure of the RNA, combined with mutagenesis and bioassays. Jia et al. have reviewed crystallographic data on orthoflavivirus MTase–RNA interactions and reported the coordinates of the OHFV MTase–SAM–(GTP/GMP) ternary complex.¹⁵ They summarized the structural evidence as a part of the complete mechanisms of orthoflavivirus MTase reactions, highlighting the lack of structural information related to the N⁷-MTase activity. Recently, the cryo-EM structure of the DENV NS5–RNA complex has been determined at 3.6 Å, providing insights into the structural basis for the interactions between the NS5 protein and the 5′-SLA.¹⁶ The RNA-cap interacting with the MTase in this DENV NS5–RNA complex has been modelled in a state resembling the 2′-O-MTase binding mode.¹⁷ While the aforementioned experimental evidence suggests the importance of both the N⁷-MTase and 2′-O-MTase reactions in the survival and replication of orthoflavivirus MTase, no experimental structures directly relevant to the N⁷-MTase reaction have been reported. Only experimental structural models that trapped the substrate binding mode relevant to the 2′-O-MTase are available. Therefore, static images from the present experimental structures cannot fully explain the contributions of the conserved residues in the active site of orthoflavivirus MTase in the N⁷-MTase reaction. A model providing information about the pathway would be a step forward to understand the enzymatic mechanisms of this system.

Molecular dynamics (MD) simulations have been adapted to model the aforementioned repositioning pathways of the GTP cap on the MTase domain. Chagas et al.¹⁹ reported a computational model of one possible pathway relevant to the N⁷-MTase reaction using unbiased molecular dynamics simulation. Key residues in MTase–GTP interaction have been identified at three stages of the trajectory, corresponding to the GTP-bound state observed in crystal structures, an intermediate mid-pathway state, and a state possibly related to N⁷-methylation. MM/PBSA energy at the three stages have been calculated. Allostery induced by SAM binding has been proposed based on their observation of the conformational changes of F24, D146, V132 and W87 as GTP proceeds from the GTP-pocket towards the methyl donor SAM. From the unbiased MD simulation, one of the possible pathways towards the state of N⁷-MTase action has been analyzed. On the other hand, Chuang et al.²⁰ considered the release of MTase products and investigated the unbinding of MTase product analogues S-adenosyl-L-homocysteine (SAH) and m⁷GTP from ZIKV MTase, instead of the binding of the substrate. They have adopted Gaussian accelerated MD (GaMD) to estimate the changes in free energy throughout the product unbinding process and the residue contribution in the process of product release. Considering the complex free energy landscape and stochastic dynamics of complex protein systems like ours, there is yet to be a comprehensive computational exploration of possible transition pathways of MTase substrates that could rationalize the observations in experimental mutagenesis studies at the molecular level. Furthermore, the free energy profiles of various pathways need to be determined to estimate their statistical significance and evaluate the importance of residues for the repositioning processes.

Inspired by the success of these previous studies, we sought to have an in-depth sampling of the repositioning pathways of the RNA 5′-guanosine cap on the MTase domain. Following a previous study, we used GTP as a surrogate model of the RNA 5′-cap to simplify the system for achieving a more extensive sampling. To obtain accurate description of the repositioning process, we have conducted numerous parallel simulations accelerated by the GaMD to explore various pathways. Our results reveal two repositioning pathways that differed by the final conformations of GTP in which the base is either in a syn or anti configuration. The free energy profiles of the major pathways identified are further analyzed through umbrella sampling (US) techniques using path-based collective variables (CV).²¹ Analysis of the free energy surface (FES) along the two pathways suggests the pathway which has more interactions between GTP and the RNA-binding pocket and the pathway that sampled a syn-GTP around the methylation site to be more probable in our trajectory samples. Moreover, energy decomposition analysis is conducted for each pathway, revealing the contributions of orthoflavivirus-conserved residues in GTP reposition (residues R57, R84, H110 and E149 that are not involved in the binding of GTP in the available crystal structures). We observed a decrease in interaction energy as GTP proceeded towards the MTase cofactor SAM. Interestingly, these conserved residues were also identified to be important for the N⁷-MTase activity in orthoflavivirus MTase in mutagenesis experiments.⁸ The results reported therein not only allow a better understanding of orthoflavivirus RNA-capping, but also provide practical insights into the design strategies of cap-analogues as orthoflavivirus inhibitors.

Method

System preparation

Amber 21²² suite of program was used for simulation, input preparation and data analysis. All the crystal structures used in this work were retrieved from the RCSB PDB.²³ The initial coordinates of the protein were taken from chain A of PDB entry 5GOZ. Flipping of the N17 amide was manually corrected according to the hydrogen bond network. The N-terminal and C-terminal of the protein were capped with methyl-acetyl (ACE) and N-methyl (NME), respectively. Hydrogen atoms of the protein were modelled with the H++ server assuming pH 7.4.²⁴ Crystal waters were then re-combined with the protonated chain, and hydrogens were added to the water molecules with UCSF Chimera²⁵ considering the hydrogen bond network. GTP extracted from the same chain was protonated in tleap to ensure consistency in atom naming in the chosen forcefield, and then combined with the protonated system to form the binary MTase–GTP complex. While the crystal structures of the binary complexes of MTase–SAM and ternary complexes of MTase–SAH–GTP are available, there is no experimental structure of the MTase–SAM–GTP ternary complex. Hence, the ternary complex of ZIKV MTase–SAM–GTP was prepared from the crystal structures of MTase–SAH–GTP by manually removing MTase byproduct SAH from chain A of 5GOZ and docking SAM into the SAM-pocket of MTase. The coordinates of SAM were taken from chain A of PDB entry 5KQR and hydrogens were added assuming the protonation state at physiological pH. The protonated SAM was then docked into the SAM-pocket of the processed receptor, using AutoDockTools 1.5.7²⁶ and AutoDock Vina 1.1.2.²⁷

The simulation system was prepared with the tleap module of Amber. Standard amino acids were modelled with the AMBER FF14SB²⁸ forcefield. GTP was modelled with the parameter set derived by Meagher et al.,²⁹ as retrieved from the amber parameter database.³⁰ The geometry of SAM was optimized with ORCA 4.2.1^31,32 and processed with OpenBabel.³³ GAFF³⁴ atom types were assigned to the processed molecule with the Antechamber module. RESP charge fitting was performed with PyRED³⁵ through the R.E.D. Server Development.³⁶ The molecular electrostatic potential for partial charge assignment was calculated with GAMESS-US (version Sept2018 GNU).³⁷ The processed complex was solved into 10 Å box of TIP3P water. Chloride counter ions were randomly placed in the water box to neutralize system charge.

Conventional MD simulation

The CUDA-accelerated PMEMD module in Amber 21 was used to perform MD simulations.^38,39 A 10 Å cutoff was used for the calculation of nonbond interactions. A 2-fs timestep was used for all dynamic stages with all bonds involving hydrogen constrained with SHAKE.⁴⁰ The solvated system was minimized with a multi-stage protocol to sequentially relax solvent, solute and the whole system. Each minimization stage had 2500 steps of steepest descent and 2500 steps of conjugated gradient. The minimized system was heated to 300 K with a Langevin thermostat. A short, restrained NPT step at 1-bar was then performed to relax solvent density, before an unrestrained NPT equilibration of 5-ns. During the 5-ns unrestrained NPT equilibration, the position of GTP was monitored to ensure that the production stage started with a state close to the crystal structure to probably sample the pathways of interest.

GaMD sampling

Dual-boost GaMD^41,42 of total and dihedral potential was performed to sample the states of MTase–GTP interaction starting from equilibrated snapshots. The run average was computed every 130 000 steps, as suggested by GaMD developers to be at least four-times the number of atoms in the system. Since preliminary test trials suggest that the lower-bound threshold, although better for reweighting, was insufficient to sample enough of samples of the event we were interested in, the upper-bound threshold (IE = 2) of boost potential was applied for sufficient acceleration of system dynamics. To account for potential inaccuracies with this choice of threshold, we have performed US along the sampled pathways for a more accurate estimation of free energy. For both the total and dihedral boost, σ₀ values were set to 6.0 kcal mol⁻¹. Default values were used for other input parameters. GaMD consisted of the pre-equilibration stage, equilibration stage and production stage. The previously equilibrated snapshot prepared from the unbiased conventional MD, which has the GTP substrate around the crystallographic state, was used as the initial configuration of GaMD. The guanine ring in the GTP of the MTase–GTP crystal structure adapts an anti-conformation, and throughout the pre-equilibration of this crystallographic state the GTP is stable with this anti-conformation as in the crystal structure. The pre-equilibrated system was subjected to additional unbiased cMD of 1.04 ns as pre-equilibration before collection of potential data for 10.4 ns for the determination of boost potential. A boost potential would then be applied based on cMD data and remain unchanged for 1.04 ns to stabilize the system. The boost potential was then allowed to update regularly for 8 ns, until the convergence of potential statistics. The position of GTP was monitored during GaMD equilibration to ensure that GTP would not leave the initial state before the start of data collection. Twenty independent replicas of 100.1-ns GaMD simulations were done for the production stage using fixed boost statistics and coordinates being saved every 1 ps, resulting in 100 100 snapshots per replica and a total of 2 002 000 snapshots from 20 trials. The simulation length of GaMD was decided after comparing conformation samples from preliminary trials, to ensure efficiency in sampling GTP reposition pathways while preventing unbinding events of high-affinity MTase cofactors SAM.

Umbrella sampling of GaMD-generated pathways

GaMD trajectories were visualized, and observables such as SAM–GTP distance, RMSD of selected residues, orientation of GTP with respect to the GTP, and the χ-angle of the guanine base of GTP were compared (Fig. S3–S8, ESI†). From the GaMD trajectories, we observed that two of the trials, Trial 7 and Trial 13, have sampled relatively stable conformations around the putative N⁷-MTase state. Thus, the two trials were selected for further energetic analysis with US. Analysis of independent pathways that sampled the interested events from unbiased methods such as GaMD has been successfully applied in various studies of biomolecular pathways related to protein–ligand interactions.^41,43–46 This approach allows the investigation of time-dependent behaviors as the system adapts a specific event.

We define the crystallographic state of MTase–GTP interactions as “State 1”, and the state putatively relevant to the N⁷-MTase reaction as “State 2”. Among the two selected trials, Trial 7 of GaMD sampled a syn-GTP as the GTP approaches the MTase methyl donor SAM (State 2), so the snapshots from the trial were extracted for US along the pathway denoted as the syn-pathway. On the other hand, Trial 13 sampled an anti-GTP around State 2, so the snapshots from the trial were extracted for US along the pathway denoted as the anti-pathway. Geometric path CV¹⁷ of the reposition process S from the GTP-pocket to the putative N⁷-MTase state was used as the reaction coordinate to be biased in US. We adapted this path CV to bias the path represented by the multiple CVs directly at the cost of only one CV. To define the path CV using representative states sampled in GaMD, the two CVs adapted by Chagas¹⁹ and Chuang²⁰ have been combined. We defined the path CV of the process on a two-dimensional basis: (1) distance between the methyl group of SAM and N⁷ of GTP; and (2) distance between the center-of-mass of GTP and center-of-mass of the GTP-pocket (Fig. 2A). Hence, this path CV, S, is the combination of the dashed line in Fig. 2B and it was calculated according to the following equation as implemented in Plumed:

where the vectors connecting the current position to the first and the second closest node of the path are denoted as v₁ and v₃, respectively, and the vector connecting the first and the second closest frame is denoted as v₂. Projections of the first and second closest frames of the path are denoted as i₁ and i₂, respectively.

Fig. 2 (A) Graphical illustration of the two distances being used to define geometric path CV, and the initial definition of S = 1 and S = 2 based on GaMD simulations. D₁ represents the distance between the two substrates of the N⁷-MTase reaction, and D₂ represents the distance between the centers of mass (COM) between GTP and the experimentally identified GTP-pocket. (B) Combined 2D-PMF of D₂ against D₁ sampled from the twenty independent replicas of GaMD trajectories. (C) Combined 1D-PMF of the geometric path CV sampled from the twenty independent replicas of GaMD trajectories. (D) Superposition of the starting model built from the crystal structure (light blue) and the snapshots at the minima around S = 1 from US samples of the two selected pathways (pink and green). (E) Superposition of the snapshots at the minima around S = 2 from US samples of the two selected pathways.

Two points on the 2D-FES that represent the movement of GTP were used to define the path CV (Fig. 2A). The values of point S = 1 were D₁ = 18.55 and D₂ = 7.66; and for S = 2, D₁ = 3.63 and D₂ = 16.18. These two points S = 1 and S = 2 are labelled in cyan in the 2D-FES plot (Fig. 2B). The values were taken from the representative snapshot extracted from clustering analysis with CPPTRAJ,⁴⁷ corresponding to the two deepest minima on the 2D-FES. This definition has been selected after multiple tests of different combinations in the path CV definition. US windows were adaptively extracted from the GaMD trajectories according to the overlap of umbrella histograms along the path CV. 24 windows and 36 windows were used for the syn-pathway and the anti-pathway respectively. The full trajectory of trial 7 (syn-pathway) was used for window selection, while only the starting 60.06 ns that sample the process from State 1 to State 2 was used to select windows from trial 13 (anti-pathway) since GTP moved away from State 2 from around 60.06 ns onwards. Using snapshots from GaMD, 10-ns production windows were used for data collection in US, applying a harmonic restraint of 300 kcal mol⁻¹ on the path CV. All US simulations were performed with the CUDA-accelerated version of PMEMD as the simulation engine and Plumed 2.7.6^48–50 for the application of restraints and calculation of CVs.

Trajectory analysis and energy calculation

Trajectories were post-processed and analyzed with CPPTRAJ⁴⁷ and Plumed 2.7.6. Molecular graphics were rendered in open-source PyMOL⁵¹ and VMD 1.9.3.⁵² Orthoflavivirus conserved residues were selected from the early experimental studies of Dong et al.⁸ for interaction energy calculation in CPPTRAJ. All the free energy calculations were done at a temperature of 300 K. The FES of GaMD trajectories was calculated with the PyReweighting⁵³ toolkit. In preliminary tests in this study, the more accurate cumulant expansion to the second order was also attempted, but the energetic noise and degree of freedom in the open cavity were too high for accurate reweighting. Hence the Maclaurin series to the 10th order was adapted for reweighting, using a cutoff of 100 and the bin size adapted for different CVs through trial and error.

The weight of configurations sampled from US trials of was calculated using the weighted histogram analysis method (WHAM).^54–57 Principal component analysis (PCA) was performed on the conformations of protein C_α, projecting the samples from the US trials of both of the pathways onto the first three eigenvectors. 1-D- and 2D-FES of path CV, D₁, D₂, the guanine base orientation with respect to the protein (Fig. S8, ESI†), top eigenvectors from PCA and the S_SAM–CE_SAM–N⁷_GTP angles were calculated from histograms using 200 bins, 100 bins, 100 bins, 100 bins, 100 bins and 100 bins respectively. Interaction energies between GTP and selected conserved residues in orthoflavivirus MTase were calculated in CPPTRAJ. Residues that we have analyzed were selected from the early experimental studies of Dong et al.⁸ The WHAM weighted average of interaction energy was calculated with 100 bins along the path CV. The reported values were shifted such that the interaction energy was zero at S = 1, to highlight the change in energy contribution as the system proceeded from State 1. We note that residue 28 was selected but not completely conserved in identity among all species under orthoflavivirus. Position 28 is lysine in the MTase of DENV, YEFV and ZIKV, while an arginine in WNV and JEV. Experimental evidence reported in the literature suggested the importance of the positive charge of this residue in the binding of GTP and the comparison of residue properties suggesting that residue 28 is still charge-conserved in orthoflavivirus. Hence, K28 was considered as one of the conserved residues in our study.

Results and discussion

Initial samples of the pathways of GTP movements and implications of the combined FES on inhibitor design

Pathways of GTP transition from the crystallographic GTP-pocket towards the methyl donor SAM were first sampled via GaMD simulations. GaMD allows the acceleration of system dynamics without a pre-defined CV, by boosting the potential of the system. Twenty independent replicas of GaMD simulation were performed. Multiple parameters were monitored throughout the simulations, to capture the process of GTP reposition. To monitor the transition process from the GTP-binding pocket to the putative N⁷-MTase state, we defined the two functionally relevant states of MTase–GTP interactions, “State 1” and “State 2”. “State 1” corresponds to the state resembling the binding mode observed in the crystal structure; while “State 2” corresponds to the putative N⁷-methylation state (Fig. 1B, step (2)). Movement between the two states was monitored by two distances, D₁ and D₂, which describe the space between the GTP-pocket and SAM (Fig. 2A). For the convenience of the pathway definition, D₁ and D₂ were reduced into one dimension to be represented by the geometric path collective variable¹⁷ (path CV, denoted as S). We defined S = 1 to be around State 1, and S = 2 to be around State 2. The values of D₁ and D₂ at State 1 and State 2 were taken from representative coordinates of targeted states from GaMD.

While GTP remained bound in all the GaMD simulations (Fig. S2 and S3, ESI†) due to the strong electrostatic interactions between its triphosphate and basic residues in the MTase cavity (Fig. 3), with GaMD we sampled multiple pathways contributing to the overall FES of GTP repositioning. From the GaMD trajectories, an initial estimation of the FES was calculated along the path CV and other CVs of interest. The reweighted FES combining the samples from the twenty GaMD trajectories has provided a preliminary overview of the preferred states of the MTase–GTP interaction. Fig. 2B shows the 2D-plot of D₁ and D₂, the two distances that represent the movement of GTP between the crystallographic pocket and the N⁷-MTase catalytic state as illustrated in Fig. 2A. This plot combines the data sampled from the twenty GaMD trajectories. This 2D-plot showed two distinct minima around where we labelled as S = 1 and S = 2, and a broad free energy surface with multiple intermediate states or off-pathway states being sampled. From these two CVs, D₁ and D₂, we select representative structures from around S = 1 and S = 2 respectively, to define the path CV of GTP movements along the path of interest. The FES of the path CV was plotted using the combined statistics of GaMD which considers not only the in-pathway states but also other off-pathway states. A shallow energy well in the middle of the pathway has been observed (Fig. 2C). Minima observed around the crystallographic state around S = 1 represents the global minima, which is reasonable as the state could be captured in experiments. The high degree of freedom in GTP movements on the open cavity could explain why the free energy around S = 2 was higher than that around S = 1 in the GaMD FES combining data from 20 trajectories. From the 2D-FES of distance that defines the path CV, we observed a broad distribution of the states of GTP motion, deviating from the shortest distance from State 1 to State 2 (Fig. 2B, cyan dotted line). Orientation of the guanine base of GTP and the χ-angle of guanine that represent the conformation of the guanine base with respect to ribose in GTP have been investigated. Independent scatter plots of these parameters along path CV (Fig. S4 and S5, ESI†) revealed that GTP sampled a range of conformations at State 2, which has not been reported in previous studies. The combined FES of the twenty replicas of GaMD does not differentiate between in-pathway states and off-pathway states, and the hotspots of MTase–GTP interactions represented by the lower-energy states on the FES could be explored in the future for drug design.

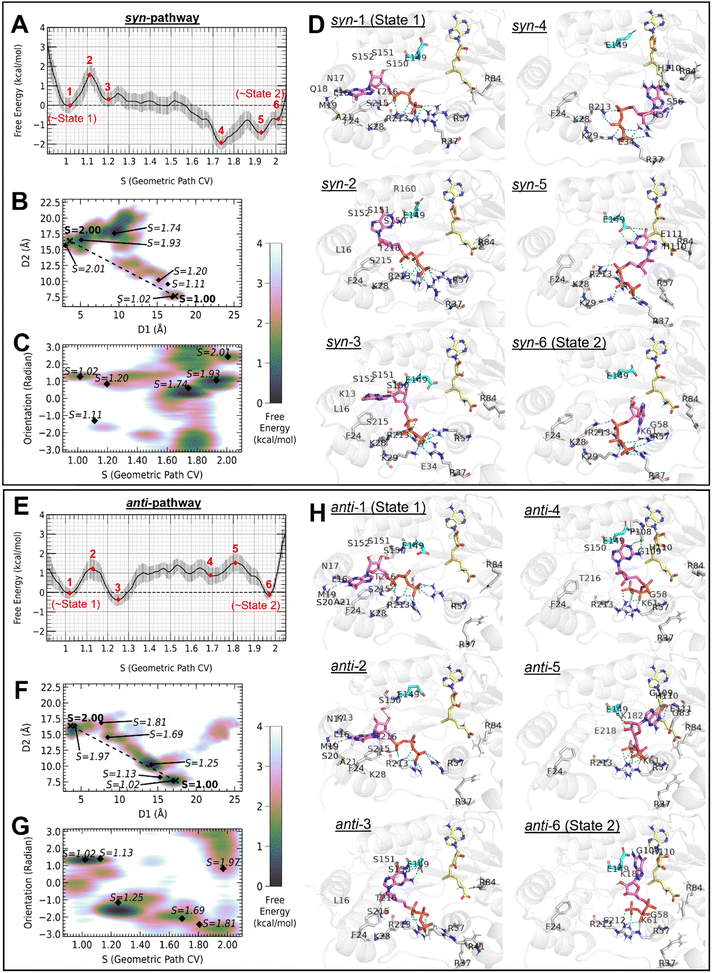Fig. 3 FES and states identified along geometric path CV sampled by the syn-pathway (top) and anti-pathway (bottom). (A) and (E) WHAM weighed FES against path CV. (B) and (F) Restored 2D-FES that defined the geometric path CV. The shortest distance from S = 1 to S = 2 is shown as dotted lines. (C) and (G) 2D-FES of the orientation of the GTP guanine base against geometric path CV. GTP orientation was defined as the dihedral angle formed by two atoms on the rigid base of GTP (exocyclic amino N2 and atom N7 in the guanine base) and two backbone C_α atoms in the K-D-K-E catalytic tetrad of the MTase protein (K61 and K182) (Fig. S8, ESI†). (D) and (H) 3D rendering of the corresponding states labeled in the FES plots. The MTase protein is colored in white, GTP is colored in pink, SAM is colored in yellow, and conserved residue E149 is colored in cyan. Polar contacts between GTP and the protein are shown as teal dashed lines, and protein residues that contributed to hydrogen bonding are shown as sticks. Residues within 4 Å of GTP are shown as wires. Non-polar hydrogens are hidden for clarity.

Characteristics of the two pathways chosen from GaMD samples and refined with US

The combined FES from GaMD provides an overall description of a relatively high-affinity position of GTP-binding on the protein surface. On the other hand, selecting pathways that sampled the events of interest reveals the mechanisms of how the orthoflavivirus MTase transfers GTP between the crystallographically observed GTP pocket to the N⁷-MTase catalytic site. Investigations of specific trajectories that sample the events of interest are commonly adapted in the study of protein–ligand binding or interaction (as detailed in Method). Of the twenty pathways from GaMD simulation, Trials 7 and 13 were able to generate complete paths leading to relatively stable modes of interactions around State 2 (Fig. S2–S7, detailed described in Method, ESI†). Hence, they were chosen for subsequent US simulations. Trial 7 of GaMD has sampled GTP in the syn-conformation around S = 2, whereas Trial 13 has sampled the anti-conformation. For the convenience in the later discussion, pathways that sampled syn-GTP and anti-GTP as the system approached State 2 were denoted as the syn-pathway and the anti-pathway respectively. Separate investigations of the trajectories have revealed pathway-dependent information about the process from State 1 to State 2 (Fig. S2–S7, ESI†), which highly varies due to the high degrees of freedom in the solvent-exposed cavity. All the GaMD trials started with GTP in the anti-conformation as in the crystal structure. Along the two pathways, we observed that as D₁ increases, i.e. as GTP proceeded towards SAM, the guanine base would be flipped from anti to syn. GTP maintained a syn-conformation when D₁ < 4 along the syn-pathway, whereas for the anti-pathway after the flip from anti to syn when leaving the pocket, it flipped back again to anti-conformation when D₁ < 4. To ensure sufficient sampling of a specific pathway for FES calculation, US was performed along pathways that sampled the transition process from State 1 to State 2 in the GaMD trajectories. The FESs of selected pathways were calculated with WHAM. Minima around State 1 and State 2 have been located along the WHAM FES calculated from US of selected pathways.

We plotted the 2D-FES of the two distances that define the path to uncover the spatial meaning of the states sampled (Fig. 3A and F). The difference in magnitude of FES changes could be explained by the mode of MTase–GTP interactions as the system visited the corresponding states through the different pathways. The anti-pathway adapted in space a path closer to the shortest linear path connecting S = 1 and S = 2, while the syn-pathway has a low-energy intermediate state at S = 1.74, at a position away from the shortest path. The FES of the 2D-distance also explained the data with S < 1 in the anti-pathway, which were off-pathway states as GTP moves away from the GTP-pocket to a direction different from the desired repositioning process. This region was also identified in the 2D-PMF in other trials of GaMD (Fig. 2B).

The orientation of the guanine base along the paths revealed the high degrees of freedom of guanine orientation as the system proceeded from State 1 to State 2 (Fig. 3C and G). This orientation was defined as a dihedral angle with two points on the rigid guanine base, and the α-carbons of two residues in the K-D-K-E catalytic tetrad in the protein (K61 and K182), along the path CV. Both the syn-pathway and anti-pathway have common minima at S = 1.02 where the orientation was around 1.3 rad. The difference between the two paths taken was also reflected by the orientation of GTP as shown in the plots. A rapid change in orientation can be observed at the global minima around S = 1.74 of the syn-pathway, before the GTP orientation started to stabilize at the minimum position as the system approached State 2 at 2.40 rad. The orientation of GTP along the anti-pathway was generally more stable as it proceeds from State 1, but the orientation was more diverse as the system approached State 2, despite the deeper energy well in the 1D-FES of the anti-pathway around this state. The orientation in this state was less restricted compared to the syn-pathway as revealed by the representative states around State 2. In the syn-pathway, when the system proceeded to around State 2 the guanine base was sandwiched between the protein and the ribose triphosphate, restricting the orientational degree of freedom (Fig. 3D, syn-6). However, in the anti-pathway, when approaching State 2 the guanine base was loosely placed on a platform formed by the cofactor SAM and the two flexible loops gating the SAM-pocket (Fig. 3H, anti-6), allowing a higher degree of orientational freedom.

We noted that the guanine base orientation in anti-6 resembles the “reaction probe” reported in Chagas et al.;³⁹ however there was a difference in the triphosphate binding mode in anti-6 compared to their work. In contrast, the guanine base orientation in syn-6 was in the opposite direction compared to that observed by Chagas et al., but the triphosphate conformation resembled their model. Interestingly, as we plot the interaction energy along the two pathways we sampled, we observed a more favorable interaction between GTP and SAM along the anti-pathway. Due to the high degree of freedom of GTP movement on the open cavity of MTase, both our samples and the results from Chagas et al. could represent a snapshot of the real biological process. The current observation indicates that the unrestricted movement of triphosphate could introduce difficulties in reaching a more energetically favorable binding mode in State 2.

FES of the two selected pathways resampled by US

From the FES obtained from US of the two selected pathways, we observed an overall decrease in free energy from S = 1 to around S = 2, indicating that the movement of GTP from the crystallographic state towards the targeted state is thermodynamically favorable. As the system proceeded from State 1 to State 2, the change in free energy started to deviate between the two pathways (Fig. 3D and H), despite the similar position on the protein being sampled (Fig. 3D and H). From the minima around S = 1 to the minima close to S = 2, the free energy decreased by 0.73 kcal mol⁻¹ and 0.06 kcal mol⁻¹ along the syn-pathway and the anti-pathway, respectively. The highest energy barrier was 1.61 kcal mol⁻¹ along the syn-pathway, corresponding to the transition from syn-1 to syn-2, and 1.95 kcal mol⁻¹ along the anti-pathway, corresponding to the transition from anti-3 to anti-5. The free energy curve implied a possible domination of the syn-pathway in the movement of GTP. The difference in the two pathways adapted can be explained by the energy contribution of conserved residues along path CV as shown in Fig. 4, which will be detailed in the next section.

Fig. 4 Relative WHAM weighted average interaction energies between GTP and selected residues along the syn-pathway (red) and anti-pathway (blue). The sum of vdW and electrostatic contribution was used as the y-axis of the plots, and the energies were shifted to zero at S = 1 to show the relative changes along the path CV. Positions of S = 1.25 and S = 1.7 were marked with dashed lines.

Residue contribution of orthoflavivirus N⁷-MTase can be rationalized by the residue-GTP interaction along the reposition pathway from the GTP-pocket to the N⁷-MTase state

The energy contribution of MTase residues to the interaction with GTP (Fig. 4) could explain the difference in the overall FES calculated along the two pathways (Fig. 3A and E). The relative energy of a specific residue as the system proceeded away from S = 1 revealed the role of this residue in the repositioning process. Energetic analysis per residue could provide a possible explanation for the conservation of MTase in the orthoflavivirus genus. The interaction energies between GTP and protein residues were calculated as the sum of vdW and electrostatic energies, and the relative contribution of each residue compared to S = 1 has been plotted along the path CV. A significantly more favorable contribution from K28 could be observed from the middle of the syn-pathway compared to the anti-pathway, that is the energy was 75 kcal mol⁻¹ lower in the syn-pathway around S = 2. Inspection of simulation trajectories confirmed that K28 interacts with the GTP phosphate along the syn-pathway (Fig. 3D), but flipped away in the middle of the anti-pathway (Fig. 3H, anti-3 to anti-4). R37 at the RNA-binding site and H110 located in a flexible loop at the entrance of the SAM-pocket also had lower energy around S = 2 along the syn-pathway.

Analysis of the pathways at different stages along the path CV reveals the role of conserved residues throughout the repositioning process. Stage I (S < 1.25) corresponds to an initiation stage where GTP starts to leave the GTP-pocket. At Stage I, K13, K28, S215 and F24 have distinct minima in the interaction energy profile along both sampled pathways. Stage II (1.25 < S < 1.7) corresponds to an intermediate stage with major contribution from residues located close to the opening of the SAM-pocket as well as from the RNA-binding site. At Stage II, minima could be found for K28, R37, R57, R84, H110, E111, E149 and R213. Stage III (S > 1.7) corresponds to MTase–GTP positioning towards a binding mode right before the N⁷-MTase reaction, where a clear energy well could be observed for R84, H110 and SAM.

The relative interaction energy curves of the conserved GTP-pocket residues K13, F24, and S215 were similar in shape, describing the contribution of guanosine-binding residues as observed in the crystal structure, which had started to level off as GTP exits the crystallographic state. E149 and R57 have a similar trend when proceeding from S = 1 to S = 2, regardless of the variety of shapes of the curves in the middle of the pathway. The relative interaction energy of R37 along the syn-pathway has a higher degree of fluctuation than along the anti-pathway, and around S = 2 its contribution along the syn-pathway was lower. Such a difference can be explained by the interaction of R37 with the triphosphate group in GTP along the syn-pathway, while R37 flipped away from GTP along the anti-pathway. For Y220, the energy has decreased along the syn-pathway while increased along the anti-pathway.

Profiles of GTP-residue interaction energy along the two sampled pathways imply the contribution of MTase residues in the GTP reposition process, which provides the reason for the experimentally observed residue contribution in the orthoflavivirus N⁷-MTase reaction.⁸ Multiple pathways and conformations were considered to identify residues critical for MTase–GTP interactions throughout the repositioning process. If a residue provides a major contribution along only one of the sampled pathways, analysis on only one of the pathways would neglect its contribution. A similar trend in the interaction energy profiles of the same residue between the syn- and anti-pathways could be an indicator of its importance, that is the residue contributes to GTP interaction at a similar magnitude regardless of the pathway taken. These residues include R57, R84, H110 and E149 (Fig. 4). All these residues are conserved in orthoflavivirus (Fig. S1, ESI†), and were identified to be critical in the orthoflavivirus N⁷-MTase activity. R57A, R84A, H110A and E149A mutants of WNV MTase were reported to have only 13%, 4%, 10% and 2% of N⁷-MTase activities, respectively.⁸ R84 in the RNA-binding site rich in basic residues mainly interacted with the triphosphate group of GTP in our simulations. H110 provides an additional platform for GTP to have a more stable binding pose as it approaches the methyl donor SAM. As we investigate the interaction between GTP and E149 at different states identified on the FES of sampled pathways, we observed that the sidechain of E149 could assist in the movement of GTP along the pathway from the GTP-pocket to the N⁷-methylation state. Representative coordinates around S = 1.11 in the syn-pathway (Fig. 3D, syn-2) and S = 1.25 in the anti-pathway (Fig. 3H, anti-3) displayed a similar geometry of GTP but only the latter displayed hydrogen bonds between GTP and E149. Along the syn-pathway, E149 formed hydrogen bonds with GTP guanine at S = 1.93 instead (Fig. 3D, syn-5). The difference in the hydrogen bonding state with E149 sidechain carboxylate at different points on the path revealed the possible role of E149 in aligning GTP for the N⁷-MTase reaction.

Considering the interaction energy between the whole MTase protein and GTP, we observed that the relative interaction energy of MTase–GTP increased from S = 1 to S = 2 (Fig. 4, MTase). The interaction energy increased more along the anti-pathway than the syn-pathway. Interestingly, as we include SAM as part of the receptor, the difference in interaction energy at S = 1 and S = 2 became close to zero, and the energy around S = 2 was now lower along the anti-pathway than the syn-pathway (Fig. 4, MTase + SAM). Interactions between GTP and SAM implied the preference in the binding mode at the state of the N⁷-MTase action. The relative interaction energy between GTP and SAM was more negative along the anti-pathway, particularly at Stages II–III. As the system approaches State 2, a more negative interaction energy between GTP and SAM could be observed in the anti-pathway (Fig. 4, SAM). At S = 2 of the syn-pathway, the GTP–SAM interaction energy was −25 kcal mol⁻¹ lower than State 1, where the distance between atom N⁷ of GTP and atom CE of SAM was 3.1 Å. Around S = 2 along the anti-pathway, SAM and GTP had more favorable interactions; from S = 1 to S = 2, the interaction energy has decreased for −75 kcal mol⁻¹. Either or both of the samples of State 2 could be a metastable state before the N⁷-MTase reaction.

Assessment of US-sampled conformations around State 2

Since it was challenging to deduce which pathway would be more probable from the FES and residue contribution along CVs that represents the process of GTP transition, we further attempted to evaluate the conformations with the concept of near-attack conformation (NAC). NAC and related models elucidate that when reactants are pre-organized and the local environment of the enzyme re-organized, stabilizing conformations close to the transition state and hence the energy barrier of the reaction can be reduced.^57,58 Various structural studies supported the mechanism of orthoflavivirus MTase to position the N7 nitrogen for nucleophilic attack on the SAM methyl group,⁸ which is also supported by the previous computational model¹⁵ and our current work. Generic mechanisms of the N⁷-MTase reaction supported by experimental studies of eukaryote MTase Ecm1⁵⁹ suggest an in-line mechanism driven by the substrate, which is consistent with the NAC-related concepts. Adapting this concept, we further assessed the relevance of the conformation around State 2 sampled along the syn-pathway and the anti-pathway of the N⁷-MTase enzymatic reaction by comparing the following two parameters: (1) the distance from atom N⁷ in GTP to the methyl carbon, atom CE of SAM (D₁), and (2) the S–CE–N⁷ angle formed by the central chiral sulfur atom S in SAM, methyl carbon CE in SAM, and atom N⁷ in GTP (Fig. 5A and F, top panel).

Fig. 5 (A) and (F) Close-up snapshot of the conformations around State 2 from a perspective slightly different from Fig. 3, syn-6 and anti-6, using a similar color scheme to that in Fig. 3 and labeling the N⁷_GTP–CE_SAM distance (D₁) and the S_SAM–CE_SAM–N⁷_GTP angle (upper panel), and the 2D-FES along D₁ and the S_SAM–CE_SAM–N⁷_GTP angle (lower panel). (B), (C), (G) and (H) 2D-FES of the first three principal components PC1–PC3 from the PCA analysis of MTase C_α coordinate samples showing the distinct conformational spaces sampled along the syn- and anti-pathway. (D), (E), (I) and (J) 2D-FES showing the correlation of PC1/PC2 with path CV, S. (K) Cyan arrows illustrating the scaled eigenmodes of the first three PCs using the normal mode wizard in VMD. Trace of protein C_α is shown as a tube and colored by the mobility with white being lower mobility and black being higher mobility. GTP (pink) and SAM (yellow) from the initial structure were aligned onto the model to show the position of binding sites.

The distance D₁ in syn-6 and anti-6 was 3.1 Å and 4.2 Å, respectively, whereas their respective S–CE–N⁷ angles were 95.5° and 67.1°. Beyond the minima, the syn-pathway further sampled an S–CE–N⁷ angle of up to 136° with D₁ < 2, and the anti-pathway sampled up to 132° (Fig. 5A and F, lower panel). While there is limited literature on the methyl-transfer process of the exact system as this work, the analogous system can be useful for comparison. Our trajectory samples from the syn-pathway has an S–CE–N⁷ angle of up to 136° aligned closely with the reactant geometry reported by Roca et al.⁶⁰ in their hybrid quantum-mechanical/molecular-mechanical (QM/MM) model of catechol O-methyltransferase (COMT), which exhibited an S–CE–N⁷ angle of 138.6°. This similarity suggests that the pathway captured reactant conformations favourable to methyl transfer, though it deviates from the transition state S–CE–N⁷ angle (165.1°) observed in COMT.⁶⁰ Moreover, the commonly referenced N⁷-MTase model by Fabrega et al.⁵⁹ from the superposition of Ecm1-SAM and Ecm1-GTP complexes had an S–CE–N⁷ angle of 168°, indicating a transition state-like alignment. The angles sampled by the syn-pathway of our study, despite not yet being optimal, reflected a pre-organized state approaching the NAC required for efficient catalysis. The syn-conformation has been sampled in 17 out of 20 GaMD trajectories as GTP successfully exited the crystallographic state (Fig. S5, ESI†), indicating that the conformation is highly accessible. The proximity to COMT's reactant geometry and partial alignment toward Ecm1's transition state angle suggests that our models were mechanistically pertinent, capturing an early stage of substrate alignment critical for reducing the energy barrier. We note that the energy barrier of this reposition event was lower compared to that of methyl transfer (15–20 kcal mol⁻¹),⁶⁰ which assumes correct positioning of guanine N⁷. We observe that both the minima conformations located from the 2D-FES around state 2, syn-6 and anti-6, yet to approach the reactant geometry, although syn-6 is closer than anti-6. Since the N⁷-MTase reaction also requires the RNA SLA structure, we believe that RNA would contribute to further stabilize the NAC closer to the transition state. Thus, the process of GTP reposition from the crystallographic pocket to the N⁷-MTase catalytic site reported in this work could reveal useful insights into the enzymatic mechanism of orthoflavivirus N⁷-MTase.

Correlation of the MTase global conformational changes along GTP reposition pathways

We further investigated the global changes in MTase conformations during each of the GTP reposition events to understand the role of protein dynamics in the process. The complex relationship between the global dynamics of the protein and GTP reposition has been revealed by analyzing the FES derived from PCA analysis on the motions of MTase C_α from the syn- and anti-pathway. The reweighted 2D-FES of the dominating principal components (PCs) and the 2D-FES of these PCs against the path CV, S, have been provided in Fig. 5B–E for the syn-pathway and in Fig. 5G–J for the anti-pathway. The first three PCs from PCA analysis accounted for 53.42%, 11.58% and 7.80% of the variance, respectively, explaining 72.8% of the variance, thus determined to be sufficient to represent system dynamics. Visualizing the eigenmodes of the PCs, we observed major conformational changes of the flexible helix E38-K45, the flexible loop gating the SAM-pocket particularly conserved residues H110 and E111, and N-terminal residues (Fig. 5K). The MTase protein has sampled different conformational space in the US trial of the syn- and the anti-pathway, as indicated by the PCA projection. US trajectories from the syn-pathway sample a broad range of values along PC1, PC2 and PC3 (Fig. 5B and C), while along PC2 the values diverged more along the anti-pathway (Fig. 5G and H). Notably, the two pathways occupied distinct regions of PC1and PC3.

Examination of the 2D-FES of the PCs along the path CV S showed a positive correlation between the global conformational changes and the GTP reposition process. At state 1 (S = 1), both systems sampled a state with PC1 around −10. Along the syn-pathway, path CV S and PC1 projections displayed a strong linear correlation from weighted linear regression (Fig. 5D and Fig. S9, R² = 0.94, ESI†). In contrast, the anti-pathway correlated more strongly with PC2 than PC1. Along the anti-pathway, the minimum of the 2D-FES around S = 1 and S = 2 was around PC1 = −10. The shape of the 2D-FES is more complicated considering the changes of path CV along PC2, as the two pathways started at different positions along PC2 at S = 1. Along the syn-pathway, PC2 projections decreased from PC2 = 11 at S = 1 to PC2 = −5 at S = 1.4, and then gradually proceeded to a narrow minimum in the FES around PC2 = −3 at S = 2. Along the anti-pathway, PC2 had a sharp decrease from PC2 = 5 at S = 1 to PC2 = −10 at S = 1.2, and then gradually increased to show two broader minima around PC2 = −5 and PC2 = 5 when approaching S = 2. These results suggested the strong correlation between global conformational changes and the GTP reposition process for the syn-pathway as PC1 captured major functional motions, particularly for the syn-pathway with PC1. The complex FES on PC2 suggested multiple metastable states in this process.

Conclusions

In this work, GaMD and US have been combined to investigate the interactions between orthoflavivirus MTase and the substrate analogue GTP. Through the energy change along the repositioning pathway and the visualization of the mode of interactions, our results have provided an explanation on protein residue contributions to the N⁷-MTase reaction reported in experimental literature. Through the analysis of residue contribution along the pathways of GTP repositioning, we were able to explain the roles of E149 and R84 in the pathway towards the N⁷-MTase reaction, of which the interactions of the two residues with GTP cannot be observed in experimental structures. Contributions of the MTase–GTP interactions out of the experimentally identified GTP-pocket also potentially reveal the design of GTP-analogue inhibitors. The mechanisms of inhibition of reported flexible nucleoside analogues such as acyclovir^61,62 should be investigated to assess the benefits of considering contributions of residues along the potential repositioning pathways. Assessment of the alignment of the N⁷-MTase reactants around the site of the N⁷-MTase reaction suggested that the conformation(s) sampled from the syn-pathway would likely be more probable based on the current results. The correlation of the global conformational changes with GTP reposition events confirmed the contribution of the flexible protein in this process. The updated insights into the enzymatic functions and actions of its inhibitors obtained from these works could furnish a new perspective to the rational design of MTase-targeted inhibitors.

Abbreviations

cMD	Conventional MD
COMT	Catechol O-methyltransferase
CV	Collective variables
DENV	Dengue virus
FES	Free energy surface
GaMD	Gaussian-accelerated molecular dynamics
GTP	Guanosine-5′-triphosphate
MD	Molecular dynamics
MTase	Methyltransferase
NAC	Near-attack conformation
OHFV	Omsk hemorrhagic fever virus
PCA	Principal component analysis
QM/MM	Hybrid quantum-mechanical/molecular-mechanical
RdRp	RNA-dependent RNA polymerase
SAH	S-adenosyl-L-homocysteine
SAM	S-adenosyl-L-methionine
SLA	Stem loop A
US	Umbrella sampling
WHAM	Weighted histogram analysis method
WNV	West Nile virus
YEFV	Yellow fever virus
ZIKV	Zika virus

Data availability

Additional data supporting this article and input parameters of simulations have been included as part of the ESI.† The code for Amber and AmberTools can be found at https://ambermd.org/. The version of the code employed for this study is version 21. The code for Plumed can be found at https://www.plumed.org/. The version of the code employed for this study is version 2.7.6. R.E.D. Server Development can be found at https://upjv.q4md-forcefieldtools.org/REDServer-Development/. The version of the code employed for this study is version 2. The code for ORCA can be found at orcaforum.kofo.mpg.de. The version of the code employed for this study is version 4.2.1. This study was carried out using publicly available structural data from the RCSB PDB at https://www.rcsb.org/ with accession numbers 5GOZ and 5KQR.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors would like to thank the Research Grants Council of Hong Kong for funding (General Research Fund #12302622). L. W. N. would also like to thank the Hong Kong Baptist University for the financial support.

References

1. T. S. Postler, M. Beer, B. J. Blitvich, J. Bukh, X. de Lamballerie, J. F. Drexler, A. Imrie, A. Kapoor, G. G. Karganova, P. Lemey, V. Lohmann, P. Simmonds, D. B. Smith, J. T. Stapleton and J. H. Kuhn, Arch. Virol., 2023, 168(9), 224.
2. WHO, 2016, https://www.who.int/emergencies/zika-virus/timeline/en/, (accessed Jul 14, 2020).
3. B. D. Lindenbach and C. M. Rice, Flaviviridae: the viruses and their replication, in Fields virology, ed. D. M. Knipe, P. M. Howley, D. E. Griffin, R. A. Lamb, M. A. Martin, B. Roizman and S. E. Straus, Lippincott, Williams & Wilkins, Philadelphia, Pa., 4th edn, 2001, pp. 991–1041.
4. A. Bateman, M.-J. Martin, S. Orchard, M. Magrane, S. Ahmad, E. Alpi, E. H. Bowler-Barnett, R. Britto, H. Bye-A-Jee, A. Cukura, P. Denny, T. Dogan, T. Ebenezer, J. Fan, P. Garmiri, L. J. da Costa Gonzales, E. Hatton-Ellis, A. Hussein, A. Ignatchenko, G. Insana, R. Ishtiaq, V. Joshi, D. Jyothi, S. Kandasaamy, A. Lock, A. Luciani, M. Lugaric, J. Luo, Y. Lussi, A. MacDougall, F. Madeira, M. Mahmoudy, A. Mishra, K. Moulang, A. Nightingale, S. Pundir, G. Qi, S. Raj, P. Raposo, D. L. Rice, R. Saidi, R. Santos, E. Speretta, J. Stephenson, P. Totoo, E. Turner, N. Tyagi, P. Vasudev, K. Warner, X. Watkins, R. Zaru, H. Zellner, A. J. Bridge, L. Aimo, G. Argoud-Puy, A. H. Auchincloss, K. B. Axelsen, P. Bansal, D. Baratin, T. M. Batista Neto, M.-C. Blatter, J. T. Bolleman, E. Boutet, L. Breuza, B. C. Gil, C. Casals-Casas, K. C. Echioukh, E. Coudert, B. Cuche, E. de Castro, A. Estreicher, M. L. Famiglietti, M. Feuermann, E. Gasteiger, P. Gaudet, S. Gehant, V. Gerritsen, A. Gos, N. Gruaz, C. Hulo, N. Hyka-Nouspikel, F. Jungo, A. Kerhornou, P. Le Mercier, D. Lieberherr, P. Masson, A. Morgat, V. Muthukrishnan, S. Paesano, I. Pedruzzi, S. Pilbout, L. Pourcel, S. Poux, M. Pozzato, M. Pruess, N. Redaschi, C. Rivoire, C. J. A. Sigrist, K. Sonesson, S. Sundaram, C. H. Wu, C. N. Arighi, L. Arminski, C. Chen, Y. Chen, H. Huang, K. Laiho, P. McGarvey, D. A. Natale, K. Ross, C. R. Vinayaka, Q. Wang, Y. Wang and J. Zhang, Nucleic Acids Res., 2022, 51, D523–D531.
5. F. Sievers, A. Wilm, D. Dineen, T. J. Gibson, K. Karplus, W. Li, R. Lopez, H. McWilliam, M. Remmert, J. Söding, J. D. Thompson and D. G. Higgins, Mol. Syst. Biol., 2011, 7, 539.
6. X. Robert and P. Gouet, Nucleic Acids Res., 2014, 42, W320–W324.
7. H. Dong, D. Ray, S. Ren, B. Zhang, F. Puig-Basagoiti, Y. Takagi, C. K. Ho, H. Li and P.-Y. Shi, J. Virol., 2007, 81, 4412–4421.
8. H. Dong, S. Ren, B. Zhang, Y. Zhou, F. Puig-Basagoiti, H. Li and P.-Y. Shi, J. Virol., 2008, 82, 4295–4307.
9. M. Issur, B. J. Geiss, I. Bougie, F. Picard-Jean, S. Despins, J. Mayette, S. E. Hobdey and M. Bisaillon, RNA, 2009, 15, 2340–2350.
10. B. J. Geiss, A. A. Thompson, A. J. Andrews, R. L. Sons, H. H. Gari, S. M. Keenan and O. B. Peersen, J. Mol. Biol., 2009, 385, 1643–1654.
11. M. Milani, E. Mastrangelo, M. Bollati, B. Selisko, E. Decroly, M. Bouvet, B. Canard and M. Bolognesi, Antiviral Res., 2009, 83, 28–34.
12. B. R. Henderson, B. J. Saeedi, G. Campagnola and B. J. Geiss, PLoS One, 2011, 6, e25795.
13. P. J. Bujalowski, W. Bujalowski and K. H. Choi, Sci. Rep., 2020, 10, 13306.
14. K. H. Choi, Viruses, 2021, 13, 1107.
15. H. Jia, Y. Zhong, C. Peng and P. Gong, J. Virol., 2022, 96(14), e00418-22.
16. T. Osawa, M. Aoki, H. Ehara and S. Ichi Sekine, Mol. Cell, 2023, 83, 2781–2791.
17. Y. Zhao, T. S. Soh, S. P. Lim, K. Y. Chung, K. Swaminathan, S. G. Vasudevan, P.-Y. Shi, J. Lescar and D. Luo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14834–14839.
18. K. Y. Chung, H. Dong, A. T. Chao, P.-Y. Shi, J. Lescar and S. P. Lim, Virology, 2010, 402, 52–60.
19. M. Chagas, W. Rocha and A. Moraes, J. Biomol. Struct. Dyn., 2020, 39, 5526–5538.
20. C.-H. Chuang, S.-J. Chiou, T.-L. Cheng and Y.-T. Wang, Sci. Rep., 2018, 8, 6336.
21. G. Díaz Leines and B. Ensing, Phys. Rev. Lett., 2012, 109, 020601.
22. D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, C. Jin, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman,T.S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O’Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, 2021, Amber 2021, University of California, San Francisco.
23. RCSB PDB, https://rcsb.org, (accessed Feb 6, 2020).
24. H++ Server, https://biophysics.cs.vt.edu/H++, (accessed Mar 29, 2020).
25. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
26. G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, J. Comput. Chem., 2009, 30, 2785–2791.
27. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461.
28. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
29. K. L. Meagher, L. T. Redman and H. A. Carlson, J. Comput. Chem., 2003, 24, 1016–1025.
30. Amber Parameter Database, https://amber.manchester.ac.uk/index.html, (accessed Jul 15, 2021).
31. F. Neese, WIREs Comput. Mol. Sci., 2011, 2, 73–78.
32. F. Neese, WIREs Comput. Mol. Sci., 2017, 8(1), e1327.
33. N. M. OBoyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
34. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
35. F. Wang, J.-P. Becker, P. Cieplak and F.-Y. Dupradeau, R.E.D. Python: Object oriented programming for Amber force fields, Université de Picardie - Jules Verne, Sanford Burnham Prebys Medical Discovery Institute, 2013.
36. E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, Nucleic Acids Res., 2011, 39, W511–W517.
37. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
38. S. Le Grand, A. W. Götz and R. C. Walker, Comput. Phys. Commun., 2013, 184, 374–380.
39. R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888.
40. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
41. Y. Miao, V. A. Feher and J. A. McCammon, J. Chem. Theory Comput., 2015, 11, 3584–3595.
42. J. Wang, P. R. Arantes, A. Bhattarai, R. V. Hsu, S. Pawnikar, Y. Ming, M. Huang, G. Palermo and Y. Miao, WIREs Comput. Mol. Sci., 2021, 11(5), e1521.
43. W. You, Z. Tang and C. A. Chang, J. Chem. Theory Comput., 2019, 15, 2433–2443.
44. Y. Miao, A. Bhattarai and J. Wang, J. Chem. Theory Comput., 2020, 16, 5526–5547.
45. A. Bhattarai, S. Pawnikar and Y. Miao, J. Phys. Chem. Lett., 2021, 12, 4814–4822.
46. H. Girame, M. Garcia-BorrÃs and F. Feixas, Front. Mol. Biosci., 2022, 9, 922361.
47. D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095.
48. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
49. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
50. The PLUMED Consortium, Nat. Methods, 2019, 16, 670–673.
51. Schrödinger, LLC, The PyMOL Molecular Graphics System, Version 2.6.0a0.
52. A. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
53. Y. Miao, W. Sinko, L. Pierce, D. Bucher, R. C. Walker and J. A. McCammon, J. Chem. Theory Comput., 2014, 10, 2677–2689.
54. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1995, 16, 1339–1350.
55. M. Souaille and B. Roux, Comput. Phys. Commun., 2001, 135, 40–57.
56. Z. Tan, E. Gallicchio, M. Lapelosa and R. M. Levy, J. Chem. Phys., 2012, 136(14), 144102.
57. T. C. Bruice, Acc. Chem. Res., 2002, 35, 139–148.
58. S. Hur and T. C. Bruice, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12015–12020.
59. C. Fabrega, S. Hausmann, V. Shen, S. Shuman and C. D. Lima, Mol. Cell, 2004, 13, 77–89.
60. M. Roca, S. Martí, J. Andrés, V. Moliner, I. Tuñón, J. Bertrán and I. H. Williams, J. Am. Chem. Soc., 2003, 125, 7726–7737.
61. D. Benarroch, M.-P. Egloff, L. Mulard, C. Guerreiro, J.-L. Romette and B. Canard, J. Biol. Chem., 2004, 279, 35638–35643.
62. J. E. Thames, C. D. Waters, C. Valle, M. Bassetto, W. Aouadi, B. Martin, B. Selisko, A. Falat, B. Coutard, A. Brancale, B. Canard, E. Decroly and K. L. Seley-Radtke, Bioorg. Med. Chem., 2020, 28, 115713.

---

Footnote

† Electronic supplementary information (ESI) available: Boost statistics of each independent GaMD trial, sequence conservation of representative species in the genus Orthoflavivirus, CV plots of each independent GaMD trial, illustration of guanine orientation with respect to the MTase protein, linear fitting of PC1 and S from the US of the syn-pathway, and input parameters of MD simulations. See DOI: https://doi.org/10.1039/d5cp00438a

---