Assessment of a foundational machine-learned potential for energy ranking of molecular crystal polymorphs

Abstract

First-principles crystal structure prediction (CSP) of isolable polymorphs of organic compounds is a grand challenge in computational chemistry. The adoption of dispersion-correction density-functional theory (DFT) has allowed great strides to be made in the accuracy of the final energy ranking of candidate crystal structures. Consequently, CSP methods are seeing increasing use in development of new pharmaceuticals, organic electronics, energetic materials, and pigments, among other applications. However, lower-cost methods, such as classical force-field potentials, are still necessary for the early stages of CSP, where hundreds of thousands of candidates are commonly generated. Recently developed foundational machine-learned potentials represent a seductive alternative to force fields for this purpose due to their promise of near-DFT accuracy at a vastly reduced computational cost. In this work, the performance of the MACE-OFF23(M) machine-learned potential is assessed for geometry optimisation and energy ranking of candidate crystal structures of 28 compounds from the first seven CSP blind tests, as well as 12 helicene compounds. The performance of MACE-OFF23(M) is found to be highly dependent on the particular compound, providing good accuracy for compounds similar to those in its training set, but failing dramatically for compounds containing unusual functional groups (such as diazo) and organic salts. Physically motivated inclusion of long-range electrostatic interactions remains an open problem for development of foundational machine-learned potentials.

---

1. Introduction

Often, more than one crystal structure can be formed from the same molecule. This phenomenon, known as polymorphism, has important consequences in industry because different polymorphs can have distinct physical properties, such as their color, solubility, electronic properties, etc. For example, pharmaceutical companies need to screen for polymorphs of the solid-form drugs that they develop to ensure that they identify (and patent) all isolable crystal structures. Consequently, there is a large incentive to develop methods for predicting possible polymorphs a priori to help avoid late-appearing¹ or “disappearing” polymorphs,² which can have devastating costs.

Crystal structure prediction (CSP)^3–7 uses the tools of computational chemistry to suggest the polymorphs that are most likely to be observed experimentally, given only a 2D diagram of the molecule. The typical process for a CSP study begins by generating an enormous landscape of pseudo-random candidate crystal structures, possibly in the range of 10⁶–10⁷ structures. The landscape is then narrowed down to the few hundred structures with the lowest potential energies according to a classical force field, or other low-cost method. Use of a low-cost method at this stage is necessary due to the vast numbers of structures involved, but they are not typically accurate enough to predict the correct stability rankings. Thus, the remaining structures then have their potential energies re-evaluated using dispersion-corrected density-functional theory (DFT-D), which is more accurate but comes with a significantly increased computational cost. Finally, all candidates within a certain threshold (perhaps ∼5 kJ mol⁻¹) of the minimum-energy structure are deemed as likely polymorphs.

The adoption of density-functional theory for the final energy ranking stage has led to much of the current success in CSP.^6–13 For example, our group has obtained highly accurate lattice energies for molecular crystals using hybrid DFT in conjunction with the XDM¹⁴ dispersion correction.^15,16 These studies employed the FHI-aims software package,^17–19 which uses numeric atom-centered orbitals (NAOs) for its basis functions.

While DFT-D has been established as the state of the art for obtaining accurate lattice energies for molecular crystals, there is still something to be desired in the way of low-cost methods suitable for use in the initial phases of CSP. Unfortunately, the degree of error when using empirical force fields (or tight-binding DFT) is often much larger than the energy differences between real polymorphs, which can lead to the correct structure being discarded before making it to the DFT phase of the study.²⁰ One potential avenue for improved low-cost energy-ranking methods is the emergence of machine-learned potentials as a possible alternative to empirical force fields.

There exist a number of machine-learned potentials that have been developed for organic chemistry, the most noteworthy of which are the series of ANI^21–24 and AIMNet potentials.^25–27 ANI makes use of neural networks based on local symmetry functions²⁸ to create transferable potentials. In recent years, the ANI-2X model has become the most widely adopted machine-learned force field. The AIMNet models make use of a message passing architecture²⁹ and they extend their applicability to a larger selection of chemical elements, as well as to charged species. Both ANI-2X and AIMNet were utilized for energy ranking by two groups in the seventh CSP blind test;^30,31 however, both of these groups began by enhancing the model with further training. Results showed that the system-specific AIMNet machine-learned potentials ranked consistently well, whereas the other machine-learned methods performed inconsistently.

MACE-OFF23³² is a recently developed set of machine-learned potentials for organic molecules that demonstrates improved accuracy compared to the ANI-2X model. More specifically, MACE-OFF23 encompasses a series of three distinct machine-learned potentials denoted (S)mall, (M)edium, and (L)arge, which are designed to provide three different levels of accuracy and cost. Like the ANI models, the MACE method makes use of only the local atomic environment of each atom in order to calculate the energy. MACE-OFF23 was trained primarily to a subset of the SPICE dataset,³³ consisting of only neutrally charged species composed of up to ten elements: H, C, N, O, F, P, S, Cl, Br, and I. SPICE contains slightly over 1.1 million conformers of selected small molecules, molecular dimers, dipeptides, and solvated amino acids, and uses reference energies and forces computed at the ωB97M-D3(BJ)^34–36/def2-TZVPPD level of theory. Additionally, MACE-OFF23 was also trained on some larger systems (composed of 50–90 atoms) from the Qmugs³⁷ dataset, as there were no systems of this size present in SPICE. Qmugs consists of minimum-energy conformations of 665 000 neutral molecules comprised of the same 10 elements noted above. In the development of MACE-OFF23, the energies and forces of these molecules were reevaluated using the same level of theory as used for the SPICE reference data.

The MACE-OFF23 potential is of particular interest to us because of its proposed applicability for molecular crystals. In their work, the creators of MACE-OFF23 tested its performance on several distinct tasks, which included predicting lattice parameters and sublimation enthalpies for the X23 set^38,39 of molecular crystals. For these systems, MACE-OFF23(M) resulted in a mean absolute error (MAE) of only 7.5 kJ mol⁻¹ when comparing the computed sublimation enthalpies to experimental data;³² this represents a massive improvement compared to ANI-2X, which gave a MAE of 20.5 kJ mol⁻¹. For comparison, the best dispersion-corrected DFT methods typically give MAEs of 2–5 kJ mol⁻¹ for the X23 benchmark.^16,38,39 This suggests that MACE-OFF23 may be directly applicable to molecular polymorph ranking without the need for additional system-specific training.

Ideally, a universal ML potential such as MACE-OFF23(M) could be a direct replacement for the FIT⁴⁰ or W99⁴¹ classical force fields, which are routinely used in CSP without parameterization. We wish to avoid any system-specific training of the ML potential (akin to construction of tailor-made force fields⁴²) as this would requires extensive DFT reference data to be generated at the outset of a CSP study. In the usual hierarchical CSP workflow, DFT calculations are performed only in the final stages, on a small set of low-energy candidates already identified by the force field. Any initial system-specific training of the ML potential to DFT would drastically increase both the complexity and computational cost and, thus, is not desirable for practical first-principles CSP on new compounds. For CSP applications, this makes bespoke ML potentials impractical and less appealing compared to foundational models that are broadly applicable to organic chemistry.

The goal of the present work is to further test the applicability of the MACE-OFF23(M) potential for molecular crystals in order to assess whether it will be a good choice as the initial energy ranking method in CSP studies going forward. Specifically, we considered the ability of the MACE-OFF23 potential to reproduce DFT geometries and relative energies for two sets of molecular crystal polymorphs: 28 organic compounds from the seven CSP blind tests^{9,20,30,31,43–46} and 12 helicene compounds.^47,48 The results presented here will help researchers decide whether or not to use MACE-OFF23(M) as an alternative to empirical force fields in the early stages of a CSP protocol.

2. Data sets

Two distinct sets of compounds were considered in this work. The first data set spans 28 compounds from the seven CSP blind tests organized by the Cambridge Crystallographic Data Centre (CCDC).^{9,20,30,31,43–46} While a total of 33 targets have appeared in the blind tests to date, compounds III, XXVII, and XXVIII were excluded as they contain elements for which the MACE-OFF23(M) potential was not trained (B, Si, and Cu, respectively). Also, compounds XXIX and XXX were excluded as these were the experimentally assisted and stoichiometry challenges from the seventh blind test and were not included in the energy-ranking stage.³⁰ The second set of compounds includes the [n] helicenes with n = 2–12, along with 1-aza[6]helicene, which have been the subject of previous CSP studies by our group.^47,48 The structures of the considered compounds are shown in Fig. 1 and 2.

Fig. 1 Structures of all blind test compounds considered in this work. The boxes encapsulate the various components for cocrystals and salts.

Fig. 2 Structures of selected helicene compounds considered in this work; structures for [n]helicenes with n = 7–12 are not shown due to the difficulty of representing their helical structures in two dimensions.

Sets of candidate crystal structures were obtained from the ESI† of ref. 15 for blind-test compounds I–XXVI, ref. 49 for blind-test compounds XXXI–XXXIII, ref. 47 for the [n] helicenes, and ref. 48 for 1-aza[6]helicene. All of these structures were already fully geometry optimized with the B86bPBE density functional,^50,51 the XDM dispersion correction,^14,16 and the ‘lightdenser’ basis set and integration grid settings, using a modified copy of FHI-aims¹⁷ version 210513. The one exception was 1-aza[6]helicene, where the geometries had previously been optimized with the same functional, but with a planewave basis set, using Quantum ESPRESSO.⁵² The 1-aza[6]helicene structures were consequently re-optimized here using the same methodology as above for consistency.

3. Computational methods

Geometries of all candidate crystal structures were re-optimized from the DFT starting point using the MACE-OFF23(M) potential³² and the atomic simulation environment (ASE)⁵³ python modules. Atomic positions and lattice vectors were optimized using the PreconLBFGS algorithm to a force tolerance of 0.2 eV Å⁻¹ (although this value was changed in a very few cases that proved difficult to converge), followed by the LBFGS algorithm to a tighter force tolerance of 0.005 eV Å⁻¹, the same as used in the previous FHI-aims optimizations.^15,47,49 A total of five candidate structures (one for compound XII and four for compound XXII) gave extremely large initial forces with MACE-OFF23(M). Closer examination revealed that these were all Z = 1 structures (i.e. a single molecule within the unit cell), and optimizations on a 2 × 2 × 2 supercell proceeded normally. This may have occurred because the Z = 1 unit-cell dimensions are smaller than the cutoff distances defining the atomic environments within MACE-OFF23(M).

Single-point energy evaluations were then performed on (i) the MACE-OFF23(M) optimized structures and (ii) the B86bPBE-XDM optimized structures using version 240206 of FHI-aims.^17,18 The B86bPBE0-XDM hybrid functional¹⁶ (25% exact exchange) was used for the blind test compounds, while the B86bPBE-XDM functional was used for the helicenes, as in our previous works.^15,47,49 The lightdense basis set and integration grids were used for both data sets. Due to some modifications to FHI-aims between versions, and the change from the lightdenser (recommended for geometry optimisations) to lightdense basis (recommended for single-point energies), the results for the DFT single-point energies at the DFT geometries are slightly different to those previously reported^15,47,49 in some cases.

When tabulating results, we use the standard energy//geometry notation, where the method used for single-point energies is given first, followed by //, and then the method used for geometry optimization. Thus, MACE//MACE means MACE-OFF23(M) energies evaluated at the MACE-OFF23(M) geometries; DFT//DFT means B86bPBE-XDM or B86bPBE0-XDM energies evaluated at the B86bPBE-XDM geometries, and DFT//MACE means B86bPBE-XDM or B86bPBE0-XDM energies evaluated at the MACE-OFF23(M) geometries. This latter combination is an example of a composite method, which should ideally yield results of similar quality to the high-level method (DFT in this case) used for the single-point energies, with a greatly reduced computational cost compared to performing full geometry optimizations with that high-level method. Composite methods combining DFT with classical force fields have previously shown promise in molecular CSP.⁵⁴ In theory, the DFT//MACE approach should give similar or better results than MACE//MACE in nearly all cases, with the only exceptions being due to accidental error cancellation between the geometry and the energy.

Finally, the similarity of the MACE-OFF23(M) structures, compared to the B86bPBE-XDM reference structures, was evaluated using the variable-cell powder difference (VC-PWDF) method,⁵⁵ as implemented in critic2.⁵⁶ These calculations compare simulated powder X-ray diffractograms of various unit-cell descriptions of a candidate crystal structure to a reference crystal structure using the de Gelder cross-correlation function.⁵⁷ In this case, the candidate is the MACE-OFF23(M) optimized crystal structure and the reference is the B86bPBE-XDM optimized structure. By its construction, VC-PWDF accounts for changes in lattice constants (due to different temperatures, pressures, or computational methods used) when comparing pairs of crystal structures to determine if they are the same form or different polymorphs.

4. Results and discussion

4.1. Crystal geometries

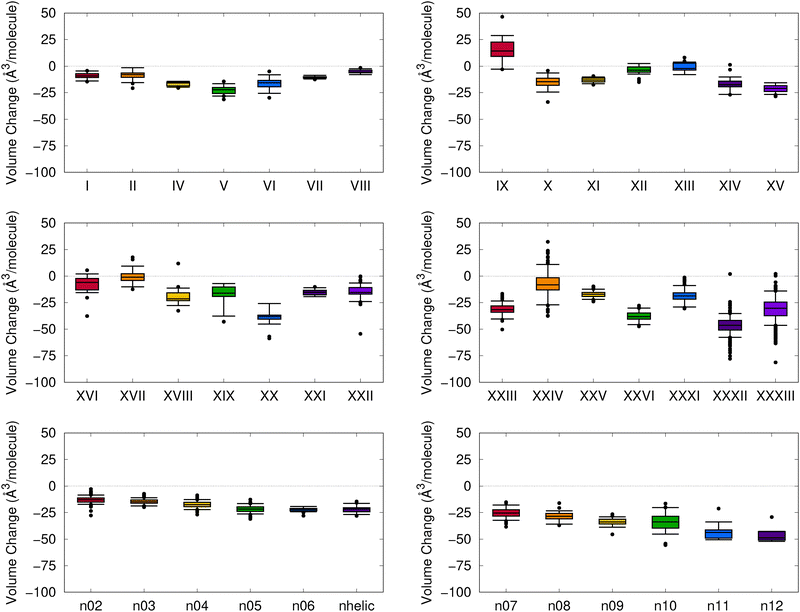
We begin by assessing the degree of change in the molecular crystal geometries upon optimizing their lattice constants and atomic positions with MACE-OFF23(M), as opposed to B86bPBE-XDM. Fig. 3 shows the results of VC-PWDF comparison of the two sets of structures in the form of a box-and-whiskers plot for each compound studied. The VC-PWDF method provides a dissimilarity score, with a value of zero indicating identical crystal structures and a value of one indicating maximum dissimilarity. Thus, if MACE-OFF23(M) provides crystal structures in good agreement with the DFT optimizations, the distribution of computed VC-PWDF values would be very narrowly clustered near zero.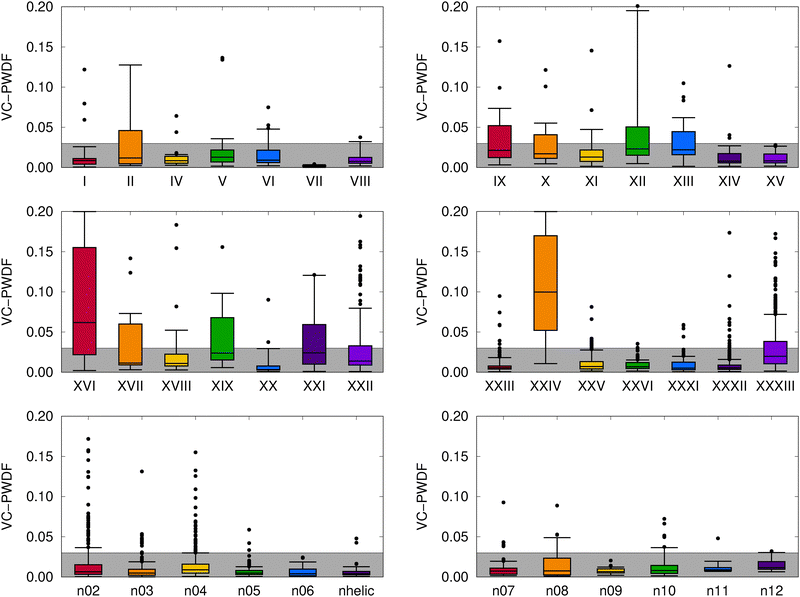

Fig. 3 Distributions of computed VC-PWDF scores obtained for comparison of the MACE-OFF23(M) optimized crystal structures to the reference B86bPBE-XDM optimized crystal structures for each compound. The boxes show the interquartile ranges, the whiskers encompass 90% of the data, and remaining outliers are shown as individual points. The grey box shows the range of VC-PWDF scores where two structures can confidently be deemed the same polymorph (i.e. <0.03).⁵⁵ For visual clarity, the plots are truncated at a VC-PWDF score of 0.2, despite a few outliers having scores exceeding this value. In the bottom row of plots, the [n]helicene structures are denoted by their n value, while “nhelic” refers to 1-aza[6]helicene.

From the results in Fig. 3, it can be seen that the distributions of VC-PWDF scores tend to be tightly clustered near zero for many of the compounds considered. In these cases, there were only minimal geometry changes upon re-optimization with the MACE-OFF23(M) potential, such that the same polymorph was recovered as opposed to a migration to some other polymorph on the potential-energy surface. However, despite generally high packing similarity between the two sets of optimized structures, some of the blind test compounds were notable outliers. These included compounds II, IX, X, XII, XIII, XVII, XIX, XXI, XXII, and XXXIII, although at least half of the structures were still identified as the same polymorph before and after MACE-OFF23(M) optimization based on VC-PWDF scores of <0.03.⁵⁵

The broadest distributions of VC-PWDF scores were observed for compounds XVI and XXIV, where more than half of the structures transitioned to different crystal forms during MACEOFF23(M) optimization. Compound XVI contains a diazo (=N=N) functional group, which is not well represented in the training data, so it is unsurprising that the MACE-OFF23(M) energy landscape differs from the DFT one to the point where many local minima are no longer stable. We note that MACEOFF23(M) shows significantly better performance for compound XVIII, which also contains a diazo group; this is likely due to the other functional groups having a proportionally greater influence on the crystal packing.

The other large outlier, compound XXIV, is a 3-component organic salt. Thus, the poorer performance of MACE-OFF23(M) is again expected as this potential was only trained for neutral molecules and included no ions, let alone ionic solids. Accurate modeling of electrostatic interactions with machine-learned potentials is problematic due to the incompatibility in their length scales—electrostatic interactions decay as −1/r and are inherently long range, while only short-range atomic environment information is typically used as input. This is indeed the case for the MACE-OFF23(M) potential, which uses a radial cutoff of 5.0 A and contains no charge or spin information. Owing to its message-passing architecture, there is a receptive field that allows atoms to exchange information up to 10.0 Å; however, this still remains too short to properly capture electrostatic interactions.³²

The VC-PWDF method is designed to assess whether the two input structures have the same packing and are the same polymorph, while ignoring volume changes.⁵⁵ Thus, low VC-PWDF scores are necessary, but not sufficient, to guarantee that the MACE-OFF23(M) geometries are in good agreement with those obtained with DFT, as significant changes in unit-cell volumes are still possible. Fig. 4 plots the volume changes, expressed per molecule in the unit cell, between the MACE-OFF23(M) optimized structures and the B86bPBE-XDM optimized structures. This plot reveals that the MACE-OFF23(M) unit cells are typically more compact. This error appears quite systematic for the helicenes, where the extent of volume compaction seems to increase with ring size. However, there are some notable exceptions for some of the blind-test compounds, with the cell volumes being consistently overestimated for compound IX, and some structures having expanded volumes for compounds XVII and XXIV. Large spreads in computed volumes between MACE-OFF23(M) and B86bPBE-XDM will likely translate to poorer performance of the composite DFT//MACE approach, which relies on the MACE-OFF23(M) geometries being a good proxy for their DFT counterparts.

Fig. 4 Distributions of volume changes (per molecule) between the MACE-OFF23(M) optimized crystal structures and the reference B86bPBE-XDM optimized crystal structures for each compound. The boxes show the interquartile ranges, the whiskers encompass 90% of the data, and remaining outliers are shown as individual points. In the bottom row of plots, the [n]helicene structures are denoted by their n value, while “nhelic” refers to 1-aza[6]helicene.

4.2. Energy ranking

4.2.1. Blind-test compounds. Table 1 shows the results of polymorph ranking studies performed using MACE-OFF23(M) and a hybrid DFT//MACE approach, compared to DFT reference data. It should be noted that the MACE-OFF23(M) potential was in no way retrained for CSP using this DFT data or any other data. Hence, the comparisons made here are drawn between two independent methodologies, analogous to comparisons between electronic structure theory and experiment. However, experimental energy differences between candidate crystal structures are, naturally, not available since the vast majority of structures generated during CSP are not seen experimentally.

Table 1 Results for selected blind test compounds. Shown are the rankings of the experimental polymorphs and their energies, in kJ mol⁻¹ per molecule, relative to the global minimum identified with each computational method, specified as energy//geometry

Polymorph	MACE//MACE		DFT//MACE		DFT//DFT
	Rank	ΔE	Rank	ΔE	Rank	ΔE
Rigid molecules
I-1	9	3.8	1	0.0	2	0.1
I-2	4	1.2	3	1.3	1	0.0
II	1	0.0	2	1.0	2	0.7
IV	1	0.0	1	0.0	1	0.0
V	1	0.0	3	1.6	4	2.0
VII	1	0.0	1	0.0	1	0.0
VIII	1	0.0	1	0.0	1	0.0
IX	9	16.1	1	0.0	1	0.0
XI	7	2.8	2	0.4	1	0.0
XII	4	1.9	1	0.0	1	0.0
XIII	1	0.0	2	0.0	1	0.0
XVI	2	0.3	16	9.0	1	0.0
XVII	10	4.4	2	0.3	1	0.0
XXII	18	3.9	25	7.0	3	0.4
Multi-component crystals
XV	2	0.3	1	0.0	2	0.6
XXI	1	0.0	2	0.8	1	0.0
XXV	1	0.0	1	0.0	1	0.0
Organic salts
XIX	1	0.0	14	28.5	4	2.3
XXIV	86	60.5	50	31.4	3	0.8
XXXIII-A	93	24.6	7	8.2	4	4.5
XXXIII-B	192	33.5	1	0.0	1	0.0
Flexible molecules
VI	2	1.8	1	0.0	1	0.0
X	12	26.5	1	0.0	2	0.6
XIV	1	0.0	1	0.0	1	0.0
XVIII	2	0.1	1	0.0	1	0.0
XX	3	1.3	6	5.8	4	6.4
XXIII-A	37	8.6	55	6.2	10	2.1
XXIII-B	4	2.2	3	0.3	3	0.5
XXIII-C	1	0.0	1	0.0	2	0.3
XXIII-D	34	8.3	36	4.9	13	2.9
XXIII-E	51	10.7	7	1.6	9	1.9
XXVI	1	0.0	3	0.2	1	0.0
XXXI-AMaj	7	6.6	3	1.8	4	2.5
XXXI-AMin	42	12.5	8	3.0	10	4.2
XXXI-B	6	5.9	18	6.5	12	5.0
XXXI-C	85	19.8	53	11.6	70	11.5
XXXII-AMaj	31	14.9	17	9.2	22	8.8
XXXII-B	135	22.0	19	10.5	26	9.1

---

The reported data in Table 1 are the ranks of all experimentally observed polymorphs (i.e. 1 indicates this is the most stable structure, 2 indicates the second-most stable, and so forth), along with their relative energies above the global minimum obtained with that particular level of theory. As the sets of candidate structures contain duplicates in some cases (i.e. the same crystal structure was generated by multiple groups participating in the blind tests), duplicate structures were eliminated from the energy ranking in Table 1 if they had a powder difference score of less than 0.01 when compared with critic2.⁵⁶ Typically, the experimentally isolated polymorphs would be expected to be among the lowest-ranked structures, with energies within <2 kJ mol⁻¹ of the global minima (with this range combining both expected uncertainties in the DFT relative energies and the magnitude of thermal free-energy corrections,⁵⁸ which are neglected here). However, there are some exceptions where experimental screening can result in formation of metastable polymorphs, for example due to solvent loss from a solvate, as in the case of polymorph C of compound XXXI.³⁰

To aid assessment of the performance of the MACE-OFF23(M) and DFT//MACE approaches, the results in Table 1 are divided into four groups based on the types of compounds included in the blind tests. These groups are rigid molecules, multi-component crystals composed of neutrally charged molecules (i.e. cocrystals and solvates), organic salts, and flexible molecules with multiple rotatable bonds. Molecules are considered to be rigid if they have no rotatable bonds, other than those that result in changing only H-atom positions (as in compound II), or when steric factors prevent rotation (as in XVII).

The results in Table 1 show that MACE-OFF23(M) performs somewhat well for the majority of the rigid molecules, ranking the experimental structure within 2 kJ mol⁻¹ of the minimum in 9/14 cases, and within 5 kJ mol⁻¹ of the minimum in another 4 cases. The only large outlier is compound IX, where the experimental structure is predicted to lie 16.1 kJ mol⁻¹ above the MACE-OFF23(M) energy minimum. Notably, IX is the only compound in our data set than contains iodine, so perhaps this element was insufficiently well represented in the original SPICE and Qmugs data used to train the MACE-OFF23(M) potential. Coincidentally, it is also the only compound for which MACE-OFF23(M) consistently overestimates the unit-cell volumes (Fig. 4).

The DFT//MACE composite approach also appears promising for rigid molecules, with the experimental structure being ranked first, second, or third, and lying within 2 kJ mol⁻¹ of the minimum-energy structure in 12/14 cases. The only two exceptions are compounds XVI and XXII, where the experimental polymorphs are 9 and 7 kJ mol⁻¹, respectively, above the corresponding minimum. For compound XXII, Fig. 3 shows that the distribution in VC-PWDF scores is clustered near zero, indicating generally high similarity between the MACE-OFF23(M) and B86bPBE-XDM structures, and this includes the experimental structure. However, this compound does contain three cyano (C≡N) groups, a fused ring system with three sulfur atoms, and no hydrogens, so it is quite far removed from the compounds in the SPICE training set.

Compound XVI includes the diazo (=N=N) functional group and, as noted above, is one of the two cases showing large deviations between the MACE-OFF23(M) and B86bPBE-XDM geometries. It is, therefore, expected that this would be a problem case for the DFT//MACE composite method. The VC-PWDF score obtained from comparing the MACE-OFF23(M) and B86bPBE-XDM optimized structures for the experimental polymorph is 0.184, and COMPACK comparison^59,60 yields only a 2/20 molecule match. This indicates a change in form upon MACE-OFF23(M) optimization, meaning that the experimental polymorph is not a stable minimum with the machine-learned potential. Thus, using MACE-OFF23(M) in the initial stages of CSP would cause the experimental structure of compound XVI to be missed. Reoptimization of the MACE-OFF23(M) “experimental” structure with B86bPBE-XDM gives a yet another structure, with a 16/20 molecule match with COMPACK, and a VC-PWDF score of 0.061, compared to the MACE-OFF23(M) result.

For the three neutral co-crystals, the results in Table 1 show that both the MACE-OFF23(M) and DFT//MACE methods perform very well. The experimental polymorphs are ranked either first or second in energy, within 1 kJ mol⁻¹ of the minimum, in each case. Conversely, the results for the three organic salts are extremely poor. While MACE-OFF23(M) happens to identify the experimental polymorph as lowest in energy for compound XIX, isolated forms are ranked 86th, 93rd, and 192nd for the other two salts, with relative energies ranging from roughly 25–60 kJ mol⁻¹ above the corresponding minimum. As such, these structures would not be carried forward to further study in most CSP protocols. Again, catastrophic failure of the MACE-OFF23(M) potential for salts is completely expected given that it was not trained on systems with net charges (or on ionic crystals). Also as expected, based on the high VC-PWDF scores in Fig. 3, the DFT//MACE approach predicts the experimental polymorphs to be 28 and 31 kJ mol⁻¹ above the minima for compounds XIX and XXIV, respectively. The performance of DFT//MACE for compound XXXIII is quite good, however, which is consistent with the much lower VC-PWDF scores seen in Fig. 3. Likely the quality of the MACE-OFF23(M) geometries for salts is, in part, related to the extent of charge localization and resemblance to the zwitterionic solvated amino acids in the SPICE training set, with the chloride salt (XXIV) proving particular problematic.

Turning to the flexible molecules, Table 1 shows that these can be challenging CSP cases even for DFT methods. It has been shown that inclusion of thermal free-energy corrections is necessary to identify the experimental structure as the most stable for compounds XX, XXIII, and XXXI.^11,49,61,62 In the most recent blind test, none of the methods considered ranked the two isolated polymorphs of compound XXXII as particularly low in energy,³¹ implying either consistent errors for several dispersion-corrected density functionals, importance of kinetic effects on crystal growth, and/or the possibility of a more-stable, late-appearing polymorph not yet characterised experimentally.⁶³ Overall, the DFT calculations predict the experimental forms to be within 10 kJ mol⁻¹ of the minimum for all cases except form C of compound XXXI; however, this polymorph was the result of solvent loss from a solvate, leaving large crystal voids, and is expected to be highly unstable. As shown in Table 1, the MACE-OFF23(M) potential provides good agreement with DFT results for compounds VI, XIV, XVIII, XX, and XXVI, but its performance for the various polymorphs of the remaining flexible molecules is erratic. In general, the DFT//MACE results are in much better agreement with the DFT reference data, illustrating the promise of this composite approach using geometries optimized with MACE-OFF23(M) for the early stages of CSP.

4.2.2. Helicene compounds. The [n]helicene compounds may represent a more ideal case for machine-learned potentials, such as MACE-OFF23(M), as they contain only aromatic rings and no other functional groups. However, the polymorph ranking will be controlled by small energy differences between various π-stacking and T-shaped intermolecular interaction motifs (synthons) within the crystal structures, which were not extensively sampled in the training data. The results obtained for the helicenes are summarized in Table 2. Overall, MACE-OFF23(M) performed reasonably well, predicting the experimentally isolated polymorphs to lie within 5 kJ mol⁻¹ of the corresponding minimum for most cases. One exception is [5]helicene, where the DBPHEN05 polymorph was ranked quite high (73rd) in energy, just over 9 kJ mol⁻¹ above the minimum. The other exception is the entantiopure form of 1-aza[6]helicene (KAWRUY), although the MACE-OFF23(M) prediction is actually in good agreement with both DFT and experiment.⁴⁸ This polymorph is known to be significantly less stable than the racemic form (COBNUD), but can be isolated from enantiopure starting material.

Table 2 Results for selected helicene compounds. Shown are the rankings of the experimental polymorphs and their energies, in kJ mol⁻¹ per molecule, relative to the global minimum identified with each computational method, specified as energy//geometry. CCDC⁶⁴ refcodes are given for each experimental polymorph, except for phenanthrene, where the experimental structure was reported in ref. 65, and the intergrowth form of [6]helicene, which was reported in ref. 66

Compound	Polymorph	MACE//MACE		DFT//MACE		DFT//DFT
		Rank	ΔE	Rank	ΔE	Rank	ΔE
Naphthalene	NAPTHA18	1	0.0	2	0.1	1	0.0
Phenanthrene	Ref. 65	22	2.7	1	0.0	1	0.0
[4] helicene	BZPHAN	1	0.0	30	4.4	4	1.3
[5] helicene	DBPHEN05	73	9.1	5	1.4	2	0.0
	DBPHEN04	25	5.1	9	1.8	3	0.4
	DBPHEN02	2	0.1	22	4.0	4	0.6
	DBPHEN03	28	5.3	14	2.8	5	0.8
[6] helicene	Intergrowth	1	0.0	1	0.0	1	0.0
	HEXHEL	2	0.6	3	1.0	2	0.2
1-aza[6] helicene	COBNUD	12	3.0	1	0.0	1	0.0
	KAWRUY	38	13.3	36	11.6	31	10.0
[7] helicene	IMEJIW	1	0.0	1	0.0	1	0.0
	HPTHEL01	3	4.7	5	4.6	3	3.4
[9] helicene	QUJNEQ	1	0.0	3	3.2	1	0.0
[10] helicene	THELIC	1	0.0	1	0.0	1	0.0
[11] helicene	UHELIC	1	0.0	1	0.0	1	0.0

---

The results in Table 2 show that the composite DFT//MACE approach offers improvement over MACE-OFF23(M) alone for phenanthrene, 1-aza[6]helicene, and most polymorphs of [5]helicene. However, agreement with DFT reference data worsens when applying the composite approach to [9]helicene and, particularly, [4]helicene, where the experimental structure is ranked 30th. Visualisation of the MACE-OFF23(M) structure for the experimental form of [4]helicene reveals a large volume contraction that resulted in very short intermolecular H⋯H contacts of <2.2 Å, which explains its lesser stability with DFT. A similarly short contact is also found in the MACE-OFF23(M) structure of only one of the four experimental forms of [5]helicene, DBPHEN02, which was ranked spuriously high in energy with DFT//MACE. Nevertheless, except for the enantiopure form of 1-aza[6]helicene discussed above, all experimental forms are predicted to lie within 5 kJ mol⁻¹ of the corresponding energy minimum with the composite method. As such, they would still be carried forward to full DFT calculation in a practical CSP protocol.

5. Summary

In this work, we applied the recent machine-learned MACE-OFF23(M) potential to two sets of molecular crystals to investigate its effectiveness as a low-cost method for use in the early phases of CSP. The agreement between MACE-OFF23(M) and DFT results was assessed for both relative energies and crystal geometries. The performance of a composite DFT//MACE approach, which uses DFT energies evaluated at MACE geometries, was also evaluated. It should be emphasized that the MACE-OFF23(M) potential was used as originally formulated³² and was not retrained using any DFT data for molecular crystals.

The MACE-OFF23(M) geometries were compared to their DFT counterparts using the VC-PWDF method, which provides a packing similarity score between two crystals while allowing for distortions of the unit cell. The VC-PWDF scores were frequently clustered near zero, indicating that the MACE-OFF23(M) geometry optimizations converged to the same crystal polymorph as the B86bPBE-XDM optmizations in the majority of cases. Even in cases with broader distributions of VC-PWDF scores, more than 50% of the candidate crystal structures were deemed as matching (VC-PWDF <0.03) the DFT reference structure after optimization with the MACE-OFF23(M) potential. The two noted exceptions were the blind-test compounds XVI and XXIV. Poor performance in these cases is unsurprising since compound XVI contains a diazo (=N=N) group, which is not well represented in MACE-OFF23(M)'s training data, while compound XXIV is an organic salt. Ions are inherently problematic for local models such as MACE-OFF23(M) because of the long range of the electrostatic interaction. In addition to VC-PWDF scores, we also considered changes in unit-cell volumes between the B86bPBE-XDM and MACE-OFF23(M) geometries. The MACE-OFF23(M) geometries were typically more compact, with the notable exception of the blind-test molecule IX, which was the only iodine-containing compound present in our study and, again, was not well represented in MACE-OFF23(M)'s training data. Machine-learned potentials are naturally limited by their training data, so it is expected to obtain good performance for compounds or intermolecular interaction motifs similar to those in the training set, and uncertain or poor performance for new or little-sampled regions of chemical space.

The energy ranking of each experimentally isolated polymorph was evaluated relative to the most-stable candidate structure provided by each method (MACE//MACE, DFT//MACE, DFT//DFT). MACE//MACE performed reasonably well for the rigid blind-test molecules, where 9/14 experimental polymorphs were ranked within 2 kJ mol⁻¹ of the minimum-energy structure. The rankings were further improved by DFT//MACE, which predicted 12/14 experimental polymorphs to lie within this energy range. For the helicene compounds, the MACE//MACE method ranked the experimental forms within 6 kJ mol⁻¹ of the minimum-energy structures in 14/16 cases, with the DFT//MACE method generally providing improved agreement with the DFT//DFT reference data. The flexible blind-test molecules, which are challenging even for DFT, were also unsurprisingly challenging for the MACE-OFF23(M) potential. Here, the performance of the MACE//MACE method was somewhat erratic, with large fluctuations in rankings of experimental structures, although there was again improvement when using the composite DFT//MACE approach. Finally, we saw a complete failure of the MACE-OFF23(M) potential for the experimental form of molecule XVI, where geometry optimization resulted in a different crystal structure, meaning that it would never be found in a CSP study using this methodology. A catastrophic failure of the MACE-OFF23(M) potential was also seen for organic salts, which is entirely expected due to the neglect of long-range electrostatics and lack of any ionic compounds in the training data. Developing machine-learned potentials that include a physically reasonable description of long-range electrostatic interactions remains an outstanding challenge.

We conclude that the MACE-OFF23(M) potential provides a promising step forward for the use of machine-learned potentials in CSP. For crystals composed of rigid molecules, containing common functional groups, the MACE method gives remarkably good results for both geometries and energy ranking, and the latter is improved by the DFT//MACE composite approach. Furthermore, our results suggest that this composite approach may even be accurate enough for application to flexible molecules, for selection of candidate structures that would progress to the final DFT energy ranking stage of a CSP study. Unfortunately, it does not seem possible to know a priori how well the MACE structure will approximate the DFT structure for specific compounds, which detracts significantly from the reliability of the DFT//MACE approach. Users of MACE-OFF23(M) should be aware of its pitfalls: it should never be used for ionic systems, and should also be avoided when considering compounds with any uncommon functionals groups, or elements, which may be poorly represented by its training data.

Data availability

The data supporting this article have been included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge Drs. Paramvir Ahlawat, R. Alex Mayo, and Ross Dickson for technical assistance, as well as Dr Flaviano Della Pia and Profs. Angelos Michaelides and Gabor Csányi for helpful discussions. We also thank the Natural Sciences and Engineering Research Council (NSERC) of Canada, the Government of Nova Scotia, and the Royal Society for financial support, and the Atlantic Computing Excellence Network (ACENET) for computational resources.

References

1. S. R. Chemburkar, J. Bauer, K. Deming, H. Spiwek, K. Patel, J. Morris, R. Henry, S. Spanton, W. Dziki and W. Porter, et al., Org. Process Res. Dev., 2000, 4, 413–417.
2. D.-K. Bucar, R. W. Lancaster and J. Bernstein, Angew. Chem., 2015, 54, 6972–6993.
3. S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111.
4. S. L. Price and J. G. Brandenburg, in Non-Covalent Interactions in Quantum Chemistry and Physics, ed A. Otero-de-la Roza and G. A. DiLabio, Elsevier, 2017, ch. 11, pp. 333–363.
5. J. Nyman and S. M. Reutzel-Edens, Faraday Discuss., 2018, 211, 459–476.
6. R. Nikhar and K. Szalewicz, Nat. Commun., 2022, 13, 3095.
7. G. J. O. Beran, Chem. Sci., 2023, 14, 13290–13312.
8. M. A. Neumann, F. J. J. Leusen and J. Kendrick, Angew. Chem., 2008, 47, 2427–2430.
9. G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk and H. L. Ammon, et al., Acta Crystallogr., Sect. B: Struct. Sci., 2009, B65, 107–125.
10. M. A. Neumann, J. Van De Streek, F. P. A. Fabbiani, P. Hidber and O. Grassmann, Nat. Commun., 2015, 6, 7793.
11. J. Hoja, H. Y. Ko, M. A. Neumann, R. Car, R. A. Distasio and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338.
12. M. Mortazavi, J. Hoja, L. Aerts, L. Quéré, J. van de Streek, M. A. Neumann and A. Tkatchenko, Commun. Chem., 2019, 2, 1–7.
13. C. R. Taylor, M. T. Mulvee, D. S. Perenyi, M. R. Probert, G. M. Day and J. W. Steed, J. Am. Chem. Soc., 2020, 142, 16668–16680.
14. E. R. Johnson, in Non-covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero-de-la-Roza and G. A. DiLabio, Elsevier, 2017, ch. 5, pp. 169–194.
15. A. J. A. Price, R. A. Mayo, A. Otero-de-la-Roza and E. R. Johnson, CrystEngComm, 2023, 25, 953–960.
16. A. J. A. Price, A. Otero de la Roza and E. R. Johnson, Chem. Sci., 2023, 14, 1252–1262.
17. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
18. S. Levchenko, X. Ren, J. Wieferink, R. Johanni, P. Rinke, V. Blum and M. Scheffler, Comput. Phys. Commun., 2015, 192, 60–69.
19. V. W. Yu, F. Corsetti, A. García, W. P. Huhn, M. Jacquelin, W. Jia, B. Lange, L. Lin, J. Lu and W. Mi, et al., Comput. Phys. Commun., 2018, 222, 267–285.
20. A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole and K. Cosburn, et al., Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459.
21. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
22. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733.
23. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903.
24. C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202.
25. R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490.
26. R. Zubatyuk, J. S. Smith, B. T. Nebgen, S. Tretiak and O. Isayev, Nat. Commun., 2021, 12, 4870.
27. D. Anstine, R. Zubatyuk and O. Isayev, AIMNet2: a neural network potential to meet your neutral, charged, organic, and elemental-organic needs, 2024 DOI:10.26434/chemrxiv-2023-296ch-v3.
28. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
29. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, pp. 1263–1272.
30. L. M. Hunnisett, J. Nyman, N. Francia, N. S. Abraham, C. S. Adjiman, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli and D. M. Anstine, et al., Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2024, 80, 517–547.
31. L. M. Hunnisett, N. Francia, J. Nyman, N. S. Abraham, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli, D. M. Anstine and J. E. Anthony, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2024, 80, 548–574.
32. D. P. Kovács, J. H. Moore, N. J. Browning, I. Batatia, J. T. Horton, V. Kapil, W. C. Witt, I.-B. Magdău, D. J. Cole and G. Csányi, MACE-OFF23: Transferable Machine Learning Force Fields for Organic Molecules, 2023, https://arxiv.org/abs/2312.15211.
33. P. Eastman, P. K. Behara, D. L. Dotson, R. Galvelis, J. E. Herr, J. T. Horton, Y. Mao, J. D. Chodera, B. P. Pritchard and Y. Wang, et al., Sci. Data, 2023, 10, 11.
34. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110.
35. A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738.
36. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
37. C. Isert, K. Atz, J. Jiménez-Luna and G. Schneider, Sci. Data, 2022, 9, 273.
38. A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705.
39. G. A. Dolgonos, J. Hoja and A. D. Boese, Phys. Chem. Chem. Phys., 2019, 21, 24333–24344.
40. D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352–7360.
41. D. E. Williams, J. Comput. Chem., 2001, 22, 1154–1166.
42. M. P. Metz, M. Shahbaz, H. Song, L. Vogt-Maranto, M. E. Tuckerman and K. Szalewicz, Cryst. Growth Des., 2022, 22, 1182–1195.
43. J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz and A. Gavezzotti, et al., Acta Crystallogr., Sect. B: Struct. Sci., 2000, B58, 647–661.
44. W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko and P. Erk, et al., Acta Crystallogr., Sect. B: Struct. Sci., 2002, B58, 647–661.
45. G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter and R. G. Della Valle, et al., Acta Crystallogr., Sect. B: Struct. Sci., 2005, B61, 511–527.
46. D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich and S. X. M. Boerrigter, et al., Acta Crystallogr., Sect. B: Struct. Sci., 2011, B67, 535–551.
47. J. A. Schmidt, E. H. Wolpert, G. M. Sparrow, E. R. Johnson and K. E. Jelfs, Cryst. Growth Des., 2023, 23, 8909–8917.
48. Y. Yang, B. Rice, X. Shi, J. R. Brandt, R. Correa da Costa, G. J. Hedley, D.-M. Smilgies, J. M. Frost, I. D. W. Samuel, A. Otero-de-la-Roza, E. R. Johnson, K. E. Jelfs, J. Nelson, A. J. Campbell and M. J. Fuchter, ACS Nano, 2017, 11, 8329–8338.
49. R. A. Mayo, A. J. A. Price, A. Otero-de-la-Roza and E. R. Johnson, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2024, 80, 595–605.
50. A. D. Becke, J. Chem. Phys., 1986, 85, 7184.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
52. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, J. Phys.: Condens. Matter, 2017, 29, 465901.
53. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
54. L. M. LeBlanc and E. R. Johnson, CrystEngComm, 2019, 21, 5995–6009.
55. R. A. Mayo, A. Otero-de-la-Roza and E. R. Johnson, CrystEngComm, 2022, 24, 8326–8338.
56. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
57. R. de Gelder, R. Wehrens and J. A. Hageman, J. Comput. Chem., 2001, 22, 273–289.
58. J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165.
59. S. Motherwell and J. A. Chisholm, J. Appl. Crystallogr., 2005, 38, 228–231.
60. C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
61. J. Hoja and A. Tkatchenko, Faraday Discuss., 2018, 211, 253–274.
62. C. J. Nickerson and E. R. Johnson, Manuscript in preparation.
63. S. L. Price, Faraday Discuss., 2018, 211, 9–30.
64. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171–179.
65. J. Trotter, Acta Crystallogr., 1963, 16, 605–608.
66. B. Rice, L. M. LeBlanc, A. Otero-de-la-Roza, M. J. Fuchter, E. R. Johnson, J. Nelson and K. E. Jelfs, Nanoscale, 2018, 10, 1865–1876.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00593k

---