 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Excitations in lanthanide ions: a systematic evaluation of two-component CAS-CI and GW†
Roman
Zielke
 ,
Florian
Weigend
,
Florian
Weigend
 * and
Christof
Holzer
* and
Christof
Holzer
 *
*
Institute for Quantum Materials and Technologies, Karlsruhe Institute of Technology, Kaiserstrasse 12, D-76131 Karlsruhe, Germany. E-mail: florian.weigend@kit.edu; holzer@kit.edu
First published on 16th May 2025
Abstract
This paper presents a thorough prediction and investigation of ionization energies, atomic levels, and crystal-field splittings in lanthanide ions. We show that a two-component complete active space (CAS) configuration interaction (CI) approach based on two-component density functional theory (DFT) reference states is suitable to yield accurate excitation energies for lower energy terms. DFT references are further shown to be superior to Hartree–Fock (HF) references for predicting both atomic levels and ionization energies. Especially in the Green's function based GW method used to determine ionization energies, the deficiencies of the wave function based HF references are severe, leading to sizable errors. Two-electron contributions to spin–orbit coupling are found to be an important ingredient for obtaining accurate atomic levels. These contributions are taken into account using a screened-nuclear-spin–orbit (SNSO) approach, which is shown to be very accurate. DFT based CAS-CI is further used to calculate crystal-field splittings. The results are well suited to predict the subtle splittings in complexes with unpaired 4f electrons.
1 Introduction
High performance methods are needed to describe the excited states of lanthanide ions and their corresponding complexes. Multiple electronic effects, including electron correlation, spin–orbit coupling (SOC), and spin-other-orbit coupling (SOOC) need to be included to properly describe ground and especially excited states. Standard (time-dependent) density functional theory is often invalid in this regime,1 as any functional currently available is unable to appropriately describe the multireference character of lanthanides. This even includes specialized functionals designed to describe strong (static) correlation.2,3 The ground state term is often already divided into multiple states, many of them slightly or significantly above the ground state level. Although density functional theory (DFT) has recently seen some success in predicting properties of trivalent lanthanide ion complexes,4,5 as for example EPR properties, excited states are currently out of reach for DFT. The required time-dependent (TD) DFT description of relativistic open-shell systems is often qualitatively wrong. This hampers the use of TD-DFT at least when aiming to include the f–f transitions in the predicted optical spectra. This is rather unfortunate, as nowadays TD-DFT represents the most important method to predict optical spectra in silico.6 While recently it was further outlined that also Green's function based methods can be applied to these highly interesting complexes with unpaired 4f electrons,7 the latter approach remains constricted to non-degenerate ground states. This effectively limits its applicability to complexes containing Eu3+ and Sm2+ ions, and to some extent also Ce3+ and Yb3+.7 It is well known, however, that complete active space (CAS) methods are in principle able to describe the electronic situations prevalent in lanthanide ions,8–15 though at steeply increasing costs. Initially, perturbation theory was used to include SOC and other relativistic effects a posteriori,16,17 CAS+SOC frameworks are broadly available within the OpenMolcas18 and GAMESS-US19 packages, and have subsequently been applied to selected states of lanthanide atoms and ions with some success.12,20In a more recent evaluation,21 it has, however, been found that the errors of treating SOC non-variationally are significant. According to this study, the overall errors could be halved for excited states of lanthanide atoms if SOC was instead treated variationally using a relativistic two-component (2c) framework. The necessity to perform fully relativistic configuration interaction simulations significantly adds to the computational effort, requiring enormous computational facilities to tackle even comparably simple problems, as for example presented within the GRASP,22 DIRAC,23 or Gaussian packages.24 While these are capable of conducting the required relativistic CI calculations, performing simulations for sizable molecular systems is currently out of reach for these programs.22–29 Reported relativistic large-scale calculations using CASSCF programs have so far only been reported for the BAGEL program,30 using a relativistic CI applied to the ground states of rhenium, uranium, and dysprosium complexes.31,32 Relativistic CASSCF proves to be numerically very demanding, even with comparably small systems and active space sizes requiring hundreds of cores to be carried out on a feasible time scale.32,33
Therefore, we draw attention to a method developed by Grimme and Marian to ease the computational demands of these kind of calculations: mixing DFT and multireference CI calculations.34–37 The resulting DFT-MRCI method tries to incorporate parts of the dynamic correlation from DFT, allowing for a reduction of the active space for which the CI or CAS procedures are carried out. This is considered to be very advantageous as it reduces the size of the active space to the minimum orbital space required to describe the static correlation.37 This statement is even more true for fully relativistic references, where the orthogonality of alpha and beta electrons and choosing a desired multiplicity of the reference wave functions via configuration state functions (CSFs) cannot be used to reduce the computational complexity. Instead, Slater determinants have to be used directly, which is conceptually convenient, yet computationally demanding. Still, including SOC directly instead of via perturbation theory has proven to be very beneficial, reducing overall errors when SOC is sizable.21
Using DFT references for lanthanides has also become more natural recently given the success of Green's function based methods.7,38–40 And while certainly lanthanides do put a lot of strain on any method used in theoretical chemistry, the GW method has successfully been proven to be applicable even if the underlying DFT reference is not optimal. In this work, we therefore aim at conducting a thorough investigation of DFT references of lanthanide ions, using them to perform subsequent CAS-CI and Green's function based GW calculations to determine their spectroscopic properties.
2 Theory
In the fully relativistic CI ansatz, the wave function |Ψ〉 is expanded in terms of Slater determinants |ψ〉,28 | (1) |
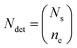 | (2) |
The Slater determinants ψ can be obtained as a properly antisymmetrized product of molecular orbitals or spinors ϕ, which are themselves constructed from chosen basis functions χ and the spinor expansion coefficients. Within the exact-2-component (X2C) theory,41–43 they are given as
 | (3) |
As outlined before, a construction of CSFs is superficial, as no computational savings can be achieved. Instead, in a fully relativistic ansatz we can directly aim at optimizing the CI coefficients C minimizing the CAS-CI energy
| E = eHF + 〈Ψ|ĤCAS-CI|Ψ〉 | (4) |
The CAS-CI Hamiltonian is given by24
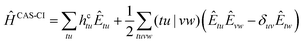 | (5) |
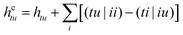 | (6) |
We note that within the CAS-CI procedure, eqn (5) is evaluated using the spinor coefficients obtained from either DFT or HF, with no further differentiation being necessary. (tu|vw) denotes a standard two-electron Coulomb integral, and Êtu are the generators of the unitary group44
| Êtu = â†tâu | (7) |
Within DFT, only the question about the most suitable starting reference arises. The single determinant ansatz used in Kohn–Sham theory is, however, not able to describe the (nearly) degenerate orbital situation in many open-shell systems containing heavy elements. We therefore suggest instead using a fractional occupation approach that can yield qualitatively correct density distributions for atomic and molecular systems containing lanthanides or other heavy elements. The fractional occupation is chosen in a way that restores the spherical symmetry of the reference density of an atom, automatically leading to the correct degeneracy patterns. This avoids conceptual issues of introducing multiple Slater determinants in density functional theory, while still yielding suitable starting points for further CAS-CI treatments. Contrary, as outlined by McWeeny,45 and Thyssen,46 the average-of-configuration (AOC) ansatz, merging restricted open-shell HF (ROHF) and CASSCF is well suited to provide good initial guesses for wave function theory. This ansatz is therefore preferred by wave function theory, yielding reliable values also for electronically complicated systems.47,48
This is, however, improper for DFT, because in the latter, only density dependent variables can formally arise, not wave function based determinants from a restricted open shell scheme. We note that the CI energy is computed explicitly within the chosen active space and is not simply added to the DFT correlation energy. As such, the DFT correlation contributions are not double-counted within the active space. This avoids the typical double counting issue that arises in more empirical DFT-CI methods, where correlation corrections are directly added to the DFT total energy.
3 Computational details
A two-component Slater determinant based CAS-CI code was implemented in the TURBOMOLE package,49,50 allowing us to perform CAS-CI calculations using various HF and DFT starting points. The hybrid PBE051,52 and local hybrid CHYF5 density functional approximations have been used. The x2c-QZVPPall-2c basis set53 was employed for lanthanide ions, while x2c-TZVPPall-2c was used for the remaining lighter elements if applicable. HF and KS reference states were converged to at least 10−8Eh and 10−7Eh for differences in energy and difference density, respectively. Fine integration grids (gridsize 3a) were used for DFT.54 Eigenvalue self-consistent evGW was used as described in ref. 7, further making use of a frequency sampling algorithm.40 As an HF or KS reference in the evGW@DFT method, the canonical reference state with integer occupation numbers was used. For CAS-CI calculations, the respective fractional occupied reference density was employed, | (8) |
The structure of the aquatic [Nd(H2O)9]3+ complex has been taken from ref. 60. For the [Nd(H2O)9](BrO3)3 complex, the crystal structure was taken from ref. 61 and the position of the hydrogen was optimized using PBE0 and a ECP49MWB basis set for Nd3+, with the f-electrons being absorbed into the effective core potential (ECP).62 The def2-TZVP basis set was used for the remaining atoms.58,63,64
4 Results
Before diving into the prediction of atomic levels of lanthanide atoms, we will perform an evGW@HF and evGW@DFT investigation of trivalent lanthanides to mainly detect qualitative differences in the underlying HF and DFT references. While GW yields ionization energies, i.e. charged excitations, those are also closely connected to the excited states via the Bethe–Salpeter equation.65 Intrinsic information about the quality of excited states is therefore tightly linked to the ionization energies recovered from a given reference.4.1 Ionization energies of trivalent lanthanide ions
As outlined in ref. 7, the GW method is a formidable tool to tackle ionization energies of lanthanide ions. Table 1 and Fig. 1 show that modern local hybrid functionals such as CHYF are an excellent basis for GW, in contrast to Hartree–Fock, which yields large errors, possibly related to its inability to correctly describe the ground state of lanthanide ions.| HF | PBE0 | CHYF | |||
|---|---|---|---|---|---|
| SNSO | No SNSO | SNSO | No SNSO | ||
| Ce3+ | 0.07 | 0.85 | 0.64 | 0.77 | 0.57 |
| Pr3+ | 0.34 | 0.90 | 0.72 | 0.88 | 0.78 |
| Nd3+ | 0.43 | 0.63 | 0.45 | 0.59 | 0.53 |
| Pm3+ | 0.63 | 0.61 | 0.68 | 0.39 | 0.52 |
| Sm3+ | 0.90 | 0.55 | 0.80 | 0.27 | 0.41 |
| Eu3+ | 0.99 | 0.53 | 0.68 | 0.19 | 0.38 |
| Gd3+ | 1.24 | 0.37 | 0.73 | 0.05 | 0.40 |
| Tb3+ | 1.44 | 0.73 | 0.72 | 0.32 | 0.33 |
| Dy3+ | 1.44 | 0.86 | 0.52 | 0.54 | 0.46 |
| Ho3+ | 1.71 | 0.63 | 0.65 | 0.22 | 0.29 |
| Er3+ | 2.00 | 0.60 | 0.83 | 0.00 | 0.33 |
| Tm3+ | 2.27 | 0.40 | 0.69 | −0.24 | 0.04 |
| Yb3+ | 2.12 | 0.24 | 0.64 | −0.40 | 0.01 |
| MAD | 1.38 | 0.64 | 0.68 | 0.45 | 0.44 |
| STD | 0.71 | 0.20 | 0.10 | 0.37 | 0.21 |
 | ||
| Fig. 1 Trend of ionization energies (in eV) for the trivalent lanthanoid ions Ln3+, calculated using evGW@HF and evGW@DFT approaches. The x2c-QZVPPall-2c basis set was used for all ions. For the dashed lines, the SNSO approach was used. Experimental references have been taken from the NIST database.66 All values in eV. | ||
A first remarkable trend is observed for HF. As the nuclear charge increases, the inability of HF to describe the ground states sufficiently well becomes obvious, and the error of the obtained evGW@HF ionization energies amounts to several eV. As seen in Table 1, the error of evGW@HF increases monotonically with higher nuclear charge Z. A population analysis of the HF wave function reveals that for Ce3+, instead of the correct 4f1 configuration, a mixture of 4f1 and 5d1 reference states is found, while a population analysis of the CHYF density reveals the correct 4f1 occupation. Due to error cancellation, the obtained ionization energy of HF is nevertheless remarkably close to the experimental value, while the error is highest for Ce3+ for CHYF.
In contrast, ionization energies predicted by evGW@DFT improve as the nuclear charge increases, with the CHYF local hybrid functional outperforming all previously tested functionals.7 As shown in Table 1, the deviations from experimental ionization energies monotonically decrease with increasing nuclear charge Z, though at an overall significantly smaller magnitude compared to the HF reference. Especially from Sm3+ on, evGW@CHYF yields accurate ionization energies and the correct 4fn occupation in every case. evGW@PBE0 finally yields a more uniform distribution of errors as outlined by both Fig. 1 and Table 1, with the overall error being approximately independent from Z, though at an significantly elevated level of errors compared to CHYF.
Furthermore, in Fig. 1 and Table 1 the impact of relativistic effects on two-electron integrals was assessed by also incorporating an SNSO approach.57,58 For ionization energies, this effect leads only to minor corrections in the resulting GW values. However, the effect is rather dependent on the actual lanthanide with, for example, Gd3+ and Yb3+ seeing rather large corrections from the inclusion of SNSO, while Pr3+ and Tb3+ only see a minor change in the overall obtained ionization energy. Nevertheless, this effect should not be overemphasized, as parts of these deviations can also arise from the full neglection of changes in the underlying spinors from the evGW update, as in the latter still only the quasiparticle eigenvalues are updated in each iteration. The relativistic effects induced by the modified two-electron interactions are significant, though rather unsystematic. Their magnitude has been described by Boettger,57 and is generally below the intrinsic error of the evGW method, essentially producing the same mean average deviation as clearly shown in Table 1. In general, DFT references can be assumed to be superior to HF references. Concerning the choice of the basis set, x2c-QZVPall-2c was found to yield converged values. We note that significant deviations can be found for smaller triple-ζ basis sets as shown in ref. 7, and currently we recommend using quadruple-ζ basis sets for investigations of excited and ionized states of lanthanide ions.
We therefore also assume that starting CI procedures from DFT references can be advantageous, as the complete negligibility of correlation can lead to qualitatively wrong reference states in HF theory, as do pure DFT functionals for lanthanide ions.
We note that for any system an optimal specific amount of exact exchange can be obtained by tuning the density functional. However, modern local hybrid functionals like CHYF have shown to be rather robust in this respect,4,5 being able to intrinsically adapt the amount of exact exchange incorporated.
4.2 Atomic levels of lanthanide ions
In terms of excited states of lanthanide ions, the GW-BSE method has severe drawbacks when trying to describe excitations from systems with (nearly) degenerate ground states.7 CAS-CI and also CASSCF resolve this issue, leading to well defined atomic levels, though with the restriction of CAS-CI requiring a reference state of viable symmetry. Fig. 2–4 outline a set of CAS-CI calculations at three different references, namely PBE0, CHYF and HF.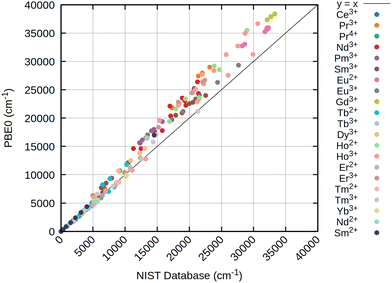 | ||
| Fig. 2 Scatter plot of calculated atomic levels of 21 lanthanide ions at the CAS-CI@PBE0/x2c-QZVPPall-2c level of theory with an SNSO 2e SOC correction. As reference on the the x-axis, atomic levels from the NIST database66 are taken. All values in cm−1. | ||
 | ||
| Fig. 3 Scatter plot of calculated atomic levels of 21 lanthanide ions at the CAS-CI@CHYF/x2c-QZVPPall-2c level of theory with an SNSO 2e SOC correction. As reference on the the x-axis, atomic levels from the NIST database66 are taken. All values in cm−1. | ||
 | ||
| Fig. 4 Scatter plot of calculated atomic levels of 19 lanthanide ions at the CAS-CI@HF/x2c-QZVPPall-2c level of theory with an SNSO 2e SOC correction. As reference on the the x-axis, atomic levels from the NIST database66 are taken. All values in cm−1. | ||
The results obtained for all three references are rather similar, pointing out that for atomic levels both HF and DFT can achieve good starting points if an initial wave function or density with the correct spherical symmetry is generated. Especially for the low energy states below 7000 to 8000 cm−1, usually belonging to the ground state term symbol, only very small deviations are obtained for all references. This is strictly tied to the inclusion of at least approximate two-electron spin–orbit contributions (2e SOC). For example, in this work as well as in ref. 21 the SNSO approach is used to ensure this. The exact details of the chosen SNSO approach are only of minor importance for the investigated lanthanide ions, and testing of modern SNSO approaches yields only small overall differences well below the error of the initial CAS-CI method, which is very likely carried over to CASSCF.59 We also expect other atomic mean field approaches, as for example the AMFI approach,16,67 to yield similar results. If no correction for 2e SOC effects is included, the splitting of the ground state term symbols can be off by several thousand wave numbers. This is further emphasized through Fig. 5, where the deterioration of calculated atomic levels is obvious when compared to the HF variant including SNSO correction as shown in Fig. 4. The same is also observed for the DFT cases, as seen in the ESI.† Involving these 2e SOC effects is therefore absolutely crucial in the prediction of the atomic levels of all lanthanide ions if two-component or four-component Hamiltonians are used. In the case of perturbative spin–orbit corrections, the results presented by Freidzon and co-workers however outline that this issue is unproblematic.12 This is consistent with recent calculations of lanthanide complexes using the same perturbative CASSCF-SO approach for Eu3+, Sm3+, Tb3+, and Yb3+ ions.68–71 In case of perturbation theory, 2e SOC effects are recovered by the Breit–Pauli spin–orbit operator if the one- and averaged two-electron parts are both included in the perturbation operator used to calculate the spin–orbit coupling matrix elements (SOCMEs).17,72 The above-mentioned studies on lanthanide ions and lanthanide complexes also show that a CAS treatment that only considers the 4f shell is often sufficient to obtain qualitatively correct results for the lowest terms.12,71 Statistical analysis of the resulting data, presented in Table 2, already indicates that CAS-CI@DFT is sufficient to reliably yield atomic levels with less than 4% error across all tested lanthanide ions. In absolute numbers, this translates to an average error of less than 200 cm−1. CAS-CI@HF yields higher errors for the ground state terms, amounting to above 5% and absolute errors of up to 300 cm−1, which is nevertheless still acceptable. However, HF completely fails to converge to the correct electronic ground state for Ce3+, Nd2+, and Sm2+, which therefore have been omitted from the statistical analysis. While for the Ce3+ ion, simply including the 5d orbital into the active space cures the otherwise incorrect results, no simple solution is found for Nd2+ and Sm2+. With even simple atoms being problematic, this points at molecular complexes being even more troublesome. Contrary, neither CHYF nor PBE0 have deficiencies when trying to converge to the correct state of Ce3+, Nd2+, and Sm2+, yielding the correct 4fn configuration with no artificial 5d admixtures. A special case is Pr2+, which also did not converge to the correct state with PBE0, whereas solely CHYF managed to correctly predict the ground state occupation of this ion. CAS-CI@DFT can therefore have a double advantage in real applications: not only does it lead to a slightly better description of the excited states, but it also has a higher chance of finding the right starting point to enable the calculation of excited states.
 | ||
| Fig. 5 Scatter plot of calculated atomic levels of 19 lanthanide ions at the CAS-CI@HF/x2c-QZVPPall-2c level of theory without 2e SOC correction. As reference on the the x-axis, atomic levels from the NIST database66 are taken. All values in cm−1. | ||
| HF | PBE0 | CHYF | ||||
|---|---|---|---|---|---|---|
| STD | MD | STD | MD | STD | MD | |
| Rel. error [%] | 5.1 | 5.7 | 3.2 | 3.8 | 3.2 | 3.7 |
| Abs. error [cm−1] | 242 | 289 | 164 | 201 | 156 | 190 |
For excited states belonging to higher terms, the deviations found with respect to data from the NIST atomic level database66 increase with increasing excitation energy. Observed deviations are roughly proportional to the energy of the atomic level. Deviations further are monotonically growing, being too large in nearly all cases. These effects are nearly independent from the chosen reference functions, with CAS-CI@HF and CAS-CI@DFT yielding similar deviations for all lanthanide ions as described in Fig. 2–4. It can be attributed to dynamic correlation becoming increasingly important for excited state terms. However, as shown in earlier work,47 simply increasing the active space only slowly leads to a lowering of the energies of these atomic states. Increasing the active space size is therefore inefficient, and future developments that improve higher excited states of lanthanides should therefore focus on more efficient ways to recover dynamic correlation. The detailed data presented in these figures show that the error patterns are rather intuitive. For example, for Sm2+ and Eu3+, both featuring a 4f6 electron configuration, nearly identical deviations are found. For the lowest F manifold, deviations of only a few hundred wave numbers are observed, while the first D manifold is off by 2000–3000 cm−1, depending on the reference. Consequently, if higher lying terms are taken into account, the subsequent statistical deviations from the NIST atomic levels increase as shown in Table 3. Notably, the order of error is now turned upside down, with CAS-CI@HF being superior to CAS-CI@DFT, at least as long as 2e SOC is taken into account using the SNSO approximation. Table 3 also shows that neglecting the 2e SOC leads to a drastic increase in overall errors. The obtained results are, as outlined previously, not meaningful for any lanthanide ion and can deviate by tens of thousands of wave numbers from the NIST values.
| HF | PBE0 | CHYF | ||||
|---|---|---|---|---|---|---|
| STD | MRD | STD | MRD | STD | MRD | |
| SNSO | 7.7 | 9.2 | 9.8 | 11.2 | 10.7 | 12.2 |
| No SNSO | 31.3 | 42.0 | 27.0 | 35.5 | 25.8 | 35.7 |
In Table 4, detailed values of the 7FJ and 5DJ states of the Eu3+ ion are listed to give a concise comparison of various feasible approaches for calculating excited states of this ion. Throughout the literature, the optical properties of the Eu3+ ion are the most thoroughly theoretically investigated, with various studies also focusing on the atomic ion.7,12,13,47,73,74
| Eu3+:LaCl366 Exp. | COSCI13 4c + ΔSOO | COSCI47 | KRCI47 4c + ΔSOO | MCDF-CI73 4c + Breit | CAS-CI 2c HF | CAS-CI 2c CHYF | CAS-CI + d 2c CHYF | evGW-BSE7 2c TPSSh | SO-CASSCF12 1c + XMCQPDT2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 7FJ | ||||||||||
| J = 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| J = 1 | 370 | 375 | 340 | 374 | 347 | 366 | 329 | 332 | 690 | 380 |
| J = 2 | 1040 | 1058 | 964 | 1041 | 964 | 1026 | 933 | 939 | 732 | 1040 |
| J = 3 | 1890 | 1962 | 1801 | 1916 | 1773 | 1899 | 1743 | 1753 | 801 | 1880 |
| J = 4 | 2860 | 3022 | 2793 | 2931 | 2711 | 2920 | 2702 | 2716 | 2370 | 2830 |
| J = 5 | 3910 | 4192 | 3893 | 4040 | 3734 | 4042 | 3770 | 3784 | 3443 | 3860 |
| J = 6 | 4940 | 5429 | 5069 | 5210 | 4810 | 5233 | 4912 | 4926 | 5229 | 4970 |
| 5DJ | ||||||||||
| J = 0 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 565 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 706 706 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 476 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 969 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 892 892 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046 046 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298 298 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 830 830 |
| J = 1 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213 213 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 202 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 138 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607 607 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 987 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 450 |
| J = 2 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746 746 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556 556 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991 991 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 546 546 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 017 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 140 |
| J = 3 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 478 478 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 823 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864 864 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598 598 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 372 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
||
| J = 4 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 640 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 795 795 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 239 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719 719 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 678 678 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
|||
The overview given in Table 4 indicates that it is still challenging to extract accurate excitation energies for even a single lanthanide ion. Eu3+, featuring a 7F0 ground state is one of the simplest examples, as this state is non-degenerate. Even the simple complete open shell CI (COSCI) variants13 are capable of well describing the 7FJ manifold, especially if 2e SOC corrections are taken into account. However, there are no significant advantages of using the 4c COSCI formalism compared to our simple 2c CAS-CI ansatz, with overall errors being basically identical. In fact, the 1c ansatz that includes SOC perturbatively yields excellent values,12 being nearly indistinguishable even from the 4c results. The only outlier is the evGW-BSE based calculation on the bare ion,7 which, however, acts on the true (symmetry broken) KS ground state instead of a CAS or a spherically averaged reference state. evGW-BSE is therefore not able to capture any significant multireference character, leading to substantial deviations in the 7FJ manifold.
For the 5DJ states, deviations are elevated as demonstrated in Fig. 2–4. All CI based approaches yield too high energies for this state. The 4c COSCI and the 2c CAS-CI approach deliver values of roughly 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, being approximately 2000–3000 cm−1 larger than the experimental reference values. The CAS-CI@DFT calculations are slightly more accurate, indicating that the inclusion of dynamic correlation is more important than a full 4c treatment of the underlying reference state. Furthermore, even extensive Kramers-restricted CI spaces as used in the KRCI and MCDF-CI approaches are merely able to lower this to 18
000 cm−1, being approximately 2000–3000 cm−1 larger than the experimental reference values. The CAS-CI@DFT calculations are slightly more accurate, indicating that the inclusion of dynamic correlation is more important than a full 4c treatment of the underlying reference state. Furthermore, even extensive Kramers-restricted CI spaces as used in the KRCI and MCDF-CI approaches are merely able to lower this to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–19
000–19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1,47,73 still yielding deviations of 1000–1500 cm−1 with respect to the NIST database. While it can be shown that including more and more correlation by expanding the active space indeed recovers the dynamic correlation needed to yield improved atomic levels, the convergence with respect to included states is slow. This is confirmed by our CAS-CI+d calculation, which sets the active space to the 4f+5d orbitals. The latter only lowers the 5D0 state by 250 cm−1, and has no significant effect on the already excellent 7F states at all. 1c SO-CASSCF used in ref. 12 delivers lower deviations than the 2c and 4c approaches, even though they also only use an active space composed of the 4f orbitals and electrons. This can largely be amounted to the “extended multi-configuration quasi-degenerate second order perturbation theory” (XMCQDPT2) correction that is used to include dynamic electron correlation.75 Surprisingly, the 2c evGW-BSE approach yields values closest to those of the experiment, even though it is unable to capture important static correlation effects. Yet, evGW-BSE likely captures a large amount of the dynamic electron correlation, yielding good results overall – although the results likely are also artificially enhanced by error cancelation.
000 cm−1,47,73 still yielding deviations of 1000–1500 cm−1 with respect to the NIST database. While it can be shown that including more and more correlation by expanding the active space indeed recovers the dynamic correlation needed to yield improved atomic levels, the convergence with respect to included states is slow. This is confirmed by our CAS-CI+d calculation, which sets the active space to the 4f+5d orbitals. The latter only lowers the 5D0 state by 250 cm−1, and has no significant effect on the already excellent 7F states at all. 1c SO-CASSCF used in ref. 12 delivers lower deviations than the 2c and 4c approaches, even though they also only use an active space composed of the 4f orbitals and electrons. This can largely be amounted to the “extended multi-configuration quasi-degenerate second order perturbation theory” (XMCQDPT2) correction that is used to include dynamic electron correlation.75 Surprisingly, the 2c evGW-BSE approach yields values closest to those of the experiment, even though it is unable to capture important static correlation effects. Yet, evGW-BSE likely captures a large amount of the dynamic electron correlation, yielding good results overall – although the results likely are also artificially enhanced by error cancelation.
4.3 Nonaaqua complexes of neodymium(III)
Crystal-field splittings of lanthanide ions are still difficult to grasp, yet can also be obtained from the approach outlined above for the bare ions. The difficulty of receiving crystal-field splittings is then redirected to calculating a suitable reference for the molecular ground state. It can still be assumed that the 4f shells are mainly atomic, with no significant mixing with the valence orbitals of the surrounding ligands. While this can be troublesome for many DFT functionals, modern local hybrid functionals constructed from first principles as CHYF can handle the required situations, providing enough flexibility and the rigor to yield qualitatively correct starting points for a subsequent fully relativistic CAS treatment.First, we investigate the aquatic [Nd(H2O)9]3+ complex, as for this complex experimental and theoretical investigations of the crystal-field splitting have recently been carried out.60,76 Nielsen and co-workers found that in solution, a capped square antiprism (cSAP) is prevalent, rather than the commonly assumed tricapped trigonal prism (TTP).60,77Table 5 compares the splitting of the I9/2 state of Nd3+ for these two configurationally different variants using the structures provided by ref. 60. Starting from a PBE0 or CHYF reference using the fractional occupation ansatz described for atoms in the previous section, we find that the experimentally observed crystal-field splitting of the I9/2 ground state is too large for a tricapped trigonal prism. The latter only amounts to 148–222 cm−1 for TTP, while cSAP produces significantly larger splittings of up to 256–289 cm−1, better aligning with the experimental findings of 350–374 cm−1.76 Employing a perturbative spin–orbit correction a posteriori to a CASSCF reference wave function leads to generally larger splittings, yielding 304 cm−1 for the highest crystal-field splitted state of the I9/2 manifold. Although this is in slightly better agreement with the experiment than the CAS-CI approach, the latter is much closer for the first excited state of the I9/2 manifold, predicting 33–35 cm−1, being in line with experimental measurements of 23–39 cm−1, while CASSCF-SO overestimates this splitting by a factor of 4.
| TTP | cSAP | Ref. 60 (cSAP) | Exp. | |||
|---|---|---|---|---|---|---|
| PBE0 | CHYF | PBE0 | CHYF | CASSCF-SO | Abs. | Em. |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 69 | 5 | 35 | 33 | 123 | 23 | 39 |
| 129 | 95 | 175 | 124 | 146 | — | — |
| 180 | 142 | 220 | 188 | 292 | 153 | 164 |
| 222 | 148 | 289 | 256 | 304 | 350 | 374 |
Given the assumption that the actual structure of Nd3+ is highly dynamic, which leads to even larger crystal-field splittings,60 our CAS-CI results are well suited to predict subtle splittings in this complicated lanthanide ion. As determined by Satten, the splitting of the I9/2 manifold is even larger in the [Nd(H2O)9](BrO3)3 crystal.61Table 6 illustrates the values calculated for this structure. Fully relativistic CAS-CI calculations confirm that the splitting found in this crystal is overall slightly larger than for the aquatic solution. For the CHYF reference, this effect is predicted to be moderate, while the PBE0 reference anticipates a more pronounced shift, which fits the overall observed splittings better. However, the differences between the splittings found in solution and in the crystal are overestimated by the PBE0 reference, which especially estimates state 4 to shift by 150 cm−1, though only an actual change of 8–32 cm−1 is found experimentally. The latter predicted change is more in line with the CAS-CI calculated in the CHYF reference, which anticipates a change of roughly 43 cm−1. Furthermore, CAS-CI@CHYF exhibits a nearly constant shift with respect to the experimental values of ref. 61, while CAS-CI@PBE0 yields less systematic deviations in that specific case. We note in passing that the HF reference state leads to no meaningful results in the case of the [Nd(H2O)9](BrO3)3 crystal, due to converging to the wrong state. Therefore, it is omitted from the discussion.
| State mJ | PBE0 | CHYF | ΔPBE0 | ΔCHYF | Exp. |
|---|---|---|---|---|---|
| ±9/2 | 0 | 0 | 0 | 0 | 0 |
| ±7/2 | 83 | 46 | −34 | −71 | 117 |
| ±5/2 | 136 | 85 | −48 | −99 | 184 |
| ±3/2 | 421 | 281 | 58 | −82 | 363 |
| ±1/2 | 442 | 299 | 60 | −83 | 382 |
Conclusions
We have investigated the optical spectra of all relevant lanthanide ions using a newly implemented 2c CAS-CI approach based on KS determinants. Taking the 4f shell and electrons as active space on top of the Kohn–Sham reference yields very good agreement for the ground state terms. For higher lying terms, still significant errors are observed, though they are slightly lower than their 4c CAS based counterparts. We therefore conclude that for ground state terms, the static and dynamic correlation captured by including the 4f shell in the CAS treatment is sufficient. Our CAS-CI@DFT is therefore especially well suited to predict crystal-field splittings in lanthanide ions, as long as excitations are solely described by the 4f manifold. In ref. 7 it has been demonstrated for Eu3+, that the excited 5DJ state can participate in charge-transfer excitations, exceeding the pure 4f orbital space. This has recently been shown experimentally using time-resolved emission spectroscopy.78 In this case, only including the 4f shell in the active space may lead to acceptable excitation energies, although the transition properties will be off. The correlation between the 4f shell and the surrounding ligands needs to be carefully taken into account to correctly predict these properties.Author contributions
Roman Zielke: conceptualization (equal); investigation (lead); methodology (equal); software (lead); validation (equal); visualization (lead); writing – original draft (supporting); writing – review & editing (equal). Florian Weigend: conceptualization (equal); investigation (supporting); methodology (equal); validation (supporting); writing – original draft (supporting); writing – review & editing (equal). Christof Holzer: conceptualization (equal); investigation (supporting); methodology (equal); software (supporting); validation (equal); visualization (supporting); writing – original draft (lead); writing – review & editing (equal).Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Roman Zielke thanks the Turbomole GmbH for financial support. Florian Weigend gratefully acknowledges financial support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the Collaborative Research Centre “4f for Future” (CRC 1573, project number 471424360), project Q.References
- L. Petit, A. Borel, C. Daul, P. Maldivi and C. Adamo, Inorg. Chem., 2006, 45, 7382–7388 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 2003, 119, 2972–2977 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 2005, 122, 064101 CrossRef PubMed.
- C. Holzer and Y. J. Franzke, J. Chem. Phys., 2022, 157, 034108 CrossRef CAS PubMed.
- C. Holzer and Y. J. Franzke, J. Chem. Theory Comput., 2025, 21, 202–217 CrossRef CAS PubMed.
- M. Marques and E. Gross, Annu. Rev. Phys. Chem., 2004, 55, 427–455 CrossRef CAS PubMed.
- C. Holzer, J. Chem. Theory Comput., 2023, 19, 3131–3145 CrossRef CAS PubMed.
- H. Moriyama, Y. Watanabe, H. Nakano, S. Yamamoto and H. Tatewaki, J. Chem. Phys., 2010, 132, 124310 CrossRef PubMed.
- S. Yamamoto and H. Tatewaki, J. Chem. Phys., 2011, 134, 164310 CrossRef PubMed.
- M. Sekiya, F. Sasaki and H. Tatewaki, Phys. Rev. A:At., Mol., Opt. Phys., 1997, 56, 2731–2740 CrossRef CAS.
- P. A. Tanner, Y.-Y. Yeung and L. Ning, J. Phys. Chem. A, 2014, 118, 8745–8752 CrossRef CAS PubMed.
- A. Y. Freidzon, I. A. Kurbatov and V. I. Vovna, Phys. Chem. Chem. Phys., 2018, 20, 14564–14577 RSC.
- O. Visser, L. Visscher, P. J. C. Aerts and W. C. Nieuwpoort, J. Chem. Phys., 1992, 96, 2910–2919 CrossRef CAS.
- W. Van den Heuvel, S. Calvello and A. Soncini, Phys. Chem. Chem. Phys., 2016, 18, 15807–15814 RSC.
- Y. S. Kim and Y. S. Lee, J. Chem. Phys., 2003, 119, 12169–12178 CrossRef CAS.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- C. M. Marian, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fdez. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- R. Feng, X. Yu and J. Autschbach, J. Chem. Theory Comput., 2021, 17, 7531–7544 CrossRef CAS PubMed.
- C. Liao, C. E. Hoyer, R. Banerjee Ghosh, A. J. Jenkins, S. Knecht, M. J. Frisch and X. Li, J. Phys. Chem. A, 2024, 128, 2498–2506 CrossRef CAS PubMed.
- K. Dyall, I. Grant, C. Johnson, F. Parpia and E. Plummer, Comput. Phys. Commun., 1989, 55, 425–456 CrossRef CAS.
- T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher, I. A. Aucar, R. Di Remigio, K. G. Dyall, E. Eliav, E. Fasshauer, T. Fleig, L. Halbert, E. D. Hedegård, B. Helmich-Paris, M. Iliaš, C. R. Jacob, S. Knecht, J. K. Laerdahl, M. L. Vidal, M. K. Nayak, M. Olejniczak, J. M. H. Olsen, M. Pernpointner, B. Senjean, A. Shee, A. Sunaga and J. N. P. van Stralen, J. Chem. Phys., 2020, 152, 204104 CrossRef CAS PubMed.
- A. J. Jenkins, H. Liu, J. M. Kasper, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2019, 15, 2974–2982 CrossRef CAS PubMed.
- T. Fleig, J. Olsen and C. M. Marian, J. Chem. Phys., 2001, 114, 4775–4790 CrossRef CAS.
- L. K. Sørensen, J. Olsen and T. Fleig, J. Chem. Phys., 2011, 134, 214102 CrossRef PubMed.
- T. Kagawa, Y. Honda and S. Kiyokawa, Phys. Rev. A:At., Mol., Opt. Phys., 1991, 44, 7092–7107 CrossRef CAS PubMed.
- T. Fleig, J. Olsen and L. Visscher, J. Chem. Phys., 2003, 119, 2963–2971 CrossRef CAS.
- H. Hu, A. J. Jenkins, H. Liu, J. M. Kasper, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2020, 16, 2975–2984 CrossRef CAS PubMed.
- T. Shiozaki, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2018, 8, e1331 Search PubMed.
- J. E. Bates and T. Shiozaki, J. Chem. Phys., 2015, 142, 044112 CrossRef PubMed.
- R. D. Reynolds, T. Yanai and T. Shiozaki, J. Chem. Phys., 2018, 149, 014106 CrossRef PubMed.
- S. Knecht, H. J. A. Jensen and T. Fleig, J. Chem. Phys., 2008, 128, 014108 CrossRef PubMed.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- A. B. J. Parusel and S. Grimme, J. Porphyrins Phthalocyanines, 2001, 5, 225–232 CrossRef CAS.
- M. Kleinschmidt, J. Tatchen and C. M. Marian, J. Comput. Chem., 2002, 23, 824–833 CrossRef CAS PubMed.
- C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2019, 9, e1394 Search PubMed.
- H. Jiang, P. Rinke and M. Scheffler, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 125115 CrossRef.
- H. Jiang, R. I. Gomez-Abal, P. Rinke and M. Scheffler, Phys. Rev. Lett., 2009, 102, 126403 CrossRef PubMed.
- M. Kehry, W. Klopper and C. Holzer, J. Chem. Phys., 2023, 159, 044116 CrossRef CAS PubMed.
- W. Kutzelnigg, Int. J. Quantum Chem., 1984, 25, 107–129 CrossRef CAS.
- K. G. Dyall, J. Chem. Phys., 1997, 106, 9618–9626 CrossRef CAS.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104 Search PubMed.
- B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189 Search PubMed.
- R. McWeeny, Mol. Phys., 1974, 28, 1273–1282 CrossRef CAS.
- J. Thyssen, PhD thesis, University of Southern Denmark, Odense, Denmark, 2001 Search PubMed.
- C. Holzer, A. M. Wernbacher, J. M. Senekowitsch, K. Gatterer and A.-M. Kelterer, J. Phys. Chem. A, 2014, 118, 11499–11511 CrossRef CAS PubMed.
- O. Visser, L. Visscher, P. J. C. Aerts and W. C. Nieuwpoort, Theor. Chim. Acta, 1992, 81, 405–416 CrossRef CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 Search PubMed.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. J. Franzke, L. Spieske, P. Pollak and F. Weigend, Segmented Contracted Error-Consistent Basis Sets of Quadruple-ζ Valence Quality for One- and Two-Component Relativistic All-Electron Calculations, J. Chem. Theory Comput., 2020, 16(9), 5658–5674, DOI:10.1021/acs.jctc.0c00546.
- O. Treutler, Dissertation (Dr. rer. nat.), University of Karlsruhe (TH), Germany, 1995 Search PubMed.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed.
- Y. J. Franzke, N. Middendorf and F. Weigend, J. Chem. Phys., 2018, 148, 104410 CrossRef PubMed.
- J. C. Boettger, Phys. Rev. B:Condens. Matter Mater. Phys., 2000, 62, 7809–7815 CrossRef CAS.
- M. Filatov, W. Zou and D. Cremer, J. Chem. Phys., 2013, 139, 014106 Search PubMed.
- J. Ehrman, E. Martinez-Baez, A. J. Jenkins and X. Li, J. Chem. Theory Comput., 2023, 19, 5785–5790 CrossRef CAS PubMed.
- V. R. M. Nielsen, M. Grasser, B. Le Guennic and T. J. Soørensen, Inorg. Chem., 2025, 64, 3463–3475 Search PubMed.
- R. A. Satten, J. Chem. Phys., 1953, 21, 637–648 CrossRef CAS.
- M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Cremer, W. Zou and M. Filatov, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 436–467 CAS.
- X. Blase, I. Duchemin, D. Jacquemin and P.-F. Loos, J. Chem. Phys. Lett., 2020, 11, 7371–7382 CrossRef CAS PubMed.
- A. Kramida, Yu. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.12), [Online], Available: https://physics.nist.gov/asd [2025, February 24], National Institute of Standards and Technology, Gaithersburg, MD, 2024 Search PubMed.
- M. Iliaš, V. Kellö, L. Visscher and B. Schimmelpfennig, J. Chem. Phys., 2001, 115, 9667–9674 CrossRef.
- F. Gendron, B. Moore II, O. Cador, F. Pointillart, J. Autschbach and B. Le Guennic, J. Chem. Theory Comput., 2019, 15, 4140–4155 CrossRef CAS PubMed.
- K. A. Romanova, A. Y. Freidzon, A. A. Bagaturyants and Y. G. Galyametdinov, J. Phys. Chem. A, 2014, 118, 11244–11252 Search PubMed.
- F. Gendron, M. Grasser and B. Le Guennic, Phys. Chem. Chem. Phys., 2022, 24, 5404–5410 Search PubMed.
- M. Grasser and B. Le Guennic, Phys. Chem. Chem. Phys., 2024, 26, 7203–7210 RSC.
- O. Vahtras, H. Ågren, P. Jørgensen, H. Jørgen Aa. Jensen, T. Helgaker and J. Olsen, J. Chem. Phys., 1992, 96, 2118–2126 CrossRef CAS.
- M. Seth, K. G. Dyall, R. Shepard and A. Wagner, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2383 CrossRef CAS.
- C. Naleway, M. Seth, R. Shepard, A. F. Wagner, J. L. Tilson, W. C. Ermler and S. R. Brozell, J. Chem. Phys., 2002, 116, 5481–5493 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- V. R. M. Nielsen, P. R. Nawrocki and T. J. Sørensen, J. Phys. Chem. A, 2023, 127, 3577–3590 CrossRef CAS PubMed.
- P. R. Nawrocki and T. J. Sørensen, Phys. Chem. Chem. Phys., 2023, 25, 19300–19336 RSC.
- Y. Kitagawa, T. Tomikawa, K. Aikawa, S. Miyazaki, T. Akama, M. Kobayashi, M. Wang, S. Shoji, K. Fushimi, K. Miyata, Y. Hirai, T. Nakanishi, K. Onda, T. Taketsugu and Y. Hasegawa, Commun. Chem., 2025, 8, 24 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00780a |
| This journal is © the Owner Societies 2025 |
