Proton transfer in methylated G–C: nuclear quantum effects and water-assisted hopping

Abstract

Methylation of DNA nucleobases is a naturally occurring process in living organisms. Usually, it functions as a gene regulation marker and is connected to inheritable epigenetic effects. However, the methylation of guanine in the O⁶ position due to external agents disrupts the hydrogen bonding between pairing bases and may have mutagenic effects. In this paper, we use density functional theory (DFT) to investigate the double proton transfer (DPT) between methyl-guanine (mG) and cytosine. We compare the DPT dynamics between mG–C and nonmethylated G–C using ab initio nuclear quantum dynamics as implemented in the nuclear-electronic orbital (NEO-DFT) approach, where the protons involved in the transfer are described at the same quantum-mechanical level as the electrons of the system. We find that nuclear quantum effects facilitate the DPT for both systems but increase the rate of point mutations for the canonical base pair G–C more significantly. Noteworthy, when similar calculations are performed in the presence of explicit solvent and strand separation, the DPT mechanism becomes assisted by water, lowering the energy barrier of the reaction.

---

1 Introduction

DNA's ability to replicate accurately underlies life continuity, but even a minor deviation in its molecular arrangement can result in mutations. One such deviation is a reorientation of hydrogen-bound protons between base pairs.^1–3 Alternative base forms, tautomers, can form through proton migration, and these can replicate incorrectly, potentially creating genetic mutations.^4,5 To understand mutation rates and genetic information stability, one must understand the processes of proton migration in DNA.^6–8

Methylation of DNA nucleobases facilitates the occurrence of mutations through various mechanisms. Some examples are the misincorporation of matching pairs,^9,10 increasing its susceptibility to reactions like deamination,¹¹ or because they alter the photochemistry of DNA.¹² This study aims to answer whether the methylation of a specific site sufficiently modifies the structure so that the tunnelling phenomenon influences its reactivity.

The methylation of nucleobases is a naturally occurring process in living organisms. Its primary function is regulating gene expression by marking specific sequences,¹³ sometimes as a response to environmental conditions. This feature is, therefore, reversible, but despite not being encrypted in the genetic sequence, it is also inheritable, belonging to the realm of epigenetics.¹⁴ However, methylation of bases may also occur due to the presence of alkylating agents in the cell, either from environmental or endogenous sources.¹⁵

Guanine can be methylated in the O⁶ position when organisms are exposed to smoke from different sources, like pollutants,¹⁶ tobacco or cooked meat,¹⁵ or anticancer drugs.¹⁷ When this happens, the hydrogen bonds between pairing bases are disrupted (see Fig. 1a), which might affect reactions and dynamics in DNA. Thus, it might be a cause of point mutations, given that O⁶-methyl-guanine (hence labelled O⁶mG or simply mG) can pair with thymine instead of cytosine, forming a wobble mismatch.⁹ Although the frequency of guanine methylation varies among individuals, it is considered a highly mutagenic modification.¹⁸

Fig. 1 Structures of (a) O⁶mG–C base pair and (b) G–C base pair, as analysed in implicit solvent. The yellow arrows indicate the direction of the DPT. (c) The protein environment around the base pairs when the strand separation takes place.¹⁹ The green circle indicates the separation site, where DPT takes place. (d) O⁶mG–C in the presence of explicit water molecules as a solvent and the moiety of helicase.

Another source of point mutation is double proton transfer (DPT) between bases, giving rise to tautomers.⁵ Proton tunnelling has been suggested²⁰ to affect the rate of tautomerism in guanine–cytosine (G–C) base pairs, which might result in base pair mismatches after the DNA replication process. Moreover, when it occurs for the O⁶mG–C base pair, the tautomeric form of cytosine (from here labelled C*, whereas the methyl-guanine tautomer will be referred to as mG*, and guanine tautomer as G*) might also mistakenly pair with adenine²¹ instead of guanine during the replication process.¹⁸ In this paper, we use this modified base to illustrate how such modifications can alter tautomeric equilibria, and the two DPT reactions under investigation have been explicitly depicted in Fig. S1 in the ESI.†

The tunnelling phenomenon influences the DPT reaction due to the quantum properties of protons, which allow them to occupy a different position even though they do not have the thermal energy to overcome the respective reaction barrier. With few exceptions, most of the previous studies apply semiclassical corrections to classical reaction rates to measure the relevance of tunnelling for the DPT reaction. Semiclassical quantum correction methods, such as the Wigner or Eckart approaches, often struggle with proton transfer rates, especially in deep or asymmetric potential energy surfaces. These methods also tend to overestimate classical recrossing, leading to inaccuracies in reaction rate predictions.²² To overcome these limitations, in this work we employ the nuclear-electronic orbital density functional theory (NEO-DFT) approach, which considers the protons involved in the DPT at the same quantum-mechanical level as the electrons of the system. Instead of applying a correction, the quantum mechanical properties of the protons are embedded in our calculations, including the system's zero-point energy.²³ In particular, we apply NEO-DFT to calculate the DPT reaction rates in G–C and mG–C. For the protons involved in the DPT, the Born–Oppenheimer approximation is no longer applied, and they are thus subject to delocalisation and anharmonicity.²³ This method should be more befitting to ponder Löwdin's original hypothesis that this mechanism is a possible cause of point mutations, where quantum mechanics is suggested to play an important role.⁶

It is essential to highlight that the lifetime of the tautomeric form in double-stranded DNA is expected to be very short.^3,24,25 Hence, the study of the DPT must be carried out in the context of DNA replication, particularly during DNA strand separation, to assess the impact that tautomerisation effectively has on point mutations.²⁶ For the regular base pair G–C, it is established that the double-strand separation that precedes DNA replication affects the energy landscape of this reaction, causing an increase in the barrier for the DPT.² For this reason, the investigations carried out in the present work have focused on the environmental framework that the replication entails,²⁷ namely explicit solvent and a moiety of the asparagine present in the helicase enzyme, and a static double-strand separation,² implemented by taking screenshots of the base pairs separated by different distances.

To address the influence of the environment, two different systems have been compared. Firstly, all calculations were performed in the presence of an implicit solvent, considering the force field of a protein (see Fig. 1c), since the base pair is not only part of an oligomer but is also in the presence of an enzyme in the context of separation. The second system includes a small moiety of helicase, considering only the atoms closer to the base pair, and four molecules of solvating water (see Fig. 1d). In this manner, it is possible to analyse how the explicit presence of these molecules during the replication process affects the reaction.

Introducing the explicit solvent in the model changes the mechanism of proton transfer between separating base pairs when the distance is enough for a water molecule to approach the intermediate site and assist in this transfer, lowering the energy barriers of the reaction. This behaviour is similar to what was observed by Cerón–Carrasco and co-workers,²⁸ who found that water molecules form a strong hydrogen bond with the bases in G–C, acting as a catalyst for the DPT. Water assistance has also been suggested to play an essential role in other types of DNA tautomerisation.^29,30 Therefore, this study aims to make a thorough investigation of the DPT reaction between base pairs, by assessing how methylation, nuclear quantum effects (NQEs) and the presence of solvent affect the tautomer population that survive DNA replication.

2 Methods

The two structures under analysis are the base pairs O⁶-methyl-guanine–cytosine (mG–C), compared to the canonical base pair guanine–cytosine (G–C). For the systems in implicit solvent (Fig. 1a and b), structures were optimised with the software QChem,³¹ using density functional theory (DFT) at the B3LYP/6-311++G** level of theory. The D4 dispersion correction³² accounts for the long-range interactions the hydrogen bonds add between base pairs. The functional and basis set was recently validated in similar studies.² Our calculations were also benchmarked against a higher level of theory (ωB97X-V functional³³). Gheorghiu et al. have extensively reviewed the accuracy of DFT methods for describing DNA base pairs,²⁴ choosing to stick with B3LYP but using the aug-cc-pVDZ basis set. A comparison between the reaction path obtained from these three different methods is shown in Table T1 and Fig. S2 in the ESI.† All the optimisations are implemented through the atomic simulation environment (ASE) Python package³⁴ and using the BFGS algorithm, with a force tolerance of 0.05 eV Å⁻¹. The presence of implicit solvent is inserted by the PCM model³⁵ with dielectric constant ε = 8.0³⁶ (see Section S3 in ESI† for a more detailed discussion), emulating the proximity with the enzyme helicase, the DNA chain itself and the surrounding aqueous solution, better depicted in Fig. 1c.

The double proton transfer mechanism (DPT reaction) is described with the machine-learning nudged elastic band (ML-NEB) method,³⁷ providing the one-dimensional potential energy surfaces (PES) through an algorithm that finds the minimal energy path (MEP) between an initial and final state. The reaction paths are obtained for six different distances, simulating a static strand separation by separating the base pairs in increments of 0.23 Å until 1.14 Å. Effectively, this strand separation consists of the stretch of hydrogen bonds established between the DNA bases.

Next, a single point energy (SPE) scan is performed on 15 images along the PES using the NEO-DFT method³⁸ to assess how nuclear quantum effects affect the PES of the reaction. Analogous to the DFT approach to the electronic structure, in NEO-DFT, selected protons are included in the nuclear-electronic wave functions that describe the molecular orbital and are expanded with appropriately developed nuclear basis sets.³⁹ Thus, it is possible to find significant changes in the tunnelling probability by considering the protons as quantum delocalised wave functions.

Using the PES obtained from DFT and NEO-DFT, the classical forward and reverse reaction rates are obtained according to eqn (1).

The ħ is the Planck constant, E^f,r stand for the respective forward and reverse reaction barriers and 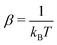, where k_B is the Boltzmann constant, and T is the system's temperature, namely 298 K.

The reaction rates are, in turn, used to build a microkinetic model through the reaction network^40,41 algorithm. A reaction network uses the energy barriers and the equilibrium constants in a system involving multiple reactions to predict each species' concentration as a function of time. This is achieved by solving a set of coupled differential equations, where each equation describes the kinetic rate of a specific reaction. Using the separation speed of helicase-mediated DNA strand separation as 1.2 Å ps⁻¹, it is possible to translate the distance-dependent DPT rates into time-dependent ones. This way, strand separation can be treated as a competing reaction to DPT, and it is possible to determine the fraction of tautomeric species that survives separation, thus leading to misincorporation.

The effect of explicit solvent on the reaction rates was then assessed by adding four water molecules to the DNA during the separation process, as shown in Fig. 1d. This setup has been chosen based on previous molecular dynamics simulations conducted in the context of a helicase-bound DNA system with explicit solvent,²⁷ where the positions of the water molecules in the first solvation shell were extracted from an equilibrated configuration obtained via umbrella sampling. Four molecules of water was also the minimal model employed in the study of proton transfer between base pairs by Cerón–Carrasco.²⁸ This time, the strand separation was performed every 0.35 Å on average, reaching a maximum separation of 1.41 Å for G–C and 1.31 Å for mG–C. Note that strand separation in our model is simulated by increasing the distance between the nitrogen atoms that would be covalently bonded to the backbone, being the initial equilibrium distances 8.67 Å for G–C and 9.56 Å for mG–C. In this case, MACE-ANI-CC⁴² was employed as a machine learning (ML) calculator instead of the QChem calculator and DFT method.

Finally, a molecular dynamics (MD) simulation of B-DNA in a water solvent box was performed with the software GROMACS 2021.1⁴³ using the force field CHARMM36.⁴⁴ Solvent effects were taken into account through the explicit solvent model TIP3P.⁴⁵ MD calculations at a constant number of atoms, volume and temperature (NVT ensemble), at 310.15 K, were performed on a DNA model of twelve alternating G–C pairs built with Avogadro.⁴⁶ Hydrogen bond analysis was performed using the MDAnalysis software at every 2.5 ps timestep over the 20 ns simulation period.^47–49 The occurrence of a hydrogen bond between the surrounding water molecules and G–C pairs was defined according to standard geometric criteria.^50–53 A hydrogen bond was considered if the donor–acceptor (D–A) distance was less than 3.5 Å and the donor–hydrogen–acceptor (D–H–A) angle was greater than 150°.

3 Results

3.1 Double-proton transfer in implicit solvent

The reaction paths regarding the double proton transfer (DPT) between the nucleobases were obtained for six different separation distances between (methyl-)guanine and cytosine to consider the DNA replication scenario. The results of these calculations are shown in Fig. 2 for the mG–C (a) and G–C (b) systems, describing the energetic profile of the DPT reaction. The potential energy surfaces of G–C feature two barriers, where the second barrier is generally significantly smaller than the first. This double-barrier feature characterises the asynchronous nature of the proton transfer,² where the zwitterion intermediate^24,54 G⁻–C⁺ (Fig. 4) emerges after the first proton transfer. This asynchronicity is only observed when the calculations are performed with an implicit solvent, whereas when performed in vacuum this mechanism is veiled, as reported by other authors.^25,55

Fig. 2 One-dimensional potential energy surfaces (PES) regarding the double-proton transfer (DPT) reaction between (a) mG–C and (b) G–C as a function of separating distance. The further the bases are separated, the higher the barriers get. For G–C, the PES feature a small second barrier, reflecting the asynchronous character of the transfer, with the zwitterion G⁻–C⁺ as an intermediate.

As previously mentioned, the tautomerisation reaction must be investigated in the context of DNA double-strand separation. It will only lead to point mutations if the modified bases survive the replication process. The DPT energy barriers significantly increase with the separation of methylated and nonmethylated systems. In contrast, the reaction asymmetry, defined as the difference in energy between canonical and tautomeric base pairs, decreases for G–C but increases for mG–C (Fig. 3).

Fig. 3 (a) Energy barrier of the DPT reaction between bases and (b) difference in energy (asymmetry) between their respective canonical and tautomeric forms, as a function of strand separating distance. The energy barrier increases for both systems, whilst the asymmetry increases for G–C and decreases for mG–C as the bases separate. The panels show the results obtained from DFT and NEO-DFT to compare the effects of nuclear quantum effects on these energies.

During strand separation in the G–C pair, reaction asymmetry decreases while energy barriers increase, making classical over-the-barrier transitions less likely and enhancing the importance of tunnelling in promoting the DPT reaction. In contrast, in mG–C, the barriers become more asymmetric with distance, reducing the tunnelling probability by making the quantum states in the tautomer potential well less accessible. An energy scan of the PES using NEO-DFT was performed (Table T2 in ESI†). We observed that the quantum nuclear motion in hydrogen atoms lowered the tautomerisation energy barriers by an average of 17.7%, and stabilised the tautomeric species by 22.8%. These results indicate how DPT is favoured when considering quantum effects, whereas the reverse reaction of tautomers restoring to the canonical form is not preferred. This is in contrast to a recent study with DFTB and inclusion of NQEs with ring polymer dynamics for the G–C base pair,²⁵ where the authors conclude that NQEs would destabilise tautomerisation since they observe lowering of the DPT barrier but no significant stabilisation of the tautomeric form G*–C*.

The equilibrium constants obtained from the classical tautomerisation rates (see eqn (1) in Section 2) are always one or two orders of magnitude lower than the quantum-corrected ones produced by NEO-DFT calculations when the two protons are allowed to tunnel. These results are shown in Table T3 in ESI,† where they are also compared to equilibrium constants obtained from the Eckart potential tunnelling correction,⁵⁶ analogous to other semiclassical corrections implemented in previous studies.³⁶ We note that the Eckart correction, despite taking into consideration the width and reverse barrier height, leads to reaction rates that are closer to the classical ones than to the rates obtained from NEO-DFT calculations, underestimating the tunnelling probability, which is uncovered when the nuclear quantum effects (NQEs) of the hydrogen atoms are considered, underscoring the necessity of explicitly treating NQEs to capture proton transfer dynamics accurately. By using NEO-DFT, the impact of barrier height and width are captured implicitly through the nuclear wavefunction solution, rather than being treated as explicit inputs. In this case, the delocalised proton may explore a broader region of the potential energy surface than classical approaches would predict, particularly in asymmetric or distorted geometries (like the ones seen for both G–C and mG–C), which significantly alter the effective tunnelling pathway. The success of NEO-DFT in revealing these effects for the first time in DNA base pair DPT further establishes its value in studying biologically relevant hydrogen transfer processes.

3.1.1 Microkinetics model. Using the tautomerisation energy barriers obtained with the two aforementioned methods (DFT and NEO-DFT) to calculate the forward and reverse reaction rates (see eqn (1)), the reaction networks⁴⁰ microkinetic model was applied to account for the equilibrium populations of the system. Here, we consider helicase strand separation as a competing reaction to the DPT, as shown in the insets of Fig. 5. Recall that the proton transfer in mG–C is synchronous, while the DPT in G–C presents a more asynchronous character. For this reason, the zwitterionic form G⁻–C⁺ (Fig. 4) must also be considered when solving the coupled differential equations of the model.

Fig. 4 Intermediate of the DPT reaction, the zwitterion G⁻–C⁺ of the canonical base pair after the first proton transfer.

Fig. 5 shows the equilibrium population of the non-canonical base pairs obtained from the reaction networks model as a function of time. We find that the final population of the tautomer mG*–C* (Fig. 5a) is in the order of 10⁻¹⁵ when the protons involved in the transfer are treated as classical particles, but increases five thousand times when treated with NEO-DFT as quantum nuclei (Fig. 5b), reaching the population of 5 × 10⁻¹², meaning that five tautomers in every trillion base pairs survive the replication machinery. This rate is still lower than the rate of spontaneous mutations, in the order of 10⁻⁸ per nucleotide,⁵⁷ suggesting that even having considered quantum effects, the DPT rates in the methylated system are considerably low.

Fig. 5 Equilibrium population of non-canonical species as a function of time, within the context of strand separation. The dashed lines in all panels show the decrease of the paired bases population as double-strand separation occurs, while the continuous lines show the respective separated forms of the non-canonical species. (a) Tautomer population in the methylated system mG*–C* when the protons are treated as classical nuclei and (b) if considered as quantum nuclei subject to tunnelling. (c) Tautomeric (G*–C*) and zwitterionic (G⁻–C⁺) populations of the regular nonmethylated system for classical protons and (d) when protons are treated as quantum nuclei. The insets in panels (b) and (d) show the competing reactions in the systems that are considered in the reaction networks, namely proton transfer and strand separation by helicase.

As for the classically treated nonmethylated case (Fig. 5c), we find a population of 10⁻⁹ tautomers, but 2.5 times more zwitterions. The populations of both non-canonical species (G⁻–C⁺ and G*–C*) increase a hundred times when adopting a quantum treatment of the nuclei (Fig. 5d), coming to the order of 10⁻⁷, and placing it above the spontaneous point mutation threshold. This makes of NQEs a strong candidate of being the cause of spontaneous mutations in DNA.

It is worth noticing that despite being 50 times more pronounced in the methylated case, it is for G–C that the quantum nuclear effects play a relevant role in increasing mutation rates. Therefore, whereas point mutations in methyl-guanine are more likely to derive from the well-established pairing mG–T,⁹ it can be inferred that point mutations in G–C are strongly influenced by tautomerisation driven by quantum effects.

Moreover, introducing the kinetic frame of reference with the reaction networks has proven to be essential² for deepening our understanding of the G–C system: the most relevant species at equilibrium is, in fact, the zwitterion (G⁻–C⁺) that arises from a single-proton transfer. This result adds to previous ones, where strand separation is not considered, and therefore conclude that the presence of this intermediate would be insignificant.^24,58 Angiolari and co-workers²⁵ also identified the zwitterion as an intermediate form to the DPT reaction in G–C, but suggested it would be destabilised by NQEs, a conclusion that differs from ours. To the best of our knowledge, this is the first study that considers NQEs and strand separation to determine respectively formation and persistence of point-mutation-relevant species. Our results emphasise how incorporating a more dynamic model can improve our understanding of proton transfer and its potential mutagenic consequences.

3.2 Double-proton transfer in explicit solvent

As we aim to understand how the DPT reaction is affected during DNA replication, a simplified model of the helicase and explicit solvent were included in our calculations. The moiety of helicase has been tailored following a previous study by Winokan et al.²⁷ The number of degrees of freedom introduced by the four unconstrained water molecules would make the cost of the DFT NEB prohibitive; hence, the reaction paths for these systems were obtained using the MACE-ANI-CC model⁴² combined with ML-NEB.

The ML force field introduced by the MACE calculator are well-suited to provide molecular structures throughout the reaction paths. However, it is not always capable of reproducing reliable energy values. A comparison between DFT-obtained NEBs and MACE ones is made in Section 5 in the ESI,† where we demonstrate that running an energy scan with DFT on the structures amends this deficiency. For this reason, fifteen images were collected along the reaction paths, including the canonical form, transition state, and tautomeric form of the base pair, on which a single-point energy (SPE) scan was run using the QChem calculator both at the DFT and NEO-DFT levels of theory. Fig. 6 summarises the energy barrier values for the DPT reaction obtained from the three methods, where we see that MACE respects the same trends given by DFT, but differs by 11.4% on average for the barrier energy values obtained from DFT.

Fig. 6 Energy barriers for the DPT reaction in (a) mG–C and (b) G–C with explicit solvent. Black lines represent protons treated classically, orange lines correspond to quantum delocalised nuclei, and blue lines show energies from the ML-trained MACE-ANI-CC calculator. Solid symbols indicate energy barriers where water does not assist proton transfer, while open symbols highlight water-assisted DPT. The solid symbols at the largest separation distance represent values obtained for a forcibly non-water-assisted transfer.

In a study using quantum mechanics/molecular mechanics (QM/MM) umbrella sampling (US), Winokan and co-authors.²⁷ suggest that the presence of the included moiety increases the reaction barrier from 0.47 to 1.35 eV, indicating that the replissome machinery itself is preventing point mutations from occurring by forming hydrogen bonds with the DNA bases. In their study, this is verified by substituting the same asparagine moiety (reproduced in the present work) with an alanine moiety, thus removing the extra hydrogen bond formation from the picture and reaching a relatively lower barrier of 1.18 eV. However, when we compare the reaction barrier of G–C in the presence of asparagine moiety (and no strand separation), we consistently find a barrier of 0.485 eV. The differences in barrier energy might be due to the moiety not having been included in the QM region and to the different functional used, BLYP instead of B3LYP. Hence, the stabilising effect they find arguably stems from other environmental components, like the rest of the helicase enzyme and solvent described in the MM region. On the other hand, our study does not intend to address the general picture introduced by environmental effects but to discuss the role of explicit solvents in proton transfer.

For the first four separating distances, the energy barrier increase observed for the implicit solvent case is reproduced in the explicit solvent scenery as the double-strand separates. The barrier heights are similar to those obtained in an implicit solvent. However, when the separation distance reaches 1.31 Å for mG–C and 1.41 Å for G–C, this pattern breaks. Under closer investigation, a water-assisted mechanism is revealed to transfer one of the protons; this mechanism reduces the barrier concerning what would be expected for a direct-transfer mechanism. The floating solid symbols at the largest separating distance in Fig. 6 display the energy values associated with the proton transfer when the DPT is forcibly performed without the assistance of water by moving it away from the vicinity of the transferring site. The open symbols denote barrier energies for a water-assisted proton transfer, indicating how the explicit presence of water molecules allows for a kinetically favourable reaction.

Fig. 7a shows the water-assisted mechanism found for mG–C: one of the water molecules approaches the site between bases and receives H1 from guanine as it donates H2 to cytosine. At the same time, H3 is transferred directly from N3 in cytosine to N4 in guanine. All three proton transfers occur in a concerted mechanism. In Fig. 7b, we see a somewhat more intricate process for the regular base pair G–C, described in two main steps: first, H1 in guanine is transferred to the water molecule, as it donates H2 to oxygen O1 in cytosine. H1 and H2 hop roughly simultaneously, as H3 transfers from N2 in cytosine to O2 in guanine. Next, the water molecule concomitantly exchanges two protons with cytosine, donating H1 to the amino group as it recovers H2 from oxygen O1, finally leading to the expected tautomeric form. Note that this water-assisted DPT mechanism was only possible for the furthest double-strand separation, when the bases are separated to at least 1.31 Å, and the water molecule can approach the inter-base site without hindrances.

Fig. 7 Water-assisted mechanism of DPT between base pairs when DNA strands are separated by 1.31 Å for mG–C and 1.41 Å for G–C. (a) One-step mechanism for the DPT in mG–C, where one of the protons hops from methyl-guanine to the water molecule and from water to cytosine. (b) A two-step mechanism for the DPT in G–C. First, the proton hops from guanine to water and from water to the oxygen in cytosine. Then, the water molecule exchanges two protons with cytosine to get to the final tautomeric form G*–C*.

In order to confirm that this mechanism was possible, a MD simulation of nonmethylated DNA in water was performed and the formation of hydrogen bonds analysed. The donor–acceptor (D–A) pairs considered for this analysis were N1–OW, OW–O2 and OW–N3, where OW corresponds to the oxygen in a solvent water molecule. The N1–OW hydrogen bond count was significantly less than the other D–A pairs (see Fig. 8a), being the one selected for further analysis since this interaction is the first step in the reaction coordinate, and is limited to a single hydrogen. Within the 20 ps of simulation, 45 occurrences were found where the separation distance between the bases was greater than or equal to 1.41 Å, considering the starting equilibrium distance between the nitrogen atom connected to the backbone in each base as 8.67 Å. The exact interaction that allows for the mechanism described in our paper, where water is bound to the inner nitrogen in guanine (N1), occurred in 46.7% of these cases. The results from the hydrogen bond analysis closely align with the previously discussed findings, highlighting the significance of DNA strand separation. The formation of hydrogen bonds elucidates the potential for the interaction between solvent water molecules and G–C pairs, where water can act as a bridge between the bases (Fig. 8b).

Fig. 8 (a) Number of hydrogen bonds detected for the following D–A pairs: N1–OW (blue), OW–O2 (orange) and OW–N3 (grey). The darker colours represent the total number of hydrogen bonds, while the lighter colours represent the total number of hydrogen bonds with unique water (OW) molecules, to avoid double–counting. (b) Representative snapshot of a timestep for separation distance of 1.41 Å where the water molecule is bridging the N1 and O2 atoms. Included are the N1–OW, OW–O2 and OW–N3 distances in Å.

This result differs from the work of Tolosa,⁵⁴ who performed an investigation of possible mechanisms for proton transfer in G–C using molecular dynamics (MD). Their findings suggest that a concerted mechanism without the assistance of water would be more favourable both kinetically and thermodynamically, but this might be because they use the potential of mean force (PMF) as a method to obtain the PES, stiffening the reaction path taken by the protons. Other studies, however, support that the presence of explicit water creates a more accessible path for the proton transfer by changing the polarisation⁵⁹ of the atoms involved and weakening the hydrogen bond between bases.²⁸ The same is reported in the presence of more complex environmental effects in a study by Cerón–Carrasco and co-workers⁶⁰ using QM/MM, where three base pairs are considered in the QM region to account for stacking effects. They propose that the assisted mechanism promotes tautomerisation, consistent with the spontaneous mutation rates in biological systems. It is worth mentioning that the water-chain mechanism also plays an imperative role in the case of the proton-coupled electron transfer (PCET) that occurs in DNA under excitation,^61,62 where the ionised protons are transferred from molecule to molecule through the Grotthuss mechanism.⁶³

4 Conclusions

This study analysed the effects of methylation, solvent, and strand separation in the tautomerisation reaction of guanine and cytosine due to double proton transfer (DPT). Nuclear quantum effects of the protons involved in the tautomerisation were accounted for via the NEO-DFT framework. This proved to be an effective computational methodology that allows for a thorough investigation of these effects at a reasonable cost.

Nuclear quantum effects were observed to facilitate the reaction in both methylated and nonmethylated base pairs. Still, in the methylated case (mG–C), the rate of tautomerisation remains below the rates of spontaneous point mutations. In contrast, in the canonical system (G–C), these effects can play a significant role in the occurrence of point mutations. Therefore, O⁶mG high mutagenicity is probably associated with its predisposition to pair with thymine instead of cytosine. In contrast, point mutations in canonical G–C are more likely to occur due to tautomerisation, especially considering that nuclear quantum effects are at play. Performing these calculations by modelling the replication scenario through reaction networks was essential to understanding the relevance of the tautomerisation reaction in generating point mutations.

Finally, including explicit solvents unveiled another reaction mechanism, water-assisted double proton transfer. This mechanism reveals the critical role of the environment in spontaneous point mutations and the importance of going beyond simple implicit solvent corrections when modelling DNA reactions.

Author contributions

M. S. and L. S. conceived and designed this research. J. G. A. performed all calculations and data analysis with the assistance of L. S. in preparing the codes. A. P. M. performed hydrogen-bond analysis for the MD calculation. I. R. contributed to editing the original manuscript and the revised version. All authors have approved the final version of the manuscript.

Data availability

The codes used for the calculations and the analysis performed can be found on the GitHub repository at https://github.com/LouieSlocombe/MethylatedProtonTransfer.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. S. acknowledges the Royal Society for funding his research through the University Research Fellowship URF/R/191029. L. S. acknowledges funding from the John Templeton Foundation grant number 62210. This project made use of time on HPC granted via the UK High-End Computing Consortium for Biomolecular Simulation, HECBioSim (https://hecbiosim.ac.uk), supported by EPSRC (grant no. EP/X035603/1). We would also like to thank George Ferguson for the assistance in preparation of MD scripts.

References

1. Y. Kim, F. Bertagna, E. M. D'Souza, D. J. Heyes, L. O. Johannissen, E. T. Nery, A. Pantelias, A. Sanchez-Pedreño Jimenez, L. Slocombe, M. G. Spencer, J. Al-Khalili, G. S. Engel, S. Hay, S. M. Hingley-Wilson, K. Jeevaratnam, A. R. Jones, D. R. Kattnig, R. Lewis, M. Sacchi, N. S. Scrutton, S. R. P. Silva and J. McFadden, Quantum Rep., 2021, 3, 80–126.
2. L. Slocombe, M. Winokan, J. Al-Khalili and M. Sacchi, Commun. Chem., 2022, 5, 144.
3. O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2019, 37, 1880–1907.
4. D. Li, B. I. Fedeles, V. Singh, C. S. Peng, K. J. Silvestre, A. K. Simi, J. H. Simpson, A. Tokmakoff and J. M. Essigmann, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3252–E3259.
5. J. D. Watson and F. H. C. Crick, Cold Spring Harbor Symp. Quant. Biol., 1953, 18, 123–131.
6. P.-O. Löwdin, Rev. Mod. Phys., 1963, 35, 724–732.
7. E. S. Kryachko, Int. J. Quantum Chem., 2002, 90, 910–923.
8. V. L. Golo and Y. S. Volkov, Int. J. Mod. Phys. C, 2011, 133–156.
9. T. Spratt, Nucleic Acids Res., 1997, 25, 3354–3361.
10. L. R. Felske, S. A. P. Lenz and S. D. Wetmore, J. Phys. Chem. A, 2018, 122, 410–419.
11. L. D. Moore, T. Le and G. Fan, Neuropsychopharmacology, 2013, 38, 23–38.
12. X. Wang, L. Martínez-Fernández, Y. Zhang, P. Wu, B. Kohler, R. Improta and J. Chen, J. Am. Chem. Soc., 2024, 146, 1839–1848.
13. R. Murín, M. Abdalla, N. Murínová, J. Hatok and D. Dobrota, Physiol. Res., 2018, 383–389.
14. S. McGraw and S. Kimmins, Nature, 2023, 615, 800–802.
15. W. M. Grady and C. M. Ulrich, Gut, 2007, 56, 318–320.
16. R. Schrott, J. I. Feinberg, C. J. Newschaffer, I. Hertz-Picciotto, L. A. Croen, M. D. Fallin, H. E. Volk, C. Ladd-Acosta and A. P. Feinberg, Environ. Epigenet., 2024, 10, dvae003.
17. Y. Li, P. Mao, E. Y. Basenko, Z. Lewis, M. J. Smerdon and W. Czaja, Sci. Rep., 2021, 11, 18393.
18. J. J. Warren, L. J. Forsberg and L. S. Beese, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19701–19706.
19. R. P. D. Bank, RCSB PDB – 6DGD: PriA helicase bound to dsDNA of a DNA replication fork, https://www.rcsb.org/structure/6DGD.
20. A. D. Godbeer, J. S. Al-Khalili and P. D. Stevenson, Phys. Chem. Chem. Phys., 2015, 17, 13034–13044.
21. O. O. Brovarets and D. M. Hovorun, Phys. Chem. Chem. Phys., 2015, 17, 15103–15110.
22. O. O. Brovarets and D. M. Hovorun, J. Biomol. Struct. Dyn., 2015, 33, 2716–2720.
23. S. Hammes-Schiffer, J. Chem. Phys., 2021, 155, 030901.
24. A. Gheorghiu, P. V. Coveney and A. A. Arabi, Interface Focus, 2020, 10, 20190120.
25. F. Angiolari, S. Huppert, F. Pietrucci and R. Spezia, J. Phys. Chem. Lett., 2023, 14, 5102–5108.
26. J. Florian and J. Leszczyński, J. Am. Chem. Soc., 1996, 118, 3010–3017.
27. M. Winokan, L. Slocombe, J. Al-Khalili and M. Sacchi, Sci. Rep., 2023, 13, 21749.
28. J. P. Cerón-Carrasco, A. Requena, J. Zúñiga, C. Michaux, E. A. Perpète and D. Jacquemin, J. Phys. Chem. A, 2009, 113, 10549–10556.
29. J. Gu and J. Leszczynski, J. Phys. Chem. A, 1999, 103, 2744–2750.
30. A. Furmanchuk, O. Isayev, L. Gorb, O. V. Shishkin, D. M. Hovorun and J. Leszczynski, Phys. Chem. Chem. Phys., 2011, 13, 4311.
31. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al., Mol. Phys., 2015, 113, 184–215.
32. E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512.
33. N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
34. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
35. J. M. H. Lange and W. Adrian, in Many-Body Effects and Electrostatics in Biomolecules, Jenny Stanford Publishing, 2016, ch. 11, pp. 363–416.
36. L. Slocombe, J. S. Al-Khalili and M. Sacchi, Phys. Chem. Chem. Phys., 2021, 23, 4141–4150.
37. E. L. Kolsbjerg, M. N. Groves and B. Hammer, J. Chem. Phys., 2016, 145, 094107.
38. S. P. Webb, T. Iordanov and S. Hammes-Schiffer, J. Chem. Phys., 2002, 117, 4106–4118.
39. Q. Yu, F. Pavošević and S. Hammes-Schiffer, J. Chem. Phys., 2020, 152, 244123.
40. I. J. Kimsey, E. S. Szymanski, W. J. Zahurancik, A. Shakya, Y. Xue, C.-C. Chu, B. Sathyamoorthy, Z. Suo and H. M. Al-Hashimi, Nature, 2018, 554, 195–201.
41. H. Warman, L. Slocombe and M. Sacchi, RSC Adv., 2023, 13, 13384–13396.
42. D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, J. Chem. Phys., 2023, 159, 044118.
43. H. J. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
44. J. Huang and A. D. MacKerell Jr, CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data, J. Comput. Chem., 2013, 34(25), 2135–2145,  DOI:10.1002/jcc.23354.
45. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
46. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17.
47. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
48. R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux, I. M. Kenney, et al., MDAnalysis: a Python package for the rapid analysis of molecular dynamics simulations, Los alamos national laboratory (lanl), los alamos, nm (united states) technical report, 2019.
49. P. Smith, R. M. Ziolek, E. Gazzarrini, D. M. Owen and C. D. Lorenz, Phys. Chem. Chem. Phys., 2019, 21, 9845–9857.
50. M. Z. Brela, P. Kubisiak and A. Eilmes, J. Phys. Chem. B, 2018, 122, 9527–9537.
51. J. Liu, X. He, J. Z. Zhang and L.-W. Qi, Chem. Sci., 2018, 9, 2065–2073.
52. H. Liu, S. Xiang, H. Zhu and L. Li, Molecules, 2021, 26, 5403.
53. T. Wang, X. He, M. Li, Y. Li, R. Bi, Y. Wang, C. Cheng, X. Shen, J. Meng and H. Zhang, et al., Nature, 2024, 1–9.
54. S. Tolosa, J. A. Sansón and A. Hidalgo, J. Mol. Liq., 2018, 251, 308–316.
55. E. E. Romero and F. E. Hernandez, Phys. Chem. Chem. Phys., 2018, 20, 1198–1209.
56. C. Eckart, Phys. Rev., 1930, 35, 1303.
57. A. S. Kondrashov, Hum. Mutat., 2003, 21, 12–27.
58. A. Pérez, M. E. Tuckerman, H. P. Hjalmarson and O. A. Von Lilienfeld, J. Am. Chem. Soc., 2010, 132, 11510–11515.
59. Z. Lv, S. Cui, F. Guo and G. Zhang, AIP Adv., 2019, 9, 015015.
60. J. P. Cerón-Carrasco, J. Zuniga, A. Requena, E. A. Perpete, C. Michaux and D. Jacquemin, Phys. Chem. Chem. Phys., 2011, 13, 14584–14589.
61. R. N. Barnett, J. Joseph, U. Landman and G. B. Schuster, J. Am. Chem. Soc., 2013, 135, 3904–3914.
62. T. Cherneva and V. Delchev, Turk. J. Chem., 2022, 46, 1909–1917.
63. K. Khistyaev, A. Golan, K. B. Bravaya, N. Orms, A. I. Krylov and M. Ahmed, J. Phys. Chem. A, 2013, 117, 6789–6797.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00854a

‡ Present address: Beyond Center for Fundamental Concepts in Science, Arizona State University, Tempe, Arizona 85287-0506, USA.

---