Effect of heteroatom incorporation on electronic communication in metal chalcogenide nanoclusters

Abstract

Metal chalcogenide nanoclusters (NC), specifically of type TM₆E₈(L)₆ (TM = transition metal, E = chalcogen, L = ligand) have garnered attention in recent years as promising catalysts and biosensors due to their remarkable electronic and magnetic properties, as well as their ability to undergo supramolecular assembly into 2D materials. Furthermore, the undercoordinated metal chalcogenide NCs have shown distinct surface reactivity, which is strongly dependent on the composition of the TM core. The differences in the reactivity of the undercoordinated species have been attributed to differences in ligand binding energies. Although ligand binding energies in homometallic NCs have been extensively studied, little is known about the effect of heteroatoms in the core on the strength of ligand binding in metal chalcogenide NCs. In this work, we provide new insights into this topic by examining the relative stability of [Co_6−xFe_xS₈(PEt₃)₆]⁺ (x = 0–6) NCs towards fragmentation using collision energy-resolved collision-induced dissociation (CID) experiments. We observe that the ligand binding energy gradually decreases until four Fe atoms are incorporated into the cluster core and then gradually increases until all the Co atoms are replaced with Fe. This experimental trend was compared with the results of density functional theory (DFT) calculations, which indicate drastic differences in the electronic communication between Co and Fe atoms in the TM core. By understanding the effect of heteroatom incorporation on ligand binding energy to the NC core, our work provides important insights into the effect of atom-by-atom substitution on the functional properties of tunable nanostructures.

---

Introduction

Atomically precise nanoclusters (NC) are an exciting class of mixed inorganic–organic systems that exhibit properties of both molecular species and nanoparticles. Ligand-capped NCs are typically composed of a well-defined, ultrasmall multi-metal core protected by a covalently bound organic ligand layer.¹ Similar to transition metal systems, a unique aspect of NCs is that different ligands favor specific metal core sizes.² Moreover, the composition of the ligand shell influences structure, reactivity, and chirality, thereby imparting distinct physical and chemical properties of NCs. For example, the achiral ligands in Au₁₃Cu₂,⁶ enzyme-inspired ligands in [Au₂₅(pMBA)₁₈]⁻,³ and alkynyl-protected ligands in Au₃₈,⁷ have been tailored to promote CO₂ reduction. In metal chalcogenide NCs, specifically of type TM₆S₈(PEt₃)₆, (TM = transition metal) the ligands can be systematically removed from the NC with blue light as reported for Co NCs,³ or altered to change the electrochemical properties of the NC as reported for Fe NCs.⁵ For the neutral and cationic Co₆ NC systems, the ligands are thermally labile, and can therefore be removed with heat or collision induced dissociation (CID).^4–6 Systematically removing a ligand significantly enhances the NCs catalytic activity and charge transfer properties.^7,8 Additional research has shown ligand-mediated surface restructuring in comparison with bare copper nanoclusters for catalysis.⁹ Furthermore, ligand removal promotes the formation of dimers and larger oligomers of NCs on surfaces.¹⁰ The undercoordinated species, which are known to be chemically and catalytically active, are of interest to a broad range of applications.¹¹

In addition to the ligand shell, heteroatom incorporation has been widely used for tailoring the electronic and magnetic properties of metal chalcogenide NCs.^12,13 Tuning the multi-metallic core is an effective route to changing the activity and selectivity of the NCs. Mass-selected ion deposition experiments, for example, show that the undercoordinated [Co₅FeS₈(PEt₃)₅]⁺ species do not react on surfaces while the analogous [Co₆S₈(PEt₃)₅]⁺ species undergoes selective dimerization.¹⁰ Moreover, significant differences in ligand binding energies among [Co₅MS₈(PEt₃)₆]⁺ (M = Mn, Fe and Ni) NCs have been observed in collision energy-resolved CID experiments.¹⁴ Interestingly, NCs with higher ligand binding energy generate undercoordinated species that undergo selective dimerization on surfaces while species with low ligand binding energy produce stable, unreactive fragments.¹⁸ These studies have demonstrated the influence of heteroatom incorporation on the surface reactivity and gas-phase stability of atomically precise NCs.

In our previous study, we synthesized a series of [Co_6−xFe_xS₈(PEt₃)₆]⁺ (x = 0–6) (Co_6−xFe_x for short) by varying the ratio of FeCl₂ to CoCl₂ precursors.¹⁵ Using electrospray ionization mass spectrometry (ESI-MS), we found that by increasing the concentration ratio of FeCl₂ to CoCl₂, up to six Fe atoms can be incorporated into the core of the NCs. We used high resolution ion mobility spectrometry measurements to examine structural changes associated with the incorporation of Fe atoms into the Co₆ core. Our results demonstrated that when Co atoms are successively replaced with Fe atoms, the collision cross section of [Co_6−xFe_xS₈(PEt₃)₆]⁺ gradually increases, indicating that the cluster size increases with the number of Fe atoms in the core.^15,16 It is remarkable that density functional theory (DFT) calculations combined with trajectory method collision cross section simulations successfully reproduced the experimentally observed trend. This close agreement between experimental data and theoretical predictions highlights the potential of using [Co_6−xFe_xS₈(PEt₃)₆]⁺ NCs as a benchmark for validating theoretical models. However, modeling ligand binding energy in these systems is difficult due to the multiple possible spin configurations and the variety of dissociation pathways, where ligand detachment can occur from different metal atoms within the core.

In this study, we address this challenge by systematically investigating the effect of each Fe atom on the structure, relative stability, core-ligand interaction, and fragmentation pathways of these NCs. Specifically, we examine the relative stability of each [Co_6−xFe_xS₈(PEt₃)₆]⁺ (x = 0–6) species towards fragmentation using collision energy-resolved CID experiments. By comparing the values of collision energies required to observe the loss of the first neutral ligand for this series of NCs, we determined that the ligand binding energy gradually decreases until four Fe atoms are incorporated into the cluster core and then gradually increases until all the Co atoms are replaced with Fe. In other words, the cluster with the Co₆ core is the most stable and the cluster with the Co₂Fe₄ core is the least stable towards ligand loss across this series. This trend is rationalized using DFT calculations of the most stable spin states of the precursor ions and their undercoordinated analogs. Furthermore, the NBO analysis shows that the Fe atoms in the NC core exhibit electronic interactions similar to a bulk material or nanoparticle. Specifically, we observe the adjustment of the d-orbital occupancy of all Fe atoms in the core, which helps compensate for the local alteration in the electronic structure following ligand removal. In contrast, Co atoms retain the same average d-orbital occupancy, even when the ligand is removed. Our results indicate that Fe and Co exhibit distinctly different atomic characteristics, despite self-assembling into geometrically similar NCs. This work provides insights into the effect of atom-by-atom incorporation on the stability of atomically precise metal chalcogenide NCs towards ligand loss. The qualitative correspondence between experimental data and theoretical predictions establishes a robust foundation for investigating structural changes of transition metal NCs of interest to a broad range of applications.

Methods

Mass spectrometry experiment

ESI-MS experiments were conducted using a trapped ion mobility time-of-flight mass spectrometer (Bruker timsTOF Pro2, Bruker Daltonics, Bremen, Germany). Details of synthesis are provided in Note S1 (ESI†). The as-synthesized solution containing Co_6−xFe_x NCs was diluted in methanol to 10–20 μM. A custom-designed ESI source was operated in positive ionization mode. Samples were delivered through a fused silica capillary (OD 150 μm ID 50 μm, Polymicro Technologies L.L.C., Phoenix, AZ) to the mass spectrometer inlet using a syringe pump (LEGATO 180, KD Scientific, Holliston, MA) at a flow rate of 0.3 μL min⁻¹. Positive ions were generated by applying a high voltage of +4.5 kV to the front of the glass capillary of the timsTOF inlet. Mass spectra were acquired over an m/z range of 200–2000 with a mass resolution (m/Δm) of 20 000. Mass calibration was performed using the ESI-L tune mix (Agilent Technologies). Collision energy-resolved CID experiments were performed on mass-selected cations using nitrogen as the collision gas. The isolation window was 1.3 m/z with collision energies ranging from 0 to 60 eV. Additional parameters in the timsTOF system that could influence the in-source fragmentation are provided in Table S1 (ESI†).

Computational details

Geometry optimizations on [Co_6−xFe_xS₈(PEt₃)₆]⁺ and [Co_6−xFe_xS₈(PEt₃)₅]⁺ (x = 0, 1, 3, 6) NCs were completed with density functional theory (DFT) in ORCA 5.0.3.¹⁷ Every NC was optimized at the PBE0-D3/def2TZVP level of theory. PBE0 is a one parameter hybrid functional with 25% exact Hartree–Fock exchange,¹⁸ ‘-D3’ incorporate dispersion effects according to the Grimme3 model,¹⁹ and def2TZVP is an all-electron valence triple-ζ basis set with polarization functions.^20,21 The RIJ(COSX) approximation was used,²² and all calculations were completed in the gas phase without symmetry constraints. As these clusters have an open electronic shell, several spin multiplicities were optimized, and the lowest energy was deemed most stable. To verify the spin multiplicities, spin-polarized geometry optimizations were completed in Vienna ab initio Simulation Package (VASP), version 5.4.4, with the PBE functional to obtain the magnetic moment of each NC (Table S2, ESI†).^23,24 VASP calculations were completed with the projector augmented wave (PAW) method to represent the ionic cores,²⁵ with a cutoff energy of 400 eV and gamma k-points. Natural bond orbital analysis (NBO)^26,27 and frequency calculations were completed on the lowest energy spin state for each NC using PBE0-D3/CEP-31G in Gaussian 16,²⁸ where CEP-31G is an effective core potential double-ζ basis set.^29,30 The zero-point energy and Gibb's free energy corrections from the frequency calculations were added to the absolute energy from ORCA to calculate ΔE_ZPE and ΔG_298.15 values for ligand binding. Partial oxidation states were calculated using the concepts and perl script provided in the work of Webster et al.,^31,32 and Patel et al.³³ Using NBO calculations, the NAO occupation matrix for the valence electrons of transition metal atoms is computed, resulting in a 5 × 5 array for spin up and spin down electrons. The array is diagonalized, resulting in eigenvalues (between 0 and 1) that represent the d-orbital occupancy. These values are then used to establish an oxidation state using different threshold values.³¹ Partial density of states (DOS) were computed on each NC using GaussSum³⁴ with a 0.30 eV FWHM.

Results

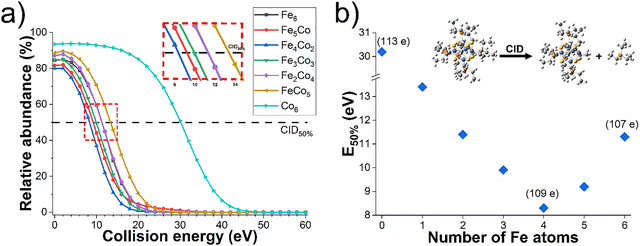
To investigate the influence of each incorporated Fe atom on the relative stability, core-ligand interaction, and fragmentation pathways of Co_6−xFe_x NCs, we conducted collision energy-resolved CID experiments. Survival curves obtained for each species in this series of NCs are shown in Fig. 1a. Each curve shows the relative abundance of a mass-selected precursor ion as a function of collision energy. The relative stability of each Co_6−xFe_x NC towards fragmentation can be evaluated using the values of collision energies corresponding to 50% fragmentation of the precursor ion (E_50%).³⁵ Because the loss of one triethyl phosphine ligand (PEt₃) is the major pathway for all Co_6−xFe_x NCs, the relative stability is largely determined by the loss of the first ligand from the NC resulting from the M–P bond cleavage. A comparison of the survival curves of each Co_6−xFe_x NC shown in Fig. 1a indicates that the Co₆ NC is a considerably more stable precursor than all other NCs in this series with a value of E_50% of 30.2 eV. The values of E_50% obtained for all the NCs are plotted in Fig. 1b. The stability of Co_6−xFe_x NCs toward ligand loss in the gas phase is in this order: Co₆ ≫ Co₅Fe > Co₄Fe₂ ≈ Fe₆ > Co₃Fe₃ > CoFe₅ > Co₂Fe₄. The incorporation of one Fe atom into the Co₆ core is associated with a dramatic decrease in the value of E_50% to 13.4 eV indicating a substantially lower stability of the Co₅Fe NC towards ligand loss. This observation is partially explained by the lower Fe-PEt₃ binding energy of 1.13 eV as compared to 1.65 eV reported for Co-PEt₃.¹⁴ Although the survival curves of all the NCs except for Co₆ are close to each other, we observe an interesting systematic trend in the values of E_50% across the series. Specifically, we observe that ligand binding energy gradually decreases until four Fe atoms are incorporated into the cluster core and then increases until all the Co atoms are replaced with Fe. Our results indicate that the Co₂Fe₄ core is the least stable NC towards ligand loss across this series. This finding is consistent with theoretically predicted electronic shell closure in related NCs.^36,37 While previous literature attributing the stability of the transition metal core to the electronic shell closure was solely based on theoretical analysis,^36,37 this work provides the first experimental observation of such a periodic trend.

Fig. 1 (a) Survival curves showing the relative abundance of mass-selected precursor ions of Co_6−xFe_x NCs as a function of collision energy in CID experiments. The horizontal dashed line corresponds to 50% fragmentation of the precursor ions. (b) The values of collision energies corresponding to 50% fragmentation (E_50%) versus the number of Fe atoms in Co_6−xFe_x NCs. The inset illustrates ligand removal from the fully coordinated Co₆ NC.

To better understand the periodic trend in energies required to remove the first ligand from the NCs observed experimentally, we examined the structures and stability of [Co_6−xFe_xS₈(PEt₃)₆]⁺ and [Co_6−xFe_xS₈(PEt₃)₅]⁺ (x = 0, 1, 3, 6) species using DFT calculations. To accurately model Co_6−xFe_x NCs, we examined multiple spin states and isomeric structures. Considering the number of possible states and symmetrically different geometries as the ligand is removed, only a subset of the experimental NCs were modelled. Each NC was optimized using PBE0-D3/def2-TZVP level of theory, which demonstrated excellent correspondence between DFT-calculated geometries and experimentally measured collision cross section values, with deviations of less than 3%, as reported in our previous work.¹⁵ Notably, the PBE0 functional used in this study has been shown to provide accurate geometries, band gaps, and optical gaps for similar transition metal NC systems.³⁸

Initially, each fully ligated NC was optimized at different spin multiplicities, where the lowest energy isomer was deemed most stable. Our previous study provides a detailed discussion of the fully ligated NCs from this series,¹⁵ but for reference, the relative energies of different spin states of these species are summarized in Table S3 (ESI†). Unlike the fully ligated NCs, the undercoordinated NCs exhibit different structural isomers as the ligand can be removed from any metal of the core. To reduce the number of structural isomers, we initially calculated geometry optimizations for the undercoordinated species starting with structures we expected to be symmetrically equivalent. For example, in homometallic NC cores such as Fe₆ and Co₆, it is expected that the energy would be nearly degenerate regardless of which metal loses the ligand, due to the symmetry of the TM core. The symmetrically equivalent isomers were used as the initial geometries for each NC in the series. For Fe₆ and Co₆ cores, we removed the ligand from one of the metal atoms in the NC core as depicted in the image in Fig. S1 (ESI†). For Co₅Fe, the ligand removal generates three distinct isomers shown in Fig. S2 (ESI†): (1) the ligand is removed from the Fe atom, (2) the ligand is removed from the Co atom across from Fe (Co – trans), and (3) the ligand is removed from the Co atom adjacent to Fe (Co – cis). For Co₃Fe₃, four different isomers shown in Fig. S3 (ESI†) can be formed by (1) removing the ligand from the Fe atom adjacent to Co (Fe – 1), (2) removing the ligand from the Fe atom that resides between two other Fe atoms (Fe – 2), (3) removing the ligand from the Co atom adjacent to Fe (Co – 1), and (4) removing the ligand from the Co atom located between two other Co atoms (Co – 2). The relative energies of all the optimized structures and their spin states are summarized in Table S4 (ESI†). The results shown in this table indicate that, for NCs with mixed Co/Fe cores, ligand removal from Fe atoms is more energetically favorable than ligand removal from Co atoms. For example, the lowest-energy structure of the undercoordinated Co₅Fe is the species generated by removing the ligand from the Fe atom. Meanwhile, the lowest-energy structures of the Co-cis and Co-trans isomers are 0.23 eV and 0.18 eV higher in energy, respectively.

One thing to note is that the initial set of isomers for the undercoordinated NCs were not energetically degenerate. For example, when the ligand is removed from the second Co atom (M2) in [Co₆S₈(PEt₃)₅]⁺, the optimized geometry is 0.11 eV higher in energy than when the ligand is removed from the first Co (M1) in [Co₆S₈(PEt₃)₅]⁺. This energetic difference can be attributed to Jahn–Teller distortion. Specifically, when the ethyl groups of triethylphosphine ligands rotate, they change the ligand shell of the NCs, which distorts the symmetry of the TM core. While Jahn–Teller distortion is most commonly observed in octahedral compounds, there are several examples where symmetry breaking in the ligand shell leads to a distortion in the symmetry of the NC. For example, square pyramidal Cu complexes, which share a similar bonding environment with the Co/Fe NCs, are known to exhibit structural distortions.³⁹ Due to this energetic difference, the initial geometries were not sufficient to cover the number of structural isomers. We therefore examined the geometries produced by removing one ligand from each metal atom in the core in all NCs of the series. The relative energies between different undercoordinated NCs with the ligand removed from each metal center (M1–M6) are summarized in Table S5 (ESI†). This table outlines that the ligand removed from different metals in all the heteroatom and Fe₆ species have larger energetic gaps between structural isomers compared to Co₆. For example, in Fe₆, ligand removal from the Fe atom at position M3 is 0.97 eV less favorable than ligand removal from the Fe atom at position M2 in [Fe₆S₈(PEt₃)₅]⁺ at the same spin multiplicity. Further, in mixed Fe/Co NCs, ligand removal from any of the Fe atoms is more energetically favorable than ligand removal from Co atoms. For example, the undercoordinated species is 0.20 eV higher in energy, or less favorable, when the ligand is removed from any of the Co atoms than if it is removed from the Fe atom. Additionally, the lowest energy isomer in [Fe₆S₈(PEt₃)₅]⁺ is when the ligand is removed from the second Fe atom (M2) with a spin multiplicity of 6; however, there are two other structural isomers nearly degenerate, 0.01 and 0.03 eV higher in energy. These nearly degenerate isomers are when the ligand is removed from Fe atom (M4) or removed from Fe atom (M1) in [Fe₆S₈(PEt₃)₅]⁺ respectively, with the NC at spin multiplicity 8. Overall, the lowest energy structural isomers of the undercoordinated species are when the ligand is removed from: (1) Co atom, M1, in Co₆ with spin multiplicity 4, (2) Fe atom, M5, in Co₅Fe with a spin multiplicity of 5, (3) Fe atom, M1, in Co₃Fe₃ with a spin multiplicity of 9, and (4) Fe atom M2 in Fe₆ at a spin multiplicity of 6.

From the optimized geometries, we calculated ligand binding energies using the lowest energy isomeric structures and spin state multiplicities of [Co_6−xFe_xS₈(PEt₃)₆]⁺ and [Co_6−xFe_xS₈(PEt₃)₅]⁺ (x = 0 (Co₆), 1 (Co₅Fe), 3 (Co₃Fe₃), and 6 (Fe₆)) species. The ligand binding energy was calculated from the difference in energy of the lowest energy structures shown in reaction 1 (ΔE). Single point calculations were performed on the structures at the PBE0-D3/CEP-31G level of theory to obtain zero-point energy (ZPE) and thermodynamic corrections at 298.15 K. The CEP-31G basis set was used for single point calculations as the calculation of vibrational spectra is computationally expensive at the def2TZVP basis set. The vibrational frequencies obtained at this level of theory were used to calculate ligand binding energies with the ZPE correction (ΔE_ZPE) as well as Gibbs free energies at room temperature (ΔG_298.15) using reaction 1. The ZPE and Gibbs free energy corrections are shown in Table S6 (ESI†) for the lowest energy structural isomers and spin multiplicity. The ligand binding energies are summarized in Table 1.

[Co_6−xFe_xS₈(PEt₃)₆]⁺ → [Co_6−xFe_xS₈(PEt₃)₅]⁺ + (PEt₃) (1)

Table 1 Ligand binding energies of [Co_6−xFe_xS₈(PEt₃)₆]⁺ (x = 0, 1, 3, and 6) species calculated at the PBE0-D3/def2TZVP level of theory (L = PEt₃; ZPE = zero point energy)

	Spin multiplicities		ΔE (eV)	ΔEZPE,298.15 (eV)	ΔG298.15 (eV)
	[Co6−xFexS8L6]^+	[Co6−xFexS8L5]^+
Co6	2	4	2.24	2.16	1.53
Co5Fe	3	5	2.00	1.93	1.29
Co3Fe3	3	9	1.50	1.33	0.74
Fe6	4	6	1.57	1.49	0.86

---

As shown in Table 1, the calculated values qualitatively reproduce the experimental trend in ligand binding energies. Specifically, the stability of Co_6−xFe_x NCs toward ligand loss in the gas phase is in the order: Co₆ > Co₅Fe > Fe₆ > Co₃Fe₃. To further compare with experiments, ligand binding energies were calculated on the multi metal NCs with the undercoordinated lowest energy isomer such that the ligand is removed from the Co atom. These values are summarized in Table S7 (ESI†), where we observe that the removal of a ligand from the Fe atom is energetically more favorable than its removal from the Co atom. These results are consistent with previously published calculations for Co₅Fe NC.¹⁸

Notably, for all the NCs examined in this study, the electrons in the undercoordinated species rearrange to a higher spin multiplicity. For example, the lowest energy undercoordinated Co₆ is in the quartet state while the fully ligated species is in the doublet state. Multiplicity often changes in TM systems when a ligand is lost due to changes the coordination environment of a metal center.⁴⁰ To further examine differences in ligand binding energies of the NCs, we calculated the energy gap between the highest occupied and lowest unoccupied electronic orbitals (SOMO–LUMO). The results are summarized in Table S8 (ESI†). We observe that all the undercoordinated NCs have a lower SOMO–LUMO gap compared to their fully ligated counterparts. This indicates the reduced electronic stability of the undercoordinated NCs compared to their fully ligated counterparts. Overall, there is a good qualitative correspondence between the experimental and computational results presented in this study. Notably, DFT calculations reproduce the following experimental findings: (1) the Co₆ NC has the highest ligand binding energy in the series; (2) the incorporation of one Fe atom into the Co₆ core substantially decreases the stability of the NC towards ligand loss; (3) the calculated ligand binding energy follows the order Co₆ > Co₅Fe > Fe₆ > Co₃Fe₃, which is consistent with the experimental data.

To better understand the trend in ligand binding energies, we performed detailed NBO calculations for the lowest energy isomers of the NCs with six and five ligands. Specifically, the natural atomic orbitals (NAO) occupation matrix for the valence electrons was diagonalized to obtain the spin-up and spin-down d-orbital occupancy for each metal center in the NCs. Applying a threshold value to the electronic occupancies, depending on the electron withdrawing nature of the ligands, a partial oxidation state (POS) for each metal center as can be obtained. For completeness, we calculated the POS at different threshold values as seen in Tables S9 and S10 (ESI†), however the threshold value is unknown for these types of NCs. Due to this, it is more meaningful to analyze the electronic communication between Co and Fe atoms using the total d-orbital occupancy. For each NC, we calculated the d-orbital occupancy from the NAO matrix by adding the spin up and spin down electron occupancies for each metal atom in the NC. The values of spin up and spin down occupancies are summarized in Tables S11 and S12 (ESI†). The average d-orbital occupancy was then computed for atoms of the same type, i.e., Fe or Co. Fig. 2 shows the average d-orbital occupancy for different metal centers, Fe and Co, in both the fully ligated (L6) and undercoordinated (L5) Co_6−xFe_x (x = 0, 1, 3, 6) NCs.

Fig. 2 Average d-electron occupancies of Fe and Co atoms in the fully ligated and undercoordinated Co_6−xFe_x (x = 0, 1, 3, 6) NCs at the PBE0-D3/def2TZVP level of theory.

Notably, the d-orbital occupancy of the Co atoms remains nearly constant across all NCs, with a value ∼8.46 e. Given that Fe has a valence of 8 and Co has a valence of 9, one would expect Fe to exhibit a lower d-orbital occupancy than Co, which is indeed observed in all cases. In contrast, the average occupancy of Fe atoms fluctuates significantly, ranging from 6.60 e to 7.53 e. Additionally, in the undercoordinated mixed Co/Fe NCs, the average Fe occupancy decreases by ∼0.50 e compared to their fully ligated counterparts. This suggests that Fe d-orbital occupancy is highly sensitive to changes in the local environment, such ligand removal and heteroatom doping. Notably, the decrease in the Fe d-orbital occupancy upon ligand removal indicates that the surrounding ligand shell exhibits redox noninnocent characteristics, actively tuning the electronic structure of the Fe d-orbitals.

Another interesting observation is that in all the L5 systems containing Fe, the d-orbital occupancy changes not only in the Fe atom that loses the PEt₃ ligand but also in all other Fe atoms within the NC (see Tables S11 and S12, ESI†). This suggests all the Fe atoms electronically “communicate” with each other, a phenomenon characteristic of transition metal bulk materials.⁴¹ In contrast, the d-orbital occupancy of Co atoms is largely unaffected by heteroatom incorporation or ligand removals, indicating a lower susceptibility to local environmental changes. The only notable exception is [Co₆S₈(PEt₃)₆]⁺, where Co d-orbital occupancy significantly shifts upon ligand removal. However, because the overall charge of the NC remains unchanged, the electron redistribution must still occur to compensate for the change in partial charge of the metal atom, from which the ligand is removed. Interestingly, this change is localized to only two Co atoms: the one losing the ligand with a d-orbital occupancy of 7.65 e, (M1 Table S12, ESI†) and its symmetry-equivalent position across the C3 axis with a d-orbital occupancy of 8.06 e, (M5 Table S12, ESI†) while the remaining Co atoms retain the occupancy of ∼8.46 e. These differences in d-orbital occupancy shifts upon ligand removal suggest that Fe atoms respond differently than Co atoms to local electronic perturbations caused by ligand loss.

Table 2 shows the total d-orbital occupancy for each metal center in the fully ligated and undercoordinated Co₅Fe NC. The total occupancy for each metal center in the rest of the series is shown in Tables S8 and S9 (ESI†). In Co₅Fe, the sole Fe atom has a d-orbital occupancy of 7.15 e, which is significantly lower than the ∼8.45 e occupancy of the Co atoms. Upon ligand removal, the d-orbital occupancy of the Fe atom further decreases to 6.60 e while the occupancies of Co atoms remain unchanged. This decrease in occupancy suggests that the Fe atom exhibits more redox noninnocent characteristics than the Co atoms. Similarly, in Co₃Fe₃, the Fe atom that preferentially loses the ligand has a d-orbital occupancy of 7.15 e while Co atoms retain their ∼8.45 e occupancies. Meanwhile, the other two atoms exhibit higher d-orbital occupancies of ∼7.50 e. This higher value is consistent with the occupancy of Co atoms in the core corrected for the difference in the valence electron counts between Fe and Co. Overall, these results indicate that ligand loss preferentially occurs at the Fe atom with the lowest d-orbital occupancy. This local change suggests that the Fe atom(s) exhibits more redox noninnocent characteristics than the Co atoms. Additionally, ligand removal from one Fe atom in Co₃Fe₃ leads to a significant decrease in the d-orbital occupancy of all three Fe atoms, while the Co atoms remain unaffected. This indicates that the Fe atoms electronically communicate with each other in a manner similar to bulk materials.

Table 2 Total d-orbital occupancy for each metal center in the fully ligated, [Co₅FeS₈(PEt₃)₆]⁺, and undercoordinated, [Co₅FeS₈(PEt₃)₅]⁺, NC at the PBE0-D3/def2TZVP level of theory. M1–M6 represent each metal in the TM core (scheme: bold = Co atom, italic = Fe atom)

	Total d-orbital occupancy			Total d-orbital occupancy
[Co5FeS8L6]^+	M1	8.45	[Co5FeS8L5]^+	M1	8.46
	M2	8.45		M2	8.44
	M3	8.46		M3	8.46
	M4	8.44		M4	8.45
	M5	7.15		M5	6.60
	M6	8.46		M6	8.46

---

The collective response of the d-orbital occupancy of Fe atoms to ligand removal is much less pronounced for Fe₆ NC indicating that the observed phenomenon cannot simply be attributed to reduced core stability due to the incorporation of electron-poor Fe atoms. Further insights can be gained by analyzing the total electronic occupancy of all metal atoms in the core. The results obtained for both fully ligated and undercoordinated NCs are shown in Table S13 (ESI†). We observe a decrease in overall d-orbital occupancy with an increasing number of Fe atoms, from 50.76 e in Co₆ to 44.68 e in Fe₆. However, the largest difference in overall d-orbital occupancy of 1.52 e between the fully ligated and undercoordinated NC is observed in Co₃Fe₃. As discussed earlier, atoms with the lowest d-orbital occupancy are the preferred sites for ligand loss. The large difference in overall d-orbital occupancy observed for Co₃Fe₃ may contribute to its lower stability toward ligand loss. Overall, the qualitative differences in d-orbital occupancy between Fe and Co atoms suggest that NCs with lower occupancy are generally less stable. For an additional point of analysis, the partial density of states (PDOS) was calculated for each NC in the series as seen in Fig. S4–S7 (ESI†). It is notable that [Co₆S₈(PEt₃)₆]⁺ is the only NC in the series that has a large occupation from the Co atoms within the occupied frontier orbitals. The other NC have large ligand contributions along with their metal counterparts. Considering the large contributions from the ligand shell in the PDOS in all the NCs with Fe, these observations further corroborate with our NBO analysis in that there are redox noninnocent characteristics in these clusters through the sulfur and phosphorus atoms. Through our analysis, the distinct interactions between Fe and Co atoms provide insight into why these NCs exhibit characteristics of both molecules and nanoparticles.

Conclusion

In this study, we examined the relative stability of the Co_6−xFe_x (x = 0–6) clusters towards fragmentation using collision energy-resolved CID experiments and DFT calculations. Loss of a neutral ligand is the major primary dissociation pathway for this series of clusters. By comparing the collision energies corresponding to 50% fragmentation, we determined that Co₆ is the most stable species while Co₂Fe₄ is the least stable toward ligand loss. The ligand binding energy gradually decreases until four Fe atoms are incorporated into the cluster core and then increases until all the Co atoms are replaced with Fe. This trend is rationalized using DFT calculations of ligand binding energies by considering different isomeric structures and species with different multiplicities. Overall, Co₃Fe₃ NC has the largest d-orbital occupancy difference between the fully ligated and undercoordinated NCs, which is reflected in the NBO calculations and ligand binding energies. It is notable that the Fe atoms communicate electronically with each other more like a bulk material, whereas the Co atoms retain the same average occupancy in all NCs. The matching trend between experimental data and theoretical predictions establishes a robust foundation for investigating these transition metal NCs for a broad range of applications.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests to influence the work reported in this paper.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences at Argonne National Laboratory under Contract No. DE-AC02-06CH11357. X. L. and J. L. were supported by the grant FA9550-23-1-0137 from the Air Force Office of Scientific Research (AFOSR). The authors gratefully acknowledge the computing resources provided on Bebop and Improv; high-performance computing clusters operated by the Laboratory Computing Resource Center at Argonne National Laboratory, in addition to the computing resources provided by National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC awards BES-ERCAP0028945 and BES-ERCAP0027337.

References

1. M. F. Matus and H. Häkkinen, Nat. Rev. Mater., 2023, 8, 372–389.
2. J. S. Kim, H. Chang, S. Kang, S. Cha, H. Cho, S. J. Kwak, N. Park, Y. Kim, D. Kang, C. K. Song, J. Kwag, J.-S. Hahn, W. B. Lee, T. Hyeon and J. Park, Nat. Commun., 2023, 14, 3201.
3. G. Liu, V. Chauhan, A. P. Aydt, S. M. Ciborowski, A. Pinkard, Z. Zhu, X. Roy, S. N. Khanna and K. H. Bowen, J. Phys. Chem. C, 2019, 123, 25121–25127.
4. H. Gholipour-Ranjbar, L. Sertse, D. Forbes and J. Laskin, J. Phys. Chem. C, 2024, 128, 8232–8238.
5. D. A. Reed, T. J. Hochuli, N. A. Gadjieva, S. He, R. A. Wiscons, A. K. Bartholomew, A. M. Champsaur, M. L. Steigerwald, X. Roy and C. Nuckolls, J. Am. Chem. Soc., 2022, 144, 306–313.
6. N. A. Gadjieva, A. M. Champsaur, M. L. Steigerwald, X. Roy and C. Nuckolls, Eur. J. Inorg. Chem., 2020, 1245–1254.
7. Y. Xu, J. Chen, A. P. Aydt, L. Zhang, I. Sergeyev, E. G. Keeler, B. Choi, S. He, D. R. Reichman, R. A. Friesner, C. Nuckolls, M. L. Steigerwald, X. Roy and A. E. McDermott, Chem. Phys. Chem., 2024, 25, e202300064.
8. A. K. Bartholomew, E. Meirzadeh, I. B. Stone, C. S. Koay, C. Nuckolls, M. L. Steigerwald, A. C. Crowther and X. Roy, J. Am. Chem. Soc., 2022, 144, 1119–1124.
9. A. Akhuli, A. Mahanty, D. Chakraborty, J. R. Biswal and M. Sarkar, J. Phys. Chem. C, 2024, 128, 15380–15392.
10. H. Gholipour-Ranjbar, H. Y. Samayoa-Oviedo and J. Laskin, ACS Nano, 2023, 17, 17427–17435.
11. T. Sengupta and S. N. Khanna, Commun Chem, 2023, 6, 53.
12. A. F. M. Ward, A. C. Reber and S. N. Khanna, J. Phys. Chem. A, 2023, 127, 38–45.
13. Deepika, H. Gholipour-Ranjbar, H. Fang, L. Sertse, J. Laskin and P. Jena, J. Phys. Chem. C, 2022, 126, 6512–6522.
14. H. Gholipour-Ranjbar, Deepika, P. Jena and J. Laskin, Commun Chem, 2022, 5, 130.
15. X. Li, S. Havenridge, H. Gholipour-Ranjbar, D. Forbes, W. Crain, C. Liu and J. Laskin, ACS Nano, 2024, 18, 33681–33695.
16. A. Baksi, E. K. Schneider, P. Weis, I. Chakraborty, O. Fuhr, S. Lebedkin, W. J. Parak and M. M. Kappes, ACS Nano, 2020, 14, 15064–15070.
17. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
18. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
19. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
20. F. Weigend, J. Comput. Chem., 2008, 29, 167–175.
21. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
22. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109.
23. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
24. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
25. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
26. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
27. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016.
29. W. J. Stevens, M. Krauss, H. Basch and P. G. Jasien, Can. J. Chem., 1992, 70, 612–630.
30. W. J. Stevens, H. Basch and M. Krauss, J. Chem. Phys., 1984, 81, 6026–6033.
31. A. J. Webster, C. M. Mueller, N. P. Foegen, P. H. L. Sit, E. D. Speetzen, D. W. Cunningham and J. S. D’Acchioli, Polyhedron, 2016, 114, 128–132.
32. P. H. L. Sit, R. Car, M. H. Cohen and A. Selloni, Inorg. Chem., 2011, 50, 10259–10267.
33. P. Patel, Z. Lu, M. G. Jafari, C. Hernández-Prieto, P. Zatsepin, D. J. Mindiola, D. M. Kaphan, M. Delferro, A. J. Kropf and C. Liu, J. Phys. Chem. C, 2022, 126, 11949–11962.
34. N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845.
35. M. Philliber, E. T. Baxter and G. E. Johnson, J. Am. Soc. Mass Spectrom., 2022, 33, 2138–2146.
36. A. C. Reber, T. Sengupta, D. Bista and S. N. Khanna, Inorg. Chem., 2022, 61, 16003–16008.
37. S. N. Khanna, A. C. Reber, D. Bista, T. Sengupta and R. Lambert, J. Chem. Phys., 2021, 155, 120901.
38. S. Havenridge and C. Liu, J. Phys. Chem. A, 2024, 128, 3947–3956.
39. M. Bacci, Chem. Phys., 1986, 104, 191–199.
40. D. T. Richens, Chem. Rev., 2005, 105, 1961–2002.
41. K. M. Neyman and S. M. Kozlov, NPG Asia Mater., 2022, 14, 59.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00946d

---