Tiling, propensity for planarity of the group-XIV pentatomic dihydrides XYZH₂(X, Y, Z = C, Si, Ge), and beyond

Abstract

A general (3+4)-atom partitioning scheme, quasi-molecule theory or simply tiling, is briefly reviewed and used anew for rationalizing the propensity to planarity of the families of Group-XIV pentatomic dihydrides. Ab initio molecular orbital theory is used to calculate the structures of such dihydrides in their electronic ground states, as well as the tiles [tri- and tetratomic quasi-molecules (quasi-radicals)] embedded on them. Using cc-pVXZ and aug-cc-pVXZ basis sets up to quadruple-ζ in conjunction with coupled-cluster theory, and its explicitly correlated variant, including single, double, and perturbative triple excitations, a brief study of the involved potential energy surfaces is presented, including equilibrium geometries and harmonic vibrational frequencies of many reported stationary points. Unveilled are the structural shapes of the title species, aiming in particular to explain why they all tend to assume planar forms. Although a cyclic structure is frequently the global minimum, in striking similitude with the also unusual purely carbonated structure recently conjectured to be present in the atmosphere of Titan, other variants turn out to be more stable in some cases. The relative stabilities of the isomers of the title species are also determined. Although not at the focal point, optimizations of other molecules and radicals were also done aiming at put in perspective recent work while providing further benchmark tests on linearity, planarity or otherwise.

---

1 Introduction

Molecular geometries shape almost every aspect of molecular behavior, from reactivity to biological function. Their prediction is therefore a fundamental task in chemistry. Rationales for explaining them, their differences and similarities, have been offered based on molecular orbital (MO) and density functional theory (DFT),^1–3 the effect of electron correlation on the geometries and energetics,⁴ spin-coupled generalized valence bond^5,6 (SCGVB) theory, and intrinsic quasi-atomic bonding analysis.⁷ Although quantum chemistry is expected to predict or explain in detail the intrinsic properties of a given species, the reliability of the explanation is anticipated to loose sharpness with increasing molecular size and when moving down a column of the periodic table of the elements. The aim in this work is to discuss a rationale that may complement the existing theoretical tools by explaining the propensity to linearity or planarity of molecules, irrespective of size and atomic diversity. Specifically, a detailed quantum mechanical study is reported for the title families of compounds. At the focal point are then the various families of group-XIV tetratomic mono- and tetratomic-dihydrides as well as pentatomic dihydrides involving carbon, silicium, and germanium (C, Si, and Ge), aiming to answer whether there is a simple way to explain the propensity of the pentatomics to be planar from the structures of the tetratomic tiles they embed. The studied molecules are best viewed in Fig. 1 where they are depicted in a triangular plot by the number of distinct atoms (C, Si and Ge). Of the pentatomic dihydrides, only the pristine ones that are located at the corners of the triangle, and the fully hybridized one at its center (all signaled by a red dot) are considered. Besides the above primary goal, a short perspective is hoped aiming at introducing the tiling approach while offering the reader examples as diverse as possible that are themselves mostly reported in the current work for the first time.

Fig. 1 Triangular plot in number of atoms of C, Si and Ge of the title penta-atomic dihydrides. Indicated in light blue are their linear (L) or planar (P) shapes.

Following Xu et al.,⁵ we begin by surveying some marked differences between the hydrides of Group-XIV elements. At diatomic level, the lowest-lying excited states of (SiH, GeH) are known to be markedly weakly bound in comparison to CH.^8–10 In turn, CH₂ and (SiH₂, GeH₂) have different ground state multiplicities and geometries,^11,12 while CH₃ and (SiH₃, GeH₃) have different ground state geometries.¹³ The list is larger,⁵ and the differences even more pronounced for other compounds, e.g., the ground-state of C₂H₂ is linear but the ground states of Si₂H₂ and Ge₂H₂ have a “butterfly” structure,^14–16 while the ground states of Si₂H₄ and Ge₂H₄ have a trans-bent structure, not a planar geometry as in C₂H₄,^4,17–21 a point where we return in Section 4.

The so-called “first row anomaly²²” was examined by Kutzelnigg²³ in 1984, which implies that the chemistry of the first row elements differs from that of elements in subsequent rows. By focusing on concepts that were justified for first row elements, but which, contrary to widespread belief, cannot be generalized to the higher main group elements, he noted “If one assumes that the lower the promotional energy the more readily hybridization occurs, one would expect more hybridization in heavy atoms-contrary to what is observed.” From his analysis, he concluded that the decrease in ns participation in the X-atom bond orbitals was the cause of the changes in the chemical behavior of the main group elements down a column; X = C, Si, Ge. This was corroborated by Xu et al.⁵ in their analysis of the SCGVB orbitals of the (CH_n, SiH_n, GeH_n) series where the X-atom bond orbitals were found to have more np character in (SiH_n, GeH_n) than in CH_n. They also noted⁵ that the case is even more complicated due to the difference in the bond energies of the C-, Si- and Ge-hydrides which plays another key role in the encountered anomalies.

The literature on bonding in the first versus subsequent rows of the periodic table is too vast to address it all, but the work by Thomas et al.²⁴ on the formation of the elusive dibridged germaniumsilylene molecule [(Ge(μ-H₂)Si)] via reaction of ground-state Ge with silane (SiH₄) under single-collision conditions deserves attention. While the thermodynamically most stable isomer of the acetylene potential energy surface²⁵ (PES) is linear (H–C≡C–H), vinylidene carbene (H₂C=C) is less stable²⁶ by 186 kJ mol⁻¹. Additionally, as also discussed in Section 3, the stability sequence is reversed in the SiCH₂ and GeCH₂ isomers: silavinylidene (H₂CSi)²⁷ and germavinylidene (H₂CGe)²⁸ represent the global minima being thermodynamically favored by 145 and 177 kJ mol⁻¹ relative to the trans bent isomers silaacetylene (HCSiH)²⁹ and germaacetylene (HCGeH).^30,31 This has been rationalized from the reduced overlap of the valence s and p orbitals of the Si and Ge atoms as compared to C, which hinders their ability to form the sp orbital hybrids that explain the linear geometry of acetylene,^24,32,33 while promoting the stability of hydrogen-double-bridged molecules in contrast to acetylenic or carbene-type structures.²⁴ Such an exotic chemical bonding and unusual molecular structures of Si and Ge have actually been demonstrated by spectroscopic detection of the hydrogen-bridged Si(μ-H₂)Si,³⁴ HSi(μ-H)Si,³⁵ Ge(μ-H₂)Ge and HGe(μ-H)Ge³⁶ isomers, which are energetically favored when compared to their carbene [H₂SiSi, H₂GeGe], and trans-acetylenic-type isomers [HSiSiH, HGeGeH].^36–38

Although it is well established that ab initio quantum chemistry followed by MO analysis leads in principle to the correct explanation of bonding in any polyatomic, there are clearly limitations imposed by the physical size of the system. Additionally, the analysis is clean-cut only up to tetratomics when accuracy is best attained and concepts such as hybridization are easier to understand and vizualize. One then wonders whether the known facts from small molecules may help on rationalizing the geometries of larger ones. Such an approach, quasi-molecule theory or tiling, has recently been suggested³⁹ and the method applied to a variety of medium and large molecules.^40–44 It will be briefly reviewed in Section 2 and put on perspective by considering novel examples, while further illustrated later anew by focusing on the title pentatomic dihydrides. Naturally, the exotic chemical bonding and unusual molecular structures of Si and Ge demonstrated above (whose C-analogs do not exist as equilibrium structures) may presage difficulties, thus posing additional challenges. Unravelling them is the goal of the present work.

2 General theory

The question now raised is: can the geometry of a molecule be rationalized from the geometries of the tetratomic quasi-molecules that are embedded in it? The following considerations guide on the analysis.

2.1 Many-body expansion versus tiling

Consider a typical group-XIV pentatomic dihydride XYZH₂. Remove a single atom. According to the Wigner–Witmer spin-spatial correlation rules, the result may be XYZH(²A) + H(²S) or YZH₂(¹A) + X(¹D), with two other possibilities for the removal of atoms Y(¹D) or Z(¹D); for convenience, the lowest molecular symmetry point group (C₁) labelling is used for molecules with three or more atoms if no need exists for further specification. Of course, possible breakups into YZH₂(³A) + X(³P) or XZH₂(³A) + Y(³P) or XYH₂(³A) + Z(³P) would also be allowed. If the singlet state is assumed to prevail near the equilibrium geometry of the pentatomic-dihydride, the full dissociation scheme assumes the form:

→ 3X(¹D) + 2H(²S) (5)

where eqn (1) [equations labelled top down as (a) to (c)] refers to removal of one atom, eqn (2) to dissociation into a triatomic plus a diatomic, eqn (3) into two diatomics plus an atom, eqn (4) into a diatomic plus two atoms, and full atomization in eqn (5).

It turns out that the energy separation between the singlet and triplet electronic states of the group-XIV atoms,⁴⁵³P → ¹D, is 1.26 eV for C, 0.78 eV for Si, and 0.88 eV for Ge. So, it is reasonable to consider the lowest energy separation between the singlet and triplet potential energy surfaces (PESs) of the pentatomic dihydride to decide which of the singlet versus triplet mechanistic routes is likely the dominant process. For example, consider the C(³P, ¹D) + C₂H₂ reactions that may occur on the singlet C₃H₂ PES where the minima of several isomers are present as we will discuss later: propynylidene (i.e., propargylene, HCCCH, the simplest acetylenic carbene), propadienylidene (the simplest vinylidene carbene, H₂CCC), and cyclopropenylidene (the smallest aromatic carbene, c-C₃H₂). It turns out that cyclic-propenylidene c-C₃H₂ is energetically the lowest structure, but roughly only by 17 kcal mol⁻¹ ≈ 70 kJ mol⁻¹ ≈ 0.725 eV (units are used interchangeably according to common use in the literature) when compared with the lowest triplet isomer (propargylene).⁴⁶ Since intersystem crossing and even crossings are likely to occur on the 9-dimensional PES of the pentatomic, one then expects that dissociation to both C(³P, ¹D) + C₂H₂ may occur:

with the triplet being likely the dominant process if the minimum energy separation between the X₂H₂(³A) and X₂H₂(¹A) PESs turns out to be larger in absolute value than between the singlet and triplet electronic states of the X atom. Using optimized energies reported in the present work, the following energy separations, calculated at the equilibrium geometry of the singlet state species with the coupled-cluster singles and doubles method including the connected perturbative triples correction⁴⁷ [CCSD(T)], may be advanced without consideration of zero-point energy (ZPE) corrections: −3.085 eV for C₂H₂(¹A–³A) at the optimum triplet trans-bent geometry with CCSD(T)/AVQZ, −0.932 eV for Si₂H₂(¹A–³A) and −0.782 eV for Ge₂H₂(¹A–³A) with the latter two at the optimum CCSD(T)/AVTZ trans-bent geometry of the singlet state. Clearly, there is a preference for the reaction of the above pentatomic dihydrides to occur in the singlet PES, although less clearly so when the Ge atom is involved. We concentrate on their singlet states in any analysis hereinafter, since we are mostly interested on their equilibrium geometries.

Suffice it to note here that the above partitions should be observed for a given geometry of the parent molecule and, if such breakups are unique, they can be the basis for the construction of a global PES for the title pentatomics via a many-body expansion⁴⁸ of the total potential energy, using either the MBE formalism^49,50 or double-MBE^50,51 (DMBE) whereby the total energy is first split into short- and long-range components, eventually in its combined-hyperbolic-inverse-power-representation^52–54 (CHIPR) form. This is not the aim of the present work. In fact, the only partitions here involve three- and four-atom fragments as in eqn (1) and (2), and hence the approach may be referred to as (3+4)-atom partitioning ((3+4)AP), commonly referred to as “tiling”.^39–44 Since the tiles are quasi-molecules in the sense specified later, it may be equivalently referred as quasi-molecule theory. At stake is to know in what extent can such a split help on understanding the geometrical shape of the parent molecules. As already noted, other systems rather than the title group-XIV pentatomic dihydrides will be considered anew as testing grounds. Note that only the electronic and spin state of the fragment species is indicated in eqn (1), (2) and (4) for a specific state of the parent, while no reference is made to the specific isomers of the product species in case there are more than one.

2.2 Triads and tetrads of atoms

The question raised is then: is there a consistency between the geometry of the parent and the tiles? The following principles guide on this endeavour:

Lemma 1. If all triads of points in a set are on a line, they all are on the same line (are collinear in an Euclidean sense).

Lemma 2. If all tetrads of points in a set are on a plane, they all are on the same plane (are coplanar in an Euclidean sense).

The term triad should not be confused with Döbereiner's homologue in the history of Chemistry⁵⁵ (where the elements were sort out into groups of three elements – triads – whose physical properties were similarly related⁵⁶). Such Lemmas, proven elsewhere,³⁹ are here briefly sketched for completeness. Recalling the inherent vector spaces, each atom (assumed a point) of a linear triatomic 123 is the tip of an arrow, with the associated vectors v⃑₁, v⃑₂, v⃑₃ spanning a vector space V. Since all atoms are on the same line, there is a vector subspace W, W⊂V, that is a minimal spanning set. In fact, any of the three vectors (e.g., v⃑₁) is enough, since there is such that any vector on the assumed line may be written as, e.g., v⃑₂ = αv⃑₁, thus implying collinearity. In matrix form, if A is formed by the coordinates of the three atoms, it will be a matrix with three column vectors and three row vectors in , but two are the vector 0. Although for an m × n matrix, where n > m, the rows may form a basis for a vector space, the columns cannot because (n–m) of them and any space that they span must be a subspace of : at most m vectors are required (the columns are a linear dependent set). For linearity, the matrix is 1 × 1, thence a scalar.

Consider next a second triad of atoms (234). Since the rank of the corresponding B matrix is 1, the coordinates of the additional atom (4) are simply a multiple scalar times those of atoms 2 and 3 of previous set: all atoms are collinear. An even easier way to reach the same conclusion is to note that with two atoms common to both triads, the line must be common to both pairs.

A similar analysis may be extended to the case of planarity, sufficing to note that one is now dealing with a vector space of four vectors in lying on a plane. Thence, there is a set of vectors that span V′, but there is also a subspace W′, W′⊂V′, that is a minimal spanning set, now of rank 2.

2.2.1 Triads and linearity. Let 1234 be a tetratomic to be tested for linearity. Choose three atoms (123), with two bonds formed: 12 and 23. If noncyclic (if cyclic, it is nonlinear), a tetratomic involves three bonds. However, only 2 require examination, e.g., 123 and 234. If the latter is linear, the answer is consistent with the tetratomic being linear. Rather than the combinatorial 4 triads (the number implied by Lemma 1), only 2 are required (123 and 234). As an example, consider C₂H₂. Numbering the first three atoms in H¹–C²≡C³–H⁴ as 123, they should mentally form in isolation a collinear^57–59 HC₂ fragment, sufficing it to verify that the same applies to the other triad C²C³H⁴ (234). Because such molecules must be considered as virtual before fragmentation viaeqn (1) and (2), they are referred to as quasi-molecules (tiles) in allusion to the quasiatom concept.⁷ Of course, there is no way to specify a priori its electronic state, except for warranting the Wigner–Witmer spin-spatial correlation rules. In the present case, the ground-state HC₂ is a doublet, since there is no other way for it to yield a singlet when added an hydrogen atom.⁶⁰ So, there is no need to consider the triads HHC that arise from the full combinatorics (and which are essential in the MBE formalism^49–54). Indeed, if the above two triads fit on a line, the remaining triads and hence the whole molecule must fit on that line. The same argument extends to a larger molecule: if N atoms are involved, (N − 2) triads require examination.

As a further example, consider tetracarbon dioxide, also regarded as butatriene dione, the double ketone of butatriene or 1,2,3-butatriene-1,4-dione.⁶¹ Is its linear structure expected and consistent with the geometries of the tiles with which it correlates? The answer is yes, since both X̃³Σ⁻ and ã¹Δ states of ketenylidene⁶² (C₂O) are linear, and also ground singlet C₃.^63–65

A similar reasoning is applicable to C₅O₂ (pentacarbon dioxide or penta-1,2,3,4-tetraene-1,5-dione), a linear⁶⁶ singlet (X¹Σ⁺_g) that was suggested to serve as a powerful tracer of the temperature history of formerly carbon monoxide rich ices in molecular clouds and star-forming regions [stick-and-ball plot obtained via CCSD(T)/VDZ optimization in the Graphical Abstract].⁶⁷ Analogously, C₄O₂ is a triplet⁶¹ that is indefinitely stable in matrices but decomposes by light into tricarbon monoxide C₃O and carbon monoxide.^61,68,69 Although this raises the question of stability, such an issue requires a quantitaive explanation either experimentally or via accurate quantum chemistry. It turns out that ab initio calculations seem to deny existence to the O(=C)_n=O family with large even n values which appear unstable.⁷⁰ In fact, their existence and shape is unknown, and hence cannot afford a test of consistency with its tiles. One wonders though whether this may be due to the possibility of forming carbon clusters, that may also be nonlinear with increasing number of C atoms.⁵⁸ Of course, linearity is also present in cumulenes⁷¹ as well as linear C clusters,^44,72,73 which are not here discussed.

Examining all possible triads or tetrads (to be discussed in the next subsection) of atoms is not cumbersome in the present case. However, it can be for large molecules, although a scheme for overcoming it has been suggested.^39–44 On the other hand, examining the triads for linearity may occasionally help when assessing planarity of a molecule (see the next paragraph). For example, consider an atom bonded to 4 other atoms or groups of atoms, where two or more at the fringe are free from any other bonding. This is the case of CH₃ in methane (CH₄) or when capping alkanes (e.g., CH₃ in butane C₄H₁₄). Let the three terminal H atoms be labelled 1,2,3 with C being number 4. For simplicity, assume further that the fifth atom is a H atom (but can be any other). Noting that the two tetrads 1234 and 2345 would relate to CH₃, which is known to be planar, it might appear (from reasons discussed in Section 2.2.2) that CH₄ would be planar. However, this would imply two linear HCH triads. Since these relate to CH₂, the answer invalidates the previous assessment since methylene (CH₂) is bent both in its triplet (ground-state) and singlet states.⁷⁴

The above argument might lead to predict that cyclobutane is nonplanar, and indeed it is not planar, with strained non-ideal angles ∠CCC of 90 deg rather than 109.5 deg that one would expect from the sp³ hybridized carbon atom. The same argument holds for cyclopropane, since not all atoms are in a single plane, thus contradicting conventional wisdom that considers it to be a planar molecule. In fact, the ∠CCC angle is now 60 deg with the three carbon atoms forming a planar C-ring granting the molecule to possess D_3h symmetry, but not with all atoms on the same plane: they occupy three parallel planes, one defined by 3 C atoms and two other planes by 3 H atoms each.

2.2.2 Tetrads and planarity. From the preceding paragraphs, it seems that not all (3+4)-atom fragments are required for the analysis. A pre-requisite though is that the inherent spin-spatial rules of the parent are satisfied. Consider then a pentatomic molecule. If the starting tetrad of atoms 1234 is planar, it suffices to ask whether the second (2345) is also planar. In fact, if the parent forms a ring, an extra 3451 tetrad may be considered. In case all tiles are planar, the parent pentatomic is itself planar. The argument follows from the fact that all tetrads share 3 atoms (thence a plane) with the previous tetrad in the sequence 1234, 2345, 3451. Thence, N − 2 tetrads need inspection to assess planarity of a N-atom molecule. This is so even when all atoms but one (say atom #1) sit on a line. Indeed, 1234 and 3451 are in this case planar tetrads, with the line where 2345 stands being on the plane of the other two tetrads.

Even simpler by analogy with the case of linearity, is to consider triads of bonds rather than tetrads of atoms, say . For a pentatomic, only the triads , and would require consideration.

To illustrate the above, consider benzene, C₆H₆. With 495 possible tetrads, the analysis to examine its planarity would start to be prohibitive. However, the actual number reduces to 10 involving HCCH and CCCH tetrads, 5 of each, as long as we are interested in geometries close to equilibrium. No need exists to consider the C or H atoms separately, which simplifies the analysis. The second of the above tetrads is the C₃H quasimolecule, which is planar in its ground-doublet⁵⁹ state and remains so in its lowest quartet state, although as a saddle point of index 1, with an imaginary frequency of 81.6 cm⁻¹ for out-of-plane bending, at the geometry of the doublet. (Parenthetically, this is located 37.4 kcal mol⁻¹ above the linear minimum at the CCSD(T)/AVTZ level of theory; 141.3 cm⁻¹ and 37.5 kcal mol⁻¹ with a VQZ basis, in the same order.) In turn, the HCCH tetrads have C₂H₂ as the quasimolecule, linear in its ground-singlet state²⁵ (planar²⁵ on its high-lying vynilidene isomer) but trans-planar^75,76 in its lowest triplet state (see Fig. 2 and the ESI,† where it is optimized at the CCSD(T)/AVQZ level of theory). Both such tiles are therefore consistent with benzene being planar. Note that C₆H₆(¹A) → 3C₂H₂(³A) and C₆H₆(¹A) → 2C₃H(²A) + 4H(²S). Note further that the quartet state of HC₃ is irrelevant in the present case. As already noted, the CCCC tetrads are of no concern (as long as the focus is on regions close to the equilibrium geometry of the parent) for two reasons. First, the formation of a C₄ quasimolecule would require at least four C–H bonds to be broken, thence a high energetic process. Second, even so, it might form a linear C₄, which could be assumed to lie on the plane defined by the HCCH and HCCC tetrads that edge the CCCC ones. So, they can be discarded. Regarding HHHH, such tetrads share difficulties common to CCCC besides not being bound: thence, may be assumed to satisfy any geometry implied by other tetrads.

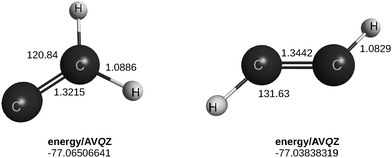Fig. 2 Optimized geometrical parameters for triplet acetylene calculated to in the present work. Distances in Å, angles in deg. All calculations here reported are run without imposing symmetry.

A similar analysis as for benzene is valid for naftalene (C₁₀H₈) and anthracene (C₁₄H₁₀): only the HCCH and HCCC tiles need consideration. This is not so for the anthracene photodimer^77,78 (dianthracene), since a pair of new C–C bonds is formed as a result of the [4+4] cycloaddition. The tetrads will then be HCCH, CCCH, and CCCC. Because ground-state C₄ is linear in its triplet state, and its singlet is rombohedral [although there are predictions⁵⁸ of a linear isomer and a weakly bound singlet C_s monocyclic ring (distorted kite, d-C₄(¹A′)) that lies high up in energy], it is impossible to warrant the parent's planarity without further analysis.^41–43

Consider next anthraquinone. Formed from the oxidation of anthracene, C₁₄H₈O₂ has HCCH, CCCH, HCCO and CCCO tiles that require consideration. The quasimolecules are now H₂C₂, HC₃, and C₃O. The novel tetrad is tricarbon monoxide, the first known interstellar carbon chain molecule containing oxygen.^79,80 Classified as a ketene or oxocumulene, it is linear in its ground-singlet state. However, CCCO can be associated to cyclopropynone, an isomer that is planar in its triplet state, as shown⁸¹ with B3PW91/6-311+G* and confirmed in Fig. 3 at CCSD(T)/AVTZ level of theory. Furthermore, it assumes an open (∠CCO = 167.5 deg) planar structure in its singlet state. So, all tiles are consistent with anthraquinone being planar.

Fig. 3 Optimized geometrical parameters of propynone. Units as in Fig. 2.

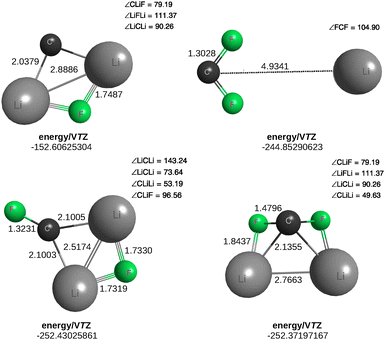
It may appear from the paragraph before the last in Section 2.2.1 that molecules with tetracoordinated atoms could hardly be planar. Yet, a paper titled “Carbon flatland: planar tetracoordinate carbon and fenestranes” highlights the broad topic of planarizing distortions of tetracoordinated carbon.⁸² Pople and coworkers⁸³ report there minimal basis set ab initio (RHF/STO-3G) calculations on the geometries of both tetrahedral and planar structures for various species. An intriguing one is CLi₂F₂, which they suggested to be cis-planar in its most stable configuration, rather than tetrahedral. Without diving on the topic, one wonders whether such a proposal is consistent with the structures of the CF₂Li or CLi₂F tiles. The answer is yes, although no attempt has been made to check whether any of the structures shown in Fig. 4 is the absolute minimum in the CLi₂F₂ PES. Nevertheless, all their calculated harmonic vibrational frequencies are real. However, rather than tetrabonded, the C atom in the present CCSD(T)/VTZ optimizations emerges as tribonded in the planar structure, possibly due to accounting for electron correlation. It is tetrabonded, but in the pyramidal structure optimized at the same level of theory, thus confirming our expectation.

Fig. 4 Shown at the bottom are geometries of two minima encountered in the CLi₂F₂ singlet PES at CCSD(T)/VTZ level of theory, the minima encountered for CLi₂F and CLiF₂ are displayed at the top. Distances are in Å, angles in deg.

Of course, the number of molecules has to be limited by necessity, with the reader addressed elsewhere^40–44 for further examples. To conclude this section, suffice it to recall the hypercoordinated arenes or hyparenes (families of molecules with planar pentacoordinated carbons),⁸⁴ and others alike.⁸² Are they consistent with the propensity of C₂B₂ and CB₃ to planarity, as shown in Fig. 5? The answer is positive but this and other questions are left for brevity without details.

Fig. 5 Optimized CCSD(T)/VTZ geometries of CB₃ (lhs) and C₂B₂ (rhs). Units as in Fig. 2.

2.2.3 Ions, strain, clusters. Noteworthy, we have not considered partitions forming ion-pairs. Would the approach still apply? Although, polyatomic ions are everywhere (e.g., trigonal planar carbonate ion CO₃²⁻ and others important in various metabolic processes), they usually form salts and are not known in the gas phase to which the above mostly applies. However, some anions have been recently studied theoretically due to their relevance in capturing CO₂.^85,86 A first question arises: can single-reference methods such as the ones here utilized be still applicable? Although the answer cannot be a full yes, it is positive if the system is near its equilibrium geometry, since no significant multiconfigurational character (no strong near-degeneracy in orbitals) is expected when the molecule (closed-shell or well-behaved open-shell) has not highly stretched bonds or high-spin states with low HOMO–LUMO (Highest Occupied MO – Lowest Unoccupied MO) gap. There is a second question though: where should the charge be placed in quasi-molecule theory? In this case too, any possibility that obeys the spin-spatial correlation rules seems plausible. Consider, e.g., C₆H₅O⁻. There are HCCH, HCCC, HCCO, and CCCO tetrads. For simplicity, the charge is assumed to be carried by the fragment containing the oxygen atom, thence C₂H₂, C₃H, HCCO⁻,⁸⁷ and C₃O⁻⁸⁸ will be the tiles. The first two are neutrals that have been discussed above, and shown to support planarity. The same is done for the quasi-anions, with the available data also supporting the planarity of C₆H₅O⁻ predicted from DFT and Møller Plesset perturbation theory (MP2) calculations.^85,86 A similar analysis could be done for gas phase C₆H₅NH⁻, with HCCH, CCNH, and NCCH neutrals and the charge transported by the quasi-ion containing N. The novel tetranions would be cyanocarbene (HCCN⁻) and possibly isocyano-carbene (HCNC⁻). Both are planar,^89,90 thus supporting planarity of the parent anion; see Fig. 6.

Fig. 6 Except for the top parent anions, optimized at the DFT/B3LYP,⁹¹ including Grimme's D3 dispersion,⁹² and M06-2X⁹³ functionals,⁸⁵ the tetranions are from the present work at CCSD(T) level of theory. All optimizations employed AVTZ basis sets. Units as in Fig. 2.

We now turn to molecules that are known to experience strain when their chemical structures undergo stress which raises the internal energy in comparison to a strain-free structure. Well known is cyclopropane discussed in Section 2.2.2. Others may be just hypothetical like benzotriyne (cyclo[6]carbon), a C₆ allotrope of carbon where the C atoms are connected by alternating triple and single bonds.⁹⁴ Yet, this is just the beginning of the so-called cyclo[n]carbon family which has attracted much experimental and theoretical research;^95,96 see also elsewhre.⁴⁰

The last paragraph leads one to well established examples of strain in clusters, in particular the C_n clusters. These vary from small⁵⁸ to large, from linear chains to rings to closed cages to nanotubes, with increasing size of the cluster.⁹⁷ When the cluster size exceedes 6 atoms or so, they have been suggested to present ring forms whose stability tends to increase due to reduction in angle strain. In fact, isomers of C₆, C₈ and C₁₀ rings are often predicted at high level of theory to be near isoenergetic or even lower in energy than their linear counterparts^58,95 (and references therein). Experimentally, Raman spectra observed for C₁₄, C₁₆, C₁₈, and C₂₀ clusters led to assigned them to linear chains, while the fluorescence observed spectra of C₁₄ and C₁₈ in the same experimental conditions suggested instead to cumulene rings.^98,99 In turn, the observed electronic spectra of C₁₈ and C₂₂ in gas phase were assigned to several transitions of monocyclic cumulenic rings with D_9h (for C₁₈) and D_11h (for C₂₂) symmetries.¹⁰⁰ So, despite the intense research activity and continuing progress, the predictions diverge depending on the experimental set up and employed level of theory. The possible shapes should though show conformity with the predictions from quasi-molecule theory as it appears to be the case from previous work.^40–44 Of course, one cannot exclude to attribute the many possible shapes to the flatening of their high-dimensional PESs. This may explain the natural appearance of multiple shallow minima (stable or metastable) with increasing cluster size, and also lead one to conjecture that the shape of how they are “visible” may depend on the way they are looked upon.

To sum up, it seems unfruitful any attempt to rationalize the multiple minima of clusters as they cannot be distinguished even by quantitative quantum chemistry, particularly when the cluster size grows. Abridged is also any discussion on van der Waals molecules. Involving mostly interacting closed shell systems, they may assume almost any geometry due to resting on a delicate balance of short- and long-range interactions. We turn in the following to the title group-XIV pentatomic dihydrides.

3 Case-study group-XIV pentatomic dihydrides

The calculations reported in this section cover the optimization of at least 30 tetratomic mono- and di-hydrides (tiles) and 31 pentatomic dihydrides (parents) of elements of the group-XIV of the periodic table. All calculations employed the CCSD(T) method and the default SCF convergence threshold in the MOLPRO¹⁰¹ code for electronic structure calculations. Both conventional correlation-consistent^102–106 basis sets of the cc-pVXZ (or VXZ) Dunning's family and their aug-cc-pVXZ (AVXZ) variants have been utilized, where the prefix aug- implies that tight diffuse functions are added to the VXZ basis sets; X = D, T. In a few noted cases, computational cost-expensive optimizations with VQZ and AVQZ basis sets have also been done. Additionally, optimizations were performed with tighter (typically ≲10⁻⁵E_ha₀⁻¹) convergence requirements than the default criterion in MOLPRO to warrant as much as possible good stationary point predictions. When involving Si, the so-called (X+d) basis sets are employed. Since the results with and without +d show good agreement for the pure silicium compounds, the extra computational labour has been avoided except where mentioned. No restrictions of symmetry have been imposed. So, any minor differences in the tabular material (for convenience, the number of significant figures is kept the same) and plots reflect the numerical accuracy achieved in the optimization procedure. Restricted Hartree–Fock calculations have always been employed hoping to avoid large spin-contamination effects, particularly when dealing with open-shell species.

For accuracy, the relative energies of the predicted isomers for the group-XIV pentatomic dihydrides have been determined using both canonical CCSD(T)/V5Z and explicitly correlated CCSD(T)-F12 calculations at the optimized geometries. Such F12 calculations employed the specialized VXZ-F12 ansätze¹⁰⁷ jointly with the VXZ-F12/OPTRI basis sets, which entered by default to construct the complementary auxiliary orbital basis (CABS). In all these cases, the CABS singles correction was used to improve the Hartree–Fock reference energy.^108,109 Only the pure pentatomic hydrides of C and Si have been considered at the explicitly correlated level since, to our knowledge, no specialized VXZ-F12 basis sets have been reported for germanium.

A summary of the numerical output from the calculations in the previous paragraph is gathered in Table 1, while a summary of the calculations performed in the present work is given in the ESI.† It should be noted that all reported calculations are valence only, thus disregarding core and core-valence correlations.

Table 1 Best CCSD(T) and CCSD(T)-F12 energies at optimized geometries. Energies are in Hartree, except relative energies (ΔE and ΔE_ZPE) that are in kcal mol⁻¹

Molecule	Isomer	CCSD(T)^a			CCSD(T)-F12b^b			Other^f
		E	ΔE^d	ΔEZPE^e	E	ΔE^d	ΔEZPE^e
a With V5Z basis. b With V5Z-F12 basis. c At optimized CCSD(T)/VTZ geometry. d Without ZPE. e At CCSD(T)/VTZ level with ZPE. f From Vázquez et al.^110 using CCSDTQ/VQZ. From Ernst et al.^111 for Si3H2 at CI level with triple-ζ polarization basis. g At optimized CCSD(T)/AV(T+d)Z geometry. h n.c. = not calculated. i At CCSD(T)/AVTZ level, with ZPE. j At the minimum; see the text. k At the saddle point.
C3H2^c	A	−115.17673701	0.000	0.000	−115.18297587	0.000	0.000	0.0
	B	−115.15342488	14.628	13.735	−115.15920978	14.913	14.020	13.751
	C	−115.13434515	26.601	24.205	−115.14029053	26.785	24.061
	D	−115.12085708	35.065	32.479	−115.12685580	35.216	32.630
	E	−115.09376404	52.066	49.670	−115.09975603	52.221	49.825
Si3H2^c	A	−868.31401950	0.000	0.000	−868.31980538	0.000	0.000	0.0
	B	−868.31262419	0.876	0.893	−868.31818859	1.014	1.031	1.4
	C	−868.30995348	2.552	2.395	−868.31542240	2.806	2.649	1.7
	D	−868.30641860	4.770	4.184	−868.31183712	5.000	4.414	4.9
	E	−868.30519013	5.540	5.381	−868.31071932	5.702	5.543	6.6
Si3H2^g	A	−868.31414472	0.000	0.000	−868.31995184	0.000	0.000
	B	−868.31274409	0.879	0.896	−868.31832631	1.020	1.037
	C	−868.31003124	2.581	2.424	−868.31533455	2.897	2.740
	D	−868.30652380	4.782	4.196	−868.31195629	5.017	4.424
	E	−868.30531370	5.542	5.383	−868.31086229	5.704	5.545
Ge3H2^c	A	−6227.73807857	0.000	0.000	n.c.^h	n.c.
	B	−6227.73795297	0.079	0.562	n.c.	n.c.
	C	−6227.73533125	1.724	2.093	n.c.	n.c.
	D	−6227.72811421	6.253	6.844	n.c.	n.c.
	E	−6227.72736783	6.721	7.076	n.c.	n.c.
CSiGeH2^d^i	A	−2403.77628475	0.000	0.000	n.c.	n.c.
	B	−2403.75710130	12.038	11.850	n.c.	n.c.
	C	−2403.74560337	19.253	19.828	n.c.	n.c.
	D	−2403.74459499	19.886	18.927	n.c.	n.c.
	E^j	−2403.73293091	27.205	25.615	n.c.	n.c.
	E^k	−2403.73226210	27.625	25.690	n.c.	n.c.
	F	−2403.70915954	42.122	39.618	n.c.	n.c.
	G	−2403.68007800	60.371	56.605	n.c.	n.c.

---

For the tetratomics, the predicted optimized structures are in Fig. 7, and ordered from bottom to top according to their energy in relation to that of the most stable isomer which is at the bottom of each column. To avoid a larger computational burden, only the mono- and dihydride tetratomics of relevance for the present work are here considered, thus leaving aside hybrid species such as SiC₂H, CSi₂H, and so on.

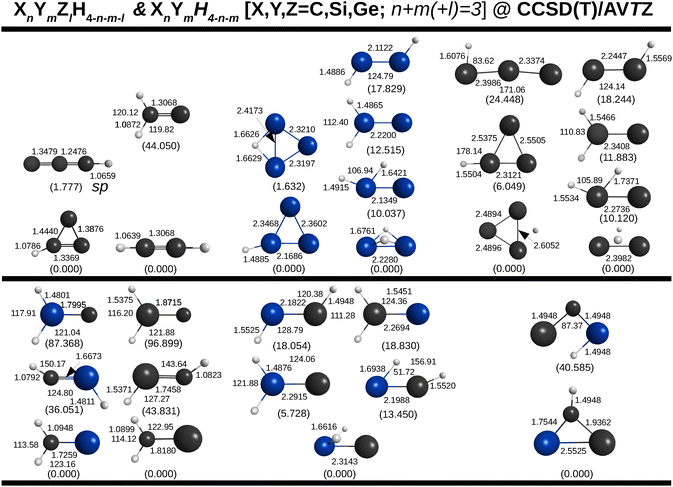Fig. 7 Tetratomic mono- and dihydrides of C, Si and Ge optimized at the CCSD(T)/AVTZ level of theory. Given in brackets are relative energies in kcal mol⁻¹. Due to lack of space, not all relevant coordinates may have been indicated. They may be obtained from the ESI.† Also there are the harmonic vibrational frequencies.

The optimized pentatomic dihydride structures are in the compilation of Fig. 8. Although an attempt has been made to locate all possible minima (thence, stable or metastable structures), such an effort has not been extended to other stationary points, but some that turned out to appear during the calculations are also indicated. Although the survey is fairly extensive at the CCSD(T) level of theory, there is no warranty that further stationary points cannot be found for higher energies.

Fig. 8 Pentatomic dihydrides of carbon, silicium and germanium optimized at CCSD(T)/AVTZ level of theory [CCSD(T)/AV(T+d)Z for Si₃H₂]; optimized energies and coordinates with several basis sets are in the SI. Similar background colors indicate similar minimal structures, with a red background signaling saddle points of index 1. Shown are cyclic structures equivalent to cyclopropenylidene in C₃H₂ (in yellow), cyclic C_s structures with one H-bridged atom (brownish), cyclic structures with two H-bridged atoms (pink), open structures with one H-bridged atom (light green), cyclic C_s structure with two H-atoms bound to the same Group-XIV atom (light blue), open-chains with two hydrogen atoms bound to the same Group-XIV atom (darker blue), and open structures with H-atoms bound to distinct Group-XIV atoms (also in pink). Indicated at the bottom rhs corner of every square is the relative energy without consideration of the ZPE correction.

3.1 Tri-carbon dihydrides

The title C₃H₂ molecule (known as carbine) is known to makeup Titan's atmosphere.¹¹² Known to have isomers,^110,113 the cyclic structure (cyclopropenylidene) illustrated in the top left-hand-side of Fig. 9 turns out to be the minimum of the C₃H₂ PES in its singlet ground state. Only another minimum is commonly reported (shown next at the right-hand-side of the previous one in the same plot), while we report a third lying 26 kcal mol⁻¹ or so above the most stable one. For C₂H₂, Thomas et al.²⁴ reported CBS extrapolated values (including ZPE) of 0.0 and 44.5 kcal mol⁻¹, which are in good agreement with the value of 44.05 kcal mol⁻¹ for the second higher isomer here reported.

Fig. 9 CCSD(T)/AVTZ geometries and energies of the three isomers of C₃H₂, and two saddle point structures (see the text). They are labelled A to E relative to the isomer of lowest energy. At the bottom right-hand-side corner of each structure is the maximum deviation in the two dihedral angles.

In an attempt to search for further extremal, we have employed the optimized reaction coordinate for stimulated evolution⁵⁸ (ORCSE) scheme as illustrated in the top panel of Fig. 10. Briefly, the following three-point premise is accepted: (1) all intermediates are well approximated at CCSD(T)/VDZ level of theory; (2) all are accessible through a reaction coordinate that involves the stretch of a bond (this is marked with a star in the corresponding plot), once all other degrees of freedom are fully optimized; (3) given the limitations of the optimization process, other paths may be potentially useful and hence have been tried in an attempt to unveil possible stationary points. Although, a wider variety of procedures has been suggested,⁵⁸ they were not attempted (or deemed necessary) in the present work. As seen, the ORCSE path climbs too fast in energy and shows no evidence of additional minima up to a reasonable energy above the most stable isomer. Indeed, the geometry of other structures are shown in Fig. 8 but they turn out to be saddle points in the C₃H₂ PES. As shown there is no evidence of any marked break in the ORCSE path that could suggest the existence of any further extremal point in that energy range. Note that all optimized structures are planar showing dihedral angles of 0 or 180 deg.

Fig. 10 ORCSE paths for C₃H₂ and Si₃H₂ searching for possible structural isomers as obtained by varying the distance between atoms separated by a star. With this bond treated as inactive coordinate, all other DOF are optimized, and energies measured relative to starting-geometry one. In this plot and that of Fig. 13, n.c. stands for non-converged.

Because the structures of the tiles (tetratomics at their equilibrium geometries in isolation) are either linear (C₂H₂ in its ground-singlet state) or planar (C₂H₂ in the triplet state, and C₃H), the (3+4)-atom partitioning scheme implies that the lowest isomers of C₃H₂ should be planar, as is actually the case without exception up to more than 26 kcal mol⁻¹ or so above the energy of reference isomer. In fact, even the highest lying saddle point (sp) structure here reported at 51 kcal mol⁻¹ above the reference energy is planar at the CCSD(T)/AVTZ level of theory. Indeed, one of the dihedral angles in this structure is rather small (0.8 deg), while the other is nearly 180 deg (179.1 deg). However, when tightening the convergence criterion, such deviations from planarity become smaller than ±0.1 deg. So, there is a clear propensity for planarity in C₃H₂ as it is also visible from the ORCSE profiles in Fig. 10, which cover basically planar structures all the way up to where shown.

3.2 Tri-silicium dihydrides

The geometric structures, isomeric stabilities, and potential energy profiles of various isomers and transition states in Si₃H₂ have been determined by Ikuda et al.¹¹⁴ for the neutral as well as for the cation at the CCSD(T)/VTZ level of theory, and for the anion with CCSD(T)/AVDZ. For the energetics, they employed single-point calculations with AVTZ and VQZ basis sets (the latter for the neutral, the former for the cation and anion). The reported¹¹⁴ structures correspond in Fig. 11 to the ones labelled as A to D (by increasing energy difference relative to the most stable isomer), with the global minimum of the neutral (¹A₁ state) having the same framework as the cyclopropenylidene of the C₃H₂ molecule. The next low-lying isomers, B to D, are predicted there¹¹⁴ to be within 20 kJ mol⁻¹. Our results compare well with the results of Ikuda et al.,¹¹⁴ although we report a fifth isomer still lying within the range of ≈5 kcal mol⁻¹, but here predicted to be in a somewhat flatter environment of the PES. Furthermore, five transition states have been located¹¹⁴ as well as their energy relationships with the isomers. The ORCSE search for other extrema did not yield evidence of other minima as illustrated in the two panels of Fig. 10.

Fig. 11 CCSD(T)/AVTZ geometries and energies of the five lowest isomers (up to ≃5 kcal mol⁻¹) of Si₃H₂, denoted A to E by increasing relative energy. At the bottwon right-hand-side corner of each structure is the maximum deviation in the two dihedral angles.

As in the case of C₃H₂, we may now try to find whether the pristine tri-silicium dihydrides could be predicted to be planar from those of the tetratomic fragments Si₂H₂ and Si₃H. The basis for the prediction appears to be less confortable in the present case due to the fact that the most stable structure of Si₂H₂ has a butterfly structure, thence non-planar. Yet, it should be highlighted the fact that there is no implication in the order of the tetratomic planar isomers, sufficing it to appear in the list of possible isomers that obey the appropriate spatial-spin state of the parent pentatomic dihydride. This is actually the case, with all tri-silicium monohydrides and all but one di-silicium dihydride being planar (eventually, quasiplanar within 1–2 deg) depending on the employed optimization constraints. In this regard, it should be noted that they have all been optimized with default convergence parameters. Indeed, both the H₂SiSi and trans-bent HSiSiH singlet structures are planar and local minima.¹⁴ Moreover, in the triplet state, the planar H₂SiSi is the global minimum, and the planar trans-bent HSiSiH plus a bridged structure are local minima.¹⁴ CBS extrapolated energies for the tetratomic silicium dihydrides, Si₂H₂, have been reported by Thomas et al.²⁴ who reported values of 0.0, 9.1, 12.0, and 16.5 kcal mol⁻¹, here too in good agreement with our estimates.

3.3 Tri-germanium dihydrides

Molecules containing Ge atoms have been intensively investigated not only for fundamental reasons but also for their role in vapor deposition processes, film formation, and synthesis of ceramic materials.^115–118 Numerous references to such work are given in the literature.^119,120 Specifically for the title system, Antoniotti et al.¹²⁰ reported a theoretical investigation on the structure, stability, and thermochemistry of various Ge₃H_n⁻ isomers (n = 0–5) and their neutral analogues using B3LYP/6-311+G(d), MP2(full)/6-31G(d), and Gaussian-2 (G2) levels of theory. Regarding Ge₃, their B3LYP/6-311+G(d) calculations confirm the near degeneracy of the and states, which have geometries qualitatively similar to MP2(full)/6-31G(d) ones.^121,122 As for the neutral tri-germanium monohydrides, they report three optimized structures at the B3LYP/6-311+G(d) and MP2(full)/6-31G(d) which agree qualitatively with those reported in Fig. 12. In the case of Ge₃H₂, they located¹²⁰ two energy minima on the singlet PES, a cyclic structure of C_s symmetry with two H atoms bound to the same Ge atom and an open-chain H-bridged isomer, whose structure is fully planar with MP2 but slightly distorted from planarity (C₁ symmetry) at B3LYP level of theory. Clearly, these show more significant differences from the ones here reported in Fig. 12. In fact, the structure 2b of ref. 120 is similar to the one reported at the bottom right of the left panel of Fig. 13, which has been optimized at the CCSD(T)/VDZ level of theory. As depicted in Fig. 13, no further minima have been encountered by exploring the ORCSE⁵⁸ profiles here reported. Optimized structures have also been recently reported by Thomas et al.²⁴ employing CCSD(T), with the energetics obtained by extrapolating to the CBS limit¹²³ from the CCSD(T)/VDZ, CCSD(T)/VTZ, and CCSD(T)/VQZ energies, and including CCSD/VTZ ZPE corrections. They report, from bottom to top structures (at the top most right-hand-side column of Fig. 7), the values: 0, 8.6, 13.6, and 17.7 kcal mol⁻¹. Good agreement is observed with the results here reported; see also Fig. 12 and 13 from this work for the geometry and energetics (without ZPE), and the ESI,† for further details. Indeed, such an agreement extends to the heteronuclears SiCH₂ and GeCH₂, for which they report from bottom up (in all cases after CBS extrapolation and inclusion of ZPE correction, in kcal mol⁻¹): (0.0, 34.2, 83.9) and (0.0, 42.3, 104.2), respectively. Despite the lack of ZPE corrections (not quite the goal here), there is good agreement.

Fig. 12 CCSD(T)/AVTZ geometries and energies of five lowest isomers (≲20 kcal mol⁻¹) of Ge₃H₂. Indicated at the bottwon right-hand-side corner of each structure is the maximum deviation found in the two dihedral angles.

Fig. 13 As in Fig. 10 but for Ge₃H₂.

As for the pure silicium analog in the previous subsection, in this case too the most stable di-germanium tetratomic dihydride is butterfly shaped, and hence the explanation for planarity of the pentatomic dihydrides may appear in this case too to be somewhat questionable. This is not so. As for Si₃H₂, it suffices to recall that the remaining isomeric structures reported in Fig. 7 are essentially, if not strictly, planar. Similarly, all tri-germanium monohydrides are planar within the employed optimization constraints. Additionally, the lowest isomer of triplet Ge₂H₂ is planar as we have also found in the present study (see the ESI†).

3.4 Carbon–silicium–germanium dihydrides

We consider next the CSiGeH₂ molecule which, to the best of our knowledge, has not been studied before. The optimized structures are reported in Fig. 14.

Fig. 14 CCSD(T)/AVTZ geometries and energies of the lowest isomers [A to G, with sp indicating a saddle point (see the text)] of CSiGeH₂. At the bottwon right-hand-side corner of each structure is the maximum deviation in the two dihedral angles.

As seen from Fig. 7 and 14, except for the relative energy ordering, basically all isomeric forms are present in all pentatomic dihydrides here studied. In fact, when not showing as stable isomers (minima), they appear as saddle points, in all cases of index 1. Indeed, they were often rerun with high convergence criteria to warrant that the stationary point shows the correct index.

Regarding the tetratomic fragments, the calculations predict the existence of up to five stable structural isomers (depending on the group-XIV atomic combination) in their singlet ground states. Interesting is the Siμ-H₂Ge butterfly molecule, which is here too predicted as the most stable structure.^24,30 As already emphasized, this shows the preferential stability of hydrogen-bridged dinuclear molecules in the absence of carbon, which in contrast favors acetylenic or carbene-type structures. The agreement with the five stable isomeric structures predicted in the present work is excellent; see Fig. 7. In fact, a similar observation goes for the tetratomic CSiGeH with the two structural isomers here reported being also planar. With all but the energetically lowest tetratomic structures being planar, this should explain the propensity of CSiGeH₂ to be itself a planar molecule as illustrated by the whole set of structures shown in Fig. 8 and 14.

A query then emerges from a further look to Fig. 8 and the fact that CGeSiH₂ is a sadlle point of index 1 with a very small imaginary bending frequency of −14.4 cm⁻¹. If so, is there a non-planar minimum nearby? Prompted by this, we have performed a further optimization with a tight convergence of 10⁻⁵E_ha₀⁻¹ for the gradient. This led to the prediction of a broad minimum with a well dept of 0.25 kcal mol⁻¹ (0.25 kcal mol⁻¹ at the CCSD(T)/V5Z level of theory; see Table 1) relative to the top of the barrier and an angle of ∠GeCSi = 127.4 deg; the bond distances are in an obvious correspondence with those of the saddle point in Fig. 14: 1.4838, 1.7165, and 1.7859a₀. This should not at all be disappointing. Although one can hardly tell for sure whether such details are correct (as it is located relatively far from the absolute minimum of the CGeSiH₂ PES and the method is single-reference), one should recall that the configuration space of a pentatomic is expected to be mostly nonplanar in its 9D configurational space (a plane has zero-dimensionality in such a space). Can the same reasoning apply to the two saddle point structures reported for C₃H₂? The answer is “not necessarily”, since the involved imaginary frequencies are fairly large, thus suggesting that they connect relatively distant minima. Although one could answer by tracing the intrinsic reaction coordinate starting at each saddle point, this is beyond the scope of the present work.

Having analysed the various group-XIV pentatomic dihydrides, a further question arises: why is lacking the open structure with H-atoms bound to the terminal atom in both tri-Si and tri-Ge dihydrides (panel B of Fig. 8 and 9 for C₃H₂)? This encounters an explanation in the fact that Si₃ and Ge₃ have nonlinear minima, conversely to C₃ which can be easily shown to have a linear singlet ground state structure, with a real double-degenerate frequency for bending of 102.4 cm⁻¹ at B3LYP/AVTZ level of theory. In fact, for Si₃, the linear geometry is at B3LYP/AVTZ level predicted to be a saddle point of index 1 with an imaginary frequency of −60.8 cm⁻¹ and energy of 15.327 kcal mol⁻¹ above the minimum (for Ge₃, the corresponding values are −23.8 cm⁻¹ and 10.898 kcal mol⁻¹). Similarly, for GeCSi the above values read −41.1 cm⁻¹ and 0.262 kcal mol⁻¹ in the same order, somehow explaining by the latter the appearance of both a saddle point and a minimum with similar structures (panels E and F of Fig. 8).

4 Back to the start: C₂H₄versus Si₂H₄ and Ge₂H₄

We emphasized in the Introduction that the list of structural differences between C₂H₄ and the other group-IV compounds (Si₂H₄ and Ge₂H₄) was quite significant: the ground-state of former has a planar structure while the latter have a trans-bent one.^4,17–21 Can this be also rationalized with quasi-molecule theory.

Quoting McCarthy et al.,¹²⁴ “Ab initio calculations of Si₂H₄ have focused almost exclusively on the stability and structures of two isomers: disilene (H₂SiSiH₂) and silylsilylene (H₃SiSiH). The most recent studies conclude that disilene is the ground state and that silylsilylene lies 5–10 kcal mol⁻¹ higher in energy, but there is little agreement as to the precise geometry of disilene, with roughly half predicting a planar structure and the rest a trans-bent structure”.¹⁷ This noted, they reported yet another isomer on the basis of CCSD(T)/AVTZ calculations. Predicted to lie only 7 kcal mol⁻¹ above disilene, the most stable Si₂H₄ isomeric arrangement, this new monobridged isomer has been denoted H₂Si(H)SiH and detected from its rotational spectrum by Fourier transform microwave spectroscopy of a supersonic molecular beam through the discharge products of silane. It was then made clear that conversely to C₂H₄ none of the three isomers of Si₂H₄ was planar. The same has been established¹²⁵ for the digermene molecule, Ge₂H₄(X¹A_g), in low temperature matrices via infrared spectroscopy, and DFT/B3LYP/6-311G(d,p) calculations. In this case, the relative energies among the Ge₂H₄ system are somewhat different from the relative energies obtained for Si₂H₄, but the order of relative energies are identical between Si₂H₄ and Ge₂H₄. Regarding the most stable Ge₂H₄ isomer, it was predicted to be the trans-bent H₂GeGeH₂, immediately followed by the H₃GeGeH type structure, with the bond angles of such structures being found similar to those of the corresponding Si₂H₄ isomers. Additionally, mono-bridged H₂Ge(H)GeH, square di-bridged trans-HGeHHGeH, and square di-bridged cis-HGeHHGeH were also predicted lying 20, 48, and 57 kJ mol⁻¹ above the most stable one, which is much less than those of the corresponding isomers of Si₂H₄, respectively 30, 83, and 94 kJ mol⁻¹. Apart the details, it is obvious that none of the isomers of singlet Si₂H₄ and Ge₂H₄ is planar. Why such a marked difference? To better understand what is going on, and despite being much studied and known to have distinct geometries,^5,13 we have optimized the structure of the singlet (¹A) and triplet (³A) states of CH₂, SiH₂ and GeH₂, as well as the ground-doublet (²A) states of CH₃, SiH₃ and GeH₃, all employing the level of theory that we have mostly utilized thus far, namely CCSD(T)/AVTZ for CH₃ and GeH₃, CCSD(T)/AV(Q+d) Z for SiH₃. As also shown, the results differ only slightly from the ones obtained at the quadruple-ζ level by Xu et al.⁵ and hence indicate that the conclusions do not depend on the level of theory that is employed.

Fig. 15 depicts the optimum structures so obtained for such triatomic and tetratomic fragments. In addition to the fact that the triplet (rather than the singlet) is the lowest state (by 9.56 kcal mol⁻¹ at AVTZ level versus 9.28 kcal mol⁻¹ at AVQZ) for CH₂, the notable difference in shape arises for CH₃ which is predicted to be planar while the other tetratomics for Si and Ge are nonplanar. This may be the key explanation for the different structural forms assumed by the X₂H₄ molecules when X is one of the group-XIV elements C, Si or Ge. Indeed, since we have 6 atoms, we hope to encounter differences from planarity in 3 possible tetrads: HXXH (or XXHH), XHHH, and HHHH. Since H₄ is a van der Waals species, thence disposable to some extent, and the trend for planarity is common to all isomers via the HCCH tetrads, the key point that distinguishes them is CHHH as clearly shown through the corresponding ground-doublet species. Note, for this, that the doublet of XH₃ is the only state that satisfies the spin-spatial correlation rules via X₂H₄(¹A) → XH₃(²A) + H(²S), with X a group-XIV element.

Fig. 15 Geometries and energies of ground-state singlet and lowest-triplet XH₂ plus ground-state doublet XH₃ (X = C, Si, Ge) studied in the present work at the triple-ζ (top two entries in roman for XH₂, top entry in roman for CH₃) and quadruple-ζ (italicized bottom entries, in the same order) basis set levels. The bluish letters P and N stand for planar and non-planar, respectively.

5 Epilogue

The (3+4) AP scheme (tiling or quasimolecule theory) has been discussed and employed to explain the propensity to linearity and planarity (or otherwise) of molecules regardless of their size and atom-location in the periodic table of the elements. The approach stems from analyzing with rigorous quantum chemistry calculations only the shape of the triatomic and tetratomic quasimolecules (tiles) that emerge from the Wigner–Witmer spin-spatial correlation rules for fragmentation of the parent. To avoid the expected combinatorial outburst when dealing with large molecules, a partitioning scheme has been proposed elsewhere^40–44 which, due to the small (or medium) size of the molecules here examined, is unnecessary to discuss.

Although theoretical tools based on molecular orbital, density functional theory, spin-coupled generalized valence bond, and intrinsic quasi-atomic bonding analysis can provide accurate predictions of the geometry, energetics and electronic structure^1–7 of a molecule, it is well recognized that they have difficulty in establishing global properties, relationships between sets of elements (such as the properties here studied) or even establish the trends common to a family of related compounds. For example, the structures need often optimization at various levels of theory and basis sets to ascertain that planarity is not an artifact of the employed methodology. Having an external guidance for consistency may therefore be comforting. Naturally, despite extensively used with success for a variety of other systems,^39–44 it is too soon to conclude that exceptions will not arise. Nevertheless, it is reassuring that the present approach is based on geometrical principles and basic theory, while employing rigorous quantum chemical calculations only for the tiles. Because databases are emerging in an impressive cadence and size, one may think of databases on molecular shapes for the tiles that can be used to check the consistency of the structure of a panoply of large molecules for which rigorous quantum chemical calculations may not be affordable.

From the studies here reported, numerous stationary points on the PESs of mono- and di-hydride group-XIV molecules have also been located and characterized. Much studied in the literature, some were just confirmed while others were reported anew for the pristine pentatomic dihydrides involving C, Si and Ge as well as the fully mixed one, CSiGeH₂. The results show both cyclic and noncyclic structures, which should be experimentally observable as actually done already in some cases. Regarding the cyclic c-CHSiHGe structure, it is predicted to be the global minimum followed by a c-CHGeHSi isomer with the hydrogens bound to the C and Ge atoms. Showing like all others a significant dipole moment, they should be themselves experimentally observable. A final query remains: being the title hydrides of atoms of the same group (XIV) of the periodic table, why does the topography of the PESs (not to mention the energy ordering) of the ground state compounds of Si or Ge (even when mixed with C) tend to show distinct isomers from those involving only C? A related query has recently been raised¹²⁶ for the XH₄⁺ (X = C, Si, Ge) cations, which justifies being here also asked. Is it a problem of method, basis set or simply more than that?

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author acknowledges the support provided by Chinas Shandong Province Double Hundred Experts project WSP2023008, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and the CQC-IMS which is supported by the Foundation for Science and Technology (FCT), Portugal, in the framework of the projects UI0313B/QUI/2020 (DOI: https://doi.org/10.54499/UIDB/00313/2020), UI0313P/QUI/2020 (DOI: https://doi.org/10.54499/UIDP/00313/2020) and LA/P/0056/2020.

Notes and references

1. J. P. Malrieu and G. Trinquier, J. Am. Chem. Soc., 1989, 111, 5916–5921.
2. G. Trinquier and J. P. Malrieu, J. Am. Chem. Soc., 1987, 109, 5303–5315.
3. M. Lein, A. Krapp and G. Frenking, J. Am. Chem. Soc., 2005, 127, 6290–6299.
4. K. Somasundram, R. D. Amos and N. C. Handy, Theor. Chim. Acta, 1986, 70, 393–406.
5. L. T. Xu, J. V. Thompson and T. H. Dunning, J. Phys. Chem. A, 2019, 123, 2401–2419.
6. T. H. Dunning, Jr., L. T. Xu, D. L. Cooper and P. B. Karadakov, J. Phys. Chem. A, 2021, 125, 2021–2050.
7. E. B. Guidez, M. S. Gordon and K. Ruedenberg, J. Am. Chem. Soc., 2020, 142, 13729–13742.
8. A. Kalemos, A. Mavridis and A. Metropoulos, J. Chem. Phys., 1999, 111, 9536–9548.
9. A. Kalemos, A. Mavridis and A. Metropoulos, J. Chem. Phys., 2002, 116, 6529–6540.
10. R. Li, Z. Zhai, X. Zhang, M. Jin, H. Xu and B. Yan, J. Quant. Spectrosc. Radiat. Transfer, 2015, 157, 42–53.
11. A. R. McKellar, P. R. Bunker, T. J. Sears, K. M. Evenson, R. J. Saykally and S. R. Langhoff, J. Chem. Phys., 1983, 79, 5251–5264.
12. A. Kasdan, E. Herbst and W. C. Lineberger, J. Chem. Phys., 1975, 62, 541–548.
13. G. S. Jackel and W. Gordy, Phys. Rev., 1968, 176, 443–452.
14. H. Lischka and H. J. Kohler, J. Am. Chem. Soc., 1983, 105, 6646–6649.
15. G. Dolgonos, Chem. Phys. Lett., 2008, 454, 190–195.
16. R. S. Grev, B. J. Deleeuw and H. F. Schaefer, Chem. Phys. Lett., 1990, 165, 257–264.
17. G. Olbrich, Chem. Phys. Lett., 1986, 130, 115–119.
18. L. Sari, M. C. McCarthy, H. F. Schaefer and P. Thaddeus, J. Am. Chem. Soc., 2003, 125, 11409–11417.
19. G. Dolgonos, Chem. Phys. Lett., 2008, 466, 11–15.
20. G. Trinquier, J. Am. Chem. Soc., 1990, 112, 2130–2137.
21. R. S. Grev, Adv. Organomet. Chem., 1991, 33, 125–170.
22. T. H. Dunning, Jr., D. E. Woon, J. Leiding and L. Chen, Acc. Chem. Res., 2013, 46, 359–368.
23. W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295.
24. A. M. Thomas, B. B. Dangi, T. Yang, G. Tarczay, R. I. Kaiser, B. J. Sun, S. Y. Chen, A. H. Chang, T. L. Nguyen, J. F. Stanton and A. M. Mebel, J. Phys. Chem. Lett., 2019, 10, 1264–1271.
25. S. Joseph and A. J. C. Varandas, J. Phys. Chem. A, 2010, 114, 13277–13287.
26. J. A. Devine, M. L. Weichman, X. Zhou, J. Ma, B. Jiang, H. Guo and D. M. Neumark, J. Am. Chem. Soc., 2016, 138, 16417–16425.
27. A. M. Mebel and R. I. Kaiser, Chem. Phys. Lett., 2002, 360, 139–143.
28. M. C. McCarthy and P. Thaddeus, Phys. Rev. Lett., 2003, 90, 2130031–2130034.
29. J. Koput, J. Comput. Chem., 2016, 37, 2395–2402.
30. A. J. Boone, D. H. Magers and J. Leszczyński, Int. J. Quantum Chem., 1998, 70, 925–932.
31. Q. Wu, Q. Hao, J. J. Wilke, A. C. Simmonett, Y. Yamaguchi, Q. Li, D.-C. Fang and H. F. Schaefer, Mol. Phys., 2012, 110, 783–800.
32. M. R. Hoffmann, Y. Yoshioka and H. F. Schaefer, J. Am. Chem. Soc., 1983, 105, 1084–1088.
33. J. M. Galbraith and H. F. Schaefer, J. Mol. Struct.: THEOCHEM, 1998, 424, 7–20.
34. M. Bogey, H. Bolvin, C. Demuynck and J. L. Destombes, Phys. Rev. Lett., 1991, 66, 413–416.
35. M. Cordonnier, M. Bogey, C. Demuynck and J. L. Destombes, J. Chem. Phys., 1992, 97, 7984–7989.
36. X. Wang, L. Andrews and G. P. Kushto, J. Phys. Chem. A, 2002, 106, 5809–5816.
37. R. S. Grev and H. F. Schaefer, J. Chem. Phys., 1992, 97, 7990–7998.
38. T. Yang, B. B. Dangi, R. I. Kaiser, K.-H. Chao, B.-J. Sun, A. H. H. Chang, T. L. Nguyen and J. F. Stanton, Angew. Chem., Int. Ed., 2017, 56, 1264–1268.
39. A. J. C. Varandas, Phys. Chem. Chem. Phys., 2022, 24, 8488–8507.
40. A. J. C. Varandas, Int. J. Quantum Chem., 2023, 123, e27036.
41. A. J. C. Varandas, Mol. Phys., 2023, 0, e2285032.
42. A. J. C. Varandas, J. Phys. Chem. A, 2023, 127, 5048–5064.
43. A. J. C. Varandas, Chem. Phys. Lett., 2023, 140836.
44. A. J. C. Varandas, Int. J. Quantum Chem., 2024, 124, e27287.
45. NIST: Atomic Spectra Database – Energy Levels Form, https://physics.nist.gov/PhysRefData/ASD/levels_form.html (accessed at March 25, 2025).
46. D. C. Clary, E. Buonomo, I. R. Sims, I. W. Smith, W. D. Geppert, C. Naulin, M. Costes, L. Cartechini and P. Casavecchia, J. Phys. Chem. A, 2002, 106, 5541–5552.
47. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
48. J. N. Murrell, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular Potential Energy Functions, Wiley, Chichester, 1984.
49. K. S. Sorbie and J. N. Murrell, Mol. Phys., 1975, 29, 1387–1407.
50. A. J. C. Varandas, Adv. Chem. Phys., 1988, 74, 255–338.
51. A. J. C. Varandas, Mol. Phys., 1984, 53, 1303–1325.
52. A. J. C. Varandas, J. Chem. Phys., 2013, 138, 054120.
53. A. J. C. Varandas, J. Chem. Phys., 2013, 138, 134117.
54. A. J. C. Varandas, in Reaction Rate Constant Computations: Theories and Applications, ed. K.-L. Han and T. S. Chu, Theoretical and Computational Chemistry Series, Royal Society of Chemistry, Cambridge, 2013, pp. 408–445.
55. J. W. Dobereiner, Ann. Phys. Chem., 1829, 15, 301–307.
56. E. Scerri, Found. Chem., 2010, 12, 69–83.
57. S. Joseph and A. J. C. Varandas, J. Phys. Chem. A, 2010, 114, 2655–2664.
58. A. J. C. Varandas, Eur. Phys. J. D, 2018, 72, 134.
59. C. M. R. Rocha and A. J. C. Varandas, Phys. Chem. Chem. Phys., 2019, 21, 24406–24418.
60. S. Carter, I. M. Mills and J. N. Murrell, Mol. Phys., 1980, 41, 191.
61. J. Buckingham and F. Macdonald, Dictionary of Organic Compounds, Chapman & Hall, London, 6th edn, 1997, Supplement 1, vol. 10.
62. H. Choi, D. H. Mordaunt, R. T. Bise, T. R. Taylor and D. M. Neumark, J. Chem. Phys., 1998, 108, 4070–4078.
63. K. Ahmed, G. G. Balint-Kurti and C. M. Western, J. Chem. Phys., 2004, 121, 10041–10051.
64. C. M. R. Rocha and A. J. C. Varandas, Phys. Chem. Chem. Phys., 2018, 20, 10319–10331.
65. C. M. R. Rocha and A. J. C. Varandas, J. Phys. Chem. A, 2019, 123, 8154–8169.
66. G. Maier, H. P. Reisenauer, U. Schäfer and H. Balli, Angew. Chem., Int. Ed. Engl., 1988, 27, 566–568.
67. M. Förstel, P. Maksyutenko, A. M. Mebel and R. I. Kaiser, Astrophys. J., 2016, 818, L30.
68. N. G. Adams, D. Smith, K. Giles and E. Herbst, Astron. Astrophys., 1989, 220, 269–271.
69. G. Maier, H. P. Reisenauer, H. Balli, W. Brandt and R. Janoschek, Angew. Chem., Int. Ed. Engl., 1990, 29, 905–908.
70. V. Krishnamurthy and V. H. Rawal, J. Org. Chem., 1997, 62, 1572–1573.
71. D. Wendinger and R. R. Tykwinski, Acc. Chem. Res., 2017, 50, 1468–1479.
72. S. Yang and M. Kertesz, J. Phys. Chem. A, 2008, 112, 146–151.
73. S. Xu, Y. Cui and C. Wang, J. Mol. Struct.: THEOCHEM, 2009, 895, 30–33.
74. Y. Apeloig, R. Pauncz, M. Karni, R. West, W. Steiner and D. Chapman, Organometallics, 2003, 22, 3250–3256.
75. R. W. Wetmore and H. F. Schaefer, J. Chem. Phys., 1978, 69, 1648–1654.
76. H. T. Le, M. Flock and M. T. Nguyen, J. Chem. Phys., 2000, 112, 7008–7010.
77. H. D. Becker, Chem. Rev., 1993, 93, 145–172.
78. H. Bouas-Laurent, A. Castellan, J. P. Desvergne and R. Lapouyade, Chem. Soc. Rev., 2000, 29, 43–55.
79. R. L. Dekock and W. Weltner, J. Am. Chem. Soc., 1971, 93, 7106.
80. H. E. Matthews, W. M. Irvine, P. Friberg, R. D. Brown and P. D. Godfrey, Nature, 1984, 310, 125–126.
81. M. Gicquel, J.-L. Heully, C. Lepetit and R. Chauvin, Phys. Chem. Chem. Phys., 2008, 10, 3578.
82. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
83. J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. V. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427.
84. Z. X. Wang and P. Von Ragué Schleyer, Science, 2001, 292, 2465–2469.
85. M. Torrent-Sucarrat and A. J. C. Varandas, Chem. – Eur. J., 2016, 22, 14056–14063.
86. D. G. S. Quattrociocchi, A. R. Oliveira, J. W. D. M. Carneiro, C. M. R. Rocha and A. J. C. Varandas, Int. J. Quantum Chem., 2020, 26583.
87. B. Schäfer-Bung, B. Engels, T. R. Taylor, D. M. Neumark, P. Botschwina and M. Perić, J. Chem. Phys., 2001, 115, 1777–1788.
88. J. T. Snodgrass, C. M. Roehl, P. A. Van Koppen, W. E. Palke and M. T. Bowers, J. Chem. Phys., 1990, 92, 5935–5943.
89. Z. X. Zhao, H. X. Zhang and C. C. Sun, J. Phys. Chem. A, 2008, 112, 12125–12131.
90. M. R. Nimlos, G. Davico, C. M. Geise, P. G. Wenthold, W. C. Lineberger, S. J. Blanksby, C. M. Hadad, G. A. Petersson and G. B. Ellison, J. Chem. Phys., 2002, 117, 4323–4339.
91. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
92. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
93. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
94. G. A. Adamson and C. W. Rees, J. Chem. Soc., Perkin Trans. 1, 1996, 1535–1543.
95. S. Arulmozhiraja and T. Ohno, J. Chem. Phys., 2008, 128, 114301.
96. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301.
97. J. A. Alonso, Structure and properties of atomic nanoclusters, Imperial College Press, 2nd edn, 2011, pp. 1–475.
98. A. K. Ott, G. A. Rechtsteiner, C. Felix, O. Hampe, M. F. Jarrold, R. P. Van Duyne and K. Raghavachari, J. Chem. Phys., 1998, 109, 9652–9655.
99. G. A. Rechtsteiner, C. Felix, A. K. Ott, O. Hampe, R. P. Van Duyne, M. F. Jarrold and K. Raghavachari, J. Phys. Chem. A, 2001, 105, 3029–3033.
100. A. E. Boguslavskiy, H. Ding and J. P. Maier, J. Chem. Phys., 2005, 123, 034305.
101. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. Miller III, M. E. Mura, A. Nicklaß, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, 2020, 2, 242–253.
102. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
103. T. H. Dunning, Jr., K. A. Peterson and D. E. Woon, Encycl. Comput. Chem., Wiley, Chichester, 1998, p. 88.
104. R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
105. T. H. Dunning, Jr., J. Phys. Chem. A, 2000, 104, 9062–9080.
106. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 2975–2988.
107. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 84102.
108. G. Knizia, T. B. Adler and H. J. Werner, J. Chem. Phys., 2009, 130, 054104.
109. H. J. Werner, G. Knizia, T. B. Adler and O. Marchetti, Z. Physiol. Chem., 2010, 224, 493–511.
110. J. Vázquez, M. E. Harding, J. Gauss and J. F. Stanton, J. Phys. Chem. A, 2009, 113, 12447–12453.
111. M. C. Ernst, A. F. Sax, J. Kalcher and G. Katzer, J. Mol. Struct.: THEOCHEM, 1995, 334, 121–126.
112. C. A. Nixon, A. E. Thelen, M. A. Cordiner, Z. Kisiel, S. B. Charnley, E. M. Molter, J. Serigano, P. G. J. Irwin, N. A. Teanby and Y.-J. Kuan, Astron. J., 2020, 160, 205.
113. J. C. Loison, M. Agúndez, V. Wakelam, E. Roueff, P. Gratier, N. Marcelino, D. N. Reyes, J. Cernicharo and M. Gerin, Mon. Not. R. Astron. Soc., 2017, 470, 4075–4088.
114. S. Ikuta and S. Wakamatsu, J. Chem. Phys., 2004, 120, 11071–11081.
115. D. J. Ehrlich and J. Y. Tsao, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1983, 969–984.
116. J. Barrau, J. Escudie and J. Satgé, Chem. Rev., 1990, 90, 283–319.
117. J. Pola and R. Taylor, J. Organomet. Chem., 1992, 437, 271–278.
118. J. M. Riveros, Probing the gas-phase ion chemistry of simple Ge systems, 2002.
119. Q.-S. Li, R.-H. Lü, Y. Xie and H. F. Schaefer, J. Comput. Chem., 2002, 23, 1642–1655.
120. P. Antoniotti, S. Borocci and F. Grandinetti, J. Phys. Chem. A, 2006, 110, 9429–9437.
121. P. W. Deutsch, L. A. Curtiss and J. P. Blaudeau, Chem. Phys. Lett., 1997, 270, 413–418.
122. P. W. Deutsch, L. A. Curtiss and J. P. Blaudeau, Chem. Phys. Lett., 2001, 344, 101–106.
123. A. J. C. Varandas, Annu. Rev. Phys. Chem., 2018, 69, 177–203.
124. M. C. Mccarthy, Z. Yu, L. Sari, H. F. Schaefer and P. Thaddeus, J. Chem. Phys., 2006, 124, 74303.
125. W. Carrier, W. Zheng, Y. Osamura and R. I. Kaiser, Chem. Phys., 2006, 330, 275–286.
126. T. Mondal, A. Guerra-Barroso, J. Fang, J. Li and A. J. C. Varandas, J. Chem. Phys., 2025, 162, 114309.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01143d

---