Revisiting a large and diverse data set for barrier heights and reaction energies: best practices in density functional theory calculations for chemical kinetics

Abstract

Accurate prediction of barrier heights and reaction energies is of paramount importance for reaction kinetics. For computational efficiency, such calculations are typically performed with density functional theory (DFT) methods, with accuracy that depends critically on the choice of functional. The RDB7 dataset (K. A. Spiekermann, L. Pattanaik and W. H. Green, High Accuracy Barrier Heights, Enthalpies, and Rate Coefficients for Chemical Reactions, Sci. Data, 2022, 9, 417) is a diverse chemical kinetics data set that covers 11 926 reactions and their barriers to assess present-day functionals. Strikingly, the RDB7 barrier heights reported using a reputable rung 4 hybrid functional (ωB97X-D3) exhibited significantly larger errors than seen in other benchmarks. Here, we identify the sources of error, and to the extent possible, address those sources. We categorize the barrier heights and reaction energies into three subsets based on orbital stability analysis. The “easy” subset has orbitals that are stable at the mean-field Hartree–Fock (HF) level, which implies weak correlation effects. An “intermediate” subset exhibits spin symmetry breaking at the HF level, but the restricted orbitals are stable at the dynamically correlated κ orbital optimized second order Møller–Plesset (κ-OOMP2) level with κ = 1.45. While more challenging than the easy category, this implies that correlation effects are still not strong. The remaining “difficult” subset is expected to be significantly affected by strong electron correlations, which potentially affects the accuracy of standard DFT. With this data classification, we performed new benchmarks with unrestricted ωB97X-D3 as well as two other hybrid functionals, ωB97M-V, and MN15, and the double hybrid ωB97M(2) functional. The RMSD values on the easy subset are comparable to prior high-quality benchmark studies, while the performance of all functionals on the intermediate subset is consistently less good. By far the largest errors lie in the difficult subset involving strongly correlated species. We refined some of the previous reference values to further assess the two key error sources: the density functional and its associated orbitals, and the reduced reliability of the previous RHF:RCCSD(T)-F12 reference. We propose our orbital stability classification as a best-practice approach for DFT calculations in chemical kinetics involving even numbers of electrons, as it provides useful information about the expected accuracy. We strongly recommend the routine use of orbital stability analysis in DFT calculations, as the spin-polarized solutions significantly reduce the strong correlation errors seen with spin-restricted orbitals.

---

1 Introduction

Rates of chemical kinetics are controlled by reaction barrier heights (BHs), and, in standard transition state theory,¹ that dependence is exponential:At room temperature, an error of just 1.5 kcal mol⁻¹ in the enthalpy of activation, ΔH^†, which is directly related to the activation energy, ΔE^†, will lead to a factor of 10 error in the resulting rate. However, for reasons of computational cost, highly accurate wavefunction-based methods^2,3 that yield significantly smaller errors are typically not used in large-scale chemical kinetics calculations. Instead it is common to employ density functional theory (DFT) methods,⁴ which are far less computationally costly. The best hybrid density functionals have root mean square deviations (RMSDs) that only just approach 1.5 kcal mol⁻¹, such as ωB97M-V (is 1.48 kcal mol⁻¹) for the barrier heights in the MGCDB84 database.⁴ Other widely used hybrid functionals are typically somewhat poorer, as illustrated by the data shown in Fig. 1. Such data is very useful for comparative assessment of density functionals, as well as for setting some expectations about the level of performance that is possible for chemical kinetics. For example, it is noteworthy that some of the best double hybrid functionals yield substantially improved predictions of barrier heights. For instance, ωB97M(2) achieves an RMSD of only 0.84 kcal mol⁻¹.⁵ On the other hand, lower rung functionals are considerably poorer.

Fig. 1 The geometric means (GM) of the RMSD values (in kcal mol⁻¹) of all subsets in the BH tasks for the representative functionals from all 5 rungs in the MGCDB84 database.

How transferable are such conclusions? It must be noted that there are relatively few data points for barrier heights in MGCDB84: only 206 values are included. It is therefore very likely that the results of benchmarking on those 206 barriers are not entirely representative of even the chemistry of the light main group elements that MGCDB84 focuses on. A similar critique can be applied to the other leading dataset used to assess density functionals: the widely used GMTKN55 dataset contains only 194 barrier heights.⁶ In fact many of their BH test cases are identical. Accordingly there is a need to assess density functionals across much larger and more diverse BH datasets. To partially fill this need, a number of high quality barrier height benchmarks have appeared in recent years. While we cannot document them all, we can list some that we are aware of. For example, TMB50 contains 50 transition metal BHs,⁷ and MOBH35 contains 35 transition metal BHs.^8,9 BH28 contains 28 diverse BHs for pericyclic, bipolar cycloaddition, cycloreversion, and proton transfer reactions,¹⁰ Criegee22 contains 22 BHs for ring-closing reactions involving atmospherically important Criegee intermediates,¹¹ CopeBH-22 contains 22 diverse BHs for Cope rearrangements in substituted shape-shifting bullvalenes.¹² BH2O-36 contains 36 BHs for hydrolysis reactions,¹³ and concerted proton transfer (CPT) BHs in 9 cyclic hydrogen bonded clusters have been reported.¹⁴ MME55 contains 55 metalloenzyme model BHs,¹⁵ and BH9 is a set of 449 diverse BHs.^16,17

While very valuable, those recent results provide only about a factor of 5 enhancement over the number of reference barrier heights available in 2017. To generate much higher volumes of data is also possible, although inevitably it is hard to do so at the same level of quality (i.e. targeting at least coupled cluster theory with perturbative triples¹⁸ (CCSD(T)) close to the complete basis set (CBS) limit).¹⁹ One notable effort that comes close to maintaining benchmark level accuracy is the RDB7 dataset.²⁰ RDB7 contains nearly 12 000 reactions and their corresponding reaction energies and barrier heights (forward and reverse), or roughly 120 times more kinetics data than either GMTN55 or MGCDB84. Briefly, the transition structures contain up to 7 heavy atoms, built from the light main group elements H, C, N, and O. The geometries were optimized at ωB97X-D3/def2-TZVP from prior work^21,22 that used the single-ended growing string method²³ to automatically identify thousands of transition structures (TSs) and products from a set of reactant species chosen from GDB-7.²⁴ RDB7 then refined the energetics at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory, which is close to the CBS limit,^25–30 thereby producing near-benchmark quality results. 15 representative reactions exhibited root mean square deviations within 0.25 kcal mol⁻¹ between CCSD(T)-F12a/cc-pVDZ-F12 and CCSD(T)-F12a/cc-pVTZ-F12 for both barrier heights and reaction energies. The RDB7 dataset has been used as ground truth data for AI-enhanced methods,^31,32 as well as a direct benchmark for evaluating the performance of various AI models.³³

The RDB7 reference results were used to assess two density functionals, a rung 2 GGA, B97-D3,³⁴ and a rung 4 range-separated hybrid GGA, ωB97X-D3 (as was used to obtain the geometries).^35–37 The results are very interesting for reasons that prompted this present study. First, the RMSD reported for the B97-D3 functional in the relatively small def2-mSVP basis set was 8.5 kcal mol⁻¹ for RDB7, which is remarkably consistent with the value of 8.3 kcal mol⁻¹ obtained from the 206 data points in MGCDB84 at the CBS limit.⁴ This would appear to suggest that conclusions drawn from the small dataset transfer quite well to the vastly larger, more diverse, RDB7 set. However, one must then confront the following apparent paradox. In RDB7, an RMSD of 5.3 kcal mol⁻¹ is obtained with the more advanced ωB97X-D3 hybrid using the larger def2-TZVP basis set, which is more than a factor of two larger than the value of 2.3 kcal mol⁻¹ obtained with the same functional at the CBS limit with the MGCDB84 data set!

Why are the range-separated hybrid results for RDB7 so much poorer than for MGCDB84? Does it reflect the greater diversity of the data? If so, then there are important limitations on how transferable the results obtained in MGCDB84 and GMTKN55 are to other systems containing the same light elements. Or are there critical differences in how the DFT reaction barrier heights are evaluated in the RDB7 study versus the MGCDB84 benchmarking? Certainly there are no obvious issues, such as numerical convergence problems. All systems were formally closed shell which meant that spin-restricted DFT calculations could be used. Yet if there are differences in benchmarking protocols, then there could be important implications for best practices in the evaluation of barrier heights by standard DFT methods that deserve to be more widely known. This work presents a systematic exploration of these two questions. While all results are revealed at the appropriate moment, we can foreshadow the conclusions a bit by observing that in fact both factors are at play in accounting for the much poorer hybrid GGA performance reported for RDB7 than in other smaller benchmarks such as GMTKN55 and MGCDB84.

To address the first question, let us remember that DFT has two main modes of breakdown. The first is delocalization or self-interaction (SIE) error^38,39 which is often associated with localized electrons or holes, and a defect of the exchange functional. SIE causes the sign of the barrier height for H + H₂ → H₂ + H to be inverted with semi-local functionals⁴⁰ (the Perdew–Zunger self-interaction-correction⁴¹ can usefully improve such results⁴²). SIE is certainly responsible for the much poorer performance of semi-local versus hybrid density functionals discussed above, as the latter cancel some SIE by use of a fraction of exact exchange. The second source of functional failure is strong correlation error^38,43,44 associated with the use of only a single Kohn–Sham determinant of molecular orbitals (MOs). Barrier heights associated with transition structures that exhibit strong correlations could indeed be significantly more difficult than those that are not. We will therefore categorize the reactions into three subsets, based on strength of correlations: easy, intermediate, and difficult. The easy category will be defined as corresponding to a sufficient absence of strong correlations that the mean-field Hartree–Fock orbitals are stable against artificial symmetry-breaking.⁴⁵ That is well known to be a signature of the absence of strong correlation effects.^46–48

The second, intermediate, category will be defined as being when a correlated method that excludes strong correlations remains stable against spin symmetry-breaking while HF is not. For this purpose we use the κ-regularized orbital-optimized second order Møller–Plesset (κ-OOMP2) method.^49,50 This method damps the matrix elements of MP2 theory in an energy-dependent way,⁵¹ based on the orbital energy differences between pairs of virtuals (a,b) and occupied (i,j), Δ^ab_ij and a parameter κ:

〈ij‖ab〉′ = 〈ij‖ab〉[1 − exp(−κΔ^ab_ij)] (2)

The strongest damping is for integrals associated with zero gaps, where they vanish. Thus κ-OOMP2 is a correlated theory which completely neglects the strongest small-gap correlations. As a result, stability of the spin-restricted κ-OOMP2 orbitals is a valid measure of the lack of very strong correlation.⁵² Assessing orbital symmetry breaking as a function of κ (i.e. a κ-scan) is the best way to fully characterize such behavior. Such results suggest that the use of κ = 1.45 is a reasonable choice for routine assessments.^49,52

If the κ-OOMP2 orbitals do not break spin-symmetry while HF orbitals do break spin-symmetry, we must conclude, on the one hand, that correlation effects are more challenging than for the easy category. On the other hand, we must also conclude that species in this category do not exhibit truly strong correlations. This definition is therefore a category of intermediate difficulty. The third, truly difficult category, will be the cases where κ-OOMP2 orbitals also break spin-symmetry, suggesting that there are genuine multi-reference effects at play.^48,52

By the same token, if there are large numbers of systems that fall into the intermediate and difficult categories, we must then confront the question of how to properly perform the DFT calculations. Our view is that the answer is to permit the DFT orbitals to break spin-symmetry whenever the spin-restricted orbitals are not stable. One can intuitively appreciate the reason for preferring this choice by recalling that in the separation of a closed shell molecule such as H₂ into two radical fragments, the correct answer will be obtained at dissociation by using spin-polarized orbitals because the fragments are becoming more and more weakly coupled. By contrast, the spin-restricted orbitals perform very poorly with almost all commonly used density functionals, as a manifestation of strong correlation error associated with entangling the two fragments.

Another aspect of the same view is that breaking spin-symmetry whenever possible provides the lowest possible energy, which is very suitable definition for the ground electronic state. While this may appear obvious as written, it is worth recalling that it is not typical to test spin-restricted DFT calculations for instability to spin-polarization, so this is certainly not the common view of practitioners of DFT. By contrast, every calculation performed in MGCDB84 assessments was tested for orbital instabilities.⁴ Most quantum chemistry codes provide this capability, at a cost that is not much greater than a self-consistent field (SCF) calculation itself. So it is computationally viable to do this for RDB7, and indeed it is viable to do this in general if needed. We note that in studies which use multiple functionals, it is typically sufficient to perform the stability analysis using the method most likely to break spin-symmetry (in our case, the mean-field Hartree–Fock method).

In the remainder of this work, we present a careful reassessment of the RDB7 dataset focusing on the nature and extent of spin symmetry breaking as motivated above. To broaden the scope of our assessment and test the transferability of our conclusions, together with ωB97X-D3, we also conducted new benchmarks with three additional functionals: ωB97M-V,⁵³ MN15,⁵⁴ and ωB97M(2).⁵ These functionals were selected both for their reported accuracy in other high-quality benchmarks^4,6,55,56 and for their slightly different ingredients and positions on the Jacob's ladder of functionals, allowing a more comprehensive evaluation.

2 Methods

The geometries for reactants, transition states, and products of all the 11 926 reactions are taken from the original RDB7 dataset. All the transition state geometries were verified in the original work of Grambow et al.^21,22 to have just one imaginary frequency that matched bond changes occurring between the reactant and product(s) at the restricted DFT level of theory (without internal stability analysis). Subsequent work by Spiekermann et al.^20,57 improved upon the Grambow geometries by refining product-side structures and computing high-level single-point energies. Considering the relatively small ratio of reactions with multiple products (27.7% 2-product reactions, 1.9% 3-product reactions in the full set), we combine the forward and reverse barrier height data as the barrier height task. With the 3-step workflow foreshadowed above, and detailed in the Results and discussion section, we categorized the reactions into “easy”, “intermediate”, and “difficult” subsets. The classifications for barrier heights and reaction energies were performed independently.

DFT calculations of all species were done with Q-Chem 5.4.^58,59 For the 4 functionals ωB97X-D3, ωB97M-V, MN15, ωB97M(2), unrestricted DFT calculations are performed with a spin polarized, unrestricted initial guess (10% β-LUMO/α-HOMO mixing from the restricted solution) and the geometric direct minimization (GDM) algorithm.⁶⁰ The def2-TZVP basis set⁶¹ was used for consistency with the original work. This is amongst the smallest basis sets that are reasonable for evaluation of barrier heights with hybrid density functionals.⁴ Internal stability analysis at the Hartree–Fock SCF level,⁴⁵ and unrestricted κ-OOMP2 〈S²〉 evaluations were also performed using Q-Chem. All κ-OOMP2 calculations used κ = 1.45 as previously recommended.⁴⁹

For the “easy” and “intermediate” subsets, the original RHF:RCCSD(T)-F12a/cc-pVDZ-F12 energetic reference values²⁰ are used without change. For the “difficult” subset, reference values for 150 selected outliers (selected as described in the Results section) were refined by applying Yamaguchi approximate spin projection,⁴⁶ which projects out the triplet contamination in the broken symmetry solution:

where the spin coupling coefficient, α, is:The M_s = 0 subscript indicates the spin-projected state, which is obtained from the broken symmetry (BS) singlet with M_s = 0 and the triplet (M_s = 1) state. We use UHF:UCCSD(T)-F12/cc-pVDZ-F12 for energies and UHF:UCCSD-F12/cc-pVDZ for 〈S²〉. Note that eqn (3) requires the triplet state to be higher than the singlet; reactions not meeting this criterion were removed from our list of refined benchmarks as shown in Fig. 2. It is also worth noting that while spin-projection surely improves the reference values for these difficult cases relative to not projecting, the improved reference values are nevertheless likely to be less accurate than for the easy and intermediate categories.

Fig. 2 Barrier height (BH) and reaction energy (RE) data are separately categorized into “easy”, “intermediate”, and “difficult” subsets leading to the distribution shown here in (a) and (b). Forward and reverse barriers are combined for the barrier height category.

For these calculations, the internal stability analysis of the UHF/cc-pVDZ-F12 solutions are done with ORCA 5.0.4,⁶² together with UCCSD(T)-F12/cc-pVDZ-F12 calculations based on the stable UHF orbitals. The resolution of the identity (RI) approximation⁶³ is applied only for the CCSD(T)-F12 part with cc-pVDZ-F12-CABS near-complete auxiliary basis set⁶⁴ and cc-pVTZ auxiliary basis set for correlation.⁶⁵ All of the correlated wavefunction calculations apply the frozen core approximation. Finally, the unrestricted Hartree–Fock based unrestricted CCSD 〈S²〉 calculations required in eqn (4) were performed with the cc-pVDZ basis set⁶⁶ using Q-Chem. The Q-Chem and ORCA input templates can be found in Section 7 of ESI.†

3 Results and discussion

3.1 Data classification

We set up a 3-step workflow to classify the data points into easy, intermediate, and difficult, as already foreshadowed:

(1) RHF stability analysis with the cc-pVDZ basis. The purpose of this step is two-fold: to check the fidelity of the spin unpolarized DFT test data and the RHF:RCCSD(T)-F12a/cc-pVDZ-F12 reference. As established in previous studies,⁶⁷ Kohn–Sham orbitals are usually less sensitive to spin polarization than Hartree–Fock orbitals, due to the inclusion of correlation effects. For instance, the onset of spin symmetry breaking with DFT is usually at longer bond-stretches than for HF. Using the relatively small cc-pVDZ basis set keeps the compute cost of stability analysis relatively low. For barrier height and reaction energy data points involving only RHF stable species, the corresponding data point is categorized into the “easy” subset. The unstable species enter step 2.

(2) The 〈S²〉 expectation value for the “not easy” species is evaluated at the unrestricted, κ-OOMP2/cc-pVDZ level of theory. If 〈S²〉 is less than 0.005 (i.e. spin symmetry is restored), we consider that the corresponding species exhibited “artificial” symmetry breaking at the HF level which is removed by use of κ-UOOMP2. The corresponding data point is categorized into the “intermediate” difficulty subset, because κ-UOOMP2 cannot describe strong correlation without spin symmetry-breaking. Species with spin-polarized κ-UOOMP2 solutions are thus considered to exhibit “essential” symmetry breaking indicating the presence of strong correlation characteristics, thus defining the “difficult” category.

(3) Species in the “difficult” category are not only difficult for DFT calculations: they may also not be reliably treated by the benchmark level of theory used previously.²⁰ Instead, a higher level of theory may be required, and ideally all reference data in the difficult category would be re-evaluated. However, this is very computationally costly, and so was not attempted. As an intermediate step, we selected 3 collections of 50 data points each as described later for closer assessment of the origin of some of the large discrepancies between ωB97X-D3 and the existing reference values. These data points were refined using spin-projection as described in the Methods section.

After the data classification (as shown in Fig. 2), spin-polarized DFT calculations with the 4 selected functionals ωB97X-D3, ωB97M-V, MN15, ωB97M(2) and def2-TZVP basis set are then performed. By contrast, the published RDB7 results are spin-restricted due to the use of a restricted initial guess. They are therefore reported as “R-ωB97X-D3”, in contrast to the true unrestricted DFT solutions in this new benchmark that carry U prefixes in all of the following data.

3.2 Easy subset

After RHF stability analysis, we categorized 5985 forward barrier heights, 4426 reverse barrier heights, and 6852 reaction energies that involve only RHF stable species into the easy subset. Of the 11 926 reactions in the full set, the easy subset is 43.6% of the barrier heights and 57.5% of the reaction energies. In Fig. 3, we present the barrier height error distribution of the easy subset compared to the whole set. Here the right panel only includes forward barrier heights for consistency with the original plot and statistics in ref. 20. We observe no significant difference between FBH and RBH error statistics and details can be found in the ESI.† The ωB97X-D3 RMSD value reduces from 5.32 kcal mol⁻¹ to 2.25 kcal mol⁻¹, which matches the reported MGCDB84 RMSD value for barrier heights⁴ of 2.28 kcal mol⁻¹ remarkably nicely! This error reduction is primarily attributed to the exclusion of systems with unstable SCF solutions, as evidenced by the near-complete overlap of the R-ωB97X-D3 and U-ωB97X-D3 error distribution curves in the left panel. Moreover, the long tail over-estimating the forward barrier height (e.g. >10 kcal mol⁻¹) in R-ωB97X-D3 in the right panel, is almost entirely eliminated in the easy subset (left panel) for both forward and reverse barrier heights.

Fig. 3 Comparison of the easy subset BH statistics with the unclassified full set FBH statistics from the original RDB7 paper.²⁰ (a) Easy set BH error distribution (with forward and reverse barriers combined). (b) Full set FBH error distribution as reported in the original paper.²⁰

A comparison of error statistics across different functionals further underscores the importance of the stability of orbitals. In the right panel, ωB97M-V, MN15, and ωB97M(2) show approximately the same RMSD for forward barrier height (∼2.70 kcal mol⁻¹) on the full RDB7 set. However, their performance diverges significantly for tasks of different levels of difficulty. When evaluating the easier tasks where all species are RHF stable, the ωB97M(2) functional performs notably better than all other functionals, with an RMSD of 1.14 kcal mol⁻¹, which is near chemical accuracy. ωB97M-V also performs well, with an RMSD of 1.55 kcal mol⁻¹ and MAD of 1.20 kcal mol⁻¹ consistent with the findings from other benchmarks.^4,16,17,68 On the easy subset, the performance of ωB97X-D3 slightly outperforms MN15, which directly contradicts the conclusions drawn from the full set in the right panel.

For reaction energies (REs), the general trends of the difference in the performance of different functionals are very similar. However, much smaller error reduction from excluding the unstable SCF solutions is achieved compared to the barrier height tasks. Overall, ωB97M(2) and ωB97M-V also perform well on reaction energy tasks with RMSDs of 1.36 and 1.47 kcal mol⁻¹, although their performance here (panel (a) of Fig. 4) is slightly worse than on barrier heights Fig. 3a). Surprisingly, the performance of MN15 is a little worse on the supposedly easy subset than on the full set!

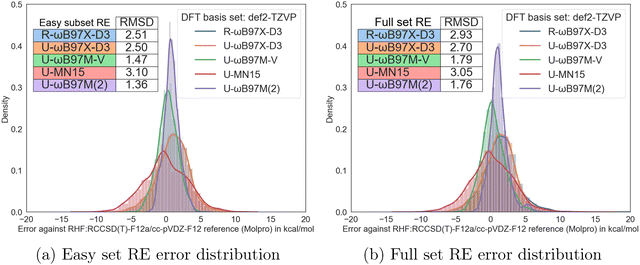Fig. 4 Comparison of the easy subset RE statistics with the unclassified full set RE statistics from the original RDB7 paper.²⁰ (a) Easy set RE error distribution. (b) Full set RE error distribution.

3.3 Intermediate subset

Recall that the intermediate subset involves at least one species with an unstable RHF solution, but no species for which κ-OOMP2 is unstable. Therefore the intermediate subset is more challenging to describe than the easy subset, but is not considered to involve truly strong correlations. After executing the classification workflow, we find the intermediate subset contains 9760 barrier heights (4513 forward and 5247 reverse) and 4054 reaction energies.

In Fig. 5, we present the error distribution of the intermediate subset. The minor difference between R-ωB97X-D3 and U-ωB97X-D3 RMSD shows that (by contrast with HF) there is relatively little spin-polarization occurring in this subset for DFT. This is consistent with previous work, which demonstrates that Kohn–Sham orbitals are less sensitive to spin symmetry breaking compared to Hartree–Fock orbitals. Therefore, the restricted DFT description is often sufficient even when HF orbitals exhibit spin symmetry breaking. Similarly, the RHF:RCCSD(T)-F12 reference can still be reliable. For our purposes, this distinction was built into the classification process by using κ-OOMP2 〈S²〉 metric. It is reassuring to see that a very similar subset would have been defined by choosing based on stability of R-ωB97X-D3 rather than κ-OOMP2.

Fig. 5 Intermediate set error distribution. (a) Intermediate set BH error distribution. (b) Intermediate set RE error distribution.

Turning to the statistical performance, as expected, almost all DFT methods perform worse on the intermediate subset than on the easy subset. For barrier heights, the double hybrid functional ωB97M(2) continues to outperform the other 3 functionals, despite its RMSD almost doubling to 2.11 kcal mol⁻¹ relative to its RMSD on the easy set (1.14 kcal mol⁻¹). Smaller fractional increases (though of similar magnitude) are found for ωB97X-D3 (2.50 kcal mol⁻¹ to 3.81 kcal mol⁻¹) and ωB97M-V (1.47 kcal mol⁻¹ to 2.65 kcal mol⁻¹). In contrast, the MN15 functional shows only a minor increase in error, bringing its performance closer to ωB97M-V in this subset.

Reaction energy tasks generally follow the same trend when comparing intermediate set errors to easy set errors. A consistent error increase of 0.4–0.5 kcal mol⁻¹ is found for ωB97X-D3, ωB97M-V, and ωB97M(2). MN15 shows a minimal decrease in error on the intermediate subset relative to the easy subset, yet its overall performance remains the worst of the 4 functionals in both subsets.

3.4 Difficult subset

Together, the easy subset and the intermediate subset account for 84.5% of the barrier heights and 91.5% of the reaction energies of the full RDB7 set. The remaining cases are significantly more challenging, as they typically exhibit much larger discrepancies between the restricted DFT and RHF:RCCSD(T)-F12 values. They account for most of the performance gap between the originally reported RDB7 RMSD of 5.32 kcal mol⁻¹ for R-ωB97X-D3, and the 2.28 kcal mol⁻¹ reported for BHs in the MGCDB84 dataset. For instance, 83 reactions from the original data have forward barrier heights differing by 20 kcal mol⁻¹ or more (R-ωB97X-D3 vs. RHF:RCCSD(T)-F12a), which corresponds to about 0.70% of the full RDB7 set. With κ-UOOMP2 〈S²〉 values greater than 0, these strongly correlated cases require more careful refinement.

There are three potential contributors to the large errors seen for R-ωB97X-D3 on the difficult subset. (1) The likely instability of restricted Kohn–Sham orbitals, which fail to describe strong correlation well, (2) strong correlation errors that remain when the restricted DFT orbitals are allowed to spin polarize, and (3) the questionable validity of the RHF:RCCSD(T)-F12 reference values in this strongly correlated regime. The first issue can be mitigated by ensuring stable, unrestricted Kohn–Sham orbitals. Breaking spin-symmetry provides the lowest possible energy and hence improves the single-determinantal description of strongly correlated system.

The second issue can be assessed properly if reliable benchmark values are available, but is not readily correctable. Spin polarization often introduces considerable spin contamination. Although this cannot strictly be measured in Kohn–Sham theory, it is likely to raise the energy relative to the properly correlated low spin solution. One may attempt to use spin projection methods to correct for the error associated with spin contamination,⁴⁶ but the results are ambiguous because the Kohn–Sham orbitals correspond to a fictitious, non-interacting system, and yet that wavefunction is used to evaluate 〈S²〉. We consider this to be out of scope for our assessment. By contrast, the third issue is addressable, as discussed in detail in the Methods section, although due to high compute costs, we only improve the benchmark values for a fraction of the difficult cases.

3.4.1 1st collection: largest R-ωB97X-D3 deviations vs. RCCSD(T)-F12. In Fig. 6, we present the forward barrier height error distribution for the 50 data points with the largest R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 discrepancy. Let us first consider the role of DFT orbital stability. The error statistics improve quite drastically upon replacing the unstable RDFT results (left panel) by stable UDFT calculations (right panel; orange bars), with absolute error reduction of up to ∼30 kcal mol⁻¹ (bottom panel: blue vs. orange bars). For these reactions, the leading source of error is the use of unstable RDFT orbitals.

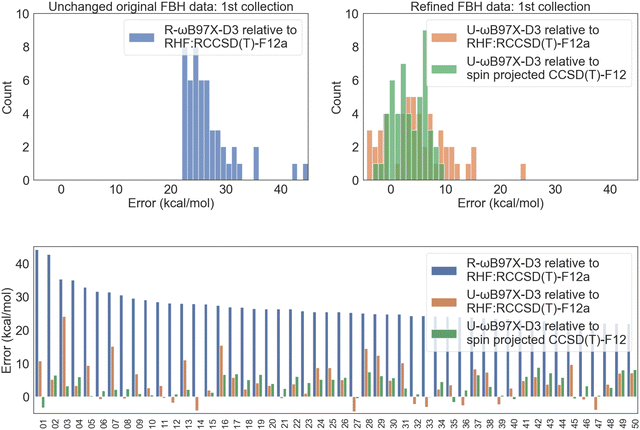Fig. 6 FBH error distribution for the 50 reactions with the largest R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 discrepancy. The indices of the reactions included in this selection are provided in the Excel sheet in the ESI.†

The next factor to address is the quality of the benchmarks themselves. Spin projected UHF:UCCSD(T)-F12 energies further improve the agreement with unrestricted DFT results as can be seen in the right and bottom panels of Fig. 6. While the refined, spin-projected CCSD(T)-F12 reference values may still carry errors of a few kcal mol⁻¹, it is impractical to further improve their quality with excessive computational cost, and such errors are still (typically) much smaller than DFT errors. In principle, the remaining errors may now be attributed to problems in a density functional when treating energy differences that involve differential strong correlation effects. An assessment of those errors for the 4 tested functionals is shown in Table 1. All functionals have consistently larger errors on this difficult FBH collection compared to easy and intermediate BH results. The mean signed deviation is significant. Since the transition structure is typically more strongly correlated than the reactants, the positive MSD is a signature of spin contamination raising the barrier height for each of the functionals. More specifically, the performance of ωB97M(2) is particularly poor: for this difficult collection it shows an RMSD of ∼6 kcal mol⁻¹ which is larger than the other 3 functionals. We infer that the double hybrid is somewhat more sensitive to strong correlation effects, perhaps consistent with its use of un-regularized PT2.⁵ A similar trend also holds for RBH, and we refer the readers to the detailed statistics in Section 4 of the ESI.†

Table 1 FBH error statistics of unrestricted DFT compared against spin projected UHF:UCCSD(T)-F12 reference, for the 50 reactions with largest R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 FBH discrepancy (unit: kcal mol⁻¹). MSD, MAD, and RMSD represent the mean signed deviation, mean absolute deviation, and root mean square deviation, respectively. These abbreviations are used consistently in the following tables in the main text and the ESI

Functional	Min	Max	MSD	MAD	RMSD
U-ωB97X-D3	−3.24	8.78	3.38	3.67	4.49
U-ωB97M-V	−0.95	8.93	4.34	4.38	4.99
U-MN15	−3.68	10.79	3.21	3.68	4.57
U-ωB97M(2)	1.53	9.42	5.48	5.48	5.93

---

For reaction energies, we do similar reaction selection and refinement as summarized in (Fig. 7). With spin-polarized Kohn–Sham orbitals, the biggest outliers with deviations of ∼15 kcal mol⁻¹ or above in the R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 collection are all fixed. Replacing the reference by spin projected UHF:UCCSD(T)-F12 allows us to report the detailed error statistics in Table 2. Again, the performance of all functionals is consistently worse than on the easy and intermediate subsets (Fig. 3a and 5a). Relatively, MN15 performs less badly than the other 3 functionals, but its RMSD is still greater than 5 kcal mol⁻¹.

Table 2 RE error statistics of unrestricted DFT compared against spin projected UHF:UCCSD(T)-F12 reference, for the 50 reactions with largest R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 RE discrepancy (unit: kcal mol⁻¹)

Functional	Min	Max	MSD	MAD	RMSD
U-ωB97X-D3	−0.43	13.06	6.26	6.28	6.81
U-ωB97M-V	2.86	11.30	6.90	6.90	7.09
U-MN15	−0.85	9.46	4.65	4.69	5.17
U-ωB97M(2)	4.33	12.24	7.43	7.43	7.56

---

Fig. 7 RE error distribution for the 50 reactions with the largest R-ωB97X-D3 vs. RHF:RCCSD(T)-F12 discrepancy. The indices of the reactions included in this selection are provided in the Excel sheet of ESI.†

3.4.2 2nd collection: largest U-ωB97X-D3 deviations vs. RCCSD(T)-F12. When we identify the 50 data points with the largest deviations between U-ωB97X-D3 and RHF:RCCSD(T)-F12, we find the data points included have changed substantially from the 1st collection. Additionally, the barrier height errors relative to the spin-projected UHF:UCCSD(T)-F12 reference increase significantly. While large discrepancies between R-ωB97X-D3 and RHF:RCCSD(T)-F12 are primarily driven by the instability of restricted Kohn–Sham orbitals, the large discrepancies between U-ωB97X-D3 and RHF:RCCSD(T)-F12 are largely due to strong correlation errors! Fixing the benchmark values, of course, does not address the intrinsic challenges for DFT (whether spin-restricted or unrestricted) to properly describe strongly correlated systems. This pronounced difference makes the error statistics of the 1st and 2nd collections remarkably different for both barrier heights and reaction energies.

Fig. 8 illustrates the forward barrier height error distribution for these 50 data points. Notably, for several of the biggest outliers, spin projection cleans up the errors in the reference level. However, in many other cases, the refined reference does not bring the difference closer, as DFT in general does not perform well in the strong correlation regime. The chief exception is the limit of complete separation of radical fragments, where good performance is recovered; however there are no such cases in this dataset, of course! Detailed error statistics in Table 3 show much poorer DFT performance even compared to the previous collection of 50 reactions. All functionals exhibit very large RMSD values, with ωB97X-D3 even exceeding 11 kcal mol⁻¹!

Fig. 8 FBH error distribution for the 50 reactions with the largest U-ωB97X-D3 vs. RHF:RCCSD(T)-F12 discrepancy. The indices of the reactions included in this selection are provided in the Excel sheet in the supplementary files.† To simplify the visualization and better highlight the difference purely from refining the CCSD(T)-F12 reference, R-ωB97X-D3 values are excluded.

Table 3 FBH error statistics of unrestricted DFT compared against spin projected UHF:UCCSD(T)-F12 reference, for the 50 reactions with largest U-ωB97X-D3 vs. RHF:RCCSD(T)-F12 FBH discrepancy (unit: kcal mol⁻¹)

Functional	Min	Max	MSD	MAD	RMSD
U-ωB97X-D3	−3.24	17.26	10.53	10.66	11.18
U-ωB97M-V	0.20	14.61	8.95	8.95	9.40
U-MN15	−2.13	12.90	7.92	8.09	8.76
U-ωB97M(2)	1.58	12.74	8.43	8.43	8.75

---

When we similarly refine 50 reaction energy data points, we observe no significant difference in the RE error statistics for the new collection (as shown in Table 4) with the largest U-ωB97X-D3 vs. RHF:RCCSD(T)-F12 reaction energy discrepancy (Fig. 9), in contrast to the RE error statistics of the 1st collection (as shown in Table 2). This may be due to the generally lower degree of spin contamination involved in the products than in the transition state structures, where some bonds are quite stretched. The detailed error statistics shown in Table 4 only change marginally (less than 0.2 kcal mol⁻¹) for ωB97M-V, MN15, and ωB97M-V relative to the REs used in the 1st collection. However, the performance of ωB97X-D3 is slightly worse compared to the 1st collection.

Table 4 RE error statistics of unrestricted DFT compared against spin projected UHF:UCCSD(T)-F12 reference, for the 50 reactions with largest U-ωB97X-D3 vs. RHF:RCCSD(T)-F12 RE discrepancy (unit: kcal mol⁻¹)

Functional	Min	Max	MSD	MAD	RMSD
U-ωB97X-D3	2.42	13.06	7.36	7.36	7.60
U-ωB97M-V	4.25	11.30	7.14	7.14	7.25
U-MN15	0.24	9.46	4.80	4.80	5.22
U-ωB97M(2)	4.71	12.24	7.40	7.40	7.54

---

Fig. 9 RE error distribution for the 50 reactions with the largest U-ωB97X-D3 vs. RHF:RCCSD(T)-F12 discrepancy. The indices of the reactions included in this selection are provided in the Excel sheet in the supplementary files.† To simplify the visualization and better highlight the difference purely from refining the CCSD(T)-F12 reference, R-ωB97X-D3 values are excluded.

For the reverse barrier heights in this collection, similar quantitative and qualitative conclusions can be drawn as for the forward barrier heights, based on the corresponding tables and plots in Section 5 of the ESI.† Additionally, we identify a 3rd collection based on the largest U-ωB97M-V deviations from RCCSD(T)-F12 values (see the Section 6 of ESI† for details), where the observed trends in barrier height and reaction energy remain consistent with the 2nd collection.

4 Conclusions

In this work, we have explored the origin of quite striking errors in ωB97X-D3 barrier heights reported for the RDB7 dataset with the generally well-regarded ωB97X-D3 functional.²⁰ Once this first purpose was achieved, we then also sought to assess the performance of three other well-regarded functionals on RDB7. First is ωB97M-V, which is a ranged-separated hybrid meta-GGA that typically out-performs ωB97X-D3, which is an older range-separated hybrid GGA. Second is MN15, which is another more recent hybrid meta-GGA that performs quite well for barrier heights and thermochemistry. Third is ωB97M(2), which is a double-hybrid functional that has the best reported performance on the MGCDB84 dataset, and, until very recently,⁶⁹ the best reported performance on the GMTKN55 dataset.

To explore the origin of the large reported errors, we used a 3-step workflow to categorize the barrier height and reaction energy data points into easy, intermediate, and difficult subsets, based on the likely strength of electron correlation effects. Our main observations are as follows:

(1) In the easy subset (defined as all species involved yielding restricted Hartree–Fock (RHF) orbitals that are stable to spin polarization), our new benchmarks align well with other prior studies. The good performance on these cases where correlation effects are not strong clearly indicates that the origin of the reported discrepancies lies elsewhere.

(2) In the intermediate subset (where some species are not RHF stable but remain stable against spin polarization with κ-OOMP2) the correlation effects become more challenging to correctly capture. Hence all 4 functionals tested perform less well than in the easy subset, although the outcomes are not out of line with other independent benchmark tests.

(3) For the 84.6% barrier heights and 91.4% reaction energies in the easy and intermediate subsets, the descending order of DFT performance for BHs is ωB97M(2) > ωB97M-V > MN15 > ωB97X-D3, while for REs it is ωB97M(2) > ωB97M-V > ωB97X-D3 > MN15.

(4) The difficult subset (where κ-OOMP2 orbitals also exhibit significant spin-symmetry breaking) exhibits strong correlation effects. Statistical analysis shows clearly that these cases are the primary source of the large reported ωB97X-D3 BH errors.

(5) Benchmark results were refined for a subset of the difficult cases (particularly problematical results) using spin-projection. The improved benchmarks demonstrate that the largest restricted ωB97X-D3 errors can be significantly reduced by allowing the DFT orbitals to spin polarize. Nevertheless, the remaining errors in all 4 functionals remain quite large for strongly correlated BHs and REs.

Given these observations, we can make the following conclusions and recommendations for barrier height and reaction energy calculations using hybrid density functional theory.

(1) We strongly recommend that orbital stability analysis be performed for hybrid DFT calculations on even-electron systems in particular, but also radical systems. The use of the lowest energy (spin-polarized) solutions typically leads to significantly smaller errors versus benchmarks than use of spin-restricted orbitals, when there are orbital instabilities.

(2) To categorize the strength of electron correlations, we recommend using the workflow we describe here, to distinguish easy cases, intermediate cases and potentially difficult cases, ranging from weak to strong correlation effects.

(3) In some cases (e.g. complete separation into fragments), systems in the strong correlation category can be accurately treated by DFT calculations after allowing for spin-polarization. However, in light of the poor performance of all 4 functionals tested on the most difficult subset, we recommend caution about the accuracy of DFT with even the best functionals for systems in the difficult category.

(4) Other best practices^4,70 for benchmarking functionals (adequate choices of atomic orbital basis set, numerical quadrature grid, and suitably tight cutoffs and convergence criteria) should be followed to the extent feasible.

(5) To obtain the best quality DFT-optimized structures (i.e. corresponding to the lowest energy for a given functional), especially for the transition state, the same orbital stability recommendations given above should also be followed.

There are almost certainly other existing datasets that could be improved by following these recommendations: one example that is derived from the same original source²¹ as RDB7²⁰ is the very large Transition1x dataset,⁷¹ used for machine learning.

Data availability

The data supporting this article have been included as part of the ESI† (SI.pdf), and the raw data is organized into a separate Excel sheet (RDB7_refined.xlsx).

Conflicts of interest

MH-G is a part-owner of Q-Chem Inc, whose software was used for most of the calculations reported here.

Acknowledgements

Work at Berkeley and MIT was supported by the Gas Phase Chemical Physics Program, in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy under Contract Numbers DE-AC02-05CH11231 (Berkeley) and DE-SC0014901 (MIT) respectively. We would like to thank Dr Diptarka Hait for helpful discussions, and Linus B. Dittmer for helping with the TOC plot.

References

1. J. L. Bao and D. G. Truhlar, Variational transition state theory: theoretical framework and recent developments, Chem. Soc. Rev., 2017, 46, 7548–7596.
2. T. Helgaker, W. Klopper and D. P. Tew, Quantitative quantum chemistry, Mol. Phys., 2008, 106, 2107–2143.
3. A. Karton, Quantum mechanical thermochemical predictions 100 years after the Schrödinger equation, Annu. Rep. Comput. Chem., 2022, 18, 123–166.
4. N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315–2372.
5. N. Mardirossian and M. Head-Gordon, Survival of the most transferable at the top of Jacob's ladder: Defining and testing the ωB97M(2) double hybrid density functional, J. Chem. Phys., 2018, 148, 241736.
6. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
7. B. Chan, P. M. W. Gill and M. Kimura, Assessment of DFT methods for transition metals with the TMC151 compilation of data sets and comparison with accuracies for main-group chemistry, J. Chem. Theory Comput., 2019, 15, 3610–3622.
8. M. A. Iron and T. Janes, Evaluating transition metal barrier heights with the latest density functional theory exchange–correlation functionals: The MOBH35 benchmark database, J. Phys. Chem. A, 2019, 123, 3761–3781.
9. M. A. Iron and T. Janes, Correction to “evaluating transition metal barrier heights with the latest density functional theory exchange–correlation functionals: The MOBH35 benchmark database”, J. Phys. Chem. A, 2019, 123, 6379–6380.
10. A. Karton, Highly accurate CCSDT (Q)/CBS reaction barrier heights for a diverse set of transition structures: Basis set convergence and cost-effective approaches for estimating post-CCSD (T) contributions, J. Phys. Chem. A, 2019, 123, 6720–6732.
11. C. D. Smith and A. Karton, Kinetics and thermodynamics of reactions involving Criegee intermediates: An assessment of density functional theory and ab initio methods through comparison with CCSDT (Q)/CBS data, J. Comput. Chem., 2020, 41, 328–339.
12. A. Karton, Can density functional theory ‘Cope’with highly fluxional shapeshifting molecules?, Chem. Phys., 2021, 540, 111013.
13. A. R. Epstein, E. W. C. Spotte-Smith, M. C. Venetos, O. Andriuc and K. A. Persson, Assessing the Accuracy of Density Functional Approximations for Predicting Hydrolysis Reaction Kinetics, J. Chem. Theory Comput., 2023, 19, 3159–3171.
14. Y. Xue, T. M. Sexton, J. Yang and G. S. Tschumper, Systematic analysis of electronic barrier heights and widths for concerted proton transfer in cyclic hydrogen bonded clusters:(HF)n, (HCl)n and (H₂O)n where n = 3, 4, 5, Phys. Chem. Chem. Phys., 2024, 26, 12483–12494.
15. D. A. Wappett and L. Goerigk, Benchmarking density functional theory methods for metalloenzyme reactions: The introduction of the mme55 set, J. Chem. Theory Comput., 2023, 19, 8365–8383.
16. V. K. Prasad, Z. Pei, S. Edelmann, A. Otero-de-la Roza and G. A. DiLabio, BH9, a new comprehensive benchmark data set for barrier heights and reaction energies: Assessment of density functional approximations and basis set incompleteness potentials, J. Chem. Theory Comput., 2021, 18, 151–166.
17. V. K. Prasad, Z. Pei, S. Edelmann, A. Otero-De-La-Roza and G. A. DiLabio, Correction to “BH9, a New Comprehensive Benchmark Data Set for Barrier Heights and Reaction Energies: Assessment of Density Functional Approximations and Basis Set Incompleteness Potentials”, J. Chem. Theory Comput., 2022, 18, 4041–4044.
18. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, A fifth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479.
19. T. Helgaker, J. Gauss, P. Jorgensen and J. Olsen, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 6430.
20. K. A. Spiekermann, L. Pattanaik and W. H. Green, High Accuracy Barrier Heights, Enthalpies, and Rate Coefficients for Chemical Reactions, Sci. Data, 2022, 9, 417.
21. C. A. Grambow, L. Pattanaik and W. H. Green, Reactants, Products, and Transition States of Elementary Chemical Reactions Based on Quantum Chemistry, Sci. Data, 2020, 7, 1–8.
22. C. A. Grambow, L. Pattanaik and W. H. Green, Reactants, Products, and Transition States of Elementary Chemical Reactions based on Quantum Chemistry, 2020 DOI:10.5281/zenodo.3715478.
23. P. M. Zimmerman, Single-Ended Transition State Finding with the Growing String Method, J. Comput. Chem., 2015, 36, 601–611.
24. L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875.
25. T. B. Adler, G. Knizia and H.-J. Werner, A Simple and Efficient CCSD(T)-F12 Approximation, J. Chem. Phys., 2007, 127, 221106.
26. F. A. Bischoff, S. Wolfsegger, D. P. Tew and W. Klopper, Assessment of Basis Sets for F12 Explicitly-Correlated Molecular Electronic-Structure Methods, Mol. Phys., 2009, 107, 963–975.
27. G. Knizia, T. B. Adler and H.-J. Werner, Simplified CCSD(T)-F12 Methods: Theory and Benchmarks, J. Chem. Phys., 2009, 130, 054104.
28. F. Pfeiffer, G. Rauhut, D. Feller and K. A. Peterson, Anharmonic Zero Point Vibrational Energies: Tipping the Scales in Accurate Thermochemistry Calculations?, J. Chem. Phys., 2013, 138, 044311.
29. Y. Shang, H. Ning, J. Shi, H. Wang and S.-N. Luo, Chemical Kinetics of H-abstractions from Dimethyl Amine by H, CH3, OH, and HO2 Radicals with Multi-Structural Torsional Anharmonicity, Phys. Chem. Chem. Phys., 2019, 21, 12685–12696.
30. D. Feller, K. A. Peterson and J. G. Hill, Calibration study of the CCSD (T)-F12a/b methods for C2 and small hydrocarbons, J. Chem. Phys., 2010, 133.
31. K. A. Spiekermann, L. Pattanaik and W. H. Green, Fast predictions of reaction barrier heights: toward coupled-cluster accuracy, J. Phys. Chem. A, 2022, 126, 3976–3986.
32. X. García-Andrade, P. García Tahoces, J. Pérez-Ríos and E. Martínez Núñez, Barrier height prediction by machine learning correction of semiempirical calculations, J. Phys. Chem. A, 2023, 127, 2274–2283.
33. Y. Chen, Y. Ou, P. Zheng, Y. Huang, F. Ge and P. O. Dral, Benchmark of generalpurpose machine learning-based quantum mechanical method AIQM1 on reaction barrier heights, J. Chem. Phys., 2023, 158, 074103.
34. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1789.
35. J.-D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106.
36. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
37. Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, Long-range Corrected Hybrid Density Functionals with Improved Dispersion Corrections, J. Chem. Theory Comput., 2013, 9, 263–272.
38. A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for density functional theory, Chem. Rev., 2012, 112, 289–320.
39. K. R. Bryenton, A. A. Adeleke, S. G. Dale and E. R. Johnson, Delocalization error: The greatest outstanding challenge in density-functional theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, 13, e1631.
40. B. G. Johnson, P. M. W. Gill and J. A. Pople, A density functional study of the simplest hydrogen abstraction reaction. Effect of self-interaction correction, Chem. Phys. Lett., 1994, 220, 377.
41. J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048.
42. P. Mishra, Y. Yamamoto, J. K. Johnson, K. A. Jackson, R. R. Zope and T. Baruah, Study of self-interaction-errors in barrier heights using locally scaled and Perdew–Zunger self-interaction methods, J. Chem. Phys., 2022, 156, 014306.
43. A. J. Cohen, P. Mori-Sánchez and W. Yang, Fractional spins and static correlation error in density functional theory, J. Chem. Phys., 2008, 129, 121104.
44. F. Malet and P. Gori-Giorgi, Strong correlation in Kohn-Sham density functional theory, Phys. Rev. Lett., 2012, 109, 246402.
45. R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XVIII. Constraints and stability in Hartree–Fock theory, J. Chem. Phys., 1977, 66, 3045.
46. K. Yamaguchi, F. Jensen, A. Dorigo and K. Houk, A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals, Chem. Phys. Lett., 1988, 149, 537–542.
47. V. N. Staroverov and E. R. Davidson, Distribution of effectively unpaired electrons, Chem. Phys. Lett., 2000, 330, 161.
48. J. Lee and M. Head-Gordon, Two single-reference approaches to singlet biradicaloid problems: Complex, restricted orbitals and approximate spin-projection combined with regularized orbital-optimized Møller-Plesset perturbation theory, J. Chem. Phys., 2019, 150, 244106.
49. J. Lee and M. Head-Gordon, Regularized orbital-optimized second-order Møller–Plesset perturbation theory: A reliable fifth-order-scaling electron correlation model with orbital energy dependent regularizers, J. Chem. Theory Comput., 2018, 14, 5203–5219.
50. A. Rettig, J. Shee, J. Lee and M. Head-Gordon, Revisiting the Orbital Energy-Dependent Regularization of Orbital-Optimized Second-Order Møller–Plesset Theory, J. Chem. Theory Comput., 2022, 18, 5382–5392.
51. J. Shee, M. Loipersberger, A. Rettig, J. Lee and M. Head-Gordon, Regularized secondorder Møller–Plesset theory: A more accurate alternative to conventional MP2 for noncovalent interactions and transition metal thermochemistry for the same computational cost, J. Phys. Chem. Lett., 2021, 12, 12084–12097.
52. J. Lee and M. Head-Gordon, Distinguishing artificial and essential symmetry breaking in a single determinant: Approach and application to the C60, C36, and C20 fullerenes, Phys. Chem. Chem. Phys., 2019, 21, 4763–4768.
53. N. Mardirossian and M. Head-Gordon, ωB97M-V: A combinatorially optimized, rangeseparated hybrid, meta-GGA density functional with VV10 nonlocal correlation, J. Chem. Phys., 2016, 144, 214110.
54. S. Y. Haoyu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051.
55. A. Najibi and L. Goerigk, The nonlocal kernel in van der Waals density functionals as an additive correction: An extensive analysis with special emphasis on the B97M-V and ωB97M-V approaches, J. Chem. Theory Comput., 2018, 14, 5725–5738.
56. G. Santra, N. Sylvetsky and J. M. L. Martin, Minimally empirical double-hybrid functionals trained against the GMTKN55 database: revDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4, J. Phys. Chem. A, 2019, 123, 5129–5143.
57. K. A. Spiekermann, L. Pattanaik and W. H. Green, High Accuracy Barrier Heights, Enthalpies, and Rate Coefficients for Chemical Reactions version 1.0.1, 2022 DOI:10.5281/zenodo.6618262.
58. Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kús, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Dop, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, P. A. Pieniazek, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, N. Sergueev, S. M. Sharada, S. Sharmaa, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, V. Vanovschi, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhou, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xua, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2015, 113, 184–215.
59. E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al., Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155, 084801.
60. T. Van Voorhis and M. Head-Gordon, A geometric approach to direct minimization, Mol. Phys., 2002, 100, 1713.
61. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
62. F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
63. S. Ten-no and J. Noga, Explicitly correlated electronic structure theory from R12/F12 ansätze, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 114–125.
64. E. F. Valeev, Improving on the resolution of the identity in linear R12 ab initio theories, Chem. Phys. Lett., 2004, 395, 190–195.
65. F. Weigend, A. Kohn and C. Hättig, Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations, J. Chem. Phys., 2002, 116, 3175.
66. T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007.
67. C. D. Sherrill, M. S. Lee and M. Head-Gordon, On the performance of density functional theory for symmetry-breaking problems, Chem. Phys. Lett., 1999, 302, 425–430.
68. G. Santra, R. Calinsky and J. M. Martin, Benefits of range-separated hybrid and doublehybrid functionals for a large and diverse data set of reaction energies and barrier heights, J. Phys. Chem. A, 2022, 126, 5492–5505.
69. A. D. Becke, A remarkably simple dispersion damping scheme and the DH24 double hybrid density functional, J. Chem. Phys., 2024, 160, 204118.
70. A. Karton and M. T. De Oliveira, Good Practices in Database Generation for Benchmarking Density Functional Theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e1737.
71. M. Schreiner, A. Bhowmik, T. Vegge, J. Busk and O. Winther, Transition1x – a dataset for building generalizable reactive machine learning potentials, Sci. Data, 2022, 9, 779.

---

Footnote

† Electronic supplementary information (ESI) available: SI.pdf: the ESI provides detailed statistical analyses of BH and RE errors across different subsets of the RDB7 dataset. Error statistics are presented in tables embedded within violin plots, with explicit comparisons between forward and reverse barrier heights for the easy and intermediate subsets and the 3 collections from the difficult subset. Q-Chem and ORCA input templates for the data categorization are also included. RDB7_refined.xlsx: this file contains raw data for the full RDB7 set and its subsets, organized into corresponding subsheets for easy access. See DOI: https://doi.org/10.1039/d5cp01181g

---