 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Point + Gaussian charge model for electrostatic interactions derived by machine learning
David
van der Spoel
 * and
A. Najla
Hosseini
* and
A. Najla
Hosseini

Dept. Cell and Molecular Biology, Uppsala University, Box 596, SE-75124 Uppsala, Sweden. E-mail: david.vanderspoel@icm.uu.se
First published on 12th June 2025
Abstract
At short distances between atoms, point charges are a poor approximation of the electrostatic interaction. Due to overlapping electron clouds, charges are effectively shielded and the electrostatic interaction energy is modified. In molecular simulations, two main approaches have surfaced to deal with this. First, the Thole-screening [B. T. Thole, Chem. Phys., 1981, 59, 341–350], which introduces a mathematical modification of the Coulomb interaction at short range, and second, the use of Gaussian-distributed charges [C. M. Smith and G. G. Hall, Theor. Chim. Acta 1986, 69, 63–69]. Here, we show that these approaches are practically equivalent, that is the screening functions are numerically very similar and their parameters related by a simple expression. A quantitative comparison between electrostatic interactions in alkali-halide ion pairs, computed using high level symmetry-adapted perturbation theory (SAPT), and in point charge models shows that the electrostatic interactions are not always weaker than those predicted by point charge approximations, highlighting that more complex atomic models may be needed. We then proceed to use machine learning with the Alexandria Chemistry Toolkit to train models for alkali-halides based on a positive core and a virtual site with a negative Gaussian-distributed charge and show that this model yields energies very close to SAPT.
Understanding the limitations of charge models is essential for accurately representing electrostatics in molecular systems. Standard point-charge approaches can overestimate dipole moments, particularly in systems with significant charge overlap or polarization effects. For instance, the experimental dipole of alkali halide ion-pairs at their minimum energy distance is 15–30% smaller than what would be expected from point charges (see Table S2 in ref. 1). This shows that charge penetration has to be taken into account when computing electrostatic interactions and several, relatively simple, modifications of the Coulomb equation can be used to incorporate this effect.
In the early 1980s, Thole introduced a smeared interaction between point dipoles i and j at distance rij to better model short range interactions:2
 | (1) |
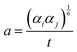 | (2) |
Some years after the Thole paper, it was realized that both the electron density and the electrostatic potential generated by small molecules can be reproduced by a combination of point charges and a Gaussian-distributed charge.4–6 The Coulomb interaction between two Gaussian-distributed charges qi and qj with screening widths ζi and ζj, respectively, is given by
 | (3) |
 | (4) |
Both the Thole screening function (eqn (1)) and the error function in eqn (3) converge to 1 rapidly with increasing distance r. By integrating the difference between the functions from zero to infinity it is possible to approximate ζ in terms of a:
 | (5) |
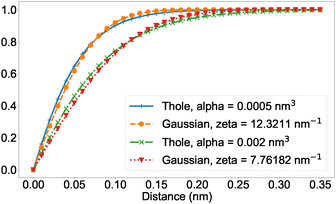 | ||
| Fig. 1 Screening function due to Thole with polarizabilities αi and αj both set to α as indicated, and t = 2.6, compared to the screening due to two Gaussian-distributed charges with ζ as computed from eqn (5). Distance corresponds to rij in eqn (1) and (3). | ||
It is tempting to compare screened Coulomb functions to real electrostatic interactions as can be computed using SAPT.13,14 Based on the ratio of the SAPT electrostatic energy component and the Coulomb interaction between two point charges, ζ or a can be computed. Table 1 lists, for nine alkali halide ion-pairs, the energy corresponding to point charges (PC), and from SAPT. Then, ζ is computed from
 | (6) |
| r (nm) | E PC (kJ mol−1) | E SAPT (kJ mol−1) | a (nm) | ζ (nm−1) | ζ′ (nm−1) | |
|---|---|---|---|---|---|---|
| LiF | 0.1640 | −847.0 | −826.4 | 0.03300 | 9.72 | 11.40 |
| LiCl | 0.2060 | −674.3 | −648.7 | 0.04638 | 7.12 | 8.11 |
| LiBr | 0.2260 | −614.6 | −591.8 | 0.05061 | 6.52 | 7.43 |
| NaF | 0.2020 | −687.6 | −708.8 | — | — | — |
| NaCl | 0.2480 | −560.1 | −573.8 | — | — | — |
| NaBr | 0.2540 | −546.9 | −562.6 | — | — | — |
| KF | 0.2260 | −614.6 | −667.9 | — | — | — |
| KCl | 0.2760 | −503.3 | −540.1 | — | — | — |
| KBr | 0.2820 | −492.6 | −538.1 | — | — | — |
The electrostatic energies computed by SAPT were compared to a polarizable alkali-halide model by Walz and co-workers.1Fig. 2 shows that the SAPT electrostatic energies for nine ion pairs and a range of distances are reproduced poorly by this relatively advanced model. Indeed, the Walz et al. model is quantitatively (ion pairs involving Li+) and even qualitatively (ion pairs involving Na+ or K+) incorrect. The reason for this is, that core and shell share the same Gaussian screening width in this model, and hence the electrostatic interaction at short distance is weaker than a point charge, which is not consistent with SAPT for ion pairs involving Na+ or K+ (see also Table 1). Despite this, the model was found to be quite accurate in applications such as the prediction of molten salt properties, melting points, and conductivity20–23 because it relies on error compensation between the energy components, like most classical FFs.24,25 The CHARMM-Drude model for ions mentioned above3 employs point charges and therefore yields the exact same electrostatic energy as a pair of point charges.
 | ||
| Fig. 2 Difference between electrostatic energy from SAPT2+3(CCD)δMP2/aug-cc-pVTZ, the Walz et al. model (Gaussian), and ACT (positive point charge + negative Gaussian + distributed charge) and the interaction of two point charges. For calculations of interaction involving the model for alkali halides due to Walz et al.,1 the exact same charges and ζ were used as in the original study. Where positive (ion-pairs involving Li+), the interaction is weaker than that between a pair of point charges and vice versa. Dashed lines indicate the minimum energy distances from gas-phase experimental data19: LiF (1.56 Å), LiCl (2.02 Å), LiBr (2.17 Å), NaF (1.93 Å), NaCl (2.36 Å), NaBr (2.50 Å), KF (2.17 Å), KCl (2.67 Å), and KBr (2.82 Å). | ||
Taken together, this analysis suggests that FF models should be constructed from the combination of a positive point charge and a Gaussian-distributed “electron cloud” with a compensating negative charge. The latter can be implemented as a virtual site located at the ion position, such that the net charge is +1 for Na+ and K+ and −1 for the halide ions. Li+ can be modeled as a point charge. The Alexandria Chemistry Toolkit (ACT)25 was used to train such a model, by optimizing atomic charges and Gaussian distribution widths (ζ, eqn (4)) to reproduce the SAPT electrostatic interactions for all ion pairs at the same time. The resulting parameters are listed in Table 2.
| Parameter | q C | q VS | ζ VS (nm−1) |
|---|---|---|---|
| F− | 1.24604 | −2.24604 | 11.7866 |
| Cl− | 1.84001 | −2.84001 | 8.87883 |
| Br− | 1.488 | −2.488 | 7.80382 |
| Li+ | 1 | — | — |
| Na+ | 5.70319 | −4.70319 | 20.4367 |
| K+ | 9.80622 | −8.80622 | 14.1548 |
The ACT point + Gaussian model yields energy curves that adhere closely to SAPT (Fig. 2). In fact, the ACT model is an order of magnitude more accurate than point charges or the model due to Walz et al.1 (Table 3), showing that accuracy of force field electrostatics can be improved vastly over simple point charges.
| Compound | Walz et al. | PC | ACT |
|---|---|---|---|
| LiF | 36.2 | 18.6 | 3.9 |
| LiCl | 13.6 | 22.0 | 3.1 |
| LiBr | 10.1 | 30.0 | 2.0 |
| NaF | 32.0 | 16.2 | 1.1 |
| NaCl | 32.5 | 16.0 | 1.2 |
| NaBr | 28.2 | 13.2 | 1.8 |
| KF | 64.5 | 54.2 | 4.2 |
| KCl | 68.0 | 57.2 | 2.4 |
| KBr | 39.4 | 32.2 | 1.4 |
| Average | 40.4 | 32.1 | 2.7 |
In a recent review of the Open Force Field project, Wang et al. coined the term “Force Field Science” to describe the study of potential functions and algorithms in a systematic manner.27 They went on to suggest that this new branch of computational chemistry was virtually unexplored. Indeed, systematic design of FFs28 is needed and the long history of model building by hand29,30 should be incorporated in these efforts. Our group has focused on highlighting the effect different potentials have on simulations for alkali halides,1,20–23 for noble gases31 and most recently on alcohol-water mixtures.25 The introduction of the Alexandria Chemistry Toolkit25 will make it easy to perform Force Field Science experiments by deriving FFs using different potentials and charge models from scratch with the purpose to critically evaluate their properties.32,33 As we show here, both Thole screening and Gaussian-distributed charges give very similar reduction of the interaction strength at short distance and the complexity of the eqn (3) and (1) is similar as well. A careful analysis of the chemistry involved (Table 1 and Fig. 2) shows, however, that charge interactions can be more complex than that given by just (screened) Coulomb interactions. For the alkali halide ion pairs studied here, the still relatively simple combination of a point charge and a Gaussian charge distribution provides an order of magnitude more accurate rendering of the electrostatic interactions than previous models. Further research is needed to determine whether such a model is needed for all atoms, or just a subset. The Alexandria Chemistry Toolkit can be used for this kind of studies in Force Field Science.25,34
Author contributions
DvdS conceived the study and wrote the first version of the manuscript. He created scripts to produce Fig. 1 and Table 1. ANH made suggestions to extend the work, performed calculations, compiled Tables 2, 3 and Fig. 2 and she contributed to writing.Conflicts of interest
There are no conflicts to declare.Data availability
All scripts and SAPT datasets are openly available on https://github.com/AlexandriaChemistry/Data/GitHub.Notes and references
- M. M. Walz, M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, J. Chem. Theory Comput., 2018, 14, 5933–5948 CrossRef CAS PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- H. Yu, T. W. Whitfield, E. Harder, G. Lamoureux, I. Vorobyov, V. M. Anisimov, A. D. MacKerell, Jr. and B. Roux, J. Chem. Theory Comput., 2010, 6, 774–786 CrossRef CAS PubMed.
- G. G. Hall and C. M. Smith, Int. J. Quantum Chem., 1984, 25, 881–890 CrossRef CAS.
- C. M. Smith and G. G. Hall, Theor. Chim. Acta, 1986, 69, 63–69 CrossRef CAS.
- G. G. Hall and K. Tsujinaga, Theor. Chim. Acta, 1986, 69, 425–436 CrossRef CAS.
- D. Elking, T. Darden and R. J. Woods, J. Comput. Chem., 2007, 28, 1261–1274 CrossRef CAS PubMed.
- D. M. Elking, G. A. Cisneros, J.-P. Piquemal, T. A. Darden and L. G. Pedersen, J. Chem. Theory Comput., 2010, 6, 190–202 CrossRef CAS PubMed.
- P. T. Kiss, P. Bertsyk and A. Baranyai, J. Chem. Phys., 2012, 137, 194102–194111 CrossRef PubMed.
- P. T. Kiss and A. Baranyai, J. Chem. Phys., 2014, 141, 114501 CrossRef PubMed.
- M. M. Ghahremanpour, P. J. van Maaren, C. Caleman, G. R. Hutchison and D. van der Spoel, J. Chem. Theory Comput., 2018, 14, 5553–5566 CrossRef CAS PubMed.
- L. Zhang, H. Wang, M. C. Muniz, A. Z. Panagiotopoulos, R. Car and W. E, J. Chem. Phys., 2022, 156, 124107 CrossRef CAS PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- T. H. Dunning, Jr. and K. A. Peterson, J. Chem. Phys., 2000, 1113, 7799–7808 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 556–565 Search PubMed.
- F. Lovas, Diatomic Spectral Database, NIST Standard Reference Database 114, 2002, https://www.nist.gov/pml/data/msd-di/index.cfm.
- M.-M. Walz and D. van der Spoel, Phys. Chem. Chem. Phys., 2019, 21, 8516–18524 RSC.
- M.-M. Walz and D. van der Spoel, Chem. Commun., 2019, 55, 12044–12047 RSC.
- M.-M. Walz and D. van der Spoel, J. Phys. Chem. C, 2019, 123, 25596–25602 CrossRef CAS.
- M.-M. Walz and D. van der Spoel, Commun. Chem., 2021, 4, 1–10 CrossRef PubMed.
- M. Zgarbova, M. Otyepka, J. Sponer, P. Hobza and P. Jurecka, Phys. Chem. Chem. Phys., 2010, 12, 10476–10493 RSC.
- D. van der Spoel, J. Marrades, K. Kříž, A. N. Hosseini, A. T. Nordman, J. P. A. Martins, M.-M. Walz, P. J. van Maaren and M. M. Ghahremanpour, Evolutionary Machine Learning of Physics-Based Force Fields in High-Dimensional Parameter-Space, chemrxiv, 2025, preprint, chemrxiv:2025-0tw95 DOI:10.26434/chemrxiv-2025-0tw95.
- D. van der Spoel, P. J. van Maaren and M. M. Ghahremanpour, Alexandria Chemistry Toolkit Reference and User Manual version 1.0, The Alexandria Chemistry Project, Uppsala, Sweden, 2025 Search PubMed.
- L. Wang, P. K. Behara, M. W. Thompson, T. Gokey, Y. Wang, J. R. Wagner, D. J. Cole, M. K. Gilson, M. R. Shirts and D. L. Mobley, J. Phys. Chem. B, 2024, 128, 7043–7067 CrossRef CAS PubMed.
- D. van der Spoel, Curr. Opin. Struct. Biol., 2021, 67, 18–24 CrossRef CAS PubMed.
- P. Dauber-Osguthorpe and A. T. Hagler, J. Comput. Aid. Mol. Des., 2019, 33, 133–203 CrossRef CAS PubMed.
- A. Hagler, J. Comput. Aid. Mol. Des., 2019, 33, 205–264 CrossRef CAS PubMed.
- K. Kříž, P. J. van Maaren and D. van der Spoel, J. Chem. Theory Comput., 2024, 20, 2362–2376 CrossRef PubMed.
- W. F. van Gunsteren and A. E. Mark, J. Chem. Phys., 1998, 108, 6109–6116 CrossRef CAS.
- D. van der Spoel, J. Zhang and H. Zhang, Wiley Interdiscip. Rev.-Comput. Mol. Sci., 2022, 12, e1560 CrossRef CAS.
- K. Kříž and D. van der Spoel, J. Phys. Chem. Lett., 2024, 15, 9974–9978 CrossRef PubMed.
| This journal is © the Owner Societies 2025 |
