Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Barkhausen noise in the columnar hexagonal organic ferroelectric BTA†
Andrey Alekseevich Butkevich ,
Fabian T. Thome
,
Fabian T. Thome ,
Toni Seiler,
Marcel Hecker and
Martijn Kemerink
,
Toni Seiler,
Marcel Hecker and
Martijn Kemerink *
*
Institute for Molecular Systems Engineering and Advanced Materials, Im Neuenheimer Feld 225, Heidelberg, 69120, Germany. E-mail: martijn.kemerink@uni-heidelberg.de
First published on 2nd June 2025
Abstract
Upon a polarization reversal within a ferroelectric material, one stable state changes into another, which is typically described by a progression of switching events of smaller fractions of the material. These events give rise to crackling or Barkhausen noise and follow a characteristic distribution in their sizes. Barkhausen noise has been studied to better understand the switching processes of ferroelectrics and has been applied for inorganic ferroelectric materials and perovskites. In this work, we present results from kinetic Monte Carlo simulations investigating the switching process of the small organic molecular ferroelectric benzene-1,3,5-tricarboxamides (BTAs). For temperatures below 175 K and sufficiently strong structural disorder, the system exhibits self-organized critical behavior; for higher temperatures, a creep regime is entered. Our extracted power-law exponents are smaller than those typically measured in inorganic crystals and ceramics, which indicates that in the more disordered material BTA larger spanning avalanches are possible. The system was experimentally investigated with a high-sensitivity setup. No Barkhausen noise was observed, which is consistent with the simulated event sizes, lying several orders beneath the noise threshold of the experimental setup. This finding corroborates the notion that switching in BTA progresses along the 1D columns in the hexagonal liquid crystal lattice, with little coupling between the columns that could give rise to larger lateral avalanches.
1. Introduction
While crackling – or Barkhausen – noise appearing during ferroelectric polarization reversal has been thoroughly investigated, most previous studies were confined to inorganics and specifically perovskites.1–7 It was established that different inorganic ferroelectric materials indeed show Barkhausen noise in their switching processes. Statistical analyses showed that power-law behavior is present in multiple quantities describing the switching process, although the expected exponential cut-off at large event sizes is not always present. The recovered critical exponents varied between different materials, depending on the strength of correlations present, but the overall similar behavior suggests universality in systems exhibiting Barkhausen noise.2–4,6,7 The only investigation into thermal Barkhausen noise of organic ferroelectrics was performed on PVDF thin films where the measured current peaks are generated due to the reordering of dipoles while crossing the Curie-temperature and clear deviations from a continuous switching process with different shapes were observed.8 As such, univocal evidence of critical behavior in the switching of organic ferroelectric materials is still lacking. Observation, or the lack thereof, would, however, provide important information about the microscopic details of switching in organic ferroelectrics, including the size of and the interaction strength between the switching entities.If a physical system is driven, meaning that it is constantly pushed out of equilibrium by a, typically slowly increasing, external force, one of the possible responses can be crackling noise, which constitutes the transition between the snapping and popping. The former is characterized by a singular large event and the latter is given by many smaller events of similar amplitude. In the intermediate – the crackling – case, the occurrence of sudden and jerky events whose corresponding amplitudes, durations and energies are typically power-law distributed on a large scale arises.9 Crackling is interpreted as a dynamical critical phenomenon.9,10 In the case of ferroelectrics, one manifestation of crackling noise is Barkhausen noise, which arises from the irregular movement of domain walls through the sample.11
The mean field plasticity model was originally applied to materials under shear stress, displaying step-like stress–strain curves that showed material-independent power-law behavior.12 Considering the property of universality in critical systems, it was found that the model could also be related to switching process in soft ferroic materials.13 This process would then be described as a depinning transition where the local failure stress τf has to be overcome for a slip to start that then continues until the local stress is below the sticking stress τs. Due to disorder, both quantities vary depending on the location inside the material. The slip itself can cause further slips in the surrounding area, leading to an avalanche propagating through the material as the external force F causes the stress to slowly increase and the medium to deform elastically. Applying a mean field theory, the evolution of the accumulated slip u(r, t) is described as
 | (1) |
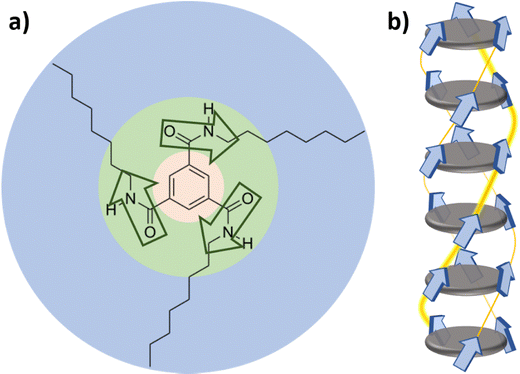
In this work, the prototypical small organic molecular ferroelectric benzene-1,3,5-tricarboxamide (BTA) is investigated. It is a columnar hexagonal liquid crystal and hence combines the properties like flexibility and easy-processability of a liquid and anisotropy for macroscopic polarization of a crystal. Furthermore, the basic BTA molecule discussed here has many structural derivatives with quantitatively different properties and potential applications.17 The herein investigated BTA-C8 is representative of the larger family of materials. BTAs consist of a benzene core with three attached amide groups and alkyl tails of varying length, as shown in Fig. 1a. BTAs tend to self-assemble into columnar stacks via π–π stacking and hydrogen bonding, hence making it a supramolecular columnar discotic, which possesses a cooperative effect, meaning that longer stacks generally become more stable and have larger dipole moments per monomer, which is indicated in Fig. 1b.18–21 The ferroelectric character of BTA is based on the dipole moments of the amide groups along the columns forming a macrodipole and has been studied and proven by several experimental studies.17,20,22,23 It has been established that the polarization switching relies on the reorientation of the amide groups and thus on sufficiently flexible side chains.24 The quasi-1D ferroelectric switching in BTA is described by the thermally-activated nucleation-limited switching model and fulfills all the common criteria for ferroelectricity.17,22,25,26 Despite the high grade of organization, BTA systems show a high amount of disorder due to amorphous regions in the material and defects in the molecular columns.
It has to be noted that the mean field plasticity model and the description of Barkhausen noise are valid for quasi-2D systems, reduced from 3D. In marked contrast, due to the weak intercolumnar coupling, ferroelectric switching in BTA happens predominantly along the columnar axis as a quasi-1D process. While crackling noise and the corresponding critical behavior has been investigated for a variety of dimensions, we are not aware of similar studies on 1D systems.10 Therefore, one of the goals of this manuscript is to investigate whether the common phenomenology and description of crackling noise is applicable to quasi-1D systems as well.
Previously, we have hypothesized that the structural disorder in BTA gives rise to small microdomains that strongly interact internally but only weakly with their surroundings.27 As such, they could be treated as the hysterons in a Preisach model, which allowed to reproduce the shape of the hysteresis curve as well as the dispersion in the switching kinetics. As the Preisach model neglects all interactions between the hysterons beyond the offset on the Preisach plane, the question whether any relevant interaction occurs between the hysterons, that were identified as sub-columns in hexagonal columnar morphology, is still open.
In this work, the fluctuations that naturally emerge in kMC simulations are used to simulate crackling noise. The analysis thereof suggests a universal character of irreversible switching of BTA, which occurs via critical dipole avalanches of different sizes as further discussed below. The avalanches propagate along the BTA columns. The power-law exponents extracted from the size and energy distribution functions are seemingly invariant to the disorder of the system and agree well with the mean field theory. While for higher temperatures the exponents are subject to thermal effects, which is attributed to creep behavior, the exponents observed at lower temperatures are robust, in agreement with self-organized criticality. Experimentally, no Barkhausen noise was measured in BTA samples, which is attributed to the current signals produced by switched dipoles being too low to be observed with the noise threshold of the used measuring setup.
2. Model
In order to study the critical behavior and crackling noise, both processes on the macroscopic scale and molecular level have to be considered. This is achieved via a kinetic Monte Carlo (kMC) simulation that focusses on electrostatic interactions; other, e.g. steric, interactions are accounted for by a prescribed morphology and especially the rotation rates and the angles of the amide dipoles. In previous work we found these parameters to be the most relevant ones and, importantly, sufficient to describe the thermally driven switching in BTA.25–27 Switching rates, based on classical energy calculations, determine which dipoles are likely to flip and thus the evolution of the system. Additionally, disorder is implemented as deviations, specified in more detail below, from the perfect crystal symmetry.The BTA morphology in the simulation has been adopted from what was discussed above. The hydrogen bonds forming between the dipolar amide groups have an out-of-plane rotation of 30° to 40°, which leads to a helical pitch of six molecules with an interdiscular distance of 3.5 Å and an intercolumnar distance 17.2 Å for an alkyl chain with eight carbon atoms (BTA-C8).28–32 The only explicitly appearing part of the BTA structure are the amide groups in form of dipole vectors, while other parts are included implicitly, i.e. in lattice parameters such as intercolumnar distance (alkyl chain length) or distance between middle of a BTA molecule and the dipoles (size of benzene core). As opposed to molecular dynamics (MD) simulations, all particles are fixed in their position as given by the morphology throughout the simulation and the only mobile aspect is the orientation of the dipole vectors. Similar to an Ising model, the dipoles can take two states, which are distinguished only by the z-component of the permanent dipole moment. As thin films are modelled, periodic boundary conditions in x- and y-directions are used; in the z-direction mirror boundary conditions are applied to account for the metal electrodes. They make use of the fact that the effect of a conducting plane on a charge Q is equivalent to that of an oppositely charged mirror image −Q on the other side of the electrode.
The final morphological aspect of disorder is implemented by separating the columns that would extend from electrode to electrode in an ideal situation into subcolumns of different lengths. The general simulated structure is columnar with the benzene cores of the BTA molecules stacking on top of each other until a defined height nz is reached. There are x·y columns that are simulated. The length for each subcolumn is drawn from a Gaussian distribution with a mean value N and variance σN and only integer values are allowed. The molecules within a column have a fixed rotation of α = 60° with respect to each other. To simulate defects, each subcolumn is separated from the others in the same stack by a shift σxyz, a randomized rotation around the column axis and a potential change in helicity. At the start of a simulation run, the grid forming the BTA columns is formed with the specified parameters. An illustration of the different parameters and the symmetry breaking can be found in Fig. S1.1 in the ESI.† The parameters for a typical simulation are given in Table S1.1 in the ESI.†
The flipping rates determining the evolution during the kMC simulation arise from the electrostatic interactions and the resulting energy calculations. The energy of a dipole i is given by
Ui = −![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i· i·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) I, I,
| (2) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i and the local electric field
i and the local electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) i. The total dipole moment consists of the permanent and induced contribution with the latter determined by the local field Ei and the polarizability α of the material:
i. The total dipole moment consists of the permanent and induced contribution with the latter determined by the local field Ei and the polarizability α of the material:
 | (3) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) app is assumed to be constant throughout the simulation box and its x- and y-components are chosen as zero. Then, the contribution to the electric field induced by and different dipole j is given as
app is assumed to be constant throughout the simulation box and its x- and y-components are chosen as zero. Then, the contribution to the electric field induced by and different dipole j is given as
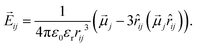 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij = rij
ij = rij![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij is the real-space vector (distance) separating the dipoles i and j. Due to numerical limitations, the dipole–dipole interactions calculated this way need to be confined to a certain number of nearest neighbors. This defines a sphere with a cut-off radius rc = 30 inside of which all interactions are considered explicitly. The contribution of the remaining dipoles is not negligible due to the long-range nature of Coulomb interactions and is approximated using the reaction field method.33 Within of this framework, it is assumed that all dipoles inside the sphere induce a polarization charge density
ij is the real-space vector (distance) separating the dipoles i and j. Due to numerical limitations, the dipole–dipole interactions calculated this way need to be confined to a certain number of nearest neighbors. This defines a sphere with a cut-off radius rc = 30 inside of which all interactions are considered explicitly. The contribution of the remaining dipoles is not negligible due to the long-range nature of Coulomb interactions and is approximated using the reaction field method.33 Within of this framework, it is assumed that all dipoles inside the sphere induce a polarization charge density  on the sphere surface and hence polarize the surrounding material. This leads to the following reaction-field at the center position:
on the sphere surface and hence polarize the surrounding material. This leads to the following reaction-field at the center position:
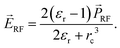 | (5) |
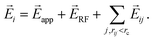 | (6) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) i and
i and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i, which are taken as the real values. Thus, the energies for all dipoles in any given dipole configuration can be obtained.
i, which are taken as the real values. Thus, the energies for all dipoles in any given dipole configuration can be obtained.
In particular, the energy difference ΔUi between a state with dipole i up with respect to a state with dipole i down, is the important factor for the flipping rate and is referenced to as the flipping energy. The value of ΔUi depends on the surrounding environment, which changes significantly during the evolution of a simulation. Instead of solving the problem of the induced dipoles at each step of the kMC, an approximation of the change of the flipping energy is obtained beforehand. In addition to calculating ΔUi,1 for a given surrounding, ΔUi,2 is also obtained, where the neighboring dipole j has been flipped. The difference of both yields djΔUi, which is a measure of the effect of reversal of a neighboring dipole on the flipping energy of dipole i and thus its flipping rate. Upon doing this calculation for all dipoles j in the interaction sphere of dipole i, the flipping rate ΔUi can at all times throughout the evolution of one simulation be kept at the approximately correct value without recalculating the induced dipoles. Expanding this to all dipoles in the simulation box saves a significant amount of computational time.
The flipping energies are solely based on electrostatic interactions, which depend on the morphology and can be calculated as
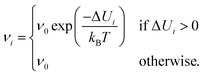 | (7) |
During the kMC simulation, the flipping rates serve as weight factors in determining which dipole flips. The probability for a dipole i to be selected for a flip is given by νi/νtot with the sum of all flipping rates  . At each simulation step, a random number between zero and one is drawn, which decides which dipole is flipped. A second random number r2 ∈ [0,1] is used to calculate the increment of time associated with the current step:
. At each simulation step, a random number between zero and one is drawn, which decides which dipole is flipped. A second random number r2 ∈ [0,1] is used to calculate the increment of time associated with the current step:
 | (8) |
3. Simulation and analysis procedure
In all numerical experiments, the BTA system was driven with a slowly varying external field while measuring the polarization. All dipoles initially pointed downwards, hence providing a fully saturated starting condition. The parameter representing the electric field was ramped from −0.8 V nm−1 to 0.8 V nm−1 and back again. The complete driving was spread over 1 microsecond and 120 different field values where each field value represents a sub-simulation with recalculated induced dipole problem. Typical simulation settings are provided in Table S1.1 in the ESI.†Fig. 2a shows a typical result for a simulated switching process over time with the driving field E (blue), the permanent polarization Pp (orange) and the obtained current of a complete loop I (green), i.e. the concatenation of all sub-simulations. The current represents the number of flipped dipoles per time bin and bundled up over longer time frames as jerks. Large jumps in the permanent polarization and spikes in the current are observed once the applied electric field is large enough, i.e. approaches the coercive field of the simulated system. Some of the spikes are numerical artifacts as seen by their regular occurrence and are due to the abrupt changes of the applied field and the corresponding recalculation of the linear polarization and flipping rates. Filtering out those data points leads to the curves of total polarization shown in Fig. 2b, where the majority of the current peaks remains, indicating the presence of crackling noise.
To identify the individual events, a threshold level was set, as is indicated in Fig. 2b (horizontal black lines). This is required since dipole flips are often initiated due to thermal fluctuations, although they reverse shortly afterwards due to the local field still pointing in the other direction. While many relatively small events arise this way, they do not contribute to the switching process and have to be filtered out. An event starts when the absolute of the polarization current first exceeds the threshold level and ends once it falls below it again. As an alternative to the polarization current, events can be defined by counting the dipoles that flipped per time step, which is the preferred method as it offers an immediate measure of the avalanche sizes while the polarization current depends on the sample geometry. However, these two quantities are linearly proportional, hence the current is the obvious choice as a proxy for the avalanche sizes in a real experiment.
Setting the threshold level is a trade-off between losing small crackling events and adding events that are thermal noise generated, as illustrated in Fig. 2c showing the number of detected events as a function of the threshold level normalized to the largest measured spike xmax of one loop. Furthermore, as the typical number of events collected from a single loop is insufficient for statistical analysis, multiple single numerical experiments were combined, as shown in Fig. 2d. The full description of the threshold settings, the analysis of simulated events and combination of similar data sets is provided in Section S2 in the ESI.†
The results of an exemplary set of simulations and the corresponding probability densities are shown in Fig. 3. Here, the size S is defined as the highest number of flipped dipoles per time step during one avalanche and the summed size SΣ is obtained by adding up all dipoles that flipped per time step in the course of one event. The latter was not further analyzed as it is subjected to artifacts arising from large fraction of singular events. The energy of an avalanche U is defined via its proportionality to the integral of the electrical power and the inter-event time δt is the time-span between events. The probability density functions for the sizes and energies show a similar structure with an initial region of small events that are not captured by the power-law, followed by a large part of the distribution showing the power-law behavior. The distribution shows a steep decline for the biggest events due to the limitations arising from the system size. For size S and summed size SΣ distributions, a clear shift towards larger events as a result of summing over all points within an event is visible. The energy distribution shows same trend as the distribution of event sizes and the proportionality U ∝ I2 ∝ S2 is clearly visible from the spread of the values. The inter-event times are directly tied to the time given by the sweeping frequency of the applied electric field. Here, the simulated time was t = 10−3 s and all the simulated events happened within the time frame of δt = 2 × 10−4 s.
4. Simulation results
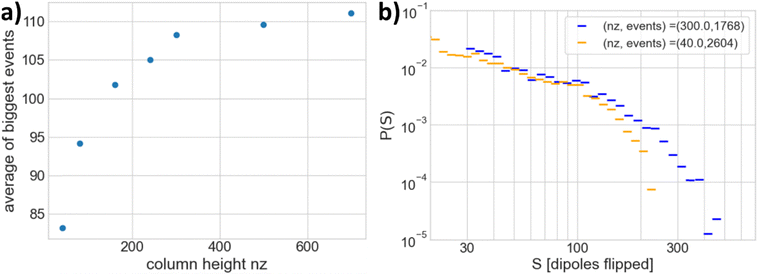
A general concern with the numerical simulation of potentially critical behavior of finite systems is that a relatively higher number of larger events could happen in bigger simulation boxes. To assure that finite size effects do not affect our results, additional simulations with gradually increased system size nz were carried out. Fig. S3.1 in the ESI† shows the probability densities for six different sizes between 40 and 700 molecules in the z-direction. It was observed that the occurrence of larger event sizes increased with increasing column length until nz ≈ 300. For even larger systems, barely an effect was found, hence the main simulations were carried out with a system size of nz = 300 We note that this corresponds to a film thickness of ∼105 nm, which is less than the film thicknesses typically investigated experimentally.Furthermore, to investigate the effect of the column height on the event sizes, the mean of the event sizes was analyzed for different system sizes. A strong initial increase that diminishes with the increase of the system size was observed, as depicted in Fig. 4a. The same effect was also investigated for systems with a larger number of shorter columns in the x- and y-directions, which is shown in Fig. 4b. The resulting distribution showed generally smaller events. Additionally, the effect of adding more columns while keeping their length constant was investigated, which is presented in Fig. S3.2 in the ESI.† As no limitations due to the geometry are apparent in contrast to varying the box height (see Fig. 4a), one dimensional avalanche propagation along the column axis is recognized as the dominant mode of switching. This behavior is attributed to the morphology, in particular the large difference between hexagonal packing distance and interdisc distance, as the dipoles are closer packed along the z-direction and hence an initial thermal perturbation is also more likely to be communicated along that direction, thus leading to needle-like dipole avalanches.
In summary, two conclusions can be drawn here. First, dipole avalanches propagate almost exclusively along the column axis. Second, for the parameter settings used above, the size of the largest avalanche was found to not be limited by the height of the system, provided the systems thickness exceeds ∼100 nm. Combined, this puts a rather stringent upper limit on the maximum event size that occur, in turn implying that truly critical behavior, which is scale-invariant over all investigated length scales, does not occur at the used temperature T = 300 K. In the following, we will see that critical behavior does occur at lower temperatures.
Having established the occurrence of jerky behavior in the polarization switching of BTA and of power-law distributions of event characteristics, we now focus on the specific values of these exponents and their dependence on temperature T, sweeping frequency f and material characteristics. A brief discussion on the role of temperature T and sweeping frequency f can be found in Section S4 in the ESI.† First, we focus on the role of temperature, that was swept between 100 and 300 K. As expected for ferroelectric materials, lower temperatures require higher fields to start the switching process and – depending on the chosen applied electric field – not the whole simulation box may be switched for a constant maximum field at the lowest temperatures. A comparison of typical simulations for 100 and 250 K is shown in Fig. S4.1 in the ESI.†
A comparison of the corresponding distributions is displayed in Fig. 5, showing a shift to bigger event sizes for lower temperatures in both the size and energy distributions. This is expected as fewer thermal excitations lead to a higher electric field required for switching and thus one event is more probable to cause bigger avalanches. This leads to the exponents recovered from the power-law to be significantly smaller for the simulation at 100 K.
The results of the systematic temperature sweep are displayed in Fig. 6a. For the used (experimentally realistic) parameters, temperatures below 100 K would often result in only very little switching throughout the process, whereas above 300 K, the thermal noise present in the system led to large variations in the datasets, which are already visible for the highest temperatures shown. Both the size and energy distributions show a similar trend for the entire temperature range. At low temperatures, the extracted exponents are consistent with mean field predictions of system-spanning avalanches, which are indicated by horizontal lines. The agreement of the numerical values with those predicted from theory in combination with their relatively constancy at lower temperatures, suggest that the field-driven switching process in BTA shows self-organized criticality at temperatures below ∼170 K.
With increasing temperature, the exponents increase, implying that the system favors smaller, localized events, which leads to a deviation from the mean-field prediction and indicates the system enters a creep-regime: as the thermal energy present in the system increases, purely field-induced events are more likely to get replaced by smaller and (partially) thermally induced events. In contrast, at lower temperatures, the switching happens at higher electric fields, which increases the probability for the flipping of one subcolumn to cause further events in one avalanche, leading to bigger events having a higher probability and, ultimately, self-organized criticality.
Furthermore, we investigated the effect of the sweeping frequency f on the power-law exponents, as shown in Fig. 6b. As we established the self-organized criticality in BTA below 170 °C, the sweeping frequency was varied at T = 160 °C. Both the size and energy exponents are consistent with the mean field prediction at higher sweeping frequencies and increase with decreasing sweeping frequencies at lower investigated sweeping frequencies. It is apparent that the power-law exponent trends for T and log(1/f) are similar.
A probable explanation of the similar trends is related to the thermally activated nature of switching processes in organic ferroelectrics. The thermally activated nucleation limited switching (TA-NLS) model assumes switching to be limited by the activation of pre-existing nucleation sites in the small regions of which the material consists of ref. 34 and 35. The activation of a nucleation site is described as the thermally driven polarization reversal of a critical volume V*. The model yields the following expression for the coercive field Ec dependent on the voltage sweeping frequency νexp:
 | (9) |
The TA-NLS model predicts that the coercivity of a ferroelectric system grows as the driving frequency increases and lower driving frequencies accordingly make thermal fluctuations more pronounced. Eqn (9) shows that the coercive field decreases linearly with temperature. The logarithm of the inverse frequency has the same effect. Based on Fig. 6, a strong similarity of the trends for power-law exponents as functions of temperature and logarithm of the inverse frequency is apparent. Therefore, we conclude that the power-law exponents are anti-correlated to the coercivity of the system.
If indeed the chiral columnar BTA system shows self-organized criticality upon field-driven polarization reversal at lower temperatures, the observed exponents should be invariant to modest changes in system parameters. In order to verify that, further simulations were performed in the low temperature range where the critical exponents stay consistently around the predicted mean field values. The investigated disorder parameters included the variance of the distribution from which the subcolumn sizes were generated and the chirality of the defects.
Investigating the different types of defects, the obtained result was that having a single type of defect can lead to either stabilization or destabilization of the system, depending on the geometrical details of the defect and the corresponding deviations in exponents. Qualitatively spoken, a ‘sufficient’ variation in defects is needed to obtain universal exponents. Specifically, the introduced disorder needs to be big enough to prevent completely intrinsic switching whereas too much disorder in the system leads to small events dominating the switching process. This behavior is consistent with the earlier mentioned Random-Field-Ising model.36 For the present system, this implies that both heterogeneity in defect type as well as in subcolumn length are necessary conditions to recover the universal exponents. The details of the investigation are discussed in Section S5 in the ESI.†
5. Experimental results
To investigate whether the simulated results could be experimentally confirmed, measurements on both out-of-plane and in-plane BTA-C10 samples were conducted. The biggest challenge was to reduce the noise level of the measurement setup while keeping sufficient time resolution as the expected currents associated with single jerks are very small. The finalized measuring setup is described in the experimental details section. The measured noise floor is depicted in Fig. S6.1 in the ESI† and the corresponding noise levels are given in Table S6.1 in the ESI.†Despite the carried-out noise reduction we did not succeed in measuring Barkhausen noise in the investigated BTA-C10 samples. Typically measured current transients and the corresponding obtained probability densities are presented in Fig. S6.2 and S6.3 in the ESI,† respectively. Also, in view of the fact that we successfully measured Barkhausen noise in P(VDF-TrFE),37 this raises the suspicion that the switching events are too small in BTAs. To verify this, we estimate the number of dipoles flipped within our samples and compare this number to both the simulations and noise level of the setup. The corresponding calculation can be found in Section S7 in the ESI.† As of our findings, the number of regions that would need to be simultaneously switched in order to achieve a measurable current is far larger than what is plausible on basis of the weak inter-columnar coupling. In other words, the negative result of the experiments, i.e. Barkhausen noise being below the resolution threshold of the used setup, is consistent with the predictions of the numerical model.
6. Summary
Barkhausen-noise in the columnar hexagonal liquid crystalline ferroelectric BTA was investigated. Numerical simulations by kinetic Monte Carlo show that the material exhibits critical behavior over long ranges of the event sizes at temperatures T ≲ 175 K for a wide range of disorder parameters, while a minimum amount (but not too much) of the latter is required. The disorder present in the system was varied by changing the subcolumn size and its variation, which corresponds to the defect density, as well as by varying the nature of the defect. The resulting behavior is similar to that of a random field Ising model. The behavior of the system and changes in power-law exponents were investigated for a wide range of temperatures. At lower temperatures (≲ 175 K), and equivalently higher driving frequencies, the extracted power-law exponents were found to be similar to the mean field predictions for self-organized critical behavior, while higher temperatures and lower driving frequencies led to systematically larger values, indicating thermal creep, i.e. many switching events originating from thermal excitations rather than the driving field. While the critical power-law exponents were affected to at least some degree for all examined parameters, the changes were significant only outside a certain regime (identified as the self-organized critical regime), hence justifying the assumption of self-organized criticality in the simulated system. Hence, the common crackling noise description for 3D systems seemingly also applies to the quasi-1D ferroelectric switching in the BTA system.Measuring Barkhausen noise of BTA-C10 experimentally was unsuccessful due to too small current signals produced by the material during the switching process, in agreement with the event sizes expected on basis of the numerical simulations. To experimentally measure Barkhausen noise in such columnar liquid crystalline molecules, stronger intermolecular and especially intercolumnar coupling is likely required to increase domain and avalanche sizes. This may be hard to achieve in (the liquid crystalline phase of) materials. For BTAs, this can in principle be achieved by reducing the temperature of the system, introducing shorter alkyl tails and, possibly, also chiral groups that generally induce more order.17 However, such materials or conditions would also cause significantly larger coercive fields, potentially making them unswitchable.
7. Experimental details
7.1. Measurement setup
The input signal was supplied by a Keysight 33600A Arbitrary Waveform Generator (AFG) and was amplified by a TReK PZD350A high voltage amplifier. Multiple AFGs (Keysight 33600A, Tektronix AFG3052C and Tektronix AFG1062) and amplifiers (TReK PZD350A and Falco System WMA-200) were tested and these were to be found to have the lowest noise level, although the difference was marginal, as shown for AFGs in Fig. S6.4 in the ESI.† The device response was measured by either a Zurich Instruments impedance analyzer (MFIA) or Lock-In amplifier (MFLI). No significant differences between the MFIA and MFLI were established and an oscilloscope could be used instead given it has sufficient resolution. The device under test was measured inside a Linkam stage in order to reduce noise and allow for precise temperature dependent measurements.7.2. Sample preparation
Both out-of-plane and in-plane electrodes were used for device fabrication of thin film BTA samples. In case of out-of-plane samples, commercially available Corning plain microscope slides with a thickness of 0.96 to 1.06 mm were cut and both bottom and top electrodes were thermally evaporated. Both aluminum on silver and gold on chromium electrodes of different thicknesses were utilized. The BTA thin films were spin coated with 900 rpm. As in-plane electrodes, interdigitated electrodes (IDEs) supplied by MicruX Technologies were used. Here, the material was drop casted from solution.Data availability
The data supporting this article have been included as part of the manuscript and its ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for support of this work (SFB 1249 and EXC-2082/1-390761711). M. K. thanks the Carl Zeiss Foundation for financial support.References
- V. Y. Shur, E. L. Rumyantsev, D. V. Pelegov, V. L. Kozhevnikov, E. V. Nikolaeva, E. L. Shishkin, A. P. Chernykh and R. K. Ivanov, Barkhausen Jumps During Domain Wall Motion in Ferroelectrics, Ferroelectrics, 2002, 267, 347–353 CrossRef CAS.
- I. S. Baturin, M. V. Konev, A. R. Akhmatkhanov, A. I. Lobov and V. Ya, Shur, Investigation of Jerky Domain Wall Motion in Lithium Niobate, Ferroelectrics, 2008, 374, 136–143 CrossRef CAS.
- V. Y. Shur, A. R. Akhmatkhanov, I. S. Baturin and E. V. Shishkina, Polarization reversal and jump-like domain wall motion in stoichiometric LiTaO3 produced by vapor transport equilibration, J. Appl. Phys., 2012, 111, 014101 CrossRef.
- C. D. Tan, C. Flannigan, J. Gardner, F. D. Morrison, E. K. H. Salje and J. F. Scott, Electrical studies of Barkhausen switching noise in ferroelectric PZT: Critical exponents and temperature dependence, Phys. Rev. Mater., 2019, 3, 034402 CrossRef CAS.
- C. Flannigan, C. D. Tan and J. F. Scott, Electrical studies of Barkhausen switching noise in ferroelectric lead zirconate titanate (PZT) and BaTiO3: critical exponents and temperature-dependence, J. Phys.: Condens. Matter, 2019, 32, 055403 CrossRef PubMed.
- E. K. H. Salje, D. Xue, X. Ding, K. A. Dahmen and J. F. Scott, Ferroelectric switching and scale invariant avalanches in $\mathrm{BaTi}{\mathrm{O}}_{3}$, Phys. Rev. Mater., 2019, 3, 014415 CrossRef CAS.
- B. Casals, G. F. Nataf and E. K. H. Salje, Avalanche criticality during ferroelectric/ferroelastic switching, Nat. Commun., 2021, 12, 345 CrossRef CAS PubMed.
- M. Mai and H. Kliem, Observation of thermal Barkhausen effect in ferroelectric films of poly(vinylidene fluoride/trifluoroethylene) copolymer, J. Appl. Phys., 2013, 114, 224104 CrossRef.
- P. Tückmantel, Scanning Probe Studies of Structural and Functional Properties of Ferroelectric Domains and Domain Walls, Springer Nature, 2021 Search PubMed.
- J. P. Sethna, K. A. Dahmen and C. R. Myers, Crackling noise, Nature, 2001, 410, 242–250 CrossRef CAS PubMed.
- H. J. Williams and W. Shockley, A Simple Domain Structure in an Iron Crystal Showing a Direct Correlation with the Magnetization, Phys. Rev., 1949, 75, 178–183 CrossRef.
- K. A. Dahmen, Y. Ben-Zion and J. T. Uhl, Micromechanical Model for Deformation in Solids with Universal Predictions for Stress-Strain Curves and Slip Avalanches, Phys. Rev. Lett., 2009, 102, 175501 CrossRef PubMed.
- E. K. H. Salje and K. A. Dahmen, Crackling Noise in Disordered Materials, Annu. Rev. Condens. Matter Phys., 2014, 5, 233–254 CrossRef CAS.
- K. A. Dahmen, in Avalanches in Functional Materials and Geophysics, ed. E. K. H. Salje, A. Saxena and A. Planes, Springer International Publishing, Cham, 2017, pp. 19–30 Search PubMed.
- M. Zaiser, B. Marmo and P. Moretti, in Proceedings of International conference on Statistical Mechanics of Plasticity and Related Instabilities—PoS(SMPRI2005), Sissa Medialab, Indian Institute of Science, Bangalore, India, 2006, p. 053 Search PubMed.
- G. Durin and S. Zapperi, The role of stationarity in magnetic crackling noise, J. Stat. Mech., 2006, 2006, P01002 CrossRef.
- I. Urbanaviciute, X. Meng, T. D. Cornelissen, A. V. Gorbunov, S. Bhattacharjee, R. P. Sijbesma and M. Kemerink, Tuning the Ferroelectric Properties of Trialkylbenzene-1,3,5-tricarboxamide (BTA), Adv. Electron. Mater., 2017, 3, 1600530 CrossRef.
- A. V. Gorbunov, Ferroelectric switching phenomena in organic dielectrics and semiconductors, Technische Universiteit Eindhoven, 2018 Search PubMed.
- I. Urbanaviciute, Multifunctional Supramolecular Organic Ferroelectrics, Linköping University Electronic Press, 2019 Search PubMed.
- I. Urbanaviciute, X. Meng, M. Biler, Y. Wei, T. D. Cornelissen, S. Bhattacharjee, M. Linares and M. Kemerink, Negative piezoelectric effect in an organic supramolecular ferroelectric, Mater. Horiz., 2019, 6, 1688–1698 RSC.
- T. Cornelissen, Switching Kinetics and Charge Transport in Organic Ferroelectrics, Linköping University Electronic Press, Linköping, 2020, vol. 2080 Search PubMed.
- A. V. Gorbunov, T. Putzeys, I. Urbanavičiūtė, R. A. J. Janssen, M. Wübbenhorst, R. P. Sijbesma and M. Kemerink, True ferroelectric switching in thin films of trialkylbenzene-1,3,5-tricarboxamide (BTA), Phys. Chem. Chem. Phys., 2016, 18, 23663–23672 RSC.
- C. F. C. Fitié, W. S. C. Roelofs, M. Kemerink and R. P. Sijbesma, Remnant Polarization in Thin Films from a Columnar Liquid Crystal, J. Am. Chem. Soc., 2010, 132, 6892–6893 CrossRef PubMed.
- C. F. C. Fitié, W. S. C. Roelofs, P. C. M. M. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, Polar Switching in Trialkylbenzene-1,3,5-tricarboxamides, J. Phys. Chem. B, 2012, 116, 3928–3937 CrossRef PubMed.
- T. D. Cornelissen, M. Biler, I. Urbanaviciute, P. Norman, M. Linares and M. Kemerink, Kinetic Monte Carlo simulations of organic ferroelectrics, Phys. Chem. Chem. Phys., 2019, 21, 1375–1383 RSC.
- T. D. Cornelissen, I. Urbanaviciute and M. Kemerink, Microscopic model for switching kinetics in organic ferroelectrics following the Merz law, Phys. Rev. B, 2020, 101, 214301 CrossRef CAS.
- I. Urbanavičiūtė, T. D. Cornelissen, X. Meng, R. P. Sijbesma and M. Kemerink, Physical reality of the Preisach model for organic ferroelectrics, Nat. Commun., 2018, 9, 4409 CrossRef PubMed.
- C. Kulkarni, E. W. Meijer and A. R. A. Palmans, Cooperativity Scale: A Structure–Mechanism Correlation in the Self-Assembly of Benzene-1,3,5-tricarboxamides, Acc. Chem. Res., 2017, 50, 1928–1936 CrossRef CAS PubMed.
- M. P. Lightfoot, F. S. Mair, R. G. Pritchard and J. E. Warren, New supramolecular packing motifs: π-stacked rods encased in triply-helical hydrogen bonded amide strands, Chem. Commun., 1999, 1945–1946 RSC.
- P. J. M. Stals, M. M. J. Smulders, R. Martín-Rapún, A. R. A. Palmans and E. W. Meijer, Asymmetrically Substituted Benzene-1,3,5-tricarboxamides: Self-Assembly and Odd–Even Effects in the Solid State and in Dilute Solution, Chem. – Eur. J., 2009, 15, 2071–2080 CrossRef CAS PubMed.
- P. J. M. Stals, J. C. Everts, R. de Bruijn, I. A. W. Filot, M. M. J. Smulders, R. Martín-Rapún, E. A. Pidko, T. F. A. de Greef, A. R. A. Palmans and E. W. Meijer, Dynamic Supramolecular Polymers Based on Benzene-1,3,5-tricarboxamides: The Influence of Amide Connectivity on Aggregate Stability and Amplification of Chirality, Chem. – Eur. J., 2010, 16, 810–821 CrossRef CAS PubMed.
- K. K. Bejagam, G. Fiorin, M. L. Klein and S. Balasubramanian, Supramolecular Polymerization of Benzene-1,3,5-tricarboxamide: A Molecular Dynamics Simulation Study, J. Phys. Chem. B, 2014, 118, 5218–5228 CrossRef CAS PubMed.
- B. A. Gil-villegas, S. C. Mcgrother and G. Jackson, Reaction-field and Ewald summation methods in Monte Carlo simulations of dipolar liquid crystals, Mol. Phys., 1997, 92, 723–734 CrossRef.
- M. Vopsaroiu, J. Blackburn, M. G. Cain and P. M. Weaver, Thermally activated switching kinetics in second-order phase transition ferroelectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 024109 CrossRef.
- M. Vopsaroiu, P. M. Weaver, M. G. Cain, M. J. Reece and K. B. Chong, Polarization dynamics and non-equilibrium switching processes in ferroelectrics, IEEE Trans. Ultrason. Eng., 2011, 58, 1867–1873 Search PubMed.
- J. P. Sethna, K. A. Dahmen and O. Perkovic, Random-Field Ising Models of Hysteresis, arXiv, 2005, preprint, arXiv:arXiv:cond-mat/0406320 DOI:10.48550/arXiv.cond-mat/0406320.
- A. A. Butkevich, M. Hecker, T. Seiler and M. Kemerink, Barkhausen noise in the organic ferroelectric copolymer P(VDF:TrFE), Phys. Chem. Chem. Phys., 2025, 27, 9637–9644 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01393c |
| This journal is © the Owner Societies 2025 |