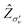Open Access Article
Open Access ArticleDynamical symmetries and selection rules in high-harmonic generation spectroscopy of nonlinear molecules†
Marco Marchettaa,
Eleonora Luppi*b and
Emanuele Coccia *a
*a
aDipartimento di Scienze Chimiche e Farmaceutiche, Università di Trieste, Trieste 34127, Italy. E-mail: ecoccia@units.it
bLaboratoire de Chimie Théorique, Sorbonne Université, CNRS, Paris F-75005, France. E-mail: eleonora.luppi@sorbonne-universite.fr
First published on 26th May 2025
Abstract
In this work we have computed high-harmonic generation (HHG) spectra of H2O and NH3, interacting with linearly polarised pulses in different orientations. All the calculations have been carried out using the real-time time-dependent configuration interaction with single excitations (RT-TD-CIS) method with a Gaussian basis set. The selection rules in the HHG spectra, as computed with RT-TD-CIS, are interpreted in the framework of dynamical symmetries (DSs). These symmetries emerge as a combination of the temporal properties of the driving pulse and the spatial characteristics of the molecular electronic Hamiltonian and of the pulse. Moreover, multiple-orbital effects have been observed and analyzed. The findings underscore the pivotal role of DSs in shaping the HHG response, highlighting their ability to bridge the complex interactions between molecular structure, electronic transitions, and the pulse. We show that Gaussian-based RT-TD-CIS is a reliable tool to study the HHG spectra of aligned nonlinear molecules, and the role of ionisation/recombination channels in the dynamics.
1 Introduction
High-harmonic generation (HHG) is a highly nonlinear process arising when matter interacts with an intense nonresonant laser pulse.1–7 Emitted photons are coherent, and can be used as sources of extreme ultraviolet6,8,9 or even X-ray light pulses10–14 to study the electron structure and dynamics of the emitter itself.2,15–22 Since the HHG is the result of ionisation and recombination processes that can possibly occur from different molecular orbitals,17,23–40 HHG spectra encode information about the electronic structure41–50 and ultrafast dynamics in atoms and molecules.18,31,51–57A fascinating aspect of HHG is the origin of the selection rules, that is, the first-principles-based understanding of the emission of a specific subset of harmonics, given the symmetry of the emitter and its interaction with the pulse.58,59 A general approach to the study of selection rules in HHG is given by the so-called dynamical symmetries (DSs),60 which combine spatial symmetry of the emitter and the pulse with that of the temporal symmetry of the pulse alone. Specifically, the pulse spatio-temporal symmetry combines with the system spatial symmetry, and selection rules emerge, dictating which harmonics are permitted and in which direction they are polarised.58–65
A theoretical understanding of selection rules in HHG is needed to rationalise experimental results and make strong-field dynamics analysis systematic and predictive. Simulations based on a first-principle quantum description of electronic degrees of freedom are a valuable tool to investigate the strong-field dynamics of complex systems.40,66–68
In real-time time-dependent configuration interaction with single excitations (RT-TD-CIS), HHG spectra are computed thanks to a real-time propagation of the time-dependent Schrödinger equation (TDSE) in the space of configuration interaction singly-excited ansatz of the wavefunction (CIS).69–81 This ab initio approach, which consists of the real-time evolution of a singly excited ansatz wavefunction constructed from a Gaussian basis set,82 was shown to be a reliable compromise between accuracy and computational cost, allowing the study of strong-field dynamics in (large) molecular systems.39,79,83–85
This approach combines the efficiency of implementing quantum chemistry methods, adapted to represent states above the ionisation threshold, with TDSE, allowing non-linear responses to be calculated in the time domain.74,78 In addition, RT-TD-CIS has recently been extended to study the partial contribution of occupied molecular orbitals (MOs) to the HHG signal of molecules.37,39,40
In this work, we investigated the HHG spectra of H2O and NH3 molecules under various orientations with respect to a linearly polarised laser pulse, interpreting the results based on the corresponding DS. Furthermore, we explored the role of MOs40 in HHG for these molecules under different pulse polarisations and configurations.
The main goal of this paper is to show that Gaussian-based ab initio time-dependent approaches, such as RT-TD-CIS, reproduces the expected selection rules in HHG spectroscopy, interpreted in the general context of DSs. DSs have been studied extensively in model systems58 or in realistic molecules using physical models, perhaps enriched quantitatively by ab initio ingredients.63 To the best of our knowledge, few examples of works that combine DSs with first-principles methods formulated in time domain be found in the literature.59,67 Here we aim to demonstrate how our RT-TD-CIS with Gaussian basis set reproduces selection rules in aligned nonlinear molecules, even in non-“standard” orientations with respect to pulse polarisation.
The article is organised as follows: in Section 2 we present the theoretical method used in this work, in Section 3 we give the computational details, in Section 4 we describe the results obtained for H2O and NH3, and in Section 5 we summarise the main results found in the work.
2 Theory
2.1 Real-time propagation
Electron dynamics in a spectroscopic molecular target irradiated by an external time-dependent electric field is described by the TDSE
 | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t)
(t)
Ĥ = Ĥ0 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t). (t).
| (2) |
In the semi-classical dipole approximation, the interaction between the molecule and the time-dependent external laser field is given in the length gauge by
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) = − (t) = −![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ·E(t), ·E(t),
| (3) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) is the molecular dipole operator and E(t) is the electric field of the laser pulse.
is the molecular dipole operator and E(t) is the electric field of the laser pulse.
For a linearly polarised pulse the electric field can be written as
E(t) = E0nα![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ω0t − φ0)f(t), sin(ω0t − φ0)f(t),
| (4) |
 | (5) |
In the RT-TD-CIS eqn (1) is numerically approached by expanding the time dependent wavefunction |Ψ(t)〉 in the space of the Ĥ0 eigenstates, i.e. the Hartree–Fock (HF) ground state (k = 0) and the excited states (k > 0)71
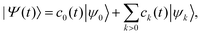 | (6) |
 | (7) |
The TDSE in eqn (1) is thus propagated in the space of electronic states from eqn (6)
 | (8) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |ψk〉. Further details are found in ref. 40 and 70.
|ψk〉. Further details are found in ref. 40 and 70.
Once the time-dependent wavefunction |Ψ(t)〉 is determined, the time-dependent dipole moment is computed as
 | (9) |
By applying the Fourier transform to μ(t), the HHG power spectrum is then obtained
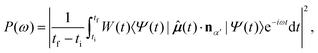 | (10) |
2.2 MO decomposition of the HHG signal
For a singly-excited ansatz wavefunction, the time-dependent dipole can be further analyzed by decomposing it into the sum of occupied MO contributions37,39,40
 | (11) |
| μi(t) = μG,i(t) + μG–E,i(t) + μE–E,i(t), | (12) |
μG,i(t) = |c0(t)|2〈i|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |i〉, |i〉,
| (13) |
 | (14) |
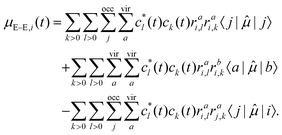 | (15) |
By inserting the MO contribution μi(t) in eqn (10) one can compute the partial HHG spectrum coming from the i-th MO as
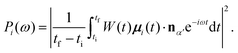 | (16) |
 | (17) |
 | (18) |
Dyson orbitals can be used to analyse physical processes, such as ionisation.86,87 Dyson orbitals represent the overlap between the many-electron wavefunction of the neutral molecule and that of the corresponding ionised state.86 At HF level, Dyson orbitals coincide with the standard occupied MOs. This equivalence implies that HF orbitals provide a valid and practical basis for interpreting HHG spectra, as they approximate the Dyson orbitals that govern the ionisation and recombination pathways. Therefore, rather than working directly with Dyson orbitals, which may be computationally demanding or difficult to extract with more sophisticated electronic-structure theories, we use HF MOs as an effective alternative for describing the HHG process. The same approach was also used in ref.34 and 40.
Our channel analysis, while based on a formally arbitrary decomposition of the total dipole, e.g. the observable, is nonetheless physically meaningful for interpretative purposes, as also discussed in ref. 40, since the non-invariance under orbital phase choice for the third term of eqn (15) does not affect the total result, as this term is numerically negligible.
3 Computational details
The strong-field real-time calculations have been carried out using fixed nuclear geometries obtained from DFT geometry optimizations. For H2O the optimization was performed using a PBE functional, resulting into an equilibrium distance of 1.831 a0 and a bond angle of 104.2°. For NH3 we used the B3LYP functional, obtaining an equilibrium distance of 1.915 a0 and a bond angle of 107.2°. Q-Chem quantum-chemistry package has been used.88CIS calculations using Q-Chem have been then carried out to determine the excited-state energies and transition dipole moments, essential for simulating electron dynamics. Special attention must be given to the basis set choice,82 as it must accurately describe Rydberg and continuum energy states. The basis set is constructed by starting from a cc-pVTZ basis89 and then augmenting it with five diffuse functions and five optimised Gaussian functions designed for the continuum90 (K) for each angular momentum, thus obtaining a basis set named 5aug-cc-pVTZ+5K basis set. The use of K90 optimal continuum Gaussian basis sets, along with other optimised continuum basis sets, has been extensively investigated,71,82,91,92 highlighting the importance of achieving a proper balance with diffuse Gaussian functions to get accurate HHG spectra. Furthermore, we stress that by including in the basis set the continuum-optimised Gaussians, we addressed one of the main challenges associated with Gaussian basis sets, their inherent limitation in representing continuum states. We have previously developed and validated an approach that systematically augments standard basis sets with additional diffuse and continuum-adapted functions. Our benchmarks against grid-based methods82 demonstrate that such tailored basis sets can accurately reproduce the main features of HHG spectra, including the position of the harmonic cutoff, plateau structure, and orbital-specific contributions.37,39,40,72
When constructing the basis set, special care was taken to preserve the overall symmetry of the molecular system. Diffuse and continuum functions were added symmetrically across all angular momenta to avoid asymmetric distortions in the wavefunction representation. This approach ensures that symmetry-related selection rules are respected, for instance, in centrosymmetric systems where only odd harmonics should be observed due to the parity of the dipole response.70,71 A detailed discussion of the methodology and its validation can be found in ref.71 and 82, to which we refer the reader for further information.
For H2O, 800 electronically excited states were used to expand the time-dependent wavefunction, while 703 states were employed for NH3. This choice ensures that all ionisation channels investigated in this study are included for both systems.
TDSE propagation has been done by means of Light,70,85 interfaced with Q-Chem. For all the HHG spectra simulated in this work we employed a cos2-shaped pulse (eqn (5)) with frequency ω0 = 0.057 Ha (1.55 eV, 800 nm) and intensity I = E02/2 = 8.5 × 1013 W cm−2. The pulse duration is 23 optical cycles (oc), with σ = 23 oc (eqn (5)), where 1 oc = 2π/ω0. The discrete time step used in the propagation is 1.21 attoseconds (0.05 a.u.).
A further crucial aspect is the treatment of artificial reflections and basis set incompleteness in the description of the outgoing electronic wavepacket. In this regard, we use a heuristic lifetime model.93 This model consists of adding to the CIS energies Ek an imaginary term −iΓk/2 where 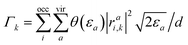 represents the inverse lifetime of the excited state n above the ionisation threshold, with εa being the energy of the virtual MO a and θ being the Heaviside step function. The parameter d represents the characteristic escape length that the electron is allowed to travel during the lifetime 1/Γk. The value of d is taken equal to the quiver radius d = E0/ω02, i.e., d = 15.143 a0. While more sophisticated approaches for the representation of states above the ionisation threshold exist, the strategy adopted here provides a computationally efficient and physically reliable framework for HHG simulations in molecular systems. The ionisation potentials can be determined using Koopmans’ theorem, considering Ip = 19.3 eV (HOMO−2) for H2O and Ip = 17.1 eV (HOMO−1) for NH3.
represents the inverse lifetime of the excited state n above the ionisation threshold, with εa being the energy of the virtual MO a and θ being the Heaviside step function. The parameter d represents the characteristic escape length that the electron is allowed to travel during the lifetime 1/Γk. The value of d is taken equal to the quiver radius d = E0/ω02, i.e., d = 15.143 a0. While more sophisticated approaches for the representation of states above the ionisation threshold exist, the strategy adopted here provides a computationally efficient and physically reliable framework for HHG simulations in molecular systems. The ionisation potentials can be determined using Koopmans’ theorem, considering Ip = 19.3 eV (HOMO−2) for H2O and Ip = 17.1 eV (HOMO−1) for NH3.
We applied a Lorentzian broadening to all the spectra reported in this work.
4 Results and discussion
In the present work, we study how the selection rules for harmonics arise from the DS that involves a linearly polarised pulse and the field-free Hamiltonian. We report and discuss results for H2O and NH3 aligned molecules, obtained using the RT-TD-CIS method and the MO decomposition shown in Section 2. These two systems represent a case study for HHG spectroscopy of aligned nonlinear molecules, including partial contributions from MOs.A DS generates selection rules in the HHG spectrum if it commutes with the Hamiltonian symmetry Ĥ0, and consequently with the molecular symmetry.59,60 A linearly polarised pulse is symmetric with respect to the Ẑ and Ĉ2 DS operations, which coincide for a linear pulse. The Ẑ operation corresponds to a time translation by half a period (![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 2) and to reflection through a plane (
2) and to reflection through a plane (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ) perpendicular to the polarisation direction. For the Ẑ DS, odd harmonics are polarised linearly and orthogonally to the plane, while only even harmonics are allowed within the plane. Similarly, the Ĉ2 operation is defined by a time translation by half a period (
) perpendicular to the polarisation direction. For the Ẑ DS, odd harmonics are polarised linearly and orthogonally to the plane, while only even harmonics are allowed within the plane. Similarly, the Ĉ2 operation is defined by a time translation by half a period (![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 2) and a π rotation around an axis (C2) perpendicular to the polarisation direction. For the Ĉ2 DS, linearly polarised odd harmonics are allowed in the plane orthogonal to the C2 rotational axis, while only even harmonics are polarised parallel to the C2 rotational axis.60
2) and a π rotation around an axis (C2) perpendicular to the polarisation direction. For the Ĉ2 DS, linearly polarised odd harmonics are allowed in the plane orthogonal to the C2 rotational axis, while only even harmonics are polarised parallel to the C2 rotational axis.60
4.1 H2O
In Fig. 1, the H2O molecule is represented with the symmetry elements characterizing the C2v symmetry, that are: the two reflection planes (σν and ) and the C2 rotational axis. The analysed MOs, computed at HF level of theory, are also reported. While in Table 1, we list the irreducible representation and ionisation energies of the H2O MOs, evaluated according to Koopmans' theorem, and the channel label associated with the MOs. MOs are representative of the ionisation channel, as widely reported in the literature.23,26,30,34–36,40,67
) and the C2 rotational axis. The analysed MOs, computed at HF level of theory, are also reported. While in Table 1, we list the irreducible representation and ionisation energies of the H2O MOs, evaluated according to Koopmans' theorem, and the channel label associated with the MOs. MOs are representative of the ionisation channel, as widely reported in the literature.23,26,30,34–36,40,67
 | ||
Fig. 1 Representation of the H2O molecule with σν and  reflection planes and the C2 rotational axis, and H2O HF occupied MOs studied in this work. reflection planes and the C2 rotational axis, and H2O HF occupied MOs studied in this work. | ||
| Channel | Irred. repr. | MO | Energy (eV) |
|---|---|---|---|
| X | B2 | HOMO | 13.9 |
| A | A1 | HOMO−1 | 15.9 |
| B | B1 | HOMO−2 | 19.3 |
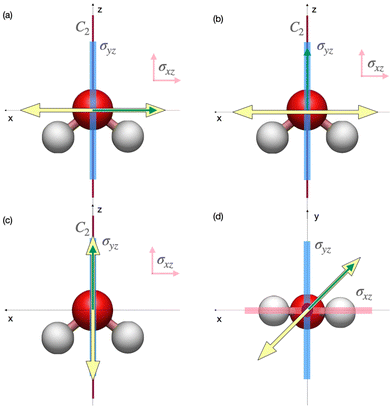
In Fig. 2 we represent the specific orientation of the pulse and the harmonic polarisation that have been investigated in this work, and reported in the main text. Within this reference frame, the molecule lies in the xz plane, with the principal rotation axis C2 oriented along the z axis. This orientation results in two reflection planes:  and σyz (σν).
and σyz (σν).
In Fig. 3, we report the HHG spectra and channel decomposition for the pulse polarisation x, which corresponds to cases (a) (detection along the same direction) and (b) (detection perpendicular to the polarisation direction and parallel to the C2 axis, that is, the z axis) collected in Fig. 2. With this molecule + pulse configuration, the pulse is invariant under a time translation of a half period (![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 2) and reflection with respect to the yz plane (
2) and reflection with respect to the yz plane (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz), which corresponds to Ẑyz DS, i.e. Ẑyz =
yz), which corresponds to Ẑyz DS, i.e. Ẑyz = ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) 2·
2·![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) yz, as also shown in Table 2. DS is conserved along the dynamics, thus partial HHG spectra also exhibit the same selection rules as the total signal. Indeed, due to the DS, panel (a) of Fig. 3 shows that only odd harmonics polarised along the x direction, i.e. along the pulse polarisation direction, are observed. While panel (b) of Fig. 3 displays only even harmonics polarised along the z direction, i.e., perpendicular to the pulse polarisation direction. The generation of even harmonics polarised perpendicular to the laser polarisation can also be physically attributed to the interaction between the molecular permanent dipole and the external field.94,95 From this interpretation, it is also possible to understand why odd harmonics in panel (a) have, on average, higher intensities than even harmonics in panel (b). The same conclusions are obtained by considering the Ĉ2 DS. From the analysis of the time-dependent dipole moments (Fig. S1 and S2 of the ESI†) one observes that the time variation of the dipole perpendicular to the pulse polarisation is much smaller than the variation along the polarisation direction. Moreover, oscillations in the permanent dipole occur with a frequency of half-period, thus explaining the presence of even harmonics only.
yz, as also shown in Table 2. DS is conserved along the dynamics, thus partial HHG spectra also exhibit the same selection rules as the total signal. Indeed, due to the DS, panel (a) of Fig. 3 shows that only odd harmonics polarised along the x direction, i.e. along the pulse polarisation direction, are observed. While panel (b) of Fig. 3 displays only even harmonics polarised along the z direction, i.e., perpendicular to the pulse polarisation direction. The generation of even harmonics polarised perpendicular to the laser polarisation can also be physically attributed to the interaction between the molecular permanent dipole and the external field.94,95 From this interpretation, it is also possible to understand why odd harmonics in panel (a) have, on average, higher intensities than even harmonics in panel (b). The same conclusions are obtained by considering the Ĉ2 DS. From the analysis of the time-dependent dipole moments (Fig. S1 and S2 of the ESI†) one observes that the time variation of the dipole perpendicular to the pulse polarisation is much smaller than the variation along the polarisation direction. Moreover, oscillations in the permanent dipole occur with a frequency of half-period, thus explaining the presence of even harmonics only.
 | ||
| Fig. 3 Panel (a): Total and partial HHG spectra of H2O, with pulse polarisation and detection along the x direction, corresponding to the configuration (a) of Fig. 2. Panel (b): Total and partial HHG spectra of H2O obtained using a pulse polarised in the x direction, and the signal is detected along the z direction, i.e. the configuration (b) in Fig. 2. In both panels, the pulse polarisation is represented by the big yellow double arrow, while the direction of detection for HHG spectra is represented by the small green arrow. | ||
| Pulse polarisation | DS | Detection | Harmonics |
|---|---|---|---|
| x axis | Ẑyz | x axis | Odd |
| z axis | Even | ||
| z axis | Ẑxy | z axis | Even and odd |
| 45° in the xy plane | Ĉ2 | 45° in the xy plane | Odd |
Furthermore, the HHG spectrum also arises from a multichannel contribution for directions of detection. To rationalise the MO contributions to the HHG spectra, we have to consider the ionisation energy and the symmetry with respect to the pulse.23,37 For x detection, the multichannel behavior can be explained by noticing that the symmetry of the B channel (HOMO−2) allows a better pulse-channel interaction (no nodal surfaces), but the B channel still results in a minor contribution due to the higher ionisation energy if compared with those of the X (HOMO) and A (HOMO−1) channels, that give a higher contribution despite their symmetry. For z detection, the weight of B is even smaller, while the contribution of A becomes larger also at low harmonics, due to the absence of nodal surfaces.
In Fig. 4, the HHG spectra for the z polarisation of the pulse and detection in the same direction are shown. This configuration is the case (c) in Fig. 2, characterised by the reflection plane that defines the DS is the xy plane. For this polarisation, the spatial part of the DS (Ẑ or Ĉ2) does not commute with the molecular symmetry, and therefore all odd and even harmonics are admitted. The A channel has the most favorable coupling with the pulse, and it thus represents the predominant channel in the range H1–H8 and from H19 onward. While from H9 to H18, the X and B channels give a relevant contribution and, resulting in some case in the largest one, such as H10 for the channel X and H16 for B channel. HN notation means the N-th harmonic of the spectrum. Corresponding dipole moments are given in Fig. S3 of ESI.†
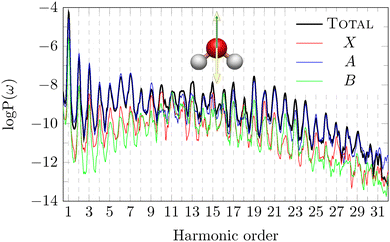 | ||
| Fig. 4 Total and partial HHG spectra of H2O, with pulse polarisation parallel to the principal axis (z axis). This system corresponds to the configuration (c) of Fig. 2. The yellow double arrow represents the pulse polarisation, while a green arrow represents the direction of detection of the HHG signal. | ||
To conclude the study on H2O, in Fig. 5, we present the HHG spectrum for a pulse linearly polarised in the xy plane, oriented at an angle of 45° with respect to the molecular plane (xz), i.e., bisecting the xy angle. This is the configuration (d) of Fig. 2. The HHG signal has been computed along the same direction, and in the z direction. In this configuration, the reflection plane of the Ẑ DS does not correspond to any reflection plane of the molecule. However, considering the Ĉ2 DS for the pulse, the molecule exhibits the same rotational symmetry as the pulse. Consequently, only odd polarised harmonics are expected in the plane orthogonal to the C2 rotational axis, while even harmonics are polarised parallel to the C2 axis, as shown in Fig. 5. The MO decomposition of the HHG signal for the pulse polarisation at 45° in the xy plane with detection in the same direction is also given in Fig. S4 of ESI.† As the HOMO has the lower Ip and the most favorable symmetry, it represents the predominant channel in the spectrum, while the A and the B channels give a much smaller contribution. Time-dependent dipoles are reported in Fig. S5 of ESI.† In Fig. S6 and S7 of ESI,† other examples are shown in which the pulse polarisation is orthogonal to the molecular C2 axis, with angles of 135° and 30°, giving only odd harmonics polarised in the plane orthogonal to the rotational axis. These results confirm that the involved DS is Ĉ2.
 | ||
| Fig. 5 Total HHG spectra of H2O obtained with pulse polarisation of 45° in the xy plane, i.e. the configuration (d) in Fig. 2. In green the spectrum recorded in the same direction of pulse polarisation, in violet the spectrum detected along the z axis. | ||
The selection rules for the various H2O + pulse configurations discussed in the main text are summarised in Table 2.
4.2 NH3
In Fig. 6, the symmetry elements of the NH3 molecule, which has a C3v symmetry, are represented: C3 rotational axis and three reflection planes σν, and
and  along each of the three NH bond. The analysed MOs, i.e. HOMO (channel X) and HOMO−1 (channel A), computed at the HF level of theory, are also given. We oriented the molecule to make the z axis coincident with the C3 rotational axis. In Table 3, the ionisation energy for each channel, together with the irreducible representation of the corresponding MO, are collected.
along each of the three NH bond. The analysed MOs, i.e. HOMO (channel X) and HOMO−1 (channel A), computed at the HF level of theory, are also given. We oriented the molecule to make the z axis coincident with the C3 rotational axis. In Table 3, the ionisation energy for each channel, together with the irreducible representation of the corresponding MO, are collected.
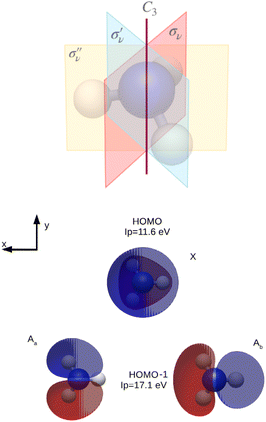 | ||
| Fig. 6 Representation of the NH3 molecule with the reflection planes and the C3 rotational axis, and NH3 HF occupied MOs studied in this work. | ||
| Channel | Irred. repr. | MO | Energy (eV) |
|---|---|---|---|
| X | A1 | HOMO | 11.6 |
| A | E | HOMO−1 | 17.1 |
Since the DS is conserved along the dynamics by construction, the appearance of a symmetry breaking, like in the case of degenerate HOMO−1 of NH3, is an artifact of the representation. Aa and Ab are therefore not physical ionisation/recombination channels. Only the combination of the two MOs restores the correct symmetry and the corresponding selection rules in the HHG signal.
In Fig. 7, we present the specific orientation for the laser and the HHG polarisation that have been analysed in the main text, together with the symmetry elements. We have computed HHG spectra with the polarisation of the pulse orthogonal to the  plane (which is not xz) and along the z direction, as schematically shown in Fig. 7.
plane (which is not xz) and along the z direction, as schematically shown in Fig. 7.
In the case of the laser polarisation with pulse polarisation orthogonal to the  plane, we expect, because of the Ẑ DS, that only odd harmonics are observed in the total spectrum along the same direction of the laser pulse polarisation.60 This is clearly confirmed by the data (“TOTAL”) in Fig. 8, where the MO decomposition of HHG spectra obtained with pulse polarisation orthogonal to the
plane, we expect, because of the Ẑ DS, that only odd harmonics are observed in the total spectrum along the same direction of the laser pulse polarisation.60 This is clearly confirmed by the data (“TOTAL”) in Fig. 8, where the MO decomposition of HHG spectra obtained with pulse polarisation orthogonal to the  plane is also presented. As expected, the X channel (HOMO) is characterised by only odd harmonics in the HHG spectrum, with the only exceptions of H12 and H14 whose presence can be attributed to numerical noise. In contrast, this is not the case for the two Aa and Ab channels, for which symmetry is broken, thus giving rise to both odd and even harmonics. We point out that the two HOMO−1 are defined arbitrarly, and as a consequence their partial HHG signal are physically meaningless. Only the combination of the degenerate MOs recovers the appropriate selection rule. Indeed, we have investigated the phase of the interference between Aa and Ab, according to eqn (18), which is reported in the panel (b) of Fig. 8. A constructive interference (+1) is found for odd harmonics, whereas even harmonics are characterised by a destructive interference (−1). In panel (c) of Fig. 8, the spectrum for the channel A now computed by summing the contribution to the dipole of Aa and Ab channels, is shown. The resulting spectrum has only odd harmonics with intensities comparable to those of the X channel, as a consequence of the destructive interference of even harmonics. This is a clear signal that the overall system
plane is also presented. As expected, the X channel (HOMO) is characterised by only odd harmonics in the HHG spectrum, with the only exceptions of H12 and H14 whose presence can be attributed to numerical noise. In contrast, this is not the case for the two Aa and Ab channels, for which symmetry is broken, thus giving rise to both odd and even harmonics. We point out that the two HOMO−1 are defined arbitrarly, and as a consequence their partial HHG signal are physically meaningless. Only the combination of the degenerate MOs recovers the appropriate selection rule. Indeed, we have investigated the phase of the interference between Aa and Ab, according to eqn (18), which is reported in the panel (b) of Fig. 8. A constructive interference (+1) is found for odd harmonics, whereas even harmonics are characterised by a destructive interference (−1). In panel (c) of Fig. 8, the spectrum for the channel A now computed by summing the contribution to the dipole of Aa and Ab channels, is shown. The resulting spectrum has only odd harmonics with intensities comparable to those of the X channel, as a consequence of the destructive interference of even harmonics. This is a clear signal that the overall system  reflection symmetry is recovered. X (HOMO) contribution is larger than the A (HOMO−1) one, except for H21 and following. It is worth mentioning that this interference pattern is only the consequence of the HOMO−1 representation; it is completely different from what, e.g., is observed in the aligned CO2, for which the minimum in the HHG spectrum is physically derived from the negative interference between HOMO and HOMO−2.40 Time-dependent dipole moments for X, Aa and Ab channels are collected in Fig. S8 of ESI.†
reflection symmetry is recovered. X (HOMO) contribution is larger than the A (HOMO−1) one, except for H21 and following. It is worth mentioning that this interference pattern is only the consequence of the HOMO−1 representation; it is completely different from what, e.g., is observed in the aligned CO2, for which the minimum in the HHG spectrum is physically derived from the negative interference between HOMO and HOMO−2.40 Time-dependent dipole moments for X, Aa and Ab channels are collected in Fig. S8 of ESI.†
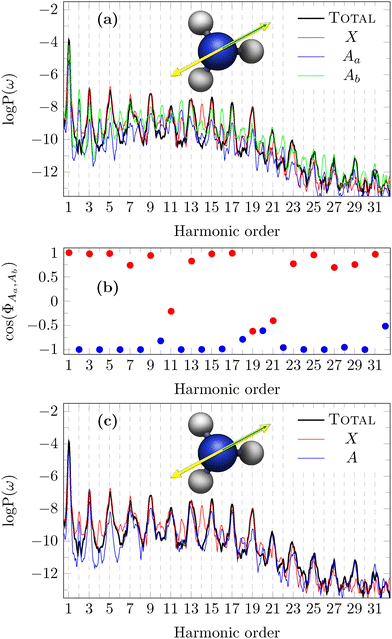 | ||
| Fig. 8 Panel (a): Total and partial HHG spectra of NH3, with pulse polarisation and detection direction perpendicular to one reflection plane, according to the configuration (a) of Fig. 7. The pulse polarisation is represented by the yellow double arrow, while the recording direction of HHG spectra is represented by a green arrow. Panel (b): Phase of the interference between Aa and Ab channels. Panel (c): Same as in panel (a), but with the A partial spectrum (see the text for details). | ||
Conversely, for a pulse polarisation perpendicular to the  plane, only even harmonics are expected when the detection is along any direction perpendicular to the pulse polarisation direction,60 i.e., in any direction belonging to the
plane, only even harmonics are expected when the detection is along any direction perpendicular to the pulse polarisation direction,60 i.e., in any direction belonging to the  plane, such as, for example, the z-direction, as shown in panel (b) of Fig. 7. Indeed, the total HHG spectrum of this configuration shows even harmonics only, as one observes in Fig. 9. In terms of MO decomposition, the X channel provides the main contribution to the spectrum. Only even harmonics appear in the spectrum of the channel X. By summing the contributions from Aa and Ab channels, i.e. defining the physical A channel, the partial HHG spectrum due to HOMO−1 is seen to follow the selection rule, with only even harmonics. These harmonics are generally less intense than those of the X channel. The interference of odd (even) harmonics between Aa and Ab channels is destructive (constructive), as reported in Fig. S9 of ESI;† few exceptions are observed, perhaps due to numerical inaccuracy. The X channel provides the largest contribution until H18, while A channel is not negligible at higher harmonics. Fig. S10 of ESI† collects the time evolution of the total and partial dipole moments.
plane, such as, for example, the z-direction, as shown in panel (b) of Fig. 7. Indeed, the total HHG spectrum of this configuration shows even harmonics only, as one observes in Fig. 9. In terms of MO decomposition, the X channel provides the main contribution to the spectrum. Only even harmonics appear in the spectrum of the channel X. By summing the contributions from Aa and Ab channels, i.e. defining the physical A channel, the partial HHG spectrum due to HOMO−1 is seen to follow the selection rule, with only even harmonics. These harmonics are generally less intense than those of the X channel. The interference of odd (even) harmonics between Aa and Ab channels is destructive (constructive), as reported in Fig. S9 of ESI;† few exceptions are observed, perhaps due to numerical inaccuracy. The X channel provides the largest contribution until H18, while A channel is not negligible at higher harmonics. Fig. S10 of ESI† collects the time evolution of the total and partial dipole moments.
 | ||
| Fig. 9 Total and partial HHG spectra of NH3, with pulse polarisation perpendicular to one reflection plane and HHG signal detected along the z axis, corresponding to the configuration (b) in Fig. 7. | ||
In Fig. 10, we present the spectra obtained using a z-polarised pulse (see panel (c) of Fig. 7). In this configuration, the DS is Zxy, and the reflection plane that defines the DS is the xy plane. However, this is not a symmetry plane for the molecule, and therefore, the spatial part of the DS does not commute with the molecular symmetry; this results in all odd and even harmonics being allowed. The X channel dominates across the spectrum due to its more favorable ionisation energy compared to the A, i.e. Aa + Ab, channel. In this case, the interference is constructive for the most of the harmonics (Fig. S11 of ESI†). As observed in Fig. 8–10, the interference among Aa and Ab restores the expected symmetry leading to the A channel, as must be for a conserved symmetry in the dynamics. Time-dependent dipole moments for this configuration are given in Fig. S12 of ESI.†
 | ||
| Fig. 10 Total and partial HHG spectra of NH3, with pulse polarisation oriented parallel to the z axis, i.e. the configuration (c) shown in Fig. 7. The pulse polarisation is represented by the yellow double arrow, while the recording direction of HHG spectra is represented by a green arrow. | ||
With a pulse polarised along the x axis and detection along the same axis, we observe that the partial spectrum by Ab, which couples favorably with the pulse polarisation, is larger than that by Aa for all the harmonics (Fig. S13 of ESI†). This result is similar to what occurs in HHG simulations of atomic systems with a p character, in which one “selects” the p orbital parallel to the pulse polarisation.
Table 4 collects the selection rules for various pulse polarisations for NH3 explicitly shown in the main text.
5 Conclusions
In this work, we have studied the DS and selection rules in HHG spectra of H2O and NH3 interacting with a linear pulse with different polarisation directions. HHG spectra have been computed at RT-TD-CIS level of theory, i.e. using an ab initio method in time domain. Within the same approach, an exact decomposition of the HHG spectrum in terms of individual MO contributions has also been applied.In the case of H2O, with pulse polarisation along x, only odd harmonics are found when the direction of detection of the HHG signal is x. In contrast, only even harmonics are observed when the detection is perpendicular to the x direction. Instead, odd and even harmonics are present in the HHG spectrum with pulse polarisation along the z axis and detection in the same direction since, in this case, the spatial part of DS does not commute with the molecular symmetry. With pulse polarisation with an angle of 45° in the xy plane, the HHG spectrum is characterised by odd harmonics only if the direction of detection of HHG spectra is contained in the plane orthogonal to the C2 rotational axis. In contrast, even harmonics are produced when the detection is parallel to the C2 rotational axis. Additionally, the generated harmonics can stem from either multichannel or single-channel contributions. For the configurations (a) and (b) of Fig. 2, HOMO, HOMO−1 and HOMO−2 contribute to the HHG signal; the relative weight among the channels changes with the direction of detection. While, in cases with strong single-channel character, the predominant channel is the HOMO, as in the alignment with the 45° pulse polarisation or HOMO−1, as in the alignment with z pulse polarisation.
For NH3, with the pulse polarisation orthogonal to the  reflection plane, only odd harmonics are observed when the direction of detection is perpendicular to the reflection plane, while even harmonics are observed if the direction of is contained within the molecular reflection plane. This selection rule is apparently lost with the doubly degenerate HOMO−1. However, the interference between the two degenerate MOs restores the symmetry, and the spectra obtained by summing the two contributions recover the shape dictated by the selection rules, i.e., even harmonics disappear in the HHG polarisation detection orthogonal to the reflection plane. With a pulse polarisation along the z axis, even and odd harmonics are found, when detected along the z direction since, in this case, the DS does not commute with the molecular symmetry. Moreover, multichannel effects characterise HHG spectra resulting from a pulse orthogonal to the reflection plane. While the HHG spectrum produced from a pulse polarised along the z axis is a strongly single-channel process, with HOMO providing the largest contribution to the total spectrum.
reflection plane, only odd harmonics are observed when the direction of detection is perpendicular to the reflection plane, while even harmonics are observed if the direction of is contained within the molecular reflection plane. This selection rule is apparently lost with the doubly degenerate HOMO−1. However, the interference between the two degenerate MOs restores the symmetry, and the spectra obtained by summing the two contributions recover the shape dictated by the selection rules, i.e., even harmonics disappear in the HHG polarisation detection orthogonal to the reflection plane. With a pulse polarisation along the z axis, even and odd harmonics are found, when detected along the z direction since, in this case, the DS does not commute with the molecular symmetry. Moreover, multichannel effects characterise HHG spectra resulting from a pulse orthogonal to the reflection plane. While the HHG spectrum produced from a pulse polarised along the z axis is a strongly single-channel process, with HOMO providing the largest contribution to the total spectrum.
In conclusion, simulations based on a time-resolved Gaussian-based ab initio method are a valuable tool to investigate the stong-field dynamics of complex systems.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU is gratefully acknowledged. This work has been supported by the project CHANGE funded by the PRIN 2022 – Progetti di Rilevante Interesse Nazionale (grant 20224KAC28).Notes and references
- J. L. Krause, K. J. Schafer and K. C. Kulander, Phys. Rev. Lett., 1992, 68, 3535 CrossRef CAS PubMed.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994 CrossRef CAS PubMed.
- M. Lewenstein, P. Balcou, M. Y. Ivanov, A. L'Huillier and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 2117 CrossRef PubMed.
- K. Schafer, B. Yang, L. DiMauro and K. Kulander, Phys. Rev. Lett., 1993, 70, 1599 CrossRef CAS PubMed.
- M. Ferray, A. L'Huillier, X. Li, L. Lompre, G. Mainfray and C. Manus, J. Phys. B: At., Mol. Opt. Phys., 1988, 21, L31 CrossRef CAS.
- F. Calegari, G. Sansone, S. Stagira, C. Vozzi and M. Nisoli, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 062001 CrossRef.
- T. Brabec and F. Krausz, Rev. Mod. Phys., 2000, 72, 545 CrossRef CAS.
- P.-M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Augé, P. Balcou, H. G. Muller and P. Agostini, Science, 2001, 292, 1689 Search PubMed.
- M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2001, 414, 509 Search PubMed.
- N. Ishii, K. Kaneshima, K. Kitano, T. Kanai, S. Watanabe and J. Itatani, Nat. Commun., 2014, 5, 3331 Search PubMed.
- F. Silva, S. M. Teichmann, S. L. Cousin, M. Hemmer and J. Biegert, Nat. Commun., 2015, 6, 6611 CrossRef CAS PubMed.
- Y. Pertot, C. Schmidt, M. Matthews, A. Chauvet, M. Huppert, V. Svoboda, A. von Conta, A. Tehlar, D. Baykusheva, J.-P. Wolf and H. J. Wörner, Science, 2017, 355, 264 CrossRef CAS PubMed.
- A. S. Johnson, D. R. Austin, D. A. Wood, C. Brahms, A. Gregory, K. B. Holzner, S. Jarosch, E. W. Larsen, S. Parker, C. S. Str
![[b with combining umlaut]](https://www.rsc.org/images/entities/char_0062_0308.gif) er, P. Ye, J. W. G. Tisch and J. P. Marangos, Sci. Adv., 2018, 4, eaar3761 CrossRef PubMed.
er, P. Ye, J. W. G. Tisch and J. P. Marangos, Sci. Adv., 2018, 4, eaar3761 CrossRef PubMed. - J. Li, J. Lu, A. Chew, S. Han, J. Li, Y. Wu, H. Wang, S. Ghimire and Z. Chang, Nat. Commun., 2020, 11, 2748 CrossRef CAS PubMed.
- C. Vozzi, F. Calegari, E. Benedetti, J.-P. Caumes, G. Sansone, S. Stagira and M. Nisoli, Phys. Rev. Lett., 2005, 95, 153902 CrossRef CAS PubMed.
- D. Faccialá, S. Pabst, B. D. Bruner, G. Ciriolo, S. De Silvestri, M. Devetta, M. Negro, H. Soifer, S. Stagira, N. Dudovich and C. Vozzi, Phys. Rev. Lett., 2016, 117, 093902 CrossRef PubMed.
- J. Marangos, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 132001 CrossRef.
- B. D. Bruner, Z. Masin, M. Negro, F. Morales, D. Brambila, M. Devetta, D. Faccialá, A. G. Harvey, M. Ivanov, Y. Mairesse, S. Patchkovskii, V. Serbinenko, H. Soifer, S. Stagira, C. Vozzi, N. Dudovich and O. Smirnova, Faraday Discuss., 2016, 194, 369 RSC.
- P. Peng, C. Marceau and D. M. Villeneuve, Nat. Rev. Phys., 2019, 1, 144 CrossRef.
- M. Negro, M. Devetta, D. Faccialá, S. De Silvestri, C. Vozzi and S. Stagira, Faraday Discuss., 2014, 171, 133 RSC.
- T. T. Gorman, T. D. Scarborough, I. P. M. Abanador, F. Mauger, D. Kiesewetter, P. Sándor, S. Khatri, K. Lopata, K. J. Schafer, P. Agostini, M. B. Gaarde and L. F. DiMauro, J. Chem. Phys., 2019, 150, 184308 CrossRef CAS PubMed.
- D. R. Tuthill, T. D. Scarborough, T. T. Gorman, K. A. Hamer, R. R. Jones, M. B. Gaarde, K. Lopata, F. Mauger, K. J. Schafer and L. F. DiMauro, J. Phys. Chem. A, 2022, 126, 8599 CrossRef PubMed.
- X. X. Zhou, X. M. Tong, Z. X. Zhao and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 061801 CrossRef.
- B. K. McFarland, J. P. Farrell, P. H. Bucksbaum and M. Guhr, Science, 2008, 322, 1232 CrossRef CAS PubMed.
- A.-T. Le, R. Lucchese and C. Lin, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 211001 CrossRef.
- C. Jin, A.-T. Le and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 053409 CrossRef.
- C. Vozzi, M. Negro, F. Calegari, G. Sansone, M. Nisoli, S. D. Silvestri and S. Stagira, Nat. Phys., 2011, 7, 822 Search PubMed.
- D. Dundas, J. Chem. Phys., 2012, 136, 194303 CrossRef PubMed.
- J. Li, P. Liu, H. Yang, L. Song, S. Zhao, H. Lu, R. Li and Z. Xu, Opt. Express, 2013, 21, 7599 CrossRef CAS PubMed.
- Z. Diveki, R. Guichard, J. Caillat, A. Camper, S. Haessler, T. Auguste, T. Ruchon, B. Carré, A. Maquet, R. Taïeb and P. Salières, Chem. Phys., 2013, 414, 121 CrossRef CAS.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972 CrossRef CAS PubMed.
- H. J. Wörner, J. B. Bertrand, P. Hockett, P. B. Corkum and D. M. Villeneuve, Phys. Rev. Lett., 2010, 104, 233904 CrossRef PubMed.
- J. Troß, X. Ren, V. Makhija, S. Mondal, V. Kumarappan and C. A. Trallero-Herrero, Phys. Rev. A, 2017, 95, 033419 CrossRef.
- M. Ruberti, P. Decleva and V. Averbukh, Phys. Chem. Chem. Phys., 2018, 20, 8311 RSC.
- K. A. Hamer, D. R. Tuthill, T. D. Scarborough, L. F. DiMauro, K. Lopata, K. J. Schafer, M. B. Gaarde and F. Mauge, Phys. Rev. A, 2021, 104, 033114 CrossRef CAS.
- Z. Shu, H. Liang, Y. Wang, S. Hu, S. Chen, H. Xu, R. Ma, D. Ding and J. Chen, Phys. Rev. Lett., 2022, 128, 183202 CrossRef CAS PubMed.
- E. Luppi and E. Coccia, J. Phys. Chem. A, 2023, 127, 7335 CrossRef CAS PubMed.
- Z. Ren, B. Zhang, Y. Yang, Y. Zhu, J. Zhao and Z. Zhao, Results Phys., 2023, 55, 107181 CrossRef.
- C. Morassut, A. Ravindran, A. Ciavardini, E. Luppi, G. De Ninno and E. Coccia, J. Phys. Chem. A, 2024, 128, 2015 CrossRef CAS PubMed.
- M. Marchetta, C. Morassut, J. Toulouse, E. Coccia and E. Luppi, J. Chem. Phys., 2024, 161, 204111 CrossRef CAS PubMed.
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J.-C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867 CrossRef CAS PubMed.
- M. Lein, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, R135 CrossRef CAS.
- D. Shafir, Y. Mairesse, D. Villeneuve, P. Corkum and N. Dudovich, Nat. Phys., 2009, 5, 412 Search PubMed.
- M. Lein, N. Hay, R. Velotta, J. P. Marangos and P. Knight, Phys. Rev. Lett., 2002, 88, 183903 CrossRef CAS PubMed.
- S. Odžak and D. Milošević, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 023414 CrossRef.
- E. V. van der Zwan and M. Lein, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 033405 CrossRef.
- A. Etches, M. B. Gaarde and L. B. Madsen, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 023418 CrossRef.
- B. Augstein and C. F. de Morisson Faria, Mod. Phys. Lett. B, 2012, 26, 1130002 CrossRef.
- B. Zhang, Y. Chen, X. Jiang and X. Sun, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 053428 CrossRef.
- E. Hasović, S. Odžak, W. Becker and D. Milošević, Mol. Phys., 2017, 115, 1750 CrossRef.
- A. Shiner, B. Schmidt, C. Trallero-Herrero, H. J. Wörner, S. Patchkovskii, P. B. Corkum, J. Kieffer, F. Légaré and D. Villeneuve, Nat. Phys., 2011, 7, 464 Search PubMed.
- A. Ferré, A. Boguslavskiy, M. Dagan, V. Blanchet, B. Bruner, F. Burgy, A. Camper, D. Descamps, B. Fabre and N. Fedorov, et al., Nat. Commun., 2015, 6, 5952 Search PubMed.
- S. Baker, J. S. Robinson, C. Haworth, H. Teng, R. Smith, C. C. Chirila, M. Lein, J. Tisch and J. P. Marangos, Science, 2006, 312, 424 CrossRef CAS PubMed.
- D. Baykusheva, D. Zindel, V. Svoboda, E. Bommeli, M. Ochsner, A. Tehlar and H. J. Wörner, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23923 CrossRef CAS PubMed.
- D. R. Tuthill, F. Mauger, T. D. Scarborough, R. R. Jones, M. B. Gaarde, K. Lopata, K. J. Schafer and L. F. DiMauro, J. Mol. Spectrosc., 2020, 372, 111353 CrossRef CAS.
- Z. Shu, H. Liang, Y. Wang, S. Hu, S. Chen, H. Xu, R. Ma, D. Ding and J. Chen, Phys. Rev. Lett., 2022, 128, 183202 CrossRef PubMed.
- A. Tehlar, J. T. Casanova, A. Dnestryan, F. Jensen, L. B. Madsen, O. I. Tolstikhin and H. J. Wörner, Struct. Dyn., 2024, 11, 014304 CrossRef CAS PubMed.
- O. E. Alon, V. Averbukh and N. Moiseyev, Phys. Rev. Lett., 1998, 80, 3743 CrossRef CAS.
- X. Liu, X. Zhu, L. Li, Y. Li, Q. Zhang, P. Lan and P. Lu, Phys. Rev. A, 2016, 94, 033410 CrossRef.
- O. Neufeld, D. Podolsky and O. Cohen, Nat. Commun., 2019, 10, 405 CrossRef PubMed.
- N. Ben-Tal, N. Moiseyev and A. Beswick, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 3017 CrossRef CAS.
- P. M. Kraus, A. Rupenyan and H. J. Wörner, Phys. Rev. Lett., 2012, 109, 233903 CrossRef CAS PubMed.
- O. Neufeld, D. Ayuso, P. Decleva, M. Y. Ivanov, O. Smirnova and O. Cohen, Phys. Rev. X, 2019, 9, 031002 CAS.
- M. E. Tzur, O. Neufeld, E. Bordo, A. Fleischer and O. Cohen, Nat. Commun., 2022, 13, 1312 CrossRef CAS PubMed.
- G. Lerner, O. Neufeld, L. Hareli, G. Shoulga, E. Bordo, A. Fleischer, D. Podolsky, A. Bahabad and O. Cohen, Sci. Adv., 2023, 9, eade0953 CrossRef CAS PubMed.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni, A. A. Correa, U. De Giovannini, A. Delgado, F. G. Eich, J. Flick, G. Gil, A. Gomez, N. Helbig, H. Hübener, R. Jestädt, J. Jornet-Somoza, A. H. Larsen, I. V. Lebedeva, M. Lüders, M. A. L. Marques, S. T. Ohlmann, S. Pipolo, M. Rampp, C. A. Rozzi, D. A. Strubbe, S. A. Sat, C. Schäfer, I. Theophilou, A. Welden and A. Rubio, J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- X. Chu, Phys. Rev. A, 2023, 108, 013116 CrossRef CAS.
- O. Neufeld, N. Tancogne-Dejean and A. Rubio, J. Phys. Chem. Lett., 2024, 15, 7254 CrossRef CAS PubMed.
- P. Krause, T. Klamroth and P. Saalfrank, J. Chem. Phys., 2007, 127, 034107 CrossRef PubMed.
- E. Coccia, B. Mussard, M. Labeye, J. Caillat, R. Taeb, J. Toulouse and E. Luppi, Int. J. Quantum Chem., 2016, 116, 1120 CrossRef CAS.
- E. Coccia and E. Luppi, Theor. Chem. Acc., 2016, 135, 1 Search PubMed.
- E. Coccia and E. Luppi, Theor. Chem. Acc., 2019, 138, 96 Search PubMed.
- C. F. Pauletti, E. Coccia and E. Luppi, J. Chem. Phys., 2021, 154, 014101 CrossRef CAS PubMed.
- E. Coccia and E. Luppi, J. Phys.: Condens. Matter, 2021, 34, 073001 CrossRef PubMed.
- A. P. Woźniak, M. Przybytek, M. Lewenstein and R. Moszyński, J. Chem. Phys., 2022, 156, 174106 CrossRef PubMed.
- A. P. Woźniak, M. Lewenstein and R. Moszyński, Adv. Quantum Chem., Elsevier, 2023, vol. 87, p. 167 Search PubMed.
- P. Krause, T. Klamroth and P. Saalfrank, J. Chem. Phys., 2005, 123, 074105 CrossRef PubMed.
- P. Saalfrank, F. Bedurke, C. Heide, T. Klamroth, S. Klinkusch, P. Krause, M. Nest and J. C. Tremblay, Adv. Quantum Chem., Elsevier, 2020, vol. 81, p. 15 Search PubMed.
- F. Bedurke, T. Klamroth and P. Saalfrank, Phys. Chem. Chem. Phys., 2021, 23, 13544 RSC.
- S. Carlström, M. Spanner and S. Patchkovskii, Phys. Rev. A, 2022, 106, 043104 CrossRef.
- A. P. Woźniak and R. Moszyński, Phys. Rev. A, 2024, 109, 013523 CrossRef.
- C. Morassut, E. Coccia and E. Luppi, J. Chem. Phys., 2023, 159, 124108 CrossRef CAS PubMed.
- F. Bedurke, T. Klamroth, P. Krause and P. Saalfrank, J. Chem. Phys., 2019, 150, 234114 CrossRef PubMed.
- A. P. Woźniak and R. Moszyński, J. Phys. Chem. A, 2024, 128, 2683–2702 CrossRef PubMed.
- E. Luppi and E. Coccia, Phys. Chem. Chem. Phys., 2021, 23, 3729 RSC.
- J. V. Ortiz, J. Chem. Phys., 2020, 153, 070902 CrossRef CAS PubMed.
- V. Pomogaev, S. Lee, S. Shaik, M. Filatov and C. H. Cho, J. Phys. Chem. Lett., 2021, 12, 9963 CrossRef CAS PubMed.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. Gilbert, L. V. Slipchenko, S. V. Levchenko and D. P. O’Neill, et al., Phys. Chem. Chem. Phys., 2006, 8, 3172 RSC.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 2223 CrossRef CAS.
- M. Labeye, F. Zapata, E. Coccia, V. Veniard, J. Toulouse, J. Caillat, R. Taïeb and E. Luppi, J. Chem. Theory Comput., 2018, 14, 5846 CrossRef CAS PubMed.
- A. P. Woźniak, M. Lesiuk, M. Przybytek, D. K. Efimov, J. S. Prauzner-Bechcicki, M. Mandrysz, M. Ciappina, E. Pisanty, J. Zakrzewski and M. Lewenstein, et al., J. Chem. Phys., 2021, 154, 094111 CrossRef PubMed.
- S. Klinkusch, P. Saalfrank and T. Klamroth, J. Chem. Phys., 2009, 131, 114304 CrossRef PubMed.
- X. Chu, Phys. Rev. A, 2024, 109, 053103 CrossRef CAS.
- H. Hu, N. Li, P. Liu, R. Li and Z. Xu, Phys. Rev. Lett., 2017, 119, 173201 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Time-dependent dipole moments for H2O and NH3 in the studied configurations. Partial HHG spectra of H2O with pulse polarisation and detection in the xy plane, along a direction at 45° with respect to the molecular plane. Total HHG spectra of H2O with pulse polarisation and detection in the xy plane, along a direction at 135° and 30° with respect to the molecular plane. Phase of interference between Aa and Ab channels of NH3 for the cases (b) and (c) of Fig. 7. See DOI: https://doi.org/10.1039/d5cp01624j |
| This journal is © the Owner Societies 2025 |