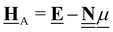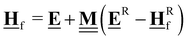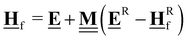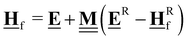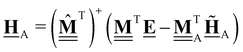DOI:
10.1039/D4CS00768A
(Tutorial Review)
Chem. Soc. Rev., 2025,
54, 560-589
Unifying thermochemistry concepts in computational heterogeneous catalysis†
Received
2nd August 2024
First published on 29th November 2024
Abstract
Thermophysical properties of adsorbates and gas-phase species define the free energy landscape of heterogeneously catalyzed processes and are pivotal for an atomistic understanding of the catalyst performance. These thermophysical properties, such as the free energy or the enthalpy, are typically derived from density functional theory (DFT) calculations. Enthalpies are species-interdependent properties that are only meaningful when referenced to other species. The widespread use of DFT has led to a proliferation of new energetic data in the literature and databases. However, there is a lack of consistency in how DFT data is referenced and how the associated enthalpies or free energies are stored and reported, leading to challenges in reproducing or utilizing the results of prior work. Additionally, DFT suffers from exchange–correlation errors that often require corrections to align the data with other global thermochemical networks, which are not always clearly documented or explained. In this review, we introduce a set of consistent terminology and definitions, review existing approaches, and unify the techniques using the framework of linear algebra. This set of terminology and tools facilitates the correction and alignment of energies between different data formats and sources, promoting the sharing and reuse of ab initio data. Standardization of thermochemistry concepts in computational heterogeneous catalysis reduces computational cost and enhances fundamental understanding of catalytic processes, which will accelerate the computational design of optimally performing catalysts.

Bjarne Kreitz
| Bjarne Kreitz is a postdoctoral researcher at Brown University funded by a Feodor Lynen Postdoctoral Scholarship, working with Prof. C. Franklin Goldsmith since 2021. He obtained his PhD from Clausthal University of Technology (Germany) in 2021 under the guidance of Prof. Thomas Turek. Before joining Brown, he briefly worked as a postdoc at the Karlsruhe Institute of Technology (Prof. Olaf Deutschmann). He is an incoming Assistant Professor at the Georgia Institute of Technology in the School of Chemical & Biomolecular Engineering starting in 2025. His research focuses on the multiscale modeling of heterogeneously catalyzed reactions with detailed chemical kinetics. |

Left to right: Dingqi Nai, Dr. A. J. Medford, Dr. Gabriel Gusmão, Dr. Jagriti Sahoo
| A. J. Medford is an associate professor at the Georgia Institute of Technology in the School of Chemical & Biomolecular Engineering. He obtained his PhD in Chemical Engineering from Stanford University in 2015, he was a Fulbright Student at the Technical University of Denmark in 2009 and received a BS degree from North Carolina State University in 2009. His research group focuses on the intersection of computational catalysis, electronic structure theory, and machine learning approaches. Gabriel Gusmão, Dingqi Nai, and Jagriti Sahoo are students in the Medford Group. Gabriel Gusmão received a BEng degree in Chemical Engineering from the University of Campinas in 2013 and defended his PhD thesis in 2023. Dingqi Nai received his BS degree in Chemical Engineering from UC Davis in 2018 and an MS degree in Chemical Engineering from Carnegie Mellon University in 2019. Jagriti Sahoo received a BTech degree in Chemical Engineering from IIT Delhi in 2019 and defended her PhD thesis in 2024. |

Andrew A. Peterson
| Andrew Peterson is an Associate Professor of chemical engineering at Brown University. He received his BChE in chemical engineering from the University of Minnesota and spent four years in industry before starting his graduate studies at the Massachusetts Institute of Technology. He performed postdoctoral research at the Technical University of Denmark and at Stanford University. Research in the Peterson group focuses on computational catalysis, electrochemistry, and acceleration of simulations with machine learning models. |

David H. Bross
| David Bross is a chemist in the Gas Phase Chemical Physics group in the Chemical Sciences and Engineering Division at Argonne National Laboratory. He received his PhD at Washington State University in 2015 and did a postdoc at Argonne National Laboratory (2015–2017). His current research is focused on developing scientific databases to enable data sciences approaches to physical chemistry. |

C. Franklin Goldsmith
| Franklin Goldsmith is an associate professor in the School of Engineering at Brown University. He obtained his PhD in Chemical Engineering from the Massachusetts Institute of Technology in 2010. From 2010–2012, he was an Alexander von Humboldt Postdoctoral Scholar at the Fritz-Haber Institute of the Max Planck Society, and from 2012–2013 he was an Argonne Director's Fellow in the Chemical Sciences Division at Argonne National Laboratory. |
Key learning points
(1) Explain the difference between formation and reaction energies
(2) Understand the role of relative quantities in thermochemistry
(3) Calculate enthalpies from DFT data with different reference sets
(4) Combine DFT data with gas-phase enthalpies of formation
(5) Evaluate different referencing approaches for adsorbate enthalpies (of formation)
|
1 Introduction
Density functional theory (DFT) has emerged as a crucial tool in computational chemistry over the last decades, revolutionizing the field of heterogeneous catalysis by providing an effective approach to predict energetic properties.1–6 This quantum-mechanical (QM) modeling method offers insight into surface chemistry and catalysis.7,8 First-principles-based multiscale modeling provides the bridge between experiments and theory that enables optimizations of catalysts and reactors.9–11 The DFT developments combined with advances in computational power have led to a surge of large-scale open-source databases, such as the Materials Project,12 the Open Catalyst Project (OCP),13–15 the Novel Materials Discovery Laboratory (NoMaD),16–18 Catalysis Hub,19 Automatic FLOW for Materials Discovery (AFLOW),20 CatApp,21 and the Open Quantum Material Database (OQMD).22,23 These databases have enabled the proliferation of energetic data, which has allowed a deeper understanding of catalytic processes at the atomic level.
Although these databases provide a vast amount of computed information, the absence of standardized data formats and naming conventions poses a challenge for researchers. The databases typically do not contain the raw DFT energies of the structures but rather the derived quantities such as thermophysical properties and activation barriers. In principle, these derived quantities are more general and transferable than raw DFT energies. However, the processes used to derive them and the terminology used to describe them can lead to inconsistencies between different studies.24 This challenge is further compounded by the variety of DFT codes and the different levels of theory used to generate the data.25,26 Due to computational cost, most large-scale databases are based on DFT calculations with the generalized gradient (GGA) approximation. Such DFT codes include The Vienna ab initio simulation package (VASP),27,28 Quantum ESPRESSO,29,30 NWChem,31 GPAW,32 Jaguar,33 and SPARC,34 each of which has its own features, functionalities, and specializations. The atomic simulation environment (ASE)35 or Python materials genomics (pymatgen)36 have helped standardize the interfaces to these codes, but numerical differences persist due to differences in exchange–correlation (xc) functionals, settings (e.g. plane-wave cutoff energy, k-point sampling) and pseudopotentials.25 For metal oxides and magnetic systems, this is further complicated by the spin state optimization and Hubbard correction (DFT+U),37,38 while electrochemical systems are affected by the potential and solvent model.39–44 Advanced techniques such as quantum Monte Carlo, the random phase approximation, or time-dependent DFT can improve physical accuracy but also introduce additional sources of numerical error and ambiguity.45–50
Consequently, it is challenging to efficiently access, compare, integrate, and analyze this data because different studies and databases often present their findings in different formats.25,51–53 Web applications for surface chemistry such as CatApp21 and Catalysis-Hub19 aim to provide systematic data for activation energies of elementary surface reactions and binding energies from a variety of studies. Yet, the broader challenge of standardizing data across various platforms and integrating existing gas-phase databases remains. The rise of machine learning (ML) in heterogeneous catalysis research has been facilitated by the availability of these databases and the development of cutting-edge approaches to handle the data, leading to the discovery of optimized catalysts.54–57 However, the inconsistencies between datasets impedes the seamless data integration and (re)use, which hinders the development of better ML models.24,51,58–60 These discrepancies underscore the need for standardized practices and benchmarks in DFT calculations to ensure consistency and reproducibility across studies.61,62 Due to all of the reasons above, it is common for every investigator of a catalytic reaction to perform electronic structure calculations for all species with a consistent set of DFT settings to obtain meaningful results. Given the millions of calculations present in emerging DFT energy databases,14,15 it is imperative that researchers find ways to leverage and reuse existing DFT data whenever possible.
Beyond the challenges posed by non-standardized data formats and different DFT methods, another critical issue that must be addressed is the potential inconsistency between experimental and ab initio data. Understanding catalytic processes relies on microkinetic modeling based on DFT-derived energetics.9,10,63 However, the uncertainties in the energetics lead to discrepancies between theory and experiment, which impact the applicability and reliability of the multiscale model.9,64,65 Discrepancies can arise from various factors, such as incorrect active site models,66 missing pathways in the mechanism, inadequate consideration of surface environment under reaction conditions,67 and intrinsic errors in the DFT xc functional.68 DFT suffers from relatively large physical errors arising primarily from the xc approximation, which yields adsorption energies errors of ≈20 kJ mol−1.68 While DFT has been instrumental in studying catalytic materials, intrinsic parametric errors translate to uncertainties in reaction rates of multiple orders of magnitude in multiscale models.69–73 Error cancellation improves the reliability of trends calculated with DFT, but the errors are still too large for quantitative predictions of reaction rates for individual materials with first-principles-based kinetic models in most cases.
The relatively mature field of gas-phase chemistry has made significant progress in establishing common references and protocols for aligning thermochemical data from various sources. Together with highly accurate electronic structure methods, this has led to the development of databases with highly accurate thermochemical properties, i.e. enthalpies of formation (ΔfH) such as the NIST Chemistry Webbook,74 JANAF,75 or the Active Thermochemical Tables (ATcT).76,77 The accuracy and consistency of the gas-phase thermochemical data are the cornerstone of quantitative predictions of reaction rates, which bridge the gap between theoretical predictions and experimental observations. When a gas-phase microkinetic model is developed, it is possible to simply use tabulated values and append only the thermophysical properties of missing species.
Drawing inspiration from the approaches the gas-phase community uses for aligning thermochemical states offers a promising route for standardizing approaches in the heterogeneous catalysis community. However, heterogeneous catalysis has distinct challenges, as outlined above. Errors in electronic structure methods for heterogeneous systems at the GGA-level are larger,78 and there is no clear hierarchy of methods that can be universally applied across different systems.61,79,80 Furthermore, the energies of adsorbates are intricately linked to the surface chemistry, making them highly dependent on the specific catalyst surface, adsorbate coverage, and reaction conditions.81–84 Given the intricate nature of heterogeneous catalysis, a more nuanced strategy is necessary to standardize methodologies, emphasizing the urgency and importance of this task.
In this review, we first define a consistent notation of thermochemical quantities that the heterogeneous catalysis community can use in the future and provide a bridge to the gas-phase thermochemical frameworks. The structure of this review ensures that the methods of deriving thermophysical properties from QM calculations are integrated into the general thermochemistry framework to provide a clear learning pathway. We review the available approaches to derive thermochemical properties of adsorbates from ab initio data using our introduced standardized notation that can be condensed into a simple set of linear algebra equations. These linear algebra tools provide a straightforward method for combining data from numerous sources, integrating experiments with ab initio data, converting between different formats, identifying and minimizing inconsistencies, and guaranteeing that the combined dataset is complete and consistent. The various approaches are used to calculate the thermophysical parameters for a case study to showcase differences and similarities. We restrict the discussion to heterogeneous catalysis for gas/solid systems for simplicity, although extensions to solution-phase chemistry39 and electrochemistry44,85 are expected to be relatively straightforward. Our aim is not to promote any single method but rather to unify thermochemistry concepts, notations, and terminology to demonstrate the differences, benefits, and drawbacks of available techniques while providing an approachable introduction to a topic often perplexing to novice researchers in the field. We hope that this review will serve as a valuable resource for navigating this complex topic and facilitate the improved use of the wealth of existing data to analyze and understand heterogeneous catalysis.
2 Overview of computational thermodynamics
This review aims to be self-contained and thus we begin with a brief overview of the relevant thermochemical properties and relationships. When working with thermochemical data related to heterogeneous catalysis or any other system, it is imperative to recognize that any thermochemically meaningful quantity will be a relative quantity that satisfies a mass balance. Here, we focus on chemical processes occurring at a fixed temperature and pressure; hence, we use Gibbs free energy ΔG as the relevant thermochemical potential. Thermodynamic equilibrium governs the maximum achievable conversion and selectivity for a chemical conversion process. The equilibrium constant K for a reaction is calculated from the Gibbs free energy change ΔrG at a temperature T| | 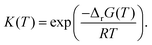 | (1) |
ΔrG is the sum of the products of the free energies of formation ΔfGi of species i and their stoichiometric coefficient νi| |  | (2) |
Thus, it is crucial to accurately know the thermochemical quantities of species participating in the reactions to make quantitative predictions with kinetic models. In microkinetic models (gas-phase or surface reaction mechanism), thermophysical properties of all species and intermediates are required to determine the equilibrium constants of the elementary steps. Commonly, an elementary reaction is specified in the forward direction with rate constant kfwd and the rate constant for the reverse direction krev is determined from the concentration equilibrium constant Kc,| | 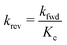 | (3) |
which ensures microscopic reversibility and thermodynamic consistency. The free reaction energy is related to the enthalpy ΔrH and entropy ΔrS of reaction:| | | ΔrG(T) = ΔrH(T) − TΔrS(T) | (4) |
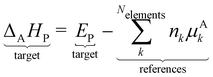
The reaction enthalpy is calculated from the enthalpy of formation ΔfHi(T), also known as the heat of formation, of the species,| | 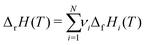 | (5) |
where ΔfHi(T) is a critical thermochemical quantity since it captures the majority of the influence of chemical bonds. The enthalpy of formation is a relative quantity, meaning it is always defined relative to other species or reference states, whereas entropy and heat capacity are properties of an individual species. Defining a set of reference species is necessary to obtain a set of internally consistent ΔfH for all species. The thermodynamic community has defined the elements in their standard configuration as the standard reference species,86 so the enthalpy of formation of a species is defined as a formation reaction from the elements in their most stable form at a constant temperature. For example, for C2H6| | 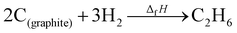 | (6) |
where the reference species are graphite and H2. Accordingly, the ΔfH of the standard reference species are 0 since it is a null reaction. Experimental ΔfH can only be obtained directly for a limited set of species such as H2O (oxidation of H2) and CO2 (oxidation of graphitic C). In nearly all other cases, ΔfH are derived from other measured reaction enthalpies, using the fact that the enthalpy is a state variable. Hess's law states that ΔfH of a species is invariant to the reaction through which it is formed. This law can be exploited since it is relatively easy to measure the combustion enthalpy of C2H6 in a bomb calorimeter.| | 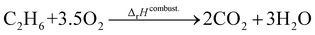 | (7) |
Alternatively, this reaction can be written as:| | 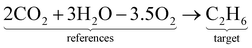 | (8) |
where the reference species to form our target species are located on the reactant side. If ΔfH of O2, CO2, and H2O are known (ΔfHO2 = 0 kJ mol−1, ΔfHCO2 and ΔfHH2O can directly be measured), it is simple to back out ΔfHC2H6 with the measured ΔrHcombust.:| | 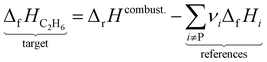 | (9) |
where νi is the stoichiometric coefficient of species i (e.g., νCO2 = −2, νO2 = 3.5 in eqn (8)). Fig. 1 shows the thermodynamic cycle to determine ΔfHC2H6.
 |
| | Fig. 1 Thermochemical cycle to determine the ΔfHC2H6 from the experimentally measured combustion enthalpy and the known enthalpies of formation of the reference species. | |
However, ΔfH of many species have never been measured and probably will never be measured, especially for highly reactive species such as radicals and other short-lived intermediates. Consequently, QM methods are used instead to compute ΔfH of species that cannot be measured. In all equations, we use the general QM instead of DFT since all methods can be used with any level of theory of electronic structure data. QM methods can provide only electronic energies of individual species that are internally referenced to the QM reference frame of the software, which can then be used to compute the reaction enthalpies and finally deduce ΔfH. To determine ΔfH of a target molecule P from an electronic structure method, we form a hypothetical reaction from a set of reference species A, B, and C with known ΔfH.
The first step is to compute the reaction enthalpy using the zero-point corrected QM energies (
Ei).
| |  | (11) |
With Δ
rHQM, we can now back out Δ
fH of the target:
| | 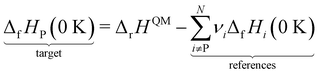 | (12) |
| | 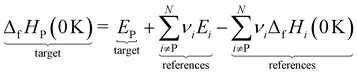 | (13) |
eqn (12) is identical to
eqn (9); the only difference is the source of the reaction enthalpy. Since the reaction is hypothetical, it is possible to use any stoichiometrically balanced reaction. QM calculations are performed at a temperature of 0 K, so Δ
fH derived from the QM reaction enthalpy are at 0 K, too. They can be converted to Δ
fH at 298 K by applying temperature corrections.
87 In principle, all the approaches described in this work are mathematically identical to
eqn (13); they only differ in the choice of reference species and the value of Δ
fH of the reference species.
2.1 Anchors, references, and thermochemical networks
Enthalpies are always derived from a set of reference species, so without a common set of references, the values of enthalpies are meaningless. When building microkinetic models, we are not only interested in the enthalpies or Gibbs free energies of a single species but rather the entire reaction pathway or mechanism. In heterogeneous catalysis, this includes the adsorption of gas-phase reactants, a series of surface reaction steps, and the desorption of gas-phase products. Thus, it is necessary to align the enthalpies of all species to the same set of reference species, which creates a thermochemical network. In this work, we introduce the term anchor species as a special case of these reference species that form the basis of a thermochemical network. The introduction of this term helps to resolve ambiguity in approaches where multiple or non-standard references are used. As we will show, the anchor species of a thermochemical network will have a relative enthalpy of zero within their own reference frame. In contrast, reference species may have zero or non-zero values.
The gas-phase thermodynamic community has defined the enthalpies of formation ΔfH (see eqn (6)), which use the elements in their most stable configuration as the reference thermochemical species.86 By referencing all species to the standard set of anchor species (i.e. the elements in their IUPAC standard states86), it is possible to integrate data from multiple sources, e.g., experimental and theoretical determinations with various degrees of accuracy, into a global thermochemical network. There are many highly accurate QM methods available for gas-phase molecules (e.g., W4,88 HEAT,89 focal point,90 and ANL091) that are capable of computing reaction enthalpies with an accuracy of ±1 kJ mol−1. With these accurate reaction enthalpies, the gas-phase chemistry community has established standard methods to convert the electronic energies from QM into highly accurate ΔfH in thermochemical networks, which can be created in two ways: sequential or using the Active Thermochemical Tables approach.77,92 We briefly describe these two different approaches in this review, but the reader is referred to ref. 87, 92 and 93 for a complete description.
In the sequential approach, a single species is added by referencing it to species already in the thermochemical network. These species can be the elements in their standard states (anchors) or species that are connected to the elements, i.e. their ΔfH is known (references). The expansion of the thermochemical network is most commonly done one species at a time, which introduces a few issues. Foremost, it requires the constructor of the sequential compilation to choose at the onset which species to add and in which order. Imagine that there are two species with similar quality thermochemical determinations (e.g. two different reaction enthalpies forming the target from references) that relate both to the existing compilation. The constructor of a sequential compilation must arbitrarily choose which to add first, artificially diminishing the impact that the second has on all subsequent determinations. Once a species is added, values for its enthalpy and partition function are adopted, and all additional species that include a reference to that species, even indirectly, depend explicitly upon the previous values. The choice of partition function determines how a species thermochemical information is converted to the reference temperature of 298.15 K under standard conditions at which the thermochemical network is solved. Thus, partition functions can limit the accuracy as many determinations occur at temperatures far from the reference temperature. The third issue is bias because constructors have to weigh all the available information when choosing what values to recommend for a given reaction enthalpy. Frequently, the constructors adopts a single “best” determination to add a new species to the network, discarding the remaining information. Importantly, new information that becomes available after a value has been adopted cannot be included without redoing the entire compilation of the network, which is the largest problem with the sequential compilation. By the time a sequential network is compiled there is likely better or contradictory information that cannot be included without introducing inconsistencies. Examples of these sequential thermochemical networks are the JANAF tables75 or the NIST Chemistry WebBook.74
The dynamic ATcT76,77,93 approach overcomes the pitfalls of the adopt-and-freeze sequential approach. At the time of compilation of the thermochemical network, a set of partition functions is chosen for each species. The entire thermochemical network is constructed by fitting trial ΔfH to that network using a weighted least squares regression.93 All determinations within the network are then checked against the trial solution using the “worst offenders” algorithm. The determination that is least consistent with the trial ΔfH has their uncertainty increased marginally. This procedure is repeated until the entire thermochemical network consists of ΔfH with uncertainties that are internally consistent. The ATcT approach uses all data available at the time of solution and can be painlessly updated with new information, including additional ab initio or experimental data, new species, or improved partition functions for species. Thus, the ATcT incorporates all available data from experimental and theoretical into a single thermochemical network. This approach can determine ΔfH with an astonishing sub kJ mol−1 accuracy. The current version of the ATcT contains 3000 gas-phase species,76 and it can easily be accessed at https://atct.anl.gov/. Our current study uses the ATcT database as the global thermochemical network. Accordingly, we will use the terms ATcT or global thermochemical network interchangeably in the remainder of this paper.
In computational catalysis it is more common to create a self-consistent local thermochemical network. A local thermochemical network may be anchored to any valid set of anchor species. These anchor species can be part of the reaction mechanism or additional species not present in the mechanism, and they can even be abstracted into elemental chemical potentials. In the context of ab initio thermodynamics, we can think of these reference species as being in a reservoir that is in equilibrium with our target species (adsorbate, gas-phase, or surface).94 The reactions to form the target from the reference species can take or donate these references to the reservoir as an isothermal and isobaric process.95 This work details the numerous approaches to construct these local networks and the approaches that integrate the formation enthalpies of adsorbates into the global thermochemical network by anchoring the species to the standard reference set according to the IUPAC definition.
2.2 Thermochemistry in heterogeneous catalysis
The gas-phase thermochemical data from the global thermochemical network is relevant for catalysis because it determines the overall thermochemical equilibrium of a catalyzed gas-phase reaction. However, no ΔfH of adsorbates are included in the ATcT, except *H on Pt(111). The lack of adsorbates in these databases is due to the structural complexity of the active site motifs, finite coverage effects, the accuracy of electronic structure calculations for adsorbates, and the limited availability of accurate experimental values. The ΔfH of the adsorbate depends on the active site (e.g., metal (oxide) facet), which drastically increases the space of possible species to integrate into a thermochemical network. Additionally, the atomic-scale structure of surfaces may vary even for a single facet, resulting in multiple possible binding sites with distinct ΔfH.
The accuracy of electronic structure calculations for gas/solid catalysis is typically limited to DFT because of the prohibitive computational cost of more advanced methods. Wellendorff et al.68 benchmarked predicted reaction energies for the adsorption of gas-phase molecules on transition metals with a range of different xc functionals with known experimental values96 and obtained the best results for the BEEF-vdW functional with uncertainties of ±30 kJ mol−1 (mean absolute error compared to the benchmark dataset).68 Some studies employed higher levels of theory such as combinations of GGA and meta-GGA functionals,97,98 embedding techniques,99–101 random-phase approximation (RPA),49,102–106 composite DFT/MP2/CCSD(T) methods,107–110 CCSD(T),48,111 and Quantum Monte Carlo47,112 to derive more accurate adsorption enthalpies. A review of beyond DFT methods is provided by Sauer.113 However, even with high-level methods, heterogeneous systems typically require pseudopotentials and other numerical approximations, leading to lower accuracy than what can be achieved for gas-phase systems. Another source of parametric uncertainty is the partition function used to compute the entropy and heat capacity, which are often approximated by assuming an ideal gas, harmonic oscillator, or hindered translator/rotor.114–116 The errors are typically smaller than errors in enthalpy but can still be substantial, as shown by more advanced techniques that account for anharmonicity.117–119
Experimental adsorption and reaction enthalpies can be significantly more accurate than DFT data. Adsorption enthalpies can be derived from temperature-programmed desorption (TPD) spectra or measured using single-crystal adsorption calorimetry (SCAC). An excellent review on SCAC is provided by Campbell.120 Determining ΔfH of the adsorbates anchored to the global thermochemical network from experimental adsorption enthalpies is straightforward. For associative adsorption, the adsorbate is directly referenced to the gas-phase precursor; for example, the adsorption enthalpy of CH4 on Pt(111) was measured by Tait et al.121via TPD:
| CH4 + * → CH4* ΔrH(63 K) = −15 kJ mol−1 |
Assuming that ΔfHPt(111) is zero (a common assumption that we will discuss later), ΔfHCH4* can be calculated directly with ΔfHCH4 from the ATcT database in the thermochemical cycle in Fig. 2. Temperature corrections have to be applied to convert between the experimental and the reference temperature. However, many species dissociate easily once adsorbed or do not have a stable gas-phase precursor, requiring specialized precursors to measure their adsorption energy. For example, Karp and coworkers122,123 used CH3I as a precursor to determine ΔfH*CH3
| CH3I2 + 2* → *CH3 + *I ΔrH(320 K) = −212 kJ mol−1 |
and measured a reaction enthalpy for the dissociative adsorption on Pt(111) of −212 kJ mol
−1 with SCAC.
122 Δ
fH*CH3 can then be derived using a thermodynamic cycle as displayed in
Fig. 3.
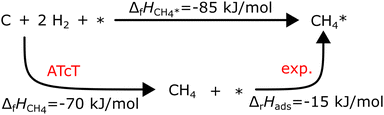 |
| | Fig. 2 Thermodynamic cycle to compute the formation enthalpy of CH4* on Pt(111) from the experimental enthalpy of adsorption at 63 K. | |
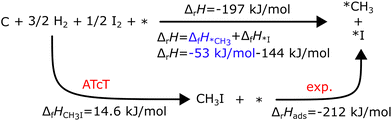 |
| | Fig. 3 Thermodynamic cycle to determine the ΔfH*CH3 on Pt(111) adapted from ref. 123. ΔfH*I (−144 kJ mol−1) was obtained from a different experiment. The figure is adapted from Karp et al.123 | |
The experimental determination of the accurate ΔfH of adsorbates is challenging since single-crystal adsorption calorimeters are expensive and intricate systems. Creating single crystals and ensuring no transformation during the operation is challenging. Additionally, ΔfH of the co-adsorbates have to be known with high accuracy,124 and coverage effects caused by self- or cross-interaction can distort the measurement.122,123 Another challenge for more complex adsorbates is finding suitable gas-phase precursors and preventing unwanted dissociation of the adsorbate. Due to all these factors, only a few dozen experimental adsorption enthalpies exist for a limited number of systems, summarized by Silbaugh and Campbell.96 Consequently, it is fair to assume that most adsorbate ΔfH will never be experimentally determined, and they have to be derived from QM data instead.
3 Definition of terms and variables
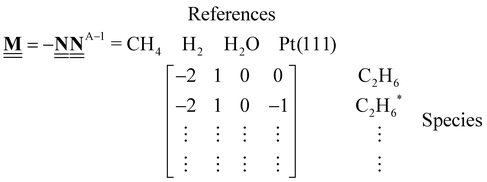
All pertinent definitions and associated notation are collected and concisely summarized in this section. We follow existing definitions and notations from the gas-phase chemistry literature where possible. Throughout this work, we assume that all thermochemical quantities are evaluated at 0 K and in the low-coverage limit, consistent with computational chemistry methods. For simplicity and readability, we drop the temperature in the equations below and only indicate if a quantity is evaluated at a different temperature. However, the definitions hold at all temperatures, and all mathematical relationships are valid as long as all quantities are evaluated at a consistent temperature. We only discuss the application of the methods to derive the enthalpies of adsorbates, which are (local) minima on the potential energy surface. The enthalpies of the adsorbates can be used to parameterize microkinetic models typically in the form of NASA polynomials, which requires the inclusion of entropy and heat capacity of the adsorbates.125 Additionally, the construction of the microkinetic models requires transition state calculations to elucidate the rate constants of the elementary steps of the reaction mechanism. Transition states, which are first-order saddle points, are outside the scope of this review since they require a different treatment to evaluate the rate constants, although we note that some of the reviewed methods are applied to transition states to develop microkinetic models. We also note that the existing computational catalysis literature may use different terms and contains many ambiguities. Thus, the definitions and notation below are inconsistent with some prior studies in computational catalysis, but are largely consistent with the gas-phase literature. Table 1 summarizes all the quantities used in this review. We provide a notation for a single species whenever possible and a linear algebra notation for a set of species (e.g., full mechanism). The general notation uses a Δ for all relative quantities, with the subscript on the Δ indicating whether it is a formation f or reaction enthalpy r. The subscript on the H indicates the identity of the species, while the superscript on the H denotes the method used. We introduce another subscript A on the Δ that indicates whether the enthalpy is relative to a non-standard set of anchor species. For example “ΔAH*CO where A = [CH4, H2O, H2, Pt(111)]” would fully specify an enthalpy of *CO adsorbed on Pt(111) anchored to the DFT energies of CH4, H2O, and H2 and Pt(111). By definition, ΔAH of the anchor species A are zero in this local thermochemical network. The specification of the subscript on the Δ is critical when reporting enthalpies of adsorbed species relative to non-standard anchors since, as shown later, the absolute values of the enthalpies vary widely with different anchor species. In this work, we reserve the name of formation enthalpies to its agreed upon definition by the chemistry community. Only enthalpies that are relative to the standard IUPAC anchors, either directly or indirectly, and, thus, are appended to the global thermochemical network are called enthalpies of formation.
Table 1 Definition of terms and variables. We drop the T for simplicity in the manuscript and only mention it if the temperature is relevant
| Symbol |
Definition |
|
E
i
|
Zero-point corrected electronic (DFT) energy of a species i, Ei = EDFT,i + EZPVE,i, where 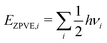 |
| ΔfHi(T) |
Enthalpy of formation of a species i at temperature T anchored to the global thermochemical network (here ATcT) |
| ΔAHi(T) |
Enthalpy of a species i at temperature T relative to the anchor species A in a local thermochemical network |
| ΔrHi,ads(T) |
Enthalpy of adsorption (or enthalpy of the adsorption reaction) of species i at temperature T |
| ΔrH(T) |
Reaction enthalpy of a stoichiometrically balanced reaction (gas-phase, surface, and adsorption reaction) calculated from enthalpies (of formation). This quantity is free of any anchor/reference species. |
| ΔrHQM |
Enthalpy of reaction j calculated only from DFT energies 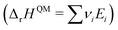 |
|
|

|
Stoichiometry vectors with stoichiometry coefficients νi of each species i in a reaction |

|
Stoichiometry matrix that encompasses a set of stoichiometry vectors (species × references) |
|
Elemental composition matrix of a set of species (species × elements) |

|
Fragment composition matrix of a set of species (species × fragments, e.g., bond types) |
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) f(T)
f(T) |
Vector of enthalpies of formation at temperature T |
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) A(T)
A(T) |
Vector of enthalpies relative to the defined anchor species A at temperature T |
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) Rf(T)
Rf(T) |
Vector of enthalpies of formation of the reference species R at temperature T |
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r(T)
r(T) |
Vector of reaction enthalpies at temperature T |
![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif)
|
Vector of zero-point corrected DFT energies |
![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) A or
A or ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) R R |
Vector of zero-point corrected DFT energies of the anchor species A or reference species |
|
|
| Anchor |
Anchor species are a special case of reference species because they form the foundation of a thermochemical network. The IUPAC standard states of each element are the anchor species for ATcT, NIST, and other global thermochemical networks, but anchor species can be arbitrarily defined for any local thermochemical network. The enthalpy of formation of an anchor species is always 0 because referencing it to itself creates a null reaction. |
| Reference |
A species that is used to determine the reference chemical potential. We assume that the enthalpy of formation of a reference species is known, e.g, from the ATcT (global thermochemical network). The enthalpy of formation of the reference species is relative to the energy of an anchor species or other reference species. |
4 Types of tasks in thermochemistry
The case study clarifies that diverse and often inconsistent datasets are prevalent in heterogeneous catalysis. Here, we seek to classify the various tasks that are often performed to make it more convenient to work with these quantities and correct or combine the values consistently. All tasks aim to construct a consistent thermochemical network that can be used to compute reaction energies that will be used as inputs to microkinetic models or other analyses. We broadly classify these into tasks of “comparison and conversion”, which involve only arbitrary modifications of data such that all relative quantities within a dataset remain unchanged, and approaches for “combining and correcting” energies, which involve changes to relative quantities within a dataset. The first class of tasks aims to create a local thermochemical network with anchors that do not correspond to the standard states, whereas the latter class of tasks integrates the data into a global thermochemical network with the standard anchors that facilitates combining data from multiple sources (gas-phase species, experimental data, etc.). The tasks for combining and correcting require decisions and compromises for selecting or combining inconsistent data. Different decisions and compromises may yield different reaction energies. It is further possible to divide the approaches into two categories. Most described methods use an atomic reference basis set, where a single reference/anchor species is selected for every element. The basis set terminology was first introduced by Mhadeshwar et al.126 for computational catalysis. Another approach has recently emerged that uses a molecular fragment reference basis set, where a reference species is defined for a particular feature of the target, e.g., bond type.
This work aims to provide a standardized way of considering the various compromises involved with each approach and provide researchers with convenient mathematical tools for implementing them. Fig. 4 summarizes the different approaches graphically. All methods are discussed assuming CxHyOz molecules and adsorbates, but it is straightforward to extend the methods to an arbitrary number of chemical elements (e.g., N or S) by adding additional reference species. Examples of all methods are provided in tutorial Jupyter Notebooks included in the ESI,† and in ref. 127.
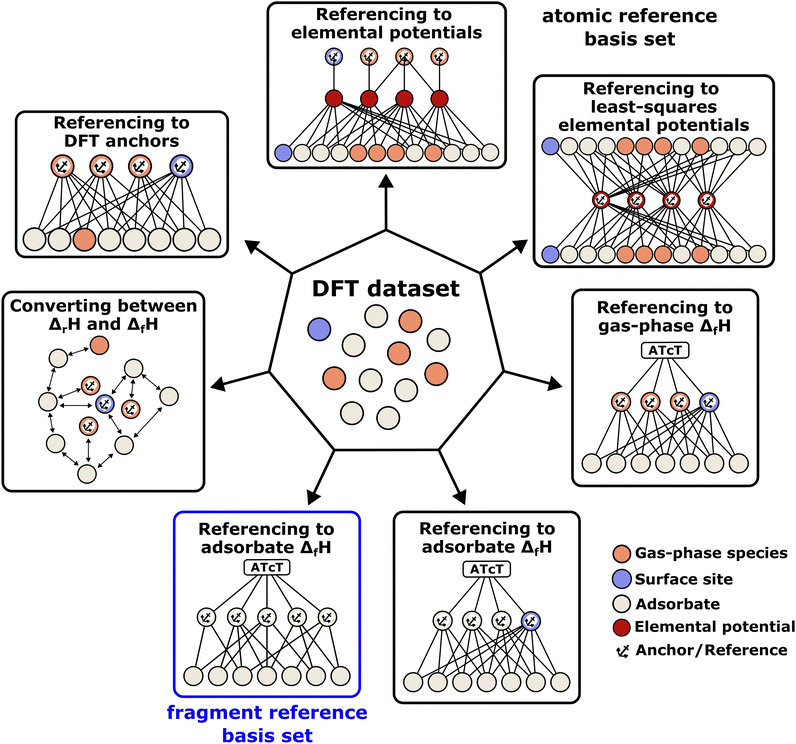 |
| | Fig. 4 Overview of the different methods to convert a DFT dataset to enthalpies of formation and construct a global or local thermochemical network. The methods can be grouped into atomic reference basis sets that conserve surface reaction energies from DFT and molecular fragment reference basis sets that exploit error cancellation. The methods can use only DFT energies, apply direct corrections to DFT energies, and consider experimental gas-phase species or adsorbate data. | |
4.1 Case study
We choose the oxidative dehydrogenation of ethane on Pt(111) using the mild oxidant CO2 as a case study to test the different approaches to compute the enthalpies (of formation) of the species in a reaction mechanism and to construct the thermochemical networks.
| C2H6 + CO2 ⇌ C2H4 + CO + H2O ΔrH(0 K) = 169.7 kJ mol−1 |
This reaction is of interest to convert the large amounts of C2H6 in shale gas to C2H4 while at the same time reducing the greenhouse gas CO2 to valuable CO. Pt and Pt-based alloys are promising catalysts for this reaction.128,129 The considered mechanism is based on the pathways discussed by Jalid et al.,130 and we only consider one possible path of the complex reaction mechanism.
| *CH2CH3 + 2* ⇌ *CH2*CH2 + *H |
We do not claim to provide new insights into this intricate reaction system, nor do we assume that the presented mechanism is complete. The case study serves purely as a demonstration purpose. Pt(111) was chosen as a model surface as it has a large amount of experimental data for ΔfH of adsorbates.96 The * indicates that the species is bound to the surface. If it is on the left-hand side of an atom, it indicates that the species is bound to the surface through this atom (e.g., *OH). If it is on the right-hand side, it indicates that the species is physisorbed (e.g., H2O*). The DFT data used in this study is published in ref. 131. DFT calculations were performed with Quantum Espresso using the BEEF-vdW xc functional132 on a (3 × 3) slab, which corresponds to a coverage of 1/9th monolayer. The reader is referred to ref. 131 for further details. Additionally, the RPBE133 xc functional was employed to provide context on how to compare different functionals. Energetic data for the relevant species is summarized in Table S1 (ESI†).
Some methods construct the thermochemical network using only the species that are part of this mechanism and derive a set of internally consistent ΔfH. However, in other methods, it is necessary to introduce a set of additional gas-phase or adsorbed species to determine ΔfH of the target species using hypothetical reactions and not the elementary reactions in the mechanism. These approaches connect the target to the existing global thermochemical network. In Table 2, we list all gas-phase species (either part of the mechanism or in a hypothetical reaction) and their ΔfH taken from the ATcT database (version 1.13076,77). We also assume that Pt(111) represents bulk Pt, which is why ΔfHPt(111) is always 0 kJ mol−1. Technically, assuming that Pt(111) is bulk Pt is not in agreement with the IUPAC standard states since there is an enthalpy of formation to form Pt(111) from bulk Pt (proportional to the surface energy of Pt(111)). However, assuming the active site as a reference is the standard procedure in determining adsorption enthalpies from experiments or theory.96 We note that in cases where multiple active sites are present, additional consideration is required to determine whether the difference in energies between active sites should be accounted for or not. Having multiple active sites with ΔfH of zero is not thermodynamically consistent but may be appropriate if the relative concentrations of active sites are known or if surfaces are not assumed to be in equilibrium. Consistent with standard practice in heterogeneous catalysis theory, we also ignore the impact of phonons on the adsorption enthalpies, as ways of calculating the interaction of adsorbates and phonons are just emerging.134
Table 2 Enthalpies of formation of the gas-phase species at 0 K from the Active Thermochemical Tables (ATcT), version 1.130.76,93 The vacant site * is Pt(111) in our case study
| Species |
ΔfH(0 K) (kJ mol−1) |
Uncertainty (kJ mol−1) |
Source |
| * |
0 |
Exact |
Assumption |
| H2 |
0 |
Exact |
ATcT |
| O2 |
0 |
Exact |
ATcT |
| CH4 |
−66.549 |
±0.044 |
ATcT |
| C2H6 |
−68.38 |
±0.12 |
ATcT |
| H2O |
−238.902 |
±0.022 |
ATcT |
| CO |
−113.8 |
±0.026 |
ATcT |
| CO2 |
−393.11 |
±0.015 |
ATcT |
| C2H4 |
60.89 |
±0.11 |
ATcT |
4.2 Tasks for comparison and conversion of datasets
DFT total energies are anchored to a consistent zero energy, typically related to the vacuum level energy. However, the specifics will depend on the DFT code used, the xc functional, the pseudopotentials, and numerical settings. Nonetheless, the enthalpy H(T, p) of a species (gas-phase or adsorbed) can be defined directly from a total DFT energy (EDFT) by including the zero-point vibrational energy (EZPVE) and a temperature correction δHfinitei(T, p), which is based on the partition functions of the species.| | | Hi(T, p) = EDFT,i + EZVPE,i + δHfinitei(T, p) | (14) |
| | 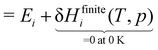 | (15) |
For simplicity, we assume throughout this work that DFT energies Ei have already been zero-point corrected, and we assume a temperature of 0 K so that the finite-temperature correction can be neglected. The quantity Hi(T, p) does not have a Δ as it is not an enthalpy of formation defined in a formation reaction; instead, it is defined based on the relative energies of the (valence) electrons. It is often more common in the catalysis literature to work with the Gibbs free energy G(T, p), which is similarly defined as:
| | 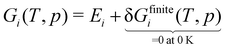 | (16) |
We reiterate that in this work, we are only evaluating the state variables at 0 K since the focus of this review is solely on species-interdependent enthalpic contributions to the Gibbs free energy (of formation). The temperature corrections δHfinitei(T) or δGfinitei(T) to evaluate Hi(T) or Gi(T) at a finite temperature T are derived from the partition functions of the adsorbates assuming a harmonic oscillator model or using more advanced methods that account for anharmonicity.116–118 However, at 0 K,
| | | Gi(0 K) = Hi(0 K) = Ei. | (17) |
The review focuses only on enthalpies and free energies of adsorbates in the low-coverage limit. Lateral adsorbate-adsorbate interactions are typically repulsive at higher coverages, leading to a destabilization of the adsorbates which affects their thermophysical properties.135 The enthalpy or free energy at a higher coverage can be determined by applying a correction factor to the low-coverage limit value, which is frequently derived from the change in the binding energy of the adsorbates with increasing coverage.72,136 All DFT energies from a consistent set of calculations create a local thermochemical network anchored to the same QM zero of energy. This local thermochemical network can be used to determine the relative quantities of interest for the researcher to evaluate the energetics of possible pathways of a mechanism.137–139 It can also be used to develop microkinetic models for complex reactions over intricate active site motifs. For example, Foppa et al.140 constructed a microkinetic model with this method for the dry reforming of methane over a Ni nanoparticle on a Al2O3 support.
However, using the DFT reference energy frame is inconvenient when comparing data from different sources, codes, and different levels of fidelity because the internal reference may change by tens or hundreds of eV depending on the code, pseudopotentials, or numerical settings selected. Therefore, converting the QM energies from the original internal electronic reference frame to an atomic reference basis set allows for easier data evaluation and comparison.
4.2.1 Referencing QM energies to elemental chemical potentials.
A straightforward method to create a local thermochemical network of consistent ΔAH from the computed DFT energies is provided by the framework of ab initio thermodynamics.94,95 In this framework, we formulate a reaction in which the target species is formed from the constituent elements to calculate ΔAH or the relative Gibbs free energy,
where P is a generic CxHyOz gas-phase species or a CxHyOz* adsorbate. We will start the derivations with the relative Gibbs free energy, which is more common in the ab initio thermodynamics literature. The Gibbs free energy Gi of a species is defined as:| | | Gi(T, p) = Gi(0 K, p) + δGfinitei(T, p) | (18) |
| | | Gi(T, p) = Ei + δGfinitei(T, p) | (19) |
When defining our atomic reference basis set A as the DFT energies of the elements in the reaction above, we can simply determine the Gibbs free energy ΔAG in this reference frame from the reaction free energy.
| | | ΔAG(T, p) = ΔrG(T, p) | (20) |
| |  | (21) |
The Gibbs free energy of the elements Gk is equal to the elemental chemical potential μk(T, p), which is more commonly used in the literature.
| | 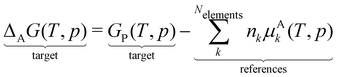 | (22) |
nk is the number of atoms of the element
k in species
i (identical to the stoichiometric coefficient in the reaction above). Since we focus only on a temperature of 0 K, we can use
eqn (17) to reduce
eqn (21) to
| | 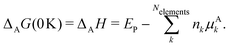 | (23) |
In this ab initio thermodynamics framework, ΔAH of the target is anchored to the chemical potentials of the elements μk, which we need to determine. Theoretically, it is possible to use the DFT energies of the elements as the chemical potentials. However, it is impractical to reliably determine the chemical potentials (or electronic energies) of the standard states of the elements with DFT. For example, the graphite formation energy is sensitive to vdW forces, which are not accurately accounted for in many functionals, and the O2 energy requires an accurate treatment of the triplet spin state of oxygen, which is difficult at the DFT level of theory and depends on the spin state. Total atomization energies offer a convenient alternative in principle, but in practice, they suffer from similar issues. Treatment of bare atoms in DFT is generally inaccurate due to unpaired electrons. Also, it requires careful convergence of spin states that can cause ambiguity in the results due to potentially large numerical errors. Calculating accurate atomization energies demands the highest level of theory and presents the most demanding calculations. To avoid these challenges, we can derive the chemical potentials of the elements via two different approaches: (i) by hand-picking closed-shell reference species that are supposedly more accurate and use them to calculate the chemical potentials in a sequential approach, or (ii) by formulating a linear algebra problem that can be solved via linear regression, avoiding explicitly defined reference species. The first approach is described in this section, and the second is described in Section 4.2.3.
In principle, the choice of reference species is arbitrary, but there are some constraints. Reference species have to be chosen so that there is a species for every element. For example, we can use A = [CH4, H2O, H2] as closed-shell anchor species to determine the chemical potentials. It is assumed that these reference species are available in thermodynamic reservoirs.94 These reservoirs are connected with the unit cell of the target molecule/adsorbate/structure, and the reference species can be drawn from the reservoirs or vanish in them without affecting the pressure or temperature of the target.95 The chemical potentials are then derived, assuming a thermoneutral reaction to form the element from the closed-shell reference species.
The chemical potential
μAC is then calculated from the DFT energies and other
μAk are derived similarly.
We have now abstracted the DFT energies of the chosen anchor species into the elemental chemical potential. We can also assume that the Pt(111) slab is one entity and define the chemical potential of this reference as the DFT energy of the surface site  . ΔAHP referenced to the anchors A = [CH4, H2O, H2, Pt(111)] is then defined as:
. ΔAHP referenced to the anchors A = [CH4, H2O, H2, Pt(111)] is then defined as:
| |  | (27) |
It immediately follows that ΔAHk = 0. The linear algebra notation of eqn (27) is,
| | 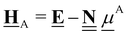 | (28) |
where

is the elemental composition matrix (number of molecules × number of elements) of the target species.
| |  | (29) |
A Jupyter notebook that applies this method with an extensive description is provided in the ESI,† with the same title as this section and also in PDF format on page 10 of the ESI.† The extension of this method to other heteroatoms (e.g. N or halogens) requires additional elemental anchors and the chemical potentials can be similarly derived from closed-shell gas-phase species as in eqn (24) (by using e.g. NH3). For a set of reference species to determine the chemical potentials, it is also possible to determine the chemical potentials by using the inverse of the elemental composition matrix of the anchors.
| | 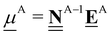 | (30) |
For simplicity, we integrated the entire slab directly into the elemental composition matrix, which is convenient when determining only ΔAH of adsorbate and gas-phase species. It is possible to parameterize a microkinetic model with the derived ΔAH from this method.141 However, the chemical potential of the slab can also be broken down into every atom, which is useful when investigating mixed transition metal, metal oxide, or metal carbide surfaces and supported metal catalysts.95,142–145 Explicitly defining the chemical potentials of all atoms is often used to derive surface free energies γ.95
| |  | (31) |
The surface free energies can be used to construct phase diagrams and compare the stability of materials for catalytic and electrocatalytic systems under specific reaction conditions.142–144,146–150 However, they may also be related to specific reaction conditions such as temperatures, environment, applied potentials, or pH. In the cases where the chemical potential is evaluated at different temperatures than 0 K, it is necessary to work with the Gibbs free energy of formation in eqn (21) and consider finite temperature and other corrections. An example is the computational hydrogen electrode (CHE), which also uses the concept of elemental chemical potentials.151–153 For electrocatalytic systems, an additional reference potential is required for the proton–electron pair, defined as the reversible hydrogen electrode (RHE).
| The proton–electron pair chemical potential is then defined via |
| | | μH+ + μe− = 0.5μH2 − eU | (32) |
| |  | (33) |
where
U is the applied potential and
e the elementary positive charge. The chemical potential of H
2,
μH2, is the sum of the electronic energy
EH2 and the finite free energy corrections

. With this definition of the chemical potential of the proton–electron pair, it is possible to evaluate,
e.g., the surface morphology or stability of alloys at different applied potentials.
It is important to note that the numerical values of the ΔAH will vary drastically depending on the choice of anchor species used to derive the chemical potentials of the elements. Consequently, directly combining energetic data with different anchors is erroneous. To illustrate this variation, we chose three different sets of anchors corresponding to closed-shell molecules to determine the chemical potentials, which are A = [CH4, H2O, H2, Pt(111)], B = [CO, H2O, H2, Pt(111)], and C = [C2H6, CO, H2, Pt(111)].
Fig. 5 shows the calculated enthalpy profiles using the different anchor species for the oxidative C2H6 dehydrogenation. Indeed, it can be seen that ΔAH for the species are very different as seen by the offsets between the profiles on the y-axis. Thus, a naive comparison of energies from ΔAH and ΔBH would result in a large discrepancy. However, the relative enthalpy differences between the adsorbates, i.e. the reaction enthalpies, which are ultimately the quantity that matters in microkinetic models, are identical. This is easily seen by setting the starting point in the enthalpy diagram to 0, which results in the collapse of the three different profiles. Thus, the reaction enthalpies predicted from DFT are always conserved, leading to identical predictions of a microkinetic model, regardless of the reference/anchor basis set.
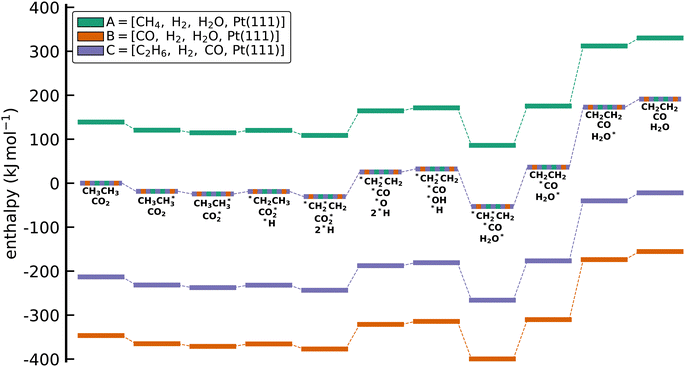 |
| | Fig. 5 Enthalpy diagram for the approach to reference the DFT energies to a set of anchor species through elemental chemical potentials. While the absolute values of the formation enthalpies depend on the set of anchor species, the reaction enthalpies for all elementary steps are conserved. This conservation can be seen when all lines are collapsed (multicolored line). No activation barriers are included in this diagram. | |
For pedagogical purposes, we show explicitly that the reaction enthalpies are independent of the chosen references for any atomic reference basis set, i.e. when there is a single chemical potential for each chemical element. A relative reaction enthalpy can be calculated using ΔAH derived from the chemical potentials, which is written as:
| |  | (34) |
| | 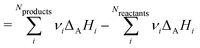 | (35) |
| |  | (36) |
| |  | (37) |
| | 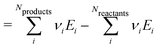 | (38) |
Therefore, for every stoichiometrically balanced reaction, it is evident that
k∈products and
k∈reactants will be equivalent and
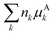
will cancel, making the choice of
μAk arbitrary. This invariance proves that as long as a dataset is anchored to the same set of atomic reference species, it is internally consistent and the relative quantities required for microkinetic models will be identical regardless of the anchors selected. The following techniques for comparison and conversion of enthalpies of formation exploit this invariance, selecting “convenient”
μAk that allow for comparison of energies under different thermodynamic scenarios or between different levels of theory and for conversion of energies between relative and absolute reference states.
4.2.2 Referencing QM data to a set of anchor species.
In the previous approach, we created a local thermochemical network where ΔAH are referenced to the elemental chemical potentials derived from a set of anchor species A. Here, we show that it is possible to cut the “middleman” of elemental potentials and use the anchor species directly to compute ΔAH (see page 18 of the ESI†). As demonstrated above, the choice of reference species is in principle arbitrary, but there are some constraints that must be followed. One reference species must be chosen for every element to form an atomic basis set. As we will see in this section, the stoichiometry of anchor species must also not be linearly dependent. Common choices for the sets of reference species in computational catalysis are typically gas-phase molecules like CO, H2, H2O154,155 or, CH4, H2, H2O.156,157 A vacant metal slab, e.g., Pt(111), has to be added for adsorbed species. The construction of local thermochemical networks is frequently used in the literature, although anchor species often vary between studies and are not always explicitly stated. Referencing a single target species directly to a set of anchor species works as follows: we construct a hypothetical reaction to form the target (either gas-phase species or adsorbate) from the set of anchor species, i.e., CH4, H2O, H2, and Pt(111).
Additional anchor species are required for other heteroatoms, e.g. NH3 for N. When using the DFT values of the reference species as the anchor, it follows that ΔAH of the target referenced to this set of anchor species is equal to the reaction enthalpy of the reaction above.
| | 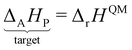 | (39) |
We can compute this reaction enthalpy from the electronic energies.
| | 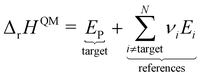 | (40) |
To determine ΔAHP, we can now substitute ΔrH in eqn (39) with eqn (40).
| | 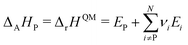 | (41) |
The subscript A is the set of anchor species, in this case, A = [CH4, H2O, H2, Pt(111)]. ΔAH of our chosen anchor species are 0 because it is a null reaction to form the anchor species from themselves. Eqn (41) converts the zero-point corrected DFT energy of a single species into ΔAH referenced to the set of anchor species, A. This problem can also be cast as a linear algebra problem for a set of species, typically the entire reaction mechanism. The linear algebra notation using the definitions in Table 1 is as follows:
| | 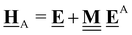 | (42) |
where
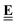
is the vector of the zero-point corrected DFT energies,
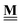
is an
m ×
n stoichiometry matrix with
m anchor species and
n reactions to form the target from the anchors (not to be confused with the elementary reactions in the mechanism), and
![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) A
A is the vector of the DFT energies of the anchor species. The stoichiometry matrix
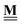
can be constructed by hand, but it is also possible to use linear algebra to determine this from the elemental composition matrix

.

an
m ×
n matrix, but consists of the elemental composition of each species and is, thus, easier to construct and more general since it is independent of the anchor set. We have to construct an elemental matrix for the anchor species

to determine
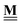
.
| |  | (43) |
To convert between the elemental composition matrix  of the species to the stoichiometry matrix
of the species to the stoichiometry matrix  that forms the species from the anchor basis set, we can use the inverse of the elemental matrix of the reference species
that forms the species from the anchor basis set, we can use the inverse of the elemental matrix of the reference species 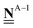 .
.
| |  | (44) |
Note that this places an explicit constraint on any possible anchor set: the composition matrix  must be invertible. This method of referencing DFT energies to a set of anchor species with their DFT values is commonly used. It is suitable for investigating a catalyst for a specific process,158–160 it can be used to screen across the material space,154,161–164 coverage effects on the thermophysical parameters can be included,155 it has been combined with uncertainty quantification,70,165 and it has also been applied to investigate electrocatalytic systems.166 Since the method is identical to the elemental chemical potentials, it is also possible to directly combine it with the CHE model to calculate free energies at applied potentials.167 This method is also the default for calculating ΔAH in the open-source CatMap168 software package, although the notation and nomenclature used in the CatMap package and manuscript are different from the more consistent ones used in this work.
must be invertible. This method of referencing DFT energies to a set of anchor species with their DFT values is commonly used. It is suitable for investigating a catalyst for a specific process,158–160 it can be used to screen across the material space,154,161–164 coverage effects on the thermophysical parameters can be included,155 it has been combined with uncertainty quantification,70,165 and it has also been applied to investigate electrocatalytic systems.166 Since the method is identical to the elemental chemical potentials, it is also possible to directly combine it with the CHE model to calculate free energies at applied potentials.167 This method is also the default for calculating ΔAH in the open-source CatMap168 software package, although the notation and nomenclature used in the CatMap package and manuscript are different from the more consistent ones used in this work.
4.2.3 Referencing QM data to least-squares elemental chemical potentials.
For a typical DFT dataset, there is a myriad of possible anchor species to calculate the chemical potentials. For example, we can calculate μO with different reference anchors, A = [H2O, H2] and B = [CO, CO2] through| | μAO = EH2O − EH2 = −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 kJ mol−1 799 kJ mol−1 | (45) |
| | μBO = ECO2 − ECO = −55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 kJ mol−1 878 kJ mol−1 | (46) |
Clearly, different anchor species will lead to different values of the chemical potentials for the elements, which in turn affects the relative enthalpies as shown in Fig. 5. However, as demonstrated by eqn (34), the reaction enthalpies of any stoichiometrically balanced reaction will be conserved in an atomic reference basis set. Instead of manually selecting the anchor species to determine the chemical potentials of the elements in a sequential approach, it is possible to exploit the invariance and select convenient numerical values for the chemical potentials. In particular, it is often convenient to select chemical potentials that minimize the (sum of squared) errors between relative enthalpies computed using different codes, levels of fidelity, or reference sets. As we will show, this can be achieved using linear algebra and least-squares regression and avoids the need to specify any explicit chemical species as anchors.
To calculate the least-squares anchor elemental potentials, we take the elemental composition matrix  that contains all the formation reactions of the target species from the constituent elements to derive the chemical potentials. Rather than selecting a set of explicit anchor species with defined stoichiometries, we seek the set of chemical potentials that minimizes the squared magnitude of the resulting relative enthalpies. The linear algebra formulation offers a convenient way to perform the minimization of squared relative enthalpies magnitudes, which is closely related to the least-squares regression problem and is given in eqn (47).
that contains all the formation reactions of the target species from the constituent elements to derive the chemical potentials. Rather than selecting a set of explicit anchor species with defined stoichiometries, we seek the set of chemical potentials that minimizes the squared magnitude of the resulting relative enthalpies. The linear algebra formulation offers a convenient way to perform the minimization of squared relative enthalpies magnitudes, which is closely related to the least-squares regression problem and is given in eqn (47).
| | 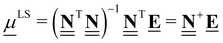 | (47) |
The least-squares regression result can also be written as the product of the pseudo-inverse of the elemental composition matrix  and the energy vector
and the energy vector ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) . Calculation of ΔLSH is then performed by replacing the chemical potentials in eqn (47) with the expression in eqn (28), leading to
. Calculation of ΔLSH is then performed by replacing the chemical potentials in eqn (47) with the expression in eqn (28), leading to
| | 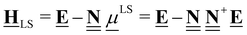 | (48) |
where we use the LS symbol to denote a “least-squares” anchor set that does not explicitly depend on specific molecular anchor species, but rather implicitly depends on the entire set of target species included (
i.e. the species in the rows of

). The Python implementation of this method can be found on page 26 of the ESI.
†
The least-squares anchor set is particularly advantageous for comparing energies from different sources or approximations. When using specific molecular species as anchors A, any error associated with the species will propagate through ΔAH of the entire dataset. To illustrate this, Fig. 6a compares the relative enthalpies of species in the oxidative dehydrogenation of ethane for two different xc functionals, RPBE and BEEF-vdW. Relative enthalpies are computed using the elemental chemical potential approach with two different reference anchor sets and the least-squares anchor. Using the molecular anchors, the deviation between the two functionals varies widely depending on the choice of anchor species. Naive comparisons could lead to very different conclusions about the relative performance of these two xc functionals. On the other hand, using the entire reaction mechanism to determine the anchor chemical potentials by minimizing the sum of squared errors removes the arbitrary dependence on the choice of anchor species. When using these fitted chemical potentials, the scatter and, accordingly, the deviation between the xc functionals are significantly smaller. This behavior is also displayed in Fig. 6b, where ΔLSH derived from the RPBE and BEEF-vdW functional give similar results with only small deviations. Determining the chemical potentials via linear regression does not make the DFT energetics more accurate; all reaction energies will be unaffected, as shown in eqn (34). However, it makes the energetic data from different xc functionals more comparable, as seen in Fig. 6b.
 |
| | Fig. 6 (a) Comparison of the difference between the enthalpies of formation from the BEEF-vdW and RPBE functional using different sets of references to determine the elemental chemical potentials: least-squares regression, CH4/H2/H2O, and C2H6/H2/CO. The mean absolute deviation (MAD) is reported in the legend. (b) Aligning the two DFT datasets for the test case with different xc-functionals using linear regression to determine the elemental chemical potentials. | |
Using the least-squares chemical potentials as an anchor is similar to determining atomization energy corrections (AEC) often employed in the gas-phase community.169 Known experimental atomization energies for species are used to determine the correction factors for the DFT energies. In a more generic way, this can be formulated as determining corrections to a set of energies to align them with known energies of higher fidelity. In the case of two DFT datasets obtained from two different functionals, we can either compare the relative enthalpies or determine atomic correction factors to align the energies of, e.g., the RPBE functional with the BEEF energy values. In fact, it can be shown that the least-squares anchor is also the anchor set that minimizes the sum of squared deviation between two different datasets obtained from different sources. Thus, the minimum sum of squares chemical potentials can also be used directly to align data from different sources, e.g., from different functionals such as BEEF-vdW and RPBE or different levels of theory.
| |  | (49) |
where
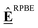
are the aligned energies of the RPBE functional to the BEEF-vdW functional.
Eqn (49) allows to align the data from various sources to the same QM zero-of-energy, which is useful in data science and machine learning for providing an unbiased error between different levels of theory.
98,170 The method is mathematically similar to the Δ-ML approach, where the thermochemical quantity from one level of theory can be mapped onto another level of theory.
171 Here, we present how to do this using least-squares regression to determine elemental chemical potentials. However, the least-squares regression can be replaced with a machine learning model to regress other structural features using
e.g. a LASSO (least absolute shrinkage and selection operator) optimization.
172,173 The downside of this approach is that the anchor chemical potentials will depend implicitly on all the species present in the dataset and technically need to be re-computed any time the network is expanded, similar to the ATcT.
77
4.3 Approaches for correcting and combining datasets in atomic reference basis sets
The approaches presented above are convenient for converting energies into various frameworks such as ab initio thermodynamics and assist in comparing different energy sets while ensuring that all relative quantities for any reaction are conserved. Thus, using these approaches, all microkinetic models will be identical regardless of the choice of anchor species. However, the resulting reaction enthalpies may not be consistent with accurately known enthalpies of the overall gas-phase reaction from global thermochemical networks, such as the ATcT. For example, a reaction enthalpy of 191.2 kJ mol−1 is calculated for C2H6 dehydrogenation with CO2 at 0 K using BEEF-vdW. This reaction enthalpy is identical for all previously described approaches. However, this value is in stark disagreement with the known reaction enthalpy of 169.7 kJ mol−1 determined from the accurate ΔfH of the ATcT database. The difference results in an equilibrium constant K for the ODH reaction that is off by a factor of ∼20 for a typical reaction temperature of 873 K as shown in Fig. 7. Therefore, the methods for comparison and conversion do not lead to microkinetic models that are thermodynamically consistent with the known ΔfH of gas-phase species. The methods described above are commonly used techniques for manipulating DFT energies in computational catalysis, and lay the foundation for subsequent approaches that enable datasets that are more consistent with known thermochemical information.
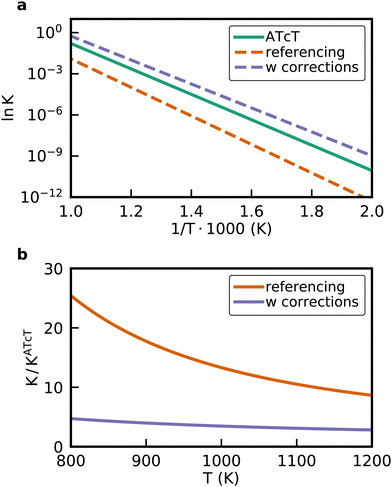 |
| | Fig. 7 (a) van't Hoff diagram of the equilibrium constant K derived from the enthalpies of reaction calculated from the ATcT database, the referencing approach, and the referencing approach with corrections. We assumed the same reaction entropy for all different cases. (b) Ratio of the equilibrium constants from the computational chemistry methods compared to the exact equilibrium constant derived from the ATcT. Note that the inverse ratio of the referencing approach is shown. | |
The error in the gas-phase reaction energies is typically caused by the inaccuracy of common GGA xc functionals, which are on the order of 30 to 50 kJ mol−1.68 When computing the reaction enthalpy of surface reactions from DFT energies, it is often assumed that error cancellation improves the accuracy.70 However, the degree of error cancellation can vary widely, depending on the specific reaction.131 Thus, we hope for error cancellation for surface reaction energies, but it is not guaranteed that surface reaction energies are accurate.94 Additionally, DFT calculations perform poorly for gas-phase species due to the approximate treatment of electron exchange and correlation.174 The most commonly used xc functionals in heterogeneous catalysis, such as BEEF-vdW and RPBE, are semi-empirical. They are specifically selected to predict experimental adsorption enthalpies, which reduces accuracy for gas-phase reaction energies.132
Combining thermochemical data from various sources (typically of very different fidelity) is necessary to achieve better agreement with experimental gas-phase reaction enthalpies or more accurate ΔfH of the adsorbates. This combination of data leads to changes in relative quantities in the thermochemical network that either implicitly or explicitly “correct” reaction enthalpies to be more consistent with higher-fidelity data. Schemes are available that apply these corrections to a few species, many species, or sometimes all species in the thermochemical network. Here, we classify approaches as “direct” correction schemes, where individual DFT energies are explicitly corrected, and “indirect” correction schemes, where corrections are made implicitly through error cancellation reactions. The direct methods tend to be simpler because they apply fewer corrections and can be understood intuitively, but they typically do not exactly reproduce all known quantities. In contrast, indirect methods are generally capable of reproducing known quantities exactly, but they do so at the expense of greater complexity and less transparency.
4.3.1 Corrections to the DFT energies of gas-phase species.
It is possible to improve the accuracy of the overall reaction enthalpy by adjusting the DFT energies of individual gas-phase species. Correction factors include atomic energy corrections (AEC), bond additivity corrections (BAC), or corrections to fragments or specific molecules.169,175 AECs and BACs are standard correction methods in the gas-phase community but are less frequently used in catalysis. In computational catalysis, correction factors have mainly been applied to specific molecules.
The most prominent introduction of molecular corrections in heterogeneous catalysis is the correction of the O2 molecule, first introduced by Nørskov et al. to explain the origin of the overpotential for oxygen reduction.151 They recognized that the high-spin ground state of O2 is poorly described with DFT, leading to large errors of ∼70 kJ mol−1 in the water splitting/formation reaction. To avoid this issue, they used the experimental reaction energy for water formation 1/2O2 + H2 → H2O (equal to ΔfHH2O) to avoid calculating O2 with DFT, leading to the widely used “O2 correction” that ensures the correct enthalpy of the water formation reaction.151,176–178
| | 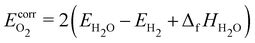 | (50) |
where Δ
fHH2O = −238.9 kJ mol
−1 (ATcT
76). Another widely used correction to DFT energies of gas-phase species for catalytic systems was proposed by Peterson
et al.152 for the electrochemical reduction of CO
2 on Cu(211). The authors applied a statistical sensitivity analysis to identify correction factors that align the reaction enthalpies from DFT with the experimental values. To determine these correction factors, they compared the DFT-derived reaction enthalpies of 21 hand-picked gas-phase reactions involving CO
2, CO, H
2, and H
2O with experimental values from the NIST database. Perturbing the energy of CO
2 and all species with an OCO backbone by 43.4 kJ mol
−1 for the RPBE functional led to a minimum deviation between the experimental and DFT values. However, the agreement with all test reactions is not exact, and a discrepancy of ≈6 kJ mol
−1 remained. In the same study, very different correction factors were necessary when using the PBE functional, highlighting the functional dependence of these corrections. In a follow-up study, Studt
et al.179 repeated the same analysis using the BEEF-vdW functional in GPAW, and they obtained the closest agreement when perturbing the CO
2 as well as the H
2 energy by 31.8 kJ mol
−1 and 8.7 kJ mol
−1. In a different study by Studt
et al.,
180 a slightly different correction value for CO
2 of 39.6 kJ mol
−1 was obtained using QuantumEspresso while the H
2 correction remained 8.7 kJ mol
−1. This discrepancy in correction factors highlights the slight differences between different electronic structure codes and numerical settings, making it challenging to generalize correction factors. Following these pioneering studies, a range of corrections for the gas-phase energies were proposed in the literature for nitrogen-containing species,
61,176 O
2,
181 CO, CO
2 and other species depending on the xc-functional.
78,182–184 Urrego-Ortiz
et al.185 reviewed the gas-phase errors and corrections of DFT calculations for computational catalysis.
Fig. 8 shows the enthalpy diagram with the applied corrections to CO2 and H2 of 31.8 kJ mol−1 and 8.7 kJ mol−1 for the BEEF-vdW functional,179 respectively. The derivation of the ΔAH follows the equations described in Section 4.2.2, with corrections added to the DFT gas-phase energies of CO2 and H2O. Notably, the reaction enthalpies will be the same regardless of whether corrections are added before or after anchoring the thermochemical network; however, if corrected species are used as anchors, then the correction will be distributed throughout the network, and the individual ΔAH will depend on whether the correction was applied before or after anchoring. Thus, it is recommended that corrected species should not be used as anchors to avoid ambiguity about which species have been “corrected”. Using these standard corrections, the overall reaction enthalpy with the gas-phase corrections is 159.4 kJ mol−1, which still deviates from the experimental value by 10 kJ mol−1. This error leads to an equilibrium constant that deviates by a factor of ∼4 from the exact value (see Fig. 7b). Compared to the “non-corrected” free energy diagram constructed directly from DFT energies, the only change is for the adsorption enthalpy of CO2, which is increased by 31.8 kJ mol−1, making CO2* more stable. Since H2 desorption does not appear in this reaction mechanism, the H2 correction cancels out, and all other DFT reaction enthalpies are conserved. In general, the approach changes only the reaction energies for the adsorption/desorption steps where corrected molecules are involved.
 |
| | Fig. 8 Enthalpy diagram with the relative enthalpies derived from the corrected DFT energies of CO2 (+31.8 kJ mol−1) and H2 (+8.7 kJ mol−1) using referencing approach compared with the ΔAH from the uncorrected DFT energies. The enthalpy diagrams are aligned to C2H6* + CO2* to demonstrate that the adsorption enthalpy of CO2 was corrected. | |
Instead of applying corrections to specific molecules, it is possible to determine correction factors for bond types. The OCO correction of Peterson et al.152 is a simple example, but more sophisticated approaches are possible. The usage of bond-additivity corrections to improve the accuracy of low level of theory methods is a well-established procedure in the gas-phase community.175,186 Bond-additivity corrections are increasingly used in catalysis. Christensen et al.187 identified that the error is not associated with the OCO backbone but rather with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. They obtained a slightly better agreement with the experimental reaction enthalpies when applying corrections of 9.7 kJ mol−1 to H2 and 14.5 kJ mol−1 for the C
O bond. They obtained a slightly better agreement with the experimental reaction enthalpies when applying corrections of 9.7 kJ mol−1 to H2 and 14.5 kJ mol−1 for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Additional bond-additivity correction factors were obtained for a range of functionals by Granda-Marulanda et al.78 for CO2, CO, –CHx, –OH, C
O bond. Additional bond-additivity correction factors were obtained for a range of functionals by Granda-Marulanda et al.78 for CO2, CO, –CHx, –OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and (C
O, and (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O. These fragments were hand-picked by experts, which requires chemical intuition and experience. Alternatively, it is possible to use machine-learning techniques like LASSO regression to determine the subgraphs that lead to the best results.173,188 Bond-additivity correction factors for N-containing molecules were determined by Urrego-Ortiz et al.189 using an automated procedure. It has also been shown that the correction factors are correlated across the DFT xc functionals.61,78,185,187,190,191 For example, Urrego-Ortiz et al.190 demonstrated that the correction factor for H2O2 and O2 exhibits a linear correlation for a range of xc functionals. Christensen et al.187,191 observed a linear relation of gas-phase reaction enthalpies when evaluating the ensemble of energies spanned by the BEEF-vdW functional. These correlations suggest that it is possible to construct correction factors that reduce dependence on the chosen xc functional,191 although such schemes will increase the complexity of the bond correction approach. Overall, these correction schemes provide chemically intuitive ways to understand the corrections, and in the simplest cases are very straightforward to apply. The usage of tabulated correction factors in the literature for specific molecules or bond-types can significantly improve the agreement of the overall gas-phase thermodynamics with the accurate thermodynamic data from the global thermochemical network. However, to achieve the best or even exact agreement, it is necessary to determine the correction factors in every self-consistent DFT study.
O)O. These fragments were hand-picked by experts, which requires chemical intuition and experience. Alternatively, it is possible to use machine-learning techniques like LASSO regression to determine the subgraphs that lead to the best results.173,188 Bond-additivity correction factors for N-containing molecules were determined by Urrego-Ortiz et al.189 using an automated procedure. It has also been shown that the correction factors are correlated across the DFT xc functionals.61,78,185,187,190,191 For example, Urrego-Ortiz et al.190 demonstrated that the correction factor for H2O2 and O2 exhibits a linear correlation for a range of xc functionals. Christensen et al.187,191 observed a linear relation of gas-phase reaction enthalpies when evaluating the ensemble of energies spanned by the BEEF-vdW functional. These correlations suggest that it is possible to construct correction factors that reduce dependence on the chosen xc functional,191 although such schemes will increase the complexity of the bond correction approach. Overall, these correction schemes provide chemically intuitive ways to understand the corrections, and in the simplest cases are very straightforward to apply. The usage of tabulated correction factors in the literature for specific molecules or bond-types can significantly improve the agreement of the overall gas-phase thermodynamics with the accurate thermodynamic data from the global thermochemical network. However, to achieve the best or even exact agreement, it is necessary to determine the correction factors in every self-consistent DFT study.
4.3.2 Deriving enthalpies of formation of adsorbates using gas-phase reference species.
It is possible to combine the ΔfH of the adsorbates with the known global thermochemical network of gas-phase reactions to achieve reaction enthalpies of gas-phase reactions that are in exact agreement with the known ΔfH from the ATcT. The approach to reference the DFT energies to the ATcT is similar to the approach described in Section 4.2.2 (see ESI,† page 36). Assuming an atomic reference basis set with CH4, H2O, H2, and Pt(111), we can again create a reaction to form the target from the references.
| νCH4CH4 + νH2OH2O + νH2H2 + ν** → P |
In Section 4.2.2, we assumed that these species are our anchors from which all other species are formed. Using the DFT energies of these species as the anchor values, it followed that the ΔAH of CH4, H2O, H2, and Pt(111) in the anchor frame A are 0 because it is a null reaction. In the global thermochemical network, ΔfH of these species are referenced to the IUPAC anchor species in their standard state. Thus, ΔfH of the reference species have known values as listed in Table 2. To utilize the tabulated ΔfH of the gas-phase species from the global network, we have to reference the DFT data to the IUPAC anchors, which we do through our chosen reference species in the atomic basis set, shown in the thermochemical cycle in Fig. 9.
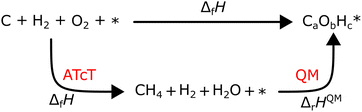 |
| | Fig. 9 Thermodynamic cycle to determine the ΔfH of the species connected to the global thermochemical network. | |
From the thermochemical cycle, it can be easily seen that ΔfHP in the IUPAC anchor frame is the sum of the ΔfH of the reference species and the reaction enthalpy to form the target from the references.
| |  | (51) |
| |  | (52) |
We can also formulate this in a linear algebra notation leading to the following equation:
| | 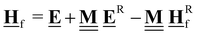 | (53) |
| | 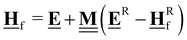 | (54) |
Including the slab into the matrix of stoichiometric coefficients leads to an equation that is similar to eqn (42), with an additional term  , which references enthalpies of formation to the ATcT thermochemical network. As shown previously in Section 4.2.2,
, which references enthalpies of formation to the ATcT thermochemical network. As shown previously in Section 4.2.2,  can conveniently be determined from
can conveniently be determined from  and
and  viaeqn (44). An alternative derivation of this approach was developed by Blöndal et al.,192 which relies on an adsorption reaction of the target species.
viaeqn (44). An alternative derivation of this approach was developed by Blöndal et al.,192 which relies on an adsorption reaction of the target species.
where the adsorption enthalpy is derived from the DFT energies and Δ
fH* = 0 kJ mol
−1 by assertion as discussed in Section 4.1. Thus, the only unknown to solve is Δ
fH of the gas-phase precursor of the adsorbate. Many gas-phase precursors are unstable and, therefore, not tabulated in the ATcT. An
isogyric reaction
91,193 to form the species from CH
4, H
2O, and H
2 is used to estimate Δ
fH of the precursor, which is similar to the ANL0 approach.
91 Δ
fH of the gas-phase precursor also provides the reference to an existing thermochemical network as illustrated in
Fig. 10. We derive the approach in detail in the Section 3 of the ESI
† and show how it is mathematically equivalent to
eqn (54).
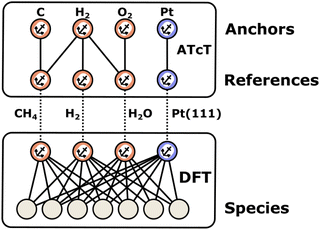 |
| | Fig. 10 Schematic illustration of referencing the DFT data to the global thermochemical network (here ATcT) using gas-phase reference species. | |
The method depends on the DFT energies of the reference species, in this case CH4, H2O, and H2. The approach is typically used with this reference species set since it is equivalent to an isogyric reaction.91,193 However, other reference sets could be selected, in which case the final ΔfH of the resulting reaction network and the resulting adsorption enthalpies will vary slightly depending on the selected reference species. For example, it is possible to use the least-squares anchor set introduced in Section 4.2.3 to combine data from two thermochemical networks without explicitly selecting molecular references. In this case, all adsorption/desorption energies would be corrected by some amount, but on average, the squared difference between the DFT-derived and ATcT enthalpies of formation would be minimized.
Referencing the DFT energies to the existing ATcT database through the reference species allows us to integrate the available accurate ΔfH of gas-phase species, which always ensures thermodynamically consistent mechanism. By using the highly accurate ΔfH of the gas-phase species from the ATcT instead of the DFT values, we implicitly correct all DFT-derived adsorption/desorption reaction energies except for those of the reference species (see Fig. 11). The adsorption enthalpies of the references match the DFT energies (see ESI†). All reaction enthalpies of the surface reactions from DFT are still conserved and identical to those of the referencing approach. This method also reduces the computational workload, as it is no longer necessary to compute the energies of gas-phase species other than the references.
 |
| | Fig. 11 Enthalpy diagram with the enthalpies of formation derived with the standard referencing approach, using the gas-phase ΔfH as references, and using experimental enthalpies of formation of adsorbates as reference. The enthalpy diagrams are aligned to C2H6* + CO2* to demonstrate the changes in the adsorption enthalpies, while all surface reaction enthalpies are conserved. | |
This approach has been widely employed by Vlachos and co-workers194–197 to convert DFT energies to ΔfH referenced to the global thermochemical network. Vorotnikov et al.194 used the method to construct a database of adsorbates for furan chemistry on Pd(111). Further, they used eqn (52) to determine the ΔfH of all gas-phase species (that are not the references) with the G4 level of theory rather than using ATcT values. This application illustrates an alternative use of the approach where gas-phase species and adsorbates are computed with different levels of theory but can be combined in a single thermochemical network since both are referenced to the same global network. Integrating the accurate ΔfH of gas-phase species and the ΔfH of adsorbates derived from DFT in a global thermochemical network is crucial when building coupled homogeneous/heterogeneous reaction mechanisms192 or for open-ended mechanism exploration with automated mechanism generation software.69,71,136,198,199 Some of the authors have used the method for the microkinetic modeling of the transient CO2 methanation on Ni(111)72 or the temperature-programmed desorption of CO2.200
It is also possible to derive elemental chemical potentials from this approach that are conveniently referenced to the global thermochemical network. Using the actual ΔfH of the reference species basically results in the correction of the DFT-derived elemental chemical potentials to match the experimental ΔfH of the reference species via
| | | μC = (ECH4 − 2EH2) + (ΔfHCH4 − 2ΔfHH2) | (55) |
| | | μO = (EH2O + EH2) + (ΔfHH2O − ΔfHH2) | (56) |
| | | μH = 0.5EH2 + 0.5ΔfHH2 | (57) |
| | | μ* = EPt(111) + ΔfHPt(111) | (58) |
With these corrected elemental chemical potentials, the method described in Section 4.2.1 can be used to derive Δ
fH of the adsorbates, which can be combined with accurate Δ
fH of gas-phase species from the ATcT to achieve thermodynamic consistency.
4.3.3 Deriving enthalpies of formation of adsorbate connected to the global thermochemical network through adsorbates.
Blaylock et al.201,202 developed a similar approach, where they also used an expression similar to eqn (54). Instead of gas-phase reference species, they used adsorbates as reference species for the atomic reference basis set. They determined ΔfH of *H, *O, and *CO on Ni(111) from experimentally measured adsorption enthalpies.203–205 In combination with the known ΔfH of the gas-phase precursors (H2, O2, CO) from a global thermochemical network like ATcT, we can derive ΔfH of the reference adsorbates using the thermochemical cycle in Fig. 2. ΔfH of the adsorbed reference species are referenced to the global thermochemical network, and all other adsorbates are then referenced to these reference species according to| | | ν*H*H + ν*O*O + ν*CO*CO + ν** → P* | (59) |
which is illustrated in the thermochemical cycle in Fig. 12.
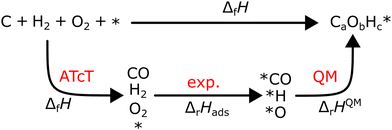 |
| | Fig. 12 Thermodynamic cycle for the connection of the DFT energies to the global thermochemical network via experimentally determined enthalpies of adsorption for a reference basis set. | |
The method to determine ΔfHP* is straightforward and similar to the method in Section 4.3.2 and can be found in the ESI,† on page 45. ΔfHP* is calculated from the reaction enthalpy to form the target from the references from DFT and the sum of the ΔfH of the references.
| | 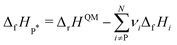 | (60) |
| | 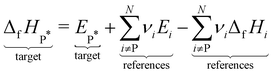 | (61) |
In linear algebra form this reads as
| | 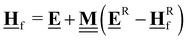 | (62) |
This is mathematically identical to the prior approach (eqn (54)), with the difference being that the enthalpies of adsorbed species, rather than gas-phase species, are used as references. For the construction of the stoichiometry matrix  , we refer the reader to Section 4.2.2. Since the approach connects the DFT data with the ATcT, it is possible to replace all DFT energies of gas-phase species with accurate ΔfH form the ATcT to achieve thermodynamic consistency. The resulting enthalpy diagram using this approach is shown in Fig. 12. Similar to the previous method, this approach does not affect the reaction enthalpies of surface steps since it uses an atomic reference basis set. However, all adsorption/desorption reaction enthalpies are changed except for the reference species. In the previous approach, the adsorption enthalpies of CH4, H2, and H2O were fixed at the DFT values. The difference in this approach is that the adsorption enthalpies of CO, H2, and O2 correspond now to experimental values (see Fig. 13). This adjustment leads to noticeable changes in the adsorption enthalpies of some species. The biggest change occurs for the adsorption of CO2, which changes from strongly exothermic to mildly endothermic. Typically, CO2 binds only weakly through physisorption on the Pt(111) surface.206 Using gas-phase reference ΔfH indicates that the CO2 binds strongly to the surface in disagreement with experiments. Mhadeshwar et al.126 also describe the use of the experimental ΔfH of adsorbates as a basis set to reference the DFT energies to the global thermochemical network, thereby ensuring thermodynamic consistency of the reaction mechanism with known adsorption enthalpies.
, we refer the reader to Section 4.2.2. Since the approach connects the DFT data with the ATcT, it is possible to replace all DFT energies of gas-phase species with accurate ΔfH form the ATcT to achieve thermodynamic consistency. The resulting enthalpy diagram using this approach is shown in Fig. 12. Similar to the previous method, this approach does not affect the reaction enthalpies of surface steps since it uses an atomic reference basis set. However, all adsorption/desorption reaction enthalpies are changed except for the reference species. In the previous approach, the adsorption enthalpies of CH4, H2, and H2O were fixed at the DFT values. The difference in this approach is that the adsorption enthalpies of CO, H2, and O2 correspond now to experimental values (see Fig. 13). This adjustment leads to noticeable changes in the adsorption enthalpies of some species. The biggest change occurs for the adsorption of CO2, which changes from strongly exothermic to mildly endothermic. Typically, CO2 binds only weakly through physisorption on the Pt(111) surface.206 Using gas-phase reference ΔfH indicates that the CO2 binds strongly to the surface in disagreement with experiments. Mhadeshwar et al.126 also describe the use of the experimental ΔfH of adsorbates as a basis set to reference the DFT energies to the global thermochemical network, thereby ensuring thermodynamic consistency of the reaction mechanism with known adsorption enthalpies.
 |
| | Fig. 13 Connecting the DFT data with the global thermochemical network (here ATcT) by referencing DFT data to experimental ΔfH of adsorbates. | |
4.4 Indirect correction schemes with molecular fragment reference basis sets
The methods that have been introduced in prior sections rely on an atomic basis set, with one reference species defined per element. Depending on the scheme, these references may be gas-phase or adsorbed species, but the approaches presented thus far effectively act as adsorption energy corrections. They ensure that gas-phase reaction energies are consistent with ATcT, and that surface reactions are consistent with DFT, while adsorption energies are adjusted in various ways to ensure this is the case. Each method makes different assumptions about how to adjust the adsorption energies. However, since surface reaction enthalpies are rarely known, the most common approach is to assume that DFT surface reaction enthalpies are accurate. The logic for this is that error cancellation in DFT is likely the largest for surface reactions since both products and reactants have similar electronic environments (adsorbates on surfaces).
While there is certainly a higher degree of error cancellation for pure surface elementary steps than adsorption reactions, error cancellation is not automatically guaranteed, and the degree of cancellation can vary widely depending on the nature of the adsorbed species. To demonstrate, we show the computed reaction enthalpy for a set of surface reactions using the BEEF-vdW and RPBE functional compared to the experimental values in Fig. 14. The experimental ΔfH of the adsorbates were derived from the adsorption enthalpies reported by Silbaugh and Campbell.96 While most of the predicted reaction enthalpies are within ±25 kJ mol−1, there are deviations of up to 90 kJ mol−1 from the experiment. Additionally, results from the different functionals can vary substantially. For example, the reaction enthalpy for the dissociation of *OH determined from the RPBE xc-functional agrees within chemical accuracy with the experiments, while the BEEF-vdW value deviates by 35 kJ mol−1. This large deviation and sensitivity to functional choice indicates a low degree of error cancellation. There are also reactions for which both functionals give similar results, indicating a higher degree of error cancellation since the specific errors of each xc functional are canceled out. Consequently, the generalization of accurate reaction enthalpies from DFT for all surface elementary reactions due to error cancellation is not possible.
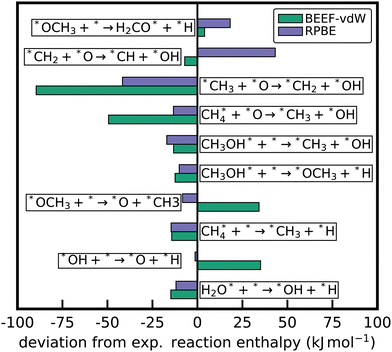 |
| | Fig. 14 Comparison of predicted reaction enthalpies from the BEEF-vdW and RPBE functional compared to the experimental value for a set of surface reactions. | |
It is possible to maximize the degree of error cancellation by constructing reactions that conserve the bonding environment and hybridization on both sides of the reaction. This approach moves away from atomic reference sets, instead selecting reference reactions by maximizing the similarity of molecular fragments. The gas-phase community has used these error-cancellation reactions to derive ΔfH of species with chemical accuracy at the DFT level of theory.207,208 Instead of conserving the reaction enthalpies of surface reactions that are relevant to a given chemical reaction network, the goal is to conserve the reaction enthalpies for reactions with the highest degree of error cancellation. The key is to construct reactions that conserve the molecular structure and bonding environment of the target molecule to maximize error cancellation.193,209–211 Raghavachari and co-workers209,210 developed the connectivity-based hierarchy (CBH) that automatically constructs error cancellation reactions for a gas-phase target. The order of the CBH approach is conservation of spin pairs (isogyric, CBH-0), bond types (isodesmic reaction, CBH-1), immediate connectivity of the heavy atoms (hypohomodesmotic, CBH-2), or immediate connectivity of the bonding environment (hyperhomodesmotic, CBH-3). Climbing this ladder leads to increasing error cancellation and more accurate ΔfH. Fig. 15 shows the order of the error cancellation reactions with a gas-phase example for 1-propyl.
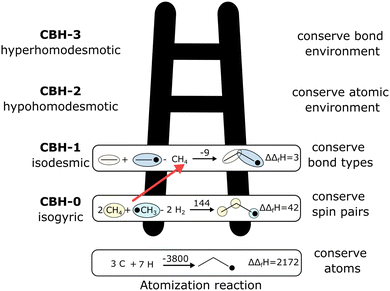 |
| | Fig. 15 Types of error cancellation reactions in the CBH209,210 scheme to determine the enthalpy of formation of the 1-propyl radical using BEEF-vdW DFT energies. The reported differences in ΔfH are with respect to the ATcT value of 118 kJ mol−1. The value above the arrow is the reaction enthalpy and all values are reported in kJ mol−1. The atomization reaction is not part of the CBH method. | |
To illustrate this concept, we calculate gas-phase reaction enthalpies at various rungs of the CBH ladder using BEEF-vdW and also compared this with the atomization energy approach, illustrated in Fig. 15. The 3 different reference reactions for 1-propyl shown in Fig. 15:
The simplest approach to calculate the Δ
fH is
via the total atomization energy from the BEEF-vdW energies. This approach results in a Δ
fH that deviates wildly from the experimental value, with an error of 2172 kJ mol
−1. This error arises due to the implicit assumption that the atomization energies are correctly computed with BEEF-vdW, but it is well known that much higher levels of theory are needed to accurately compute total atomization energies.
87,209–212 The isogyric reaction gives a much better agreement with the experiment, with a deviation of only 42 kJ mol
−1, but the deviation is still large enough to cause equilibrium constants to be off by orders of magnitude. The highest possible rung in the CBH scheme for 1-propyl is an isodesmic reaction. With this reaction, Δ
fH is determined to within chemical accuracy (3 kJ mol
−1) of the accurate ATcT value from BEEF-vdW energies. Although the gas-phase community has highly accurate electronic structure methods, error cancellation is still a very active field of research.
212,213 This example illustrates the power of error cancellation in a gas-phase context, and the same concepts hold for surface reactions, although some modifications are required.
4.4.1 Deriving enthalpies of formation of adsorbates using adsorbate reference species in isodesmic reactions.
Recently, Kreitz et al.131 introduced the concept of error cancellation reactions for adsorbates by extending the CBH approach. The CBH approach provides a convenient way to connect the DFT data with the global thermochemical network by using accurate and independent reference ΔfH for the adsorbates that serve as the bond-type fragments used in the reference reactions. This necessity is a limitation for many catalytic surfaces where experimental or high-level theory data is not available. However, for Pt(111) (and some other close-packed facets), there is enough experimental data available in the literature, which is summarized by Silbaugh and Campbell,96 to decompose all CxHyOz adsorbates into bond types using isodesmic reactions (CBH-1). It is not possible to use the lower CBH-0 rung due to inconsistencies with the conservation of surface sites, which conveniently cancel out at the CBH-1 rung, as explained in detail in ref. 131. The ΔfH of the adsorbates used as the reference fragments are referenced to the ATcT and all other adsorbates are referenced to the set of reference adsorbates. Similarly to Section 4.3.3, we avoid the use of a gas-phase precursors and combine DFT with experimental adsorbate ΔfH directly. Table 3 contains a list of the ΔfH of all the species that were used for the bond types and additional experimental values for the case study. In the literature, these experimental values are only used to benchmark the DFT calculations; here, we show how to combine them with DFT values so that they can all be included in a consistent thermochemical network. ΔfH of the target is determined from an isodesmic reaction using the fragments F, where F are adsorbates. An example of the isodesmic reaction for adsorbed ethyl (*CH2CH3) is given in Fig. 16.
Table 3 ΔfH at 0 K of the species that were used as fragments for the bond types to construct the isodesmic reactions. All enthalpies are in kJ mol−1. The table is adapted from Kreitz et al.131 and details for the derivation of the ΔfH can be found there
| Bond type |
Species |
ΔfH (0 K) |
Ref. |
| C–O |
CH3OH* |
−245.0 |
124
|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
CH2CH2* |
22.1 |
214
|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
H2CO* |
−159.3 |
215
|
| C–C |
CH3CH3* |
−96.0 |
68
|
| C–H |
CH4* |
−81.3 |
68
|
| O–H |
H2O* |
−267.9 |
68
|
| Pt–C |
*CH3 |
−47.2 |
123
|
Pt![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C C |
*CH |
−35.8 |
216
|
Pt![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
*CH2 |
46.5 |
216
|
| Pt–O |
*OH |
−164.7 |
217
|
| Pt–H |
*H |
−32.7 |
68
|
Pt![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
*O |
−103.7 |
68
|
Pt![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
*CO |
−230.9 |
68
|
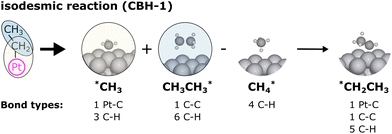 |
| | Fig. 16 Isodesmic reaction to determine the ΔfH of adsorbed ethyl (*CH2CH3) using the CBH approach for adsorbates developed by Kreitz et al.131 This illustration shows that the C to which ethyl binds to the surface is counted twice, which is why a CH4 needs to be subtracted. | |
The various bond types in this reaction are summarized in Fig. 16 for demonstration purposes and show that all bond types are perfectly balanced on both sides of the reaction. An open-source software tool is available to construct these structure-preserving reactions automatically for adsorbates.131,218 The method for calculating the ΔfH*CH2CH3 from this reference reaction is similar to the approaches described before. First, the zero-point corrected DFT energies are used to compute the reaction enthalpy.
| |  | (63) |
| | | ΔrHQM = E*CH2CH3 − E*CH3 − EC2H6* + ECH4* | (64) |
Assuming that ΔrHQM = ΔrH, we can calculate ΔfH of the target with the known ΔfH of the reference adsorbates.
| | 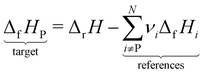 | (65) |
| | | ΔfH*CH2CH3 = ΔrHQM + ΔfHCH3CH3* + ΔfH*CH3 − ΔfHCH4* | (66) |
The missing additional species for which isodesmic reactions can be used from our case study are *CH2*CH2 and *CO2.
| CH3CH3* + 2*CH3 − 2CH4* → *CH2*CH2 |
The linear algebra notation for this approach is straightforward and identical to eqn (54) (see ESI,† page 53),
| |  | (67) |
| | 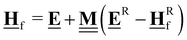 | (68) |
where
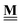
is the matrix of stoichiometric coefficients for the isodesmic reactions, which can be enumerated using the algorithm or software described in ref.
131. The stoichiometric matrix can again be derived using linear algebra, but in this case, from a matrix

(number of molecules × number of fragments) containing the composition of fragments of the target.
| | 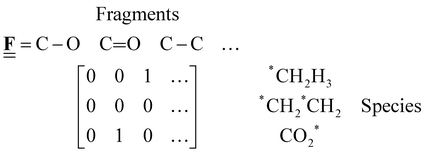 | (69) |
Analogously, we can define a matrix with the fragments of the reference species  .
.
| | 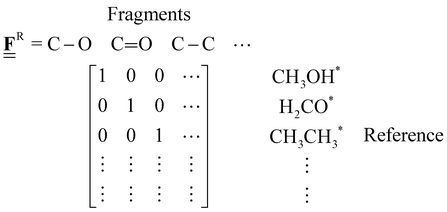 | (70) |
The stoichiometry matrix is then calculated via
| | 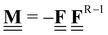 | (71) |
which can be compared to
eqn (43) to highlight the use of a “fragment” basis rather than an “atomic” basis in this approach. See Section 4 of the ESI,
† for the full matrix
,

, and
.
The CBH methodology for adsorbates can only be applied for molecules that can be broken down into isodesmic reactions. Thus, the method cannot be used for small adsorbates like *O, *H, or *CO. In this work, we can use experimental ΔfH for the parameterization of the microkinetic model (see Table 3). Alternatively, it is possible to perform higher-level of theory calculations for these adsorbates to determine accurate ΔfH. The CBH approach integrates available experimental data for the reference adsorbates, accurate gas-phase species from the ATcT, and DFT energies into a global thermochemical network as shown in Fig. 17. Additionally, systematic error cancellation provides a more accurate ΔfH of adsorbates from DFT. Kreitz et al.131 obtained a ΔfH for *OCH3 and C3H8* that is within chemical accuracy of the experimental value using BEEF-vdW DFT energies. However, isodesmic reactions do not necessarily have the maximum degree of error cancellation,209,211e.g., the degree of error cancellation for CO2* is rather low. Conserving only the bond types does not always conserve the correct hybridization and the molecular orbitals. A good indicator for the effectiveness of the error cancellation is the reaction enthalpy of eqn (63).218 High reaction enthalpies indicate a low degree of error cancellation, and climbing to the next highest rung would be preferable. Unfortunately, this depends on the size of the target adsorbate. Additionally, independent and accurate reference ΔfH are needed to populate the fragments for the hypohomodesmotic level. Yet, the approach provides a way to leverage a relatively small number of strategically selected highly accurate reaction enthalpies from experiment or wavefunction theories and use these to elevate the accuracy of other reaction enthalpies by maximizing cancellation of error.
 |
| | Fig. 17 Thermochemical cycle for the isodesmic reactions. | |
While the molecular fragment reference basis sets still conserve the stoichiometry, they also conserve the bond types in the molecule, which leads to differences between the reference fragments in the products and reactants. Consequently, these approaches do not necessarily conserve the surface reaction enthalpies of a mechanism at the DFT values. Instead, they conserve surface reaction enthalpies of alternative reactions that maximize error cancellation for a given electronic structure method.193,207–209
Fig. 18 shows the enthalpy diagram with ΔfH from experiments, ATcT, and the isodesmic reactions. Since the enthalpies of the gas-phase species are directly from the ATcT, we match the reaction enthalpy exactly, which is identical to the adsorption reaction approach in Section 4.3.2. The DFT energy of the empty slab is also no longer needed. The reaction enthalpies now vary considerably in comparison to the previous methods. The dissociation of ethane to ethyl changed from endothermic to exothermic and the subsequent dissociation step is even more exothermic. Furthermore, the formation of *OH is also exothermic, while the endothermicity for the dissociation of CO2* increased significantly. Assuming the experimentally measured adsorption enthalpies are more accurate than DFT, it follows that the free energy pathway constructed from the CBH approach should also be more accurate. However, it is only possible to calculate ΔfH using the CBH approach in cases where the experimental (or other highly accurate) reaction enthalpies of the requisite reference species are known.
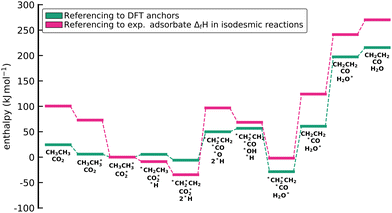 |
| | Fig. 18 Enthalpy diagram with enthalpies of formation derived with the standard referencing approach and using the molecular fragment basis set with isodesmic reactions. The enthalpy diagrams are aligned to C2H6* + CO2* to demonstrate that using a molecular fragment basis set changes the adsorption enthalpies and the surface reaction enthalpies. | |
5 Converting between reaction enthalpies and formation enthalpies
The approaches in Sections 4.2.1–4.2.3 have shown that the reaction enthalpies calculated from the total DFT energies are conserved, regardless of the choice of atomic reference species. We can use this fact and calculate ΔAH if only reaction enthalpies are reported for a mechanism. This problem cannot be formulated for a single species, and it directly becomes a linear algebra problem. For a chemical kinetics network involving n chemical species, a total of na + ns reference species must be defined, where na is the number of unique atomic elements of which all species consist and ns is the number of surface sites (typically one). Let be the zero-point corrected energies of chemical species, ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) A be the enthalpies of formation of the same species given defined references A and
A be the enthalpies of formation of the same species given defined references A and ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r be the reaction energies according to the stoichiometry matrix
r be the reaction energies according to the stoichiometry matrix  . The relationship between
. The relationship between ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r and
r and ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) is a simple linear combination, shown in eqn (72).
is a simple linear combination, shown in eqn (72).| |  | (72) |
Since the number of elementary reactions is typically greater than or equal to the number of chemical species, i.e., m ≥ n, there exists a direct mapping between ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) and
and ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r. Yet, no obvious mapping exists in the opposite direction since this is an under-constrained linear system of equations. The Moore-Penrose219–221 pseudo-inverse of the stoichiometry matrix
r. Yet, no obvious mapping exists in the opposite direction since this is an under-constrained linear system of equations. The Moore-Penrose219–221 pseudo-inverse of the stoichiometry matrix  can be used to construct the inverse mapping. To solve this inverse mapping, it is first necessary to select anchor species for each element from the mechanism, e.g., A = [C2H6, CO, H2O, Pt(111)]. We can separate the stoichiometry matrix into the anchor
can be used to construct the inverse mapping. To solve this inverse mapping, it is first necessary to select anchor species for each element from the mechanism, e.g., A = [C2H6, CO, H2O, Pt(111)]. We can separate the stoichiometry matrix into the anchor  species
species 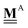 and non-anchor species
and non-anchor species  , leading to eqn (73).
, leading to eqn (73).
| |  | (73) |
In eqn (73), we separate ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) A into the anchor species
A into the anchor species 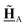 and the unknown
and the unknown  . All enthalpies are referenced to the DFT energies of the anchor species. Thus, the relative enthalpies of the anchor species
. All enthalpies are referenced to the DFT energies of the anchor species. Thus, the relative enthalpies of the anchor species 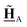 are 0. We can now rearrange the equation to compute the unknown
are 0. We can now rearrange the equation to compute the unknown  from the reaction enthalpies referenced to the set of anchor species.
from the reaction enthalpies referenced to the set of anchor species.
| |  | (74) |
| | 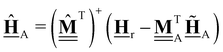 | (75) |
| |  | (76) |
This general form allows intuitive change of references. It is possible to use this method to create a thermochemical network that is referenced to the ATcT by defining the enthalpies of formation of the reference species to have the actual experimental values (instead of using the DFT values, which is equivalent to assuming  ). When using gas-phase reference species, this results in the same enthalpies of formation as the method in Section 4.3.2, and when using adsorbates, this is equivalent to Section 4.3.3. Integrating the DFT data into the global thermochemical network allows to replace gas-phase DFT energies with accurate ΔfH from the ATcT. The interested reader is referred to Section 5 of the ESI,† for a more detailed discussion of the linear algebra of this approach and the Jupyter notebook for this method is provided on page 62 of the ESI.† This approach of calculating enthalpies of formation directly from reaction enthalpies can serve as a convenient framework for new methods of combining data from various sources or identifying discrepancies in existing databases.
). When using gas-phase reference species, this results in the same enthalpies of formation as the method in Section 4.3.2, and when using adsorbates, this is equivalent to Section 4.3.3. Integrating the DFT data into the global thermochemical network allows to replace gas-phase DFT energies with accurate ΔfH from the ATcT. The interested reader is referred to Section 5 of the ESI,† for a more detailed discussion of the linear algebra of this approach and the Jupyter notebook for this method is provided on page 62 of the ESI.† This approach of calculating enthalpies of formation directly from reaction enthalpies can serve as a convenient framework for new methods of combining data from various sources or identifying discrepancies in existing databases.
6 Summary & conclusions
This review paper presents a cohesive collection of thermochemical concepts and linear algebra methods for calculating key thermochemical quantities in computational catalysis. These methods provide tools to combine data from various sources, to integrate experimental and ab initio data, and to convert between different formats. We have defined a notation for evaluating the thermochemistry of adsorbates from DFT data that is consistent with the existing gas-phase thermochemical conventions. All available methods in the literature for converting a set of DFT data into enthalpies of formation were described and explained following the consistent notation. The summary of the methods in Table 4 highlights that they can all be reduced to a simple linear algebra equation to anchor/reference the DFT data and to create a local or global thermochemical network. The difference in the methods is the choice of the anchor/reference species and the source of their enthalpies of formation. This review focused only on the enthalpy of formation at 0 K as it is the foundation of all thermochemistry and has the biggest contribution to the Gibbs free energy. ΔfH at 0 K can be converted to ΔfH at other temperatures or to Gibbs free energies of formation by applying finite-temperature corrections through e.g., entropic contributions.
Table 4 Summary of all discussed methods using the consistent notation with additional information on the specifics of each method
| Method |
Equation |
Reference set |
References |
Data |
Network type |
Comments |
| Chemical elemental potentials |
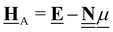
|
Atomic |
Gas-phase species |
DFT |
Local |
Convenient framework for dealing with non-standard reaction conditions (T, p, environment, applied potential) |
| Regression of elemental potentials |

|
Atomic |
Entire mechanism |
DFT |
Local |
Aligning DFT data from different sources |
| DFT anchors |

|
Atomic |
Gas-phase species |
DFT |
Local |
Easy to use |
| DFT anchors with corrections |

|
Atomic |
Gas-phase species |
DFT |
Local |
Increased accuracy of overall reaction enthalpy |
| Gas-phase references |
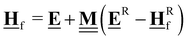
|
Atomic |
Gas-phase species |
DFT, ATcT |
Global |
Accurate gas-phase ΔfH |
| Adsorbate references |
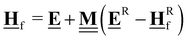
|
Atomic |
Adsorbates |
DFT, ATcT, Exp. |
Global |
Accurate gas-phase ΔfH and 3 experimental Hads |
| Isodesmic reactions |
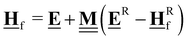
|
Bond type |
Adsorbates |
DFT, ATcT, Exp. |
Global |
Accurate gas-phase ΔfH, many experimental Hads, and error-cancellation for surface reactions |
| Converting ΔrH to ΔAH |
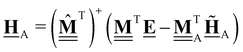
|
Atomic |
Gas-phase species or adsorbates |
DFT, (ATcT, Exp.) |
Local (or global) |
Useful if only reaction enthalpies are reported |
The approaches can be classified according to their use of an atomic reference basis sets or molecular fragment reference basis sets. In an atomic reference basis set method, every element must be assigned a single reference species (typically a closed-shell gas-phase molecule), which can be abstracted into elemental chemical potentials. The atomic reference basis set methods always conserve the reaction enthalpies as if they were calculated from the plain DFT energies, so long as correction factors are not applied and data from different sources are not mixed together. Conserving all DFT reaction enthalpies does not reproduce the thermodynamics of the overall gas-phase reaction from the accurate gas-phase ΔfH of global thermochemical networks like the ATcT. Therefore, correction factors are applied to DFT energies to reduce discrepancies by adjusting adsorption enthalpies. However, the only method to ensure an exact agreement is to integrate the DFT data into the global thermochemical networks by anchoring it to the gas-phase or adsorbates ΔfH of the references.
Instead of atomic references, a fragment reference basis set using e.g. isodesmic reactions can be used to integrate data from various sources (DFT, accurate gas-phase ΔfH from the ATcT, and experimental adsorption enthalpies) into a global thermochemical network. The isodesmic reference reactions of this basis set lead to an increased accuracy of ΔfH of adsorbates by maximizing error cancellation. Finally, we show how the linear algebra framework can also be used to “invert” the problem of constructing reaction enthalpies from ΔfH. This approach allows direct calculation of ΔfH from tabulated reaction enthalpies, providing an alternative perspective on how thermochemical data can be converted and combined.
In conclusion, these tools can help researchers make better use of existing DFT datasets and facilitate the storage of new DFT data, preventing unnecessary waste of computational resources. The usage of a standardized reference frame has led to the proliferation of accurate thermochemical data in the gas-phase community, with wide-ranging implications on better reaction mechanisms and accurate models. The goal for the catalysis community should be to establish similar standards and methods. It is necessary to align the adsorbate thermochemistry concepts with the gas-phase community to integrate accurate thermophysical data of gas-phase species and adsorbates into a single global thermochemical network like the ATcT. Through the integration in this global network, it will be possible to simply search for the enthalpy of formation of an adsorbate in a database that contains the most accurate thermochemical information.
Author contributions
B. K. – conceptualization, funding acquisition, data curation, formal analysis, investigation, software, writing – original draft, writing – review & editing; G. S. G. – conceptualization, data curation, formal analysis, software, writing – original draft; S. J. S. – formal analysis, investigation, software; A. A. P. – funding acquisition, writing – review & editing; D. H. B. – writing – review & editing; D. N. – writing – original draft, investigation; C. F. G. – conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing; A. J. M. – conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.
Data availability
All data is publicly available via Zenodo: https://zenodo.org/records/13143954.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
BK, AAP, CFG, and AJM gratefully acknowledge support by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award #0000232253 and #DE-SC0019441, as part of the Computational Chemical Sciences Program. The work at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, under Contract No. DE-AC02-06CH11357, through the Computational Chemical Sciences Program (DHB). BK acknowledges financial support from the Alexander von Humboldt Foundation. The authors thank Zachary Ulissi for helpful discussions.
Notes and references
- C. Chizallet and P. Raybaud, Catal. Sci. Technol., 2014, 4, 2797–2813 RSC.
- P. Sit and L. Zhang, Heterog. Catal., 2021, 2, 405–418 Search PubMed.
-
T. Van Mourik, M. Bühl and M.-P. Gaigeot, Density functional theory across chemistry, physics and biology, 2014 Search PubMed.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, J. Comput. Chem., 2019, 40, 1305–1318 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2018, 119, 2453–2523 CrossRef PubMed.
- A. Ishikawa, Sci. Rep., 2022, 12, 11657 CrossRef CAS PubMed.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- C. A. Gaggioli, S. J. Stoneburner, C. J. Cramer and L. Gagliardi, ACS Catal., 2019, 9, 8481–8502 CrossRef CAS.
- G. D. Wehinger, M. Ambrosetti, R. Cheula, Z.-B. Ding, M. Isoz, B. Kreitz, K. Kuhlmann, M. Kutscherauer, K. Niyogi, J. Poissonnier, R. Réocreux, D. Rudolf, J. Wagner, R. Zimmermann, M. Bracconi, H. Freund, U. Krewer and M. Maestri, Chem. Eng. Res. Des., 2022, 184, 39–58 CrossRef CAS.
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- J. Resasco, F. Abild-Pedersen, C. Hahn, Z. Bao, M. T. M. Koper and T. F. Jaramillo, Nat. Catal., 2022, 5, 374–381 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder,
et al.
, APL Mater., 2013, 1, 011002 CrossRef.
-
C. L. Zitnick, L. Chanussot, A. Das, S. Goyal, J. Heras-Domingo, C. Ho, W. Hu, T. Lavril, A. Palizhati and M. Riviere, et al., arXiv, 2020, preprint, arXiv:2010.09435 DOI:10.48550/arXiv.2010.09435.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, F. Therrien, J. Abed, O. Voznyy, E. H. Sargent, Z. Ulissi and C. L. Zitnick, ACS Catal., 2023, 13, 3066–3084 CrossRef CAS.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef.
- C. Draxl and M. Scheffler, JPhys Mater., 2019, 2, 036001 CrossRef CAS.
- M. Scheffler, M. Aeschlimann, M. Albrecht, T. Bereau, H.-J. Bungartz, C. Felser, M. Greiner, A. Groß, C. T. Koch and K. Kremer,
et al.
, Nature, 2022, 604, 635–642 CrossRef CAS PubMed.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. Hart, S. Sanvito and M. Buongiorno-Nardelli,
et al.
, Comput. Mater. Sci., 2012, 58, 227–235 CrossRef CAS.
- J. S. Hummelshøj, F. Abild-Pedersen, F. Studt, T. Bligaard and J. K. Nørskov, Angew. Chem., Int. Ed., 2012, 51, 272–274 CrossRef PubMed.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1–15 Search PubMed.
- V. I. Hegde, C. K. H. Borg, Z. del Rosario, Y. Kim, M. Hutchinson, E. Antono, J. Ling, P. Saxe, J. E. Saal and B. Meredig, Phys. Rev. Mater., 2023, 7, 053805 CrossRef CAS.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark and A. Dal Corso,
et al.
, Science, 2016, 351, aad3000 CrossRef PubMed.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439–10452 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo,
et al.
, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni,
et al.
, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- E. Aprà, E. J. Bylaska, W. A. De Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. Van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin Del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. Schäfer, E. Ö. Jónsson, E. D. Hermes, F. A. Nilsson, G. Kastlunger, G. Levi, H. Jónsson, H. Häkkinen, J. Fojt, J. Kangsabanik, J. Sødequist, J. Lehtomäki, J. Heske, J. Enkovaara, K. T. Winther, M. Dulak, M. M. Melander, M. Ovesen, M. Louhivuori, M. Walter, M. Gjerding, O. Lopez-Acevedo, P. Erhart, R. Warmbier, R. Würdemann, S. Kaappa, S. Latini, T. M. Boland, T. Bligaard, T. Skovhus, T. Susi, T. Maxson, T. Rossi, X. Chen, Y. L. A. Schmerwitz, J. Schiøtz, T. Olsen, K. W. Jacobsen and K. S. Thygesen, J. Chem. Phys., 2024, 160, 092503 CrossRef CAS PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- Q. Xu, A. Sharma, B. Comer, H. Huang, E. Chow, A. J. Medford, J. E. Pask and P. Suryanarayana, SoftwareX, 2021, 15, 100709 CrossRef.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- M. Capdevila-Cortada, Z. Odziana and N. López, ACS Catal., 2016, 6, 8370–8379 CrossRef CAS.
- B. Meredig, A. Thompson, H. A. Hansen, C. Wolverton and A. van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195128 CrossRef.
- R. Sundararaman, D. Vigil-Fowler and K. Schwarz, Chem. Rev., 2022, 122, 10651–10674 CrossRef CAS PubMed.
- X.-H. Yang, Y.-B. Zhuang, J.-X. Zhu, J.-B. Le and J. Cheng, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1559 CAS.
- R. Sundararaman, W. A. Goddard and T. A. Arias, J. Chem. Phys., 2017, 146, 114104 CrossRef PubMed.
- C. R. Tezak, N. R. Singstock, A. W. Alherz, D. Vigil-Fowler, C. A. Sutton, R. Sundararaman and C. B. Musgrave, ACS Catal., 2023, 13, 12894–12903 CrossRef CAS.
- S. M. R. Islam, F. Khezeli, S. Ringe and C. Plaisance, J. Chem. Phys., 2023, 159, 234117 CrossRef CAS PubMed.
- Z. Levell, J. Le, S. Yu, R. Wang, S. Ethirajan, R. Rana, A. Kulkarni, J. Resasco, D. Lu, J. Cheng and Y. Liu, Chem. Rev., 2024, 124, 8620–8656 CrossRef CAS PubMed.
- X. Andrade, J. Alberdi-Rodriguez, D. A. Strubbe, M. J. Oliveira, F. Nogueira, A. Castro, J. Muguerza, A. Arruabarrena, S. G. Louie and A. Aspuru-Guzik,
et al.
, J. Phys.: Condens. Matter, 2012, 24, 233202 CrossRef PubMed.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- G. R. Iyer and B. M. Rubenstein, J. Phys. Chem. A, 2022, 126, 4636–4646 CrossRef CAS PubMed.
-
H.-Z. Ye and T. C. Berkelbach, Ab Initio Surface Chemistry with Chemical Accuracy, 2024 Search PubMed.
- C. Sheldon, J. Paier and J. Sauer, J. Chem. Phys., 2021, 155, 174702 CrossRef CAS PubMed.
-
H. Kim, N.-K. Yu, N. Tian and A. J. Medford, Assessing exchange–correlation functionals for heterogeneous catalysis of nitrogen species, 2024, https://arxiv.org/abs/2403.14482 Search PubMed.
- B. R. Goldsmith, J. Esterhuizen, J.-X. Liu, C. J. Bartel and C. Sutton, AIChE J., 2018, 64, 2311–2323 CrossRef CAS.
- A. J. Medford, M. R. Kunz, S. M. Ewing, T. Borders and R. Fushimi, ACS Catal., 2018, 8, 7403–7429 CrossRef CAS.
- K. Suzuki, T. Toyao, Z. Maeno, S. Takakusagi, K.-I. Shimizu and I. Takigawa, ChemCatChem, 2019, 11, 4537–4547 CrossRef CAS.
- M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C.-T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C.-S. Tan, M. Askerka, F. Che, M. Liu, A. Seifitokaldani, Y. Pang, S.-C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Nature, 2020, 581, 178–183 CrossRef CAS PubMed.
- T. Williams, K. McCullough and J. A. Lauterbach, Chem. Mater., 2019, 32, 157–165 CrossRef.
- D. Roy, S. C. Mandal and B. Pathak, ACS Appl. Mater. Interfaces, 2021, 13, 56151–56163 CrossRef CAS PubMed.
- S. Pablo-García, S. Morandi, R. A. Vargas-Hernández, K. Jorner, Ž. Ivković, N. López and A. Aspuru-Guzik, Nat. Comput. Sci., 2023, 3, 433–442 CrossRef PubMed.
- P. Schlexer Lamoureux, K. T. Winther, J. A. Garrido Torres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, ChemCatChem, 2019, 11, 3581–3601 CrossRef CAS.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, npj Comput. Mater., 2021, 7, 84 CrossRef CAS.
- J. T. Margraf, H. Jung, C. Scheurer and K. Reuter, Nat. Catal., 2023, 6, 112–121 CrossRef.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, ACS Catal., 2022, 12, 4784–4791 CrossRef CAS PubMed.
- C. Carbogno, K. S. Thygesen, B. Bieniek, C. Draxl, L. M. Ghiringhelli, A. Gulans, O. T. Hofmann, K. W. Jacobsen, S. Lubeck and J. J. Mortensen,
et al.
, npj Comput. Mater., 2022, 8, 69 CrossRef.
- A. H. Motagamwala and J. A. Dumesic, Chem. Rev., 2020, 121, 1049–1076 CrossRef PubMed.
- W. Xie, J. Xu, J. Chen, H. Wang and P. Hu, Acc. Chem. Res., 2022, 55, 1237–1248 CrossRef CAS PubMed.
- A. A. Gokhale, S. Kandoi, J. P. Greeley, M. Mavrikakis and J. A. Dumesic, Chem. Eng. Sci., 2004, 59, 4679–4691 CrossRef CAS.
- S. Bhandari, S. Rangarajan and M. Mavrikakis, Acc. Chem. Res., 2020, 53, 1893–1904 CrossRef CAS PubMed.
- T. Avanesian, S. Dai, M. J. Kale, G. W. Graham, X. Pan and P. Christopher, J. Am. Chem. Soc., 2017, 139, 4551–4558 CrossRef CAS PubMed.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- B. Kreitz, P. Lott, F. Studt, A. J. Medford, O. Deutschmann and C. F. Goldsmith, Angew. Chem., Int. Ed., 2023, 62, e202306514 CrossRef CAS PubMed.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Nørskov, Science, 2014, 345, 197–200 CrossRef CAS PubMed.
- B. Kreitz, K. Sargsyan, K. Blöndal, E. J. Mazeau, R. H. West, G. D. Wehinger, T. Turek and C. F. Goldsmith, JACS Au, 2021, 1, 1656–1673 CrossRef CAS PubMed.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, ChemCatChem, 2022, 14, e202200570 CrossRef CAS.
- J. E. Sutton, W. Guo, M. A. Katsoulakis and D. G. Vlachos, Nat. Chem., 2016, 8, 331–337 CrossRef CAS PubMed.
-
NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, ed. P. J. Linstrom and W. G. Mallard DOI:10.18434/T4D303, (accessed 2023-11-30).
-
M. Chase, N. I. of Standards and T. (U.S.), NIST-JANAF Thermochemical Tables, American Chemical Society, 1998 Search PubMed.
-
B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) Values Based on ver. 1.130 of the Thermochemical Networkhttps://atct.anl.gov, (accessed 2023-11-30) Search PubMed.
- B. Ruscic, J. Phys. Chem. A, 2015, 119, 7810–7837 CrossRef CAS PubMed.
- L. P. Granda-Marulanda, A. Rendon-Calle, S. Builes, F. Illas, M. T. Koper and F. Calle-Vallejo, ACS Catal., 2020, 10, 6900–6907 CrossRef CAS.
- B. W. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2020, 121, 1007–1048 CrossRef PubMed.
- C. P. Marshall, J. Schumann and A. Trunschke, Angew. Chem., Int. Ed., 2023, 62, e202302971 CrossRef CAS PubMed.
-
G. Ertl, H. Knözinger, F. Schüth and J. Weitkamp, Handbook of heterogeneous catalysis, 2008 Search PubMed.
- K. F. Kalz, R. Kraehnert, M. Dvoyashkin, R. Dittmeyer, R. Gläser, U. Krewer, K. Reuter and J.-D. Grunwaldt, ChemCatChem, 2017, 9, 17–29 CrossRef CAS PubMed.
- M. Zhang, M. Wang, B. Xu and D. Ma, Joule, 2019, 3, 2876–2883 CrossRef.
-
J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental concepts in heterogeneous catalysis, John Wiley & Sons, 2014 Search PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- J. D. Cox, Pure Appl. Chem., 1982, 54, 1239–1250 CrossRef.
-
B. Ruscic and D. H. Bross, Mathematical Modelling of Gas-Phase Complex Reaction Systems: Pyrolysis and Combustion, Elsevier, 2019, vol. 45, pp. 3–114 Search PubMed.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- H. M. Jaeger, H. F. Schaefer, J. Demaison, A. G. Császár and W. D. Allen, J. Chem. Theory Comput., 2010, 6, 3066–3078 CrossRef CAS PubMed.
- S. J. Klippenstein, L. B. Harding and B. Ruscic, J. Phys. Chem. A, 2017, 121, 6580–6602 CrossRef CAS PubMed.
-
B. Ruscic, R. E. Pinzon, G. Von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoy and A. F. Wagner, J. Phys.: Conf. Ser., 2005, p. 561 Search PubMed.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- K. Reuter, Catal. Lett., 2016, 146, 541–563 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- T. L. Silbaugh and C. T. Campbell, J. Phys. Chem. C, 2016, 120, 25161–25172 CrossRef CAS.
- R. B. Araujo, G. L. S. Rodrigues, E. C. dos Santos and L. G. M. Pettersson, Nat. Commun., 2022, 13, 6853 CrossRef CAS PubMed.
- R. S. Kingsbury, A. S. Rosen, A. S. Gupta, J. M. Munro, S. P. Ong, A. Jain, S. Dwaraknath, M. K. Horton and K. A. Persson, npj Comput. Mater., 2022, 8, 195 CrossRef.
- B. T. G. Lau, G. Knizia and T. C. Berkelbach, J. Phys. Chem. Lett., 2021, 12, 1104–1109 CrossRef CAS PubMed.
- F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775 CrossRef CAS PubMed.
- Q. Zhao and E. A. Carter, J. Chem. Theory Comput., 2020, 16, 6528–6538 CrossRef CAS PubMed.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Nat. Mater., 2010, 9, 741–744 CrossRef CAS PubMed.
- N. A. Szaro, M. Bello, C. H. Fricke, O. H. Bamidele and A. Heyden, J. Phys. Chem. Lett., 2023, 14, 10769–10778 CrossRef CAS PubMed.
- X. Ren, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045402 CrossRef.
- P. S. Schmidt and K. S. Thygesen, J. Phys. Chem. C, 2018, 122, 4381–4390 CrossRef CAS.
- J. A. Garrido Torres, B. Ramberger, H. A. Früchtl, R. Schaub and G. Kresse, Phys. Rev. Mater., 2017, 1, 060803 CrossRef.
- P. N. Plessow, A. Smith, S. Tischer and F. Studt, J. Am. Chem. Soc., 2019, 141, 5908–5915 CrossRef CAS PubMed.
- P. N. Plessow, A. E. Enss, P. Huber and F. Studt, Catal. Sci. Technol., 2022, 12, 3516–3523 RSC.
- S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825 CrossRef CAS PubMed.
- N. Hansen, T. Kerber, J. Sauer, A. T. Bell and F. J. Keil, J. Am. Chem. Soc., 2010, 132, 11525–11538 CrossRef CAS PubMed.
- B. X. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372–25381 CrossRef CAS PubMed.
- R. O. Sharma, T. T. Rantala and P. E. Hoggan, J. Phys. Chem. C, 2020, 124, 26232–26240 CrossRef CAS.
- J. Sauer, Acc. Chem. Res., 2019, 52, 3502–3510 CrossRef CAS PubMed.
- C. T. Campbell and J. R. V. Sellers, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, ACS Catal., 2020, 10, 9236–9260 CrossRef CAS.
- L. H. Sprowl, C. T. Campbell and L. Árnadóttir, J. Phys. Chem. C, 2016, 120, 9719–9731 CrossRef CAS.
- K. Blöndal, K. Sargsyan, D. H. Bross, B. Ruscic and C. F. Goldsmith, J. Phys. Chem. C, 2021, 125, 20249–20260 CrossRef.
- K. Blöndal, K. Sargsyan, D. H. Bross, B. Ruscic and C. F. Goldsmith, ACS Catal., 2023, 13, 19–32 CrossRef.
- C. Waitt, A. R. Miles and W. F. Schneider, J. Phys. Chem. C, 2021, 125, 20331–20342 CrossRef CAS.
- C. T. Campbell, Acc. Chem. Res., 2019, 52, 984–993 CrossRef CAS PubMed.
- S. L. Tait, Z. Dohnálek, C. T. Campbell and B. D. Kay, J. Chem. Phys., 2006, 125, 234308 CrossRef PubMed.
- E. M. Karp, T. L. Silbaugh and C. T. Campbell, J. Phys. Chem. C, 2013, 117, 6325–6336 CrossRef CAS.
- E. M. Karp, T. L. Silbaugh and C. T. Campbell, J. Am. Chem. Soc., 2013, 135, 5208–5211 CrossRef CAS PubMed.
- E. M. Karp, T. L. Silbaugh, M. C. Crowe and C. T. Campbell, J. Am. Chem. Soc., 2012, 134, 20388–20395 CrossRef CAS PubMed.
- M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355 CrossRef CAS.
- A. B. Mhadeshwar, H. Wang and D. G. Vlachos, J. Phys. Chem. B, 2003, 107, 12721–12733 CrossRef CAS.
-
B. Kreitz, G. S. Gusmão, D. Nai, S. J. Sahoo, A. A. Peterson, D. H. Bross, C. F. Goldsmith and A. J. Medford, Data for Unifying thermochemistry concepts in computational heterogeneous catalysis, 2024 DOI:10.5281/zenodo.13143954.
- M. D. Porosoff, M. N. Z. Myint, S. Kattel, Z. Xie, E. Gomez, P. Liu and J. G. Chen, Angew. Chem., Int. Ed., 2015, 54, 15501–15505 CrossRef CAS PubMed.
- M. Myint, B. Yan, J. Wan, S. Zhao and J. G. Chen, J. Catal., 2016, 343, 168–177 CrossRef CAS.
- F. Jalid, T. S. Khan and M. A. Haider, Catal. Sci. Technol., 2021, 11, 97–115 RSC.
- B. Kreitz, K. Abeywardane and C. F. Goldsmith, J. Chem. Theory Comput., 2023, 19, 4149–4162 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- A. Farahvash, M. Agrawal, A. A. Peterson and A. P. Willard, J. Chem. Theory Comput., 2023, 19, 6452–6460 CrossRef CAS PubMed.
- L. C. Grabow, B. Hvolbæk and J. K. Nørskov, Top. Catal., 2010, 53, 298–310 CrossRef CAS.
- B. Kreitz, P. Lott, J. Bae, K. Blöndal, S. Angeli, Z. W. Ulissi, F. Studt, C. F. Goldsmith and O. Deutschmann, ACS Catal., 2022, 12, 11137–11151 CrossRef CAS.
- D. W. Flaherty, D. D. Hibbitts, E. I. Gürbüz and E. Iglesia, J. Catal., 2014, 311, 350–356 CrossRef CAS.
- A. Almithn and D. Hibbitts, ACS Catal., 2018, 8, 6375–6387 CrossRef CAS.
- D. D. Hibbitts, D. W. Flaherty and E. Iglesia, ACS Catal., 2016, 6, 469–482 CrossRef CAS.
- L. Foppa, T. Margossian, S. M. Kim, C. Müller, C. Copéret, K. Larmier and A. Comas-Vives, J. Am. Chem. Soc., 2017, 139, 17128–17139 CrossRef CAS PubMed.
- Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, Nat. Commun., 2017, 8, 14621 CrossRef PubMed.
- H. Li and K. Reuter, ACS Catal., 2022, 12, 10506–10513 CrossRef CAS.
- T. P. Senftle, A. C. T. Van Duin and M. J. Janik, ACS Catal., 2015, 5, 6187–6199 CrossRef CAS.
- D. Opalka, C. Scheurer and K. Reuter, ACS Catal., 2019, 9, 4944–4950 CrossRef CAS.
- P. Ghanekar, J. Kubal, Y. Cui, G. Mitchell, W. N. Delgass, F. Ribeiro and J. Greeley, Top. Catal., 2020, 63, 673–687 CrossRef CAS.
- N. Bergmann, N. G. Hörmann and K. Reuter, J. Chem. Theory Comput., 2023, 19, 8815–8825 CrossRef CAS PubMed.
- A. J. Medford, A. Vojvodic, F. Studt, F. Abild-Pedersen and J. K. Nørskov, J. Catal., 2012, 290, 108–117 CrossRef CAS.
- A. Banerjee, V. Navarro, J. W. M. Frenken, A. P. van Bavel, H. P. C. E. Kuipers and M. Saeys, J. Phys. Chem. Lett., 2016, 7, 1996–2001 CrossRef CAS PubMed.
- S. P. Vicchio, Z. Chen, K. W. Chapman and R. B. Getman, J. Am. Chem. Soc., 2023, 145, 2852–2859 CrossRef CAS PubMed.
- R. Cheula, A. Soon and M. Maestri, Catal. Sci. Technol., 2018, 8, 3493–3503 RSC.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311 RSC.
- P. Lindgren, G. Kastlunger and A. A. Peterson, J. Chem. Phys., 2022, 157, 180902 CrossRef CAS PubMed.
- A. J. Medford, A. C. Lausche, F. Abild-Pedersen, B. Temel, N. C. Schjødt, J. K. Nørskov and F. Studt, Top. Catal., 2014, 57, 135–142 CrossRef CAS.
- A. C. Lausche, A. J. Medford, T. S. Khan, Y. Xu, T. Bligaard, F. Abild-Pedersen, J. K. Nørskov and F. Studt, J. Catal., 2013, 307, 275–282 CrossRef CAS.
- S. Wang, V. Petzold, V. Tripkovic, J. Kleis, J. G. Howalt, E. Skúlason, E. M. Fernández, B. Hvolbæk, G. Jones, A. Toftelund, H. Falsig, M. Björketun, F. Studt, F. Abild-Pedersen, J. Rossmeisl, J. K. Nørskov and T. Bligaard, Phys. Chem. Chem. Phys., 2011, 13, 20760 RSC.
- M. Andersen, C. P. Plaisance and K. Reuter, J. Chem. Phys., 2017, 147, 152705 CrossRef PubMed.
- N. Yang, A. J. Medford, X. Liu, F. Studt, T. Bligaard, S. F. Bent and J. K. Nørskov, J. Am. Chem. Soc., 2016, 138, 3705–3714 CrossRef CAS PubMed.
- J. L. Snider, V. Streibel, M. A. Hubert, T. S. Choksi, E. Valle, D. C. Upham, J. Schumann, M. S. Duyar, A. Gallo, F. Abild-Pedersen and T. F. Jaramillo, ACS Catal., 2019, 9, 3399–3412 CrossRef CAS.
- G. T. K. K. Gunasooriya, A. P. van Bavel, H. P. C. E. Kuipers and M. Saeys, ACS Catal., 2016, 6, 3660–3664 CrossRef CAS.
- R. García-Muelas and N. López, Nat. Commun., 2019, 10, 4687 CrossRef PubMed.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- M. H. Hansen, J. K. Nørskov and T. Bligaard, J. Catal., 2019, 374, 161–170 CrossRef CAS.
- A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Nørskov, Nat. Mater., 2017, 16, 225–229 CrossRef CAS PubMed.
- C. Fricke, B. Rajbanshi, E. A. Walker, G. Terejanu and A. Heyden, ACS Catal., 2022, 12, 2487–2498 CrossRef CAS.
- G. Kastlunger, L. Wang, N. Govindarajan, H. H. Heenen, S. Ringe, T. Jaramillo, C. Hahn and K. Chan, ACS Catal., 2022, 12, 4344–4357 CrossRef CAS.
- M. Valter, E. C. Dos Santos, L. G. M. Pettersson and A. Hellman, J. Phys. Chem. C, 2020, 124, 17907–17915 CrossRef CAS.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807 CrossRef CAS.
- H. Wu, A. M. Payne, H.-W. Pang, A. Menon, C. A. Grambow, D. S. Ranasinghe, X. Dong, A. Grinberg Dana and W. H. Green, J. Phys. Chem. A, 2024, 128, 4335–4352 CrossRef CAS PubMed.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115 CrossRef.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- H. Bhattacharjee and D. G. Vlachos, J. Chem. Inf. Model., 2020, 60, 4673–4683 CrossRef CAS PubMed.
- H. Bhattacharjee, N. Anesiadis and D. G. Vlachos, Sci. Rep., 2021, 11, 14372 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- C. F. Goldsmith, G. R. Magoon and W. H. Green, J. Phys. Chem. A, 2012, 116, 9033–9057 CrossRef CAS PubMed.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, ChemCatChem, 2021, 13, 2508–2516 CrossRef CAS.
- C. P. Plaisance and R. A. Van Santen, J. Am. Chem. Soc., 2015, 137, 14660–14672 CrossRef CAS PubMed.
- E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, Electrochim. Acta, 2022, 426, 140799 CrossRef CAS.
- F. Studt, F. Abild-Pedersen, J. B. Varley and J. K. Nørskov, Catal. Lett., 2013, 143, 71–73 CrossRef CAS.
- F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111 CrossRef CAS.
- V. Streibel, H. A. Aljama, A.-C. Yang, T. S. Choksi, R. S. Sánchez-Carrera, A. Schäfer, Y. Li, M. Cargnello and F. Abild-Pedersen, ACS Catal., 2022, 12, 1742–1757 CrossRef CAS.
- B. Zijlstra, R. J. Broos, W. Chen, I. A. Filot and E. J. Hensen, Catal. Today, 2020, 342, 131–141 CrossRef CAS.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- R. Cheula and M. Maestri, Catal. Today, 2022, 387, 159–171 CrossRef CAS.
- R. Urrego-Ortiz, S. Builes, F. Illas and F. Calle-Vallejo, EES Catal., 2024, 2, 157–179 RSC.
- C. A. Grambow, Y.-P. Li and W. H. Green, J. Phys. Chem. A, 2019, 123, 5826–5835 CrossRef CAS PubMed.
- R. Christensen, H. A. Hansen and T. Vegge, Catal. Sci. Technol., 2015, 5, 4946–4949 RSC.
- G. H. Gu, P. Plechac and D. G. Vlachos, React. Chem. Eng., 2018, 3, 454–466 RSC.
- R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, Ind. Eng. Chem. Res., 2022, 61, 13375–13382 CrossRef CAS PubMed.
- R. Urrego-Ortiz, M. O. Almeida and F. Calle-Vallejo, ChemSusChem, 2024, e202400873 CrossRef PubMed.
- R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, J. Phys. Chem. C, 2016, 120, 24910–24916 CrossRef CAS.
- K. Blöndal, J. Jelic, E. Mazeau, F. Studt, R. H. West and C. F. Goldsmith, Ind. Eng. Chem. Res., 2019, 58, 17682–17691 CrossRef.
- S. E. Wheeler, K. N. Houk, P. V. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560 CrossRef CAS PubMed.
- V. Vorotnikov, S. Wang and D. G. Vlachos, Ind. Eng. Chem. Res., 2014, 53, 11929–11938 CrossRef CAS.
- V. Vorotnikov and D. G. Vlachos, J. Phys. Chem. C, 2015, 119, 10417–10426 CrossRef CAS.
- G.
H. Gu, B. Schweitzer, C. Michel, S. N. Steinmann, P. Sautet and D. G. Vlachos, J. Phys. Chem. C, 2017, 121, 21510–21519 CrossRef CAS.
- G. H. Gu and D. G. Vlachos, J. Phys. Chem. C, 2016, 120, 19234–19241 CrossRef CAS.
- B. Kreitz, K. Blöndal, K. Badger, R. H. West and C. F. Goldsmith, Digital Discovery, 2024, 3, 173–185 RSC.
- E. J. Mazeau, P. Satpute, K. Blöndal, C. F. Goldsmith and R. H. West, ACS Catal., 2021, 11, 7114–7125 CrossRef CAS.
- B. Kreitz, G. D. Wehinger, C. F. Goldsmith and T. Turek, J. Phys. Chem. C, 2021, 125, 2984–3000 CrossRef CAS.
- D. W. Blaylock, T. Ogura, W. H. Green and G. J. O. Beran, J. Phys. Chem. C, 2009, 113, 4898–4908 CrossRef CAS.
- D. W. Blaylock, Y.-A. Zhu and W. H. Green, Top. Catal., 2011, 54, 828–844 CrossRef CAS.
- J. T. Stuckless, N. Al-Sarraf, C. Wartnaby and D. A. King, J. Chem. Phys., 1993, 99, 2202–2212 CrossRef CAS.
- J. T. Stuckless, C. E. Wartnaby, N. Al-Sarraf, St. J. B. Dixon-Warren, M. Kovar and D. A. King, J. Chem. Phys., 1997, 106, 2012–2030 CrossRef CAS.
- J. Lapujoulade and K. S. Neil, J. Chem. Phys., 1972, 57, 3535–3545 CrossRef CAS.
- J. Segner, C. Campbell, G. Doyen and G. Ertl, Surf. Sci., 1984, 138, 505–523 CrossRef CAS.
- W. J. Hehre, R. Ditchfield, L. Radom and J. A. Pople, J. Am. Chem. Soc., 1970, 92, 4796–4801 CrossRef CAS.
- J. A. Pople, L. Radom and W. J. Hehre, J. Am. Chem. Soc., 1971, 93, 289–300 CrossRef CAS.
- R. O. Ramabhadran and K. Raghavachari, J. Chem. Theory Comput., 2011, 7, 2094–2103 CrossRef CAS PubMed.
- R. O. Ramabhadran and K. Raghavachari, Acc. Chem. Res., 2014, 47, 3596–3604 CrossRef CAS PubMed.
- S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 204–220 CAS.
- S. N. Elliott, M. Keçeli, M. K. Ghosh, K. P. Somers, H. J. Curran and S. J. Klippenstein, J. Phys. Chem. A, 2023, 127, 1512–1531 CrossRef CAS PubMed.
- P. Buerger, J. Akroyd, S. Mosbach and M. Kraft, Combust. Flame, 2018, 187, 105–121 CrossRef CAS.
- J. Kubota, S. Ichihara, J. N. Kondo, K. Domen and C. Hirose, Surf. Sci., 1996, 357, 634–638 CrossRef.
- N. M. Abbas and R. J. Madix, Appl. Surf. Sci., 1981, 7, 241–275 CrossRef CAS.
- C. A. Wolcott, I. X. Green, T. L. Silbaugh, Y. Xu and C. T. Campbell, J. Phys. Chem. C, 2014, 118, 29310–29321 CrossRef CAS.
- E. M. Karp, C. T. Campbell, F. Studt, F. Abild-Pedersen and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 25772–25776 CrossRef CAS.
- K. Abeywardane and C. F. Goldsmith, ACS Phys. Chem. Au, 2024, 4, 247–258 CrossRef CAS PubMed.
- E. H. Moore, Bull. Am. Math. Soc., 1920, 26, 394–395 Search PubMed.
- A. Bjerhammar, Bull. Géodésique, 1951, 20, 188–220 CrossRef.
- R. Penrose, Math. Proc. Cambridge Philos. Soc., 1955, 51, 406–413 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: DFT data, additional mathematical derivations, and Jupyter notebooks. See DOI: https://doi.org/10.1039/d4cs00768a |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Gabriel S.
Gusmão
*a,
Gabriel S.
Gusmão
 b,
Dingqi
Nai
b,
Sushree Jagriti
Sahoo
b,
Andrew A.
Peterson
b,
Dingqi
Nai
b,
Sushree Jagriti
Sahoo
b,
Andrew A.
Peterson
 a,
David H.
Bross
a,
David H.
Bross
 c,
C. Franklin
Goldsmith
c,
C. Franklin
Goldsmith
 *a and
Andrew J.
Medford
*a and
Andrew J.
Medford
 *b
*b
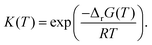

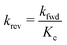
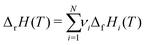
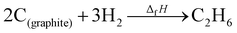
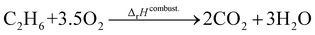
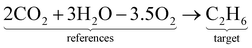
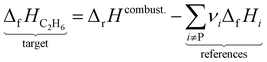


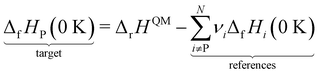
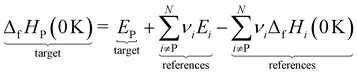
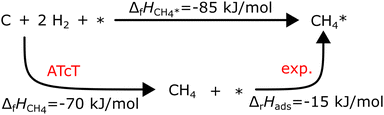
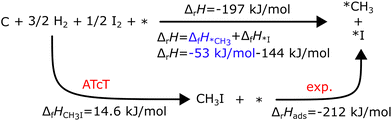
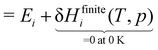
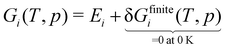

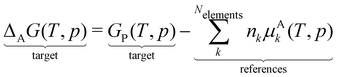
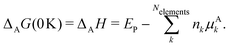
 . ΔAHP referenced to the anchors A = [CH4, H2O, H2, Pt(111)] is then defined as:
. ΔAHP referenced to the anchors A = [CH4, H2O, H2, Pt(111)] is then defined as:
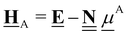
 is the elemental composition matrix (number of molecules × number of elements) of the target species.
is the elemental composition matrix (number of molecules × number of elements) of the target species.
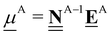


 . With this definition of the chemical potential of the proton–electron pair, it is possible to evaluate, e.g., the surface morphology or stability of alloys at different applied potentials.
. With this definition of the chemical potential of the proton–electron pair, it is possible to evaluate, e.g., the surface morphology or stability of alloys at different applied potentials.

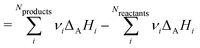


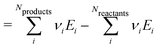
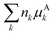 will cancel, making the choice of μAk arbitrary. This invariance proves that as long as a dataset is anchored to the same set of atomic reference species, it is internally consistent and the relative quantities required for microkinetic models will be identical regardless of the anchors selected. The following techniques for comparison and conversion of enthalpies of formation exploit this invariance, selecting “convenient” μAk that allow for comparison of energies under different thermodynamic scenarios or between different levels of theory and for conversion of energies between relative and absolute reference states.
will cancel, making the choice of μAk arbitrary. This invariance proves that as long as a dataset is anchored to the same set of atomic reference species, it is internally consistent and the relative quantities required for microkinetic models will be identical regardless of the anchors selected. The following techniques for comparison and conversion of enthalpies of formation exploit this invariance, selecting “convenient” μAk that allow for comparison of energies under different thermodynamic scenarios or between different levels of theory and for conversion of energies between relative and absolute reference states.
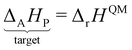
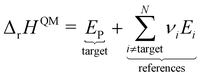
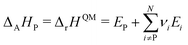
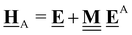
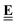 is the vector of the zero-point corrected DFT energies,
is the vector of the zero-point corrected DFT energies, 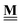 is an m × n stoichiometry matrix with m anchor species and n reactions to form the target from the anchors (not to be confused with the elementary reactions in the mechanism), and
is an m × n stoichiometry matrix with m anchor species and n reactions to form the target from the anchors (not to be confused with the elementary reactions in the mechanism), and ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) A is the vector of the DFT energies of the anchor species. The stoichiometry matrix
A is the vector of the DFT energies of the anchor species. The stoichiometry matrix 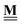 can be constructed by hand, but it is also possible to use linear algebra to determine this from the elemental composition matrix
can be constructed by hand, but it is also possible to use linear algebra to determine this from the elemental composition matrix  .
.  an m × n matrix, but consists of the elemental composition of each species and is, thus, easier to construct and more general since it is independent of the anchor set. We have to construct an elemental matrix for the anchor species
an m × n matrix, but consists of the elemental composition of each species and is, thus, easier to construct and more general since it is independent of the anchor set. We have to construct an elemental matrix for the anchor species  to determine
to determine 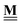 .
.
 of the species to the stoichiometry matrix
of the species to the stoichiometry matrix  that forms the species from the anchor basis set, we can use the inverse of the elemental matrix of the reference species
that forms the species from the anchor basis set, we can use the inverse of the elemental matrix of the reference species 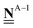 .
.
 must be invertible. This method of referencing DFT energies to a set of anchor species with their DFT values is commonly used. It is suitable for investigating a catalyst for a specific process,158–160 it can be used to screen across the material space,154,161–164 coverage effects on the thermophysical parameters can be included,155 it has been combined with uncertainty quantification,70,165 and it has also been applied to investigate electrocatalytic systems.166 Since the method is identical to the elemental chemical potentials, it is also possible to directly combine it with the CHE model to calculate free energies at applied potentials.167 This method is also the default for calculating ΔAH in the open-source CatMap168 software package, although the notation and nomenclature used in the CatMap package and manuscript are different from the more consistent ones used in this work.
must be invertible. This method of referencing DFT energies to a set of anchor species with their DFT values is commonly used. It is suitable for investigating a catalyst for a specific process,158–160 it can be used to screen across the material space,154,161–164 coverage effects on the thermophysical parameters can be included,155 it has been combined with uncertainty quantification,70,165 and it has also been applied to investigate electrocatalytic systems.166 Since the method is identical to the elemental chemical potentials, it is also possible to directly combine it with the CHE model to calculate free energies at applied potentials.167 This method is also the default for calculating ΔAH in the open-source CatMap168 software package, although the notation and nomenclature used in the CatMap package and manuscript are different from the more consistent ones used in this work.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 kJ mol−1
799 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 kJ mol−1
878 kJ mol−1 that contains all the formation reactions of the target species from the constituent elements to derive the chemical potentials. Rather than selecting a set of explicit anchor species with defined stoichiometries, we seek the set of chemical potentials that minimizes the squared magnitude of the resulting relative enthalpies. The linear algebra formulation offers a convenient way to perform the minimization of squared relative enthalpies magnitudes, which is closely related to the least-squares regression problem and is given in eqn (47).
that contains all the formation reactions of the target species from the constituent elements to derive the chemical potentials. Rather than selecting a set of explicit anchor species with defined stoichiometries, we seek the set of chemical potentials that minimizes the squared magnitude of the resulting relative enthalpies. The linear algebra formulation offers a convenient way to perform the minimization of squared relative enthalpies magnitudes, which is closely related to the least-squares regression problem and is given in eqn (47).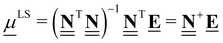
 and the energy vector
and the energy vector ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) . Calculation of ΔLSH is then performed by replacing the chemical potentials in eqn (47) with the expression in eqn (28), leading to
. Calculation of ΔLSH is then performed by replacing the chemical potentials in eqn (47) with the expression in eqn (28), leading to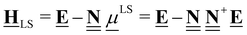
 ). The Python implementation of this method can be found on page 26 of the ESI.†
). The Python implementation of this method can be found on page 26 of the ESI.†

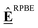 are the aligned energies of the RPBE functional to the BEEF-vdW functional. Eqn (49) allows to align the data from various sources to the same QM zero-of-energy, which is useful in data science and machine learning for providing an unbiased error between different levels of theory.98,170 The method is mathematically similar to the Δ-ML approach, where the thermochemical quantity from one level of theory can be mapped onto another level of theory.171 Here, we present how to do this using least-squares regression to determine elemental chemical potentials. However, the least-squares regression can be replaced with a machine learning model to regress other structural features using e.g. a LASSO (least absolute shrinkage and selection operator) optimization.172,173 The downside of this approach is that the anchor chemical potentials will depend implicitly on all the species present in the dataset and technically need to be re-computed any time the network is expanded, similar to the ATcT.77
are the aligned energies of the RPBE functional to the BEEF-vdW functional. Eqn (49) allows to align the data from various sources to the same QM zero-of-energy, which is useful in data science and machine learning for providing an unbiased error between different levels of theory.98,170 The method is mathematically similar to the Δ-ML approach, where the thermochemical quantity from one level of theory can be mapped onto another level of theory.171 Here, we present how to do this using least-squares regression to determine elemental chemical potentials. However, the least-squares regression can be replaced with a machine learning model to regress other structural features using e.g. a LASSO (least absolute shrinkage and selection operator) optimization.172,173 The downside of this approach is that the anchor chemical potentials will depend implicitly on all the species present in the dataset and technically need to be re-computed any time the network is expanded, similar to the ATcT.77
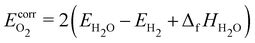
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. They obtained a slightly better agreement with the experimental reaction enthalpies when applying corrections of 9.7 kJ mol−1 to H2 and 14.5 kJ mol−1 for the C
O bond. They obtained a slightly better agreement with the experimental reaction enthalpies when applying corrections of 9.7 kJ mol−1 to H2 and 14.5 kJ mol−1 for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Additional bond-additivity correction factors were obtained for a range of functionals by Granda-Marulanda et al.78 for CO2, CO, –CHx, –OH, C
O bond. Additional bond-additivity correction factors were obtained for a range of functionals by Granda-Marulanda et al.78 for CO2, CO, –CHx, –OH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and (C
O, and (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O. These fragments were hand-picked by experts, which requires chemical intuition and experience. Alternatively, it is possible to use machine-learning techniques like LASSO regression to determine the subgraphs that lead to the best results.173,188 Bond-additivity correction factors for N-containing molecules were determined by Urrego-Ortiz et al.189 using an automated procedure. It has also been shown that the correction factors are correlated across the DFT xc functionals.61,78,185,187,190,191 For example, Urrego-Ortiz et al.190 demonstrated that the correction factor for H2O2 and O2 exhibits a linear correlation for a range of xc functionals. Christensen et al.187,191 observed a linear relation of gas-phase reaction enthalpies when evaluating the ensemble of energies spanned by the BEEF-vdW functional. These correlations suggest that it is possible to construct correction factors that reduce dependence on the chosen xc functional,191 although such schemes will increase the complexity of the bond correction approach. Overall, these correction schemes provide chemically intuitive ways to understand the corrections, and in the simplest cases are very straightforward to apply. The usage of tabulated correction factors in the literature for specific molecules or bond-types can significantly improve the agreement of the overall gas-phase thermodynamics with the accurate thermodynamic data from the global thermochemical network. However, to achieve the best or even exact agreement, it is necessary to determine the correction factors in every self-consistent DFT study.
O)O. These fragments were hand-picked by experts, which requires chemical intuition and experience. Alternatively, it is possible to use machine-learning techniques like LASSO regression to determine the subgraphs that lead to the best results.173,188 Bond-additivity correction factors for N-containing molecules were determined by Urrego-Ortiz et al.189 using an automated procedure. It has also been shown that the correction factors are correlated across the DFT xc functionals.61,78,185,187,190,191 For example, Urrego-Ortiz et al.190 demonstrated that the correction factor for H2O2 and O2 exhibits a linear correlation for a range of xc functionals. Christensen et al.187,191 observed a linear relation of gas-phase reaction enthalpies when evaluating the ensemble of energies spanned by the BEEF-vdW functional. These correlations suggest that it is possible to construct correction factors that reduce dependence on the chosen xc functional,191 although such schemes will increase the complexity of the bond correction approach. Overall, these correction schemes provide chemically intuitive ways to understand the corrections, and in the simplest cases are very straightforward to apply. The usage of tabulated correction factors in the literature for specific molecules or bond-types can significantly improve the agreement of the overall gas-phase thermodynamics with the accurate thermodynamic data from the global thermochemical network. However, to achieve the best or even exact agreement, it is necessary to determine the correction factors in every self-consistent DFT study.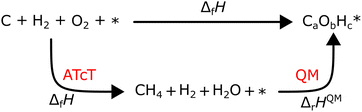


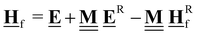
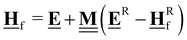
 , which references enthalpies of formation to the ATcT thermochemical network. As shown previously in Section 4.2.2,
, which references enthalpies of formation to the ATcT thermochemical network. As shown previously in Section 4.2.2,  can conveniently be determined from
can conveniently be determined from  and
and  viaeqn (44). An alternative derivation of this approach was developed by Blöndal et al.,192 which relies on an adsorption reaction of the target species.
viaeqn (44). An alternative derivation of this approach was developed by Blöndal et al.,192 which relies on an adsorption reaction of the target species.

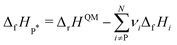
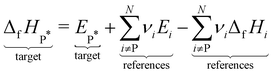
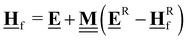
 , we refer the reader to Section 4.2.2. Since the approach connects the DFT data with the ATcT, it is possible to replace all DFT energies of gas-phase species with accurate ΔfH form the ATcT to achieve thermodynamic consistency. The resulting enthalpy diagram using this approach is shown in Fig. 12. Similar to the previous method, this approach does not affect the reaction enthalpies of surface steps since it uses an atomic reference basis set. However, all adsorption/desorption reaction enthalpies are changed except for the reference species. In the previous approach, the adsorption enthalpies of CH4, H2, and H2O were fixed at the DFT values. The difference in this approach is that the adsorption enthalpies of CO, H2, and O2 correspond now to experimental values (see Fig. 13). This adjustment leads to noticeable changes in the adsorption enthalpies of some species. The biggest change occurs for the adsorption of CO2, which changes from strongly exothermic to mildly endothermic. Typically, CO2 binds only weakly through physisorption on the Pt(111) surface.206 Using gas-phase reference ΔfH indicates that the CO2 binds strongly to the surface in disagreement with experiments. Mhadeshwar et al.126 also describe the use of the experimental ΔfH of adsorbates as a basis set to reference the DFT energies to the global thermochemical network, thereby ensuring thermodynamic consistency of the reaction mechanism with known adsorption enthalpies.
, we refer the reader to Section 4.2.2. Since the approach connects the DFT data with the ATcT, it is possible to replace all DFT energies of gas-phase species with accurate ΔfH form the ATcT to achieve thermodynamic consistency. The resulting enthalpy diagram using this approach is shown in Fig. 12. Similar to the previous method, this approach does not affect the reaction enthalpies of surface steps since it uses an atomic reference basis set. However, all adsorption/desorption reaction enthalpies are changed except for the reference species. In the previous approach, the adsorption enthalpies of CH4, H2, and H2O were fixed at the DFT values. The difference in this approach is that the adsorption enthalpies of CO, H2, and O2 correspond now to experimental values (see Fig. 13). This adjustment leads to noticeable changes in the adsorption enthalpies of some species. The biggest change occurs for the adsorption of CO2, which changes from strongly exothermic to mildly endothermic. Typically, CO2 binds only weakly through physisorption on the Pt(111) surface.206 Using gas-phase reference ΔfH indicates that the CO2 binds strongly to the surface in disagreement with experiments. Mhadeshwar et al.126 also describe the use of the experimental ΔfH of adsorbates as a basis set to reference the DFT energies to the global thermochemical network, thereby ensuring thermodynamic consistency of the reaction mechanism with known adsorption enthalpies.



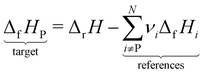

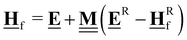
 is the matrix of stoichiometric coefficients for the isodesmic reactions, which can be enumerated using the algorithm or software described in ref. 131. The stoichiometric matrix can again be derived using linear algebra, but in this case, from a matrix
is the matrix of stoichiometric coefficients for the isodesmic reactions, which can be enumerated using the algorithm or software described in ref. 131. The stoichiometric matrix can again be derived using linear algebra, but in this case, from a matrix  (number of molecules × number of fragments) containing the composition of fragments of the target.
(number of molecules × number of fragments) containing the composition of fragments of the target.
 .
.
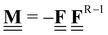
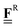 ,
,  , and
, and 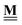 .
.
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) A be the enthalpies of formation of the same species given defined references A and
A be the enthalpies of formation of the same species given defined references A and ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r be the reaction energies according to the stoichiometry matrix
r be the reaction energies according to the stoichiometry matrix  . The relationship between
. The relationship between ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r and
r and ![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) is a simple linear combination, shown in eqn (72).
is a simple linear combination, shown in eqn (72).
![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) and
and ![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) r. Yet, no obvious mapping exists in the opposite direction since this is an under-constrained linear system of equations. The Moore-Penrose219–221 pseudo-inverse of the stoichiometry matrix
r. Yet, no obvious mapping exists in the opposite direction since this is an under-constrained linear system of equations. The Moore-Penrose219–221 pseudo-inverse of the stoichiometry matrix  can be used to construct the inverse mapping. To solve this inverse mapping, it is first necessary to select anchor species for each element from the mechanism, e.g., A = [C2H6, CO, H2O, Pt(111)]. We can separate the stoichiometry matrix into the anchor
can be used to construct the inverse mapping. To solve this inverse mapping, it is first necessary to select anchor species for each element from the mechanism, e.g., A = [C2H6, CO, H2O, Pt(111)]. We can separate the stoichiometry matrix into the anchor 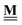 species
species 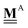 and non-anchor species
and non-anchor species  , leading to eqn (73).
, leading to eqn (73).
![[H with combining low line]](https://www.rsc.org/images/entities/b_char_0048_0332.gif) A into the anchor species
A into the anchor species 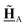 and the unknown
and the unknown  . All enthalpies are referenced to the DFT energies of the anchor species. Thus, the relative enthalpies of the anchor species
. All enthalpies are referenced to the DFT energies of the anchor species. Thus, the relative enthalpies of the anchor species 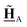 are 0. We can now rearrange the equation to compute the unknown
are 0. We can now rearrange the equation to compute the unknown  from the reaction enthalpies referenced to the set of anchor species.
from the reaction enthalpies referenced to the set of anchor species.
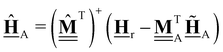

 ). When using gas-phase reference species, this results in the same enthalpies of formation as the method in Section 4.3.2, and when using adsorbates, this is equivalent to Section 4.3.3. Integrating the DFT data into the global thermochemical network allows to replace gas-phase DFT energies with accurate ΔfH from the ATcT. The interested reader is referred to Section 5 of the ESI,† for a more detailed discussion of the linear algebra of this approach and the Jupyter notebook for this method is provided on page 62 of the ESI.† This approach of calculating enthalpies of formation directly from reaction enthalpies can serve as a convenient framework for new methods of combining data from various sources or identifying discrepancies in existing databases.
). When using gas-phase reference species, this results in the same enthalpies of formation as the method in Section 4.3.2, and when using adsorbates, this is equivalent to Section 4.3.3. Integrating the DFT data into the global thermochemical network allows to replace gas-phase DFT energies with accurate ΔfH from the ATcT. The interested reader is referred to Section 5 of the ESI,† for a more detailed discussion of the linear algebra of this approach and the Jupyter notebook for this method is provided on page 62 of the ESI.† This approach of calculating enthalpies of formation directly from reaction enthalpies can serve as a convenient framework for new methods of combining data from various sources or identifying discrepancies in existing databases.





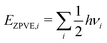
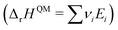














![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C
C