NH₃-induced activation of hydrophilic Fe–N–C nanocages for enhanced oxygen reduction reaction

Abstract

Non-noble metal electrocatalysts for the oxygen reduction reaction (ORR) are urgently needed in metal–air batteries, seawater batteries and fuel cells. Fe–N–C materials are among the most active catalysts for the ORR. Fe–N–C synthesis usually requires post-heat treatment after pyrolysis which is time-consuming and inevitably triggers inactive aggregate Fe species due to difficulties in controllable atom-level modulation. Here, highly active Fe–N–C catalysts were prepared by a simple process involving an ammonia etching treatment by using ZIF-8 as a hard template and a mixture of FeSO₄ and 2-methylimidazole as the Fe, N and C precursors. The direct ammonia treatment modulates N and Fe active species and removes the unstable carbon framework to form pyrolyzed Fe–N–C nanocages with a well-dispersed pore structure. The obtained Fe–N–C exhibits a potential of 0.89 V vs. RHE at a kinetic current density of −1 mA cm⁻² (E₋₁) for the ORR, similar to commercial Pt/C, but outperforming it in terms of stability and methanol tolerance. In situ electrochemical Raman and density functional theory provide insights into the origin of the activity of Fe–N–C materials and the underlying ORR electrocatalytic mechanisms at the molecular level.

---

Introduction

The massive development of renewable energy-based technologies that are required in the next decades represents a global challenge that is necessary to alleviate the current dependence on fossil fuel-based energy supply. The oxygen reduction reaction (ORR) plays a major role in a wide range of electrochemical energy conversion and storage devices involving renewable energy, including metal–air batteries and fuel cells.^1,2 Although current platinum-group metal (PGM) catalysts can provide good activity and stability for the kinetically sluggish ORR, their high cost, low abundance and vulnerability remain grand challenges that limit the wide applications of these energy devices.^1,3–5 To address this, tremendous efforts have been devoted to developing precious metal-free electrocatalysts for the ORR. Transition metal–N complexes on carbon matrices (M–N–C), such as Fe(Co)–N–C, have attracted great interest because of their inherent high activity toward the ORR.^6–8 Among various types of metal centers, the Fe–N–C catalyst created by depositing iron single atoms as metal centers on a nitrogen-doped carbon matrix has been demonstrated to be the most active one to date,⁷ although most of the reported Fe–N–C catalysts currently being pursued do not yet meet the demands of high activity (at least comparable to Pt/C), long-term durability, and low cost. Recently, substantial efforts have been devoted to developing Fe–N–C catalysts with enhanced activity and increased density of FeN₄ active sites for an overall improvement of the ORR activity.^6,9,10 Compared to traditional Fe–N–C catalysts, zeolite imidazole frameworks (ZIF-8) and their derived microporous carbon, which was first studied by Proietti et al.,¹¹ have been identified as ideal precursors to produce FeN_x active sites for the ORR without containing inactive Fe aggregate species due to the abundant pores in ZIF-8 that can serve as the host for the Fe precursor, thus promoting the dispersion and formation of the active Fe metal centers.¹² However, the conventional high-temperature pyrolysis method for the synthesis of Fe–N–C catalysts is time-consuming and usually leads to considerable structural and compositional heterogeneity, such as the content of metal loading, the coordination environment of isolated metal sites, and the structure of the nitrogen-containing carbon matrix.^13,14 Such heterogeneity in structure and composition hinders the establishment of a definitive correlation between the atomistic structure of the isolated metal sites and the exhibited ORR catalytic properties.

Within the preparation of Fe–N–C catalysts, annealing in ammonia is often used to either form active sites¹⁵ or to improve catalytic performance.¹¹ As confirmed by several studies, using an Fe precursor with a high iron content during a pyrolysis step in an argon atmosphere prevents a well-dispersed atomic dispersion of iron (FeN₄ formation) and thus leads to a lower catalytic activity.¹⁵ In contrast to pyrolysis in Ar, an additional heat treatment in NH₃ afterward increases the absolute amount of Fe in FeN₄ coordination.^11,15 Moreover, NH₃ etching can modulate Fe–N_x active sites by forming different N species.¹⁵ However, while enhancing the performance of Fe–N–C catalysts, post-heat treatment after pyrolysis is time-consuming and inevitably gives rise to a non-uniform structure.¹⁶ Moreover, a secondary heat treatment after pyrolysis probably conducts the formation of a carbon framework rich in disordered micropores, which are hardly accessible and lead to the inhomogeneous distribution of active sites, thus hindering optimization of activity due to steric hindrance and the large mass transport resistance.¹⁷

In this study, a Fe–N–C material was synthesized via an ammonia etching strategy by using ZIF-8 as the hard template and a mixture of FeSO₄ and 2-methylimidazole as the Fe, N and C precursors. Exposure to ammonia was correlated with the modulation of N and Fe active species and removal of the unstable carbon framework to form well-dispersed pore structures in the pyrolyzed Fe–N–C catalysts. The Fe–N–C catalyst is far superior to the N–C species in catalyzing the ORR, although their N content is quite similar, demonstrating the dominant role of the Fe–N₄ active site over N₄–C species. Both the ordered mesoporous structure of the carbon framework and the FeN₄ active site along with small clustering of Fe are confirmed with X-ray diffraction (XRD), X-ray absorption spectroscopy (XAS) and aberration-corrected high-angle annular dark field scanning transmission electron microscopy (HAADF-STEM). This work provides a new strategy for effectively manipulating the ORR electrocatalytic performances of Fe–N–C materials by direct NH₃ etching for a sustainable energy conversion system.

Experimental section

Materials synthesis

Synthesis of ZIF-8 and pure NC samples. All syntheses were conducted at room temperature. Typically, 1 g of zinc nitrate hexahydrate was dissolved in 100 mL of methanol with stirring. Then 50 mL of methanol containing 4 g of 2-methylimidazole was added with vigorous stirring for 24 h to form ZIF-8. The solid product (ZIF-8) was collected by centrifugation, washed with ethanol three times, and dried at 60 °C under vacuum overnight. Metal-free N-doped carbon (NC) samples were prepared by pyrolyzing ZIF-8 in a tube furnace at 1000 °C for 1 h with a heating rate of 5 °C min⁻¹ under flowing argon.

Synthesis of Fe-ZIF-8. Typically, FeSO₄·7H₂O (20 mg) and as-made ZIF-8 (1.2 g) were dissolved in 50 mL ethanol and vigorously stirred for 15 min at 60 °C to form a yellow suspension. The solid yellow product (Fe-ZIF-8) was collected by centrifugation, washed with ethanol three times, and dried at 60 °C under vacuum overnight.

Synthesis of Fe–N–C–Ar. The Fe-ZIF-8 samples were pyrolyzed in a tube furnace at 1000 °C for 1 h with a heating rate of 5 °C min⁻¹ under flowing argon. After cooling down, Fe–N–C–Ar was obtained.

Synthesis of Fe–N–C–NH₃. The Fe-ZIF-8 samples were pyrolyzed in a tube furnace at 1000 °C for 1 h with a heating rate of 5 °C min⁻¹ under flowing ammonia gas. After cooling down, Fe–N–C–NH₃ was obtained.

Material characterization

Scanning electron microscopy (SEM) was carried out on a LEO 1550-Gemini microscope operating at 3.00 kV. A platinum layer was sputtered on the samples to increase their surface conductivity. Transmission electron microscopy (TEM) and high-resolution TEM (HR-TEM) images, together with elemental mapping images, were acquired on a Tecnai G2 F30 S-Twin (FEI, Netherlands) working at 200 kV. High-angle annular dark-field scanning TEM (HAADF-STEM) and aberration-corrected HAADF-STEM 3 (AC-HAADF-STEM) images were collected using a Themis Z field emission electron microscope (FEI, Netherlands) working at 200 kV equipped with a probe spherical aberration corrector. X-ray photoelectron spectroscopy (XPS) experiments were conducted on an Axis Ultra DLD imaging XPS using hybrid mode (700 × 300 μm) with 80 eV pass energy for survey spectra, as well as 20 eV pass energy for high-resolution spectra of elements. The excitation source was an Al anode operating at 15 kV and 10 mA emission. The X-ray photoelectron spectra were fitted with a Voigt function and a Shirley background and calibrated to the C 1s. Powder X-ray diffraction (PXRD) patterns were recorded on a Bruker D8 Advance diffractometer equipped with a scintillation counter detector with Cu Kα radiation (λ = 0.15184 nm) applying a 2θ step size of 0.02°. Raman spectra were recorded using a Witec (focus innovations) Raman microscope operating with an objective (Nikon, 10×/0.25, ∞/− WD 6.1) and an excitation wavelength of 532 nm with an intensity of 3.5 mW. The nitrogen sorption isotherms were measured with a Belsorp Max automatic volumetric adsorption system at liquid nitrogen temperature (77 K) using N₂ as the probe gas after a degassing process at 120 °C for 12 h under vacuum. The specific surface areas and pore size distribution were obtained by using the Brunauer–Emmett–Teller (BET) equation and the nonlinear density functional theory (NL-DFT) model. The XA spectra at the Fe L-edge were acquired in total electron yield (TEY) mode by measuring the drain current of the Fe–N–C materials spread uniformly on double-sided copper tape. The XAS measurements were performed at the U49/2 PGM-1 beamline of the synchrotron BESSY II using the LiXEdrom endstation.¹⁸ For the Fe L_2,3-edges, the spectra were normalized to the XAS area calculated over the region 700–730 eV. The photon flux was adjusted to avoid sample damage during the measurement. The RIXS measurements were performed at the U41-PEAXIS beamline using the endstation PEAXIS of BESSY II.¹⁹ The samples were prepared using the same procedure as for XAS. The RIXS spectra were acquired with an incident angle of 30° from the sample surface and a scattering angle, 2θ, of the CCD detector at 60°. Carbon tape was used to determine the energy resolution to 150 meV at the Fe L-edge. Fe L-edge spectra were acquired for 30 min per incident energy. Due to the sensitivity of the sample to X-ray exposure, the spectra were acquired while the sample was moving at a meandering pattern at a horizontal speed of 100 μm s⁻¹ and vertical speed of 1000 μm s⁻¹. The XAS measurements at the Fe K-edge were performed at the KMC-2 beamline of the synchrotron BESSY II.²⁰ Further details of the experimental setup are described elsewhere in depth.^20,21 For the sample preparation, a thin and uniform layer of the powder was evenly spread on Kapton tape. Excess powder was carefully brushed away, and the tape was then folded multiple times to create 1 cm × 1 cm measurement windows. The Fe–N–C NH₃ and Fe–N–C Ar samples were measured in fluorescence mode, along with commercial Fe-oxides in transmission mode. The energy calibration was conducted by aligning the first inflection point of a simultaneously measured Fe metal foil to 7112 eV. All spectral normalization involved the subtraction of a linear baseline obtained by fitting the data before the Fe K-edge and division by a polynomial function of order 3 obtained by fitting the data after the Fe K-edge for analysis near the edge and division by a knot spline for the extended X-ray absorption fine structure (EXAFS) analysis. The Fourier transform (FT) of EXAFS was performed in the energy range from 35 to 340 eV above the Fe K-edge (corresponding to 3 to 9.45 Å⁻¹), with the reference energy (E₀) set at 7112 eV for the Fe K-edge.

In situ electrochemical Raman characterization

A controlled active area of 3.5 cm² with 5 μL catalyst ink dropcast on an Au-coated film was used as the working electrode with counter (carbon) and reference (Ag/AgCl) electrodes onto the SP 200 (BioLogic) potentiostat and the in situ Raman experiment was conducted in 0.1 M KOH electrolyte. Raman spectra were collected using a Raman spectrometer LabRAM HR Evolution with a 532 nm excitation laser with a power of 0.5 mW on the sample. The Raman frequencies were calibrated using an Si substrate. A 50× long working distance objective (Olympus, 0.5 NA) was used, focusing on the sample surface and avoiding contact with the electrolyte. Before the backscattered light entered the CCD, a 532 nm notch filter was added to eliminate the laser beam. The acquisition time was set as 30 s for the spectral Raman shift ranging from 400 to 2000 cm⁻¹ using a 300 g mm⁻¹ grating.

Electrochemical measurements

The electrochemical measurements were carried out in a 100 mL three-electrode cell made from polymethyl pentene with a Teflon lid (ALS Inc. part # 013271, 013580) using a Reference 600+ potentiostat (Gamry Inc.) equipped with an RRDE-3A rotator (ALS Inc.). A glassy carbon (GC) rotating disk electrode (RDE) of 3 mm in diameter (0.071 cm²) was coated with a catalyst ink and used as the working electrode. Hg|HgO (ALS Inc.) filled with 1 M NaOH solution and a graphite rod were used as the reference electrode and the counter electrode, respectively. The catalyst deposition on the working electrode was achieved by dropcasting 2.8 μL catalyst ink which was then dried naturally under air. The ink consisted of 5 mg mL⁻¹ catalyst dispersed by 15 min sonication in a mixture of water and ethanol (1 : 1 volume ratio) in the presence of 2 vol% Nafion solution (∼5% Nafion in a mixture of alcohols, Sigma-Aldrich). The total catalyst loading on the GC electrode was 200 μg cm⁻². The electrochemical experiments were conducted in O₂-saturated or Ar-saturated 0.1 M KOH solution and 0.5 M H₂SO₄ solution (Sigma-Aldrich) at room temperature after purging the electrolyte with Ar or O₂ for 30 min. For each sample, three freshly prepared electrodes were measured under the same conditions to assess the reproducibility of the measurements.

Prior to the ORR activity characterization, 10 cyclic voltammograms (CVs) were recorded at a scan rate of 100 mV s⁻¹ in the potential range from 0.2 to −0.4 V vs. Hg|HgO|NaOH and no change of the voltammetric response was observed during the last CVs. Subsequently, electrochemical impedance spectra were collected in the frequency range from 100 kHz to 1 Hz with an AC amplitude of 10 mV (RMS) to determine the uncompensated resistance (R_u) and later correct the measured data (E_measured) by the iR_u-drop according to eqn (1), where i_measured is the measured current. All potentials were converted to the reversible hydrogen electrode (RHE) scale by measuring the voltage between an RHE electrode (Gaskatel) and the reference electrode for 10 min at the beginning of each measurement day. The last value recorded (V_RE) was applied to calculate the potentials vs. RHE according to eqn (1) each measurement day. The average value obtained for different experiment days was 0.87 ± 0.01 V. The obtained R_u values were on average 74.9 ± 3 Ω for all samples.

E_corrected = E_measured + V_RE − i_measuredR_u (1)

To investigate the ORR activity, linear sweep voltammograms (LSVs) were recorded in the potential range from 0.2 to −0.8 V vs. Hg|HgO|NaOH reference electrode at a scan rate of 5 mV s⁻¹ and rotation rate of 1600 rpm. All activity measurements were performed in triplicate to ensure the reproducibility of the measurements (Fig. S7†). An additional LSV was recorded in Ar-saturated electrolyte, at the same scan rate to determine the background current, which was later subtracted from the measured voltammograms (Fig. S7†).

To investigate the ORR stability, 100 CVs were recorded with the catalyst-modified electrodes at a scan rate of 50 mV s⁻¹ in the potential range from 0.2 to −0.8 V vs. Hg|HgO|NaOH reference electrode at a rotation rate of 1600 rpm. The current densities at 0.5 V vs. RHE were then extracted at different cycling rates and plotted as a function of the corresponding number of cycles.

The CH₃OH tolerance tests were carried out by chronoamperometric measurements at 0.45 V vs. RHE in an O₂-saturated 60 mL 0.1 M KOH electrolyte. After 240 s, the measurement was paused to inject 0.5 M CH₃OH (1.22 mL) into the electrochemical cell and the solution was mixed with a magnetic stirrer without disassembling any cell component. The chronoamperometric measurement was then resumed for 240 s more.

The electrochemical double layer capacitance was estimated from the CVs in the non-faradaic potential window from 0.2 to −0.4 V vs. Hg|HgO|NaOH at various scan rates (10, 25, 50, 75, 100 and 150 mV s⁻¹). The fitting model is based on an allometric regression with the variables Y and X as the current and the scan rate, respectively.²² The slope b corresponds to the capacitance while an exponent α is associated with compensating deviations from linearity (eqn (2)).²²

Y = bX^α (2)

RDE voltammetry was performed at various rotating speeds ranging from 100 to 1600 rpm with a sweep rate of 5 mV s⁻¹ to assess the selectivity of the different samples. This experiment was performed in duplicate for each catalyst to ensure that the results are reproducible (Fig. S7†). The number of electrons transferred during the ORR was determined using the Koutechý–Levich (K–L) equation (eqn (3)):

1/J = 1/(0.62nFC₀D₀^2/3V^−1/6ω^1/2) + 1/J_K (3)

where J is the measured current density, n is electron transfer number, F is the Faraday constant (96 485 C mol⁻¹), C₀ is the bulk concentration of O₂ (1.2 × 10⁻⁶ mol cm⁻³), D₀ is the diffusion coefficient of O₂ in 0.1 M KOH (1.9 × 10⁻⁵ cm² s⁻¹), V is the kinematic viscosity of the electrolyte (0.01 cm² s⁻¹), ω is the angular velocity of the disk electrode, and J_K is the kinetic-limited current density.²³ The kinetically controlled potential region is defined here by the potential region at which the current density remains below 20% of the limiting current density.

A rotating ring disk electrode (RRDE) consisting of a GC disc (∅ = 4 mm, 0.126 cm²) and a concentric platinum (Pt) ring (∅ = 7 mm, 0.188 cm²) in polyether ether ketone was used as the working electrode (WE). The GC/Pt-RRDE was polished using deagglomerated alumina (Al₂O₃) pastes with particle sizes of 0.05 μm. The electrode was sonicated in 18 MΩ water after the polishing steps. LSV was performed in an O₂-saturated 0.1 M KOH electrolyte using the RRDE to calculate the collection rate, electron transfer number, and yield of intermediate HO₂⁻. The disk potential is scanned from 1.2 to 0.0 V (vs. RHE), and the platinum ring potential is fixed at 1.2 V vs. RHE with a rotation speed of 1600 rpm at a sweep rate of 5 mV s⁻¹. The ring electrode potential is higher than the disk electrode potential to collect the signal of hydrogen peroxide oxidation. The ring electrode potential of 1.2 V vs. RHE can ensure the oxidation of hydrogen peroxide ions diffusing from the disk electrode to the ring electrode.

The hydrogen peroxide yield and the electron transfer number (n) were calculated with the following eqn (4) and (5) assuming the absence of any side reactions:

H₂O₂ (%) = 200 × (I_R/N)/(I_D + I_R/N) (4)

n = 4 × (I_D)/(I_D + I_R/N) (5)

where I_D is the disk current, I_R is the ring current, and N is the ring collection efficiency (experimental determination of N = 0.36 for Fe–N–C NH₃ and 0.39 for Pt/C 20%).

DFT methods

DFT calculations were performed using the all-electron, numeric atomic orbital FHI-aims software package.²⁴ Calculations were performed using the PBE²⁵ exchange–correlation functional coupled with the many-body dispersion method (DFT + MBD),^26,27 as implemented in FHI-aims, to account for long-range van der Waals effects. Structures were created using periodic boundary conditions with several structures of the Fe–N–C system created with increasing amounts of oxidation in the form of the addition of OH groups to carbons atoms (structures shown in Fig. 9a). To represent the ORR process, O, OH and OOH molecules were added onto the central Fe atom and the geometry was allowed to relax until all convergence criteria were below each threshold of 10⁻⁶ eV for the total energy, 10⁻³ eV for the sum of the eigenvalues, 10⁻⁴ e/a₀³ for the charge density, and 0.01 eV Å⁻¹ for the forces. All calculations were performed at the gamma-point (1 × 1 × 1 Monkhorst–Pack²⁷k-grid) and performed with the built-in ‘tight’ basis set of FHI-aims.

Results and discussion

Electrocatalyst material characterization

Fig. 1 illustrates the synthetic method for preparing the Fe–N–C catalyst. First, ZIF-8 was prepared by mixing Zn(NO₃)₂·6H₂O and 2-methylimidazole (2-MI) in methanol and subsequently the iron precursor FeSO₄·7H₂O was encapsulated in the cages of the zeolite imidazolate frameworks (ZIF-8) via the assembly of Zn²⁺ and 2-methylimidazole (2-MI) in ethanol by oil-bath heating. The obtained solid yellow product (denoted as Fe-ZIF-8) was then collected by centrifugation, washed three times with ethanol, and dried under vacuum overnight. Finally, after pyrolysis of Fe-ZIF-8 at 1000 °C under a pure ammonia or an argon atmosphere with a flow rate at 0.1 L min⁻¹, for carbonization and Zn removal, Fe-ZIF-8 was correspondingly converted into two types of catalysts (denoted as Fe–N–C NH₃ and Fe–N–C Ar according to the atmosphere used during the pyrolysis step). The crystal structures of Fe-ZIF-8 and ZIF-8 (before modification with the Fe precursor) are compared from the XRD patterns in Fig. S1,† showing that the two materials share a similar crystalline structure. ZIF-8 and Fe-ZIF-8 display similar Fourier transform infrared (FTIR) spectra (Fig. S2†), indicating that the introduction of Fe did not change the functional groups on ZIF-8. The O=S=O stretching of sulfate is also revealed by the bands at 1104 cm⁻¹ while the band at 612 cm⁻¹ corresponds to S–O stretching in FeSO₄·7H₂O.²⁸ These two characteristic peaks related to SO₄²⁻ of FeSO₄·7H₂O are not present in Fe-ZIF-8, indicating that the Fe species in this material is not in the form of sulfate salt. The sharp peaks at around 422 cm⁻¹ and 688 cm⁻¹ corresponding to the stretching vibration of Zn–N bonds formed between zinc and imidazole can be observed in the two cases,²⁹ suggesting that the incorporated Fe species are not substituting Zn in the ZIF structure. Furthermore, the characteristic peaks in the range of 700–1600 cm⁻¹ originating from the stretching vibration of the 2-methylimidazole ligands only can be seen in Fe-ZIF-8 and ZIF-8, and the stretching vibration peak of the C=N bond in the imidazole ring appears at 1585 cm⁻¹ of Fe-ZIF-8 and ZIF-8, indicating that Fe doping does not cause the disappearance of organic ligands.³⁰ The rigid structure of ZIF-8 nanocages can reduce the Fe species from aggregation during the heat treatment at high temperatures.

Fig. 1 Schematic procedure for the synthesis of Fe–N–C electrocatalysts for the ORR.

Several characterization techniques were used to confirm the chemical structure and morphology of the Fe–N–C catalyst. Scanning electron microscopy (SEM) images of Fe–N–C NH₃ (Fig. 2a), Fe–N–C Ar (Fig. S3a†), and NC (Fig. S4a†) samples demonstrate that after heat treatment, Fe–N–C samples and NC (prepared by skipping the step involving the Fe precursor during the synthesis) retain their initial dodecahedral shape while the surface becomes rougher. In the transmission electron microscopy (TEM) images (Fig. 2b and c) of Fe–N–C NH₃, there are no nanoparticles or nanoclusters observed over the entire carbon matrix and the images demonstrate a dodecahedral shape as well. The Fe–N–C Ar and pure NC exhibited the same morphology as Fe–N–C NH₃ as shown in Fig. S3 and S4.†Fig. 2d shows the aberration-corrected high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of Fe–N–C NH₃. Single-site iron atoms are clearly identified by isolated bright dots marked with red circles, indicating that single metal sites were uniformly distributed in the carbon skeleton matrix. Similar observations for Fe–N–C Ar are shown in Fig. S3.† Selected-area electron diffraction (SAED) patterns of Fe–N–C NH₃ (Fig. 2e) and Fe–N–C Ar (Fig. S3e†) display clear crystalline diffraction rings corresponding to the (100) and (002) facets of the carbon matrix.³¹ This demonstrates the formation of mostly single atom structure in Fe–N–C materials, and agrees well with the XRD pattern. In addition, energy-dispersive X-ray spectroscopy (EDS) mapping images exhibit that Fe, N, and C are uniformly distributed on the whole architecture of Fe–N–C samples (Fig. 2 and S3†). There is no Fe distribution in the carbon matrix of pure NC as shown in Fig. S4.† Small traces of Zn are homogeneously detected over the whole sample (Fig. S5†). These results demonstrate at well-dispersed structures derived from the pyrolysis of ZIF-8 under NH₃ and Ar could serve as an excellent matrix to host atomically dispersed Fe-based active sites and thus maximize the density of single-atom catalytic sites. Knowing the limitation of TEM in terms of resolving single atoms and signals from a very small area of scanning, XAS studies were performed to further understand the distribution in the N-doped carbon matrix which is discussed later.

Fig. 2 (a) SEM image of Fe–N–C NH₃. (b) and (c) TEM images of Fe–N–C NH₃. (d) Aberration-corrected HAADF-STEM image of Fe–N–C NH₃. (e) SAED pattern of Fe–N–C NH₃. (f)–(i) Elemental mapping analysis of C, N, and Fe of Fe–N–C NH₃ by HAADF-STEM.

From the XRD patterns obtained with the annealed samples (Fe–N–C NH₃, Fe–N–C Ar and NC, Fig. 3a), two broad diffraction peaks at 25° and 43° indexed to the (002) and (100) planes of the N-doped graphitic carbon can be observed for all three samples.³² No clear differences were found between samples annealed under NH₃ and Ar, both presenting amorphous and graphitic carbon characteristic peaks. Raman spectra were collected for the same three samples and are shown in Fig. 3b. The spectra exhibit two peaks at 1347 cm⁻¹ (D band) and 1591 cm⁻¹ (G band) with an intensity ratio (I_D/I_G) of 1.00 for all samples, indicating a similar degree of graphitization.³³ The pore properties were analysed by nitrogen adsorption/desorption isotherms. The pure NC has a significantly larger specific surface area (497 m² g⁻¹) than Fe–N–C NH₃ (380 m² g⁻¹), Fe–N–C Ar (345 m² g⁻¹) and Pt/C 20% (131 m² g⁻¹). As shown in Fig. 3c, all samples displayed type IV isotherms with a steep increase in V_ads at relatively low N₂ pressures (P/P₀ = 0–0.015) due to micropores and a well-defined hysteresis loop at higher N₂ pressures (P/P₀ = 0.45–0.95) due to mesopores. Such a mesoporous structure can be further verified by the pore size distribution plots in Fig. 3d. The Fe–N–C NH₃ and pure NC samples showed a very similar pore distribution with an average pore size of ≈3.5 nm, while Fe–N–C Ar demonstrated an average pore size of ≈3 nm.

Fig. 3 (a) XRD patterns, (b) Raman spectra, and (c) N₂ adsorption–desorption isotherms with (d) corresponding pore size distributions of Fe–N–C NH₃, Fe–N–C Ar, NC and Pt/C 20%.

X-ray photoelectron spectroscopy (XPS) allows the identification of the binding states of Fe, N, and C in the Fe–N–C catalyst, as shown in Fig. 4, 5 and S6.† The presence of Fe is identified in the survey spectrum of Fe–N–C (Fig. S6a†) and represents less than 1 at% (Table S1†). The nitrogen (oxygen) content of Fe–N–C NH₃ is 7.1 (9.7) at%, while those of Fe–N–C Ar and pure NC are 7.4 (6.5) at% and 6.3 (6.3) at%, respectively. The highest O contents of Fe–N–C NH₃ can be ascribed to a higher density of oxygen defects.³⁴ Some residues of Zn (∼0.1 wt%) are identified in Fe–N–C NH₃ and NC as evidenced by the Zn Auger peak at 499.4 eV and Zn 2p peaks from 975 to 1046 eV. The C 1s XPS spectra (Fig. 4a, c and e) of Fe–N–C NH₃, Fe–N–C Ar and pure NC can be deconvoluted into three peaks at around 284.3 eV, 285.3 eV, and 289 eV, attributed to C–C, C–N and C=O, respectively. Meanwhile, the component C–N of Fe–N–C NH₃ exhibits a slight shift to higher energy compared to Fe–N–C Ar, suggesting a lower electron cloud density and thus a higher electron transfer from Fe to the N-doped graphitic matrix at the Fe–N–C NH₃ interfaces.³⁵ N-doping in carbon can change the charge or spin distribution, which facilitates the O₂ adsorption and thus is expected to enhance the ORR performance.^34,35 The N 1s XPS spectra of the three catalysts reveal three dominant peaks at around 398.2 eV, 400.2 eV and 403.8 eV, assigned to pyridinic N, pyrrolic N or pyridonic (N adjacent to a C–O group), and oxidized N, respectively, as shown in Fig. 4b, d and f. Note that defective sites related to C–O and C–N at the C 1s and pyrrolic and oxidized N in the N 1s exhibit broader peaks than the C–C and pyridinic N components (Table S2†), which are mostly related to the well-defined graphitic carbon and Fe–N–C active sites. The broadening is most likely related to slight chemical shifts due to the different chemical environment that cannot be resolved by XPS. The content of pyridinic N in Fe–N–C NH₃, Fe–N–C Ar and pure NC is 35 (±2) % while the content of pyrrolic N is 57% in Fe–N–C NH₃, 54% in Fe–N–C Ar and 53% in pure NC as summarized in Table S2.† The amount of pyrrolic/pyridonic N in Fe–N–C NH₃ and Fe–N–C Ar is therefore increased compared to the pure NC, which instead presents more oxidized N. Pyridinic and pyrrolic N sites are believed to be beneficial for ORR chemistry due to improved oxygen adsorption resulting from a weak bonding energy of oxygen molecules.³⁴ In addition, O 1s XPS spectra confirm the existence of C–OH as shown in Fig. S6b–d,† which is in line with C 1s XPS spectra. Moreover, the peak at around 531.5 eV can be assigned to C=O bonds, suggesting the possible presence of pyrrolic-like nitrogen groups, which were shown to play a role in the ORR of metal-free catalysts.³⁶ The C–OH and C=O groups represent roughly 18% and 82% of the XPS O 1s based on the fitting results (Table S2†), which are related to ∼1.7 at% and 8 at%, respectively for Fe–N–C NH₃. C=O bonds are probably not situated close to Fe₄N sites as they would lead to strong distortion of the carbon framework. On the other hand, C–OH groups may be stable near the active sites for the ORR and affect the catalytic activity, and it will be discussed in the following sections based on DFT calculations. N=O bonds coming from oxidized nitrogen detected at the N 1s may also contribute to this peak.³⁷ From the XPS Fe 2p spectra in Fig. 5a, both Fe–N–C NH₃ and Fe–N–C Ar exhibit similar compositions with Fe 2p_3/2, Fe(II) satellite and Fe 2p_1/2 components, respectively.^38,39 Notably, the Fe 2p XPS spectrum of Fe–N–C NH₃ appears at lower binding energy than that of Fe–N–C Ar, which may be related to the presence of slightly more oxidized Fe atoms in the Fe–N–C Ar catalyst.

Fig. 4 High-resolution C 1s XPS spectra of Fe–N–C NH₃ (a), Fe–N–C Ar (c) and pure NC (e), respectively. High-resolution N 1s XPS spectra of Fe–N–C NH₃ (b), Fe–N–C Ar (d) and pure NC (f), respectively.

Fig. 5 (a) High-resolution Fe 2p XPS spectra of Fe–N–C NH₃ and Fe–N–C Ar. (b)–(d) XAS and RIXS of Fe–N–C materials. (b) XAS at the Fe L_3,2-edge for Fe–N–C NH₃ and Fe–N–C Ar. (c) and (d) Energy loss feature detected from Fe L₃ RIXS of Fe–N–C NH₃ and Fe–N–C Ar, respectively. Zero energy loss (E = 0 eV) corresponds to the elastic line. The excitation energies for the RIXS are labeled as black lines in (b). (e) XANES spectra at the Fe K-edge for Fe–N–C NH₃ and Fe–N–C Ar along with the reference sample Fe₃O₄, Fe₂O₃ and FePc. (f) FT of EXAFS spectra at the Fe K-edge for Fe–N–C NH₃ and Fe–N–C Ar along with the reference sample Fe₃O₄, Fe metal foil and FePc.

The X-ray absorption (XA) spectra at the Fe L-edge of Fe–N–C NH₃ and Fe–N–C Ar are shown in Fig. 5b. This indicated the signature of Fe moieties with an oxidation state close to +3. The Fe³⁺ features are related to the Fe–N bonds, with an L₃-edge composed of two peaks resulting from ligand field splitting. Similar features appear in Fe-doped carbon nanotubes and polymeric carbon nitride.^40,41 The weak shoulder at 713.1 eV may be related to a charge transfer state resulting from the hybridization with oxygen atoms, and possibly nitrogen atoms.⁴² The Fe L₃-edge resonant inelastic X-ray scattering (RIXS) spectra of Fe–N–C NH₃ were also recorded at selected photon energies corresponding to the main XA features and are plotted as a function of the energy loss (Fig. 5c). Two energy loss features at 1.3 eV (A) and 2.6 eV (B), attributed to d–d excitations, are detected for excitation energy below the main L₃ peak.^42,43 Peak A is most clearly observed around 708.4 eV, whereas peak B is more intense at 709.6 eV excitation energy. When the incident energy is detuned above the L₃ resonance (713.1 eV), a broad band around 5 eV is observed, which is related to transitions from 3d to 2p states localized at the Fe atom,⁴⁴ but could also potentially result from the hybridization with the nitrogen ligand. The Fe L₃-edge RIXS of Fe–N–C Ar in Fig. 5d also shows the same features as that of Fe–N–C NH₃, suggesting a similar chemical environment of Fe atoms in both materials. This RIXS signature supports the fact that Fe atoms are incorporated in the N-doped carbon matrix with an oxidation state close to +3. Fe–N–C active sites with a high Fe oxidation state were found to increase ORR activity compared to Fe with an oxidation state closer to +2.⁴⁵

The bulk sensitive XA spectra at the Fe K-edge of Fe–N–C NH₃ and Fe–N–C Ar were obtained. Fig. 5e shows the X-ray absorption near-edge structure (XANES) spectra of Fe–N–C NH₃ and Fe–N–C Ar along with reference samples Fe₃O₄ and Fe₂O₃ and iron phthalocyanine (FePc). The edge position of Fe–N–C NH₃ and Fe–N–C Ar (Fe K-edge at 0.5 of normalized absorption intensity) is overlapped with the Fe₂O₃ reference sample, indicating the bulk oxidation state close to +3, which is well aligned with XAS at the Fe L₃ edge and RIXS analysis. The local structure around the absorbing atom in Fe–N–C NH₃ and Fe–N–C Ar was further tracked by EXAFS at the Fe K-edge (Fig. 5f). The Fourier transform (FT) of the EXAFS spectra of Fe–N–C NH₃ and Fe–N–C Ar showed multiple peaks, which did not support a pure single-site phase. The distinct peak for Fe–N around 1.5 Å reduced distance was clearly observed in Fe–N–C NH₃ and Fe–N–C Ar, confirming the presence of Fe–N_x coordination.⁴⁶ We note that the FT of FePc showed a peak at 2.46 Å reduced distance which had been assigned to Fe–C bonds.⁴⁷ The FT peaks in our samples were clearly distinct. The second coordination peak in Fe–N–C NH₃ overlaps with that of the Fe metal foil at 2.2 Å reduced distance, suggesting the presence of Fe–Fe bonding along with single atom sites.⁴⁸ Meanwhile, in Fe–N–C Ar a small peak around 3.0 Å reduced distance coincided with the second coordination peak of Fe₃O₄ reference oxides,⁴⁹ which suggests the presence of small metal oxide nanoparticles along with Fe–N_x sites. Overall, both Fe–N–C NH₃ and Fe–N–C Ar exhibited single atom sites along with small Fe metal clusters on Fe–N–C NH₃ and FeO_x nanoparticles on Fe–N–C Ar.

Profiting from a series of merits, such as rich defects and a high total content of nitrogen and oxygen species as well as large specific surface area, Fe–N–C catalysts (both Fe–N–C NH₃ and Fe–N–C Ar) display extreme hydrophilicity with a contact angle (θ) of approximately 0°, much better than pure NC (15°) and commercial Pt/C (150°) (Fig. S7†). The favourable hydrophilicity has been proven to increase the transport and adsorption of hydrated O₂ to the active sites, further improving ORR activity.^34,35 While this may have a relatively small impact on half-cell performances, it may impact more significantly full membrane electrode assembly.

Electrochemical evaluation of Fe–N–C for the ORR

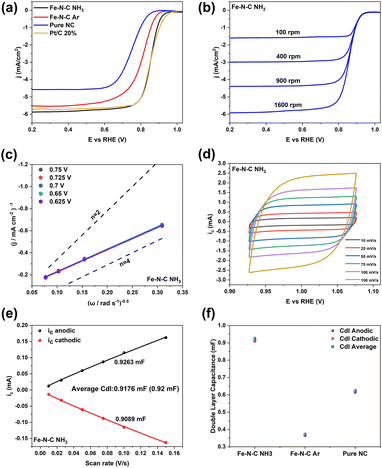
The activity of Fe–N–C NH₃ catalysts toward the ORR was investigated by rotating disk electrode (RDE) measurements. Linear sweep voltammetry (LSV) was performed at a scan rate of 5 mV s⁻¹ and electrode rotation at 1600 rpm as shown in Fig. 6a. The procedure for the background correction is shown in Fig. S8a–d.† The reproducibility of three consecutive measurements was validated as shown in Fig. S8e–h.† To compare the electrocatalytic activity in the kinetic-control voltametric region, three parameters were determined, namely, the onset potential (E_onset), defined here as the potential at which the current density reaches −0.1 mA cm⁻², the potential at a current density of −1 mA cm⁻² (E₋₁) and the half-wave potential (E_1/2).^50,51 These parameters were estimated from the LSV curves (Fig. 6a) to E₋₁ = 0.89 ± 0.002 V (E_1/2 = 0.86 ± 0.002 V) vs. RHE for Fe–N–C NH₃, comparable with that of Pt/C 20% (E₋₁ = 0.9 ± 0.005 V; E_1/2 = 0.86 ± 0.005 V) and higher than for Fe–N–C Ar (E₋₁ = 0.85 ± 0.006 V; E_1/2 = 0.81 ± 0.006 V) and pure NC (E₋₁ = 0.79 ± 0.004 V; E_1/2 = 0.75 ± 0.004 V). This is also observed in terms of the E_onset, which was 0.97 ± 0.005 V vs. RHE for Fe–N–C NH₃, while it was found more negative for NC (0.88 ± 0.006 V vs. RHE) and Fe–N–C Ar (0.93 ± 0.009 V vs. RHE). Furthermore, the ORR performance of the most active sample Fe–N–C NH₃ was also investigated in acidic media (0.5 M H₂SO₄) by RDE. Interestingly, Fe–N–C NH₃ was also active for the ORR in an acidic solution. As shown in Fig. S8i,† the E_onset and E₋₁ of Fe–N–C NH₃ were 0.85 ± 0.01 V and 0.79 ± 0.006 V, respectively, which were comparable to those of Pt/C and higher than some of other non-precious metal–based catalysts in acidic electrolyte^52–54 but still significantly lower than those in alkaline electrolyte. The Fe–N–C active site may be less stable in acidic electrolyte or experience a decrease in ORR activity due to competitive carbon surface oxidation and corrosion reaction with protons in acidic solution.

Fig. 6 (a) Background-corrected linear sweep voltammograms of Fe–N–C NH₃, Fe–N–C Ar, pure NC and Pt/C 20% recorded at a scan rate of 5 mV s⁻¹ with an electrode rotating rate of 1600 rpm. (b) Background-corrected linear sweep voltammograms of Fe–N–C NH₃ recorded at a scan rate of 5 mV s⁻¹ with electrode rotation rates of 100, 400, 900 and 1600 rpm. (c) The fitted Koutecký–Levich plots of Fe–N–C NH₃ at different electrode potentials for the determination of the number of electrons transferred (n); line plots corresponding to the theoretical n = 2 and n = 4 are shown to facilitate visual comparison. (d) Cyclic voltammograms recorded at different scan rates from 10 to 150 mV s⁻¹ in the potential range of 0.9 to 1.1 V vs. RHE for Fe–N–C NH₃. (e) The extraction of the C_dl of Fe–N–C NH₃. (f) Average C_dl comparison of Fe–N–C NH₃, Fe–N–C Ar and pure NC. All measurements were conducted using an O₂-saturated 0.1 M KOH solution as an electrolyte.

The diffusion-limited current density J_L (determined here at a potential of 0.2 V vs. RHE) of Fe–N–C NH₃ (−5.9 ± 0.06 mA cm⁻²) is comparable to that of commercial Pt/C 20% (−5.8 ± 0.1 mA cm⁻²), and higher than that of Fe–N–C Ar (−5.5 ± 0.08 mA cm⁻²) and pure NC (−4.6 ± 0.07 mA cm⁻²), which could be correlated to differences in selectivity between these materials. To gain further insight into the electron-transfer pathway of all samples, the RDE measurements were conducted at various rotation speeds from 100 to 1600 rpm.⁵⁴ The measurements show again a high reproducibility (Fig. S9†). Fig. 6b and S10a, c and e† show that the current densities were enhanced with the increasing rotation speed, while the onset potentials remained constant at different rotation speeds. Fig. 6c and S10b, d, f† illustrate the Koutecký–Levich (K–L) plots of all samples, which displayed excellent linearity between the inverse of the current density (1/j) and the negative of the square root of the scan rate (ω^−0.5) at different potentials. Moreover, the numbers of transferred electron per oxygen molecule in the ORR of Fe–N–C NH₃ were almost the same between 0.625 and 0.75 V vs. RHE, implying first-order reaction kinetics for the ORR.⁵⁵ The transfer numbers of these three catalysts are estimated to be 3.54 (pure NC), 3.95 (Fe–N–C Ar) and 3.98 (Fe–N–C NH₃) from the slopes of the linear fitting plots. The values of the Fe–N–C samples approach n = 4, corroborating a four-electron oxygen reduction process (Fig. 6c and S10†).

The correlation between specific surface area and electrochemically active surface area (ECSA) is highly important to confirm the extent of the surface area involved in the electrochemical reaction.⁵⁶ Specific surface area refers to the total surface area of a material per unit mass or volume, while ECSA refers to the portion of the surface area that is electrically conductive and exposed to the electrolyte.^57,58 Since the electrochemical reactions, including the ORR, take place at the interface between the electrode and the electrolyte, a larger ECSA indicates higher availability of catalytic sites and better conductivity. Therefore, we used the non-faradaic capacitive double-layer current as a proxy of the ECSA to further evaluate the relative catalyst activity of the materials in this study. It was measured using the scan-rate dependence of cyclic voltammograms (CVs).^57,58 For this purpose, CVs were collected with each of the catalysts at scan rates ranging from 10 to 1000 mV s⁻¹ in the non-faradaic potential range between 0.9 and 1.1 V vs. RHE for Fe–N–C NH₃, Fe–N–C Ar and pure NC. The obtained voltammograms are shown in Fig. 6d, S11a, c and e† for Fe–N–C NH₃, Fe–N–C Ar, pure NC and Pt/C 20%, respectively. From the obtained voltammograms, the anodic and cathodic currents measured at a potential of 1.0 V vs. RHE for Fe–N–C NH₃, Fe–N–C Ar and pure NC were extracted and plotted as a function of the scan rate as shown in Fig. 6e, S11b and d,† respectively. The double-layer capacitance (C_dl) values can be calculated by determining the slope using an allometric fit according to a previously reported procedure (fitting details are shown in Table S3†).²² As shown in Fig. 6f, the average C_dl is 0.92 mF for Fe–N–C NH₃, higher than that of Fe–N–C Ar (0.37 mF) and pure NC (0.62 mF), indicating the higher electrochemical active surface area of the Fe–N–C NH₃ catalyst among N–C materials, which is attributed to the large surface area and defective network of the Fe–N–C NH₃ catalyst, elucidating numerous active site exposure and thus profiting mass transfer and charge transport during the ORR. It is noted that the specific surface areas of Fe–N–C NH₃ and Fe–N–C Ar are very similar whereas the average C_dl and expected ECSA of Fe–N–C NH₃ are much higher than those of Fe–N–C Ar, indicating that a larger portion of the surface area in Fe–N–C NH₃ is in electrochemical contact with the electrolyte compared to Fe–N–C Ar, leading to relatively superior ORR performance.

Additionally, long-term stability and methanol tolerance are two other critical factors for application in fuel cells.⁵⁹ Thus, we examined the stability through recording 100 CVs and then extracted the current at 0.5 V vs. RHE of Fe–N–C NH₃, Fe–N–C Ar and Pt/C 20% (Fig. 7a and S12a and b†). Fig. 7b shows the currents recorded with the different samples as a function of the cycle number, relative to the current recorded during the first cycle. Fe–N–C NH₃ had the best durability with almost 99.4% of the current maintained in the system by the end of the test compared to that of Fe–N–C Ar (96.8%) and commercial Pt/C (98.2%). In addition, methanol tolerance was measured by i–t chronoamperometric response under the same conditions with the addition of 0.5 M methanol. As shown in Fig. 7c, the current density of Pt/C dropped sharply. In contrast, it recovered rapidly after a tiny transitory disturbance for Fe–N–C NH₃ and Fe–N–C Ar, indicating the superb methanol tolerance ability of Fe–N–C materials.⁵³ After recording 100 cycles for the stability test and 6-min methanol tolerance test, LSVs were recorded to compare the activity before and after the stability and methanol tolerance test. As shown in Fig. 7d and S12c and d,† negligible negative shifts were detected for the E₋₁ and E_onset of Fe–N–C NH₃, while a 40 mV loss for E₋₁ of Pt/C 20% and a large decline for J_L of Fe–N–C Ar were observed, indicating that Fe–N–C NH₃ had a better stability than other catalysts. Also, LSV curves of Fe–N–C NH₃, Fe–N–C Ar and Pt/C 20% were obtained before and after the methanol tolerance test (Fig. 7d and S12c and d†); Pt/C 20% and Fe–N–C Ar produced an obvious oxidation peak of methanol in the LSV curve and a large potential loss of 25 mV with a large decrease of J_L,0.2, respectively, while the E₋₁ of Fe–N–C NH₃ has only a slight 10 mV positive shift compared to its LSV curve before the methanol tolerance test. These results indicate that Fe–N–C NH₃ has the best durability and tolerance to methanol compared with commercial Pt/C and Fe–N–C Ar. Longer stability tests on real fuel cells will be needed to assess the potential of Fe–N–C NH₃ for practical applications.

Fig. 7 (a) Stability test recording 100 cyclic voltammograms of Fe–N–C NH₃ at a scan rate of 50 mV s⁻¹. (b) Relative current as a function of time for the evaluation of the stability of Fe–N–C NH₃, Fe–N–C Ar and Pt/C 20% determined by extracting each current density value at 0.5 V vs. RHE of each cycle. (c) Methanol tolerance test for Fe–N–C NH₃, Fe–N–C Ar, pure NC and Pt/C 20%. (d) ORR activity plots of the Fe–N–C NH₃ catalyst before and after stability test and methanol tolerance in O₂-saturated 0.1 M KOH electrolyte. (e) RRDE voltammograms of the Fe–N–C NH₃ catalyst and Pt/C 20% measured at a scan rate of 5 mV s⁻¹ using the RRDE in O₂-saturated 0.1 M KOH electrolyte at a rotation speed of 1600 rpm while the Pt-ring was kept at 1.2 V_RHE and (f) the corresponding H₂O₂ yield and electron transfer number from (e).

To further evaluate the ORR efficiency, an electrocatalytic experiment using a rotating ring disk electrode (RRDE) was carried out in O₂-saturated 0.1 M KOH aqueous solution. The potential of the Pt ring on the RRDE was set as at 1.2 V vs. RHE during the ORR test to monitor the concentration change of HO₂⁻. The ring current density of both Fe–N–C NH₃ and Pt/C 20% are lower compared to disk counterparts, indicating a low amount of HO₂⁻ formation (Fig. 7e). As shown in Fig. 7f, the yield of HO₂⁻ remains below 3% over the potential ranging from 0.2 to 0.8 V vs. RHE. Moreover, the average numbers of electron transfer (n) for Fe–N–C NH₃ and Pt/C 20% are 3.98 and 3.97 from 0.2 to 0.8 V vs. RHE, leading to the average yield of HO₂⁻ being strikingly suppressed to average 1.3% and 1.6%, respectively. This result highly supports the calculation results derived from K–L plots, confirming that the Fe–N–C NH₃ electrode advances a four-electron ORR process as commercial Pt/C 20%. Thus, the low production of peroxide is evidence of a four-electron ORR pathway over the Fe–N–C NH₃ electrode, indicating enhanced catalytic efficiency. The ORR performance in terms of the activity and number of electrons transferred of recently reported PGM-free Fe-based catalysts is listed in Table S4,† demonstrating the excellent ORR catalytic performance of Fe–N–C NH₃ materials.

In situ Raman spectroscopy investigation of Fe–N–C NH₃ in 0.1 M KOH

Monitoring the structural variation of the active sites in the reaction environment allows the exploration of the catalytic mechanism that can lead to a tailored design of advanced catalysts. Therefore, in situ Raman was carried out for the most active Fe–N–C NH₃ in the ORR process as shown in Fig. 8. The in situ Raman spectra give evidence for the generation of O-containing intermediates on the surface of Fe–N_x in Fe–N–C and exhibit a broad Raman band around 650 cm⁻¹, due to O–O stretching of OOH bound to Fe (Fig. 8).^60–63 The intensity increases when shifting the potential from 0.9 to 0.2 V vs. RHE, suggesting an accumulation of OOH intermediates. The appearance of a shoulder around 1000 and 1200 cm⁻¹, especially for potentials below 0.7 V vs. RHE, is attributed to the formation of superoxo species (O₂⁻) adsorbed on the Fe active site.⁶⁴ Note that no contribution is detected around 1500 cm⁻¹, as reported in previous Fe–N–C catalysts and attributed to C–N active sites for the ORR.⁶⁴ Previous studies suggest that the metallic nanoparticles are less active for oxygen electrocatalysis as compared to Fe–N–C. Fe–N_x sites appear therefore to be the main ORR active sites in Fe–N–C NH₃ catalysts.^65,66

Fig. 8 In situ Raman measurements at applied potentials (vs. Ag/AgCl) for the Fe–N–C NH₃ electrocatalyst in 0.1 M KOH during the ORR process.

DFT simulation

Based on previous XPS results, Fe–N–C NH₃ has more oxygen defects than Fe–N–C Ar and pure NC. Thus density-functional theory calculations (DFT) were carried out to provide an in-depth understanding of the role of oxygen in the form of OH groups next to the Fe–N–C structure in influencing the ORR process. Perfect FeN₄ sites are known to be active sites for the ORR, also with vacancies next to the nitrogen atoms.⁶⁷ However, based on our XPS results, it appears that defect sites may contain oxygen groups based on the large amount of oxygen detected, forming C–O bonds with carbon atoms. We have therefore considered different FeN₄ models with varying amounts of hydroxyl groups next to the FeN₄ site, as shown in Fig. 9a. The adsorption energies for three different oxygen-containing intermediates in the ORR process (addition of O, OH and *OOH to the Fe atom) were calculated using the following equation:

E_ads = E_system − (E_clean + E_molecule)

where E_system is the total energy of the whole system, E_clean is the total energy of the Fe–N–C molecule with no oxygen group adsorbed onto the central Fe atom and E_molecule is the total energy of the isolated O, OH or OOH molecule. A larger, more negative adsorption energy (E_ads) corresponds to a more favourable configuration.

Fig. 9 (a) Top-down (top) and side-on (bottom) view of structures of DFT calculated clean FeN₄ active centres with additional hydroxyl groups increasing from 1 to 4 from left to right, (b) DFT calculated adsorption energies of O (green), OH (orange) and OOH (blue) onto the Fe–N–C catalyst with increasing number of OH groups added to the Fe–N–C structure.

The results for the addition of up to 4 OH groups for each of the three ORR structures are shown in Fig. 9b. For an increasing amount of OH groups, the adsorption energy for each of the three oxygen intermediates becomes smaller meaning a weaker bond between the Fe–N–C structure and the intermediate. The more labile chemical bonding of oxygen intermediates on more oxidized surfaces may explain the higher catalytic activity and durability of Fe–N–C NH₃. While the oxygen adsorption on FeN₄ centers remains highly favourable (negative adsorption energies), the oxygen intermediates are more loosely bonded and therefore more likely to evolve further.

Conclusion

In summary, we describe an Fe–N–C electrocatalyst fabricated by a microporous ZIF-8-assisted and NH₃ etching-induced strategy and demonstrated its superior ORR activity. The obtained Fe–N–C NH₃ shows excellent electrocatalytic activity toward the ORR with an onset potential of 0.97 V vs. RHE, a potential of 0.89 V vs. RHE at a current density of −1 mA cm⁻² and a limiting current density of −5.91 mA cm⁻² at 1600 rpm, implying a four-electron transfer. Additionally, this catalyst also demonstrates excellent durability and reproducibility. It can also work in acidic media although with poorer ORR performance as in alkaline media. RRDE results corroborate that the ORR catalyzed by Fe–N–C NH₃ is a four-electron reaction and produces little peroxide. Experimental investigations combining XPS, XAS and RIXS with electrochemical in situ Raman spectroscopy indicate that Fe active sites with an oxidation state close to +3, possibly coordinated with nitrogen adjacent to oxidized carbon atoms, can effectively promote the key intermediate *OOH at low overpotentials during the ORR process. The higher accessibility of the electrochemically active site after NH₃ annealing and the lower adsorption energy of oxygen intermediates due to the presence of oxygen defects contribute to the higher ORR activity of the Fe–N–C catalyst. This work provides a facile synthesis approach to promote activity and durability of the Fe–N–C system and can be easily extended to other transition metal-based systems, offering new directions for the exploration of inexpensive and highly efficient ORR electrocatalysts.

Data availability

The data for the DFT calculations are openly available and can be found at the URL/DOI: https://doi.org/10.17172/NOMAD/2024.12.02-1. Other data are available upon request to the authors.

Author contributions

B. Wu performed the electrochemical experiments and wrote the manuscript. B. Wu and D. M. Morales collected and analyzed the electrochemical data under the supervision of M. Risch. H. B. Meng carried out TEM, HAADF-STEM, SEM, BET, XRD and Raman measurements. D. Wong and C. Schulz carried out soft XAS and RIXS measurement. G. Zuliani, M. Zoli, O. Y. Bisen and M. Risch carried out hard XAS and analyzed the data of XAS. S. Hall, A. Bande, B. Liu and Z. B. Wang performed DFT calculations. T. Petit initiated and supervised the whole project. All the authors discussed the results and assisted during the manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Volkswagen Foundation (Freigeist Fellowship No. 89592) and CSC scholarship (No. 201904910594). The authors also acknowledge support from the Federal Ministry of Education and Research in the framework of the project CatLab (03EW0015A/B). The authors thank Dr. Peter Bogdanoff and Prof. Ulrike Kramm for fruitful discussions. We thank the Helmholtz-Zentrum Berlin für Materialien und Energie for the allocation of synchrotron radiation beamtime and providing computing resources along with additional resources from LUH, funded by the Deutsche Forschungsgemeinshaft (DFG, German Research Foundation) – Projektnummer (INST 187/742-1 FUGG). The authors thank Konstantin Rücker, Darius Hayes, Elliot Brim, Imke Mönkeberg, Jasmin Schmeling and Carla Terboven for helping with XAS data collection, Götz Schuck for support at the KMC-2 beamline and Louis Godeffroy for support with SEM–EDX.

References

1. B. Wu, H. Meng, D. M. Morales, F. Zeng, J. Zhu, B. Wang, M. Risch, Z. J. Xu and T. Petit, Adv. Funct. Mater., 2022, 32, 2204137.
2. W. Deng, Z. Song, M. Jing, T. Wu, W. Li and G. Zou, Carbon Neutralization, 2024, 3, 501–532.
3. W. Wei and W. Chen, Int. J. Smart Nano Mater., 2013, 4, 62–71.
4. P. Rao, Y. Yu, S. Wang, Y. Zhou, X. Wu, K. Li, A. Qi, P. Deng, Y. Cheng, J. Li, Z. Miao and X. Tian, Exploration, 2024, 4, 20230034.
5. J. Kundu, T. Kwon, K. Lee and S.-I. Choi, Exploration, 2024, 4, 20220174.
6. F.-X. Ma, Z.-Q. Liu, G. Zhang, Y.-X. Xiong, M.-T. Zhang, L. Zheng, L. Zhen and C.-Y. Xu, Small, 2022, 18, 2205033.
7. J. Li, S. Ghoshal, W. Liang, M.-T. Sougrati, F. Jaouen, B. Halevi, S. McKinney, G. McCool, C. Ma, X. Yuan, Z.-F. Ma, S. Mukerjee and Q. Jia, Energy Environ. Sci., 2016, 9, 2418–2432.
8. A. Zitolo, V. Goellner, V. Armel, M.-T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937–942.
9. K. Strickland, E. Miner, Q. Jia, U. Tylus, N. Ramaswamy, W. Liang, M.-T. Sougrati, F. Jaouen and S. Mukerjee, Nat. Commun., 2015, 6, 7343.
10. U. I. Kramm, I. Herrmann-Geppert, J. Behrends, K. Lips, S. Fiechter and P. Bogdanoff, J. Am. Chem. Soc., 2016, 138, 635–640.
11. E. Proietti, F. Jaouen, M. Lefèvre, N. Larouche, J. Tian, J. Herranz and J.-P. Dodelet, Nat. Commun., 2011, 2, 416.
12. Y. Li, P. Zhang, L. Wan, Y. Zheng, X. Qu, H. Zhang, Y. Wang, K. Zaghib, J. Yuan, S. Sun, Y. Wang, Z. Zhou and S. Sun, Adv. Funct. Mater., 2021, 31, 2009645.
13. Z. Miao, X. Wang, M.-C. Tsai, Q. Jin, J. Liang, F. Ma, T. Wang, S. Zheng, B.-J. Hwang, Y. Huang, S. Guo and Q. Li, Adv. Energy Mater., 2018, 8, 1801226.
14. U. I. Kramm, L. Ni and S. Wagner, Adv. Mater., 2019, 31, 1805623.
15. J. Herranz, F. Jaouen, M. Lefèvre, U. I. Kramm, E. Proietti, J.-P. Dodelet, P. Bogdanoff, S. Fiechter, I. Abs-Wurmbach, P. Bertrand, T. M. Arruda and S. Mukerjee, J. Phys. Chem. C, 2011, 115, 16087–16097.
16. M. Chen, Y. He, J. S. Spendelow and G. Wu, ACS Energy Lett., 2019, 4, 1619–1633.
17. M. Kang, Y.-S. Bae and C.-H. Lee, Carbon, 2005, 43, 1512–1516.
18. E. F. Aziz, J. Xiao, R. Golnak and M. Tesch, Journal of large-scale research facilities JLSRF, 2016, 2, A80.
19. C. Schulz, K. Lieutenant, J. Xiao, T. Hofmann, D. Wong and K. Habicht, J. Synchrotron Radiat., 2020, 27, 238–249.
20. A. Erko, I. Packe, C. Hellwig, M. Fieber-Erdmann, O. Pawlizki, M. Veldkamp and W. Gudat, AIP Conf. Proc., 2000, 521, 415–418.
21. O. Y. Bisen, M. Baumung, M. Tatzel, C. A. Volkert and M. Risch, Energy Adv., 2024, 3, 504–514.
22. D. M. Morales and M. Risch, JPhys Energy, 2021, 3, 034013.
23. Z. Jin, H. Nie, Z. Yang, J. Zhang, Z. Liu, X. Xu and S. Huang, Nanoscale, 2012, 4, 6455–6460.
24. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
26. R. A. DiStasio, V. V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
28. F. P. Franguelli, B. Barta-Holló, V. M. Petruševski, I. E. Sajó, S. Klébert, A. Farkas, E. Bódis, I. M. Szilágyi, R. P. Pawar and L. Kótai, J. Therm. Anal. Calorim., 2021, 145, 2907–2923.
29. P. Raju and S. Natarajan, Appl. Nanosci., 2023, 13, 1919–1937.
30. J. Li, T. Tian, Y. Jia, N. Xu, S. Yang, C. Zhang, S. Gao, W. Shen and Z. Wang, Environ. Sci. Pollut. Res., 2023, 30, 4123–4136.
31. R. Ma, G. Lin, Q. Ju, W. Tang, G. Chen, Z. Chen, Q. Liu, M. Yang, Y. Lu and J. Wang, Appl. Catal., B, 2020, 265, 118593.
32. J. Han, X. Meng, L. Lu, J. Bian, Z. Li and C. Sun, Adv. Funct. Mater., 2019, 29, 1808872.
33. G. Long, K. Wan, M. Liu, X. Li, Z. Liang and J. Piao, Chin. J. Catal., 2015, 36, 1197–1204.
34. X. Wei, X. Luo, H. Wang, W. Gu, W. Cai, Y. Lin and C. Zhu, Appl. Catal., B, 2020, 263, 118347.
35. Z. Sun, Y. Wang, L. Zhang, H. Wu, Y. Jin, Y. Li, Y. Shi, T. Zhu, H. Mao, J. Liu, C. Xiao and S. Ding, Adv. Funct. Mater., 2020, 30, 1910482.
36. D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365.
37. S. Abujarada, A. S. Walton, A. G. Thomas, U. K. Chohan and S. P. K. Koehler, Phys. Chem. Chem. Phys., 2019, 21, 10939–10946.
38. F. Mirabella, J. Balajka, J. Pavelec, M. Göbel, F. Kraushofer, M. Schmid, G. S. Parkinson and U. Diebold, ChemPhysChem, 2020, 21, 1788–1796.
39. B. Wu and W. Gao, J. Mater. Sci., 2018, 53, 4433–4443.
40. J. Zhou, P. N. Duchesne, Y. Hu, J. Wang, P. Zhang, Y. Li, T. Regier and H. Dai, Phys. Chem. Chem. Phys., 2014, 16, 15787–15791.
41. J. Ren, L. Lin, K. Lieutenant, C. Schulz, D. Wong, T. Gimm, A. Bande, X. Wang and T. Petit, Small Methods, 2021, 5, 2000707.
42. J. Miyawaki, S. Suga, H. Fujiwara, M. Urasaki, H. Ikeno, H. Niwa, H. Kiuchi and Y. Harada, Phys. Rev. B, 2017, 96, 214420.
43. L.-C. Duda, J. Nordgren, G. Dräger, S. Bocharov and Th. Kirchner, J. Electron Spectrosc. Relat. Phenom., 2000, 110–111, 275–285.
44. K. Atak, S. I. Bokarev, M. Gotz, R. Golnak, K. M. Lange, N. Engel, M. Dantz, E. Suljoti, O. Kühn and E. F. Aziz, J. Phys. Chem. B, 2013, 117, 12613–12618.
45. M. Wang, L. Wang, Q. Li, D. Wang, L. Yang, Y. Han, Y. Ren, G. Tian, X. Zheng, M. Ji, C. Zhu, L. Peng and G. I. N. Waterhouse, Small, 2023, 19, 2300373.
46. H. Tu, H. Zhang, Y. Song, P. Liu, Y. Hou, B. Xu, T. Liao, J. Guo and Z. Sun, Adv. Sci., 2023, 10, 2305194.
47. M. Xiao, J. Zhu, L. Ma, Z. Jin, J. Ge, X. Deng, Y. Hou, Q. He, J. Li, Q. Jia, S. Mukerjee, R. Yang, Z. Jiang, D. Su, C. Liu and W. Xing, ACS Catal., 2018, 8, 2824–2832.
48. H. Tu, H. Zhang, Y. Song, P. Liu, Y. Hou, B. Xu, T. Liao, J. Guo and Z. Sun, Adv. Sci., 2023, 10, 2305194.
49. L. Signorini, L. Pasquini, L. Savini, R. Carboni, F. Boscherini, E. Bonetti, A. Giglia, M. Pedio, N. Mahne and S. Nannarone, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195423.
50. K. J. J. Mayrhofer, D. Strmcnik, B. B. Blizanac, V. Stamenkovic, M. Arenz and N. M. Markovic, Electrochim. Acta, 2008, 53, 3181–3188.
51. W. Chen, Q. Xiang, T. Peng, C. Song, W. Shang, T. Deng and J. Wu, iScience, 2020, 23, 101532.
52. L. Jin, B. Zhu, X. Wang, L. Zhang, D. Song, J. Guo and H. Tao, Materials, 2020, 13, 4551.
53. J. L. Chen, W. B. Li and B. Q. Xu, J. Colloid Interface Sci., 2017, 502, 44–51.
54. L.-J. Yuan, B. Liu, L. Shen, Y.-K. Dai, Q. Li, C. Liu, W. Gong, X.-L. Sui and Z.-B. Wang, Adv. Mater., 2023, 35, 2305945.
55. I.-Y. Jeon, S. Zhang, L. Zhang, H.-J. Choi, J.-M. Seo, Z. Xia, L. Dai and J.-B. Baek, Adv. Mater., 2013, 25, 6138–6145.
56. S. M. Unni, S. Ramadas, R. Illathvalappil, S. N. Bhange and S. Kurungot, J. Mater. Chem. A, 2015, 3, 4361–4367.
57. P. Connor, J. Schuch, B. Kaiser and W. Jaegermann, Z. Phys. Chem., 2020, 234, 979–994.
58. G.-Q. Han, Y.-R. Liu, W.-H. Hu, B. Dong, X. Li, X. Shang, Y.-M. Chai, Y.-Q. Liu and C.-G. Liu, J. Electrochem. Soc., 2015, 163, H67.
59. L. Zhang, J. Niu, L. Dai and Z. Xia, Langmuir, 2012, 28, 7542–7550.
60. M. Jiang, F. Wang, F. Yang, H. He, J. Yang, W. Zhang, J. Luo, J. Zhang and C. Fu, Nano Energy, 2022, 93, 106793.
61. M. Jiang, C. Fu, R. Cheng, W. Zhang, T. Liu, R. Wang, J. Zhang and B. Sun, Adv. Sci., 2020, 7, 2000747.
62. Y.-H. Wang, J.-B. Le, W.-Q. Li, J. Wei, P. M. Radjenovic, H. Zhang, X.-S. Zhou, J. Cheng, Z.-Q. Tian and J.-F. Li, Angew. Chem., Int. Ed., 2019, 58, 16062–16066.
63. M. Li, H. Zhu, Q. Yuan, T. Li, M. Wang, P. Zhang, Y. Zhao, D. Qin, W. Guo, B. Liu, X. Yang, Y. Liu and Y. Pan, Adv. Funct. Mater., 2023, 33, 2210867.
64. J. Wei, D. Xia, Y. Wei, X. Zhu, J. Li and L. Gan, ACS Catal., 2022, 12, 7811–7820.
65. Y. J. Sa, D.-J. Seo, J. Woo, J. T. Lim, J. Y. Cheon, S. Y. Yang, J. M. Lee, D. Kang, T. J. Shin, H. S. Shin, H. Y. Jeong, C. S. Kim, M. G. Kim, T.-Y. Kim and S. H. Joo, J. Am. Chem. Soc., 2016, 138, 15046–15056.
66. O. Y. Bisen, R. Nandan, A. K. Yadav, B. Pavithra and K. Kar Nanda, Green Chem., 2021, 23, 3115–3126.
67. K. Liu, J. Fu, Y. Lin, T. Luo, G. Ni, H. Li, Z. Lin and M. Liu, Nat. Commun., 2022, 13(1), 1–8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cy00124b

---