Understanding alkali-metal driven hydrophosphorylation: mechanism and challenges in the Pudovik reaction

Abstract

The addition of H–P(V) bonds of phosphane oxides across alkynes (hydrophosphorylation reaction) presents an effective synthetic strategy to generate alkenylphosphane oxides. This reaction requires a strong P-nucleophile, such as phosphinite, which can be generated by the reaction of a phosphane oxide with alkali metal amides, such as hexamethyldisilazanides (M-HMDS). Hydrophosphorylation exemplifies an important synthetic reaction facilitated by s-block metal bases. Extensive experimental studies have demonstrated the crucial impact of both the alkali cation and the P-bound substituent on reaction rates, product distribution, and the regio- and stereoselectivity of phosphane oxide addition. This study aims to provide a comprehensive mechanistic interpretation of the alkali metal-catalysed hydrophosphorylation reactions, employing density functional theory (DFT) calculations to clarify experimental findings. Our analysis focuses on two critical stages: 1) formation of the active alkali metal phosphinite species through the metalation–deprotonation of phosphane oxide by M-HMDS, and 2) the subsequent H–P addition onto the alkyne. Additionally, the study addresses side processes that may deactivate the active species by lowering its concentration in solution, potentially impacting the overall reaction efficiency. Computational modelling of reaction mechanisms involving s-block metal cations has been less explored than those with transition metal complexes and faces solvation and speciation as major challenges. This article also discusses the computational requirements necessary for accurate chemical modelling of these systems, as well as the limitations inherent in the employed approach.

---

Introduction

In the quest for sustainable catalysis, there is an increasing interest in the use of s-block metal bases as catalysts in organic synthesis.^1–3 Particularly appealing is their role in hydrofunctionalisation (hydroelementation) reactions, i.e. the addition of H—E bonds (E = N, P) across multiple bonds such as alkenes and alkynes.⁴ These reactions are atom-efficient, enabling a chemoselective formation of C–N and C–P bonds. However, they imply the approach of a base lone pair to an electron-rich π-system of a unsaturated bond. Furthermore, intermolecular hydrofunctionalization reactions are entropically highly disfavored. Thus, the use of a catalyst is mandatory to overcome the high activation barrier and enable the reaction to proceed. s-Block metal based precatalysts can deprotonate the protic substrate, generating a highly nucleophilic species that can add to the carbon atoms of the unsaturated bonds, resulting in formation of new C–E bonds. Although the general mechanism of this reaction is known, key aspects, such as the influence of the metal and the origin of the regio- and stereoselectivity, are not yet fully understood. Computational modelling of s-block metal promoted processes, able to provide answers to these questions, has received comparatively less attention than that centred on transition metal-catalysed processes. Transition metals are able to direct a reaction via overlapping orbitals (Dewar–Chatt–Duncanson model) whereas it is accepted that s-block interactions with electron-rich sites (Lewis bases) are mainly of non-directional ionic nature.

The direct addition of P–H bonds onto unsaturated substrates is an attractive synthetic strategy for creating new C–P bonds, facilitating the preparation of organophosphorous compounds. s-Block metal catalysts are particularly well-suited for catalysing these reactions.^5,6 In this vein, hydrophosphorylation reactions, that is, the addition of H–P(V) bonds of phosphane oxides across alkynes (Pudovik reaction), yield alkenylphosphane oxides (E- and Z-1-R) and alkane-1,2-diy-bis(phosphane oxides) (2-R) (Scheme 1). A significant number of experimental results have been collected on the s-block metal mediated Pudovik reaction,^7–10 which makes it a very appealing subject for computational studies aimed at both rationalising these findings and evaluating the computational methodologies applicable to s-block metal catalysis, revealing their successes and limitations.

Scheme 1 Alkali metal-mediated hydrophosphorylation of phenylacetylene with di(organyl)phosphane oxides R₂P(O)H (R = Mes, Ph, OEt and Cy) via M-HMDS (M = Li, Na, and K) depicting the possible products.

The reaction demands the presence of a strong P-nucleophile.¹¹ Alkali metal hexamethyldisilazanides (M-HMDS: M–N(SiMe₃)₂) have been employed as precatalysts for these reactions to generate alkali metal phosphinites, which serve as the ultimate nucleophiles, by deprotonation and metalation of phosphane oxides. Lithium, sodium, and potassium bis(trimethylsilyl)amides are commercially available and are soluble in a range of polar and nonpolar organic solvents. However, in solution they are involved in aggregation and solvation processes, complicating the accurate assessment of their chemical speciation in specific solvents.^12–14

The proposed mechanism of the Pudovik reaction promoted by M-HMDS is illustrated in Scheme 2.¹⁰ The initial step involves the metalation of di(organyl)phosphane oxide by M-HMDS of the alkali metals, resulting in the formation of the active species, the alkali metal diorganyl phosphinite (M-OPR₂). The ensuing step involves a nucleophilic attack by the phosphorous atom of M-OPR₂ (active species) on the C≡C functional group. Subsequently, the intermediate undergoes protonation with a proton donated by an additional molecule of R₂P(O)H. This step regenerates M-OPR₂ and yields E/Z-mixtures of mono-phosphorylated 1-R. Experimentally, this addition exclusively yields the anti-Markovnikov product, indicating that regioselectivity is decided in the initial step. Depending on the P-bound substituent of the phosphane oxide and the alkali cation present in the active species, a second phosphinite may be added to the newly formed alkene moiety. The subsequent and final step involves another protonation step, resulting in the formation of bis-phosphorylated 2-R. Experimental evidence demonstrates that bis-phosphorylated 2-R precipitates from the reaction mixture, preventing 2-R from interfering with the equilibrium by reverting back to 1-R.¹⁰ Additionally, the M-OPAr₂ molecules formed as by-products in the protonation steps can be reused in subsequent catalytic cycle. Phosphane oxides with bulky substituents, such as Mes₂P(O)H do not form the bis-phosphorylated product 2-R. Instead, the mono-phosphorylated 1-R undergoes a cyclization process to yield a phosphindole 1-oxide.¹⁰

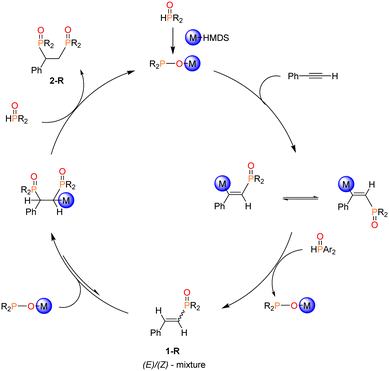Scheme 2 Proposed mechanism for the formation of the (E)/(Z)-mixture of 1-R and the subsequent bis-phosphorylated 2-R.

In the Pudovik reaction, the reaction rate and product ratio exhibit a notable dependency on both the alkali metal and the P-bound substituent utilised in the experiment. When comparing the three alkali cations in the case of P-bound mesityl group, it was observed that the lighter metal-based precatalyst (Li-HMDS) was unable to mediate the reaction within 1 h, achieving only 8% conversion with 5/1 ratio for E/Z isomers after 27 h. In contrast, precatalysts based on heavier alkali metals such as Na and K, successfully mediated the reaction within 1 h, resulting in conversion rates of 31% and 93% respectively. This resulted in the formation of E and Z isomers in a 3 : 1 ratio (Na) and 5 : 1 ratio (K). Interestingly, the same trend was found in the hydrophosphorylation of styrenes catalysed by monometallic group 1 alkyls M–CH₂SiMe₃, with the order of conversion being K (99%) ≈ Na (81%) > Li (19%).¹⁵ Furthermore, using M-HMDS as a base, similar effects of alkali-metal cations, with Li-HMDS failing to give the desired product, were also noted in the direct nucleophilic trifluoromethylation using fluoroform, which proceeded by the initial generation of MCF₃ from CF₃H and M-HMDS.¹⁶ However, a computed energy profile for this reaction indicated no significant alkali-metal-dependent variations in the barriers during the trifluoromethylation. It was proposed that the failure in trifluoromethylation when using Li-HMDS was due to a decomposition reaction suffered by the LiCF₃ reagent.¹⁷

The influence of the P-bound group on the hydrophosphorylation reaction has been investigated using potassium amide (K-HMDS). In the case of dimesitylphosphane oxide, hydrophosphorylation generated only phenylethenyl-dimesitylphosphane oxide (1-Mes). When one mesityl substituent was substituted by a phenyl ((Ph)(Mes)P(O)H) the reaction rate decreased slightly, resulting in a drop in conversion from 93% to 76% after 1 h, with minimal formation of the Z-isomer. Additionally, double-hydrophosphorylated phenylacetylene 2-Ar was detected in this case. Substituting all mesityl P-bound substituents by phenyl groups (Ph₂P(O)H) fast-tracks the second hydrophosphorylation to the extent that only 2-Ph product was observed despite incomplete conversion. Conversely, under the same conditions, potassium-mediated hydrophosphorylation of phenylacetylene via alkyl (Cy₂P(O)H) and alkoxy ((OEt)₂P(O)H) P-bound substituents is inhibited.

The experimental results commented on above were obtained in tetrahydrofuran (THF) solutions. Potassium-mediated hydrophosphorylation of phenylacetylene with dimesitylphosphane oxide in various solvents showed that increasing the polarity and donor strength of the solvent increases the reaction rate, achieving quantitative conversions after one hour for acetonitrile (ε = 36.0).¹⁰

This article aims to rationalise the complete set of experimental results on the Pudovik reaction promoted by alkali metal cations, by means of density functional theory (DFT) calculations. The main issues to be addressed in this study are the effect of the metal and the substituents, as well as the origin of the regio- and stereo-selectivity of the Pudovik reaction. Computational modelling of reaction mechanisms involving s-block metal cations has been less thoroughly explored than that of transition metal complexes and faces significant challenges related to solvation and speciation. The article will also discuss the computational requirements for the chemical modelling of the system to tackle these issues, as well as its limitations.

Experimental

Computational details

The exploration of the potential energy surface, including location of minima and transition states, has been carried out using the Gaussian16 suite of programs¹⁸ at DFT level of theory with the B3LYP functional,^19–21 combined with the D3 version of Grimme's dispersion with Becke–Johnson damping correction (D3BJ) to account for dispersion effects.²² The structures of all the intermediates and transition states were optimized using the BS1 basis set in the tetrahydrofuran solvent (THF, ε = 7.426), as described with the SMD continuum model.²³ The BS1 basis set includes the 6-31G(d,p) basis set for all the atoms.^24,25 Frequency calculations were carried out for all the optimized geometries in order to characterise the stationary points as either minima or transition states. Connections between the transition states and the corresponding minima were verified by displacing the geometry of the transition states along the transition vector in both directions, followed by subsequent geometry optimization until a minimum was reached.

As discussed later, accurately describing the solvent is essential for reproducing some of the experimental trends. Therefore, in some parts of the study the solvent was represented using a cluster–continuum approach, also referred to as a hybrid implicit–explicit solvation scheme.²⁶ In this case, alongside the SMD polarizable continuum model for THF, explicit solvent molecules (ranging from 1 to 4) were introduced to describe the solvation sphere of the cation.

Energies in solvent were refined using single-point calculations at the optimised BS1 geometries using an extended basis set (BS2). BS2 comprises the def2-TZVP basis set for all the atoms.^27,28 The Gibbs energies in THF solvent were calculated at 298.15 K by adding the thermal and entropic corrections obtained with BS1 to the BS2 energies in solvent. An additional correction of 1.9 kcal mol⁻¹ was applied to all Gibbs energies to change the standard state from the gas phase (1 atm) to the condensed phase (1 M) at 298.15 K (ΔG^1atm→1M).²⁹ In this way, all the energy values given in the article are Gibbs energies in solution calculated using the formula:

G = E(BS2) + G(BS1) − E(BS1) + ΔG^1atm→1M

3D-structures were generated using CYLview.³⁰

Results and discussion

Formation and deactivation of active species

The active species in the s-block metal-mediated hydrophosphorylation of alkynes are the highly nucleophilic alkali metal diorganylphosphinites (M-OPR₂). In the studied process, these species are generated by the metalation of secondary phosphane oxides, R₂P(O)H, with the hexamethyldisilazanide complexes of the alkali metals (M-HMDS). Prior to the study of the hydrophosphorylation mechanism we will first analyse the formation of the active species and their potential deactivation pathways.

A preliminary consideration regarding the speciation of the phosphorous substrate involves its prototropic tautomerism. Phosphinylidene compounds typically exist in two forms: P(V) and P(III).³¹ The so-called P(V) form A₁/A₂ is almost invariably the most stable species; however, in cases with strong electron acceptors, the less stable P(III) form B may become the more stable species (Scheme 3).^31,32 An experimental and computational study by Montchamp et al. on this tautomerism indicated that the direct P,O-proton transfer would proceed through a strained three-membered ring, via unaffordable reaction barrier.³³ This tautomerism therefore requires catalysis by a proton shuttle, such as a water molecule. Gas-phase calculations for the diphenylphosphane oxide favoured the P(V) P–H form by 6.8 kcal mol⁻¹ with an energy barrier of 30.8 kcal mol⁻¹ assuming catalysis by a single H₂O molecule.³³ Our own calculations yielded a Gibbs energy difference between both isomers of 10.2 kcal mol⁻¹ in THF, also favouring the P(V) tautomer. Hence, it can be concluded that the predominant species in our solution will be the A₁/A₂ configuration, with no presence of B configuration. Consequently, all further calculations will be conducted with the A configuration of the Ar₂P(O)H reagent.

Scheme 3 Prototropic tautomerism within phosphinylidene compounds.

The formation of the metal-phosphinites (active species) from the corresponding M-HMDS precatalysts and R₂P(O)H can be described by reaction 1.

However, this reaction involves two steps: i) the deaggregation of the alkali-metal amides M–N(SiMe₃)₂ in THF (step 1), and ii) the metalation–deprotonation of the phosphane oxide by monomeric and solvated M–N(SiMe₃)₂ (step 2) (Scheme 4).

Scheme 4 General scheme for the two steps involved in the generation of active species M-OPR₂ (M = Li, Na and K; R = Mes). For M = K also R = Mes, Ph, OEt, and Cy.

Deaggregation of the alkali-metal amides. Speciation and solvation of M-HMDS and M-OPR₂ species in solution pose a significant challenge due to the complex interplay between solvation and aggregation exhibited by alkali metal hexamethyldisilazanide reagents. A variety of M-HMDS aggregates have been characterized in solid state by X-ray diffraction analysis, appearing in both unsolvated forms and with several solvent molecules coordinated. For example, unsolvated Li-HMDS is known to exist as a trimer or tetramer in the solid state,^34,35 although disolvated dimers and solvent coordinate monomers have also been structurally characterized.^36,37 The solid-state structure of Na-HMDS is also a trimer, while X-ray structures of solvated homoleptic K-HMDS aggregates have been shown to adopt a dimeric structure.^12,13 However, these structures are highly solvent-dependent in solution. In THF as solvent, Li-HMDS has been reported as a mixture of dimers and monomers.¹³ Two recent studies have analysed aggregation and solvation behaviour for Na- and K-hexamethyldisilazanide complexes across various solvents, showing that disolvated dimers predominate in solvents of intermediate donor strength, such as THF.^12,13 Therefore, for comparison across the three alkali-cations, we have considered disolvated dimeric M-HMDS structures to compute the thermodynamics of the formation of solvated M-OPR₂ species in THF solution (Scheme 4).^13,38–40 Although a crystal structure of K-HMDS revealed only a bis-THF solvated dimer, tetrasolvated dimers have been proposed in THF solution; therefore, for K-HMDS we have also considered the tetrasolvated dimer as initial state.^12,40 We have confirmed that steric constraints hinders the stabilization of such tetrasolvated dimers for the Na- and Li-HMDS. Fig. 1 displays the optimised structures in THF of M-HMDS reagents.

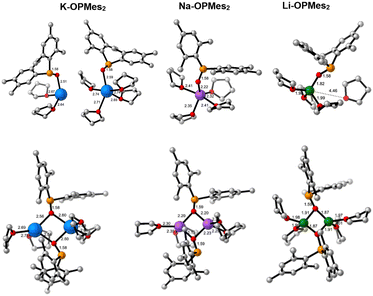
Fig. 1 Optimised structures in THF solvent of ligated M-HMDS reagents considered in the computational study. The distances presented are given in Å.

For step 1 (Scheme 4), we computed ΔG_R of 18.8, 22.3 and 16.6 kcal mol⁻¹, respectively, for the deaggregation of disolvated K-, Na- and Li-HMDS dimers, respectively. For potassium, using the tetrasolvated dimer as starting structure, ΔG_R is 17.1 kcal mol⁻¹. A recent study reported a deaggregation energy of 15 kcal mol⁻¹ at 195 K for the non-solvated dimer.¹² These ΔG_R values suggest that deaggregation is thermodynamically hindered. Experimentally, dimers are observed in concentrated solutions, whereas dilution prompts deaggregation to monomeric species.^12,37 The aforementioned ΔG_R values describe monomeric species as monosolvated adducts, which would be the case in highly concentrated solutions with relatively low THF content.

In diluted THF solutions, tetrasolvated (THF)₄M-HMDS monomers have been proposed as the most abundant species. When describing the deaggregation step as depicted in Scheme 5, significantly different ΔG_R values are obtained: −18.3 kcal mol⁻¹ (K, disolvated dimer), −1.5 kcal mol⁻¹ (K, tetrasolvated dimer), −12.8 kcal mol⁻¹ (Na) and 1.0 kcal mol⁻¹ (Li). These results indicate that solvation of the monomers is the driving force shifting the reaction toward deaggregation. In these calculations we have employed a cluster model of six THF molecules ((THF)₆) for disolvated dimers and four ((THF)₄) for tetrasolvated K-dimer to describe the process in which tetrasolvated monomers are formed (Scheme 5). This model has been previously been shown to yield reliable values for solvent coordination processes.⁴¹ Fig. 2 illustrates the optimised structures of the THF-saturated M-HMDS monomers.

Scheme 5 Deaggregation of M-HMDS disolvated dimers to yield tetrasolvated monomers.

Fig. 2 Optimised structures in THF solvent of solvated M-HMDS monomers considered in the computational study. For K-HMDS mono- and tetrasolvated species are compared. C–H hydrogen atoms are omitted in tetrasolvated species for clarity reasons. The distances are given in Å.

Considering the stabilization of the deaggregated monomer through tetrasolvation, the dissociation of the M-HMDS dimer is relatively easy for potassium and sodium bis(trimethylsilyl) amides. However, Li-HMDS deaggregation is considerably less favourable, resulting in significantly lower concentration of monomer in solution. This may partly explain the reduced efficiency of Li-HMDS as precatalyst in the Pudovik reaction.

Metalation–deprotonation of the phosphane oxide. In the second step of the reaction (Scheme 4) when M = K, we also examined the impact of various P-bound groups on the formation of the active species. Both monosolvated (THF)₁ and tetrasolvated (THF)₄ species have been considered. The results, summarised in Table 1, show that cation solvation has a much smaller effect on this proton transfer than on the deaggregation step.

Table 1 Computed Gibbs reaction (ΔG_R) and activation (ΔG†) energies (kcal mol⁻¹) for the proton transfer step (step 2, Scheme 4) in the generation of active species

Entry	Metal	P-bound group (R)	ΔGR		ΔG†
			(THF)1^a	(THF)4^b
a Monosolvated species.b Tetrasolvated species (numbers in italics).
1	Li	Mes	−5.7	−19.7	16.6 (17.3)^b
2	Na	Mes	−8.0	−9.9	11.7
3	K	Mes	−8.1	−9.2	11.2 (9.5)^b
4	K	Mes/Ph	−8.1	−9.3	12.0
5	K	Ph	−11.7	−13.1	7.1
6	K	Cy	8.6	7.8	13.0
7	K	OEt	−15.3	−13.6	6.4

---

The ΔG_R values for monosolvated and tetrasolvated species are similar, with the exception of the lithium dimesitylphosphinite case in which the tetrasolvated species is much more stabilized (Table 1, entry 3). Therefore, to simplify calculations, we have computed the Gibbs energy profiles by locating all structures (intermediates and transition state) for the P- to N-proton transfer (Scheme 6) using monosolvated structures. To verify the validity of this simplification, we have also computed the energy profile for the tetrasolvated species in the case of K-OPMes₂ and Li-OPMes₂ (entries 1 and 3, Table 1). The barriers (ΔG†) for mono- and tetrasolvated species were found to be comparable. The optimized structures for the pathway with M = K and R = Mes are depicted in Fig. 3.

Scheme 6 General scheme for the proton transfer step in the formation of alkali metal diorganylphosphinites (M-OPR₂).

Fig. 3 Optimised structures of intermediates (RI and PI) and transition state (TS) in THF in the proton transfer step for the generation of K-OPMes₂ with monosolvated (top) and tetrasolvated (bottom) structures. Carbon-bound hydrogen atoms are omitted for clarity reasons. The distances presented are given in Å.

Coordination of the alkali metal to the oxygen atom of the phosphane oxide in the initial intermediate RI positions the P–H proton in the vicinity of the N-centre where the proton transfer will occur (Fig. 3).

The Gibbs energy profiles for the proton transfer step are presented in the ESI† (Fig. S1 and S2). For all the three cations with R = Mes, the reaction is exergonic and proceeds with low barriers, although lithium exhibits a notably higher barrier (16.6 kcal mol⁻¹) compared to sodium and potassium, which exhibit similar values (11.7 and 11.2 kcal mol⁻¹, respectively). A Gibbs activation energy of 21.5 kcal mol⁻¹ was computed for the lithium/proton exchange between LiN(SiMe₃)₂ and benzylamine.⁴² The Gibbs energy of the reaction depends strongly on the P-bound group of the phosphane oxide. With aryl substituents on phosphorous the reaction is highly exergonic, whilst when the substituent is an alkyl (R = Cy) the process is highly unfavourable (ΔG_R = 7.8 kcal mol⁻¹), indicating an inefficient stabilization of the alkyl phosphinite. When the P-substituent is an aryl, the cation engages in interactions with both the oxygen atom of the phosphinite and the aryl ring. However, this intramolecular cation–aryl π-interaction is not present when R = Cy. The unfeasibility to form K-OPCy₂ appears to be the primary reason for the absence of hydrophosphorylation with Cy₂P(O)H. With R = OEt the cation interacts with both the oxygen atom in the phosphinite functionality and an oxygen atom in one ethoxy group, making the reaction highly exergonic. Nonetheless, hydrophosphorylation does not proceed with (EtO)₂P(O)H either, indicting that another factor must be responsible for the lack of reactivity in this case.

Deactivating processes. So far, we have examined the formation of alkali metal phosphinites, which act as catalysts in the Pudovik reaction. However, the concentration of these active species in solution may be considerably reduced due to two side-reactions: i) dimerization and ii) dismutation, both of which are deactivating processes (Scheme 7).

Scheme 7 Deactivation processes of alkali metal diorganylphosphinites M-OPR₂: dimerization (top) and dismutation (bottom).

The crystal structures of alkali metal diarylphosphinites show a tendency to aggregate. Tetranuclear lithium and potassium diarylphosphinites featuring central M₄O₄ cages have been characterised.^7,43 However, understanding of the coordination chemistry of the alkali metal diarylphosphinites remains limited. A recent study described the metalation of dimesitylphosphane oxide with n-butyllithium as well as with sodium and potassium hexamethyldisilazanides in THF, leading to the formation of alkali metal dimesitylphosphinites M-OPMes₂.⁴⁴ From the lithium reagent, the dinuclear complex [(THF)₃(Li–O–PMes₂)₂] was crystalized, while tetranuclear species of the form [(THF)M–O–PMes₂]₄ with central heterocubane cages were obtained from Na- and K-HMDS. In the potassium reaction with bulky P-bound 2,4,6-triisopropylphenyl substituents, a dimeric complex [(THF)₄(K–O–PMes₂)₂] forms in which each potassium ion is coordinated by two THF molecules.⁴⁴

We have computationally examined the dimerization of the alkali metal diorganylphosphinites. Our analysis revealed that, due to the reduced steric pressure induced by the P-substituents compared to the two trimethylsilyl groups of HMDS, two THF molecules are able to coordinate to each cation, resulting in the formation of tetrasolvated dimers (Scheme 8).

Scheme 8 Dimerization process of M-OPR₂ phosphinites considering disolvalted (top) or tetrasolvated (bottom) monomers.

In akin manner to the M-HMDS case, we have examined the solvation state of the monomer by calculating the reaction for both disolvated and tetrasolvated species. Fig. 4 displays the optimised structures of dimesitylphospinites.

Fig. 4 Optimised structures of monomeric (top) and dimeric (bottom) alkali metal dimesityl phosphinites in THF. For monomeric K complexes di- and tetrasolvated species are depicted. All hydrogen atoms are omitted for clarity reasons. The distances presented are given in Å.

Table 2 presents the computed Gibbs reaction energies for the dimerization reactions depicted in Scheme 8. As observed in the deaggregation of dimeric M-HMDS (Scheme 5), the solvation state of the monomer significantly influences the thermodynamics of the reaction. The values for the tetrasolvated monomers provide a more accurate representation of the conditions in pure THF. For the potassium case (ΔG_R = −0.7 kcal mol⁻¹) there is a significant amount of monomeric active species present. In contrast, for sodium and lithium (ΔG_R = −3.8 and −4.4 kcal mol⁻¹, respectively) the equilibrium shifts towards the dimer side, leading to a notable reduction in the concentration of the active species in THF solution.

Table 2 Computed Gibbs reaction energies (ΔG_R, kcal mol⁻¹) for the dimerization of the phosphinites M-OPR₂ (Scheme 8)

Entry	Metal	P-bound group (R)	ΔGR
			(THF)2^a	(THF)4^b
a Disolvated species.b Tetrasolvated species (numbers in italics).
1	Li	Mes	−18.7	−3.8
2	Na	Mes	−21.1	−4.4
3	K	Mes	−21.0	−0.7
4	K	Mes/Ph	−19.7	−1.7
5	K	Ph	−25.1	−0.2
6	K	OEt	−20.4	−3.4

---

It is known that certain alkali metal phosphinites, such as Li-OPMes₂, undergo dismutation into phosphinate (M(O₂PMes₂)) and phosphanide (M-PR₂) (Scheme 7, bottom).⁴⁵ Similarly, homologous potassium diphenylphosphinite also undergoes dismutation.⁸ Increasing the steric requirements of the P-bound substituents hampers the disproportionation reaction. We have evaluated the thermodynamics of dismutation by examining tetrasolvated species (Scheme 7, bottom, with (THF)₄). The Gibbs reaction energies (ΔG_R) for the dismutation reaction are summarized in Table 3.

Table 3 Computed Gibbs reaction energies (ΔG_R, kcal mol⁻¹) for the dismutation of phosphinites M-OPR₂ yielding phosphinates (M(O₂PR₂)) and phosphanides (M-PR₂) (Scheme 7)

Entry	Metal	P-bound group (R)	ΔGR
1	Li	Mes	−5.7
2	Na	Mes	−13.4
3	K	Mes	−19.3
4	K	Mes/Ph	−17.2
5	K	Ph	−20.0
6	K	OEt	−17.1

---

The results highlight that dismutation is thermodynamically favoured for all the three alkali metal cations, following the trend K > Na > Li. For potassium, comparable Gibbs reaction energies are obtained across the P-substituents (R = Mes, Mes/Ph and Ph). In contrast, disproportionation is unfavourable when R = OEt, as this leads to the formation of a species with four oxygen atoms bonded to phosphorous. Since dismutation requires the approach of solvated M-OPR₂ phosphinites, it is evident that steric effects significantly influence the reaction kinetics.

The complexities of speciation and solvation entail significant challenges in the computational simulation of the formation and deactivation of the alkali metal phosphinite active species in the Pudovik reaction within THF solution. Achieving more accurate results would require performing DFT-based molecular dynamics simulations, akin to those conducted for the Schlenk equilibrium in Grignard reagents, which are beyond the scope of this study.⁴⁶ Moreover, the reactions of dimerization and dismutation involve two alkali metal phosphinite molecules and are influenced by concentration effects, which were not taken into account when conducting the calculations. However, static DFT calculations can provide useful insights in the behaviour of these systems in solution, especially when solvation is carefully modelled by including explicit THF molecules in the computational model. Although our investigation focused on a limited number of species, it should be noted that other species might also exist in solution. Nevertheless, our study points out that the concentration of active species in solution is highly dependent on both the alkali metal cation present and the P-bound substituents. Specifically, the combination of a potassium cation combined with bulky mesityl groups at the phosphorous atom, which hinder aggregation and dismutation of the phosphinite, appears as the best combination to affording high concentration of active species in solution.

Nucleophilicity of alkali metal phosphinites

As previously discussed, s-block metal precatalysts promote the generation of metal phosphinites M-OPR₂ which act as nucleophilic intermediates capable of reacting with unsaturated substrates to generate new P–C bonds.⁴⁷ As nucleophiles, metal phosphinites possess a high-lying HOMO, primarily attributed to the lone pair on the phosphorous atom, which interacts in an antibonding way with a p orbital on the oxygen atom. Fig. 5 illustrates the HOMO of K-OPMes₂, highlighting this electronic structure.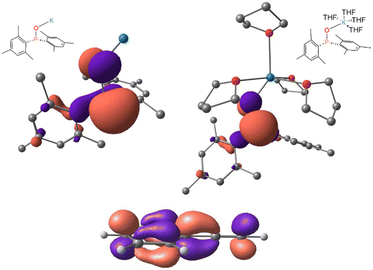

Fig. 5 Top: calculated HOMO of K-OPMes₂ without explicit THF molecules solvating the cation (left) and with four THF solvent molecules (right). Bottom: LUMO of phenylacetylene.

To analyse the relative nucleophilicity of the species involved in the nucleophilic addition, as well as the influence of solvation, we have calculated the empirical global nucleophilicity index (N) for each species. This nucleophilicity index is derived from the HOMO energies obtained within the Kohn–Sham scheme, and is defined as N = ε_HOMO (Nu) − ε_HOMO (TCE), where tetracyanoethylene (TCE) serves as the reference, due to its particularly negative ε_HOMO, enabling the calculation of positive values of N.⁴⁸ Within this framework, organic molecules with N ≥ 3.0 eV are classified as strong nucleophiles, while those with N ≥ 4.0 eV are categorised as supernucleophiles.⁴⁹

The nucleophilicity index N in Table 4 clearly demonstrates that deprotonating phosphane oxide substantially increases the nucleophilicity of P-nucleophiles. Specifically, N increases from 3.11 in dimesitylphosphane oxide to over 4.00 in alkali metal phosphinites, classifying them as supernucleophiles. The influence of the cation is minor but follows the trend K > Na > Li in agreement with an increasing electronegativity difference. Phosphorous substituents have a greater influence on nucleophilicity, with a notable decrease when R = OEt. Furthermore, the inclusion of four explicit THF molecules to solvate the cation has very little impact on N, only causing a slight increase. Charge model 5 (CM5) atomic charges⁵⁰ on the metal indicate a primarily ionic interaction between the potassium or sodium and the oxygen atom of the phosphinite (charges about 0.9 e in the potassium and 0.8 e in the sodium dimesitylphosphinite). This ionic character is notably decreased with lithium.

Table 4 Energy of HOMO molecular orbital, nucleophilicity index and CM5 atomic charge⁵⁰ at the alkali metal of alkali metal phosphinites

Entry	Metal phosphinites (M-OPR2)	No explicit THF molecules			(THF)4
		HOMO energy (eV)	N^a (eV)	M^b charge	HOMO energy (eV)	N^a (eV)	M^b charge
a Relative nucleophilicity index, taking tetracyanoethylene (TCE), which is the expected least nucleophilic neutral species, as a reference: N = εHOMO(Nu) − εHOMO(TCE). In THF εHOMO(TCE) = −8.64 eV.b CM5 atomic charge at the alkali metal.c H instead of M.
1	[OPMes2]^−	−3.26	5.38	—	—	—	—
2	K-OPMes2	−4.15	4.49	0.90	−4.09	4.55	0.88
3	Na-OPMes2	−4.32	4.32	0.82	−4.12	4.52	0.73
4	Li-OPMes2	−4.55	4.09	0.69	−4.29	4.35	0.52
5	H-OPMes2	−5.53	3.11	0.35^c	—	—	—
6	K-OPPhMes	−4.26	4.38	0.91	−4.09	4.55	0.87
7	K-OPPh2	−4.45	4.19	0.89	−4.32	4.32	0.87
8	K-OPCy2	−3.97	4.67	0.89	−3.84	4.80	0.85
9	K-OPOEt2	−5.19	3.45	0.96	−4.97	3.67	0.88

---

Modes of interaction of the alkali metal cation with the alkyne

Alkali metal cations are known to interact with π systems through what is known as cation–π interaction.⁵¹ Thus, prior to entering into the exploration on the reaction mechanism we investigated how the metal cation from the active species (M-OPMes₂) interacts with the π-system of the phenylacetylene. In this context, the cation may form two distinct types of interaction: i) a π-interaction with the C≡C triple bond and ii) a π-interaction with the aryl moiety (Scheme 9).

Scheme 9 Possible modes of interaction between M-OPMes₂ and phenylacetylene.

Two key observations emerge from the calculations. First, the interactions between the metal cation and the π-system are notably weak. For the most stable structures, the computed phosphinite–alkyne binding energies (ΔG) are −0.8 (K), −1.6 (Na) and −2.9 (Li) kcal mol⁻¹. The most stable conformations for the three alkali cations are depicted in Fig. 6. As shown, all interactions exhibit slightly attraction, indicating a weak M–π binding in a highly dynamic environment where the metal cation has a minimal impact on the π system. Our findings on the metal effects in cation–π interaction align with Schleyer's observations regarding the conformational “floppiness” of the metal cations.⁵² This “floppiness” of the metal cations relative to the π system posed significant challenges in identifying transition states as significant positional changes led to small variations in energy values.

Fig. 6 Top: most stable conformations computed for phenylacetylene·M-OPMes₂ (M = Li⁺ (green), Na⁺ (purple), and K⁺ (blue)) adducts. Bottom: X-ray structures of PhCH₂M·Me₆TREN (M = Li, Na, and K) complexes.⁵³ ΔG binding in kcal mol⁻¹. Certain H atoms are omitted for clarity reasons. The distances are given in Å.

The second key observation relates to the preferred orientation of the metal cation relative to the π-system in its most stable conformation. Potassium cation preferably interacts with the aryl-system rather than the triple bond C≡C π-system, whereas lithium cation shows the opposite preference favouring interaction with the π-system of the C≡C triple bond. Sodium cation's coordination preference falls somewhere in the middle. This behaviour mirrors the shift observed in X-ray structures of PhCH₂M·Me₆TREN⁵⁴ and alkali metal aryl methyl anions, where increasing the size of the alkali metal and hence its softness leads to displacement of the metal from the lateral ‘carbanionic’ carbon towards the softer aromatic π-system (Fig. 6).⁵⁵

Hydrophosphorylation of phenylacetylene with potassium dimesitylphosphinite

Assuming that K-OPMes₂ has already been formed, as discussed above, we have computed the energy profile for the P–H addition to phenylacetylene, following the proposed mechanism (Scheme 2).¹⁰ The computed energy profile for the formation of the Z-mono-phosphorylated alkene is presented in Fig. 7.

Fig. 7 Computed Gibbs energy profile in THF (ΔG_THF in kcal mol⁻¹) at 298 K for the hydrophosphorylation of phenylacetylene catalysed by potassium dimesitylphosphinite yielding the Z-dimesityl(styryl)phosphane oxide.

The reaction proceeds in two steps: i) nucleophilic addition of the P-nucleophile and ii) subsequent protonation. During the first step, the nucleophilic attack can target either the internal carbon (Markovnikov) or the terminal carbon (anti-Markovnikov) of the C≡C triple bond of phenylacetylene. We have computed both additions and our computational results are consistent with experimental findings, indicating that only the anti-Markovnikov addition occurs. We have found a much higher barrier for the addition to the internal carbon atom (19.1 kcal mol⁻¹) compared to the terminal carbon atom (10.3 kcal mol⁻¹) (details provided in Fig. S3 and S4, ESI†). The presence of phenyl group polarises the alkyne π* orbital, increasing the contribution of the terminal carbon in the π* (Fig. 5), thereby rendering the terminal carbon more electrophilic and promoting it as the site for nucleophilic attack.^56,57

The second step involves the protonation of the internal carbon. There are two possible protonating agents in the reaction medium: Mes₂P(O)H and H-HMDS, the latter being a product formed during the generation of the active phosphinite species K-OPMes₂. Our calculations indicate that protonation with Mes₂P(O)H occurs with a lower barrier (10.5 kcal mol⁻¹) compared to H-HMDS (15.8 kcal mol⁻¹) (refer to Fig. S5 and S6 in the ESI† for details). The formation of the Z-alkene is very exergonic, with a computed ΔG of −20.8 kcal mol⁻¹.

The preceding calculations considered the unsolvated cation, treating THF solvent as a continuum medium with the dielectric constant ε = 7.43 (SMD model), without including explicit THF molecules in our system. To evaluate the validity of this assumption, we have computed the Gibbs energy profile for the formation of the Z-isomer, this time solvating the potassium cation with one or two explicit THF molecules. Since the potassium cation interacts with both the π system and the oxygen atom of the phosphinite, coordinating two THF molecules to the cation yields a more realistic description of its first coordination sphere. A comparison of the transition states for the nucleophilic addition (TS-1-Mes-K) and the protonation (TS-2-Mes-K) with 0, 1 and 2 explicit THF molecules coordinated to K is illustrated in Fig. S7 in the ESI.† Table 5 summarizes the Gibbs energy barriers (ΔG†) for both steps with 0, 1 and 2 explicit THF molecules. This comparison sheds light to how explicit solvation affects the reaction energies.

Table 5 Gibbs activation energies (ΔG†, kcal mol⁻¹) for the two steps involved in the formation of the Z-alkene isomer with a different number of explicit solvent molecules (THF)_n

Entry	(THF)n	Nuc attack	Protonation
1	n = 0	10.3	10.5
2	n = 1	12.0	10.0
3	n = 2	11.2	9.7

---

Results in Table 5 demonstrate that coordinating explicit THF molecules to the potassium cation has a minor impact on the reaction barriers. For this reason and considering the added complexity in optimization steps when explicit THF molecules are included, as well as the significant number of calculations required, we opted out to proceed without explicit THF molecules in the model for future computations. This approach streamlines the computational process while maintaining a reliable level of accuracy for the system under study.

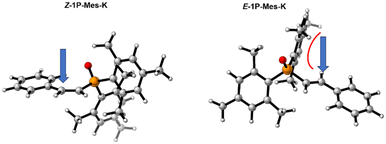
Numerous attempts were conducted to attain the direct nucleophilic attack for formation of the E-hydrophosphorylated product E-1I-Mes-K but all proved unsuccessful. Interestingly, a similar preference for the Z isomer was found in the study of the Na-HMDS mediated enolization of ketone.⁵⁸ A thermal study on the E/Z isomerization of Mes₂–P(O)–C(Me)=C(H)Ph showcased that at slightly elevated temperature (80 °C) rotation around the C=C double bond is feasible with a low barrier of 14.1 kcal mol⁻¹.⁹ This observation prompted us to investigate the possibility of a transition state for an isomerization from Z-1I-Mes-K to E-1I-Mes-K intermediates occurring before protonation. We successfully located this transition state (TS-3-Mes-K), which corresponds to bending of the C_terminal–C_internal–C_Ph angle from 135^○ in the Z-intermediate to almost 180^○ in the transition state. TS-3-Mes-K exhibits an allene-like nature, as indicated by its similar C_terminal–C_internal and C_internal–C_Ph distances (1.31 and 1.36 Å, respectively, Fig. 8). The change in the coordination of the potassium cation during the isomerization is remarkable. In the Z-1I-Mes-K intermediate the cation interacts with the π system of the aryl moiety, whilst in E-1I-Mes-K intermediate the cation becomes σ coordinated to the C_internal (Fig. 8). This isomerization occurs with a barrier of only 4.9 kcal mol⁻¹, low enough to be easily surpassed at the temperature at which the reaction proceeds. This transformation is additionally thermodynamically assisted as E-1I-Mes-K is found at −9.9 kcal mol⁻¹ in the Gibbs energy profile, whilst intermediate Z-1I-Mes-K is located at −6.2 kcal mol⁻¹.

Fig. 8 Optimised structures of intermediates and transition state involved in the Z/E isomerization. The distances presented are given in Å.

The computed Gibbs energy profile for the formation of the E-mono-phosphorylated alkene is presented in Fig. 9. In the final step, the E-1I-Mes-K intermediate is protonated by an additional molecule of Mes₂P(O)H through transition state TS-4-Mes-K, with a barrier of 12.9 kcal mol⁻¹. This step yields the final product at −25.6 kcal mol⁻¹ below the starting reagents in the Gibbs energy profile, while simultaneously regenerating the catalytically active species as side product.

Fig. 9 Computed Gibbs energy profile in THF (ΔG_THF in kcal mol⁻¹) at 298 K for the hydrophosphorylation of phenylacetylene catalysed by potassium dimesitylphosphinite yielding the E-dimesityl(styryl)phosphane oxide.

By comparing the Gibbs energy profiles for the formation of both Z and E isomers it can be inferred that the outcome of this reaction is governed by the thermodynamics: the E-isomer (−25.6 kcal mol⁻¹) exhibits greater thermodynamic stability than the Z-isomer (−20.8 kcal mol⁻¹). This difference in stability suggests a thermodynamic driving force that favours the formation of the E-isomer over the Z-isomer.

Formation of bishydrophosphorylated alkanes and cyclization. Based on experimental evidences, the reaction with Mes₂P(O)H does not progress to form bishydrophosphorylated alkanes (2-R, Scheme 1). This behaviour stands in stark contrast to reactions involving smaller phosphorous-bound substituents, such as phenyl groups. In cases where phosphane oxides possess bulky substituents like Mes₂P(O)H, the expected bis-phosphorylated product 2-Mes is not formed. Instead, the mono-phosphorylated alkene 1-Mes undergoes a cyclization process, resulting in the formation of a phosphindole 1-oxide (3-Mes).¹⁰

The second nucleophilic attack in the hydrophosphorylation process proceeds at C_internal. It is important to highlight that Z-1P-Mes-K is less stable than E-1P-Mes-K, yet it offers more spatial room. This increased space in Z-1P-Mes-K facilitates a more favourable environment for the second hydrophosphorylation to take place, in contrast to E-1P-Mes-K, where steric constrains are more pronounced (Fig. 10). Consequently, the second hydrophosphorylation is expected to preferentially occur at Z-1P-Mes-K, which is consistent with experimental results involving P-bound phenyl groups.

Fig. 10 Accessibility for a second addition in Z- and E-mono-hydrophosphorylated alkenes.

We have computed the second addition starting from Z-1P-Mes. The mechanistic steps for the second addition closely mirror those of the first addition, as depicted in Scheme 2. The Gibbs energy diagram for the formation of the bishydrophosphorylated alkane is depicted in Fig. S8 in the ESI.† The optimised structures for the transition states involved in the formation of bishydrophosphorylated alkane are presented in Fig. S9 in the ESI.† The second nucleophilic attack proceeds at C_internal and displays a significantly higher barrier compared to the first nucleophilic attack (16.2 vs. 10.3 kcal mol⁻¹). Furthermore, the energy barrier for the protonation step (ΔG† = 26.6 kcal mol⁻¹, TS-2-Mes-DA) is even higher, rendering the second addition unfeasible for the dimesitylphosphane oxide. These results give us an insight why the formation of bishydrophosphorylated alkynes is not observed under these conditions.

Experimentally, only very low concentrations of the double-hydrophosphorylation product have been observed.¹⁰ Calculations indicate that the rather high barrier computed for the second P-addition renders the addition of a second Mes₂P(O)H onto the alkenyl moiety formed in the first addition highly disadvantageous. Conversely, experiments revealed the formation of 2-benzyl-1-mesityl-5,7-dimethyl-2,3-dihydrophosphindole 1-oxide. In the original paper it was proposed that this product arises from a cyclization reaction, initiated by deprotonation of an ortho-methyl group of a mesityl substituent in the Z-product of the first addition. This is followed by cyclization triggered by an intramolecular nucleophilic attack at the alkenyl substituent of the resulting carbanion. The final product is expected to form via protonation by H–N(SiMe₃)₂.¹⁰ We have computationally assessed the proposed mechanism. Fig. 11 displays the computed Gibbs energy profile for the cyclization, including the optimised structures of the transition states involved.

Fig. 11 Computed Gibbs energy profile in THF (ΔG_THF kcal mol⁻¹) at 298 K for the potassium-mediated cyclization process of Z-hydrophosphorylated phenylethene (Z-1P-Mes) yielding 2-benzyl-1-mesityl-5,7-dimethyl-2,3-dihydrophosphindole 1-oxide (3-Mes).

The formation of the phosphindole 1-oxide product (3-Mes) proceeds through a sequence of three steps. Initially, a strong interaction occurs between the oxygen of Z-1P-Mes and the potassium ion from K-HMDS. This interaction facilitates the approach of the nitrogen center of K-HMDS to a C–H bond of an ortho-methyl group of the mesityl substituent, enabling an easy deprotonation, which requires a barrier of only 18.8 kcal mol⁻¹ (TS-1-Mes-CYC, Fig. 11). The second step involves cyclization, wherein the carbanion, formed from the deprotonation, attacks the alkenyl carbon bonded to phosphorous, thereby closing the cycle. This second step has a Gibbs energy barrier of 10.6 kcal mol⁻¹ (TS-2-Mes-CYC, Fig. 11). Finally, protonation at the benzylic carbon atom by H-HMDS occurs, yielding the phosphindole 1-oxide product 3-Mes after overcoming a Gibbs energy barrier of 15.3 kcal mol⁻¹ (TS-3-Mes-CYC, Fig. 11). This step also regenerates the catalytic species K-HMDS. The cyclization product is found 22.3 kcal mol⁻¹ below Z-1P-Mes-K, indicating a strong thermodynamic driving force favouring cyclization. Furthermore, the cyclic 3-Mes product is 1.9 kcal mol⁻¹ more stable than the double-added product 2-Mes.

Influence of the metal in the hydrophosphorylation reaction

With the reaction mechanism for potassium-mediated hydrophosphorylation of phenylacetylene to mono- and bishydrophosphorylated products analysed, we can now turn our attention to investigating sodium- and lithium-mediated hydrophosphorylation of phenylacetylene to monohydrophosphorylated products. The addition of dimesitylphosphane oxide onto phenylacetylene, which results in Z- and E-monohydrophosphorylated products when employing Na-OPMes₂ or Li-OPMes₂ as catalysts, was investigated using an analogous mechanism as the one computed for K-OPMes₂ (Fig. 7 and 9). The computed barriers associated with these reactions are summarized in Table 6, while Gibbs energy profiles and optimised transition states can be found in the ESI† (Fig. S10–S17).

Table 6 Computed Gibbs energy barriers in THF (ΔG† kcal mol⁻¹) at 298 K for the two steps of Pudovik reaction (addition of dimesitylphosphane oxide across phenylacetylene) depending on the alkali metal M of the dimesitylphosphinite M-OPMes₂

Entry	Metal	N^a (eV)	Z-isomer (ΔG†)		E-isomer (ΔG†)
			Nuc attack	Protonation	Nuc attack	Isomerization	Protonation
a Relative nucleophilicity index of M-OPMes2.
1	Li	4.09	11.7	9.7	11.7	8.2	3.2
2	Na	4.32	10.2	9.5	10.2	9.4	9.6
3	K	4.49	10.3	10.5	10.3	4.9	12.9
4	H	3.11	22.7	—	—	—	—

---

The results in Table 6 display a minimal influence of the alkali metal cation on the nucleophilic addition, which aligns with the comparable nucleophilicities of the three M-OPMes₂ nucleophiles, as reflected in their nucleophilicity index (N in Table 6). Notably, a slightly high addition barrier is found with lithium consistent with the lower nucleophilicity index of Li-OPMes₂ (Table 6). Overall, the barriers are very similar and low, suggesting that, if the alkali metal phosphinite forms, the addition could proceed under the reaction conditions without significant variation attributable to the alkali metal. This result seems to contradict the experimental results, which show almost no conversion with Li-HMDS. However, the reaction does successfully yield bisphosphorylethane (in THF solvent, at 70 °C, 4 h) when employing t-BuOLi and diphenylphosphane oxide, as reported by Yoshimura et al.⁵⁹ This fact suggests that the lack of activity observed with Li-HMDS precatalyst may stem more from the low concentration of the active species Li-OPMes₂ in the reaction medium, rather than from any inherent limitation in the reaction mechanism itself. Indeed, dismutation and sparing solubility of lithium dimesitylphosphinate lead to the precipitation of dinuclear [(thf)₂Li(O₂PMes₂)]₂ when Mes₂P(O)H is lithiated with BuⁿLi in THF.⁴⁵

To further assess the impact of the metal cation over the reaction barriers we conducted calculations using a hydrogen atom (formally a proton) in the place of the metal ion, considering H-OPMes₂ as the nucleophile (Fig. S18 in the ESI†). Our findings indicate that replacing the alkali cation with a proton indeed results in doubling the barrier for the nucleophilic attack (Table 6), which corresponds to the decrease in nucleophilicity of H-OPMes₂ compared with alkali metal phosphinites (K⁺: N = 4.49; H⁺: N = 3.11, Table 6). This suggests that substitution of the proton with the alkali cation, thereby generating supernucleophilic species, is necessary for the reaction to ensue. However, if the active species were accessible only minor differences between the three alkali cations can be expected.

The effect of the P-bound group

We have analysed the dependence of the Pudovik reaction on the substituents of the potassium di(organyl)phosphinite catalyst, K-OPR₂, with R = Ph, Cy and OEt by computing the reaction yielding the Z-alkene. The reaction mechanism follows the previously discussed sequence of nucleophilic addition followed by protonation step. The computed barriers associated with these reactions are summarized in Table 7, while Gibbs energy profiles and optimised transition states can be found in the ESI† (Fig. S19–S26).

Table 7 Computed Gibbs energy barriers in THF (ΔG† kcal mol⁻¹) at 298 K for the two steps of hydrophosphorylation across phenylacetylene yielding the Z-alkene depending on the P-bound group of the potassium di(organyl)phosphite (K-OPR₂)

Entry	P-bound group	N^a (eV)	Z-isomer (ΔG†)
			Nuc attack	Protonation
a Relative nucleophilicity index of K-OPR2.
1	Mes	4.49	10.3	10.5
2	Mes/Ph	4.38	9.0	7.5
3	Ph	4.19	11.4	9.5
4	Cy	4.67	9.1	5.4
5	OEt	3.45	18.1	6.7

---

In Table 7 the computed reaction barriers have been summarized. The results show a clear correlation with the nucleophilicity of the phosphinite species. Specifically, the lowest nucleophile K-OP(OEt)₂ exhibits the highest barrier (18.1 kcal mol⁻¹), which is comparable to that of the phosphane oxide H-OPMes₂ (22.7 kcal mol⁻¹). Accordingly, this indicates that (EtO)₂P(O)H cannot efficiently mediate the addition reaction. In contrast, K-OPCy₂, identified as the highest nucleophilic species, shows the lowest computed barrier (9.1 kcal mol⁻¹). Notably, in the presence of t-BuOLi, dicyclohexylphosphane oxide was able to proceed with the addition reaction onto phenylacetylene readily, resulting in quantitative formation of the 1,2-bisphosphoryl compound (in THF solution, at 70 °C, 4 h).⁵⁹ However, deprotonation of phosphane oxide Cy₂P(O)H by K-HMDS is endergonic (ΔG = 7.8 kcal mol⁻¹, Table 1), suggesting that the active species is not formed through this pathway, which ultimately explains the lack of observed reactivity.

Experimentally, in contrast to the reaction outcome observed with R = Mes, when the P-bound group is phenyl, the second hydrophosphorylation occurs, leading exclusively to the bis-hydrophosphorylated product. We have computed the Gibbs energy profile for the formation of the bis-phosphorylated alkane product from the Z-alkenyl diphenylphosphane oxide (Fig. S27 and S28 in the ESI†). The nucleophilic addition associated with the second phosphorylation displays a barrier comparable to that of the first phosphorylation (11.8 and 11.4 kcal mol⁻¹, respectively), much lower than that for the second addition involving the mesityl system (16.2 kcal mol⁻¹). The protonation barrier for the diphenylphosphane oxide (7.6 kcal mol⁻¹) is much lower than that for the mesityl-substituted phosphane oxide (26.6 kcal mol⁻¹). The bis-phosphorylated product is highly stable (−56.1 kcal mol⁻¹), showing a strong thermodynamic driving force for the reaction. Overall, these theoretical findings align with the experimental observance of a >99% conversion to the bis-hydrophosphorylation product when utilizing diphenylphosphane oxide. It appears that steric effects, due to the bulkiness of the mesityl groups, are responsible for the lack of formation of the double-hydrophosphorylation product in reactions involving Mes₂P(O)H.

Conclusions

The addition of P–H bonds of phosphane oxides across alkynes requires a strong nucleophile. Our calculations demonstrate that alkali metal dimesitylphosphinites (M-OPMes₂, where M = Li, Na, K) exhibit sufficient nucleophilicity to serve as the active species in this addition, facilitating the formation of P–C bonds. Notably, the influence of the alkali metal cation on the addition process is minimal, resulting in only slight variations in the nucleophilicity of the phosphinite. The active species can be generated by deprotonation of dimesitylphosphane oxide by alkali metal hexamethyldisilazanides (M-HMDS). However, the formation of the active species may be affected by deactivation processes, such as aggregation and dismutation, which can reduce the concentration of catalytically active species in the reaction medium. While our computed barriers for the addition reaction involving the three cations are quite similar, it is noteworthy to mention that experimentally Li-HMDS does not facilitate the reaction. Our results suggest that the primary challenge associated with lithium is not inherent to the reaction mechanism, but rather pertains to the generation of the active species Li-OPMes₂.

We have analysed the regio- and stereoselectivity in the reaction, finding a clear preference for the anti-Markovnikov addition at the terminal carbon of the triple bond. The anti-Markovnikov regioselectivity is governed by the polarization of the π* orbital caused by the phenyl group, making the terminal carbon more electrophilic and promoting the site for nucleophilic attack. Regarding Z/E-stereoselectivity, our analysis indicates that only the Z-addition occurs initially. The formation of the E-alkene phosphane oxide results from isomerization of the initially formed pro-Z intermediate. This isomerization step has a low barrier and leads to a more stable dimesityl(styryl)phosphane oxide, providing a thermodynamic driven force for the formation of the E-alkene phosphane oxide. Furthermore, our calculations suggest that the double addition of dimesitylphosphane oxide to yield the 1,2-bisphosphoryl product is primarily hindered by steric factors. Conversely, the Z-alkene product from the first addition can undergo cyclization. This pathway beginning with the deprotonation of the ortho-methyl group of the mesityl substituent, ultimately forming a phosphindole 1-oxide product. The energy barrier for this cyclization (22.4 kcal mol⁻¹) is lower than that for the second addition (26.6 kcal mol⁻¹), demonstrating that the cyclization pathway is more favourable for this system.

Substituents on the phosphorous atom significantly influence the nucleophilicity of the phosphinite. Overall, there is a good correlation between the barriers for the addition of the P-nucleophile (ΔG†) and the nucleophilicity index N (Fig. 12).

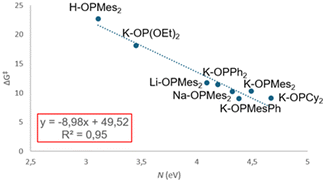Fig. 12 Plot of the Gibbs energy barriers for the addition of the P-nucleophile (ΔG†, kcal mol⁻¹) versus nucleophilicity index (N, eV).

For instance, when R = OEt the nucleophilicity index decreases to a value comparable to that of the phosphane oxide, preventing the reaction from proceeding. Surprisingly, even the most nucleophilic substituent (R = Cy) does not react. This outcome may be attributed to the high endergonic deprotonation of Cy₂P(O)H phosphane oxide by K-HMDS, which has a Gibbs energy change of ΔG = 7.8 kcal mol⁻¹. This suggests that the active species is not generated under these conditions and no reaction occurs. Additionally, the impact of steric effects is evident in the calculation for the second addition reaction with diphenylphosphane oxide. Contrarily to the case with Mes₂P(O)H, the reduced steric pressure exerted by phenyl enables the formation of the bis-hydrophosphorylated product.

Experimentally, an increase in solvent polarity increases the reaction rate. The active species, alkali metal phosphinite M-OPMes₂, generally exists as a contact ion-pair, characterised by a strong electrostatic interaction between the cation and the phosphinite oxygen. As the solvent polarity increases, this interaction is expected to shift from contact ion-pair to solvent separated ion-pair. Calculations indicate that the anionic dimesitylphosphinite, when uncoupled from the cation, emerges as the strongest nucleophile (Table 4). Therefore, detaching the cation from [OPMes₂]⁻ in a more polar solvent is expected to reduce the activation barrier of the nucleophilic addition, thereby increasing the overall reaction rate.

Computational studies of reaction mechanisms of s-block metal promoted processes have garnered less attention compared to those centred on transition-metal catalysed processes. From a computational perspective this study highlights the difficulties associated with computationally modelling reaction mechanisms for catalytic processes involving s-block metal cations. Key issues include speciation and solvation, particularly evident in the analysis of the formation and deactivation of the alkali metal phosphinite active species. In contrast, these factors have a reduced impact in the P–H addition reaction, where the cations play a minor role. Achieving more quantitative insights into the formation and stability of the active species would require performing expensive time-consuming DFT-based molecular dynamics simulations, using a box with tens of solvent molecules, an approach beyond the scope of this work. Nonetheless, our findings depict that static DFT calculations, using a careful choice of a cluster–continuum solvent model, incorporating a limited number of explicit THF solvent molecules, can provide valuable insights and outline key trends to understand the behaviour of such systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

IB: DFT calculations and data analysis, review and editing of the draft. GU: supervision, review and edition; MW: supervision, conceptualization, review and editing; AL: DFT calculations, conceptualization, funding acquisition, formal analysis, and original draft preparation. All authors have corrected the final manuscript. All authors have read and approved the final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 860322, for which I. B. would also like to express gratitude for the awarded scholarship. G. U. and A. L. thank the Spanish Ministerio de Ciencia, Innovación y Universidades for Grant PID2023-150881NB-I00 funded by MCIN/AEI/10.13039/501100011033. The allocation of computer time at Consorci de Serveis Universitaris de Catalunya (CSUC) is also gratefully acknowledged.

References

1. S. Harder, Early Main group Metal Catalysis: Concepts and Reactions, Wiley-VCH, 2020,  DOI:10.1002/9783527818020.
2. S. Krieck and M. Westerhausen, Kudos and Renaissance of s-Block Metal Chemistry, Inorganics, 2017, 5, 17,  DOI:10.3390/inorganics5010017.
3. M. J. Rodríguez-Álvarez, N. Ríos-Lombardía, S. E. García-Garrido, C. Concellón, V. del Amo, V. Capriati and J. García-Álvarez, Recent Advancements in the Utilization of s-Block Organometallic Reagents in Organic Synthesis with Sustainable Solvents, Molecules, 2024, 29, 1422,  DOI:10.3390/molecules29071422.
4. S. Krieck and M. Westerhausen, H–N and H–P Bond Addition to Alkynes and Heterocumulenes, in Early Main group Metal Catalysis: Concepts and Reactions, Wiley-VCH, 2020, ch. 5, pp. 123–150,  DOI:10.1002/9783527818020.ch5.
5. Y. Sarazin and J.-F. Carpentier, Molecular s-Block Catalysts for Alkene Hydrophosphination and Related Reactions, in Early Main group Metal Catalysis: Concepts and Reactions, Wiley-VCH, 2020, ch. 4, pp. 93–121,  DOI:10.1002/9783527818020.ch4.
6. I. Banerjee and T. K. Panda, Recent advances in the carbon-phosphorus (C-P) bond formation from unsaturated compounds by s- and p-block metals, Org. Biomol. Chem., 2021, 19, 6571–6587,  10.1039/D1OB01019K.
7. S. M. Härling, H. Görls, S. Krieck and M. Westerhausen, Potassium-Mediated Hydrophosphorylation of Heterocumulenes with Diarylphosphane Oxide and Sulfide, Inorg. Chem., 2016, 55, 10741–10750,  DOI:10.1021/acs.inorgchem.6b01973.
8. S. M. Härling, S. Krieck, H. Görls and M. Westerhausen, Influence of 18-Crown-6 Ether Coordination on the Catalytic Activity of Potassium and Calcium Diarylphosphinites in Hydrophosphorylation Reactions, Inorg. Chem., 2017, 56, 9255–9263,  DOI:10.1021/acs.inorgchem.7b01314.
9. S. M. Härling, B. E. Fener, S. Krieck, H. Görls and M. Westerhausen, Potassium Dimesitylphosphinite Catalyzed Intermolecular Hydrophosphorylation of Alkynes, Organometallics, 2018, 37, 4380–4386,  DOI:10.1021/acs.organomet.8b00368.
10. B. E. Fener, P. Schüler, N. Ueberschaar, P. Bellstedt, H. Görls, S. Krieck and M. Westerhausen, Scope and Limitations of the s-Block Metal-Mediated Pudovik Reaction, Chem. – Eur. J., 2020, 26, 7235–7243,  DOI:10.1002/chem.201905565.
11. A. A. Sobanov, A. V. Zolotukhin, V. I. Galkin, R. A. Cherkasov and A. N. Pudovik, Kinetics and Mechanism of the Pudovik Reaction in the Azomethine Series: I. Addition of Dimethyl Hydrogen Phosphite to N-Isopropylbenzalimines, Russ. J. Gen. Chem., 2002, 72, 1141–1144,  DOI:10.1023/a:1020794530963.
12. J. A. Spivey and D. B. Collum, Potassium Hexamethyldisilazide (KHMDS): Solvent-Dependent Solution Structures, J. Am. Chem. Soc., 2024, 146, 17827–17837,  DOI:10.1021/jacs.4c03418.
13. R. A. Woltornist and D. B. Collum, Aggregation and Solvation of Sodium Hexamethyldisilazide: Across the Solvent Spectrum, J. Org. Chem., 2021, 86, 2406–2422,  DOI:10.1021/acs.joc.0c02546.
14. B. L. Lucht and D. B. Collum, Lithium Hexamethyldisilazide: A View of Lithium Ion Solvation through a Glass-Bottom Boat, Acc. Chem. Res., 1999, 32, 1035–1042,  DOI:10.1021/ar960300e.
15. A. W. J. Platten, A. M. Borys and E. Hevia, Hydrophosphinylation of Styrenes Catalysed by Well-Defined s-Block Bimetallics, ChemCatChem, 2022, 14, e202101853,  DOI:10.1002/cctc.202101.
16. G. K. S. Prakash, P. V. Jog, P. T. D. Batamack and G. A. Olah, Taming of Fluoroform: Direct Nucleophilic Trifluoromethylation of Si, B, S, and C Centers, Science, 2012, 338, 1324–1327,  DOI:10.1126/science.1227859.
17. G. Luo, Y. Luo and J. Qu, Direct nucleophilic trifluoromethylation using fluoroform: a theoretical mechanistic investigation and insight into the effect of alkali metal cations, New J. Chem., 2013, 37, 3274–3280,  10.1039/C3NJ00686G.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr , J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian Inc., Wallingford CT, 2016.
19. C. T. Lee, W. T. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789,  DOI:10.1103/physrevb.37.785.
20. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206,  DOI:10.1016/0009-2614(89)87234-3.
21. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652,  DOI:10.1063/1.464913.
22. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465,  DOI:10.1002/jcc.21759.
23. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396,  DOI:10.1021/jp810292n.
24. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 1972, 56, 2257–2261,  DOI:10.1063/1.1677527.
25. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654–3665,  DOI:10.1063/1.444267.
26. G. Norjmaa, G. Ujaque and A. Lledos, Beyond Continuum Solvent Models in Computational Homogeneous Catalysis, Top. Catal., 2022, 65, 118–140,  DOI:10.1007/s11244-021-01520-2.
27. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305,  10.1039/B508541A.
28. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065,  10.1039/B515623H.
29. V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, Calculation of Solvation Free Energies of Charged Solutes Using Mixed Cluster/Continuum Models, J. Phys. Chem. B, 2008, 112, 9709–9719,  DOI:10.1021/jp802665d.
30. C. Y. Legault, CYLview20, Université de Sherbrooke, 2020 (https://www.cylview.org).
31. J. P. Guthrie, Tautomerization equilibria for phosphorous acid and its ethyl esters, free energies of formation of phosphorous and phosphonic acids and their ethyl esters, and pKa values for ionization of the P—H bond in phosphonic acid and phosphonic esters, Can. J. Chem., 1979, 57, 236–239,  DOI:10.1139/v79-039.
32. D. Vincze, P. Ábrányi-Balogh, P. Bagi and G. A. Keglevich, A Mechanistic Study on the Tautomerism of H-Phosphonates, H-Phosphinates and Secondary Phosphine Oxides, Molecules, 2019, 24, 3859,  DOI:10.3390/molecules24213859.
33. B. G. Janesko, H. C. Fisher, M. J. Bridle and J.-L. Montchamp, P(=O)H to P–OH Tautomerism: A Theoretical and Experimental Study, J. Org. Chem., 2015, 80, 10025–10032,  DOI:10.1021/acs.joc.5b01618.
34. S. Popenova, R. C. Mawhinney and G. Schreckenbach, Density functional study of lithium hexamethyldisilazide (LiHMDS) complexes: effects of solvation and aggregation, Inorg. Chem., 2007, 46, 3856–3864,  DOI:10.1021/ic061599s.
35. A. Koch, H. Görls, S. Krieck and M. Westerhausen, Coordination behavior of bidentate bis(carbenes) at alkali metal bis(trimethylsilyl)amides, Dalton Trans., 2017, 46, 9058–9067,  10.1039/C7DT01538K.
36. D. Mootz, A. Zinnius and B. Böttcher, Assoziation im festen Zustand von Bis(trimethylsilyl)amidolithium und Methyltrimethylsilanolatoberyllium, Angew. Chem., 1969, 81, 398–399,  DOI:10.1002/ange.19690811015.
37. K. W. Henderson, A. E. Dorigo, Q.-Y. Liu and P. G. Williard, Effect of Polydentate Donor Molecules on Lithium Hexamethyldisilazide Aggregation: An X-ray Crystallographic and a Combination Semiempirical PM3/Single Point ab Initio Theoretical Study, J. Am. Chem. Soc., 1997, 119, 11855–11863,  DOI:10.1021/ja971920t.
38. A. I. Ojeda-Amador, A. J. Martínez-Martínez, A. R. Kennedy and C. T. O'Hara, Structural Studies of Cesium, Lithium/Cesium, and Sodium/Cesium Bis(trimethylsilyl)amide (HMDS) Complexes, Inorg. Chem., 2016, 55, 5719–5728,  DOI:10.1021/acs.inorgchem.6b00839.
39. R. E. Mulvey and S. D. Robertson, Synthetically Important Alkali-Metal Utility Amides: Lithium, Sodium, and Potassium Hexamethyldisilazides, Diisopropylamides, and Tetramethylpiperidides, Angew. Chem., Int. Ed., 2013, 52, 11470–11487,  DOI:10.1002/anie.201301837.
40. A. I. Ojeda-Amador, A. J. Martínez-Martínez, G. M. Robertson, S. D. Robertson, A. R. Kennedy and C. T. O'Hara, Exploring the solid state and solution structural chemistry of the utility amide potassium hexamethyldisilazide (KHMDS), Dalton Trans., 2017, 46, 6392–6403,  10.1039/C7DT01118K.
41. J. Del Pozo, M. Pérez-Iglesias, R. Álvarez, A. Lledós, J. A. Casares and P. Espinet, Speciation of ZnMe₂, ZnMeCl, and ZnCl₂ in Tetrahydrofuran (THF), and Its Influence on Mechanism Calculations of Catalytic Processes, ACS Catal., 2017, 7, 3575–3583,  DOI:10.1021/acscatal.6b03636.
42. P. Horrillo-Martínez, K. C. Hultzsch, A. Gil and V. Branchadell, Base-Catalyzed Anti-Markovnikov Hydroamination of Vinylarenes – Scope, Limitations and Computational Studies, Eur. J. Org. Chem., 2007, 3311–3325,  DOI:10.1002/ejoc.200700147.
43. C. Berthold, L. R. Thomas-Hargreaves, S. I. Ivlev and M. R. Buchner, An approach towards the synthesis of lithium and beryllium diphenylphosphinites, Z. Naturforsch., B:J. Chem. Sci., 2021, 76, 651–658,  DOI:10.1515/znb-2021-0104.
44. B. E. Fener, P. Schüler, P. Liebing, H. Görls and M. Westerhausen, Syntheses and Structures of Dimesitylphosphinite Complexes of the Alkali Metals as well as their Catalytic Activity in Hydro-phosphorylation Reactions, Dalton Trans., 2025, 54, 181–197,  10.1039/d4dt02721c.
45. M. A. Beswick, N. L. Cromhout, C. N. Harmer, J. S. Palmer, P. R. Raithby, A. Steiner, K. L. Verhorevoort, D. S. Wright, A. Steiner, K. L. Verhorevoort and D. S. Wright, Metal selection of ligand functionality in [(mes)₂P(··O)₂Li·₂thf]₂ and [{(Me₃Si)₂N}Cd{(mes)₂P··O}₂Li·₂thf] (mes = C₆H₂Me₃-2,4,6), Chem. Commun., 1997, 583–584,  10.1039/A608202E.
46. R. M. Peltzer, O. Eisenstein, A. Nova and M. Cascella, How Solvent Dynamics Controls the Schlenk Equilibrium of Grignard Reagents: A Computational Study of CH₃MgCl in Tetrahydrofuran, J. Phys. Chem. B, 2017, 121, 4226–4237,  DOI:10.1021/acs.jpcb.7b02716.
47. Z.-Y. Wang, Q. Guo, S. Xu and K.-K. Wang, Nucleophilic H-Phosphites, H-Phosphinates, and H-Phosphine Oxides in Organic Reactions, Synthesis, 2021, 53, 3683–3698,  DOI:10.1055/a-1511-0382.
48. P. Jaramillo, L. R. Domingo, E. Chamorro and P. Pérez, A further exploration of a nucleophilicity index based on the gas-phase ionization potentials, J. Mol. Struct.:THEOCHEM, 2008, 865, 68–72,  DOI:10.1016/j.theochem.2008.06.022.
49. M. Ríos-Gutiérrez, A. S. Sousa and L. R. Domingo, J. Phys. Org. Chem., 2023, 36, e4503.
50. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8, 527–541,  DOI:10.1021/ct200866d.
51. D. A. Dougherty, The Cation−π Interaction, Acc. Chem. Res., 2013, 46, 885–893,  DOI:10.1021/ar300265y.
52. C. Lambert and P. V. R. Schleyer, Are Polar Organometallic Compounds “Carbanions”? The Gegenion Effect on Structure and Energies of Alkali-Metal Compounds, Angew. Chem., Int. Ed. Engl., 1994, 33, 1129–1140,  DOI:10.1002/anie.199411291.
53. D. R. Armstrong, M. G. Davidson, D. Garcia-Vivo, A. R. Kennedy, R. E. Mulvey and S. D. Robertson, Monomerizing alkali-metal 3,5-dimethylbenzyl salts with tris(N, N-dimethyl-2-aminoethyl)amine (Me6TREN): structural and bonding implications, Inorg. Chem., 2013, 52, 12023–12032,  DOI:10.1021/ic401777x.
54. M. G. Davidson, D. Garcia-Vivo, A. R. Kennedy, R. E. Mulvey and S. D. Robertson, Exploiting σ/π coordination isomerism to prepare homologous organoalkali metal (Li, Na, K) monomers with identical ligand sets, Chem. – Eur. J., 2011, 17, 3364–3369,  DOI:10.1002/chem.201003493.
55. A. Rae, K. M. Byrne, S. A. Brown, A. R. Kennedy, T. Krämer, R. E. Mulvey and S. D. Robertson, Sigma/pi Bonding Preferences of Solvated Alkali-Metal Cations to Ditopic Arylmethyl Anions, Chem. – Eur. J., 2022, 28, e202104260,  DOI:10.1002/chem.202104260.
56. A. Couce-Rios, A. Lledós, I. Fernández and G. Ujaque, Origin of the Anti-Markovnikov Hydroamination of Alkenes Catalyzed by L−Au(I) Complexes: Coordination Mode Determines Regioselectivity, ACS Catal., 2019, 9, 848–858,  DOI:10.1021/acscatal.8b03843.
57. J. Escorihuela, A. Lledós and G. Ujaque, Anti-Markovnikov Intermolecular Hydroamination of Alkenes and Alkynes: A Mechanistic View, Chem. Rev., 2023, 123, 9139–9203,  DOI:10.1021/acs.chemrev.2c00482.
58. R. A. Woltornist and D. B. Collum, Ketone Enolization with Sodium Hexamethyldisilazide: Solvent- and Substrate-Dependent E–Z Selectivity and Affiliated Mechanisms, J. Am. Chem. Soc., 2021, 143, 17452–17464,  DOI:10.1021/jacs.1c06529.
59. A. Yoshimura, Y. Saga, Y. Sato, A. Ogawa, T. Chen and L.-B. Han, An efficient base-catalyzed double addition of H-phosphine oxides to alkynes, Tetrahedron Lett., 2016, 57, 3382–3384,  DOI:10.1016/j.tetlet.2016.06.079.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cy00269a

---