Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insight into the activity and mechanism of FeNiB LDH electrocatalysts in alkaline OER via operando DRIFTS†
Emilia M.
Kazek
 a,
Rocco
Villano
a,
Rocco
Villano
 a,
M. Veronica
Sofianos
b,
Jeannie Z. Y.
Tan
a,
M. Veronica
Sofianos
b,
Jeannie Z. Y.
Tan
 c and
Leila
Negahdar
c and
Leila
Negahdar
 *a
*a
aSchool of Chemistry, University College Dublin, Belfield, Dublin 4, Ireland. E-mail: leila.negahdar@ucd.ie
bSchool of Chemical and Bioprocess Engineering, University College Dublin, Belfield, Dublin 4, Ireland
cResearch Centre for Carbon Solutions (RCCS), Heriot−Watt University, Edinburgh EH14 4AS, UK
First published on 7th May 2025
Abstract
Green H2 shows significant promise as an energy carrier capable of replacing fossil fuels and meeting global energy demands. Understanding the oxygen evolution reaction (OER) mechanism is crucial for the development of efficient electrocatalysts for green H2 production. In this study, we investigated the activity and stability of FeNiB layered double hydroxide (LDH) catalysts with varying Fe/Ni ratios (0.9/1, 1/1, 1/0.9) using steady-state polarisation, electrochemical impedance spectroscopy (EIS), electrochemical kinetic modelling, and surface characterisation techniques, including X-ray photoelectron spectroscopy (XPS) and operando diffuse reflectance Fourier transform infrared spectroscopy (DRIFTS). Tafel slope and EIS analysis revealed that FeNiB 0.9/1 exhibited the best stability among the three catalysts. In the low Tafel region slopes of 34, 23, and 32 mV dec−1 were obtained for FeNiB 0.9/1, 1/1, and 1/0.9, respectively, whereas 80, 102, and 100 m Vdec−1 were obtained in the high Tafel region. Kinetic studies indicated that FeNiB 0.9/1 and 1/1 followed the first step of Bockris' pathway as the rate-determining step, whereas FeNiB 1/0.9 proceeded through the second step. XPS evidenced the superior performance of FeNiB 0.9/1 in the high overpotential region, attributed to its enhanced stability from the higher Ni content. Operando DRIFTS provided further mechanistic insights, showing that at lower Fe concentrations, OH− bound to Ni plays a dominant role in OER, while Fe-bound OH− governs the reaction in the Fe-rich catalysts.
Introduction
Global warming, climate change due to massive greenhouse gas emissions such as CO2, and the depletion of fossil fuels have brought significant attention to the need for new renewable and sustainable energy sources.1 H2 is one of the most promising alternative energy resources to fossil fuels. Among the many ways to generate H2 gas, electrochemical water splitting has presented a feasible and renewable route.2 Water splitting involves two half-reactions, the kinetically hindered four-electron transfer oxygen evolution reaction (OER) at the anode and the mechanistically simpler and faster two-electron transfer hydrogen evolution reaction (HER) at the cathode. In OER under alkaline conditions, OH− groups are oxidised to H2O and O2 with the accompanying release of e−.3 The sluggish kinetics of the OER determine the overall rate of H2 production, therefore a highly active electrocatalyst is required to overcome the energy barrier of OER.4 Theoretically, the OER catalyst should operate at a low overpotential and have a high stability, as well as earth abundance, and be available at a low cost for ease of its implementation at an industrial scale.Transition metal-based OER catalysts have been extensively investigated because of their superior OER catalytic activities. Specifically, transition bimetallic borides, hydroxides, sulphides, and phosphides have shown improved OER performance in comparison to their monometallic counterparts. By adjusting the relative ratios, a new bimetallic compound with a tuneable electronic structure can be synthesised.5 NiFe-LDH (layered double hydroxide) are among the best performing transition metal OER catalysts. Specifically, the synergistic effect of Ni and Fe has been shown to surpass the performance of Ni and Fe-based catalysts on their own. The Fe-to-Ni ratio in NiFe-LDH has been shown to regulate OER activity, even with small differences in the amount of Ni and Fe.5 The metal ratio has been described to influence the pre-oxidation of Ni2+ species to catalytically active high-valence species like NiOOH, which is regarded as a prerequisite to catalyse the OER.6Operando X-ray absorption (XAS) and Raman spectroscopy have been used to show that when anodic potential is applied, Ni exhibits electronic shifts to higher oxidation states, and the apparent NiOOH phase evolution occurs.7 Many catalyst design strategies have therefore focused on modifying the Fe-to-Ni ratio or introducing foreign anions and heteroatoms to induce high Ni oxidation states, which is known to stabilise OER intermediates and promote oxygen production.7 Agreement has not been conclusively found on the precise active sites in OER on NiFe-LDH, but it is believed that interactions between Ni and Fe atoms influence the electronic structures around the active sites, thus influencing OER kinetics.6 The activity of Fe species at edge, corner, and defect sites within LDH has been studied. For example, Shi et al. observed that as the Fe content in NiFe-LDH increases, the grain size decreases while the interlayer spacing increases, which leads to abundant edge sites for OER activity and the large spacing can expose active sites and accommodate NiOOH formation.8 With this in mind, our focus is on observing the effects of different Fe-to-Ni ratios to the OER activity.
Combining Fe and Ni with intercalated boron (B) ions can greatly increase the efficiency of water splitting. Han et al. detailed an amorphous nickel–iron boride coated (NiFeB@NiFeBi) prepared through a facile NaBH4 reduction which exhibited excellent oxygen evolution activity with an overpotential of 237 mV at 10 mA cm−2.9 In another study, Hong et al. synthesised NixFe1−xB nanoparticles by a facile borothermal reduction method in molten salt, which exhibited an overpotential of 282 mV at 10 mA cm−2 for OER in an alkaline electrolyte.10 Boron can improve the catalytic properties of Fe and Ni by increasing the interlayer distance in the LDH structure of NiFe-LDH, which enhances the surface activity of the catalyst.11 Boron can facilitate the enrichment of electrons at metal sites via reverse electron transfer, inducing metal lattice strain and enhancing electrochemical reactions.12 Boron intercalation within the OH− layers is proposed to be capable of modulating the electronic structure of the metal sites and influencing the bonding between the metal and non-metal atoms, which makes way for surface reconstruction, creating defects, or moderating charge transfer to improve OER activity.7 In one study, Bai et al.13 observed that the Ni2+/Ni3+ oxidation peak in NiFeB during CV experienced a cathodic shift compared to their NiFe catalyst without any boron, which indicated that boron lowers the potential required for the oxidation of Ni2+ in FeNiB catalysts. This is favourable for the formation of highly oxidised Ni3+ active sites. A more robust oxidation of Fe was observed via operando UV-vis spectroscopy and XAS analysis by Hong et al. when boron was present in NiFe hydroxide, indicating the production of OER active Fe and thus, enhancing the catalytic activity of NiFe hydroxide. Boron also influenced the rate of Fe redeposition onto the surface of the catalyst and preserved the homogeneity of Fe spatial distribution on the catalyst surface.7 Additionally, incorporating boron into transition metal catalysts offer a way to reduce costs without compromising performance.
The underlying mechanism behind the activity of Ni and Fe-based OER catalysts has been investigated.11,14,15 For instance, Berger et al. found that Bockris' physisorbed hydrogen peroxide pathway fit with the experimentally observed Tafel slope and reaction order for FeNiB electrocatalysts.11 While Tafel analysis helps explain the OER kinetics of an electrocatalyst, incorporating operando characterisation provides a more detailed mechanistic understanding. Operando DRIFTS enables real-time monitoring of reaction intermediates on the catalyst surface by detecting changes in metal-adsorbate bond strengths and their corresponding infrared absorbance.
This study aims to investigate the OER activity over FeNiB electrocatalysts with Fe-to-Ni ratio through a combination of steady-state polarisation, electrochemical impedance spectroscopy, electrochemical kinetic modelling, and surface characterisation techniques, including XPS and operando DRIFTS, to elucidate the factors influencing catalytic performance and stability.
Experimental
a. Synthesis of FeNiB electrocatalysts and working electrode
The catalyst synthesis procedure has been reported by Sofianos et al.5 The catalyst samples with Fe/Ni mole ratios of 1/0.9, 1/1, and 0.9/1 were prepared by adding 5 mg of electrocatalyst powder to a mixture of 490 μL deionised water, 490 μL ethanol, and 20 μL of 5% Nafion solution (Ion Power). For the working electrode (WE), 72 μL of catalyst ink was drop-cast onto a Toray carbon paper surface with dimensions of 1.8 cm × 1.8 cm, with a catalyst loading of 2.8 mg cm−2.b. Material characterisation
Chemical analysis of the electrocatalyst powders was conducted using a Kratos AXIS Ultra DLD X-ray photoelectron spectrometer (XPS) in ultra-high vacuum utilising an Al-Kα X-ray source (1486.7 eV). Casa XPS software was used for data analysis and calibrated using the surface adventitious C 1s peak at 284.5 eV.c. Electrochemical testing
The catalyst activity was tested using a customised flow cell setup with exposed electrocatalyst area of 1 cm2, with graphite sheets as the counter electrode (CE) and an Ag/AgCl (3.0 M KCl) electrode as the reference electrode (RE), controlled by a Metrohm Autolab potentiostat model PGSTAT204 connected to a computer with Nova 2.1.7 software. A 1 M potassium hydroxide (KOH) solution prepared with deionised water was used as the electrolyte. To prepare the WE surface, the electrode was cleaned before each electrochemical measurement by performing 50 cyclic voltammetry (CV) scans from 1 to 2 V vs. RHE at a scan rate of 200 mV s−1.For electrochemical surface area (ECSA) measurements, CV scans were conducted from 1 to 1.1 V vs. RHE at varying scan rates (20, 40, 60, 80, 100 and 120 mV s−1). For electrochemical impedance spectroscopy (EIS) analysis, measurements were performed with an amplitude of 10 mV across a frequency range of 100 kHz to 0.1 Hz, at nine different potentials from 1.4 to 1.6 V vs. RHE in 0.025 V increments, with a waiting time of 150 seconds to reach equilibrium at each step. Reaction order analysis was conducted using CV scans (1 to 2 V vs. RHE) at various KOH electrolyte concentrations (1 M, 0.8 M, 0.6 M, 0.4 M, and 0.2 M) at a scan rate of 5 mV s−1.Operando diffuse reflectance Fourier transform infrared spectroscopy (DRIFTS) was performed on a Bruker Vertex 70 spectrometer with a liquid nitrogen–cooled HgCdTe (MCT) detector connected to our customised flow reaction cell. Similar to the actual electroreduction experiments, in each DRIFT measurement, 72 μL of electrocatalyst ink was drop-cast on the Toray carbon paper and placed on the cathode holder with exposed electrocatalyst area of 1 cm2. The anode compartment, in which the anode was place, was separated from cathode compartment using AEM. The graphite background was collected prior to the start of the experiment. 24 scans were collected per spectrum with a spectral resolution of 1 cm−1 and in the spectral range of 4000–400 cm−1. FTIR measurements were taken of the catalyst in the absence of KOH, the catalyst in the presence of KOH, and the catalyst during and after surface cleaning with 50 CV scans. Operando FTIR measurements of each catalyst sample were preformed while an LSV scan was taken from 1 to 2 V vs. RHE at a scan rate of 5 mV s−1.
Results and discussion
The electrochemically active surface area (ECSA) of FeNiB 0.9/1, 1/1, and 1/0.9 were studied using CV cycling at different scan rates. The ECSA was calculated using the method reported by Bai et al., with 2.8 mg cm−2 of catalyst per electrode.13 FeNiB 0.9/1 exhibited the largest ECSA (2.5 cm2), followed by FeNiB 1/1 (2.2 cm2), and lastly FeNiB 1/0.9 (1.7 cm2) (Fig. 1). Generally, materials with a large ECSA have a higher catalytic activity than materials with a low ECSA, as in the former, more area of the electrode material is available to react with the electrolyte and be used for charge transfer.16 A loss of ECSA can occur if the number of available active sites decreases, e.g. via Ni or Fe dissolution, or via blockage by gas bubble evolution on the catalyst surface during OER. As the ECSA measurements were taken before a significant loss of active sites or gas evolution could occur, the data proves that FeNiB 0.9/1 had more accessible electrode material for charge transfer to begin with than FeNiB 1/1 and 1/0.9. | ||
| Fig. 1 Electrochemically active surface area (ECSA) of FeNiB 0.9/1 (black), FeNiB 1/1 (red), and FeNiB 1/0.9 (blue). The Cdl is indicated for each catalyst. | ||
The electrocatalytic activity of the FeNiB samples in OER was compared using polarisation curves generated from steady-state linear sweep voltammetry (LSV) experiments. To compensate for the electrolyte resistance, which was determined using EIS, the LSV values shown in Fig. 2 were iR corrected. A favourable polarisation curve for an OER electrocatalyst exhibits a high current density at a low overpotential. The current density conventionally used to compare the OER activity of electrocatalysts is 10 mA cm−2.17 FeNiB 0.9/1, 1/1, and 1/0.9 reached a current density of 10 mA cm−2 at overpotentials of 300, 360, and 320 mV, respectively (Fig. 2). A current density of 50 mA cm−2 was attained by FeNiB 0.9/1, 1/1, and 1/0.9 at overpotentials of 340, 540, and 490 mV, respectively. The best performance was exhibited by FeNiB 0.9/1, followed by FeNiB 1/0.9, and lastly FeNiB 1/1. The superior performance exhibited during LSV by FeNiB 0.9/1 was possibly due to its comparatively larger ECSA.
 | ||
| Fig. 2 Polarisation curves of FeNiB 0.9/1 (black), FeNiB 1/1 (red), and FeNiB 1/0.9 (blue), showing the overpotentials at 10 mA cm−2 (bottom line) and 50 mA cm−2 (top line). | ||
Electrochemical impedance spectroscopy (EIS)
Electrochemical impedance spectroscopy (EIS) spectra for FeNiB catalyst samples were recorded across increasing potentials from 1.4 to 1.6 V vs. RHE with an increment of 0.025 V and are presented in Bode and Nyquist plots (Fig. S1–S3†). The raw impedance data was analysed using an equivalent circuit model, as shown in Fig. 3. The fitted impedance data to the equivalent circuit model are reported in Fig. S4–S6.†The circuit consists of Rs, the uncompensated solution resistance and two R-CPE parallel combinations. In this model, the capacitance C (parameter for electrode with ideal behaviour) is replaced by CPE, accounting for sample inhomogeneities e.g., roughness and porosity of the electrodes.18–20 The high frequency R-CPE parallel combination, denoted as Rf-CPE_f is attributed to the properties of a resistive interlayer on the electrode due to the possible formation of hydroxide/oxide on the surface given by the exposure in ambient air and immersion in an alkaline solution, while the second R-CPE combination is attributed to Rct - CPE_dl .21–23
The impedance data were fitted using the electrochemical circle fit command on Nova2.1.8 Software. The optimised parameters from the fitting are summarised in Tables S1–S3.† To further analyse the contributions of each faradaic element, the fitted values of the circuit components were plotted as a function of applied potential (Fig. 4).
 | ||
| Fig. 4 A plot of the fitted values as a function of applied potential, with (a) charge transfer resistance (Rct); (b) double-layer capacity (Cdl); (c) resistance (Rf); (d) capacitance (Cf). | ||
The Rct of all the synthesised samples decreases and approaching 0 as the applied potential increases from 1.4 to 1.6 V vs. RHE (Fig. 4a). This observation suggested high electron transfer kinetics when the applied potential goes beyond 1.42 V vs. RHE, which is consistent with a Faradaic process.24 Before reaching the water oxidation onset potential, all three catalysts exhibit similar behaviour, with Cdl increasing as the potential rises from 1.4 to 1.45 V vs. RHE (Fig. 4b). This increase is likely due to charge accumulation at the electrode–electrolyte interface, enhancing the double-layer capacitance. However, at potentials greater than 1.5 V vs. RHE, Cdl begins to decrease, which can be attributed to extensive gas bubble evolution that reduces the active surface area of the electrode. The higher Cdl value observed for FeNiB 0.9/1 suggests greater OER activity, as evidenced in the LSV measurements and its larger ECSA (Fig. 1 and 2).
Fig. 4(c) presents the film resistance (Rf) as a function of potential. For FeNiB 0.9/1, Rf decreases slightly at higher potentials, whereas FeNiB 1/1 exhibited a more pronounced decline. In contrast, FeNiB 1/0.9 initially showed an increase in Rf before the water oxidation onset potential, followed by a gradual decrease thereafter. The film capacitance (Cf) behaviour is depicted in Fig. 4(d). Prior to the water oxidation onset potential, Cf remained stable for FeNiB 0.9/1 and FeNiB 1/1, while for FeNiB 1/0.9, it decreased as the potential increased. After the onset of water oxidation, Cf showed a slight increase for all three catalysts. The stability of Cf and Rf in FeNiB 0.9/1 indicated enhanced surface stability, whereas the significant variations in Cf and Rf observed for FeNiB 1/0.9 suggest structural reorganisation of the resistive interlayer at low overpotentials.
Tafel analysis
In order to investigate the activity and mechanism of the OER on FeNiB, a Tafel analysis was performed on CV and EIS data. The analysis of Tafel slopes and reaction order plots is frequently utilised in the determination of OER catalyst mechanisms. The following Tafel relation has been confirmed empirically:25η = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log (j) log (j) | (1) |
| j = j0{exp(−αfη) − exp [(1 − α)fη]} | (2) |
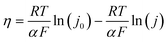 | (3) |
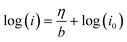 | (4) |
 | (5) |
From the CV Tafel plot, Tafel slopes of 34, 23, and 32 mV dec−1 were observed in the low overpotential region (150–300 mV) for FeNiB 0.9/1, FeNiB 1/1, and FeNiB 1/0.9, respectively. In the high overpotential region (250–400 mV), Tafel slopes of 80, 102, and 100 mV dec−1 were observed for sample FeNiB 0.9/1, FeNiB 1/1, and FeNiB 1/0.9, respectively. The performance data in the high overpotential region was in line with FeNiB 0.9/1 having the largest ECSA (2.5 cm2) and lowest operational overpotential. However, its inferior performance in the low overpotential region (150–300 mV) does not agree with these results. This may be a result of its high stability and will be discussed in the next section. A change in the Tafel slope was observed for all three catalysts at an overpotential between 250 and 350 mV in both CV and EIS data. The Tafel slope can increase at high overpotentials as a result of deactivation of the catalyst, for example by gas bubble evolution which blocks the active sites, or mass transfer limitations, leading to a loss of current.26 The presence of dual-Tafel behaviour across both methodologies suggests that the change in slope is mechanistically significant, implying a different the rate-determining step (RDS) in the low and high overpotential regions.11
Electrochemical reaction order
In electrocatalytic reactions, the reaction orders depend on the isotherm adsorption of the reactants at the electrode interface and the adsorption of reaction intermediates. The reaction order reflects the relationship between the reaction rate and the concentration of the reactants, which is the key in mechanistic interpretations. The reaction order is described by (eqn (6)):26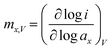 | (6) |
 | ||
| Fig. 6 Electrochemical reaction order of FeNiB 0.9/1 (0.71, black), FeNiB 1/1 (0.52, red) and FeNiB 1/0.9 (1.21, blue). | ||
Tafel slope and order of reaction are two key aspects depicting the differences in intrinsic catalytic activities. The Langmuir and Temkin isotherms are commonly used to describe adsorption conditions at the catalyst surface, which influence the reaction order. The Langmuir isotherm is based on the assumption that the apparent free energy of adsorption is independent of the surface coverage of OH, while the Temkin isotherm states that the free energy of adsorption may decrease linearly with coverage, either due to heterogeneity of the surface or to lateral interactions between adsorbates.26,27 The Langmuir isotherm is used to describe an integer reaction order, where the surface coverage (θ) is 0 or unity, whereas the Temkin isotherm describes fractional reaction orders, where 0.2 < θ < 0.8.26 Langmuir conditions indicate strong adsorption, while Temkin conditions indicate weak adsorption or competing reactions, which is often the case in complex reactions, including OER.11,26 The Temkin isotherm condition is also more applicable when two or more adsorbed intermediate species are present simultaneously on an electrode surface, giving rise to a fractional reaction order.28
The reaction orders of FeNiB 0.9/1, 1/1, and 1/0.9 in the high overpotential region were all fractional, and therefore will be evaluated under Temkin conditions in the section detailing the mechanism of OER. The value of the reaction order indicates the number of OH− equivalents involved in reactions at each active site in the OER prior to and including the RDS, but also the fraction of catalytically active sites promoting each of the individual pathways.26 FeNiB 0.9/1 and 1/1 had reaction orders less than 1, whereas FeNiB 1/0.9 had a reaction order greater than 1. A change in reaction orders arises from changes of adsorption conditions and therefore changes of the degree of coverage by intermediates like OH−.26 Therefore, we can deduce that the two catalysts containing the lowest proportion of Fe-to-Ni had a lower coverage of OH−, and a lower dependence of the rate on OH−, whereas the catalyst containing the highest proportion of Fe-to-Ni had a higher OH− coverage and larger dependence of the rate of reaction on OH−. This will be discussed in more detail in the operando DRIFTS section.
Mechanism of OER
In 1935, Eyring, Evans, and Polanyi described the theory of activated complexes, which can be extended to homogeneous and heterogeneous catalytic processes. Chemisorption of reactant species A* and B* proceeds via an activated chemisorbed complex (BA*)‡, which is subsequently transformed to the activated chemisorbed complex of products (RS*)‡. (RS*)‡ then splits into chemisorbed species R* and S* and finally, products are desorbed from the surface.29 In OER, most of the proposed mechanisms starts with adsorption of OH− onto the catalyst active site, followed by the formation of a range of adsorbed intermediates on the surface which react with each other via various disproportionation or bimolecular decomposition reactions, or undergo nucleophilic attack releasing O2.26 OH− not only attach to and detach from the surface, but also mutually interact with the growing surfaces on the catalyst and with the transient intermediates that are formed and consumed as the OER proceeds.4 Reaction sequences for the OER have been developed to better understand these surface processes.30Under typical electrochemical conditions all reaction intermediates before the transition state (TS) with the highest free energy are in quasi-equilibrium, in which the rate of the electrochemical reaction is determined by the TS with the highest free energy, or the TS involved in the RDS. The transition between consecutive reaction intermediates with the highest free energy difference defines the potential-determining step (PDS) in case of an electrochemical reaction step, where it can be assumed that the PDS = RDS if the additional kinetic barriers are small, such as the proton transfer reactions for OER.31 Such quasi-equilibrium conditions are assumed in the development of rate equations for the OER.
Therefore, in order to derive a rate expression for OER, it is necessary to describe the overall reaction as a sequence of elementary one electron transfer steps, and assume steady-state and quasi-equilibrium conditions.11 The overall rate of OER can then be expressed in terms of the RDS, and depending on which step is rate determining, the reaction sequences lead to different Tafel slope and reaction orders.26 Rate equations have been generated for OER pathways in the literature that describe the Tafel slope and reaction order for different rate determining steps.11,15,26 For instance, in a publication by Berger et al., the second step of Bockris' physisorbed hydrogen peroxide mechanism (Table 1) was assumed to be the rate determining step and Temkin conditions were used to generate rate equations to reflect their experimentally obtained fractional reaction orders.14 They were able to explain their experimental Tafel slopes and reaction orders with Bockris' path.
| Bockris' path11 |
| M + OH− → MOH + e− |
| MOH + OH− → MH2O2 + e− |
| MH2O2 + OH− → MHO2− + H2O |
| MH2O2 + MHO2− → O2 + H2O + OH− + 2M |
In the low Tafel region a slope of 34, 23, and 32 mVdec−1 were obtained for FeNiB 0.9/1, FeNiB 1/1, and FeNiB 1/0.9, respectively, whereas 80, 102, and 100 mVdec−1 were obtained in the high Tafel region. To explain the mechanism of NiFeB, we followed the proposed OER pathways by Bockris (Table 1). Assuming the first step of Bockris' path under Temkin adsorption conditions to be rate determining step, the Tafel slope and the order of reaction was derived from the following equations:11
 | (7) |
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dec−1, close to the experimental Tafel slope of b = 80 mV
dec−1, close to the experimental Tafel slope of b = 80 mV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dec−1, corresponding to β = 1. FeNiB 1/1 displays a reaction order of 0.52 in the high overpotential region, resulting in γ = 0.48. This produces a Tafel slope of b = 113 mV dec−1, also close to the experimental Tafel slope of b = 102 mV
dec−1, corresponding to β = 1. FeNiB 1/1 displays a reaction order of 0.52 in the high overpotential region, resulting in γ = 0.48. This produces a Tafel slope of b = 113 mV dec−1, also close to the experimental Tafel slope of b = 102 mV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dec−1. This calculated Tafel slope corresponds to β = 1. Assuming the second step of Bockris' path under Temkin adsorption conditions to be rate determining, the following equations were used to derive the Tafel slope and reaction order:11
dec−1. This calculated Tafel slope corresponds to β = 1. Assuming the second step of Bockris' path under Temkin adsorption conditions to be rate determining, the following equations were used to derive the Tafel slope and reaction order:11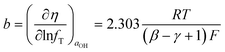 | (9) |
 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dec−1, corresponding to a symmetrical potential energy barrier constant of β = 0.38 (Fig. 7).
dec−1, corresponding to a symmetrical potential energy barrier constant of β = 0.38 (Fig. 7).
 | ||
| Fig. 7 Schematic of Bockris' physisorbed hydrogen peroxide path with the rate determining steps of FeNiB 0.9/1 (black), FeNiB 1/1 (red) and FeNiB 1/0.9 (blue) labelled. | ||
The meaning of the symmetrical potential energy barrier constant β has been interpreted based on models by Butler and Marcus.32 Based on Butler, β represents the fraction of the potential distance profile across the electrical double layer that enhances the electron transfer rate by bringing the reactant on top of the potential-energy barrier, where the transition state complex is located. If the potential energy barrier is symmetric meaning it is symmetrically located within the electrical double layer, the value of β equals 0.5. According to Marcus' theory, β is regarded as a multicomponent term that depends upon reorganisation of the solvent necessary to attain the transition state, and is a function of the applied overpotential.33 When the asymmetric form of the Marcus–Hush model is considered, β takes values different from 0.5 at the formal potential.34 Deviations from β = 0.5 such as those seen in FeNiB 0.9/1, 1/1, and 1/0.9 can be interpreted as a measure of the earliness or lateness of the transition state. A highly unfavourable step would be expected to show a β near unity when the overall reaction is at equilibrium, while β would shift nearer to 0.5 at the overpotentials where this step becomes downhill.35 Different factors can shift β away from 0.5. These include structural changes due to different ratios of Fe/Ni, lattice strain from size and coordination mismatches between Fe3+ and Ni2+/Ni3+, or B doping which alters the electronic environment and modifies the adsorption energies of oxygen intermediates.36 The β values of FeNiB 0.9/1, 1/1, and 1/0.9 reflect the impact of these structural factors through their deviations from β = 0.5, implying that the Fe/Ni ratios and presence of B had an effect on the electron transfer symmetry.
Large deviations of β from the 0.5 value are also expected if the reactant exchanges an electron with the metal while being in the adsorbed state.33 The deviation from β = 0.5 for FeNiB 0.9/1, 1/1, and 1/0.9 implies asymmetry in the location of the potential energy barrier within the electrical double layer, and the exchange of an electron with the metal while OH− is adsorbed, which is in line with steps 1 and 2 of Bockris' path being rate determining.
Catalyst surface analysis
X-ray photoelectron spectroscopy (XPS) analysis
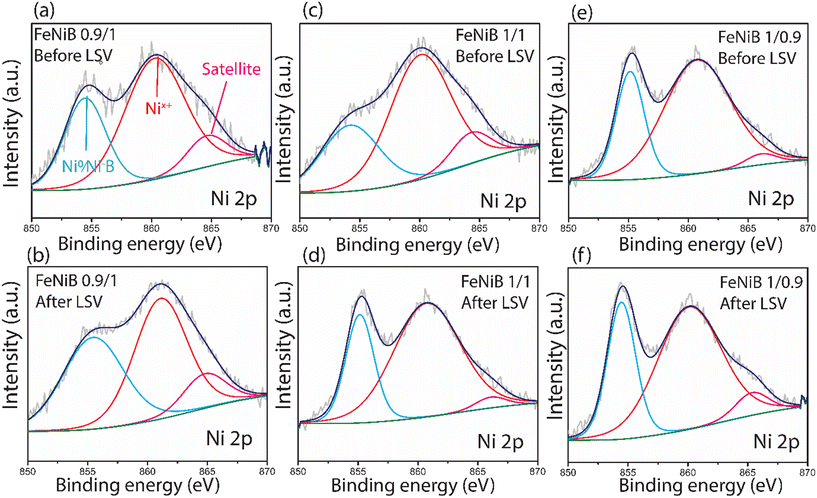
The surface compositions of FeNiB samples were compared using XPS. Fig. 8 and 9 present one set of FeNiB samples before LSV but after 50 CV scans, and another set after an LSV scan. In the high-resolution spectra of Ni 2p, the first peak at ∼852 eV is assigned to metallic Ni or Ni bonded to B (Fig. 8).5 The second peak at ∼856 eV is attributed to Ni2+ and Ni3+.37 Analysis of the area under the deconvoluted peaks indicated that FeNiB 1/0.9 had the most Ni2+ present both before and after LSV (Fig. 8e and f), followed by FeNiB 0.9/1 (Fig. 8a and b), and lastly FeNiB 1/1 (Fig. 8c and d). The analysis also showed that FeNiB 1/0.9 experienced the biggest increase in Ni2+ after LSV (Fig. 8f). The peak at ∼855 eV with its satellite at 866 eV was attributed to Ni(OH)2 (Fig. 8a–e).38In the high-resolution Fe 2p spectra, the peak observed at low binding energy of ∼705 eV originates from metallic Fe or Fe bonded to B (Fig. 9).5 Analysis of the area of deconvoluted peaks shows that FeNiB 1/0.9 had the highest concentration of metallic Fe or Fe bonded to B before LSV (Fig. 9e). The two peaks at ∼711![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and ∼723 eV correspond to Fe3+ 2p3/2 and Fe3+ 2p1/2, respectively (Fig. 9f).5,39 The spectrum after LSV of FeNiB 1/0.9 had the strongest Fe3+ 2p1/2 signal of all the XPS spectra (Fig. 9f), which shows that more Fe3+ was detected on the surface of FeNiB 1/0.9 following LSV than FeNiB 1/1 and 0.9/1, something we will return to in the operando DRIFTS section. Furthermore, the peak at ∼704 eV corresponding to metallic Fe or Fe bonded to B, present in the spectrum of FeNiB 1/0.9 before LSV (Fig. 9e) disappears in the spectrum after LSV (Fig. 9f), indicating the intense surface oxidation of Fe during OER. All three catalysts experienced an increase in the valency of Fe between the spectra before and after LSV, indicated by an increase in the binding energy of each peak.
and ∼723 eV correspond to Fe3+ 2p3/2 and Fe3+ 2p1/2, respectively (Fig. 9f).5,39 The spectrum after LSV of FeNiB 1/0.9 had the strongest Fe3+ 2p1/2 signal of all the XPS spectra (Fig. 9f), which shows that more Fe3+ was detected on the surface of FeNiB 1/0.9 following LSV than FeNiB 1/1 and 0.9/1, something we will return to in the operando DRIFTS section. Furthermore, the peak at ∼704 eV corresponding to metallic Fe or Fe bonded to B, present in the spectrum of FeNiB 1/0.9 before LSV (Fig. 9e) disappears in the spectrum after LSV (Fig. 9f), indicating the intense surface oxidation of Fe during OER. All three catalysts experienced an increase in the valency of Fe between the spectra before and after LSV, indicated by an increase in the binding energy of each peak.
Comparatively fewer changes were observed between the XPS spectra before and after LSV for FeNiB 0.9/1 (Fig. 8a and b and 9a and b), which combined with the relatively weak intensity of its Ni2+ signal before and after LSV (Fig. 8a and b), leads us to conclude that FeNiB 0.9/1 had the best stability of the three catalysts. This is supported by the EIS data, where the superior stability of 0.9/1 FeNiB is expressed in the highest Cdl out of all the three samples, and a low Rct. An increase in charge transfer resistance (Rct) and a sharp decrease in double layer capacitance (Cdl) can occur if excessive gas bubbles evolve and cover the active surface area.26 A large Cdl, and a decrease in Rct with increasing potential due to the favourable reconstruction of the catalyst surface, result in higher catalytic longevity. Furthermore, the EIS data indicated structural reorganisation of the surface of FeNiB 1/1 and 1/0.9, which is confirmed by the XPS data. FeNiB 1/1 exhibited a large increase in Ni2+ detected after LSV (Fig. 8d), and FeNiB 1/0.9 showed a large increase in Fe3+ following LSV (Fig. 9f).
The OER activity and stability of FeNiB appeared to improve with increasing Ni content, however the Tafel slopes in the low overpotential region for FeNiB 1/1 and 1/0.9, which have a lower Ni content, were better than FeNiB 0.9/1. On the other hand, the Tafel slope of FeNiB 0.9/1 was better in the high overpotential region than FeNiB 1/1 and 1/0.9. The greater concentration of Ni2+ detected in FeNiB 1/1 and 1/0.9 compared to FeNiB 0.9/1 could be an indicator for more readily formed highly oxidised Ni species during OER, such as NiOOH groups, which are recognised in some cases as active sites for OER and may contribute to the high activity of FeNiB 1/1 and 1/0.9 in the low overpotential region.13,40 The presence of Fe and its synergistic effect with Ni in FeNiB LDH electrocatalysts has, in fact, been shown to enhance the formation of these highly oxidised Ni active sites. Zhang et al. discussed the behaviour of NiFe-LDH catalysts for OER, and described that different bulk Fe-to-Ni ratios significantly affect the OER performance, with NiFe-LDH showing higher activity and stability as the level of Fe doping decreases.41 The superior performance in the high overpotential region of FeNiB 0.9/1, which has a larger proportion of Ni to Fe, could therefore be attributed to a higher overall stability with the caveat of comparatively worse performance when a low overpotential is applied. As for the involvement of Ni in the OER, we observed increasing ECSA with increasing Ni content, which supports the hypothesis that Ni acts as an active site in the OER on FeNiB. However, it should be noted that our data does not discount Fe as an active site, and the amount of Fe present has significant effects on the OER performance. These effects will be discussed in more detail in the operando section.
Operando DRIFTS
Operando diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) (Fig. 10a–d) was utilised alongside with the kinetic modelling of experimental data to Bockris' path in order to identify the formation of reaction intermediates and enhance our understanding of the OER mechanism of FeNiB. Firstly, it is worth mentioning that FeNiB 0.9/1 (Fig. 10a) showed more drastic changes in intensity over the course of LSV compared to FeNiB 1/1 and 1/0.9 (Fig. 10b and c, respectively). The DRIFTS spectrum of FeNiB 0.9/1 before CV (light grey line, Fig. 10a) and during the LSV at 0 minutes (red line, Fig. 10a) show a small difference in absorbance intensity (Fig. 10a, 3250–2750 cm−1 region highlighted in yellow). The equivalent spectral lines of FeNiB 1/1 and 1/0.9 have greater differences in absorbance (Fig. 10b and c). This shows that FeNiB 0.9/1 exhibited a higher stability during CV than FeNiB 1/1 and 1/0.9, which agrees with the XPS and EIS results.For FeNiB 0.9/1, the peaks at 886 cm−1 and 1423 cm−1 corresponding to H2O2 and 914 cm−1 and 1149 cm−1 corresponding to NiO2 (Fig. 10a, region highlighted in green) reach their maximum intensity at 3 min (Fig. 10a, orange line), which may correspond to the formation of the MH2O2 species in step 2 of Bockris' path. Their subsequent decrease in intensity may be due to the consumption of MH2O2 in the formation of the MHO2− species in step 3. The maximum absorbance of the peak at 3644 cm−1, corresponding to OH− species coordinated to the catalyst, is reached at 7 minutes (Fig. 10a, yellow region, yellow line). Also at 7 minutes, the intensity of the H2O2 peak (1423 cm−1) decreases. This could be a result of an accumulation of OH− groups on the surface and consumption of MH2O2 in step 3 of Bockris' path. Subsequently, at 8 minutes (Fig. 10a, green line), we observed the maximum absorbance of the H2O peak (1652 cm−1). The species detected on the FeNiB 0.9/1 catalyst surface during LSV closely reflected the intermediates described in Bockris' path.
According to our Tafel analysis, FeNiB 1/1 and FeNiB 0.9/1 shared a common RDS, therefore the similarities between their DRIFTS spectra could be mechanistically significant (Fig. 10a and b). The M–OH peak at 3644 cm−1 for FeNiB 1/1 also reached maximum absorbance at 7 minutes (Fig. 10b, yellow region, yellow line), as did the H2O peak at 1650 cm−1 (Fig. 10b, green region, yellow line), similar to FeNiB 0.9/1. Another commonality is in the NiO2 peaks at 905 cm−1 and 1143 cm−1, which momentarily increases in intensity at 3 minutes (Fig. 10b, green region, orange line), and subsequently drops (yellow line), which may be due to the formation and consumption of the MH2O2 species. Overall, the catalysts exhibited similar behaviour (Table 2 and 3).
| Surface species | Assignment | Frequency (cm−1) | |
|---|---|---|---|
| Observed | Literature | ||
| M = Ni, Fe | v(M–O–M) within LDH | 600–890 | <1000 (ref. 43) |
| v(O–H) of surface OH− in MOH | 3605–3748 | 3600–3700 (ref. 44) | |
| Ni(OH)2 | v(OH) of free OH | 3644 | 3637 (ref. 45), 3648 (ref. 46) |
| NiO2 | v(O–O) peroxidic stretch | 905, 914, 1143–1149 | 900–1150 (ref. 47) |
| NiOOH | v(O–O) | 1059, 1060 | 1062 (ref. 48) |
| FeOOH | ν(μ–OH) | 3624 | 3624 (ref. 49), 3626 (ref. 50), 3648 (ref. 50) |
| B(O)33− | v(B–O) | 1279–1284 | 1280 (ref. 39) |
| H2O2 | v(O–O) | 880–900 | 874 (ref. 51) |
| v(H–O–O) | 1423–1430 | 1426 (ref. 52) | |
| O–H stretch | 3270–3274 | 3273 (ref. 51) | |
| H2O | v(H2O) within LDH | 1635 | 1630 (ref. 43) |
| v(H–O–H) | 1650, 1652 | 1650 (ref. 53) | |
| Fe/Ni ratio | 0.9/1 | 1/1 | 1/0.9 |
| Tafel slope CV, EIS (low OP) (mV dec−1) | 34, 43 | 23, 23 | 32, 32 |
| Tafel slope CV, EIS (high OP) (mV dec−1) | 80, 99 | 102, 118 | 100, 186 |
| Reaction order (high OP) | 0.71 | 0.52 | 1.21 |
| RDS (high OP) | Step 1 | Step 1 | Step 2 |
| DRIFTS O–H stretching mode maximum absorbance | 3644 cm−1 | 3644 cm−1 | 3624 cm−1 |
| Time of DRIFTS H2O vibrational mode maximum absorbance | 8 minutes | 7 minutes | 1 minute |
The DRIFTS spectrum of FeNiB 1/0.9 has some notable differences to the remaining catalysts (Fig. 10c). Firstly, the maximum absorbance in the 3600–3700 cm−1 region is at 3624 cm−1, as opposed to 3644 cm−1 (FeNiB 0.9/1 and 1/1) (Fig. 10c, region highlighted in yellow). Unlike the other catalysts, the peak at 3624 cm−1 reaches its maximum absorbance at 0 minutes (Fig. 10c, yellow region, red line), followed by the H2O peak at 1652 cm−1 reaching its maximum absorbance at 1 min (Fig. 10b, green region, orange line). While the maximum detection of H2O was preceded by the highest detected absorbance of M–OH, similar to FeNiB 0.9/1 and 1/1, it occurred far earlier. This may be due to the presence of H2O2 groups after CV, visible by the presence of the peak at 1425 cm−1 at 0 minutes (Fig. 10c, region highlighted in green, red line). If the RDS is step 2 (Table 1), which involves the adsorption of OH− to MOH in order to form MH2O2, having peroxide species present prior to LSV could increase the rate of OER momentarily while they are consumed. The deprotonation of MH2O2 to form MHO2− in step 3 of Bockris' path is quick due to the instability of the MH2O2 intermediate and is further facilitated by the alkaline reaction medium. Step 4 is favourable due to gas evolution and Le Chatelier's principle.11 Therefore, by providing the catalyst with peroxide species, the slow formation of MH2O2 may have been “skipped” and in response, the reaction rate increased. This is in line with step 2 being the RDS for FeNiB 1/0.9, as was calculated earlier, as it is the RDS that governs the rate of reaction.42 Interestingly, it appears that the OER repeated. While the NiO2 peaks at 905 cm−1 and 1148 cm−1 are present in all scans (Fig. 10c, green region), their absorbance increased momentarily at 5 minutes (Fig. 10c, green region, yellow line), which may be due to the generation of more MH2O2. An increase in the absorbance of the peak at 1652 cm−1 was observed at 8 minutes (Fig. 10c, green region, blue line), in line with H2O production in steps 3 and 4 of Bockris' path.
The 3600–3700 cm−1 region corresponds to free, and H-bonded OH− groups. FeNiB 1/1 had the highest maximum absorbance in this region, followed by 0.9/1, where both maxima appear at a frequency of 3644 cm−1, corresponding to free OH− on Ni(OH)2. The identification of this peak as Ni(OH)2 is supported by the XPS data, where the Ni2+ peaks in the spectra of all three catalysts were attributed to Ni(OH)2 (Fig. 8). FeNiB 1/0.9 had the lowest maximum absorbance in this region, at a frequency of 3624 cm−1, which corresponds to doubly coordinated OH− groups on FeOOH.49,54 Similar peaks at a lower wavenumber of 3620 cm−1 have been reported as free OH− on catalysts consisting of nickel and silicon, such as that described by Peri et al.,55 whereas peaks attributed to FeOOH were at wavenumbers of ∼3625 cm−1.55–57 Therefore, the peak has been ascribed to Fe species rather than Ni species. Furthermore, there was a greater concentration of Fe3+ detected in the XPS analysis of FeNiB 1/0.9 compared to FeNiB 0.9/1 and 1/1 (Fig. 9). It is therefore likely that the strong Fe3+ signal arose from FeOOH that formed on the surface of FeNiB 1/0.9 during the OER. In addition, the Fe3+ signal in the XPS analysis was weaker for FeNiB 0.9/1 and 1/1, however oxidation of Ni was evident. This may explain why the maximum absorbance in the 3600–3700 cm−1 region corresponded to Ni species for FeNiB 0.9/1 and 1/1.
FeNiB 1/0.9 showcased a different RDS to FeNiB 0.9/1 and 1/1 in our Tafel analysis, therefore the difference in the wavenumber at which the maximum absorbance in this region is observed may be mechanistically significant. The peak at 3624 cm−1 had the highest absorption in the 3600–3700 cm−1 region (Fig. 10a–c, highlighted in yellow) throughout most of the OER. This was not the case for both FeNiB 0.9/1 and 1/1, indicating a different surface coverage of OH− on FeNiB 1/0.9. The lower intensity and red shift of the peak with the maximum absorbance between 3600–3700 cm−1 may indicate more hydrogen bonding between OH− groups. The stretching vibration peaks of free OH− without hydrogen bonding are located between 3600 and 3700 cm−1, and after the hydroxyl groups form hydrogen bonds, the O–H stretching vibration frequency shifts towards a lower wavenumber and the peaks broaden.44
The operando DRIFTS data implied a prevalence of surface FeOOH participating in the OER on FeNiB 1/0.9 (Fig. 10c), as opposed to more prevalent Ni(OH)2 in FeNiB 0.9/1 and 1/1 (Fig. 9a and b). Fe3+, which was shown to be present in the FeNiB 1/0.9 sample by XPS, can be further oxidised to form relatively stable [FeO4]2− ions which can leach out from the LDH structure. NiOOH has a strong attraction for these ions, which facilitates their adsorption on the NiOOH surface during OER, and at high [FeO4]2− concentrations, kinetically stable Fe(OH)x complexes preferentially form and deposit on the surface.41 As FeNiB 1/0.9 had the highest Fe concentration, this may have contributed to the different surface species detected during operando DRIFTS, and to its different catalytic behaviour. It appears that at lower Fe concentrations, OH− bound to Ni was a key participant in the OER, whereas Fe-bound OH− dominated in the catalyst containing more Fe than Ni. In addition, a study on NiFeOOH catalysts by Ahn and Bard58 has shown that FeOOH acts as a “fast” active site during the OER, which exhibited different behaviour to the “slow” Ni active sites. Following on from this, since FeNiB 0.9/1 and 1/1 had step 1 as the RDS and more Ni participating in the OER, it is possible that having more Ni present slowed the adsorption of OH− onto the catalysts' surface. In contrast, FeNiB 1/0.9 with more Fe participating in the OER had step 2 as the RDS, which indicates Fe may increase the rate of initial adsorption of OH−. Therefore, tying back to our previous discussion on active sites, Fe cannot be discounted as an active site in FeNiB, and modifying its bulk concentration plays a major role in optimising the catalytic performance of FeNiB.
Conclusion
In this study, the kinetic and stability behaviours of FeNiB electrocatalysts with varying Fe-to-Ni ratios were investigated, aiming to understand the factors affecting their OER performance. Our results indicated that the FeNiB sample with a ratio of Fe and Ni at 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 achieved the best performance in the high overpotential region (250–400 mV), with the lowest Tafel slope (80 mVdec−1). On the other hand, samples FeNiB 1/1 and 1/0.9 demonstrated better performance in the low overpotential region (150–300 mV). The reaction orders revealed that the catalysts with lower Fe-to-Ni ratios (FeNiB 0.9/1 and 1/1) exhibit a lower OH− coverage and weaker dependence on OH−, whereas FeNiB 1/0.9, with a higher Fe content, shows a greater OH− coverage and stronger dependence on OH−. EIS and XPS data suggested that the structural reorganisation of FeNiB 1/1 and 1/0.9 surfaces, which correlates with increased Ni2+ and Fe3+ formation, respectively, had improved the electrocatalytic activity of the samples in the low overpotential region (150–300 mV). The operando DRIFTS data further revealed that, at higher Fe concentrations, Fe-bound OH− dominates the OER; while Ni-bound OH− is more prevalent at lower Fe concentrations. Overall, these results emphasised the importance of Fe-to-Ni ratio optimisation, revealing that increasing the Ni content could improve the stability of FeNiB. However, modifying the Fe content can enhance the electrocatalytic performance, highlighting the synergy between Fe and Ni in boosting OER activity and stability.
1 achieved the best performance in the high overpotential region (250–400 mV), with the lowest Tafel slope (80 mVdec−1). On the other hand, samples FeNiB 1/1 and 1/0.9 demonstrated better performance in the low overpotential region (150–300 mV). The reaction orders revealed that the catalysts with lower Fe-to-Ni ratios (FeNiB 0.9/1 and 1/1) exhibit a lower OH− coverage and weaker dependence on OH−, whereas FeNiB 1/0.9, with a higher Fe content, shows a greater OH− coverage and stronger dependence on OH−. EIS and XPS data suggested that the structural reorganisation of FeNiB 1/1 and 1/0.9 surfaces, which correlates with increased Ni2+ and Fe3+ formation, respectively, had improved the electrocatalytic activity of the samples in the low overpotential region (150–300 mV). The operando DRIFTS data further revealed that, at higher Fe concentrations, Fe-bound OH− dominates the OER; while Ni-bound OH− is more prevalent at lower Fe concentrations. Overall, these results emphasised the importance of Fe-to-Ni ratio optimisation, revealing that increasing the Ni content could improve the stability of FeNiB. However, modifying the Fe content can enhance the electrocatalytic performance, highlighting the synergy between Fe and Ni in boosting OER activity and stability.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Author contributions
Emilia Kazek: investigation, methodology, conceptualization, data curation, writing – original draft, Rocco Villano: methodology, data curation, writing – review & editing Veronica Sofianos: methodology, data curation, writing – review & editing M., Jeannie Z. Y. Tan: methodology, data curation, writing – review & editing Leila Negahdar: conceptualization, supervision, writing – original draft, funding acquisition, validation.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
LN wishes to thank Science Foundation Ireland for the support (grant number 22/FFP–P/11527). Dr Ahmed Alanazi is acknowledged for his support with data collections. MVS acknowledges the financial support from the UCD Ad Astra fellowship programme, and the Royal Chemical Society for the Research Enablement Grant number 72049. Special thanks to Prof. James Sullivan for providing access to the laboratory facilities.References
- A. Mostafaeipour, A. Bidokhti, M.-B. Fakhrzad, A. Sadegheih and Y. Zare Mehrjerdi, Energy, 2022, 238, 121602 CrossRef CAS.
- K. Zhang and R. Zou, Small, 2021, 17, 2100129 CrossRef CAS PubMed.
- Q. Liang, G. Brocks and A. Bieberle-Hütter, JPhys Energy, 2021, 3, 026001 CrossRef CAS.
- Z. Chen, Q. Fan, J. Zhou, X. Wang, M. Huang, H. Jiang and H. Cölfen, Angew. Chem., Int. Ed., 2023, 62, e202309293 CrossRef CAS PubMed.
- B. Schmitt, E. Murphy, S. J. Trivedi, Q. Zhang, B. J. Rodriguez, A. Rafferty, R. Bekarevich, G. Ersek, G. Portale and M. V. Sofianos, Sustainable Energy Fuels, 2024, 8, 5793–5805 RSC.
- J. Zhao, J. J. Zhang, Z. Y. Li and X. H. Bu, Small, 2020, 16, e2003916 CrossRef PubMed.
- Y. Hong, J. Choi, E. Lee and Y. J. Hwang, Nanoscale, 2024, 16, 11564–11574 RSC.
- H. Shi, Y. Zhu, J. Chen, Z. Wang, J. Zhan, S. Li, P. Han and X. Guo, Int. J. Hydrogen Energy, 2025, 97, 874–881 CrossRef CAS.
- P. Han, T. Tan, F. Wu, P. Cai, G. Cheng and W. Luo, Chin. Chem. Lett., 2020, 31, 2469–2472 CrossRef CAS.
- W. Hong, S. Sun, Y. Kong, Y. Hu and G. Chen, J. Mater. Chem. A, 2020, 8, 7360–7367 RSC.
- M. Berger, I. M. Popa, L. Negahdar, S. Palkovits, B. Kaufmann, M. Pilaski, H. Hoster and R. Palkovits, ChemElectroChem, 2023, 10, e202300235 CrossRef CAS.
- M. Song, X. Yang, J. Ma, X. Deng and H. Gao, Mater. Today Chem., 2024, 36, 101957 CrossRef CAS.
- Y. Bai, Y. Wu, X. Zhou, Y. Ye, K. Nie, J. Wang, M. Xie, Z. Zhang, Z. Liu, T. Cheng and C. Gao, Nat. Commun., 2022, 13, 6094 CrossRef CAS PubMed.
- M. Berger, A. Markus, S. Palkovits and R. Palkovits, ChemElectroChem, 2024, 11, e202400457 CrossRef CAS.
- M. E. G. Lyons and M. P. Brandon, Int. J. Electrochem. Sci., 2008, 3, 1386–1424 CrossRef CAS.
- M. Dupont, A. F. Hollenkamp and S. W. Donne, Electrochim. Acta, 2013, 104, 140–147 CrossRef CAS.
- S. Wang, A. Lu and C.-J. Zhong, Nano Converg., 2021, 8, 4 CrossRef CAS PubMed.
- L. Birry and A. Lasia, J. Appl. Electrochem., 2004, 34, 735–749 CrossRef CAS.
- A. Lasia, J. Electroanal. Chem., 1995, 397, 27–33 CrossRef.
- B. Hirschorn, M. E. Orazem, B. Tribollet, V. Vivier, I. Frateur and M. Musiani, Electrochim. Acta, 2010, 55, 6218–6227 CrossRef CAS.
- W. Peng, Y. Li, B. Yuan, R. Hu, Z. Luo and M. Zhu, Appl. Catal., A, 2023, 323, 122171 CrossRef CAS.
- A. Alobaid, C. Wang and R. Adomaitis, J. Electrochem. Soc., 2018, 165, J3395–J3404 CrossRef CAS.
- G. Niklasson, Z. Qiu, I. Bayrak Pehlivan and T. Edvinsson, IOP Conf. Ser.:Mater. Sci. Eng., 2019, 503, 012005 CAS.
- R. Attias, B. Dlugatch, M. Chae, Y. Goffer and D. Aurbach, Electrochem. Commun., 2021, 124, 106952 CrossRef CAS.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- L. Negahdar, F. Zeng, S. Palkovits, C. Broicher and R. Palkovits, ChemElectroChem, 2019, 6, 5588–5595 CrossRef CAS.
- A. Saraby-Reintjes, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 271–279 RSC.
- B. E. Conway and E. Gileadi, Trans. Faraday Soc., 1962, 58, 2493–2509 RSC.
- M. Králik, Chem. Pap., 2014, 68, 1625–1638 Search PubMed.
- J. O. M. Bockris and T. Otagawa, J. Phys. Chem., 1983, 87, 2960–2971 CrossRef CAS.
- K. S. Exner and H. Over, Acc. Chem. Res., 2017, 50, 1240–1247 CrossRef CAS PubMed.
- M. Ganser, F. E. Hildebrand, M. Klinsmann, M. Hanauer, M. Kamlah and R. M. McMeeking, J. Electrochem. Soc., 2019, 166, H167 CrossRef CAS.
- R. Guidelli, R. G. Compton, J. M. Feliu, E. Gileadi, J. Lipkowski, W. Schmickler and S. Trasatti, Pure Appl. Chem., 2014, 86, 245–258 CrossRef CAS.
- E. Laborda, M. C. Henstridge and R. G. Compton, J. Electroanal. Chem., 2012, 667, 48–53 CrossRef CAS.
- A. M. Román, J. Dudoff, A. Baz and A. Holewinski, ACS Catal., 2017, 7, 8641–8652 CrossRef.
- X. Zhao, B. Wen, Q. Dong, P. Wang and X. Lyu, Int. J. Hydrogen Energy, 2025, 105, 556–564 CrossRef CAS.
- L. Wang, P. Wang, S. Li, H. Shang, D. Wang, Y. Zhao and B. Zhang, Surf. Interfaces, 2024, 47, 104215 CrossRef CAS.
- M. Oliver-Tolentino, R. Cabrera-Sierra, L. Lartundo-Rojas, J. Lucero-Guerrero, R. Sotelo-Boyás and A. Manzo-Robledo, J. New Mater. Electrochem. Syst., 2013, 16, 183–188 CrossRef CAS.
- H. Liao, G. Ni, P. Tan, Y. Liu, K. Chen, G. Wang, M. Liu and J. Pan, Appl. Catal., A, 2022, 317, 121713 CrossRef CAS.
- J. Gallenberger, H. Moreno Fernández, A. Alkemper, M. Li, C. Tian, B. Kaiser and J. P. Hofmann, Catal. Sci. Technol., 2023, 13, 4693–4700 RSC.
- Q. Zhang, W. Xiao, H. C. Fu, X. L. Li, J. L. Lei, H. Q. Luo and N. B. Li, ACS Catal., 2023, 13, 14975–14986 CrossRef CAS.
- J. R. Murdoch, J. Chem. Educ., 1981, 58, 32 CrossRef CAS.
- J. Long, J. Zhang, L. Li, Y. Wen, X. Xu and F. Wang, Int. J. Hydrogen Energy, 2024, 90, 1424–1434 CrossRef CAS.
- K. Hadjiivanov, in Advances in Catalysis, ed. F. C. Jentoft, Academic Press, 2014, vol. 57, pp. 99–318 Search PubMed.
- D. P. Dubal, V. J. Fulari and C. D. Lokhande, Microporous Mesoporous Mater., 2012, 151, 511–516 CrossRef CAS.
- H. Du, L. Jiao, K. Cao, Y. Wang and H. Yuan, ACS Appl. Mater. Interfaces, 2013, 5, 6643–6648 CrossRef CAS PubMed.
- O. Diaz-Morales, D. Ferrus-Suspedra and M. T. M. Koper, Chem. Sci., 2016, 7, 2639–2645 RSC.
- D. Rathore, M. D. Sharma, A. Sharma, M. Basu and S. Pande, Langmuir, 2020, 36, 14019–14030 CrossRef CAS PubMed.
- C. Rémazeilles and P. Refait, Polyhedron, 2009, 28, 749–756 CrossRef.
- X. Song and J.-F. Boily, J. Phys. Chem. A, 2016, 120, 6249–6257 CrossRef CAS PubMed.
- J. Żeglin'ski, G. P. Piotrowski and R. Piękoś, J. Mol. Struct., 2006, 794, 83–91 CrossRef.
- Y. Zhao, Z. Chen, X. Shen and X. Zhang, Environ. Sci. Technol., 2011, 45, 3317–3324 CrossRef CAS PubMed.
- T. Seki, K.-Y. Chiang, C.-C. Yu, X. Yu, M. Okuno, J. Hunger, Y. Nagata and M. Bonn, J. Phys. Chem. Lett., 2020, 11, 8459–8469 CrossRef CAS PubMed.
- X. Zhang, H. Yao, X. Lei, Q. Lian, A. Roy, D. Doucet, H. Yan, M. E. Zappi and D. D. Gang, Environ. Res., 2021, 199, 111223 CrossRef CAS PubMed.
- J. B. Peri, Discuss. Faraday Soc., 1966, 41, 121–134 RSC.
- J. Ashok, M. L. Ang, P. Z. L. Terence and S. Kawi, ChemCatChem, 2016, 8, 1308–1318 CrossRef CAS.
- S. Jahangiri and N. J. Mosey, Phys. Chem. Chem. Phys., 2018, 20, 11444–11453 RSC.
- H. S. Ahn and A. J. Bard, J. Am. Chem. Soc., 2016, 138, 313–318 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cy00392j |
| This journal is © The Royal Society of Chemistry 2025 |