Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Balancing molecular information and empirical data in the prediction of physico-chemical properties†
Johannes
Zenn
 *a,
Dominik
Gond
b,
Fabian
Jirasek
*a,
Dominik
Gond
b,
Fabian
Jirasek
 b and
Robert
Bamler
b and
Robert
Bamler
 c
c
aTübingen AI Center, University of Tübingen, IMPRS, 72076 Tübingen, Germany. E-mail: johannes.zenn@uni-tuebingen.de
bLaboratory of Engineering Thermodynamics (LTD), RPTU Kaiserslautern, 67663 Kaiserslautern, Germany
cTübingen AI Center, University of Tübingen, 72076 Tübingen, Germany
First published on 15th January 2025
Abstract
Predicting the physico-chemical properties of pure substances and mixtures is a central task in thermodynamics. Established prediction methods range from fully physics-based ab initio calculations, which are only feasible for very simple systems, over descriptor-based methods that use some information on the molecules to be modeled together with fitted model parameters (e.g., quantitative-structure–property relationship methods or classical group contribution methods), to representation-learning methods, which may, in extreme cases, completely ignore molecular descriptors and extrapolate only from existing data on the property to be modeled (e.g., matrix completion methods). In this work, we propose a general method for combining molecular descriptors with representation learning using the so-called expectation maximization algorithm from the probabilistic machine-learning literature, which uses uncertainty estimates to trade off between the two approaches. The proposed hybrid model exploits chemical structure information using graph neural networks, but it automatically detects cases where structure-based predictions are unreliable, in which case it corrects them by representation-learning based predictions that can better specialize to unusual cases. The effectiveness of the proposed method is demonstrated using the prediction of activity coefficients in binary mixtures as an example. The results are compelling, as the method significantly improves predictive accuracy over the current state of the art, showcasing its potential to advance the prediction of physico-chemical properties in general.
1 Introduction
Information on physico-chemical properties is crucial for the conceptual design and optimization of processes in many industries, including chemistry, pharmacy, and biotechnology. Among the most important thermodynamic properties are the activity coefficients of the components in a mixture, which describe the deviation of a mixture from the ideal mixture and enable the accurate prediction of reaction and phase equilibria of mixtures. Activity coefficients at infinite dilution are more sensitive thermodynamic properties than activity coefficients at finite concentration (and the subsequently calculated reaction and phase equilibria) and knowing the activity coefficients at infinite dilution allows to predict the activity coefficients in binary mixtures of any finite concentration as well as the activity coefficients in multi-component mixtures. Unfortunately, measuring activity coefficients, as measuring thermodynamic properties of mixtures in general, is costly and time-consuming, and the number of relevant mixtures exceeds the ones that can be studied experimentally by orders of magnitude.1 Consequently, prediction methods for thermodynamic properties of mixtures are paramount. Recently, research on such prediction methods has split into two branches.On the one hand, descriptor-based methods correlate information on the molecules to be modeled with properties of interest. Among these, group-contribution methods, which use the composition of the components in terms of structural groups as molecular descriptors and whose underlying equations are usually derived from physical theories, have succeeded and are still the gold standard for property prediction in many (industrial) fields.2,3 The most successful group-contribution method for predicting activity coefficients is UNIFAC,4–6 which is available in different versions and established in most process simulation software. Besides the physics-based group-contribution methods, also other descriptor-based methods that rely on various descriptors, such as molecular weight, surface area, or boiling point, have been proposed for predicting activity coefficients.7–14
In statistics parlance, such descriptor-based models are called parametric models as they fit model parameters that affect several related components (e.g., those containing a given structural group). Thus, parametric models can leverage statistical strength across chemically similar components.
On the other hand, recent idea transfer from the machine-learning community has led to an alternative approach to predicting activity coefficients and other mixture properties, which is based solely on learned representations without relying on descriptors. So-called matrix completion methods (MCMs)15–19 ignore the chemical structure of components and fit individual representation vectors for each mixture component that appears in a set of available experimental data. While this approach makes MCMs more flexible than descriptor-based methods, it prevents them from exploiting structural similarities across components, and from extrapolating to new components. In statistics parlance, one says that MCMs are “nonparametric in the components” (note that nonparametric models tend to have many parameters, similar to how a “stepless” controller has infinitely many steps).
It was shown empirically15,16,20 that purely nonparametric MCMs make more accurate predictions for activity coefficients compared to the descriptor-based (parametric) state-of-the-art UNIFAC. However, since each fitted parameter (i.e., each representation vector) in an MCM only describes a single component, MCMs can only make predictions for mixtures where each component appears in some (other) mixtures in the available experimental data (“in-domain predictions”). By contrast, descriptor-based methods can exploit the structural similarity of components to extrapolate to components that appear in no mixture in the available experimental data (“out-of-domain predictions”).
In this work, we propose a new method for predicting activity coefficients in binary mixtures that combines the strengths of both the parametric (descriptor-based) and the nonparametric (representation-based) approach while avoiding their respective weaknesses. To do this, we phrase both a parametric and a nonparametric model in a probabilistic framework, and we fit them jointly using the so-called variational expectation maximization (variational EM) algorithm. This algorithm finds an optimal compromise between the parametric and the nonparametric part of a model, taking into account how confident each part is in its fitted or predicted parameters, as discussed in the next section. Our evaluation shows that weighing off the respective confidences of the parametric and nonparametric models indeed improves the accuracy of both in-domain and out-of-domain predictions.
While this paper focuses on the concrete task of predicting activity coefficients of pure solutes at infinite dilution in pure solvents at room temperature, the proposed method can, e.g., be generalized to arbitrary temperatures and concentrations following the procedure described in Jirasek et al.,20 and to other thermodynamic properties of binary mixtures by fitting it to a corresponding dataset. More generally, we argue that the variational EM algorithm is a valuable tool in thermodynamic modeling since it allows for combining the strengths of descriptor-based (parametric) and representation-based (nonparametric) models, which is a powerful approach beyond the modeling single thermodynamic properties of binary mixtures.
In the remaining sections of this paper, we first formalize the problem setup, present the proposed method, and discuss several variants of its concrete execution. We then empirically evaluate the accuracy of predicted activity coefficients and compare them to existing methods and simplified variants of our proposed method (ablation studies).
2 Method
2.1 Problem setting
As in Jirasek et al.,15 we start from a data set of 4094 measured activity coefficients γ∞i,j of solutes i at infinite dilution in solvents j at 298.15 (±1) K. We use the same data set as in previous work,15 which was taken from the Dortmund Data Bank (DDB),21 the largest database for physico-chemical properties covering the most relevant molecular components for technical processes. We refrain from using synthetic datasets because this only demonstrates how well a method can reproduce an available model and does not results in a practically useful new model. The DDB dataset is illustrated in the yellow/black matrix on the right of Fig. 1 (which is discussed in more detail in Section 2.2 below). The matrix has M = 240 rows and N = 250 columns corresponding to the M distinct solutes and N distinct solvents that appear in the data set, and each black pixel indicates an available experimental data point γ∞i,j. Our goal is to predict activity coefficients for the yellow parts of the matrix (“in-domain predictions”), and to also extend the rows and columns of the matrix, i.e., predict activity coefficients that involve yet unstudied solutes or solvents (“out-of-domain predictions”).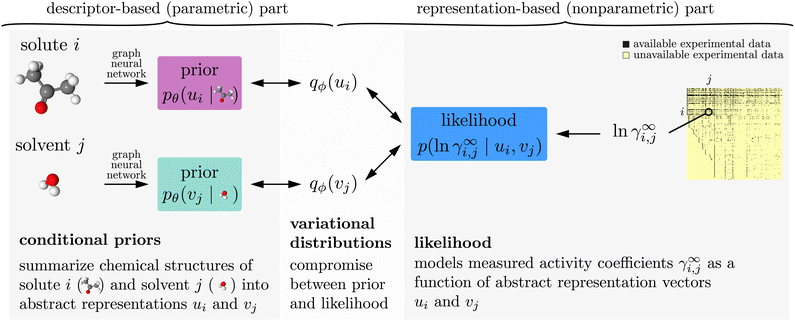 | ||
| Fig. 1 Model and data flow for training the proposed model. (Left) graph neural networks take chemical structure information and output the parameters of conditional prior probability distributions (eqn (1)) over abstract representation vectors. (Right) the likelihood (eqn (2)) models how well given representation vectors explain experimentally measured activity coefficients γ∞i,j. We use variational EM (Sections 2.3 and 2.4) to fit the neural network weights θ (parametric, descriptor-based part), and to find variational distributions for each solute and solvent (nonparametric, representation-based part). | ||
A previous deep-learning-based approach14 addressed this prediction problem with a combination of three neural networks. The first two networks are so-called graph neural networks (GNNs) that take as input the molecular graph structures of the solute and solvent, respectively, i.e., each atom kind, their hybridizations and formal charges, and the type of bond between each pair of atoms. The GNNs map the molecular graphs to so-called abstract representation vectors u ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K and v ∈
K and v ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K, respectively, where the dimension K is a modeling choice. The third neural network combines u and v and outputs a prediction for the activity coefficient for the respective solute at infinite dilution in the respective solvent. This existing approach can perform out-of-domain predictions because the neural networks can extrapolate to new molecular structures as long as they share some common substructures with the ones in the training data. But this approach has the downside that it uses an entirely parametric model, i.e., it is limited by the expressiveness of the neural networks and cannot make any exceptions in case some anomalous components behave very differently than structurally similar components. Our proposed method, described below, accounts for exceptions with anomalous behavior in a nonparametric way.
K, respectively, where the dimension K is a modeling choice. The third neural network combines u and v and outputs a prediction for the activity coefficient for the respective solute at infinite dilution in the respective solvent. This existing approach can perform out-of-domain predictions because the neural networks can extrapolate to new molecular structures as long as they share some common substructures with the ones in the training data. But this approach has the downside that it uses an entirely parametric model, i.e., it is limited by the expressiveness of the neural networks and cannot make any exceptions in case some anomalous components behave very differently than structurally similar components. Our proposed method, described below, accounts for exceptions with anomalous behavior in a nonparametric way.
2.2 Probabilistic model
Like in Medina et al.14 discussed in Section 2.1 above, our proposed model has a descriptor-based part (left half of Fig. 1) that processes the chemical structures of the solute and solvent independently using two neural networks (one for solutes and one for solvents), and our main results were also obtained by using GNNs here. Unlike in the previous work, these neural networks parameterize probabilistic models, i.e., their outputs are not representation vectors u and v but instead parameters that define so-called conditional prior probability distributions pθ(u | r) and pθ(v | s), respectively. Here, θ are the neural network weights, and the bar “|” denotes conditioning on the chemical structure r and s of the solute and solvent, respectively. Specifically, the conditional priors in our empirical analysis are normal distributions, | (1) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K and variances uσθ2(r), vσθ2(s) ∈
K and variances uσθ2(r), vσθ2(s) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K>0 are extracted from the outputs of the two neural networks. Here, diag(u/vσθ2(·)) is a covariance matrix with the components of u/vσθ2(·) on its diagonal, and zeros on all off-diagonal entries. The inference algorithm, described in and Section 2.4 below, ensures that u/vσθ2(·) estimates an uncertainty region around the corresponding mean prediction u/vμθ(·) of the parametric part of the model. These uncertainty estimates affect how strongly the parametric part of the model constrains (“regularizes”) the nonparametric part of the model (described next) during training.
K>0 are extracted from the outputs of the two neural networks. Here, diag(u/vσθ2(·)) is a covariance matrix with the components of u/vσθ2(·) on its diagonal, and zeros on all off-diagonal entries. The inference algorithm, described in and Section 2.4 below, ensures that u/vσθ2(·) estimates an uncertainty region around the corresponding mean prediction u/vμθ(·) of the parametric part of the model. These uncertainty estimates affect how strongly the parametric part of the model constrains (“regularizes”) the nonparametric part of the model (described next) during training.
The representation-based (nonparametric) part of our model is a probabilistic MCM.15 It represents each solute i and each solvent j that appears in the experimental data with an individual representation vector ui, vj ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K, respectively, which it uses to predict the activity coefficients γ∞i,j. Since activity coefficients range over several orders of magnitude, we model their logarithm, ln
K, respectively, which it uses to predict the activity coefficients γ∞i,j. Since activity coefficients range over several orders of magnitude, we model their logarithm, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞i,j. We use a simple Gaussian likelihood,
γ∞i,j. We use a simple Gaussian likelihood,
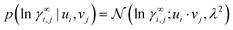 | (2) |
2.3 Fitting the model: intuition
While the inference algorithm that we use is easy to implement (see Algorithm 1 discussed in Section 2.4 below), understanding why it works requires more explanation. We therefore first motivate the algorithm in this section before formalizing it mathematically in Section 2.4.We propose to train the nonparametric and parametric parts of the model jointly using the so-called variational expectation maximization (variational EM)22,23 algorithm. Variational EM allows us to fit a model that can generalize across components with similar chemical structures while still being able to learn exceptions for individual components where the experimental data shows evidence for anomalous behavior.
The arrows in Fig. 1 show the direction of data flow in variational EM. The algorithm concurrently fits both the neural network weights θ of the conditional priors and a so-called variational distribution qϕ(ui) and qϕ(vj) for each solute i and each solvent j that appears in the experimental data. The weights θ of the conditional priors are fitted to model the data as well as one can with a parametric model. By contrast, the variational distributions are fitted in a nonparametric way. They are fitted to find a compromise between the conditional priors (which can share statistical strength across chemically similar components but cannot make exceptions for anomalous cases) and the experimental data (which may contain evidence for anomalous behaviors, but which is often scarce and generally affected by measurement errors).
In our setup, the necessary constraint on the prior comes from the finite expressiveness of the neural networks: unless the neural network for, e.g., solute representation vectors ui is exorbitantly large, it cannot output completely independent prior parameters (uμθ(ri), uσθ2(ri)) for all solutes i in the dataset. Thus, fitting the neural network weights θ cannot perfectly overfit the prior to the data. By contrast, the variational distributions qϕ(ui) and qϕ(vj) are fitted nonparametrically, i.e., with individual parameters for each solute and solvent. The reason why these do not perfectly overfit the data is because they are not fitted solely to the data but instead obtained by (approximate) Bayesian inference with the (non-overfitting) prior, as explained in Section 2.4 below.
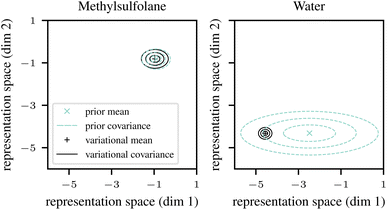
The positions of the ellipses in representation space are not directly interpretable, but their sizes indicate uncertainty estimates. For example, the prior predictions for methylsulfolane (left panel in Fig. 2) have low uncertainty (the turquoise ellipses are small). This is expected to happen for solvents (and equally for solutes) where the dataset contains structurally similar solvents that empirically behave similarly in mixtures, thus allowing the neural network to effectively and confidently interpolate between them. The low prior uncertainty causes variational EM to trust the prior predictions, and to fit a variational distribution qϕ(vj) (solid black ellipses) that closely follows the prior.
By contrast, the prior predictions for water (right panel in Fig. 2) have high uncertainty (the turquoise ellipses are large). This is expected to happen if the dataset contains solvents that are structurally similar to water but behave very differently in mixtures. Such anomalous cases prevent the neural network from interpolating effectively. However, as we discuss in Section 2.4 below, the neural network is at least fitted to detect such cases, and to reflect them by outputting a large uncertainty estimate vσθ2(s). As can be seen in the right panel of Fig. 2, the high prior uncertainty allows variational EM to fit the variational distribution (black ellipses) more freely, thus, in a sense, overriding the descriptor-based prior (mean) prediction vμθ(s) (turquoise cross) in this case. Note that the uncertainty of the (approximate) posterior (size of the black ellipses) for water is small despite the large prior uncertainty. This is expected since the data set contains a lot of experimental data where the solvent is water.
2.4 Inference algorithm
We now formally discuss the variational EM algorithm22,23 in the concrete context of the model for activity coefficients in binary mixtures introduced in Section 2.2. Combining the conditional priors (eqn (1)) and the likelihood (eqn (2)), our probabilistic model defines a joint probability density over all representation vectors ui and vj, and all logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞i,j in all binary mixtures i–j in the data set,
γ∞i,j in all binary mixtures i–j in the data set,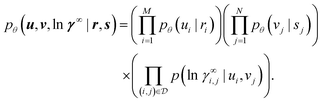 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞ on the left-hand side denotes the collection of all representation vectors ui and vj and all chemical structures ri and sj for all solutes i and all solvents j, respectively, that appear at least once in the experimental data
γ∞ on the left-hand side denotes the collection of all representation vectors ui and vj and all chemical structures ri and sj for all solutes i and all solvents j, respectively, that appear at least once in the experimental data  , and all logarithmic activity coefficients ln
, and all logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞i,j of all binary mixtures i–j for which experimental data is available. Similarly, the first two products on the right-hand side of eqn (3) run over all M solutes i and all N solvents j, respectively, and the third product runs over all pairs (i, j) where we have experimental data for the binary mixture i–j (i.e., the black pixels in the yellow/black matrix on the right of Fig. 1).
γ∞i,j of all binary mixtures i–j for which experimental data is available. Similarly, the first two products on the right-hand side of eqn (3) run over all M solutes i and all N solvents j, respectively, and the third product runs over all pairs (i, j) where we have experimental data for the binary mixture i–j (i.e., the black pixels in the yellow/black matrix on the right of Fig. 1).
A naive approach to training the neural networks would attempt to find the network weights θ that maximize the so-called marginal likelihood pθ(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞ | r, s), i.e., the probability density of predicting the experimentally measured logarithmic activity coefficients ln
γ∞ | r, s), i.e., the probability density of predicting the experimentally measured logarithmic activity coefficients ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞ for all binary systems where experimental data is available. Unfortunately, the marginal likelihood is not accessible in our model because obtaining it would require marginalizing eqn (3) over u and v,
γ∞ for all binary systems where experimental data is available. Unfortunately, the marginal likelihood is not accessible in our model because obtaining it would require marginalizing eqn (3) over u and v,
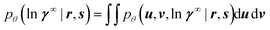 | (4) |
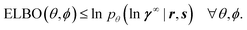 | (5) |
To derive a valid expression for the ELBO, variational inference replaces the integral on the right-hand side of eqn (4) with a form of biased importance sampling.28 One first chooses a family of typically simple probability distributions qϕ(u, v) that are parameterized by ϕ and called variational distributions. For simplicity, we use the so-called Gaussian mean-field approximation, i.e., we choose a family of fully factorized normal distributions  with
with
 | (6) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e0.gif) i, v
i, v![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e0.gif) j ∈
j ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K and variances u
K and variances u![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/char_e10d.gif) i2, v
i2, v![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/char_e10d.gif) j2 ∈
j2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) K>0 together make up the variational parameters ϕ. The ELBO is then26
K>0 together make up the variational parameters ϕ. The ELBO is then26 | (7) |
 of the log likelihood under the variational distribution, which can be estimated by averaging the logarithm of eqn (2) over samples ui ∼ qϕ(ui), vj ∼ qϕ(vj). The last two terms on the right-hand side of eqn (7) are Kullback–Leibler (KL) divergences,24,25 which quantify how much the variational distributions differ from the conditional priors. For normal distributions, the KL divergence can be calculated analytically,25
of the log likelihood under the variational distribution, which can be estimated by averaging the logarithm of eqn (2) over samples ui ∼ qϕ(ui), vj ∼ qϕ(vj). The last two terms on the right-hand side of eqn (7) are Kullback–Leibler (KL) divergences,24,25 which quantify how much the variational distributions differ from the conditional priors. For normal distributions, the KL divergence can be calculated analytically,25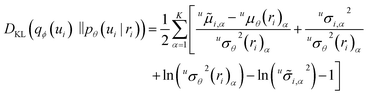 | (8) |
Maximizing the ELBO in eqn (7) over both θ and ϕ trades off between three objectives:
(i) maximizing the first term on the r.h.s. of eqn (7) over ϕ tries to fit variational distributions qϕ(ui) and qϕ(vj) such that samples from them explain the experimental data in  ;
;
(ii) maximizing the last two terms in eqn (7) over ϕ (i.e., minimizing the KL-divergences over ϕ) regularizes the fits, i.e., it keeps the variational distributions qϕ(ui) and qϕ(vj) close to the conditional priors. Here, the first term on the r.h.s. of eqn (8) penalizes deviations between prior mean and variational mean stronger for smaller prior variance uσθ2(ri)α. Thus, the (parametric) prior model has a stronger effect on the (nonparametrically fitted) variational distributions when it is confident in its prediction, as claimed in the discussion of Fig. 2;
(iii) minimizing the KL-divergences in eqn (7) also over θ fits the neural networks that define the conditional priors to the variational distributions, and thus indirectly to the data. This includes fitting the prior variances u/vσθ2(·) to model the aleatoric uncertainty observed in the data plus any changes between the variational distributions of structurally similar components that cannot be resolved by the prior due to the finite expressiveness of the neural networks.
We maximize the ELBO over θ and ϕ with stochastic gradient descent, using reparameterization gradients29 for the first term on the right-hand side of eqn (7), and automatic differentiation provided by common software frameworks for machine-learning.30 Algorithm 1 summarizes the algorithm. Our implementation is available online (see section “Data and software availability”). Training our largest model variant (GNN MCM, see below) took about four hours on a single GPU (Nvidia GeForce RTX 2080 Ti).
2.5 Predictions
Once our model is trained with variational EM, we use it for predicting activity coefficients for binary mixtures whose components can each be either in-domain (i.e., appearing in other mixtures in the available experimental data) or out-of-domain (i.e., previously unstudied components). Fig. 3 shows an example where the solute i is out-of-domain whereas the solvent j is in-domain. For the out-of-domain solute i, we apply the trained neural network to its chemical structure ri, which outputs the means and variances of the conditional prior pθ(ui|ri) (eqn (1)). For the in-domain solvent j, we directly use the variational distribution qϕ(vj) (eqn (6)), which was fitted to the data under consideration of its conditional prior. We then obtain a prediction![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) ∞i,j = exp(ln
∞i,j = exp(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) ∞i,j) by calculating the modes,
∞i,j) by calculating the modes, | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞i,j | ûi,
γ∞i,j | ûi,![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) j) is the likelihood (eqn (2)). For different combinations of in-domain and out-of-domain mixture components, we adapt the first two lines of eqn (9) accordingly.
j) is the likelihood (eqn (2)). For different combinations of in-domain and out-of-domain mixture components, we adapt the first two lines of eqn (9) accordingly.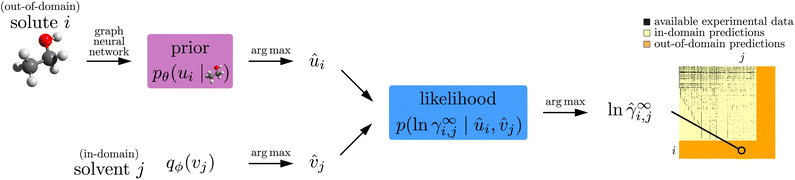 | ||
Fig. 3 Data flow for a prediction where the solvent appears in the training set (in-domain) but the solute does not (out-of-domain). We thus predict the solute representation vector ûi from the prior, and the solvent representation vector ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) j from the variational distribution qϕ, see eqn (9). j from the variational distribution qϕ, see eqn (9). | ||
2.6 Model details and variants
In our experiments, we investigate two model variants that differ in how they represent chemical structures of solutes and solvents, and how they parameterize the means and variances of the conditional prior distributions (eqn (1)) as functions of these chemical structures. A simple model variant, which we call “MoFo MCM”, represents chemical structures by the molecular formula (MoFo) (e.g., water is represented as H2O). A more expressive model variant, which we call “GNN MCM”, represents chemical structures by their topological molecular graphs (e.g., water is represented as the graph H–O–H), and it employs graph neural networks (GNNs).31–33In detail, the MoFo MCM uses two neural networks (one for solutes and one for solvents) that receive a fixed-size integer-valued vector as input. Each entry of the input vector corresponds to a given atom or bond type, and the values at these entries count the number of occurrences of the given atom or bond type in the molecule. Specifically, we use 16-dimensional input vectors for the 12 atoms O, Si, I, F, Br, P, H, S, Sn, N, C, and Cl present in the data set and the 4 bond types single, double, triple, and aromatic. The network outputs a 2K-dimensional vector that is the concatenation of the prior means u/vμθ(·) and variances u/vσθ2(·).
The GNN MCM uses two graph neural networks, whose inputs are the molecular graphs of the solute and solvent, respectively. More specifically, we encode atoms and bonds from the same vocabulary as in the MoFo MCM with learnable real-valued vectors, which we use as initial node and edge features for the GNN. In general, message-passing GNNs operate on such graph-structured inputs by performing transformations of the node and edge features over multiple layers via a message-passing scheme.34 The output of a GNN is computed from all node features (and possibly edge features) at the last layer with a readout function. Generally, the message-passing scheme consists of a message step, an aggregation step, and an update step. In each layer, a message is computed for each directed edge utilizing a message function whose parameters are part of the learnable neural network parameters θ. Incoming messages are aggregated by a sum for each node. The update function produces new node features depending on the previous node features and the aggregated message, and its parameters are also part of θ.
Message, aggregation, and update steps are specific to the architecture of the GNN. In this work, we utilize the Feature-wise Linear Modulation (FiLM) GNN.35 The FiLM model uses the target features of a directed edge as input to a hyper-network that determines element-wise affine transformation parameters. Messages are computed by scaling and shifting the input features with the element-wise affine transformation parameters, where the input features result from multiplying a learnable matrix with previous features. The update function of a node sums over the aggregated messages for each edge type, where also transformation parameters are computed for each edge type.
3 Evaluation setup
In Section 4 below, we compare the two variants of our proposed method to existing prediction methods in the literature (“baselines”) and to simplified variants of our models (“ablations”).3.1 Models and baselines
We evaluate the two variants “MoFo MCM” and “GNN MCM” of our proposed method. As baselines, we compare to the group-contribution method modified UNIFAC (Dortmund)5,6 (referred to simply as “UNIFAC” in the following) and to two machine-learning based methods: the fully nonparametric MCM method by Jirasek et al.15 and the fully parametric neural-network-based method by Medina et al.14 The latter uses a different GNN architecture34 than our conditional priors, and it assumes knowledge of more chemical information (such as orbital hybridizations and formal atom charges).3.2 Ablation studies
We perform two ablation studies where we remove parts of our method to investigate their contribution to the method's performance. For the first ablation study, we use the same trained MoFo MCM and GNN MCM models as for our main results, but we perform predictions for in-domain components as if they were out of domain, i.e., using the mode of the conditional prior as representation vector (see first line of eqn (9)), thus ignoring the variational distributions at prediction time.For the second ablation study, we simplify the model by removing its nonparametric part, and we train it by simple maximum likelihood estimation (MLE) rather than variational EM. Thus, in this ablation, the neural networks only output means uμθ(ri) and vμθ(sj) and no variances, and we use these means directly as representation vectors ui and vj, respectively, in the likelihood (eqn (2)), which our training objective maximizes over the neural network parameters θ (similar to Medina et al.14). Since this simplified model has no variational distributions, predictions are again done as if all mixture components were out of domain.
3.3 Training
We train our models with 10-fold cross validation.36 For each split, we use 80% of the dataset for training, 10% for testing, and 10% for a validation set. The 10 resulting test set splits are pairwise disjoint, and their union equals the full dataset. We use the test set splits to evaluate the accuracy of model predictions, where we consider a mixture “i–j” in the test set to be out-of-domain if at least one of solute i or solvent j does not appear in the corresponding training split. Note that our 10-fold cross validation is different from the work of Jirasek et al.,15 which uses more computationally expensive leave-one-out cross validation.We implement our models in PyTorch30 and use PyTorch Geometric37 for the GNN. All models are trained for 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 epochs using the Adam38 optimizer. In the MoFo (MLE) ablation study, we use early stopping,39,40i.e., we compute validation errors every 10 epochs and use the model with the lowest validation mean squared error (MSE) to evaluate on the test set. This is done to be as lenient as possible to the ablation study, and because MLE training is more prone to overfitting than variational EM. When training with variational EM, we do not use the validation set.
000 epochs using the Adam38 optimizer. In the MoFo (MLE) ablation study, we use early stopping,39,40i.e., we compute validation errors every 10 epochs and use the model with the lowest validation mean squared error (MSE) to evaluate on the test set. This is done to be as lenient as possible to the ablation study, and because MLE training is more prone to overfitting than variational EM. When training with variational EM, we do not use the validation set.
To find well-performing hyperparameters (e.g., the learning rate schedule and the dimension K of the abstract representation space), we utilize a sparse random grid search. See ESI† for more information on this process and the hyperparameters that we search over. We choose the best model of the grid search according to its MSE on a predefined dataset split that is the same for all models and different from any other split. In order to fairly compare all models, we exclude the test data of the predefined dataset (that is used to determine the hyperparameters) from the evaluation.
Medina et al.14 use a different dataset and train an ensemble of 30 models for prediction where each model has been trained on randomized train/validation splits. For a fair comparison against this baseline, we train a separate GNN MCM for each of these train/validation splits, using again a sparse random grid search for hyperparameter tuning.
4 Results and discussion
Fig. 4 and Table 1 summarize our results by showing the mean absolute error (MAE) and mean squared error (MSE) of the predicted logarithmic activity coefficients of all evaluated models. Solid bars in Fig. 4 show evaluations based on our full dataset. As the UNIFAC baseline cannot be applied to all mixtures in our dataset, we also trained and evaluated all models on a reduced dataset, which contains only those data points that can be modeled by UNIFAC (light hatched bars). The neural-network baseline method by Medina et al.14 uses yet a different dataset. Therefore, we trained and evaluated an additional instance of our proposed GNN MCM method on their dataset, and we compare its predictive accuracy to results reported by the authors of Medina et al.14 in Table 1. In the following, we discuss all results in detail.| Model | MAE | MSE |
|---|---|---|
| GNN MCM | 0.1542 ± 0.0046 | 0.0905 ± 0.0071 |
| Medina et al.14 | 0.1973 ± 0.0067 | 0.1196 ± 0.0074 |
4.1 Comparison to baselines
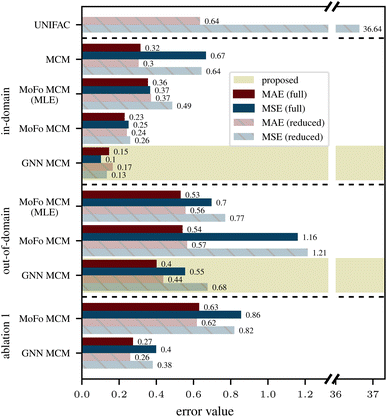
The proposed GNN MCM (highlighted in gold in Fig. 4) provides more accurate predictions than all considered baselines, both in terms of MAE and MSE, and for both in-domain and out-of-domain predictions. Compared to UNIFAC5,6 (first row in Fig. 4), the GNN MCM makes significantly more accurate predictions even if we restrict the test set for GNN MCM to the more difficult out-of-domain predictions (eighth row in Fig. 4). Predictive accuracy is further improved significantly for in-domain predictions (fifth row in Fig. 4). Recall that, even for an in-domain prediction, the training data never contains the precise mixture i–j for which we predict the activity coefficient; it only contains other mixtures that may involve either solute i or solvent j or neither, but never both. This is in sharp contrast to UNIFAC, whose training set has not been disclosed. However, one must assume that a significant share of the dataset considered in this work was used to fit UNIFAC, so the UNIFAC results should rather be seen as correlations than predictions, making the performance of the proposed GNN MCM even more impressive.The comparison to the fully nonparametric MCM15 (second row in Fig. 4) is only possible for in-domain predictions as this baseline cannot perform out-of-domain predictions. Here, the GNN MCM (fifth row) approximately halves MAE, and it reduces MSE (which is more sensitive to outliers) even more significantly.
The published evaluation results in Medina et al.14 do not distinguish between in-domain and out-of-domain predictions, effectively averaging over both. Using the same training data and evaluation setup, our proposed GNN MCM significantly reduces both MAE and MSE (Table 1).
The fourth and seventh rows in Fig. 4 show prediction errors of the MoFo MCM variant of our model, whose conditional priors condition only on the molecular formula of mixture components but not on their chemical structures. We find that this model variant performs worse than the GNN MCM model on both in-domain and out-of-domain prediction tasks. For in-domain predictions, we can compare again to the fully nonparametric MCM (second row in Fig. 4), which does not exploit any chemical information about the mixture components. We find, as expected, that performance improves with increasing granularity of exploited chemical information: MoFo MCM performs better than the fully nonparametric MCM but worse than GNN MCM.
4.2 Ablation 1: predicting without the nonparametric model part
As discussed under “Ablation Studies” above, our first ablation discards the nonparametric part of the model after training and performs predictions for in-domain mixtures as if they were out-of-domain (i.e., using the conditional priors). The last two rows in Fig. 4 show prediction errors of our MoFo MCM and GNN MCM models for this ablation. Here, we evaluate on the same dataset splits as in the in-domain predictions since the splits for out-of-domain predictions contain tasks where this ablation study would not change anything. Comparing the last two rows of Fig. 4 to rows four and five, we observe that discarding the nonparametric part of the model at prediction time hurts predictive accuracy significantly, thus confirming that the nonparametric fits of our method are useful where they are available.4.3 Ablation 2: relevance of variational EM
Our second ablation study goes one step further and removes the nonparametric part of the model already at training time, so that the model can no longer be trained with variational EM and has to be trained with standard maximum likelihood estimation (MLE) instead (see “Ablation Studies” above). We performed this ablation study only on the MoFo MCM model as performing the same ablation for the GNN MCM model would result in a simplified variant of the method by Medina et al.,14 which is already part of our baselines (see Table 1).The results for in-domain and out-of-domain predictions are labeled “MoFo MCM (MLE)” in Fig. 4. For in-domain predictions, we observe that models trained with MLE perform significantly worse than models trained with variational EM, but better than if we train with variational EM and then discard the nonparametric part (see Ablation 1 above). For out-of-domain predictions, the picture is less clear. Here, models trained with MLE perform slightly better than their variational EM counterparts, in particular in terms of MSE, which penalizes outliers more strongly. A possible explanation is that variational EM allows the parametric prior models to effectively ignore any mixture components that can be better modeled in a nonparametric way. This makes the priors in variational EM less regularized, so they are more susceptible to overfitting to the training data, which can result in worse generalization to unseen mixture components in out-of-domain predictions. However, this slight improvement of MoFo MCM (MLE) over MoFo MCM on out-of-domain predictions comes at the cost of significantly reduced performance on in-domain predictions, where the lack of a nonparametric model part prevents MoFo MCM (MLE) from specializing to anomalous components. Further, the proposed GNN MCM model improves performance over both MoFo MCM and MoFo MCM (MLE) significantly on both in-domain and out-of-domain predictions.
4.4 Comparison by chemical structure
We analyze whether the improved predictive accuracy of our proposed GNN MCM method is systematic across all mixture types or limited to specific types of mixtures. For this purpose, we manually assign each solute and solvent to a category based on its chemical structure, e.g., category “XALK” for substituted alkanes and alkenes, or category “HET_ARO” for heteroaromatic compounds. Fig. 5 and 6 show the improvement of our proposed GNN MCM over both UNIFAC (olive) and MCM (terracotta), grouped by the category of the solute and solvent, respectively. We show in-domain predictions here so that we can compare to MCM. Positive values in the figures indicate that GNN MCM has a lower mean average error (MAE) within the corresponding category than the baseline, whereas negative values indicate that the baseline performs better within a given category.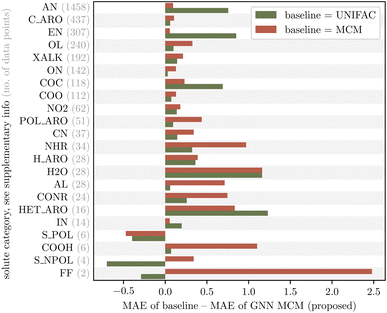 | ||
| Fig. 5 Improvement (in terms of mean average error, MAE) of the proposed GNN MCM method over UNIFAC and MCM, grouped by chemical category of the solute (see Table 6 in the ESI† for a definition of the categories). Our method consistently improves over both UNIFAC and MCM across almost all solute categories; we see regressions (negative improvements) only on three categories with poor statistics in this evaluation due to small sample sizes (see gray numbers). | ||
 | ||
| Fig. 6 Improvement of the proposed GNN MCM over UNIFAC and MCM, by chemical category of the solvent (see Table 6 in the ESI† for a definition of the categories). Our method consistently improves over both UNIFAC and MCM across all solvent categories. | ||
We observe that the improvements of our proposed GNN MCM are systematic across almost all categories of solutes and solvents. The only regressions occur within the solute categories “S_POL” (strongly polar sulfurous compounds), “S_NPOL” (weakly polar sulfurous compounds), and “FF” (perfluorinated compounds). The results in these three categories should be taken with a grain of salt as the dataset contains only very few mixtures that involve a solute from one of these categories (gray numbers in Fig. 5). Thus, within these categories, the MAE averages only over 6, 4, or 2 values, respectively, making it highly susceptible to outliers.
4.5 Comparison by data availability
We finally analyze if the improvement in predictive accuracy for a given mixture depends on the amount of training data that is available for the two mixture components. This analysis is motivated as our proposed GNN MCM trades off between a parametric and a nonparametric part, where parametric models tend to perform better in the low-data regime (because they can share statistical strength across structurally similar components) while nonparametric models tend to perform better in the high-data regime (because they can fit the data better due to fewer constrains). We therefore investigate whether our method manages to use the best of both approaches in both regimes.For each solute i, we set n(i) to the number of times that i appears as a solute in the data set  . The inverse of this function,
. The inverse of this function, 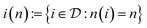 maps each possible solute count
maps each possible solute count  to all solutes in the data set that appear n times in
to all solutes in the data set that appear n times in  . For each n where i(n) is not empty, we now calculate the average prediction error for all binary mixtures in the data set whose solute is in i(n). We proceed analogously for the solvents.
. For each n where i(n) is not empty, we now calculate the average prediction error for all binary mixtures in the data set whose solute is in i(n). We proceed analogously for the solvents.
Fig. 7 shows the improvement of our proposed GNN MCM over both UNIFAC (olive) and MCM (terracotta) as a function of the frequency n of solutes (top) and solvents (bottom). We observe that GNN MCM improves over both UNIFAC and MCM consistently across all solute and solvent frequencies n (i.e., almost all points in the plots lie above the dashed zero line). The improvement over MCM (terracotta lines) is most pronounced in the regime of small n, i.e., where few data points with the same solute or solvent exist. This is to be expected since this is the regime where a fully nonparametric model like MCM tends to perform poorly. The strong improvement for the solvent with highest n (right end of lower plot) can be explained as this solvent is water, for which a lot of data points with infrequent solutes exist in the dataset.
In summary, we find that our proposed method significantly improves predictive accuracy over both fully parametric and fully nonparametric baselines (Fig. 4 and Table 1), and that this improvement is consistent across mixture components from different chemical categories (Fig. 5 and 6) and across varying amounts of training data for involved components (Fig. 7).
5 Summary and outlook
In this work, we propose a method for predicting physico-chemical properties that combines a structure-based approach using graph neural networks (which are able to extrapolate across substances with similar chemical structure) with a representation-learning based approach (which allows the model to override structure-based predictions in anomalous cases). The method significantly improves predictive accuracy over the state of the art in the studied example problem of predicting activity coefficients in binary mixtures.Our ablation studies identify the variational EM algorithm to be crucial for the success of the prediction method. We think that variational EM can be a useful tool for many physico-chemical prediction problems since it balances structure-based and representation-learning based predictions by weighing off their respective uncertainties.
Future work should explore the application of our method to other properties like diffusion coefficients or even fundamental quantities like interaction energies, which are at the core of established physical models of mixtures and based on with diverse mixture properties can be described. In a broader context, our work provides additional evidence for the efficacy of graph neural networks for processing chemical structure information. It would be interesting to study whether activations of hidden layers of the graph neural networks can be made interpretable to human domain experts, whether correlations between the hidden activations of different atoms can be used to identify relevant substructures of molecules, and whether such substructures correspond to the structural groups considered in established group contribution methods.
Data availability
We evaluate our methods on two datasets: a dataset that is licensed from the Dortmund Data Bank (DDB)21 and a dataset collected by Brouwer et al.41. The software packages for preprocessing and training our models are freely available. We provide the source code to replicate our results at . For the comparison of our method to the model proposed by Medina et al.,14 we directly use the files available from the GitHub repository by Medina et al.14
. For the comparison of our method to the model proposed by Medina et al.,14 we directly use the files available from the GitHub repository by Medina et al.14
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Johannes Zenn thanks Tim Xiao for helpful comments and discussions. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC number 2064/1 – Project number 390727645. This work was supported by the German Federal Ministry of Education and Research (BMBF): Tübingen AI Center, FKZ: 01IS18039A. The authors would like to acknowledge support of the ‘Training Center Machine Learning, Tübingen’ with grant number 01|S17054. The authors thank the International Max Planck Research School for Intelligent Systems (IMPRS-IS) for supporting Johannes Zenn. Robert Bamler acknowledges funding by the German Research Foundation (DFG) for project 448588364 of the Emmy Noether Program. Fabian Jirasek gratefully acknowledges funding by DFG for project 528649696 of the Emmy Noether Program and for project 497201843 in the Priority Program Molecular Machine Learning (SPP 2363).Notes and references
- F. Jirasek and H. Hasse, Annu. Rev. Chem. Biomol. Eng., 2023, 14, 31–51 CrossRef CAS PubMed.
- J. Gmehling, D. Constantinescu and B. Schmid, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 267–292 CrossRef CAS PubMed.
- F. Jirasek, N. Hayer, R. Abbas, B. Schmid and H. Hasse, Phys. Chem. Chem. Phys., 2023, 25, 1054–1062 RSC.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- U. Weidlich and J. Gmehling, Ind. Eng. Chem. Res., 1987, 26, 1372–1381 CrossRef CAS.
- D. Constantinescu and J. Gmehling, J. Chem. Eng. Data, 2016, 61, 2738–2748 CrossRef CAS.
- A. R. Katritzky, M. Kuanar, S. Slavov, C. D. Hall, M. Karelson, I. Kahn and D. A. Dobchev, Chem. Rev., 2010, 110, 5714–5789 CrossRef CAS PubMed.
- E. Estrada, G. A. Díaz and E. J. Delgado, J. Comput.-Aided Mol. Des., 2006, 20, 539–548 CrossRef CAS PubMed.
- F. Giralt, G. Espinosa, A. Arenas, J. Ferre-Gine, L. Amat, X. Girones, R. Carbó-Dorca and Y. Cohen, AIChE J., 2004, 50, 1315–1343 CrossRef CAS.
- B. E. Mitchell and P. C. Jurs, J. Chem. Inf. Comput. Sci., 1998, 38, 200–209 CrossRef CAS.
- K. Paduszynski, J. Chem. Inf. Model., 2016, 56, 1420–1437 CrossRef CAS PubMed.
- S. Ajmani, S. Rogers, M. Barley, A. Burgess and D. Livingstone, QSAR Comb. Sci., 2008, 27, 1346–1361 CrossRef CAS.
- H. A. Behrooz and R. B. Boozarjomehry, Fluid Phase Equilib., 2017, 433, 174–183 CrossRef.
- E. I. S. Medina, S. Linke, M. Stoll and K. Sundmacher, Digital Discovery, 2022, 216–225 RSC.
- F. Jirasek, R. A. Alves, J. Damay, R. A. Vandermeulen, R. Bamler, M. Bortz, S. Mandt, M. Kloft and H. Hasse, J. Phys. Chem. Lett., 2020, 11, 981–985 CrossRef CAS PubMed.
- F. Jirasek, R. Bamler and S. Mandt, Chem. Commun., 2020, 56, 12407–12410 RSC.
- N. Hayer, F. Jirasek and H. Hasse, AIChE J., 2022, 68, e17753 CrossRef CAS.
- O. Großmann, D. Bellaire, N. Hayer, F. Jirasek and H. Hasse, Digital Discovery, 2022, 1, 886–897 RSC.
- J. Damay, F. Jirasek, M. Kloft, M. Bortz and H. Hasse, Ind. Eng. Chem. Res., 2021, 60, 14564–14578 CrossRef CAS.
- F. Jirasek, R. Bamler, S. Fellenz, M. Bortz, M. Kloft, S. Mandt and H. Hasse, Chem. Sci., 2022, 13, 4854–4862 RSC.
- U. Onken, J. Rarey-Nies and J. Gmehling, Int. J. Thermophys., 1989, 10, 739–747 CrossRef.
- A. P. Dempster, N. M. Laird and D. B. Rubin, J. Roy. Stat. Soc. B, 1977, 1–38 Search PubMed.
- M. J. Beal and Z. Ghahramani, Bayesian statistics, 2003, vol. 7, pp. 453–464 Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- K. P. Murphy, Probabilistic machine learning: an introduction, MIT press, 2022 Search PubMed.
- D. M. Blei, A. Kucukelbir and J. D. McAuliffe, J. Am. Stat. Assoc., 2017, 112, 859–877 CrossRef CAS.
- C. Zhang, J. Bütepage, H. Kjellström and S. Mandt, IEEE Trans. Pattern Anal. Mach. Intell., 2018, 41, 2008–2026 Search PubMed.
- R. Bamler, C. Zhang, M. Opper and S. Mandt, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- D. P. Kingma and M. Welling, International Conference on Learning Representations, 2013 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, in Advances in Neural Information Processing Systems 32, ed. H. Wallach, H. Larochelle, A. Beygelzimer, F. d' Alché-Buc, E. Fox and R. Garnett, Curran Associates, Inc., 2019, pp. 8024–8035 Search PubMed.
- M. Gori, G. Monfardini and F. Scarselli, Proceedings. 2005 IEEE International Joint Conference on Neural Networks, 2005, pp. 729–734 Search PubMed.
- F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, IEEE Trans. Neural Network., 2008, 20, 81–102 Search PubMed.
- M. M. Bronstein, J. Bruna, T. Cohen and P. Veličković, arXiv, preprint, 2021, arXiv:2104.13478 Search PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International Conference on Machine Learning, 2017 Search PubMed.
- M. Brockschmidt, International Conference on Machine Learning, 2020. Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- M. Fey and J. E. Lenssen, ICLR Workshop on Representation Learning on Graphs and Manifolds, 2019 Search PubMed.
- D. P. Kingma and J. Ba, International Conference on Learning Representations, 2015 Search PubMed.
- N. Morgan and H. Bourlard, Advances in neural information processing systems, 1989 Search PubMed.
- A. Zhang, Z. C. Lipton, M. Li and A. J. Smola, Dive into deep learning, Cambridge University Press, 2023 Search PubMed.
- T. Brouwer, S. R. Kersten, G. Bargeman and B. Schuur, Separ. Purif. Technol., 2021, 272, 118727 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00154k |
| This journal is © The Royal Society of Chemistry 2025 |