A materials discovery framework based on conditional generative models applied to the design of polymer electrolytes

Abstract

In this work, we introduce a computational polymer discovery framework that efficiently designs polymers with tailored properties. The framework comprises three core components—a conditioned generative model, a computational evaluation module, and a feedback mechanism—all integrated into an iterative framework for material innovation. To demonstrate the efficacy of this framework, we used it to design polymer electrolyte materials with high ionic conductivity. A conditional generative model based on the minGPT architecture can generate candidate polymers that exhibit a mean ionic conductivity that is greater than that of the original training set. This approach, coupled with molecular dynamics (MD) simulations for testing and a specifically planned acquisition mechanism, allows the framework to refine its output iteratively. Notably, we observe an increase in both the mean and the lower bound of the ionic conductivity of the new polymer candidates. The framework's effectiveness is underscored by its identification of 14 distinct polymer repeating units that display a computed ionic conductivity surpassing that of polyethylene oxide (PEO).

---

1 Introduction

Polymers cater to a wide range of applications, spanning from biodegradable materials and high-performance aerospace composites to conducting elements in electronic devices and smart materials in sensor technologies. Notably, polymer electrolytes are a promising direction in the field of energy storage.^1–4 Currently, several challenges are associated with liquid electrolytes, which are the commercially used materials in Li-ion batteries, including flammability,^5,6 toxicity,^7,8 and instability of the electrode–electrolyte interface due to lithium dendrite formation.^9,10 Polymer electrolytes can address these issues due to their inherent properties.^2–4 Additionally, several other advantages of polymer electrolytes, such as better adaptability to current manufacturing processes compared to ceramics¹¹ and lower cost compared to ionic liquids,¹² highlight the potential of polymer materials to revolutionize energy storage technologies.

Recent advancements in polymer electrolytes have emerged from strategies including crosslinking, blending with additives, and copolymerization.^13–17 For example, He et al.¹⁸ improved Li-ion mobility and electrochemical stability by moving the carbonate group to the side chain and using a hydrocarbon backbone, achieving a conductivity of about 1.1 mS cm⁻¹ at room temperature. Similarly, Zhang et al.¹⁹ enhanced polyethylene oxide (PEO) electrolytes through crosslinking, resulting in a conductivity of 2.7 × 10⁻⁴ S cm⁻¹. Sun et al.²⁰ developed PEO-based electrolytes with fast Li⁺ transport and dendrite-free Li-metal deposition, maintaining cell capacity over 1200 cycles. Lin et al.²¹ designed block copolymer electrolytes with three-dimensional networks, achieving a conductivity of 5.7 × 10⁻⁴ S cm⁻¹ and a high lithium ion transference number. Despite these advances, solid polymer electrolytes still face challenges in matching the ion transport properties of liquid counterparts.

The vastness of polymer electrolyte design space, combined with the necessity to balance multiple properties like mechanical strength, electrical conductivity, and thermal stability, makes the discovery process highly intricate. Given the need to rapidly identify innovative materials, including advanced polymer electrolytes for next-generation energy storage solutions, more efficient and comprehensive approaches to polymer discovery are needed.

Machine learning, particularly in the realm of generative modeling, presents a potentially transformative approach to this challenge. Generative models in machine learning have shown promise in various domains, including material science,^22–26 by enabling the exploration of vast chemical spaces with unprecedented efficiency. These models can quickly navigate the intricacies of polymer chemistry, suggesting novel and plausible compositions and structures for investigation, thereby streamlining the discovery process.

Within this realm, conditioned generative modeling presents a particularly relevant technique.^22,27–30 By training models on specific conditions or properties, it becomes possible to generate content that meets predetermined criteria. In the current landscape, while the concept of integrating machine learning with material science to tailor polymer properties is gaining traction, conditioned generative models specifically for polymers are still emerging. We, therefore, introduce a comprehensive polymer discovery framework that leverages the principles of conditioned generative modeling. This framework is designed to iteratively improve and refine its suggestions based on continuous feedback and evaluation, and such a system could offer a more holistic and efficient pathway to polymer material innovation.^31–33

This proof-of-concept study demonstrates the application of our discovery framework in the realm of polymer electrolytes. We limit the scope of this study to dry (solid) linear chain homopolymers and utilize the HTP-MD database,³⁴ a recently developed large database of polymer electrolyte properties computed from MD simulations. Building on prior work exploring conditional generation of polymer electrolytes using a variety of model architectures,³⁵ this work proposes an iterative discovery framework and discusses its outcomes. We show that our framework successfully designs polymer electrolytes with ion conductivities superior to PEO, as assessed by molecular dynamics (MD) simulations. It is worth mentioning that PEO currently holds the record for one of the highest ion conductivity in the form of dry (solid) polymers with around 1 mS cm⁻¹ conductivity at 353 K, and Li⁺·TFSI⁻ molality of 1.5 mol kg⁻¹ and is still considered a benchmark material in this field.

While this study only explores a limited region of the polymer design space and does not specifically target other requirements, such as thermal stability or varied operational conditions, the framework has the potential to be extended in future work to address these critical challenges, potentially leading to safer, more durable, and higher-capacity energy storage solutions.

2 Framework

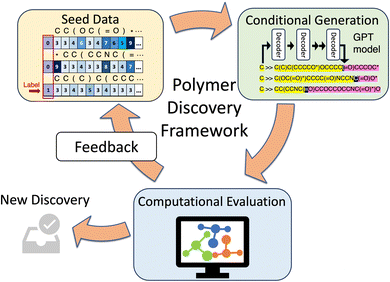
Our framework (Fig. 1) is structured around an iterative and self-sustaining workflow comprising three essential components: a conditional generative model, a computational evaluation module, and a feedback mechanism. This integrated system allows for continuous refinement and evolution of the discovery process, which we term a “discovery campaign”.

Fig. 1 Schematic illustration of the framework.

The conditioned generative model, the heart of this framework, is tasked with proposing potential polymer candidates. Tailored to incorporate specific target properties, this module is responsible for generating polymers, either by constructing repeating units, oligomers, polymer chains, or 3D structures. For this work, our focus is on generating the 2D representation of repeat units of polymers. Several aspects heavily influence the performance of the generative model: the (seed) data, the model architecture and hyperparameters, and the training strategies. Different from traditional regression models, where a numerical loss is clearly defined, the generative tasks are more ambiguous and difficult to evaluate and often require domain knowledge. The process of formulating a comprehensive and domain-relevant evaluation schema and performing the benchmarking across a series of model architectures and training strategies presents its own set of challenges studied in our related work.³⁵

Once a batch of polymers is proposed by the generative model, the evaluation module takes over. This component is responsible for assessing the target properties of the proposed polymers, employing both simulation and experimental validations. In the current study, we rely on MD simulations for computational validation. While experimental validation would serve as the definitive confirmation for computationally discovered polymers, it is significantly more costly in time and resources and has not been integrated into the current framework.

Establishing a feedback mechanism is pivotal to allowing active learning and continuously guiding the model to newly found promising search space. At the end of each campaign iteration, all computed results are recorded in a database, and strategically sampled for enriching the training data. The model is then retrained to the new data to become increasingly adept at targeting the desired polymers. Acquisition strategies could range from the simple scheme used in this work to more sophisticated models, perhaps in the future leveraging uncertainty quantification of the generative model to balance exploration and exploitation.

The initialization and deployment of the framework are crucial steps of the discovery campaign. The seed data chosen by the user describes the initial design space, and its quality and variety are paramount for each campaign's success. With the chosen dataset and clearly defined target properties, the framework is designed to be capable of operating with minimal subjective intervention. This capability underlies the framework's potential for high-throughput, efficient discovery campaigns.

3 Experiment setup

3.1 Conditional generation

The core of this demonstration revolves around a conditional generative model based on the minGPT³⁶ architecture, which is trained to generate a polymer electrolyte candidate given lead, prompt signaling what kind of property is needed (with high or low ionic conductivity), just like the popular large language models. We use the Simplified Molecular Input Line Entry System (SMILES)³⁷ code of polymers' repeating units to represent the polymer electrolyte candidates. To direct the model towards polymers with high ionic conductivity, we implement a method to incorporate the properties of the input during training. This involves the modification of tokenized SMILES strings of known polymer electrolytes prefixed by their ionic conductivity classes. Specifically, given the range (0.007–0.506 mS cm⁻¹) and distribution (mean = 0.062 mS cm⁻¹, std = 0.036 mS cm⁻¹) of ionic conductivity in our dataset, we assign different class labels to high-conductive (top 5%) and low-conductive (lower 95%) polymers and use this class as the leading digit in the input to the model. The dividing line between the “high-conductivity” (labeled with class 1) and “low-conductivity” (labeled with class 0) categories is set to be 0.012 mS cm⁻¹, and this is fixed throughout the experiment. Additionally, to maintain the importance of the property class in comparison to the lengthy SMILES, and to ensure the model can be effectively guided towards desirable structures, we replicate the property class tokens five times, which we find results in better polymer electrolyte candidates. Therefore, the effective prompt that signals the conditioned generative model to generate polymer electrolyte candidates with high ionic conductivity is a leading string of “11111”, and the model will then complete the string by generating a SMILES code that represents a specific polymer candidate.

Inspired by the simple design of the benchmark PEO, which has a very short repeat unit (OCC), we use the model to generate small repeating units with SMILES strings containing 10 or fewer tokens (excluding the end tokens) during the iterative polymer generation loops. This approach proves crucial for the model's ability to generate high-conductivity polymers. Short repeat units often result in the short distance between negatively charged atoms, such as oxygen atoms, in the polymer backbone that coordinates with Li ions, and this is an effective coordination environment can help with salt dissociation to individual ions and the easier hopping of cations from one coordination site to another.^38,39 Regardless of the imposed restriction on the length of repeat units, the model shows a tendency toward generating short repeat units, which is mainly due to oversampling PEO that will be discussed in Section 3.3.

It is worth mentioning that, given our goal of designing new polymers, we address duplicate generated polymers in two ways. First, exact matches for SMILES in the training set and in each batch of generation are automatically ignored. For SMILES that are not exact duplicates but still represent the same polymer (due to mirror and translational symmetries, repeated patterns, and combinations of these scenarios), we filter them out during post-processing. In our discovery campaign, we generate 50 candidates in each iteration which are not exact duplicates. We identified 2 duplicates during post-processing in the first iteration, 7 in the second, and 20 in the third (not included in the manuscript). A list of all generated SMILES strings in the first two iterations, also including these post-processed duplicates and those that failed MD simulations, is provided in our GitHub repository.

3.2 Model details

In this study, we use a transformer-based generative model and a workflow described in full in our concurrent study,³⁵ which is tailored for polymer design.

The generative model is based on a minimal implementation of the GPT model.³⁶ The model first converts a sequence of tokens (SMILES vocabulary) to two embeddings, including token embedding and positional embedding. Token embedding represents the meaning of individual words or symbols in a high-dimensional space, while positional embedding encodes the order or position of tokens within a sequence to provide contextual information to the model. These embeddings are then passed through multiple layers of transformer blocks. Each transformer block mainly consists of a multi-head masked self-attention layer and a feed-forward neural network, following the original transformer architecture.⁴⁰ The loss function is cross entropy loss comparing tokens in the generated and actual sequences.

We perform a grid search to tune the hyperparameters of minGPT. The mean values of six metrics assessing the generated polymers (chemical validity, uniqueness, novelty, synthesizability, similarity, diversity) are utilized as the evaluation metric for each model's performance. It is important to note that in this study, novelty is defined as a polymer structure that has not been seen by the model during the training process and is not based on literature novelty. We search over three independent hyperparameters: model architecture, temperature, and the total number of training epochs. For model architecture we choose between various transformer-based architectures, specifically “gpt-2”, “gpt-mini” and “gpt-nano” from HuggingFace.⁴¹ The model temperature is varied between 0.1, 0.5 and 1.0, where higher temperature results in higher “creativity” for the model. Models are trained between 1000 to 10 000 epochs with a uniform interval of 1000. The best performance is obtained with the “gpt-nano” model (which has 0.12 million parameters) with temperature set to 1.0 and trained for 6000 epochs. Additional hyperparameter selection and the grid search details can be found in the ESI Tables S1–S4.†

3.3 Data

The initial dataset used in this study is a subset of polymers from HTP-MD database,^34,42 consisting of 6024 linear chain homopolymers. The polymers in HTP-MD database are composed of the elements H, C, F, S, P, O, and N, previously filtered from 53 362 structures in the ZINC database⁴³ to improve the likelihood of synthesizability and potential application as electrolytes.⁴⁴ To skew the model towards high-conductivity polymers, we randomly oversample the top 5% ionic conducting polymers to provide a training set that includes the same number of polymers from low-conductive and high-conductive classes. Additionally, PEO is added and oversampled 4000 times in the seed data. This method of selective oversampling is instrumental in guiding the model towards generating more promising polymer candidates. It should be noted that in the current study, oversampling is performed by including duplicate SMILES strings, and we have not tried other methods, such as randomization.⁴⁵

3.4 Evaluation and feedback

For evaluation purposes, the 50 polymer candidates generated at each iteration of the discovery process have their ionic conductivities evaluated through MD simulations. These simulations adhere to the same protocol previously used in creating the initial dataset (HTP-MD: ref. 42).^34,44

We carry out MD simulations on polymer–(Li⁺·TFSI⁻) systems at a temperature of 353 K and a salt concentration of 1.5 mol kg⁻¹ using LAMMPS⁴⁶ with the PCFF+.⁴⁷ The charges of Li and TFSI ions were adjusted using a scale factor of 0.7 according to ref. 48. The PCFF+ force field has been employed in previous studies to explore various properties of electrolyte systems.^44,49–54 Additionally, multiple studies have compared the MD predictions obtained using the PCFF+ force field with experimental data and density functional theory (DFT) calculations for both polymer^44,55,56 and liquid^57–59 electrolytes.

The simulation process includes initial relaxation and equilibration of the polymer–salt mixture, followed by a production phase to gather data for computing ion transport properties, such as ionic conductivity. The equilibration stage involves running sequential NVT (constant number of particles, volume, and temperature) and NPT (constant number of particles, pressure, and temperature) ensembles to achieve densities close to theoretical values. For the production run, an NVT simulation at 353 K is conducted for 5 ns with a 2.0 fs time step. The resulting trajectories are then analyzed to compute ion transport properties using the cluster Nernst–Einstein equation.⁴⁹ The analysis code used to compute ionic conductivity is consistent with the one used to generate the HTP-MD database and is available at https://github.com/TRI-AMDD/htp_md. More details about MD simulations, dataset composition, and computing ionic conductivity have been included in 3.3 section, as well as previous studies.^34,42,44,60

The repeat units of the generated polymers are polymerized to have at least 150 heavy atoms (non-H) in their backbone, with the two ends terminated by methyl groups. This approach is consistent with the method used to generate the HTP-MD database, allowing us to compare the performance of newly generated polymers with the training set. Also, to ensure robustness, each candidate undergoes five independent simulation replicas to determine its conductivity. Given the randomness in MD simulation results originating from different conformation sampling, this rigorous step is crucial for ascertaining the potential of each proposed polymer.

The feedback mechanism of our framework plays a vital role in its iterative learning process. After evaluation, we add both PEO and newly discovered polymers showing conductivity higher than PEO to the training set and oversample 4000 in total from all newly added polymers. This is to ensure the model can still explore polymers that are different from PEO. This enriched dataset is then used to retrain the generative model, with the aim of proposing increasingly relevant and high-performance polymers in subsequent iterations.

4 Application: polymer electrolyte discovery

4.1 Framework iterations

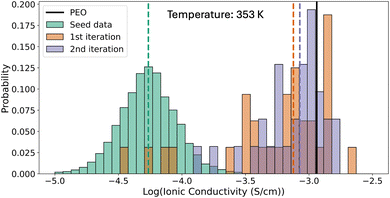
We examine how the distribution of polymers evolves across iterations of our framework (Fig. 2). In the initial iteration, the generated polymer candidates exhibit a shifted distribution of ion conductivity with a notably higher mean value (0.75 mS cm⁻¹) when compared to the training set (0.06 mS cm⁻¹, excluding the added PEO polymers), an improvement by a factor of 11.5. At the second iteration, the average ion conductivity of the generated polymers (0.85 mS cm⁻¹) improves by a further 15%. Further, the lowest ion conductivity resulting from the second iteration batch (0.136 mS cm⁻¹) is 3.6 times that of the first iteration (0.037 mS cm⁻¹, ignoring the 0 conductivity of polyethylene).

Fig. 2 Distribution of MD-predicted ionic conductivities of polymers in the training set (green), first iteration (orange), and second iteration (purple). The dotted vertical lines show the mean ionic conductivity in each distribution, and the solid black line is the MD-predicted ionic conductivity of PEO.

Although we observe an increase in the minimum and average ionic conductivity, there is a decrease in the maximum ionic conductivity of generated polymers from the first iteration (1.61 mS cm⁻¹) to the second iteration (2.04 mS cm⁻¹). We believe this decrease is due to the exhaustion of the limited search space. Since we are exploring linear chain homopolymers composed of only a few heavy atoms, the search space is narrow. The increasing number of duplicate candidates generated (mentioned in Section 3.1) also provides evidence of search space saturation. We, therefore, only perform two full iterations of exploration. We believe that by extending the chemistry to a wider range of atom types and incorporating more diverse polymer structures (e.g., aromatic structures), a saturation of performance increase would occur at later stages. This highlights the necessity of developing more creative generative models that can extrapolate the search space, which has been the focus of other researchers' studies.³¹

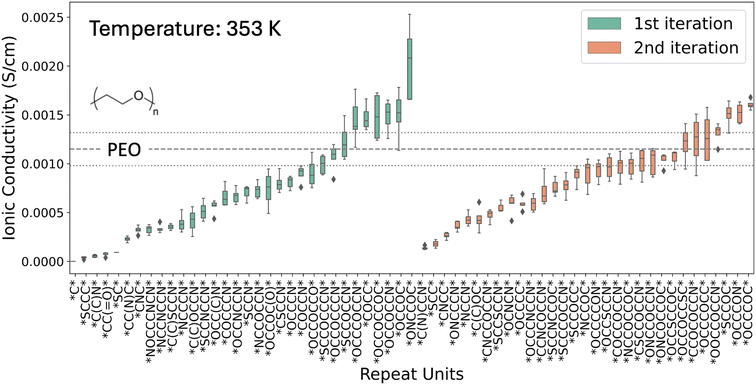
Despite this limited search space, the framework generates polymer electrolyte candidates with high conductivity, including those exceeding the PEO benchmark. The box-and-whisker plot in Fig. 3 highlights the new repeating units discovered through this process and their ionic conductivity computed from MD simulations. In the first iteration, 7 polymers have MD-computed conductivities greater than PEO, and in the second iteration, again 7 polymers exceed PEO. The distribution of computed conductivity for individual polymers is due to the effect of random initialization of different simulation replicas with a standard deviation within the range of 20% of the average conductivity values consistent with previous studies.⁶¹ Other ion transport properties of the generated polymer in the two iterations, including density, ion diffusivity, ionic conductivity, and transference number, are listed in the ESI (Tables S5 and S6†).

Fig. 3 Ionic conductivity of polymers generated from two iterative candidate generations computed from MD simulations. The box plots show the mean and standard deviation in 5 MD simulations performed for each listed polymer, and the diamond symbols are outlier conductivity values. The dashed and dotted lines show the mean and the standard deviation of ionic conductivity of PEO as computed from MD simulation.

4.2 High-performing polymers

In Fig. 4, we introduce the 14 generated polymer repeating units whose ionic conductivities, as predicted by MD simulations, surpass that of PEO. To facilitate discussion, we assign a unique ID to each polymer in Fig. 4, where the first number in the ID represents the iteration number and the second indicates the polymer's ranking in terms of average conductivity. Polymers 1–2, 1–4, 1–5, 2–1, and 2–5 are polyacetals, which are polymers with a high oxygen-to-carbon ratio, similar to PEO, which facilitates efficient lithium salt solvation and creates effective pathways for lithium ion transport. A few of these polyacetals, while not part of our initial dataset, have been previously reported. For example, polymer 1–2 is poly(1,3-dioxolane) (P(EO-MO), *OCCOC*), a polyacetal with a repeating unit of 1,3-dioxolane. MD simulations in this work predict its ion conductivity to be 1.515 (±0.199) mS cm⁻¹, but its experimentally measured conductivity has been reported to be lower at 0.4 mS cm⁻¹.⁶² Nevertheless, its potential as a polymer electrolyte candidate remains significant due to its improved ion transport efficacy. Similarly, polymer 1–4 is poly(diethylene oxide-alt-oxymethylene) (P(2EO-MO), *OCCOCCOC*), which has been previously synthesized and investigated, and shows slightly lower ionic conductivity of 1.1 mS cm⁻¹ compared to PEO's 1.5 mS cm⁻¹ at 90 °C.⁶³ Finally, polymer 2–5 is polyethylene oxide-alt-trimethylene oxide (P(EO-TMO) *OCCCOCC*). Previous MD simulations have supported the higher ionic conductivity of P(EO-TMO) compared to PEO.⁶⁴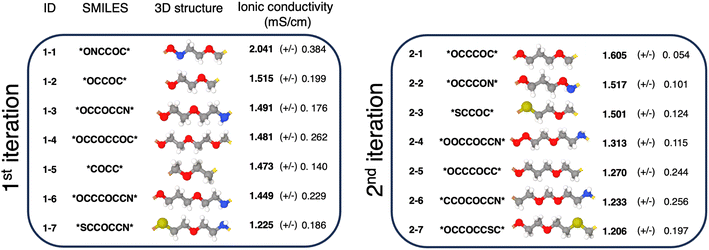

Fig. 4 Discovered polymers from two iterative generation cycles. The polymer listed for each iteration exhibited an ionic conductivity superior to that of PEO.

The remaining candidate polymers feature elements like nitrogen and sulfur (1–1, 1–3, 1–6, 1–7, 2–2, 2–3, 2–4, 2–6, and 2–7), marking a shift from the conventional focus on polycarbonates composed solely of carbon and oxygen. Polymer 1–1 (ONCCOC) has the highest conductivity among all polymers in our study – roughly twice that of PEO. Unfortunately, most of these polymers, including 1–1, have unstable bonds and motifs such as N–O, S–O, S–N, O–O–NH, and O–NH–O bonds (1–1, 1–3, 1–6, 1–7, 2–2, 2–4, and 2–6). Likely due to difficulties in synthesizability and stability, there are no previous experimental or theoretical studies on these specific polymers. However, related research on polyethylenimine (PEI, CCN) polymer electrolytes^65,66 and their blends with PEO^67,68 have been documented. Polymers 2–3 and 2–7 do not have the unstable bonds, and we did not find any prior studies of these candidates.

4.3 Factors influencing conductivity

The calculated ionic conductivity, derived from the cluster Nernst–Einstein equation, arises from both ion diffusivity and clustering. To elucidate the mechanisms underpinning the superior ionic conductivity observed in generated polymers, we conduct a comparative analysis of conductivity, ion diffusivity, and concentrations of free ions between PEO and the polymers exhibiting enhanced performance (see Fig. S1†). In this context, “free ions” denote those not incorporated into any clusters and moving freely, with their concentration determined as an average across simulation durations. The analysis reveals that the augmented conductivity in the most effective polymers from the first two iterations is attributed to both an increase in ion diffusivity and a higher prevalence of free ion clusters. Interestingly, it is also noted that several of the developed polymers exhibit a more efficient dissociation of the Li⁺·TFSI⁻ salt compared to PEO, indicating a potential for improved ion transport properties.

Salt concentration is a crucial design parameter that influences ion pairing in polymer electrolytes. Both ionic conductivity and free ion concentration initially increase with higher salt concentration, but at very high concentrations, ion clusters of cations and anions form. These clusters reduce effective conductivity due to charge cancellation within each cluster.⁴⁹ The optimal salt concentration depends on how strongly polymer atoms coordinate with ions, which affects salt dissociation. Consequently, this optimal concentration varies for different polymers. Generally, a practical electrolyte system for lithium-ion batteries requires a moderate to high salt concentration to achieve enhanced ionic conductivity,⁶⁹ mechanical strength,⁷⁰ electrochemical stability,⁷¹ and solid electrolyte interphase (SEI) formation.⁷² We examined the ionic conductivity of several top candidates across various salt concentrations at 353 K to illustrate this concept (see Fig. S2†). The MD simulation results indicated that maximum conductivity occurs at slightly different salt molalities, generally around 1.5–2.0 mol kg⁻¹. Although the salt concentration in the training set used to generate the polymers in this study was 1.5 mol kg⁻¹, exploring this parameter further as a design factor is recommended for future research.

5 Outlook

In this manuscript, we presented an iterative polymer discovery framework and applied it to generate new polymer electrolytes in their SMILES representations. We have demonstrated that this approach generates polymer structures that outperform benchmark materials like PEO in MD simulations. The generated candidates include polymer candidates that other researchers have investigated in recent years, as well as new candidates that are as of yet unstudied.

While this study demonstrates the capabilities of our framework, it also highlights important directions for refinement and improvement, which will strengthen our ability to translate discoveries to experiment and the real-world performance of new materials.

One direction would be to include other relevant properties or metrics for optimization, as well as enabling multi-property optimization. In this study, we selected ionic conductivity as the primary metric to identify new polymer electrolytes. However, a more holistic measure is efficacy, defined as the product of conductivity and cationic current fraction.^62,73 Furthermore, conductivity and efficacy could be more accurately predicted by using more accurate MD – reactive force fields, machine learned potentials, and ab initio MD – and by incorporating experimental feedback. Our framework could also potentially be adapted to evaluate additional polymer properties such as glass transition temperature (T_g), bulk density, and mechanical properties. Another important metric would be the synthesizability of polymers, which can be approximated through the SA score, based on factors such as the number of plausible synthesis recipes, required synthesis conditions, and the kinetics of the routes, and/or determined through a feedback loop incorporating real-world testing of the synthesis recipes.⁷⁴

The second direction would be to improve the models integrated into the framework. Models could be refined with improved data (over)sampling and to account for polymer symmetries. Furthermore, a deeper understanding on metrics of generative model performance would aid in identifying the best models during hyperparameter searches.³⁵ In addition, the use of SMILES strings limits the information available to the model, since they represent molecules as linear sequences and may be inadequate for capturing the complexity of branched or cross-linked polymer structures. Models that incorporate 3D structural information may be more performant.

The third direction is to expand the search space available to the framework. The current work focuses on the design of monomers of linear chain homopolymers via SMILES string consisting of just a few atom types. The use of this representation in fact allows us to easily extend our discovery framework to use cases including molecular discovery, e.g., for liquid electrolytes composed of small molecules. However, to thoroughly exploit the polymer design space, we must enhance the framework to accommodate more complex representations. These should capture the multiscale and stochastic characteristics of polymers, enabling the exploration of diverse structures such as cyclic and aromatic backbones, copolymers, and variations in tacticity. Further strategies to expand the search space might involve the incorporation of additives like plasticizing solvents, blending of distinct polymer architectures, or the integration of various salts. These tactics have demonstrated potentials in experimentally optimizing ionic conductivity.^{13,14,67,75–81}

Finally, the implementation of our approach presents an opportunity for further improvement. The workflow of our framework could be further modularized and automated to provide more flexibility and expedite development. Regardless, throughout the discovery campaign, the current process already includes minimal subjective intervention, laying the groundwork for developing a fully automated system. The existing platform and available code provide a basis for future efforts, which could enable compatibility with various generative models and evaluation methods, streamline the discovery process, and also expand the platform's utility across different domains of polymer research.

Code and data availability

A subset of HTP-MD dataset (https://www.htpmd.matr.io/) has been used for training the generative models. This dataset can be accessed at https://github.com/TRI-AMDD/PolyGen/blob/main/PolyGen-train-set-from-HTP-MD.csv [https://doi.org/10.5281/zenodo.14261933]. The code for training the generative models can be found at: https://github.com/TRI-AMDD/PolyGen/tree/main/minGPT [https://doi.org/10.5281/zenodo.14261787]. The code for running the MD simulations can be found here: https://github.com/TRI-AMDD/PolyGen/tree/main/Example-simulation-files. Consistent with the trainset, the MD simulation trajectories were analyzed, and the ionic conductivity of the generated polymers has been computed using HTP-MD code available at https://github.com/TRI-AMDD/htp_md.

Conflicts of interest

The authors wish to acknowledge that the discovery framework and materials discovered using our generative model framework, as described within this manuscript, are subject to a provisional patent application. This application has been submitted with the following details: U.S. Patent Application No. 63/582,871 titled “Methods of Designing Polymers and Polymers Designed Therefrom” with TEMA Reference No. IP-A-6823PROV and Darrow Reference No. TRI-1107-PR.

Acknowledgements

This work has been performed at the Toyota Research Institute without an external source of funding. We thank Professors Jeffrey Grossman, Yang Shao-Horn, Jeremiah Johnson, and Rafael Gomez-Bombarelli, and Drs Tian Xie, Sheng Gong, and Arthur France-Lanord at the Massachusetts Institute of Technology for their support in our MD simulations and polymer electrolyte research. Their guidance and insightful discussions have greatly enhanced our study's development and robustness.

References

1. K. Wu, J. Huang, J. Yi, X. Liu, Y. Liu, Y. Wang, J. Zhang and Y. Xia, Recent advances in polymer electrolytes for zinc ion batteries: Mechanisms, properties, and perspectives, Adv. Energy Mater., 2020, 10(12), 1903977.
2. J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Designing polymers for advanced battery chemistries, Nat. Rev. Mater., 2019, 4(5), 4.
3. Y. Hu, X. Xie, W. Li, Q. Huang, H. Huang, S.-M. Hao, L.-Z. Fan and W. Zhou, Recent progress of polymer electrolytes for solid-state lithium batteries, ACS Sustain. Chem. Eng., 2023, 11(4), 1253–1277.
4. Q. Zhao, S. Stalin, C.-Z. Zhao and L. A. Archer, Designing solid-state electrolytes for safe, energy-dense batteries, Nat. Rev. Mater., 2020, 5(3), 2.
5. L. Han, L. Wang, Z. Chen, Y. Kan, Y. Hu, H. Zhang and X. He, Incombustible polymer electrolyte boosting safety of solid-state lithium batteries: A review, Adv. Funct. Mater., 2023, 33(32), 2300892.
6. P. Jaumaux, J. Wu, D. Shanmukaraj, Y. Wang, D. Zhou, B. Sun, F. Kang, B. Li, M. Armand and G. Wang, Non-flammable liquid and quasi-solid electrolytes toward highly-safe alkali metal-based batteries, Adv. Funct. Mater., 2021, 31(10), 2008644.
7. N. P. Lebedeva and L. Boon-Brett, Considerations on the chemical toxicity of contemporary li-ion battery electrolytes and their components, J. Electrochem. Soc., 2016, 163(6), A821.
8. J. Strehlau, T. Weber, C. Lürenbaum, J. Bornhorst, H.-J. Galla, T. Schwerdtle, M. Winter and S. Nowak, Towards quantification of toxicity of lithium ion battery electrolytes-development and validation of a liquid-liquid extraction gc-ms method for the determination of organic carbonates in cell culture materials, Anal. Bioanal. Chem., 2017, 409, 6123–6131.
9. J. Xiao, How lithium dendrites form in liquid batteries, Science, 2019, 366(6464), 426–427.
10. Y. Takeda, O. Yamamoto and N. Imanishi, Lithium dendrite formation on a lithium metal anode from liquid, polymer and solid electrolytes, Electrochemistry, 2016, 84(4), 210–218.
11. X. Yu and A. Manthiram, A review of composite polymer-ceramic electrolytes for lithium batteries, Energy Storage Mater., 2021, 34, 282–300.
12. X. Ma, J. Yu, Y. Hu, J. Texter and F. Yan, Ionic liquid/poly (ionic liquid)-based electrolytes for lithium batteries, Ind. Chem. Mater., 2023, 1(1), 39–59.
13. C. Tang, K. Hackenberg, Q. Fu, P. M. Ajayan and H. Ardebili, High ion conducting polymer nanocomposite electrolytes using hybrid nanofillers, Nano Lett., 2012, 12(3), 1152–1156,  DOI:10.1021/nl202692y.
14. L. R. A. K. Bandara, M. A. K. L. Dissanayake and B.-E. Mellander, Ionic conductivity of plasticized(peo)-licf3so3 electrolytes, Electrochim. Acta, 1998, 43, 1447–1451.
15. B. Arouca Maia, N. Magalhães, E. Cunha, M. H. Braga, R. M. Santos and N. Correia, Designing versatile polymers for lithium-ion battery applications: a review, Polymers, 2022, 14(3), 403.
16. R. Bouchet, S. Maria, R. Meziane, A. Aboulaich, L. Lienafa, J.-P. Bonnet, T. N. T. Phan, D. Bertin, D. Gigmes and D. Devaux, et al., Single-ion bab triblock copolymers as highly efficient electrolytes for lithium-metal batteries, Nat. Mater., 2013, 12(5), 452–457.
17. Y. Tominaga and K. Yamazaki, Fast li-ion conduction in poly(ethylene carbonate)-based electrolytes and composites filled with tio2 nanoparticles, Chem. Commun., 2014, 50, 4448–4450.
18. Y. He, N. Liu and P. A. Kohl, High conductivity, lithium ion conducting polymer electrolyte based on hydrocarbon backbone with pendent carbonate, J. Electrochem. Soc., 2020, 167(10), 100517.
19. Y. Zhang, W. Lu, L. Cong, J. Liu, L. Sun, A. Mauger, C. M. Julien, H. Xie and J. Liu, Cross-linking network based on poly (ethylene oxide): Solid polymer electrolyte for room temperature lithium battery, J. Power Sources, 2019, 420, 63–72.
20. C. Sun, Z. Wang, L. Yin, S. Xu, Z. Ali Ghazi, Y. Shi, B. An, Z. Sun, H.-M. Cheng and F. Li, Fast lithium ion transport in solid polymer electrolytes from polysulfide-bridged copolymers, Nano Energy, 2020, 75, 104976.
21. Z. Lin, X. Guo, Y. Yang, M. Tang, Q. Wei and H. Yu, Block copolymer electrolyte with adjustable functional units for solid polymer lithium metal battery, J. Energy Chem., 2021, 52, 67–74.
22. Z. Yao, B. Sánchez-Lengeling, N. Scott Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha and R. Q. Snurr, et al., Inverse design of nanoporous crystalline reticular materials with deep generative models, Nat. Mach. Intell., 2021, 3(1), 76–86.
23. C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, S. Shysheya, J. Crabbé, L. Sun, J. Smith, et al., Mattergen: a generative model for inorganic materials design, arXiv, 2023, preprint, arXiv:2312.03687,  DOI:10.48550/arXiv.2312.03687.
24. D. Wines, T. Xie and K. Choudhary, Inverse design of next-generation superconductors using data-driven deep generative models, J. Phys. Chem. Lett., 2023, 14(29), 6630–6638.
25. P. Lyngby and K. Sommer Thygesen, Data-driven discovery of 2d materials by deep generative models, npj Comput. Mater., 2022, 8(1), 232.
26. M. Alverson, S. G. Baird, R. Murdock, J. Johnson and T. D. Sparks, et al., Generative adversarial networks and diffusion models in material discovery, Digital Discovery, 2024, 3(1), 62–80.
27. N. W. A. Gebauer, M. Gastegger, S. S. P. Hessmann, K.-R. Müller and K. T. Schütt, Inverse design of 3d molecular structures with conditional generative neural networks, Nat. Commun., 2022, 13(1), 973.
28. Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, Generative adversarial networks (gan) based efficient sampling of chemical composition space for inverse design of inorganic materials, npj Comput. Mater., 2020, 6(1), 84.
29. N. Fu, L. Wei, Y. Song, Q. Li, R. Xin, S. Sadeed Omee, R. Dong, E. M. D. Siriwardane and J. Hu, Material transformers: deep learning language models for generative materials design, Mach. Learn.: Sci. Technol., 2023, 4(1), 015001.
30. R. Okabe, M. Cheng, A. Chotrattanapituk, N. T. Hung, X. Fu, B. Han, Y. Wang, W. Xie, R. J. Cava, T. S. Jaakkola, et al., Structural constraint integration in generative model for discovery of quantum material candidates, arXiv, 2024, preprint, arXiv:2407.04557,  DOI:10.48550/arXiv.2407.04557.
31. R. Gurnani, D. Kamal, H. Tran, H. Sahu, K. Scharm, U. Ashraf and R. Ramprasad, polyg2g: A novel machine learning algorithm applied to the generative design of polymer dielectrics, Chem. Mater., 2021, 33(17), 7008–7016.
32. R. Ma and T. Luo, Pi1m: A benchmark database for polymer informatics, J. Chem. Inf. Model., 2020, 60(10), 4684–4690 , PMID: 32986418..
33. C. Kim, R. Batra, L. Chen, H. Tran and R. Ramprasad, Polymer design using genetic algorithm and machine learning, Comput. Mater. Sci., 2021, 186, 110067.
34. T. Xie, H.-K. Kwon, D. Schweigert, S. Gong, A. France-Lanord, A. Khajeh, E. Crabb, M. Puzon, C. Fajardo, W. Powelson, Y. Shao-Horn and J. C. Grossman, A cloud platform for automating and sharing analysis of raw simulation data from high throughput polymer molecular dynamics simulations, APL mach. learn., 2023, 1(4), 046108.
35. Z. Yang, W. Ye, X. Lei, H.-K. Kwon, D. Schweigert and A. Khajeh, De novo design of polymer electrolytes with high conductivity using gpt-based and diffusion-based generative models, npj Comput. Mater., 2023 DOI:10.1038/s41524-024-01470-9.
36. Mingpt, https://github.com/karpathy/mingpt.
37. A. A. Toropov, A. P. Toropova, D. V. Mukhamedzhanoval and I. Gutman, Simplified molecular input line entry system (smiles) as an alternative for constructing quantitative structure-property relationships (qspr), Indian J. Chem., 2005, 44A, 1545–1552.
38. A. Roy, B. Dutta and S. Bhattacharya, Correlation of the average hopping length to the ion conductivity and ion diffusivity obtained from the space charge polarization in solid polymer electrolytes, RSC Adv., 2016, 6(70), 65434–65442.
39. Y. Zhang, J. Wang, P. Apostol, D. Rambabu, A. E. Lakraychi, X. Guo, X. Zhang, X. Lin, S. Pal and V. Rao Bakuru, et al., Bimetallic anionic organic frameworks with solid-state cation conduction for charge storage applications, Angew. Chem., Int. Ed., 2023, 62(42), e202310033.
40. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. ukasz Kaiser, and I. Polosukhin, Attention is all you need, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, Curran Associates, Inc., 2017, vol. 30.
41. T. Wolf, L. Debut, V. Sanh, J. Chaumond, C. Delangue, A. Moi, P. Cistac, T. Rault, R. Louf, M. Funtowicz, J. Davison, S. Shleifer, P. von Platen, C. Ma, Y. Jernite, J. Plu, C. Xu, T. Le Scao, S. Gugger, M. Drame, Q. Lhoest, and A. M. Rush, Huggingface's transformers: State-of-the-art natural language processing, 2019, vol. 10.
42. htpmd web app, https://www.htpmd.matr.io.
43. J. J. Irwin and B. K. Shoichet, Zinc - a free database of commercially available compounds for virtual screening, J. Chem. Inf. Model., 2005, 45(1), 177–182 , PMID: 15667143..
44. T. Xie, A. France-Lanord, Y. Wang, J. Lopez, M. A. Stolberg, M. Hill, G. M. Leverick, R. Gomez-Bombarelli, J. A. Johnson and Y. Shao-Horn, et al., Accelerating amorphous polymer electrolyte screening by learning to reduce errors in molecular dynamics simulated properties, Nat. Commun., 2022, 13(1), 1–10.
45. J. Arús-Pous, S. V. Johansson, O. Prykhodko, E. Jannik Bjerrum, C. Tyrchan, J.-L. Reymond, H. Chen and O. Engkvist, Randomized smiles strings improve the quality of molecular generative models, J. Cheminf., 2019, 11, 1–13.
46. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19.
47. H. Sun, Force field for computation of conformational energies, structures, and vibrational frequencies of aromatic polyesters, J. Comput. Chem., 1994, 15(7), 752–768.
48. M. J. Monteiro, F. F. C. Bazito, L. J. A. Siqueira, M. C. C. Ribeiro and R. M. Torresi, Transport coefficients, Raman spectroscopy, and computer simulation of lithium salt solutions in an ionic liquid, J. Phys. Chem. B, 2008, 112(7), 2102–2109.
49. A. France-Lanord and J. C. Grossman, Correlations from ion pairing and the nernst-einstein equation, Phys. Rev. Lett., 2019, 122, 136001.
50. A. France-Lanord, Y. Wang, T. Xie, J. A. Johnson, Y. Shao-Horn and J. C. Grossman, Effect of chemical variations in the structure of poly (ethylene oxide)-based polymers on lithium transport in concentrated electrolytes, Chem. Mater., 2019, 32(1), 121–126.
51. Y. Wang, T. Xie, A. France-Lanord, A. Berkley, J. A. Johnson, Y. Shao-Horn and J. C. Grossman, Toward designing highly conductive polymer electrolytes by machine learning assisted coarse-grained molecular dynamics, Chem. Mater., 2020, 32(10), 4144–4151.
52. J. Wahlers, K. D. Fulfer, D. P. Harding, D. G. Kuroda, R. Kumar and R. Jorn, Solvation structure and concentration in glyme-based sodium electrolytes: A combined spectroscopic and computational study, J. Phys. Chem. C, 2016, 120(32), 17949–17959.
53. H. Meng, X. Yu, H. Feng, Z. Xue and N. Yang, Superior thermal conductivity of poly (ethylene oxide) for solid-state electrolytes: A molecular dynamics study, Int. J. Heat Mass Transfer, 2019, 137, 1241–1246.
54. J. Feng, J. Wang, Q. Gu, W. Thitisomboon, D. Yao, Y. Deng and P. Gao, Room-temperature all-solid-state lithium metal batteries based on ultrathin polymeric electrolytes, J. Mater. Chem. A, 2022, 10(26), 13969–13977.
55. N. Molinari, J. P. Mailoa and B. Kozinsky, Effect of salt concentration on ion clustering and transport in polymer solid electrolytes: A molecular dynamics study of peo–litfsi, Chem. Mater., 2018, 30(18), 6298–6306.
56. F. S. Genier and I. D. Hosein, Effect of coordination behavior in polymer electrolytes for sodium-ion conduction: A molecular dynamics study of poly(ethylene oxide) and poly(tetrahydrofuran), Macromolecules, 2021, 54(18), 8553–8562.
57. E. Crabb, A. France-Lanord, G. Leverick, R. Stephens, Y. Shao-Horn and J. C. Grossman, Importance of equilibration method and sampling for ab initio molecular dynamics simulations of solvent–lithium-salt systems in lithium-oxygen batteries, J. Chem. Theory Comput., 2020, 16(12), 7255–7266.
58. X. Rozanska, P. Ungerer, B. Leblanc, P. Saxe and E. Wimmer, Automatic and systematic atomistic simulations in the medea® software environment: Application to eu-reach, Oil Gas Sci. Technol., 2015, 70(3), 405–417.
59. M. J. Tillotson, N. I. Diamantonis, C. Buda, L. W. Bolton and E. A. Müller, Molecular modelling of the thermophysical properties of fluids: expectations, limitations, gaps and opportunities, Phys. Chem. Chem. Phys., 2023, 25, 12607–12628.
60. htpmd source code, https://github.com/tri-amdd/htp_md.
61. A. Khajeh, D. Schweigert, S. B. Torrisi, L. Hung, B. D. Storey and H.-K. Kwon, Early prediction of ion transport properties in solid polymer electrolytes using machine learning and system behavior-based descriptors of molecular dynamics simulations, Macromolecules, 2023, 56(13), 4787–4799.
62. R. L. Snyder, Y. Choo, K. W. Gao, D. M. Halat, B. A. Abel, S. Sundararaman, D. Prendergast, J. A. Reimer, N. P. Balsara and G. W. Coates, Improved li+ transport in polyacetal electrolytes: Conductivity and current fraction in a series of polymers, ACS Energy Lett., 2021, 6(5), 1886–1891.
63. Qi Zheng, D. M. Pesko, B. M. Savoie, K. Timachova, A. L. Hasan, M. C. Smith, T. F. Miller III, G. W. Coates and N. P. Balsara, Optimizing ion transport in polyether-based electrolytes for lithium batteries, Macromolecules, 2018, 51(8), 2847–2858.
64. M. A. Webb, B. M. Savoie, Z.-G. Wang and T. F. Miller III, Chemically specific dynamic bond percolation model for ion transport in polymer electrolytes, Macromolecules, 2015, 48(19), 7346–7358.
65. İ. Bayrak Pehlivan, C. G. Granqvist and G. A. Niklasson, Ion conduction mechanism of nanocomposite polymer electrolytes comprised of polyethyleneimine–lithium bis(trifluoromethylsulfonyl)imide and silica, Electrochim. Acta, 2014, 119, 164–168.
66. D. Yang, H. Yang, X. Guo, H. Zhang, C. Jiao, W. Xiao, P. Guo, Q. Wang and D. He, Robust polyethylenimine electrolyte for high performance and thermally stable atomic switch memristors, Adv. Funct. Mater., 2020, 30(50), 2004514.
67. S. J. Pritam, A. Arya and A. L. Sharma, Selection of best composition of na+ ion conducting peo-pei blend solid polymer electrolyte based on structural, electrical, and dielectric spectroscopic analysis, Ionics, 2020, 26(2), 745–766.
68. M. L. Lehmann, G. Yang, J. Nanda and T. Saito, Well-designed crosslinked polymer electrolyte enables high ionic conductivity and enhanced salt solvation, J. Electrochem. Soc., 2020, 167(7), 070539.
69. N. A. Stolwijk, M. Wiencierz, C. Heddier and J. Kösters, What can we learn from ionic conductivity measurements in polymer electrolytes? a case study on poly(ethylene oxide) (peo)–nai and peo–litfsi, J. Phys. Chem. B, 2012, 116(10), 3065–3074 , PMID: 22316082..
70. D. Mohanty, S.-Y. Chen and I.-M. Hung, Effect of lithium salt concentration on materials characteristics and electrochemical performance of hybrid inorganic/polymer solid electrolyte for solid-state lithium-ion batteries, Batteries, 2022, 8(10), 173.
71. K. Kimura, J. Motomatsu and Y. Tominaga, Highly concentrated polycarbonate-based solid polymer electrolytes having extraordinary electrochemical stability, J. Polym. Sci., Part B: Polym. Phys., 2016, 54(23), 2442–2447.
72. T. Yoon, N. Chapman, D. M. Seo and B. L. Lucht, Lithium salt effects on silicon electrode performance and solid electrolyte interphase (sei) structure, role of solution structure on sei formation, J. Electrochem. Soc., 2017, 164(9), A2082.
73. D. M. Halat, R. L. Snyder, S. Sundararaman, Y. Choo, K. W. Gao, Z. J. Hoffman, B. A. Abel, L. S. Grundy, M. D. Galluzzo and M. P. Gordon, et al., Modifying li+ and anion diffusivities in polyacetal electrolytes: a pulsed-field-gradient nmr study of ion self-diffusion, Chem. Mater., 2021, 33(13), 4915–4926.
74. L. Chen, J. Kern, J. P. Lightstone and R. Ramprasad, Data-assisted polymer retrosynthesis planning, Appl. Phys. Rev., 2021, 8(3), 031405.
75. J. Chai, Z. Liu, J. Zhang, J. Sun, Z. Tian, Y. Ji, K. Tang, X. Zhou and G. Cui, A superior polymer electrolyte with rigid cyclic carbonate backbone for rechargeable lithium ion batteries, ACS Appl. Mater. Interfaces, 2017, 9(21), 17897–17905 , PMID: 28488847..
76. Z. Li, L. Wang, M. Yu, Y. Liu, B. Liu, Z. Sun, W. Hu and G. Zhu, Lithium-rich porous aromatic framework-based quasi-solid polymer electrolyte for high-performance lithium ion batteries, ACS Appl. Mater. Interfaces, 2022, 14(48), 53798–53807 , PMID: 36441518..
77. A. Vöge, V. Deimede, F. Paloukis, S. G. Neophytides and J. K. Kallitsis, Synthesis and properties of aromatic polyethers containing poly (ethylene oxide) side chains as polymer electrolytes for lithium ion batteries, Mater. Chem. Phys., 2014, 148(1–2), 57–66.
78. D. Zhang, L. Zhang, K. Yang, H. Wang, C. Yu, D. Xu, B. Xu and L.-M. Wang, Superior blends solid polymer electrolyte with integrated hierarchical architectures for all-solid-state lithium-ion batteries, ACS Appl. Mater. Interfaces, 2017, 9(42), 36886–36896 , PMID: 28985458..
79. N. Ihrner and M. Johansson, Improved performance of solid polymer electrolytes for structural batteries utilizing plasticizing co-solvents, J. Appl. Polym. Sci., 2017, 134(23) DOI:10.1002/app.44917.
80. Q. Liu, G. Yang, X. Li, S. Zhang, R. Chen, X. Wang, Y. Gao, Z. Wang and L. Chen, Polymer electrolytes based on interactions between [solvent-li+] complex and solvent-modified polymer, Energy Storage Mater., 2022, 51, 443–452.
81. I. Shaji, D. Diddens, N. Ehteshami, M. Winter and J. R. Nair, Multisalt chemistry in ion transport and interface of lithium metal polymer batteries, Energy Storage Mater., 2022, 44, 263–277.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00293h

‡ These authors contributed equally.

---