Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Data efficiency of classification strategies for chemical and materials design†
Quinn M.
Gallagher
 and
Michael A.
Webb
and
Michael A.
Webb
 *
*
Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: mawebb@princeton.edu
First published on 3rd December 2024
Abstract
Active learning and design–build–test–learn strategies are increasingly employed to accelerate materials discovery and characterization. Many data-driven materials design campaigns require that materials are synthesizable, stable, soluble, recyclable, or non-toxic. Resources are wasted when materials are recommended that do not satisfy these constraints. Acquiring this knowledge during the design campaign is inefficient, and many materials constraints transcend specific design objectives. However, there is no consensus on the most data-efficient algorithm for classifying whether a material satisfies a constraint. To address this gap, we comprehensively compare the performance of 100 strategies for classifying chemical and materials behavior. Performance is assessed across 31 classification tasks sourced from the literature in chemical and materials science. From these results, we recommend best practices for building data-efficient classifiers, showing the neural network- and random forest-based active learning algorithms are most efficient across tasks. We also show that classification task complexity can be quantified by task metafeatures, most notably the noise-to-signal ratio. These metafeatures are then used to rationalize the data efficiency of different molecular representations and the impact of domain size on task complexity. Overall, this work provides a comprehensive survey of data-efficient classification strategies, identifies attributes of top-performing strategies, and suggests avenues for further study.
1 Introduction
Computational workflows are increasingly used to design materials more efficiently than the trial-and-error nature of traditional laboratory discovery.1–3 These workflows often utilize high-throughput screening or design-of-experiments strategies applied to automated laboratory equipment and computational models. Examples include the design of π-conjugated peptides for organic electronics,4 metal–organic frameworks for gas separation,5 small molecules for organic light-emitting diodes,6 phase-separating intrinsically disordered proteins,7 and many others.8–15 Using active learning and Bayesian optimization (AL/BO), these campaigns have produced materials with desired figures of merit despite characterizing a small fraction of the possible design space. Such workflows promise to drastically accelerate materials discovery in increasingly complex spaces.Materials optimization often targets a constrained domain. Consequently, resources can be wasted on candidates unsuitable for further characterization. Common constraints on materials domains include synthesizability, unwanted phase behavior, instability, and toxicity. For example, when surveying a polymer library for enzyme-stabilizing candidates, Tamasi et al. encountered phase-separating or aggregating polymers unsuitable for physical assays with the target enzyme.9 Likewise, Körbel et al. surveyed 1276 hybrid organic-inorganic halide perovskites of the form A+B2+X3−, from which only 203 compounds were considered stable for further density functional theory calculations.16 An et al. sought to find peptide sequences that would form condensed phases and disparate dynamical properties,7 yet no phase-separating systems were identified in an initial survey of 1266 peptides listed in the DisProt database.17 Ideally, such behavior would be known or predicted from the outset and incorporated into the data-selection process for any given design campaign. Additionally, knowledge of materials classification can be applied across varied design objectives. Therefore, a viable strategy is to allocate a portion of the resource budget to accurately classify viability within a materials domain, avoiding wasted resources on unsuitable candidates. To maximize resource use, it is desirable to use a data-selection strategy and classification algorithm that achieves the highest accuracy with the fewest measurements.
Numerous and varied classification schemes can be found across the literature. Terayama et al. used uncertainty-based active learning to build phase diagrams of H2O, glass-ceramic glazes, block copolymers, and more18–20 using label propagation, a semi-supervised machine learning model.21 Citing the computational expense of the label propagation algorithm, Telleria-Allika et al. used a random forest-based active learning scheme to build magnetic and covalency phase diagrams for few electron Hooke atoms and helium dimers.22 Dai and Glotzer used active learning based on a Gaussian process least-squares classifier and a novel acquisition function to learn the phase diagram of active Brownian particles and quasi-crystals.23 Hickman et al. used Gaussian processes to simultaneously classify viability and optimize performance for several materials design tasks, including small molecule drugs and perovskites.24 Focusing on the low-data regime, Bhat and Kitchin used heuristics, rather than active learning, to identify classification boundaries in several engineering problems, asserting that active learning would be ineffective in their low-data limit.25 Other works have continued the trend of applying novel active learning schemes to custom design tasks.26–30 The diversity of considered tasks and proposed algorithms indicates no consensus on what constitutes an optimal approach or how to select reasonable strategies.
Here, we investigate the performance of various algorithms across a set of 31 classification tasks primarily sourced from chemical and materials science. From these results, we identify algorithms that perform optimally and the attributes that lead to maximum data efficiency. We also explore approaches to building classification algorithms that are robust to task variation. To explain algorithm performance across tasks, we demonstrate that metafeatures (i.e., properties of classification tasks) predict an algorithm's performance, with a few metafeatures strongly correlating with classification accuracy regardless of algorithm choice. Additional metafeature analysis demonstrates why a limited set of physico-chemical descriptors can outperform common high-dimensional representations and also highlights the influence of domain size on task complexity. Through this study, we identify best practices for selecting data-efficient classification algorithms and explain why these practices improve performance.
2 Overview of strategies
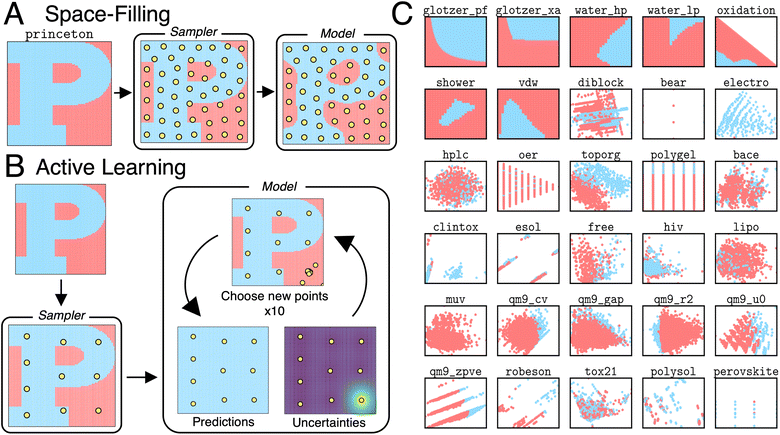
We consider space-filling and active learning algorithms, both of which rely on a sampler and a model. Space-filling algorithms (Fig. 1A) use the sampler to select a batch of points. The model is then trained on this batch and used to make predictions on the rest of the task domain. The accuracy of the algorithm is measured by comparing the predicted labels of the model to the ground truth labels. In this way, space-filling algorithms rely on a one-shot data selection scheme. Active learning algorithms (Fig. 1B) use the sampler to select an initial batch of points. The model is trained on these points and used to compute the predicted labels and uncertainties of all points in the task domain. A new batch of points is chosen based on the most uncertain points. Model training, uncertainty calculations, and batch selection are repeated until the total allowable number of points is reached. The accuracy of the algorithm is measured by comparing the predicted labels of the final model to the ground truth labels. In this way, active learning algorithms rely on an iterative, rather than one-shot, data selection scheme. Considering multiple samplers and models produces a combinatorial space of 100 space-filling and active learning algorithms that are applied to a diverse set of 31 binary classification tasks (mostly) relevant to chemical and materials science. The tasks are visualized in Fig. 1C. Further details on the tasks, samplers, models, batch selection schemes, and accuracy metrics are provided in Methods.3 Methods
3.1 Tasks
Task domains vary in size (285–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and dimensionality (2–14). For active learning algorithms, batch sizes are chosen for each classification task so that less than 10% of the task domain and a maximum of 100 points is sampled. A description of the included tasks and their sources is included in Table 1. Briefly, tasks include the classification of phase behavior in active Brownian particles, polymer systems, and water; figures of merit in metal alloys, catalysts, and perovskites; performance of experimental equipment for high-performance liquid chromatography and additive manufacturing; and small-molecule properties like aqueous solubility, band gap, heat capacity, and others.
000) and dimensionality (2–14). For active learning algorithms, batch sizes are chosen for each classification task so that less than 10% of the task domain and a maximum of 100 points is sampled. A description of the included tasks and their sources is included in Table 1. Briefly, tasks include the classification of phase behavior in active Brownian particles, polymer systems, and water; figures of merit in metal alloys, catalysts, and perovskites; performance of experimental equipment for high-performance liquid chromatography and additive manufacturing; and small-molecule properties like aqueous solubility, band gap, heat capacity, and others.
| Name | Size | Dim. | Domain | Label | Ref. |
|---|---|---|---|---|---|
| bace | 1513 | 10 | Small molecules | Inhibition of human β-secretase 1 | 31 |
| bear | 1800 | 4 | 3D-printed structures | High mechanical toughness | 32 |
| clintox | 1480 | 10 | Small molecules | FDA approval | 31 |
| diblock | 5376 | 3 | Diblock copolymers | Lamellar phase | 33 |
| electro | 285 | 4 | Electrocatalysts | High stability | 34 |
| esol | 1128 | 10 | Small molecules | Low aqueous solubility | 31 |
| free | 642 | 10 | Small molecules | Low hydration free energy | 31 |
| glotzer_pf | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | ABP phase diagram (constant PF) | Phase separating | 23 |
| glotzer_xa | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | ABP phase diagram (constant xA) | Phase separating | 23 |
| hiv | 7215 | 10 | Small molecules | Active HIV inhibitors | 31 |
| hplc | 1385 | 5 | HPLC process parameters | Low photodegradation | 35 |
| lipo | 4200 | 10 | Small molecules | Low lipophilicity | 31 |
| muv | 5000 | 10 | Small molecules | Toxicity | 31 |
| oer | 2121 | 6 | OER catalysts | Low overpotential | 36 |
| oxidation | 1275 | 2 | Ternary alloys | Oxidation susceptibility | 25 |
| perovskite | 1276 | 14 | Perovskites | Stability | 24 |
| polygel | 9856 | 9 | Polymethacrylates | Predicted solubility | |
| polysol | 6524 | 11 | Common polymers and solvents | Solubility | 37 |
| princeton | 6390 | 2 | Princeton “P” | Inside the “P” | |
| qm9_cv | 6695 | 10 | Small molecules | Low CV | 38 |
| qm9_gap | 6695 | 10 | Small molecules | Low band gap | 38 |
| qm9_r2 | 6695 | 10 | Small molecules | Low spatial extent | 38 |
| qm9_u0 | 6695 | 10 | Small molecules | Low internal energy at 0 K | 38 |
| qm9_zpve | 6695 | 10 | Small molecules | Low ZPVE | 38 |
| robeson | 353 | 10 | Linear homopolymer membranes | Above the 1999 Robeson bound | 39 |
| shower | 625 | 2 | Flow rates | Satisfactory temperature | 25 |
| toporg | 1342 | 8 | Polymer topologies | Low radius of gyration | 40 |
| tox21 | 7831 | 10 | Small molecules | Toxicity | 31 |
| vdw | 625 | 2 | Thermodynamic conditions | Phase separation | 25 |
| water_hp | 625 | 2 | Thermodynamic conditions (high P) | Ice | 19 |
| water_lp | 625 | 2 | Thermodynamic conditions (low P) | Liquid water | 19 |
Some tasks require a molecular representation. For these tasks, molecules are represented as the ten most informative physico-chemical features calculated by the Mordred descriptor calculator41 for the given property. The chosen descriptors are selected by training a logistic regression model with an L1 loss on the full dataset, with molecules represented by all available Mordred descriptors, and keeping the ten descriptors with the largest absolute coefficients. This scheme emulates molecular design campaigns that use a set of expert-informed features as a molecular representation.42 Viable alternatives to this choice of molecular representation, like graphs43 and physics-informed structural representations,44 are not considered in this study. The impact of alternative molecular representations is examined in Section 4.7.
Some tasks are prepared from datasets with continuous properties. For these datasets, the task is to classify elements of the domain with property values below the 20th percentile of the property distribution. Some tasks, like those derived from QM9,38 are taken from large datasets that would be too computationally intensive for exhaustive consideration in our high-throughput survey. If such datasets have continuous properties as labels, we subsample the dataset with stratification to preserve the property distribution. If such datasets have discrete properties as labels, we subsample the dataset, such that the minority class is approximately 20% of the observations. While the high-throughput survey is restricted to datasets with domain sizes of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 or fewer, the impact of domain size is further examined in Section 4.8.
000 or fewer, the impact of domain size is further examined in Section 4.8.
3.2 Samplers
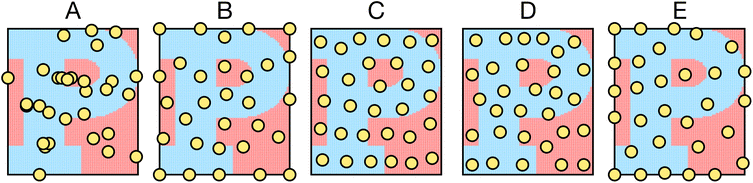
Five samplers are considered for generating complete datasets for space filling or initial datasets for active learning. These are referred to as (i) random, (ii) maximin, (iii) medoids, (iv) max entropy, and (v) Vendi samplers. For demonstrative purposes, Fig. 2 shows the points selected by these five samplers on the princeton dataset. These samplers represent different data-selection paradigms from the field of “Design of Experiments”,45 including geometry, information theory, and diversity. Common alternatives like Latin hypercube sampling46 and Sobol sequences47 are not considered due to their applicability only on (hyper)cubic domains, which differ from the non-cubic domains present in many of the materials spaces considered here. Extension of such approaches may be feasible, in certain scenarios, but not facile. Thus, we restrict our testing to approaches that can be readily applied, irrespective of the input space.While the random sampler chooses points at random, non-random samplers choose points that optimize a specific metric. Maximin sampling, also called furthest-point sampling, sequentially selects points that maximize the minimum Euclidean distance between the current point and all previously chosen points. A medoids sampler chooses the centroids produced by the k-medoids algorithm, which selects a set of points that minimizes the average squared Euclidean distance between any point in the domain to a point in the sample. A max entropy sampler, a method created by Paiva,48 chooses a maximally informative set of points by sequentially selecting the point in the domain x* to solve
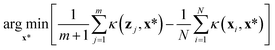 | (1) |
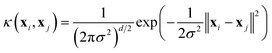 | (2) |
3.3 Models
Models include random forests (RFs), gradient boosted decision trees (XGBs), support vector machines (SV), label propagation (LP), neural networks (NNs), Gaussian processes (GPs), and Bayesian kernel density estimation (BKDE). Models predict labels and uncertainties on the task domain. For models without inherent uncertainty estimates (XGBs and NNs), ensembles of models are built using bootstrap aggregation to calculate uncertainties. Gaussian processes are implemented as both least-squares classifiers (GPRs) and as classifiers with a Bernoulli likelihood (GPCs) using both isotropic and anisotropic (ARD) squared exponential kernels.51 The uncertainties of GPRs use the scheme developed by Dai and Glotzer in ref. 23. All models are subject to hyperparameter tuning after each new batch of data is selected. A full description of the chosen models and hyperparameter tuning is available in the ESI (see Section S1†).The BKDE model is inspired by the Gryffin52 and Phoenics53 algorithms. The kernel density of each point is measured using the outputs of a Bayesian autoencoder fit to the training data. Specifically, the kernel density at point x due to a measured point xk can be written as:
 | (3) |
 | (4) |
3.4 Batch selection
All active learning algorithms use the “Kriging believer” scheme to select batches of points.54 The Kriging believer scheme operates as follows. First, uncertainties are computed across the domain, and the point with the highest uncertainty is added to the training set. The model then assumes its prediction for that point is correct and retrains accordingly. Updated uncertainties are then recomputed on the domain to identify the next point with the greatest uncertainty. This process is repeated until the desired batch size is reached. Hyperparameter tuning is not repeated during retraining with assumed labels.For BKDE-based active learning algorithms, a custom batch-selection scheme is used due to the computational expense of refitting BKDE to new data. We define ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) k(x) = ρk(x)/ρk,max as the normalized kernel density, so that
k(x) = ρk(x)/ρk,max as the normalized kernel density, so that ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) k(x) ∈ [0, 1].
k(x) ∈ [0, 1]. ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) k(x) represents the influence of point xk on every point x in the domain with a value between 0 and 1. Before batch selection, the uncertainties of every point in the domain are computed, denoted u0(x). Batch selection begins by selecting the point with the highest uncertainty, denoted x1. When this point is selected,
k(x) represents the influence of point xk on every point x in the domain with a value between 0 and 1. Before batch selection, the uncertainties of every point in the domain are computed, denoted u0(x). Batch selection begins by selecting the point with the highest uncertainty, denoted x1. When this point is selected, ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 1(x) is computed. The uncertainties are then recomputed by reducing their magnitude by a factor proportional to the influence of x1 at that point, producing a new uncertainty function u1(x) = u0(x) × (1 −
1(x) is computed. The uncertainties are then recomputed by reducing their magnitude by a factor proportional to the influence of x1 at that point, producing a new uncertainty function u1(x) = u0(x) × (1 − ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 1(x)). By consequence, uncertain points uninfluenced by x1 remain uncertain, while those near x1 are less likely to be chosen. The point x2 that maximizes u1(x) is then chosen, and the process is repeated until the desired batch size is reached. This method allows for a diverse batch of points to be selected by BKDE-based active learning algorithms without retraining the model for each acquired point.
1(x)). By consequence, uncertain points uninfluenced by x1 remain uncertain, while those near x1 are less likely to be chosen. The point x2 that maximizes u1(x) is then chosen, and the process is repeated until the desired batch size is reached. This method allows for a diverse batch of points to be selected by BKDE-based active learning algorithms without retraining the model for each acquired point.
3.5 Metrics
Classification accuracy is assessed using the Macro F1 score for its robustness to class imbalance, equal weighting of precision and recall, and use in prior studies.19 For a given class, the F1 score is defined as: | (5) |
For any given task, what differentiates “good” from “bad” Macro F1 scores can be ambiguous. Inspired by the use of random selection as a baseline in optimization literature,55 we define a new metric, ξ, as the number of randomly selected points a nearest neighbor classifier requires to achieve the same Macro F1 score as the specified algorithm. We further define ξmax as the maximum ξ achieved by any algorithm on the task. Then, ξ/ξmax describes how close an algorithm is to the best performance on a given task. Metrics like ξ and ξ/ξmax quantify efficiency in terms of resources saved by employing a given algorithm compared to a naive approach.
3.6 Metafeatures analysis
Algorithm performance on tasks is predicted based on metafeatures of the task. Metafeatures include basic characteristics of a classification task (e.g., dimensionality, dataset size, class proportion), information theory-based properties (e.g., feature entropies, mutual information, noise-to-signal ratio), and properties quantifying task complexity (e.g., Fisher's discriminant ratio, feature efficiency, hub score).56 A total of 213 metafeatures, computable by the PyMFE Python package,57 are considered.Predictive metafeatures for each algorithm are identified by fitting a linear regression model of metafeatures to the algorithm's 31 Macro F1 scores across all tasks. A minimal set of predictive metafeatures common to all algorithms is determined using sequential feature addition. Sequential feature addition starts by constructing linear models of individual metafeatures for all algorithms. The metafeature ψ1 that results in the lowest mean absolute error (MAE) is added to the set of selected metafeatures, with MAE computed via leave-one-out cross-validation. The process is repeated with combinations of ψ1 and additional metafeatures, adding the metafeature ψ2 that results in the lowest MAE. This iterative process continues until MAE decreases by less than 1%. The final set of metafeatures {ψi} is used to build maximally predictive linear models of algorithm performance across tasks. BKDE-based algorithms are excluded from this analysis due to the inability of metafeatures to predict their performance.
4 Results and discussion
4.1 Active learning with neural networks and random forests generally outperforms other strategies
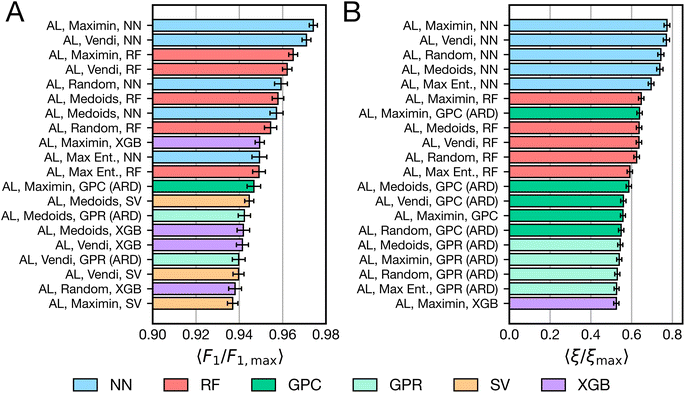
All combinations of samplers and models (totaling 100 algorithms) were applied as space-filling and active learning algorithms to all tasks in Fig. 1C. This process was repeated with 30 different random seeds to assess performance variability due to stochastic factors such as sampler initialization, model random states, and hyperparameter tuning. Performance was assessed in terms of overall accuracy and in terms of data efficiency.Fig. 3A shows the 20 highest-performing algorithms, by accuracy, as measured by average relative Macro F1 score across all tasks for ten rounds of active learning. NN- and RF-based active learning algorithms are the most accurate classifiers regardless of sampler choice, representing 10 out of the top 11 algorithms. Most variants of XGB-based active learning algorithms are also present in the top 20, along with a few GP- and SV-based active learning algorithms. Space-filling algorithms are notably missing from the top performers, suggesting the value of iterative data acquisition, which is further analyzed in Section 4.3. The choice of sampler does not clearly affect performance of these algorithms, with roughly equal representation of all samplers. The presence of all NN- and RF-based active learning algorithms in the top 20 suggests that choice of model is more important than choice of sampler. While the results are statistically robust, we note that the top 20 most accurate algorithms differ in relative Macro F1 scores by at most ca. 0.04; the practical implication of such a difference would require additional external evaluation.
To better characterize the data efficiency of algorithms, we consider 〈ξ/ξmax〉, the performance relative to a naive algorithm that achieves equivalent accuracy. For example, on a given task, an algorithm may achieve a Macro F1 score of 0.7, while the best algorithm achieves a Macro F1 score of 0.8. The naive method may require 1000 measurements to reach the score of the first algorithm and 2000 measurements to match the best algorithm. In this case, the value of ξ/ξmax is given by 1000/2000 = 0.5. This process can be repeated for each random seed of every algorithm applied to each task, enabling estimation of 〈ξ/ξmax〉 across all tasks.
Fig. 3B ranks the top 20 algorithms by 〈ξ/ξmax〉 for all tasks after ten rounds of active learning. Fig. 3B shows that NN-based active learning algorithms are the clear top performers, regardless of sampler, when using this metric. RF-based active learning algorithms follow closely behind, followed by a variety of Gaussian process-based active learning methods. Compared to Fig. 3A, the metric in Fig. 3B provides greater stratification in algorithm performance for high values of Macro F1. As F1 scores tend to 1.0, more and more points are required by a naive algorithm to improve its accuracy, which is reflected only by small increases in Macro F1 score. When appropriately weighting the relative “effort” required for getting a high-resolution understanding of the task, NN-based active learning algorithms emerge as a consistent top performer. However, the maximum value of 〈ξ/ξmax〉 achieved by any algorithm is less than 0.8, indicating that even the top-performing algorithms are not necessarily optimal for many tasks.
The ordering in Fig. 3 reflects an average across all tasks and specifically follows after ten rounds of active learning. Variants of Fig. 3 for different subsets of tasks and fewer points selected are available in the ESI (see Section S2†). We find that performance varies depending on the dimensionality of the tasks. Fig. S1† shows that when only low-dimensional tasks (d ≤ 8) are considered, NN-based active learning algorithms greatly outperform all alternatives. Fig. S2† shows that when higher dimensional tasks are considered (d > 8), tree-based algorithms perform better, and there is not a clear advantage to using either NN- or RF-based active learning algorithms.
Fig. S3–S5† show how the results in Fig. 3 change when fewer points are selected. At only three rounds of active learning, space-filling algorithms with a variety of models are present in the top 20 algorithms (Fig. S3†). The top space-filling algorithm, which uses the medoids sampler and neural network model, remains in the top 20 until five rounds of active learning (Fig. S4†), closely followed by GP-based space-filling algorithms. NN-based active learning algorithms are the top-performing algorithms for three rounds of active learning onwards, while RF-based active learning algorithms do not emerge as the clear second best choice until five rounds of active learning. Results are mostly consistent with Fig. 3 for seven rounds of active learning (Fig. S5†). Therefore, the results of Fig. 3 are consistent for many rounds of active learning, but when few batches have been selected, NN-based active learning algorithms are optimal.
From these results, we suggest using NN- or RF-based active learning algorithms for building accurate classification models on domains with a limited experimental budget. RFs seem preferred for higher-dimensional tasks. This guidance seemingly runs counter to conventional wisdom regarding the relative ineffectiveness of neural networks in low-data regimes and the common utilization of Gaussian processes for AL/BO. It may be interesting to consider whether prior studies (such as ref. 18, 20 and 23–25) might be more data-efficient by opting for a different strategy.
4.2 Many algorithms fail to perform well across all tasks
While the preceding analysis shows that selecting an optimal strategy a priori can be challenging, we find certain algorithms are consistently “suboptimal.” We define performance as suboptimal if ξ/ξmax < 0.9 for every task. Fig. 4 displays the fraction of suboptimal algorithms based on algorithm type and model choice. Of the 100 algorithms studied, 61 are suboptimal. Space-filling algorithms are more often suboptimal compared to active learning algorithms. Among active learning algorithms, model choice significantly affects performance. NN- and RF-based active learning algorithms are never suboptimal, while BKDE- and LP-based active learning algorithms are always suboptimal. SV- and isotropic GPC-based active learning schemes are also commonly suboptimal. | ||
| Fig. 4 Summary of suboptimal algorithms. Algorithms are considered suboptimal if ξ/ξmax < 0.9 on every task. Data is stratified by algorithm type and model choice. | ||
The poor performance of BKDE-based algorithms may be attributed to several factors. First, unlike GPs and SVs, BKDE does not use training labels when estimating kernel densities, reducing predictive accuracy. Second, BKDE relies on a Bayesian autoencoder to estimate kernel densities, which can be inaccurate with limited training data. Third, BKDE's kernel density estimates rapidly decay to zero with distance, leading to high uncertainties across much of the task domain. This causes BKDE-based active learning algorithms to fail in prioritizing points near classification boundaries, reducing accuracy. Consequently, BKDE-based active learning and space-filling algorithms perform similarly across tasks.
The poor performance of LP-based algorithms is likely due to two reasons. First, LP models assign classes to unlabeled points based on neighboring labeled points defined by Euclidean distance. Unlike anisotropic GPs, XGBs, RFs, and NNs, LP models do not have a mechanism to ignore irrelevant features. Second, LP models assign high uncertainties to points near an identified classification boundary but not to points far from those already chosen. As a result, LP models can miss classification boundaries not initially discovered by the sampler. This likely explains why space-filling LP algorithms outperform active learning LP algorithms. Other methods address this issue by explicitly increasing the uncertainty of distant points (e.g., GPs) or using model ensembles to encourage uncertainties in less sampled regions (e.g., RFs, NNs, XGBs).
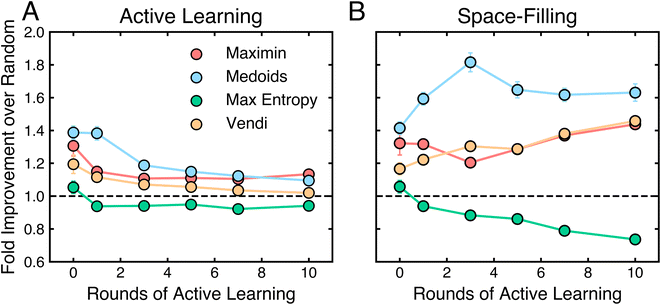
4.3 Space filling occasionally outperforms active learning
Fig. 3 and 4 together suggest that active learning, or iterative data selection, is more data-efficient than one-shot space filling. To quantify this, we compare the performance of every seed of every active learning algorithm to that of the space-filling algorithm with the same seed, sampler, and model. For each number of points selected on each task, we compute how often the active learning variant outperforms the space-filling variant.Fig. 5 shows that active learning does not always outperform space filling, especially with few rounds of active learning. In the first round, active learning outperforms space filling in less than 50% of cases, suggesting little initial benefit. This fraction increases to about 65% by round 10. To avoid misleading results from poorly performing models, we also analyze the top-performing models from Fig. 3B. In this case, active learning outperforms space filling about 50% of the time in the first round, increasing to nearly 80% by round 10. While active learning generally outperforms space filling, these results indicate that an arbitrary active learning scheme may not always surpass its space-filling variant on a given task.
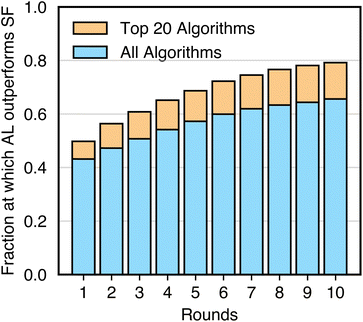 | ||
| Fig. 5 Controlled comparison of active learning (AL) and space filling (SF). Data corresponds to the fraction of instances that AL outperforms SF when using the same sampler, model, and seed. Data is also stratified for different rounds of AL. For a given round of AL, the AL algorithm is compared to a SF algorithm that has selected the same number of points. The fractions considering all sampler, model, and seed choices are shown in blue. The fractions considering only the top 20 sampler, model, and seed choices in Fig. 3B include the blue and orange bars. Statistics are aggregated over all tasks. | ||
The results in Fig. 5 depend on the tasks considered. Some tasks (e.g., princeton, tox21, electro) deviate from aforementioned trends (Fig. S6–S8†). In these cases, space-filling algorithms consistently outperform active learning algorithms. We note that these are also among the most difficult classification tasks, as indicated by the mean performance of all algorithms. When all algorithms struggle, the performance gap between active learning and space filling is less meaningful. Additionally, datasets like princeton have complex classification boundaries that benefit from allocating more experimental budget to exploring the task domain rather than refining an already discovered boundary.
Based on these results, we recommend using active learning algorithms for data-efficient classifiers but acknowledge that factors such as (i) the number of active learning rounds and (ii) the expected complexity of the classification task can influence the relative performance of active learning and space filling. Determining the optimal choice of active learning, space filling, or combinations thereof is left for future work.
4.4 Sampler choice has disparate impact on active learning versus space filling
The role of initial data selection is an often overlooked aspect of active learning algorithms and their outcomes. To assess this impact, we compare the performance of each active learning algorithm with non-random samplers to the same algorithm with a random sampler across all tasks after 10 rounds of active learning. Here, the performance metric is ξ, as defined in Methods.Fig. 6 shows the impact of sampler choice on performance for both active learning and space-filling algorithms. For active learning algorithms (Fig. 6A), sampler choice has a minor effect, with maximin and medoids samplers providing a slight improvement over random sampling, though the difference diminishes with increasing rounds of active learning. Vendi and max entropy samplers perform similarly to or worse than random sampling, with max entropy showing lower performance overall. In contrast, for space-filling algorithms (Fig. 6B), the medoids sampler consistently outperforms other options at all training set sizes, while maximin and Vendi samplers are only modestly better than random sampling. Here, the max entropy sampler also performs worse than random selection. Notably, sampler choice has a more sustained influence in space-filling algorithms than in active learning, where additional rounds of selection reduce the initial impact of the sampler. These results suggest that while active learning reduces the dependency on the initial sampling strategy over time, for space-filling algorithms, the medoids sampler provides the most robust performance across training set sizes. Thus, the medoids sampler is recommended for both active learning algorithms with limited rounds and for space-filling algorithms generally.
4.5 Model ensembles provide robust performance
Given that the maximum 〈ξ/ξmax〉 in Fig. 3B is only about 0.77, we hypothesized that more data-efficient classification algorithms could be developed using ensembling. Based on observed performance, we consider ensemble-based algorithms featuring NNs, RFs, and anisotropic GPCs. Several ensembling strategies were considered, including treating model choice as a hyperparameter, “stacking” models to combine predictions and uncertainties, and “arbitrating” by using the model with the lowest uncertainty for each prediction, and others58 (see ESI, Section S4†). From this survey, treating model choice as a hyperparameter was found to be the best-performing scheme, and all “Ensemble” results in the main text refer to this method.Fig. 7A shows the relative performance based on 〈ξ/ξmax〉 of NN-, RF-, and ensemble-based active learning algorithms across all tasks. While ensembles rank among the top-performing algorithms, they do not consistently outperform NN-based active learning algorithms. However, the results in Fig. 7 are task-dependent, suggesting that ensemble-based active learning may be beneficial for certain types of tasks.
To determine if ensemble-based active learning algorithms outperform NN- and RF-based algorithms on specific tasks, we analyze two task sets. Fig. 7B shows tasks where NN-based algorithms are the top performers (n = 9). Fig. 7C shows tasks where RF-based algorithms excel (n = 10). Ensemble schemes generally outperform individual models on tasks for which they are not optimal. This effect is strongest for tasks where NN-based algorithms excel and less pronounced for RF-based tasks. Thus, using ensemble-based active learning may mitigate the risk of selecting a suboptimal model for any given task.
4.6 Metafeatures are predictive of task difficulty
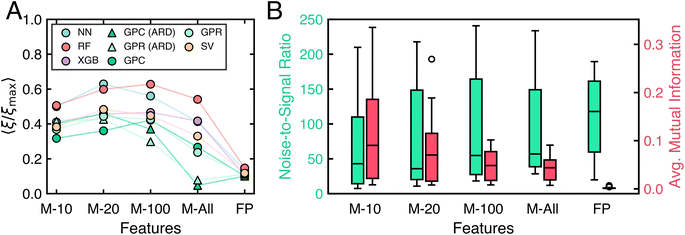
To understand the factors behind algorithm performance variability across tasks, we identify metafeatures that predict learning algorithm accuracy. This approach allows us to quantify what makes one classification task more challenging than another.Fig. 8 shows that a limited set of task metafeatures identified by sequential feature addition can reasonably predict task complexity. Fig. 8A shows results of using just four metafeatures (noise-to-signal ratio,56 maximum weighted distance between two points in the task domain,59 maximum mutual information between features and labels, and the performance of the linear discriminant classifier) to predict the accuracy of all algorithms across all tasks. To reduce the influence of poorly performing algorithms, the same analysis is performed using just the top 20 algorithms. This yields Fig. 8B, which uses noise-to-signal ratio, the average mutual information between features and labels, and the performance of the naive Bayes classifier. In both cases, simple linear models based on these few features capture the data well.
The particular metafeatures selected resonate with intuition. Noise-to-signal ratio is the most predictive metafeature of algorithm performance across all tasks. Linear models using only this ratio achieve an MAE of 11.260% and R2 = 0.619 for all algorithms, and an MAE of 8.370% and R2 = 0.696 for top-performing algorithms. Tasks with low noise-to-signal ratios require fewer measurements because each measurement provides valuable information about labels. Related to the noise-to-signal ratio, mutual information and the performance of the naive Bayes classifier indicate how useful individual features are for predicting labels. When features are individually predictive of labels, less data is required for accurate predictions than for tasks where features are uninformative. The maximum weighted distance between point pairs59 likely identifies outliers in the task domain, which require more measurements to account for their influence. The performance of the linear discriminant classifier indicates the linear separability of a task. Linearly separable tasks have simple classification boundaries, requiring less data for accurate prediction. In simple and expected terms, less data is needed to train accurate models for tasks with informative features, few outliers, and linearly separable classes.
4.7 Low-dimensional representations with molecular descriptors improve data efficiency
The preceding analysis represents molecules using a feature vector of the ten Mordred descriptors most correlated with the target property. However, many machine learning applications in chemical sciences use higher-dimensional representations (d ≈ 1000), such as extended vectors of physico-chemical properties41 or molecular fingerprints.60 To evaluate how featurization strategies impact algorithm performance on molecular tasks, we apply the same set of active learning and space-filling algorithms to 13 molecular classification tasks using these different representations. Specifically, we compare representations using the 10, 20, or 100 Mordred descriptors most correlated with the property of interest, all available Mordred descriptors, and 1024-dimensional Morgan fingerprints.61 BKDE- or LP-based algorithms are excluded due to poor prior performance. For Morgan fingerprints, all Euclidean distance metrics are replaced with Tanimoto distances as necessary. Vendi-based space-filling algorithms are also excluded for Morgan fingerprints due to high computational cost.Fig. 9A shows the performance of active learning algorithms, grouped by model type, for different molecular feature sets after ten rounds of active learning. Increasing the number of Mordred descriptors from 10 to 20 or 100 generally improves performance. However, using all available Mordred descriptors often leads to only slight gains or even notable performance drops compared to using just 10 descriptors. Replacing 10 Mordred descriptors with 1024 bit Morgan fingerprints significantly reduces performance for all algorithms. Tree-based models (i.e., RF and XGB) exhibit smaller declines in performance with larger feature sets than neural networks or kernel-based methods, consistent with the observed superiority of tree-based models over deep learning models on high-dimensional, tabular datasets.62
To elucidate the results of Fig. 9A, we examine distributions of noise-to-signal ratio and average mutual information values obtained across tasks for each representation (Fig. 9B). As the number of Mordred descriptors increases, the noise-to-signal ratio distribution shifts upward, indicating more uncorrelated variation in the feature vectors relative to the property of interest. In contrast, Morgan fingerprints exhibit a consistently higher noise-to-signal ratio than Mordred descriptors. Conversely, the average mutual information decreases as more Mordred descriptors are added, with Morgan fingerprints displaying markedly low mutual information across all tasks, as expected for binary fingerprints. These trends suggest that larger feature sets introduce more noise, complicating model training by requiring more complex functions to predict outputs accurately. Consequently, data efficiency declines as models must process additional, often irrelevant, information. These findings support the use of minimal feature sets highly correlated with the property of interest to maximize data efficiency in classification tasks, aligning with recent work highlighting the effectiveness of using fewer features for molecular property prediction.63
4.8 Relative performance remains consistent across larger domain sizes
For computational expediency, the number of prospective samples in the task domain was limited to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidates or fewer for analysis up to this point. However, active learning is often considered for much larger domains. To evaluate the impact of domain size, we assessed the performance of selected algorithms (again excluding LP- and BKDE-based algorithms due to expense and prior performance) when applied to an expanded domains of five tasks (glotzer_pf, water_lp, qm9_gap, qm9_r2, and qm9_cv). For glotzer_pf and water_lp, we increased the resolution of phase diagrams to expand the domain to 100
000 candidates or fewer for analysis up to this point. However, active learning is often considered for much larger domains. To evaluate the impact of domain size, we assessed the performance of selected algorithms (again excluding LP- and BKDE-based algorithms due to expense and prior performance) when applied to an expanded domains of five tasks (glotzer_pf, water_lp, qm9_gap, qm9_r2, and qm9_cv). For glotzer_pf and water_lp, we increased the resolution of phase diagrams to expand the domain to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 samples. For the QM9 datasets, we used the full set of 133
489 samples. For the QM9 datasets, we used the full set of 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 molecules rather than a subset, as described in Methods.
885 molecules rather than a subset, as described in Methods.
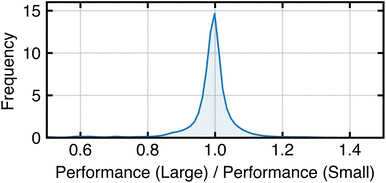
Fig. 10 shows the distribution of performance changes when domain size increases. For all tasks, the performance of each algorithm (measured by Macro F1) on the smaller domain is within the standard error of its performance on the larger domain. The symmetric shape and small bandwidth of the distribution indicate that domain size does not systematically affect algorithm performance. These results suggest that in a low-data regime, where training sets are much smaller than the domain size, domain size has little impact on the data efficiency of algorithms. We speculate this is because task complexity influences algorithm performance more than domain size. To show this, we compute metafeatures predictive of algorithm performance (as determined in Section 4.6) for both small and large versions of the tasks (Table 2). The datasets exhibit minimal changes in noise-to-signal ratio, average mutual information, and maximum mutual information with increased domain size. These findings support the idea that domain size does not inherently beget task complexity, which ultimately dictates algorithm performance.
| Task | Noise-to-signal ratio | Mutual information (mean) | Mutual information (max) | |||
|---|---|---|---|---|---|---|
| Small | Large | Small | Large | Small | Large | |
| glotzer_pf | 14.4 | 18.3 | 0.285 | 0.286 | 0.285 | 0.286 |
| water_lp | 15.7 | 27.8 | 0.179 | 0.192 | 0.210 | 0.203 |
| qm9_gap | 65.5 | 65.1 | 0.044 | 0.056 | 0.112 | 0.110 |
| qm9_r2 | 20.5 | 23.1 | 0.150 | 0.198 | 0.410 | 0.424 |
| qm9_cv | 16.4 | 21.2 | 0.198 | 0.174 | 0.402 | 0.408 |
5 Conclusion
We characterized the relative efficiency and performance of strategies for building effective machine learning classifiers with relevance across chemical and materials science. In total, 100 space-filling and active learning algorithms were evaluated across 31 classification tasks. Our findings indicated that NN- and RF-based active learning algorithms were the most data-efficient, while BKDE and LP algorithms performed poorly in comparison. Space-filling methods were competitive with active learning, particularly when few rounds of active learning were used. We also demonstrated that using the k-medoids algorithm for point selection improved accuracy over other sampling strategies in both active learning and space filling. Ensemble-based algorithms were found to perform generally well, irrespective of task. Additionally, task metafeatures were predictive of algorithm performance, with a few key metafeatures, particularly the noise-to-signal ratio, effectively quantifying classification task complexity and its relationships to task domain size as well as explaining the efficiency of low-dimensional molecular representations. These results have implications for data-driven materials design in constrained domains.This study opens several avenues for future research. Key areas for further investigation include exploring algorithm design choices not covered here, such as feature and label transformations, batch-selection schemes, and batch sizes. Additionally, applying the current findings to materials design campaigns that involve simultaneous optimization and classification, as discussed by Hickman et al.,24 could be valuable. Beyond algorithm design, incorporating domain knowledge could enhance data efficiency. Utilizing pre-trained models, incorporating priors from foundation models, and applying physical constraints on model predictions may offer significant improvements in data efficiency compared to changes in sampler or model. Specifically, constructing pre-trained material representations optimized for metafeatures predictive of algorithm performance, like the noise-to-signal ratio, could boost data efficiency across materials domains. This approach could be beneficial for both classification and regression tasks.64 Finally, establishing a unified set of classification tasks for testing would strengthen the generalizability of the findings here and for future studies.
Data availability
All code required to reproduce measurements of classification algorithm performance on all tasks is available in the following GitHub repository: https://github.com/webbtheosim/classification-suite.git. The produced data, along with scripts for reproducing the analysis presented in this work are available in the following GitHub repository: https://github.com/webbtheosim/classification-analysis.git.Author contributions
Conceptualization: Q. M. G., M. A. W. Data curation: Q. M. G. Formal analysis: Q. M. G. Funding acquisition: Q. M. G., M. A. W. Investigation: Q. M. G. Methodology: Q. M. G., M. A. W. Project administration: M. A. W. Resources: M. A. W. Software: Q. M. G. Supervision: M. A. W. Validation: Q. M. G. Visualization: Q. M. G. Writing: Q. M. G., M. A. W.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Q. M. G. acknowledges support from the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-2039656 and from the National Science Foundation under Grant No. 2118861. M. A. W. also acknowledges support from the National Science Foundation under Grant No. 2118861. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. Simulations and analyses were performed using resources from Princeton Research Computing at Princeton University, which is a consortium led by the Princeton Institute for Computational Science and Engineering (PICSciE) and Office of Information Technology's Research Computing.Notes and references
- D. Reker and G. Schneider, Drug Discovery Today, 2015, 20, 458–465 CrossRef.
- C. Kim, A. Chandrasekaran, A. Jha and R. Ramprasad, MRS Commun., 2019, 9, 860–866 CrossRef CAS.
- R. A. Patel and M. A. Webb, ACS Appl. Bio Mater., 2023, 7, 510–527 CrossRef.
- K. Shmilovich, R. A. Mansbach, H. Sidky, O. E. Dunne, S. S. Panda, J. D. Tovar and A. L. Ferguson, J. Phys. Chem. B, 2020, 124, 3873–3891 CrossRef CAS.
- Z. Yao, B. Sanchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. Farha, R. Q. Snurr and A. Aspuru-Guzik, Inverse Design of Nanoporous Crystalline Reticular Materials with Deep Generative Models, 2020, https://chemrxiv.org/engage/chemrxiv/article-details/60c74f70337d6c9a51e28124 Search PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Nat. Mater., 2016, 15, 1120–1127 CrossRef.
- Y. An, M. A. Webb and W. M. Jacobs, Sci. Adv., 2024, 10, eadj2448 CrossRef.
- M. Reis, F. Gusev, N. G. Taylor, S. H. Chung, M. D. Verber, Y. Z. Lee, O. Isayev and F. A. Leibfarth, J. Am. Chem. Soc., 2021, 143, 17677–17689 CrossRef CAS.
- M. J. Tamasi, R. A. Patel, C. H. Borca, S. Kosuri, H. Mugnier, R. Upadhya, N. S. Murthy, M. A. Webb and A. J. Gormley, Adv. Mater., 2022, 34, 2201809 CrossRef CAS PubMed.
- E. A. Pogue, A. New, K. McElroy, N. Q. Le, M. J. Pekala, I. McCue, E. Gienger, J. Domenico, E. Hedrick, T. M. McQueen, B. Wilfong, C. D. Piatko, C. R. Ratto, A. Lennon, C. Chung, T. Montalbano, G. Bassen and C. D. Stiles, npj Comput. Mater., 2023, 9, 1–8 CrossRef.
- G. Wu, H. Zhou, J. Zhang, Z.-Y. Tian, X. Liu, S. Wang, C. W. Coley and H. Lu, Nat. Synth., 2023, 2, 515–526 CrossRef CAS.
- I. J. Gomez, J. Wu, J. Roper, H. Beckham and J. C. Meredith, ACS Appl. Polym. Mater., 2019, 1, 3064–3073 CrossRef CAS.
- R. Kumar, N. Le, Z. Tan, M. E. Brown, S. Jiang and T. M. Reineke, ACS Nano, 2020, 14, 17626–17639 CrossRef CAS PubMed.
- S. Kosuri, C. H. Borca, H. Mugnier, M. Tamasi, R. A. Patel, I. Perez, S. Kumar, Z. Finkel, R. Schloss, L. Cai, M. L. Yarmush, M. A. Webb and A. J. Gormley, Adv. Healthcare Mater., 2022, 11, 2102101 CrossRef CAS PubMed.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Nat. Commun., 2021, 12, 2312 CrossRef CAS PubMed.
- S. Körbel, M. A. L. Marques and S. Botti, J. Mater. Chem. A, 2018, 6, 6463–6475 RSC.
- A. Hatos, B. Hajdu-Soltész, A. M. Monzon, N. Palopoli, L. Álvarez, B. Aykac-Fas, C. Bassot, G. I. Benítez, M. Bevilacqua, A. Chasapi, L. Chemes, N. E. Davey, R. Davidović, A. K. Dunker, A. Elofsson, J. Gobeill, N. S. G. Foutel, G. Sudha, M. Guharoy, T. Horvath, V. Iglesias, A. V. Kajava, O. P. Kovacs, J. Lamb, M. Lambrughi, T. Lazar, J. Y. Leclercq, E. Leonardi, S. Macedo-Ribeiro, M. Macossay-Castillo, E. Maiani, J. A. Manso, C. Marino-Buslje, E. Martínez-Pérez, B. Mészáros, I. Mičetić, G. Minervini, N. Murvai, M. Necci, C. A. Ouzounis, M. Pajkos, L. Paladin, R. Pancsa, E. Papaleo, G. Parisi, E. Pasche, P. J. B. Pereira, V. J. Promponas, J. Pujols, F. Quaglia, P. Ruch, M. Salvatore, E. Schad, B. Szabo, T. Szaniszló, S. Tamana, A. Tantos, N. Veljkovic, S. Ventura, W. Vranken, Z. Dosztányi, P. Tompa, S. C. E. Tosatto and D. Piovesan, Nucleic Acids Res., 2020, 48, D269–D276 CAS.
- K. Terayama, K. Tsuda and R. Tamura, Jpn. J. Appl. Phys., 2019, 58, 098001 CrossRef CAS.
- K. Terayama, R. Tamura, Y. Nose, H. Hiramatsu, H. Hosono, Y. Okuno and K. Tsuda, Phys. Rev. Mater., 2019, 3, 033802 CrossRef CAS.
- K. Terayama, K. Han, R. Katsube, I. Ohnuma, T. Abe, Y. Nose and R. Tamura, Scr. Mater., 2022, 208, 114335 CrossRef CAS.
- X. Zhu and Z. Ghahramani, Learning from labeled and unlabeled data with label propagation, Technical Report CMU-CALD-02-107, Carnegie Mellon University, 2002 Search PubMed.
- X. Telleria-Allika, J. M. Mercero, X. Lopez and J. M. Matxain, AIP Adv., 2022, 12, 075206 CrossRef CAS.
- C. Dai and S. C. Glotzer, J. Phys. Chem. B, 2020, 124, 1275–1284 CrossRef CAS.
- R. Hickman, M. Aldeghi and A. Aspuru-Guzik, 2023, https://chemrxiv.org/engage/chemrxiv/article-details/651bd338a69febde9e23dd1c.
- M. Bhat and J. R. Kitchin, Ind. Eng. Chem. Res., 2023, 62, 15326–15339 CrossRef CAS.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 21 CrossRef.
- J. He, X. Su, C. Wang, J. Li, Y. Hou, Z. Li, C. Liu, D. Xue, J. Cao, Y. Su, L. Qiao, T. Lookman and Y. Bai, Acta Mater., 2022, 240, 118341 CrossRef CAS.
- R. Katsube, K. Terayama, R. Tamura and Y. Nose, ACS Mater. Lett., 2020, 2, 571–575 CrossRef CAS.
- S. Dasetty, I. Coropceanu, J. Portner, J. Li, J. J. d. Pablo, D. Talapin and A. L. Ferguson, Mol. Syst. Des. Eng., 2022, 7, 350–363 RSC.
- Y. Tian, R. Yuan, D. Xue, Y. Zhou, Y. Wang, X. Ding, J. Sun and T. Lookman, Adv. Sci., 2021, 8, 2003165 CrossRef CAS.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530 RSC.
- A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, Sci. Adv., 2020, 6, eaaz1708 CrossRef PubMed.
- A. Arora, T.-S. Lin, N. J. Rebello, S. H. M. Av-Ron, H. Mochigase and B. D. Olsen, ACS Macro Lett., 2021, 10, 1339–1345 CrossRef CAS.
- M. Kodera and K. Sayama, Digital Discovery, 2023, 2, 1683–1687 RSC.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. E. Yunker, J. E. Hein and A. Aspuru-Guzik, ChemOS: An Orchestration Software to Democratize Autonomous Discovery, 2018, https://chemrxiv.org/engage/chemrxiv/article-details/60c73d939abda2181df8b72d Search PubMed.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen, E. Liles, J. E. Hein and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2021, 2, 035021 Search PubMed.
- J. G. Ethier, R. K. Casukhela, J. J. Latimer, M. D. Jacobsen, B. Rasin, M. K. Gupta, L. A. Baldwin and R. A. Vaia, Macromolecules, 2022, 55, 2691–2702 CrossRef CAS.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- Q. Yuan, M. Longo, A. W. Thornton, N. B. McKeown, B. Comesaña-Gándara, J. C. Jansen and K. E. Jelfs, J. Membr. Sci., 2021, 627, 119207 CrossRef CAS.
- S. Jiang, A. B. Dieng and M. A. Webb, npj Comput. Mater., 2024, 10, 139 CrossRef CAS.
- H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminf., 2018, 10, 4 Search PubMed.
- N. Angello, D. Friday, C. Hwang, S. Yi, A. Cheng, T. Torres-Flores, E. Jira, W. Wang, A. Aspuru-Guzik, M. Burke, C. Schroeder, Y. Diao and N. Jackson, Nature, 2024, 633, 351–358 CrossRef CAS PubMed.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- R. Fisher, The design of experiments, Oliver and Boyd Ltd, Edinburgh: Tweeddale Court, 2nd edn, 1937 Search PubMed.
- M. D. McKay, R. J. Beckman and W. J. Conover, Technometrics, 1979, 21, 239–245 Search PubMed.
- I. M. Sobol', USSR Comput. Math. Math. Phys., 1967, 7, 86–112 CrossRef.
- A. R. C. Paiva, 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 2017, pp. 2088–2095 Search PubMed.
- B. W. Silverman, Density estimation for statistics and data analysis, Chapman & Hall/CRC, Boca Raton, Fla., 1st edn, 1998 Search PubMed.
- D. Friedman and A. B. Dieng, The Vendi Score: A Diversity Evaluation Metric for Machine Learning, arXiv, 2023, preprint, arXiv:2210.02410 [cond-mat, stat], DOI:10.48550/arXiv:2210.02410.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, MIT Press, Cambridge, Mass, 2006 Search PubMed.
- F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Applied Physics Reviews, 2021, 8, 031406 CrossRef.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145 CrossRef PubMed.
- D. Ginsbourger, R. Le Riche and L. Carraro, A Multi-points Criterion for Deterministic Parallel Global Optimization based on Gaussian Processes, 2008 Search PubMed.
- R. Turner, D. Eriksson, M. McCourt, J. Kiili, E. Laaksonen, Z. Xu and I. Guyon, arXiv, 2021, preprint, arXiv:2104.10201v2 [cs, stat], DOI:10.48550/arXiv.2104.10201.
- Machine learning, neural and statistical classification, ed. D. Michie, Ellis Horwood, New York, 1st edn, 1995 Search PubMed.
- E. Alcobaça, F. Siqueira, A. Rivolli, L. P. F. Garcia, J. T. Oliva and A. C. P. L. F. d. Carvalho, J. Mach. Learn. Res., 2020, 21, 1–5 Search PubMed.
- P. Brazdil, J. N. Van Rijn, C. Soares and J. Vanschoren, Metalearning: Applications to Automated Machine Learning and Data Mining, Springer International Publishing, Cham, 2022 Search PubMed.
- R. Vilalta, Proceedings of the ICML-99 workshop on recent advances in meta-learning and future work, 1999, pp. 3–9 Search PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS.
- H. L. Morgan, J. Chem. Doc., 1965, 5, 107–113 CrossRef CAS.
- L. Grinsztajn, E. Oyallon and G. Varoquaux, arXiv, 2022, preprint, arXiv:2207.08815 [cs, stat], DOI:10.48550/arXiv.2207.08815.
- T. Jin, V. Singla, H.-H. Hsu and B. M. Savoie, Faraday Discuss., 2024 10.1039/D4FD00113C.
- M. Aldeghi, D. E. Graff, N. Frey, J. A. Morrone, E. O. Pyzer-Knapp, K. E. Jordan and C. W. Coley, J. Chem. Inf. Model., 2022, 62, 4660–4671 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00298a |
| This journal is © The Royal Society of Chemistry 2025 |