High-throughput robotic collection, imaging, and machine learning analysis of salt patterns: composition and concentration from dried droplet photos

Abstract

Macroscopic deposit patterns resulting from dried solutions and dispersions are often perceived as random and without meaningful information. Their formation is governed by a bewildering interplay of evaporation, crystal nucleation and growth, capillary flows, Marangoni convection, diffusion, and heat exchange that severely hinders mechanistic studies. It is therefore remarkable that the patterns contain subtle clues about the chemical nature of the original solution. To utilize this information, extensive reference image libraries and advanced analysis methods are essential. For this purpose, we developed a robotic drop imager (RODI) that, under non-stop operation, produces up to 2500 high-resolution images of sample deposits daily. Utilizing RODI, we have assembled an initial library of 23 417 images for seven inorganic salts and five concentration levels. Each image is analyzed and distilled into 47 metric values that capture distinct characteristics of the deposit patterns. This compact dataset is utilized for machine learning and artificial intelligence training, specifically with Random Forest, XGBoost, and a deep learning multi-layer perceptron. We achieved prediction accuracies of 98.7% for the salt type and 92.2% for the combined salt type and initial concentration. Expanded databases will likely enable the rapid identification of broad compositional features from mere photographic images, with possible applications ranging from phone-based apps to field-based analytical and lab safety tools.

---

1 Introduction

Microscopic chemical processes can drive profound transformations in the macroscopic world that manifest as unexpected dynamics and complex patterns.^1–4 However, chemistry's ability to provoke and program such events remains largely unexplored and even modern biological research has deemphasized morphogenetic studies in favor of molecular and machine-like descriptions.^5,6 This knowledge gap is in stark contrast to the intellectual and technological potential of this causal micro-to-macro chain that for living systems orchestrates cells and organisms from molecular events.⁷ The advent of laboratory automation and machine learning/artificial intelligence, however, provides powerful tools to study these intriguing connections.^8–10

Two essential components of such length scale and complexity escalation are far-from-equilibrium conditions and transport processes such as diffusion, fluid flow, and active motion.^11,12 The far from equilibrium thermodynamic state does not necessarily require the continuous supply of reactants or energy, but can often be reached as a long-lived transient along the system's path toward equilibrium. The transport modes promote mixing and spatial homogenization but in conjunction with nonlinear processes can create steep gradients and patterns. This counterintuitive effect is evident in the Turing instability¹ and impacts crystal growth and other solidification events, such as periodic Liesegang bands, fingering instabilities during directional melt solidification, and dendritic electrodeposition.^13–16

A pattern-forming process that at first glance appears exceedingly simple, is the drying of solution and dispersion drops on nonporous, horizontal surfaces.^17–19 However, certain salts such as NH₄Cl induce salt creep during the drying of such sessile drops.²⁰ Driven by evaporation, crystallization, and capillary action, this creeping phenomenon greatly increases the footprint of the drops and the resulting deposit.²¹ Another counter-intuitive example is the coffee-ring effect that occurs when a drop with small suspended particles dries on a flat surface.^22,23 The ring of dry particulate matter results from the pinning of the contact line and flow that transports particles to the edge of the evaporating drop. In many crystallizing solutions, the patterns formed can be complex, ranging from isolated small crystals to dendritic structures or featureless disks.^19–21

Previous studies have demonstrated that the deposit patterns formed by drying droplets might reveal compositional features of the employed solution,^24,25 including tap water²⁶ and alcoholic beverages.²⁷ For human tears, the drying patterns have been suggested as an inexpensive diagnostic tool for conditions such as dry-eye disease, where the resulting fern-like structures are indicative of the tear's composition.²⁸ Similarly, blood drops from patients with various medical conditions, including leukemia and anemia, tend to form distinctive patterns upon drying, potentially serving as diagnostic markers.^29,30 In addition, mixtures of KCl or KCl/MgCl₂ solutions with urine produce drop deposits that deep neural networks can potentially analyze to diagnose bladder cancer.³¹

Our team recently applied these ideas to a set of deposit patterns of 42 different, mainly inorganic salts.³² Based on 7500 images, we identified distinct pattern families including the NaCl–KCl–KBr group which shows compact deposits with small crystals and the RbCl–NaNO₃–NH₄Cl group of creeping salts. In addition, we showed that the chemical composition can be accurately predicted from the deposit pattern with a surprisingly high degree of accuracy reaching 75% even for small training sets of 14 images and >90% for larger sets. The study also revealed possible complications for the analysis of salt mixtures, which likely will require substantially large image libraries.

The analysis employed in this earlier work was based on the extraction of 16 image metrics that allowed us to represent each deposit pattern as a characteristic point in a 16-dimensional morphospace. These metrics were calculated from binary image versions that only distinguished the dark background from the bright deposit. Specific metrics included the total salt area, the total area of salt-free holes, their ratio, the number of connected salt areas, and the eccentricity of the salt area based on a fitted ellipse. In the Z-scored version of this morphospace, the deposits of different salts form well-separated regions despite the, sometimes strong, variations among individual deposit patterns.

While providing a relatively large set of images (available at ref. 33), our study was limited by the time required for manually pipetting the drops and positioning the resulting deposits for subsequent photography. In addition, the work is highly repetitive and prone to undesired variations in the release height and angle of the drop onto the sample substrates. For example, Lippi et al. reported a mean inter-individual imprecision of 8.1% for pipetting 10 μL volumes.³⁴ Further exploration of this morphogenic analysis method would therefore benefit from automated approaches.

Here, we report the construction of an automated system that creates 676 drops per run and subsequently records high-resolution photos of the deposit patterns. Using this robotic drop imager, we study the concentration-dependencies of seven different salts based on a total of over 23 000 images. We also describe an expanded set of 47 metrics and demonstrate that machine learning (ML) methods can predict both the salt type and concentration with high fidelity.

2 Experimental methods

All salts were used as received. We prepared solutions in water by continuously adding and stirring the respective salt into high-purity water (Barnstead EASYpure UV, resistivity of 18.3 MΩ cm) until no further solute could be dissolved as indicated by the presence of undissolved salt particles. Then these saturated solutions were diluted to the desired percentages. The suppliers and purity levels for all salts were: ammonium chloride (NH₄Cl, Fisher Scientific: Certified A.C.S.); sodium chloride (NaCl, Sigma-Aldrich: A.C.S. reagent); potassium chloride (KCl, Fisher Scientific: Certified A.C.S.); sodium sulfate (Na₂SO₄, Fisher Chemical: Certified A.C.S.); potassium nitrate (KNO₃, Sigma-Aldrich: A.C.S. reagent); sodium sulfite (Na₂SO₃, Sigma-Aldrich: 98%); sodium nitrate (NaNO₃, Fisher Scientific: Certified A.C.S.).

We performed all experiments at ambient conditions in a climate-controlled laboratory. The temperature and relative humidity (RH) were monitored with two identical probes (ThermoPro sensors). The times required for solvent evaporation depended on the employed salt and sample drop, varying between 2 and 18 h; the typical wait time was 3 h. These times were judged by visual inspection of the deposit patterns.

3 Results and discussion

3.1 Robotic drop imager (RODI)

3.1.1 Basic components. RODI is housed in an air-conditioned laboratory ensuring temperatures of 21.0 ± 0.5 °C and a relative humidity between 40 and 50%. While not essential, it is mounted on an optical table that dampens mechanical vibrations. An overview photo is shown in Fig. 1. Excluding the PC, the construction cost was about US$5000 of which US$2000 was spent on RODI's main camera and lens. A detailed list of RODI's parts and suppliers is provided in the ESI (see also Fig. S1 and Table S1†). All 3D printed parts were produced in-house on a Creality Ender 3 device from polylactic acid filaments.

Fig. 1 Photo of the robotic drop imager RODI. The main components include a motorized two-dimensional positioning system to which a camera and a dispensing system are mounted. The photo also shows the electronic control interface (top) and the syringe pump (right). The width of the optical table is 1.2 m.

The main component of RODI is a two-dimensional positioning system consisting of three linear ball-screw guides with a stroke range of 1 m and an accuracy of up to ±0.03 mm (Fuyu FSK40). The table-mounted x-drive uses two rails and stepper motors, while the elevated y-drive operates with one stepper motor. The three motors (NEMA 23) are connected to motor controllers (MECCANIXITY 4 A). The controllers are connected to an external power supply (Corsair RM1000E) and an Arduino Uno board (Rev 3). The Arduino is interfaced with a personal computer allowing full control of the set-up's positioning via the Arduino IDE 2.0.4 software. The corresponding Arduino control script and the Tinkercad OBJ files are available for download at GitHub.³⁵ Four stop-contacts are mounted at the ends of the y-rail and one of the x-rails to avoid instrument damage.

Mounted to the y-drive is the heart of the instrument, consisting of a camera and fluid-delivery unit, which appear rear- and front-mounted in Fig. 1, respectively. The 24.3 MP full-frame mirrorless camera (Nikon Z5) uses a high-quality macro lens (Nikkor Z MC 105 mm f/2.8). Mounted to the lens is a 3D-printed hood with 50 internal white LED lights, illuminating the drop deposit at a low angle from all directions. The delivery unit consists of a disposable pipette tip (10 μL, Corning microvolume pipet tips) with a conical shape and an approximate hole diameter of 400 μm. It is connected to a syringe pump (New Era Pump Systems, Inc.) located on a small adjacent table. The pump's syringe (20 mL, NORM-JECT Luer Solo) via a ∼3 m long tubing (Saint-Gobain, Tygon, ID 1/16′′, OD 1/8′′, wall 1/32′′) and a disposable glass capillary (Pasteur style). The connection between tip and glass capillary is secured by a 3D-printed adapter. If excessive pressure builds up in the injection system, leakage will occur at this adapter and will not contaminate the y-rail or other sensitive components.

A small 3D-printed case positions a white LED (5 mm) and a photocell (GL5516, 5 mm CdS photoresistor) at a distance of 7 mm from the location of the growing drops (Fig. 2). This holder moves with the delivery system and measures the light reflected from the drop if present. The voltage of the photocell is monitored by the Arduino board. The tubing and the electric wires for all LEDs and the photocell are contained in a towline (two black drag chains, see Fig. 1) above the y-rail that prevents sharp bends and minimizes wear.

Fig. 2 (a) Image sequence of pendant solution drops expanding and detaching. (b) Close-up photo showing RODI's pipette tip and LED-photocell detector. (c) Voltage signal of the photocell (blue) and the drops' local image intensity as recorded by an auxiliary video camera (red). The sharp decrease corresponds to the detachment of a drop.

RODI delivers the solution drops onto four glass panes (HOME4, fulfilled by Amazon), each measuring 40.5 × 40.5 × 0.3 cm³. The use of four units allows for easier removal and washing of the glass substrate in between runs. They are held by 16 3D-printed posts, secured within the holes of the optical table. These posts create a gap of 10 mm to a black cardboard background which is slightly out-of-focus for the main camera. Additional components include a large post next to the optical table for guiding the moving wires and tubing as well as a webcam on top of this post that we occasionally use for live streaming of experiments.³⁶

3.1.2 Operation. RODI has two main modes of operation, drop production and deposit imaging. The delivery of the drops utilizes the principle of a “dripping faucet”, which is much simpler than alternative techniques based on automatic pipettes that load and eject predetermined volumes.

As a controlled experiment, the dripping faucet is a classic physics problem. For decreasing flow rates, its flow behavior changes from the release of a steady jet to individual droplets.³⁷ While the rhythm of the drop detachment can show deterministic chaos and quasi-periodic behavior, it is typically periodic.³⁸ The critical drop volume V_c at detachment follows from the balance of the downward directed weight force and the force due to the surface tension γ, which holds the pendant liquid to the faucet's orifice of radius r. This balance is expressed by Tate's law³⁹

2πrγ = FρV_cg, (1)

where ρ and g are the solution density and the acceleration due to gravity, respectively. Empirical equations for the correction factor F ⪅ 1 have been reported elsewhere and also include minor flow-rate dependencies.^40–42

During drop production, the main camera is off and the pump delivers solution to the pipette tip at a constant flow rate of typically 12 mL h⁻¹. This rate causes drops to form at the tip, expand, and detach at a frequency of 12–16 drops per min (Fig. 2a). The vertical distance between the pipette tip and the glass substrate is 7.5 mm. The detachment event is detected by the aforementioned photocell (Fig. 2b) as a sudden drop in voltage (Fig. 2c) or precisely a voltage below a threshold value around 2.5 V. Once this decrease is registered by our control software, the motors move the solution dispenser to the next target site. This movement step requires 2.4 s, which is sufficiently short to ensure that the next drop is released from a stationary pipette tip. The distance between the target sites is 3.0 cm in both the x- and y-direction. To avoid the drop release over or near the seams of the four glass panels, we carefully control the starting position, offsetting it by Δx = Δy = 1.5 cm from the outer corner.

Following the drop production stage, we wait for at least 2 h for all drops to dry. Depending on the salt solution's equilibrium relative humidity⁴³ and the deposit characteristics, some samples require longer drying times (see Fig. S2† for such an example). Once no visual changes in the deposit patterns are detected anymore, we proceed to the imaging stage which commences with the manual positioning of the camera over the first deposit pattern. Then, our software moves to the 3 cm spaced target sites, waits 2.6 s for minor vibrations of the camera and set-up to diminish, and then automatically acquires a photo. The image acquisition software (digiCamControl) and Arduino script are currently not integrated and require appropriately timed initiation. The total imaging phase lasts 1 h.

3.1.3 Performance. As our facile drop delivery method differs from conventional approaches, we performed numerous measurements of the generated drop volumes. For these tests, individual drops were collected on microscope slides and quickly transferred to a microbalance (Mettler-Toledo XSR105). Results for all salt solutions studied are shown in Fig. S3.† Overall, the drop weight distributions yield small standard deviations of not more than 4% of the mean volume, which is significantly smaller than the errors generated by humans pipetting comparable volumes.³⁴ After measurement of the solution densities and conversion of weights to volumes, we also noticed small but statistically significant differences between the average volumes of the salts. We attribute this finding to slightly different surface tensions and densities of the solutions that affect the volume V_c of the drops detaching from the pipette tip (see eqn (1)). To compensate at least partially for this small but undesired effect, we decrease the pump rate from 12 mL h⁻¹ to values as low as 10 mL h⁻¹ for Na₂SO₃. This semi-quantitative adjustment is performed based on measuring the weight of a few drops prior to the run. We also note that the dependence of V_c on the tip radius r should allow for variations of the drop volumes if desired.

Excluding early tests, we performed over 30 runs with RODI to date. While all of these runs completed satisfactorily, yielding over 600 images each, we noticed one undesired performance issue. On occasion, we observed a smeared-out appearance of the deposit, which indicates a millimeter-scale movement of the solution drop prior to settling as well as occasional small satellite deposits that were caused by splashing. These data correspond to less than 1% of all drops imaged and were removed by visual inspection (see Fig. S4 and Table S2†), although automatic exclusion during image processing could easily be integrated by demanding a sufficiently centered deposit centroid. Furthermore, we believe that careful reduction of the drops' fall height (currently 3.0 mm) could further reduce the already low image rejection rate.

3.2 A 23 000-image dataset

Over only two months, we used RODI to collect a library of over 23 000 high-resolution photos of dried salt solutions. On a typical day, two runs were performed, requiring intervention only for the preparation of the solution and the clean-up of the four glass panes. The resulting image library comprises data for seven salts at five concentrations each. These 35 categories are represented by a maximum of 676 images, corresponding to the 26 × 26 layout of drops created by RODI during one run. After the removal of smeared-out drop deposits, the image library is comprised of 23 417 photos. These high-resolution, uncropped, and unprocessed images are available for free downloading at ref. 44. The photos are organized by salt with each zipped set equaling about 14 GB (average).

Fig. 3 shows representative sample images for the different experimental categories with the initial salt concentration increasing in the downward direction and each column representing the specified salt. The first impression confirms the expectation that higher concentrations create more precipitate than lower ones. For each given salt, a qualitative comparison of the images further suggests that the main characteristics are preserved regardless of the employed concentration. For example, NaCl and KCl form small crystallites that often appear cubic and either clump together near the original drop center or arrange along a ring-like curve. NH₄Cl shows the strongest tendency to creep, meaning that its deposit area is much larger than the footprint of the initial solution drop. Na₂SO₄ forms a dense ring-like deposit for all concentrations studied while the ring diameter increases with increasing concentration. A similar feature in KNO₃, however, emerges only for higher concentrations while its needle-like appearance is always discernible.

Fig. 3 Representative deposit patterns formed by seven different salts (columns) at five different initial concentrations (rows). The concentration values are given as vol/vol percent of the saturated salt solution. Saturation concentrations are given in Table S3.† The scale bar (lower right) denotes 1 cm and applies to all panels.

While the photos in Fig. 3 aim to represent the most common pattern types for each salt and concentration, differences exist between the individual samples. These differences are predominantly due to the stochastic nature of crystallization, the sensitivity of Marangoni flow patterns, and possibly other minor factors such as imperfections of the glass substrate, vibrations, and airflow. To provide a qualitative indication of the pattern variations, randomly selected sets of ten deposit photos are shown for each salt and concentration in Fig. S5–S11.†

RODI's camera system acquires photos of the deposit patterns at a high spatial resolution (see Table S4†) and quality that is not discernible in the image collection of Fig. 3. In Fig. 4, we therefore show magnified views of the deposits obtained at the highest concentration of 90%. These images confirm the presence of cubic crystallites in the deposit patterns of NaCl and KCl, but also reveal intricate details for the other salts. For example, NH₄Cl features a multitude of very small, cell-like structures (most likely crystals) that scatter light at their grain boundaries. This architecture is visually reminiscent of a web or foam and dominant in the periphery of the overall deposit (compare Fig. 3). The brighter core consists of larger needle-like crystals that can be aligned locally and create larger salt-free inclusion that appear as dark holes. Na₂SO₄ shows dendritic features that are reminiscent of tiny brushes. These and other characteristics at small length scales contribute to the fingerprint-like nature of the salts' deposit patterns.

Fig. 4 Magnified views of deposit patterns created by the seven salts at 90% concentration. These examples demonstrate the intricate nature of the patterns and high quality of RODI's image data. Samples are not identical to those in Fig. 3. Field of view: 5 × 5 mm².

3.3 Dimensional reduction

In our earlier study,³² we reduced each deposit photo to a binary image and then to a vector containing 16 numbers, representing different aspects of the pattern. Here, we expand the information content of this metric vector by adding 31 new characteristics to yield a 47-dimensional description of each photo. Notice that each new vector still requires less than 328 bytes, yielding a compression factor of over 30 000 compared to the 10 megabyte raw image. A complete description of the old and new metrics is given in the ESI (Table S4†), but a few key features are summarized in the following. All image analyses and machine learning tasks were performed using custom MATLAB scripts developed in-house.

3.3.1 Original metrics. The 16 original image metrics were derived after converting the raw photo to a grayscale image and applying a constant intensity threshold. This process yields a binary image distinguishing the dark background (“0”) from the brighter deposit regions (“1”). Four key metrics specify the overall deposit area (numWhitePixels), total boundary length, the number of connected bright regions, and the overall deposit's eccentricity. We also compute the distribution of the bright pixel distances from the deposit's centroid. From this radial distribution, five metrics are derived, namely the mean, median, mode, standard deviation, and skewness. Two additional values characterize the image erosion behavior, while the remaining five are related to the dark regions embedded within the bright regions.

3.3.2 New metrics. The 31 additional metrics derived from the images enhance our understanding of the deposit's structural and textural properties. These metrics, computed from either grayscale or thresholded images, offer detailed insights into various aspects of the pattern:

Edge characteristics: by measuring the density of edge points at both low and high thresholds, we gain insights into the boundary's jaggedness or smoothness. Comparisons between the total area of the precipitate and the number of edge points further elucidate the boundary's complexity relative to the overall size of the deposit.

Statistical analyses: we explore the uniformity or heterogeneity within the deposit by evaluating the standard deviation of pixel intensities across different thresholds. This analysis is complemented by metrics that focus on the shapes and sizes of the more distinct, brighter regions. These metrics provide median values for the eccentricity and area of these regions, highlighting typical dimensions and elongation.

Spatial distribution: metrics assessing the concentration and brightness within a central defined area shed light on the core density and luminance of the deposit. Additionally, the proportion of darker areas within this zone highlights the internal contrast and composition of the frequently encountered core.

Radial variations: we capture the distribution's 'tailedness' and asymmetry of intensity distributions, alongside comparisons of average intensities between different sections. This provides a detailed view of radial intensity variations throughout the deposit.

Structural complexity: the relationships between the deposit's skeletonization and its area are computed to assess connectivity, branching, and terminal structures. We also provide an estimate of the deposit's fractal dimension to quantify its structural complexity.

Textural analysis: the expanded analysis includes entropy measures that quantify the randomness and complexity of textures at multiple scales. Intensity variations along radial directions reveal differences in boundary distances and the structural highlights near the center. Moreover, texture consistency and uniformity are analyzed using correlation and energy metrics from the gray-level co-occurrence matrix, which explore the spatial dependencies of pixel intensities.

Detailed textural variations: a comprehensive examination of textural variations across different scales is presented, along with a quantification of the complexity of distinct regions within the deposit at high thresholds. This reveals the diversity and intricacy of the deposit's textural features, providing a deeper understanding of its unique characteristics.

While guided by the visual appearance of various deposit patterns, the process of developing and selecting these metrics is partly intuitive. During this process, however, we performed cursory correlation analyses on a small set of 18 images to avoid the introduction of metrics that correlate strongly with existing ones. In this context, we often found strong correlations or anti-correlations with the deposit area (i.e. numWhitePixels) and, for ten cases, minimized this connection by simple division. These metrics are log10Entropy, meanStd5, meanStd25, numContours, skeletonBranchPoints, skeletonEndPoints, skeletonLength, sumEdgesHigh, sumEdgesLow, and waveletEntropy. Future work could further expand and refine this approach by inclusion of additional metrics such as Hu moments and other methods for computer vision.^45,46

3.4 Basic analysis results

In this section, we characterize the new, expanded set of metrics in terms of averages and correlations. After extraction of the 47-dimensional metric vectors (see Fig. S12 and Table S5† for representative examples), the next processing step is the Z-scoring of each metric over the entire data set. This step sets the global mean for each metric to zero and expresses distances from this mean as multiples of the metric's standard deviation. Notice that for a given category (i.e. a salt at a specific concentration) the average of the Z-scored metrics differs from the global average.

Fig. 5a shows a heatmap of the metrics' absolute correlation matrix with red colors indicating strong correlation or anti-correlation between the respective metrics pair. Notice that the matrix is symmetric. The metrics are sorted according to their average absolute correlation with all other metrics. This ordering places metrics that are closely coupled or similar to other metrics near the top (and left), while displaying distinct metrics—that on average are unlike other metrics—near the bottom (and right). Notice that the diagonal corresponds to self-correlations which equal 1.0. Numerous details can be discerned from the heatmap in Fig. 5a. For example, we see that the metrics meanStd25 and meanStd5 are tightly correlated and hence capture closely related features of the images. More surprisingly, both of these metrics also correlate strongly with waveletEntropy.

Fig. 5 Correlation analysis of the metrics based on the Z-scored data. (a) Heatmap of the reordered absolute correlation coefficient matrix. The color scale represents the absolute value of the correlation coefficients. Metrics are sorted according to their average absolute correlations with the other metrics. Metrics listed near the bottom stand out as having little similarity to the other metrics. (b) Alternative grouping of the metrics using hierarchical clustering. The dendrogram shows relationships and groupings of the metrics. The x-axis represents the Euclidean distance calculated from the absolute correlation values, where shorter distances indicate stronger relationships and higher similarity between metrics.

Fig. 5b explores a different sorting approach that follows hierarchical clustering, placing the metrics into various families and super-families. We identify nine main groups in the dendrogram, highlighted by different colors. Revisiting the earlier example, meanStd25 and meanStd5 fall within the lowest level bracket of the blue group, indicating close similarity, and waveletEntropy joins this pair at the next bracket level. Even closer relationships are observed for the mean, median, and mode of the bright pixels' (i.e., deposit's) radial distribution around the overall pattern's centroid. A heatmap similar to Fig. 5a that reflects this hierarchical clustering is shown in Fig. S13.†

While rationalizing these groupings in detail is challenging, we can outline some underlying similarities within these families. For example, the blue family focuses on overall texture, entropy, and spatial distribution, the pink family emphasizes structural and geometrical features such as skeletonization and edge detection, and the cyan family examines intensity and compactness within the core region of the precipitate. These insights into the metrics' categories provide a possible basis for future attempts to expand or reduce the number of metrics and the information they provide.

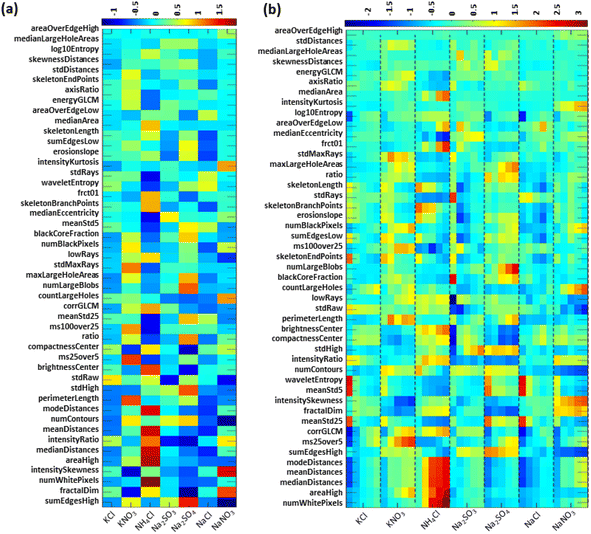
We re-state that the global average of each metric is zero for the Z-scored data set, whereas the averages for individual salts and different concentrations deviate from zero. These deviations provide additional insights into the nature of the metrics and their potential for predicting the salt type and concentration for test images. Fig. 6a shows a heatmap of the averages for the seven salts by metric, disregarding the concentration information. The metrics are sorted from top to bottom by how strongly they vary between the different salts. This ordering reveals that sumEdgesHigh, fractalDim, and numWhitePixels show the largest variability, while areaOverEdgeHigh and medianLargeHoleAreas barely distinguish between the selected salts. Furthermore, numWhitePixels, which measures the deposit area, is the largest for the expansive patterns formed by the creeping salt NH₄Cl.

Fig. 6 Category averages of the Z-scored data. Heatmaps of the averages for (a) the seven salt types regardless of concentration and (b) the 7 × 5 salts and concentrations. For each salt in (b), the concentration increases in the right direction. The metrics are sorted according to their standard deviations, with the most variable metrics appearing at the bottom.

Applying the same sorting approach, the heatmap in Fig. 6b shows the averages for all 35 categories (i.e. the seven salts and their five concentrations). Notice that, within the columns delimited by dashed lines, concentration increases from left to right. The five most varied metrics show a systematic increase with increasing concentration for all salts, most strikingly for NH₄Cl. The metrics sumEdgesHigh and numLargeBlobs are similar indicators for Na₂SO₄. These results suggest a possible determination of the solution's initial concentration solely from the final deposit pattern.

3.5 Machine learning

We employed three different ML/AI techniques to evaluate whether the salt type and original concentration can be determined from single photos of the dried deposit. The first one, Random Forest, is an ensemble learning method that constructs multiple decision trees during training and outputs the mode of the classes for classification tasks.⁴⁷ The second, XGBoost (Extreme Gradient Boosting), is an optimized gradient boosting framework that builds additive prediction models in a sequential manner.⁴⁸ This method is known for its speed and performance, but the interpretation of its results is more difficult than for Random Forest. Finally, we used a Multilayer Perceptron (MLP), which belongs to the class of feedforward artificial neural networks that consist of at least three layers of nodes: an input layer, one or more hidden layers, and an output layer, which can capture complex patterns in the data through backpropagation.⁴⁹ In all analyses, the total image library was split into 16 392 photos for training (70%) and 7025 photos for testing (30%). To prevent data leakage, Z-scoring was applied to the training data, and the resulting mean and standard deviation were then used to normalize the test data.

First, we investigated the possible identification of the salt type while disregarding the different solution concentrations. Fig. 7 shows the results of these analyses as confusion matrices for the corresponding seven categories. The two panels differ in the applied method with (a) being the results from Random Forest and (b) from XGBoost. The dark blue columns right of the two matrices show the accuracies of predicting the correct salt type that are listed along the left edge of each matrix. We find mean accuracies of (98.0 ± 0.2)% and (98.7 ± 0.1)% for (a) and (b), respectively. For the Random Forest method, most misidentifications occurred for KCl patterns which were misrepresented as either NaCl or NaNO₃. Out-of-bag error estimates indicate the use of an appropriate number of trees (N = 100, Fig. S14†). For XGBoost, the few misassignments are more equally spread out among the categories. Overall, these results are excellent, demonstrating that salt identification is possible despite varying concentrations.

Fig. 7 Confusion matrices for identifying the salt type regardless of concentration. The results follow from the ML classifier (a) “Random Forest” with 100 decision trees and (b) XGBoost. Both sets of results are based on 20 repeats with different random number seeds. We used 70% of the 23 417 sample entries for training and 30% (N = 7025) for testing. The numbers in the matrix cells denote the averages per run and the right column shows the correct predictions per salt. As obtained from the mean and standard deviation of the repeated runs, the overall accuracy is (a) (98.0 ± 0.2)% and (b) (98.7 ± 0.1)%.

Next, we used MLP, a deep learning model, to classify our data into the 35 categories that not only distinguish between the different salts but also the initial solution concentrations. The model architecture of the MLP included an input layer, followed by four fully connected layers with 1024, 512, 256, and 128 neurons, respectively. Each fully connected layer was followed by batch normalization, ReLU activation, and a dropout layer with a 50% dropout rate to prevent overfitting. The final output layer was a fully connected layer corresponding to the number of unique categories, followed by a softmax layer for classification. The model was trained using the Adam optimizer⁵⁰ with a mini-batch size of 128, an initial learning rate of 0.001, and a piecewise learning rate schedule. Early stopping was implemented with a patience of 10 epochs to avoid overfitting. The performance of the model was evaluated over 20 runs, achieving a mean accuracy of (92.2 ± 1.2)%.

Additional details are provided by the confusion matrix in Fig. 8 where the labels along the axes indicate the salt name and the percent concentration. The submatrices along the diagonal that correspond to the particular salts, are highlighted by blue boxes and show that most of the overall infrequent misassignments occur within the correct salt category. Very infrequent exceptions include KCl patterns that are misidentified as NaCl. In addition, we find that the concentration assignment is most challenging for NaNO₃. A comparison to the image examples in Fig. 3 shows that the NaNO₃ deposits for the higher concentrations are indeed very similar.

Fig. 8 Confusion matrix for identifying the salt type and the initial concentration. The results are obtained from deep learning using a Multi-Layer Perceptron (MLP) architecture. We used 70% (N = 16 392) of the 23 417 sample entries for training and 30% (N = 7025) for testing. The confusion matrix presented here represents the average results over 20 runs. The numbers in the matrix cells denote the average occurrences per run. As determined by the mean and standard deviation across the repeated runs, the overall accuracy of the model is (92.2 ± 1.2)%.

We also performed the same 35-category analysis using the Random Forest and XGBoost methods. The corresponding confusion matrices are shown in Fig. S15 and S16† and indicate results of slightly lower quality; the mean accuracies are (89.2 ± 0.4)% and (90.1 ± 0.4)%, respectively. Interestingly, XGBoost performs better at resolving the initial concentrations of NaNO₃ patterns, but worse for NaCl. Overall, all three methods are suitable approaches, with Random Forest offering rather straightforward interpretability and MLP providing the best performance.

Lastly, we computed the feature importance of our 47 metrics in the context of our Random Forest analyses (Fig. S17†). This analysis yields the highest scores for intensitySkewness, areaHigh, and stdHigh, which are scattered in the mid-section of the map in our correlation analysis (Fig. 5a), possibly indicating a compromise of uniqueness and broad coverage with respect to the features captured by the other metrics. Regarding the category averages in Fig. 6a, they fall in the lower third of the map, indicating strong variations across the salt types. These characteristics of important features might be helpful for the future formulation of further improved sets of metrics. However, since the performance of our workflow and ML/AI analysis depends on the specific salts involved, incorporating metrics that are currently of lesser importance might enhance the identification of additional salt types.

4 Conclusions

We have reported the construction of a robotic imaging setup (RODI) capable of generating large databases of patterns formed during the drying of sessile solution drops. Leveraging RODI's capabilities, we compiled a database of over 23 000 images featuring seven inorganic salts at five different concentrations. Building on earlier results, we also developed a workflow for compressing high-resolution images into 47 metrics that capture essential textural and structural features of the patterns. This overall approach enabled us to accurately determine both the salt type and initial concentration with machine learning analyses, achieving an overall accuracy of 92%. Remarkably, when concentration is disregarded, the accuracy increases to 99%.

Given the complexity of the underlying physico-chemical processes and the sometimes striking variations in patterns formed from identical solution drops, these accuracies are particularly noteworthy. This suggests that high accuracies could also be achieved for much larger sets of salts, as well as for organic compounds and biological fluids. The integration of our feature-extraction workflow with RODI's high-throughput sample collection could democratize traditionally expensive (bio)analytical measurements that are often reliant on mass spectrometry and similar specialized instruments. In an ideal scenario, these applications could be performed using solely a phone camera and an app.

Finally, our results suggest that the complexities of crystallization in drying solution drops converge on reliable pattern attractors. These “Platonic ideals” of deposit patterns and stains provide tangible targets for theoretical studies aiming to describe the multitude of involved processes.

Data availability

All images (∼96.4 GB) are deposited at https://www.chem.fsu.edu/~steinbock/saltscapes2.php. All MATLAB scripts, files with all image metrics, the Arduino script, and 3D design files are available at https://github.com/osteinbock/RODI2024. The same files are also available at https://zenodo.org/viahttps://doi.org/10.5281/zenodo.14907154.

Author contributions

Conceptualization: B. C. B. and O. S. Experimental work: B. C. B. and A. S. V. Funding acquisition: B. B. D., J. Y., and O. S. Computational analyses: B. C. B., A. S. V., and O. S. Writing—original draft: B. C. B. and O. S. Writing—review and editing: B. C. B., A. S. V., J. Y., B. B. D., and O. S.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based on work supported by NASA under grant no. 80NSSC23M0050. We thank Dr Jéssica A. Nogueira, Dr Suman Sinha Ray, Dr Ruth Agada, and Srinivasakranthikiran Kolachina for discussions.

References

1. A. M. Turing, Philos. Trans. R. Soc. London, 1952, 327, 37–72,  DOI:10.1098/rstb.1952.0012.
2. I. Prigogine and G. Nicolis, J. Chem. Phys., 1967, 46, 3542–3550,  DOI:10.1063/1.1841255.
3. A. Gierer and H. Meinhardt, Kybernetik, 1972, 12, 30–39,  DOI:10.1007/BF00289234.
4. P. Knoll, B. Ouyang and O. Steinbock, ACS Phys. Chem. Au, 2023, 4, 19–30,  DOI:10.1021/acsphyschemau.3c00050.
5. B. Alberts, Cell, 1998, 92, 291,  DOI:10.1016/S0092-8674(00)80922-8.
6. D. J. Nicholson, J. Theor. Biol., 2019, 477, 108,  DOI:10.1016/j.jtbi.2019.06.002.
7. T. C. Tang, B. An and Y. Huang, et al. , Nat. Rev. Mater., 2021, 6, 332–350,  DOI:10.1038/s41578-020-00265-w.
8. S. Back, et al. , Digital Discovery, 2024, 3, 23,  10.1039/D3DD00213F.
9. J. Lebert, M. Mittal and J. Christoph, Phys. Rev. E, 2023, 107, 014221,  DOI:10.1103/PhysRevE.107.014221.
10. G. Tom, et al. , Chem. Rev., 2024, 124, 9633–9732,  DOI:10.1021/acs.chemrev.4c00055.
11. P. Knoll and O. Steinbock, Isr. J. Chem., 2018, 58, 682–692,  DOI:10.1002/ijch.201700136.
12. W. Zhu, P. Knoll and O. Steinbock, J. Phys. Chem. Lett., 2024, 15, 5476–5487,  DOI:10.1021/acs.jpclett.4c01031.
13. M. Tanaka, S. M. Montgomery, L. Yue, Y. Wei, Y. Song, T. Nomura and H. J. Qi, Sci. Adv., 2023, 9, eade4381,  DOI:10.1126/sciadv.ade4381.
14. A. De Wit, Annu. Rev. Fluid Mech., 2020, 52, 531–555,  DOI:10.1146/annurev-fluid-010719-060349.
15. A. D. Nikolov, D. T. Wasan and P. Wu, Curr. Opin. Colloid Interface Sci., 2021, 51, 101387,  DOI:10.1016/j.cocis.2020.08.012.
16. V. Fleury, Nature, 1997, 390, 145–148,  DOI:10.1038/36522.
17. E. R. Washburn, J. Phys. Chem., 1927, 31, 1246–1248,  DOI:10.1021/j150278a009.
18. T. H. Hazlehurst Jr, H. C. Martin and L. Brewer, J. Phys. Chem., 1935, 40, 439–452,  DOI:10.1021/j150373a003.
19. N. Shahidzadeh, M. Schut and J. Desarnaud, et al. , Sci. Rep., 2015, 5, 10335,  DOI:10.1038/srep10335.
20. E. R. Townsend, W. J. P. van Enckevort, J. A. M. Meijer and E. Vlieg, Cryst. Growth Des., 2017, 17, 3107–3115,  DOI:10.1021/acs.cgd.7b00023.
21. W. J. P. van Enckevort and J. H. Los, Cryst. Growth Des., 2013, 13, 1838–1848,  DOI:10.1021/cg301429g.
22. P. Yunker, et al. , Nature, 2011, 476, 308–311,  DOI:10.1038/nature10344.
23. H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094,  DOI:10.1021/jp0609232.
24. D. Zang, S. Tarafdar, Y. Y. Tarasevich, M. D. Choudhury and T. Dutta, Phys. Rep., 2019, 804, 1–56,  DOI:10.1016/j.physrep.2019.01.008.
25. K. Sefiane, G. Duursma and A. Arif, Adv. Colloid Interface Sci., 2021, 298, 102546,  DOI:10.1016/j.cis.2021.102546.
26. X. Li, A. R. Sanderson, S. S. Allen and R. H. Lahr, Analyst, 2020, 145(4), 1511–1523,  10.1039/C9AN01624D.
27. J. González-Gutiérrez, R. Pérez-Isidoro and J. C. Ruiz-Suárez, Rev. Sci. Instrum., 2017, 88, 074101,  DOI:10.1063/1.4991818.
28. S. Akhtar, A. Masmali, A. Khan and T. Almubrad, Acta Ophthalmol., 2018, 92, 1,  DOI:10.2174/18743641-v17-e230116-2022-11.
29. T. A. Yakhno, O. A. Sedova, A. G. Sanin and A. S. Pelyushenko, Tech. Phys., 2003, 48, 399–403,  DOI:10.1134/1.1568479.
30. L. Hamadeh, S. Imran, M. Bencsik, G. R. Sharpe, M. A. Johnson and D. J. Fairhurst, Sci. Rep., 2020, 10, 3313,  DOI:10.1038/s41598-020-59847-x.
31. R. Demir, S. Koc and D. G. Ozturk, et al. , Sci. Rep., 2024, 14, 2488,  DOI:10.1038/s41598-024-52728-7.
32. B. C. Batista, S. D. Tekle, J. Yan, B. B. Dangi and O. Steinbock, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2405963121,  DOI:10.1073/pnas.2405963121.
33. Steinbock Group, SaltScapes 1.0, https://www.chem.fsu.edu/%7Esteinbock/saltscapes.php, accessed 09 September 2024.
34. G. Lippi, G. Lima-Oliveira, G. Brocco, A. Bassi and G. L. Salvagno, Clin. Chem. Lab. Med., 2017, 55, 962–966,  DOI:10.1515/cclm-2016-0810.
35. File repository, https://github.com/osteinbock/RODI2024, accessed 14 October 2024.
36. O. Steinbock, YouTube Channel @RodiOneFSU, https://www.youtube.com/@RodiOneFSU, accessed 09 September 2024.
37. B. Ambravaneswaran, H. J. Subramani, S. D. Phillips and O. A. Basaran, Phys. Rev. Lett., 2004, 93, 034501,  DOI:10.1103/PhysRevLett.93.034501.
38. H. J. Subramani, H. K. Yeoh, R. Suryo, Q. Xu, B. Ambravaneswaran and O. A. Basaran, Phys. Fluids, 2006, 18, 03106,  DOI:10.1063/1.2185111.
39. T. Tate, Philos. Mag., 1864, 27, 176–180,  DOI:10.1080/14786446408643645.
40. J. P. Garandet, B. Vinet B and P. Gros, J. Colloid Interface Sci., 1994, 165, 351–154,  DOI:10.1006/jcis.1994.1240.
41. J. C. Earnshaw, E. G. Johnson, B. J. Carroll and P. J. Doyle, J. Colloid Interface Sci., 1996, 177, 150–155,  DOI:10.1006/jcis.1996.0015.
42. M. Soni, J. Pharmacogn. Phytochem., 2019, 8, 2197–2202 . https://www.phytojournal.com/archives/2019.v8.i2.8620/a-simple-laboratory-experiment-to-measure-the-surface-tension-of-a-liquid-in-contact-with-air.
43. A. Wexler and S. Hasegawa, J. Res. Natl. Bur. Stand., 1954, 53, 19,  DOI:10.6028/jres.053.003.
44. Image repository, https://www.chem.fsu.edu/~steinbock/saltscapes2.php, accessed 14 October 2024.
45. M. K. Hu, IRE Trans. Inf. Theory, 1962, 8, 179–187,  DOI:10.1109/TIT.1962.1057692.
46. J. Serra, Image Analysis and Mathematical Morphology, Academic Press, 1982.
47. T. K. Ho, IEEE Trans. Pattern Anal. Mach. Intell., 1998, 20, 832–844,  DOI:10.1109/34.709601.
48. T. Chen and C. Guestrin, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ed. B. Krishnapuram, M. Shah, A. J. Smola, C. C. Aggarwal, D. Shen and R. Rastogi, San Francisco, CA, 2016, pp. 785–794,  DOI:10.1145/2939672.2939785.
49. M.-C. Popescu, V. E. Balas, L. Perescu-Popescu and N. Mastorakis, WSEAS Trans. Circuits Syst., 2009, 8, 579–588.
50. D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980,  DOI:10.48550/arXiv.1412.6980, https://arxiv.org/abs/1412.6980, accessed 15 October 2024.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00333k

---