Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
AI-powered exploration of molecular vibrations, phonons, and spectroscopy
Bowen Han†
 a,
Ryotaro Okabe†bc,
Abhijatmedhi Chotrattanapituk†bd,
Mouyang Cheng†bef,
Mingda Li
a,
Ryotaro Okabe†bc,
Abhijatmedhi Chotrattanapituk†bd,
Mouyang Cheng†bef,
Mingda Li *beg and
Yongqiang Cheng
*beg and
Yongqiang Cheng *a
*a
aNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA. E-mail: chengy@ornl.gov
bQuantum Measurement Group, MIT, Cambridge, MA 02139, USA. E-mail: mingda@mit.edu
cDepartment of Chemistry, MIT, Cambridge, MA 02139, USA
dDepartment of Electrical Engineering and Computer Science, MIT, Cambridge, MA 02139, USA
eCenter for Computational Science & Engineering, MIT, Cambridge, MA 02139, USA
fDepartment of Materials Science and Engineering, MIT, Cambridge, MA 02139, USA
gDepartment of Nuclear Science and Engineering, MIT, Cambridge, MA 02139, USA
First published on 14th February 2025
Abstract
The vibrational dynamics of molecules and solids play a critical role in defining material properties, particularly their thermal behaviors. However, theoretical calculations of these dynamics are often computationally intensive, while experimental approaches can be technically complex and resource-demanding. Recent advancements in data-driven artificial intelligence (AI) methodologies have substantially enhanced the efficiency of these studies. This review explores the latest progress in AI-driven methods for investigating atomic vibrations, emphasizing their role in accelerating computations and enabling rapid predictions of lattice dynamics, phonon behaviors, molecular dynamics, and vibrational spectra. Key developments are discussed, including advancements in databases, structural representations, machine-learning interatomic potentials, graph neural networks, and other emerging approaches. Compared to traditional techniques, AI methods exhibit transformative potential, dramatically improving the efficiency and scope of research in materials science. The review concludes by highlighting the promising future of AI-driven innovations in the study of atomic vibrations.
1. Introduction
Today, over 90% of global energy consumption involves generating or manipulating thermal energy, yet 70% of the generated energy – clean energy included – is lost as waste heat. This inefficiency poses a significant challenge to harnessing, storing, and transporting thermal energy effectively to combat global climate change. On a microscopic level, thermal energy is carried by various energy carriers such as electrons, photons, and atomic vibrations.1 In this review, we focus on the atomic vibrations, represented as molecular vibrations in non-interacting molecules and collective lattice vibrations (phonons) in solids. Molecular vibrations, such as the bending and stretching modes in CO2, directly contribute to the greenhouse effect by absorbing and re-emitting infrared radiation, intensifying global climate change.2 In solid-state materials, heat primarily dissipates through phonons, leading to substantial energy loss in applications, such as energy harvesting and information processing devices. Therefore, a deeper understanding of molecular vibrations, phonons, and the advanced spectroscopic techniques are crucial for developing technologies in areas related to carbon capture, thermal storage, and waste heat recovery. However, conventional computational techniques using ab initio methods have extremely high computational costs, while experimental measurements are resource intensive and frequently encounter technical challenges. Considering this, artificial intelligence (AI)-driven approaches provide a crucial solution that can afford orders-of-magnitude improvement in computation efficiency with comparable accuracy, real-time experimental data simulation and interpretation, and eventually inverse design of materials with superior performance. In this review, we examine the role of AI in advancing the understanding of atomic vibrations, focusing on overcoming current computational and experimental limitations. We begin this in Section 1 by reviewing the theoretical, experimental, and computational foundations of atomic vibrations. Section 2 focuses on the foundational preparation for AI-driven atomic vibrations, including data preparation and structural and spectral representations. Section 3 covers various AI-powered approaches to predict atomic vibrational spectra, and we conclude in Section 4 with a perspective of future opportunities.1.1. Fundamental theory of atomic vibrations
The vibration of atoms in molecules and solids is a fundamental process that underlies the material's properties.1 Dictated by quantum mechanics, the interacting atoms will never stop moving even at zero temperature, and their vibrational behavior changes with internal structure, surrounding environment, and external stimuli. Quantitative characterization and description of atomic vibrations constitute the foundation of the structure–dynamics–property relationship in materials science.3Within the harmonic model, the vibrations in an isolated molecule can be described by its normal modes, which can be obtained by diagonalizing the Hessian matrix — the matrix of second derivatives of the potential energy with respect to the atomic coordinates. The eigenvalues correspond to a molecule's signature vibrational frequencies, and the eigenvectors describe the displacement of each atom associated with the normal modes.4 These vibrational features are characteristics of the molecule, and they vary as the molecule's physical and chemical status changes (e.g., when the molecule is adsorbed on a surface or activated for a chemical reaction).
In a crystalline solid, the vibrations extend to the three-dimensional (3D) space on a periodic lattice. The discrete normal modes thus spread out to percolate in the solid, and the coupled motions with various spatial correlations form continuous bands in the energy domain and dispersion curves when examined as a function of wavevectors in the reciprocal space. Solving the 3D periodic Hamiltonian allows us to extract all eigenmodes at each wavevector and their corresponding frequencies. These are the quanta for vibrational excitations named phonons.3
To quantitatively describe the vibrational dynamics, the potential energy of an atomistic system can be written as a Taylor expansion:5,6
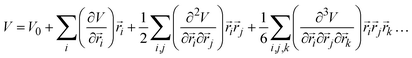 | (1) |
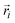 represents the position vector of atom i, and the inner products of each term are between the position vectors and their corresponding gradients. In eqn (1), the negatives of the first derivatives represent interatomic forces, and the second derivatives represent force constants. The higher-order derivatives are neglected under harmonic approximation, which assumes the potential energy profile takes a parabolic shape near equilibrium. A normal mode with angular frequency
represents the position vector of atom i, and the inner products of each term are between the position vectors and their corresponding gradients. In eqn (1), the negatives of the first derivatives represent interatomic forces, and the second derivatives represent force constants. The higher-order derivatives are neglected under harmonic approximation, which assumes the potential energy profile takes a parabolic shape near equilibrium. A normal mode with angular frequency 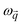 and wavevector
and wavevector 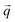 corresponds to the displacement of atom a in the unit cell k:
corresponds to the displacement of atom a in the unit cell k:
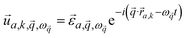 | (2) |
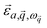 is the mode's polarization vector of atom a, and
is the mode's polarization vector of atom a, and 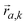 is the position vector of atom a in the unit cell k. Applying Newton's second law to each atom, we have the following equation describing the vibrational dynamics of the solid:
is the position vector of atom a in the unit cell k. Applying Newton's second law to each atom, we have the following equation describing the vibrational dynamics of the solid:
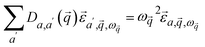 | (3) |
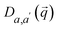 is a block of the dynamical matrix corresponding to the interaction between atoms a and a′ at
is a block of the dynamical matrix corresponding to the interaction between atoms a and a′ at 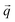 . Solving eigenvalues and eigenvectors leads to phonon frequencies
. Solving eigenvalues and eigenvectors leads to phonon frequencies 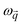 and polarization vectors
and polarization vectors 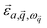 at this wavevector
at this wavevector 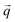 .
.
On a microscopic level, the molecular vibrations and phonons are sensitive indicators of the high-dimensional potential energy surface (PES), which is ultimately determined by the atomic level structure and the interatomic interactions dictated by the electronic structure. Therefore, vibrational spectroscopy has been used to understand a wide range of phenomena in chemistry, physics, and biology, providing critical information on where atoms/molecules are and what they do. For example, the vibrational spectra of a molecule can tell us where it is adsorbed, how it interacts with its surroundings, what its charge status is, and whether it is undergoing a reaction to produce a different molecule. The phonon dispersion of a crystal tells us how much energy and momentum it takes to excite each vibrational quantum, and this can be influenced by defects, disorder, stress, and coupling with electrons, spins, and other degrees of freedom.
On a macroscopic level, phonons are directly responsible for the vibrational entropy, free energy, and specific heat capacity of a solid, which can be calculated following:
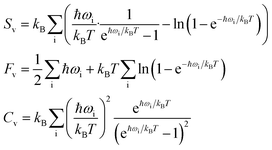 | (4) |
A harmonic system has no phonon–phonon interaction; all phonons are independent and have an infinite lifetime. In an anharmonic system (when the third and/or higher-order derivatives are non-zero), however, phonon–phonon scattering occurs, which leads to finite phonon lifetime (τω) and varying frequencies. The intrinsic phonon–phonon scattering rate due to anharmonic three-phonon processes can be expressed as
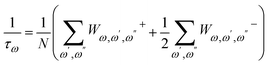 | (5) |
The anharmonic phonon–phonon scattering will cause heat dissipation and, therefore, finite thermal conductivity. Such lattice thermal conductivity can be accounted for by:
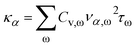 | (6) |
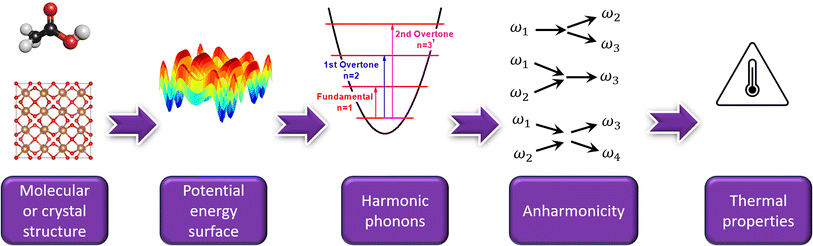 | ||
| Fig. 1 A typical workflow to compute a material's vibrational and thermal properties from its molecular or crystal structure. | ||
1.2. Experimental measurements of atomic vibrations
A common approach to probing atomic vibrations is to shine a beam of quantum particles such as photons, neutrons, or electrons onto the material of interest. These particles exchange energy (and/or momentum) with the sample; thus, measuring the differences between the incident beam and the outgoing beam will tell us about the material's vibrational excitations.Infrared (IR) spectroscopy and Raman spectroscopy are two of the most widely used techniques to measure atomic vibrations.8 Since the wavevector (momentum) of the photons in the laser beam is negligibly small compared to the size of the Brillouin zone, IR/Raman essentially measures the Brillouin-zone-center (Γ-point) phonons. The complex interactions between the photons and the electron cloud ultimately determine the peak intensities of the spectra. The IR intensities are related to the IR linear absorption cross-section. For a specific normal mode k, it can be calculated as:9
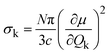 | (7) |
The Raman activity of the mode is defined as:9
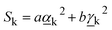 | (8) |
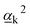 and
and 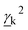 are Raman rotational invariants expressed as
are Raman rotational invariants expressed as
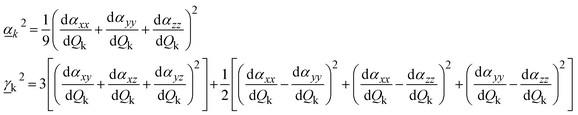 | (9) |
Inelastic Neutron Scattering (INS) is arguably the most powerful method to directly and comprehensively measure phonons.10 Since the probing particles have energy and momentum comparable to phonons, INS is an ideal tool to measure the full phonon dispersion and density of states (DOS). It is also not subject to the selection rules that limit the capability of IR/Raman to observe certain modes. Fig. 2 shows IR/Raman/INS spectra measured on the same material, illustrating their advantages, disadvantages, and complementary roles in the comprehensive understanding of vibrational dynamics.11 With a single crystal sample, INS can also measure phonon dispersion with high resolution in the reciprocal space. Neutrons interact directly with the nuclei. The strength of the interaction can be accurately described by the neutron scattering lengths and cross-sections. Thus, translation from atomic dynamics to neutron scattering intensities can be straightforward and rigorous. Specifically, the dynamical structure factor due to one-phonon excitations can be written as:
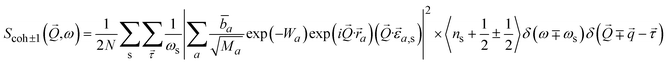 | (10) |
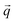 and its mode order, Ma, and
and its mode order, Ma, and ![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) a are the atomic mass and the average neutron scattering length of atom a, respectively,
a are the atomic mass and the average neutron scattering length of atom a, respectively, 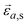 is the phonon polarization vector, and
is the phonon polarization vector, and 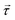 is a reciprocal lattice vector, exp(−Wa) is the Debye-Waller factor with
is a reciprocal lattice vector, exp(−Wa) is the Debye-Waller factor with 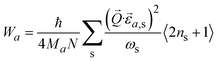 .12
.12
 | ||
| Fig. 2 Various experimental techniques used to measure vibrations. An example is shown for N-phenylmaleimide in this figure. INS-D in the legend refers to spectrum measured on partially deuterated N-phenylmaleimide (with the phenyl ring deuterated). Image produced using data published and provided by Parker.11 | ||
Inelastic X-ray scattering (IXS) provides yet another venue to measure phonons.13 The working mechanism is similar to INS, except that the probing beam is synchrotron X-ray. While the momentum of synchrotron X-ray photons is comparable to thermal neutrons, the energy of X-ray photons (e.g., ∼10 keV) is orders of magnitude higher than thermal neutrons (e.g., tens of meV). It is, therefore, technically challenging to resolve the signal in the energy-momentum space relevant to the phonon dispersion. The measured intensity is often energy-integrated containing thermal diffuse scattering, or with broad elastic line width and poor energy resolution. This is in contrast to INS, which has been routinely used to measure the full 4D dynamical structure factor in single crystals. Despite the technical challenges, recent developments in IXS instrumentation have enabled better resolution and potentially broader applications of this technique reaching to the meV resolution level.14,15
Electron Energy Loss Spectroscopy (EELS) can be conducted in Transmission Electron Microscopy (TEM) and Scanning Transmission Electron Microscopy (STEM) experiments to measure local vibrations and phonons at the nanometer scale.16,17 Since the energy of the incident electron beam is orders of magnitude higher than phonon energies, the challenge is energy resolution, especially near the broad elastic line. The newest vibrational EELS techniques have enabled measurements of vibrations of individual atoms or atomic clusters, offering unprecedented insight that cannot be obtained with macroscopic measurements.18 Another type of EELS, high-resolution EELS (HREELS), does not involve a TEM. It utilizes lower-energy electron-beam and a reflection geometry, which can also measure phonon properties but is less commonly used.19
In addition to the above methods, there are more specialized approaches when the material of interest contains certain elements. For example, synchrotron-X-ray-based nuclear resonant scattering can measure partial phonon DOS of certain isotopes (notably 57Fe).20 All these techniques have advantages and disadvantages, and they should be used as complementary tools to provide a full picture of atomic vibrations and lattice dynamics. Some important specifications of these techniques are listed in Table 1.
| Probing particles | Spatial resolution | Energy resolution | Momentum resolution | |
|---|---|---|---|---|
| IR/Raman | Photons (laser) | 1−10 μm | ∼0.1 meV | Γ Only |
| INS | Neutrons | ∼10 mm | 0.01–1 meV | 0.001–0.1 Å−1 |
| IXS | Photons (X-ray) | 0.01–1 mm | 1−10 meV | 0.01–0.1 Å−1 |
| EELS | Electrons | ∼1 nm | ∼10 meV | 0.01–0.1 Å−1 |
While technical specifications are important, the accessibility of these methods is also a crucial consideration for practical applications. IR/Raman spectrometers are widely available even in individual research groups. EELS requires more complex and expensive equipment, especially the more advanced ones that can probe phonons, but it is still affordable and can be available in many research universities, institutes, and companies. IXS and INS can only be performed at limited scientific user facilities because complex, large, and expensive accelerators, reactors, and instruments need to be built to produce, control, and measure synchrotron X-rays and neutrons. As a result, access to IXS and INS can be highly competitive. Interested users are required to submit research proposals to obtain beam time, and even for the winning proposals, it usually takes a long time for the experiment to be reviewed, approved, scheduled, and executed. This lack of accessibility to IXS and INS further highlights the need for an AI-powered approach.
1.3. Atomistic modeling and spectral simulation using ab initio methods before the AI era
The goal of analyzing the data from vibrational spectroscopy is to understand the vibrational frequencies and modes from the peak positions and intensities. Additionally, the peak shape and profile can also be analyzed to extract further details, such as structural disorder or anharmonicity (knowing the resolution of the instrument). However, direct answers to such inverse problems are often difficult to obtain. A handy tool to assist data analysis and interpretation is atomistic modeling.21 In this process, a structural model that can represent the sample is first built. We then run simulations of the atomic vibrations, usually with density functional theory (DFT),22,23 and calculate the expected vibrational spectra to compare with the experiment. The comparison helps us to decipher the spectra and extract useful information. One can then modify the model and reiterate the simulations until a satisfactory agreement with the experiment is achieved. Alternatively, one can make hypotheses or conclusions based on discrepancies between the simulation and the experiment. Fig. 3 shows an example of using INS to validate DFT model parameters by measuring and simulating the phonon dynamical structure factor in a single crystal of RuCl3, a Kitaev quantum spin liquid candidate.24 Since vibrational frequencies and polarization vectors are often very sensitive to the structure, interatomic interactions, and defects, the verification with vibrational spectra is usually considered a higher level model validation than other commonly used criteria, such as lattice constants or bond lengths. | ||
| Fig. 3 Phonon dynamical structure factor in a RuCl3 single crystal. (a) From INS experiment, (b) and (c) from DFT simulation using Hubbard effective U of 3.0 eV and 1.0 eV, respectively. The better agreement between (a) and (b) indicates that U = 3.0 eV can capture the correct electronic structure and is the parameter to use when modeling this material with DFT. Reprinted under CC BY 4.0 license from ref. 24. | ||
This data analysis workflow has several key components. The first is to understand the PES around the equilibrium configuration. The potential energy as a function of atomic coordinates allows us to evaluate the interatomic forces when atoms deviate from their equilibrium positions. This is typically done using first-principles methods such as DFT (popular DFT packages include ABINIT,25 Quantum Espresso,26 VASP,27 CP2K,28 etc.) or force fields in either parameterized analytical form or numerical tabulated form.
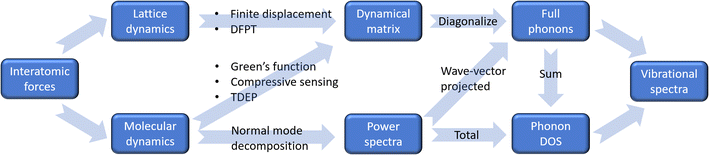
The second component concerns the way how atomic vibrations are computed. There are two widely used methods: lattice dynamics and molecular dynamics. The lattice dynamics approach directly computes the second derivatives of the energy in an optimized structure, using finite displacement method or density functional perturbation theory (DFPT), extracts the force constants, constructs the dynamical matrix for each wavevector, and then diagonalizes the dynamical matrix to solve the phonon frequencies and polarization vectors (as implemented in phonopy,5 for example). This method is suitable for less complex crystals, as well as non-interacting/single molecules (gas phase systems), and it is based on harmonic approximation. Anharmonic force constants can also be solved using predetermined finite displacements (as implemented in phono3py6). However, the degrees of freedom grow rapidly with system size, rendering it only feasible for small or high-symmetry unit cells. The molecular dynamics approach involves simulations of the atomic trajectories (time evolution of atomic coordinates) at finite temperatures. The time-dependent positions, velocities, and forces of each atom are then used to extract the phonon information. For example, the phonon DOS can be calculated as the Fourier transform of the velocity autocorrelation function. One can also take a step further by calculating the wavevector-projected power spectra to obtain phonon dispersion using the normal mode decomposition method.29,30 Alternatively, phonon dispersion may be extracted from the trajectory using Green's function method,31 which is less demanding computationally but involves consideration on quality of force constants and self-energy. One could also use methods such as compressive sensing32,33 or temperature-dependent effective potentials (TDEP)34 to find the “effective” force constants that best match the sampled configurations and then follow the same diagonalization procedures as in lattice dynamics to solve the phonon frequencies and eigenmodes. An advantage of utilizing the molecular dynamics approach is that the anharmonicity is inherently considered, at least to some extent. While the conventional velocity autocorrelation function method does not allow the assignment of the spectral peaks to specific vibrational modes, the effective force constants method can have advantages in both lattice dynamics and molecular dynamics – it can provide full information about the phonon modes while effectively accounting for (part of) the anharmonicity. Recently, progress has been made in conventional lattice dynamics, where on-the-fly training of polynomial machine learning potential has been introduced. This machine learning-based approach facilitates accurate computation of anharmonicity and thermal conductivity while significantly reducing computational cost.35 Multiple software packages have been developed to convert molecular dynamics trajectories into second and higher order force constants, such as Alamode,36–40 TDEP,41 and hiPhive.42 A flow chart summarizing these different approaches is illustrated in Fig. 4.
The third component involves converting phonon information into various spectra for direct comparison with experiments. It is usually based on theoretical descriptions of the coupling between the vibrational modes and the probing particles. Equations to calculate IR, Raman, and INS are given in the previous section. While theories on these calculations have been well developed, the implementation is not always trivial. For instance, complex resolution functions need to be considered when performing INS simulations.43 Some quantum chemistry or DFT software packages contain modules to calculate IR/Raman spectra, such as Gaussian44 and CASTEP.45,46 Auxiliary tools47,48 to convert DFT calculation results into IR,49 Raman,50,51 or INS52–54 spectra also exist.
The workflow from the molecular/crystal structure to the vibrational spectra is usually a time-consuming and resource-intensive process, although conceptually, it may seem straightforward. One (or more) of the three components can hold up the data pipeline. For example, despite rapid growth in computing power, first-principles or DFT phonon calculations are usually only feasible for relatively simple systems (with up to a few hundred atoms in the unit cell) and can take many hours on a powerful computer to complete. The simulation of Raman intensities requires additional steps based on each eigenmode and is thus even more computationally expensive. Phonon calculations of large, complex, disorder, or heterogeneous systems are especially challenging. Going beyond harmonic approximation, explicit calculations of the anharmonicity (higher-order derivatives) require enormous computing resources and are currently only affordable for very simple systems (simple crystal structures with small unit cells). These bottlenecks call for an alternative approach to obtain information on lattice dynamics, simulated vibrational spectra, and thermal properties in a high-throughput fashion. In the rest of this review, we will discuss alternative AI-powered approaches, including the methods, applications, and future developments.
2. AI-driven insights to atomic vibrations: foundations
2.1. Database preparation
The foundation of any data-driven approach obviously depends on “data”, in both quality and quantity. High-quality training datasets are crucial for applicable predictive models. With more and faster computing resources, large synthetic datasets are being produced at a record speed. There are already many datasets that are relevant to the topic of this review. For example, the Materials Project (MP),55 the JARVIS-DFT,56 phonondb database,57 Alexandria database,58 OMat24,59 and INS database.60 Most of these datasets are generated using DFT, albeit with different software, levels of accuracy, and computational details.Some experimental databases are also available for IR/Raman61 and INS.62 However, one major challenge associated with using the experimental database for AI-related applications is the intrinsic consistency across different materials, i.e., whether the data were collected under comparable conditions with the same/similar background, resolution, noise level, etc. So far, most of the data-driven results have been obtained using synthetic data, either from published databases or generated by the researchers. Even within synthetic databases, one should be careful when mixing data from different sources, as they may be calculated using various methods or parameters. Table 2 lists some publicly and freely available datasets that have been used or are potentially helpful for data-driven methods to understand atomic vibrations.
| Name | Description | # of entries | URL |
|---|---|---|---|
| DFPT DOS | Phonon DOS and full dispersion from ABINIT, semiconductors | ∼1500 | https://doi.org/10.6084/m9.figshare.c.3938023 |
| JARVIS-DFT | Force constants from VASP, inorganic crystals | ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://jarvis.nist.gov/jarvisdft/ |
| Phonondb | Force constants from VASP, inorganic crystals | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://github.com/atztogo/phonondb |
| MP | Force constants from VASP, inorganic crystals | ∼1500 | https://next-gen.materialsproject.org/ |
| Topological phonon database | Based on dynamical matrices from phonondb and MP crystals | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://www.topologicalquantumchemistry.com/topophonons/ |
| INS crystals | INS spectra based on phonondb crystals | ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://zenodo.org/records/7438040 |
| INSPIRED | Force constants from VASP, inorganic crystals | ∼2000 | https://zenodo.org/records/11478889 |
| TPDB | Phonon DOS and dispersion from VASP, topological phonons | ∼5000 | https://www.phonon.synl.ac.cn/ |
| INS molecules | INS spectra for GDB-8 molecules, Gaussian DFT | ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://zenodo.org/records/7438040 |
| TOSCA | Experimental INS database | ∼1000 | https://www.isis.stfc.ac.uk/Pages/INS-database.aspx |
| Raman-db | Raman spectra database for inorganic compounds, calculated with crystal | ∼300 | https://raman-db.streamlit.app/ |
| CCCBDB | Vibrational frequencies of molecules, both experimental and calculated | ∼500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
https://cccbdb.nist.gov/anivib1x.asp |
| SDBS | Spectral database for organic compounds, experimental | ∼32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (IR) 000 (IR) |
https://sdbs.db.aist.go.jp/ |
| ∼3500 (Raman) | |||
| MPtrj | Dataset containing 1.58 million structures, 1.58 million energies, 7.94 million magnetic moments, 49.30 million forces, and 14.22 million stresses | ∼1.58 million | https://figshare.com/articles/dataset/Materials_Project_Trjectory_MPtrj_Dataset/23713842 |
| Alexandria | DFT calculations for periodic three-, two-, and one-dimensional compounds | ∼30.5 million | https://alexandria.icams.rub.de/ |
| OMat24 | DFT energies, forces, and stresses on non-equilibrium structures, offered with EquiformerV2 models | ∼110 million | https://huggingface.co/datasets/fairchem/OMAT24 |
In addition to databases containing information on vibrational modes and phonons, other relevant contributions include those containing DFT-calculated forces for many atomic configurations. For example, the MP trajectory (MPtrj) database63 and the Alexandria database64 contain DFT forces along the structural optimization steps for many compounds. Such information can be used to train neural network force field models that represent the potential energy profile and, therefore, can be further used to calculate phonons and thermal properties.
The key information in the synthetic datasets, such as the atomic coordinates, energies, forces, and vibrational properties, can be obtained by atomistic modeling using different methods and level of theories. For example, CCSD(T) is a highly accurate quantum chemistry method that is often considered the gold standard for energy calculations of molecules. It is, however, computationally expensive and can only be used for relatively small molecules and datasets. DFT strikes a desired balance between accuracy and efficiency and is thus most widely used to produce the larger datasets. There are different implementations of DFT, from the representation of the core electrons to the wave-functions of the valence electrons, and there are also various levels of approximations within the DFT framework.65 All these will affect the accuracy of the results, and it is important to take these into consideration when choosing the training data.
The accuracy of the models will not exceed the accuracy of the training data, and the models usually do not “extrapolate” well on elements or bonds or local environment that are completely absent or poorly represented in the training dataset. Due to the difficulty to deal with out-of-distribution (OOD) scenarios66 and the high-dimensional and complex nature of the phases space, it is crucial to understand, for example, how the datasets were produced, what compounds are covered, what local atomic arrangements have been surveyed, and under what internal and external conditions. Also, careful discussion on the research background and proposed methodologies is important, including what has not been learned, and the associated limitations of the model. It is only within such a context that one can make meaningful evaluations of whether the prediction of a specific scenario is reliable. Thus, statistical information on the training dataset matters, and it should be made clear to the readers and potential users, as it is crucial for correctly interpreting the results obtained from the data-driven approach. It is also essential to remember the intended applications when designing and creating new training datasets for specific applications. Efficiently covering the phase space for the intended applications is a topic that has not received sufficient attention, and rigorous approaches to reliable and reproducible machine-learning-based materials research should be explored. Active learning that selects the most informative data points to calculate and label is a potential strategy to improve data efficiency when generating the training datasets on the fly.67–69
2.2. The representation of atomic structures
When trying to establish a connection between the structure of the material and its vibrational properties using AI-powered approaches, one critical step is to find an efficient and discriminative way to represent the atomic structure. Intuitively, since the Cartesian coordinates of atoms contain all the essential structural information, it would be most straightforward to use them as a direct structural descriptor. However, Cartesian coordinates are neither necessarily suitable as representations of atomic structures nor appropriate to serve as direct inputs for machine learning models. This is because the Cartesian representation of a molecule varies with its orientation and absolute position in space, as well as the sequence in which the atoms are ordered. As a result, theoretically, equivalent configurations can produce significantly different Cartesian values, making Cartesian coordinates ineffective in certain machine-learning tasks.To address this, many strategies have been developed to impart translation, rotation, inversion, and atomic permutation symmetries to the structure descriptors. These efforts have given rise to a wide range of efficient representations. The principle of symmetry plays such a central role in these developments, as illustrated by the “phylogenetic tree” in Fig. 5.70
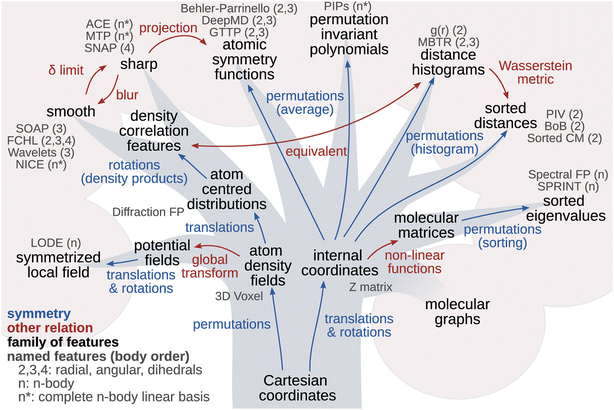 | ||
| Fig. 5 Phylogenetic tree of representations of atomic structures. Arrows indicate the relationship (blue: symmetry; red: other relation) between different hierarchies of structural features. The atomic density fields and the internal coordinates of an atom are two approaches for molecular and crystal structure representation. Reprinted under CC BY 4.0 license from ref. 70. | ||
A well-designed representation of the atoms should at least be translationally invariant and rotationally equivariant since many physical properties of materials only depend on relative positions. For instance, the Z matrix, also known as internal coordinate representation, is widely used in quantum chemistry software to represent molecules. However, the effectiveness of the Z matrix was questioned because it lacks a standardized and unique definition.71,72 This limitation is largely attributed to its lack of permutation invariance when exchanging two atoms. Another widely used representation of atomic structures is the pair distribution function, g(r), which can be readily measured from diffraction experiments. This function captures the radial distribution of atomic pairs, providing insight into the short-range order. Based on the two-body radial correlation, the Smooth Overlap of Atomic Positions (SOAP)73 descriptor extends beyond g(r) by encoding density correlations of both radial basis functions and spherical harmonics. Such integration of radial and angular information makes SOAP very effective for capturing intricate structural features and tackling complex machine-learning tasks, such as learning properties at grain boundaries.74 In recent years, many more representations have been developed, largely driven by the need to encode the structure for neural networks and machine learning applications. Several review articles have been published specifically on or with extensive coverage of structural representations.75–80
Structural representations can be classified into two conceptual categories: pre-defined representations and end-to-end representations. Before the advancement of graph-like representation, most representations, including SOAP and g(r), belong to the pre-defined category, where the descriptor of the material follows a fixed rule that captures the geometrical environment of atoms or densities. Recent developments, such as graph representations, offer a more flexible strategy to encode structural information, where representations are learned and updated during the model training. In the following sections, we focus on the advancements that may be suitable for studying vibrational dynamics.
Despite the many models explored to represent a molecular or crystal structure, recent efforts have gradually converged to graph neural networks (GNNs), which have a natural connection with the 3D atomic coordinates. A graph G = (V, E) is a structure that describes entities with nodes V and their connections through edges E. It comprises a set of vertices (or nodes) v ∈ V and a set of edges eu,v = (u,v) ∈ E, which represent the connections between nodes. The definition of a graph renders it a straightforward way to encode molecules/materials, where atoms are the nodes and bonds correspond to the edges. The GNN architecture follows the intuition that atoms of the neighborhood have interactions, and the local interactions cumulatively affect the global property of materials. Specifically, the graph representation is realized through message-passing neural networks (MPNNs), which iteratively aggregate and propagate information between nodes and edges in graph structures.81,82 Because of these desired features, GNNs are widely used in many studies for material property predictions, showing great efficiency, accuracy, and flexibility.82
CGCNN83 is one of the pioneering GNNs applied to materials property prediction, representing crystals as graphs where atoms are nodes and bonds are edges. MEGNet84 built on this by incorporating global state inputs such as temperature and pressure. Later, GATGNN85 improves expressiveness with local attention layers for atomic environments and a global attention layer for aggregating these features, excelling in single-property prediction. Another approach, Mat2Spec,86 predicts phonon and electron DOS with a GNN encoder coupled with probabilistic embedding generation and contrastive learning.
An important feature of a GNN is how it transforms upon operations such as translation, rotation, reflection. Some properties, such as potential energy and atomic charges, are scalars and invariant under these operations. Some others, such as forces, dipole moment, or polarizability, are vectors, which are equivariant, meaning the properties should also change according to the symmetry operations. Mathematically, a function f: X → Y is equivariant with respect to a group G that acts on X and Y if:
| DY[g]f(x) = f(DX[g]x)∀g ∈ G,∀x ∈ X | (11) |
In early GNN models, the edges only contain information on distance or 2-body interactions between atoms. It is then demonstrated that the angular information (3-body interaction) is also essential for more accurate predictions. These GNNs are translationally and rotationally invariant, and they may fall short in distinguishing certain stereochemical features.87 Equivariant GNNs can represent tensor properties and tensor operations of physical systems. They are guaranteed to preserve the known transformation properties of physical systems under a change of coordinates because they are explicitly constructed from equivariant operations.88
Tensor-field network (TFN)89 is one of the most popular rotationally equivariant neural networks. A TFN is invariant to translation and equivariant to parity and rotation, a feature of most physical properties of materials. The convolutional filters comprise learnable radial functions and spherical harmonics (Fig. 6).90 Features of various orders can be represented by the order of the spherical harmonics, including scalars (l = 0), vectors (l = 1) and higher-order tensors (l ≥ 2) with parity p ∈ (1,−1). A series of GNNs (including the widely used e3nn91) have been developed based on this concept. They have shown excellent data efficiency and accuracy in various applications.90,92,93 Here, we only briefly introduce the realization of e3nn, which builds on TFN for additional inversion symmetry and preserves E(3) (including translation, rotation, and inversion) group equivariance. As illustrated in Fig. 6 below,90 the key idea to preserve E(3) equivariance in e3nn is to separate input encoding into radial and angular components and propagate the nodal information via tensor product, i.e.
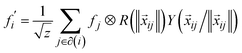 | (12) |
 are node features before and after the graph convolution layer of atom i, respectively, and the summation is over all neighboring atoms, i.e., those who have an edge connecting them to i (normally determined by a cut off radius, rmax), xij is the edge vector pointing from i to j, ‖·‖ represents the norm (length) of a vector. R is a parametrized neural network encoding the radial distance information and Y is spherical harmonics encoding the directional/angular information.
are node features before and after the graph convolution layer of atom i, respectively, and the summation is over all neighboring atoms, i.e., those who have an edge connecting them to i (normally determined by a cut off radius, rmax), xij is the edge vector pointing from i to j, ‖·‖ represents the norm (length) of a vector. R is a parametrized neural network encoding the radial distance information and Y is spherical harmonics encoding the directional/angular information.
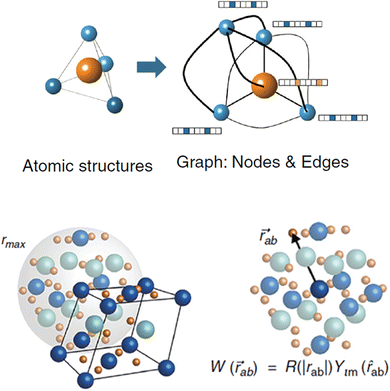 | ||
| Fig. 6 Sketch of a symmetry-aware representation of atomic structure using e3nn. (Top) An atomic structure is converted into a crystal graph with nodes and edges, and when structural information passes within a cutoff radius rmax for a given atom, the angular information and radial information between two atoms are encoded in spherical harmonics Ylm(rab) and a radial neural network R(|rab|), respectively. Reprinted under CC BY 4.0 license from ref. 90. | ||
Scalars like bond lengths are always invariant under E(3) transformation, and spherical harmonics preserve the rotational equivariance. Thus, e3nn ensures E(3) equivariance by decomposing the tensor product of spherical harmonics into a direct sum of spherical harmonics of different orders and passing on E(3) equivariance throughout every layer.
Different from equivariant features, invariant features remain invariant under group transformation. Following similar strategies from above, we can design invariant GNNs, such as SchNet,94 which are also extremely useful for certain property prediction tasks. For example, these invariant representations could be applied to predict spectral properties such as DOS, which are functions of frequency and invariant with respect to rotation. It is straightforward to accommodate such invariance into existing equivariant frameworks such as e3nn, where an invariant GNN architecture was applied to predict phonon DOS.90 Additionally, there are also invariant representations which are not based on GNNs, such as SOAP and atom-centered symmetry functions (ACSFs).95
Another approach, the symmetry-enhanced equivariance network (SEN), avoids using tensor products while still achieving equivariance. SEN builds material representations by jointly encoding structural and chemical patterns, capturing significant clusters within the crystal structure, and learning equivariant patterns across different scales using capsule transformers.96
In a conventional GNN model, the number of nodes is the number of atoms in the system, and the dimension of the predicted output is predetermined. This excludes the possibility of predicting size-dependent properties, such as molecular normal modes (depending on the size of the molecule) and phonon dynamical matrix (depending on the size of the unit cell). Recently, Okabe et al.93 proposed virtual node GNNs to address this challenge. This approach gains full flexibility in the output dimension by allowing an arbitrary number of virtual nodes to be added anywhere in the GNN. The message passing is unidirectional from the real nodes and the virtual nodes and bidirectional within the real nodes set or virtual nodes set. This design, as illustrated in Fig. 7, ensures that the predicted properties are ultimately rooted in the material structure itself (represented by the real nodes), and not a consequence of the added virtual nodes. In other words, the added virtual nodes can effectively introduce flexibility without violating the chain of causation. This new model enables direct prediction of the full phonon dispersion with higher efficiency than other traditional or data-driven calculations. It also enables large-scale materials screening and design for specific vibrational or thermal properties. In fact, the method is very general, and it opens the door to predicting many other properties with material-dependent dimensions.
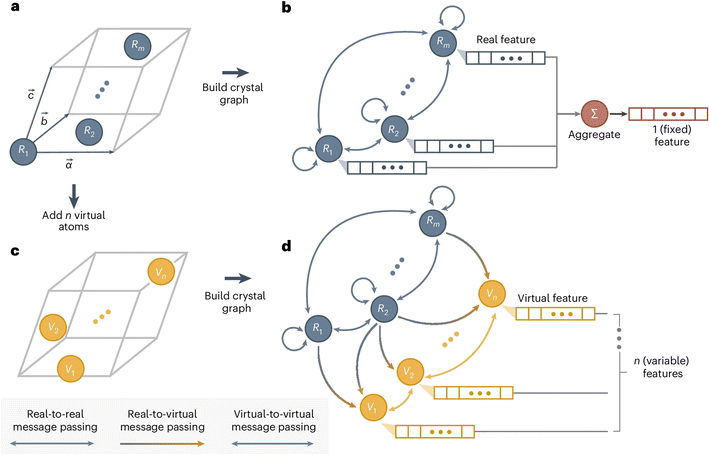 | ||
| Fig. 7 Design of virtual node GNN. (a) A crystal structure, which is converted into (b) a crystal graph in a GNN with real nodes. (c) By adding virtual nodes to the crystal structures, the (d) virtual node graph can be used to represent both atoms and collective excitations, where the unidirectional information passing from real nodes to virtual nodes ensures the training quality. Reprinted with permission from Springer Nature Copyright (2024).93 | ||
When predicting a crystalline material's properties, especially those that are sensitive to periodicity and long-range correlations, it is essential to have a GNN that can uniquely and comprehensively represent the periodic crystal structure. Thus, periodic invariance and explicit representation of the global periodicity could be important. Yan et al. proposed periodic graph transformers for complete and efficient representation of crystal structures and prediction of various forms of properties, including tensors (e.g., dielectric, piezoelectric, and elastic tensors).97–99 A key feature in this model is the node-specific lattice representation, which is uniquely defined with the node-of-interest as the origin and the vectors connecting the nearest periodic “mirror” atoms. This representation guarantees the periodic invariance of the model.
In addition to the representation of a structure, it is equally important to have a proper representation for each atomic species in the structure. Different atomic species have different masses and charges, which influence the structure's potential energy, leading to different dynamical matrices and, ultimately, band structures and thermal properties. The most straightforward way is to represent each atom by its descriptors, including atomic number, atomic mass, formal charge, atomic group, electronic configuration, negativity, radius, metal/nonmetal, etc. However, directly using all these descriptors as is (numerical encoding) can be a poor choice since numbers give a sense of high/low value while the actual atomic descriptors can be categorical, and not all descriptors are equally important in predicting a certain property. Moreover, some descriptors can be correlated, and very high-dimensional descriptors can be detrimental to model learning. These problems require feature engineering, which can be either deterministic or small learnable processes to preprocess the input features for the main machine learning model.
One of the first tasks in feature engineering concerns input features that are categorical. In these situations, it is common to use one-hot encoding. For instance, if the descriptors can be grouped into ten categories; the feature of the 8th category would be represented with an array of length ten filled with 0's except the 8th array element, which is equal to 1:
| [0, 0, 0, 0, 0, 0, 0, 1, 0, 0] |
One natural application is the one-hot encoding of elements, where the representation is a length 118 (total number of known elements on the periodic table) array filled with 0's except an array element corresponding to the atomic number that is filled with that atom's descriptor value. For example, the encoding for the atomic mass of H, C, and O can be:
| [1, 0, 0, 0, 0, 0, 0, 0, 0, …] |
| [0, 0, 0, 0, 0, 12, 0, 0, 0, …] |
| [0, 0, 0, 0, 0, 0, 0, 16, 0, …] |
This deviation from a simple one-hot encoding can capture both categorical information of each atom and ordinal information of each atomic feature. This encoding can also effectively represent uniform substitution alloy and defect systems with virtual crystal approximation (VCA) without losing information on composite elements. For instance, an alloy system AxB1−x and defect Cy have mass encoding as [⋯, xmA, ⋯, (1−x)mB, ⋯] and [⋯, ymC, ⋯], respectively.90
Although the one-hot encoding is straightforward to implement, it renders the model inputs to be high-dimensional and sparse arrays. This increases the model complexity (i.e., more parameters to learn), making it difficult to train effectively. Hence, it is also common to send the high-dimensional input features through dimensionality reduction algorithms before passing it to the main model. The simplest and most straightforward method is a shallow, fully connected neural network or multi-layer perceptron (MLP), as used by Chen et al.90 Other available methods include principal component analysis (PCA), autoencoder, and feature selection.
Departing from the one-hot and numerical encoding, Antunes et al. performed unsupervised learning on the co-occurrence of atoms in materials from the MP database55 and constructed distributed atomic representation. Unlike one-hot encoding, where each element is independent of another, the distributed representation contains information on the similarity between atomic species. The work shows that this kind of representation is especially effective in situations where only the atomic compositions of the materials are known.100
For a machine learning model targeting the thermal properties of materials, it is often assumed that the atomic number and atomic mass should be the most natural descriptors since they are explicitly present in the dynamical matrix. However, the relevance of other descriptors is less apparent. One can either try multiple combinations of atomic descriptors and eliminate the descriptors that have insignificant effects on the model performance or add more descriptors until the performance plateaus. Recently, Hung et al. proposed a universal ensemble-embedding method for feature learning (Fig. 8).92 A shallow neural network independently embeds each input atomic descriptor before it is passed through a learnable gate that controls their mixture. The individual embedding allows the model to find the optimized way each descriptor can improve the performance, while the gate determines the importance of each descriptor to the overall prediction.
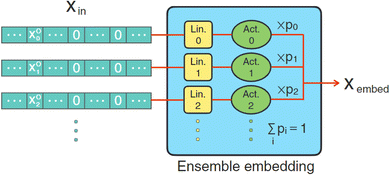 | ||
| Fig. 8 Universal ensemble-embedding. Different atomic descriptors are fed into an ensemble layer to mix before passing through other layers in the GNN. Reprinted under CC BY 4.0 license from ref. 92. | ||
2.3. The compression of the spectroscopic data
The spectra of interest can be complex and/or multi-dimensional, posing challenges for the analysis and prediction. However, the spectral data often exhibit certain general features, making significant dimensionality reduction and compression possible. PCA is a widely used method for dimensionality reduction.101 It uses a linear transformation to project the data to a set of new coordinates, one at a time, in descending order of the data variation along the coordinate. One can then choose the first N coordinates and represent (the majority of) the data in N-dimension. Beyond the linear PCA, an autoencoder is a type of neural network (which can be nonlinear) to learn efficient coding of input data, usually for dimensionality reduction or feature extraction.102 It consists of an encoder and a decoder: the encoder compresses the input data into a lower-dimensional representation, known as the latent space, while the decoder reconstructs the original data from the latent space. It aims to capture the essential features of the initial data in the latent space that may be used for noise reduction, anomaly detection, and data visualization, with broad applications in vibrational spectroscopy.Samarakoon et al. explored the application of autoencoder in the compression of 3D neutron magnetic diffuse scattering data into a small latent space, followed by parameter optimization in latent space and inverse problem solving.103–105 These successful examples illustrate the great potential to compress the high-dimensional phonon spectra following a similar approach. There are autoencoders of diverse architectures. Even a simple fully connected autoencoder may work well for some 2D or 3D vibrational spectra where features are relatively broad and smooth; see Fig. 9 for an example.106 More complex spectra may require more sophisticated models, such as convolutional autoencoder or variational autoencoder (VAE), to describe. Su and Li107 systematically compared the performance of four types of autoencoders in the compression of 2D INS spectral data, including the fully connected autoencoder (FCAE), fully connected variational autoencoder (FCVAE), convolutional autoencoder (CNNAE) and convolutional variational autoencoder (CNNVAE). They demonstrated that the variational autoencoders generally perform better at disentangling the features, with different latent dimensions showing less correlation. They are, therefore, potentially more efficient at data compression. It should be noted that this comparative study was performed on simulated aluminum spectra with varying force constants. The intrinsic similarities in the dataset (all for aluminum) may play a role in the results. It would be interesting to perform a similar study on a general database with a more extensive variety of spectra patterns. Regardless of the model used and their varying performance, compression of 2D and 3D spectral data has been achieved from up to millions of pixels into a small latent space with a few tens of dimensions. The autoencoder architectures are applied to reconstruct powder INS spectra and single crystal diffuse scattering.103,106 The much-reduced dimension in latent space will enable many applications, such as feature extraction, tracking, filtering, and prediction. It can also be used in generative models to explore broader spectral space.
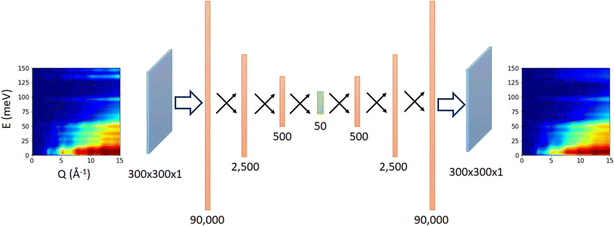 | ||
| Fig. 9 A simple fully connected autoencoder is used to compress and reconstruct a 2D INS spectrum. Adapted under CC BY 4.0 license from ref. 106. | ||
Apart from these encoder-decoder-based neural networks, another family of data compression technique relies on learning the topological manifold of high-dimensional data distributions. Some popular machine learning methods in this category include Stochastic Neighbor Embedding (SNE),108 its variant t-SNE,109 and Uniform Manifold Approximation and Projection (UMAP).110 These methods outperform linear methods (e.g., PCA) in capturing complex, nonlinear structures in data. Moreover, topological data analysis (TDA)111 further provides a complementary approach by focusing on the global shape and connectivity of data. TDA, such as persistent cohomology,112,113 encompasses machine learning techniques that not only reduce dimensions but also preserve and quantify key topological features, such as loops, voids, and higher-dimensional structures. This makes TDA particularly effective for capturing the intricate relationships within high-dimensional data in ways that other local-transformation methods might miss. For example, the 4D phonon dispersion as measured in a single crystal INS experiment is where TDA can be potentially useful.
Fig. 10 illustrates TDA and its applications in representing experimental spectroscopy data. As shown in Fig. 10(a), a general TDA functions through a series of steps: partitioning the dataset, performing cluster analysis within each partition, and generating a final network that reflects the relationships among clusters. This multi-step approach allows TDA to capture subtle topological features of the data, which are typically robust against noise, spectral shifts, or resolution variations in high-dimensional spectroscopy data. For example, in Fig. 10(b), TDA effectively separates bacterial strains based on Raman spectroscopy data, demonstrating its ability to differentiate and visualize all four subpopulations.111 Linear methods, such as PCA, failed to resolve these clusters, particularly in noisy conditions or when spectral preprocessing was bypassed. TDA's robustness makes it suitable for extracting fundamental properties or features hidden within high-dimensional experimental spectroscopy data and making interpretable inferences and predictions.
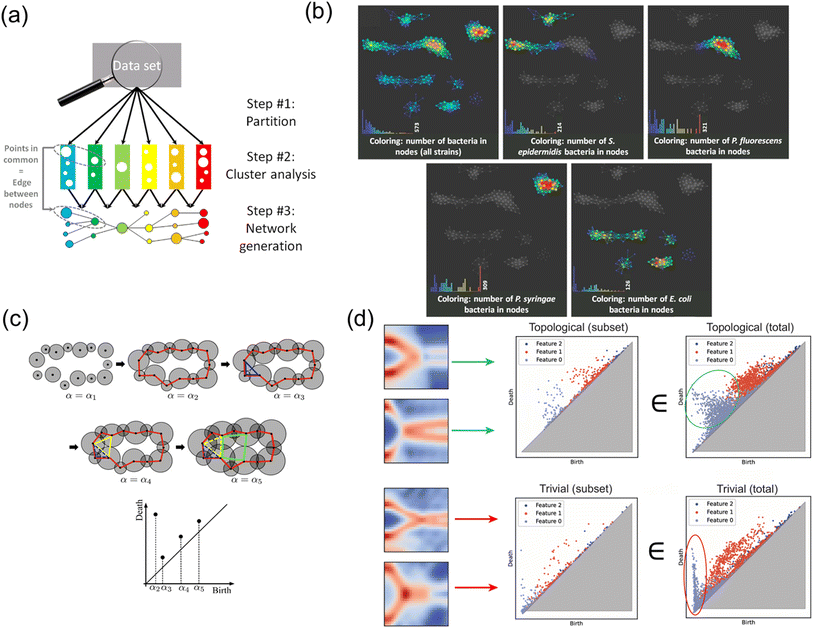 | ||
| Fig. 10 Illustration of TDA and its applications in reducing high-dimensional spectroscopy data. (a) General framework of TDA. Reprinted with permission from Elsevier Copyright (2016).111 (b) Colored TDA predicted networks for all bacterial strains and four types of bacterial strains, respectively, based on Raman spectroscopy data. Reprinted with permission from Elsevier Copyright (2016).111 (c) Illustration of persistent cohomology, a type of TDA technique. Reprinted with permission from ref. 112. (d) Persistent cohomology analysis on topological Majorana zero mode and trivial classes, respectively, based on scanning tunneling spectroscopy (STS) data. Reprinted with permission from Elsevier Copyright (2024).113 | ||
Among various TDA techniques, persistent cohomology, a variant technique illustrated in Fig. 10(c), has extra potential in capturing multi-scale topological features.112 As the threshold parameter changes, persistent cohomology tracks the “birth” and “death” of topological structures, such as lines and closed loops, revealing insights into robust and global features within the spectroscopic data. Results from persistent cohomology are often displayed as persistence diagrams, as shown in Fig. 10(d).113 In these diagrams, sweeping through different threshold values leads to the emergence and annihilation of features, which are represented as points in a birth-death scatter plot.114 This visualization provides global information on the topological manifold of the data and makes persistent cohomology a powerful tool for uncovering hidden structures in complex datasets.
As shown in Fig. 10(d), Cheng et al. used persistent cohomology to distinguish between topological and trivial classes in Majorana zero modes (MZMs) using scanning tunneling spectroscopy (STS) data.113 By analyzing the persistence diagrams, one can observe obvious differences between the topological MZM class and the trivial class, although their STS signals seem hard to distinguish by human eyes. This example and the analysis of bacterial strains demonstrate TDA can robustly handle variations in high-dimensional data, resolve substructures, and isolate meaningful features that are difficult to extract from experimental signals directly. Given the power of TDA in analyzing other spectroscopic data, we expect TDA will one day play a positive role in encoding vibrational spectroscopy data.
In conclusion, encoder–decoder neural network approaches and manifold-based machine learning techniques show great promise in compressing complex experimental spectroscopy data and other high-dimensional datasets. By leveraging their ability to identify and retain essential structures while discarding irrelevant details, these techniques can efficiently transform intricate data into more manageable and interpretable forms.
3. AI-driven approaches to atomic vibrations: applications
The previous sections covered the basic principles of atomic vibrations, the experimental and theoretical methods, and the foundation for data-driven approaches. This section discusses some successful applications of machine learning methods in studying atomic vibrations, lattice dynamics, vibrational spectroscopy, and thermal properties.3.1. Machine learning interatomic potentials (MLIPs) for efficient simulation of atomistic systems
A critical step in calculating the atomic vibrations is to determine the system's PES, from which the interatomic forces are calculated. While DFT has been widely used to map out the PES, its high computational costs make it impractical to study complex systems. Machine learning Interatomic Potentials (MLIPs), such as the surrogate models that predict PES, offer a powerful alternative to obtain the interatomic forces in a shorter time with substantial accuracy.115 MLIPs are typically trained on datasets containing energies and forces provided by DFT calculations. This enables the model to learn the relationship between the atomic structures and their corresponding energies or/and forces.MLIPs have become valuable tools in chemistry and material science due to their capacity to predict interatomic forces Fi efficiently for each atom i. These forces are derived as the gradients of the potential energy V with respect to atomic positions ri.
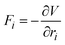 | (13) |
MLIPs stand out in computationally intensive tasks such as phonon calculations, which require accurate calculation of interatomic forces. The robust predictive power of MLIPs is founded on their ability to capture many-body interactions with proper representations, including ACSF,95 SOAP,116 and GNNs. These descriptors allow machine learning models to learn effectively the local environment and spatial relationship of the atomic systems to extract the factors contributing to the PES. Recently, models leveraging equivariant GNNs have emerged as an efficient approach for representing atomic systems by considering the symmetries, including rotation and inversion. By training the MLIP with a sufficiently large DFT dataset, universal interatomic potentials (UIPs) have been built so that the model applies to a wide range of atomistic systems covering a large portion of the periodic table.
Training of MLIPs requires the generation of ground-truth datasets using accurate theory and calculations, such as DFT. With a well-trained MLIP, we can run lattice or molecular dynamics simulations much faster and on much more complex systems. To do that, we need high-quality training datasets with DFT energies and forces. The size and diversity of the dataset significantly impact the generalization of MLIP models. The MP database55 provides the computed information of over 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 known and predicted materials, making it a substantial database for building foundation models. The MPtrj dataset63 contains over 1.5 million structures, the corresponding energies, and nearly 50 million forces. Many universal MLIPs available so far are trained using the MPtrj database.
000 known and predicted materials, making it a substantial database for building foundation models. The MPtrj dataset63 contains over 1.5 million structures, the corresponding energies, and nearly 50 million forces. Many universal MLIPs available so far are trained using the MPtrj database.
If computational resources are limited, we will need an efficient strategy for collecting training datasets. Active learning can be employed117 to start from a small subset of material datasets and then decide which additional datasets are needed based on the acquisition functions. The idea is to run the expensive DFT calculations only when necessary, and in a way that is most efficient to enhance the overall model accuracy.
During the past few years, researchers have developed a wide range of MLIPs and relevant GNN models for materials. Here we summarize the publicly available MLIP packages in Table 3 and describe three recent examples in more details: M3GNet, CHGNet and MACE.
| Name | Description | Molecular dynamics engine | URL |
|---|---|---|---|
| eqv2 (ref. 59) | Built upon EquiformerV2 | ASE118 | https://github.com/FAIR-Chem/fairchem |
| ORB MPtrj | Attention augmented graph network-based simulator (GNS), a type of MPNN | ASE118 | https://github.com/orbital-materials/orb-models/tree/main |
| SevenNet119 | Built on NequIP, support parallel molecular dynamics simulations | LAMMPS,120 ASE118 | https://github.com/MDIL-SNU/SevenNet |
| MACE121 | ACE for higher order interactions | ASE118 | https://github.com/ACEsuit/mace |
| CHGNet122 | Prediction of charge and magnetic moments | ASE118 | https://github.com/CederGroupHub/chgnet |
| M3GNet123 | GNN incorporating 3-body interaction | ASE118 | https://github.com/materialsvirtuallab/m3gnet |
| DeePMD124 | Built on DeepPot-SE, MPI and GPU support, interfaced with multiple atomistic modeling tools | LAMMPS,120 ASE,118 i-PI,125 GROMACS,126 AMBER,127 CP2K,28 etc. | https://github.com/deepmodeling/deepmd-kit |
| NequIP128 | E(3)-equivariant convolutions using e3nn | LAMMPS,120 ASE118 | https://github.com/mir-group/nequip |
| Allegro129 | Built upon NequIP and learn local equivariant representations | LAMMPS120 | https://github.com/mir-group/allegro |
| DP-GEN130 | On-the-fly learning, based on DeePMD, HPC-ready | LAMMPS,120 GROMACS,126 AMBER127 | https://github.com/deepmodeling/dpgen |
| ALIGNN131 | GNN for message passing on both the interatomic bond graph and its line graph | ASE118 | https://github.com/usnistgov/alignn |
| NEP132 | Neuroevolution potential using Chebyshev and Legendre polynomials to represent atomic environment and trained using an evolutionary strategy | GPUMD133 | https://gpumd.org/potentials/nep.html |
M3GNet123 is a GNN-based MLIP designed for high-throughput simulations. The GNN-based architecture incorporates the three-body interactions, enabling the model to capture the spatial relation of atoms efficiently. While it lacks the equivariant nature seen in MACE, M3GNet excels in predicting relaxed structures and capturing the interactions necessary for structural optimization and stability evaluation. Its architecture has enabled researchers to screen large datasets and predict the total energy of diverse materials. With Atomic Simulation Environment (ASE),118 Chen and Ong demonstrated M3GNet could run high-throughput phonon calculations.123 These utilities have made it a valuable resource for materials discovery and property predictions.
CHGNet122 is an MLIP model incorporating the prediction of magnetic moments on top of energy and force calculations. Using the MPTrj dataset, CHGNet included charge and magnetic moments information in the training, allowing it to capture electronic configurations more accurately than the models utilizing sorely atomic positions. CHGNet is a powerful tool for studying material physics where magnetic properties play a crucial role in their stability and dynamics, offering insights into atomic and electronic degrees of freedom in complex systems.
One of the latest contribution in MLIPs is MACE,121 which is built upon the advanced equivariant GNN model leveraging atomic cluster expansion (ACE).134 MACE is the state-of-the-art MLIP framework as it can represent the high-order interactions between atoms, capturing complex multi-body interactions while preserving rotational and translational symmetries using E(3)-equivariant architectures. This model design allows MACE to simulate atomic dynamics in molecular and crystalline systems without exploding computational costs. Using the MPTrj dataset of relaxation trajectories, MACE stands out as one of the most potent UIPs due to its high evaluation scores and applicability to diverse targets.135
Together, these models represent a trajectory of innovation in MLIP development, with each new contribution addressing specific challenges in the field by improving the representation of atomic environments, incorporating magnetic properties, or achieving a better balance between accuracy and scalability.
The Matbench Discovery website provides a ranking list of the performance for UIPs (Fig. 11).136 Among the top-performing models, MatterSim138 and GNoME,139 developed by Microsoft and DeepMind, respectively, exceed the performance of MACE, CHGNet, and M3GNet. ORB and ORB MPtrj were published very recently,140 and the combined training using both MPtrj and Alexandria datasets helped the ORB model to surpass MatterSim and GNoME. At the time of writing![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) this review, eqV2 developed by Meta is on top of the list, which included OMat24 containing over 100 million training structures.59 SevenNet (Scalable EquiVariance Enabled Neural Network)119 is a GNN interatomic potential package that supports parallel and large-scale molecular dynamics simulations with LAMMPS,120 which provides a pre-trained UIP based on NequIP architecture. ALIGNN131 and MEGNet84 are both based on GNNs, and these can be potentially used to calculate the vibrational properties. A recent benchmark revealed that available UIPs underestimate the vibrational frequencies systematically, as indicated in Fig. 12.141 In fact, these pre-trained UIPs are not designed to predict the vibrational properties, as they only include the energies and forces along the optimization trajectories. Structural optimization algorithms usually favor the shortest path to the optimized structure, which saves computing time but may result in insufficient training datasets to explore the local PES adequately for vibration and phonon calculations. Indeed, although the trained forces seem to compare well with the ground truth, the calculated phonon dispersion and DOS can be unsatisfactory and sometimes unphysical. Deng et al.141 found that even with a single additional data point sampling the high-energy region, the MLIP can be fine-tuned to improve accuracy significantly.
this review, eqV2 developed by Meta is on top of the list, which included OMat24 containing over 100 million training structures.59 SevenNet (Scalable EquiVariance Enabled Neural Network)119 is a GNN interatomic potential package that supports parallel and large-scale molecular dynamics simulations with LAMMPS,120 which provides a pre-trained UIP based on NequIP architecture. ALIGNN131 and MEGNet84 are both based on GNNs, and these can be potentially used to calculate the vibrational properties. A recent benchmark revealed that available UIPs underestimate the vibrational frequencies systematically, as indicated in Fig. 12.141 In fact, these pre-trained UIPs are not designed to predict the vibrational properties, as they only include the energies and forces along the optimization trajectories. Structural optimization algorithms usually favor the shortest path to the optimized structure, which saves computing time but may result in insufficient training datasets to explore the local PES adequately for vibration and phonon calculations. Indeed, although the trained forces seem to compare well with the ground truth, the calculated phonon dispersion and DOS can be unsatisfactory and sometimes unphysical. Deng et al.141 found that even with a single additional data point sampling the high-energy region, the MLIP can be fine-tuned to improve accuracy significantly.
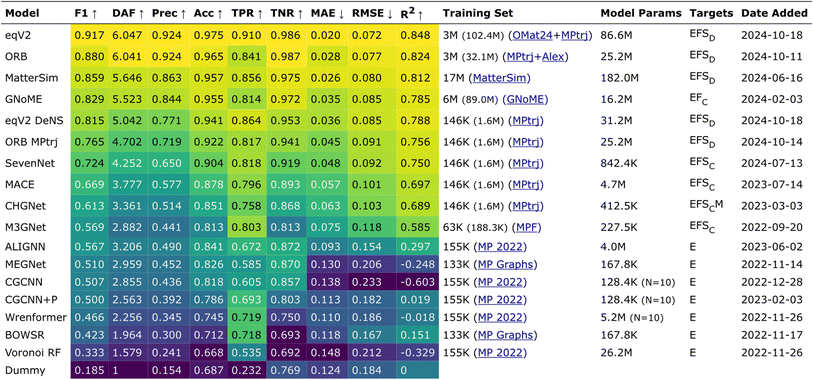 | ||
| Fig. 11 A list of foundation models from the Matbench Discovery website as of October 2024, released under CC BY 4.0 license.136,137 | ||
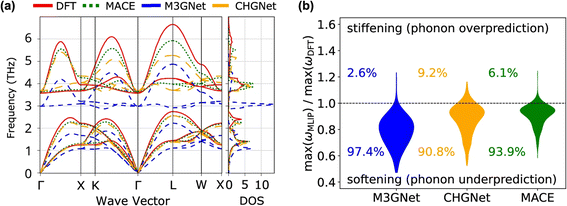 | ||
| Fig. 12 Comparison of three UIPs and DFT for phonon calculations. (a) Phonon dispersion and DOS of CsF, calculated using DFT and various UIPs. (b) Violin plots showing the distribution of ratios between maximum frequencies calculated by UIPs and DFT, for 229 crystals. Systematic and significant softening is observed in the phonon frequencies calculated by the UIPs. Reprinted under CC BY 4.0 license from ref. 141. | ||
While MLIPs have shown great promise, their performance depends heavily on the quality and diversity of training datasets. This suggests that existing models, especially the UIPs, need further refinement to explore the local PES relevant to vibrational dynamics effectively. Nevertheless, MLIPs have become essential tools in high-throughput materials screening, structure relaxation, and the prediction of thermodynamic properties. As the field continues to develop, a combination of specialized training datasets, advanced model architectures, and innovative learning strategies, such as active learning, will further enhance the capabilities of MLIPs. These developments set the stage for their applications in more specialized areas of materials science, such as the study of atomic vibrations and phonon behavior, which we explore in the next section.
3.2. MLIP applications in atomic vibrational spectra prediction
Building on the general principles and benchmarks discussed in the previous section, we now focus on the specific applications of MLIPs in understanding atomic vibrations, lattice dynamics, and phonon properties. We will discuss several key studies highlighting the role of MLIPs in studying anharmonicity, simulating complex phonon behaviors, and exploring the coupling between electronic and vibrational properties. These examples illustrate how MLIPs are accelerating simulations and enabling new insights into vibrational dynamics.Anharmonicity has been a long-standing challenge in the description of lattice dynamics. Properly interpreting spectroscopic data measured on anharmonic systems requires comprehensive modeling beyond the harmonic approximation. Explicit calculation of anharmonicity at the DFT level can be costly computationally. Alternative solutions that are both fast and accurate are desired. Fan et al.132 developed neuroevolution machine learning potentials (NEPs) to simulate heat transport in anharmonic systems. They used Chebyshev and Legendre polynomials as descriptors of the atomic environment and an evolutionary strategy to train the models. Combining with a molecular dynamics engine optimized for GPUs (GPUMD133), they achieved superior speed compared to several other models and obtained thermal conductivity of PbTe in excellent agreement with experiments. Ren et al.142 used molecular dynamics simulations with MLIPs trained by DeePMD-kit to effectively capture the phonon vibrational dynamics within a superionic material, Ag8SnSe6, which shows a rapid broadening of phonon DOS with increased temperatures. The anomaly is caused by strongly anharmonic PES, manifested by phonon–phonon scattering between acoustic and low-energy optical phonons. This leads to a glass-like ultralow thermal conductivity at elevated temperatures. The MLIP allowed direct simulation on a supercell of the superionic cubic phase with 480 atoms to generate molecular dynamics trajectories of 1 ns duration. The combination of length scale and timescale is crucial to capture the phonon–phonon scattering at low energies, which is beyond the range that DFT can cover. Gupta et al.143 used a similar approach to simulate the atomic vibrations and neutron-weighted phonon DOS for another superionic material, Cu7PSe6,144 that reveals a significant broadening of the Cu phonon peak, consistent with the behavior observed in the INS experiments. The MLIP approach was also employed to study other materials, such as MoSe2 and WSe2, particularly to understand the temperature-dependent behavior and to reproduce the signature of anharmonicity in the INS spectra (Fig. 13).145
 | ||
| Fig. 13 Phonon spectral energy density calculated by Gupta et al.145 for MoSe2 and WSe2 using molecular dynamics and MLIPs. The effects of anharmonicity can be clearly seen in the 500 K spectra as the broadening of the lines and the diffusive intensities. Reprinted with permission from Royal Society of Chemistry Copyright (2023). | ||
Another factor that has long been neglected in spectroscopic data analysis is the nuclear quantum effects (NQEs). NQEs can be strong for light elements such as H, and the zero-point motion can be coupled with anharmonicity, making rigorous modeling and data interpretation challenging. In atomistic modeling, NQEs are usually studied with path-integral molecular dynamics (PIMD) and its variations,125 but a converged PIMD simulation can be two orders of magnitude more expensive than a traditional molecular dynamics simulation, making DFT-based PIMD only feasible in the smallest systems. By developing an MLIP for ammonia, Linker et al.146 used the Allegro model129 based on GNN to perform large-scale simulations on solid and liquid ammonia that are computationally efficient yet maintain near quantum mechanical accuracy. The PIMD simulations with MLIP show excellent agreement with experimental INS spectra, while the standard DFT lattice dynamics and molecular dynamics simulations fail, see Fig. 14. The calculation specifically reveals that the potential energy profile associated with ammonia libration/vibration is highly anharmonic. However, unlike in previous cases associated with heavy elements such as Ag and Cu, the anharmonicity here does not require an elevated temperature to activate. Even at base temperature (T = 5 K), the anharmonicity is manifested by major discrepancies in peak positions between the experiment and DFT simulations at the same temperature. The large zero-point motion due to NQEs of the hydrogen is responsible for the anharmonic behavior, and only PIMD can correctly capture this. The study unambiguously revealed the coupling effects of anharmonicity and NQEs on the vibrational dynamics and spectroscopy.
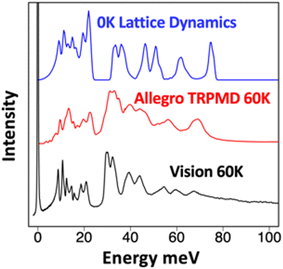 | ||
| Fig. 14 INS spectra of solid ammonia: (black) experimentally measured at the VISION spectrometer, (blue) simulated using lattice dynamics and harmonic approximation, and (red) simulated using thermostatted ring-polymer molecular dynamics (TRPMD), an implementation of PIMD, with Allegro. The conventional lattice dynamics produce major discrepancies in peak positions and profile, notably the overestimation of the higher energy band by >30%.146 | ||
Training of MLIPs can be performed after the DFT training datasets are generated, but it is also possible to perform on-the-fly learning while the DFT simulation is running. This approach belongs to active learning, which requires an integration of the MLIPs and the DFT software to interactively decide the batch of training data to run DFT. The active learning framework has been recently implemented in VASP6,147–149 which efficiently expands the set of reference configurations, enhancing the force fields' accuracy. With this capability, Wieser and Zojer150 benchmarked the MLIPs against DFT calculations for various metal–organic frameworks (MOFs), assessing their accuracy in predicting forces, phonon band structures, etc. Three other methods are included for comparison: direct DFT, moment tensor potentials (MTPs), another type of MLIP, and UFF4MOF, a classical universal force field adapted for MOFs. In most cases, the performance of VASP6 MLIP is similar to or slightly better than the MTP and significantly better than UFF4MOF, as indicated by the phonon DOS in Fig. 15. The gain of using MLIPs to model MOFs can be particularly appealing, not only because MOFs usually have large unit cells containing many atoms but also because the atoms are loosely packed, leaving large space/vacuum undesirable for the commonly used plane-wave DFT. MLIPs are also expected to play a major role in studying defects, deformation, and gas adsorption in MOFs, where the structural disorder can make conventional lattice dynamics prohibitively expensive.
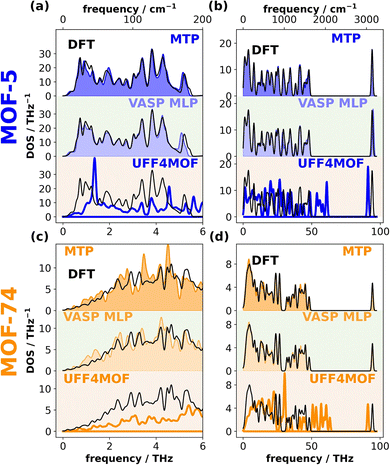 | ||
| Fig. 15 Phonon DOS for two MOFs, calculated using DFT, VASP MLP, MTP, and UFF4MOF. (a and c) Highlight the low frequency range and (b and d) show the full range. Reprinted under CC BY 4.0 license from ref. 150. | ||
Compared to a phonon or INS calculation, simulating IR and Raman spectra requires the prediction of other physical properties, such as dipole moment or polarizability, from the atomic coordinates of the molecules. Han et al. wrote a concise review on machine learning for the prediction of IR/Raman spectra.80 Here, we mainly focus on methods related to charge property predictions.
An early effort by Gastegger et al.151 employed high-dimensional neural network potentials (HDNNPs) to model the PES, with the local environment around an atom described by ACSFs. Additionally, they used HDNNPs to predict the atomic charges and then used the environment-dependent partial charges to construct the molecular dipole moment. The IR spectra obtained for methanol, n-alkanes, and protonated alanine tripeptide agreed well with the experiments.
It has also been explored to predict the dipole moment for IR spectra or polarizability for Raman spectra based on the molecular dynamics trajectories using different neural network architectures in various systems. For example, Han et al.152 used ACSFs and kernel ridge regression model to re-assign the point charges in liquid water for a rigid non-polarizable water model. They obtained a dipole moment surface that accurately reproduces the low-frequency IR spectrum of water, revealing the importance of charge transfer for the peak associated with hydrogen bond stretching. Xu et al.153 used a tensorial neuroevolution potential framework to perform molecular dynamics simulations and IR/Raman predictions for liquid water, PTAF− molecule and BaZrO3. Schienbein154 introduced a machine learning model to train the atomic polar tensor that can predict the dipole moment of liquid water on molecular dynamics trajectories leading to the IR spectrum. Berger and Komsa155 compared three polarizability models for obtaining Raman spectra with trajectories generated from MLIPs on various materials, including BAs, MoS2, and cesium halide perovskites. Fang et al.156 explored the transferability of a neuroevolution machine learning model trained on smaller alkane molecules to predict the polarizability and Raman spectra of larger alkanes. Berger et al.157 trained machine learning models, including neural network and Gaussian process regressor, to predict polarizabilities and Raman spectra of amino acids and small peptides against DFT data. Chen et al.158 developed a multitask machine learning model (predicting energy, force, dipole moment, and polarizability simultaneously) termed Vibrational Spectra Neural Network (VSpecNN) to simulate IR and Raman spectra for a pyrazine molecule. Grumet et al.159 developed a Δ-ML method to predict polarizabilities and then generate Raman spectra from molecular dynamics trajectories. It uses a linear-response model to provide an initial approximation of polarizabilities. Then it uses a kernel-based machine learning method to refine the predictions, which eventually outperform direct machine learning predictions.
Built upon the studies on individual systems, recent development suggests that machine learning models can also predict the atomic charge/dipole moment and the polarizability for a large collection of molecules, such as the GDB-9/QM9 database containing over 133k molecules with up to nine heavy atoms (C, O, N, F). Wilkins et al.160 performed an accurate calculation of polarizabilities with coupled cluster theory on over 7000 small organic molecules (QM7b dataset) and trained a symmetry-adapted model to predict the polarizability tensors in larger molecules with an accuracy that exceeds the hybrid DFT (Fig. 16). Veit et al.161 made comparable achievements in predicting dipole moments on the QM9 dataset by combining a partial-charge model and a partial-dipole model and training the model using the QM7b dataset calculated with coupled cluster theory. Schütt et al.162 proposed the polarizable atom interaction neural network (PaiNN) to use equivariant MPNNs to predict tensorial properties. They demonstrated fast calculations of IR and Raman spectra using PaiNN in ethanol and aspirin. Zhao et al.163 developed and trained a model to predict the molecular polarizability using a subset of GDB-9. The hierarchical interacting particle neural network (HIP-NN) was used to predict the atomic charges of the molecules in GDB-5 and ANI-1x datasets. The predicted atomic charges reproduce the dipole moments of the molecules, which were further used to calculate IR spectra with molecular dynamics simulations and then compared to the results from quantum mechanical calculations.164,165
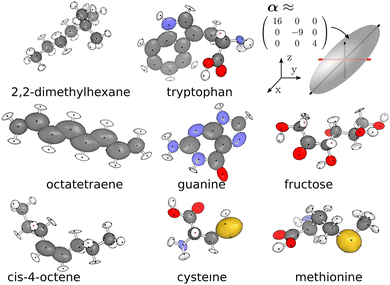 | ||
| Fig. 16 Predicted polarizability tensor for selected molecules. Tensors are represented by ellipsoids around the atoms. Reprinted under CC BY-NC-ND 4.0 license from ref. 160. | ||
In addition to predicting the full spectra, it is sometimes helpful to focus on a specific peak and monitor how its profile changes with the environment.166 For example, Ye et al.167,168 developed models to predict the amide I and amide II IR spectra of proteins based on the AIMD configurations, allowing for efficient secondary structure determination, temperature variation probing, and protein folding monitoring. Kwac and Cho169 presented machine learning approaches to describe the frequency shifts of the amide I mode vibration of N-methyl acetamide due to solute–solvent interactions and to predict the frequencies of OH stretching mode with different configurations in liquid water. Kananenka et al.170 developed a Δ-ML method to improve the accuracy of vibrational spectroscopic maps for OH stretch frequencies in water.
In general, molecular spectroscopy measures the field responses of the molecule. Instead of treating the dipole moment and polarizability tensor as individual quantities to predict, a more general approach is to predict the potential energy as a function of the external field, from which multiple responses (various derivatives) can be calculated. Two recent models, FieldSchNet171 and FIREANN,172 were specifically designed for this purpose. In these models, neural networks representing field dependence are trained and incorporated either directly into the potential energy term (FieldSchNet), or the orbital description of the atoms (FIREANN). By doing so, one can solve the gradient to access multiple responses using a single model, making it much more versatile comparing to those directly and explicitly predicting dipole moment or polarizability.
A neural network surrogate of DFT is trained with quantities that can be directly calculated from DFT, such as atomic energies, forces, stresses, charges, etc., and used to make quick predictions of these quantities in unseen (but related) structures without running the time-consuming and resource-demanding DFT calculations. One still needs to go through the workflow to obtain the spectra from the structure, albeit much faster by replacing DFT (the bottleneck in the workflow) with a high-throughput surrogate. The surrogate can be trained for a specific composition under some specific conditions (such as temperature) or can be trained with a broader coverage of the PES. The scope of the training data determines the scenarios under which the trained model can be considered reliable. Three factors are key to the successful application of this method: sufficient but not redundant sampling of training structure models, efficient neural network model, and optimized training hyperparameters.
Apart from the ambitious attempt to develop UIPs, which is undoubtedly very challenging due to the sheer number of possibilities in the many-body interatomic relationship even if we only focus on the local structure, a compromised approach is to develop MLIPs for a specific group of materials sharing some similarities. Rodriguez et al.173 used an elemental spatial density neural network force field with an active learning scheme to predict atomic forces and phonon properties of approximately 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cubic crystals across 63 elements. This method facilitates the high-throughput search for materials with specific thermal properties, such as ultralow lattice thermal conductivity. One can train domain-specific MLIPs for metals, semiconductors, oxides, organic molecules, metal–organic frameworks, etc. Since each category of materials share more structural, chemical, or functional similarities, the training is more likely to converge with smaller average errors.
000 cubic crystals across 63 elements. This method facilitates the high-throughput search for materials with specific thermal properties, such as ultralow lattice thermal conductivity. One can train domain-specific MLIPs for metals, semiconductors, oxides, organic molecules, metal–organic frameworks, etc. Since each category of materials share more structural, chemical, or functional similarities, the training is more likely to converge with smaller average errors.
One can also fine-tune the foundation models for specific applications. Lee and Xia174 developed a universal harmonic interatomic potential (MLUHIP) to predict phonon properties in crystalline solids more accurately. The study leverages existing phonon databases, transforming interatomic force constants into a force-displacement representation suitable for training MLIPs. In follow-up research, Lee et al. fine-tuned MACE on a dataset containing 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 structures with random atomic displacements of 2738 unary or binary materials covering 77 elements across the periodic table to predict forces. Subsequently, they used the fine-tuned potential to derive phonon properties. It is shown that the fine-tuned MACE model can predict full harmonic phonon spectra and calculate key thermodynamic properties with significantly improved accuracy compared to out-of-the-box UIPs.175
670 structures with random atomic displacements of 2738 unary or binary materials covering 77 elements across the periodic table to predict forces. Subsequently, they used the fine-tuned potential to derive phonon properties. It is shown that the fine-tuned MACE model can predict full harmonic phonon spectra and calculate key thermodynamic properties with significantly improved accuracy compared to out-of-the-box UIPs.175
3.3. Direct prediction of energy derivatives
Under harmonic approximation, vibrational properties, such as frequencies and displacements of normal modes, are obtained from the second derivative of the energy with respect to atomic coordinates. With an interatomic potential or force field, the second derivative is usually calculated by the finite displacement method. An alternative approach would be to predict the second derivative directly from the structure, bypassing the finite displacement calculations. The key difference between this approach and the MLIPs is that ground truth force constants are explicitly used during the training process to optimize the parameters.Domenichini and Dellago176 developed a model that utilizes a random forest regression algorithm to predict the energy's second derivatives (molecular Hessian) with respect to redundant internal coordinates (Fig. 17), ensuring rotational and translational invariance. They demonstrated the transferability of the model by training on the smaller QM7 dataset and testing the model on larger molecules from the QM9 dataset. Zou et al.177 introduced a deep-learning model, DetaNet, to predict molecular spectra with improved efficiency and accuracy. DetaNet combines E(3)-equivariance and self-attention mechanisms to predict various molecular properties, including scalars, vectors, and tensors, achieving near quantum-chemistry accuracy. To split the large Hessian matrix into manageable sizes, the DetaNet treats the atomic tensor for each atom and interatomic tensor for each atom pair with separate models. Combined with additional models to predict the derivative of the dipole moment and polarizability, one can then use all the predicted information to calculate the IR and Raman spectra. Besides vibrational spectroscopy, DetaNet also performed well in predicting UV-vis and NMR spectra.177 While DetaNet is focused on molecular spectroscopy, Fang et al.178 presented an approach using E(3)-equivariant GNNs to predict vibrational and phonon modes of periodic crystals. By evaluating the dynamical matrices of a trained energy model, the method can efficiently calculate phonon dispersion and the DOS for inorganic crystal materials. The approach can also be applied to predict molecular vibrational modes.
 | ||
| Fig. 17 Parity plots comparing predicted and calculated non-diagonal terms of the Hessian matrix. (a) Consecutive bond–bond, (b) included bond–angle, (c) adjacent bond–angle, (d) adjacent angle–angle, (e) consecutive angle–angle, (f) opposite angle–angle, (g) external bond–dihedral, and (h) internal bond–dihedral. Reprinted under CC BY 4.0 license from ref. 176. | ||
3.4. Direct prediction methods for atomic vibrational spectra: beyond MLIPs
Methods reviewed in previous sections can dramatically accelerate the lattice and molecular dynamics by predicting the potential energy and its derivatives from the molecular or crystal structure. The predicted properties are then used to calculate the end results, such as phonons and vibrational spectra. Alternatively, one can bypass the atomistic modeling altogether and use machine learning models to predict the end results directly.For instance, Gurunathan et al.179 developed ALIGNN, a graph-based neural network model, to directly predict phonon DOS and other thermodynamic properties, including heat capacity and vibrational entropy. Chen et al.90 used a graph-based E(3) equivariant neural network (E(3)NN) to predict phonon DOS from the atomic species and positions. The model effectively captures phonon properties and generalizes well to unseen materials. Mat2Spec by Kong et al.86 utilizes a probabilistic encoder and supervised contrastive learning on atomic structure and its corresponding phonon and electron DOS. The encoder concentrates atomic structure and spectral information in their latent spaces, while contrastive learning guides those spaces to coincide with each other, mapping structure-spectrum pairs to the same point in latent space. With a predictor for decoding latent space, the model can then effectively predict the spectrum, as shown in Fig. 18.
 | ||
| Fig. 18 Mat2Spec prediction of phonon and electron DOS. Reprinted under CC BY 4.0 license from ref. 86. | ||
Built on the work of Chen et al., a hybrid model combining autoencoders and E(3)NN was developed and trained against a large synthetic database of INS spectra from DFT calculations. The resulting model could predict one-dimensional and two-dimensional INS spectra with the 3D atomic coordinates as the only input (Fig. 19). This method enabled rapid and accurate predictions that can facilitate experimental design and data analysis in neutron scattering.106 These models are also implemented in the INSPIRED software,180 which has a graphic user interface to help users with no or little experience with computer simulations.
 | ||
| Fig. 19 A neural network for direct prediction of 2D INS spectra from the crystal structure (left) architecture of the neural network (right) predicting performance. Adapted under CC BY 4.0 license from ref. 106. | ||
Going beyond the prediction of histograms (phonon DOS or INS spectra), which have predetermined dimensions, it is sometimes desirable to predict individual phonons (frequencies and modes). Nguyen et al. trained the deeper GATGNN, a GNN with a global attention mechanism, to predict vibrational frequencies. However, unlike spectral prediction, the number of phonon modes is different for each material, resulting in variable output dimensions, which could be a problem for conventional neural networks. This work addressed the variable dimension issue using the zero-padding scheme.181 One could also adopt a new neural network architecture, such as the virtual node GNN.93 The additional virtual nodes in the graph enable dimensional flexibility, as shown in Fig. 7. For the full phonon prediction, the virtual nodes are constructed to have the shape of the dynamical matrix and trained to produce the wavevector-dependent eigenfrequencies. Furthermore, because of the flexibility in atomic embedding, the model can also be applied to structure models with partial occupancies, allowing the prediction of phonon dispersions in alloys, as shown in Fig. 20.93 The work demonstrates that any graph-based machine-learning model with proper atomic embedding has the potential to describe high-entropy systems where certain sites are occupied nearly randomly by multiple elements.182,183
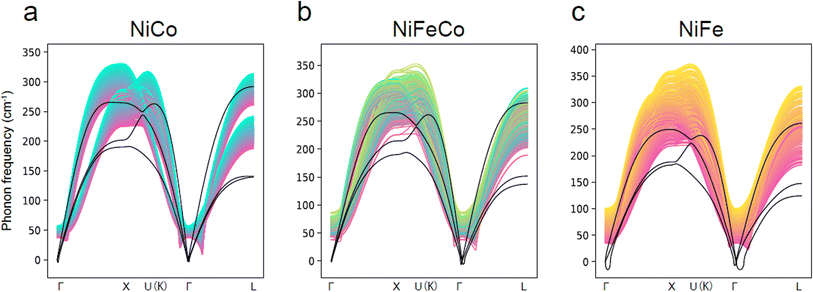 | ||
| Fig. 20 Phonon dispersion of substitution alloys (a) NiCo (b) NiFeCo and (c) NiFe – prediction under virtual crystal approximation with virtual node GNN. Red, blue, and yellow indicate pure Ni, Co, and Fe, respectively, and the intermediate colors represent alloys with different composition ratios. The black lines in each figure are ground truth computed by DFPT. Reprinted with permission from Springer Nature Copyright (2024).93 | ||
Machine learning models for direct prediction of IR spectra have also been developed. For instance, McGill et al.184 used an MPNN to construct vector representations (fingerprints) of the molecules. A feedforward neural network (FFNN) was then used to predict the IR spectra from the molecular vector representation. The model was first trained with computed spectra for over 85k molecules from PubChem and then further trained with nearly 57k experimental spectra measured on molecules in five different phases (Fig. 21). The phase information is introduced to the MPNN by a one-hot vector of size five. To evaluate the accuracy of the predicted spectra, they proposed a spectral information similarity metric, which applies Gaussian broadening and normalization to the spectra for them to be comparable. This study demonstrates that accurate IR spectra can be obtained efficiently, and the developed tool, Chemprop-IR, is potentially valuable for high-throughput screening and generation of large-scale databases of molecular spectra.
 | ||
| Fig. 21 Workflow of the chemprop-IR model, which was pretrained with computed spectra on ∼85k PubChem molecules and retrained with ∼57k experimental spectra. Reprinted with permission from the American Chemical Society Copyright (2021).184 | ||
Taking a different approach, Saquer et al. predicted the IR spectra from chemical structures via attention-based GNNs. They compared several GNN models, including AttentiveFP, which incorporates the message passing and graph attention mechanisms, MorganFP/DNN, graph attention network, graph convolutional network, and MPNN. AttentiveFP was shown to outperform other models.185 The performance enhancement in AttentiveFP is believed to be associated with the capability of the attention mechanism to learn not only from neighboring atoms but also from distant atoms. The attention weights in the trained model also provide insight into the relative importance of certain molecular features on the resulting spectra. This study highlights the potential benefit of introducing the attention mechanism into the graph neural networks for property predictions, as well as the importance of interpretability of the machine learning models. The interpretability can be achieved through multiple routes. In the case of AttentiveFP, the physical information on the atomic correlations is encoded in the attention weights. Predicting the Hessian, rather than the spectra, is another way to enhance interpretability, as the Hessian contains more fundamental information about interatomic interactions, which can be used to study other properties of the material. Although interpretability sometimes comes at the cost of efficiency, the knowledge we extract, which can guide material screening and design, is otherwise difficult to obtain with other data-driven approaches.
4. Future perspectives
Atomistic modeling of vibrational dynamics and spectral simulations have been widely used to understand structure–dynamics–property relationships in materials. They serve as a crucial bridge between theory and experiments. This bridge, however, is often challenging to navigate through, with roadblocks and barriers caused by the requirements for resources or expertise. The rapid development of AI for science, in terms of advanced software and hardware, has opened the door to new data-driven approaches. Successful data-driven methods are built on three key components: high-quality training data, efficient structure representation, and flexible feature encoding, as illustrated in Fig. 22.Within the overarching data-driven scheme, there can be different routes to achieve the goal. One approach is to use MLIP to accelerate the simulation of vibrational spectra. The MLIPs leverage neural networks as surrogates for predicting interatomic energies based on a given atomic configuration, achieving high accuracy when trained on DFT datasets. However, even with an appropriately trained MLIP, calculating vibrational spectra can still be time-consuming for large and complex systems. An alternative approach is, therefore, to predict the Hessian (force constants) matrix or the end results, which are the experimentally measurable vibrational spectra. While these methods can be more straightforward, they may render the results less interpretable and transferable. Fig. 23 summarizes the various data-driven approaches to the rapid prediction or calculation of the vibrational dynamics and spectra.
 | ||
| Fig. 23 Various routes towards data-driven prediction or calculation of the vibrational dynamics and spectra. | ||
Although significant progress has been made, especially in the past few years, there are still many areas where new data, models, and algorithms are needed to gain a more accurate and in-depth understanding of vibrational dynamics. Below, we outline several key aspects for advancing atomic vibration prediction using machine learning techniques.
4.1. Challenges and strategies on vibrational spectra predictions using machine learning
Machine learning models have revolutionized the study of atomic vibrations, providing extremely efficient and reasonably accurate solutions for vibrational spectra and other material properties. However, significant challenges persist in ensuring the robustness, generalizability, and applicability of these models, particularly in the areas of model transferability, extrapolation capability, and addressing dataset limitations.A fundamental issue in applying machine learning models to vibrational and spectral predictions is model transferability.186 Transferability refers to the capacity of a trained model to generalize its predictive power to different but related systems. Transfer learning techniques can fine-tune pre-trained models for specific material classes with limited data. Such approaches are particularly useful in domains such as quantum materials, which often contain heavy/magnetic elements and are computationally expensive to simulate using DFT. Another example is the use of models trained on computational datasets to predict properties in experimental datasets, where the computational data serve as a foundation for fine-tuning. Similarly, pre-training models on simpler molecular datasets and subsequently adapting them to more complex systems, such as crystals or polymers, have shown promise.187 For instance, Sanyal et al.188 leveraged multi-task learning to simultaneously predict formation energy, band gap, and Fermi energy, enhancing transferability by exploiting shared knowledge across these properties. However, achieving reliable transferability remains a significant hurdle when models are applied to vastly dissimilar systems, such as moving from inorganic solids to organic molecules, or when modeling phase transitions. Enhanced datasets representing diverse material systems and the development of domain adaptation techniques will be essential to bridging gaps between distinct datasets and improving transferability.
Another pressing challenge in machine learning for vibrational spectra predictions is the limited extrapolation capability of current models. While these models excel at interpolating within the distribution of their training datasets, they often fail when tasked with predicting properties for OOD materials.189 For example, materials with distinct chemical compositions or structures not represented in the training dataset often exhibit poor prediction performance. This issue is particularly evident in tasks such as predicting phonon DOS for materials with unique or rare elemental distributions. GNN-based models, for instance, show a marked drop in performance when applied to OOD scenarios.190 Studies by Segal et al. on bilinear transduction have addressed this issue by considering the positional relationship of data points in vector space to estimate representations for OOD materials.191 Similarly, adversarial learning methods, such as those proposed by Li et al., have been used to highlight data points with higher prediction uncertainties, thereby improving generalization.192 While significant progress has been made, the extrapolation of machine learning models to unprecedented material configurations remains an open area of research, requiring suitable application of domain adaptation and physics-informed modeling.190
The challenges of transferability and extrapolation are compounded by the risk of overfitting and underfitting. Overfitting occurs when a model becomes overly tailored to the training data, resulting in poor performance on unseen datasets. This issue is especially prevalent when using small datasets, as the model captures noise and spurious correlations rather than generalizable patterns. In contrast, underfitting arises when a model lacks sufficient complexity to capture the underlying relationships in the data, leading to overly simplified predictions. For instance, underfitting can manifest as an inability to predict accurately detailed peak positions in the vibrational spectra. These issues are further exacerbated in OOD scenarios, where current evaluation metrics often focus on interpolation ability rather than true extrapolation performance. Mitigation strategies include using regularization techniques, such as L2 regularization and dropout, as well as ensuring access to larger and more diverse datasets. Cross-validation and early stopping during training are also effective in reducing overfitting. Incorporating domain knowledge, such as symmetry constraints or physical laws, can guide model training and improve generalizability.
Dataset limitation is another critical issue to address in improving machine learning models for vibrational and spectral predictions. The scarcity of high-quality, diverse datasets has been a bottleneck in advancing machine learning approaches. Data augmentation techniques, such as generating synthetic vibrational spectra using VAEs or introducing controlled noise to expand dataset diversity, can alleviate this limitation. Active learning frameworks offer a complementary solution by identifying the most informative data points for labeling or computation, thus optimizing dataset creation. Transfer learning also provides a powerful tool for addressing small dataset challenges, enabling pre-trained models to act as a foundation for specialized tasks, such as predicting properties for rare material systems or unconventional lattice dynamics.
4.2. Prediction of higher-order derivatives and anharmonicity
Current methods to quantify anharmonicity, such as calculating the higher-order force constants, are extremely expensive even for very simple solids. Anharmonic phonons play a crucial role in understanding thermal conductivity, phonon lifetimes, and other temperature-dependent properties of materials such as thermal expansion, making their accurate prediction critical for advancing materials design. The computational cost increases significantly with the inclusion of higher-order terms due to the need for larger supercells, additional displacement configurations, and the inherently higher computational demand of DFT. It is thus highly valuable to have an AI-based method to predict the higher-order derivatives. The main barrier, however, is the lack of a ground truth dataset. So far, there is no high-quality database of higher-order force constants. High-throughput calculations, combined with active learning frameworks, offer a promising solution to effectively expand these datasets, balancing accuracy and computational cost. Furthermore, synthetic data augmentation, such as generating additional displacement configurations or utilization of MLIPs can increase dataset diversity. For example, pypolymlp193 has been used to accelerate the generation of anharmonic phonon datasets. Once the training dataset has been generated, further efforts can be devoted to efficient representations of higher-order force constants (e.g., as the three-dimensional tensor with equivariance principles) to ensure physically meaningful predictions without data augmentation.The alternative approach to train MLIPs requires a significantly larger number of configurations to capture the higher order derivatives quantitatively, compared to what is needed for just the forces or Hessian matrix. Preliminary attempt by Okabe et al.93 included anharmonic phonon calculations with around 200 simple solids, which showed the possibility of data-driven rapid computation of lattice thermal conductivity and Grüneisen parameters in simple solids. However, there is a large room for improvement in accuracy (e.g., by increasing the supercell size), and a truly useful model may require a much larger database to predict renormalized phonon frequencies and lifetimes caused by three-phonon scattering. A database of phonon anharmonicity covering a wide range of materials is thus highly desirable as a starting point. In contrast, molecular dynamics serve as an alternative approach to study anharmonicity, although the quality of the potentials will play a key role in extracting all anharmonic parameters. On another front, there has been growing interest in materials driven far away from equilibrium. For example, terahertz waves194,195 have been used to excite systems to a regime of high anharmonicity where even DFPT may breakdown with large, higher-order lattice displacement in selected phonon branches. We expect AI-powered approach will play a role in identifying the phases in the regime far away from equilibrium.
4.3. Design and production of training data
High-quality training data is the foundation of a good model. There are certain guidelines we can follow when preparing the training dataset. The first and foremost criterion is accuracy and consistency. For any machine learning model to be useful (i.e., not just a technical demo), the training data should be sufficiently accurate for the intended applications, and the accuracy should ideally be consistent throughout the dataset. Accurate descriptions of molecular vibration and phonons require accurate determination of atomic forces and energies, as the frequencies can be sensitive to minor errors in the derivatives of these quantities. Therefore, although many databases are already available, as listed in Table 2, they may still fall short of describing molecular vibrations and phonons. A practical solution may be to focus on certain categories of material first to produce high accuracy data. Once such dataset is available for a group of materials, the downstream components in the data pipeline can be developed and tested. The divide-and-conquer strategy may eventually lead to more efficient overall development in the area. On the other hand, high throughput experimental techniques, including the rapidly growing fourth-generation synchrotron-radiation sources, next generation spallation neutron sources, as well as emerging autonomous laboratory initiatives, may provide a venue for large-scale, accurate, and consistent experimental data suitable for machine learning applications. Besides the quality of the data itself, the format of the data and the user interface are also crucial. The FAIR (Findable, Accessible, Interpretable, Reusable) principles should be followed. Specifically, the datasets should be prepared and published in a way that is easy to access and interpret by users, which may require preprocessing, cleaning, and an interface for search and inference. Unambiguous labeling (such as atom species, quantity, physical unit, etc.), consistent formatting, and clear organization are necessary. Data curation can be as important as data generation to enhance its accessibility and impact. Some of the widely used datasets have user-friendly interfaces that can be easily integrated into the users' own workflow for searching, training, and visualization.Some experimental techniques, such as INS, can be intrinsically slow due to technical limitations (in the case of INS, it is mainly the low flux of the neutron beam). This makes producing experiment-based training data impractical, at least for the near future. In such cases, a digital twin can be developed to produce “realistic” synthetic data for model training. For example, Lin et al.196 have demonstrated a digital twin at a direct geometry neutron spectrometer using Monte Carlo ray tracing method to achieve super resolution. Using the synthetic data produced by the digital twins, the trained model can then be applied to the real instrument, and the available experimental data can be used to fine-tune the model further. Integrating the digital twin with the actual instrument may also allow active training, where the starting training data can be synthetic, and targeted experimental data are collected to efficiently fine-tune the model, reducing errors and uncertainties.
4.4. Improvement in representations
4.5. Generative models and inverse problems
As discussed in the previous sections, studying atomic vibrations and phonons is critical for understanding material properties, especially those linked to thermal behavior. However, the materials currently included in the existing databases represent only a tiny fraction of the vast material space, consisting of many combinations of atomic types, symmetries, and structural complexities.197 Relying solely on existing data limits the ability of computational approaches to become comprehensive tools for material discovery due to the challenges in dealing with OOD.190,198 Datasets suitable to describe higher-order derivatives and anharmonicity still need to be improved, partly because generating such data from DFT is very challenging. To truly explore the potential of novel molecules or crystal structures, it is essential to generate new materials that extend beyond the boundaries of current databases. Combined with autonomous laboratory technologies,199 exploration of new material candidates is expected to accelerate both experimentally and computationally, offering large-scale accurate and consistent data for further development of data-driven methods.Generative models have emerged as a promising approach to identifying new compounds that do not yet exist, providing a direct means to generate novel atomic structures without resorting to exhaustive searches.200,201 Crystal Structure Prediction (CSP) is a subfield of material discovery that seeks optimal structures with given known atomic compositions.202 In contrast, de novo generation (DNG) simultaneously explores atomic types, coordinates, and unit cell structures.203 Historically, CSP and DNG have relied on generating numerous candidate structures, which are then evaluated using high-throughput quantum mechanical calculations (e.g., DFT) to determine their stability. Early approaches have been foundational in this field, such as simple substitution rules204,205 or genetic algorithms.206 However, challenges remain in exploring the broad combinatorial space of atomic types and optimizing atomic positions within crystal lattices. Generative models, particularly diffusion models, have formulated the procedure to generate material structures from simple distributions into complex structures. Crystal Diffusion Variational Autoencoder (CDVAE) is a pioneering material generation model that optimizes the atom types and coordinates using Langevin dynamics.207 There emerged approaches focusing on jointly diffusing atomic positions, lattice parameters, and atomic types, such as DiffCSP208 and UniMat.209 Incorporating space groups as inductive biases has further improved these models in finding stable and diverse compounds.210,211
Additionally, structural constraints can be applied during the generation process when specific geometric configurations are known to yield unique physical properties.212 For instance, periodic crystals arranged in Kagome or Lieb lattice patterns exhibit distinctive magnetic and electronic characteristics, making them highly desirable for electronic applications (Fig. 24(a)).214,215 Furthermore, methods other than diffusion models have recently emerged. For example, fine-tuned LLM can write CIF files presenting stable crystal structures.216 Flow matching is another emerging approach to optimize the material structures by learning the optimal transport processes from the prior noise (Fig. 24(b)).213 Once a massive dataset of new materials is produced, the properties, including the stability and spectroscopic data, can be evaluated and characterized. This workflow is becoming mainstream for accessing unexplored material datasets to improve machine learning methods further.
 | ||
| Fig. 24 Examples of generative models for discovering new materials. (a) SCIGEN. Reprinted under CC BY 4.0 license from ref. 212. (b) FlowMM. Reprinted under CC BY 4.0 license from ref. 213. | ||
Our discussion on machine learning in this review before this section focuses on effective models that, given any atomic structure, can shortcut their dynamical property determinations (forward problem). Much less development happens in the opposite direction (inverse problem), i.e., determining the materials that satisfy given properties. One major reason roots from the fundamental nature of the inverse problem where the atomic structure is, in general, not a function of the target properties, i.e., multiple structures can give the same or similar property such that it is hard for a machine learning model to distinguish, or some desired property might be unobtainable with any stable material. This results in an ill-posed inverse problem and the ambiguity often leads to the failure of most machine learning models, which are essentially functions that uniquely map any input to a prediction.
Because of these, most inverse problems are generally tackled with either screening (pseudo-inverse) or global optimization methods, both utilizing the machine learning model for the forward problem to rapidly evaluate a large collection of known stable materials or a sequence of continuously perturbed structures through chemical space. While easier to implement, these methods can be very computationally expensive, and impossible to predict novel materials outside the known structure database or search space allowed by the optimization method. Fortunately, the development of generative models unlocks the possibilities beyond the massive screening of millions of generated structures. Because of the probabilistic nature of the generative model, the issue of the inverse problem can be alleviated since the generation can output different structures that are not in the training dataset each time, thanks to the random process in the initialization of each generation (Fig. 25).217
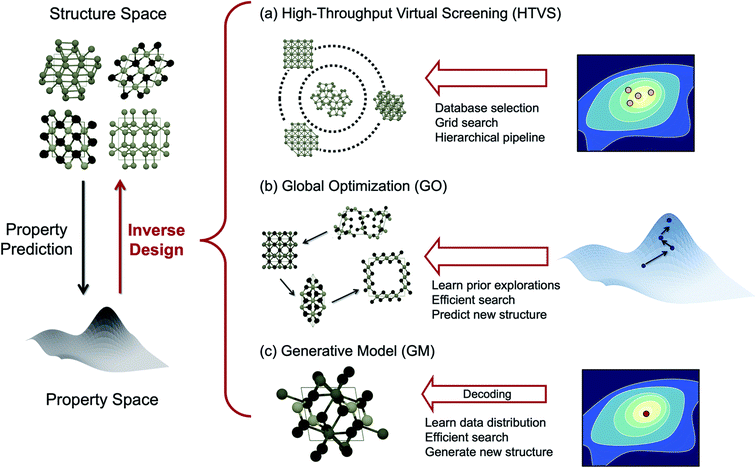 | ||
| Fig. 25 Inverse problem paradigms proposed by Noh et al. Reprinted under CC BY-NC 3.0 license from ref. 217. | ||
In image generation models, the input prompt can influence the generation through a conditional generative process. Similarly, in our generative models, we can potentially use input containing partial information to influence the generation of materials toward having such properties. For instance, Li et al.218 used a conditional graph generative model for drug design based on drug-likeness and synthetic accessibility. Ren et al.219 developed a variational autoencoder-based generative model framework to predict candidate materials not in the training dataset with user-defined target properties, including formation energy, band-gap, and thermoelectric power factor with up to 40% success rate. Recently, Liu et al.220 employed a diffusion-based generative model that can predict design parameters of a metamaterial periodic structure that exhibits the desired thermal response for thermal transparency application. At different runs, the model also predicts multiple sets of design parameters from the same input, allowing the selection of the most promising structure for fabrication.
While direct inverse problem solving using machine learning has intrinsic challenges, statistical approaches, such as Bayesian inference,221 could be a viable solution in some cases. The idea is to connect the spectrum with multiple candidate models, with each assigned a predicted probability. Different from the forward problem, where a unique solution is found for a given input, here the feature to be predicted is not a unique solution, but rather the likelihood of a list of solutions. This effectively tackles the possibly ill-posed inverse problems. Additional constraints (prior information) can also be applied to guide the prediction.
4.6. Advancement in neural network architectures
Machine learning's rapid progress yields a continuous flow of innovative neural network designs, enhancing models for materials science and broadening machine learning applications. Here, we propose several directions that might be worthwhile of incorporating into the material research arsenal, along with the motivations of applying each: Bayesian inference (confidence level to the model prediction), Kolmogorov–Arnold network (model interpretability), physics-informed machine learning (model that respects known physical laws), and foundation model (reusable multipurpose representation).In many machine learning studies in the materials science community, the primary aim of the models is to predict the assigned target properties as accurately as possible. While the models' overall performance can be evaluated from their average results, it is extremely challenging to determine the confidence of individual prediction on each input or even each part of the prediction from the same input. For instance, if the training data is not properly distributed, it is more likely that the model would perform poorly for those under-represented samples. However, a normal machine learning model could not intrinsically recognize this, requiring manual dataset analysis to understand the performance. For example, predicting phonon DOS of materials containing H, which forms different bonds with other atomic species, is generally more difficult if our representation utilizes atomic mass but neglects electrostatic effects.90 In this case, without proper knowledge of the fundamental rules behind the data, it is extremely hard to evaluate the confidence level for each of the testing data points. This is where Bayesian inference comes into play. By itself, Bayesian inference is a statistical framework that holistically manages prediction probability based on new prior knowledge that the model obtains. Applying Bayesian inference to machine learning is not new. It has been incorporated into many machine learning models, including Bayesian neural networks to evaluate prediction uncertainties and enhance robustness against overfitting,222,223 Bayesian optimization for efficient search,224,225 and Bayesian Markov chain Monte Carlo (BMCMC) for complex distribution sampling.226,227 Moreover, because of prior distribution management, the Bayesian framework is also robust against outlier data. It allows prior knowledge of the training tasks, e.g., dataset bias, to be included in the training. Hence, Bayesian inference can improve the current state of vibrational and other spectra predictions by providing information on whether a prediction, or part of the prediction from a particular input, has a high probability of being a poor prediction and requires attention from the user.
Another aspect of most machine learning models for forward problems is that they were developed as a black box that predicts the correct properties with given structural inputs. If we consider the predicted properties as our end goal, these models already serve their purposes. However, with the recent development in the Kolmogorov–Arnold Network (KAN) by Liu et al.,228,229 the possibility has emerged to use machine learning to help us understand the fundamental physics that builds up our data. Fundamentally, all neural networks (which will be called universal approximation network, or UAN, only in this part for clear distinction with KAN) are based on the universal approximation theorem (UAT), in which all well-behaved functions can be approximated by alternating between learnable linear and fixed non-linear layers in the models. In contrast, KANs are based on the Kolmogorov–Arnold theorem (KAT), in which all well-behaved multivariate functions can be approximated by stacking learnable non-linear layers. Ultimately, UAT can be considered as a special case of KAT, which implies that KAN should be able to replicate any neural network models with the following additional benefits. First, since each layer of KAN is a learnable non-linear function, it should, in principle, be more expressive than a layer of UAN. This implies that a smaller number of KAN layers can potentially emulate a larger UAN model, making the model easier to interpret for the functional form of the black box. Second, together with the attention mechanism, KAN can meaningfully reduce its connectivity either interactively or automatically, since each connection can be considered a simple dependence function. This aids the discovery of the simplest underlying functional form of the black box.228,229 So far, there have been many implementations of KAT including convolutional KAN,230 graph KAN,231 equivariant KAN,232 molecular dynamic KAN,233 residual KAN,234 etc. Recent development shows that KAN models trade off their model simplicity and accuracy with tremendous amounts of computational power during the training. There is still not much progress, except by Liu et al.,228,229 in pushing the research paradigm toward interpretability of the models – the current effort is more focused on the models' accuracy. Nonetheless, we believe the interpretability potential of KAN can lead to a better or more efficient approximation formula for thermal transport, discovery of new phase of matter, and, ultimately, discovery of new thermal physics.
When training a machine learning model, the goal is to minimize the prediction losses subject to some model regularizations. Often, these losses and regularizations are not based on the physical nature of the prediction target but purely on how close the prediction and target are and how many model parameters we have. These ad hoc optimizations and training restrictions are one of the main reasons why, in general, machine learning models cannot extrapolate out of the training dataset distribution even when the underlying physics is the same. A potential solution to this issue is a model incorporating physical laws into the training, which is called physics-informed machine learning. If the training data is large (big data) such that no extrapolation of the model is needed, one can simply use a normal deep neural network model with standard losses and regularizations. However, when the data amount is smaller, such that it does not represent the whole input space, more constraints reflecting physical laws need to be added to either losses or regularizations to compensate for the lost information. The smaller the dataset size provided, the greater the amount of physics needed.235 In one of the pioneer work by Zhou et al., a physics-informed neural network (PINN) that fully integrates partial differential equations into the loss function shows that if all physics required for understanding Boltzmann transport is supplied, there is no need for training data at all.236 Work by Okabe et al. on virtual node GNN shows better extrapolation power of the model to predicting Γ-phonon spectra of materials that are out of distribution when the harmonic model regularization is implemented.93 Zubatiuk and Isayev developed MLIP models to incorporate Hamiltonian of molecular systems so that the neural network is physics-informed or physics aware. This is shown to greatly increase the transferability of the model.237 Therefore, physics-informed machine learning can incorporate known vibrational physics as the model bias, making it possible for the model to be trained with smaller amounts of data while having a greater extrapolation power. This is crucial for the model that aims to use experimental data that are expensive to collect and might not be sufficiently diverse to cover the whole material space.
Currently, a significant amount of computational time and power in a machine learning project is used in data preprocessing. Moreover, each model usually has its own embedding layers, an additional data processing step before any actual training. However, since the chemical space of material, though vast, is fixed, it is reasonable to expect the latent space learned by all machine learning projects for property prediction can be very similar or directly correlated. Therefore, recently, there have been significant efforts on foundation models for science research.238–243 The foundation model is part of an unsupervised machine learning paradigm in which the purpose is not to train the model for a specific prediction task. Rather, it is for processing (pretraining) the raw data into a unified representation ready to be used in fine-tuning (training) for specialized tasks. Conceptually, this is similar to how one organizes space in a cupboard. There is no clear goal for this organization except making everything neat and easy to access for extraction and future additions. Of course, to produce a high-quality foundation model for all material research tasks, a large amount of high-quality data is required. Ideally, we would like to include all the data used for training the published models, as well as all data produced from both simulations and experiments in the foreseeable future to update the foundation model. Cumulatively, this should increase the quality of all machine learning research for materials science while saving time, effort, and energy from redundant data preprocessing. This can only happen with the cooperation of many research facilities.
4.7. Training strategies and software communities
In addition to the development of the model architecture, in this section, we highlight a few crucial components related to comprehensive strategies for model training, as well as the development of user-friendly software packages for the community.The structure–dynamics–property relationship has long been a foundational theme in materials science. In the era of AI, emerging tools are enabling us to explore this relationship at unprecedented speeds. This review highlights recent advancements in AI-driven investigations of molecular vibrations, phonons, and spectroscopy. These innovative approaches facilitate significantly faster simulations and calculations of atomic vibrations, even in complex systems. When integrated into experimental synthesis and characterization pipelines, they offer the potential to accelerate and deepen our understanding of the structure–dynamics–property relationship, effectively closing the loop in materials research. Furthermore, the transformative potential of AI methods paves the way for new materials discovery and inverse design. As computing power continues to expand, large-scale datasets grow, and novel models and methods emerge, we are entering a new AI-powered era in materials research.
Data availability
This is a review article. No original data or research results have been included.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
B. H. and Y. C. were supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy, under Contract No. DE-AC0500OR22725 with UT Battelle, LLC. This research was partially sponsored by the Artificial Intelligence Initiative as part of the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory. R. O. acknowledged the support from the U.S. Department of Energy (DOE), Office of Science (SC), Basic Energy Sciences (BES), Award No. DE-SC0021940. A. C. thanks the National Science Foundation (NSF) Designing Materials to Revolutionize and Engineer the Future (DMREF) Program with Award No. DMR-2118448. M. C. acknowledges support from DOE BES No. DE-SC0020148. M. L. was partially supported by NSF ITE-2345084. We thank the reviewers for valuable suggestions which helped to improve the paper. This manuscript has been authored in part by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).References
- G. Chen, Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons, Oxford University Press, 2005 Search PubMed.
- J. Barrett, Greenhouse Molecules, Their Spectra and Function in the Atmosphere, Energy Environ., 2005, 16(6), 1037–1045, DOI:10.1260/095830505775221542.
- J. A. Reissland, The Physics of Phonons, Wiley, 1973 Search PubMed.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, 1980 Search PubMed.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- A. Togo, First-principles Phonon Calculations with Phonopy and Phono3py, J. Phys. Soc. Jpn., 2022, 92(1), 012001, DOI:10.7566/JPSJ.92.012001.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, ShengBTE: A solver of the Boltzmann transport equation for phonons, Comput. Phys. Commun., 2014, 185(6), 1747–1758, DOI:10.1016/j.cpc.2014.02.015.
- P. Larkin, Infrared and Raman Spectroscopy: Principles and Spectral Interpretation, Elsevier, 2011 Search PubMed.
- D. Porezag and M. R. Pederson, Infrared intensities and Raman-scattering activities within density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(11), 7830–7836, DOI:10.1103/PhysRevB.54.7830.
- S. W. Lovesey and T. Springer, Dynamics of solids and liquids by neutron scattering, Springer-Verlag, New York, NY, 1977 Search PubMed.
- S. F. Parker, Vibrational spectroscopy of N-phenylmaleimide, Spectrochim. Acta, Part A, 2006, 63(3), 544–549, DOI:10.1016/j.saa.2005.06.001.
- G. L. Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications, 1996 Search PubMed.
- O. H. Seeck and B. Murphy, X-Ray Diffraction: Modern Experimental Techniques, Pan Stanford Publishing, 2015 Search PubMed.
- B. Eberhard, Phonon spectroscopy by inelastic x-ray scattering, Rep. Prog. Phys., 2000, 63(2), 171, DOI:10.1088/0034-4885/63/2/203.
- A. Q. R. Baron, High-Resolution Inelastic X-Ray Scattering I: Context, Spectrometers, Samples, and Superconductors, in Synchrotron Light Sources and Free-Electron Lasers: Accelerator Physics, Instrumentation and Science Applications, ed. E. J. Jaeschke, S. Khan, J. R. Schneider and J. B. Hastings, Springer International Publishing, 2020, pp. 2131–2212 Search PubMed.
- R. F. Egerton, Electron energy-loss spectroscopy in the TEM, Rep. Prog. Phys., 2009, 72(1), 016502, DOI:10.1088/0034-4885/72/1/016502.
- F. Hofer, F. P. Schmidt, W. Grogger and G. Kothleitner, Fundamentals of electron energy-loss spectroscopy, IOP Conf. Ser. Mater. Sci. Eng., 2016, 109(1), 012007, DOI:10.1088/1757-899X/109/1/012007.
- M. Xu, D.-L. Bao, A. Li, M. Gao, D. Meng, A. Li, S. Du, G. Su, S. J. Pennycook and S. T. Pantelides, et al., Single-atom vibrational spectroscopy with chemical-bonding sensitivity, Nat. Mater., 2023, 22(5), 612–618, DOI:10.1038/s41563-023-01500-9.
- M. J. Lagos, I. C. Bicket, S. S. Mousavi M and G. A. Botton, Advances in ultrahigh-energy resolution EELS: phonons, infrared plasmons and strongly coupled modes, Microscopy, 2022, 71(Supplement_1), i174–i199, DOI:10.1093/jmicro/dfab050.
- W. Sturhahn, T. S. Toellner, E. E. Alp, X. Zhang, M. Ando, Y. Yoda, S. Kikuta, M. Seto, C. W. Kimball and B. Dabrowski, Phonon Density of States Measured by Inelastic Nuclear Resonant Scattering, Phys. Rev. Lett., 1995, 74(19), 3832–3835, DOI:10.1103/PhysRevLett.74.3832.
- P. C. H. Mitchell, S. F. Parker, T. A. J. Ramirez-cuesta and J. Tomkinson, Vibrational Spectroscopy With Neutrons - With Applications In Chemistry, Biology, Materials Science And Catalysis, World Scientific Publishing Company, 2005 Search PubMed.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871, DOI:10.1103/PhysRev.136.B864.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138, DOI:10.1103/PhysRev.140.A1133.
- S. Mu, K. D. Dixit, X. Wang, D. L. Abernathy, H. Cao, S. E. Nagler, J. Yan, P. Lampen-Kelley, D. Mandrus and C. A. Polanco, et al., Role of the third dimension in searching for Majorana fermions in alpha-RuCl3 via phonons, Phys. Rev. Res., 2022, 4(1), 013067, DOI:10.1103/PhysRevResearch.4.013067.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet and E. Bousquet, et al., The Abinitproject: Impact, environment and recent developments, Comput. Phys. Commun., 2020, 248, 107042, DOI:10.1016/j.cpc.2019.107042.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29(46), 465901, DOI:10.1088/1361-648X/aa8f79.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561, DOI:10.1103/PhysRevB.47.558.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al., CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152(19), 194103, DOI:10.1063/5.0007045.
- A. Carreras, A. Togo and I. Tanaka, DynaPhoPy: A code for extracting phonon quasiparticles from molecular dynamics simulations, Comput. Phys. Commun., 2017, 221, 221–234, DOI:10.1016/j.cpc.2017.08.017.
- T. Sun, X. Shen and P. B. Allen, Phonon quasiparticles and anharmonic perturbation theory tested by molecular dynamics on a model system, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(22), 224304, DOI:10.1103/PhysRevB.82.224304.
- L. T. Kong, Phonon dispersion measured directly from molecular dynamics simulations, Comput. Phys. Commun., 2011, 182(10), 2201–2207, DOI:10.1016/j.cpc.2011.04.019.
- F. Zhou, W. Nielson, Y. Xia and V. Ozoliņš, Compressive sensing lattice dynamics. I. General formalism, Phys. Rev. B, 2019, 100(18), 184308, DOI:10.1103/PhysRevB.100.184308.
- F. Zhou, B. Sadigh, D. Åberg, Y. Xia and V. Ozoliņš, Compressive sensing lattice dynamics. II. Efficient phonon calculations and long-range interactions, Phys. Rev. B, 2019, 100(18), 184309, DOI:10.1103/PhysRevB.100.184309.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Temperature dependent effective potential method for accurate free energy calculations of solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(10), 104111, DOI:10.1103/PhysRevB.87.104111.
- A. Togo and A. Seko, On-the-fly training of polynomial machine learning potentials in computing lattice thermal conductivity, J. Chem. Phys., 2024, 160(21), 211001, DOI:10.1063/5.0211296.
- T. Tadano, Y. Gohda and S. Tsuneyuki, Anharmonic force constants extracted from first-principles molecular dynamics: applications to heat transfer simulations, J. Phys.: Condens. Matter, 2014, 26(22), 225402, DOI:10.1088/0953-8984/26/22/225402.
- T. Tadano and S. Tsuneyuki, Self-consistent phonon calculations of lattice dynamical properties in cubic SrTiO3 with first-principles anharmonic force constants, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(5), 054301, DOI:10.1103/PhysRevB.92.054301.
- Y. Oba, T. Tadano, R. Akashi and S. Tsuneyuki, First-principles study of phonon anharmonicity and negative thermal expansion in ScF3, Phys. Rev. Mater., 2019, 3(3), 033601, DOI:10.1103/PhysRevMaterials.3.033601.
- R. Masuki, T. Nomoto, R. Arita and T. Tadano, Ab initio structural optimization at finite temperatures based on anharmonic phonon theory: Application to the structural phase transitions of BaTiO3, Phys. Rev. B, 2022, 106(22), 224104, DOI:10.1103/PhysRevB.106.224104.
- R. Masuki, T. Nomoto, R. Arita and T. Tadano, Full optimization of quasiharmonic free energy with an anharmonic lattice model: Application to thermal expansion and pyroelectricity of wurtzite GaN and ZnO, Phys. Rev. B, 2023, 107(13), 134119, DOI:10.1103/PhysRevB.107.134119.
- F. Knoop, N. Shulumba, A. Castellano, J. P. A. Batista, R. Farris, M. J. Verstraete, M. Heine, D. Broido, D. S. Kim and J. Klarbring, et al., TDEP: Temperature Dependent Effective Potentials, J. Open Source Softw., 2024, 9(94), 6150, DOI:10.21105/joss.06150.
- F. Eriksson, E. Fransson and P. Erhart, The Hiphive Package for the Extraction of High-Order Force Constants by Machine Learning, Adv. Theory Simul., 2019, 2(5), 1800184, DOI:10.1002/adts.201800184.
- G. Shirane, S. M. Shapiro and J. M. Tranquada, Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques, Cambridge University Press, 2002, DOI:10.1017/CBO9780511534881.
- Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220(5–6), 567–570, DOI:10.1524/zkri.220.5.567.65075.
- K. Refson, P. R. Tulip and S. J. Clark, Variational density-functional perturbation theory for dielectrics and lattice dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(15), 155114, DOI:10.1103/PhysRevB.73.155114.
- Phonopy-Spectroscopy, https://github.com/skelton-group/Phonopy-Spectroscopy, accessed 2024/10/31.
- ASE vibration analysis, https://wiki.fysik.dtu.dk/ase/ase/vibrations/vibrations.html, accessed 2024/10/31.
- VASP-infrared-intensities, https://github.com/dakarhanek/VASP-infrared-intensities, accessed 2024/10/31.
- A. Fonari and S. Stauffer, vasp_raman.py, 2013, https://github.com/raman-sc/VASP/.
- N. T. Hung, J. Huang, Y. Tatsumi, T. Yang and R. Saito, QERaman: An open-source program for calculating resonance Raman spectra based on Quantum ESPRESSO, Comput. Phys. Commun., 2024, 295, 108967, DOI:10.1016/j.cpc.2023.108967.
- Y. Q. Cheng, L. L. Daemen, A. I. Kolesnikov and A. J. Ramirez-Cuesta, Simulation of Inelastic Neutron Scattering Spectra Using OCLIMAX, J. Chem. Theory Comput., 2019, 15(3), 1974–1982, DOI:10.1021/acs.jctc.8b01250.
- K. Dymkowski, S. F. Parker, F. Fernandez-Alonso and S. Mukhopadhyay, AbINS: The modern software for INS interpretation, Phys. B, 2018, 551, 443–448, DOI:10.1016/j.physb.2018.02.034.
- R. Fair, A. Jackson, D. Voneshen, D. Jochym, D. Le, K. Refson and T. Perring, Euphonic: inelastic neutron scattering simulations from force constants and visualization tools for phonon properties, J. Appl. Crystallogr., 2022, 55(6), 1689–1703, DOI:10.1107/S1600576722009256.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002, DOI:10.1063/1.4812323.
- K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne and A. Centrone, et al., The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6(1), 173, DOI:10.1038/s41524-020-00440-1.
- A. Togo, Phonondb database, https://github.com/atztogo/phonondb, accessed 2024/10/31.
- J. Schmidt, T. F. T. Cerqueira, A. H. Romero, A. Loew, F. Jäger, H.-C. Wang, S. Botti and M. A. L. Marques, Improving machine-learning models in materials science through large datasets, Mater. Today Phys., 2024, 48, 101560, DOI:10.1016/j.mtphys.2024.101560.
- L. Barroso-Luque, M. Shuaibi; X. Fu, B. M. Wood, M. Dzamba, M. Gao, A. Rizvi, C. L. Zitnick and Z. W. Ulissi, Open Materials 2024 (OMat24) Inorganic Materials Dataset and Models, arXiv, 2024, preprint, arXiv:2410.12771, DOI:10.48550/arXiv.2410.12771.
- Y. Cheng, M. B. Stone and A. J. Ramirez-Cuesta, A database of synthetic inelastic neutron scattering spectra from molecules and crystals, Sci. Data, 2023, 10(1), 54, DOI:10.1038/s41597-022-01926-x.
- SDBS (National Institute of Advanced Industrial Science and Technology), https://sdbs.db.aist.go.jp/Disclaimer.aspx, accessed 2024/10/31.
- S. F. Parker, TOSCA INS database, https://www.isis.stfc.ac.uk/Pages/INS-database.aspx, accessed 2024/10/31.
- B. Deng, Materials Project Trajectory (MPtrj) Dataset, figshare, 2023 Search PubMed.
- Alexandria database, https://alexandria.icams.rub.de/, accessed 2024/10/31.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Wiley, 2005 Search PubMed.
- J. Liu, Z. Shen, Y. He, X. Zhang, R. Xu, H. Yu and P. Cui, Towards Out-Of-Distribution Generalization: A Survey, arXiv, 2023, preprint, arXiv:2108.13624, DOI:10.48550/arXiv.2108.13624.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design, npj Comput. Mater., 2019, 5(1), 21, DOI:10.1038/s41524-019-0153-8.
- P. Xu, X. Ji, M. Li and W. Lu, Small data machine learning in materials science, npj Comput. Mater., 2023, 9(1), 42, DOI:10.1038/s41524-023-01000-z.
- M. Kulichenko, B. Nebgen, N. Lubbers, J. S. Smith, K. Barros, A. E. A. Allen, A. Habib, E. Shinkle, N. Fedik and Y. W. Li, et al., Data Generation for Machine Learning Interatomic Potentials and Beyond, Chem. Rev., 2024, 124(24), 13681–13714, DOI:10.1021/acs.chemrev.4c00572.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Physics-Inspired Structural Representations for Molecules and Materials, Chem. Rev., 2021, 121(16), 9759–9815, DOI:10.1021/acs.chemrev.1c00021.
- J. Baker and W. J. Hehre, Geometry optimization in cartesian coordinates: The end of the Z-matrix?, J. Comput. Chem., 1991, 12(5), 606–610, DOI:10.1002/jcc.540120510.
- J. Baker and F. Chan, The location of transition states: A comparison of Cartesian, Z-matrix, and natural internal coordinates, J. Comput. Chem., 1996, 17(7), 888–904, DOI:10.1002/(SICI)1096-987X(199605)17:7<888::AID-JCC12>3.0.CO;2-7.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87(18), 184115, DOI:10.1103/PhysRevB.87.184115.
- M. Wagih, P. M. Larsen and C. A. Schuh, Learning grain boundary segregation energy spectra in polycrystals, Nat. Commun., 2020, 11(1), 6376, DOI:10.1038/s41467-020-20083-6.
- D. S. Wigh, J. M. Goodman and A. A. Lapkin, A review of molecular representation in the age of machine learning, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12(5), e1603, DOI:10.1002/wcms.1603.
- S. Raghunathan and U. D. Priyakumar, Molecular representations for machine learning applications in chemistry, Int. J. Quantum Chem., 2022, 122(7), e26870, DOI:10.1002/qua.26870.
- Y. Harnik and A. Milo, A focus on molecular representation learning for the prediction of chemical properties, Chem. Sci., 2024, 15(14), 5052–5055, 10.1039/D4SC90043J.
- L. David, A. Thakkar, R. Mercado and O. Engkvist, Molecular representations in AI-driven drug discovery: a review and practical guide, J. Cheminf., 2020, 12(1), 56, DOI:10.1186/s13321-020-00460-5.
- G. M. Jones, B. Story, V. Maroulas and K. D. Vogiatzis, Molecular Representations for Machine Learning, Am. Chem. Soc., 2023 DOI:10.1021/acsinfocus.7e7006.
- R. Han, R. Ketkaew and S. Luber, A Concise Review on Recent Developments of Machine Learning for the Prediction of Vibrational Spectra, J. Phys. Chem. A, 2022, 126(6), 801–812, DOI:10.1021/acs.jpca.1c10417.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for Quantum chemistry, in Proceedings of the 34th International Conference on Machine Learning – Volume 70, Sydney, NSW, Australia, 2017 Search PubMed.
- P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. van Hoesel, H. Schopmans and T. Sommer, et al., Graph neural networks for materials science and chemistry, Commun. Mater., 2022, 3(1), 93, DOI:10.1038/s43246-022-00315-6.
- T. Xie and J. C. Grossman, Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties, Phys. Rev. Lett., 2018, 120(14), 145301, DOI:10.1103/PhysRevLett.120.145301.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31(9), 3564–3572, DOI:10.1021/acs.chemmater.9b01294.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Graph convolutional neural networks with global attention for improved materials property prediction, Phys. Chem. Chem. Phys., 2020, 22(32), 18141–18148, 10.1039/D0CP01474E.
- S. Kong, F. Ricci, D. Guevarra, J. B. Neaton, C. P. Gomes and J. M. Gregoire, Density of states prediction for materials discovery via contrastive learning from probabilistic embeddings, Nat. Commun., 2022, 13(1), 949, DOI:10.1038/s41467-022-28543-x.
- K. T. Schütt, O. T. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, arXiv, 2021, preprint, arXiv:2102.03150, DOI:10.48550/arXiv.2102.03150.
- V. G. Satorras, E. Hoogeboom and M. Welling, E(n) Equivariant Graph Neural Networks, arXiv, 2022, preprint, arXiv:2102.09844, DOI:10.48550/arXiv.2102.09844.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, Tensor field networks: Rotation- and translation-equivariant neural ne tworks for 3D point clouds, arXiv, 2018, preprint, arXiv:1802.08219, DOI:10.48550/arXiv.1802.08219.
- Z. Chen, N. Andrejevic, T. Smidt, Z. Ding, Q. Xu, Y.-T. Chi, Q. T. Nguyen, A. Alatas, J. Kong and M. Li, Direct Prediction of Phonon Density of States With Euclidean Neural Networks, Adv. Sci., 2021, 8(12), 2004214, DOI:10.1002/advs.202004214.
- M. Geiger; T. Smidt e3nn: Euclidean Neural Networks, arXiv, 2022, preprint, arXiv:2207.09453, DOI:10.48550/arXiv.2207.09453.
- N. T. Hung, R. Okabe, A. Chotrattanapituk and M. Li, Universal Ensemble-Embedding Graph Neural Network for Direct Prediction of Optical Spectra from Crystal Structures, Adv. Mater., 2024, 2409175, DOI:10.1002/adma.202409175.
- R. Okabe, A. Chotrattanapituk, A. Boonkird, N. Andrejevic, X. Fu, T. S. Jaakkola, Q. Song, T. Nguyen, N. Drucker and S. Mu, et al., Virtual node graph neural network for full phonon prediction, Nat. Comput. Sci., 2024, 4(7), 522–531, DOI:10.1038/s43588-024-00661-0.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, SchNet – A deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148(24), 241722, DOI:10.1063/1.5019779.
- J. Behler, Atom-centered symmetry functions for constructing high-dimensional neural network potentials, J. Chem. Phys., 2011, 134(7), 074106, DOI:10.1063/1.3553717.
- C. Liang, Y. Rouzhahong, C. Ye, C. Li, B. Wang and H. Li, Material symmetry recognition and property prediction accomplished by crystal capsule representation, Nat. Commun., 2023, 14(1), 5198, DOI:10.1038/s41467-023-40756-2.
- K. Yan, Y. Liu, Y. Lin and S. Ji, Periodic Graph Transformers for Crystal Material Property Prediction, arXiv, 2022, preprint, arXiv:2209.11807, DOI:10.48550/arXiv.2209.11807.
- K. Yan, C. Fu, X. Qian, X. Qian and S. Ji, Complete and Efficient Graph Transformers for Crystal Material Propert y Prediction, arXiv, 2024, preprint, arXiv:2403.11857, DOI:10.48550/arXiv.2403.11857.
- K. Yan, A. Saxton, X. Qian, X. Qian and S. Ji, A Space Group Symmetry Informed Network for O(3) Equivariant Crystal T ensor Prediction, arXiv, 2024, preprint, arXiv:2406.12888, DOI:10.48550/arXiv.2406.12888.
- L. M. Antunes, R. Grau-Crespo and K. T. Butler, Distributed representations of atoms and materials for machine learning, npj Comput. Mater., 2022, 8(1), 44, DOI:10.1038/s41524-022-00729-3.
- H. Abdi and L. J. Williams, Principal component analysis, Wiley Interdiscip. Rev. Comput. Stat., 2010, 2(4), 433–459, DOI:10.1002/wics.101.
- D. Bank, N. Koenigstein and R. Giryes, Autoencoders, arXiv, 2021, preprint, arXiv:2003.05991, DOI:10.48550/arXiv.2003.05991.
- A. M. Samarakoon, K. Barros, Y. W. Li, M. Eisenbach, Q. Zhang, F. Ye, V. Sharma, Z. L. Dun, H. Zhou and S. A. Grigera, et al., Machine-learning-assisted insight into spin ice Dy2Ti2O7, Nat. Commun., 2020, 11(1), 892, DOI:10.1038/s41467-020-14660-y.
- A. Samarakoon, D. A. Tennant, F. Ye, Q. Zhang and S. A. Grigera, Integration of machine learning with neutron scattering for the Hamiltonian tuning of spin ice under pressure, Commun. Mater., 2022, 3(1), 84, DOI:10.1038/s43246-022-00306-7.
- A. M. Samarakoon and D. Alan Tennant, Machine learning for magnetic phase diagrams and inverse scattering problems, J. Phys.: Condens. Matter, 2022, 34(4), 044002, DOI:10.1088/1361-648X/abe818.
- Y. Cheng, G. Wu, D. M. Pajerowski, M. B. Stone, A. T. Savici, M. Li and A. J. Ramirez-Cuesta, Direct prediction of inelastic neutron scattering spectra from the crystal structure, Mach. Learn.: Sci. Technol., 2023, 4(1), 015010, DOI:10.1088/2632-2153/acb315.
- Y. Su and C. Li, Uncovering obscured phonon dynamics from powder inelastic neutron scattering using machine learning, Mach. Learn.: Sci. Technol., 2024, 5(3), 035080, DOI:10.1088/2632-2153/ad79b6.
- G. Hinton and S. Roweis, Stochastic neighbor embedding, in Proceedings of the 15th International Conference on Neural Information Processing Systems, 2002 Search PubMed.
- L. Maaten and G. Hinton, Visualizing Data using t-SNE, J. Mach. Learn. Res., 2008, 9(86), 2579–2605 Search PubMed.
- L. McInnes, J. Healy, N. Saul and L. Großberger, UMAP: Uniform Manifold Approximation and Projection, J. Open Source Softw., 3(29), 861, DOI:10.21105/joss.00861.
- M. Offroy and L. Duponchel, Topological data analysis: A promising big data exploration tool in biology, analytical chemistry and physical chemistry, Anal. Chim. Acta, 2016, 910, 1–11, DOI:10.1016/j.aca.2015.12.037.
- Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue and Y. Nishiura, Hierarchical structures of amorphous solids characterized by persistent homology, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(26), 7035–7040, DOI:10.1073/pnas.1520877113.
- M. Cheng, R. Okabe, A. Chotrattanapituk and M. Li, Machine learning detection of Majorana zero modes from zero-bias peak measurements, Matter, 2024, 7(7), 2507–2520, DOI:10.1016/j.matt.2024.05.028.
- G. Carlsson, Topological methods for data modelling, Nat. Rev. Phys., 2020, 2(12), 697–708, DOI:10.1038/s42254-020-00249-3.
- F. L. Thiemann, N. O'Neill, V. Kapil, A. Michaelides and C. Schran, Introduction to machine learning potentials for atomistic simulations, arXiv, 2024, preprint, arXiv:2410.00626, DOI:10.48550/arXiv.2410.00626.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Comparing molecules and solids across structural and alchemical space, Phys. Chem. Chem. Phys., 2016, 18(20), 13754–13769, 10.1039/C6CP00415F.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, On-the-fly active learning of interpretable Bayesian force fields for atomistic rare events, npj Comput. Mater., 2020, 6(1), 20, DOI:10.1038/s41524-020-0283-z.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002, DOI:10.1088/1361-648X/aa680e.
- Y. Park, J. Kim, S. Hwang and S. Han, Scalable Parallel Algorithm for Graph Neural Network Interatomic Potentials in Molecular Dynamics Simulations, J. Chem. Theory Comput., 2024, 20(11), 4857–4868, DOI:10.1021/acs.jctc.4c00190.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- I. Batatia, D. P. Kovács, G. N. C. Simm, C. Ortner and G. Csányi, MACE: higher order equivariant message passing neural networks for fast and accurate force fields, in Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 2024 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5(9), 1031–1041, DOI:10.1038/s42256-023-00716-3.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, Nat. Comput. Sci., 2022, 2(11), 718–728, DOI:10.1038/s43588-022-00349-3.
- J. Zeng, D. Zhang, D. Lu, P. Mo, Z. Li, Y. Chen, M. Rynik, L. a. Huang, Z. Li and S. Shi, et al., DeePMD-kit v2: A software package for deep potential models, J. Chem. Phys., 2023, 159(5), 054801, DOI:10.1063/5.0155600.
- Y. Litman, V. Kapil, Y. M. Y. Feldman, D. Tisi, T. Begušić, K. Fidanyan, G. Fraux, J. Higer, M. Kellner and T. E. Li, et al., i-PI 3.0: A flexible and efficient framework for advanced atomistic simulations, J. Chem. Phys., 2024, 161(6), 062504, DOI:10.1063/5.0215869.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25, DOI:10.1016/j.softx.2015.06.001.
- D. A. Case, T. E. Cheatham Iii, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26(16), 1668–1688, DOI:10.1002/jcc.20290.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13(1), 2453, DOI:10.1038/s41467-022-29939-5.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning local equivariant representations for large-scale atomistic dynamics, Nat. Commun., 2023, 14(1), 579, DOI:10.1038/s41467-023-36329-y.
- Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang and H. E. Wang, DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models, Comput. Phys. Commun., 2020, 253, 107206, DOI:10.1016/j.cpc.2020.107206.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 185, DOI:10.1038/s41524-021-00650-1.
- Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Neuroevolution machine learning potentials: Combining high accuracy and low cost in atomistic simulations and application to heat transport, Phys. Rev. B, 2021, 104(10), 104309, DOI:10.1103/PhysRevB.104.104309.
- Z. Fan, Y. Wang, P. Ying, K. Song, J. Wang, Y. Wang, Z. Zeng, K. Xu, E. Lindgren and J. M. Rahm, et al., GPUMD: A package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations, J. Chem. Phys., 2022, 157(11), 114801, DOI:10.1063/5.0106617.
- R. Drautz, Atomic cluster expansion for accurate and transferable interatomic potentials, Phys. Rev. B, 2019, 99(1), 014104, DOI:10.1103/PhysRevB.99.014104.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, et al., A foundation model for atomistic materials chemistry, arXiv, 2024, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096.
- Matbench Discovery, https://matbench-discovery.materialsproject.org/, accessed 2024/10/31.
- J. Riebesell, R. E. A. Goodall, P. Benner, Y. Chiang, B. Deng, A. A. Lee, A. Jain and K. A. Persson, Matbench Discovery – A Framework to Evaluate Machine Learning Crystal Stability Predictions, arXiv, 2024, preprint, arXiv.2308.14920, DOI:10.48550/arXiv.2308.14920.
- H. Yang, C. Hu, Y. Zhou, X. Liu, Y. Shi, J. Li, G. Li, Z. Chen, S. Chen, C. Zeni, et al., MatterSim: A Deep Learning Atomistic Model Across Elements, Temperatur es and Pressures, arXiv, 2024, preprint, arXiv:2405.04967, DOI:10.48550/arXiv.2405.04967.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624(7990), 80–85, DOI:10.1038/s41586-023-06735-9.
- Orbital Materials, https://github.com/orbital-materials/orb-models/tree/main, accessed 2024/10/31.
- B. Deng, Y. Choi, P. Zhong, J. Riebesell, S. Anand, Z. Li, K. Jun, K. A. Persson and G. Ceder, Overcoming systematic softening in universal machine learning interato mic potentials by fine-tuning, arXiv, 2024, preprint, arXiv:2405.07105, DOI:10.48550/arXiv.2405.07105.
- Q. Ren, M. K. Gupta, M. Jin, J. Ding, J. Wu, Z. Chen, S. Lin, O. Fabelo, J. A. Rodríguez-Velamazán and M. Kofu, et al., Extreme phonon anharmonicity underpins superionic diffusion and ultralow thermal conductivity in argyrodite Ag8SnSe6, Nat. Mater., 2023, 22(8), 999–1006, DOI:10.1038/s41563-023-01560-x.
- M. K. Gupta, J. Ding, D. Bansal, D. L. Abernathy, G. Ehlers, N. C. Osti, W. G. Zeier and O. Delaire, Strongly Anharmonic Phonons and Their Role in Superionic Diffusion and Ultralow Thermal Conductivity of Cu7PSe6, Adv. Energy Mater., 2022, 12(23), 2200596, DOI:10.1002/aenm.202200596.
- A. Ghata, T. Bernges, O. Maus, B. Wankmiller, A. A. Naik, J. Bustamante, M. W. Gaultois, O. Delaire, M. R. Hansen and J. George, et al., Exploring the Thermal and Ionic Transport of Cu+ Conducting Argyrodite Cu7PSe6, Adv. Energy Mater., 2024, 2402039, DOI:10.1002/aenm.202402039.
- M. K. Gupta, S. Kumar, R. Mittal, S. K. Mishra, S. Rols, O. Delaire, A. Thamizhavel, P. U. Sastry and S. L. Chaplot, Distinct anharmonic characteristics of phonon-driven lattice thermal conductivity and thermal expansion in bulk MoSe2 and WSe2, J. Mater. Chem. A, 2023, 11(40), 21864–21873, 10.1039/D3TA03830K.
- T. M. Linker, A. Krishnamoorthy, L. L. Daemen, A. J. Ramirez-Cuesta, K. Nomura, A. Nakano, Y. Q. Cheng, W. R. Hicks, A. I. Kolesnikov and P. D. Vashishta, Neutron scattering and neural-network quantum molecular dynamics investigation of the vibrations of ammonia along the solid-to-liquid transition, Nat. Commun., 2024, 15(1), 3911, DOI:10.1038/s41467-024-48246-9.
- R. Jinnouchi, F. Karsai and G. Kresse, On-the-fly machine learning force field generation: Application to melting points, Phys. Rev. B, 2019, 100(1), 014105, DOI:10.1103/PhysRevB.100.014105.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phase Transitions of Hybrid Perovskites Simulated by Machine-Learning Force Fields Trained on the Fly with Bayesian Inference, Phys. Rev. Lett., 2019, 122(22), 225701, DOI:10.1103/PhysRevLett.122.225701.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, Descriptors representing two- and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials, J. Chem. Phys., 2020, 152(23), 234102, DOI:10.1063/5.0009491.
- S. Wieser and E. Zojer, Machine learned force-fields for an Ab-initio quality description of metal-organic frameworks, npj Comput. Mater., 2024, 10(1), 18, DOI:10.1038/s41524-024-01205-w.
- M. Gastegger, J. Behler and P. Marquetand, Machine learning molecular dynamics for the simulation of infrared spectra, Chem. Sci., 2017, 8(10), 6924–6935, 10.1039/C7SC02267K.
- B. Han, C. M. Isborn and L. Shi, Incorporating Polarization and Charge Transfer into a Point-Charge Model for Water Using Machine Learning, J. Phys. Chem. Lett., 2023, 14(16), 3869–3877, DOI:10.1021/acs.jpclett.3c00036.
- N. Xu, P. Rosander, C. Schäfer, E. Lindgren, N. Österbacka, M. Fang, W. Chen, Y. He, Z. Fan and P. Erhart, Tensorial Properties via the Neuroevolution Potential Framework: Fast Simulation of Infrared and Raman Spectra, J. Chem. Theory Comput., 2024, 20(8), 3273–3284, DOI:10.1021/acs.jctc.3c01343.
- P. Schienbein, Spectroscopy from Machine Learning by Accurately Representing the Atomic Polar Tensor, J. Chem. Theory Comput., 2023, 19(3), 705–712, DOI:10.1021/acs.jctc.2c00788.
- E. Berger and H.-P. Komsa, Polarizability models for simulations of finite temperature Raman spectra from machine learning molecular dynamics, Phys. Rev. Mater., 2024, 8(4), 043802, DOI:10.1103/PhysRevMaterials.8.043802.
- M. Fang, S. Tang, Z. Fan, Y. Shi, N. Xu and Y. He, Transferability of Machine Learning Models for Predicting Raman Spectra, J. Phys. Chem. A, 2024, 128(12), 2286–2294, DOI:10.1021/acs.jpca.3c07109.
- E. Berger, J. Niemelä, O. Lampela, A. H. Juffer and H.-P. Komsa, Raman Spectra of Amino Acids and Peptides from Machine Learning Polarizabilities, J. Chem. Inf. Model., 2024, 64(12), 4601–4612, DOI:10.1021/acs.jcim.4c00077.
- Y. Chen, S. V. Pios, M. F. Gelin and L. Chen, Accelerating Molecular Vibrational Spectra Simulations with a Physically Informed Deep Learning Model, J. Chem. Theory Comput., 2024, 20(11), 4703–4710, DOI:10.1021/acs.jctc.4c00173.
- M. Grumet, C. von Scarpatetti, T. Bučko and D. A. Egger, Delta Machine Learning for Predicting Dielectric Properties and Raman Spectra, J. Phys. Chem. C, 2024, 128(15), 6464–6470, DOI:10.1021/acs.jpcc.4c00886.
- D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio and M. Ceriotti, Accurate molecular polarizabilities with coupled cluster theory and machine learning, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(9), 3401–3406, DOI:10.1073/pnas.1816132116.
- M. Veit, D. M. Wilkins, Y. Yang, R. A. DiStasio Jr and M. Ceriotti, Predicting molecular dipole moments by combining atomic partial charges and atomic dipoles, J. Chem. Phys., 2020, 153(2), 024113, DOI:10.1063/5.0009106.
- K. Schütt, O. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, in International Conference on Machine Learning, PMLR, 2021, pp. 9377–9388 Search PubMed.
- G. Zhao, W. Yan, Z. Wang, Y. Kang, Z. Ma, Z.-G. Gu, Q.-H. Li and J. Zhang, Predict the Polarizability and Order of Magnitude of Second Hyperpolarizability of Molecules by Machine Learning, J. Phys. Chem. A, 2023, 127(29), 6109–6115, DOI:10.1021/acs.jpca.2c08563.
- A. E. Sifain, N. Lubbers, B. T. Nebgen, J. S. Smith, A. Y. Lokhov, O. Isayev, A. E. Roitberg, K. Barros and S. Tretiak, Discovering a Transferable Charge Assignment Model Using Machine Learning, J. Phys. Chem. Lett., 2018, 9(16), 4495–4501, DOI:10.1021/acs.jpclett.8b01939.
- B. Nebgen, N. Lubbers, J. S. Smith, A. E. Sifain, A. Lokhov, O. Isayev, A. E. Roitberg, K. Barros and S. Tretiak, Transferable Dynamic Molecular Charge Assignment Using Deep Neural Networks, J. Chem. Theory Comput., 2018, 14(9), 4687–4698, DOI:10.1021/acs.jctc.8b00524.
- M. Gandolfi, A. Rognoni, C. Aieta, R. Conte and M. Ceotto, Machine learning for vibrational spectroscopy via divide-and-conquer semiclassical initial value representation molecular dynamics with application to N-methylacetamide, J. Chem. Phys., 2020, 153(20), 204104, DOI:10.1063/5.0031892.
- S. Ye, K. Zhong, J. Zhang, W. Hu, J. D. Hirst, G. Zhang, S. Mukamel and J. Jiang, A Machine Learning Protocol for Predicting Protein Infrared Spectra, J. Am. Chem. Soc., 2020, 142(45), 19071–19077, DOI:10.1021/jacs.0c06530.
- S. Ye, K. Zhong, Y. Huang, G. Zhang, C. Sun and J. Jiang, Artificial Intelligence-based Amide-II Infrared Spectroscopy Simulation for Monitoring Protein Hydrogen Bonding Dynamics, J. Am. Chem. Soc., 2024, 146(4), 2663–2672, DOI:10.1021/jacs.3c12258.
- K. Kwac and M. Cho, Machine learning approach for describing vibrational solvatochromism, J. Chem. Phys., 2020, 152(17), 174101, DOI:10.1063/5.0005591.
- A. A. Kananenka, K. Yao, S. A. Corcelli and J. L. Skinner, Machine Learning for Vibrational Spectroscopic Maps, J. Chem. Theory Comput., 2019, 15(12), 6850–6858, DOI:10.1021/acs.jctc.9b00698.
- M. Gastegger, K. T. Schütt and K.-R. Müller, Machine learning of solvent effects on molecular spectra and reactions, Chem. Sci., 2021, 12(34), 11473–11483, 10.1039/D1SC02742E.
- Y. Zhang and B. Jiang, Universal machine learning for the response of atomistic systems to external fields, Nat. Commun., 2023, 14(1), 6424, DOI:10.1038/s41467-023-42148-y.
- A. Rodriguez, C. Lin, C. Shen, K. Yuan, M. Al-Fahdi, X. Zhang, H. Zhang and M. Hu, Unlocking phonon properties of a large and diverse set of cubic crystals by indirect bottom-up machine learning approach, Commun. Mater., 2023, 4(1), 61, DOI:10.1038/s43246-023-00390-3.
- H. Lee and Y. Xia, Machine learning a universal harmonic interatomic potential for predicting phonons in crystalline solids, Appl. Phys. Lett., 2024, 124(10), 102202, DOI:10.1063/5.0199743.
- H. Lee, V. I. Hegde, C. Wolverton and Y. Xia, Accelerating High-Throughput Phonon Calculations via Machine Learning Universal Potentials, arXiv, 2024, preprint, arXiv:2407.09674, DOI:10.48550/arXiv.2407.09674.
- G. Domenichini and C. Dellago, Molecular Hessian matrices from a machine learning random forest regression algorithm, J. Chem. Phys., 2023, 159(19), 194111, DOI:10.1063/5.0169384.
- Z. Zou, Y. Zhang, L. Liang, M. Wei, J. Leng, J. Jiang, Y. Luo and W. Hu, A deep learning model for predicting selected organic molecular spectra, Nat. Comput. Sci., 2023, 3(11), 957–964, DOI:10.1038/s43588-023-00550-y.
- S. Fang, M. Geiger, J. G. Checkelsky and T. Smidt, Phonon predictions with E(3)-equivariant graph neural networks, arXiv, 2024, preprint, arXiv:2403.11347, DOI:10.48550/arXiv.2403.11347.
- R. Gurunathan, K. Choudhary and F. Tavazza, Rapid prediction of phonon structure and properties using the atomistic line graph neural network (ALIGNN), Phys. Rev. Mater., 2023, 7(2), 023803, DOI:10.1103/PhysRevMaterials.7.023803.
- B. Han, A. T. Savici, M. Li and Y. Cheng, INSPIRED: Inelastic neutron scattering prediction for instantaneous results and experimental design, Comput. Phys. Commun., 2024, 304, 109288, DOI:10.1016/j.cpc.2024.109288.
- N. Nguyen, S.-Y. V. Louis, L. Wei, K. Choudhary, M. Hu and J. Hu, Predicting Lattice Vibrational Frequencies Using Deep Graph Neural Networks, ACS Omega, 2022, 7(30), 26641–26649, DOI:10.1021/acsomega.2c02765.
- E. P. George, D. Raabe and R. O. Ritchie, High-entropy alloys, Nat. Rev. Mater., 2019, 4(8), 515–534, DOI:10.1038/s41578-019-0121-4.
- B. L. Musicó, D. Gilbert, T. Z. Ward, K. Page, E. George, J. Yan, D. Mandrus and V. Keppens, The emergent field of high entropy oxides: Design, prospects, challenges, and opportunities for tailoring material properties, APL Mater., 2020, 8(4), 040912, DOI:10.1063/5.0003149.
- C. McGill, M. Forsuelo, Y. Guan and W. H. Green, Predicting Infrared Spectra with Message Passing Neural Networks, J. Chem. Inf. Model., 2021, 61(6), 2594–2609, DOI:10.1021/acs.jcim.1c00055.
- N. Saquer, R. Iqbal, J. D. Ellis and K. Yoshimatsu, Infrared spectra prediction using attention-based graph neural networks, Digit. Discov., 2024, 3(3), 602–609, 10.1039/D3DD00254C.
- N. Hoffmann, J. Schmidt, S. Botti and M. A. L. Marques, Transfer learning on large datasets for the accurate prediction of mat erial properties, arXiv, 2023, preprint, arXiv:2303.03000, DOI:10.48550/arXiv.2303.03000.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, Predicting Materials Properties with Little Data Using Shotgun Transfer Learning, ACS Cent. Sci., 2019, 5(10), 1717–1730, DOI:10.1021/acscentsci.9b00804.
- S. Sanyal, J. Balachandran, N. Yadati, A. Kumar, P. Rajagopalan, S. Sanyal and P. Talukdar, MT-CGCNN: Integrating Crystal Graph Convolutional Neural Network with Multitask Learning for Material Property Prediction, arXiv, 2018, preprint, arXiv:1811.05660, DOI:10.48550/arXiv.1811.05660.
- K. Li, A. N. Rubungo, X. Lei, D. Persaud, K. Choudhary, B. DeCost, A. B. Dieng and J. Hattrick-Simpers, Probing out-of-distribution generalization in machine learning for materials, arXiv, 2024, preprint, arXiv:2406.06489, DOI:10.48550/arXiv.2406.06489.
- S. S. Omee, N. Fu, R. Dong, M. Hu and J. Hu, Structure-based out-of-distribution (OOD) materials property prediction: a benchmark study, npj Comput. Mater., 2024, 10(1), 144, DOI:10.1038/s41524-024-01316-4.
- N. Segal, A. Netanyahu, K. P. Greenman, P. Agrawal and R. Gomez-Bombarelli, Known Unknowns: Out-of-Distribution Property Prediction in Materials and Molecules. 2024, 2024 Search PubMed.
- Q. Li, N. Miklaucic and J. Hu, Out-of-distribution materials property prediction using adversarial le arning based fine-tuning, arXiv, 2024, preprint, arXiv:2408.09297, DOI:10.48550/arXiv.2408.09297.
- A. Seko, Tutorial: Systematic development of polynomial machine learning potentials for elemental and alloy systems, J. Appl. Phys., 2023, 133, 011101, DOI:10.1063/5.0129045.
- X. Li, T. Qiu, J. Zhang, E. Baldini, J. Lu, A. M. Rappe and K. A. Nelson, Terahertz field–induced ferroelectricity in quantum paraelectric SrTiO3, Science, 2019, 364(6445), 1079–1082, DOI:10.1126/science.aaw4913.
- S. W. Teitelbaum, T. Shin, J. W. Wolfson, Y.-H. Cheng, I. J. P. Molesky, M. Kandyla and K. A. Nelson, Real-Time Observation of a Coherent Lattice Transformation into a High-Symmetry Phase, Phys. Rev. X, 2018, 8(3), 031081, DOI:10.1103/PhysRevX.8.031081.
- J. Y. Y. Lin, G. Sala and M. B. Stone, A super-resolution technique to analyze single-crystal inelastic neutron scattering measurements using direct-geometry chopper spectrometers, Rev. Sci. Instrum., 2022, 93, 025101, DOI:10.1063/5.0079031.
- A. M. Mroz, V. Posligua, A. Tarzia, E. H. Wolpert and K. E. Jelfs, Into the Unknown: How Computation Can Help Explore Uncharted Material Space, J. Am. Chem. Soc., 2022, 144(41), 18730–18743, DOI:10.1021/jacs.2c06833.
- S. Bulusu, B. Kailkhura, B. Li, P. K. Varshney and D. Song, Anomalous Example Detection in Deep Learning: A Survey, IEEE Access, 2020, 8, 132330–132347, DOI:10.1109/ACCESS.2020.3010274.
- N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He, D. Milsted, M. J. McDermott, M. Gallant, E. D. Cubuk and A. Merchant, et al., An autonomous laboratory for the accelerated synthesis of novel materials, Nature, 2023, 624(7990), 86–91, DOI:10.1038/s41586-023-06734-w.
- D. M. Anstine and O. Isayev, Generative Models as an Emerging Paradigm in the Chemical Sciences, J. Am. Chem. Soc., 2023, 145(16), 8736–8750, DOI:10.1021/jacs.2c13467.
- M. Alverson, S. G. Baird, R. Murdock, S.-H. Ho, J. Johnson and T. D. Sparks, Generative adversarial networks and diffusion models in material discovery, Digit. Discov., 2024, 3(1), 62–80, 10.1039/D3DD00137G.
- K. Ryan, J. Lengyel and M. Shatruk, Crystal Structure Prediction via Deep Learning, J. Am. Chem. Soc., 2018, 140(32), 10158–10168, DOI:10.1021/jacs.8b03913.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de-novo design through deep reinforcement learning, J. Cheminf., 2017, 9(1), 48, DOI:10.1186/s13321-017-0235-x.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Data Mined Ionic Substitutions for the Discovery of New Compounds, Inorg. Chem., 2011, 50(2), 656–663, DOI:10.1021/ic102031h.
- M. Kusaba, C. Liu and R. Yoshida, Crystal structure prediction with machine learning-based element substitution, Comput. Mater. Sci., 2022, 211, 111496, DOI:10.1016/j.commatsci.2022.111496.
- P. C. Jennings, S. Lysgaard, J. S. Hummelshøj, T. Vegge and T. Bligaard, Genetic algorithms for computational materials discovery accelerated by machine learning, npj Comput. Mater., 2019, 5(1), 46, DOI:10.1038/s41524-019-0181-4.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Crystal Diffusion Variational Autoencoder for Periodic Material Genera tion, arXiv, 2022, preprint, arXiv:2110.06197, DOI:10.48550/arXiv.2110.06197.
- R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu and Y. Liu, Crystal Structure Prediction by Joint Equivariant Diffusion, arXiv, 2024, preprint, arXiv:2309.04475, DOI:10.48550/arXiv.2309.04475.
- S. Yang, K. Cho, A. Merchant, P. Abbeel, D. Schuurmans, I. Mordatch and E. D. Cubuk, Scalable Diffusion for Materials Generation, arXiv, 2024, preprint, arXiv:2311.09235, DOI:10.48550/arXiv.2311.09235.
- C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, S. Shysheya, J. Crabbé, L. Sun, J. Smith, et al., MatterGen: a generative model for inorganic materials design, arXiv, 2024, preprint, arXiv:2312.03687, DOI:10.48550/arXiv.2312.03687.
- R. Jiao, W. Huang, Y. Liu, D. Zhao and Y. Liu, Space Group Constrained Crystal Generation, arXiv, 2024, preprint, arXiv:2402.03992, DOI:10.48550/arXiv.2402.03992.
- R. Okabe, M. Cheng, A. Chotrattanapituk, N. T. Hung, X. Fu, B. Han, Y. Wang, W. Xie, R. J. Cava, T. S. Jaakkola, et al., Structural Constraint Integration in Generative Model for Discovery of Quantum Material Candidates, arXiv, 2024, preprint, arXiv:2407.04557, DOI:10.48550/arXiv.2407.04557.
- B. K. Miller, R. T. Q. Chen, A. Sriram and B. M. Wood, FlowMM: Generating Materials with Riemannian Flow Matching, arXiv, 2024, preprint, arXiv:2406.04713, DOI:10.48550/arXiv.2406.04713.
- M. Kang, S. Fang, L. Ye, H. C. Po, J. Denlinger, C. Jozwiak, A. Bostwick, E. Rotenberg, E. Kaxiras and J. G. Checkelsky, et al., Topological flat bands in frustrated Kagome lattice CoSn, Nat. Commun., 2020, 11(1), 4004, DOI:10.1038/s41467-020-17465-1.
- M. R. Slot, T. S. Gardenier, P. H. Jacobse, G. C. P. van Miert, S. N. Kempkes, S. J. M. Zevenhuizen, C. M. Smith, D. Vanmaekelbergh and I. Swart, Experimental realization and characterization of an electronic Lieb lattice, Nat. Phys., 2017, 13(7), 672–676, DOI:10.1038/nphys4105.
- N. Gruver, A. Sriram, A. Madotto, A. G. Wilson, C. L. Zitnick, Z. Ulissi, Fine-Tuned Language Models Generate Stable Inorganic Materials as Text, arXiv, 2024, preprint, arXiv:2402.04379, DOI:10.48550/arXiv.2402.04379.
- J. Noh, G. H. Gu, S. Kim and Y. Jung, Machine-enabled inverse design of inorganic solid materials: promises and challenges, Chem. Sci., 2020, 11(19), 4871–4881, 10.1039/D0SC00594K.
- Y. Li, L. Zhang and Z. Liu, Multi-objective de novo drug design with conditional graph generative model, J. Cheminf., 2018, 10(1), 33, DOI:10.1186/s13321-018-0287-6.
- Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle and S. Sun, et al., An invertible crystallographic representation for general inverse design of inorganic crystals with targeted properties, Matter, 2022, 5(1), 314–335, DOI:10.1016/j.matt.2021.11.032.
- B. Liu, L. Xu, Y. Wang and J. Huang, Diffusion model-based inverse design for thermal transparency, J. Appl. Phys., 2024, 135(12), 125101, DOI:10.1063/5.0197999.
- F. G. Waqar, S. Patel and C. M. Simon, A tutorial on the Bayesian statistical approach to inverse problems, APL Mach. Learn., 2023, 1, 041101, DOI:10.1063/5.0154773.
- L. V. Jospin, H. Laga, F. Boussaid, W. Buntine and M. Bennamoun, Hands-On Bayesian Neural Networks—A Tutorial for Deep Learning Users, IEEE Comput. Intell. Mag., 2022, 17(2), 29–48, DOI:10.1109/MCI.2022.3155327.
- E. Goan and C. Fookes, Bayesian Neural Networks: An Introduction and Survey, in Case Studies in Applied Bayesian Data Science: CIRM Jean-Morlet Chair, Fall 2018, ed. K. L. Mengersen, P. Pudlo and C. P. Robert, Springer International Publishing, 2020, pp. 45–87 Search PubMed.
- Y. Jin and P. V. Kumar, Bayesian optimisation for efficient material discovery: a mini review, Nanoscale, 2023, 15(26), 10975–10984, 10.1039/D2NR07147A.
- Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada and S. A. Khan, et al., Benchmarking the performance of Bayesian optimization across multiple experimental materials science domains, npj Comput. Mater., 2021, 7(1), 188, DOI:10.1038/s41524-021-00656-9.
- P. Dellaportas, J. J. Forster and I. Ntzoufras, On Bayesian model and variable selection using MCMC, Stat. Comput., 2002, 12(1), 27–36, DOI:10.1023/A:1013164120801.
- J. Deleeuw, H. Goldstein and E. Meijer, Handbook of Multilevel Analysis, Springer, New York, 2007 Search PubMed.
- Z. Liu, Y. Wang, S. Vaidya, F. Ruehle, J. Halverson, M. Soljačić, T. Y. Hou, M. Tegmark, KAN: Kolmogorov-Arnold Networks, arXiv, 2024, preprint, arXiv:2404.19756, DOI:10.48550/arXiv.2404.19756.
- Z. Liu, P. Ma, Y. Wang, W. Matusik and M. Tegmark, KAN 2.0: Kolmogorov-Arnold Networks Meet Science, arXiv, 2024, preprint, arXiv:2408.10205, DOI:10.48550/arXiv.2408.10205.
- A. D. Bodner, A. S. Tepsich, J. N. Spolski and S. Pourteau, Convolutional Kolmogorov-Arnold Networks, arXiv, 2024, preprint, arXiv:2406.13155, DOI:10.48550/arXiv.2406.13155.
- M. Kiamari, M. Kiamari, B. Krishnamachari, GKAN: Graph Kolmogorov-Arnold Networks, arXiv, 2024, preprint, arXiv:2406.06470, DOI:10.48550/arXiv.2406.06470.
- L. Hu, Y. Wang and Z. Lin, EKAN: Equivariant Kolmogorov-Arnold Networks, arXiv, 2024, preprint, arXiv:2410.00435, DOI:10.48550/arXiv.2410.00435.
- Y. Nagai and M. Okumura, Kolmogorov–Arnold networks in molecular dynamics, arXiv, 2024, preprint, arXiv:2407.17774, DOI:10.48550/arXiv.2407.17774.
- R. C. Yu, S. Wu and J. Gui, Residual Kolmogorov-Arnold Network for Enhanced Deep Learning, arXiv, 2024, preprint, arXiv:2410.05500, DOI:10.48550/arXiv.2410.05500.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Physics-informed machine learning, Nat. Rev. Phys., 2021, 3(6), 422–440, DOI:10.1038/s42254-021-00314-5.
- J. Zhou, R. Li and T. Luo, Physics-informed neural networks for solving time-dependent mode-resolved phonon Boltzmann transport equation, npj Comput. Mater., 2023, 9(1), 212, DOI:10.1038/s41524-023-01165-7.
- T. Zubatiuk and O. Isayev, Development of Multimodal Machine Learning Potentials: Toward a Physics-Aware Artificial Intelligence, Acc. Chem. Res., 2021, 54(7), 1575–1585, DOI:10.1021/acs.accounts.0c00868.
- J. Yin, S. Dash, F. Wang and M. Shankar, FORGE: Pre-Training Open Foundation Models for Science, in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 2023 Search PubMed.
- R. Bommasani, D. A. Hudson, E. Adeli, R. Altman, S. Arora, S. Arx, M. S. Bernstein, J. Bohg, A. Bosselut, E. Brunskill, et al., On the Opportunities and Risks of Foundation Models, arXiv, 2022, preprint, arXiv:2108.07258, DOI:10.48550/arXiv.2108.07258.
- S. Takeda, A. Kishimoto, L. Hamada, D. Nakano and J. R. Smith, Foundation model for material science, in Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence and Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence and Thirteenth Symposium on Educational Advances in Artificial Intelligence, 2023 Search PubMed.
- K. L. K. Lee, C. Gonzales, M. Spellings, M. Galkin, S. Miret and N. Kumar, Towards Foundation Models for Materials Science: The Open MatSci ML Toolkit, in Proceedings of the SC '23 Workshops of The International Conference on High Performance Computing, Network, Storage, and Analysis, Denver, CO, USA, 2023 Search PubMed.
- X. Wang, S. Liu, A. Tsaris, J.-Y. Choi, A. Aji, M. Fan, W. Zhang, J. Yin, M. Ashfaq, D. Lu, et al., ORBIT: Oak Ridge Base Foundation Model for Earth System Predictability, arXiv, 2024, preprint, arXiv:2404.14712, DOI:10.48550/arXiv.2404.14712.
- T. Nguyen, R. Shah, H. Bansal, T. Arcomano, R. Maulik, V. Kotamarthi, I. Foster, S. Madireddy and A. Grover, Scaling transformer neural networks for skillful and reliable medium-r ange weather forecasting, arXiv, 2024, preprint, arXiv:2312.03876, DOI:10.48550/arXiv.2312.03876.
- M. P. Prange, N. Govind, P. Stinis, E. S. Ilton and A. A. Howard, A Multifidelity and Multimodal Machine Learning Approach for Extracting Bonding Environments of Impurities and Dopants from X-ray Spectroscopies, United States, 2023, DOI:10.2172/2263311.
- M. Alberts, O. Schilter, F. Zipoli, N. Hartrampf and T. Laino, Unraveling Molecular Structure: A Multimodal Spectroscopic Dataset for Chemistry, arXiv, 2024, preprint, arXiv:2407.17492, DOI:10.48550/arXiv.2407.17492.
- X. Liu, P.-P. De Breuck, L. Wang and G.-M. Rignanese, A simple denoising approach to exploit multi-fidelity data for machine learning materials properties, npj Comput. Mater., 2022, 8(1), 233, DOI:10.1038/s41524-022-00925-1.
- C. Fare, P. Fenner, M. Benatan, A. Varsi and E. O. Pyzer-Knapp, A multi-fidelity machine learning approach to high throughput materials screening, npj Comput. Mater., 2022, 8(1), 257, DOI:10.1038/s41524-022-00947-9.
- K. P. Greenman, W. H. Green and R. Gómez-Bombarelli, Multi-fidelity prediction of molecular optical peaks with deep learning, Chem. Sci., 2022, 13(4), 1152–1162, 10.1039/D1SC05677H.
- G. Pilania, J. E. Gubernatis and T. Lookman, Multi-fidelity machine learning models for accurate bandgap predictions of solids, Comput. Mater. Sci., 2017, 129, 156–163, DOI:10.1016/j.commatsci.2016.12.004.
- S. Gong, S. Wang, T. Xie, W. H. Chae, R. Liu, Y. Shao-Horn and J. C. Grossman, Calibrating DFT Formation Enthalpy Calculations by Multifidelity Machine Learning, JACS Au, 2022, 2(9), 1964–1977, DOI:10.1021/jacsau.2c00235.
- R. Batra and S. Sankaranarayanan, Machine learning for multi-fidelity scale bridging and dynamical simulations of materials, JPhys Materials, 2020, 3(3), 031002, DOI:10.1088/2515-7639/ab8c2d.
- A. Zhu, S. Batzner, A. Musaelian and B. Kozinsky, Fast uncertainty estimates in deep learning interatomic potentials, J. Chem. Phys., 2023, 158(16), 164111, DOI:10.1063/5.0136574.
- M. Kulichenko, K. Barros, N. Lubbers, Y. W. Li, R. Messerly, S. Tretiak, J. S. Smith and B. Nebgen, Uncertainty-driven dynamics for active learning of interatomic potentials, Nat. Comput. Sci., 2023, 3(3), 230–239, DOI:10.1038/s43588-023-00406-5.
- A. R. Tan, S. Urata, S. Goldman, J. C. B. Dietschreit and R. Gómez-Bombarelli, Single-model uncertainty quantification in neural network potentials does not consistently outperform model ensembles, npj Comput. Mater., 2023, 9(1), 225, DOI:10.1038/s41524-023-01180-8.
- Y. Hu, J. Musielewicz, Z. W. Ulissi and A. J. Medford, Robust and scalable uncertainty estimation with conformal prediction for machine-learned interatomic potentials, Mach. Learn.: Sci. Technol., 2022, 3(4), 045028, DOI:10.1088/2632-2153/aca7b1.
- E. Annevelink and V. Viswanathan, Statistical methods for resolving poor uncertainty quantification in m achine learning interatomic potentials, arXiv, 2023, preprint, arXiv:2308.15653, DOI:10.48550/arXiv.2308.15653.
- S. Pathrudkar, P. Thiagarajan, S. Agarwal, A. S. Banerjee and S. Ghosh, Electronic structure prediction of multi-million atom systems through uncertainty quantification enabled transfer learning, npj Comput. Mater., 2024, 10(1), 175, DOI:10.1038/s41524-024-01305-7.
- Y. Wei, Z. Liu and G. Qin, Prediction methods for phonon transport properties of inorganic crystals: from traditional approaches to artificial intelligence, Nanoscale Horiz., 2025, 10, 230–257, 10.1039/D4NH00487F.
- A. Ghosh, B. G. Sumpter, O. Dyck, S. V. Kalinin and M. Ziatdinov, Ensemble learning-iterative training machine learning for uncertainty quantification and automated experiment in atom-resolved microscopy, npj Comput. Mater., 2021, 7(1), 100, DOI:10.1038/s41524-021-00569-7.
- H. Valladares, T. Li, L. Zhu, H. El-Mounayri, A. M. Hashem, A. E. Abdel-Ghany and A. Tovar, Gaussian process-based prognostics of lithium-ion batteries and design optimization of cathode active materials, J. Power Sources, 2022, 528, 231026, DOI:10.1016/j.jpowsour.2022.231026.
- Y. Li, S. Rao, A. Hassaine, R. Ramakrishnan, D. Canoy, G. Salimi-Khorshidi, M. Mamouei, T. Lukasiewicz and K. Rahimi, Deep Bayesian Gaussian processes for uncertainty estimation in electronic health records, Sci. Rep., 2021, 11(1), 20685, DOI:10.1038/s41598-021-00144-6.
- J. Li, X. Long, X. Deng, W. Jiang, K. Zhou, C. Jiang and X. Zhang, A principled distance-aware uncertainty quantification approach for enhancing the reliability of physics-informed neural network, Reliab. Eng. Syst. Saf., 2024, 245, 109963, DOI:10.1016/j.ress.2024.109963.
- W. Blokland, K. Rajput, M. Schram, T. Jeske, P. Ramuhalli, C. Peters, Y. Yucesan and A. Zhukov, Uncertainty aware anomaly detection to predict errant beam pulses in the Oak Ridge Spallation Neutron Source accelerator, Phys. Rev. Spec. Top. Accel. Beams, 2022, 25(12), 122802, DOI:10.1103/PhysRevAccelBeams.25.122802.
- H. M. Bui and A. Liu, Density-Regression: Efficient and Distance-aware Deep Regressor for Uncertainty Estimation under Distribution Shifts, in Proceedings of The 27th International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research, 2024 Search PubMed.
- H. Hayashi, A Hybrid of Generative and Discriminative Models Based on the Gaussian-Coupled Softmax Layer, IEEE Transact. Neural Networks Learn. Syst., 2024, 1–11, DOI:10.1109/TNNLS.2024.3358113.
- N. Dionelis, R. Jackson, S. A. Tsaftaris and M. Yaghoobi, SLX: Similarity Learning for X-Ray Screening and Robust Automated Disassembled Object Detection, in 2023 International Joint Conference on Neural Networks (IJCNN), 18-23 June 2023, 2023, pp, 1–8, DOI:10.1109/IJCNN54540.2023.10190997.
- A. P. Soleimany, A. Amini, S. Goldman, D. Rus, S. N. Bhatia and C. W. Coley, Evidential Deep Learning for Guided Molecular Property Prediction and Discovery, ACS Cent. Sci., 2021, 7(8), 1356–1367, DOI:10.1021/acscentsci.1c00546.
- Z. Fan, C. Zuo, C. Guo, Z. Yang, X. Yan and X. Li, Uncertainty Quantification in Predicting Physical Property of Porous Medium With Bayesian Evidential Learning, IEEE Trans. Geosci. Rem. Sens., 2024, 62, 1–17, DOI:10.1109/TGRS.2024.3428575.
- G. Singh, G. Moncrieff, Z. Venter, K. Cawse-Nicholson, J. Slingsby and T. B. Robinson, Uncertainty quantification for probabilistic machine learning in earth observation using conformal prediction, Sci. Rep., 2024, 14(1), 16166, DOI:10.1038/s41598-024-65954-w.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |