 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unveiling CO2 reactivity with data-driven methods†
Maike Eckhoff ,
Kerstin L. Bublitz
,
Kerstin L. Bublitz and
Jonny Proppe
and
Jonny Proppe *
*
TU Braunschweig, Institute of Physical and Theoretical Chemistry, Gauss Str 17, 38106 Braunschweig, Germany. E-mail: j.proppe@tu-braunschweig.de
First published on 26th February 2025
Abstract
Carbon dioxide is a versatile C1 building block in organic synthesis. Understanding its reactivity is crucial for predicting reaction outcomes and identifying suitable substrates for the creation of value-added chemicals and drugs. A recent study [Li et al., J. Am. Chem. Soc., 2020, 142, 8383] estimated the reactivity of CO2 in the form of Mayr's electrophilicity parameter E on the basis of a single carboxylation reaction. The disagreement between experiment (E = −16.3) and computation (E = −11.4) corresponds to a deviation of up to ten orders of magnitude in bimolecular rate constants of carboxylation reactions according to the Mayr–Patz equation, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(E + N). Here, we introduce a data-driven approach incorporating supervised learning, quantum chemistry, and uncertainty quantification to resolve this discrepancy. The dataset used for reducing the uncertainty in E(CO2) represents 15 carboxylation reactions in DMSO. However, experimental data is only available for one of these reactions. To ensure reliable predictions, we selected a training set composed of this and 19 additional reactions comprising heteroallenes other than CO2 for which experimental data is available. With the new data-driven protocol, we can narrow down the electrophilicity of carbon dioxide to E(CO2) = −14.6(5) with 95% confidence, and suggest an electrophile-specific sensitivity parameter sE(CO2) = 0.81(6), resulting in an extended reactivity equation, log
k = sN(E + N). Here, we introduce a data-driven approach incorporating supervised learning, quantum chemistry, and uncertainty quantification to resolve this discrepancy. The dataset used for reducing the uncertainty in E(CO2) represents 15 carboxylation reactions in DMSO. However, experimental data is only available for one of these reactions. To ensure reliable predictions, we selected a training set composed of this and 19 additional reactions comprising heteroallenes other than CO2 for which experimental data is available. With the new data-driven protocol, we can narrow down the electrophilicity of carbon dioxide to E(CO2) = −14.6(5) with 95% confidence, and suggest an electrophile-specific sensitivity parameter sE(CO2) = 0.81(6), resulting in an extended reactivity equation, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sEsN(E + N) [Mayr, Tetrahedron, 2015, 71, 5095].
k = sEsN(E + N) [Mayr, Tetrahedron, 2015, 71, 5095].
1 Introduction
Carbon dioxide, as an abundant waste product, is a desirable C1 building block in organic synthesis.1–5 There are two chemical recycling paths for CO2 with different foci, the energy pathway and the functionalisation pathway. The former represents the reduction of CO2 up to methane and enables energy storage and conversion to potential fuel substitutes.6Functionalisation through carboxylation and further derivatisation, on the other hand, creates value-added chemicals and is the pathway relevant to this study. For instance, carboxylic acids transformed into esters and amides are key components in pharmaceuticals, particularly in prodrugs, which can be activated through biotransformation into active drugs.7 Furthermore, CO2 can be fixated into carbamates, which serve as key building blocks not only in pharmaceuticals but also in agricultural chemicals.8
Given the environmental impact of CO2 as a greenhouse gas in the Earth's atmosphere, the topic of CO2-binding has become increasingly important. In this context, carbamates again play a crucial role. Successful direct CO2-binding from the air as carbamates as well as by metal–organic frameworks has already been demonstrated.9–12
Carboxylation reactions initiated by C–H activation are particularly relevant due to their high step and atom economy as well as versatility in constructing complex molecules from simple precursors.13,14 There are various strategies for C–H functionalisation with CO2, including catalysis by transition metal complexes or enzymes and mediation by Lewis acids or Brønsted bases.14
A frequent and prominent approach in C–H carboxylation is transition metal catalysis, where the nucleophile is activated for a subsequent reaction with CO2. Metal-N-heterocyclic carbene complexes, e.g. with Cu(I) and Au(I), have proven to be successful catalysts for carboxylation reactions with aromatic heterocycles.15,16 1,2,3-Triazol-5-ylidene copper complexes were also shown to catalyse these reactions effectively.17
Of particular interest are base-mediated carboxylations as these can be carried out under mild and transition-metal-free conditions and are therefore more environmentally friendly and potentially more economical.18 Reactions promoted by Cs2CO3 have been reported for electron-deficient aromatic heterocycles by Vechorkin et al.19 Fenner and Ackermann showed that these reactions are possible under even milder conditions with KOt-Bu. The resulting highly nucleophilic carbanion enables the subsequent CO2 insertion step at low to moderate temperatures and atmospheric pressure of CO2.20 Felten et al. also pursued a base-mediated approach in their work on the carboxylation of azoles activated and stabilised by silyl triflate reagents.21
Due to their highly nucleophilic nature, N-heterocyclic carbenes (NHCs) have come into focus for CO2 fixation in organocatalysis.5,22 Several examples showing the ability of NHCs to bind CO2 have been reported.23–25
While highly reactive nucleophiles offer significant advantages in carboxylation reactions, they also present notable drawbacks related to selectivity, stability, handling, and environmental impact. Understanding the reactivity of CO2 is crucial for optimising reaction conditions and developing tailored nucleophiles that are milder but still reactive enough to form products with CO2, thereby expanding the scope of CO2-based syntheses towards late-stage functionalisation. Unveiling the reactivity of CO2 therefore is key to creating value-added chemicals and drugs in a more sustainable and controlled manner.
One way to characterise the reactivity of CO2 is Mayr's electrophilicity parameter E, which can be determined by calibration against a series of reference nucleophiles according to the Mayr–Patz equation,26–28
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(E + N) k = sN(E + N)
| (1) |
A recent study by Mayr, Ofial, and co-workers suggests two distinct values for E of carbon dioxide (experiment, E = −16.3; computation, E = −11.4), which encompass the values for benzaldehyde and fairly strong Michael acceptors.29 This gap represents a deviation of about five orders of magnitude in bimolecular rate constants of carboxylation reactions if sN is close to one, a discrepancy that is clearly too pronounced to enable reasonable estimates of the rate and selectivity of carboxylation reactions. Both E(CO2)-values were derived from a single identical reaction, i.e. the carboxylation of the indenide anion,
 | (2) |
Nicoletti et al.30 calculated E(CO2) for four additional reactions by using adopted versions of eqn (2), suggesting a range of lower reactivity (−18.7 < E(CO2) < −15.3). No calibration of E was applied. Instead, every nucleophile was linked to an individual value of E for carbon dioxide, an issue to be avoided in the construction of a global reactivity scale. An alternative approach was taken by Liu et al.,31 who created a machine-learning-based web prediction tool trained on experimental E parameters from Mayr's Database of Reactivity Parameters,32,33 placing the electrophilicity value of CO2 at E = −15.02 without providing a species-specific error estimate. Another web prediction tool based on methyl anion affinities (correlated to E) and methyl cation affinities (correlated to N) created by Ree et al. includes error estimates for specific electrophilic and nucleophilic sites.34,35 A direct estimation of Mayr's reactivity parameters, however, is not possible with this tool.
The goal of this work is to reduce the aforementioned uncertainty in CO2 reactivity by narrowing down the range of E(CO2). For this purpose, we investigate reactions of CO2 with 15 carbanions (Fig. 1) in DMSO by means of quantum chemical calculations involving transition state searches to obtain estimates of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k. These carbanions have been selected from Mayr's database and span a wide nucleophilicity range. However, for only one of these reactions (CO2 + indenide anion N01) experimental data is available. To assess the validity of different quantum chemical methods, we benchmark calculated rate constants against experimental reference values for this and six similar reactions involving the chemically related heteroallene carbon disulphide.29 To improve the quality of calculated rate constants, we train a multivariate linear (ML) model on these seven and 13 additional heteroallene–carbanion reactions for which experimental data is available (also from Li et al.29). Finally, by combining least-squares optimisation with Bayesian bootstrapping,36,37 we quantify E by calibration against ML-derived log
k. These carbanions have been selected from Mayr's database and span a wide nucleophilicity range. However, for only one of these reactions (CO2 + indenide anion N01) experimental data is available. To assess the validity of different quantum chemical methods, we benchmark calculated rate constants against experimental reference values for this and six similar reactions involving the chemically related heteroallene carbon disulphide.29 To improve the quality of calculated rate constants, we train a multivariate linear (ML) model on these seven and 13 additional heteroallene–carbanion reactions for which experimental data is available (also from Li et al.29). Finally, by combining least-squares optimisation with Bayesian bootstrapping,36,37 we quantify E by calibration against ML-derived log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values.
k values.
 | ||
| Fig. 1 Carbanions (15 in total) considered in this study for reactions with CO2 in DMSO, including identifiers and reactivity parameters (N, sN). | ||
2 Methods
2.1 Quantum chemical protocol
We took the experimental protocol applied by Li et al.29 into account, which is adapted from work by Fenner and Ackermann.20 The reaction is transition-metal-free and carried out under mild conditions, namely at 20 °C and atmospheric pressure. After deprotonation of a carbon-centred nucleophile with KOt-Bu, the carbanion formed reacts with CO2, which was previously dissolved in DMSO.
 | (3) |
| Abbreviation | Computational setting for the energy |
|---|---|
| B3LYP | B3LYP-D3(BJ)/def2-TZVPD/SMD(DMSO) |
| DLPNO-B2PLYP | DLPNO-B2PLYP-D3(BJ)/def2-TZVPD/SMD(DMSO) |
| DLPNO-CCSD(T) | DLPNO-CCSD(T)/CBS/SMD(DMSO) |
2.2 Data-driven protocol
All data analysis tools presented in this section can be accessed through the project-related GitLab repository.67 = 10−6,
= 10−6, 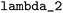 = 0.003,
= 0.003, 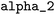 = 0.27, and
= 0.27, and 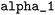 = 3.0. These parameters were refined through an extensive grid search, with success determined by the highest cross-validation score. To validate the resulting model, a leave-one-out approach was employed: with n = 20 reactions in the dataset, n − 1 data points were used to train n models. The left-out reaction was used for evaluating the model's performance.
= 3.0. These parameters were refined through an extensive grid search, with success determined by the highest cross-validation score. To validate the resulting model, a leave-one-out approach was employed: with n = 20 reactions in the dataset, n − 1 data points were used to train n models. The left-out reaction was used for evaluating the model's performance.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(E + N) and only E is determined. In the second problem, log
k = sN(E + N) and only E is determined. In the second problem, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sEsN(E + N) and both E and sE are determined. The least-squares method was applied to calibrate these electrophile-specific parameters against n reactions for which experimental rate constants are available,
k = sEsN(E + N) and both E and sE are determined. The least-squares method was applied to calibrate these electrophile-specific parameters against n reactions for which experimental rate constants are available,
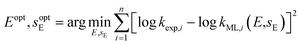 | (4) |
Optimisation of these nonlinear calibration problems was performed using the basin-hopping method70 implemented in SciPy 1.10.1.71
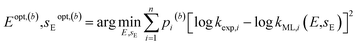 | (5) |
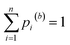 . Since every bootstrap sample is represented by a unique set of weights, the optimal reactivity parameters were slightly different for each set, hence the designations Eopt,(b) and sEopt,(b).
. Since every bootstrap sample is represented by a unique set of weights, the optimal reactivity parameters were slightly different for each set, hence the designations Eopt,(b) and sEopt,(b).We chose B = 1000 for this study. The optimal values for E and sE were estimated as medians (50th percentiles) of their respective B bootstrapped values. To estimate the probability P that E or sE are located within a certain range of values, we calculated both the [(1 − P)/2]th and the [(1 + P)/2]th percentiles, which define the lower and upper bounds of the corresponding confidence interval. For instance, for a 95% confidence interval, P = 0.95, [(1 − P)/2] = 0.025, and [(1 + P)/2] = 0.975.
3 Results and discussion
3.1 Assessment of quantum chemical methods
Prior to determining the electrophilicity of CO2, we benchmarked different electronic-structure methods of varying sophistication (based on B3LYP, DLPNO-B2PLYP, DLPNO-CCSD(T); see Section 2.1.4 and Table 1) against the experimental rate constants listed in Table S10.† Since there is only a single experimental rate constant available for the reaction of CO2 with a nucleophile (N01) from Mayr's database, we included six additional experimental rate constants for reactions of the chemically related carbon disulphide (E1)29 with carbanions (N01, N07, N16, N17, N18, N19; see Fig. 2) in DMSO.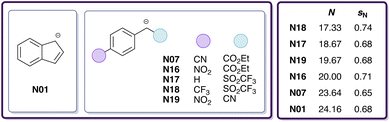 | ||
Fig. 2 Carbanions involved in reactions with E1 (CS2) in DMSO, including identifiers and reactivity parameters (N, sN), for which experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values were determined.29 k values were determined.29 | ||
In Table 2, the root mean square error (RMSE) and maximum absolute error (max. AE) are shown for the Gibbs free activation energy ΔG‡sol and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k in comparison to the experimental results. All values correspond to a temperature of 20 °C. The RMSE values are smallest for DLPNO-CCSD(T). However, the max. AE is largest for DLPNO-CCSD(T) but smallest for B3LYP. When including the reaction of CO2 with N01, both RMSE and max. AE are smallest for B3LYP. Since all results in Table 2 are based on B3LYP-optimised structures, the assumption that the reactants and the transition states are structurally similar across the different electronic-structure methods could be critical for explaining the increasing max. AE in DLPNO-B2PLYP and DLPNO-CCSD(T) in comparison to B3LYP.
k in comparison to the experimental results. All values correspond to a temperature of 20 °C. The RMSE values are smallest for DLPNO-CCSD(T). However, the max. AE is largest for DLPNO-CCSD(T) but smallest for B3LYP. When including the reaction of CO2 with N01, both RMSE and max. AE are smallest for B3LYP. Since all results in Table 2 are based on B3LYP-optimised structures, the assumption that the reactants and the transition states are structurally similar across the different electronic-structure methods could be critical for explaining the increasing max. AE in DLPNO-B2PLYP and DLPNO-CCSD(T) in comparison to B3LYP.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for different quantum chemical approximations applied to reactions of E1 (CS2) with six carbanions in DMSO in comparison to experimental data. Statistics including the reaction of CO2 with the indenide anion N01 in DMSO are given in parentheses. See also Table S10
k for different quantum chemical approximations applied to reactions of E1 (CS2) with six carbanions in DMSO in comparison to experimental data. Statistics including the reaction of CO2 with the indenide anion N01 in DMSO are given in parentheses. See also Table S10
| B3LYP | DLPNO-B2PLYP | DLPNO-CCSD(T) | |
|---|---|---|---|
| RMSE ΔG‡sol | 2.44 (2.26) | 2.60 (2.47) | 2.22 (2.47) |
| max. AE ΔG‡sol | 3.25 | 3.71 | 4.12 |
RMSE log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
1.82 (1.68) | 1.94 (1.84) | 1.65 (1.84) |
max. AE log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
2.42 | 2.77 | 3.07 |
As the average error in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is comparable among the different electronic-structure approximations, B3LYP appears to be a reasonable choice given its relatively low computational cost. However, the scatter of residuals (log
k is comparable among the different electronic-structure approximations, B3LYP appears to be a reasonable choice given its relatively low computational cost. However, the scatter of residuals (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp − log
kexp − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kB3LYP) is too high for a proper quantification of electrophilicity, and the limited number of reaction data is insufficient to apply statistical corrections.
kB3LYP) is too high for a proper quantification of electrophilicity, and the limited number of reaction data is insufficient to apply statistical corrections.
To enhance our analysis, we included 15 additional experimental rate constants for reactions carried out in DMSO involving other heteroallenes (Fig. 3a) and carbanions (Fig. 3b).29 For these additional heteroallene–carbanion reactions, we followed the same computational protocol as before (see Section 2.1) but omitted further DLPNO-B2PLYP and DLPNO-CCSD(T) calculations. The reactions E4-N07 and E4-N20 were excluded due to the excessive size of their transition state conformer ensembles (see Section S3†), leading to 20 modelled reactions in total (Table 3). Table 4 shows the updated RMSE and max. AE for the Gibbs free activation energy ΔG‡sol and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k in comparison to the experimental results for this set of reactions. Both RMSE and max. AE decrease compared to the previous values (Table 2). However, the log
k in comparison to the experimental results for this set of reactions. Both RMSE and max. AE decrease compared to the previous values (Table 2). However, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values from our DFT calculations still do not align well with the experimental results. To improve the accuracy of log
k values from our DFT calculations still do not align well with the experimental results. To improve the accuracy of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k predictions and, hence, ensure a reliable quantification of the electrophilicity of CO2, we next investigated how statistical corrections can be incorporated into the workflow.
k predictions and, hence, ensure a reliable quantification of the electrophilicity of CO2, we next investigated how statistical corrections can be incorporated into the workflow.
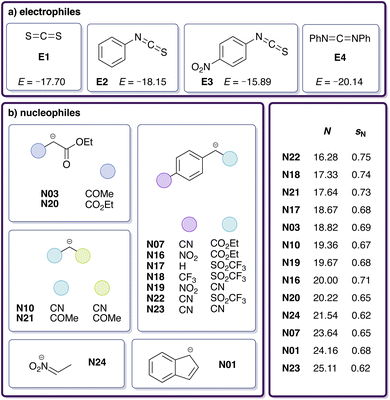 | ||
| Fig. 3 Dataset of (a) electrophiles and (b) nucleophiles involved in reactions with available experimental rate constants measured in DMSO,29 including identifiers and reactivity parameters (E, N, sN). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC) compared to their experimental values29 (log
kQC) compared to their experimental values29 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp) for each nucleophile–electrophile reaction of the ML training set. Reference IDs29 are listed in Table S5
kexp) for each nucleophile–electrophile reaction of the ML training set. Reference IDs29 are listed in Table S5
| Elec. | Nuc. | ΔG‡sol [kcal mol−1] | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC kQC |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp29 kexp29 |
|---|---|---|---|---|
| E1 | N01 | 10.25 | 5.14 | 4.99 |
| N07 | 10.32 | 5.09 | 3.25 | |
| N16 | 12.28 | 3.63 | 1.34 | |
| N17 | 12.81 | 3.24 | 1.00 | |
| N18 | 14.41 | 2.04 | −0.38 | |
| N19 | 14.50 | 1.98 | 1.42 | |
| E2 | N03 | 17.36 | −0.16 | 0.06 |
| N10 | 18.23 | −0.80 | 1.43 | |
| N17 | 15.29 | 1.38 | 0.31 | |
| N21 | 18.40 | −0.93 | −0.19 | |
| N24 | 12.77 | 3.26 | 1.72 | |
| E3 | N03 | 14.68 | 1.84 | 1.96 |
| N10 | 15.17 | 1.48 | 3.09 | |
| N20 | 12.54 | 3.44 | 2.43 | |
| N21 | 14.78 | 1.77 | 0.88 | |
| N22 | 15.20 | 1.45 | 0.39 | |
| E4 | N03 | 19.11 | −0.62 | −1.46 |
| N17 | 16.20 | 0.71 | −0.55 | |
| N23 | 14.07 | 2.30 | 2.23 | |
| CO2 | N01 | 10.20 | 5.18 | 5.32 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC) obtained from quantum chemical calculations for 19 reactions of heteroallenes with carbanions in DMSO in comparison to experimental data. Statistics including the reaction of CO2 with the indenide anion N01 in DMSO are given in parentheses. See also Table 3
kQC) obtained from quantum chemical calculations for 19 reactions of heteroallenes with carbanions in DMSO in comparison to experimental data. Statistics including the reaction of CO2 with the indenide anion N01 in DMSO are given in parentheses. See also Table 3
| ΔG‡sol | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC kQC |
|
|---|---|---|
| RMSE | 1.87 (1.82) | 1.39 (1.36) |
| max. AE | 3.25 | 2.42 |
3.2 Improving upon quantum chemical log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) k values
k values
To approximate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp of heteroallene–carbanion reactions over a wide range of reactivity, suitable parameters must be identified. Different sets of parameters were tested for this purpose: (a) individual contributions to the Gibbs free activation energy ΔG‡sol (details in Section 2 of ref. 72), (b) molecular descriptors from conceptual DFT based on recent studies,73–76 and (c) Mayr's nucleophile-specific reactivity parameters sN and N. Section S4† provides a summary of all tested parameters, which are also listed in Table S7†, together with detailed information on their selection (see also Table S6†) and leave-one-out validations (Fig. S2–S22†).
kexp of heteroallene–carbanion reactions over a wide range of reactivity, suitable parameters must be identified. Different sets of parameters were tested for this purpose: (a) individual contributions to the Gibbs free activation energy ΔG‡sol (details in Section 2 of ref. 72), (b) molecular descriptors from conceptual DFT based on recent studies,73–76 and (c) Mayr's nucleophile-specific reactivity parameters sN and N. Section S4† provides a summary of all tested parameters, which are also listed in Table S7†, together with detailed information on their selection (see also Table S6†) and leave-one-out validations (Fig. S2–S22†).
Bayesian regression with Automatic Relevance Determination (ARD)68 was performed after preprocessing the data (see Section 2.2.1 for more details). In total, 20 models were trained per examined combination of parameters, excluding each reaction once from the training dataset. With this leave-one-out approach, we attempted to mitigate the effect of overfitting in order to reliably assess log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k predictions for CO2–nucleophile reactions not included in the training set.
k predictions for CO2–nucleophile reactions not included in the training set.
The best working combination of parameters includes, from group (a), the temperature-scaled entropy of the nucleophile, TSnuc, from group (b), the electronic chemical potential77,78 of the electrophile, defined as
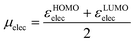 | (6) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML: = w0 + w1TSnuc + w2μelec + w3N ≈ log kML: = w0 + w1TSnuc + w2μelec + w3N ≈ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp kexp
| (7) |
In Table 5, the model coefficients w0 to w3 are listed for the final multivariate linear (ML) model including all 20 reference reactions. RMSE and max. AE of the corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML values (Table 6) are about four times smaller compared to those obtained from Gibbs free energies of activation (log
kML values (Table 6) are about four times smaller compared to those obtained from Gibbs free energies of activation (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC). This finding indicates that a statistical model combining quantum chemical (TSnuc and μelec) and empirical (N) information systematically outperforms DFT-based thermochemistry. In fact, not a single parameter combination from group (a) alone could achieve an accuracy similar to that of the best combination shown in eqn (7).
kQC). This finding indicates that a statistical model combining quantum chemical (TSnuc and μelec) and empirical (N) information systematically outperforms DFT-based thermochemistry. In fact, not a single parameter combination from group (a) alone could achieve an accuracy similar to that of the best combination shown in eqn (7).
| Coefficient | Term | Value |
|---|---|---|
| w0 | — | +1.5042 |
| w1 | TSnuc | −0.4399 |
| w2 | μelec | −0.8825 |
| w3 | N | +1.1256 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) for 19 reactions of non-CO2 heteroallenes with carbanions in DMSO (Table 3) in comparison to experimental data. Statistics for the ML model refer to leave-one-out errors
k) for 19 reactions of non-CO2 heteroallenes with carbanions in DMSO (Table 3) in comparison to experimental data. Statistics for the ML model refer to leave-one-out errors
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC kQC |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML kML |
|
|---|---|---|
| RMSE | 1.39 | 0.35 |
| max. AE | 2.42 | 0.58 |
Fig. 4 shows a leave-one-out plot of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQC values (unfilled circles) and the log
kQC values (unfilled circles) and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML values (filled circles) versus their experimental analogues for the 20 reference reactions. The prediction of the reaction left out of training in this case, CO2–N01, is shown in red. Results for the 19 other leave-one-out models and the final ML model are provided in Section S4.†
kML values (filled circles) versus their experimental analogues for the 20 reference reactions. The prediction of the reaction left out of training in this case, CO2–N01, is shown in red. Results for the 19 other leave-one-out models and the final ML model are provided in Section S4.†
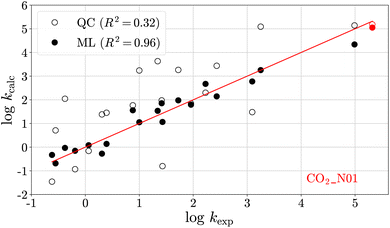 | ||
Fig. 4 Rate constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) from quantum chemical (QC) calculations (unfilled circles) and those obtained from multivariate linear (ML) regression (filled circles) versus their experimental analogues for the heteroallene–carbanion reactions listed in Table 3. The reaction shown in red has been left out for training and is predicted by the ML model. k) from quantum chemical (QC) calculations (unfilled circles) and those obtained from multivariate linear (ML) regression (filled circles) versus their experimental analogues for the heteroallene–carbanion reactions listed in Table 3. The reaction shown in red has been left out for training and is predicted by the ML model. | ||
To examine whether this approach is transferable to reactions of CO2 with nucleophiles not included in the training of the ML model, we simulated analogous scenarios, two for each of the other heteroallenes E1–E3, respectively. In each of the six simulations, the ML model was retrained using data from only one reaction of the selected heteroallene with a nucleophile that is also involved in at least one other reaction (see Section S5†). (In the original ML model, CO2 is the heteroallene for which experimental data with only one nucleophile, N01, is available, which is also present in a reaction with E1). In all cases, the agreement between experimental and ML-predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values for reactions with the underrepresented heteroallene is high, although several nucleophiles are excluded from the respective model trainings. These results indicate that the ML model is transferable to reactions with other heteroallenes as well as other carbanions, an essential prerequisite for predicting the kinetics of yet-unobserved carboxylation reactions.
k values for reactions with the underrepresented heteroallene is high, although several nucleophiles are excluded from the respective model trainings. These results indicate that the ML model is transferable to reactions with other heteroallenes as well as other carbanions, an essential prerequisite for predicting the kinetics of yet-unobserved carboxylation reactions.
In addition to delivering more accurate results, the ML model provides computational cost advantages over conventional quantum chemical calculations. The most significant computational time is required for the transition state search in the latter case. The proposed ML model effectively circumvents this time-intensive process.
3.3 Determination of E(E1): experiment vs. computation
To validate the ML model, we assess the reproducibility of E of E1 (CS2), whose experimental value is reliably known (E = −17.7). For this purpose, we compare the calibration of E against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kexp (Fig. 5a and Table 7) with that against log
kexp (Fig. 5a and Table 7) with that against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML (Fig. 5b and Table 7). The sampled distributions of experimental and ML-derived E values obtained from Bayesian bootstrapping36,37 are strongly overlapping (Fig. 5c), and the ML-predicted value (E = −17.6) is very close to its experimental reference, especially when taking into account that the resulting deviation in log
kML (Fig. 5b and Table 7). The sampled distributions of experimental and ML-derived E values obtained from Bayesian bootstrapping36,37 are strongly overlapping (Fig. 5c), and the ML-predicted value (E = −17.6) is very close to its experimental reference, especially when taking into account that the resulting deviation in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k is much smaller than the uncertainty in log
k is much smaller than the uncertainty in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k introduced by the Mayr–Patz approach.36
k introduced by the Mayr–Patz approach.36
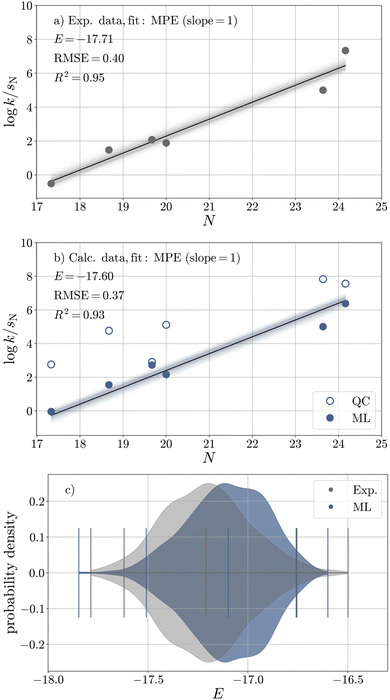 | ||
| Fig. 5 Calibration of E against (a) experimental rate constants and (b) rate constants obtained from the ML model (filled circles) for six reactions of carbanions with E1 (CS2) in DMSO based on bootstrapped least-squares optimisation with respect to the Mayr–Patz equation (MPE, eqn (1)). The quantum chemical (QC) data is shown in unfilled circles for comparison. (c) Bootstrapped distributions of E(E1) based on experimental (grey) and ML (blue) data. | ||
| Exp. | ML | QC | |
|---|---|---|---|
| Elower | −18.12 | −18.01 | −16.16 |
| E | −17.71 | −17.60 | −15.39 |
| Eupper | −17.25 | −17.26 | −14.64 |
| u95 (E) | 0.87 | 0.75 | 1.51 |
RMSE (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) k) |
0.40 | 0.37 | 0.72 |
R2 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) k) |
0.95 | 0.93 | 0.68 |
The close agreement is not particularly surprising as the corresponding reactions are part of the training set for the ML model (eqn (7)). The same holds for the calibration of E of E2 and E3, the results of which are provided in Section S5.† However, we obtain similar results (Tables S11–S13†) when the ML-predictions of the six data-sparse simulations mentioned in the previous section are employed, where only one of the experimentally investigated reactions is part of the training procedure.
3.4 Determination of E(CO2)
To quantify the electrophilicity parameter E for carbon dioxide, we applied the same calibration procedure as in the previous section. Due to the availability of only one experimental data point, we calibrated E(CO2) against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kML (Table S14†) predicted for 15 carboxylation reactions with different carbanions (Fig. 1 and Table S9†) in DMSO; see Fig. 6-1a.
kML (Table S14†) predicted for 15 carboxylation reactions with different carbanions (Fig. 1 and Table S9†) in DMSO; see Fig. 6-1a.
The resulting distribution of E(CO2) (Fig. 6-1b and Table 8) has a median of E = −15.45 and a two-sided 95% confidence interval of −16.00 < E < −14.97. This median along with its confidence interval lies between the two values determined by Li et al.29 (experiment, E = −16.3; computation, E = −11.4), which are both based on a single reaction (with the indenide anion N01). In direct comparison to the single experimental reference, the reactivity of CO2 increases from −16.3 to −15.5.
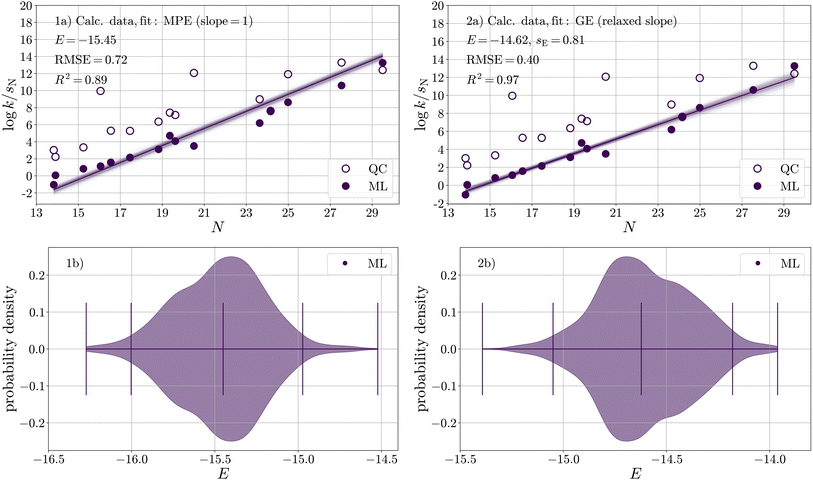 | ||
| Fig. 6 (a) Calibration of E against rate constants obtained from the ML model for 15 reactions of CO2 with carbanions in DMSO with respect to (1) the Mayr–Patz equation (MPE, fixed slope, eqn (1)) and (2) the more general equation of reactivity (GE, relaxed slope, eqn (9)). (b) Corresponding bootstrapped distributions of E(CO2). | ||
However, as evident in Fig. 6-1a, a noticeable systematic deviation exists in the ML data (filled circles). At lower N values, the data points are positioned above the median, while as N increases, the data points generally lie below the median line. A possibility to examine the underlying data for signs of autocorrelation, which may indicate systematic errors, is the Durbin–Watson test, a statistical test used to assess the independence of residuals, zij, in regression analysis,79,80
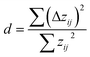 | (8) |
One assumption in the Mayr–Patz equation (eqn (1)) is that the electrophile-specific sensitivity parameter sE equals one.81 Mayr and coworkers have demonstrated that this assumption is valid for many different electrophiles,27,81 including the heteroallenes E1–E4.29 In the linear visualisation of the Mayr–Patz relationship, the slope of the plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k/sN versus N equals sE. We were curious to see if a more general equation for nucleophile–electrophile reactions that contains sE as a free parameter,
k/sN versus N equals sE. We were curious to see if a more general equation for nucleophile–electrophile reactions that contains sE as a free parameter,
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sEsN(E + N) k = sEsN(E + N)
| (9) |
Fig. 6-2a shows a significant improvement when applying the generalised equation over the Mayr–Patz equation, evidenced by an increase/decrease in R2 (from 0.89 to 0.97)/RMSE (from 0.72 to 0.40) and a significant reduction in autocorrelation (d = 1.22). Regarding the high calibration accuracy, it is worth mentioning that only four nucleophiles (N01, N03, N07, N10) were included in both the ML model as well as CO2 dataset. This result suggests that sE should be explicitly considered as a parameter in the quantification of E for CO2.
The resulting distribution of E(CO2) (Fig. 6-2b and Table 8) has a median of E = −14.62 and a two-sided 95% confidence interval of −15.05 < E < −14.18. For sE(CO2), the resulting distribution has a median of sE = 0.81 and a two-sided 95% confidence interval of 0.73 < sE < 0.87. These distributions allow us to estimate reaction-specific uncertainty in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (Section S6†), which we provide in Table S16†. With a confidence of 95%, the uncertainty in rate constants of carboxylation reactions equals about one order of magnitude. It increases slightly towards both ends of the nucleophilicity range under consideration.
k (Section S6†), which we provide in Table S16†. With a confidence of 95%, the uncertainty in rate constants of carboxylation reactions equals about one order of magnitude. It increases slightly towards both ends of the nucleophilicity range under consideration.
Building on this set of nucleophiles, we find evidence that sE takes values significantly smaller than one (0.7–0.8, see Table S20†) also for heteroallenes E1–E3, indicating a more general trend. A distinctive aspect is that heteroallenes are linear in their ground state but adopt an increasingly bent structure along the reaction coordinate. This change can affect the relative stabilisation of transition states and products, both intrinsically and through solvent interactions, thereby potentially altering the sensitivity of the activation energy to changes in the reaction energy. This sensitivity coefficient, better known as the Brønsted coefficient, has been shown to be proportional to the sN parameter in the Mayr–Patz framework.82 Assuming an analogous relationship for the sE parameter, the pronounced structural change in heteroallenes during nucleophilic attack may explain the deviation from the typical case where sE = 1. The directional nature of nucleophilic attack on CO2 may further contribute to this effect. Given the complexity of these influences, a detailed quantitative analysis would be required to draw firm conclusions. For now, we focus on the narrowness of the confidence intervals for E and sE, which allows us to explore the application scope of CO2 (and potentially other heteroallenes).
3.5 Identifying suitable substrates for CO2
Applying the extended Mayr–Patz equation (eqn (9)), kinetically suitable nucleophiles for reactions with CO2 can be identified. As a rule of thumb, electrophile–nucleophile reactions can be observed at room temperature (20 °C) if log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k > −6.81 The diffusion limit is reached at log
k > −6.81 The diffusion limit is reached at log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k ≈ 8, where the validity of the Mayr–Patz equation breaks.28To illustrate the reaction scope of CO2, we establish a “CO2 reactivity cone”, which is defined by two axes, N and 1/sN (Fig. 7). Every nucleophile with known reactivity parameters can thus be assigned a specific position in the cone plot and falls either into the cone (reaction scope) or outside of it (unobservable or diffusion-controlled reactions). Within this cone, 229 carbon-centred nucleophiles from Mayr's database32 have been included, emphasising some examples with low nucleophilicity values, highlighted in red. These nucleophiles are relatively mild but, according to the extended Mayr–Patz equation, reactive enough to form products with CO2. For instance, certain cyclic α-diazo carbonyl compounds and heteroarenes (measured in DCM) fall into this category. With a fixed sE parameter, the cone would be narrower, shifting many of these “mild” compounds outside the cone. In this light, it is an encouraging result that sE < 1, as it widens the substrate scope of carboxylation reactions.
k ≈ 8, where the validity of the Mayr–Patz equation breaks.28To illustrate the reaction scope of CO2, we establish a “CO2 reactivity cone”, which is defined by two axes, N and 1/sN (Fig. 7). Every nucleophile with known reactivity parameters can thus be assigned a specific position in the cone plot and falls either into the cone (reaction scope) or outside of it (unobservable or diffusion-controlled reactions). Within this cone, 229 carbon-centred nucleophiles from Mayr's database32 have been included, emphasising some examples with low nucleophilicity values, highlighted in red. These nucleophiles are relatively mild but, according to the extended Mayr–Patz equation, reactive enough to form products with CO2. For instance, certain cyclic α-diazo carbonyl compounds and heteroarenes (measured in DCM) fall into this category. With a fixed sE parameter, the cone would be narrower, shifting many of these “mild” compounds outside the cone. In this light, it is an encouraging result that sE < 1, as it widens the substrate scope of carboxylation reactions.
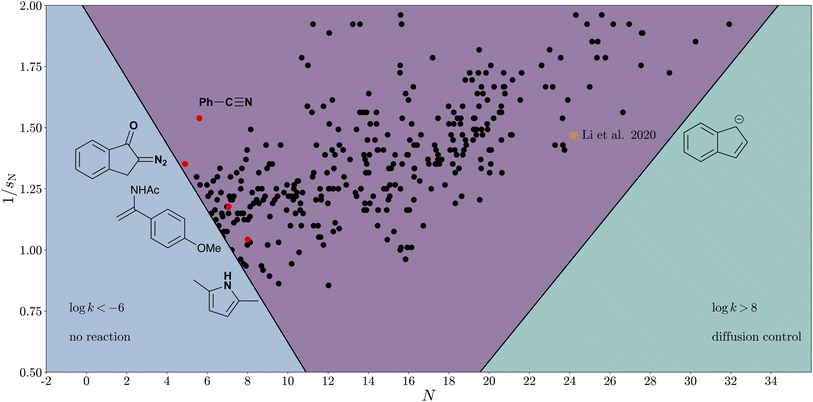 | ||
| Fig. 7 Reactivity cone for reactions of nucleophiles with CO2 according to the general Mayr–Patz equation (eqn (9)). Reactivity parameters for CO2 are set to sE = 0.81 and E(CO2) = −14.6. Here, all carbon-centered nucleophiles of Mayr's database falling into the cone are shown. | ||
By utilising available web prediction tools for fast predictions of N,31,34,35 nucleophiles not yet included in Mayr's database can be accessed. However, it is important to consider the uncertainty estimates provided by these tools.
Through various approaches for the activation of nucleophiles mentioned earlier,2,4,14 such as binding to a transition metal, but also by activating CO2 in a Lewis–acidic medium, weaker nucleophiles can become sufficiently reactive, which significantly increases the number of suitable reaction partners for carboxylation reactions further. In case of CO2 activation, the boundaries of the cone would shift, whereas nucleophile activation shifts substrates into and out of the cone.
4 Conclusions and outlook
We developed a computational pipeline integrating supervised learning, quantum chemistry, and uncertainty quantification to quantify the reactivity of heteroallenes (X = C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Y), most notably carbon dioxide (CO2), in the form of Mayr's electrophilicity parameter E. Benchmarking revealed that conventional quantum chemical calculations combined with standard thermochemistry and canonical transition state theory fail to reproduce experimental rate constants of nucleophilic attack by carbanions at heteroallenes.
Y), most notably carbon dioxide (CO2), in the form of Mayr's electrophilicity parameter E. Benchmarking revealed that conventional quantum chemical calculations combined with standard thermochemistry and canonical transition state theory fail to reproduce experimental rate constants of nucleophilic attack by carbanions at heteroallenes.
To resolve this issue, we developed and trained a multivariate linear (ML) model on experimental data for 20 heteroallene–carbanion reactions to improve the accuracy of computed rate constants by one order of magnitude compared to the ab initio protocol. Both quantum chemical and empirical reactivity information serves as input to the ML model.
ML-predicted rate constants for 15 CO2–carbanion reactions were subjected to nonlinear least-squares optimisation combined with Bayesian bootstrapping to quantify E for carbon dioxide, E(CO2) = −14.6(5), with 95% confidence. In contrast to other heteroallenes, it was necessary to relax the otherwise fixed electrophile-specific parameter sE (default value of 1), which is also done to describe electrophiles undergoing sN2 reactions.81 Here, sE(CO2) = 0.81(6). A positive implication of an sE parameter smaller than one is that it expands the substrate scope towards less reactive nucleophiles.
Through these insights, we have gained a refined understanding of the characteristics of CO2, which helps to better exploit its potential in synthetic and related applications. For example, nucleophiles located within the “CO2 reactivity cone” developed in this study (Fig. 7) are generally kinetically suitable for undergoing reactions with CO2 without additional support by transition metal catalysts, Lewis acids, or other activating media. To broaden the scope of application beyond nucleophiles that have been already characterised experimentally, web prediction tools of chemical reactivity can be utilised.31,34 Identifying new nucleophiles that can successfully undergo carboxylation creates opportunities for designing novel prodrugs or carbamates, thereby enhancing pharmaceutical development or CO2-binding strategies.
These applications underscore the need to bridge predictions with experimental validation to ensure their practical relevance. Despite the evidence provided by our computational method, further experiments are unavoidable to truly unveil the reactivity and full potential of CO2, as well as to clarify the origins of the electrophile-specific parameter sE.
Data availability
Data for this article, including optimised structures and exemplary input files for quantum chemical calculations are available at https://doi.org/10.5281/zenodo.14677023. The data analysis scripts of this article are available in the interactive notebook in the same repository.
in the same repository.
Author contributions
ME: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualisation, writing – original draft preparation, writing – review & editing. KLB: investigation, validation, visualisation, writing – original draft preparation, writing – review & editing. JP: conceptualization, project administration, resources, supervision, writing – original draft preparation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
ME and JP acknowledge funding by Germany's joint federal and state program supporting early-career researchers (WISNA) established by the Federal Ministry of Education and Research (BMBF). The authors thank Prof. Christoph R. Jacob (TU Braunschweig) for computational resources. The authors appreciate discussions with Prof. Herbert Mayr and PD Armin Ofial (LMU Munich), as well as Dr Robert Mayer (TU Munich).References
- X.-F. Liu, K. Zhang, L. Tao, X.-B. Lu and W.-Z. Zhang, Green Chem. Eng., 2022, 3, 125–137 CrossRef.
- S. Dabral and T. Schaub, Adv. Synth. Catal., 2019, 361, 223–246 CrossRef CAS.
- J. Artz, T. E. Müller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504 CrossRef CAS PubMed.
- Q. Liu, L. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 5933 CrossRef PubMed.
- G. Fiorani, W. Guo and A. W. Kleij, Green Chem., 2015, 17, 1375–1389 RSC.
- C. Das Neves Gomes, O. Jacquet, C. Villiers, P. Thuéry, M. Ephritikhine and T. Cantat, Angew. Chem., 2012, 124, 191–194 CrossRef.
- H. Maag, Prodrugs, Springer, New York (NY), United States, 2007, vol. 5, pp. 703–729 Search PubMed.
- L. Wang, C. Qi, W. Xiong and H. Jiang, Chin. J. Catal., 2022, 43, 1598–1617 CrossRef CAS.
- A. Demessence, D. M. D'Alessandro, M. L. Foo and J. R. Long, J. Am. Chem. Soc., 2009, 131, 8784–8786 CrossRef CAS PubMed.
- A. C. Forse and P. J. Milner, Chem. Sci., 2021, 12, 508–516 RSC.
- D.-H. Nam, O. Shekhah, G. Lee, A. Mallick, H. Jiang, F. Li, B. Chen, J. Wicks, M. Eddaoudi and E. H. Sargent, J. Am. Chem. Soc., 2020, 142, 21513–21521 CrossRef CAS PubMed.
- I. Sullivan, A. Goryachev, I. A. Digdaya, X. Li, H. A. Atwater, D. A. Vermaas and C. Xiang, Nat. Catal., 2021, 4, 952–958 CrossRef CAS.
- J. Hong, M. Li, J. Zhang, B. Sun and F. Mo, ChemSusChem, 2019, 12, 6–39 CrossRef CAS PubMed.
- J. Luo and I. Larrosa, ChemSusChem, 2017, 10, 3317–3332 CrossRef CAS PubMed.
- I. I. F. Boogaerts and S. P. Nolan, J. Am. Chem. Soc., 2010, 132, 8858–8859 CrossRef CAS PubMed.
- I. I. F. Boogaerts, G. C. Fortman, M. R. L. Furst, C. S. J. Cazin and S. P. Nolan, Angew. Chem., Int. Ed., 2010, 49, 8674–8677 CrossRef CAS PubMed.
- H. Inomata, K. Ogata, S.-I. Fukuzawa and Z. Hou, Org. Lett., 2012, 14, 3986–3989 CrossRef CAS PubMed.
- Y. Luo and W. Huang, Org. Biomol. Chem., 2023, 21, 8628–8641 RSC.
- O. Vechorkin, N. Hirt and X. Hu, Org. Lett., 2010, 12, 3567–3569 CrossRef CAS PubMed.
- S. Fenner and L. Ackermann, Green Chem., 2016, 18, 3804–3807 RSC.
- S. Felten, C. Q. He, M. Weisel, M. Shevlin and M. H. Emmert, J. Am. Chem. Soc., 2022, 144, 23115–23126 CrossRef CAS PubMed.
- S. Naumann, Chem. Commun., 2019, 55, 11658–11670 RSC.
- B. R. Van Ausdall, J. L. Glass, K. M. Wiggins, A. M. Aarif and J. Louie, J. Org. Chem., 2009, 74, 7935–7942 CrossRef CAS PubMed.
- L. Yang and H. Wang, ChemSusChem, 2014, 7, 962–998 CrossRef CAS PubMed.
- A. Katharina Reitz, Q. Sun, R. Wilhelm and D. Kuckling, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 820–829 CrossRef.
- H. Mayr and M. Patz, Angew. Chem., Int. Ed., 1994, 33, 938–957 CrossRef.
- H. Mayr, T. Bug, M. F. Gotta, N. Hering, B. Irrgang, B. Janker, B. Kempf, R. Loos, A. R. Ofial, G. Remennikov and H. Schimmel, J. Am. Chem. Soc., 2001, 123, 9500–9512 CrossRef CAS PubMed.
- J. Ammer, C. Nolte and H. Mayr, J. Am. Chem. Soc., 2012, 134, 13902–13911 CrossRef CAS PubMed.
- Z. Li, R. J. Mayer, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2020, 142, 8383–8402 CrossRef CAS PubMed.
- C. Nicoletti, M. Orlandi, L. Dell'Amico and A. Sartorel, Sustain. Energy Fuels, 2024, 8, 5050–5057 RSC.
- Y. Liu, Q. Yang, J. Cheng, L. Zhang, S. Luo and J.-P. Cheng, ChemPhysChem, 2023, e202300162 CrossRef CAS PubMed.
- H. Mayr and A. R. Ofial, Mayr's Database of Reactivity Parameters, https://www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/, last accessed on 07 November 2024.
- H. Mayr and A. R. Ofial, SAR QSAR Environ. Res., 2015, 26, 619–646 CrossRef CAS PubMed.
- N. Ree, A. H. Göller and J. H. Jensen, Digit. Discov., 2024, 3, 347–354 RSC.
- N. Ree, J. M. Wollschläger, A. H. Göller and J. H. Jensen, Atom-Based Machine Learning for Estimating Nucleophilicity and Electrophilicity with Applications to Retrosynthesis and Chemical Stability, 2024 Search PubMed.
- J. Proppe and J. Kircher, ChemPhysChem, 2022, 23, e202200061 CrossRef CAS PubMed.
- D. B. Rubin, Ann. Stat., 1981, 9, 130–134 Search PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford (CT), United States, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, F1000Research, 2020, 9, 291 Search PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33, 449–454 CrossRef CAS.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1606 CrossRef.
- S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042 RSC.
- P. Pinski, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2015, 143, 034108 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446 CrossRef CAS.
- M. Eckhoff, K. L. Bublitz and J. Proppe, Determination of the electrophilicity of CO2, https://git.rz.tu-bs.de/proppe-group/co2_electrophilicity, last accessed on 18 November 2024.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, New York (NY), United States, 2006 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- M. Vahl and J. Proppe, Phys. Chem. Chem. Phys., 2023, 25, 2717–2728 RSC.
- G. Hoffmann, M. Balcilar, V. Tognetti, P. Héroux, B. Gaüzère, S. Adam and L. Joubert, J. Comput. Chem., 2020, 41, 2124–2136 CrossRef CAS.
- M. Eckhoff, J. V. Diedrich, M. Mücke and J. Proppe, J. Phys. Chem. A, 2024, 128, 343–354 CrossRef CAS PubMed.
- P. Pérez, A. Toro-Labbé, A. Aizman and R. Contreras, J. Org. Chem., 2002, 67, 4747–4752 CrossRef PubMed.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- J. Durbin and G. S. Watson, Biometrika, 1950, 37, 409–428 CAS.
- J. Durbin and G. S. Watson, Biometrika, 1951, 38, 159–178 CrossRef CAS PubMed.
- H. Mayr, Tetrahedron, 2015, 71, 5095–5111 CrossRef CAS.
- C. Schindele, K. N. Houk and H. Mayr, J. Am. Chem. Soc., 2002, 124, 11208–11214 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Information on benchmarks for computational methods, comparison between isolated reactants and pre-reaction complexes, information on conformer ensembles, information on the training and validation of regression models, overview of tested model parameters, results for the determination of the electrophilicity of electrophiles E1, E2, and E3, additional information on the determination of the electrophilicity of carbon dioxide, example input structures, optimised structures, interactive notebook for (reproductive) data analyses (see also https://git.rz.tu-bs.de/proppe-group/co2_electrophilicity). See DOI: https://doi.org/10.1039/d5dd00020c |
| This journal is © The Royal Society of Chemistry 2025 |
