Classification of (dis)ordered structures as superionic lithium conductors with an experimental structure–conductivity database

Abstract

Solid-state electrolytes (SSEs) are critical for the development of high-performance all-solid-state batteries. Data-driven efforts to discover novel SSEs have been constrained by the absence of databases linking ionic conductivity with structure, as well as by challenges in encoding structural information for the disorder that is often found in superionic conductors. Here, we construct the largest database to date of experimentally measured ionic conductivity values paired with corresponding crystal structures, comprising 548 Li-containing compounds. Graph-based features, derived using a transfer learning framework, enable learning directly from disordered crystals, and AtomSets models leveraging these features outperform domain-specific features in a classification task. These models are employed to screen the Inorganic Crystal Structure Database (ICSD) and Materials Project for superionic Li-containing compounds. We identify 241 compounds with predicted superionic conductivity and band gaps greater than 1 eV. Experimental validation confirming superionic conductivity in one of these candidates, Li₉B₁₉S₃₃, demonstrates the utility of this approach for the discovery and development of advanced SSEs for all-solid-state batteries.

---

1 Introduction

All-solid-state batteries represent a transformative frontier in energy storage technology, offering the potential for enhanced safety and performance compared to conventional lithium-ion batteries.^1–4 However, the realization of their full potential hinges critically upon the discovery and development of solid-state electrolytes (SSEs) exhibiting high ionic conductivity, low electronic conductivity, stability against both Li metal anodes and highly oxidative cathodes, and suitable mechanical properties. The multi-objective search is further complicated by the observed trade-off between the conductivity and stability in commonly studied SSE material families.^5–10 Discovery of novel SSE materials is necessary to optimize these desired properties.^8,11

To expedite the exploration for suitable SSEs, researchers have increasingly explored the integration of statistical and machine learning approaches.^8,12–31 These methodologies often rely on databases consisting of compounds labelled with their experimental ionic conductivity (σ_exp) or related quantities such as migration energy (E_m), serving as the foundation for training predictive models. Features derived from these compounds serve as inputs to the models, encapsulating information about the material's composition and/or structure. Models trained solely on composition information have successfully predicted various material properties in other domains.^32–36 Such an approach has also been explored for predicting ionic conductivity, as demonstrated by Hargreaves et al., who achieved high performance using a composition-only model trained on 403 unique compositions.²⁶ However, since compounds are featurized by composition only, the model is unable to distinguish between polymorphs. Additionally, the ionic conductivity in solid-state materials is inherently linked to their crystal structure, as the arrangement of atoms and the pathways available for ion migration directly influence ion mobility. Structural features can capture information about coordination environments, atomic positions, and the potential for site disorder, all of which are critical in determining ion transport properties.

Incorporating structure-based information to identify fast ion conductors with data-driven methods has historically encountered two primary challenges: the lack of comprehensive datasets that provide both ionic conductivity values and corresponding crystal structures, and inadequate methods for representing the prevalent disorder in many fast ion conductors. In this context, disorder refers to the occurrence of atomic sites within a crystal structure that are not fully occupied by a single element. Instead, the sites are populated by a set of possible chemical species, with the partial occupancy describing the fraction of sites occupied by each species in the long-range average structure. Sendek et al. trained a logistic regression model capable of predicting if a material would exhibit superionic conductivity using interpretable structural features.¹⁵ However, their training set contained only 40 entries, preventing evaluation with a holdout test set. Moreover, their probabilistic sampling method for feature construction for disordered compounds may become computationally expensive when applied to large collections of known compounds such as the Inorganic Crystal Structure Database (ICSD), in which 6860 of 11925 Li-containing materials exhibit disorder (v5.2.0). Our own previous study implemented a semi-supervised learning strategy using a database of 219 ionic conductivity values and corresponding ICSD crystal structures. The structural descriptors used in the previous work were unable to represent disordered compounds, limiting the utilization to a subset that could be ordered through a costly supercell ordering procedure.²⁷ Excluding highly disordered compounds from consideration is particularly undesirable when searching for novel fast ion conductors, as site disorder is known to be a critical factor in realizing high conductivity in many systems.^37–43 The recently reported COSNet framework introduced by Wang et al., has shown promise in combining structural and compositional information using multimodal ensemble learning to predict material properties, including ionic conductivity.⁴⁴ However, the effectiveness of this approach for representing structural disorder was not explicitly examined in the study.

In the current work, we alleviate the data scarcity challenge by constructing the largest repository to date of 548 crystal structures and σ_exp values. To address the issue of disordered crystal structure representation, we use transfer-learned graph-based features. Graph-neural networks (GNNs) have emerged as powerful architectures for incorporating composition and crystal structure information to make property predictions.^45–47 Additionally, by representing the node features for disordered sites through combinations of elemental embeddings, GNNs have been used for learning from disordered compounds.⁴⁸ However, the flexibility of these models enabled by their vast number of trainable parameters necessitates thousands of labelled data points to be trained correctly.^49–51 To circumvent the issue, we represent our data with features derived from GNNs pre-trained on large datasets (e.g., Materials Project formation energies) and pass these graph-based features through comparatively simple multilayer perceptron (MLP) models using the AtomSets framework developed by Chen and Ong.⁵⁰ Such an approach has been demonstrated to achieve higher performance than GNNs for smaller datasets of similar size to our own.^50,52 To further overcome the challenges of a small dataset, we implement transfer learning by pre-training AtomSets models on the MatBench metal classifier dataset containing 106 113 samples and use the trained weights to initialize the network weights for ionic conductivity prediction.⁵³ The AtomSets models are tasked with classifying input materials as superionic (σ_exp > 10⁻⁴ S cm⁻¹) or not.

We examine the efficacy of representing disordered compounds using a linear combination of elemental embeddings and graph-based features. For comparison, ordered configurations are generated using a supercell approach. The performance of classification models trained using these two methods is found to be nearly equivalent. The optimal feature representation and model configurations for this task are explored through k-fold and leave-one-cluster-out (LOCO) cross-validation (CV). Transfer-learned features derived from early graph-convolutional layers of the parent model, which encode short-range structural information, achieve the highest performance for out-of-cluster predictions. Reducing the chemical diversity by replacing atoms with representative species improves extrapolation beyond the training set. A final ensemble of 100 AtomSets models is shown to achieve high test performance and is used to evaluate all Li-containing materials in the Inorganic Crystal Structure Database (v5.2.0) and Materials Project (v2023.11.1). An additional criterion requiring the electronic band gap (E_g) to be greater than 1 eV is used to prioritize compounds more likely to be electronically insulating, a critical property for SSEs. The screening identifies 241 compounds predicted to be superionic with E_g > 1 eV. To show the practical relevance of our approach, we experimentally validate superionic conductivity in one of these candidate phases, Li₉B₁₉S₃₃, achieving a σ_exp of 4.1 × 10⁻⁴ S cm⁻¹.

2 Results and discussion

2.1 Structure–conductivity database

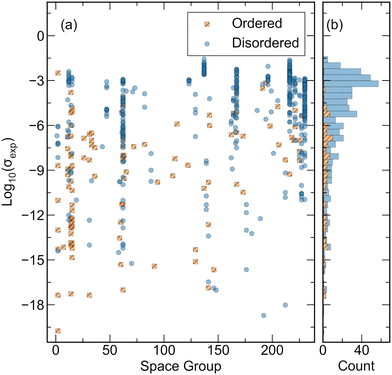
The database created for this study is comprised of experimental ionic conductivity values for 548 distinct Li-containing compounds and their corresponding crystal structures sourced from the Inorganic Crystal Structure Database (ICSD). All ionic conductivity measurements recorded are obtained from electrochemical impedance spectroscopy (EIS) data. The database includes ionic conductivity values that are both directly extracted from text and digitized from figures in reference sources. In solid-state ionics literature, particularly for low conductivity materials, measurements are frequently performed at elevated temperatures and presented in the form of Arrhenius-type plots where ln(σT) or log₁₀(σT) is plotted against T⁻¹. To capture these data, plots are digitized, and conductivity values are extrapolated to room temperature using an Arrhenius relationship. The resulting room-temperature conductivity values, along with the lowest measured temperature, are recorded in the database. To facilitate the inclusion of both structure and composition information for model training, conductivity values are paired with corresponding crystal structures. Wherever possible, Crystallographic Information Files (CIFs) associated with conductivity measurements are obtained from the ICSD using article DOIs. That is, reports are identified which included both conductivity measurements and sufficient structural characterization to generate an ICSD entry. Since the same nominal compound (i.e. Li₁₀GeP₂S₁₂) can have different lattice parameters, atomic positions, or defect concentrations depending on preparation conditions, direct matching of the CIF with the measured sample is prioritized. For articles containing conductivity measurements but lacking ICSD entries, associated crystal structures are identified by manual inspection. Only articles with sufficient structural characterization to enable matching of stoichiometry, space group, and lattice parameters to existing ICSD entries are included. Articles without structural characterization or containing conductivity values for non-crystalline compounds are excluded from the dataset. For a comprehensive list of ionic conductivity values corresponding to compounds without ICSD entries, readers are referred to the database compiled by Laskowski et al.²⁷ Structures deemed identical within a specified tolerance are identified. In cases of multiple ionic conductivity values for identical structures, the entry corresponding to the median ionic conductivity is retained and duplicate entries are removed. Notably, this process preserves highly related structures, necessitating diverse forms of CV to assess model performance, as elaborated in subsequent sections. To ensure database accuracy, the database is constructed by a single author and is verified by the other authors. Any discrepancies found during the verification process are reviewed by a third author for validation. A summary of the database created in this work is presented in Fig. 1. The compiled database contains a broad range of ionic conductivity values from crystal structures with 72 different space groups. However, certain space groups are more represented due to the bias in SSE material research which has primarily been confined to garnets, LISICON-type structures, argyrodites, NASICON-type structures, Li-nitrides, Li-hydrides, perovskites, and Li-halides.⁶ Importantly, from the histogram in Fig. 1 it is evident that most structures in the database, and especially those corresponding to materials with high conductivity, are disordered, further motivating the use of a compatible structural representation.

Fig. 1 (a) The space group and corresponding Li-ion conductivity (σ) values at room temperature are plotted as log₁₀(σ_exp) for each database entry. The database contains entries from 72 different space groups, with σ_exp values spanning over 10 orders of magnitude. (b) A histogram of the data in (a) showing the distribution of log₁₀(σ_exp). Most superionic compounds contain site disorder, necessitating an appropriate featurization method. Note that seven compounds with σ_exp < 10⁻²⁰ S cm⁻¹ are excluded from this figure for ease of visualization.

Experimental ionic conductivity measurements of the same compound with EIS can vary significantly across different laboratories.⁵⁴ Such variability has been attributed to inadequate control of sample temperature, sample geometry, the frequency range measured, choice of metal contact materials, and aging effects.⁵⁴ Extrapolating conductivity measurements performed at high temperature to room temperature is an additional source of error. The use of experimental conductivity values from our database would thus introduce considerable noise into the training of a regression model. Thus, herein we do not endeavor to predict ionic conductivity but rather determine if a material is likely to be a good conductor or not. Framing a materials discovery problem as a classification task can enhance the prediction accuracy for identifying extraordinary compounds.³² Classification models are designed to distinguish between distinct categories, allowing them to more effectively handle the binary nature of identifying extraordinary versus ordinary materials. In contrast, regression models predict continuous values, which can introduce greater uncertainty and error, particularly when extrapolating beyond the training data.

The supervised learning performed in this study involves training a classifier neural network to determine if an input crystalline compound will exhibit superionic Li conductivity (σ_exp > 10⁻⁴ S cm⁻¹). Table 1 provides summary statistics for the dataset used in this study. From the 548 labels, 10% are removed at the outset of this work and set aside as a final test set. The remainder of the data is used to determine optimal feature representations and hyperparameters using various CV techniques.

Table 1 A summary of the structure–conductivity database

Description	Number
σexp values with crystal structure	571
Unique structures	548
Space groups	72
Ordered compounds	112
Disordered compounds	436
Positive class (σexp ≥ 10^−4 S cm^−1)	211
Negative class (σexp < 10^−4 S cm^−1)	337

---

2.2 Training with disordered representations using AtomSets framework

Input compounds are transformed into graphs following the MatErials Graph Network (MEGNet) formalism outlined by Chen et al.⁴⁵ A graph is defined as G = (u, V, E) where u, V, and E are the global state, atom (node), and bond (edge) attributes, respectively. A comprehensive description of the MEGNet architecture can be found in the original works.^45,48 The graph representations are subjected to a specified number of graph-convolution (GC) layers within the pre-trained parent MEGNet model, after which atom features are extracted and provided as inputs for the AtomSets models. Within GC layers of the parent model, information is passed between atom, bond, and state vectors. Consequently, atom features following GC layers implicitly encapsulate both compositional and structural information, with a greater number of GC layers encoding longer-range interactions.⁵⁰ The AtomSets models accept the atom feature matrix V with dimensions N_a × N_f where N_a is the number of atoms in the structure and N_f is the number of features.⁵⁰ Consistent with the methodology implemented by Chen et al., the node feature for a disordered site is derived as a linear combination of elemental embeddings for the constituent elements, weighted by their reported occupancy. That is, , where x_i is the reported site occupancy of element i and W_Zi denotes the learned elemental embedding for the element with atomic number Z_i.⁴⁸ For the present study, W_Zi are learned embedding vectors of length 16 from a MEGNet model trained on 133 420 structures and their formation energies from the Materials Project database, downloaded on April 1, 2019. Importantly, this strategy for representing disorder does not consider possible occupancy correlations between disordered sites, instead treating each site independently. While the following analysis demonstrates that this approximation is sufficient for predicting superionic conductivity, we expect that other applications (e.g. force predictions between atoms) may require additional considerations to handle interactions between correlated sites.

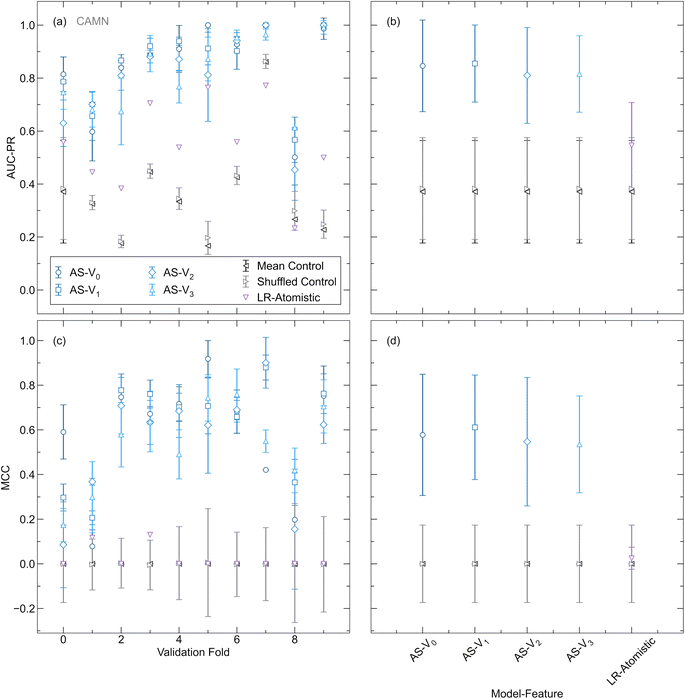
The performance of models employing a linear combination of elemental embeddings is evaluated against those using ordered representations. To create the comparison set, ordered configurations without Li atoms are generated and ranked using the OrderDisorderedStructureTransformation in the Python Materials Genomics (Pymatgen) package, with the configuration exhibiting the lowest calculated Ewald energy selected for each structure.⁵⁵ Only disorder of the non-Li atoms is considered for this comparison because the extensive disorder in the mobile ion sublattice makes supercell generation computationally prohibitive for the entire dataset. An illustration of the two strategies to create graph representations from disordered crystals is shown in Fig. 2(a). AtomSets classification models, tasked with discerning whether an input structure is superionic, are trained using both ordered and linear combination of elemental embeddings representations. A comparative analysis is presented in Fig. 2(b) and (c) where the average area under the precision–recall curve (AUC-PR) and Matthews correlation coefficient (MCC) assessed under k-fold CV for each model is shown over 500 training epochs. The AUC-PR is chosen as it provides a comprehensive evaluation of the model's precision and recall across different thresholds and is particularly well-suited for classification tasks with imbalanced datasets.⁵⁶ The AUC-PR score ranges from 0 to 1, with a perfect classifier obtaining a score of 1. MCC offers a balanced measure of classification performance, accounting for both true positives and true negatives, thereby providing a robust metric for our binary classification task.^57–59 The MCC score ranges from −1 to 1, where 1 indicates perfect agreement between predicted and actual labels and −1 indicates total disagreement between predicted and actual labels. As in the work by Hargreaves et al., these metrics are compared against those obtained from shuffled and mean controls, where predicted values are generated either by randomly shuffling the dataset labels or by using the training set mean as the prediction label.²⁶ Models trained with both ordered and disordered representations achieve AUC-PR and MCC scores significantly higher than those of the controls and comparable performance levels by 500 training epochs. The results demonstrate that the linear combination of elemental embeddings representation enables similar efficacy to the ordered representation without necessitating the computationally intensive ordering transformation. Given the substantial computational costs associated with creating ordered configurations, which can scale combinatorially with the number of disordered sites and possible substitutions, the ability to use a disordered representation while maintaining performance parity offers expedited training.⁶⁰ Moreover, this capability facilitates efficient screening of experimental databases containing disordered compounds such as the ICSD, where over half of Li-containing compounds exhibit site disorder.

Fig. 2 Different strategies to represent disordered structures. (a) On the left, the atom attributes are equal to a linear combination of elemental embeddings learned from a MEGNet model trained on a large database of Materials Project formation energies. On the right, ordered supercell configurations are generated. Configurations are compared using an Ewald summation and the lowest-energy configuration is used for graph creation. (b) The average area under the precision–recall curve (AUC-PR) and (c) Matthews correlation coefficient (MCC) for AtomSets models trained with graph representations generated through the two approaches. Metrics are averaged over 5-fold random cross-validation with the shaded regions indicating the standard deviation. Controls from random shuffling and using the mean of the training set as the predicted values are plotted as horizontal lines. Both methods for representing disordered structures offer comparable performance that exceeds the controls.

2.3 Feature and model evaluation

The present study explores two distinct feature engineering strategies: (1) the number of GC layers in the parent MEGNet model through which the graph is passed before the atom features are extracted and (2) input structure simplifications prior to graph generation. Models are trained using atom feature matrices V_i (i = 0, 1, 2, 3) where V₀ is the atom feature matrix comprised solely of the learned elemental embeddings from the parent model and V_i (i = 1, 2, 3) denote the atom feature matrices after passing the graph through i GC layers. By nature of the message passing in each GC layer, higher-i atom features encode longer-range interactions. The second feature engineering technique of pre-processing input structures before feature generation has been demonstrated to enhance learning outcomes for Li-ion conductor datasets.^17,27 Laskowski et al. found that simplifying compounds by replacing categories of atoms with representative species and removing the position of the mobile ion improved clustering efficacy of known Li-ion conductors.²⁷ To evaluate this strategy within the model architecture under investigation, we explore structural modifications involving changes to the cations (C), anions (A), mobile Li ions (M), and neutral atoms (N) within the structures. Specifically, we investigate the following representations:

• CAMN: retaining all atom types.

• CAN: removing the mobile Li ion.

• CAMNS: retaining all atom types but simplifying the structure by substituting cations with Al, anions with S, and neutral species with Mg.

• CANS: removing the mobile Li ion and performing the same substitutions as in CAMNS.

To compare the model performance for the different feature representations, we use both k-fold validation and LOCO CV. Experimental training data can exhibit a highly clustered distribution due to the inherent nature of scientific exploration – parent materials are systematically perturbed through various means (e.g. elemental substitution) to develop structure–property relationships, resulting in a large number of training data points confined to a relatively small number of parent structure frameworks. The clustering of data can lead to the inclusion of highly related compounds in both training and validation sets when data is randomly segregated. Therefore, randomized k-fold validation provides insight into a model's interpolation ability but offers limited information regarding its capacity to predict in unseen chemical spaces. Predictive models intended for materials discovery also require an evaluation of their extrapolative capabilities. We assess this using LOCO CV, a clustering-based validation method for assessing a model's ability to predict on chemically distinct compounds not present in the training set.^26,61 The dataset is clustered into n clusters using a chosen embedding representing the chemical nature of the compounds and a clustering algorithm. Training is conducted on the compounds belonging to n − 1 clusters and the model performance is evaluated on the compounds from the remaining cluster. In this work, we adhere to the procedure described by Hargreaves et al.²⁶ The compounds in our labelled database are embedded using ElMD, a metric which captures the chemical similarity between compounds based on their chemical composition. Uniform Manifold Approximation and Projection (UMAP) is applied to obtain a low-dimensional representation that retains essential chemical relationships. Density-Based Spatial Clustering of Applications with Noise (DBSCAN) is used to automate separation of the data into clusters for LOCO CV.²⁶ Detailed statistics for each cluster generated for this validation procedure are provided in the Table S3.† The effectiveness of data segregation from this clustering technique is examined by analyzing the compositional similarity between the entries in the test and validation sets and those in the training set. The results of this analysis displayed in Tables S4–S6† show that except for one fold, the LOCO CV validation sets exhibit significantly lower compositional similarity with the training set compared to the k-fold validation or test sets. This motivates the use of LOCO CV as our primary evaluation technique when comparing feature representations and performing hyperparameter optimization.

An additional benchmark for our AtomSets-based model is provided by comparing its performance with that of a logistic regression model trained using the database created in this work and a set of interpretable atomistic features defined by Sendek et al.¹⁵ This serves to validate our approach against a method that has been previously applied to the task of identifying SSE candidates using structure-based representations. The atomistic features used in the previous work include the average number of Li–Li bonds per Li atom in the crystal, the ionic character of bonds within the sublattice, the anion coordination environment, the shortest distance between Li ions and anions, and the shortest distance between Li ions.¹⁵ These features were chosen to encode information directly impacting Li mobility, potential pathways for ion conduction, and the ease of ion movement through the lattice. Detailed definitions for each feature are provided in the original work. Fig. 3 depicts the AUC-PR and MCC for AtomSets models trained using V_i (i = 0, 1, 2, 3) atom features with different structural simplifications in addition to the logistic regression model trained using the atomistic feature set. All model variations are trained using the same dataset and k folds. Both the AtomSets and logistic regression models achieve higher AUC-PR and MCC than the controls, indicating significant predictive power. However, all variations of the AtomSets model outperform the logistic regression model that is based on atomistic features. For the CAN and CAMN representations, using V₀ features achieves the highest performance, suggesting that composition-only information in the form of the learned elemental embeddings is sufficient for classifying ionic conductors in this dataset when assessed under k-fold CV. The CANS representation attains the lowest performance for all V_i, but higher performance is enabled by i > 0 which incorporates longer-range structural information through additional graph convolutions. These results suggest that AtomSets models using transfer-learned features are able to better capture the complex relationships influencing ionic conductivity, leading to higher classification accuracy.

Fig. 3 Classification performance of model–feature combinations assessed with k-fold cross-validation. (a) AUC-PR and (b) MCC of AtomSets (AS) models with graph-based atom features (V₀ to V₃, denoted as V₀–V₃ in plots for simplicity) and a logistic regression model using atomistic features. Four different structural simplifications are shown (CAMN, CAN, CAMNS, and CANS) with mean and randomly shuffled controls. The symbol locations indicate the mean from random 5-fold cross-validation and error bars represent the standard deviation.

LOCO CV is used as a complementary method for evaluating model and feature representations in the context of materials discovery. Different from the case of k-fold CV, controls are calculated separately for each cluster due to the significant variation in the ratio of positive to negative labels across clusters (as shown in Table S3†). We perform hyperparameter optimization separately for each V_i and each validation cluster. For all subsequent results, figures, and discussion, we report and compare the metrics from the highest-performing hyperparameter configurations for each representation. This approach ensures that each representation and validation cluster is evaluated based on its optimal hyperparameter settings, allowing for a consistent comparison of performance. To capture the variance of the models, the metric value averaged over 10 repeated runs is presented at the average best epoch across all folds. Reporting the variance in this way offers insight into the model performance under conditions akin to those encountered in materials discovery scenarios, where a final model is trained for a specified number of epochs before being used as a screening tool. For the logistic regression model, optimization of the regularization penalty term is performed in a similar manner and the results from the best value are shown for comparison to the AtomSets models. Fig. 4(a) and (c) depict the validation AUC-PR and MCC for AtomSets models trained with each V_i, the logistic regression model, and controls across all clusters. The logistic regression model with atomistic features performs significantly worse than the AtomSets models, showing comparable MCC to the randomized and mean controls. No single V_i outperforms all others for every cluster, despite all surpassing the random and shuffled controls. The averaged AUC-PR and MCC scores across all clusters for each V_i are illustrated in Fig. 4(b) and (d). Descriptors capturing short-range interactions (V₀, V₁) provide slightly higher classification performance than those derived from more GC layers. A similar finding was reported in the original AtomSets work where models trained using features from early GC layers exhibited higher accuracy across a variety of prediction tasks.⁵⁰ Additionally, it is observed that contrary to the k-fold validation results, the averaged metrics for V₁ are higher than those for V₀, with the average AUC-PR and MCC being (0.86, 0.61) for V₁ and (0.85, 0.58) V₀, respectively. These findings suggest that incorporating some short-range structural information can enhance the model's ability to classify ion conductors with chemistry different from the training set beyond composition-only information. We note that while LOCO CV is designed to evaluate model extrapolation by grouping compounds based on chemistry, automated clustering does not always preserve chemically intuitive boundaries. For instance, clusters 6 and 7 both include argyrodites with comparable compositions, potentially contributing to the higher observed performance.

Fig. 4 Classification performance comparison of different features assessed with leave-one-cluster-out cross-validation. (a) AUC-PR and (c) MCC for each validation cluster of pre-trained AtomSets (AS) models with graph-based atom features (V₀ to V₃) and a logistic regression model using atomistic features. The average from 10 repeated training runs with the optimal hyperparameters for each validation cluster are shown. Mean and shuffled controls are calculated for each validation cluster. (b) AUC-PR and (d) MCC from the optimal hyperparameter set for each model–feature combination averaged across all validation clusters. Error bars indicate the standard deviation. Metrics are from the best epoch across all runs and validation clusters.

Fig. 5 illustrates the performance of AtomSets models trained using V₁ atom features constructed from the CAMN, CAN, CAMNS, and CAN structure representations. The CAMN and CAMNS representations enable learning that surpasses the control tests for all validation clusters. Removing the mobile atom yields inferior performance, with the CAN representation exhibiting slightly worse MCC compared to the controls for validation cluster 0, and the CANS representation showing lower MCC than controls for validation clusters 0 and 1. This emphasizes the value of the graph-based featurization in incorporating structural information while including the disordered mobile atom sites. The mobile ion sublattice typically constitutes the source of disorder in these compounds, and it is evident that neglecting these sites due to inadequate representation would overlook crucial information for prediction. Notably, the CAMNS representation, where the identity of the cation, anion, and neutral species remains constant for all compounds, achieves nearly the same performance as the model trained on the nominal structures (CAMN) while exhibiting lower variation between clusters. Most representations exhibit lower predictive performance on validation clusters 0 and 1, which primarily consist of garnets and other oxides. This may be due to the unique structural characteristics and ionic conduction mechanisms in these materials, which are more challenging for the models to capture compared to other clusters.

Fig. 5 Classification performance of structural simplifications assessed with leave-one-cluster-out cross-validation. (a) AUC-PR and (c) MCC for each validation cluster of pre-trained AtomSets (AS) models and V₁ atom features for CAMN, CAN, CAMNS, and CANS structural simplifications. The average from 10 repeated training runs with the optimal hyperparameters for each validation cluster is shown. Mean and shuffled controls are calculated for each validation cluster. (b) AUC-PR and (d) MCC from the optimal hyperparameter set for each model–feature combination averaged across all validation clusters. Error bars indicate the standard deviation. Metrics are from the best epoch across all runs and validation clusters.

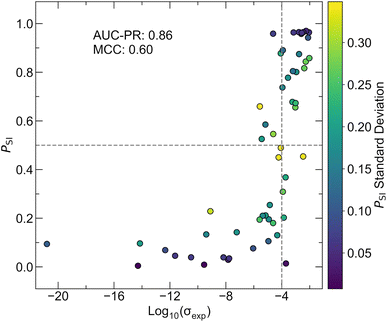
The best hyperparameter configuration is different between chosen validation clusters as shown in Table S8.† To introduce diversity in the final model parameters and reduce overfitting to one specific validation set, an ensemble comprised of AtomSets models with CAMNS-V₁ features is trained with the most effective hyperparameters for each of the 10 validation clusters. Variation for each model configuration is captured by training 10 models for each parameter set, resulting in a total of 100 AtomSets models within the ensemble. The performance of the final ensemble is examined using the test partition, which is separate from the data used for the above k-fold and LOCO CV. It is noted that the test partition, while separate from the training data, was partitioned randomly, similar to k-fold validation. This approach does not fully assess extrapolation to distinct chemistries, a limitation examined by LOCO CV in this study. Fig. 6 shows the probability of a compound being superionic (P_SI) where superionic is defined as σ_exp > 10⁻⁴ S cm⁻¹ with the log₁₀(σ_exp) for the test set. The final model ensemble achieves an AUC-PR of 0.86 and an MCC of 0.60. By contrast, the logistic regression model only achieves an AUC-PR of 0.80 and an MCC of 0.26, highlighting the superior performance of the AtomSets ensemble approach. Test set compounds that are misclassified all have σ_exp values less than two orders of magnitude from the decision boundary. Overall, the pre-trained Atomsets CAMNS-V₁ models display significantly higher predictive power than control metrics, as assessed through k-fold CV, LOCO CV, and a separate test set. The strong performance on out-of-cluster inputs suggests that this model architecture is well-suited for screening known Li-containing materials to discover novel fast ion conductors.

Fig. 6 Test set evaluation of the AtomSets-V1 CAMNS model ensemble. The predicted likelihood of test set compounds exhibiting superionic conductivity (P_SI) is plotted against their reported log₁₀(σ_exp). Dashed lines indicate boundaries for classification. The model ensemble achieves an AUC-PR of 0.86 and a MCC of 0.6. All incorrectly classified compounds have log₁₀(σ_exp) values less than two orders of magnitude from the class boundary of 10⁻⁴ S cm⁻¹.

2.4 Screening of known Li-containing materials

All Li-containing materials present in the ICSD (v5.2.0) and Materials Project (v2023.11.1) are aggregated. Structures are featurized using the CAMNS structural simplification and V₁ atom feature matrix. The P_SI is predicted for all compounds. To facilitate consideration of compounds as potential SSEs, the DFT-calculated E_g from the Materials Project is retrieved if a corresponding ICSD entry can be identified. In cases where no matching entry exists in the Materials Project, the E_g is predicted using the MEGNet model developed by Chen et al.⁴⁵ Compounds with E_g of less than 1 eV are excluded. The relatively low E_g for SSEs accounts for the systematic underestimation of experimental band gap values by approximately 40 percent in the Materials Project.⁶² The MEGNet model is trained using Materials Project band gap data and so a similar systematic underestimation of experimental band gap values is expected. This value was chosen to balance the discovery of novel material families with practical considerations for electronic insulation.

A histogram of the P_SI for all 6863 Li-containing materials with predicted E_g > 1 eV is shown in Fig. 7. Most compounds are not predicted to be fast ion conductors with 6435 of 6863 having P_SI less than 0.5. Of the 428 predicted to be superionic, 396 exhibit site disorder as highlighted in the inset of Fig. 7(a). This underscores the importance of choosing a compatible structural representation to ensure that disordered materials are retained in the screening process. The prediction confidence is quantified by the standard deviation of the ensemble P_SI and a calculated distance metric d_training. Lower standard deviations indicate greater agreement between ensemble models, increasing the confidence in the prediction. The distance metric is defined as the distance between the unlabelled compound and the nearest training sample in N_f-dimensional space where N_f is the number of features in the atom feature matrix. Similar to previous work, we normalize the distances by the training data variance using principal component analysis (PCA).¹⁵ Fig. S2† shows the PCA embedding to two dimensions of the atom features for compounds in the training set, ICSD, and Materials Project. A smaller d_training indicates that the prediction requires less extrapolation from the training data, increasing the confidence. Fig. 7(b) shows the P_SI, d_training and P_SI standard deviation for each Li-containing compound in the ICSD with predicted E_g > 1 eV.

Fig. 7 Results of screening Li-containing compounds in the ICSD using the AtomSets-V1 CAMNS model ensemble. (a) Histogram of the likelihood of superionic conductivity (P_SI) for ordered and disordered Li-containing compounds with predicted E_g > 1 eV. Inset shows region of high P_SI where most compounds are disordered. (b) P_SI vs. the distance from the nearest training sample d_training for Li-containing materials with E_g > 1 eV.

To identify novel materials that could be interesting in battery applications, we filter out any compounds with chemical formula similar to those in our training set. Specifically, compounds whose normalized compositions have all constituent elements within 5 percent of any training sample composition are excluded. This screening results in 241 materials from the ICSD and Materials Project predicted to be superionic with E_g > 1 eV. The ICSD compounds with the top 20 highest P_SI values are detailed in Table 2 for discussion. Intermetallic compounds with predicted E_g > 1 eV are also omitted. The standard deviation of the ensemble predictions is provided in parentheses next to the P_SI in addition to the d_training. Among these candidates, conductivity measurements for 5 compounds were reported recently and were not captured during the database creation process. These values are included in Table 2. Although these compounds do not directly contribute to identifying new useful materials, they serve as additional validation of the model's effectiveness, as all were correctly classified based on the experimental measurements. While a measurement of Li_1.251Cd_1.671In_0.471Cl₆ could not be identified, its structure was described as resembling that of the high-temperature polymorph of LiMnInCl₆, which adopts a layered CdCl₂-type structure, with Li⁺, Cd²⁺, and In³⁺ ions randomly distributed across the octahedral sites.⁶⁷ Li₂Zr₆MnCl₁₅ is composed of abundant elements, has a straightforward reported synthesis method, and a high P_SI with low standard deviation, making it a strong candidate for experimental investigation.⁶⁸ In a recent computational study, LiP₅ was found to have the highest ionic conductivity of all known Li–P binaries, predicted to exceed 1 mS cm⁻¹ at room temperature through molecular dynamics simulations.⁶⁹ The same study did not observe significant Li conduction in LiP₇. Nevertheless, the predictions from this study in addition to the work by Maltsev et al. suggests that these phases, particularly LiP₅, may warrant further investigation. The Li dynamics of B_xS_y compounds Li₅B₇S₁₃ and Li₉B₁₉S₃₃ studied via Li⁷ nuclear magnetic resonance (NMR) have suggested high Li mobility and ab initio molecular dynamics has also predicted high conductivity in these materials.^70–72 However, experimental measurements of the ionic conductivity are not reported in the literature. Another promising candidate, LiBSi₂, features an open tetrahedral framework with three-dimensional channels that may facilitate fast ion conduction.⁷³ Additional considerations such as the abundance or toxicity of constituent elements could make candidates such as Li_6.55Ga_0.05La_2.91Zr₂O₁₂, Li₇La_1.8Eu_1.2Zr₂O₁₂, Li_6.43Ga_0.52La_2.67Zr₂O₁₂, LiCaAs, and LiNdS₂ less desirable. However, these additional screening criteria are not applied for all compounds in the present work.

Table 2 The top 20 candidate materials from the ICSD as ranked by the average P_SI from the AtomSets-V1 CAMNS model ensemble. Compositions are rounded to two decimal places where appropriate

Compound	ICSD code	PSI (SD)	Eg (eV)	dtraining	σexp (mS cm^−1)
a Value retrieved from corresponding entries in the Materials Project. All other Eg values are predicted from the pre-trained MEGNet model.
Li1.25Cd1.67In0.47Cl6	98583	0.94 (0.09)	3.15	0.38	NA
Li2Zr6MnCl15	71146	0.91 (0.13)	1.29	0.62	NA
Li9.9SnP2S11.9Cl0.1	48716	0.9 (0.13)	2.15	0.06	0.26 (ref. 63)
LiP5	23620	0.89 (0.15)	1.26^a	1.54	NA
Li5B7S13	143927	0.89 (0.16)	2.16	0.30	NA
Li6.75La2.75Ca0.25Zr1.5Nb0.5O12	63870	0.87 (0.12)	2.68	0.05	0.20 (ref. 64)
Li6.55Ga0.05La2.91Zr2O12	430602	0.86 (0.13)	2.47	0.05	NA
LiP7	23621	0.84 (0.17)	1.65^a	1.51	NA
LiCaAs	428102	0.84 (0.20)	1.1^a	2.13	NA
LiSrAlSb2	412654	0.83 (0.17)	1.01	1.95	NA
LiBSi2	425643	0.83 (0.14)	1.17^a	1.40	NA
Li7.03La2.87Sr0.08Zr1.39Ta0.58O12.22	45740	0.83 (0.20)	3.16	0.19	0.72 (ref. 65)
Li9B19S33	73151	0.82 (0.29)	2.27	0.29	NA
Li6.41La2.90Sr0.10Zr1.6Mo0.4O12	42738	0.81 (0.21)	2.74	0.14	0.33 (ref. 66)
Li0.5ZrS2	642338	0.79 (0.26)	1.33	0.38	NA
Li1.66W6I14	256678	0.79 (0.24)	1.13	2.52	NA
Li7La1.8Eu1.2Zr2O12	27177	0.79 (0.24)	2.94	0.29	NA
Li6.43Ga0.52La2.67Zr2O12	196425	0.79 (0.17)	2.27	0.09	NA
LiNdS2	642202	0.78 (0.22)	1.5	2.21	NA
Li7.10La2.83Sr0.16Zr1.38Ta0.61O11.76	45741	0.78 (0.20)	3.16	0.19	0.85 (ref. 65)

---

2.5 Experimental demonstration of Li₉B₁₉S₃₃

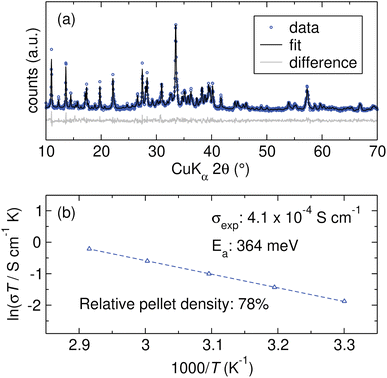
Li₉B₁₉S₃₃ is chosen for experimental characterization. Originally synthesized by Hiltmann et al., the crystal structure of Li₉B₁₉S₃₃ is composed of corner-sharing B₁₉S₃₆ units that form large channels populated by highly disordered Li⁺ cations, offering potential pathways for ion migration.⁷⁴ NMR studies by Bertermann et al. indicate anisotropic Li⁺ diffusion within these channels, associated with a low activation energy.⁷¹ Computational work by Sendek et al. predicted that Li₉B₁₉S₃₃ possesses the widest electrochemical stability window and highest oxidative stability among the materials in the Li–B–S ternary phase space, including Li₅B₇S₁₃, Li₃BS₃, and Li₂B₂S₅.⁷² Experimental studies of materials in the Li–B–S ternary phase space are relatively rare in the context of fast ion conductors, partly due to synthesis challenges posed by the reactivity of their precursors with conventional reaction vessels and the difficulty in obtaining phase-pure products. In previous work, we developed a solid-state synthesis protocol for Li₃BS₃ using Li₂S, B, and S that we find is readily adapted to the synthesis of Li₉B₁₉S₃₃.²⁷ The powder X-ray diffraction (XRD) pattern and Rietveld refinement to the reported structure shown in Fig. 8(a) confirms phase-purity. Variable-temperature EIS is used to characterize the ionic conductivity of Li₉B₁₉S₃₃. Although challenges with densification yield a pellet that is only 78% of the theoretical density, the material demonstrates a conductivity of 4.1 × 10⁻⁴ S cm⁻¹. The slope of the Arrhenius plot of ln(σT) versus T⁻¹ presented in Fig. 8(b) yields an activation energy E_a of 364 meV. Although improved pelletization is expected to increase conductivity, these findings nevertheless affirm the superionic conductivity of Li₉B₁₉S₃₃, a candidate identified by the model ensemble. True experimental validation of this approach's predictive capabilities would require the synthesis and characterization of a significant number of the identified candidates. However, this task is beyond the scope of a single group and is not pursued in the present work.

Fig. 8 Experimental characterization of Li₉B₁₉S₃₃. (a) XRD pattern and Rietveld refinement for as-prepared Li₉B₁₉S₃₃. (b) Arrhenius-type fit for Li₉B₁₉S₃₃ with ionic conductivity values obtained from electrochemical impedance spectroscopy.

3 Conclusions

We have constructed the largest known database of experimental ionic conductivity and corresponding crystal structure information for 548 unique Li-containing compounds. By comparing with ordered configurations generated through a supercell sampling approach, we demonstrate that using linear combinations of elemental embeddings is an effective means of representing the prevalent site disorder in our database with graph-based features, thereby enabling the training of structurally-aware predictive models to identify potential superionic conductors.

Using this representation and a transfer-learning approach, we train AtomSets models that display classification performance surpassing our controls under both k-fold and LOCO CV. As compared to a benchmark logistic regression model trained using domain-specific features, the AtomSets models employing transfer learning exhibit superior predictive power. We find that short-range interactions are most critical for accurate predictions, emphasizing the need to capture local structural environments. Properly including and representing Li atom positions significantly enhances predictive accuracy. Interestingly, the specific identity of anions is found to be less important, as models using simplified structural representations (e.g., CAMNS) show high performance. This observation aligns with previous findings, suggesting that capturing the overall structural framework may be sufficient for effective identification of fast ion conductors within this database.^17,27,75

An ensemble of AtomSets models is used to screen all Li-containing materials in the ICSD and Materials Project repositories. Through this screening, we find 241 materials predicted to be superionic with E_g > 1 eV and compositions significantly different from those in our training database. The prediction confidence is quantified by reporting the standard deviation of the ensemble predictions and the distance from each screened compound to the nearest training sample. The predicted likelihood of superionic conductivity (P_SI) for all Li-containing materials in the ICSD and Materials Project are provided for consideration. To validate the effectiveness of the model ensemble for screening, we experimentally demonstrate superionic conductivity in a candidate phase, Li₉B₁₉S₃₃.

Importantly, while our approach facilitates screening of materials containing disorder in the Li framework, it does not account for changes in conductivity due to defect introduction. It is possible that compounds with P_SI < 0.5 could be modified to be fast ion conductors through appropriate defect engineering strategies. Despite the strengths of the AtomSets architecture, it does not enable the direct determination of interpretable structural features to guide SSE design. While our results show that the logistic regression model using domain-specific features was less effective in this case, the identification of more refined or relevant features could potentially improve its performance. By making the structure–conductivity database used in this study publicly available, we hope to enable future works to explore and develop better structure–property relationships for ion conduction, facilitating design-focused methodologies.

4 Methods

4.1 Database processing

All 11295 Li-containing compounds cataloged in the ICSD (v5.2.0) are compiled. The constructed database for this study encompasses the experimentally measured ionic conductivities of 571 compounds alongside their corresponding ICSD crystal structures. Consequently, there remain 10724 Li-containing compounds in the ICSD without reported ionic conductivity measurements in the literature. To identify duplicate structures in the labelled database, the StructureMatcher tool within the Python Materials Genomics (Pymatgen) (v2023.11.12) library is employed. Briefly, all pairs of structures are converted to primitive cells, and checks are conducted to ensure that the number of sites, lattice parameters, unit cell angles, and atomic positions do not match within a default tolerance. Duplicate structures are consolidated by retaining the entry with the median ionic conductivity value. The resulting database, devoid of duplicate structures, is comprised of 548 entries.

4.2 Data partitioning and clustering

From the database, 10% of entries are randomly allocated to a test set, which is exclusively assessed with the final model ensemble after determination of the final structure representation and the completion of hyperparameter optimization. The remaining data is divided into training and validation sets using two distinct methods. Initially, the data undergoes random splitting for k-fold CV, with folds of equal size (80 : 20 training and validation). When assessing model performance using k-fold CV, the training and validation portion of the database is randomly partitioned into k different folds. The model is trained on k − 1 of the folds and the predictive power of the model is assessed using the remaining fold. The process is repeated for all k folds to obtain the average and variation of the model performance. In the present study, 5 folds are used for CV. Additionally, the data is partitioned into non-random training and validation sets for LOCO CV. In this scenario, the data is initially represented using the ElMD description, followed by the application of UMAP with a spread parameter of 5, which controls the scale of local neighborhood preservation, to acquire a low-dimensional representation that maintains essential chemical relationships. Subsequently, DBSCAN, using an epsilon of 4, which defines the maximum distance between points to be considered neighbors, is employed to automatically segregate the data into clusters for LOCO CV. We obtain 10 clusters of compounds, with a statistical summary of each cluster provided in the ESI.† The ElMD description, the spread parameter for UMAP, and the epsilon parameter for DBSCAN were selected to align with the leave-one-cluster-out procedure described in previous studies. Intuitive clustering of known families of ion conductors is observed, as detailed in previous works.²⁶

4.3 Descriptor generation and ML models

Crystallographic Information Files (CIFs) for each compound are parsed with Pymatgen (v2023.11.12). Simplified versions of each structure are generated by systematically removing or modifying groups of atoms. For the CAN representation the Li atoms in each structure are removed. The CAMNS representation is created by checking the oxidation state from the CIF file for each non-Li atom in the structure. Atoms with positive oxidation states are substituted with Al, negative oxidation states converted to S, and oxidation states of 0 converted to Mg. For CANS, this simplification is performed and the Li atoms are removed as well. Graph representations are created using a modified version of the MatErials Graph Network (MEGNet) library (https://github.com/materialsvirtuallab/megnet v1.3.2)⁴⁵ to accommodate disordered crystals. The MAterials Machine Learning (maml) library (https://github.com/materialsvirtuallab/maml v2023.9.9) is then used to create the atom matrix features which are used as the inputs for the AtomSets models.⁵⁰ The AtomSets models pass the atom features matrix through a series of fully connected layers before a set2set symmetry function is used to generate a readout vectors of a defined length with permutation invariance of the atom order.⁷⁶ The output of the symmetry function is subsequently passed through additional dense layers and a final sigmoid activation for classification. Atomistic features are generated using the definitions provided by Sendek et al.¹⁵ The scikit-learn library is used for training of logistic regression models with default parameters excluding the penalty for regularization.⁷⁷

4.4 Hyperparameter optimization

The default AtomSets architecture does not include conventional regularization techniques to avoid overfitting. Therefore, dropout layers and L2 kernel regularization is added. The optimal hyperparameters for each validation cluster within the LOCO CV framework are determined using the Ray library (v2.9.3). Model weights are updated using the LAMB optimizer with Lookahead mechanism and a triangular-2 cyclical learning rate schedule.^78,79 A comprehensive listing of the hyperparameter ranges explored is provided in Table S7.† For each cluster, 250 configurations are tested. The top 10 performing configurations for each are then repeated 10 times to account for run-to-run variability. Subsequently, the best performing configuration across these 10 runs is selected as the optimal configuration for that particular validation cluster. Hyperparameter trial runs are orchestrated using the Asynchronous Successive Halving Algorithm (ASHA).⁸⁰ ASHA is an advanced optimization algorithm that efficiently allocates computational resources to hyperparameter configurations, enabling parallelization and faster optimization by iteratively promoting promising configurations while discarding under performing ones through successive halving. The search space is explored employing HyperOpt, which employs Bayesian optimization to find the optimal configuration.⁸¹

4.5 Li₉B₁₉S₃₃ synthesis

Li₉B₁₉S₃₃ is prepared from lithium sulfide (Li₂S, 99.9%, Thermo Fisher Scientific), elemental boron (99.99%, SkySpring Nanomaterials, Inc.) and sulfur (S₈, >99.5%, Acros Organics). In an Ar-filled glovebox (Mbraun), a 2 gram stoichiometric mixture of the precursor materials is combined in a 50 ml YSZ milling jar along with milling media (2 10 mm diameter balls, 34 5 mm diameter balls, and 8 grams of 3 mm diameter balls). The jar is sealed before removing from the glovebox to minimize exposure to air. The precursors are milled in a planetary ball mill (MSE PMV1-0.4L) for 45 minutes at 300 rpm. After milling, the precursor mixture is extracted under Ar and 333 mg of the powder is transferred to a glassy carbon crucible (SPI Supplies). Two repeated heating steps are required to obtain pure Li₉B₁₉S₃₃. The crucible containing the powder is placed into a carbon-coated vitreous silica ampoule (inner diameter 14 mm, outer diameter 16 mm), which is evacuated to <10 mTorr and sealed. The sealed ampoule is heated to 700 °C at a rate of 1 °C min⁻¹, held at 700 °C for 16 h, and then cooled to room temperature at 1 °C min⁻¹. After the first annealing step, the material is removed under Ar, ground with a mortar and pestle, and reloaded into the crucible. The crucible is then sealed in a second carbon-coated vitreous silica ampoule, and the heating procedure is repeated to yield the desired phase.

4.6 Experimental characterization of Li₉B₁₉S₃₃

Powder X-ray diffraction is used to assess the phase purity of the prepared Li₉B₁₉S₃₃ material. The sample powder is loaded into a Rigaku air-free sample holder under Ar to prevent exposure to air during the measurement. Diffraction patterns are collected using a Rigaku Smartlab diffractometer with a Cu Kα X-ray source. The scan range is from 10° to 70° 2θ at a rate of 3° min⁻¹ with a step size of 0.04°. Rietveld refinement of the diffraction patterns was performed using GSAS-II software.⁸² To characterize the ionic conductivity of Li₉B₁₉S₃₃, 40–60 mg of the material is hot-pressed (Col-Int Tech Manual Hydraulic press) at 250 °C under 2 tons of pressure for 5 minutes, forming pellets with 6 mm diameter. The pellet surfaces are polished with 1500-grit abrasive sheets before the pellet thickness is measured. Indium metal foil is placed on stainless steel current collector rods and the pellet is assembled into Swagelok cells under ∼100 MPa of pressure using a manual vise. Electrochemical impedance spectroscopy (EIS) is performed with a Biologic VSP-300 potentiostat over a frequency range of 3 MHz to 1 Hz and an amplitude of 25 mV, across a temperature range of 25 °C to 70 °C.

Data and code availability

The database of σ_exp values and ICSD collection codes for corresponding crystal structures is made available as a supplementary comma-separated values file. The dataset and the predicted likelihood of superionic conductivity for all Li-containgin materials in the ICSD and Materials Project are available through CaltechDATA at https://doi.org/10.22002/23mvv-6gk43. The version of the codebase used to train models, perform screening, and analyze results is archived at https://doi.org/10.22002/cgx0v-wqq34.

Author contributions

Conceptualization, D. B. M., Z. W. B. I., J. M. B., F. A. L. L.,; data curation, F. A. L. L., D. B. M., Z. W. B. I., J. M. B.,; formal analysis, D. B. M.; investigation, D. B. M.; methodology, D. B. M.; software, D. B. M.; validation, D. B. M., Z. W. B. I., J. M. B.; visualization, D. B. M.; writing – original draft, D. B. M.; writing – review & editing, D. B. M., Z. W. B. I., J. M. B., F. A. L. L., K. A. S.; supervision, K. A. S.; funding acquisition, K. A. S.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Arnold and Mabel Beckman Foundation through the Beckman Young Investigator Award. The computations presented here were conducted in the Resnick High Performance Computing Center, a facility supported by Resnick Sustainability Institute at the California Institute of Technology. K. A. S. acknowledges support from the Packard Fellowship for Science and Engineering, Alfred P. Sloan Foundation, and Camille and Henry Dreyfus Foundation.

References

1. J. B. Goodenough, Rechargeable Batteries: Challenges Old and New, J. Solid State Electrochem., 2012, 16, 2019–2029.
2. J. Janek and W. G. Zeier, A Solid Future for Battery Development, Nat. Energy, 2016, 1, 16141.
3. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-Power All-Solid-State Batteries Using Sulfide Superionic Conductors, Nat. Energy, 2016, 1, 16030.
4. T. Inoue and K. Mukai, Are All-Solid-State Lithium-Ion Batteries Really Safe?–Verification by Differential Scanning Calorimetry with an All-Inclusive Microcell, ACS Appl. Mater. Interfaces, 2017, 9, 1507–1515.
5. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, A Lithium Superionic Conductor, Nat. Mater., 2011, 10, 682–686.
6. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116, 140–162.
7. W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Interface Stability in Solid-State Batteries, Chem. Mater., 2016, 28, 266–273.
8. A. D. Sendek, G. Cheon, M. Pasta and E. J. Reed, Quantifying the Search for Solid Li-Ion Electrolyte Materials by Anion: A Data-Driven Perspective, J. Phys. Chem. C, 2020, 124, 8067–8079.
9. O. Sheng, C. Jin, X. Ding, T. Liu, Y. Wan, Y. Liu, J. Nai, Y. Wang, C. Liu and X. Tao, A Decade of Progress on Solid-state Electrolytes for Secondary Batteries: Advances and Contributions, Adv. Funct. Mater., 2021, 31, 2100891.
10. J. Janek and W. G. Zeier, Challenges in Speeding up Solid-State Battery Development, Nat. Energy, 2023, 8, 230–240.
11. Y. Hu, W. Li, J. Zhu, S.-M. Hao, X. Qin, L.-Z. Fan, L. Zhang and W. Zhou, Multi-Layered Electrolytes for Solid-State Lithium Batteries, Next Energy, 2023, 1, 100042.
12. R. Jalem, T. Aoyama, M. Nakayama and M. Nogami, Multivariate Method-Assisted Ab Initio Study of Olivine-Type LiMXO₄ (Main Group M²⁺–X⁵⁺ and M³⁺–X⁴⁺) Compositions as Potential Solid Electrolytes, Chem. Mater., 2012, 24, 1357–1364.
13. K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. J. Fisher, H. Moriwake and I. Tanaka, Accelerated Materials Design of Lithium Superionic Conductors Based on First-Principles Calculations and Machine Learning Algorithms, Adv. Energy Mater., 2013, 3, 980–985.
14. R. Jalem, M. Nakayama and T. Kasuga, An Efficient Rule-Based Screening Approach for Discovering Fast Lithium Ion Conductors Using Density Functional Theory and Artificial Neural Networks, J. Mater. Chem. A, 2014, 2, 720–734.
15. A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N. Duerloo, Y. Cui and E. J. Reed, Holistic Computational Structure Screening of More than 12 000 Candidates for Solid Lithium-Ion Conductor Materials, Energy Environ. Sci., 2017, 10, 306–320.
16. Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman and V. Viswanathan, Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes, ACS Cent. Sci., 2018, 4, 996–1006.
17. Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Unsupervised Discovery of Solid-State Lithium Ion Conductors, Nat. Commun., 2019, 10, 5260.
18. A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Machine Learning-Assisted Discovery of Solid Li-Ion Conducting Materials, Chem. Mater., 2019, 31, 342–352.
19. E. D. Cubuk, A. D. Sendek and E. J. Reed, Screening Billions of Candidates for Solid Lithium-Ion Conductors: A Transfer Learning Approach for Small Data, J. Chem. Phys., 2019, 150, 214701.
20. E. Choi, J. Jo, W. Kim and K. Min, Searching for Mechanically Superior Solid-State Electrolytes in Li-Ion Batteries via Data-Driven Approaches, ACS Appl. Mater. Interfaces, 2021, 13, 42590–42597.
21. Q. Zhao, M. Avdeev, L. Chen and S. Shi, Machine Learning Prediction of Activation Energy in Cubic Li-argyrodites with Hierarchically Encoding Crystal Structure-Based (HECS) Descriptors, Sci. Bull., 2021, 66, 1401–1408.
22. H. Guo, Q. Wang, A. Urban and N. Artrith, Artificial Intelligence-Aided Mapping of the Structure–Composition–Conductivity Relationships of Glass–Ceramic Lithium Thiophosphate Electrolytes, Chem. Mater., 2022, 34, 6702–6712.
23. Z. Lu, P. Adeli, C.-H. Yim, M. Jiang, J. Rempel, Z. W. Chen, S. Yadav, P. Mercier, Y. Abu-Lebdeh and C. V. Singh, Automatically Capturing Key Features for Predicting Superionic Conductivity of Solid-State Electrolytes Using a Neural Network, ACS Appl. Energy Mater., 2022, 5, 8042–8048.
24. A. Adhyatma, Y. Xu, N. H. Hawari, P. Satria Palar and A. Sumboja, Improving Ionic Conductivity of Doped Li₇La₃Zr₂O₁₂ Using Optimized Machine Learning with Simplistic Descriptors, Mater. Lett., 2022, 308, 131159.
25. K. Kim and D. J. Siegel, Machine Learning Reveals Factors That Control Ion Mobility in Anti-Perovskite Solid Electrolytes, J. Mater. Chem. A, 2022, 10, 15169–15182.
26. C. J. Hargreaves, et al., A Database of Experimentally Measured Lithium Solid Electrolyte Conductivities Evaluated with Machine Learning, npj Comput. Mater., 2023, 9, 9.
27. F. A. L. Laskowski, D. B. McHaffie and K. A. See, Identification of Potential Solid-State Li-ion Conductors with Semi-Supervised Learning, Energy Environ. Sci., 2023, 16, 1264–1276.
28. Y.-Y. Lin, J. Qu, W. J. Gustafson, P.-C. Kung, N. Shah, S. Shrivastav, E. Ertekin, J. A. Krogstad and N. H. Perry, Coordination Flexibility as a High-Throughput Descriptor for Identifying Solid Electrolytes with Li+ Sublattice Disorder: A Computational and Experimental Study, J. Power Sources, 2023, 553, 232251.
29. J. Sun, S. Kang, J. Kim and K. Min, Accelerated Discovery of Novel Garnet-Type Solid-State Electrolyte Candidates via Machine Learning, ACS Appl. Mater. Interfaces, 2023, 15, 5049–5057.
30. X. Guo, Z. Wang, J.-H. Yang and X.-G. Gong, Machine-Learning Assisted High-Throughput Discovery of Solid-State Electrolytes for Li-ion Batteries, J. Mater. Chem. A, 2024, 12, 10124–10136.
31. J. Kim, D. Lee, D. Lee, X. Li, Y.-L. Lee and S. Kim, Machine Learning Prediction Models for Solid Electrolytes Based on Lattice Dynamics Properties, J. Phys. Chem. Lett., 2024, 15, 5914–5922.
32. S. K. Kauwe, J. Graser, R. Murdock and T. D. Sparks, Can Machine Learning Find Extraordinary Materials?, Comput. Mater. Sci., 2020, 174, 109498.
33. A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, High-Throughput Machine-Learning-Driven Synthesis of Full-Heusler Compounds, Chem. Mater., 2016, 28, 7324–7331.
34. S. K. Kauwe, J. Graser, A. Vazquez and T. D. Sparks, Machine Learning Prediction of Heat Capacity for Solid Inorganics, Integr. Mater. Manuf. Innovation, 2018, 7, 43–51.
35. D. Jha, L. Ward, A. Paul, W.-k. Liao, A. Choudhary, C. Wolverton and A. Agrawal, ElemNet: Deep Learning the Chemistry of Materials From Only Elemental Composition, Sci. Rep., 2018, 8, 17593.
36. A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, Compositionally Restricted Attention-Based Network for Materials Property Predictions, npj Comput. Mater., 2021, 7, 77.
37. G. K. Phani Dathar, J. Balachandran, P. R. C. Kent, A. J. Rondinone and P. Ganesh, Li-Ion Site Disorder Driven Superionic Conductivity in Solid Electrolytes: A First-Principles Investigation of β-Li₃PS₄, J. Mater. Chem. A, 2017, 5, 1153–1159.
38. D. Di Stefano, A. Miglio, K. Robeyns, Y. Filinchuk, M. Lechartier, A. Senyshyn, H. Ishida, S. Spannenberger, D. Prutsch, S. Lunghammer, D. Rettenwander, M. Wilkening, B. Roling, Y. Kato and G. Hautier, Superionic Diffusion through Frustrated Energy Landscape, Chem, 2019, 5, 2450–2460.
39. K. Hogrefe, N. Minafra, I. Hanghofer, A. Banik, W. G. Zeier and H. M. R. Wilkening, Opening Diffusion Pathways through Site Disorder: The Interplay of Local Structure and Ion Dynamics in the Solid Electrolyte Li_6+xP_1−xGe_xS₅I as Probed by Neutron Diffraction and NMR, J. Am. Chem. Soc., 2022, 144, 1795–1812.
40. B. J. Morgan, Mechanistic Origin of Superionic Lithium Diffusion in Anion-Disordered Li₆PS₅X Argyrodites, Chem. Mater., 2021, 33, 2004–2018.
41. M. Botros and J. Janek, Embracing Disorder in Solid-State Batteries, Science, 2022, 378, 1273–1274.
42. Y. Zeng, B. Ouyang, J. Liu, Y.-W. Byeon, Z. Cai, L. J. Miara, Y. Wang and G. Ceder, High-Entropy Mechanism to Boost Ionic Conductivity, Science, 2022, 378, 1320–1324.
43. J. Gamon, M. S. Dyer, B. B. Duff, A. Vasylenko, L. M. Daniels, M. Zanella, M. W. Gaultois, F. Blanc, J. B. Claridge and M. J. Rosseinsky, Li_4.3AlS_3.3Cl_0.7: A Sulfide–Chloride Lithium Ion Conductor with Highly Disordered Structure and Increased Conductivity, Chem. Mater., 2021, 33, 8733–8744.
44. S. Wang, S. Gong, T. Böger, J. A. Newnham, D. Vivona, M. Sokseiha, K. Gordiz, A. Aggarwal, T. Zhu, W. G. Zeier, J. C. Grossman and Y. Shao-Horn, Multimodal Machine Learning for Materials Science: Discovery of Novel Li-Ion Solid Electrolytes, Chem. Mater., 2024, 36, 11541–11550.
45. C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31, 3564–3572.
46. V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, Benchmarking Graph Neural Networks for Materials Chemistry, npj Comput. Mater., 2021, 7, 84.
47. P. Reiser, M. Neubert, A. Eberhard, L. Torresi, C. Zhou, C. Shao, H. Metni, C. Van Hoesel, H. Schopmans, T. Sommer and P. Friederich, Graph Neural Networks for Materials Science and Chemistry, Commun. Mater., 2022, 3, 93.
48. C. Chen, Y. Zuo, W. Ye, X. Li and S. P. Ong, Learning Properties of Ordered and Disordered Materials from Multi-Fidelity Data, Nat. Comput. Sci., 2021, 1, 46–53.
49. K. T. Butler, F. Oviedo and P. Canepa, Machine Learning in Materials Science, American Chemical Society, Washington, DC, USA, 2022.
50. C. Chen and S. P. Ong, AtomSets as a Hierarchical Transfer Learning Framework for Small and Large Materials Datasets, npj Comput. Mater., 2021, 7, 173.
51. P.-P. De Breuck, G. Hautier and G.-M. Rignanese, Materials Property Prediction for Limited Datasets Enabled by Feature Selection and Joint Learning with MODNet, npj Comput. Mater., 2021, 7, 83.
52. V. Gupta, K. Choudhary, B. DeCost, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Structure-Aware Graph Neural Network Based Deep Transfer Learning Framework for Enhanced Predictive Analytics on Diverse Materials Datasets, npj Comput. Mater., 2024, 10, 1.
53. A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, Benchmarking Materials Property Prediction Methods: The Matbench Test Set and Automatminer Reference Algorithm, npj Comput. Mater., 2020, 6, 138.
54. M. Müller, H. Auer, A. Bauer, S. Uhlenbruck, M. Finsterbusch, K. Wätzig, K. Nikolowski, S. Dierickx, D. Fattakhova-Rohlfing, O. Guillon and A. Weber, Guidelines to Correctly Measure the Lithium Ion Conductivity of Oxide Ceramic Electrolytes Based on a Harmonized Testing Procedure, J. Power Sources, 2022, 531, 231323.
55. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319.
56. T. Saito and M. Rehmsmeier, The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets, PLoS One, 2015, 10, e0118432.
57. B. Matthews, Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme, Biochim. Biophys. Acta, Protein Struct., 1975, 405, 442–451.
58. D. Chicco and G. Jurman, The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation, BMC Genomics, 2020, 21, 6.
59. D. Chicco, N. Tötsch and G. Jurman, The Matthews Correlation Coefficient (MCC) Is More Reliable than Balanced Accuracy, Bookmaker Informedness, and Markedness in Two-Class Confusion Matrix Evaluation, Biodata Min., 2021, 14, 13.
60. G. L. W. Hart and R. W. Forcade, Algorithm for Generating Derivative Structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224115.
61. B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons, J. Hattrick-Simpers, A. Mehta and L. Ward, Can Machine Learning Identify the next High-Temperature Superconductor? Examining Extrapolation Performance for Materials Discovery, Mol. Syst. Des. Eng., 2018, 3, 819–825.
62. A. Jain, S. P. Ong, G. Hautier, C. Moore and J. Munro, Electronic Structure | Materials Project Documentation, 2023, https://docs.materialsproject.org/methodology/materials-methodology/electronic-structure.
63. Q. Wang, D. Liu, X. Ma, X. Zhou and Z. Lei, Cl-Doped Li₁₀SnP₂S₁₂ with Enhanced Ionic Conductivity and Lower Li-Ion Migration Barrier, ACS Appl. Mater. Interfaces, 2022, 14, 22225–22232.
64. M. A. Limpert, T. B. Atwater, T. Hamann, G. L. Godbey, G. T. Hitz, D. W. McOwen and E. D. Wachsman, Achieving Desired Lithium Concentration in Garnet Solid Electrolytes; Processing Impacts on Physical and Electrochemical Properties, Chem. Mater., 2022, 34, 9468–9478.
65. T. Ning, Y. Zhang, Q. Zhang, X. Shen, Y. Luo, T. Liu, P. Liu, Z. Luo and A. Lu, The Effect of a Ta, Sr Co-Doping Strategy on Physical and Electrochemical Properties of Li₇La₃Zr₂O₁₂ Electrolytes, Solid State Ionics, 2022, 379, 115917.
66. X. Zhou, L. Huang, O. Elkedim, Y. Xie, Y. Luo, Q. Chen, Y. Zhang and Y. Chen, Sr²⁺ and Mo⁶⁺ Co-Doped Li₇La₃Zr₂O₁₂ with Superior Ionic Conductivity, J. Alloys Compd., 2022, 891, 161906.
67. R. Nagel, Ch. Wickel and H. Lutz, Crystal Structure of the Quaternary Compounds Li_1.25Cd_1.67In_0.47Cl₆ and Li_0.21Mn_1.71In_0.79Cl₆, Solid State Sci., 2003, 5, 827–832.
68. J. Zhang and J. D. Corbett, Zirconium Chloride Cluster Phases Centered by Transition Metals Mn-Ni. Examples of the Nb₆F₁₅ Structure, Inorg. Chem., 1991, 30, 431–435.
69. A. P. Maltsev, I. V. Chepkasov, A. G. Kvashnin and A. R. Oganov, Ionic Conductivity of Lithium Phosphides, Crystals, 2023, 13, 756.
70. M. Grüne, Complex Lithium Dynamics in the Novel Thioborate Li5B7S13 Revealed by NMR Relaxation and Lineshape Studies, Solid State Ionics, 1995, 78, 305–313.
71. R. Bertermann, W. Muller-Warmuth, C. Jansen, F. Hiltmann and B. Krebs, NMR Studies of the Lithium Dynamics in Two Thioborate Superionic Conductors: Li₉B₁₉S₃₃ and Li_4−2xSr_2+xB₁₀S₁₉ (x ≈ 0.27), Solid State Ionics, 1999, 117(3–4), 245–255.
72. A. D. Sendek, E. R. Antoniuk, E. D. Cubuk, B. Ransom, B. E. Francisco, J. Buettner-Garrett, Y. Cui and E. J. Reed, Combining Superionic Conduction and Favorable Decomposition Products in the Crystalline Lithium–Boron–Sulfur System: A New Mechanism for Stabilizing Solid Li-Ion Electrolytes, ACS Appl. Mater. Interfaces, 2020, 12, 37957–37966.
73. M. Zeilinger, L. van Wüllen, D. Benson, V. F. Kranak, S. Konar, T. F. Fässler and U. Häussermann, LiBSi₂: A Tetrahedral Semiconductor Framework from Boron and Silicon Atoms Bearing Lithium Atoms in the Channels, Angew. Chem., Int. Ed., 2013, 52, 5978–5982.
74. F. Hiltmann, P. Zum Hebel, A. Hammerschmidt and B. Krebs, Li₅B₇S₁₃ und Li₉B₁₉S₃₃: Zwei Lithiumthioborate mit neuen hochpolymeren Anionengerüsten, Z. Anorg. Allg. Chem., 1993, 619, 293–302.
75. Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design Principles for Solid-State Lithium Superionic Conductors, Nat. Mater., 2015, 14, 1026–1031.
76. O. Vinyals, S. Bengio and M. Kudlur, Order Matters: Sequence To Sequence For Sets, arXiv, 2016, preprint, arXiv:1511.06391,  DOI:10.48550/arXiv.1511.06391.
77. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg and others, Scikit-Learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
78. Y. You, J. Li, S. Reddi, J. Hseu, S. Kumar, S. Bhojanapalli, X. Song, J. Demmel, K. Keutzer and C.-J. Hsieh, Large Batch Optimization for Deep Learning: Training BERT in 76 Minutes, Proc. International Conference on Learning Representations (ICLR), 2020.
79. M. Zhang, J. Lucas, J. Ba and G. E. Hinton, Lookahead Optimizer: k Steps Forward, 1 Step Back, Advances in neural information processing systems, 2019, vol. 32.
80. L. Li, K. Jamieson, A. Rostamizadeh, E. Gonina, J. Ben-Tzur, M. Hardt, B. Recht and A. Talwalkar, A System for Massively Parallel Hyperparameter Tuning, Proceedings of machine learning and systems, 2020, vol. 2, pp. 230–246.
81. J. Bergstra, D. Yamins and D. Cox, Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures, International Conference on Machine Learning, 2013, pp. 115–123.
82. B. H. Toby and R. B. Von Dreele, GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package, J. Appl. Crystallogr., 2013, 46, 544–549.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00052a

---