Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A classification-based methodology for the estimation of binary surfactant critical micelle concentrations
Chetan R. Chilkunda,
John R. Kitchin and
Robert D. Tilton
and
Robert D. Tilton *
*
Department of Chemical Engineering, Carnegie Mellon University, 5000 Forbes Ave., Pittsburgh, PA 15213, USA. E-mail: tilton@andrew.cmu.edu
First published on 11th April 2025
Abstract
The commercial formulation development for multicomponent complex fluids is time-intensive and data-intensive. There is a need for tools to expedite this process. This work develops an experimental and analytical high-throughput methodology to quantify binary surfactant mixture micellization in a 96-well plate. The novelty of this work lies in (1) employing model-driven design of experiments for efficient experimentation and (2) using physics-informed classification to quantify the mixture critical micelle concentration. This work employs a novel classification-based approach to map the binary critical micelle concentration as a function of the surfactant mixture ratio. Regular solution theory is used as the physics basis for modeling the binary interactions between surfactants (quantifying the β interaction parameter). Other, more complex surfactant interaction models exist; however, this simple model is used to demonstrate the efficacy of this methodology as a high-throughput screening tool for binary surfactant mixtures. Using regular solution theory as a guide to map the critical micelle concentration against the surfactant ratio, the SDS-C8E4 surfactant system was determined to have a β = −3.6 ± 0.5, a 14.9% difference from the literature reference of β = −3.1. We demonstrate the utility of the method on the SDS-C8E4 system in 0.5 M NaCl which was determined to have a β = −3.1 ± 0.4, which is a 17.5% difference from a similar literature system of SDS-C12E8 in 0.5 M NaCl with β = −2.6. These two systems support the efficacy and generalizability of this high-throughput methodology to any binary surfactant mixture and future work involves extending this methodology to ternary surfactant mixtures.
1 Introduction
Many commercial products involve mixtures of surfactants because of their synergistic and complementary properties in solution. For example, laundry detergent formulations typically incorporate anionic surfactants to maximize solubilization power and nonionic surfactants to maximize water hardness tolerance.1 From an industrial point of view, rapidly and accurately characterizing surfactant mixture micellization is critical to developing new formulations. The formation of micelles from surfactants is required to achieve solubilization, and thus the critical micelle concentration (CMC) is an important quantity to determine in any surfactant system.Current formulation development includes testing a large number of candidate surfactant mixtures, a process that is time-intensive and data-intensive. Surfactant mixtures tend to be non-ideal, and so quantifying surfactant mixture CMCs can require many experiments to quantify the non-ideal behavior. Efficiently quantifying this behavior requires systematic and deliberate planning and experimentation. This study details the development of a high-throughput methodology based on 96-well plates that efficiently quantifies the CMC for a binary mixture of surfactants by incorporating a simple model for the CMC of a binary surfactant solution into a classification framework to determine the best decision boundary that separates points labeled below the CMC from points labeled above the CMC.
The CMC is a boundary that separates mixtures that form micelles from those that do not. In a classification model, one seeks to find a boundary that separates two classes of observations. In a conventional approach, one finds values of a CMC at various composition ratios and then fits a model using nonlinear regression through those values to obtain the CMC function. In our work we will use a machine learning classifier to fit that model directly using the boundary to most accurately separate mixtures that form micelles from those that do not. In that context, classification is a natural approach to finding the composition dependent CMC of a surfactant mixture.
There are several binary surfactant micellization models to choose from, each with its own degree of complexity. Beyond the one-constant Margules activity coefficient model as in regular solution theory, there exist more complex activity coefficient models as well as models that quantify surfactant packing in micelle formation.2,3 In this work, regular solution theory is used for its simplicity and common usage.4–7 Regular solution theory is a thermodynamic model that characterizes the interactions and the potential for synergism in a binary surfactant mixture as a function of the pure surfactant CMCs, an empirical interaction parameter, and the molar ratio of each surfactant in the binary mixture:8
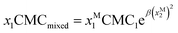 | (1) |
 | (2) |
In eqn (1) and (2), for a given binary mixture of surfactants (marked as 1 and 2), x1 and x2 where x1 + x2 = 1, represent total surfactant molar fractions, xM1 and xM2 represent the molar fractions of the two surfactants in the mixed micelle, CMC1 and CMC2 represent the pure critical micelle concentrations of the two surfactants, CMCmixed represents the mixed critical micelle concentration, and β represents an empirical interaction parameter that quantifies the deviation of the mixture from ideal mixing. β values generally fall within the range of 0 (corresponding to ideal mixing) to approximately −20 (corresponding to strong attractive interactions between the surfactant species as occurring in mixtures of anionic and cationic surfactants).9 It is also possible to have positive values of β with fluorocarbon based surfactants.10,11 At these large, negative β values, the predicted mixture CMC curve resembles the x−1 function with endpoints at the pure surfactant CMCs. This model predicts that the surfactant interactions tend towards equal molar fractions inside the micelle (xM1 ≈ xM2 = 0.5) over a wide range of overall surfactant ratios, and that less total surfactant may be required to achieve micellization than would be the case for either pure surfactant, the condition referred to as micellization synergism.8 In this study, regular solution theory serves as the basis for the model-driven DoE (Design of Experiments) and as the governing physics-imposed guide in the analysis methods.
There are several ways to experimentally determine the CMC including capillary electrophoresis,12,13 Taylor dispersion analysis,14 bipolar pulse conductance, spectroscopic methods,15 surface tension16 and even analysis of “coffee rings” formed from surfactant mixtures.17 More commonly, measuring dye solubilization via fluorescence or absorbance methods as a function of total surfactant concentration for a fixed ratio of the two surfactants in solution15,16,18,19 is used. Previous research on the high-throughput determination of the CMC leveraged a 96-well plate20 to assess the fluorescence of detergents. An alternative approach used absolute aggregation-caused quenching probes in a 96-well platform.21 In this study, the fluorescence-based dye solubilization approach is used based on its suitability for high-throughput implementation in a 96-well plate format.
This work uses Nile Red for the dye. This dye produces low fluorescence intensity when it is in a polar environment (i.e. in aqueous solution) and a relatively high fluorescence intensity when it is in a local non-polar environment (i.e. inside the non-polar micelle core).22,23 Preferential dye partitioning into the non-polar cores of micelles allows for dye solubilization experiments to measure fluorescence intensity as a function of total surfactant concentration. Fluorescence intensity serves as a proxy measurement for micelle formation. Typically there is a constant or weakly varying intensity for surfactant concentrations below the CMC, with an abrupt transition at the CMC.24 At concentrations above the CMC, the dye fluorescence intensity typically increases approximately linearly with increasing surfactant concentration, with a slope that depends on the solubilizing power of the mixed micelles.25–27
2 Methods
2.1 Materials
The anionic surfactant sodium dodecyl sulfate (SDS) was obtained from Sigma-Aldrich (>99.0%) as a white crystalline powder. The nonionic surfactant tetraethylene glycol monooctyl ether (C8E4) was purchased from Sigma-Aldrich (>98.0%) as a liquid. The surfactant solutions were prepared in distilled water and stored in a dark environment at room temperature (20–25 °C). Sodium chloride (NaCl), which is used as an electrolyte additive for methodology verification, was purchased from Alfa Aesar (Johnson Matthey Company) (>99.0%) in crystalline form. Nile Red dye, which is used for the micelle dye solubilization fluorescence intensity measurements, was obtained from Sigma-Aldrich (>99.0%) as a dark brown crystalline powder. The dye was solubilized in >99.0% ethanol on a 0.75 mg mL−1 basis.2.2 Measurements
The 96 mixed surfactant dye solubilization samples were prepared and measured at 25 °C, and all samples were prepared to contain 2.0% Nile Red solution by volume. The upper limit of dye concentration was experimentally determined to be 10% Nile Red by volume to obtain negligible interactions between the ethanol solvent and the surfactants that affect the critical micelle concentration. After preparing each of the 96 trials to a total of 1.00 mL in glass scintillation vials, each vial was gently mixed using a vortex mixing apparatus for about 10 seconds. All 96 mixed surfactant samples were randomly mapped to their own well within the 96-well plate and filled to 200 μL accordingly. Additionally, an internal standard of 10 mM SDS was used to normalize all fluorescence readings.In measuring fluorescence intensity over the 96-well plate, a SYNERGY H1 Biotek microplate spectrofluorometer was used to (1) measure the excitation and emission spectra of the highest concentration samples and internal standard and record the wavelengths at peak absorption and (2) perform a fluorescence intensity endpoint scan with a manual gain setting of 100 and bottom-plate optical readings using the mean excitation maximum wavelength and mean emission maximum wavelength as the lower and upper bounds. The output endpoint fluorescence intensity scan was measured 5–7 times to account for instrument variability and averaged to get the expected fluorescence intensity for each well.
2.3 Design of experiments
The binary surfactant system of anionic sodium dodecyl sulfate (SDS) and nonionic tetraethylene glycol monooctyl ether (C8E4) was chosen because a current literature value exists for its empirical interaction parameter, β = −3.1, and its prevalence in industrial formulations.8 Fundamentally, the incorporation of nonionic surfactants into anionic surfactant micelles will decrease the electrostatic repulsive forces between the individual anionic surfactant molecules and decrease the resistance to micellization. Accordingly, mixed micelles will form at a lower total concentration than the anionic surfactant's CMC.28 This phenomenon is indicated by the negative sign of the β interaction parameter. Solving the regular solution theory eqn (1) and (2) for xM1 and CMCmixed as a function of β over all bulk mole fractions x1, where CMC1 and CMC2 refer to the pure CMC of SDS and C8E4, respectively, yields the dependence of the CMC for different values of β.We aim to determine the CMC boundary across all mixture compositions for the SDS-C8E4 blend using regular solution theory as the reference physics-based model. For the most general scenario of binary surfactant mixtures, the experimental space is quite large, with β values in the range of [−20, 0]. To expedite the procedure one would take advantage of well-established trends. Here, the trends indicate that mixtures of anionic surfactants and nonionic surfactants with oligo(ethylene oxide) headgroups exhibit small, negative β values. Thus, we restrict the experimental sampling space to β ∈ [−6, 0].29 This restriction gives targeted information about where the boundary lies.
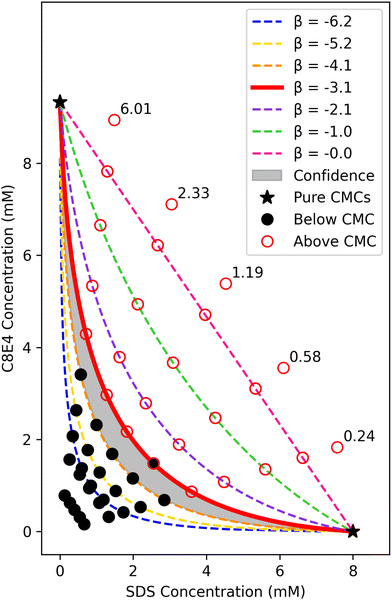
Although the literature indicates that one should expect β = −3.1 for the SDS-C8E4 system, the value of β would not generally be known a priori. Only a rough idea of the β value is needed to expedite the experiment design. To sample across the entire space, the top-most ideal mixing line (β = 0.0) is broken into six equivalent line segments as shown in Fig. 1. For surfactants with unknown β values, one might use the head group character (e.g. anionic, zwitterionic, ionic, etc.) to narrow down the search space, or rely on an iterative approach to search broadly and narrow down in subsequent experiments.
The five black lines in Fig. 1 represent five mixed surfactant blends, where each solution has a constant ratio of C8E4 concentration to SDS concentration. Experimental trial samples are prepared along each of the five lines at their intersections with the predicted regular solution theory curves with additional trials both below and above the predicted curves.
In Fig. 1, each constant composition line has a trial at each of the seven different β interaction values and an additional two trials below the lowest curve and one trial above the ideal mixing line. The two trials below the lowest curve map to 10% and 20% of the trial at the ideal mixing line and are necessary to characterize fluorescence in the system at very low surfactant concentrations that are highly likely to fall below the CMC. This information aids in determining the empirical fluorescence intensity threshold for classification. The trial above the ideal mixing line signifies a point with expected maximum fluorescence, marking an upper bound on fluorescence intensity for each respective mixture blend.
Altogether, each line corresponds to ten unique experimental trials-ten different aliquots from a premade mixed stock solution blend. Given the total 50 unique trials needed to map out the experimental space and the applicability of using a plate reading fluorescence spectrofluorometer, a 96-well plate facilitates a simple, high-throughput setup for the experiment. The 96-well plate experimental design is as follows: except for the trials above the zero interaction line, every trial is replicated twice. This amounts to 19 trials per line over five lines for a total of 95 trials. The trials above the zero interaction line are chosen to not have a second replicate because (1) the experiment needs to fit inside a single 96-well plate and (2) these trials are far from the expected CMC boundary so they do not directly influence the boundary determination. With 95 of the 96 wells occupied, the last remaining well was used to hold an internal fluorescence standard (of high fluorescence intensity) to normalize all spectrofluorometer readings between 0 and 1.
The pure CMCs of both SDS and C8E4 must first be accurately determined. These pure CMCs, marked by the starred endpoints in Fig. 1, mark the bounds of the experimental sampling space as the mixture CMC will occur at a lower total surfactant concentration. This two-stage experimental procedure of (1) determining the pure CMCs and (2) the physics-based sampling and experimentation across mixture compositions allows for the efficient quantification of the mixture's CMC across all compositions. After pure CMC determination of both SDS and C8E4, the pipeline for the experimentation is as follows: (1) use model-driven design of experiments to determine the specified 96-well plate mixed surfactant trials, (2) prepare 96 surfactant samples for the high-throughput dye solubilization experiment and measure their respective fluorescence intensity, and (3) analyze the experimental data using physics-based classification to quantify the empirical binary interaction parameter and the mixture CMC across all compositions.
3 Results
3.1 Pure CMC determination
The CMC values for pure SDS and pure C8E4 were determined by using the literature values of 8.2 mM for SDS and 9.1 for C8E4 as a basis for the sampling.30 A follow-up experiment was performed on an electrolyte-rich surfactant mixture of SDS-C8E4 in 0.5 M NaCl. The pure surfactant CMCs for both SDS and C8E4, as well as their counterparts in 0.5 M NaCl are detailed in Table 1.| Description | CMC (mM) | Literature ref. |
|---|---|---|
| SDS | 8.0 ± 0.2 | 8.2 |
| SDS (in 0.5 M NaCl) | 0.6 ± 0.1 | 0.5–0.9 |
| C8E4 | 9.3 ± 0.3 | 9.1 |
| C8E4 (in 0.5 M NaCl) | 7.0 ± 0.2 | N/A |
The CMC values for pure SDS and pure C8E4 in Table 1 have less than a 2.5% difference from their literature references detailed above. Additionally, the SDS in 0.5 M NaCl CMC value of 0.6 mM falls within the expected range of 0.5–0.9 mM based on surface tension CMC experiments.31
To determine the CMC of a binary mixture of SDS and C8E4 we prepared a 96-well plate in the design shown in Fig. 2 which shows the normalized fluorescence intensity (NFU) as a function of each of the two surfactant concentrations.
In Fig. 2, we observed a boundary between the bottom blackish points and the first colored points around NFU = 0.2. This is an indication that the sampling approach successfully encompassed the binary interaction micellization space. That boundary demarcates the onset of micellization and the shielding of the non-polar Nile Red dye from the polar aqueous solution. Qualitatively, we can assert that the binary CMC boundary between SDS and C8E4 lies at the first jump in fluorescence intensity (between the black and dark blue points).
The remainder of this section details the CMC boundary quantification via (1) Leaky ReLU analysis and (2) physics-based classification analysis. These two analysis methods are introduced in order of increasing generalizability and complexity. The ReLU approach is most subject to the local noise in the data and does not account for the underlying physics constraints. In contrast, the physics-based classification approach is the least subject to local noise and directly imposes the physics constraints to robustly identify the CMC boundary from the data.
3.2 Leaky ReLU regression analysis
The ReLU regression analysis follows two sequential steps: (1) nonlinear fitting with Leaky ReLU over each of the five constant composition lines to quantify each mixture blend's CMC and (2) orthogonally regressing regular solution theory over the determined five composition dependent CMCs and two pure endpoint CMCs to determine the β interaction parameter. In step (2), orthogonal distance regression is used over the conventional Cartesian ordinary least squares regression because of the apparent nonlinearity in the data and the curvature of the regular solution theory model. For step (1), a representative plot of the Leaky ReLU fitting upon the most SDS-rich and most C8E4-rich blends is shown in Fig. 3.From Fig. 3, we observe that the data obtained are fit well by Leaky ReLU regressions. After determining the mixed CMC for all five blends, regular solution theory is regressed upon these five CMC points and the two pure endpoint CMCs and the final result of the ReLU regression analysis is depicted in Fig. 4.
Fig. 4 illustrates the final result from the ReLU analysis approach, where β = −2.8 ± 0.2 closely agrees with the literature value of β = −3.1.8 This analysis approach is easy to understand and implement; however, it has a limitation: local noise in each constant composition line affects the fits independently. Each Leaky ReLU fit is regressed separately so the constraint of a smooth CMC boundary is not present which can introduce some uncertainty when choosing the initial guesses for the Leaky ReLU regression. Another limitation to this analysis method is that the second regression is performed on only seven points (five CMC values and two endpoints). This limits uncertainty quantification. A more robust approach than this two-step regression analysis is to enforce the mixed CMC boundary directly into the first regression, and perform the analysis over all five constant composition lines simultaneously.
3.3 Physics-based classification analysis
The piecewise, ReLU shape of the data can be leveraged to turn this regression problem into a binary classification problem. By labeling the experimental points as either 0 (below CMC) or 1 (above CMC), classification algorithms can be used to quantify the boundary that minimize the number of misclassifications.To label the points, we fit a plane to the low-curvature region (the bottom most two trials across all blends including replicates) and extrapolate this plane to determine an empirical fluorescence threshold. In Fig. 5, the blue center plane represents the fitted composition-based fluorescence threshold and the two red planes illustrate the 95% confidence interval in the fit. From Fig. 5, it is clear that there is a significant difference in the low-curvature region's fluorescence intensity when compared to the fluorescence intensity above the CMC. This difference in intensity from below to above the CMC indicates the robustness of the methodology to the choice of the confidence interval. One note is that this empirical fluorescence threshold stems directly from the two bottommost trials outlined in the DoE sampling setup, and that this threshold assumes linearity within the low-curvature region. This is used to label the points (Fig. 6).
The final results of this physics-based binary classification approach are summarized in Fig. 6 which depicts the original seven β curves, the classification truth values determined from the plane fluorescence threshold, and the predicted optimal β range. Given the literature value for the SDS-C8E4 system β = −3.1, the predicted β from this approach is β = −3.6 (midpoint of the confidence interval [−4.1, −3.1]).8 A 14.9% difference between the two values indicates that this overarching experimental and analytical methodology efficiently and accurately quantified the binary interaction parameter β for the SDS-C8E4 system.
3.4 Application to mixed surfactant CMC in an electrolyte
To demonstrate the generalizability of this methodology to more complex surfactant systems, we used the approach to estimate the composition dependent CMC of the SDS-C8E4 system in 0.5 M NaCl. The addition of the electrolyte drastically changes the surfactant electrostatic interactions and mixture properties (it reduces the SDS CMC by an order of magnitude). Although a literature value for β does not exist for the SDS-C8E4 in 0.5 M NaCl system, there is a literature value8 for the SDS-C12E8 in 0.5 M NaCl system: β = −2.6 and this literature reference is used as the basis for the DoE sampling scheme. The results are shown in Fig. 7. A key thing to note is the asymmetry in the axes caused by the interactions of anionic SDS with the ionic electrolyte solvent: the concentration sampling range for SDS is a full order of magnitude less than the concentration sampling range for C8E4.From Fig. 7, for the electrolyte system, β ∈ [−3.45, −2.71] based on the confidence (shaded) region and resolution of the data via the physics-based classification analysis. Equivalently, β = −3.1 ± 0.4 and this result highlights the applicability of the high-throughput methodology to an asymmetric binary surfactant formulation with drastically different pure surfactant CMCs. The experimentally determined β = −3.1 for the SDS-C8E4-electrolyte system sees a 17.5% difference from the value reported for a similar literature system of the SDS-C12E8-electrolyte system. As the value of β is responsive to the chemical composition of the headgroups, it is reasonable that the SDS-C8E4-electrolyte β value is close to that of the SDS-C12E8-electrolyte system.
The addition of 0.5 M NaCl to the SDS-C8E4 system decreased the predicted β from β = −3.6 ± 0.5 to β = −3.1 ± 0.4. At 95% confidence, there is an overlap between the two predicted values due to the sampling resolution of the data; however, the smaller negative β associated with the electrolyte system implies less cooperative interactions between C8E4 and SDS. The less cooperative interactions can be attributed to the already screened electrostatic repulsions among the sulfate headgroups in the presence of NaCl so there is less ethylene oxide incorporation (and interactions) among the headgroups in the micelles.32
In summary, this experiment illustrates the efficacy and accuracy of the high-throughput methodology by reproducing the literature binary interaction parameter from regular solution theory for the SDS-C8E4-electrolyte system. We note that this methodology could have been used with any physics model, and regular solution theory serves as a simple model to demonstrate the viability of this experimental and analytical framework. Additionally, in cases where the governing models turn out to be inconsistent with the data, any mathematical expression can be fit to the data to determine the nonlinear CMC boundary. Some areas of future work could include extending the physical model to include three or more surfactants, as well as other electrolyte and solvent effects.
4 Conclusions
In this work we present a novel, high-throughput methodology that rapidly and accurately determines binary surfactant mixture properties. The novelty of this work is in (1) employing model-driven design of experiments for efficient experimentation in a 96-well plate and (2) a physics-based binary classification analysis approach to quantify the CMC in a less biased, robust manner than current methods based on individual fits to subsets of data. Using regular solution theory as the governing physics, the SDS-C8E4 system had a β = −3.6 ± 0.5, with a 14.9% difference from the literature value of β = −3.1. The SDS-C8E4-electrolyte system had a β = −3.1 ± 0.4, a 17.5% difference from the similar SDS-C12E8-electrolyte system β = −2.6. These two experiments support the validity of this generalized methodology as a high-throughput screening tool for binary surfactant systems. Although regular solution theory was used to demonstrate the methodology, any physics model or mathematical expression could have been used instead. This demonstrates a new approach to using classification to regress physical parameters from data.Data availability
Data for this article, including Excel sheets of the raw data and a Jupyter notebook containing all the analysis and code used to make figures are available at Figshare at https://doi.org/10.6084/m9.figshare.28687496.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CRC thanks the Office of Undergraduate Research and Scholar Development at Carnegie Mellon University for support through a Summer Undergraduate Research Fellowship. CRC acknowledges Shipica Uddagiri and Sejal Vispute for assistance with the fluorescence 96-well-plate experimental procedures. We acknowledge Lynn Walker for the initial motivation to study the critical micelle concentration with this method and for teaching CRC lab techniques at the beginning of the project.Notes and references
- P. M. Holland and D. N. Rubingh, in Mixed Surfactant Systems, American Chemical Society, 1992, pp. 2–30 Search PubMed.
- L. Huang and P. Somasundaran, Langmuir, 1997, 13, 6683–6688 CrossRef CAS.
- S. K. Shah, G. Chakraborty, A. Bhattarai and R. De, J. Mol. Liq., 2022, 368, 120678 CrossRef.
- M. Poša, Chem. Eng. Res. Des., 2014, 92, 2826–2839 CrossRef.
- L. Kong, H. Gang, Z. Wang, T. Li, C. J. Jafta, D. Fei, R. Ye and B. Mu, Colloids Surf., A, 2018, 551, 174–184 CrossRef CAS.
- N. Suzuki, J. Mol. Liq., 2022, 367, 120597 CrossRef CAS.
- Z. F. Agatić, K. Popović, D. Kumar, D. Škorić and M. Poša, J. Mol. Liq., 2023, 379, 121682 CrossRef.
- X. Y. Hua and M. J. Rosen, J. Colloid Interface Sci., 1982, 90, 212–219 CrossRef CAS.
- A. A. Dar, G. M. Rather, S. Ghosh and A. R. Das, J. Colloid Interface Sci., 2008, 322, 572–581 CrossRef CAS PubMed.
- K. Yoda, K. Tamori, K. Esumi and K. Meguro, Colloids Surf., 1991, 58, 87–98 CrossRef CAS.
- N. Suzuki, AppliedChem, 2024, 4, 1–14 CrossRef CAS.
- J. Jacquier and P. Desbène, J. Chromatogr. A, 1995, 718, 167–175 CrossRef CAS.
- H. Liu, Y. Gao and Z. Hu, J. Anal. Chem., 2007, 62, 176–178 CrossRef CAS.
- J. Petr, J. Sep. Sci., 2017, 40, 1421–1426 CrossRef CAS PubMed.
- M. M. Mabrouk, N. A. Hamed and F. R. Mansour, Appl. Spectrosc. Rev., 2021, 58, 206–234 Search PubMed.
- A. Dominguez, A. Fernandez, N. Gonzalez, E. Iglesias and L. Montenegro, J. Chem. Educ., 1997, 74, 1227 CrossRef CAS.
- D. J. Barlow, J. Mol. Liq., 2023, 390, 123167 CrossRef CAS.
- J. K. Salem, I. M. El-Nahhal and S. F. Salama, Chem. Phys. Lett., 2019, 730, 445–450 CrossRef CAS.
- H. He, C. Liu, J. Ming, Y. Lv, J. Qi, Y. Lu, X. Dong, W. Zhao and W. Wu, Aggregate, 2022, 3, e163 CrossRef CAS.
- T. Jumpertz, B. Tschapek, N. Infed, S. H. Smits, R. Ernst and L. Schmitt, Anal. Biochem., 2011, 408, 64–70 Search PubMed.
- X. Ji, A. Raza, J. Qi, Y. Lu, H. He and W. Wu, J. Pharm. Anal., 2024, 101044 Search PubMed.
- J.-R. Daban, M. Samsó and S. Bartolomé, Anal. Biochem., 1991, 199, 162–168 Search PubMed.
- I. N. Kurniasih, H. Liang, P. C. Mohr, G. Khot, J. P. Rabe and A. Mohr, Langmuir, 2015, 31, 2639–2648 CrossRef CAS PubMed.
- D. R. Perinelli, M. Cespi, N. Lorusso, G. F. Palmieri, G. Bonacucina and P. Blasi, Langmuir, 2020, 36, 5745–5753 CrossRef CAS.
- J. W. McBain, R. C. Merrill and J. R. Vinograd, J. Am. Chem. Soc., 1941, 63, 670–676 CrossRef CAS.
- J.-H. Kim, M. M. Domach and R. D. Tilton, Langmuir, 2000, 16, 10037–10043 CrossRef CAS.
- A. Tehrani-Bagha and K. Holmberg, Materials, 2013, 6, 580–608 CrossRef CAS.
- I. Kurnia, G. Zhang, X. Han and J. Yu, Fuel, 2020, 259, 116236 CrossRef CAS.
- S. Ghosh, D. Khatua and J. Dey, Langmuir, 2011, 27, 5184–5192 CrossRef CAS PubMed.
- S. A. Markarian, L. R. Harutyunyan and R. S. Harutyunyan, J. Solution Chem., 2005, 34, 361–368 CrossRef CAS.
- J. N. Phillips, Trans. Faraday Soc., 1955, 51, 561 RSC.
- P. Kroll, J. Benke, S. Enders, C. Brandenbusch and G. Sadowski, ACS Omega, 2022, 7, 7057–7065 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |