X and Q-band EMR study of ultrasmall Zn_1−xMn_xFe₂O₄ spinel nanoparticles fabricated under nonhydrolytic conditions

Abstract

In this work, we are showing the results of the X- and Q-band electron magnetic resonance measurements of ultra-small Zn_1−xMn_xFe₂O₄ nanoparticles (ca. 8 nm) with a very narrow size distribution. The chosen synthetic route allows for precise structural modifications with a broad concentration range (x = 0, 0.2, 0.5, 0.8, 1). The crystal structure was evaluated by means of X-ray diffraction, while cell parameters were calculated using Rietveld refinement. EMR spectral studies indicated that the prepared nanoparticles were superparamagnetic. The linewidth of EMR signal for any ferrite material generally originates from two sources: (a) magnetic dipole–dipole interactions among particles and (b) interparticle superexchange interactions between magnetic ions through oxygen ions. Observed effects are more complex interactions than in pure zinc and manganese ferrites. As a result of the study, a relationship was observed between the composition of the material and the magnetic properties with striking antiferromagnetism and ferrimagnetism change. Hence, by structural modification of materials, the magnetic character (FM–AFM–FiM) can be controlled.

---

1. Introduction

Ferrite-type compounds described with the general chemical formula AFe₂O₄, where metal cation A can be commonly represented by Zn²⁺, Mn²⁺, Co²⁺, Ni²⁺, Fe²⁺, etc. are a fairly broad subgroup of inorganic materials belonging to the larger spinel family depicted by the cubic crystal structure assigned to the Fd3̄m (no. 227) space group.^1–4 The unit cell is composed of two subnets. The one with A²⁺ cations has a T_d point symmetry with tetrahedral coordination by O²⁻ anions, while the second constitutes Fe³⁺ cations in 6-fold coordination that forms high-symmetry octahedral crystallographic sites O_h. In the general case, the ionic distribution is mixed, and it can be represented by [A_1−δFe]^a[AFe_2−δ]^bO₄, where δ is called the inversion parameter that specifies the fraction of Fe³⁺ ions located at A sites. Consequently, if δ is 0 or 1 it represents the normal and inverse spinel, respectively. Interestingly, ferrites can show crystallographic site occupancy inversion between the positions of A²⁺ and Fe³⁺ cations. It leads to the formation of an inverted spinel with a net cationic disorder that can be strongly dependent on the synthetic route.^5–8 This phenomenon is more pronounced for nanomaterials, where the degree of inversion can be higher than that in bulkier crystals. It is also worth noting that ferrite structures existing in bulk form only as normal spinel at the nanoscale can show a high cationic site disorder characteristic of inverted ferrites.⁹

The most well known representative of the nanoferrite family is the magnetite Fe₃O₄ (FeFe₂O₄) where iron has a mixed Fe²⁺ and Fe³⁺ valency. However, unless it is surface-protected, magnetite is highly prone to oxidation into α-Fe₂O₃.¹⁰ This chemical transformation results in a drastic change in magnetic properties and can have a detrimental effect on certain bio-related applications due to a change of physical properties characteristic.¹¹ To avoid that, one of the possibilities relies on the usage of more chemically stable AFe₂O₄ ferrites, for instance ZnFe₂O₄ or MnFe₂O₄. Both compounds are generally defined by the normal spinel structure.^5,9 However, upon particle size reduction, some cationic disorder can be observed, especially at the nanoscale. The degree of inversion in ZnFe₂O₄ and MnFe₂O₄ was shown to depend quite strongly on the fabrication technique.^6,7,12 What makes them particularly interesting is that they offer extraordinary particle size-dependent physicochemical properties that can be fine-tuned by chemical approaches.^13–16 The range of applications is wide and includes electronic devices,¹⁷ telecommunications,¹⁸ hyperthermia,¹⁹ virus sensor detection,²⁰ batteries,²¹ catalysis,²² contrast agents for magnetic imaging resonance (MRI),^23,24 drug delivery platforms,²⁵ gas sensing,²⁶etc. Mixed zinc–manganese ferrites (Zn_1−xMn_xFe₂O₄) are of great interest, as their properties can be shaped by structural modification.^16,25,27 A careful reader can find numerous reports on the synthetic routes towards ferrite compounds such as coprecipitation,²⁸ hydrothermal,¹⁹ sol–gel,²⁹ solid-state,³⁰ rapid hot-injection,³¹ thermal decomposition,³²etc.

Many antiferromagnetic materials have been reported to have a positive Curie–Weiss temperature, which is a sign of ferromagnetic interactions.^33–36 This behaviour was explained by the coexistence of competing antiferromagnetic and ferromagnetic interactions. In fact, ZnFe₂O₄ is a model system for studying competing interactions. The normal (Zn)^a(Fe₂)^bO₄ is antiferromagnetic, but the exchange of only a few Zn–Fe cations between sites gives place to (Zn_1-δFe)^a[ZnFe_2-δ]^bO₄. Recent evidence for such coexistence of ferrimagnetic clusters within an antiferromagnetic matrix^37–39 allows for correlation of Zn–Fe exchange with the anomalous increase in positive Curie–Weiss temperature despite the antiferromagnetic character of sample.³⁶ If the A ion is magnetic, AFe₂O₄ can be decomposed into two inequivalent magnetic sublattices, denoted as O (octahedral) and T (tetrahedral), respectively.⁴⁰ The diamond-like T sublattice is not frustrated within the nearest neighbour (NN) interaction, whereas in the presence of antiferromagnetic (AFM) interactions within the sublattice, the pyrochlore-like O sublattice can host a large NN frustration.⁴¹ The ions within a sublattice often interact ferromagnetically (FM), and the ions between two sublattices interact antiferromagnetically.^40,42,43 Some spinel compounds can cause the interaction of AFM between ions at O sites, which leads to geometric frustration.^44,45 Consequently, the general magnetic behaviour depends on the strength of the exchange interactions between O–O (J_OO), T–T (J_TT) and O–T (J_OT).^44–46

All Fe³⁺ ions are coupled to each other via a superexchange pathway through A sites, and their interactions are very weak. The normal ZnFe₂O₄ spinel shows long-range antiferromagnetic ordering at T_N = 9–11 K.^47,48 Magnetization was found to increase with grain size reduction. This characteristic is generally associated with an increase in cation inversion and a decrease in grain size.^43,49,50

Electron magnetic resonance spectroscopy (EMR) is a technique used to study chemical species with unpaired electrons. EMR spectroscopy also plays an important role in understanding organic and inorganic radicals, transition-metal complexes, and biomolecules. Among many experimental research methods used to study the magnetic properties of ferrite nanoparticles, EMR proves to be a very sensitive and provides information on local magnetic properties, the correlation between particle moments and the internal field distribution.^51–55 The properties and range of EMR applications depend mainly on the frequency band used. The maximum geometrical size of the object that can be examined by the EMR method is directly proportional to the wavelength of the microwave. As the frequency of the microwave signal increases, the ability to detect closely located resonance lines increases. EMR is a universal technique that provides valuable information on a variety of paramagnetic systems. This is favoured by high measurement sensitivity, selectivity, the ability to measure a specific compound in the presence of many other unidentified compounds, relatively short measurement time, or uncomplicated sample preparation. The information extracted from EMR spectroscopy includes the identity and atomic oxidation state of atoms, properties of free radicals, the local environment around the unpaired electrons, and the hyperfine interaction of nuclei with unpaired electrons.

When Zn_1−xMn_xFe₂O₄ is subject to a strong magnetic field, an induced magnetic potential energy splits the spin state of unpaired electrons (Zeeman effect) accordingly. Afterwards, simultaneously applied microwave frequencies are absorbed by the unpaired electrons, which can cause the transition from one spin state to another. This mechanism can be affected by several interactions such as the hyperfine interaction and the zero-field interaction, etc. We focused on investigating the influence of the Zn/Mn content on the microstructure, magnetic properties, and EMR characteristics of Mn–Zn ferrite nanoparticles, without neglecting the effect of the contribution of Fe ions. It is also worth recalling that in 1947 Néel was interested in the so-called spinel ferrites of formula Fe₂O₃MO, where M is a 3d divalent metal cation (e.g. Fe²⁺). The magnetic properties of these materials, with spontaneous magnetization, were not understood in detail. Néel called them non-compensated antiferromagnets “ferrimagnets”.⁵⁶

In this work, we conducted an in-depth characterisation of the chosen physical properties of ultrasmall (ca. 8 nm) Zn_1−xMnFe₂O₄ nanoparticles with narrow size distribution fabricated by the non-hydrolytic approach. The main focus was on detailed EMR characteristics. We observed that the positive Curie–Weiss temperature obtained from macroscopic measurements of the inverse susceptibility, at temperatures well below the Curie temperature of the ferrimagnetic clusters, is assigned to the superparamagnetic behaviour of clusters of atoms with a net magnetic moment originated through A–B superexchange interactions. The linear thermal dependence of the inverse of susceptibility appears only at temperatures above the blocking temperatures of these superparamagnetic clusters. Thus, the apparent Curie–Weiss temperature was expected to be in the range of the blocking temperatures corresponding to the cluster size distribution. It is important to note that this temperature is not the critical one for a phase transition, but it corresponds to the temperature at which the relaxation time of the magnetic moment is similar to the measurement time.³⁶ The EMR method makes it possible to measure the magnetic properties of materials in a way that other methods cannot. In some respects, the EMR can be more sensitive than SQUID because it responds only to magnetic ions with unpaired spin, whereas SQUID responds to both magnetic ions (seen in the EMR) and elements (atoms).

2. Experimental

2.1. Synthesis of Zn_1−xMn_xFe₂O₄ nanoparticles

The preparation procedure of the pure ZnFe₂O₄, MnFe₂O₄, and mixed Zn_1−xMn_xFe₂O₄ ferrites was based on the non-hydrolytic thermal decomposition technique in high boiling solvent i.e. benzyl alcohol (99% Thermo Scientific) as previously described by Bilecka et al.⁵⁷ with our amendments. As a source of metal cations, the respective acetylacetonate complexes were chosen Zn(acac)₂·H₂O (99% Thermo Scientific), Mn(acac)₂ (97% Thermo Scientific) as well as Fe(acac)₃ (99% Thermo Scientific) where necessary were chosen. Since all ferrites were prepared using the same protocol, only the example of fabrication of Zn_0.5Mn_0.5Fe₂O₄ will be explained. In other cases, the recalculation of the main chemical quantities is mandatory to keep the adequate stoichiometry ratio for a given compound. The fabrication of Zn_0.5Mn_0.5Fe₂O₄ involved 1.25 mmol of Zn(acac)₂·H₂O, 1.25 mmol of Mn(acac)₂, and 5 mmol of Fe(acac)₃. Handling of all chemicals was carried out under the protective atmosphere of N₂ using an acrylic glovebox (GS Glove Box Systemtechnik GMBH P10R250T2, Germany) equipped with automatic pressure gas control to protect them from possible deterioration. The metal complexes were dissolved in 70 ml of benzyl alcohol facilitated by sonication for 20 min in a cap-protected 100 ml two-neck glass flask. Since the zinc complex contains crystalline water before synthesis, the mixture temperature was raised to 120 °C for 1 hour to remove it. Subsequently, the flask was moved directly to the set-up containing the heating mantle, reflux column, and Pt-100 sensor connected to the automatic temperature controller (LTR 2500, Juchheim, Germany). The temperature was quickly increased to the boiling point of benzyl alcohol (205 °C) and left for 4 hours under constant reflux. After that, the reaction was stopped, and the flask with the final product was cooled to room temperature. The resulting black powder was separated and purified from the mother solution by washing/centrifugation cycles with ethanol (96% Chempur, Poland) and resuspended for long-term storage. The other ferrites were prepared by repeating the same procedure. Samples for TEM imaging were prepared in the form of suspensions of ethanol, while, for other experiments, ferrites were dried in a Petri dish at 60 °C for approximately 1 hour.

2.2. Characterization of nanoparticle physicochemical properties

The powder X-ray diffraction technique was used to evaluate the structural properties of Zn_1−xMn_xFe₂O₄ nanomaterials with the help of the Bruker D8 Advance diffractometer. As an X-ray source, a Cu lamp (1.54 Å) was used, and to cut the K_α2 line Ni filter was mounted. X-ray patterns were collected in the 15–70° 2θ range with a 0.02° step while the integration time was set to 0.8 s. Zinc–manganese ferrite samples were ground before the experiment with the agate mortar and then placed in a special holder. All recorded reflections were compared with the reference standards of the Crystallography Open Database⁵⁸ following card numbers 1010130 for ZnFe₂O₄, 2300583 Zn_0.2Mn_0.8Fe₂O₄, (c) Zn_0.5Mn_0.5Fe₂O₄, (d) Zn_0.8Mn_0.2Fe₂O₄, as well as 1528316 for MnFe₂O₄, respectively. Rietveld refinement was performed using the fundamental parameters approach implemented in MAUD software.⁵⁹ A five-polynomial coefficient background, sample displacement, unit cell parameters, scale factor, Popa microstructure rules,⁶⁰ and occupancy factors (only for (II) to (IV)) were sequentially refined. The presentation of the X-ray data and the analysis were performed using Origin Pro 2019 9.6 software (OriginLab, USA).

A Tecnai Osiris X-FEG (FEI Company, USA) transmission electron microscope (TEM) operating at 200 kV was used for nanoparticle (NP) imaging and evaluation of particle size, distribution, and morphology. The sample preparation involved the sonication of ferrite-containing ethanol suspensions (ca. 25 μg ml⁻¹) and placing a droplet of colloids on a 200 mesh carbon-coated copper grid (EM Resolutions, United Kingdom). The grids with the deposited materials were dried overnight under dust protection. Image analysis was performed in ImageJ freeware software (v. 1.8.0_1720). The concentration of particles in stock solution was determined using the Radwag MYA 5.4Y scale through three independent repetitions and final mass averaging.

Elemental analysis of mixed zinc manganese ferrites was performed using a Tescan Vega 3 scanning electron microscope (SEM) equipped with a Bruker Nano XFlash 6130 detector for energy-dispersive X-ray spectroscopy analysis (EDS). All samples for SEM-EDS analysis were prepared by placing a dry powder on a carbon tape attached to the aluminium-made holder. Data analysis was performed in a dedicated Bruker Esprit software (v. 2.1.1.1.17430) provided by the manufacturer.

Magnetic resonance measurements were performed on X-band (ν ≈ 9.4 GHz) and Q-band (ν ≈ 34 GHz) with modulation of the magnetic field at 100 kHz and 50 kHz, respectively, by a Bruker multifrequency and multiresonance FT-EPR ELEXSYS E580 spectrometer with X-band with a sensitivity of 7 × 10⁹ spins per 0.1 mT having a resolution of 2.35 (micro) T or even better.⁶¹ Temperature dependence measurements were carried out at room temperature, and as a function of temperature in the X-band in the range from 95 K to 300 K using a Bruker liquid nitrogen gas-flow cryostat with 41 131 VT digital controller, and in the Q-band in the range from 4 K to 300 K, using an ESR 900 liquid helium gas-flow cryostat from Oxford Instruments with Mercury iTC digital controller. Samples containing approximately 20 mg of sample powder were placed in 4 mm diameter quartz tubes.

3. Results and discussion

3.1. Physicochemical characterization of materials

The diffraction patterns for the zinc, manganese, and zinc–manganese nanoferrites were measured using the XRD technique and are presented in Fig. 1. In all cases, characteristic reflections were recorded that match with a reference standard card (COD database), namely 1010130 and 1528316 that were ascribed to the crystalline structure of ZnFe₂O₄ and MnFe₂O₄ cubic Fd3̄m (no. 227) crystalline structure. No additional peaks were detected, which confirmed the structural purity of the obtained phases and the absence of impurities. The main feature observed for all compounds relies on a significant peak broadening. This effect was associated to the presence of a small crystallites with comparable full width at half maximum (FWHM) values (1.3 2θ, [220] plane) between samples. The average size of the crystals was calculated by using the well-known Scherrer method defined by the following equation:where k is a constant (0.89) that approximates the particle morphology, λ is an X-ray source wavelength (1.54060 Å), β₀ depicts the apparatus broadening (0.05), β stands for FWHM, and finally θ represents the angle ascribed to the maximum peak position chosen for the analysis ([220] reflection).⁶² The calculated crystallite size (D) was around 6 nm for the whole group of fabricated compounds. The parameters of the unit cells were calculated using a well-established Rietveld refinement (see Fig. 1) and collected in Table 1. In the case of mixed Zn_1−xMn_xFe₂O₄ ferrites for more accurate fitting of the COD standard card no. 2300583 was chosen, while in Fig. 1 only two referenced patterns for ZnFe₂O₄ and MnFe₂O₄ are presented for clarity. As one can see, the calculated cell parameter a and cell volume did not differ significantly. It can be seen that a parameter of pure ZnFe₂O₄ and MnFe₂O₄ due to the complete exchange of smaller Zn²⁺ to Mn²⁺ cations shows a pronounced increase. The effect was expected since the ionic radius of Mn²⁺ at the tetrahedral site is greater than Zn²⁺, 0.66 and 0.6 Å, respectively.⁶³ In the case of mixed ferrites, the effect of the Mn²⁺ substitution on a parameter is not that striking and does not follow Vegard's law as one would expect. One possible explanation for this behaviour is associated with the presence of cationic crystallographic site occupancy inversion that probably becomes less pronounced with higher concentration of Mn²⁺. This observation is in-line with previous reports on the possible formation of the inverted ferrites at the nanoscale with a strong cationic disorder that depends on the fabrication technique.^5–7

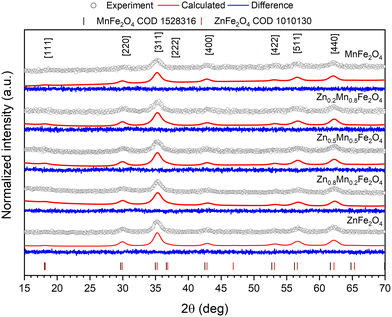Fig. 1 Graphical representation of the recorded X-ray patterns of pure and mixed zinc–manganese ferrites along with fitting results obtained through Rietveld refinement.

Table 1 Unit cell parameters, cell volume, and refine factors for the pure and mixed zinc–manganese ferrite nanoparticles calculated using the Rietveld refinement

Crystal data
Chemical Formula	ZnFe2O4	Zn0.8Mn0.2Fe2O4	Zn0.5Mn0.5Fe2O4	Zn0.2Mn0.8Fe2O4	MnFe2O4
Crystal system, space group	Regular, Fd3̄m
a, (Å)	8.4388	8.4259	8.4370	8.4355	8.4473
V (Å^3)	600.95	598.20	600.57	600.25	602.77
Z	8
Radiation type	Cu Kα
Refinement
R	0.0208	0.0216	0.0218	0.0210	0.0206
wR	0.0261	0.0269	0.0273	0.0261	0.0258
S	0.32	0.32	0.33	0.32	0.32

---

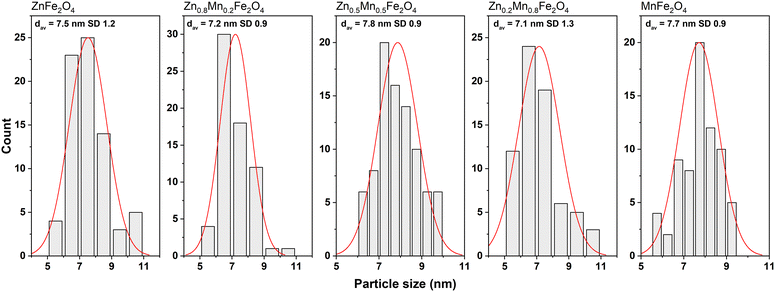
The size of the pure and mixed zinc–manganese ferrite particles, their distribution, and morphology were estimated using the TEM technique (Fig. 2 and 3). It should be noted that the fabricated nanomaterials did not differ in size, which was estimated to be 7.5 in all cases with a narrow distribution (monodisperse particles). This is beneficial since all of the observed effects will be associated only with that small particle size. The morphology of all ferrites is close to spherical with the presence of less regular particles with a tendency to form agglomerates. This behaviour is very typical for the synthesis of nanomaterials without the addition of any surface-blocking agents that will lead to a reduction of the surface energy responsible for agglomeration. Concerning particle size, good correspondence was found with the crystallite size estimated by the Scherrer formula, meaning that individual particles seen in TEM are represented as single crystallites.

Fig. 2 TEM images of the pure and mixed zinc–manganese ferrites obtained by the non-hydrolytic approach.

Fig. 3 Particle size distribution plots of pure and mixed zinc manganese ferrites.

SEM images as well as element maps of the Zn_1−xMn_xFe₂O₄ nanoferrites are shown in Fig. 4. It is evident that after manganese doping, the Mn²⁺ signal increases, while Zn²⁺ decreases significantly. It is, together with the XRD data, a straightforward proof of the Mn²⁺ incorporation into the structure of zinc ferrite for a broad concentration range. The content of the manganese ratio was calculated from the EDS data to be sufficiently close to the desired final composition, i.e., 19% for x = 0.2, 46% for x = 0.5, and 71% for the x = 0.8, respectively. Some deviation from the expected content of Mn²⁺ might be caused by the standard error of the EDS analysis (5%) and losses during substrate transfer.

Fig. 4 EDS and SEM elemental mapping of the Zn_1−xMn_xFe₂O₄ nanoparticles. EDS was performed covering a sample area of 250 μm × 250 μm in each case.

The EMR characteristics of Zn_1−xMn_xFe₂O₄ ferrites samples were studied by electron magnetic resonance spectroscopy. The authors determined the resonance field (B_res) and resonance linewidth (B_pp) from measured EMR spectra to understand the homogeneity and crystalline anisotropy of Zn_1−xMn_xFe₂O₄ ferrites. Representative EMR spectra of Zn_1−xMn_xFe₂O₄ ferrites are plotted in Fig. 5.

Fig. 5 EMR spectra of Zn_1−xMn_xFe₂O₄ nanoparticles at room temperature.

Various magnetic parameters such as resonance linewidth (B_PP), Lande's splitting factor (effective g-value) of Zn_1−xMn_xFe₂O₄ ferrite nanoparticles are listed in Table 2. The g-value is a function of the molecular motion, the symmetry of the ions, and the paramagnetic properties, which is also a constant of proportionality between the field and frequency. The effective g-value is calculated using the following relation:⁶⁴

where h is a Planck constant, ν is the microwave frequency, β is Bohr magneton, and B is the magnetic field at the resonance. The linewidth of the EMR signal for any ferrite material generally originated from two sources: (a) magnetic dipole–dipole interactions among particles and (b) interparticle superexchange interactions between magnetic ions through oxygen ions. Linewidth may get broadened or narrowed depending upon the interaction inside the material. The large linewidth and effective g-value increase due to leading dipole–dipole interactions, while the small linewidth and effective g-value increase due to leading superexchange interactions.⁶⁵ In addition, the line parameters were analyzed as a function of temperature.

Table 2 The EMR parameters and Curie temperature of the of Zn_1−xMn_xFe₂O₄ nanoparticles

	ZnFe2O4	Zn0.8Mn0.2Fe2O4	Zn0.5Mn0.5Fe2O4	Zn0.2Mn0.8Fe2O4	MnFe2O4
B pp – resonance linewidth, QCW – paramagnetic Curie temperature, C – Curie constant.
Effective g-factor	2.010	2.014	2.124	2.115 s	2.253
B pp (mT)	33.60	56.03	113.46	133.67	108.40
Q CW (K)	89.1	75.6	5.6	−112.0	−183.6
C	1.57 × 10^−10	3.88 × 10^−10	8.32 × 10^−10	14.58 × 10^−10	71.43 × 10^−10

---

The material studied Zn_1−xMn_xFe₂O₄ is a complex structure with various magnetic interactions. It is a kind of combination of two materials, MnFe₂O₄ and ZnFe₂O₄. A detailed analysis of the line parameters is planned in a separate article, including the calculation of the spin Hamiltonian. In the case of MnFe₂O₄, Fe-3d electrons occupy the crowded B-site while Mn-3d occupy the less electrons crowded A-site. From this anomalous behavior for the Fe 3d energy states position, electrons are not able to share the conduction mechanism (−8 eV away from Fermi level). The conduction mechanism in the spinel depends mainly on the super exchange between sites (A and B, for example between Mn and Fe cations through oxygen). Therefore, the Fe-3d electrons site for this cycle of conduction (Fe, O, and Mn) is missing. From the above anomalous explanation of density of states figures, it can be observed that a ferrimagnetic spin current between Fe-3d and Mn-3d through O-2p is yielded according to spin open or closed loop.⁴² Spin open loop:

(1) Fe–O spin exchange interaction in minority channel between −10 and −8 eV;

Fe-3d↓ + O-2p → Fe-3d + O-2p↓, (3)

(2) O–O spin exchange interaction between minority and majority;

O-2p↓(minority) + O-2p(majority) → O-2p↑, (4)

(3) O–Mn spin exchange interaction in majority channel between −2 and 0 eV.

O-2p↑, Mn-3d → O-2p, Mn-3d↑, (5)

Spin closed loop: this p–d overlap is the origin of the ferrimagnetic superexchange interaction between tetra and octahedral sites in ferrites, which are characterized by high hardness, further confirming the p–d overlapping for oxygen, and that TM is too much strong.⁴² In the case of ZnFe₂O₄, the susceptibility χ is the sum of all magnetic contributions, paramagnetic (PM), diamagnetic (DM), AFM, and FM-like. It can be described as:

χ = χ_PM + χ_DM + χ_AFM + χ_FM. (6)

On the other hand, at high fields, only the PM, DM, and AFM orderings vary with the field since the others are saturated.⁶⁶ Therefore, FM-like contributions can be discarded at HF, and high-field susceptibility χ_HF can be described as:

χ_HF = χ_DM + χ_PM + χ_AFM. (7)

Consequently, the ferri-, ferro-, and/or superparamagnetic contributions can be evaluated by calculating χ_HF and subtracting it from the entire magnetization curve.³⁷ Theoretical calculations show the influence of inversion within a single unit cell, the smallest local inversion (δ_c) is either 0 or 1/8, the last corresponding to the exchange of a single Zn/Fe pair in the unit cell. Assuming that only a single Zn/Fe exchange can occur in a cell, around 40% of the unit cells suffer a single Zn/Fe cations exchange when the macroscopic δ is as small as 0.05. Unit cells with δ_c = 1/8 are FiM (40%) with a magnetic moment of 5.9μ_B,³⁷ while for δ_c = 0 the cells are AFM (60%). This illustrates the dramatic effect that δ ≈ 0 can have on the magnetic and calorimetric properties.

Cobos et al.³⁸ show for ZnFe₂O₄, that the magnetic entropy increment can be associated with the AFM to PM transition, and the small experimental value of 8.7 J mol⁻¹ K⁻¹ indicates that only 29% of the sample has evolved from AFM to the paramagnetic phase. In summary, instead of the expected 60%, only 29% of the sample appears to be AFM ordered.³⁸

To briefly recap, the contribution of ZnFe₂O₄ gives a narrow line, while the line of MnFe₂O₄ is several times wider. The observed spectrum consists of a line from the Fe³⁺ ion (a line of about 150 mT), and a broad line that is a superposition of at least two components. In addition, a narrow line (about 350 mT) is also visible. As the concentration of Mn ions increases, the width of the resonance line also increases. The only exception is MnFe₂O₄, due to the fact that the effective g-factor comes from the superposition of the line. The spectrum of the Fe³⁺-coupled pair (Fe³⁺–O–Fe³⁺) in Fe₂O₃ is known to give a resonance line with an effective g-factor around 2.0. So, the effective g-value, 2.169, for the MnFe₂O₃ sample can be attributed to the superexchange interaction between the Fe³⁺ ions. A weak signal observed at about effective g-factor 4.2, in addition to the intense spectral line, can be attributed to an isolated Fe³⁺ in the orthorhombic field.^67,68

As the temperature increases, the signals gradually get sharper and more symmetrical, with a shift to a high field (see Fig. 6). Furthermore, with increasing temperature, a sharp decrease in the line width and an increase in the intensity of the EMR signal is observed (Fig. 9). This is because the thermal fluctuation of magnetic moments can reduce the extent of the anisotropic contributions to the free energy density and the effective magnetic field (the superparamagnetic effect).⁶⁹ In this event, at elevated temperatures very narrow resonance spectra are observed, while at low temperatures the thermal fluctuations are gradually frozen out, and the magnetization direction is blocked, resulting in the broadening of the resonance line.

Fig. 6 Temperature dependence of X-band EMR spectra of Zn_0.8Mn_0.2Fe₂O₄ nanoparticles.

Broadening and shift to lower magnetic fields of magnetic resonance spectra with increasing temperature are typically observed for superparamagnetic (SPM) nanoparticles, and analogous cases can be found in a number of systems.⁶⁹ However, for SPM particles, whose direction of magnetization fluctuates at a rate faster than the Larmor frequency, this results in a narrow resonance line because of an averaging effect of this fluctuation on the magnetocrystalline anisotropy. With a decrease in the temperature, the resonance line of the SPM particle broadens as the averaging effect of thermal fluctuations is reduced and the direction of magnetization is blocked, first in bigger and progressively in smaller particles. Thus, the narrow resonance line at room temperature, which progressively broadens with a reduction in temperature, once again confirms the superparamagnetic behavior of the prepared samples.⁶⁸

In ferromagnetic materials, magnetic domains are in a fragile state of equilibrium, and the Bloch wall, which is a narrow transition region at the boundary between magnetic domains, moves with very low applied fields. In fact, LFMA is associated with the dynamics of magnetic domains in material.⁷⁰ The existence of this absorption at room temperature is an indication of the ferromagnetic state of the material used to detect magnetic order. For bulk samples, the LFMA signal is used to determine the Curie temperature of ferromagnetic compounds.^71,72 Above 28 nm, the existence of LFMA shows that these compounds are in a magnetic multi-domain state, and a flat response for compounds with smaller size shows that they are in a single-domain state. The absence of the LFMA signal in ferromagnetic compounds is a good indication of the superparamagnetic state in samples.⁷³ By size reduction, the nanocrystalline passes from a particle with several magnetic domains to a monodomain particle; the latter is either in a single-domain state or in a superparamagnetic state. Low-field absorption cannot determine the intermediate state. Particles belonging to the single-domain state are characterized by the maximum magnetocrystalline anisotropy energy, consequently the direction of magnetization is ‘frozen’. This characteristic has an effect on the linewidth of resonant absorption; a comparative analysis can reveal the critical size of changes in magnetic states.

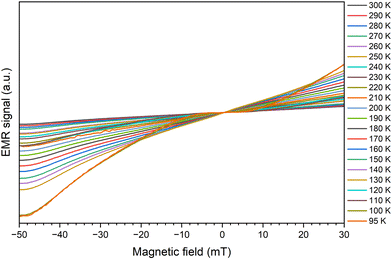
In the higher temperature range, the paramagnetic region, the line is relatively narrow and more regular. When the temperature is lower, we observe a widening of the line along with its deformation (the upper part), the centre moves along with the lower part of the line. The lower the temperature, the deformation increases. In the Q-band we observe a clear separation of the line (Fig. 7).

Fig. 7 Temperature of dependence of the Q-band EMR spectra of MnFe₂O₄ nanoparticles.

Increasing the content of manganese the value of the effective factor g increases, from 2.008 to 2.169 (for 100% Mn ions). A similar relation occurs for the width of the line. For ZnFe₂O₄, the line is the narrowest (33.6 mT). We observe an increase in line width to 130.6 mT for 80% manganese. Finally, for 100% Mn ion, the width is 108 mT, which is less than described above, due to the fact that we are facing two components of the resonance line that are offset from each other. Still, as a result of the summation, we will eventually get the widest recorded line. If the ZnFe₂O₄ component is missing, the line from the MnF₂O₄ component becomes narrower. The superposition of the two components of the line causes the relationship shown in Fig. 8 to change rapidly at temperatures around 120 K. This is particularly visible at contents of 50% or more manganese.

Fig. 8 Temperature dependence of the effective g-factor for Zn_1−xMn_xFe₂O₄ nanoparticles obtained in the X-band.

We used the Curie–Weiss law to analyze the temperature dependences of the integral intensity, which is directly proportional to the magnetic susceptibility χ. A linear increase of χ⁻¹ (T) at higher temperatures can be fitted to the Curie–Weiss law:

(χ − χ₀)⁻¹ = (T − Q_CW)/C, (8)

where C is the Curie constant. The first term describes the asymptotic high temperature behavior, with C being the asymptotic Curie temperature and Curie constant, respectively. The magnitude measures the antiferromagnetic coupling strength between the two sublattices,⁶¹ while C is the sum of the sublattice Curie constants, that is, C = CT + CO.^17,22 Observation of three magnetic states in MnFe₂O₄ single crystals.⁴⁶

Q _CW is the paramagnetic Curie temperature, χ₀ temperature independent coefficient to calculate the magnetic permeability, and the Pauli term for paramagnetism.⁷⁴ Based on the theory, the inverse relationship of intensity (1/Int) is shown as a function of temperature for Zn_1−xMn_xFe₂O₄ nanoparticles samples (Fig. 9). Obtained values of Curie temperatures and Curie constants for all samples shown in Table 2.

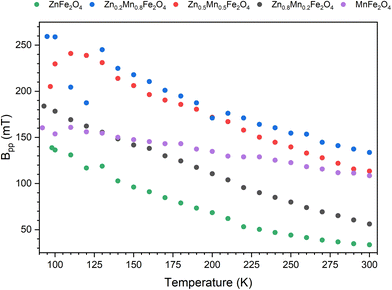Fig. 9 Temperature dependence of peak to peak line width for Zn_1−xMn_xFe₂O₄ nanoparticles obtained in X-band.

Fig. 10(a–e) show the dependence of the inverse intensity as a function of temperature for Zn_1−xMn_xFe₂O₄ nanoparticles obtained in the X-band for EMR lines in a higher magnetic field (about 350 mT). Due to the antiferromagnetic character of the B–B and A–B superexchange interactions in spinel ferrites, the experimental finding of a positive value of the apparent Curie–Weiss temperature may be surprising. As Lotgering⁷⁵ indicated, the measuring temperature should increase to 800 K to observe the straight line with negative Curie–Weiss temperature due to the antiferromagnetic A–B coupling, which gives rise to the ferrimagnetic clusters. On the other hand, the negative Curie–Weiss temperature associated with the B–B antiferromagnetic coupling could only be observed for δ = 0 (for example, with ideal ZnFe₂O₄ samples, in which there is no trace of ferrimagnetic clusters). However, since this ideal case is difficult to achieve, the previously reported anomalous sign for the Curie–Weiss temperature can be understood as a consequence of superparamagnetism associated with the almost unavoidable presence of a few ferrimagnetic clusters.³⁶ We observed a non-linear increase in Q_cw values for the increase in Zn content (Fig. 10f) as well as deviations from the designated Q_cw from the literature. We identified the following reasons for these differences (1) only values for pure compounds are given in the literature; (2) particle size affects the Curie temperature⁷⁶ that is especially manifested for nanoparticles with dimensions in the range of a few to several nanometers, thus observed changes in Q_cw of several tens of K; (3) it is not insignificant that our measurements involve materials being a combination of Zn and Mn, so more complex magnetic interactions are to be expected than for single compounds.

Fig. 10 Inverted integrated intensity as a function of temperature for (a) ZnFe₂O₄; (b) Zn_0.2Mn_0.2Fe₂O₄; (c) Zn_0.5Mn_0.5Fe₂O₄; (d) Zn_0.8Mn_0.8Fe₂O₄; (e) MnFe₂O₄, as well as dependence of the determined temperature Q_cw on chemical composition of ferrites (f).

Observed effects are more complex interactions than in pure zinc an manganese ferrites. As a result of the study, a relationship was observed between the composition of the material and the magnetic properties with striking antiferromagnetism to ferrimagnetism change (see Fig. 10f). Hence, by modifying the composition of materials, we have the possibility of controlling the magnetic properties (FM–AFM–FiM).

4. Conclusions

Ultra-small Zn_1−xMn_xFe₂O₄ nanoparticles with an average crystallite size of 8 nm were synthesized using a convenient non-hydrolytic route by thermal decomposition of zinc and manganese complexes in high-temperature boiling organic solvent. Fabricated materials did not differ in particle size and showed a narrow distribution while being close to spherical morphology. The visible tendency to form agglomerated structures is due to the lack of surface surface-blocking agents that, if necessary, can be used for applications where it is mandatory. The chosen synthetic approach allows for control of the chemical composition within a broad concentration range, which additionally has a significant effect on the final physicochemical properties as shown by EMR spectroscopy.

EMR spectral studies indicated that the prepared nanoparticles were superparamagnetic. The linewidth of EMR signal for any ferrite material generally originated from two sources: (a) magnetic dipole–dipole interactions among particles and (b) interparticle superexchange interactions between magnetic ions through oxygen ions. The presented EMR lines are obtained from contributions from ZnFe₂O₄ and MnFe₂O₄. The contribution of ZnFe₂O₄ gives a narrow line, while the line of MnFe₂O₄ is several times wider. The observed spectrum is composed of a line originating from the Fe³⁺ ion (a line around 150 mT) and a broad line that is a superposition of at least two components. A narrow line (around 350 mT) was also analyzed. An increase in the width of the resonant line was observed, proportional to the increase in Mn concentration in the sample. The only exception is MnFe₂O₄, due to the fact that the effective g-factor comes from the superposition of the line.

In the higher temperature range, the paramagnetic region, the observed lines are relatively narrow and regular. With a decrease in the temperature, a broadening of the line is observed along with a deformation of the upper part, with the centre of the line moving along with the lower part. The lower the temperature, the greater the deformation becomes. Performing measurements in the Q-band allowed us to observe separated resonant lines. Both ZnFe₂O₄ and MnFe₂O₄ can be decomposed into two inequivalent magnetic sublattices, denoted as O and T, respectively. The T sublattice is not frustrated in the NN interaction, whereas in the presence of AFM interactions within the sublattice, the O sublattice can host a large NN frustration. While the ions within a sublattice often interact FM and the ions between two sublattices interact AFM, some spinel compounds can give rise to the interaction of AFM between ions at the O sites that leads to geometric frustration. As a result, the overall magnetic behavior depends on the strength of the exchange interaction between O–O (J_OO), T–T (J_TT) and O–T (J_OT). We observe a non-linear increase in Q_cw values with an increase of Zn content. Such complex behavior is caused by the size of the particles as well as chemical structural modification that leads to more complex magnetic interactions than that expected for pure compounds.

Author contributions

M. K.-G. and A. T. synthesis of particles, TEM imaging, R. P. XRD measurements, P. K. SEM and EDS characterization, B. Z. Rietveld refinement, I. R., B. C. EMR measurements, I. R., I. S. EMR measurements analysis and interpretations of EMR spectra, I. R., B. C., M. K.-G., A. T., R. P., I. S., P. K. writing manuscript, editing, and corrections. R. P. and I. S. idea and conceptualization. All authors read the manuscript and agreed with its content.

Data availability

All data are accessible from the corresponding authors upon request.

Conflicts of interest

We declare no conflict of interest.

References

1. B. Skołyszewska, W. Tokarz, K. Przybylski and Z. Kakol, Phys. C, 2003, 387, 290–294.
2. M. Sugimoto, J. Am. Ceram. Soc., 1999, 82, 269–280.
3. K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82, 3279–3292.
4. D. Dadarlat, C. Neamtu, M. Streza, R. Turcu, I. Craciunescu, D. Bica and L. Vekas, J. Nanopart. Res., 2008, 10, 1329–1336.
5. H. S. C. O'Neill and A. Navrotsky, Am. Mineral., 1983, 68, 181–194.
6. C. Simon, A. Blösser, M. Eckardt, H. Kurz, B. Weber, M. Zobel and R. Marschall, Z. Anorg. Allg. Chem., 2021, 647, 2061–2072.
7. M. V. Nikolic, Z. Z. Vasiljevic, M. D. Lukovic, V. P. Pavlovic, J. B. Krstic, J. Vujancevic, N. Tadic, B. Vlahovic and V. B. Pavlovic, Int. J. Appl. Ceram. Technol., 2019, 16, 981–993.
8. B. Antic, A. Kremenovic, A. S. Nikolic and M. Stoiljkovic, J. Phys. Chem. B, 2004, 108, 12646–12651.
9. R. J. Hill, J. R. Craig and G. V. Gibbs, Phys. Chem. Miner., 1979, 4, 317–339.
10. R. Pązik, E. Piasecka, M. Małecka, V. G. Kessler, B. Idzikowski, Z. Śniadecki and R. J. Wiglusz, RSC Adv., 2013, 3, 12230.
11. G. Xu, L. Li, Z. Shen, Z. Tao, Y. Zhang, H. Tian, X. Wei, G. Shen and G. Han, J. Alloys Compd., 2015, 629, 36–42.
12. S. Wen, B. Chen, J. Zhang, W. Zhan, Z. He and L. Gao, Crystals, 2023, 13, 1509.
13. A. G. Niculescu, C. Chircov and A. M. Grumezescu, Methods, 2022, 199, 16–27.
14. M. D. Nguyen, H. V. Tran, S. Xu and T. R. Lee, Appl. Sci., 2021, 11, 11301.
15. H. Gavilán, S. K. Avugadda, T. Fernández-Cabada, N. Soni, M. Cassani, B. T. Mai, R. Chantrell and T. Pellegrino, Chem. Soc. Rev., 2021, 50, 11614–11667.
16. S. J. Salih and W. M. Mahmood, Heliyon, 2023, 9, e16601.
17. B. Sun, F. Chen, W. Yang, H. Shen and D. Xie, J. Magn. Magn. Mater., 2014, 349, 180–187.
18. A. Goldman and A. M. Laing, J. Phys. (Paris), Colloq., 1976, 38, 297–301.
19. P. T. Phong, P. H. Nam, D. H. Manh, D. K. Tung, I. J. Lee and N. X. Phuc, J. Electron. Mater., 2015, 44, 287–294.
20. V. D. Krishna, K. Wu, A. M. Perez and J. P. Wang, Front. Microbiol., 2016, 7, 400.
21. P. F. Teh, S. S. Pramana, Y. Sharma, Y. W. Ko and S. Madhavi, ACS Appl. Mater. Interfaces, 2013, 5, 5461–5467.
22. A. Khazaei, A. Ranjbaran, F. Abbasi, M. Khazaei and A. R. Moosavi-Zare, RSC Adv., 2015, 5, 13643–13647.
23. C. Bárcena, A. K. Sra, G. S. Chaubey, C. Khemtong, J. P. Liu and J. Gao, Chem. Commun., 2008, 2224–2226.
24. N. Dogan, G. Caliskan and M. Irfan, J. Mater. Sci.: Mater. Electron., 2023, 34, 390.
25. P. Thakur, D. Chahar, S. Taneja and N. Bhalla, Ceram. Int., 2020, 46, 15740–15763.
26. Z. M. Abdulhamid, A. A. Dabbawala, T. Delclos, R. Straubinger, M. Rueping, K. Polychronopoulou and D. H. Anjum, Sci. Rep., 2023, 13, 19705.
27. T. Sembiring, D. Siburian and M. Rianna, Mater. Sci. Energy Technol., 2023, 6, 124–129.
28. F. Ameen Ramiza, S. K. Ajmal, M. B. Khan, A. Nasim, Y. Jamil, K. Kashif and S. Amira, IOP Conf. Ser.:Mater. Sci. Eng., 2016, 146, 012029.
29. S. J. Haralkar, R. H. Kadam, S. S. More, S. E. Shirsath, M. L. Mane, S. Patil and D. R. Mane, Mater. Res. Bull., 2013, 48, 1189–1196.
30. S. F. Wang, Y. F. Hsu and C. H. Chen, J. Electroceram., 2014, 33, 172–179.
31. M. Kulpa-Greszta, A. Tomaszewska, A. Dziedzic and R. Pązik, RSC Adv., 2021, 11, 20708–20719.
32. V. I. Popkov, V. P. Tolstoy and V. G. Semenov, J. Alloys Compd., 2020, 813, 152179.
33. X. L. Wang, M. James, J. Horvat and S. X. Dou, Supercond. Sci. Technol., 2002, 15, 427–430.
34. V. Tsurkan, J. Hemberger, A. Krimmel, H. A. Krug Von Nidda, P. Lunkenheimer, S. Weber, V. Zestrea and A. Loidl, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 224442.
35. J. Hemberger, H. A. K. Von Nidda, V. Tsurkan and A. Loidl, Phys. Rev. Lett., 2007, 98, 147203.
36. A. Hernando, M. Á. Cobos, J. A. Jiménez, I. Llorente, A. García-Escorial and P. de la Presa, Materials, 2022, 15, 4789.
37. M. A. Cobos, P. De La Presa, I. Llorente, J. M. Alonso, A. Garciá-Escorial, P. Marín, A. Hernando and J. A. Jiménez, J. Phys. Chem. C, 2019, 123, 17472–17482.
38. M. A. Cobos, A. Hernando, J. F. Marco, I. Puente-Orench, J. A. Jiménez, I. Llorente, A. García-Escorial and P. de la Presa, Materials, 2022, 15, 1198.
39. M. Á. Cobos, P. de la Presa, I. Puente-Orench, I. Llorente, I. Morales, A. García-Escorial, A. Hernando and J. A. Jiménez, Ceram. Int., 2022, 48, 12048–12055.
40. M. L. Néel, Ann. Phys., 1948, 12, 137–198.
41. C. Lacroix, P. Mendels and F. Mila, Introduction to Frustrated Magnetism, Springer, 2011.
42. A. Elfalaky and S. Soliman, J. Alloys Compd., 2013, 580, 401–406.
43. D. S. Mathew and R. S. Juang, Chem. Eng. J., 2007, 129, 51–65.
44. T. A. Kaplan and N. Menyuk, Philos. Mag., 2007, 87, 3711–3785.
45. C. Ederer and M. Komelj, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 064409.
46. R. Nepal, M. Saghayezhian, J. Zhang and R. Jin, J. Magn. Magn. Mater., 2020, 497, 165955.
47. F. J. Burghart, W. Potzel, G. M. Kalvius, E. Schreier, G. Grosse, D. R. Noakes, W. Schak, W. Kockelmann, S. J. Campbell, W. A. Kaczmarek, A. Martin and M. K. Krause, Phys. B, 2000, 289–290, 286–290.
48. J. C. Ho, H. H. Hamdeh, Y. Y. Chen, S. H. Lin, Y. D. Yao, R. J. Willey and S. A. Oliver, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 52, 10122–10126.
49. J. F. Hochepied, P. Bonville and M. P. Pileni, J. Phys. Chem. B, 2000, 104, 905–912.
50. M. R. Anantharaman, S. Jagatheesan, K. A. Malini, S. Sindhu, A. Narayanasamy, C. N. Chinnasamy, J. P. Jacobs, S. Reijne, K. Seshan, R. H. H. Smits and H. H. Brongersma, J. Magn. Magn. Mater., 1998, 189, 83–88.
51. J. P. Jamet and A. P. Maiozemoff, Phys. Rev. B:Condens. Matter Mater. Phys., 1978, 8, 75–91.
52. F. Gazeau, J. C. Bacri, F. Gendron, R. Perzynski, Y. L. Raikher, V. I. Stepanov and E. Dubois, J. Magn. Magn. Mater., 1998, 186, 175–187.
53. E. De Biasi, C. A. Ramos, R. D. Zysler and H. Romero, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 1–8.
54. R. Berger, J. Kliava, J. C. Bissey and V. Baïetto, J. Appl. Phys., 2000, 87, 7389–7396.
55. A. Mendoza, J. Prado and O. Almanza, Acta Phys. Pol., A, 2012, 121, 950–953.
56. B. Barbara, C. R. Phys., 2019, 20, 631–649.
57. I. Bilecka, I. Djerdj and M. Niederberger, Chem. Commun., 2008, 886–888.
58. A. Vaitkus, A. Merkys and S. Grazulis, J. Appl. Crystallogr., 2021, 54, 661–672.
59. L. Lutterotti, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 334–340.
60. N. C. Popa, J. Appl. Crystallogr., 1998, 31, 176–180.
61. A. V. Raut, S. A. Jadhav, D. R. Shengule and K. M. Jadhav, J. Sol-Gel Sci. Technol., 2016, 79, 1–11.
62. H. P. Klug and L. E. Alexander, X-Ray Diffraction Procedures: For Polycrystalline and Amorphous Materials, Wiley, New York, 2nd edn, 1974.
63. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
64. A. Lund and M. Shiotani, Applications of EPR in radiation research, Springer International Publishing, 2014.
65. F. A. Ahmed and L. N. Singh, J. Mater. Sci. Surf. Eng., 2018, 6, 825–830.
66. C. Richter and B. A. Van Der Pluijm, Phys. Earth Planet. Inter., 1994, 82, 113–123.
67. K. Tanaka, K. Kamiya, T. Yoko, S. Tanabe, K. Hirao and N. Soga, J. Non-Cryst. Solids, 1989, 109, 289–294.
68. K. V. P. M. Shafi, A. Gedanken, R. Prozorov and J. Balogh, Chem. Mater., 1998, 10, 3445–3450.
69. X. Cao and L. Gu, Nanotechnology, 2005, 16, 180–185.
70. R. Valenzuela, G. Alvarez, H. Montiel, M. P. Gutiérrez, M. E. Mata-Zamora, F. Barrón, A. Y. Sánchez, I. Betancourt and R. Zamorano, J. Magn. Magn. Mater., 2008, 320, 1961–1965.
71. H. Gavi, B. D. Ngom, A. C. Beye, A. M. Strydom, V. V. Srinivasu, M. Chaker and N. Manyala, J. Magn. Magn. Mater., 2012, 324, 1172–1176.
72. G. Alvarez, H. Montiel, J. F. Barron, M. P. Gutierrez and R. Zamorano, J. Magn. Magn. Mater., 2010, 322, 348–352.
73. M. Yahya, F. Hosni and A. H. Hamzaoui, in Smart Nanosystems for Biomedicine, Optoelectronics and Catalysis, ed. T. Shabatina and V. Bochenkov, Intechopen, 2020, pp. 2–22.
74. K. Kambe, J. Phys. Soc. Jpn., 1950, 5, 48–51.
75. F. K. Lotgerlng, J. Phys. Chem. Solids, 1966, 27, 139–145.
76. N. S. Gajbhiye, G. Balaji and M. Ghafari, Phys. Status Solidi A, 2002, 189, 357–361.

---