Open Access Article
Open Access ArticleExploring N2 activation using novel Lewis acid/base pairs: computational insight into frustrated Lewis pair reactivity†
Xuban Gastearena a,
Jon M. Matxain
a,
Jon M. Matxain *a and
Fernando Ruipérez
*a and
Fernando Ruipérez *b
*b
aKimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU and Donostia International Physics Center (DIPC), Paseo Manuel Lardizábal 4, 20018 Donostia, Euskadi, Spain
bPOLYMAT and Physical Chemistry Department, Faculty of Pharmacy, University of the Basque Country UPV/EHU, 01006 Vitoria – Gasteiz, Euskadi, Spain. E-mail: fernando.ruiperez@ehu.eus
First published on 7th February 2025
Abstract
The activation of dinitrogen (N2) is a crucial step in synthesizing nitrogen-based compounds and remains a significant challenge due to its strong triple bond. Currently, industrial N2 conversion relies on the Haber–Bosch process, a highly energy-intensive method that utilizes transition metal-based catalysts. Frustrated Lewis pairs (FLPs) have emerged as a promising alternative for N2 activation without the need for transition metals. In this work, we employ density functional theory (DFT) to investigate the activation of N2 by transition metal-free Lewis acids (LAs) and bases (LBs). Our study demonstrates that LAs play a crucial role in capturing N2 and determining the thermodynamics of activation, while LBs play a complementary role by reducing the bond order of the N2 molecule, thereby promoting activation. The efficiency of N2 capture is directly linked to the electroaccepting characteristics of the LAs. A principal component analysis (PCA) reveals that the key factors influencing the electroaccepting power of LAs are the degree of pyramidalization and orbital occupation at the acidic site, as well as the local electrophilicity index. The LA-N2 interaction is found to be electrostatic with partially covalent character. Among the 21 LAs analyzed, triptycene-based systems exhibit the highest stability in forming LA-N2 complexes, highlighting their potential as effective N2-capturing agents. However, the N2 triple bond remains largely intact, necessitating the involvement of LBs in LA-N2-LB complexes for full activation, in a “push–pull” mechanism. Six LBs are analyzed in complexes with the most promising LAs. Bonding analysis indicates that the LB-N2 interaction can be regarded as a covalent bond, which may explain the main role of the LB in the reduction of the N2 bond order. Furthermore, the bond activation is significantly enhanced by increasing the nucleophilicity of the LB. Among all the LA–LB pair combinations, only three exhibit the defining characteristics of frustrated Lewis pairs (FLPs), with moderate interaction energies and substantial LA–LB distances. Our findings suggest that FLPs composed of triptycene-based LAs and tris-tert-butylphosphine represent the most promising candidates for N2 activation.
1 Introduction
Nitrogen is a vital element for all life forms and serves as a precursor to essential nitrogen-containing compounds such as amino acids, DNA, and fertilizers.1 It is the most abundant element in Earth's atmosphere, comprising 78% of the air in its diatomic form, N2. However, most organisms are unable to directly utilize nitrogen in its gaseous form; it must first be converted or “fixed” into a more accessible form. This process occurs naturally through two primary mechanisms. Lightning can convert atmospheric nitrogen into nitrogen oxides (NOx),2 while nitrogenase enzymes, found in certain bacteria, play a more critical role. These enzymes facilitate the multi-electron reduction of N2 to NH3, a reaction catalyzed by the iron-molybdenum cofactor (FeMoco).3,4 The nitrogen fixation process requires the hydrolysis of at least 16 equivalents of adenosine triphosphate (ATP) and achieves up to 65% selectivity. However, biological N2 fixation remains kinetically slow due to its dependence on electron tunneling, making it inadequate to support the demands of modern intensive agriculture.5 Over the past century, nitrogen activation has predominantly been achieved through the Haber–Bosch process, in which atmospheric N2 is reduced by hydrogen gas to produce ammonia, which is then converted into various fertilizers. Despite its industrial success, the initial step of nitrogen reduction is inherently challenging due to the extreme stability of the N2 triple bond. This necessitates harsh reaction conditions (elevated temperature and pressure) and the use of a metal catalyst, often powered by fossil fuels, leading to the emission of fossil-derived CO2 as a by-product.6–9 Consequently, the activation of N2 has become a focal point of scientific research, with efforts focused on developing environmentally sustainable alternatives that operate under mild conditions and utilize main-group elements rather than transition metals.The widespread use of transition metals in dinitrogen activation is due to their ability to provide both unoccupied and occupied d orbitals that are energetically and symmetrically suited for accepting electron density from N2 and back-donating it into the molecule's antibonding orbitals, thereby weakening its triple bond.10–13 Recently, the “push–pull” hypothesis has been introduced, suggesting that electron depletion caused by Lewis acid complexation (the pull effect) enhances the delocalization of d electrons from the metal center into N2 antibonding orbitals (the push effect), further promoting bond weakening. A representative example involves boron, which acts as a Lewis acid through sp3 hybridization with its 2s22p1 electronic configuration. When combined with low-valent iron (Fe), molybdenum (Mo), and tungsten (W) centers, tris(pentafluorophenyl)borane (B(C6F5)3) significantly enhances the activation of N2 in M–N–N–B(C6F5)3 complexes.14
Conceptually, the push–pull reactivity observed in frustrated Lewis pairs (FLPs) can be compared to that of transition metal systems, where a Lewis acid (LA) and Lewis base (LB) cooperate to activate small molecules. In both cases, the reactivity is driven by the synergistic action of a strong LA pulling electron density and a bulky LB pushing its electron pair into the antibonding orbitals of a substrate, facilitating activation.15 In this context, the combination of free LA and LB, which are prevented from interacting due to steric hindrance from bulky substituents, exhibits intriguing catalytic properties that mimic the role of metallic catalysts (Fig. 1). The LA mimics the empty d orbitals of a metal by interacting with nitrogen lone pairs via σ-bonding, while the LB performs the π-backdonation into the π* antibonding orbitals of the nitrogen molecule. In recent years, FLPs and other main group systems have demonstrated the ability to replicate the reactivity of various transition metal complexes, enabling both stoichiometric and catalytic reactions that were once thought to be exclusive to transition metals.16 This realization has led to the hypothesis that main group compounds could serve as viable alternatives to transition metal complexes for N2 fixation.17 Examples include experimental studies on borylene-based FLPs, such as cyclic alkyl(amino)carbene (CAAC)-supported borylene complexes [(Dur)B(CAAC)].18–20 Additionally, computational investigations of N-heterocyclic carbenes (NHC) emphasize the role of aromaticity in the activation process.21–23 The activation potential of borylenes lies in the ambiphilic character of boron, which possesses a sp hybridization with one empty 2p orbital and one filled, allowing them to function as both LA and LB, similar to transition metals. However, most FLP systems studied so far are based on intramolecular FLPs, where both acidic and basic sites are incorporated into the same molecule. Moreover, these FLPs typically involve carbenes as the basic sites and borylenes as the acidic sites.24,25 The highly reactive nature of borylenes necessitates stabilization as Lewis base adducts, usually with NHC or CAAC. The electronic characteristics of borylenes limit the selection of LA and LB for N2 activation, making it challenging to develop alternative systems with the same activation capacity but with greater stability and flexibility.
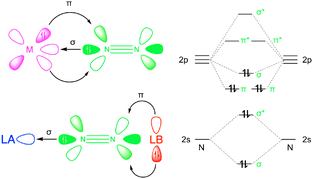 | ||
| Fig. 1 Transition metal (M-N2) vs. frustrated Lewis pairs (LA-N2-LB) complexes (left) and N2 valence molecular orbital diagram (right). | ||
In the realm of metal-free N2 activation, the use of common tricoordinate borane species presents a promising alternative, potentially broadening the range of LAs and LBs that can be utilized. Despite this potential, attempts to develop such systems are limited and still in the early stages. One of the pioneering efforts involved exploring the reactivity of diphenyldiazomethane (Ph2CNN) with B(C6F5)3,26 where the adduct formed can be viewed as a system where N2 is effectively trapped between a borane LA and a carbene LB. However, this adduct was found to be unstable, often releasing N2 rather than maintaining it in a trapped state. Other approaches have sought to capture and activate N2 through LA-N2 adducts. For instance, the (N2)BF3 species has been transiently generated, albeit under specific conditions of 170 K and 600 Torr,27 suggesting that metal-free N2 activation with tricoordinate boranes may be feasible. Consequently, the binding of N2 to Lewis acids has been a focus of several computational studies.
Given the low Lewis basicity of N2, it is necessary to use strong LAs or superacids. Computational studies have shown examples such as the use of carboranes,28 which have demonstrated successful N2 activation, although the initial LA-N2 adducts were not found to be thermodynamically stable. Additionally, computational studies on B(SiMe3)3 and B(CF3)3 have shown that these species can form stable adducts with N2, with stabilization energies around −15 kcal mol−1.29 The pyramidalization of the acidic center has been shown to significantly enhance Lewis acidity by lowering the reorganization energy and reducing the structural changes required during complex formation.30 This decrease in reorganization energy increases the effectiveness of the Lewis acid in accepting electron pairs from Lewis bases.31–35 Additionally, this characteristic contributes to the stability of Lewis acid–Lewis base (LA–LB) complexes, often resulting in higher dissociation energies for complexes involving pyramidal Lewis acids.36 Computational studies indicate that pyramidal boron-containing Lewis acids, such as 9-boratriptycene, exhibit significantly greater Lewis acidity compared to their planar analogs.37 For instance, pyramidal compounds like boraadamantane and alaadamantane are capable of forming donor–acceptor complexes with noble gases.38 Furthermore, Lewis acidity can be enhanced through fluorination, due to the electron-withdrawing properties of fluorine atoms,37,39 or via cationic effects.32–34 Despite these advances, finding common tricoordinate borane species that can form stable adducts with N2 remains a significant challenge.
Based on all this previous experience and challenges, the main goal of this work is to determine which are the key factors that determine and improve the dinitrogen capture and activation by LAs and LBs, respectively. In order to do so, different complexes of dinitrogen and various tricoordinate boron-based LAs and LBs from different families with diverse electronic and structural characteristics have been studied. Then, the nature of the interactions between LAs, LBs and dinitrogen was thoroughly analyzed by means of computational tools to understand and predict the binding patterns. These results will allow in the design of improved LA/LB and FLP combinations for further dinitrogen reduction to ammonia.
2 Computational details
All geometry optimizations and vibrational frequency calculations were carried out within density functional theory (DFT)40,41 using the Gaussian 16 program package.42 Specifically, geometries were optimized using the ωB97XD functional,43 combined with the 6-31+G(d) basis set.44 Harmonic vibrational frequencies were obtained by analytical differentiation of gradients, at the same level of theory, to identify if the characterized structures were minima in the potential energy surface. Such frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and the thermal (T = 298 K) vibrational corrections to the enthalpy (H) and the Gibbs free energy (G). These corrections are calculated in gas phase, while experiments would be carried out in solution. The simplification of our reaction model introduces entropy overestimation errors associated to the overestimation of the entrophy due to the neglect of temperature-dependent solvation effects. To partially overcome this overestimation, the Gibbs free energy correction proposed by Finkelstein and Janin is applied:45| Gcorr = H − T[Svib + 1/2(Strans + Srot)] | (1) |
This correction mitigates the overestimation of entropy changes, thus providing more accurate results for comparison with experimental values. The non-corrected Gibbs free energy values are available in the ESI.†
To refine the electronic energies single-point calculations with the 6-311++G(2df,2p) basis set46 were carried out in the optimized structures. The natural charges were computed by the natural bonding orbital (NBO) methodology.47–49 The computational approach used in this work has been validated against higher-level theoretical data from the literature29,32,50 (see Tables S1, S2, S3 and S4 in the ESI†).
2.1 Calculation of acidity and basicity
The electrophilicity of the Lewis acids has been estimated by several paramters: hydride ion affinity (HIA),51 global electrophilicity index (ω)52 and local electrophilicity index (ωB).53 The HIA is defined as the enthalpy change (ΔH) in the reaction between and acid (LA) and a hydride anion (H−) in gas phase:| LA + H− → [LA − H]− | (2) |
The HIA values have been calculated using the following isodesmic reaction:50
| LA + Me3Si − H → [LA − H]− + Me3Si+ | (3) |
| Me3Si − H → Me3Si+ + H− | (4) |
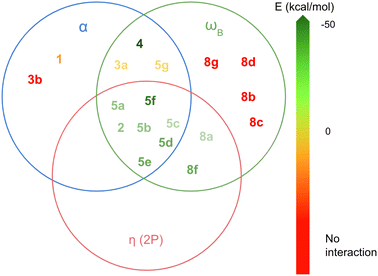
The larger the enthalpy (more negative or highest absolute value) the larger the acidity of the LA. The global electrophilicity index (ω) is a measure of the overall ability of a molecule to accept electrons from any electron-rich species (nucleophile), and is defined as:
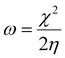 | (5) |
| ωB = ωfB+ | (6) |
| fB+ = QB(N + 1) − QB(N) = ΔQB | (7) |
The ω and ωB indexes are quantitative and base-independent metrics of Lewis acidity and provide the electroaccepting capacity of the LA, globally and locally (referred to the 2p orbital of B). Larger absolute values of these parameters should indicate a higher affinity towards binding the N2. The basicity is estimated with the empirical global nucleophilicity index (N), a relative scale based on the HOMO energy of the base (LB) referred to tetracyanoethylene (TCE). This compound shows the lowest HOMO in a large set of previously studied molecules54 and allows a positive scale of basicities:
| N = εH(LB) − εH(TCE) | (8) |
2.2 Analysis of bonding interactions
The nature of the interaction was analyzed using the Quantum Theory of Atoms in Molecules (QTAIM)55–58 and Electron Decomposition Analysis (EDA)59,60 methodologies. In QTAIM, the bond critical point (BCP) of a particular bond is characterized by the electron density (ρ), its Laplacian (∇2ρ) and the kinetic (V), potential (G) and total (H) electron energy density. A negative value of ∇2ρ denotes electron density concentration in the interatomic region, corresponding to covalent bonds. The condition |V| ≥ 2G also denotes a covalent interaction. A positive Laplacian indicates depletion of electron density, which is usually attributed to non-covalent interactions. If the Laplacian is positive but H is negative, the interaction can be classified as partially covalent. Lastly, if the density value is large enough (more than 0.03 a.u.) and H is negative, the interaction is partially covalent.The EDA method is based on Morokuma's energy partitioning scheme,61 and examines the instantaneous interaction energy (ΔEint) between two fragments (A and B) within a bond (A–B). This analysis is performed in the specific electronic reference state and with the frozen geometry of the AB complex. The interaction energy is typically divided into two main components, ΔEelstat and ΔEorb, along with an additional dispersion term (ΔEdisp). The term ΔEelstat represents the quasi-classical electrostatic interaction between the unperturbed charge distributions of the prepared atoms, which is generally attractive. Lastly, ΔEorb accounts for charge transfer and polarization effects within the system.
3 Results and discussion
The activation of N2 was studied through a two-step process: capturing nitrogen followed by its activation. Initially, the capture mechanism was investigated by examining interactions with individual Lewis acids (LAs) or Lewis bases (LBs). This was followed by an analysis of the activation process via the formation of LX-N2-LX complexes, where LX denotes either a LA or a LB. This study provides an in-depth analysis of the electroaccepting and electrodonating capacities of LAs and LBs, the molecular geometries of the formed complexes, their interaction energies, and the nature of the interactions involved.3.1 N2 capture by Lewis acids
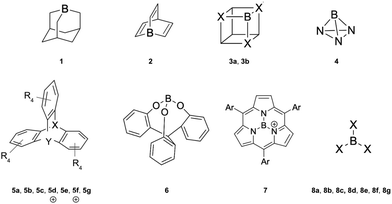
The capture of a small molecule like N2 can occur through interactions with either a Lewis acid or a Lewis base. When interacting with a Lewis acid, the process typically involves a σ-type interaction between the nitrogen lone pair and the empty orbital of the acid. In contrast, interaction with a Lewis base often involves π donation of electron density into the π* antibonding orbitals of N2. In this work, we have employed a set of 21 Lewis acids (see Fig. 2) and 6 Lewis bases (see Fig. 3) to explore their potential for capturing N2.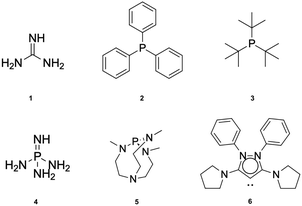 | ||
| Fig. 3 Lewis bases studied in this work: guanidine (1), triphenylphosphine (2), tris-t-butylphosphine (3), phosphazene (4), Verkade base (5) and cyclic bent allene (CBA) (6). | ||
Attempts to capture free N2 using Lewis bases have been unsuccessful, as none of the tested bases were able to form a stable LB-N2 complex. This outcome was anticipated because a Lewis base is unlikely to interact favorably with another Lewis base, such as N2. As a result, the proposed mechanism involving π donation from the Lewis base to the antibonding orbitals of N2 is inefficient for capturing N2. Therefore, the analysis of the N2 capture is performed only with Lewis acids.
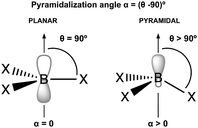
N2 is a very weak Lewis base due to its unique electronic structure. The lone pairs in N2 are located in sp hybrid orbitals, which are more localized and less available for interaction compared to sp3 hybrids or pure atomic p orbitals. Additionally, the high electronegativity of nitrogen further reduces the availability of these lone pairs for bonding with other molecules. The linear structure of N2 can also hinder effective overlap with the orbitals of other molecules approaching from different angles. Therefore, the acidity and electrophilicity of Lewis acids are crucial factors in achieving effective capture of N2. The acidity of the LAs represented in Fig. 2 is studied using the following parameters: hydride ion affinity (HIA), global (ω) and local (ωB) electrophilicity indexes and occupation number of the 2p empty orbital of boron atom (η(2p)). Note that, with the exception of two, all the acids under consideration are boron-based. The interaction of LAs with N2 is evaluated using the interaction (ΔHint, ΔGint) and deformation (Edef) energies, as well as the pyramidalization angle (α). The interaction energy is estimated as both the enthalpy (ΔH) and the Gibbs free energy (ΔG) change in the reaction between an acid and N2, while the deformation energy corresponds to the enthalpy change associated to the geometry rearrangement of the acid following the formation of the LA-N2 complex. The α angle reflects the initial geometrical configuration of the LA before interacting with N2 (see Fig. 4). The degree of pyramidalization can influence Edef, with higher values expected for planar LAs. Additionally, planar LAs may facilitate π-backbonding from substituents to the empty orbital at the acidic site (boron), thereby increasing orbital occupation (η(2p)) and reducing the capacity to accept electron density from N2.
| LA | ΔHint | ΔGint | Edef | HIA | ω | ωB | η(2p) | α | RBN | RNN | WBI1 | WBI2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Al 3p orbital.b Al–N bond distance.c Al–N bond index.d Ga 4p orbital.e Ga–N bond distance.f Ga–N bond index.g Cationic. | ||||||||||||
| 1 | 2.98 | 6.46 | 8.21 | 70.17 | 0.85 | −0.48 | 0.15 | 11.0 | 1.616 | 1.103 | 0.656 | 2.874 |
| 2 | −7.00 | −3.02 | 7.71 | 91.92 | 0.83 | −1.02 | 0.09 | 15.3 | 1.569 | 1.102 | 0.723 | 2.866 |
| 3a | −0.47 | 3.37 | 9.73 | 79.49 | 0.84 | −0.90 | 0.25 | 30.0 | 1.492 | 1.110 | 0.806 | 2.738 |
| 3b | — | — | — | 88.25 | 0.87 | −0.03 | 0.33 | 24.4 | — | — | — | — |
| 4 | −51.90 | −47.79 | 9.71 | 169.62 | 3.20 | −3.91 | 0.28 | 49.4 | 1.426 | 1.111 | 0.860 | 2.687 |
| 5a | −10.71 | −6.99 | 7.33 | 110.40 | 0.93 | −1.25 | 0.08 | 15.4 | 1.565 | 1.101 | 0.727 | 2.876 |
| 5b | −8.55 | −6.98 | 0.63 | 108.56 | 1.18 | −0.89 | 0.04a | 21.8 | 2.190b | 1.099 | 0.312c | 2.991 |
| 5c | −5.46 | −3.64 | −0.01 | 109.24 | 1.20 | −0.88 | 0.04d | 21.9 | 2.276e | 1.099 | 0.292f | 2.999 |
| 5dg | −15.36 | −11.48 | 7.23 | 200.70 | 3.71 | −5.22 | 0.07 | 13.8 | 1.589 | 1.099 | 0.706 | 2.908 |
| 5e | −17.78 | −13.52 | 7.93 | 146.12 | 1.76 | −2.45 | 0.08 | 16.6 | 1.589 | 1.098 | 0.714 | 2.906 |
| 5fg | −22.60 | −18.17 | 8.43 | 230.47 | 5.05 | −7.18 | 0.07 | 14.8 | 1.596 | 1.097 | 0.704 | 2.912 |
| 5g | −0.42 | 4.78 | 15.86 | 138.68 | 1.60 | −1.32 | 0.12 | 15.8 | 1.590 | 1.097 | 0.707 | 2.904 |
| 6 | — | — | — | 81.00 | 0.78 | 0.00 | 0.42 | 0.0 | — | — | — | — |
| 7 | — | — | — | 153.23 | 4.42 | 0.03 | 0.45 | 0.0 | — | — | — | — |
| 8a | −5.19 | −0.89 | 9.33 | 75.32 | 1.51 | −1.82 | 0.00 | 0.0 | 1.579 | 1.102 | 0.860 | 2.687 |
| 8b | — | — | — | 72.14 | 1.35 | −1.19 | 0.32 | 0.0 | — | — | — | — |
| 8c | — | — | — | 96.42 | 1.38 | −1.22 | — | 0.0 | — | — | — | — |
| 8d | — | — | — | 104.59 | 1.40 | −0.96 | — | 0.0 | — | — | — | — |
| 8e | — | — | — | 55.61 | 0.95 | −0.57 | 0.15 | 0.0 | — | — | — | — |
| 8f | −12.39 | −10.99 | 10.88 | 143.07 | 2.72 | −3.22 | 0.09 | 0.0 | 1.619 | 1.098 | 0.669 | 2.915 |
| 8g | — | — | — | 114.62 | 2.07 | −1.05 | 0.21 | 0.0 | — | — | — | — |
EWG groups enhance the acidity of LAs by withdrawing electron density from the boron atom through inductive effects.37 This trend is evident when comparing compounds such as 8a (R = H, −70.62 kcal mol−1), 8e (R = CH3, −50.92 kcal mol−1), and 8f (R = CF3, −138.38 kcal mol−1). The electronic nature of the substituents also impacts the occupation of the boron 2p orbital, with EDGs leading to higher values. For example, η(2p) is larger in 8e (0.15) compared to 8f (0.09). In general, η(2p) is influenced by the retrodonation ability of the ligands, which depends on both their electronic nature (EWG or EDG) and the geometry of the acids. For 8a, η(2p) is 0.00 due to hydrogen's inability to participate in retrodonation. Substituents with nitrogen, oxygen or halogens can exhibit dual characteristics, acting as EWGs via inductive effects (due to high electronegativity) and as EDGs through lone-pair conjugation. Nitrogen atoms directly bonded to boron increase both HIA and η(2p), as seen in compounds 3a and 3b. Notably, η(2p) values for BCl3 and BBr3 are not reported due to substantial retrodonation from halogen atoms, which leads to the formation of partial double bonds.
The importance of the local geometry at the acidic site lies in reducing the energy penalty associated with the geometric rearrangement during hydride ion binding.31,37,63 Specifically, non-planar geometries minimize this penalty while also hindering potential retrodonation from substituents to the boron 2p orbital, which would otherwise reduce acidity. This effect is evident when comparing the calculated HIA values for 8g (−109.93 kcal mol−1) and 5e (−141.42 kcal mol−1), where 5e can be considered a pyramidal analogue of 8g. The non-planar geometry of 5e leads to a higher HIA, as well as a lower η(2p) value (0.08 vs. 0.21), due to the orthogonal arrangement between the triptycene aryl p-orbitals and the boron 2p orbital, which prevents π-conjugation that would otherwise increase η(2p) (see Fig. S1 in the ESI†). The highest HIA values are observed for the cationic species 5f (−225.77 kcal mol−1) and 5d (−196.00 kcal mol−1), where the combined effects of EWGs, non-planar geometry and a cationic sulfur atom, which strongly enhances acidity through its electron-withdrawing character, are evident. Notably, this strong acidity occurs without affecting η(2p). Finally, compounds 3b, 6, 7, 8b–e and 8g were found to not bind to N2.
When examining the electrophilicity parameters, ω (global) and ωB (local), a trend similar to that observed for HIA is apparent. The highest ω values are found in pyramidal LAs with EWGs, specifically 5a–g, where ω ranges from 0.93 eV to 5.05 eV. Conversely, planar LAs with EDGs display the lowest ω values, such as 6 (0.78 eV) and 8e (1.51 eV). The largest ω is observed in cationic 5f (5.05 eV), while the smallest corresponds to 6 (0.78 eV), mirroring the HIA trends. Significant discrepancies between global (ω) and local (ωB) electrophilicity indexes are evident in compounds like 1 (ω = 0.85 eV, ωB = −0.48 eV), 3b (ω = 0.87 eV, ωB = −0.03 eV), 6 (ω = 0.78 eV, ωB = 0.00 eV) and 7 (ω = 4.42 eV, ωB = 0.03 eV). This difference arises because the global index reflects the overall electron-accepting capability of the entire molecule, while the local index specifically measures electrophilicity at the boron site. For example, compound 7 has a high global electrophilicity (ω = 4.42 eV), likely due to its cationic nature, but shows low boron-site electrophilicity (ωB = 0.03 eV), illustrating the non-uniform distribution of electrophilic character across the molecule.
Firstly, it is important to note that several acids (3b, 6, 7, 8b–e and 8g) form weakly bonded van der Waals complexes and will therefore not be considered in the discussion. These acids exhibit shared features, such as planarity, increased occupation of the boron 2p orbital and diminished electrophilicity, which contribute to their limited interaction with N2. The remaining LAs form thermodynamically favorable LA-N2 complexes through B–N interactions in almost all cases, with interaction energies (ΔGint) ranging from −0.89 kcal mol−1 for 8a to −47.79 kcal mol−1 for 4, except for compounds 1, 3a and 5g which show positive values. Compounds 5b and 5c exhibit unusually low deformation energies (0.63 kcal mol−1 and −0.01 kcal mol−1, respectively), which can be attributed to the highly electrostatic nature of the interaction, as will be discussed later. Compound 5g shows a relatively high positive deformation energy (15.86 kcal mol−1), likely due to steric hindrance between the nitrogen and the lone pairs of chlorine atoms, which hinders effective B–N coordination.
Regarding the geometries of the LA-N2 complexes, the B–N bond lengths range from 1.426 Å to 1.619 Å, with Wiberg bond indices (WBI1) between 0.706 and 0.860, indicating a weak single bond in most cases. However, 5b and 5c exhibit significantly longer B–N bond distances (2.190–2.276 Å) and lower WBI1 values (0.292–0.312), consistent with the electrostatic nature of the interaction. The N–N bond lengths range from 1.097 Å to 1.111 Å, closely matching the experimental bond distance of 1.0977 Å,64 suggesting that interaction with the LA causes only a slight weakening of the N2 bond. This minimal weakening is further reflected in the Wiberg bond indices for N2 (WBI2), which range from 2.687 (indicating a slightly weakened triple bond) to 2.999.
Fig. 5 illustrates the results of the PCA analysis and the corresponding correlation matrix for the acidity and electrophilicity parameters. In the PCA analysis (left panel), the five original parameters have been reduced to two principal components (PC1 and PC2). The orange dots represent LA-N2 complexes (labeled as 1), while the blue dots indicate LAs that do not bind to N2 (labeled as 0). The PCA results reveal that η(2p) and α are the most influential parameters. Specifically, a higher η(2p) value is associated with a reduced tendency to bind to N2, whereas a higher α value corresponds to an increased tendency to bind. HIA, ω and ωB exhibit lower vector magnitudes in the PCA, indicating their lesser relevance in the interaction with N2. Additionally it seems to be a connection between the size of the lone pair and the interaction with N2 in the boratriptycenes (5a–g) and compound 2 (see Fig. S2 and S3 in the ESI†). These findings are corroborated by the correlation matrix (right panel), which shows that the parameters most strongly correlated with interaction energy are η(2p) (−0.68) and α (0.54). ωB also shows a moderate correlation (−0.46), while ω and HIA have the weakest correlations (−0.36 and 0.12, respectively). Therefore, HIA and global electrophilicity indices alone are insufficient to fully explain the binding patterns with N2. Instead, the trends in LA-N2 interactions can be more accurately rationalized by focusing on α, ωB, and η(2p). Generally, non-planar compounds tend to have lower deformation energy (Edef) values (7.23–9.73 kcal mol−1) compared to planar compounds (9.33–10.88 kcal mol−1), and these non-planar compounds also prevent back-donation to the 2p orbital, resulting in lower η(2p) values. Additionally, higher ωB values are indicative of greater electroaccepting power.
 | ||
| Fig. 5 Left: results of the Principal Component Analysis (PCA). Right: correlation matrix of the acidity/electrophilicity parameters. | ||
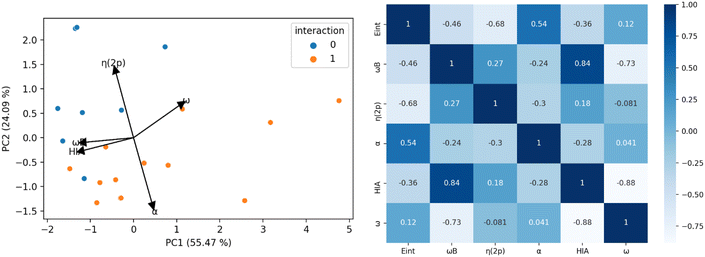
Acoording to this results, the LAs can be classified into three groups based on these three parameters. In Fig. 6, each circle represents LAs that meet the following criteria: α > 0°, ωB > 0.9 eV and η(2p) < 0.09. This classification highlights how different combinations of these parameters influence the exothermic nature of the LA-N2 binding. The group of LAs with the largest interaction energies is found at the intersection of the three circles. This intersection represents LAs that meet all the specified parameter thresholds. Notably, this group includes members of the 2 and 5 families, with the exception of 5g.
 | ||
| Fig. 6 Classification of the LAs in terms of the most important parameters in the formation of the LA-N2 complexes: α, ωB and η(2p). | ||
The next group of LAs includes those with α = 0°, but meeting the conditions for the other two parameters (intersection of the red and green circles): 8a and 8f. These LAs are planar, but their substituents attached to boron (H for 8a and CF3 for 8f) do not participate in back-donation of electron density, resulting in low η(2p) values. The third group comprises LAs that satisfy the criteria for α and ωB but not for η(2p) (intersection of the green and blue circles): 3a, 4, and 5g. Notably, 4 demonstrates a very high ωB value (−3.91 eV), which is likely due to its unusual geometry and sp2 hybridization of the boron atom, facilitating a strong interaction with N2 (ΔGint = −47.79 kcal mol−1). In contrast, 3a and 5g exhibit significantly lower ωB values (−0.90 eV and −1.32 eV, respectively). Additionally, 5g shows an unusually high deformation energy (15.86 kcal mol−1), probably due to steric hindrance between the Cl atoms and N2, resulting in a positive interaction energy (ΔGint = 4.78 kcal mol−1). The remaining LAs either meet only one of the specified parameters or none at all, leading them to either not bind with N2 or form complexes with positive ΔGint.
| LA | ΔEelstat | ΔEorb | ΔEdisp | ρ | ∇2ρ | V | G | H |
|---|---|---|---|---|---|---|---|---|
| a Cationic. | ||||||||
| 1 | −220.65 (43.6) | −271.35 (53.7) | −13.51 (2.7) | 0.093 | 0.611 | −0.243 | 0.198 | −0.045 |
| 2 | −212.60 (40.3) | −304.34 (57.7) | −10.33 (2.0) | 0.107 | 0.674 | −0.283 | 0.226 | −0.057 |
| 3a | −343.31 (42.6) | −451.46 (56.1) | −10.49 (1.3) | 0.135 | 0.775 | −0.369 | 0.281 | −0.088 |
| 4 | −214.42 (30.0) | −495.90 (69.3) | −5.45 (0.8) | 0.169 | 0.867 | −0.479 | 0.348 | −0.131 |
| 5a | −214.61 (39.7) | −308.14 (57.0) | −17.76 (3.3) | 0.109 | 0.680 | −0.288 | 0.229 | −0.059 |
| 5b | −71.78 (46.8) | −72.47 (47.3) | −8.99 (5.9) | 0.030 | 0.152 | −0.337 | 0.358 | 0.021 |
| 5c | −69.21 (50.1) | −59.95 (43.4) | −9.09 (6.6) | 0.041 | 0.144 | −0.507 | 0.433 | −0.073 |
| 5da | −700.39 (34.0) | −1341.12 (65.1) | −19.01 (0.9) | 0.104 | 0.615 | −0.267 | 0.210 | −0.057 |
| 5e | −197.69 (37.2) | −311.95 (58.7) | −22.03 (4.1) | 0.106 | 0.592 | −0.269 | 0.208 | −0.060 |
| 5fa | −637.70 (32.3) | −1315.59 (66.6) | −22.55 (1.1) | 0.107 | 0.553 | −0.264 | 0.201 | −0.063 |
| 5g | −239.46 (40.8) | −323.09 (55.1) | −24.26 (4.1) | 0.107 | 0.583 | −0.269 | 0.207 | −0.061 |
| 8a | −191.55 (38.8) | −297.98 (60.4) | −3.95 (0.8) | 0.103 | 0.688 | −0.279 | 0.225 | −0.053 |
| 8f | −191.02 (37.6) | −300.02 (59.1) | −16.89 (3.3) | 0.099 | 0.570 | −0.249 | 0.196 | −0.053 |
3.2 Activation of N2 with Lewis acids and bases
In the previous section, it was observed that several LAs can capture N2 through a donor–acceptor interaction between the nitrogen lone pair and the empty orbital of the acid. However, this interaction does not activate the strong N2 triple bond. To facilitate this activation, a second active species is required. For example, a Lewis base can interact with the LA-N2 complex to form a LA-N2-LB “push–pull” complex (see Fig. 7). In this system, the acid withdraws electron density from the N2 bond (“pull”), while the base donates electron density to the antibonding π* orbitals of N2 (“push”). This combined effect weakens the N2 triple bond in a manner similar to that observed with transition metals.15,66,67To explore the role of the bases in activating the N2 bond, the interaction of several LA-N2 complexes with the LBs shown in Fig. 3 was investigated. Initially, the basicity of these LBs was assessed using the global nucleophilicity index (N), as this property is expected to be critical for the activation process. The most basic LBs identified are LB-5 and LB-6, with nucleophilicity values of 4.80 eV and 4.79 eV, respectively (see Table 3). Compound LB-6 is a cyclic bent allene (CBA), a type of pyrazolin-4-ylidene with two nitrogens in the ring. This structure transmits a strong σ-donation capacity to the central carbon atom.68–70 LB-5 is Verkade's base, a triaminophosphine known for its exceptionally high basicity, which surpasses many traditional bases.71 LB-4 is a phosphazene (R2P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N type compound), whose basicity is significantly attributed to the resonance stabilization and the electronic characteristics of the P
N type compound), whose basicity is significantly attributed to the resonance stabilization and the electronic characteristics of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, which increases electron density over the nitrogen.72 Additionally, the well-known guanidine (LB-1), triphenylphosphine (LB-2), and tris-tert-butylphosphine (LB-3) were also included in the study for comparison.
N bond, which increases electron density over the nitrogen.72 Additionally, the well-known guanidine (LB-1), triphenylphosphine (LB-2), and tris-tert-butylphosphine (LB-3) were also included in the study for comparison.
| LB | LA-4 | LA-5a | LA-5b | LA-5da | LA-5e | LA-5fa | LA-8f | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | |
| a Cationic. | |||||||||||||||
| LB-1 | 2.64 | −29.04 | −21.97 | 26.32 | 32.33 | — | — | −3.83 | 2.22 | 6.83 | 13.85 | −21.10 | −14.15 | 7.09 | 10.87 |
| LB-2 | 3.48 | −40.25 | −34.05 | 16.81 | 22.50 | — | — | −15.02 | −9.35 | −2.70 | 3.11 | −32.57 | −25.93 | −2.29 | 1.15 |
| LB-3 | 3.74 | −50.06 | −43.35 | 6.78 | 13.93 | — | — | −22.40 | −15.37 | −11.73 | −4.02 | −38.17 | −29.91 | −13.51 | −8.36 |
| LB-4 | 4.00 | −41.75 | −33.29 | — | — | — | — | −23.30 | −14.76 | −10.57 | −13.9 | −39.31 | −32.99 | −13.66 | −6.24 |
| LB-5 | 4.80 | −57.65 | −50.52 | 0.15 | 6.11 | 9.65 | 16.81 | −32.68 | −25.24 | −20.05 | −13.06 | −44.45 | −35.65 | −13.66 | −9.33 |
| LB-6 | 4.79 | −80.50 | −72.71 | −25.52 | −17.71 | −18.94 | −12.39 | −62.46 | −54.64 | −49.27 | −40.97 | −83.77 | −75.04 | −49.23 | −42.80 |
| LA + LB + N2 → LA − N2 − LB | (9) |
LA-4, as well as the cationic acids LA-5d and LA-5f, form stable LA-N2-LB complexes with all bases, except for LA-5d with LB-1, which exhibits a slightly positive interaction energy (ΔGint = 2.22 kcal mol−1). Similarly, LA-5e and LA-8f form stable complexes with all LBs, except LB-1 and LB-2. On the other hand, LA-5a and LA-5b only form stable complexes with the exceptionally nucleophilic LB-6. The results show a correlation between the capacity of the LAs to capture N2 (ΔGint, Table 1) and the stability of the LA-N2-LB complexes (ΔGint, Table 3), with the most favorable LA-N2-LB interactions following this order (except for the exchange between LA-5e and cationic LA-5d): LA-4 > LA-5f > LA-5d > LA-5e > LA-8f > LA-5a > LA-5b. For the triptycenes (LA-5 family), these trends can be attributed to the ωB parameter, due to their identical geometric structure. Besides, for the same acid, the interaction energy appears to correlate with the nucleophilicity index (N), reflecting the influence of the base. Stronger bases yield more negative interaction energies. LB-6 shows significantly more negative interaction energies, notable greater than LB-5, despite having similar strength, even for LA-5a, which shows unfavorable interactions with the rest of the LBs and a stable complex is found with LB-6. This suggests that the remarkable stability provided by LB-6 is also linked to the nature of the interaction, as will be explained later. Thus, both the electronic characteristics of the LA and LB determine the feasibility and strength of the interaction.
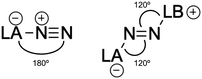
The degree of activation of the N2 molecule can also be deduced from the geometry of the complexes, especially from the N2 bond length. Upon reaction with a Lewis base, the LA-N2 complex undergoes a significant geometry rearrangement (see Fig. 7). Specifically, while the LA-N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond angles in LA-N2 complexes are nearly linear (close to 180°), the LA-N
N bond angles in LA-N2 complexes are nearly linear (close to 180°), the LA-N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and N
N and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-LB bond angles in the resulting LA-N2-LB complexes shift to around 120°, and can also be represented as the zwitterionic form LA−-N2-LB+. This structural transformation reflects the formation of a covalent bond between the Lewis base and N2.
N-LB bond angles in the resulting LA-N2-LB complexes shift to around 120°, and can also be represented as the zwitterionic form LA−-N2-LB+. This structural transformation reflects the formation of a covalent bond between the Lewis base and N2.
In Table 4 are collected selected bond distances and bond orders. The N–N bond length oscillates between 1.208–1.281 Å, notably longer than the bond length in the isolated molecule (1.10 Å). This feature is reflected in the reduction of the bond order from triple to double (WBI3, around 2.000), clearly indicating an effective bond activation. Furthermore, in some cases a weakened double bond is observed, as in the complexes formed by the acid LA-4 and bases LB-2, LB-3, LB-5 and LB-6 (WBI3 less than 1.800). The LA-N2 bond distances range between 1.415–1.563 Å and WBI1 values of 0.756–1.002, indicating a bonding interaction. For LA-5b, notably longer distances and lower WBI1 values are calculated, suggesting a weaker interaction with this acid. LB-N2 bond distances between 1.370–1.786 Å and WBI2 values between 0.790–1.111 are calculated, therefore, a bonding interaction is also expected.
| LA | LB | ΔGint | R1 | R2 | R3 | WBI1 | WBI2 | WBI3 |
|---|---|---|---|---|---|---|---|---|
| a Cationic. | ||||||||
| 4 | 1 | −21.97 | 1.445 | 1.442 | 1.236 | 0.906 | 0.970 | 1.812 |
| 2 | −34.05 | 1.415 | 1.715 | 1.281 | 1.002 | 0.933 | 1.630 | |
| 3 | −43.35 | 1.420 | 1.723 | 1.277 | 0.979 | 0.893 | 1.657 | |
| 4 | −33.29 | 1.468 | 1.455 | 1.231 | 0.850 | 0.986 | 1.873 | |
| 5 | −50.52 | 1.423 | 1.699 | 1.278 | 0.980 | 0.880 | 1.660 | |
| 6 | −72.71 | 1.450 | 1.416 | 1.261 | 0.906 | 1.069 | 1.768 | |
| 5a | 1 | 32.33 | 1.563 | 1.490 | 1.208 | 0.756 | 0.899 | 2.021 |
| 2 | 22.50 | 1.536 | 1.783 | 1.233 | 0.790 | 0.868 | 1.930 | |
| 3 | 13.93 | 1.535 | 1.764 | 1.245 | 0.792 | 0.854 | 1.903 | |
| 5 | 6.11 | 1.533 | 1.727 | 1.249 | 0.800 | 0.834 | 1.889 | |
| 6 | −17.71 | 1.536 | 1.416 | 1.249 | 0.804 | 1.066 | 1.868 | |
| 5b | 5 | 16.81 | 1.965 | 1.761 | 1.242 | 0.417 | 0.806 | 1.987 |
| 6 | −12.39 | 1.947 | 1.417 | 1.253 | 0.441 | 1.063 | 1.912 | |
| 5da | 1 | 2.22 | 1.553 | 1.436 | 1.219 | 0.782 | 0.976 | 1.975 |
| 2 | −9.35 | 1.544 | 1.781 | 1.233 | 0.793 | 0.845 | 1.963 | |
| 3 | −15.37 | 1.545 | 1.777 | 1.241 | 0.795 | 0.825 | 1.944 | |
| 4 | −14.76 | 1.545 | 1.436 | 1.224 | 0.796 | 1.007 | 1.939 | |
| 5 | −25.24 | 1.540 | 1.750 | 1.243 | 0.804 | 0.785 | 1.938 | |
| 6 | −54.64 | 1.536 | 1.410 | 1.250 | 0.816 | 1.072 | 1.872 | |
| 5e | 1 | 13.85 | 1.540 | 1.326 | 1.214 | 0.790 | 0.961 | 1.984 |
| 2 | 3.11 | 1.541 | 1.783 | 1.229 | 0.793 | 0.852 | 1.972 | |
| 3 | −4.02 | 1.547 | 1.778 | 1.234 | 0.797 | 0.845 | 1.956 | |
| 4 | −1.39 | 1.541 | 1.461 | 1.213 | 0.798 | 0.964 | 1.984 | |
| 5 | −13.06 | 1.541 | 1.740 | 1.240 | 0.800 | 0.805 | 1.944 | |
| 6 | −40.97 | 1.533 | 1.405 | 1.247 | 0.821 | 1.088 | 1.860 | |
| 5fa | 1 | −14.15 | 1.532 | 1.415 | 1.219 | 0.811 | 1.005 | 1.958 |
| 2 | −25.93 | 1.540 | 1.784 | 1.231 | 0.798 | 0.829 | 1.987 | |
| 3 | −29.91 | 1.548 | 1.786 | 1.234 | 0.813 | 0.823 | 1.972 | |
| 4 | −32.99 | 1.527 | 1.409 | 1.228 | 0.823 | 1.052 | 1.905 | |
| 5 | −35.65 | 1.538 | 1.783 | 1.235 | 0.816 | 0.756 | 1.972 | |
| 6 | −75.04 | 1.526 | 1.370 | 1.250 | 0.830 | 1.111 | 1.843 | |
| 8f | 1 | 10.87 | 1.555 | 1.439 | 1.215 | 0.783 | 0.967 | 1.984 |
| 2 | 1.15 | 1.548 | 1.774 | 1.231 | 0.792 | 0.859 | 1.968 | |
| 3 | −8.36 | 1.550 | 1.766 | 1.238 | 0.792 | 0.831 | 1.950 | |
| 4 | −6.24 | 1.547 | 1.412 | 1.228 | 0.794 | 1.035 | 1.918 | |
| 5 | −9.33 | 1.543 | 1.759 | 1.239 | 0.804 | 0.790 | 1.944 | |
| 6 | −42.80 | 1.544 | 1.410 | 1.246 | 0.816 | 1.081 | 1.877 | |
In summary, the results support the proposed model of N2 activation, where the Lewis acid plays a key role in capturing N2 and is primarily responsible of the thermodynamics of the process, stabilizing the complex and influencing the overall energy profile of the reaction. On the other hand, the Lewis base is primarily responsible for the kinetics of the activation, since the weakening of the bond directly impacts the rate at which the N2 molecule is activated. To investigate the kinetics of the Lewis base attack on the LA-N2 complex, we computed the transition states corresponding to this process in selected systems. Table 5 summarizes the calculated energies of the transition states. The Gibbs free energy values (ΔGTS) for the transition states of various Lewis bases attacking different LA-N2 complexes reveal significant variations in reactivity. Across all systems, LB-1 and LB-2 consistently show higher ΔGTS values, indicating less favorable transition states and slower reaction kinetics. For instance, with LA-4, the ΔGTS values are 28.70 kcal mol−1 for LB-1 and 23.51 kcal mol−1 for LB-2. In contrast, LB-3 and LB-5 exhibit lower values, suggesting more favorable interactions with the LA-N2 complexes. For example, LA-5d shows the lowest values, especially with LB-5 (0.75 kcal mol−1), highlighting its high reactivity in facilitating the Lewis base attack. On the other hand, LA-5a and LA-4 complexes present higher ΔGTS values, such as 39.86 kcal mol−1 for LA-5a with LB-1 and 28.70 kcal mol−1 for LA-4 with LB-1, indicating relatively less favorable transition states. These trends underscore the significant influence of both the Lewis base and the Lewis acid on the energetics of the transition states.
| LA-4 | LA-5a | LA-5da | LA-5e | LA-5fa | LA-8f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔHTS | ΔGTS | ΔHTS | ΔGTS | ΔHTS | ΔGTS | ΔHTS | ΔGTS | ΔHTS | ΔGTS | ΔHTS | ΔGTS | |
| a Cationic. | ||||||||||||
| LB-1 | 24.46 | 28.70 | 34.25 | 39.86 | 11.72 | 16.93 | 24.22 | 30.06 | 5.13 | 8.34 | 19.97 | 25.87 |
| LB-2 | 17.85 | 23.51 | 24.62 | 31.82 | 1.14 | 8.46 | 14.99 | 22.46 | −5.28 | 1.58 | 11.61 | 18.98 |
| LB-3 | 11.15 | 15.59 | 17.48 | 23.57 | −2.24 | 3.53 | 8.40 | 14.82 | −8.55 | −2.73 | 4.00 | 10.29 |
| LB-5 | 9.59 | 14.56 | 16.57 | 22.76 | −5.62 | 0.75 | 7.45 | 14.21 | −4.58 | 1.23 | 7.21 | 13.90 |
When only Lewis bases are involved (LB-N2-LB), the bond is significantly activated, resulting in bond orders corresponding to a single bond (ranging from 1.004 to 1.443). However, all LB-N2-LB complexes were found to be thermodynamically unstable. Therefore, as concluded in the previous subsection, both a Lewis acid and a Lewis base are necessary for effective activation of N2.
| LB | LA-4 | LA-5a | LA-5b | LA-5d | LA-5e | LA-5f | LA-8f | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | ΔHint | ΔGint | |
| LB-1 | −110.19 | −106.20 | −56.32 | −52.21 | — | — | −75.62 | −71.76 | −72.83 | −67.93 | −92.07 | −86.96 | −73.00 | −70.36 |
| LB-2 | −100.49 | −97.20 | −49.81 | −44.77 | — | — | −67.20 | −61.94 | −56.63 | −50.31 | −73.95 | −67.15 | −55.18 | −51.29 |
| LB-3 | −112.28 | −108.47 | −19.22 | −14.24 | — | — | −32.29 | −26.85 | −2.25 | 2.78 | −15.48 | −10.87 | −46.19 | −40.00 |
| LB-4 | −119.84 | −114.80 | −59.58 | −52.54 | — | — | −82.08 | −74.90 | −71.82 | −63.78 | −94.58 | −86.20 | −71.97 | −66.08 |
| LB-5 | −104.97 | −101.93 | −58.66 | −53.41 | −49.61 | −46.26 | −76.49 | −70.79 | −64.56 | −58.21 | −81.73 | −75.37 | −64.53 | −60.51 |
| LB-6 | −143.94 | −139.00 | −77.27 | −71.51 | −78.30 | −74.05 | −105.83 | −100.11 | −95.07 | −88.89 | −123.49 | −117.99 | −84.93 | −81.61 |
| LX | ΔGint | R1 | R2 | R3 | WBI1 | WBI2 | WBI3 |
|---|---|---|---|---|---|---|---|
| a Cationic. | |||||||
| LA-N2-LA | |||||||
| LA-4 | −97.72 | 1.389 | 1.389 | 1.131 | 0.959 | 0.959 | 2.202 |
| LA-5a | −15.63 | 1.530 | 1.530 | 1.105 | 0.753 | 0.753 | 2.643 |
| LA-5da | 27.49 | 1.562 | 1.562 | 1.102 | 0.716 | 0.716 | 2.710 |
| LA-5e | −25.09 | 1.568 | 1.568 | 1.096 | 0.713 | 0.713 | 2.744 |
| LA-5fa | 12.37 | 1.609 | 1.609 | 1.094 | 0.676 | 0.676 | 2.798 |
| LA-8f | −12.16 | 1.642 | 1.641 | 1.096 | 0.625 | 0.625 | 2.794 |
| LB-N2-LB | |||||||
| LB-1 | 132.45 | 1.363 | 1.363 | 1.417 | 1.117 | 1.117 | 1.055 |
| LB-2 | 53.41 | 1.588 | 1.588 | 1.457 | 1.197 | 1.197 | 1.015 |
| LB-3 | 44.17 | 1.596 | 1.596 | 1.456 | 1.146 | 1.146 | 1.011 |
| LB-4 | 131.81 | 1.620 | 1.514 | 1.402 | 0.969 | 0.965 | 1.063 |
| LB-5 | 29.08 | 1.576 | 1.576 | 1.465 | 1.214 | 1.214 | 1.004 |
| LB-6 | 38.57 | 1.349 | 1.399 | 1.303 | 1.071 | 1.306 | 1.443 |
Comparing these results with those available in the literature,36 which focus on boratriptycene-based Lewis acids and triphenylphosphine or tri-t-butylphosphine Lewis bases, our computations show a strong overall agreement with the reference data, reinforcing the reliability of the chosen methodology (see Table S13 in the ESI†). The B–P bond distances exhibit only minor deviations, with differences mostly within ∼0.02 Å, supporting the structural consistency between both approaches. Similarly, the computed enthalpy and Gibbs free energy values follow the expected trends, further validating the accuracy of our results. While some discrepancies are noted, particularly for LA-5e–LB-3, the overall qualitative agreement remains strong. These findings provide additional support to the assessment of LA–LB interactions and their potential classification as frustrated Lewis pairs (FLPs).
For the formation of an energetically favorable LA-N2-LB complex from an FLP, the LA–LB interaction energy must be lower than that of the LA-N2-LB complex. In all cases, the LA–LB interaction energies were higher than those of the LA-N2-LB complexes, with the exceptions of LA-5f-N2-LB-3 and LA-5e-N2-LB-3, where the LA–LB interaction is very weak (slightly positive). These findings suggest that 5e-N2-3 and 5f-N2-3 offer the most potential for further exploration due to their enhanced stability and frustrated interaction profile among the triptycene family.
In identifying the most promising compounds, it is crucial to acknowledge that many of the studied Lewis acids, especially triptycene-based derivatives, are not isolated in their free form. These acids are typically stabilized by complexation with Lewis bases. For instance, 9-boratriptycene is isolated in complexes with diethyl ether, pyridine or triphenylphosphine.32 Similarly, sulfur-containing cationic boratriptycenes require counterions such as [B(C6F5)4]− for stabilization.33 This highlights the importance of considering these stabilization factors when transitioning from computational predictions to experimental synthesis. Despite these challenges, the computational findings provide valuable insights into the design of novel Lewis acids with enhanced properties, guiding future experimental efforts.
4 Conclusions
The activation of N2 was studied by analyzing its interaction with a set of transition metal-free Lewis acids (LA) and bases (LB). The results indicate that the LAs are primarily responsible for capturing the nitrogen and ensuring the thermodynamic stability of the resulting complexes, whereas the LBs facilitate the activation of the N2 molecule by weakening its bond. To understand the capturing process, we first analyzed the electroaccepting properties of 21 LAs using various parameters, including hydride ion affinity (HIA), global (ω) and local (ωB) electrophilicity indexes and occupation of the 2p empty orbital of the boron atom (η(2p)). The electrophilicity is related to the capability of the Lewis acids to capture N2, reflecting the strength of the LA-N2 interaction. Principal Component Analysis (PCA) revealed that the trends in interaction energy can be explained by three key parameters: α (the pyramidalization angle), ωB and η(2p). Additionally, the local geometry of the boron atom, as indicated by the pyramidalization angle, plays a crucial role. A pyramidalized acidic site reduces the deformation energy associated with the rearrangement of the acid upon forming the LA-N2 complex and limits the potential retrodonation of electron density by the ligands, which would increase η(2p) and decrease the electrophilicity of the acid. In summary, LAs that meet the following criteria: ωB > 0.9 eV, η(2p) < 0.09 and α > 0° are effective in capturing N2 and forming thermodynamically stable LA-N2 complexes, specifically LA-2, LA(5a–5f) and LA-8f. EDA and QTAIM analyses indicate that the interaction is predominantly electrostatic, with a partial covalent character due to the donor–acceptor interaction between the nitrogen lone-pair and the empty 2p orbital.The LAs are responsible for capturing N2; however, analysis of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond shows that it remains unactivated, with bond lengths and orders comparable to those of the free N2 molecule. Effective activation of N2 requires the presence of a Lewis base. To explore this, six LBs were investigated to form LA-N2-LB complexes with the LAs demonstrating the highest N2 capture efficiency. Many of these complexes were found to be thermodynamically stable and led to a reduction in the nitrogen bond order from triple to double. The kinetics were explored by calculating the transition state energies for selected systems. The transition state analysis reveals that LB-3 and LB-5 show more favorable reactivity, as indicated by lower ΔGTS values, while LB-1 and LB-2 lead to higher values, suggesting slower reaction kinetics. Notably, the reaction of LB-5 with LA-5d displayed the lowest ΔGTS, highlighting its high reactivity. The extent of bond activation and the interaction energies of the LA-N2-LB complexes increased with the nucleophilicity of the LB. This reduction in nitrogen bond order is likely due to a more covalent nature of the interactions, as revealed by the QTAIM analysis.
N bond shows that it remains unactivated, with bond lengths and orders comparable to those of the free N2 molecule. Effective activation of N2 requires the presence of a Lewis base. To explore this, six LBs were investigated to form LA-N2-LB complexes with the LAs demonstrating the highest N2 capture efficiency. Many of these complexes were found to be thermodynamically stable and led to a reduction in the nitrogen bond order from triple to double. The kinetics were explored by calculating the transition state energies for selected systems. The transition state analysis reveals that LB-3 and LB-5 show more favorable reactivity, as indicated by lower ΔGTS values, while LB-1 and LB-2 lead to higher values, suggesting slower reaction kinetics. Notably, the reaction of LB-5 with LA-5d displayed the lowest ΔGTS, highlighting its high reactivity. The extent of bond activation and the interaction energies of the LA-N2-LB complexes increased with the nucleophilicity of the LB. This reduction in nitrogen bond order is likely due to a more covalent nature of the interactions, as revealed by the QTAIM analysis.
Among all the LA–LB pair combinations, only three exhibited characteristics typical of frustrated Lewis pairs (FLPs), showing moderate interaction energies and large LA–LB distances. Notably, the combinations of LA-5e and cationic LA-5f with LB-3 were the only complexes that demonstrated greater stability when binding N2 compared to the corresponding LA–LB complexes. Although the computational results suggest that the 5e-N2-3 and 5f-N2-3 complexes are promising candidates for effective nitrogen activation, experimental challenges may arise, since the triptycene-based acids have been only isolated as complexes with Lewis bases.30 Nonetheless, these systems stand out as potential candidates for further exploration in nitrogen activation.
Author contributions
The authors have contributed to this work as follows. Conceptualization: FR and JMM, data curation: XG, formal analysis: XG, funding acquisition: FR and JMM, investigation: XG, methodology: FR and JMM, project administration: FR and JMM, resources: FR and JMM, supervision: FR and JMM, visualization: XG, writing – original draft: XG and FR, writing – review and editing: XG, FR and JMM.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Technical and human support provided by IZO-SGI, SGIker (UPV/EHU, MICINN, GV/EJ, ERDF and ESF) is gratefully acknowledged for assistance and generous allocation of computational resources. We acknowledge support from grant PID2023-148587NB-I00, funded by MICIU/AEI/10.13039/501100011033 and by ERDF/EU, and from the María de Maeztu Excellence Unit CEX2023-001303-M funded by MCIN/AEI/10.13039/501100011033.References
- T. Liu, D. Zhai, B.-T. Guan and Z.-J. Shi, Nitrogen fixation and transformation with main group elements, Chem. Soc. Rev., 2022, 51, 3846–3861 RSC.
- H. Iriawan, S. Z. Andersen, X. Zhang, B. M. Comer, J. Barrio, P. Cheng, A. J. Medford, I. E. L. Stephens, I. Chorkendorff and Y. Shao-Horn, Methods for nitrogen activation by reduction and oxidation, Nat. Rev. Methods Primers, 2021, 1, 56 CrossRef CAS.
- T. Spatzal, M. Aksoyoglu, L. Zhang, S. L. A. Andrade, E. Schleicher, S. Weber, D. C. Rees and O. Einsle, Evidence for interstitial carbon in nitrogenase FeMo cofactor, Science, 2011, 334, 940–940 CrossRef CAS PubMed.
- C. Van Stappen, L. Decamps, G. E. I. Cutsail, R. Bjornsson, J. T. Henthorn, J. A. Birrell and S. DeBeer, The spectroscopy of nitrogenases, Chem. Rev., 2020, 120, 5005–5081 CrossRef CAS PubMed.
- B. M. Hoffman, D. Lukoyanov, Z.-Y. Yang, D. R. Dean and L. C. Seefeldt, Mechanism of nitrogen fixation by nitrogenase: The next stage, Chem. Rev., 2014, 114, 4041–4062 CrossRef CAS PubMed.
- V. Smil, Detonator of the population explosion, Nature, 1999, 400, 415–415 CrossRef CAS.
- D. R. MacFarlane, A. N. Simonov, T. M. Vu, S. Johnston and L. M. Azofra, Concluding remarks: Sustainable nitrogen activation - are we there yet?, Faraday Discuss., 2023, 243, 557–570 RSC.
- P. Wang, F. Chang, W. Gao, J. Guo, G. Wu, T. He and P. Chen, Breaking scaling relations to achieve low-temperature ammonia synthesis through LiH-mediated nitrogen transfer and hydrogenation, Nat. Chem., 2017, 9, 64–70 CrossRef CAS PubMed.
- Z. Kirova-Yordanova, Exergy analysis of industrial ammonia synthesis, Energy, 2004, 29, 2373–2384 CrossRef CAS.
- D. V. Yandulov and R. R. Schrock, Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum Center, Science, 2003, 301, 76–78 CrossRef CAS PubMed.
- K. Arashiba, Y. Miyake and Y. Nishibayashi, A molybdenum complex bearing PNP-type pincer ligands leads to the catalytic reduction of dinitrogen into ammonia, Nat. Chem., 2011, 3, 120–125 CrossRef CAS PubMed.
- Y. Ashida, K. Arashiba, K. Nakajima and Y. Nishibayashi, Molybdenum-catalysed ammonia production with samarium diiodide and alcohols or water, Nature, 2019, 568, 536–540 CrossRef CAS PubMed.
- J. S. Anderson, R. Jonathan and P. Jonas, , Catalytic conversion of nitrogen to ammonia by an iron model complex, Nature, 2013, 501, 84–87 CrossRef CAS PubMed.
- J. B. Geri, J. P. Shanahan and N. K. Szymczak, Testing the push-pull hypothesis: Lewis acid augmented N2 activation at iron, J. Am. Chem. Soc., 2017, 139, 5952–5956 CrossRef CAS PubMed.
- A. J. Ruddy, D. M. C. Ould, P. D. Newman and R. L. Melen, Push and pull: the potential role of boron in N2 activation, Dalton Trans., 2018, 47, 10377–10381 RSC.
- D. W. Stephan and G. Erker, Frustrated Lewis pair chemistry of carbon, nitrogen and sulfur oxides, Chem. Sci., 2014, 5, 2625–2641 RSC.
- R. Melen, A step closer to metal-free dinitrogen activation: A new chapter in the chemistry of frustrated Lewis pairs, Angew. Chem., Int. Ed., 2017, 57, 880–882 CrossRef PubMed.
- M.-A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Nitrogen fixation and reduction at boron, Science, 2018, 359, 896–900 Search PubMed.
- M.-A. Légaré, G. Bélanger-Chabot, M. Rang, R. Dewhurst, I. Krummenacher, R. Bertermann and H. Braunschweig, One-pot, room-temperature conversion of dinitrogen to ammonium chloride at a main-group element, Nat. Chem., 2020, 12, 1–5 CrossRef PubMed.
- M.-A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, The reductive coupling of dinitrogen, Science, 2019, 363, 1329–1332 Search PubMed.
- J. Zhu, Rational design of a Carbon-Boron frustrated Lewis pair for metal-free dinitrogen activation, Chem. – Asian J., 2019, 14, 1413–1417 Search PubMed.
- J. Zeng, S. Dong, C. Dai and J. Zhu, Predicting dinitrogen activation by five-electron boron-centered radicals, Inorg. Chem., 2022, 61, 2234–2241 CrossRef CAS PubMed.
- Q. Zhu, S. Chen, D. Chen, L. Lin, K. Xiao, L. Zhao, M. Solá and J. Zhu, The application of aromaticity and antiaromaticity to reaction mechanisms, Fundam. Res., 2023, 3, 926–938 CrossRef CAS PubMed.
- A. M. Rouf, C. Dai, F. Xu and J. Zhu, Dinitrogen activation by tricoordinated boron species. A systematic design, Adv. Theory Simul., 2020, 3, 2070006 CrossRef.
- A. M. Rouf, C. Dai, S. Dong and J. Zhu, Screening borane species for dinitrogen activation, Inorg. Chem., 2020, 59, 11770–11781 CrossRef CAS PubMed.
- C. Tang, Q. Liang, A. R. Jupp, T. C. Johnstone, R. C. Neu, D. Song, S. Grimme and D. W. Stephan, 1,1-Hydroboration and borane adduct of diphenyldiazomethane: A prelude to FLP-N2 chemistry?, Angew. Chem., Int. Ed., 2017, 56, 16588–16592 CrossRef CAS PubMed.
- K. C. Janda, L. S. Bernstein, J. M. Steed, S. E. Novick and W. Klemperer, Synthesis, microwave spectrum, and structure of ArBF3, BF3CO, and N2BF3, J. Am. Chem. Soc., 1978, 100, 8074–8079 CrossRef CAS.
- C. Dai, Y. Huang and J. Zhu, Predicting dinitrogen activation by carborane-based frustrated Lewis pairs, Organometallics, 2022, 41, 1480–1487 CrossRef CAS.
- T. Brinck and S. K. Sahoo, Anomalous π-backbonding in complexes between B(SiR3)3 and N2: catalytic activation and breaking of scaling relations, Phys. Chem. Chem. Phys., 2023, 25, 21006–21019 RSC.
- A. Y. Timoshkin, The Field of Main Group Lewis Acids and Lewis Superacids: Important Basics and Recent Developments, Chem. – Eur. J., 2024, 30, e202302457 CrossRef CAS PubMed.
- A. B. Saida, A. Chardon, A. Osi, N. Tumanov, J. Wouters, A. I. Adjieufack, B. Champagne and G. Berionni, Pushing the Lewis acidity boundaries of boron compounds with non-planar triarylboranes derived from triptycenes, Angew. Chem., Int. Ed., 2019, 58, 16889–16893 CrossRef PubMed.
- A. Chardon, A. Osi, D. Mahaut, T.-H. Doan, N. Tumanov, J. Wouters, L. Fusaro, B. Champagne and G. Berionni, Controlled generation of 9-boratriptycene by Lewis adduct dissociation: Accessing a non-planar triarylborane, Angew. Chem., Int. Ed., 2020, 59, 12402–12406 CrossRef CAS PubMed.
- A. Osi, D. Mahaut, N. Tumanov, L. Fusaro, J. Wouters, B. Champagne, A. Chardon and G. Berionni, Taming the Lewis superacidity of non-planar boranes: C-H bond activation and non-classical binding modes at boron, Angew. Chem., Int. Ed., 2022, 61, e202112342 CrossRef CAS PubMed.
- M. Henkelmann, A. Omlor, M. Bolte, V. Schünemann, H.-W. Lerner, J. Noga, P. Hrobárik and M. Wagner, A free boratriptycene-type Lewis superacid, Chem. Sci., 2022, 13, 1608–1617 RSC.
- S. E. Prey, J. Gilmer, S. V. Teichmann, L. Čić, M. Wenisch, M. Bolte, A. Virovets, H.-W. Lerner, F. Fantuzzi and M. Wagner, Synthesis, bridgehead functionalization, and photoisomerization of 9,10-diboratatriptycene dianions, Chem. Sci., 2023, 14, 5316–5322 RSC.
- A. V. Pomogaeva and A. Y. Timoshkin, Hydrogen Activation by Frustrated and Not So Frustrated Lewis Pairs Based on Pyramidal Lewis Acid 9-Boratriptycene: A Computational Study, ACS Omega, 2022, 7, 48493–48505 CrossRef CAS PubMed.
- L. A. Mück, A. Y. Timoshkin and G. Frenking, Design of Neutral Lewis Superacids of Group 13 Elements, Inorg. Chem., 2012, 51, 640–646 Search PubMed.
- L. A. Mück, A. Y. Timoshkin, M. v. Hopffgarten and G. Frenking, Donor Acceptor Complexes of Noble Gases, J. Am. Chem. Soc., 2009, 131, 3942–3949 CrossRef PubMed.
- A. Y. Timoshkin and G. Frenking, Gas-Phase Lewis Acidity of Perfluoroaryl Derivatives of Group 13 Elements, Organometallics, 2008, 27, 371–380 CrossRef CAS.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods, XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 10, 650–654 CrossRef.
- A. Finkelstein and J. Janin, The price of lost freedom: entropy of bimolecular complex formation, Protein Eng., 1989, 3, 1–3 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- A. E. Reed and F. Weinhold, Natural localized molecular orbitals, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- P. Erdmann and L. Greb, Multidimensional Lewis Acidity: A Consistent Data Set of Chloride, Hydride, Methide, Water and Ammonia Affinities for 183 p-Block Element Lewis Acids, ChemPhysChem, 2021, 22, 935–943 CrossRef CAS PubMed.
- R. Vianello and Z. B. Maksić, Hydride affinities of borane derivatives: Novel approach in determining the origin of Lewis acidity based on triadic formula, Inorg. Chem., 2005, 44, 1095–1102 CrossRef CAS PubMed.
- R. G. Parr, L. v. Szentpály and S. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- L. Domingo, M. Aurell, P. Pérez and R. Contreras, Quantitative Characterization of the Local Electrophilicity of Organic Molecules. Understanding the Regioselectivity on Diels-Alder Reactions, J. Phys. Chem. A, 2002, 106, 6871–6875 CrossRef CAS.
- L. R. Domingo, E. Chamorro and P. Pérez, Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study, J. Org. Chem., 2008, 73, 4615–4624 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, USA, 1994 Search PubMed.
- R. F. W. Bader, A bond path: a universal indicator of bonded interactions, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- S. Jenkins and I. Morrison, The chemical character of the intermolecular bonds of seven phases of ice as revealed by ab initio calculation of electron densities, Chem. Phys. Lett., 2000, 317, 97–102 CrossRef CAS.
- W. D. Arnold and E. Oldfield, The chemical nature of hydrogen bonding in proteins via NMR: J-couplings, chemical shifts, and AIM theory, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- T. Ziegler and A. Rauk, CO, CS, N2, PF3 and CNCH3 as σ donors and π acceptors. A theoretical study by the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1755–1759 CrossRef CAS.
- M. Van Hopffgarten and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 Search PubMed.
- K. J. Morokuma, Molecular orbital studies of hydrogen bonds. III. C=O⋯O-H hydrogen bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS.
- A. J. Kalita, S. S. Rohman, C. Kashyap, S. S. Ullah and A. K. Guha, Stabilization of neutral tricoordinate pyramidal boron: Enhanced Lewis acidity and profound reactivity, Polyhedron, 2019, 175, 114193 CrossRef.
- A. Chardon, A. Osi, D. Mahaut, A. B. Saida and G. Berionni, Non-planar boron Lewis acids taking the next step: development of tunable Lewis acids, Lewis superacids and bifunctional catalysts, Synlett, 2020, 1639–1648 CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Springer New York, NY, 1979 Search PubMed.
- M. Galdeano, F. Ruipérez and J. M. Matxain, Theoretical characterization of new frustrated lewis pairs for responsive materials, Polymers, 2021, 13, 1573 CrossRef CAS PubMed.
- A. Simonneau and M. Etienne, Enhanced activation of coordinated dinitrogen with p-block Lewis acids, Chem. – Eur. J., 2018, 24, 12458–12463 CrossRef CAS PubMed.
- A. Coffinet, A. Simonneau and D. Specklin, Push-pull activation of N2: coordination of Lewis acids to dinitrogen complexes, Encycl. Inorg. Bioinorg. Chem., 2020, 1–25 Search PubMed.
- V. Lavallo, C. A. Dyker, B. Donnadieu and G. Bertrand, Synthesis and ligand properties of stable five-membered-ring allenes containing only second-row elements, Angew. Chem., Int. Ed., 2008, 47, 5411–5414 CrossRef CAS PubMed.
- S. Klein, R. Tonner and G. Frenking, Carbodicarbenes and related divalent carbon(0) compounds, Chem. – Eur. J., 2010, 16, 10160–10170 CrossRef CAS PubMed.
- A. Peuronen, M. M. Hänninen and H. M. Tuononen, Pyrazolium- and 1,2-cyclopentadiene-based ligands as σ-donors: a theoretical study of electronic structure and bonding, Inorg. Chem., 2012, 51, 2577–2587 CrossRef CAS PubMed.
- J. G. Verkade and S. Urgaonkar, Proazaphosphatrane, Encyclopedia of Reagents for Organic Synthesis, 2012 Search PubMed.
- J. Saame, T. Rudima, S. Tshepelevitsh, A. Kütt, I. Kaljurand, T. Haljasorg, I. A. Koppel and I. Leito, Experimental basicities of superbasic phosphonium ylides and phosphazenes, J. Org. Chem., 2016, 81, 7349–7361 CrossRef CAS PubMed.
- S. Dong and J. Zhu, Predicting small molecule activation including catalytic hydrogenation of dinitrogen promoted by a dual Lewis acid, Chem. – Asian J., 2023, 18, e202200991 CrossRef CAS PubMed.
- S. Dong and J. Zhu, Predicting activation of small molecules including dinitrogen via a carbene with a σ0π2 electronic configuration, Inorg. Chem., 2024, 63, 15931–15940 CrossRef CAS PubMed.
- G. Bistoni, A. A. Auer and F. Neese, Understanding the role of dispersion in frustrated Lewis pairs and classical Lewis adducts: A domain-based local pair natural orbital coupled cluster study, Chem. – Eur. J., 2017, 23, 865–873 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt03425b |
| This journal is © The Royal Society of Chemistry 2025 |