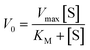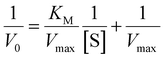Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cationic−anionic complexes of Cu(II) and Co(II) with N-scorpionate ligand – structure, spectroscopy, and catecholase activity†
Małgorzata
Zienkiewicz-Machnik
 *a,
Roman
Luboradzki
*a,
Roman
Luboradzki
 a,
Justyna
Mech-Piskorz
a,
Justyna
Mech-Piskorz
 a,
Gonzalo
Angulo
a,
Gonzalo
Angulo
 a,
Wojciech
Nogala
a,
Wojciech
Nogala
 a,
Tomasz
Ratajczyk
a,
Tomasz
Ratajczyk
 a,
Pavlo
Aleshkevych
a,
Pavlo
Aleshkevych
 b and
Adam
Kubas
b and
Adam
Kubas
 *a
*a
aInstitute of Physical Chemistry Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: mzienkiewiczmachnik@ichf.edu.pl; akubas@ichf.edu.pl
bInstitute of Physics Polish Academy of Sciences, Al. Lotników 32/46, 02-668 Warsaw, Poland
First published on 27th February 2025
Abstract
We report structural and physicochemical characterization supported by quantum chemical studies of two novel copper(II) [CuLCl]2[CuCl4] (1) and cobalt(II) [CoLCl][CoL′Cl3] (2) cationic−anionic complexes with N-scorpionate type ligand, N,N,N-tris(3,5-dimethylpyrazol-1-ylmethyl)amine (L), where L′ is 1-methylamine-3,5-dimethylpyrazole. The obtained complexes are the first reported examples of cationic−anionic coordination compounds tested for catecholase activity. Interestingly, only copper complex (1) shows catalytic activity in the oxidation of 3,5-di-tert-butylcatechol (3,5-DTBC), which turned out to be solvent dependent. Here, experimental UV-vis spectroscopy of 1 shows that essential features of the solid-state spectrum are maintained in DMSO and MeOH solvents. In contrast, the build-up of a new feature around 465 nm for 1 in CH3CN was noted, along with negligible activity. According to quantum chemical calculations, this feature could be attributed to ligand-to-metal excitations within the [CuCl4]2− fragment disturbed by adjacent [CuLCl]+ species. The band shifts to lower energies compared to solid-state measurements as the two charged fragments get closer due to Coulomb interactions. In DMSO, the solvent molecule serves as an inert ligand in a [CuLCl]+ fragment and blocks the catalytic center, disturbing the formation of the [catalyst–substrate] complex and decreasing activity, while in MeOH, the solvent effectively stabilizes [CuCl4]2−via a H-bond network and the free coordination site is accessible, thus allowing a substrate molecule to bind. The critical advantage of the investigated complexes, in the context of their possible catalytic activity, was the fact that their usage would not introduce any unnecessary counterions.
Introduction
The design of the ligand is the most crucial step for developing new metal complexes with novel structures and reactivity. The nature of the ligand and its architecture has a significant impact on the structure and properties of the resulting coordination compound. Hence, developing new heteroaromatic molecules with donor properties is an essential driving force in the progress of modern coordination chemistry.N-heteroaromatic alcohol – 1-hydroxymethyl-3,5-dimethylpyrazole (3,5-DMePzCH2OH) – is a unique molecule that plays various functions in coordination chemistry, especially as a proligand for complexes synthesized in situ1,2 and as a precursor for the synthesis of multipodal chelating ligands.3,4 Among pyrazole-based multidentate donors, N-scorpionate-type compounds represent a very important class of ligands. They appear to be chemical analogues of poly(pyrazole)borates, introduced in the late 1960s by Trofimenko.5 Scorpionate ligands obtained by Trofimenko and their C- and N-analogues, like tris-(pyrazolyl)amines, have a widespread application in coordination chemistry. They act as ligands in metal complexes with applications such as (i) structural and functional models of metal active sites in metalloenzymes,6,7 (ii) molecular wires3 and (iii) new selective catalysts or their precursors.3,8,9
The oxidation of organic substrates with molecular oxygen under mild conditions is of great interest for industrial and synthetic processes from both economic and environmental points of view.10,11 Therefore, the synthesis and investigation of metal complexes as functional models of metalloenzymes with oxidase or oxygenase activity are of great promise for developing new and efficient catalysts for oxidation reactions.
Catechol oxidases (EC 1.10.3.1) are natural examples of enzymes that utilize molecular oxygen as an oxidant. They are type 3 copper metalloproteins that contain a dinuclear Cu(II) active site, where metal ions are linked by an OH bridge and coordinated to the nitrogen atoms of three histidine molecules. This metalloenzyme catalyzes the oxidation of catechol to o-quinone, which plays an important role in the natural production of melanin. Therefore, the oxidation of catechol to quinone remains a subject of broad industrial and scientific interest. From an industrial point of view, quinones are intermediate products for synthesizing fine chemicals, perfumes, cosmetics, drugs, and adhesives, among others.12–15 At the same time, the study of chemical models that mimic oxidases has been developed to provide bases for understanding enzymatic activity and developing simple catalytic systems that exhibit promising catalytic activity under mild conditions. So far, none of the reported mono- or binuclear Cu(II) complexes has reached an activity close to the native enzyme. Hence, it is worth expanding the search for active biomimetics to include structurally different systems, such as cationic–anionic compounds. Such systems feature the same metallic centers in both fragments but with different ligands in the first coordination sphere. The critical advantage of cationic–anionic complexes, in the context of their possible catalytic activity or potential bio-related applications, is the fact that their usage would not introduce any unnecessary counterions.
Moreover, besides copper(II) complexes,16–18 other metal ions, such as manganese,19–21 iron,22,23 nickel24–26 and cobalt27–29 with structural diversity, have also shown catechol oxidation activity. Furthermore, a wide variety of cobalt(II) complexes are known to bind dioxygen and are, therefore, frequently studied as model compounds for natural oxygen carriers and for their use in O2 storage and organic synthesis due to their catalytic properties.30 In this respect, Co(II) complexes with N-donor ligands containing binding units suitable either for the coordination of a single metal ion or for assembling dimeric centers are particularly useful.31,32
Herein, we report the syntheses and structural and spectroscopic characterization supported by quantum chemical studies of two novel Cu(II) and Co(II) cationic–anionic complexes with an N-scorpionate type ligand. For the analyzed complexes, the N-scorpionate ligand coordinates to the metal centres in the same manner, leaving free coordination sites on the metal atom where the substrate can successfully bind, which is crucial for the catalytic activity. The obtained complexes are the first reported examples of cationic–anionic coordination compounds tested for catecholase activity and may represent a structurally new and interesting group of functional mimetics of catechol oxidase. Hence, in this paper, the reported studies constitute the analysis of the structure–activity relationship, where the experimental catecholase activity is well corroborated by quantum chemical calculations. Moreover, the solvent dependency of the catalytic activity was investigated for the obtained complexes.
Results and discussion
Molecular and crystal structure of [CuLCl]2[CuCl4] (1)
The molecular structure of 1 with the formula [CuLCl]2[CuCl4] crystallizes in a monoclinic space group I2/c (Table 1) and consists of two Cu(II) cationic units and one tetrachloro cuprate(II) anion. The crystal field of copper atoms in the cationic and anionic forms is different (Fig. 1). In each cation, the Cu(II) ion (Cu(2)) is bound by the four nitrogen atoms of the polypyrazole amine ligand (L): three from three different pyrazole rings and one tertiary amine. The coordination sphere is completed by one chloride and forms a square-pyramidal geometry. Interestingly, in 1, the coordination mode of the N-scorpionate ligand differs from that found in the literature in the copper(II) complex with the same ligand and chloride ions.33 In the case of [Cu(L0N4)Cl2] coordination compound,33 the polypyrazole ligand (L0N4) binds the Cu(II) ion as a tridentate ligand, with one arm remaining uncoordinated. Therefore, [Cu(L0N4)Cl2] pentacoordinate complex consists of a copper(II) ion surrounded by three nitrogen atoms from the organic ligand and two chloride ions.33 A similar tridentate coordination mode of the polypyrazole ligand was also observed for [Cu(L1N4)Cl2], where the L1 molecule contains –CH(CH3)2 substituents instead of methyl groups in the pyrazole rings of the N-scorpionate ligand.33 Despite the heteroaromatic ligand's different binding mode in the abovementioned literature complexes, the copper(II) coordination environment possesses square-pyramidal geometry, similar to complex 1. In the polyhedron of 1, two pyrazole N atoms (N(3) and N(5)) and the amine N(1) atom occupy the equatorial positions. The remaining site of the pyramid's equatorial plane is occupied by a chloride ion. One of the nitrogen atoms (N(7)) from the third N-scorpionate ligand arm occupies the axial position. In terms of the trigonality index for five-coordinated environments (τ) introduced by Addison et al.34 (τ = (α − β)/60°, where α and β are the largest angles (α ≥ β) around a five-coordinated metal centre, τ is 0 for a perfect square pyramid and 1 for a trigonal bipyramid), the coordination geometry in the analyzed complex can be described as a slightly distorted square pyramid (τ = 0.05). The axial Cu–N(7) bond length (2.3583(16) Å) is longer than the other Cu–N bond lengths from the equatorial plane of [CuLCl]+, and the Cu–Cl distance (2.2258(5) Å) is shorter than the Cu–N(7) distance (Table S1†). This atypical arrangement of the copper(II) coordination sphere in [CuLCl]+ results from the specific chemical structure of the N-scorpionate ligand.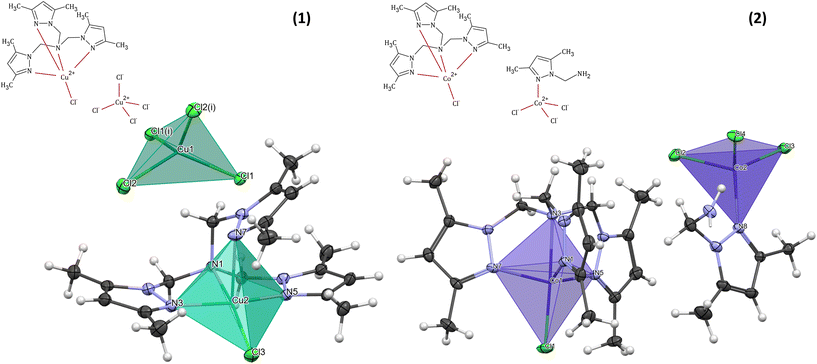 | ||
| Fig. 1 Schematic representations and coordination spheres with coordination polyhedra in cationic and anionic forms of [CuLCl]2[CuCl4] (1) and [CoLCl][CoL′Cl3] (2). | ||
| [CuLCl]2[CuCl4] (1) | [CoLCl][CoL′Cl3] (2) | |
|---|---|---|
| Empirical formula | C18H27N7Cu1.5Cl3 | C24H38N10Co2Cl4 |
| Moiety formula | 2(C18H27N7CuCl), CuCl4 | C18H27N7CoCl, C6H11N3CoCl3 |
| Formula weight | 543.12 | 726.313 |
| CCDC | 2212853† | 2213450† |
| Wavelength | 0.71073 | 0.71073 |
| Crystal system | Monoclinic | Triclinic |
| Space group | I2/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Unit cell dimensions | a = 13.5359(2) Å | a = 10.4702(4) Å |
| b = 11.7557(2) Å | b = 11.8660(5) Å | |
| c = 29.3343(5) Å | c = 12.9663(3) Å | |
| α = 101.057(2)° | α = 80.559(3)° | |
| β = 90° | β = 80.492(3)° | |
| γ = 90° | γ = 78.970(3)° | |
| Volume | 4581.14(13) Å3 | 1544.78(9) Å3 |
| Z | 8 | 2 |
| Density calc. | 1.575 g cm−3 | 1.561 g cm−3 |
| Absorption coefficient | 1.775 mm−1 | 1.454 mm−1 |
| F(000) | 2228 | 750.985 |
| Crystal | Green block | Dark-violet plate |
| Crystal size | 0.2 × 0.1 × 0.1 mm | 0.35 × 0.1 × 0.03 mm |
| Index ranges | −19 ≤ h ≤ 18, −16 ≤ k ≤ 16, −40 ≤ l ≤ 41 | −15 ≤ h ≤ 15, −17 ≤ k ≤ 17, −19 ≤ l ≤ 19 |
| Reflections collected (all/independent) | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406/6426 [Rint = 0.0562] 406/6426 [Rint = 0.0562] |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605/9225 [Rint = 0.0398] 605/9225 [Rint = 0.0398] |
| Absorption correction | Multi-scan | Multi-scan |
| Refinement method | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 |
| Restraints/parameters | 0/273 | 7/410 |
| Goodness-of-fit on F2 | 1.067 | 1.0486 |
| Final R indices [F2 > 2σ(F2)] | R 1 = 0.0314, wR2 = 0.0736 | R 1 = 0.0315, wR2 = 0.0766 |
| R indices (all data) | R 1 = 0.0389, wR2 = 0.0778 | R 1 = 0.0394, wR2 = 0.0817 |
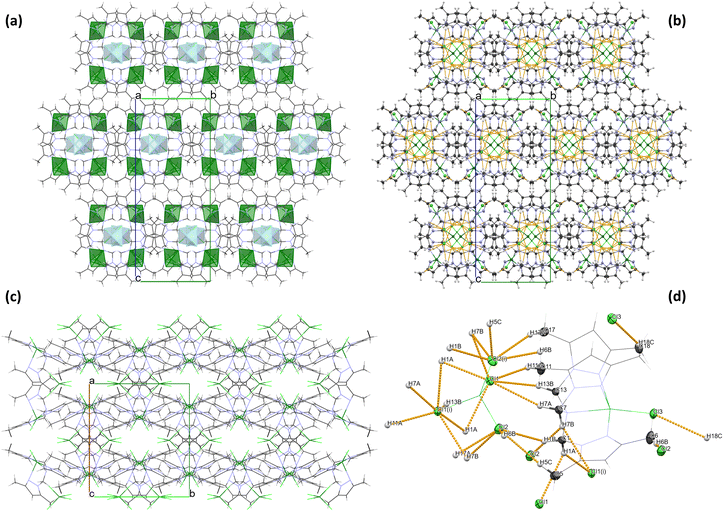
The geometry of the central metal ion (Cu(1)) in the anionic part is a slightly distorted tetrahedron occupied by four Cl− ions. Distortion in the geometry of the polyhedron is observed due to the formation of a hydrogen bond network between [CuCl4]2− species and methyl groups of the pyrazole ring in the heteroaromatic ligand (Table S2† and Fig. 2). A similar geometry of the [CuCl4]2− moiety was observed for other copper(II) cationic/anionic structures.35–37
Molecular and crystal structure of [CoLCl][CoL′Cl3] (2)
The [CoLCl][CoL′Cl3] (2) complex crystallizes in a triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Table 1). The molecular structure of 2 consists of a mononuclear complex cation [CoLCl]+ and [CoL′Cl3]− counter ion. A perspective view of the representative complex cation/anion pair is depicted in Fig. 1.
(Table 1). The molecular structure of 2 consists of a mononuclear complex cation [CoLCl]+ and [CoL′Cl3]− counter ion. A perspective view of the representative complex cation/anion pair is depicted in Fig. 1.
A coordination sphere of the cobalt(II) centre (Co(1)) in the cationic form [CoLCl]+ is pentacoordinated by four N-donor atoms of the tripodal amine (L) and one chloride ion. The Co(1) ion possesses an almost ideal tripodal bipyramidal arrangement ({CoN4Cl} chromophore) with a τ value of 1.34 The Co(1) atom is displaced by 0.496 Å from the geometric middle point of the {CoN4Cl} trigonal bipyramid, and it is shifted in the coordinated chloride Cl(1) direction. A similar finding was observed in the case of other cobalt(II) complexes with the same cationic form as described here but with a zinc coordination anion38 and for the complex with the [CdI4]2− anionic form,39 as well as for [Co(L)Cl]ClO4.40 Moreover, like in the aforementioned [CoClL1][ZnI3L2],38 [CoClL1]2[CdI4]39 and [Co(L)Cl]ClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 complexes, in compound 2, the axial Co–Namine bond length is longer than the other Co–N bond lengths from the equatorial plane of [CoLCl]+ and the Co–Cl distance (2.2580(4) Å) is shorter than the Co–Namine length (2.3053(12) Å) (Table S3†). This atypical arrangement of the cobalt(II) coordination sphere in [CoLCl]+ results from the specific chemical structure of the heteroaromatic ligand, i.e. tris(1-(3,5-dimethylpyrazolyl)-methyl)amine (L).38,39
40 complexes, in compound 2, the axial Co–Namine bond length is longer than the other Co–N bond lengths from the equatorial plane of [CoLCl]+ and the Co–Cl distance (2.2580(4) Å) is shorter than the Co–Namine length (2.3053(12) Å) (Table S3†). This atypical arrangement of the cobalt(II) coordination sphere in [CoLCl]+ results from the specific chemical structure of the heteroaromatic ligand, i.e. tris(1-(3,5-dimethylpyrazolyl)-methyl)amine (L).38,39
The [CoL′Cl3]− counter ion contains a tetracoordinated cobalt(II) centre (Co(2)) bonded to the pyrazole derivative (1-methylamine-3,5-dimethylpyrazole, L′) through the nitrogen atom from the pyrazole ring (N(8)) and three chlorides. The coordination environment of Co(2), with the {CoNCl3} chromophore, shows a slightly distorted tetrahedral geometry (Fig. 1 and Table S3†).
Analysis of the crystal packing of 2 revealed the absence of strong hydrogen bonds in the structure. However, the crystal structure analysis shows that the organic ligand (tertiary amine – L) structure promotes the formation of intramolecular C–H⋯Cl interactions of the methyl groups C(4), C(10) and C(16) in the [CoLCl]+ form (Table S4† and Fig. 3). A similar situation was described previously in the literature for other Co(II) complexes with the same polypyrazole ligand.38,39 Moreover, in the [CoL′Cl3]− form, intramolecular N–H⋯Cl non-covalent contacts with the graph set descriptor of S(7)41,42 (Table S4† and Fig. 3) are observed. Furthermore, the crystal structure of 2 is stabilized by the intermolecular C–H⋯Cl interactions between cationic and anionic fragments and the π⋯π stacking between the pyrazole rings of the neighbouring [CoLCl]+ cations (Table S4† and Fig. 3).
Hirshfeld surface analysis for complexes 1 and 2
The 2D fingerprints of all interactions around the asymmetric unit of 1 and 2 are shown in Fig. S1 and S2,† respectively. It quantifies the number of inter-contacts the molecule makes in the crystal lattice. The relative contribution percentages of the major inter-contacts existing within the crystal packing of complexes 1 and 2 are given in Fig. S1 and S2,† respectively.It is revealed that the H⋯H non-covalent interactions have made the most significant contribution to the HS for both complexes (49.3% for 1 and 55.8% for 2), and it appears to be the most important contributor to the crystal structure packing of 1 and 2. They are represented by a cluster of points accumulated at the diagonal of the graph with di = de ∼1.1 Å in 1 and di = de ∼0.7 Å in 2 and covering the most area in the total fingerprint plot (Fig. S1 and S2†). For both compounds, the H⋯Cl non-covalent contacts are the second most important factor, contributing 36% in 1 and 25.1% in 2 to the total HS, which is in agreement with the findings revealed from the X-ray analysis of crystal packing (Fig. 2 (1) and Fig. 3 (2)). In the complexes, the H⋯Cl inter-contacts are represented as two symmetrical wings located on the two sides of the diagonal of the 2D graph (Fig. S1 and S2†). Moreover, HS analysis confirmed the presence of C⋯C interactions in the crystal structure of 2 with a contribution of about 1.1% to the HS, which are related to the π⋯π interactions of pyrazole rings, as was presented by experimental X-ray data (Fig. 3). Furthermore, the attractive C⋯H and N⋯H interatomic interactions are depicted in the total fingerprint plot of 1 and 2 as two symmetrical wings and contribute significantly to the stabilization of the supramolecular structure by 7 and 4.8% for 1 and 8.9 and 5.8% for 2 of the total interactions, respectively (Fig. S1 and Fig. S2†).
FTIR spectra
The FTIR spectra of complexes 1 and 2 were recorded in the 450–4000 cm−1 range (Fig. S3†). Since the synthesis of the complexes was based on the one-pot, two-step synthetic procedure, without isolation of the ligand, the spectra of 1 and 2 were compared with the spectrum of the precursor (1-hydroxymethyl-3,5-dimethyl pyrazole). The IR analysis confirmed that condensation occurred in both cases, and a new polypyrazole ligand (L) was formed. This is associated with the disappearance of the OH stretching band at 3122 cm−1. Additionally, a new band at 1133 cm−1 for 1 and 1127 cm−1 for 2 appeared related to the ν(C–N) stretching vibrations of the tertiary amine (L) (Fig. S3†).38,39,43,44 Furthermore, new peaks at 3332, 700 and 692 cm−1 are observed in the spectrum of 2, which are related to the primary amine formation (L′) and the presence of NH stretching vibrations.45,461H NMR spectroscopy
1H NMR spectra for complexes 1 and 2 are presented in Fig. S4.† All observed signals were characterized by strong broadening resulting from the presence of a paramagnetic center within the prepared complexes. While all signals associated with the investigated complexes 1 and 2 were broadened significantly, the solvent signals were only slightly broadened. This suggests that the H atoms with significantly broadened 1H NMR resonances are within the same molecular framework as paramagnetic ions (i.e. in the first coordination sphere of the complex), while the solvent is not within this framework, and its 1H NMR signal is not broadened significantly.Electronic structure calculations
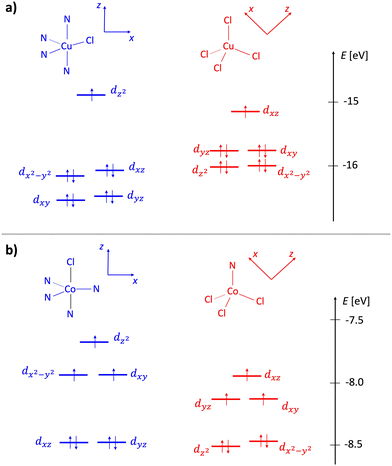
Complexes 1 and 2 were subjected to electronic structure calculations as described in the Experimental section. Molecular orbital diagrams of cationic and anionic fragments of both species are shown in Fig. 4. Cationic fragments feature crystal field splitting characteristic of a distorted trigonal bipyramid, while anionic fragments show patterns typical of distorted tetrahedral arrangements. For both systems, the energy difference between states for which metallic centers were coupled either in the ferromagnetic (high-spin) or the antiferromagnetic (low-spin) state was estimated with a multireference approach. We found the difference to be exactly 0.0 cm−1 for cobalt dimeric complex 2 and −0.1 cm−1 for copper complex 1 (a more stable low-spin state). This means that magnetic interactions between near neighbors are negligible for 2 and very weakly antiferromagnetic for 1. Considering the magnitude of these interactions, we assumed ferromagnetic coupling in all subsequent calculations. The obtained ground-state electronic structures served as a basis for subsequent calculation and interpretation of UV-vis and electrochemical data.Electronic spectra
For complexes 1 and 2, electronic spectra were recorded in the 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range, both in solution (MeOH, CH3CN and DMSO) and the solid state (Table 2 and Fig. S5†). The latter are compared with the calculated values in Fig. 5.
000 cm−1 range, both in solution (MeOH, CH3CN and DMSO) and the solid state (Table 2 and Fig. S5†). The latter are compared with the calculated values in Fig. 5.
| Complex | Method (solvent) | Colour | d–d (cm−1) |
|---|---|---|---|
| 1 | DRS | Green | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090, 15 090, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
| Abs (MeOH) | Green | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020, 14 020, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 837 |
|
| Abs (CH3CN) | Green | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165, 13 165, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625 |
|
| Abs (DMSO) | Green | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050, 13 050, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 514 |
|
| 2 | DRS | Dark blue | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225, 14 225, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577, 15 577, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552, 16 552, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, 19 610, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 120 |
| Abs (MeOH) | Purple | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860, 15 860, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950, 16 950, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722, 19 722, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
|
| Abs (CH3CN) | Blue | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905, 14 905, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 15 750, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798, 16 798, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835, 19 835, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
|
| Abs (DMSO) | Blue | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905, 14 905, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705, 15 705, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873, 16 873, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, 19 610, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 305 |
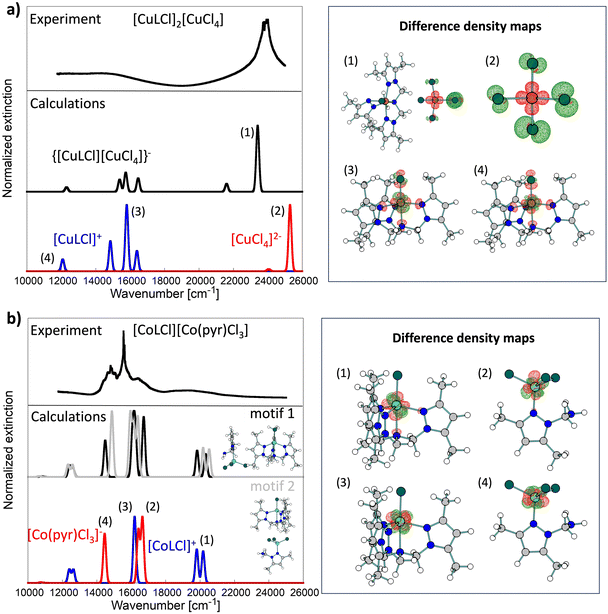
Experimental UV-vis spectroscopy of 1 shows that essential features of the solid-state spectrum are maintained in DMSO and MeOH solvents (Table 2 and Fig. S5†). In contrast, the build-up of a new feature around 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 cm−1 (465 nm) for 1 in CH3CN was noted. Using quantum chemical calculations, we found that this feature could be attributed to ligand-to-metal charge transfer transitions in the [CuCl4]2− fragment as the two charged fragments get closer due to Coulomb interactions. This band is highly affected by the presence of a positively charged fragment (see bands (1) and (2) in Fig. 5a).
505 cm−1 (465 nm) for 1 in CH3CN was noted. Using quantum chemical calculations, we found that this feature could be attributed to ligand-to-metal charge transfer transitions in the [CuCl4]2− fragment as the two charged fragments get closer due to Coulomb interactions. This band is highly affected by the presence of a positively charged fragment (see bands (1) and (2) in Fig. 5a).
In the case of copper(II) complexes with tripodal tetradentate ligands, the coordination sphere around the copper(II) centre can possess a square-pyramidal or a trigonal–bipyramidal coordination mode, with the d-d absorption bands shifted to higher energy for the compounds with a square-pyramidal configuration compared to those with a trigonal–bipyramidal geometry.33,47,48
The d–d transition bands in pentacoordinated [CuLCl]+ cationic complex 1 (τ = 0.05) are observed at around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 and 14
020 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837cm−1 in absorption spectra (MeOH) and at 12
837cm−1 in absorption spectra (MeOH) and at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 and 15
090 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cm−1 in the reflectance spectra (Table 2 and Fig. S5†). These bands are associated with the dxz ≈ dyz → dz2 transition accompanied by the dx2−y → dz2 transition. The band's positions correspond well with those in the solid state and are in agreement with those obtained from the calculations (Fig. 5). Similar spectral patterns for solid and solution measurements indicate almost the same geometries around the Cu(II) centers.49
650 cm−1 in the reflectance spectra (Table 2 and Fig. S5†). These bands are associated with the dxz ≈ dyz → dz2 transition accompanied by the dx2−y → dz2 transition. The band's positions correspond well with those in the solid state and are in agreement with those obtained from the calculations (Fig. 5). Similar spectral patterns for solid and solution measurements indicate almost the same geometries around the Cu(II) centers.49
Interestingly, the spectrum for the MeOH solution of 1 recorded after 4 months shows some changes compared to the spectrum for the “fresh” MeOH solution. The bands shift to lower energies (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 and 10
990 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 cm−1), which can be associated with higher distortion of the coordination sphere geometry around the Cu(II) ion in [CuLCl]+. Moreover, an additional maximum can be observed in the spectrum at 14
152 cm−1), which can be associated with higher distortion of the coordination sphere geometry around the Cu(II) ion in [CuLCl]+. Moreover, an additional maximum can be observed in the spectrum at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 cm−1, which can be attributed to the coordination of the MeOH molecules in [CuCl4]2− and the formation of hexacoordinated [CuCl4(MeOH)2]2− species.50,51 Changes in the spectrum are also related to the solution colour change from green to blue-greenish.
860 cm−1, which can be attributed to the coordination of the MeOH molecules in [CuCl4]2− and the formation of hexacoordinated [CuCl4(MeOH)2]2− species.50,51 Changes in the spectrum are also related to the solution colour change from green to blue-greenish.
The analysis of the electronic spectra of 2 in the d–d range supports (except in methanol) the Co(II) coordination sphere geometry determined by X-ray diffraction. The spectra in CH3CN and DMSO remain almost unchanged compared to the spectrum for the solid state of 2 (Table 2 and Fig. S5†). Nevertheless, the UV-vis spectrum in MeOH revealed some differences. The spectrum of 2 in the solid state displays quite well-separated peaks at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225, 14
225, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577, 15
577, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552, 16
552, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, and 19
610, and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 cm−1. Comparing the obtained spectrum with the one found in the literature for another cationic-anionic cobalt(II) complex [CoCl(L)][CoCl4]52 and with the calculated one, it is clear that peaks with a maximum at 12
120 cm−1. Comparing the obtained spectrum with the one found in the literature for another cationic-anionic cobalt(II) complex [CoCl(L)][CoCl4]52 and with the calculated one, it is clear that peaks with a maximum at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225, 16
225, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, and 19
610, and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 cm−1 correspond to the characteristic 4A2′(F) → 4E′′(P), 4A2′(F) → 4A2′(P) and 4A2′(F) → 4E′(F) transitions of a high-spin pentacoordinated Co(II) complex with a trigonal–bipyramidal geometry.38,39,52–55 Moreover, the spectrum of 2 shows these bands overlaid with the diagnostic peaks at 14
120 cm−1 correspond to the characteristic 4A2′(F) → 4E′′(P), 4A2′(F) → 4A2′(P) and 4A2′(F) → 4E′(F) transitions of a high-spin pentacoordinated Co(II) complex with a trigonal–bipyramidal geometry.38,39,52–55 Moreover, the spectrum of 2 shows these bands overlaid with the diagnostic peaks at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 and 15
577 and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552 cm−1 for the 4A2 → 4T1(P) transition of the [CoL′Cl3]− anion.52,55
552 cm−1 for the 4A2 → 4T1(P) transition of the [CoL′Cl3]− anion.52,55
Our calculations (see Fig. 5) show that cationic and anionic signals mix heavily in the UV-vis spectrum of 2, which was not the case for 1, where the low-energy spectrum was almost exclusively due to the cationic fragment, while the high-energy part (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) was due to the electronic transition in the anionic fragment. All key transitions in 2 have quite local characteristics (Co-centered). Interestingly, the spectrum of the dimeric [CoLCl][CoL′Cl3] depends heavily on the dimeric model used in calculations (derived from the crystal structure). Here, we studied two motifs shown in Fig. 5b. We postulate that both contribute to the experimental solid-state spectrum and, therefore, are the cause of rich and broad experimental signals.
000 cm−1) was due to the electronic transition in the anionic fragment. All key transitions in 2 have quite local characteristics (Co-centered). Interestingly, the spectrum of the dimeric [CoLCl][CoL′Cl3] depends heavily on the dimeric model used in calculations (derived from the crystal structure). Here, we studied two motifs shown in Fig. 5b. We postulate that both contribute to the experimental solid-state spectrum and, therefore, are the cause of rich and broad experimental signals.
The spectrum of 2 recorded in MeOH solution shows only three prominent peaks at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860, 16
860, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722 (with a shoulder at 15
722 (with a shoulder at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 cm−1) and 19
950 cm−1) and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 cm−1 (Fig. S5†). The changes in the spectrum in MeOH and the disappearance of high intensity peaks in the range of around 12
305 cm−1 (Fig. S5†). The changes in the spectrum in MeOH and the disappearance of high intensity peaks in the range of around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500–16
500–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 cm−1, characteristic of the tetrahedral geometry of Co(II) ions, could be associated with the coordination of MeOH molecules and octahedral geometry formation in the anionic Co(II) complex – [CoL′Cl3(MeOH)2]−. Changes in the geometry of the Co(II) metal centre in the anionic form are consistent with the purple colour of the spectroscopically analyzed solution of 2 in MeOH, while the crystals of 2 are dark blue.56
650 cm−1, characteristic of the tetrahedral geometry of Co(II) ions, could be associated with the coordination of MeOH molecules and octahedral geometry formation in the anionic Co(II) complex – [CoL′Cl3(MeOH)2]−. Changes in the geometry of the Co(II) metal centre in the anionic form are consistent with the purple colour of the spectroscopically analyzed solution of 2 in MeOH, while the crystals of 2 are dark blue.56
Similarly, as in the case of Cu(II) complex 1, the measurements in the UV-vis region for methanol solution of 2 were performed again after 4 months. No changes in the obtained spectrum support the statement on the presence of thermodynamically more stable [CoL′Cl3(MeOH)2]− octahedral species.
Electron paramagnetic resonance spectra
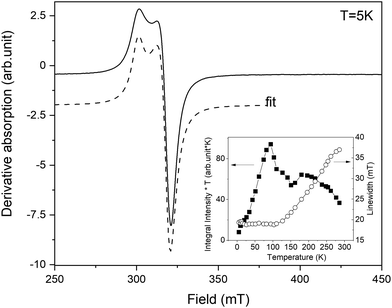
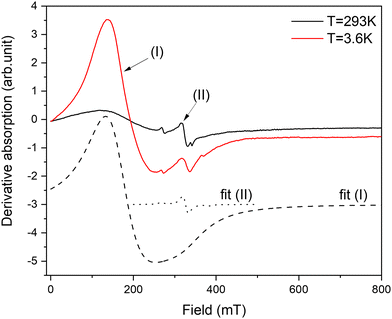
The resonance spectrum of powdered complex 1 is shown in Fig. 6. The average spectrum represents a typical Cu(II) pattern in the local environment with pronounced axial distortion. The dashed line shows the best fit to the experimentally calculated spectrum assuming the axial g-tensor with the following main values: gx = gy = 2.064 and gz = 2.29. In fact, the averaged spectrum of the powdered sample contains not one but two different crystallographic positions of Cu. This is clearly seen on the spectrum acquired on a single crystal of complex 1 (Fig. S6†). The g-tensors of both positions are similar, but the intensity is very different. While the resonance spectrum comes from paramagnetic Cu(II), the intensity of absorption does not follow Curie-like (1/T) temperature dependence. The integral intensity is proportional to magnetic susceptibility, and deviation from pure paramagnetic behaviour is better visible in the temperature evolution of the integral intensity multiplied by temperature (I × T). As is seen (inset in Fig. 6), I*T is not constant but shows nonlinear dependence on temperature. At first, the I*T value increases as the temperature increases from liquid helium up to 100 K and then it almost steadily decreases up to room temperature. The low temperature decreases cannot be explained by crystal field effects because the 3d9 electronic configuration of Cu(II) does not have ZFS. It could be explained by the presence of Cu–Cu antiferromagnetic (AFM) interactions at low temperatures. Then, at higher temperatures (T > 100 K), the AFM interaction becomes obscured by the dipolar Cu–Cu interactions, which manifests as a broadening of the resonance line.The resonance spectra of powdered complex 2 are shown in Fig. 7. The spectrum consists of two different patterns. The first one, labelled as (I) in Fig. 7, represents intensive broad absorption in the magnetic field range of ∼100–300 mT. The second pattern, labelled as (II), represents a fine structure of three lines with the central line around Hres = 330 mT and two “satellite” lines symmetrically placed around the central line. Both patterns are associated with Co(II) ions having different local environments. Out of all possible coordination, an octahedral environment of Co is ruled out as it requires an orbital triplet to be the ground state. The experiment shows that the ground state of the Co ions is an orbital singlet in a high-spin state (S = 3/2) because the resonances are visible from liquid-helium up to room temperature, so the spin–lattice constant does not become too short. It is possible for four- and five-coordinated Co, and it is in agreement with the crystallographic data. The axial and possible rhombic distortions will split the ground spin quartet into two Kramers doublets. Assuming that axial distortion is dominant, the separation between the Kramers doublet is 2|D|, where D is the axial zero-field splitting parameter. Even the tentative fit of both resonance patterns allows reaching a good agreement with the experiment. The calculated absorption is shown in Fig. 7 by dashed lines. The cobalt in position (I) is described by g-factor = ∼2.1 and parameter D = ∼3.92 cm−1, while the cobalt in position (II) is described by g-factor = ∼2.04 and parameter D = ∼0.03 cm−1. By taking into account that Cl as a ligand will produce a much smaller crystal field than N, it can be assumed that pattern (I) is associated with pentacoordinated Co(1), while pattern (2) is associated with tetracoordinated Co(2) subjected to a much smaller crystal field. In summary, EPR results strongly support the electronic structure picture obtained in calculations.
Electrochemistry
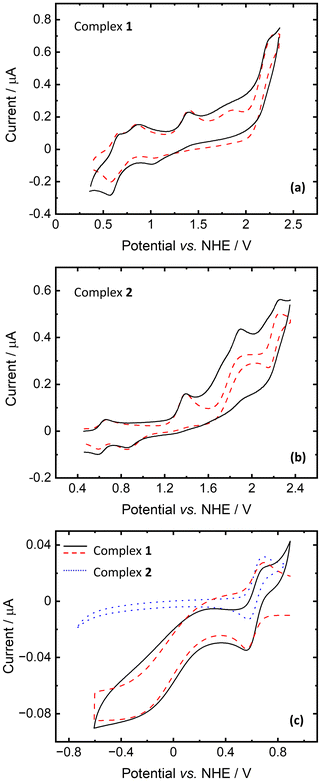
The redox properties of complexes 1 and 2 and the polypyrazole ligand (L) were investigated by cyclic voltammetry under an ambient air atmosphere in acetonitrile containing 0.1 M NBu4PF6 as a background electrolyte solution in a standard three-electrode configuration. Ferrocene (used as an internal reference) was added to the solution to assess the redox potentials of the compounds studied. All potentials are reported vs. NHE.The voltammetric curves with simulated voltammograms of complexes 1 and 2 are depicted in Fig. 8 and Fig. S7.† In the presented voltammograms, three main peaks can be observed in both cases with E° = 1.206, 1.646 and 2.056 V vs. NHE for complex 1 (Fig. 8a) and E° = 1.166, 1.476 and 2.196 V vs. NHE for 2 (Fig. 8b). Comparing the CV curves of the complexes with the free ligand curve (Fig. S8†) it could be revealed that peaks with E° above 2 V vs. NHE are associated with the scorpionate ligand oxidation. Furthermore, in the case of Cu complex (1), homogeneous oxidation of Fc to Fc+ can be detected. A similar phenomenon was observed for anhydrous CuCl2 (Fig. S9†) and other Cu(II) compounds.57
The waves with E° = 1.206 and 1.646 for 1 and 1.166 and 1.476 V vs. NHE for 2 can be assigned to the Cu(II/III) and Co(II/III) redox couples, respectively. According to calculations, anionic and cationic fragments of 1 have oxidation potentials of 1.20 and 1.75 V vs. NHE, respectively. For 2, the lower wave corresponds to the oxidation of the anionic fragment (0.91 V), and the oxidation of the cationic fragment was found to be at 1.38 V. Some discrepancies between calculations and experiment are mainly due to the fact that only separate fragments were considered in calculations and solvent effects (acetonitrile) were modelled only as a continuum.
The measurements of the cyclic voltammograms for the reduction process revealed that only complex 1 is reducible, contrary to complex 2 (Fig. 8c). The recorded voltammogram fits the simulated one with relatively slow kinetics of electron transfer (k0 = 2 × 10−4 cm s−1) and homogeneous regeneration of the oxidized form of the complex according to the catalytic EC′ mechanism. Based on quantum chemical calculations, we assign the reduction potential of 1 as E° = 0.472 V (close to Fc/Fc+) for the Cu(II/III) redox couple. Here, the computed value is 0.86 V for the reduction of the isolated cationic fragment (1.18 V for anionic). However, it decreases to 0.68 V when one acetonitrile molecule binds to the copper center (such a structure is anticipated in CH3CN solution). These findings should be compared to the reduction potentials of cationic and anionic fragments of 2 that were found to be 2.48 V and 2.86 V, respectively.
Catecholase activity: oxidation of 3,5-di-tert-butyl catechol (3,5-DTBC)
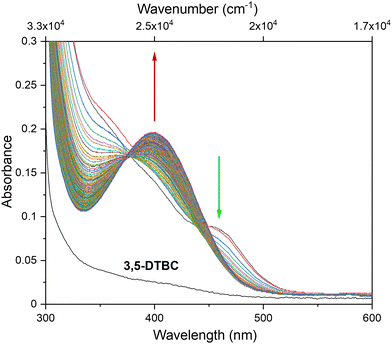
The catecholase activity of complexes 1 and 2 has been investigated according to the reaction presented in Scheme 1, using 3,5-di-tert-butyl catechol (3,5-DTBC) as a model substrate. The following reasons dictated the choice: (i) 3,5-DTBC is easily oxidized because of its low redox potential, (ii) the presence of bulky tert-butyl substituents prevents overoxidation reactions such as ring-opening and (iii) the oxidation product, 3,5-di-tert-butyl quinone (3,5-DTBQ), is highly stable.58–60 The product of the reaction exhibits a characteristic absorption band at around 400 nm.60–62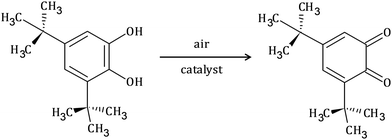 | ||
| Scheme 1 Schematic representation of catalytic oxidation of 3,5-di-tert-butyl catechol to the corresponding quinone. | ||
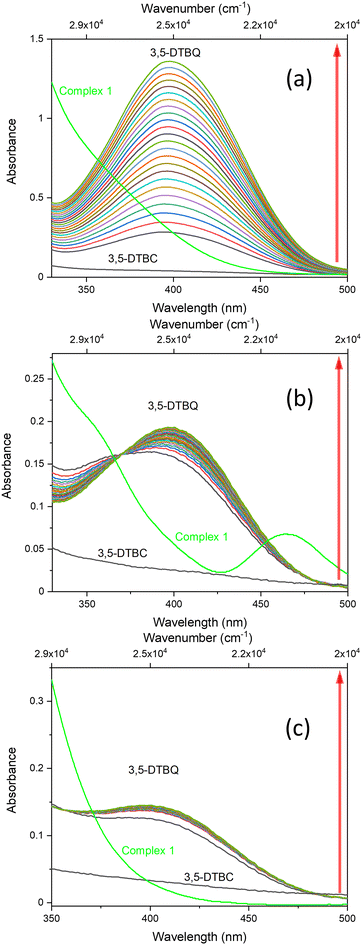
To explore the ability of the complexes to act as catalysts for catecholase activity, solutions of 1 (5 × 10−5 M) and 2 (1 × 10−4 M) were treated with a solution of 3,5-DTBC (1 × 10−2 M) under aerobic conditions in MeOH, CH3CN and DMSO, and time-dependent UV-vis spectra were recorded at intervals of 5 min up to 120 min at room temperature. For the tested Cu(II) and Co(II) complexes, only the Cu(II) complex (1) possesses catalytic activity in the oxidation of 3,5-DTBC (Fig. 9 and Fig. S10†). The obtained results for complex 1 revealed that the solvent's nature significantly affects the catecholase activity of the Cu(II) complex (Fig. 9). This is most probably related to the coordination ability of the various solvents. As far as the coordination power of the solvent is concerned, the lower the coordination power of the solvent, the higher the activity of the complexes in that solvent in catalyzing oxidation.63 Hence, kinetic experiments have been conducted to reveal solvent dependence in the tested reaction.
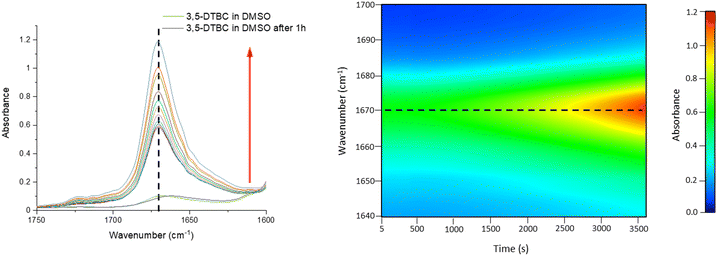
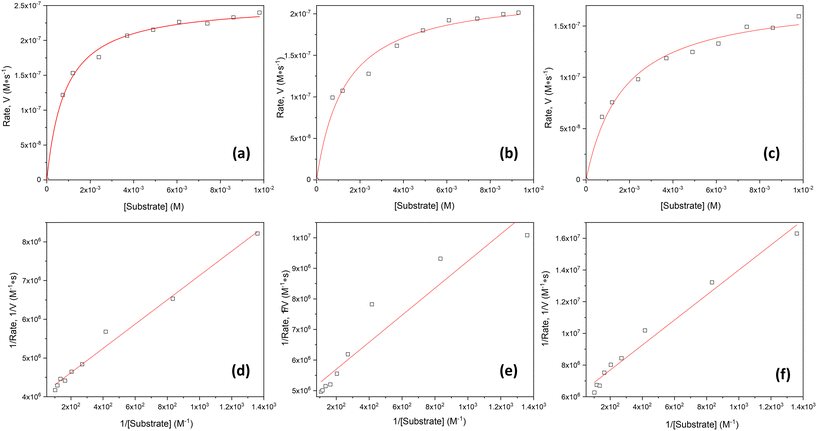
The oxidation of 3,5-DTBC in the presence of complex 1 was also confirmed by time-dependent analysis of the changes in the FT-IR spectrum (Fig. 10). The spectra of 3,5-DTBC after addition of complex 1 were recorded at intervals of 5 min up to 1 h at room temperature. The peak appearance during the reaction, with the maximum at 1670 cm−1 corresponding to the –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group vibrations, confirmed the formation of quinone molecules (3,5-DTBQ).64
O group vibrations, confirmed the formation of quinone molecules (3,5-DTBQ).64
Kinetics of catecholase activity
Because only complex 1 is catalytically active in the oxidation of 3,5-DTBC, the kinetic experiment was performed only for this complex. The reaction between the catalyst (with a constant concentration of 5 × 10−5 M) and 3,5-DTBC (with varying concentrations from 7.4 × 10−4 M to 9.8 × 10−3 M in MeOH, CH3CN and DMSO) was monitored by fiber optic UV-vis spectroscopy, which allows monitoring the changes of the spectra in a whole spectral range of interest (not only changes of absorbance at given wavelengths) online, during the catalytic experiment with very low time intervals (2 s). The experimental scheme involved the preparation of the stock solution of 1 and the substrate (3,5-DTBC) at higher concentrations in methanol, acetonitrile, and DMSO. From the stock solution, 2 ml of the substrate of appropriate concentration at appropriate dilution was taken into the UV-vis quartz cell. After that, 0.04 ml (in MeOH or DMSO) or 0.12 ml (due to poor solubility in CH3CN) of the stock solution of complex 1 was introduced into it to achieve the ultimate concentration of the catalyst as 5 × 10−5 M. The creation of 3,5-DTBQ was monitored using online UV-vis measurements of the spectra during the first 10 min of the reaction, with 2 s intervals. The whole procedure was repeated three times. The initial rate method was used to determine the rate constant value for each substrate concentration. The rate constant value versus the concentration of the substrate was analyzed based on the Michaelis–Menten approach of enzymatic kinetics to obtain the Lineweaver–Burk plot and the values of the parameters: the maximum reaction rate – Vmax, the Michaelis–Menten binding constant – KM and the turnover number – Kcat. The observed and simulated rate constant versus substrate concentration plot and the Lineweaver–Burk plot (in methanol, acetonitrile and dimethylsulfoxide) are presented in Fig. 11. The obtained results show that in the low concentration range of the substrate, first-order dependence was observed and in the higher concentration regime, zero-order saturation kinetics was followed. According to the literature,65 the dependence on the substrate concentration indicates that catalyst–substrate binding is the initial step in the catalytic mechanism.The kinetic parameters obtained for complex 1 are listed in Table 3. A comparison of turnover numbers for various nuclearity Cu(II) complexes is given in Table 4.66–77 This type of saturation rate dependency on the concentration of the substrate may be explained by considering the Michaelis–Menten equation for enzymatic kinetics as:
KM and Vmax values were calculated. The Kcat values were obtained by dividing the Vmax values by the complex concentration. The turnover numbers (Kcat) for 1 are 18.02 h−1 in MeOH, 14.95 h−1 in CH3CN and 11.79 h−1 in DMSO (Table 3) and are in agreement with the data reported in the literature (Table 4) for other Cu(II) complexes with multidentate N-donor heteroaromatic ligands. The calculated values indicate moderate catecholase activity of complex 1. Bearing in mind that 3,5-DTBC can be readily oxidized by atmospheric oxygen and even only CuCl2 catalyzes the reaction, it is worth mentioning that the rate obtained for complex 1 (Table 3) was significantly higher than those without the catalyst (Vmax = 0.68 × 10−8 M s−1)66 and with CuCl2 (Vmax = 1.15 × 10−8 M s−1).66 Additionally, to reveal that the cationic part of 1 is the main source of the catecholase activity in our cationic-anionic complex, the catalytic reaction of (NH4)2[CuCl4] with 3,5-DTBC was performed, and the kinetic parameters were calculated (Fig. S11 and Table S5†) for the same three solvents as for complex 1. The obtained values of Kcat for [CuCl4]2− are in the range of 1.27–3.62 h−1 (Table S5†) and significantly smaller than those obtained for complex 1 (Table 3). This finding is in line with the assumption about the decisive contribution of the [CuLCl]+ cationic form to the catecholase activity of 1.
| Solvent | V max (M s−1) (×10−7) | Std. error (×10−8) | K M (M) (×10−4) | Std. error (×10−5) | K cat (h−1) | K cat/KM (M−1 s−1) |
|---|---|---|---|---|---|---|
| MeOH | 2.50 | 0.48 | 7.85 | 3.34 | 18.02 | 6.38 |
| CH3CN | 2.08 | 1.34 | 9.17 | 9.09 | 14.95 | 4.53 |
| DMSO | 1.64 | 0.69 | 12.90 | 7.34 | 11.79 | 2.53 |
| Complex | Nuclearity | CN | Solvent | K cat (h−1) | Ref. |
|---|---|---|---|---|---|
| Here: L7 = 6-(Bis-pyrazol-1-ylmethyl-amino)-hexane-1-ol; pymimi = (2-(pyridyl-2-yl)ethyl)((1-methylimidazol-2-yl)methyl)imine; bpymima = (2-(pyridyl-2-yl)ethyl)((1-methylimidazol-2-yl)methyl)amine; EDTB = N,N,N′,N′-tetrakis(20-benzimidazolylmethyl)-1,2-ethanediamine; PhBIm2 = 2,2′-(1,2-phenylene)bis(1H-benzimidazole); L1NH2 = N,N-bis(2-pyridylmethyl)aminoethyl amine; Py3N = N,N,N-tris(2-pyridylmethyl)amine; L1 = bis(2-pyridyl carbonyl)amine; L1 = 1,2-bis(2-((pyridine-2-yl)methyleneamino)phenyl)ethane; L2 = tris((2-benzylideneamino)ethyl)amine; [22]py4pz = 9,22-bis(pyridin-2′-ylmethyl)-1,4,9,14,17,22,27,28,29,30-decaazapentacyclo-[22.2.17,14.111,14.117,20]triacontane-5,7(28),11(29),12,18,20(30), (24(27),25-octaene); L4 = α,α′-Bis[(6-methyl-2-pyridylmethyl)-(N-(pyrazol-1-ylmethyl))amino]-m-xylene; 2-AEP = 2-aminoethylpyridine; phen = 1,10-phenanthroline. | |||||
| [Cu(L7)Cl]Cl | Monomeric | 5 | MeOH | 11.16 | 66 |
| [Cu(pymimi)Cl2] | Monomeric | 5 | CHES buffer | 216 | 67 |
| [Cu(pymima)Cl2] | Monomeric | 5 | CHES buffer | 396 | 67 |
| Cu(EDTB)(NO3)2·C2H5OH | Monomeric | 6 | MeOH-Tris-HCl | 3.27 | 68 |
| [Cu(PhBIm2)Cl2] | Monomeric | 4 | MeOH | 5.65 | 69 |
| [Cu(L1NH2)Cl](BF4) | Monomeric | 5 | CH3CN | 340 | 70 |
| [Cu(Py3N)Cl](BF4) | Monomeric | 5 | CH3CN | 600 | 70 |
| [Cu(L1)(OCN)(H2O)] | Monomeric | 5 | MeOH | 29.2 | 71 |
| [Cu(II)(L1)(CH3OH)](ClO4)2·CH3OH | Monomeric | 5 | CH3CN | 36 | 72 |
| [Cu(L2)(CH3COO)](ClO4) | Monomeric | 5 | CH3CN | 108 | 72 |
| [Cu2L2(CH3O)2]·2(CH3OH) | Dimeric | 5, 5 | MeOH | 720 | 73 |
| [Cu2([22]py4pz)(μ-OH)](ClO4)3·H2O | Dimeric | 5, 5 | CH3CN | 104 | 74 |
| [Cu2(2-AEP)4(μ-Cl)](ClO4)2 | Dimeric | 5, 5 | DMF | 183.6 | 75 |
| [Cu2(L4)(μ-OH)2][ClO4]2·H2O | Dimeric | 5, 5 | CH3CN | 100 | 76 |
| [Cu4(μ3-OH)2(μ2-OH)2(2-AEP)4(μ2-ClO4)2](ClO4)2 | Tetrameric | 5, 5, 6, 6 | DMF | 175.68 | 75 |
| [Cu(phen)(NO3)2]n | Polymeric | 5, 5 | MeOH | 8.28 | 77 |
| 1 | Cationic–anionic | 5, 4 | MeOH | 18.02 | This work |
| CH3CN | 14.95 | This work | |||
| DMSO | 11.79 | This work | |||
To be sure that the obtained values are reliable, we have checked the correctness using suggestions included in the literature78 and compared the calculated kinetic parameters of 1 with the experimental results presented in Fig. 11. A comparison of spectral and kinetic parameters obtained during the first 10 min of the oxidation reaction for each solvent is presented in Table 5. Calc. rate/“rate” factors are close to one in each case, which confirms the accuracy of the calculations.
| Solvent | ΔAbs. in 10 min | Rate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (M s−1) a (M s−1) |
V max (M s−1) | K cat (h−1) | K M (M) | Calc. rate (V0)b | V 0/rate |
|---|---|---|---|---|---|---|---|
a Rate has been calculated using ε = 1630 M−1 cm−1 for the product.
b Calculated rate has been determined using the equation: 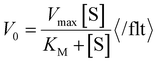 . .
|
|||||||
| MeOH | 0.34 | 3.48 × 10−7 | 2.50 × 10−7 | 18.02 | 7.73 × 10−4 | 2.32 × 10−7 | 0.67 |
| CH3CN | 0.17 | 1.74 × 10−7 | 2.08 × 10−7 | 14.95 | 8.84 × 10−4 | 1.90 × 10−7 | 1.09 |
| DMSO | 0.14 | 1.43 × 10−7 | 1.64 × 10−7 | 11.79 | 1.29 × 10−3 | 1.45 × 10−7 | 1.01 |
Based on the obtained results, we observed the highest catalytic activity in MeOH, followed by CH3CN and DMSO, and this result is in line with the fact that catecholase activity is solvent dependent. Moreover, obtained data revealed that the Kcat value is the lowest for DMSO, in which complex 1 dissolves the easiest, suggesting that the solvent molecule acts as a quite inert ligand and blocks the catalytic centre. Hence, the formation of the [catalyst–substrate] complex is harder to achieve. Also, in the case of the reaction in CH3CN, the formation of the [catalyst–substrate] complex is disturbed. This probably takes place due to the short contact between [CuCl4]2− and [CuLCl]+ species demonstrated by an additional (compared to reflectance spectrum) maximum in the UV-vis spectrum at 465 nm (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 cm−1) (vide supra). Moreover, this feature disappears in the first few seconds of the 3,5-DTBC oxidation reaction with simultaneous product formation (Fig. 12).
505 cm−1) (vide supra). Moreover, this feature disappears in the first few seconds of the 3,5-DTBC oxidation reaction with simultaneous product formation (Fig. 12).
Conversely, the highest activity in MeOH most likely follows the stabilization of [CuCl4]2− moieties by the solvent molecules via the H-bond network so the free coordination site is accessible, thus allowing a substrate molecule to bind.
These solvent trends are in line with the results of quantum chemical calculations of cationic and anionic fragments of 1 and 2 interacting with a single solvent molecule (Table 6). Here, we note that cationic−anionic fragment interaction energy was found to be ca. −28 kcal mol−1 and −9 kcal mol−1 for 1 and 2, respectively. In the latter case, the sum of solvent interaction energies for cationic and anionic fragments is always larger than the cationic−anionic fragment interaction energy. Therefore, we expect the interfragment communication in 2 to be negligible. On the other hand, the sum of solvent interaction energies for cationic and anionic fragments of 1 in acetonitrile (−22.2 kcal mol−1) is less than the fragment interaction energy in this solvent (−28.0 kcal mol−1). Therefore, in line with the UV-vis measurements, 1 in CH3CN should have a copper active site in the cationic fragment blocked largely by the anionic fragment and stay rather inactive in the tested oxidation reaction. Two other solvents tested (methanol and DMSO) with complex 1 display the sum of solvent interaction energies comparable to or more negative than the cationic−anionic fragment interaction energy.
| Solvent | 1-cation | 1-anion | 2-cation | 2-anion |
|---|---|---|---|---|
| MeOH | −15.1 | −13.2 | −12.3 | −12.1 |
| CH3CN | −10.1 | −12.1 | −10.7 | −10.3 |
| DMSO | −19.5 | −14.1 | −10.6 | −14.6 |
Various factors affect the structure–activity relationship. For an effective catechol oxidase reaction, the relationship between the nature of the central metallic atom, metal⋯metal distance, electrochemical properties, exogenous bridging ligand, ligand structure, and pH should be considered.79 Although dimeric complexes are considered more relevant for mimicking the catalytic activity owing to the active site of the naturally occurring enzyme, both mononuclear and dinuclear, as well as polymeric copper complexes, have been found to show significant catecholase activity (Table 4). Among the monomeric complexes, non-planar compounds with intermediate coordination geometry between trigonal bipyramid and square pyramidal are potential cases, while those with a square-planar environment show little or no activity.65 Furthermore, according to the literature,65 in mononuclear complexes labile ligands can be easily replaced with a substrate, leading to higher catalytic activity. Moreover, complexes with Cu⋯Cu distances in the range of 2.9–3.2 Å have been found to be the best candidates to show promising activity in catechol oxidation.65,80 Nevertheless, the literature reports dimeric copper(II) complexes in which a solid-state copper⋯copper distance is as large as 7.840 Å, which still exhibit good catecholase activity.81,82 Here, we present the first reported cationic−anionic Cu(II) complex with catecholase activity where the Cu⋯Cu distance between cationic and anionic forms is 5.593 Å and the distance between the closest situated cationic species in the crystal lattice is equal to 8.178 Å.
The analysis of Table 6 also provides hints about the lack of activity of cobalt complex 2. One should note that the interaction energies of solvent molecules are, in most cases, lower for cobalt complexes than for copper complexes. Particularly in the case of catalytically active cationic fragments, the square-pyramidal copper coordination sphere seems to provide a more convenient site for substrate binding than the trigonal bipyramidal cobalt complex. Moreover, the reduction potentials for the cationic fragment depend on the central atom (calculated to be 0.68 V and 2.48 V for Cu and Co, respectively). In fact, in the typical 3,5-DTBC oxidation reaction mechanisms catalyzed by Cu and Co complexes considered in the literature,83–86 the metallic center is reduced by the substrate in the first part of the catalytic cycle. The catalyst is then regenerated by reaction with molecular oxygen. In light of this mechanism, a relatively low reduction potential is a prerequisite for the reaction to occur. This condition is fulfilled by the examined copper complex 1.
Conclusions
In summary, we have successfully synthesized and characterized two novel cationic−anionic copper(II) and cobalt(II) complexes with the N-scorpionate type ligand. The critical advantage of the investigated complexes, in the context of their possible catalytic activity, was the fact that their usage would not introduce any unnecessary counterions. Complexes [CuLCl]2[CuCl4] (1) and [CoLCl][CoL′Cl3] (2) have been characterized by various spectral, electrochemical, single crystal X-ray and quantum chemical methods. The crystal structures of 1 and 2 revealed that in both cases, the cationic form consists of a tetradentate N-scorpionate ligand and one chloride. The central metal ion coordination environment possesses square-pyramidal or trigonal bipyramidal geometry in 1 and 2, respectively. The geometry of the central metal ion in the anionic part of complexes 1 and 2 is a slightly distorted tetrahedron occupied by four Cl− ions in 1 or the nitrogen atom from the pyrazole ring of the pyrazole derivative (L′) and three chlorides in complex 2. The analysis of crystal structures revealed the presence of various non-covalent interactions in both complexes, which were further corroborated theoretically (by Hirshfeld surface analysis). UV-visible spectra were verified by quantum chemical calculations, and a high-spin ground-state configuration with a distorted pentacoordinated geometry around the metal ions in the cationic forms of the complexes was ascertained.The obtained complexes are the first reported examples of cationic−anionic coordination compounds tested for catecholase activity. We found that copper complex 1 is a good 3,5-DTBC oxidation catalyst, while cobalt complex 2 was inactive in the reaction. The latter outcome was explained by relatively high reduction potential and a less convenient substrate binding site in 2 as compared to 1, which renders catalyst reduction by the substrate impossible. Catalytic results obtained for compound 1 revealed that the solvent's nature significantly affects the catecholase activity of the Cu(II) complex. Based on the obtained results, we observed the highest catalytic activity in MeOH, followed by CH3CN and DMSO, and this result is in line with the fact that catecholase activity is solvent dependent. We note, however, that the explanation of the observed experimental trends would not be possible without a close synergy between experiment and theory. In fact, quantum chemistry provided us with “insights and numbers”, as postulated by Neese and co-workers.87
Experimental
All reagents used in the synthesis were purchased from commercial sources and used without further purification. All the experiments were performed under an air atmosphere. 1-Hydroxymethyl-3,5-dimethylpyrazole (TCI), CuCl2 × 4H2O, CoCl2 × 6H2O, (NH4)2[CuCl4] and CH3COONH4 (WARCHEM Sp. z o.o.) have been used. Ferrocene (98%) and tetrabutylammonium hexafluorophosphate (NBu4PF6, >98%) were purchased from Sigma-Aldrich.Elemental analysis was run on a UNIcube analyzer (Elementar, Germany).
IR spectra were recorded on a PerkinElmer Spectrum Two FT-IR spectrometer, in the range of 4000–450 cm−1 using the diffusive reflection method (ATR); relative intensities are indicated (w: weak, m: medium, s: strong, vs: very strong, and br: broad).
Electronic spectra of the complexes were recorded on a UV-vis spectrophotometer UV-270 (Shimadzu, Japan) for the samples dissolved in MeOH and using the same spectrometer equipped with an integrating sphere for measuring solids. The powder samples were ground with barium sulfate for the solid measurement and then pressed in a holder. Barium sulfate, spectrally pure, was delivered by Shimadzu Corporation. Deuterated solvents for all NMR experiments were purchased from EUROISOTOP and used as obtained. All NMR samples were prepared using the same procedure. This procedure is as follows. To a standard 5 mm NMR sample, 1 mg of a complex was loaded and dissolved in 0.75 ml of deuterated solvent ([D3]MeOH). All NMR spectra were recorded on a BRUKER AVANCE II 300 MHz spectrometer equipped with a W1 5 mm z-gradient BBI probe head. The temperature was controlled using a BVT unit. A standard Bruker pulse program was utilized for the acquisition of 1H NMR spectra, and the acquisition was carried out via the TopSpin 3.2 program. Each 1H NMR spectrum was recorded with ns = 512, d1 = 5 s, and aq = 2 s parameters. The acquired spectra which are presented in all figures, were processed and produced via the TopSpin3.2 program. All spectra were calibrated on the residual signal of the solvent, which was [D3]MeOH.881H NMR spectra were calibrated on the signal of the residual –CHD2 group with resonance at 3.346 ppm.
The EPR measurements were carried out using a Bruker EMX spectrometer working at a fixed frequency 9.37 GHz (X-band) with an Oxford Instruments helium-flow cryostat operating in the temperature range from 3.8 K to 300 K. A 100 kHz magnetic field modulation and phase sensitive detection were used to record the derivative of the absorbed microwave power.
Cyclic voltammetry measurements were conducted under ambient air using a PalmSens4 potentiostat in a standard three-electrode configuration. Ferrocene (used as an internal reference) was added to the solution to assess the redox potentials of the compounds studied. Cyclic voltammograms were compared with simulated voltammograms using DigiSim 3.03b software (Bioanalytical Systems). Platinum disk ultramicroelectrodes with a diameter of 25 μm were used as the working electrode for steady-state voltammetry. Platinum wires with diameters of 0.5 mm, 0.1 mm, and 0.025 mm were sourced from the Mint of Poland. Platinum disc microelectrodes were fabricated by sealing 25 μm or 100 μm diameter microwires into borosilicate capillaries (Sutter Instruments, o.d. 1.2 mm, i.d. 0.69 mm) under vacuum using a micropipette puller (PC-10, Narishige). The resulting composite was cut with a diamond knife and polished with 0.1 μm grade diamond lapping tape (Buehler) using a custom-built microelectrode polisher. Small glass test tubes served as open electrochemical cells.
Single crystal X-ray diffraction measurements were carried out on a Rigaku Supernova diffractometer at 100 K with monochromated Mo Kα radiation (0.71073 Å). A green block crystal of 1 and a dark-violet plate crystal of 2 of approximate dimensions 0.3 × 0.1 × 0.1 and 0.35 × 0.1 × 0.03 mm were used, respectively. The data reduction was performed by using CrysAlisPro software.89 The structures were solved by direct methods and refined on F2 by full-matrix least-squares by using SHELXS97 and SHELXL97.90 All non-hydrogen atoms were refined as anisotropic, while hydrogen atoms were placed in calculated positions and refined in riding mode. The figures were made using Mercury software.91 CCDC 2212853 (1) and 2213450 (2) contain supplementary crystallographic data for this paper.†
Hirshfeld surface and 2D fingerprint calculations were performed using the Crystal Explorer package ver. 21.5.92 Crystal structures were imported from CIF files. The bond lengths of hydrogen atoms were normalized to standard neutron values (C–H = 1.083 Å, O–H = 0.983 Å, and N–H = 1.009 Å). Hirshfeld surfaces were generated for complex molecules using high resolution and mapped with the dnorm functions. 2D fingerprint plots were prepared using the same software.
To determine catecholase activity, spectrophotometric titrations of a 5 × 10−5 M solution of complexes 1 and 2 were carried out with a 1 × 10−2 M (>100-fold equivalents) concentrated solution of 3,5-DTBC, and the course of the reaction was followed by recording time-dependent UV-vis spectra of the mixture on a UV-visible spectrophotometer UV-270 (Shimadzu, Japan) under aerobic conditions up to 2 h at 5 min intervals. Kinetic parameters for 1 and (NH4)2[CuCl4] were determined based on online UV-vis spectra measurements during the first 10 min (2s intervals) of the oxidation reaction of 3,5-DTBC in the presence of 1 on an Ocean Optics USB4000 Fiber Optic Spectrometer (Ocean Optics, Inc.). Additionally, the changes in the FT-IR spectrum during the reaction of 1 (1 × 10−3 M) with 3,5-DTBC (1 × 10−1 M) in DMSO were recorded on a PerkinElmer Spectrum Two FT-IR spectrometer, using a Specac Pearl™ liquid analyser. The spectra were collected under aerobic conditions, at room temperature up to 1 h at 5 min intervals.
Preparation of the complexes
The synthesis was based on a simple one-pot, two-step synthetic protocol.93 The tetradentate ligand, tris(1-(3,5-dimethylpyrazolyl)-methyl)amine (L), was obtained as a condensation reaction product.4 In the presence of CuCl2 and CoCl2, a coordination reaction occurs, which leads to the formation of complexes 1 and 2, respectively.Synthesis of [CuLCl]2[CuCl4] (1)
In the first step, acetonitrile solution (10 ml) of 1-hydroxymethyl-3,5-dimethylpyrazole (2 mmol, 0.2523 g) and ammonium acetate (1 mmol, 0.0771 g) was stirred at room temperature for 5 days. Then, to the resulting solution, a solid of CuCl2 × 2H2O (1 mmol, 0.1705 g) was added to yield an intense green solution. The solution was stirred at 60 °C for 4 h, and after that, it was allowed to evaporate at room temperature. The next day, green, X-ray quality blocks of complex 1 were isolated from the mother solution. Yield: 73%. Anal. Calc. (%) for Cu3C36H54N14Cl6: C, 39.80; H, 5.01; N, 18.05. Found: C, 39.44; H, 4.93; N, 17.90. IR (ATR, νmax/cm−1): 3111 w, 3074 w, 2995 w, 2980 w, 2923 w, 1550 s, 1490 m, 1465 s, 1435 m, 1417 s, 1394 s, 1311 s, 1275 s, 1250 m, 1237 m, 1186 w, 1154 w, 1133 m, 1111 m, 1061 s, 1037 s, 1021 m, 983 m, 964 m, 868 m, 832 m, 800 m, 784 s, 703 w, 690 w, 676 w, 659 w, 630 w, 620 w, 605 w, 572 w, 514 w, 490 w, 466 w. UV-Vis (λmax, cm−1) in solid (DRS): 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650, 12
650, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090; (λmax, cm−1) in MeOH: 14
090; (λmax, cm−1) in MeOH: 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837, 12
837, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020; (λmax, cm−1) in CH3CN: 13
020; (λmax, cm−1) in CH3CN: 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625, 12
625, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165; (λmax, cm−1) in DMSO: 13
165; (λmax, cm−1) in DMSO: 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514, 12
514, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050.
050.
Synthesis of [CoLCl][CoL'Cl3] (2)
First, 1-hydroxymethyl-3,5-dimethylpyrazole (2 mmol, 0.2523 g) and ammonium acetate (1 mmol, 0.0771 g) were stirred in acetonitrile solution (10 ml) at room temperature for 5 days. Next, to the resulting solution, a solid of CoCl2 × 6H2O (1 mmol, 0.2379 g) was added to yield an intense violet−blue solution. The solution was stirred at 60 °C for 3.5 h and then allowed to evaporate slowly at room temperature. Violet-blue, suitable for X-ray analysis, crystals of complex 2 were isolated from the mother solution after one week. Yield: 68%. Anal. calc. (%) for Co2C24H38N10Cl4: C, 39.69; H, 5.27; N, 19.28. Found: C, 39.57; H, 5.04; N, 19.37. IR (ATR, νmax/cm−1): 3332 w, 3129 w, 3095 w, 2997 w, 2982 w, 2958 w, 2927 w, 1555 m, 1492 w, 1462 m, 1418 m, 1408 m, 1386 m, 1375 m, 1309 m, 1298 m, 1280 m, 1251 m, 1225 w, 1177 w, 1158 w, 1140 w, 1127 s, 1049 s, 1037 s, 1012 w, 1003 m, 983 m, 895 w, 836 m, 821 m, 810 m, 798 m, 786 m, 700 m, 692 m, 664 w, 631 w, 622 w, 593 w, 578 w, 548 w, 499 w, 487 w. UV-vis (λmax, cm−1) in solid (DRS): 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120, 16
120, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, 15
610, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 552, 14
552, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577, 12
577, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225; (λmax, cm−1) in MeOH: 19
225; (λmax, cm−1) in MeOH: 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305, 16
305, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 722, 15
722, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950, 11
950, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860; (λmax, cm−1) in CH3CN: 19
860; (λmax, cm−1) in CH3CN: 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340, 16
340, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835, 15
835, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798, 14
798, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750, 11
750, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905; (λmax, cm−1) in DMSO: 19
905; (λmax, cm−1) in DMSO: 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305, 16
305, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610, 15
610, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873, 14
873, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705, 11
705, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 905.
905.
Quantum chemical calculations
All calculations were performed with the DKH2 quasi-relativistic Hamiltonian94 and DKH-def2-TZVP95 basis set as implemented in the ORCA 5.0.2 suite of programs.96 Whenever possible, we took advantage of the resolution-of-identity (RI) and chain-of-spheres (COSX) approximations to speed up the calculations.97,98 If not stated otherwise, geometries were obtained with the BP86 functional augmented with D3 dispersion correction (BP86+D3); Hessian analysis confirmed fully optimized structures as true minima. Spectra were recorded using time-dependent density functional theory (TD-DFT) based on crystal structures (hydrogen atoms optimized) using the range-separated ωB97X functional99 and the usual Tamm–Dancoff approximation. We accounted for 10 excited states for monomers and 50 states for dimers. This set-up provided spectra close to those calculated with the multireference NEVPT2 method100 on [CuCl4]2− molecules (see Fig. S12†). The same method was used to estimate the magnitude of coupling between metallic centers in cationic−anionic dimers. For the cobalt complex, all 3d orbitals entered the active spaces along with associated electrons, which resulted in a (14,10) space, while a minimal space of two electrons distributed over two orbitals was employed for the Cu complex. State-averaging was carried out over single high-spin and single low-spin states.Oxidation and reduction potentials were computed using the well-established protocol described elsewhere by some of us.101 Briefly, ground and ionized states were fully optimized with the BP86+D3 setup and the CPCM solvation model with parameters chosen to model acetonitrile solvent. Single-point energies were evaluated with the B3LYP functional102,103 with D3 dispersion correction. Energy differences between ground and ionized states were referenced against a theoretical standard hydrogen electrode, for which absolute potential was obtained via the aforementioned protocol as −4.48 V, assuming a Gibbs free energy of proton solvation of −262.4 kcal mol−1.104 By computing both electrode processes at the same level, we took advantage of error cancellation to a large extent.
The XYZ coordinates of all geometries are provided in the ESI.†
Author contributions
The manuscript was written with contributions from all authors. All authors have given approval to the final version of the manuscript. Conceptualization: M. Z.-M. and A. K.; methodology: M. Z.-M. and A. K.; investigation: M. Z.-M., R. L., J. M.-P., G. A., W. N., T. R., P. A. and A. K.; writing – original draft: M. Z.-M. and A. K.; writing – review and editing: M. Z.-M., R. L., J. M.-P., G. A., W. N., T. R., P. A. and A. K; project administration: M. Z.-M. and A. K.; funding acquisition: A. K.Data availability
The data supporting this article have been included as part of the ESI.†Crystallographic data for all structures reported in this paper have been deposited with CCDC 2212853 and 2213450.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the National Science Centre of Poland, grant no. 2020/39/B/ST4/01952.References
- J. Masternak, M. Zienkiewicz-Machnik, M. Kowalik, A. Jabłońska-Wawrzycka, P. Rogala, A. Adach and B. Barszcz, Coord. Chem. Rev., 2016, 327–328, 242 CrossRef CAS.
- A. Adach, J. Coord. Chem., 2017, 70, 757 CrossRef CAS.
- M. Daoudi, N. B. Larbi, A. Kerbal, B. Bennani, J.-P. Launay, J. Bonvoisin, T. B. Hadda and P. H. Dixneuf, Tetrahedron, 2006, 62, 3123 CrossRef CAS.
- W. L. Driessen, Recl. Trav. Chim. Pays-Bas, 1982, 101, 441 CrossRef CAS.
- S. Trofimenko, J. Am. Chem. Soc., 1967, 89, 6288 CrossRef CAS.
- R. Mukherjee, Coord. Chem. Rev., 2000, 1, 151 CrossRef.
- A. Dołęga, Coord. Chem. Rev., 2010, 254, 916 CrossRef.
- L. M. D. R. S. Martins and A. J. L. Pombeiro, Coord. Chem. Rev., 2014, 265, 74 CrossRef CAS.
- A. Otero, J. Fernández-Baeza, A. Lara-Sánchez and L. F. Sánchez-Barba, Coord. Chem. Rev., 2013, 257, 1806 CrossRef CAS.
- J. Haggin, Chem. Eng. News, 1993, 71, 30 Search PubMed.
- L. I. Simándi, Catalytic Activation of Dioxygen by Metal Complexes, Kluwer Academic Publishers, Dordrecht, Boston, 1992 Search PubMed.
- G. P. Maier, C. M. Bernt and A. Butler, Biomater. Sci., 2018, 6, 332 RSC.
- J. Yang, M. Stuart and M. Kamperman, Chem. Soc. Rev., 2014, 43, 8271 RSC.
- J. Bolton and T. Dunlap, Chem. Res. Toxicol., 2017, 30, 13 Search PubMed.
- B. Kim, D. Oh, S. Kim, J. Seo, D. Hwang, A. Masic, D. Han and H. Cha, Biomacromolecules, 2014, 15, 1579 CrossRef CAS PubMed.
- K. S. Banu, T. Chattopadhyay, A. Banerjee, S. Bhattacharya, E. Suresh, M. Nethaji, E. Zangrando and D. Das, Inorg. Chem., 2008, 47, 7083 CrossRef CAS PubMed.
- S. Y. Shaban, A. E.-M. M. Ramadan, M. M. Ibrahim, F. I. Elshami and R. van Eldik, Inorg. Chim. Acta, 2019, 486, 608 CrossRef CAS.
- A. Neves, L. M. Rossi, A. J. Bortoluzzi, B. Szpoganicz, C. Wiezbicki, E. Schwingel, W. Haase and S. Ostrovsky, Inorg. Chem., 2002, 41, 1788 CrossRef CAS PubMed.
- D. Lakk-Bogáth, P. Török, M. Giorgi and J. Kaizer, J. Mol. Struct., 2022, 1262, 133100 CrossRef.
- M. Maiti, D. Sadhukhan, S. Thakurta, E. Zangrando, G. Pilet, A. Bauzá, A. Frontera, B. Dede and S. Mitra, Polyhedron, 2014, 75, 40 CrossRef CAS.
- K. S. Banu, T. Chattopadhyay, A. Banerjee, M. Mukherjee, S. Bhattacharya, G. K. Patra, E. Zangrado and D. Das, Dalton Trans., 2009, 8755 RSC.
- S.-I. Lo, J.-W. Lu, W.-J. Chen, S.-R. Wang, H.-H. Wei and M. Katada, Inorg. Chim. Acta, 2009, 362, 4699 CrossRef CAS.
- A. Chatterjee, G. Kaur, M. Joshi, A. R. Choudhury and R. Ghosh, Inorg. Chim. Acta, 2020, 513, 119933 CrossRef CAS.
- M. Shit, S. Maity, S. Bera, P. K. Mudi and B. Biswas, New J. Chem., 2021, 45, 2221 RSC.
- B. Mandal, M. C. Majee, D. Mandal and R. Ganguly, J. Mol. Struct., 2020, 1202, 127340 CrossRef CAS.
- S. Mistri, H. Puschmann and S. C. Manna, Polyhedron, 2016, 115, 155 CrossRef CAS.
- M. Mitra, P. Raghavaiah and R. Ghosh, New J. Chem., 2015, 39, 200 RSC.
- R. Modak, Y. Sikdar, S. Mandal and S. Goswami, Inorg. Chem. Commun., 2013, 37, 193 CrossRef CAS.
- S. Sarkar and H.-I. Lee, Inorg. Chim. Acta, 2020, 504, 119437 CrossRef CAS.
- E. C. Niederhoffer, J. H. Timmons and A. E. Martell, Chem. Rev., 1984, 84, 137 CrossRef CAS.
- A. Bencini, A. Bianchi, C. Giorgi, P. Paoletti, B. Valtancoli, N. Ceccanti and R. Pardini, Polyhedron, 2000, 19, 2441 CrossRef CAS.
- N. Ceccanti, R. Pardini, F. Secco, M. R. Tinè, M. Venturini, A. Bianchi and P. Paoletti, Polyhedron, 2000, 19, 2447 CrossRef CAS.
- K. Fujisawa, S. Chiba, Y. Miyashita and K. Okamoto, Eur. J. Inorg. Chem., 2009, 3921 CrossRef CAS.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, Dalton Trans., 1984, 1349 RSC.
- A. Panja, S. Goswami, N. Shaikh, P. Roy, M. Manassero, R. J. Butcher and P. Banarjee, Polyhedron, 2005, 24, 2921 CrossRef CAS.
- A. N. Protsenko, O. G. Shakirova and N. V. Kuratieva, J. Mol. Struct., 2019, 1175, 782 CrossRef CAS.
- X.-L. Cao, Y. Liu, G.-L. Li, Z.-X. Lu, S. Li, Z.-M. Cao and Y.-G. Huang, J. Mol. Struct., 2021, 1244, 130958 CrossRef CAS.
- A. Adach, M. Daszkiewicz, B. Barszcz, M. Cieślak-Golonka and G. Maciejewska, Inorg. Chem. Commun., 2010, 13, 361 CrossRef CAS.
- A. Adach, M. Daszkiewicz and B. Barszcz, Struct. Chem., 2010, 21, 331 CrossRef CAS.
- S. S. Massoud, R. C. Fischer, F. A. Mautner, M. M. Parfait, R. Herchel and Z. Trávníček, Inorg. Chim. Acta, 2018, 471, 630 CrossRef CAS.
- J. Bernstein, R. E. Davis, L. Shimoni and N. L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555 CrossRef CAS.
- M. K. Corpinot and D.-K. Bučar, Cryst. Growth Des., 2019, 19, 1426 CrossRef CAS.
- J. Masternak, J. Zienkiewicz-Machnik, K. Kazimierczuk and B. Barszcz, Polyhedron, 2018, 142, 93 CrossRef CAS.
- J. Masternak, B. Barszcz, W. Sawka-Dobrowolska, J. Wietrzyk, J. Jezierska and M. Milczarek, RSC Adv., 2014, 4, 43962 RSC.
- K. R. Surati and B. T. Thaker, J. Coord. Chem., 2006, 59, 1191 CrossRef CAS.
- Y. Sato, Y. Kayaki and T. Ikariya, Organometallics, 2016, 35, 1257 CrossRef CAS.
- Z. He, S. B. Colbran and D. C. Craig, Chem. – Eur. J., 2003, 9, 116 CrossRef CAS PubMed.
- X.-H. Bu, M. Du, Z.-L. Shang, L. Zhang, Q.-H. Zhao, R.-H. Zhang and M. Shionoya, Eur. J. Inorg. Chem., 2001, 1551 CrossRef CAS.
- Y. Yamada, H. Sakurai, Y. Miyashita, K. Fujisawa and K. Okamoto, Polyhedron, 2002, 21, 2143 CrossRef CAS.
- J. Masternak, M. Zienkiewicz-Machnik, I. Łakomska, M. Hodorowicz, K. Kazimierczuk, M. Nosek, A. Majkowska-Młynarczyk, J. Wietrzyk and B. Barszcz, Int. J. Mol. Sci., 2021, 22, 1 Search PubMed.
- M. Zienkiewicz-Machnik, J. Masternak, K. Kazimierczuk and B. Barszcz, J. Mol. Struct., 2016, 1126, 37 CrossRef CAS.
- Z. He, D. C. Craig and S. B. Colbran, J. Chem. Soc., Dalton Trans., 2002, 4224 RSC.
- U. K. Das, J. Bobak, C. Fowler, S. E. Hann, C. F. Petten, L. N. Dawe, A. Decken, F. M. Kerton and C. M. Kozak, Dalton Trans., 2010, 39, 5462 RSC.
- A. Garoufis, S. Kasselouri and C. P. Raptopoulou, Inorg. Chem. Commun., 2000, 3, 251 CrossRef CAS.
- S. S. Massoud, M. Dubin, A. E. Guilbeau, M. Spell, R. Vicente, P. Wilfling, R. C. Fischer and F. A. Mautner, Polyhedron, 2014, 78, 135 CrossRef CAS.
- J. Ren, T. Lin, L. W. Sprague, I. Peng and L.-Q. Wang, J. Chem. Educ., 2020, 97, 509 CrossRef CAS.
- J. Irangu, M. J. Ferguson and R. B. Jordan, Inorg. Chem., 2005, 44, 1619 CrossRef CAS PubMed.
- F. Zippel, F. Ahlers, W. Werner, H. Hasse, H.-F. Nolting and B. Krebs, Inorg. Chem., 1996, 35, 3409 CrossRef CAS PubMed.
- S. Kumari, K. A. Mahato, A. Maurya, V. K. Singh, N. Kesharwani, P. Kachhap, I. O. Koshevoy and C. Haldar, New J. Chem., 2017, 41, 13625 RSC.
- I. Mantasha, M. Shahid, M. Kumar, A. Ansari, M. N. Akhtar, M. A. AlDamen, Y. Song, M. Ahmad and I. M. Khan, New J. Chem., 2020, 44, 1371 RSC.
- P. Chakraborty, I. Majumder, K. S. Banu, B. Ghosh, H. Kara, E. Zangrando and D. Das, Dalton Trans., 2016, 45, 742 RSC.
- M. N. Ahmad, F. Sama, M. N. Akhtar, Y.-C. Chen, M.-L. Tong, M. Ahmad, M. Shahid, S. Hussian and K. Khan, New J. Chem., 2017, 41, 14057 RSC.
- K. S. Banu, M. Mukherjee, A. Guha, S. Bhattacharya, E. Zangrando and D. Das, Polyhedron, 2012, 45, 245 CrossRef CAS.
- R. M. Silverstein, F. X. Webster and D. J. Kiemie, Spectrometric Identification of Organic Compounds, Wiley, 7th edn, 2005 Search PubMed.
- V. K. Bhardwaj, N. Aliaga-Alcalde, M. Corbella and G. Hundal, Inorg. Chim. Acta, 2010, 363, 97 CrossRef CAS.
- R. Marion, M. Zaarour, N. A. Qachachi, F. Justaud, D. Floner, O. Lavastre and F. Geneste, J. Biol. Inorg. Chem., 2011, 105, 1391 CAS.
- F. T. Ferre, J. A. L. C. Resende, J. Schultz, A. S. Mangrich, R. B. Faria, A. B. Rocha and M. Scarpellini, Polyhedron, 2017, 123, 293 CrossRef CAS.
- Z.-F. Chen, Z.-R. Liao, D.-F. Li, W.-K. Li and X.-G. Meng, J. Inorg. Biochem., 2004, 98, 1315 CrossRef CAS PubMed.
- J. Chirinos, D. Ibarra, Á. Morillo, L. Llovera, T. González, J. Zárraga, O. Larreal and M. Guerra, Polyhedron, 2021, 203, 115232 CrossRef CAS.
- E. C. M. Ording-Wenker, M. A. Siegler, M. Lutz and E. Bouwman, Dalton Trans., 2015, 44, 12196 RSC.
- K. Das, S. Dolai, P. Vojtíšek and S. C. Manna, Polyhedron, 2018, 149, 7 CrossRef CAS.
- S. Sarkar, M. Kim and H.-L. Lee, Bull. Korean Chem. Soc., 2021, 42, 1037 CrossRef CAS.
- S. Sarkar, A. Sim, S. Kim and H.-L. Lee, J. Mol. Cat. A: Chem., 2015, 410, 149 CrossRef CAS.
- I. A. Koval, C. Belle, K. Selmeczi, C. Philouze, E. Saint-Aman, A. M. Schuitema, P. Gamez, J.-L. Pierre and J. Reedijk, J. Biol. Inorg. Chem., 2005, 10, 739 CrossRef CAS PubMed.
- P. Sureshbabu, Q. M. Junaid, C. Upadhyay, W. Victoria, V. Pitchavel, S. Natarajan and S. Sabiah, Polyhedron, 2019, 164, 202 CrossRef CAS.
- J. Mukherjee and R. Mukherjee, Inorg. Chim. Acta, 2002, 337, 429 CrossRef CAS.
- M. S. Khan, M. Khalid, M. S. Ahmad, M. Shahid and M. Ahmad, J. Struct. Chem., 2019, 60, 1907 Search PubMed.
- L. Gasque, A. Mendieta and G. Ferrer-Sueta, Dalton Trans., 2020, 49, 3365 RSC.
- I. A. Koval, P. Gamez, C. Belle, K. Selmeczi and J. Reedijk, Chem. Soc. Rev., 2006, 35, 814 RSC.
- R. Maity, M. Maity, K. Jana, T. Maity, N. Sepay and S. Chandra, New J. Chem., 2023, 47, 2673 RSC.
- K. Selmeczi, M. Reglier, M. Giorgi and G. Speier, Coord. Chem. Rev., 2003, 245, 191 CrossRef CAS.
- K. Selmeczi, M. Reglier, G. Speier and G. Peintler, React. Kinet. Catal. Lett., 2004, 81, 143 CrossRef CAS.
- P. E. M. Siegbahn, J. Biol. Inorg. Chem., 2004, 9, 577 CrossRef CAS PubMed.
- I. A. Koval, K. Selmeczi, C. Belle, C. Philouze, E. Saint-Aman, I. Gautier-Luneau, A. M. Schuitema, M. van Vliet, P. Gamez, O. Roubeau, M. Lueken, B. Krebs, M. Lutz, A. L. Spek, J.-L. Pierre and J. Reedijk, Chem. − Eur. J., 2006, 12, 6138 CrossRef CAS PubMed.
- J. Kaizer, J. Pap, G. Speier, L. Parkanyi, L. Korecz and A. Rockenbauer, J. Inorg. Biochem., 2002, 91, 190 CrossRef CAS PubMed.
- S. K. Dey and A. Mukherjee, New J. Chem., 2014, 38, 4985 RSC.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141(7), 2814 CrossRef CAS PubMed.
- H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512 CrossRef CAS PubMed.
- Agilent, CrysAlis PRO, Agilent Technologies, Yarnton, England, 2011 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A:Found. Crystallogr., 2008, A64, 112 CrossRef PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226 CrossRef CAS PubMed.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006 CrossRef CAS PubMed.
- G. Yang, J. Chem. Crystallogr., 2004, 34, 269 CrossRef CAS.
- M. Reiher, Theor. Chem. Acc., 2006, 116, 241 Search PubMed and references therein.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- A. Kubas, C. Orain, D. de Sancho, L. Saujet, M. Sensi, C. Gauquelin, I. Meynial-Salles, P. Soucaille, H. Bottin, V. Fourmond, R. B. Best, J. Blumberger and C. Léger, Nat. Chem., 2017, 9, 88 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. J. Becke, Chem. Phys., 1993, 98, 5648 CAS.
- M. Sotoudeh, K. Laasonen and M. Busch, Electrochim. Acta, 2023, 443, 141785 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Bond lengths and angles for 1 and 2, relevant interatomic contacts for 1 and 2 and π⋯π interactions for 2, HS analysis for 1 and 2, 1H NMR spectra for complexes 1 and 2, UV-vis and CV spectra for 1 and 2, EPR spectra for 1 and the kinetics for [CuCl4]2−. CCDC 2212853 and 2213450. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt03478c |
| This journal is © The Royal Society of Chemistry 2025 |