SIMDAVIS 1.2: phosphonates are outstanding SIM ligands. Crown ethers are not

Abstract

This study presents SIMDAVIS 1.2, an updated dataset and analysis tool for lanthanide-based single-ion magnets (Ln-SIMs), focusing on the role of various ligands in influencing their magnetic properties. The revised dataset, accessible via a user-friendly online dashboard, encompasses over 10 000 data points on chemical and physical properties derived from more than 400 publications. Notably, the study redefines ligand classifications, introducing phosphonate-based ligands as a distinct family and highlighting their superior performance as SIM ligands compared to less effective alternatives such as crown ethers. Phosphonates exhibit promising pentagonal bipyramidal geometries that enhance magnetic stability by minimizing low-energy vibrational interactions. Comparative analysis reveals that while phosphonates may have moderate U_eff values compared to other leading ligands, their magnetic memory and hysteresis properties are comparable to those of bis-phthalocyaninato or metallocene sandwiches. This work emphasizes the importance of rational ligand selection and frugal data-driven approaches in the design of effective Ln-SIMs, contributing valuable insights into the optimization of single-ion magnet design strategies.

---

Introduction

AI hype vs. frugal modelling for data-based chemistry

The proponents of so-called artificial intelligence, and in particular in its meaning of generative artificial intelligence, have conquered our social imagination, and as a result, the usage of tools based on large language models has exploded. This has vast consequences, both positive and negative, not just on society in general but in particular in the academic world.^1–3 As a broader, well stablished research field, artificial intelligence includes machine learning, which has also become very popular recently and which the chemistry community is struggling to use rationally and productively.^4–6 Among the motivations towards these efforts to rationalize the automated use of data to extract insights and advance scientific knowledge, we need to highlight the need to work in a way that is consistent with our understanding of the current climate crisis. Rather than just pushing for efficiency, which carries the risk of the so-called Jevons’ paradox, we need to take a frugal approach to limit the actual carbon footprint.^7,8 Currently, most of the magnetic analysis of SMMs is done using theoretical models and calculations.⁹ While, only some seminal and outstanding works have been published on the use of data-driven approach to predict the properties of SMM structures using deep learning, nonetheless the model has a 70% accuracy in predicting the SMM properties.¹⁰ Lunghi et al. explores machine learning's role in predicting, optimizing, and modelling magnetic molecules, accelerating quantum simulations, and understanding environmental interactions, crucial for applications in data storage, spintronics, and quantum information technologies.¹¹ In this context, machine learning recognizes the value of optimized, curated data as a prime resource, specifically by revisiting the SIMDAVIS dataset of lanthanide-based single-ion magnets (Ln-SIMs) to enhance its quality without increasing computational costs.¹²

SIMDAVIS is a dataset and online dashboard of Ln-SIMs, accessible at https://rosaleny.shinyapps.io/simdavis_dashboard/. It allows the visualization of chemical and physical information manually recovered from over 400 publications; the dataset contains over 10 000 independent pieces of chemical information, as well as over 5000 independent pieces of physical (magnetic) information. Its initial analysis allowed discarding most attempted strategies for Ln-SIM design as fruitless, while confirming the two historically successful ones. Namely bis-phthalocyaninato Tb³⁺ complexes and Dy(III)metallocene-like sandwiches.^13,14 While it is true that this is a somewhat trivial result, it is nevertheless also true that there is value in knowing when to stop synthetic efforts on fruitless chemical strategies. There is a publication bias, even more so if one focuses on high-impact journals that facilitates involuntary cherry-picking, which results in well-meaning researchers pursuing follow-ups on the one good result of a chemical strategy with consistently mediocre results. Note that what we write “good/bad SIMs” along the manuscript, in which we mean the robustness of their magnetic memory, in particular long relaxation times resulting in hysteretic behaviour. We consider that observing hysteresis at a relatively high temperature is the real goal, whereas observing out-of-phase ac maxima is merely an indicator of whether one is advancing in the right direction. The energy barrier one obtains from fits is merely a parameter, an attempt to describe the mechanism, not a goal in itself. A chemical family where a novel member can be safely expected to display open hysteresis at 2 K, and where the best members have maximum hysteresis temperatures in the tens of K would be a “good” one.

Crucially, our initial study also raised a promising but so far underexplored approach: heptacoordinated lanthanides where the coordination sphere takes the shape of a pentagonal bipyramid, a symmetry that not only minimizes extradiagonal contributions to the ligand field Hamiltonian but also protects diagonal crystal field terms from low-energy vibrations, as detailed in ESI Section 7.2† of Duan et al. 2022.¹² However, the dataset lacked a singular category as a chemical family for the compounds with these properties. This was a consequence from an abundance of caution on our part in aiming for epistemological quality, as we cleanly divided the design phase of the dataset from the data acquisition and posterior analysis. Indeed, unless the statistical methods are chosen before the study is started, one introduces a risk that different approaches are explored –but not reported– and in the final, published version, with the method being chosen to produce the results that are expected (or desired) by the researchers. An independent follow-up study as the present one allows us to improve this analysis while avoiding this risk.

A second major insight of the initial SIMDAVIS study was revealing an unexpected relation between Orbach and Raman parameters, for which we suggested as a possible rationalisation a common factor to the two mechanisms in the form of spin-vibrational coupling, which influences relaxation whether it involves real or virtual spin states. However, we lacked any finer details on how to relate the combination of ligands to spin-vibrational coupling. In particular, it would have been interesting to study the behaviour of systems based on mixtures of different kinds of ligands.

Herein, we present a substantial revision of the two least useful chemical classes within our previous dataset, namely “mixed ligands” and “other families”. Since they were also among the largest classes, this involved reclassifying hundreds of samples. Part of this effort served to revise the original dataset, but mostly it served to include new categories that were not defined in the previous version. Most notably these were phosphonate-based ligands and crown ethers. Additionally, for complexes with different ligands sharing their coordination sphere, the new classifications and definitions allows testing whether the spin relaxation can be best predicted by considering the “best” or the “worst” ligand in terms of Ln-SIM behaviour. Our goal is to invest a substantial amount of human time and a very moderate computational effort, with a negligible carbon footprint, on the analysis of experiments that have already been performed. This can allow one to obtain novel insights and to test hypotheses without incurring in an irresponsible waste of our carbon budget.

Methods

As in the original version of the SIMDAVIS dataset, we focus our attention on the temperature (in K) at which a maximum in out-of-phase ac susceptibility has been measured at a frequency close to 1000 Hz, which we denote T_B3, and, in the cases where hysteresis has been reported, the temperature T_hyst (in K) up to which hysteresis survives, using a sweep rate less than 0.3 T s⁻¹, to exclude pulses of magnetic field that exaggerate the apparent magnetic memory, and corresponding to highest temperature at which the system presents magnetic bistability. Additionally, in the cases where the maximum in out-of-phase ac susceptibility appears only when applying an external dc magnetic field, we record the temperature where this maximum appears (always at a frequency close to 1000 Hz) as T_B3H.

What have we changed in the dataset?

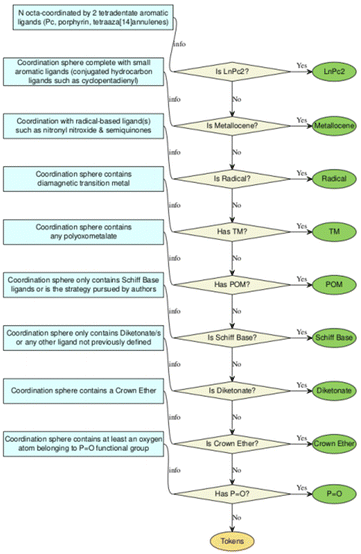
A revision of the original approach of 1411 compounds with SIM properties depicted in the dashboard-style web application SIMDAVIS was done. It depicts the original search between 2003 to 2019, which is a dashboard using R language and Shiny, an open-source R package to create the interactive web app. This interface allows for variables in the analysis, and subsets of the data, to be adjusted and chosen in real-time.

Originally, the compounds were classified into 9 chemical families, being defined according to their ligands of the Ln³⁺ complexes: LnPc₂, POM, Schiff base, metallocenes, diketonates, radicals, TM near Ln, mixed ligands, and other families. The same criteria were used to analyse the data of each complex but introducing some new considerations:

• POM family: the polyoxometalate (POM) family consists of complexes where lanthanide ions are coordinated with at least one POM ligand and is often complemented by other ligands.

• Schiff base family: this section covers complexes based on Schiff base ligands, in which the imine group in combination with others donor atoms like nitrogen, oxygen, sulfur, or phosphorus of the same molecule can coordinate lanthanide ions. No consideration is given to solvent or smaller ions that complete the coordination sphere of these complexes.

• Diketonate family: lanthanide complexes are coordinated by the 1,3-diketones or β-diketones, known for their bidentate chelating properties. The complexes need to have at least 2 β-diketones ligands coordinated to the lanthanide ion, and the coordination sphere is completed with other auxiliary ligands such as H₂O, aza-aromatic ligands, solvent molecules, etc.

Moreover, this re-categorization and revision of the data set allowed to reassign 237 complexes and to define two new families: phosphonate (P=O) and crown ether. The definitions of these two families are:

• Phosphonate family: correspond to lanthanide complexes, in which at least two P=O group that is negative charged coordinate a Ln³⁺ ion in different coordination modes, and the first coordination is complete with small and/or neutral ligand. Coordination number of 6 to 9 are found with octahedral to muffin geometries, respectively (For more details see ESI S2.1†).

• Crown-ether family: the crown ether ligands are polydentate heterocycles and are linked through the oxygen atom or some other heteroatom. This family includes complexes where the lanthanide ion is coordinated with at least one crown ether ligand and the first coordination sphere is complete with other small ligands, such as nitrate (for more details see ESI S2.2†).

Note that other interesting families have not been given their own category in the current classification, e.g. complexes based on macrocyclic ligands such as DOTA-like systems. In general, this is because we judged the number of cases to be insufficient to give statistical information. All changes done to data set can be found at SIMDAVIS web application but also is presented in Table 1.

Table 1 Data set reordering of the “mixed ligand” and “other families”, and the family destination to those compounds

Original family	New family	Count
Mixed ligands	Metallocene	1
	POM	3
	Schiff base	35
	Diketonate	108
	Crown ether	34
	P=O	45
Other families	Diketonate	2
	P=O	9

---

Data visualisation

The data visualisation on the SIMDAVIS app is based on R^15,16 a widely used software environment for statistical computing and graphics, and the shiny package to build interactive web applications.¹⁷ The R packages readr,¹⁸ dplyr,¹⁹ DT,²⁰ ggplot2²¹ have also been used. The dashboard-style web application is available at https://go.uv.es/rosaleny/SIMDAVIS.

Fig. 3 shows violin plots where the width of each one is proportional to the density of data points for this range of values, and the horizontal stripes mark the quartiles. Fig. 4 shows a lineal regression, and the shadowed area represents a 95% confidence interval. This compares very favourably with high-throughput studies²² where energy consumption can be in the order of 20 MW h, with associated emissions in the order of 5T CO₂ eq., i.e. a factor of around 10 000 higher than the present case. While knowledge cannot be easily quantified, it seems clear that a limited carbon budget would favour, for the same climate cost, 10 000 frugal studies rather than a single high-throughput one. Thus, all the work performed, including manual and automatic data processing, was performed on personal computers and resulted in a trivial carbon footprint (<10 kW h resulting in <2 kg CO₂e, equivalent to <10 km in a passenger car).

Results and discussion

New families and the particularities of phosphonate-based complexes

The rapid development of synthetic strategies that allow the design of coordination compounds with Ln³⁺ ions with potentially interesting magnetic properties has generated a large number of compounds in the last three decades. The realisation that lanthanide SIMs were not restricted to a single chemical family inspired a large community of chemists to explore different types of compounds. With no single chemical strategy dominating in terms of reported examples.

In a first approximation, Duan et al.¹² collected and categorised 1411 compounds that had been magnetically characterized between the years 2003 to 2019, developing a user-friendly dashboard-style web application named SIMDAVIS (Single Ion Magnet DAta VISualisation). As a first phase, we redefined the classification in chemical families within the SIMDAVIS dataset as depicted in the flowchart depicted as Scheme 1. We carefully analysed the categories “mixed ligands” with 553 compounds and “other families” with 202 compounds, to reassign some of the systems reported in those families. The ligand analysis of the complexes allowed us to reassign 110 records to the diketonate family, 35 to Schiff base, 3 to POM and 1 to metallocene (Fig. 1).

Scheme 1 Flowchart for the classification of chemical families in SIMDAVIS 1.2.

Fig. 1 Relation of the chemical families and the value U_eff incorporating the two new families depicted in this work. Extracted from SIMDAVIS webpage.

By the analysis of the molecular structures and their corresponding representations, already defined in the previous work and available through the dashboard, thus not shown here, allowed us to evidence the presence of two large groups of ligands that were not categorised as a family. Due to their chemical and magnetochemical relevance, we introduced the crown ether family, defined as containing a “crown ether” in the coordination sphere and the phosphonate family defined as presenting at least one oxygen atom belonging to phosphonate ligand, “P=O”. Moreover, we have re-define the family diketones, whereas in the original study we assigned to the diketonate family (barring errors) “samples with Ln³⁺ ions coordinated with diketonate ligands and diketonate ligands mixed with other molecules which are not defined in the classification”, we now consider that the complexes need to have at least 2 β-diketonate ligands coordinated to the lanthanide ion (Fig. 1). Even more, we introduced a system of data tokens, where for all compounds not pertaining to any of the defined families we considered the presence of a series of important ligands in their coordination sphere. There we register whether the complex contains ligands of any of the following categories, in any combination: carboxylate, diketonate, Schiff base, Cp*/COT or phthalocyaninato. Thus, complexes with e.g. two Pc²⁻ ligands will pertain to the category LnPc₂ whereas a complex with a single Pc⁻ and a diketonate ligand would be in the Mixed ligands category, with the two tokens: Pc and diketonate (Scheme S1†). Let us start by presenting the chemical features of the two new families before moving on to further analysis of their magnetic behaviour in the wider context of the rest of the dataset.

Crown ether family

The crown ether family includes compounds where the Ln³⁺ ion is coordinated with at least one crown ether ligand and the entire coordination sphere with other small ligands, where the lanthanide complexes have coordination numbers of 8, 9 and 10, thus 34 complexes match this depiction. An example can be found in Fig. 2. Naïvely, one could think that the presence of a 4-coordinated ligand could make this family close in behaviour to the Pc family. One needs to consider that the other coordination positions have a very large mobility. The fact is that for this family, the highest U_eff value is 75.9 K for a half-sandwich crown ether Dy³⁺ complex with coordination number 10 and a sphenocorona geometry reported by Li et al.²³ for more information see ESI (Fig. 2 and Fig. S1†).

Fig. 2 Polyhedron of crown ether-Ln³⁺ complex, [Ln(12-crown-4)(NO₃)₃] (sample_ID = 854). Colour scheme for atoms: cyan, Ln; grey, C; blue, N; red, O; white, H.

Phosphonate family

Even though we simply defined the phosphonate family as presenting at least one oxygen in the coordination sphere pertaining to a P=O phosphonate group, with 54 samples responding to that description. We verified that this chemical family is very rich in 7-coordinated complexes, in particular presenting pentagonal bipyramid geometry. This is easily rationalised chemically since these phosphonate-based ligands tend to be bulky and coordinate axially from two opposite directions, leaving 5 equatorial coordination sites for smaller ligands resulting in a 1 + 5 + 1 structure.²⁴ We found that these are almost exclusively coordinated by oxygen in published literature, but we can find no fundamental reason why these sites could not be occupied by N donors.

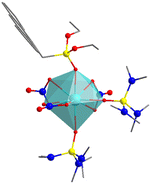
Within 7-coordinated complexes in the phosphonate family. we encounter multiple cases with 6 or 4 ligands. This of course is to be understood as the presence of bi- or tri-dentate ligands that nevertheless do not alter the basic 1 + 5 + 1 structure, but the best results are obtain with negative axial ligands and neutral ones in the equatorial plane, thus adopting D_5h symmetry.²⁵ We do find examples within this family with coordination numbers (CN) of 6, 8 and 9, with octahedral, bipyramidal pentagonal, triangular dodecahedron and muffin geometries²⁶ (Table 2).

Table 2 Molecular structures of some representative Ln³⁺ Phosphonate SIMs (define as P=O in SIMDAVIS) and some of their chemical and magnetic descriptors. Colour scheme for atoms: cyan, Ln; grey, C; blue, N; yellow, P; red, O. H atoms are not shown for clarity

	A	B	C	D
CN	6	7	8	9
U eff (K)	51.2	460	40.5	20.4
τ 0 (s)	5.89 × 10^−6	2.00 × 10^−11	5.20 × 10^−8	1.50 × 10^−8
T B3H (K)	15	30	5	2.4
Closest polyedron	Octahedron	Pentagonal bipyramid	Biaugmented trigonal prism	Muffin
Sample_ID	1214	1059	1309	1046
CCDC_COD	COD 4132550	COD 7121940	CCDC 1884676	CCDC 1833630

---

More interestingly, one needs to highlight that complex of the phosphonate family present uniquely axially compressed geometries, meaning the axial oxygens are considerably closer than the equatorial ones. This is to be expected purely for geometric reasons, in which the structural feature correlates with the magnitude of the energy barrier. Thus, if we compare the structure of [(^tBuPO(NHⁱPr)₂)₂Dy(H₂O)₅]⁺ (sample_ID = 781), which has an average axial distance of 2.206 Å (Dy–O=P) and an average equatorial distance of 2.363 Å (Dy–O–H₂).²⁷ Therefore, possessing a compressed pentagonal bipyramidal geometry, which is also expected due to the nature of both ligands, in which the phosphonate is anionic, and the water molecules are neutral, being the first should be closer to the Dy³⁺ ion than the other ones, making this complex the one with the largest U_eff value (651 K) of this family. On the other hand, complexes with octahedral geometry have Dy–O distances that do not show compression or elongation in any direction do not have good SIM behaviour like [Dy(CpCo{P(O)(OEt)₂}₃)₂]⁺ (sample_ID = 943), in which the Dy–O=P distances are almost the same, 2.256 to 2.251 Å.²⁸ However, it is interesting that this simple tendency still dominates despite the typically bulky nature of the axial phosphonate-based ligands. Examples of this type of complexes for each coordination number are shown in Table 2.

Phosphonate complexes vs. LnPc₂ and metallocene derivatives

Our initial study already included examples of phosphonate-based complexes as promising. The current analysis confirmed this. It is trivial to see that crown ethers are not particularly good as SIMs, and these data are only depicted briefly in the ESI,† with the whole information being available in the dashboard. Let us here instead focus on phosphonate complexes and compare them with the [LnPc₂]⁻ and metallocene families in Fig. 3.

Fig. 3 Violin type graph of U_eff (A), T_B3 (B) and T_hyst (C) of the families: LnPc₂. Metallocene and phosphonate. For definitions of T_B3 and T_hyst. See ESI† in Duan et al.¹²

Fig. 3a shows that complexes in the P=O family statistically tend to present a slightly above-mediocre U_eff, with a median value around 80 K, which is somewhat above all other families except [LnPc₂]⁻ and metallocene, but indeed rather low compared with median U_eff values around 200 K for [LnPc₂]⁻ and metallocene families (Fig. 3a). These results are overcompensated since it is clear from the analysis that there is group of complexes with compressed pentagonal bipyramidal geometries with axially phosphonate groups, and neutral water molecules in the equatorial plane that present large U_eff values of around 600 K. Moreover, phosphonate complexes do present an extraordinary magnetic memory, as one can see in Fig. 3b and c. Indeed, the distributions of (quantitative) maximum recorded temperatures T_B3(K) and T_hyst(K) are competitive with the best families, as is the frequency of (qualitative) recordings of hysteresis or maximum of out-phase ac signal.

Verifying the data case by case, one can see that the discrepancy with the U_eff distribution is partly due to a few systems with high hysteresis temperature where U_eff was not determined^29,30 and this can be disregarded as noise. However, one can see that this is also partly due to other systems where, despite presenting a relatively low U_eff (in the 10–150 K window) do present an intriguingly good magnetic memory.^31,32 The disparity may confirm the postulated mechanism of symmetry protection of diagonal crystal field terms from low-energy vibrations postulated in Duan et al.¹² Also, from the data is observed that all 7-coordinate Dy³⁺ phosphonate complexes have the higher U_eff values with values below 100 K, for 9, 8 and 6-coordinate Dy³⁺ complexes are in the middle section, being the lowest one the 9-coordinate complex, [Dy(depma)(NO₃)₃(hmpa)₂] (sample_ID = 1046) with a U_eff = 20.4 K. Non Dy³⁺ systems are ones with lowest energy barriers, such as Er³⁺ or Nd³⁺, see Fig. 4. In contrast, the family of crown ethers not shown here, presents mediocre properties as SIMs both in terms of T_B3 and T_hyst.

Fig. 4 Ln(U_eff) vs. Ln(τ₀) linear relation between the P=O (purple) and metallocenes (green) done using the app SIMDAVIS. Also, the graph shows the coordination number for the P=O complexes and offer an easy comparison between both families.

Let as delve deeper into the apparent minimization of spin–vibrational coupling in phosphonate complexes. Since vibrations that alter metal–ligand bond distance tend to be high-energy they are not expected to be the ones limiting the working temperature for slow relaxation of the magnetisation. Instead, low frequency vibrations affecting the angles change can be the ones mediating spin relaxation, so they should be key in an analysis of spin-vibrational coupling. As we suggested elsewhere,¹² an ideal pentagonal bipyramid presents only two types of ligands: perfectly axial ligands and perfectly equatorial ligands. This means that the positions of the donor atoms are situated on the angular maxima of the diagonal spherical harmonics (B20, B40 and B60). This means that the crystal field is quadratically protected against angular distortions: at an angular maximum, the first derivative of the spherical harmonics, and thus, the change in any diagonal term in the crystal field Hamiltonian, is zero. This special geometrical correspondence should allow pentagonal bipyramids to be especially resilient to angular (twisting, wagging, bending) vibrations which, being the lowest in energy, can be present even at low temperatures and facilitate magnetic relaxation most often. These results are consistent with the conclusions of Lunghi et al. in which rigid and bulky ligands can minimize low-energy lattice vibrations (phonons), which are responsible for Raman relaxation.³³ Finally, it is worthy to mention that just recently, a new publish work, also by the same author, which presented machine learning method for the prediction of vibrational spectra and spin-phonon couplings for molecules with a computational savings of at least 80% compared to the full ab initio approach.³⁴

Phosphonates, as metallocenes, promote Orbach-only relaxation

The Orbach relaxation mechanism is parameterised by (a) an effective barrier U_eff, associated to the energy difference with an excited state which plays a role in the relaxation process analogous to a reaction intermediate in a stepwise reaction, and (b) a characteristic time τ₀, which reflects the relaxation time at temperatures that are very high compared with U_eff expressed as an equivalent temperature. Often, this mechanism is as summed to be the dominant one when fitting experimental data, and thus the effect of other mechanisms results in unphysical corrections of U_eff and τ₀; these can include Raman mechanisms, quantum tunnelling of the magnetization, the direct relaxation process and even additional Orbach relaxation pathways over alternate barriers. It can then be interesting to have further independent information to get some insight into the validity of the assumption of Orbach as dominant mechanism. Statistical relations may be helpful on this type of study. Under a certain simplified model,³⁵ a relation of τ₀ and (U_eff)⁻³ exist between them. One can expect, then, that when plotting ln(τ₀) vs. ln(U_eff) for a sufficient number of analogous systems, the appropriate slope can be recovered, if the Orbach mechanism is dominant. However, if the parameters have been substantially altered or contaminated to correct for the effect of other relaxation mechanisms, there is no reason to expect this ideal slope (see ESI, section S.3†).

In the previous analysis,¹² we only focused on the different slopes (n) and intercepts (R_or) of the approximate equation τ₀⁻¹ = R_or·(U_eff)ⁿ and found that collectively slopes of around n = 2.5 were found both for prolate and oblate ions, although with intercepts differing in a factor of 5 (500 K^−2.5 s⁻¹ for oblate ions and 2500 K^−2.5 s⁻¹ for prolate ions). It was only in the cases where one plots U_eff.ffvs. τ_0.ffi.e. for the cases where a “full fit” was available in the bibliography, which separated the contributions of Orbach, Raman and QTM processes, where a n = 3 was found, the expected value for a two-phonon Orbach process within the Debye model for phonons.³⁵ In the present case, we considered the different chemical families and found a striking coincidence between the slopes of the metallocene and phosphonate families, which both present the closest slope to n = 3 among all the studied families (Table S2†). These similar results suggest that both systems are compatibles with the Orbach Relaxation Rate model depicted by Duan et al.¹² which means that the main relaxation mechanism is Orbach, with less or no contribution of the other mechanisms (Raman, Direct and QTM). Structurally, when we compare the P=O and metallocenes families, it is possible to observed that in both cases the axiality is induce in one case with coordination of neutral ligands in the equatorial plane and in the second case, no equatorial coordination is depicted in the structures. This means that the axial coordination is quite close to the Ln³⁺ centre, that may influence the relaxation dynamics of these complexes.

This is to be rationalized as meaning that in these families the two-phonon Orbach process, within the Debye model for phonons, is a strikingly good approximation, at least for the data that give rise to these fits i.e. relatively high frequencies and relatively high temperatures. This would mean that the Raman processes are quenched for those families. An open question is the relative importance of Orbach vs. Raman in different regimes and for different chemical families. This could be addressed by simulation of ac experiments and hysteresis experiments employing the same sets of parameters, to quantify the deviation of the simulated hysteresis in different families. Since the STOSS simulator has been employed for similar purposes,^36,37 some of us are currently working on a version of STOSS that is able to explore this inexpensively and this will be the subject of an upcoming work.

Is the best or the worst ligand the one determining relaxation?

These data let us do a first data-based test of what we can call the “bad apple” vs. “champion” hypotheses. I.e. can a single floppy ligand accelerate spin relaxation by itself, or does a high-barrier inducing ligand slow down relaxation by itself? If the overall strength of the ligand field is the main factor controlling the effective barrier and thus governing relaxation speed, one could expect that the strongest LF-inducing ligand, such as a cyclopentadienyl anion will be the one governing spin relaxation, and its influence should be noticeable regardless of the presence of other ligands. On the contrary, if the coupling between spin states and molecular vibrations is the key, the presence of a single floppy ligand with accessible vibrations would be expected to favour spin-vibrational mixing, even if the overall LF is very strong. To distinguish between the two competing qualitative hypotheses, we compare the behaviour of complexes with different kinds of ligands. Meaning if a “mixed ligand” complex based on a metallocene with another ligands this tends to result in a higher-than-average U_eff, because metallocene's tend to act as strong ligands. However, even though they are also very rigid ligand, the other ligands completing the coordination sphere are the ones which will offer rapid relaxation paths and thus the actual behaviour will be that of a mediocre SIM at best, with most cases displaying no out-of-phase ac peak. This is also consistent with the good behaviour of DyC81N, where the U_eff is weak but there is just no available floppy ligand.³⁸

The hypothesis depicted above, can be tested by comparing the experimental results of some metallocenes systems. The [Dy(Cp^iPr5)₂]⁺ (sample_ID = 1412) compound has a U_eff value of 1919.3 K, and taking this compound as reference, it is possible to infer that axiality govern the relaxation dynamics in Dy³⁺ complexes, since for the [(Cp^iPr5)Dy(Cp*)]⁺ (sample_ID = 1408) the U_eff = 2217 K, which is the highest magnetization energy barrier ever recorded. Thus, since both systems present the (Cp^iPr5)²⁻ ligand, it could be inferred that this is a strong ligand and such the combination with other ligands should not affect its energy barrier. However, compounds such as, [(Cp^iPr5)Dy(BH₄)₂(THF)] (sample_ID = 1406) and [(Cp^iPr5)Dy(Cp*)(BH₄)] (sample_ID = 1407), display much lower energy barriers, being for the first 346.7 K and 10 K, respectively. Therefore, the “other ligands” can displace around the Ln³⁺ ion disrupting the first coordination sphere inducing rapid relaxation paths, which diminish the good SIM behaviour.^14,38 The definition of best or worst ligands cannot be taken solely as a single dependency of the relaxation dynamics, since metallocene systems like [Dy(COT)₂]⁻ (sample_ID = 294) has a small U_eff value (11 K), but the Er³⁺ analogue has a larger value of 286 K that can be defined as good SIM, being the disposition of the ligands in the Dy³⁺ complex, the main cause that this compound does not have good SIM behaviour.³⁹ Thus, as for the P=O family the same behaviour can be applied, since for Ln³⁺ complexes with “strong” negatively charge phosphonate ligand axially coordinated, in all cases when water molecules complete the coordination sphere (equatorially) the U_eff value in all cases is large, circa 600 K (sample_ID = 781). When this axiality is not present in Ln³⁺ phosphonate complexes, the U_eff value dramatically decreases, like for example, to 38.2 K for [Dy(notpH₄)(H₂O)]ClO₄·3H₂O (sample_ID = 541).

Not only do some complexes show improved energy barriers, but the increase in the relaxation times (τ₀) is also an important factor since many SIMs with high energy barriers have slow relaxation times. For instance, purely inorganic Ln³⁺-POMs like [Ln(XW₁₁O₃₉)₂]ⁿ⁻, despite their near-perfect D_4d symmetry, often lack good SIM behaviour. When organic ligands are added, the energy barriers do not change, but relaxation times can improve up to 1000-fold.^40,41 In homoleptic complexes the Ln–O distances do not change much due to the nature of this type of systems. But their crystalline packing is full of cations and water molecules surrounding the Ln³⁺-POMs complex, which can affect the first coordination sphere—especially alkaline ions that can distort the Ln³⁺ centre.⁴² As a result, supramolecular structure alters the ligand field and magnetic relaxation. In contrast, metallocene and phosphonate complexes, stabilized mainly by intermolecular interactions rather than covalent bonds, remain less influenced by counter-cations or solvents, leading to reduced spin-phonon coupling and better energy barriers. Thus, while flexible and strong ligands are important for magnetization barriers in SIMs, other factors like the oblate/prolate nature of the Ln³⁺ ion and the supramolecular environment are also crucial.

Exceptions with low barrier but robust magnetic memory

Despite a relatively robust trend of U_eff having a good predicting character of the robustness of the magnetic memory, some complexes show low U_eff values, yet surprisingly high T_hyst (and vice versa). This thought-provoking disparity and apparent contradiction are perhaps most apparent in the phosphonate family, see Fig. 3. While there may be different possible reasons for this, we want to emphasize that one needs to consider the silent assumption that the same relaxation mechanism is operating in the hysteresis experiment and in the ac experiment, which may often not be the case. It would be very beneficial to the field to apply a single simulation tool for different kinds of experiments, as was recently done in an endohedral metallofullerene SIM where the decay of the magnetization could be fit with Raman and Quantum Tunnelling of the Magnetization parameters that proved inadequate to reproduce the hysteresis behaviour, revealing the role of the direct mechanism and probably also of a phonon bottleneck.^36,37 This is however outside the scope of the present study and will be the subject of an upcoming work.

Conclusions and future outlook

Firstly, this work has introduced new classifications of chemical families, highlighting the P=O ligands effectiveness for obtaining single-ion magnets, as well as improving the current classification for three of the original families (POM, Schiff base and diketonates). The P=O family presents enhanced magnetic properties due to their pentagonal bipyramidal geometries that minimize low-energy vibrational interactions. On the other hand, their effective energy barriers (U_eff) are comparable to metallocenes and bis-phthalocyaninato complexes, exhibiting similar magnetic memory and hysteresis properties. In contrast, both crown ethers and carboxylates prove ineffective, presumably due to their structural flexibility, which accelerates spin relaxation. The study also indicates that both phosphonate-based and metallocene-based SIMs predominantly follow an Orbach relaxation mechanism, with a nearly-ideal exponent n ∼2.9 in the relation between τ₀ and U_eff.

Newer chemical strategies, such as endohedral metallofullerene complexes show a lot of potential, but the limited data up to 2019 prevent us to do a comprehensive analysis using the same methods; an upcoming expanding the dataset may allow this as well as strengthen the overall statistical power of these conclusions. Finally, an updated version of the STOSS code will soon allow the reinterpretation of the SIMDAVIS dataset by simulation of hysteresis data employing parameters extracted from ac fits to clarify the main relaxation mechanisms for each family.

Author contributions

Conceptualization and software: A.G.A. and L.E.R. Methodology: A.G.A., L.E.R., W.C.M. and C.G.P. Investigation and formal analysis: W.C.M and C.G.P. Supervision: W.C.M. and A.G.A. Original draft: A.G.A. Reviewing and editing: A.G.A., L.E.R., W.C.M and C.G.P.

Data availability

The dataset collected and analyzed during this study is freely available for download at SIMDAVIS Dataset. ESI† contains the updated SIMDAVIS dataset.

Code availability: All custom code generated and employed for this study, namely the SIMDAVIS app version 1.2.0. is freely available for download at SIMDAVIS Code. In addition, it can be downloaded as the ESI Software 1 (includes a SIMDAVIS Guide file).†

Conflicts of interest

All authors state that there are no conflicts to declare.

Acknowledgements

W. C. M. and C. G. P. thanks FONDECYT Regular 1211282 and UBO for the institutional support grant for hiring a research assistant (UBO Rect. Nº 3000/1221/23). WCM also thanks ECOS 200027 (C20E04) and CEDENNA for financial support. W. C. M. also thanks FONDEQUIP-EQM130086 and French-Chilean International Research project “Cooperation in Inorganic Chemistry” (CoopIC). A. G. A. has been supported by the Generalitat Valenciana (GVA) CIDEGENT/2021/018 grant.

References

1. W. Liang, Z. Izzo, Y. Zhang, H. Lepp, H. Cao, X. Zhao, L. Chen, H. Ye, S. Liu, Z. Huang, D. A. McFarland and J. Y. Zou, arXiv, 2024, preprint,  DOI:10.48550/arXiv.2403.07183.
2. W. Liang, Y. Zhang, Z. Wu, H. Lepp, W. Ji, X. Zhao, H. Cao, S. Liu, S. He, Z. Huang, D. Yang, C. Potts, C. D. Manning and J. Y. Zou, arXiv, 2024, preprint, arXiv:2404.01268, https://arxiv.org/abs/2404.01268.
3. M. Dingemanse, OSF, 2024, preprint, osf.io/2c48n_v1, https://osf.io/preprints/osf/2c48n_v1.
4. D. Dalmau and J. V. Alegre-Requena, ChemRxiv, preprint, 2023,  DOI:10.26434/chemrxiv-2023-k994h.
5. M. Gallegos, V. Vassilev-Galindo, I. Poltavsky, Á. Martín Pendás and A. Tkatchenko, Nat. Commun., 2024, 15(1–13), 4345,  DOI:10.1038/s41467-024-48567-9.
6. S. Zavitsanou, Z. Bo, E. Casali, M. Langton and F. Duarte, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-fqdtn.
7. B. Alcott, Ecol. Econ., 2005, 54, 9–21,  DOI:10.1016/j.ecolecon.2005.03.020.
8. G. M. Gutiérrez-Finol, A. Ullah, M. González-Béjar and A. Gaita-Ariño, Green Chem., 2025, 27, 3167–3177,  10.1039/D4GC04900D.
9. A. Lunghi, in Computational Modelling of Molecular Nanomagnets, ed. G. Rajaraman, Springer International Publishing, Cham, 2023, pp. 219–289.  DOI:10.1007/978-3-031-31038-6.
10. Y. Takiguchi, D. Nakane and T. Akitsu, IUCrJ, 2024, 11, 182–189,  DOI:10.1107/S2052252524000770.
11. A. Lunghi and S. Sanvito, Nat. Rev. Chem., 2022, 6, 761–781,  DOI:10.1038/s41570-022-00424-3.
12. Y. Duan, L. E. Rosaleny, J. T. Coutinho, S. Giménez-Santamarina, A. Scheie, J. J. Baldoví, S. Cardona-Serra and A. Gaita-Ariño, Nat. Commun., 2022, 13, 7626,  DOI:10.1038/s41467-022-35336-9.
13. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695,  DOI:10.1021/ja801659m.
14. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403,  DOI:10.1126/science.aav0652.
15. R Core Team, R: A Language and Environment for Statistical Computing, R version 4.2.3, 2018, https://www.R-project.org/.
16. Posit team, RStudio: Integrated Development Environment for R, version 2024.12.1, 2024, https://www.posit.co/.
17. W. Chang, J. Cheng, J. J. Allaire, Y. Xie and J. McPherson, Shiny: Web application framework for R. R Package version 1.7.5, 2023, https://CRAN.R-project.org/package=shiny.
18. H. Wickham, J. Hester, R. Francois, S. Bearrows and J. Bryan, readr: Read rectangular text data. R package version 2.1.4, 2023, https://CRAN.R-project.org/package=readr.
19. H. Wickham, R. François, L. Henry and K. Müller, dplyr: A Grammar of Data Manipulation. R package version 1.1.3, 2023, https://CRAN.R-project.org/package=dplyr.
20. Y. Xie, J. Cheng and X. Tan, DT: A wrapper of the JavaScript library ‘DataTables’. R package version 0.30, 2023, https://CRAN.R-project.org/package=DT.
21. H. Wickham, W. Chang, L. Henry, T. L. Pedersen, K. Takahashi, C. Wilke, K. Woo, H. Yutani, D. Dunnington and T. van den Brand, ggplot2: Create elegant data visualisations using the grammar of graphics. R package version 3.4.3, 2019, https://CRAN.R-project.org/package=ggplot2.
22. L. Mariano, V. Nguyen, V. Briganti, A. Lunghi and J. Am, Chem. Soc., 2024, 146(49), 34158–34166,  DOI:10.1021/jacs.4c14076.
23. F. Gao, F. L. Yang, X. Feng, H. Xu, W. Sun, H. Liu and X. L. Li, Dalton Trans., 2017, 46, 1317–1323,  10.1039/C6DT04353D.
24. Y. S. Ding, T. Han, Y. Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y. Z. Zheng, Chem. – Eur. J., 2020, 26, 5893–5902,  DOI:10.1002/chem.202000646.
25. A. Swain, T. Sharma and G. Rajaraman, Chem. Commun., 2023, 59, 3206–3228,  10.1039/D2CC06041H.
26. J. Ali, P. Kumar and V. Chandrasekhar, Chem. – Asian J., 2024, 19(1), e202300812,  DOI:10.1002/asia.202300812.
27. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191,  10.1039/C6SC00279J.
28. K. S. Lim, J. J. Baldoví, S. Da Jiang, B. H. Koo, D. W. Kang, W. R. Lee, E. K. Koh, A. Gaita-Ariño, E. Coronado, M. Slota, L. Bogani and C. S. Hong, Inorg. Chem., 2017, 56, 4911–4917,  DOI:10.1021/acs.inorgchem.6b03118.
29. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837,  DOI:10.1021/jacs.5b13584.
30. A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chem. Commun., 2018, 54, 8273–8276,  10.1039/C8CC03929A.
31. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Commun., 2016, 52, 7168–7171,  10.1039/C6CC03066A.
32. D. Zeng, M. Ren, S.-S. Bao, J.-S. Feng, L. Li and L.-M. Zheng, Chem. Commun., 2015, 51, 2649–2652,  10.1039/C4CC09341K.
33. S. Mondal and A. Lunghi, J. Am. Chem. Soc., 2022, 144(50), 22965–22975,  DOI:10.1021/jacs.2c08876.
34. V. Briganti and A. Lunghi, npj Comput. Mater., 2025, 11(62), 1–9,  DOI:10.1038/s41524-025-01547-z.
35. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970.
36. G. M. Gutiérrez-Finol, S. Giménez-Santamarina, Z. Hu, L. E. Rosaleny, S. Cardona-Serra and A. Gaita-Ariño, npj Comput. Mater., 2023, 9, 196,  DOI:10.1038/s41524-023-01149-7.
37. Z. Hu, Y. Wang, A. Ullah, G. M. Gutiérrez-Finol, A. Bedoya-Pinto, P. Gargiani, D. Shi, S. Yang, Z. Shi, A. Gaita-Ariño and E. Coronado, Chem, 2023, 9, 3613–3622,  DOI:10.1016/j.chempr.2023.08.007.
38. K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503,  10.1039/C8SC03907K.
39. M. Li, H. Wu, S. Zhang, L. Sun, H. Ke, Q. Wei, G. Xie, S. Chen and S. Gao, Eur. J. Inorg. Chem., 2017, 811–819,  DOI:10.1002/ejic.201601188.
40. W. Cañón-Mancisidor, M. Zapata-Lizama, P. Hermosilla-Ibáñez, C. Cruz, D. Venegas-Yazigi and G. Mínguez Espallargas, Chem. Commun., 2019, 55, 14992–14995,  10.1039/C9CC07868A.
41. S. Sarwar, S. Sanz, J. van Leusen, G. S. Nichol, E. K. Brechin and P. Kögerler, Dalton Trans., 2020, 49, 16638–16642,  10.1039/D0DT03716H.
42. J. Iijima, H. Naruke and R. X. Suzuki, ACS Omega, 2023, 8, 9673–9683,  DOI:10.1021/acsomega.3c00711.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00417a

---