Metal speciation of volcanic aerosols from Mt. Etna at varying aerosol water content and pH obtained by different thermodynamic models

Abstract

Mt. Etna, an open-vent, persistently degassing volcano, is the tallest and most active volcano in Europe. Aerosols from the summit (Bocca Nuova crater), downwind (about 10 km from the crater) and control sites were collected during the EUROVOLC EPL-REFLECT field campaign in July 2019 and analysed for aerosol mass determination, major inorganic and organic ions, and soluble and insoluble metals. Computational modelling (using the models E-AIM, ISORROPIA, and Visual MINTEQ) was performed to determine the speciation of metal ions in the deliquescent aerosol phase within the volcanic plume and in aerosol collected in the town of Milo (Catania, Italy), a few km downwind of Mt. Etna and influenced by transport of the volcanic plume. The aerosol liquid water concentration at the summit was strongly dependent on the determination method – with ISORROPIA calculating a water concentration a factor of 10² lower than that of E-AIM, which itself was a factor of 10²–10³ lower than the total water content of the plume measured by infrared spectroscopy. The calculated pH was predominantly acidic (except for ISORROPIA calculations in the three samples), with the highest acidity observed where the water concentration was the lowest. Only a few metals were shown to have significant organic–ligand complexation in the aerosol, i.e., Al(III), Cu(II), and Fe(III) with oxalate, in the deliquescent aerosol within the plume. When considering the total amount of water of the plume, lower complexation was observed because of more diluted species concentration and less acidity.

---

Environmental significance

Aerosols, in which both metal content and their speciation are relevant attributes, can impact human health and the Earth's climate. Complexation with organic ligands is an important process that can lead to changes in metal solubility, dissolution kinetics, redox activity, and particle physical properties such as optical properties and hygroscopicity. We characterised atmospheric aerosols emitted by Mt. Etna within the plume and 10 km downwind in the town of Milo. We found that current models for calculating aerosol water content and pH give highly uncertain results, with the uncertainty affecting the results of the speciation of metal ions. This research lays the foundation of a more systematic enquiry into volcanic aerosol complexation and the potential health effects on nearby residents.

1 Introduction

Volcanoes emit a chemically complex cocktail of gases and aerosols into the atmosphere, which can affect human health, ecosystems, and the Earth's radiative balance and climate.^1,2 Volcanic aerosols, besides contributing to direct absorption and reflection of solar radiation and acting as a site for heterogeneous atmospheric chemical reactions, can also lead to a number of changes in cloud nucleation and distribution. The large volume of gases and aerosols released during a volcanic eruption event can cause globally remarkable physical changes in the atmosphere. For example, the 1991 Mt. Pinatubo eruption led to an average O₃ column reduction of 5% globally and significant climate impacts through stratospheric aerosol injection.³ The more recent Hunga Tonga – Hunga Ha'apai eruption in 2022 led to the largest stratospheric water vapour perturbation ever observed with consequent radiative impacts.⁴

In contrast to large eruption events, such as those experienced by Mt. Pinatubo in 1991 or Hunga Tonga – Hunga Ha'apai in 2022, many volcanoes instead undergo a lengthened period of quiescent degassing, releasing a steady plume over many years to centuries. Mt. Etna, located in Sicily, Italy, is an example of this latter type of volcano.⁵ A previous investigation dedicated to Etna quiescent degassing has estimated 2 kt of CO₂ daily emission on average, with considerable volumes of SO₂, HCl, and HF.^6–8 In the study by Aiuppa et al.,⁷ CO₂ emissions were deemed to be 10–40 times larger during the 2004–2005 summit eruption compared to the quiescent degassing periods. Even under passive degassing conditions, Mt. Etna’s emissions can have important impacts on the downwind atmospheric composition, aerosol spatial distribution, and on the local climate.⁹ This impact can extend throughout the Mediterranean region.¹⁰

Allen et al.¹¹ measured aerosol size distributions in the plume at the summit craters Voragine and Bocca Nuova, and at the northeast crater. The size distributions were dominated by the fine fraction (D_p < 3.5 μm), with a larger contribution of coarse particles (D_p > 3.5 μm) and higher mineral content aerosols at the northeast crater, compared to Bocca Nuova, attributed to Strombolian or gas puffing activity at the magma surface in the vent.¹¹ Major ions, such as F⁻, Cl⁻, NO₃⁻, SO₄²⁻, Na⁺, NH₄⁺, K⁺, and Ca²⁺, were measured in 2004 and in 2005 at the summit and downwind showing that the partitioning of F- and Cl-is predominantly in the gas phase at the summit and in the condensed phase downwind probably due to plume evolution (on a minute timescale) and meteorology.^11,12 Size-segregated measurements showed a different distribution of major ions across fine and coarse fractions with halogens, nitrate and sulphate dominating the fine fraction unlike the alkali and alkali-earth metals which contributed more to the coarse fraction. In addition, Sellitto et al.⁹ showed that hotspots of PM₁ and PM₁₀ across the plume at the Bocca Nuova and Voragine craters are not localised in the same plume section, confirming that fine and coarse particles are generated by different sources such as primary emissions of ashes (coarse) and gas-to-particle conversion of SO₂ to sulphate (fine).

Besides gasses and ashes, it has been observed that continuous degassing can lead to a high amount of volatile metals being emitted into the atmosphere, especially metals that are characterised by higher aqueous fluid-melt partition coefficients.^5,13 Measurements of metals from Mt. Etna plume date back to 1976.¹⁴ Besides the highly abundant alkali and alkali-earth metals, high concentrations of Al, Fe, Zn, Cu, Se and Pb in the range of 1–20 μg m⁻³ were found in the plume at the summit crater.¹⁴ Gauthier et al.¹⁵ collected aerosol samples from the Mt. Etna plume between 1991 and 1995 and found that primary degassing always occurs at the summit no matter how intense the volcanic activity. Except for Zn and Sn, which showed higher fluxes during eruptions, metal fluxes during eruptive and non-eruptive periods remained constant.¹⁵ In 2007, chemical abundances of the elements in aerosol samples collected in the plume at Mt. Etna were extremely variable due to variability in the plume dilution, meteorological conditions and emission rates at the crater.¹⁶ Despite the variability, Mt. Etna remains the main point source of major and trace metals in the Mediterranean region.¹⁷ Concerning water solubility of volatile metals from volcanoes, extremely scarce information is currently available in the literature. Ilyinskaya et al.¹⁸ measured water solubility of a large range of metals emitted from the Kīlauea volcano (Hawai'i) during the 2018 eruption. The results showed a very high solubility, close to 100% for most volatile metals except for Bi.

To the authors knowledge there is no study that investigated water-solubility of metals in volcanic aerosols emitted by Mt. Etna or the atmospheric aqueous phase processing of volcanic aerosols. In this study, size-segregated aerosol samples were collected from Mt. Etna at the summit within the plume at the Bocca Nuova crater, in a control location upwind, and in a 10 km downwind location in the town of Milo (Italy), in the context of the EUROVOLC EPL-REFLECT field campaign in July 2019. These samples were analysed for inorganic ions, organic ions, and soluble and non-soluble metals. Subsequently, thermodynamic modelling techniques were used to investigate the formation of metal–ligand complexes in atmospheric aqueous aerosols. Metal solubility and metal speciation together with the results obtained from different thermodynamic models (E-AIM, ISORROPIA and Visual MINTEQ) are discussed as well as uncertainties and knowledge gaps in metal speciation.

2 Experimental

2.1 Field campaign

During the summer of 2019, a multi-instrumental field campaign took place at Mount Etna in the context of the “Etna Plume Lab – near-source estimations of radiative effects of volcanic aerosols for climate and air quality studies (EPL-REFLECT)” project, funded by the European Commission under the grant Horizon 2020-EUROVOLC. One of the main objectives of the EPL-REFLECT project was to provide a near-crater size-resolved characterisation of the composition and properties of Mt. Etna's aerosol emissions, with the aim of characterising their toxicity and how this evolves depending on in-plume processes along dispersion downwind. For this latter objective, aerosol samples were collected at Mt. Etna from the 8th to the 12th of July 2019. The samples were collected at three locations: within the volcanic plume at the Bocca Nuova crater (two samples), at a control location upwind of the plume, and in the town of Milo (on the roof of “Milo La Torre”) approximately 10 km downwind of the plume (Fig. 1). The specific sampling points were chosen to allow sampling of fresh aerosol within the plume at the crater as well as aged aerosol being transported downwind. The locations were chosen based on a visual inspection of the plume direction and considering availability of a suitable location for the sampling equipment. Concerning the downwind site, the location chosen is representative of transport towards the east, which is largely dominant (over 80% of the overall transport) based on previous decadal scale trajectory analyses.¹⁰

Fig. 1 Map of Sicily (top panel), filter sampling locations at the summit of Mt. Etna (middle panel) within (S1-0807 and S2-1207 sets) and upwind (C-1207 set) of the plume and filter sampling locations in the town of Milo (bottom panel) downwind of the plume (M-1007 set). The Mt. Etna summit is located at 37.7510° N, 14.9934° E and has an altitude of 3369 m.

2.2 Sample collection and measurements

For each site, two parallel sets of samples were collected using Personal Cascade Impactor Samplers (PCISs) in the size fractions 10–2.5 μm, 2.5–1.0 μm, 1.0–0.5 μm, 0.50–0.25 μm, and <0.25 μm in aerodynamic diameters with a sampling flow rate of 9 L min⁻¹ mounted on a tripod.¹⁹ All samples were collected on Teflon membranes (Ø 25 mm Teflon filters, SKC, 0.5 μm pore size and Ø 37 mm Teflon final backup filters, SKC, 2.0 μm pore size, used as purchased). A set of field blanks was also collected. Weighing of the filters was done, before and after sampling, after conditioning at a temperature (T) of 20 ± 1 °C and relative humidity (RH) of 50 ± 5% for at least 48 h, as in previous studies.^20,21 Filter samples were then stored at −20 °C until analysis. Temperature and RH were measured at the site using sensors fitted to a low-cost Optical Particle Counter (OPC-SEN0177). A summary of the samples collected, together with recorded RH and T values are reported in Table 1.

Table 1 Summary of the filter samples collected during the EPL-RELFECT campaign in July 2019 together with average temperature (T) and relative humidity (RH)

Sample sets	Sample type/site	Sampling start date	Sampling start time	Sampling duration (min)	RH (%)	T (°C)
FB-0807	Field blank (summit, not exposed)	08 Jul 2019	—	—	—	—
S1-08-07	Summit 1 (Bocca Nuova crater)	08 Jul 2019	13 h 45	128	100	23.40
M-1007	Milo (10 km downwind)	10 Jul 2019	12 h 00	1440	89.69 (night), 50.23 (average)	23.59 (night), 27.53 (average)
S2-1207	Summit 2 (Bocca Nuova crater)	12 Jul 2019	12 h 45	120	100	4.22
C-1207	Control (summit, upwind)	12 Jul 2019	11 h 35	220	46.40	16.76

---

2.3 Analysis of metals, inorganic ions, and short-chain organic acids

One set of samples was used to determine the water soluble and total concentrations of metals using inductively coupled plasma mass spectrometry (ICP-MS). The samples were extracted in a three-step procedure – water, hot diluted HNO₃, and concentrated HNO₃. In the first step, filter samples were placed in 10 mL falcon tubes and 3 mL of ultrapure water (purified by using Millipore MilliQ equipment) containing an internal standard of ¹⁸³Re at 25 ppb were added. The samples were extracted in an ultrasonic bath (ELMA® Transsonic Digitals) for 40 min at room temperature. After that, filter samples were removed from the falcon tubes, rinsed with ultrapure water, and transferred into clean falcon tubes. Sample extracts were spiked with concentrated HNO₃ (68.5–69.5%, Aristar for trace analysis, VWR) to obtain a final HNO₃ concentration of 3.45% (w/w) before analysis. The second extraction was done in 3 mL of a 3.45% (w/w) HNO₃ solution in ultrapure water containing ¹⁵⁹Tb at 25 ppb as the internal standard, in a bain-marie (100 °C) for 2 h. After that, filter samples were removed from the falcon tubes, rinsed with ultrapure water, and transferred into clean falcon tubes. Sample extracts were analysed as is. The third and last extraction was done in 3 mL of a ∼69% (w/w) HNO₃ solution in ultrapure water containing ⁷²Ge at 25 ppb as the internal standard, in a bain-marie (100 °C) for 1 h. Sample extracts were diluted 1 : 20 with ultrapure water to obtain a final HNO₃ concentration of 3.45% (w/w) before analysis. All samples were analysed using an ICP-MS Agilent series 7700× (Agilent Technologies International Japan, Ltd, Tokyo, Japan). The instrumental operating conditions were as follows: radiofrequency power 1550 W, RF matching 1.8 V, plasma gas (Ar) flow rate 15 L min⁻¹, carrier gas (Ar) flow rate 1.05 L min⁻¹, He gas flow rate 4.3 mL min⁻¹, CeO⁺/Ce⁺ = 0.90%, nebuliser type: microflow PFA, spray chamber type: Scott double pass at 2 °C, sample introduction speed 0.1 mL min⁻¹, internal diameter of the nickel cone 1.0 mm, internal diameter of the skimmer cone 0.5 mm, sampling depth 8.5 mm, dwell time/mass = 100.^22,23 Quantification has been performed by external calibration using the isotopes ⁷²Ge, ¹⁵⁹Tb, and ¹⁸³Re as internal standards to monitor the instrumental drift. Calibration standards were prepared by diluting the following concentrated solutions: rhenium standard for ICP (1001 ± 5 mg L⁻¹, 2% HNO₃, Sigma-Aldrich), germanium standard for ICP (1005 ± 2 mg L⁻¹, 2% HNO₃, Sigma-Aldrich), terbium standard for ICP (1002 ± 5 mg L⁻¹, 2% HNO₃, Sigma-Aldrich), calibrating standard solution CCS-5 for ICP (100.00 ± 0.70 μg mL⁻¹ of B, Ge, Hf, Mo, Nb, P, Re, S, Sb, Si, Sn, Ta, Ti, W, Zr, 1.2% (v/v) HF + 7.43% (v/v) HNO₃, Inorganic Ventures), and calibrating standard solution IV-ICPMS-71A (10 ± 0.08 μg mL⁻¹ of Ag, Al, As, B, Ba, Be, Ca, Cd, Ce, Co, Cr, Cs, Cu, Dy, Er, Eu, Fe, Ga, Gd, Ho, K, La, Lu, Mg, Mn, Na, Nd, Ni, P, Pb, Pr, Rb, S, Se, Sm, Sr, Th, Tl, Tm, U, V, Yb, Zn, Inorganic Ventures).

One set of samples was used for quantification of inorganic ions and short-chain organic acids by means of ion chromatography (IC). The samples were extracted in 3 mL of ultrapure water, in an ultrasonic bath in a slurry of ice for 40 min, filtered (0.2 μm RC Membrane, Phenomenex 4 mm syringe filters), and analysed in a Dionex IC system equipped with an a GP50 gradient pump, an EG40 eluent generation system fitted with a Dionex EGC III KOH RFIC™ eluent generator cartridge, a LC25 oven, and an ED40 electrochemical detector (in conductometric detection mode). Analytical procedures are described in Tapparo et al.²⁴ for inorganic anions and short-chain organic acids and in Giorio et al.²¹ for inorganic cations.

2.4 Thermodynamic modelling

2.4.1 Extended aerosol inorganics model (E-AIM) IV. To determine the aerosol liquid water content, the E-AIM Model (Extended Aerosol Inorganics Model) IV was used. E-AIM is an online-accessible phase equilibrium thermodynamic model, developed by Wexler and Clegg,^25,26 which allows the calculation of water and ion distribution between different phases. Particulate inorganic ions NH₄⁺, Na⁺, SO₄²⁻, NO₃⁻ and Cl⁻, as well as the organic species acetic acid, succinic acid, malonic acid, and oxalic acid, were the inputs, along with H⁺ (estimated from the charge balance). In the case of an excess of positive charges, NH₄⁺ was converted to NH₃ to reach charge neutrality (and H⁺ was therefore not added in the input but then calculated by the model). RH and temperature were also required. The model partitions ions and organic acids into the liquid water phase, a possible solid phase, and a gas phase. The organic species are further divided into protonated and deprotonated forms. The model was run in ‘simple calculation’ mode (also known as reverse mode), from which the aerosol liquid water content is calculated based on the RH, T, and hygroscopicity of the aerosol components, and then the pH of the liquid water phase is calculated. The RH measured in situ was deemed unreliable in a high-water content environment (with IR measurements of 12 000 ppmv relative to the background)²⁷ of the plume, as demonstrated in Fig. S1 in the ESI.† This, along with the input restrictions of the model, meant a RH of 99.99% (the maximum allowable) was used for the summit sites for E-AIM. Temperatures used as input were those observed at 23.4 °C and 4.22 °C at the Summit 1 (8th July 2019) and 2 (12th July 2019) sites respectively. In the case of Milo (10th–11th July 2019), daytime conditions were dry, and consequently a RH of 89.69% and temperature of 23.59 °C, representing night-time conditions were used for the calculations.

2.4.2 ISORROPIA II. ISORROPIA II was developed by Fountoukis and Nenes²⁸ and was run here in reverse mode (due to unavailability of gas phase measurements), allowing solids to precipitate. The input ions were Na⁺, NH₄⁺, K⁺, Mg²⁺, Ca²⁺, SO₄²⁻, NO₃⁻ and Cl⁻, as well as T and RH. As with E-AIM, the ions are separated into solid, liquid water and gaseous phases, with the model providing water concentration and pH. The summit site temperature and RH inputs were the same as in E-AIM, yet due to less restrictive model requirements, the average RH and temperature were used, 50.23% and 27.53 °C for Milo.

2.4.3 Visual MINTEQ 3.1. To predict the speciation at equilibrium in the aerosol water phase, thermodynamic modelling program Visual MINTEQ 3.1 was used (https://vminteq.com/). For each sample, three different runs were carried out. The first run used pH, ALW, metal and ion molality inputs calculated from E-AIM. The second run used pH, ALW, metal and ion molality inputs calculated from ISORROPIA, and the third run used the metal and ion molality inputs calculated from the average water content of the plume (12 000 ppmv)²⁷ while pH was calculated by Visual MINTEQ from the charge and mass balance of the species in solution. Measured temperatures were used for all runs.

Due to the input limitation of 28 ions the following were used: NH₄⁺, Na⁺, SO₄²⁻, NO₃⁻, Cl⁻, succinate²⁻, malonate²⁻, oxalate²⁻, acetate⁻, PO₄³⁻, K⁺, Mg²⁺, Ca²⁺, Al³⁺, Cr³⁺, Cu²⁺, Fe³⁺, Fe²⁺, Pb²⁺, Zn²⁺, Mn²⁺, and Ni²⁺. The partitioning of Fe²⁺ and Fe³⁺ could not be determined by ICP-MS. As there is generally more Fe²⁺ in the day and more Fe³⁺ at night due to photochemistry, a 50 : 50 compromise was used as in a previous study.²³ Although Fe³⁺ is the thermodynamically stable form under atmospheric conditions, previous studies showed that Fe²⁺ can be the dominant species or equally present in the soluble fraction.²⁹ Fe²⁺ can be present in atmospheric aerosols in a substantial amount due to photo- and other reduction processes in aerosols, especially in the presence of secondary organic aerosols,³⁰ and it can persist in the core of atmospheric particles due to anoxic conditions being established due to particle viscosity.³¹ The remaining metals were omitted because of their low concentrations as well as their tendency to not form metal–ligand complexes. For the two summit samples the Davies method for activity correction, with a ‘b parameter’ of 0.3, was used. Whilst the SIT method gives higher accuracy for high concentration solutions, it does not converge, and the Davies model's inaccuracies at high ionic strength were deemed acceptable as used in previous studies.^23,32 At the higher molality concentrations of the Milo samples, the SIT method was used instead.

3 Results and discussion

During the EPL-REFLECT field campaign, two sets of samples were collected within the volcanic plume at the Bocca Nuova crater on two separate days. On the second day of sampling at the summit, a control sample upwind of the plume was also collected. Additionally, a set of samples in the town of Milo approximately 10 km downwind the plume in between the two days of sampling at the summit was also collected. Temperatures at the summit were very different between the first and second days of sampling, with 23.4 °C on the first day of sampling and 4.2 °C on the second day of sampling. At Milo, the temperature was higher with a daily average of 27.5 °C. During the sampling at Milo, the volcanic plume was transported towards Milo as evidenced by deposition of ashes at the sampling site. It should be noted that the plume transport towards the east, i.e. in the direction of Milo, is largely dominant (over 80% of the overall transport), based on the decadal scale high-spatiotemporal-resolution Lagrangian trajectory analyses of Sellitto et al.¹⁰ During the second day of sampling at the summit, transport of Saharan dusts was additionally observed (based on satellite observations and CAMS – Copernicus Atmosphere Monitoring Service – reanalyses, not shown here), likely overpassing the area at relatively high altitude (>5 km). Despite this, the control sample collected upwind did not contain a significant amount of aerosol mass compared to the sample collected within the plume (less than 10% contribution).

3.1 Aerosol mass, composition, and element solubility

The results of the gravimetric and chemical analysis are reported in Table 2 as averages for each size-fraction. The PM concentrations of the two samples collected at the summit on 8th and 12th July 2019 differ by approximately a factor of two (PM₁₀ of 830 and 444 μg m⁻³, respectively), probably due to a different volcanic activity across the two days. In fact, Mt. Etna entered a new active phase a few days later with initial sporadic explosions at Etna's New Southeast Crater starting as early as 15th July.³³ The observed PM were around a factor of ten lower compared to the 2004.77 and 4498.75 μg m⁻³ found by Allen et al.¹¹ in August 2004 in the coarse (D_p > 3.5 μm) and fine (D_p < 3.5 μm) fractions, respectively, and a factor of fifteen lower compared to the PM₁₀ of about 8000 μg m⁻³ found by Sellitto et al.⁹ in July 2017.

Table 2 Size-segregated concentrations of PM and major ions (μg m⁻³) in aerosol samples collected at the summit of Mt. Etna (reported as the average and standard deviation between two samples) and in Milo

Size fraction (μm)	Summit (Bocca Nuova crater)					Milo
	10–2.5	2.5–1.0	1.0–0.50	0.50–0.25	<0.25	10–2.5	2.5–1.0	1.0–0.50	0.50–0.25	<0.25
PM	106 (51)	67.6 (6.6)	31 (31)	200 (70)	268 (64)	33.44	17.48	15.2	5.32	12.92
Na^+	5.40 (3.37)	1.04 (0.08)	1.10 (0.99)	10.4 (7.9)	12.4 (5.7)	0.66	0.26	0.07	0.03	0.15
NH4^+	2.46 (0.26)	2.14 (0.34)	2.23 (0.49)	2.59 (0.46)	5.63 (0.41)	0.02	0.01	0.02	0.26	0.4
K^+	0.91 (0.35)	0.95 (0.31)	1.6 (1.2)	6.7 (3.4)	18.2 (8.8)	0.02	0.01	<DL	0.02	0.23
Mg^2+	0.37 (0.02)	0.15 (0.05)	0.10 (0.10)	<DL	0.33 (0.28)	0.09	0.04	<DL	<DL	0.03
Ca^2+	2.04 (0.13)	0.72 (0.03)	0.38 (0.38)	<DL	4.1 (3.8)	0.64	0.26	0.12	<DL	0.22
Fo^−	0.03 (0.03)	0.13 (0.02)	<DL	0.02 (0.02)	0.03 (0.03)	0	<DL	<DL	<DL	<DL
Cl^−	<DL	0.47 (0.27)	0.47 (0.47)	9.2 (9.2)	0.87 (0.26)	0.82	0.2	<DL	<DL	0.08
NO3^−	0.14 (0.06)	0.96 (0.64)	<DL	0.08 (0.08)	<DL	1.08	0.57	0.14	0	0.12
SO4^2−	21.9 (5.2)	10.9 (3.5)	18.0 (5.5)	84 (20)	107 (18)	0.6	0.26	0.16	0.69	1.27
Ox^2−	0.02 (0.02)	1.04 (0.92)	0.31 (0.06)	0.26 (0.13)	0.81 (0.48)	0.04	0.03	0.04	0.02	0.07
PO4^3−	<DL	0.04 (0.04)	0.85 (0.45)	<DL	0.40 (0.13)	<DL	<DL	0.02	<DL	0.1

---

Concerning major ions, as expected sulphate was the most abundant inorganic ion measured in the samples collected at the crater, originating from oxidation of SO₂ emitted from the volcanic vent.³⁴ Sulphate concentrations within the PM₁₀ fraction were between 199 and 283 μg m⁻³ in this study, lower compared to the 249.52 and 1629.94 μg m⁻³ found by Allen et al.¹¹ in August 2004 in the coarse (D_p > 3.5 μm) and fine (D_p < 3.5 μm) fractions, respectively. While HF and HCl are known compounds emitted by Mt. Etna,^8,35 fluoride was not detected in the condensed phase and chloride had a variable concentration across the samples collected at Bocca Nuova (20.6 and 1.3 μg m⁻³ in the first and second samples, respectively). Fluoride concentrations were below the detection limit in our study, while those between 22.59 (for D_p > 3.5 μm) and 1.02 (for D_p < 3.5 μm) μg m⁻³ at Voragine/Bocca Nuova were observed in August 2004.¹¹ Concerning chloride, concentrations within the PM₁₀ fraction were between 1.35 and 20 μg m⁻³ in this study, while they were 0.66 and 0.35 μg m⁻³ at Voragine/Bocca Nuova in August 2004 in the coarse (D_p > 3.5 μm) and fine (D_p < 3.5 μm) fractions, respectively.¹¹ Consistent results between both studies have been found for nitrate and the cations (Na⁺, NH₄⁺, K⁺, Mg²⁺, and Ca²⁺).

Oxalate and formate were also detected in the samples collected at the crater (Table 2), while they were below the detection limit in the control sample collected upwind of the plume. Organic compounds were previously detected in volcanic plumes; however, only methane was confirmed to be originated from the volcanic vent, including at Mt. Etna.^36,37 Oxalate and formate detected here are likely to be formed from oxidation of atmospheric volatile organic compounds in the aqueous environment created by the plume rather than being emitted from the volcanic vent. It is well known that organic acid formation from their gaseous precursors is promoted by aqueous phase chemistry in the troposphere.³⁸

A downwind sample (Torre del Filosofo, about 1 km from the crater) was collected in August 2004,¹¹ substantially closer to the emission source compared to the town of Milo (about 10 km downwind), which is our downwind sampling location. At Torre del Filosofo, concentrations of PM were 281.00 (D_p > 3.5 μm) and 150.06 (D_p < 3.5 μm) μg m⁻³ in August 2004, while PM₁₀ was only 76.0 μg m⁻³ and PM_2.5 was 42.1 μg m⁻³ in 2019 in Milo. Consequently, all major ion concentrations were higher at Torre del Filosofo in 2004 than in Milo in 2019.

Metal concentrations and solubility in water are reported in Tables 3 and 4, respectively for both the samples collected at the summit and in Milo. For both samples collected at the summit on 8th and 12th July 2019, the water solubility is generally higher than that in Milo for most elements for the middle three size fractions except As and P. In the smallest size fraction (<0.25 μm) about half of the species are more soluble at the summit and half are more soluble at Milo, and in the largest size fraction (10–2.5 μm) most species are more soluble at Milo. Milo is characterised by a mixture of sources, including the transport of the volcanic plume during the sampling period but also other local natural and anthropogenic sources. The likely explanation for the different solubilities might therefore be attributed to an influence of other natural and anthropogenic sources at this location. Compared to the study from Ilyinskaya et al.,¹⁸ the samples collected in the plume of Mt. Etna present a higher solubility for Fe (up to 86%) and Mn (up to 100%) compared to the samples collected at the fissure at Kīlauea volcano, Hawai'i, USA (<20% for both Fe and Mn). Furthermore, Al and Ca were not soluble at Kīlauea but show a solubility of up to 90% and 100%, respectively, at Mt. Etna. We hypothesise that these contrasting solubilities are likely to be caused by the different activities of the two volcanoes during the sample collection, with Kīlauea being in the eruption phase and therefore emitting metals embedded in crustal material (e.g., silicates) and Mt. Etna being in a quiescent degassing state and therefore emitting metals in a more volatile form. Conversely, for more volatile metals such as Cu, Zn, and Cd the solubility is somewhat consistent (close to 100%) between both studies. As and Cd are also characterised by high solubilities at both sites while Se and Pb show a lower solubility in the samples collected at Mt. Etna (<70% and <56%, respectively) compared to an almost 100% solubility at Kīlauea.

Table 3 Size-segregated concentrations of metals (ng m⁻³) in aerosol samples collected at the summit of Mt. Etna (reported as the average and standard deviation between two samples) and in Milo

Size fraction (μm)	Summit (Bocca Nuova crater)					Milo
	10–2.5	2.5–1	1–0.5	0.5–0.25	<0.25	10–2.5	2.5–1	1–0.5	0.5–0.25	<0.25
Pb	<DL	<DL	6.3 (6.3)	69.1 (9.8)	76 (31)	<DL	<DL	0.19	0.24	0.05
Tl	0.90 (0.10)	1.37 (0.04)	1.53 (0.88)	14.16 (0.21)	15.4 (4.1)	0.02	0.01	0.02	<DL	0.07
Ba	11.7 (1.4)	5.25 (0.32)	4.7 (3.1)	1.7 (1.7)	13 (12)	4.80	3.39	2.62	0.64	1.31
Sr	26.7 (8.0)	10.2 (1.2)	4.26 (0.52)	1.80 (0.87)	0.31 (0.31)	6.07	1.85	1.11	0.37	0.76
Rb	1.58 (0.25)	1.34 (0.14)	1.32 (0.94)	25.2 (1.2)	27 (10)	0.42	0.17	0.11	0.05	0.15
Br	134 (70)	20 (15)	8.27 (0.30)	41 (17)	59 (17)	14.82	0.12	3.92	0.00	5.42
La	1.88 (0.78)	0.91 (0.20)	0.24 (0.08)	0.10 (0.01)	0.04 (0.02)	0.52	0.22	0.11	0.05	0.05
Cd	0.28 (0.05)	0.44 (0.18)	0.48 (0.41)	5.1 (1.1)	5.8 (1.1)	0.01	0.01	0.01	0.01	0.04
Se	4.3 (1.6)	4.3 (1.2)	8.8 (2.5)	63 (12)	50 (13)	1.25	1.01	0.20	0.78	0.02
As	1.52 (0.90)	2.84 (0.32)	5.64 (0.25)	26.1 (1.1)	12.34 (0.63)	0.00	0.10	0.14	1.57	1.23
Ga	2.23 (0.36)	1.74 (0.26)	1.51 (0.34)	0.42 (0.18)	1.00 (0.90)	0.68	0.60	0.42	0.13	0.17
Zn	12.8 (4.3)	<DL	9.9 (1.1)	23.1 (4.2)	38 (17)	1.74	7.43	2.34	7.76	2.02
Cu	18.16 (0.47)	5.91 (0.85)	7.5 (5.6)	155 (33)	197 (95)	2.10	0.80	0.62	10.23	0.25
Ni	9.0 (8.7)	0.30 (0.08)	1.87 (0.97)	1.16 (0.03)	3.3 (1.5)	0.24	0.87	0.23	0.51	0.91
Fe	750 (420)	392 (167)	112.6 (3.6)	148.4 (2.5)	187 (12)	223.26	130.70	80.88	44.91	27.98
Mn	25 (13)	11.1 (1.8)	4.5 (1.8)	3.55 (0.24)	3.00 (0.33)	7.66	2.09	1.40	0.46	0.85
Cr	0.15 (0.15)	1.07 (0.35)	1.43 (0.67)	0.09 (0.01)	9.46 (0.52)	0.06	0.42	0.09	0.63	0.56
V	3.20 (0.93)	1.45 (0.17)	0.41 (0.40)	0.72 (0.08)	0.49 (0.14)	0.90	0.37	0.22	0.14	1.39
P	332 (332)	358 (328)	1439 (114)	415 (135)	197.64	33.44	47.18	106.34	63.97	21.43
Al	1954 (229)	600 (67)	217 (82)	119 (38)	255 (25)	348.28	199.16	115.79	50.89	13.65
B	<DL	<DL	<DL	<DL	24 (24)	<DL	0.32	5.45	<DL	1.54

---

Table 4 Metal solubility in aerosol samples collected at the summit of Mt. Etna (average between both summit samples) and in Milo. Bold values indicate in which sample (crater vs. Milo) the highest solubility was observed

Size fraction (μm)	Summit (Bocca Nuova crater)					Milo
	10–2.5	2.5–1	1–0.5	0.5–0.25	<0.25	10–2.5	2.5–1	1–0.5	0.5–0.25	<0.25
Pb	NA	NA	51%	51%	50%	NA	NA	20%	0.0%	51%
Tl	32%	63%	64%	96%	80%	60%	0.6%	2.3%	0.0%	78%
Ba	28%	54%	19%	0.0%	3.6%	50%	0.0%	1.9%	0.0%	32%
Sr	53%	66%	34%	34%	25%	71%	1.1%	8.8%	0.0%	44%
Rb	47%	75%	81%	100%	84%	68%	2.4%	3.8%	0.0%	80%
Br	5.9%	9.2%	45%	39%	41%	23%	0.0%	0.4%	NA	82%
La	55%	73%	53%	56%	53%	64%	8.6%	1.2%	0.4%	33%
Cd	61%	84%	93%	100%	81%	60%	0.0%	0.7%	5.0%	86%
Se	17%	42%	29%	70%	38%	1.9%	0.0%	0.0%	6.2%	100%
As	36%	24%	89%	99%	67%	NA	50%	2.5%	96%	82%
Ga	26%	29%	11%	21%	14%	56%	0.0%	2.2%	0.0%	40%
Zn	63%	NA	56%	100%	71%	51%	0.0%	31%	0.0%	100%
Cu	18%	100%	81%	99%	98%	59%	0.0%	0.0%	0.0%	100%
Ni	95%	36%	71%	57%	52%	59%	0.0%	21%	6.6%	66%
Fe	3.8%	22%	20%	86%	57%	46%	0.4%	0.9%	0.0%	7.4%
Mn	69%	81%	38%	79%	100%	74%	1.5%	9.4%	0.0%	61%
Cr	7.4%	12%	4.2%	100%	4.7%	100%	0.3%	2.3%	0.5%	9.4%
V	15%	39%	32%	88%	88%	58%	0.0%	0.0%	0.0%	82%
P	6.5%	6.7%	1.8%	0.0%	25%	80%	0.1%	2.9%	0.0%	16%
Al	24%	44%	32%	57%	89%	51%	0.0%	1.0%	0.0%	47%
B	NA	NA	NA	NA	0.0%	NA	0.0%	0.0%	NA	84%

---

3.2 Calculation of aerosol liquid water content and pH

Metal speciation in solution strongly depends on the amount of water available, and therefore the concentration of the dissolved species, and pH conditions. E-AIM and ISORROPIA are the two most used thermodynamic models to calculate the aerosol liquid water (ALW) content and aerosol pH. Table 5 shows the calculated ALW concentration and pH obtained with the E-AIM Model IV and ISORROPIA II for all collected samples at the summit of Mt. Etna and in Milo. At the summit, E-AIM consistently predicts a much higher water concentration than ISORROPIA under these conditions.

Table 5 Aerosol liquid water (ALW) content and pH predicted by E-AIM and ISORROPIA for the different samples as well as pH calculated using Visual MINTEQ using the averaged water content in the volcanic plume of 12 000 ppmv²⁷

Sample	Size fraction (μm)	E-AIM ALW (μg m^−3)	ISORROPIA ALW (μg m^−3)	E-AIM pH	ISORROPIA pH	Visual MINTEQ pH
Summit 1 S1-0807	10–2.5	8.72 × 10^4	1.14 × 10^3	2.85	12.31	6.47
	2.5–1.0	7.89 × 10^4	8.03 × 10^2	2.85	1.46	5.52
	1.0–0.50	1.32 × 10^5	2.04 × 10^3	2.72	1.42	7.63
	0.50–0.25	7.15 × 10^5	1.59 × 10^4	2.66	1.09	5.96
	<0.25	6.59 × 10^5	1.09 × 10^4	2.68	1.80	5.51
Summit 2 S2-1207	10–2.5	1.45 × 10^5	2.18 × 10^3	3.66	13.49	5.17
	2.5–1.0	6.35 × 10^4	1.30 × 10^3	2.91	13.03	5.46
	1.0–0.50	6.58 × 10^4	1.30 × 10^3	2.64	1.16	5.85
	0.50–0.25	3.30 × 10^5	6.66 × 10^3	2.50	1.01	5.92
	<0.25	4.66 × 10^5	9.10 × 10^3	2.59	1.16	5.73
Milo M-1007	10–2.5	16.7	14.7	−0.05	0.78
	2.5–1.0	60.7	5.21	−0.03	7.05
	1.0–0.50	1.24	0.60	0.36	7.05
	0.50–0.25	2.20	2.35	0.40	7.05
	<0.25	5.59	3.65	0.95	7.05

---

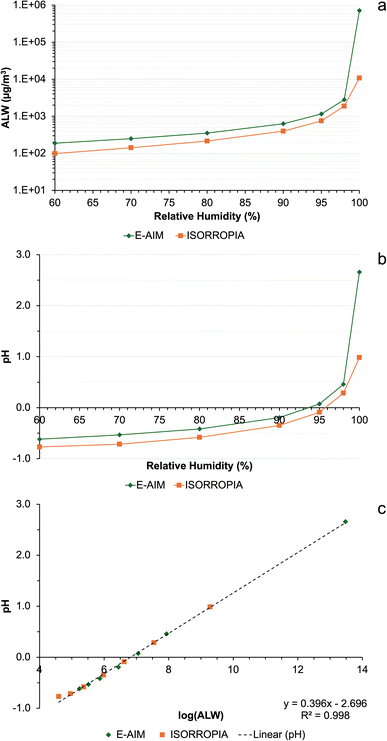
To gain a qualitative understanding of how the ALW concentration calculated by the models depends on RH, the two models (E-AIM and ISORROPIA) were run with identical ion inputs (i.e., NH₄⁺, Na⁺, SO₄²⁻, NO₃⁻ and Cl⁻, no organics or other alkali metals, but E-AIM also required H⁺ from the ion charge balance) using data from one of the samples (summit 1, 0.5–0.25 μm size fraction). This was repeated with a RH of 60% to 99.99% in 10% increments up to 90%, then at 95%, 98% and 99.99%. Fig. 2a shows how the ALW content varies, indicating that the models agree within a factor of approximately 1.5 at lower RH, but rapidly diverge at RH close to saturation. This is consistent with the data in Table 5, where the water concentration calculated for the Milo data are within the same order of magnitude in E-AIM and ISORROPIA. In contrast, values are different, by a factor of 100, at the summit sites where the humidity is at saturation.

Fig. 2 Comparison of the outputs between E-AIM and ISORROPIA using the chemical composition of sample S1-0807-PM_0.5–0.25 (summit 1, 0.5–0.25 μm size fraction) as the input and varying relative humidity, between 60% and 100%: (a) aerosol liquid water (ALW) content, (b) pH, and (c) correlation between ALW and pH.

Although E-AIM and ISORROPIA are both thermodynamic models, they use different assumptions leading to their divergence. E-AIM is a more computationally thorough model compared to ISORROPIA, which is more efficient at the expense of accuracy as it was optimised for chemical transport models.³⁹ ISORROPIA assumes that H⁺ and OH⁻ activity coefficients are unity, whereas E-AIM calculates them. To calculate the activity coefficients of other ions, ISORROPIA uses the Kusik–Meissner and the (empirical and efficient) Bromley equations, whereas E-AIM uses the more rigorous and laborious Pitzer–Simonson–Clegg (PSC) equations.⁴⁰

Given the different ALW contents calculated by E-AIM and ISORROPIA, the pH was also very different between the two models (Fig. 2b), which diverged substantially, approximately by 2 pH units, at RH close to saturation. The computed pH is highly correlated (r > 0.999) with the logarithm of ALW (Fig. 2c) which is consistent between the two models. As Table 5 shows, there are some striking differences in the pH predicted in the larger size fractions of the summit samples, S1-0807 and S2-1207. Literature studies suggest that atmospheric aerosol is acidic in nature, due to the high quantities of H₂SO₄ present and the large surface area to volume ratio.^41–43 In addition, the volcanic plume is rich in acids such as HF and HCl in addition to SO₂ emissions.³⁵ Therefore, the lower pH values predicted by E-AIM at the summit in the 10–2.5 μm (S1-0807 and S2-1207) and 2.5–1.0 μm (S2-1207) size fractions are more expected results, instead of the alkaline pH from ISORROPIA. An acidic pH, around 5.3, has also been measured previously in wet depositions at Mt. Etna.¹⁶

E-AIM and ISORROPIA were both run in reverse mode, meaning that only aerosol phase concentrations of species were used as the input. The main difference between the concentration inputs used in reverse and forward modes (which includes gas phase concentration of species) is for NH₄⁺ (as NH₃ is an important atmospheric species that partition between the gas and aerosol phases) because the other inorganic ions generally do not have high concentrations in the gas phase. The partitioning of NH₃/NH₄⁺ attempted by the models in reverse mode is the main source of error.⁴⁴ Due to the experimental setup at Mt. Etna, only the aerosol concentrations were recorded (from the analysis of the filter samples), and no information about the gas phase, especially the NH₃ concentration, is available which is essential to properly constrain ISORROPIA calculations.

As shown by Hennigan et al.,⁴⁴ the forward and reverse modes are in poor agreement concerning pH for both E-AIM and ISORROPIA models – with their data suggesting a median difference of 3.1 and 3.5 pH units between the two modes, respectively. Reverse mode calculations predicted pH much lower than that in either forward mode calculations or phase partitioning calculations of NH₃/NH₄⁺. Hennigan et al.⁴⁴ suggested that the two best proxy methods for estimating aerosol pH are thermodynamic equilibrium models run using both gas and aerosol concentrations as inputs, and the phase partitioning of ammonia while the reverse mode calculations are less reliable. In contrast, Yao et al.⁴⁵ found that reverse mode calculations gave a more accurate prediction of aerosol pH given that they do not assume that the partitioning equilibrium of NH₃/NH₄⁺ is reached in the atmosphere and most of the sulphate would remain unneutralised. However, Nault et al.⁴⁶ found that E-AIM calculations are relatively insensitive to gas phase constraints as shown by sensitivity analysis run with and without gas phase measurements.

Another issue which has undoubtedly led to inaccuracies with the pH calculations is the treatment of the organic species. To calculate the H⁺ concentration in E-AIM, a charge balance calculation involving only the inorganic ions was used. Hennigan et al.⁴⁴ highlight that neglecting the organic species in this charge balance, especially in environments at low acidities, where dissociation of the organic acids is likely, leads to inaccuracies. ISORROPIA does not require H⁺ input from charge balance but also does not have organic species input, so it likely faces similar problems by neglecting their treatment. Running E-AIM for all summit and Milo samples without including organics leads to a pH which is higher by 0.01–0.03 pH units. This very small adjustment owing to organics is consistent with findings from Guo et al.,⁴⁷ who also both calculated very minor changes in pH from neglecting organic ions (less than 0.25 pH units, although Song et al.⁴⁸ predicted an increase and Guo et al.⁴⁷ predicted a decrease). The small magnitude of the correction means that this is unlikely to be a main point of disagreement between E-AIM and ISORROPIA.

Between both models, the discrepancies in pH values can be partly attributed to the activity coefficient.²⁸ As previously discussed, whilst ISORROPIA assumes unit activity coefficient for H⁺, E-AIM calculates it. Jia et al.⁴⁹ predicted this to generally increase the pH of ISORROPIA compared to E-AIM by 0.25 pH units. This is not consistent with the results obtained in Table 5 where, except for the anomalous very high pH calculated for the larger size fractions (S1-0807-PM_10–2.5, S2-1207-PM_10–2.5, and S2-1207-PM_2.5–1), the summit samples indicate a consistently higher pH with E-AIM. Omitting the three anomalous samples, E-AIM has a pH higher by 1.36 (mean) or 1.43 (median) pH units. If all samples are considered, ISORROPIA has a higher pH by 1.99 pH units on average (mean), although the median predicts E-AIM results to be higher by 1.34 pH units.

However, probably the most important factor contributing to the lower pH in ISORROPIA is the water concentration, which is a factor of 100 smaller in ISORROPIA than E-AIM. With this discrepancy alone, ISORROPIA would predict a pH lower by 2 pH units.

Research using the models at such high RH is sparse, so a literature review was unable to determine whether E-AIM and ISORROPIA gave more reliable results under this particular condition. IR measurements of the volcanic plume showed a water concentration of 12 000 ppm (1.43 × 10⁷ μg m⁻³) – much higher than that predicted by E-AIM or ISORROPIA. The plume likely contained water droplets in addition to aerosol-bound water, so IR measurements provide the sum of both contributions.

At Milo, the water concentrations are much lower than those at the summit. Solid precipitation and supersaturation due to high ion concentrations are seen, and so unit activity coefficient for H⁺ is a poor approximation. The high, anomalous pH predicted by ISORROPIA is likely due to this. E-AIM does not face similar issues because it makes no assumptions about the H⁺ activity coefficient.

Fig. 3 summarises the main differences between ISORROPIA and E-AIM leading to different estimates of ALW and aerosol pH. Besides the aforementioned differences, disregarding the hygroscopicity of organics may cause underestimations in the ALW calculated by ISORROPIA.⁵⁰ In addition, previous studies suggested that ISORROPIA may overpredict pCl⁻ because of a too large effective equilibrium constant for HCl⁵¹ and it may overpredict particle nitrate at low RH due to possible organic–inorganic phase separations.⁵⁰ Similar investigations for E-AIM were not found so it remains unclear if these inaccuracies may affect E-AIM calculations too, keeping also in mind that E-AIM works in a narrower range of RH conditions (>60% and <100%) compared to ISORROPIA. Finally, Peng et al.⁵² showed that a different treatment of the dissociation equilibrium of HSO₄⁻ under highly acidic conditions may cause discrepancies between ISORROPIA and E-AIM with higher pH being predicted by ISORROPIA. This different way of accounting for the dissociation equilibrium of HSO₄⁻ seems to be linked with the availability of NH₃ to partition and neutralise, as well as the different way in which activity coefficients are calculated.⁵²

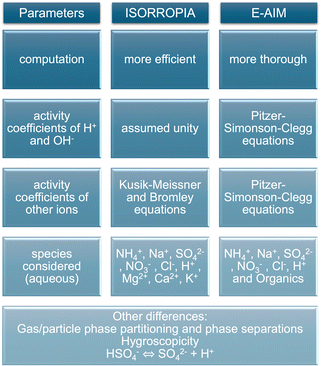Fig. 3 Infographic summarising the main known differences between the thermodynamic calculations of aerosol liquid water content and pH by the ISORROPIA and E-AIM models.

3.3 Metal speciation

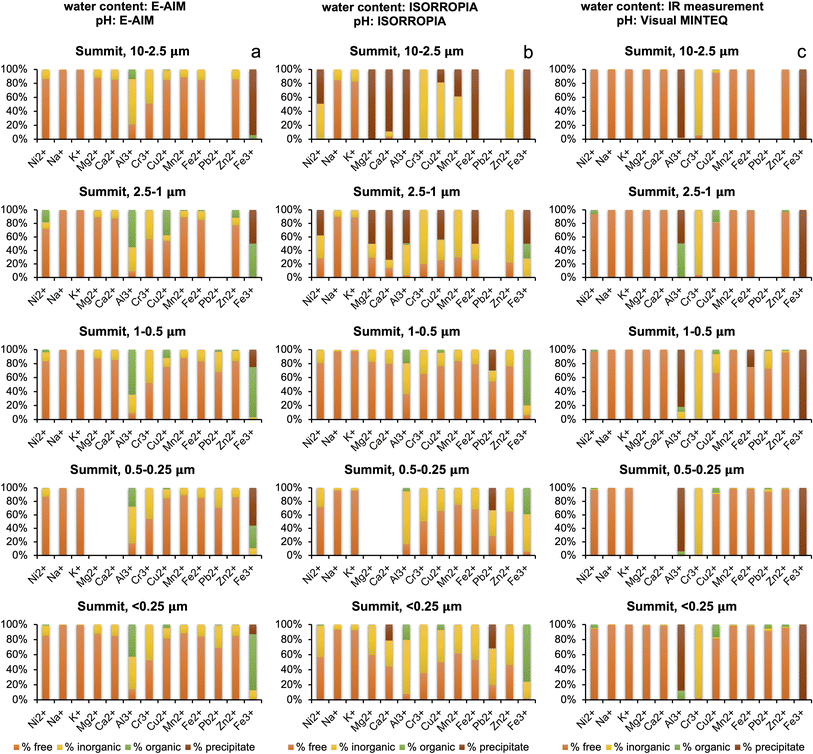
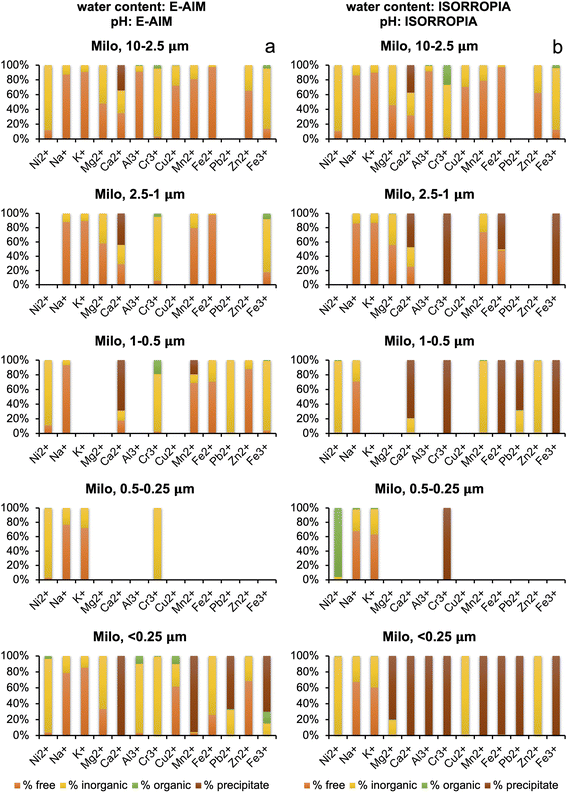
Water content and pH are important parameters that influence the speciation of metals in solution. The results obtained from E-AIM and ISORROPIA were remarkably different (see Section 3.2), and the water content of the plume measured by IR²⁷ was orders of magnitude higher than that calculated by both models. For this reason, metal speciation calculations with Visual MINTEQ for the summit aerosol were run three times – one for each both the E-AIM calculation and ISORROPIA calculation of water concentration, and once for the IR measurement of water concentration. The pH for the IR water concentration, shown in Table 5, was calculated by inputting proton concentration calculated by using the charge balance of the determined inorganic and organic ions, and then allowing Visual MINTEQ to calculate pH by using the mass balance. For the Milo aerosol, Visual MINTEQ was run twice, for both the E-AIM and ISORROPIA concentrations of water and pH.

3.3.1 Comparison of metal speciation in samples collected in the volcanic plume. Fig. 4 shows the comparison of the calculated metal speciation using water concentrations and pH derived by E-AIM and ISORROPIA, and the IR measurements with Visual MINTEQ calculations.

Fig. 4 Comparison of metal speciation for samples collected at the summit of Mt. Etna (average of the two samples), within the volcanic plume, using (a) water content and pH calculated with E-AIM, (b) water content and pH calculated with ISORROPIA, and (c) measured water content with IR and pH calculated with Visual MINTEQ.

Looking at the distribution seen at the summit with the E-AIM water concentration, shown in Fig. 4a, of the 13 metals, Ni²⁺, K⁺, Mg²⁺, Ca²⁺ and Fe²⁺ have a distribution between the free ion, inorganic–ligand complexes and organic–ligand complexes which vary by less than 10% across all the size fractions, showing a high free ion percentage, with around 10–20% inorganic–ligand complex. Cr³⁺ is distributed almost equally between its free ion form and inorganic form bound to sulphate in the form of CrSO₄⁺. In the finest size fractions (<2.5 μm), due to high oxalate concentration, two metals (Al³⁺ and Fe³⁺) display more variable speciation with a significant contribution from complexation with oxalate. Complexation by oxalate contributed up to 80% of Fe³⁺ in the smallest size fraction (<0.25 μm). The significant variation in Al³⁺ and Fe³⁺ indicates high sensitivity of complexation to water concentration, chemical composition, and pH.

Turning to the ISORROPIA calculations of water at the summit, as shown in Fig. 4b, there is significant variation between the size fractions due to the skew from the anomalous high pH values in the two larger size fractions. The three samples with high pH (S1-0807-PM_10–2.5, S2-1207-PM_10–2.5, and S2-1207-PM_2.5–1) had 60–90% of the oxalate in the free anion form, compared to 27% in S1-0807-PM_2.5–1. This aligns with the pK_a values for oxalate being 1.25 and 4.40, and thus the deprotonated form being present.⁵³ Oxalate is discussed because it is the most abundant organic species in all samples. It also complexes strongly, unlike some other organics.³² In addition, iron oxide precipitation at high pH means no iron is available for binding with oxalate. Most of the metals were seen as free ions, within inorganic complexes or as precipitates given the lower ALW content. In the remaining samples, a decrease in free ion and an increase in inorganic complex abundance was seen as the size fractions got smaller, and the organic fraction was small and invariant (except for Al³⁺, Cu²⁺, and Fe³⁺). This does not follow the trends in water or acidity.

Visual MINTEQ calculations based on IR water concentrations at the summit, shown in Fig. 4c, show an abundance of free ions for Na⁺, K⁺, Mg²⁺, Ca²⁺, Mn²⁺, Zn²⁺ and Fe²⁺ across all size fractions. Cr³⁺ and Fe³⁺ are also invariant across size fractions, with the vast majority of the metals within inorganic–ligand complexes for Cr³⁺ (as Cr(OH)₂⁺ and Cr(OH)_3(aq.)) and as precipitates for Fe³⁺ due to higher pH. Cu²⁺, Al³⁺ and Pb²⁺ show more variation, seemingly uncorrelated with water concentration (constant in all samples) and pH.

The E-AIM and ISORROPIA metal distributions at the summit differ – E-AIM water concentration predicts more free-ions, whereas ISORROPIA concentration predicts more inorganic–ligand complexation. Exceptions to this are Fe³⁺, with more organic–ligand complexation seen in E-AIM than ISORROPIA, Zn²⁺ and Cr³⁺, showing relatively high organic–ligand complexation in the 2.5–1.0 μm size ISORROPIA samples compared to E-AIM, and Al³⁺ which shows variable trends but more organic–ligand complexation in E-AIM.

Compared to E-AIM and ISORROPIA, the IR water concentration based calculations predict largely higher free-ion concentrations at the summit in 9 metals, as expected given the higher water concentrations. Cu²⁺ (E-AIM) and Fe³⁺ (E-AIM and ISORROPIA) have significant concentrations of organic complexes, not seen in IR. This could be due to the higher pH predicted using IR water concentrations compared to E-AIM and ISORROPIA water concentrations, above the pK_a values for oxalate. Al³⁺ is mostly precipitating according to the calculations based on IR input data due to the higher pH.

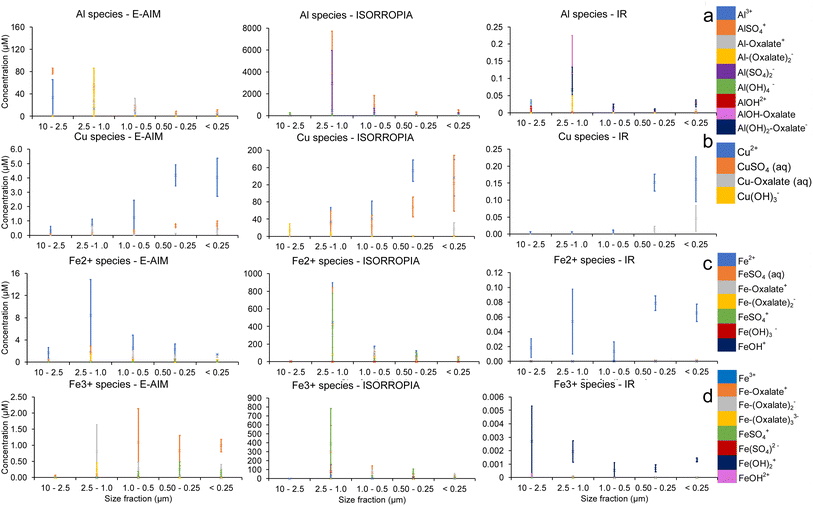
The metals with an appreciable proportion of organic–ligand complexes are Al³⁺, Cu²⁺ and Fe³⁺. The detailed speciation of their soluble fraction for samples collected at the summit is shown in Fig. 5 together with that of Fe²⁺ for comparison. Fig. 5 shows a remarkably different distribution of ions with size for the three model simulations. These different distributions can be attributed to the different conditions being simulated, in terms of water content and pH, which drives not only the ion speciation in solution but also the amount of precipitation being predicted for different ions (as can be seen also in Fig. 4).

Fig. 5 Detailed speciation of (a) Al³⁺, (b) Cu²⁺, (c) Fe²⁺, and (d) Fe³⁺ for samples collected at the summit within the volcanic plume. Bars show standard deviations between the two samples collected at the summit of Mt. Etna.

The distribution of Al³⁺, shown in Fig. 5a, is strongly dependent on water concentration. At high water concentrations (IR), the organic–ligand complexes AlOH–oxalate, Al–oxalate⁺ and Al(OH)₂–oxalate⁻ are most concentrated, except in the largest size fraction, where Al³⁺ and AlOH²⁺ are seen. The higher pH using IR water concentration inputs, allows oxalate to be more available to complex elements other than Fe as observed in previous studies.²³ For the calculations based on lower water concentration of E-AIM, inorganic–ligand complexes, organic–ligand complexes and the free ions have all large relative concentrations. The lowest water concentration, predicted by ISORROPIA, favours inorganic–ligand complexes while Al–oxalate⁺ and Al³⁺ are comparatively less concentrated than for calculations using E-AIM and IR inputs.

Fig. 5b shows the Cu²⁺ species predicted at the summit. In all cases, the free ion is the most abundant species in most size fractions. All three models also predict that CuSO₄(aq.) is the highest concentration inorganic–ligand species, and Cu–oxalate(aq.) is the highest concentration organic–ligand species. As with Al³⁺, inorganic–ligand species are more dominant at low water concentrations, with CuSO₄(aq.) more abundant in calculations based on water concentration from E-AIM and ISORROPIA than in IR, which favours Cu–oxalate(aq.).

For all three water concentrations, the free ion Fe²⁺ is the most concentrated in most size fractions, as shown in Fig. 5c. As in the Cu species, the free ion is dominant at high (IR) water concentrations. FeSO₄²⁺, Fe–oxalate⁺ and Fe(–oxalate)₂⁻ are of comparable magnitude in the lower water content scenarios (E-AIM and ISORROPIA). For the largest size fraction, using the water content and pH calculated with ISORROPIA, Fe(OH)₃⁻ is the most concentrated species by a factor of 10⁴.

Looking more specifically at Fe³⁺ species, as shown in Fig. 5d, the free Fe³⁺ ion has a low relative concentration. Unlike previous trends, the high water concentration scenario (IR) favours the inorganic–ligand complex Fe(OH)₂⁺, whereas E-AIM features organic–ligand complexes at high concentration. Organic–ligand and inorganic–ligand complexes are of comparable magnitude in ISORROPIA.

For Zn²⁺ and Ni²⁺, E-AIM calculates that a minor proportion of these two metals coordinates with oxalate (Fig. S2 and S3†).

3.3.2 Comparison of metal speciation in samples collected in Milo, downwind of the volcanic plume. Fig. 6 shows the comparison of the calculated metal speciation using water concentrations and pH derived by E-AIM and ISORROPIA for the sample collected in the town of Milo, about 10 km downwind from the crater. Fig. 6a shows the metal speciation obtained using E-AIM water concentration and pH. The largest three size fractions show similar distributions. In the 0.5–0.25 μm size fraction, only a few metals were detected, and their speciation resembles that of the largest size fractions. However, the smallest size fraction (<0.25 μm), which has less water and reduced acidity compared to the largest three size fractions, shows less free ions, more inorganic–ligand complexes, and precipitation. A few ions do not fit this trend, such as Zn²⁺ which is relatively invariant, and Pb²⁺ and Fe³⁺ mostly precipitating in the smallest size fraction. Cr³⁺ is calculated to be complexed with acetate as Cr–acetate²⁺ in the 1–0.5 μm size fraction and to a minor extent in the two largest size fractions too.

Fig. 6 Comparison of metal speciation estimated with Visual MINTEQ and based on samples collected in Milo, 10 km downwind of the plume, using (a) water content and pH calculated with E-AIM, and (b) water content and pH calculated with ISORROPIA.

Calculation based on Milo samples using ISORROPIA water concentration, as shown in Fig. 6b, had very different distributions, likely due to the large difference in pH (very acidic at 10–2.5 μm, and neutral at 2.5–1.0 μm). In eight of the metals, there are more free-ions in the largest size fraction, while the majority of metals precipitate in the smallest size fraction. This could be attributable to the decrease in water concentration by a factor of 2.8 from the largest to the smallest size fractions. In Cr³⁺, the larger size fraction had significant organic–ligand complexation, while it precipitates for all other size fractions. Ni²⁺ shows complexation with organics in the 0.5–0.25 μm size fraction in the form of Ni(oxalate)₂²⁻ and Ni–oxalate(aq.). Cu²⁺ and Zn²⁺ are mainly complexed with ammonia in the smaller size fractions, as Cu(NH₃)₄²⁺, Cu(NH₃)₃²⁺, Zn(NH₃)₄²⁺, and Zn(NH₃)₃²⁺, due to the high pH calculated by ISORROPIA.

Generally, at Milo, Visual MINTEQ estimation based on E-AIM water concentration predicts more free-ions and more soluble inorganic–ligand complexation than the one based on ISORROPIA inputs. This can partly be explained by the different T and RH inputs used in the two models for Milo (nighttime conditions of 89.69% RH and 23.59 °C for E-AIM, and average daily conditions of 50.23% and 27.53 °C for ISORROPIA). ISORROPIA generally shows higher organic–ligand complexation for Ni²⁺ in the 0.5–0.25 μm size fraction, as oxalate is found in its fully protonated form at greater relative concentrations in the very acidic environment as calculated by E-AIM. Contrastingly, E-AIM calculates Cr³⁺ to be complexed with acetate in the three largest size fractions and especially in the 1–0.5 μm size fraction, while ISORROPIA calculates it to be complexed with acetate in the largest size fraction only (acidic pH for ISORROPIA, contrary to the lowest size fractions).

3.3.3 Comparison of metal speciation in samples collected within the volcanic plume and in Milo. Looking at the summit and Milo samples from E-AIM together, generally, as water content decreases and acidity increases, the free ion concentration falls, and inorganic complex concentration grows. This is observed in Ni²⁺, K⁺, Ca²⁺ and Pb²⁺ in all size fractions. Precipitation also increases in Milo given the lower water content, especially for Ca²⁺, Mn²⁺, and Fe³⁺. Formation of organic complexes is more favoured at the summit except for Cr³⁺ for which higher organic complex concentrations are observed at Milo.

Comparing the ISORROPIA summit and Milo in the 10–2.5 μm samples, the water concentration decreases from the summit to Milo by a factor of 100. The pH goes from 12 at the summit to around 0 at Milo, which led to all metals increasing free ion concentration and decreasing inorganic–ligand complex concentration, except for Cr³⁺ where organic–ligand complex concentration (with acetate as the ligand) grew significantly. The four smallest size fractions show less uniformity in their changes in composition from the summit to Milo likely due to the neutral pH calculated using ISORROPIA inputs for the samples collected in Milo together with the decrease in water content. In Milo, despite the water content predicted by E-AIM and ISORROPIA being of comparable magnitude (unlike at the summit), Visual MINTEQ calculates very different species distributions. This is likely because E-AIM predicts a very acidic environment whereas ISORROPIA indicates almost neutral aerosols.

4 Conclusion

In this paper, we presented for the first time a detailed chemical characterisation and metal ion speciation for aerosol samples collected within the plume emitted at the Bocca Nuova crater at Mt. Etna, during continuous degassing, as well as for a 10 km downwind sample collected in the town of Milo.

Metal speciation calculations rely on knowledge concerning the water content of the aerosol and its pH. We compared two models, E-AIM and ISORROPIA, for determining water concentration and pH which have been shown to differ significantly under high relative humidity and supersaturation conditions within the plume. ISORROPIA calculates a water concentration a factor 10² lower than that of E-AIM and alkaline pH values for some of the samples. As the volcanic plume environment is characterised by high concentrations of acids, such as HF and HCl, together with SO₂ which converts to H₂SO₄,³⁵ ISORROPIA appears to be unreliable in this environment when run in reverse mode (i.e., lacking the constraint of gas phase concentrations of ammonia and acids). This is also confirmed by pH calculations being run using the Visual MINTEQ model using the plume water content measured by IR. The plume water content measured with IR was a factor of 10²–10³ larger than E-AIM, although this is not necessarily reflective of the aerosol water content within the plume.

At Milo, E-AIM and ISORROPIA calculate similar aerosol water contents. Differences in pH between E-AIM and ISORROPIA were due to supersaturation conditions making the simplifications (e.g., activity equal to one for H⁺ and OH⁻) that ISORROPIA utilises inappropriate. The results of our study show that, when run in reverse mode (i.e., without constraints on gas species concentrations), the more computationally thorough E-AIM provides reliable results which is consistent with a previous study⁴⁶ that ran sensitivity analysis with and without gas concentration constraints and found that the results were in good agreement. On the other hand, ISORROPIA, which was designed to be more computationally efficient for running with chemical transport models,³⁹ requires constraints for the partitioning of NH₃/NH₄⁺ to provide accurate results. Our study highlights large discrepancies between E-AIM and ISORROPIA, especially under more extreme conditions (dry at Milo, in supersaturation within the volcanic plume). Recording gas phase composition data, e.g., NH₃(g) concentration, would enable E-AIM and ISORROPIA to be run in their more accurate ‘forward’ mode, thus refining water concentrations and pH calculations. Nevertheless, more research is needed to understand the range of applicability of the two models but also more direct measurements of water content⁵⁴ and aerosol pH⁴² would allow filling knowledge gaps on aerosol speciation.

The large discrepancies between the water content and pH calculated by the two models impact the speciation results which are largely dependent on the absolute concentrations of dissolved species as well as pH conditions. Within the volcanic plume and using E-AIM water concentration, Visual MINTEQ predicts most metals in deliquescent aerosol to be present predominantly as free ions. Significant organic complexation, with oxalate, is calculated only for Al³⁺, Cu²⁺, and Fe³⁺ and to a minor extent also for Ni²⁺ and Zn²⁺. When considering the total content of water in the plume, Al³⁺ and Fe³⁺ predominantly precipitate due to a less acidic pH compared to that of the aerosol-bound water calculated by E-AIM. Concerning Cr³⁺, in both cases, it is calculated to be bound to inorganics but in the form of CrSO₄⁺ using input data from E-AIM and as Cr(OH)₂⁺ and Cr(OH)₃(aq.) using the total water content of the plume (measured by IR). When using input data from ISORROPIA, the speciation broadly overlaps with that obtained using E-AIM input data for the three smallest size fractions. However, due to the unreasonably very basic pH calculated by ISORROPIA for the two largest size fractions the resulting speciation appeared to be extremely different, with a large extent of precipitation for most metals, and presumably incorrect given the acidic conditions expected for a typical volcanic plume.

Downwind from the crater, in the town of Milo, large discrepancies between the speciation obtained with E-AIM and ISORROPIA inputs are also found predominantly due to the very different pH conditions calculated by the two models. At Milo, E-AIM calculates a a larger fraction of inorganic-bound metals due to the lower aerosol water concentrations compared to those of the plume environment. Additionally, Ca²⁺ is calculated to precipitate thus removing oxalate from the water phase and preventing the formation of organic–ligand complexes with other metals. A minor contribution of organic complexation is observed only for the smallest size fraction for Al³⁺, Cu²⁺, and Fe³⁺ while Cr³⁺ is predicted to be bound to acetate in the three largest size fractions. Visual MinteQ with ISORROPIA inputs calculates a large extent of precipitation for many metals in the four smallest size fractions due to the neutral pH. Organic complexation is found only for Ni²⁺ (with oxalate) in the 0.5–0.25 μm size fraction, probably due to oxalate deprotonation as well as the absence of other metals that would bind strongly with oxalate, and for Cr³⁺ (with acetate) in the 10–2.5 μm size fraction, the only one with acidic pH according to Visual MINTEQ based on ISORROPIA inputs. Due to the neutral pH in the smallest four size fraction (from ISORROPIA), Zn²⁺ and Cu²⁺ would be found to be complexed with ammonia at Milo.

As evident in the error bars in Fig. 5, the variation in concentration of species between the two summit samples recorded on different days is significant. This result highlights the need for collecting more samples within the plume. From the sample data, the solubility of metals in aerosols is size dependent, with the largest, 10–2.5 μm, and smallest, <0.25 μm, fractions more soluble at Milo, and the 2.5–0.25 μm fractions more soluble at the summit. The higher metal solubility in the coarse fraction at Milo is unexpected, given that generally the coarse fraction is made of less soluble material as observed previously in both urban⁵⁵ and more remote marine⁵⁶ environments. Also for downwind samples, there is a need for further studies to evaluate metal solubility and the impact of the volcanic plume on the local and regional outdoor air. Previous studies have shown that the oxidative potential of aerosol is influenced by the chemical form in which metals are present in the aerosols, which is influenced by coordination with organic ligands.^57,58 Similarly, reactive oxygen species production is impacted by coordination between metals and organic ligands.⁵⁹ In addition, the solubility and dissolution kinetics of metals can be enhanced by coordination chemistry making metals more bioavailable and potentially more toxic.²³ While oxidative potential and reactive oxygen species production are linked with adverse health outcomes,^60–64 to the authors' knowledge, there are no other published studies that have investigated the influence of coordination chemistry on particle toxicity, a research area that requires investigation.

Data availability

Characterisation data are available in the ESI.† The results of modelling can be provided upon request to the corresponding author.

Author contributions

CG designed the study, collected the samples, and prepared the manuscript for submission. TH performed the thermodynamic modelling work and prepared a first draft of the manuscript. SD and DB analysed the samples. SC and BH measured and provided data on RH and T. PS, SG, ALS, and GS provided support during sample collection and field campaign organisation. All authors revised and approved the manuscript before submission.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The EPL-REFLECT campaign was funded by the European Commission under the EUROVOLC grant (Programme: Horizon 2020, Grant Number: 731070). This work was funded by the Supporting TAlent in ReSearch@University of Padova STARS-StG MOCAA awarded by the University of Padova to CG and a BP Next Generation fellowship awarded by the Yusuf Hamied Department of Chemistry at the University of Cambridge to CG.

References

1. R. von Glasow, Atmospheric chemistry in volcanic plumes, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6594–6599.
2. P. Weinstein, C. J. Horwell and A. Cook, in Essentials of Medical Geology, Springer Netherlands, Dordrecht, 2013, pp. 217–238.
3. A. Robock, Climatic Impacts of Volcanic Eruptions, The Encyclopedia of Volcanoes, 2015, pp. 935–942.
4. P. Sellitto, A. Podglajen, R. Belhadji, M. Boichu, E. Carboni, J. Cuesta, C. Duchamp, C. Kloss, R. Siddans, N. Bègue, L. Blarel, F. Jegou, S. Khaykin, J.-B. Renard and B. Legras, The unexpected radiative impact of the Hunga Tonga eruption of 15th January 2022, Commun. Earth Environ., 2022, 3, 288.
5. M. Edmonds, T. A. Mather and E. J. Liu, A distinct metal fingerprint in arc volcanic emissions, Nat. Geosci., 2018, 11, 790–794.
6. A. Aiuppa, A. Franco, R. Von Glasow, A. G. Allen, W. D'Alessandro, T. A. Mather, D. M. Pyle and M. Valenza, The tropospheric processing of acidic gases and hydrogen sulphide in volcanic gas plumes as inferred from field and model investigations, Atmos. Chem. Phys., 2007, 7, 1441–1450.
7. A. Aiuppa, C. Federico, G. Giudice, S. Gurrieri, M. Liuzzo, H. Shinohara, R. Favarra and M. Valenza, Rates of carbon dioxide plume degassing from Mount Etna volcano, J. Geophys. Res.: Solid Earth, 2006, 111, 1–8.
8. T. Caltabiano, M. Burton, S. Giammanco, P. Allard, N. Bruno, F. Murè and R. Romano, Volcanic gas emissions from the summit craters and flanks of Mt. Etna, 1987–2000, Geophysical Monograph Series, 2004, vol. 143, pp. 111–128.
9. P. Sellitto, G. Salerno, A. La Spina, T. Caltabiano, S. Scollo, A. Boselli, G. Leto, R. Zanmar Sanchez, S. Crumeyrolle, B. Hanoune and P. Briole, Small-scale volcanic aerosols variability, processes and direct radiative impact at Mount Etna during the EPL-RADIO campaigns, Sci. Rep., 2020, 10, 15224.
10. P. Sellitto, C. Zanetel, A. di Sarra, G. Salerno, A. Tapparo, D. Meloni, G. Pace, T. Caltabiano, P. Briole and B. Legras, The impact of Mount Etna sulfur emissions on the atmospheric composition and aerosol properties in the central Mediterranean: A statistical analysis over the period 2000–2013 based on observations and Lagrangian modelling, Atmos. Environ., 2017, 148, 77–88.
11. A. G. Allen, T. A. Mather, A. J. S. McGonigle, A. Aiuppa, P. Delmelle, B. Davison, N. Bobrowski, C. Oppenheimer, D. M. Pyle and S. Inguaggiato, Sources, size distribution, and downwind grounding of aerosols from Mount Etna, J. Geophys. Res.: Atmos., 2006, 111, 1–10.
12. R. S. Martin, T. A. Mather, D. M. Pyle, M. Power, A. G. Allen, A. Aiuppa, C. J. Horwell and E. P. W. Ward, Composition-resolved size distributions of volcanic aerosols in the Mt. Etna plumes, J. Geophys. Res.: Atmos., 2008, 113, 1–17.
13. M. Edmonds, E. Mason and O. Hogg, Volcanic Outgassing of Volatile Trace Metals, Annu. Rev. Earth Planet. Sci., 2022, 50, 79–98.
14. P. Buat-Ménard and M. Arnold, The heavy metal chemistry of atmospheric particulate matter emitted by Mount Etna Volcano, Geophys. Res. Lett., 1978, 5, 245–248.
15. P. J. Gauthier and M. F. Le Cloarec, Variability of alkali and heavy metal fluxes released by Mt. Etna volcano, Sicily, between 1991 and 1995, J. Volcanol. Geotherm. Res., 1998, 81, 311–326.
16. S. Calabrese, A. Aiuppa, P. Allard, E. Bagnato, S. Bellomo, L. Brusca, W. D'Alessandro and F. Parello, Atmospheric sources and sinks of volcanogenic elements in a basaltic volcano (Etna, Italy), Geochim. Cosmochim. Acta, 2011, 75, 7401–7425.
17. S. Calabrese, L. Randazzo, K. Daskalopoulou, S. Milazzo, S. Scaglione, S. Vizzini, C. D. Tramati, W. D’Alessandro, L. Brusca, S. Bellomo, G. B. Giuffrida, G. Pecoraino, G. Montana, G. Salerno, S. Giammanco, T. Caltabiano and F. Parello, Mount Etna volcano (Italy) as a major “dust” point source in the Mediterranean area, Arabian J. Geosci., 2016, 9, 219.
18. E. Ilyinskaya, E. Mason, P. E. Wieser, L. Holland, E. J. Liu, T. A. Mather, M. Edmonds, R. C. W. Whitty, T. Elias, P. A. Nadeau, D. Schneider, J. B. McQuaid, S. E. Allen, J. Harvey, C. Oppenheimer, C. Kern and D. Damby, Rapid metal pollutant deposition from the volcanic plume of Kīlauea, Hawai'i, Commun. Earth Environ., 2021, 2, 78.
19. C. Misra, M. Singh, S. Shen, C. Sioutas and P. M. Hall, Development and evaluation of a personal cascade impactor sampler (PCIS), J. Aerosol Sci., 2002, 33, 1027–1047.
20. C. Giorio, S. Pizzini, E. Marchiori, R. Piazza, S. Grigolato, M. Zanetti, R. Cavalli, M. Simoncin, L. Soldà, D. Badocco and A. Tapparo, Sustainability of using vineyard pruning residues as an energy source: Combustion performances and environmental impact, Fuel, 2019, 243, 371–380.
21. C. Giorio, A. Tapparo, M. L. Scapellato, M. Carrieri, P. Apostoli and G. B. Bartolucci, Field comparison of a personal cascade impactor sampler, an optical particle counter and CEN-EU standard methods for PM10, PM2.5 and PM1 measurement in urban environment, J. Aerosol Sci., 2013, 65, 111–120.
22. V. Di Marco, A. Tapparo, D. Badocco, S. D'Aronco, P. Pastore and C. Giorio, Metal Ion Release from Fine Particulate Matter Sampled in the Po Valley to an Aqueous Solution Mimicking Fog Water: Kinetics and Solubility, Aerosol Air Qual. Res., 2020, 20, 720–729.
23. C. Giorio, S. D'Aronco, V. Di Marco, D. Badocco, F. Battaglia, L. Soldà, P. Pastore and A. Tapparo, Emerging investigator series: aqueous-phase processing of atmospheric aerosol influences dissolution kinetics of metal ions in an urban background site in the Po Valley, Environ. Sci.: Processes Impacts, 2022, 24, 884–897.
24. A. Tapparo, V. Di Marco, D. Badocco, S. D'Aronco, L. Soldà, P. Pastore, B. M. Mahon, M. Kalberer and C. Giorio, Formation of metal-organic ligand complexes affects solubility of metals in airborne particles at an urban site in the Po valley, Chemosphere, 2020, 241, 125025.
25. A. S. Wexler, Atmospheric aerosol models for systems including the ions H⁺, NH₄⁺, Na⁺, SO₄²⁻, NO₃⁻, Cl⁻, Br⁻, and H₂O, J. Geophys. Res., 2002, 107, 4207.
26. S. L. Clegg, P. Brimblecombe and A. S. Wexler, Thermodynamic model of the system H⁺-NH₄⁺-SO₄^2--NO₃^--H₂O at tropospheric temperatures, J. Phys. Chem. A, 1998, 102, 2137–2154.
27. H. Shinohara, A. Aiuppa, G. Giudice, S. Gurrieri and M. Liuzzo, Variation of H ₂ O/CO ₂ and CO ₂/SO ₂ ratios of volcanic gases discharged by continuous degassing of Mount Etna volcano, Italy, J. Geophys. Res.: Solid Earth, 2008, 113, B09203.
28. C. Fountoukis and A. Nenes, ISORROPIAII: A computationally efficient thermodynamic equilibrium model for K+-Ca2+-Mg2+-NH4+-Na+-SO42--NO3--Cl--H2O aerosols, Atmos. Chem. Phys., 2007, 7, 4639–4659.
29. L. Deguillaume, K. V. Desboeufs, M. Leriche, Y. Long and N. Chaumerliac, Effect of iron dissolution on cloud chemistry: from laboratory measurements to model results, Atmos. Pollut. Res., 2010, 1, 220–228.
30. N. M. Garner, J. Top, F. Mahrt, I. El Haddad, M. Ammann and D. M. Bell, Iron-Containing Seed Particles Enhance α-Pinene Secondary Organic Aerosol Mass Concentration and Dimer Formation, Environ. Sci. Technol., 2024, 58, 16984–16993.
31. P. A. Alpert, J. Dou, P. Corral Arroyo, F. Schneider, J. Xto, B. Luo, T. Peter, T. Huthwelker, C. N. Borca, K. D. Henzler, T. Schaefer, H. Herrmann, J. Raabe, B. Watts, U. K. Krieger and M. Ammann, Photolytic radical persistence due to anoxia in viscous aerosol particles, Nat. Commun., 2021, 12, 1769.
32. S. Scheinhardt, K. Müller, G. Spindler and H. Herrmann, Complexation of trace metals in size-segregated aerosol particles at nine sites in Germany, Atmos. Environ., 2013, 74, 102–109.
33. Report on Etna (Italy)—17 July-23 July 2019, https://volcano.si.edu/showreport.cfm?wvar=GVP.WVAR20190717-211060, accessed 9 April 2024.
34. M. Lachatre, S. Mailler, L. Menut, A. Cholakian, P. Sellitto, G. Siour, H. Guermazi, G. Salerno and S. Giammanco, Modelling SO2conversion into sulfates in the mid-troposphere with a 3D chemistry transport model: the case of Mount Etna's eruption on 12 April 2012, Atmos. Chem. Phys., 2022, 22, 13861–13879.
35. A. Aiuppa, S. Bellomo, W. D'Alessandro, C. Federico, M. Ferm and M. Valenza, Volcanic plume monitoring at Mount Etna by diffusive (passive) sampling, J. Geophys. Res.: Atmos., 2004, 109, 1–11.
36. A. Aiuppa, P. Allard, W. D'Alessandro, S. Giammanco, F. Parello and M. Valenza, Magmatic gas leakage at Mount Etna (Sicily, Italy): Relationships with the volcano-tectonic structures, the hydrological pattern and the eruptive activity, Geophys. Monogr. Ser., 2004, 143, 129–145.
37. R. D. Cadle, A comparison of volcanic with other fluxes of atmospheric trace gas constituents, Rev. Geophys., 1980, 18, 746–752.
38. H. Herrmann, T. Schaefer, A. Tilgner, S. A. Styler, C. Weller, M. Teich and T. Otto, Tropospheric Aqueous-Phase Chemistry: Kinetics, Mechanisms, and Its Coupling to a Changing Gas Phase, Chem. Rev., 2015, 115, 4259–4334.
39. H. Ling, M. Deng, Q. Zhang, L. Xu, S. Su, X. Li, L. Yang, J. Mao and S. Jia, Quantifying Contributions of Factors and Their Interactions to Aerosol Acidity with a Multiple-Linear-Regression-Based Framework: A Case Study in the Pearl River Delta, China, Atmosphere, 2024, 15, 172.
40. R. A. Zaveri, R. C. Easter and A. S. Wexler, A new method for multicomponent activity coefficients of electrolytes in aqueous atmospheric aerosols, J. Geophys. Res.: Atmos., 2005, 110, 1–23.
41. A. G. Allen, T. A. Mather, A. J. S. McGonigle, A. Aiuppa, P. Delmelle, B. Davison, N. Bobrowski, C. Oppenheimer, D. M. Pyle and S. Inguaggiato, Sources, size distribution, and downwind grounding of aerosols from Mount Etna, J. Geophys. Res.: Atmos., 2006, 111, 1–10.
42. K. J. Angle, D. R. Crocker, R. M. C. Simpson, K. J. Mayer, L. A. Garofalo, A. N. Moore, S. L. Mora Garcia, V. W. Or, S. Srinivasan, M. Farhan, J. S. Sauer, C. Lee, M. A. Pothier, D. K. Farmer, T. R. Martz, T. H. Bertram, C. D. Cappa, K. A. Prather and V. H. Grassian, Acidity across the interface from the ocean surface to sea spray aerosol, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018397118.
43. H. O. T. Pye, A. Nenes, B. Alexander, A. P. Ault, M. C. Barth, S. L. Clegg, J. L. Collett Jr, K. M. Fahey, C. J. Hennigan, H. Herrmann, M. Kanakidou, J. T. Kelly, I.-T. Ku, V. F. McNeill, N. Riemer, T. Schaefer, G. Shi, A. Tilgner, J. T. Walker, T. Wang, R. Weber, J. Xing, R. A. Zaveri and A. Zuend, The acidity of atmospheric particles and clouds, Atmos. Chem. Phys., 2020, 20, 4809–4888.
44. C. J. Hennigan, J. Izumi, A. P. Sullivan, R. J. Weber and A. Nenes, A critical evaluation of proxy methods used to estimate the acidity of atmospheric particles, Atmos. Chem. Phys., 2015, 15, 2775–2790.
45. X. Yao, T. Yan Ling, M. Fang and C. K. Chan, Comparison of thermodynamic predictions for in situ pH in PM2.5, Atmos. Environ., 2006, 40, 2835–2844.
46. B. A. Nault, P. Campuzano-Jost, D. A. Day, D. S. Jo, J. C. Schroder, H. M. Allen, R. Bahreini, H. Bian, D. R. Blake, M. Chin, S. L. Clegg, P. R. Colarco, J. D. Crounse, M. J. Cubison, P. F. DeCarlo, J. E. Dibb, G. S. Diskin, A. Hodzic, W. Hu, J. M. Katich, M. J. Kim, J. K. Kodros, A. Kupc, F. D. Lopez-Hilfiker, E. A. Marais, A. M. Middlebrook, J. Andrew Neuman, J. B. Nowak, B. B. Palm, F. Paulot, J. R. Pierce, G. P. Schill, E. Scheuer, J. A. Thornton, K. Tsigaridis, P. O. Wennberg, C. J. Williamson and J. L. Jimenez, Chemical transport models often underestimate inorganic aerosol acidity in remote regions of the atmosphere, Commun. Earth Environ., 2021, 2, 93.
47. H. Guo, L. Xu, A. Bougiatioti, K. M. Cerully, S. L. Capps, J. R. Hite, A. G. Carlton, S. H. Lee, M. H. Bergin, N. L. Ng, A. Nenes and R. J. Weber, Fine-particle water and pH in the southeastern United States, Atmos. Chem. Phys., 2015, 15, 5211–5228.
48. S. Song, M. Gao, W. Xu, J. Shao, G. Shi, S. Wang, Y. Wang, Y. Sun and M. B. McElroy, Fine-particle pH for Beijing winter haze as inferred from different thermodynamic equilibrium models, Atmos. Chem. Phys., 2018, 18, 7423–7438.
49. S. Jia, X. Wang, Q. Zhang, S. Sarkar, L. Wu, M. Huang, J. Zhang and L. Yang, Technical note: Comparison and interconversion of pH based on different standard states for aerosol acidity characterization, Atmos. Chem. Phys., 2018, 18, 11125–11133.
50. H. Guo, A. P. Sullivan, P. Campuzano-Jost, J. C. Schroder, F. D. Lopez-Hilfiker, J. E. Dibb, J. L. Jimenez, J. A. Thornton, S. S. Brown, A. Nenes and R. J. Weber, Fine particle pH and the partitioning of nitric acid during winter in the northeastern United States, J. Geophys. Res., 2016, 121, 10355–10376.
51. J. D. Haskins, L. Jaeglé, V. Shah, B. H. Lee, F. D. Lopez-Hilfiker, P. Campuzano-Jost, J. C. Schroder, D. A. Day, H. Guo, A. P. Sullivan, R. Weber, J. Dibb, T. Campos, J. L. Jimenez, S. S. Brown and J. A. Thornton, Wintertime Gas-Particle Partitioning and Speciation of Inorganic Chlorine in the Lower Troposphere Over the Northeast United States and Coastal Ocean, J. Geophys. Res.: Atmos., 2018, 123, 12897–12916.
52. X. Peng, P. Vasilakos, A. Nenes, G. Shi, Y. Qian, X. Shi, Z. Xiao, K. Chen, Y. Feng and A. G. Russell, Detailed Analysis of Estimated pH, Activity Coefficients, and Ion Concentrations between the Three Aerosol Thermodynamic Models, Environ. Sci. Technol., 2019, 53, 8903–8913.
53. National Center for Biotechnology Information, PubChem Compound Summary for CID 971, Oxalic Acid, https://pubchem.ncbi.nlm.nih.gov/compound/Oxalic-Acid#section=Computed-Properties, accessed 8 April 2024.
54. S. Canepari, C. Farao, E. Marconi, C. Giovannelli and C. Perrino, Qualitative and quantitative determination of water in airborne particulate matter, Atmos. Chem. Phys., 2013, 13, 1193–1202.
55. L. Liu, W. Li, Q. Lin, Y. Wang, J. Zhang, Y. Zhu, Q. Yuan, S. Zhou, D. Zhang, C. Baldo and Z. Shi, Size-dependent aerosol iron solubility in an urban atmosphere, npj Clim. Atmos. Sci., 2022, 5, 53.
56. K. Sakata, M. Kurisu, Y. Takeichi, A. Sakaguchi, H. Tanimoto, Y. Tamenori, A. Matsuki and Y. Takahashi, Iron (Fe) speciation in size-fractionated aerosol particles in the Pacific Ocean: The role of organic complexation of Fe with humic-like substances in controlling Fe solubility, Atmos. Chem. Phys., 2022, 22, 9461–9482.
57. P. Shahpoury, Z. W. Zhang, A. Arangio, V. Celo, E. Dabek-Zlotorzynska, T. Harner and A. Nenes, The influence of chemical composition, aerosol acidity, and metal dissolution on the oxidative potential of fine particulate matter and redox potential of the lung lining fluid, Environ. Int., 2021, 148, 106343.
58. P. Shahpoury, S. Lelieveld, C. Johannessen, T. Berkemeier, V. Celo, E. Dabek-Zlotorzynska, T. Harner, G. Lammel and A. Nenes, Influence of aerosol acidity and organic ligands on transition metal solubility and oxidative potential of fine particulate matter in urban environments, Sci. Total Environ., 2024, 906, 167405.
59. H. Tong, P. S. J. Lakey, A. M. Arangio, J. Socorro, C. J. Kampf, T. Berkemeier, W. H. Brune, U. Pöschl and M. Shiraiwa, Reactive oxygen species formed in aqueous mixtures of secondary organic aerosols and mineral dust influencing cloud chemistry and public health in the Anthropocene, Faraday Discuss., 2017, 200, 251–270.
60. M. Shiraiwa, K. Ueda, A. Pozzer, G. Lammel, C. J. Kampf, A. Fushimi, S. Enami, A. M. Arangio, J. Fröhlich-Nowoisky, Y. Fujitani, A. Furuyama, P. S. J. Lakey, J. Lelieveld, K. Lucas, Y. Morino, U. Pöschl, S. Takahama, A. Takami, H. Tong, B. Weber, A. Yoshino and K. Sato, Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 2017, 51, 13545–13567.
61. Z. Zhang, S. Weichenthal, J. C. Kwong, R. T. Burnett, M. Hatzopoulou, M. Jerrett, A. van Donkelaar, L. Bai, R. V. Martin, R. Copes, H. Lu, P. Lakey, M. Shiraiwa and H. Chen, Long-term exposure to iron and copper in fine particulate air pollution and their combined impact on reactive oxygen species concentration in lung fluid: a population-based cohort study of cardiovascular disease incidence and mortality in Toronto, Canada, Int. J. Epidemiol., 2021, 50, 589–601.
62. Z. Zhang, S. Weichenthal, J. C. Kwong, R. T. Burnett, M. Hatzopoulou, M. Jerrett, A. van Donkelaar, L. Bai, R. V. Martin, R. Copes, H. Lu, P. Lakey, M. Shiraiwa and H. Chen, A population-based cohort study of respiratory disease and long-term exposure to iron and copper in fine particulate air pollution and their combined impact on reactive oxygen species generation in human lungs, Environ. Sci. Technol., 2021, 55, 3807–3818.
63. Q. Meng, J. Liu, J. Shen, I. del Rosario, P. S. J. Lakey, M. Shiraiwa, J. Su, S. Weichenthal, Y. Zhu, F. Oroumiyeh, S. E. Paulson, M. Jerrett and B. Ritz, Fine Particulate Matter Metal Composition, Oxidative Potential, and Adverse Birth Outcomes in Los Angeles, Environ. Health Perspect., 2023, 131, 107012.
64. J. T. Bates, T. Fang, V. Verma, L. Zeng, R. J. Weber, P. E. Tolbert, J. Y. Abrams, S. E. Sarnat, M. Klein, J. A. Mulholland and A. G. Russell, Review of Acellular Assays of Ambient Particulate Matter Oxidative Potential: Methods and Relationships with Composition, Sources, and Health Effects, Environ. Sci. Technol., 2019, 53, 4003–4019.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ea00108g

---