Degradation path prediction of lithium-ion batteries under dynamic operating sequences

Abstract

Reliable battery management requires the degradation of lithium-ion batteries (LIBs) under variable usage patterns to be accurately and continuously monitored and predicted. However, the chemically entangled internal states and the nonlinear accumulation of degradation mechanisms pose challenges to establishing these management processes. Here we present our comprehensive analysis of the degradation path for different operating sequences. The analysis is based on a dataset we constructed using measurements from 72 commercial battery cells operated according to 24 dynamic operating sequences and by employing a periodic diagnostic protocol to quantify the kinetic degradation at various states of charge. By incorporating the path-dependent characteristics of battery degradation into deep learning approaches, we developed a framework capable of predicting future health states from the state at a single time-point without historical information. Our predictive framework achieves test average percent errors of 0.76% and 0.81% for the degradation paths and capacity trajectories, respectively. The proposed battery management schemes offer high prediction reliability and accuracy for dynamic operation and are anticipated to be useful for extending the operational lifetime of LIBs.

---

Broader context

The extensive use of lithium-ion batteries across various applications and end-user groups results in multiple degradation pathways depending on their diverse usage patterns. Amidst these complex real-world usage dynamics, the need to closely track and predict the future evolution of degradation has become more crucial than ever to ensure the reliability of battery management systems. However, a reliable method that can universally predict future degradation behaviors based on upcoming dynamic usage scenarios has yet to be established. In response to this challenge, we developed a deep learning-based framework that leverages the path-dependent characteristics of battery degradation. The framework enables the future degradation path to be forecasted by linking internal degradation trends with future usage plans. To this end, the kinetic parameters that depend on the state-of-charge of the battery are used as features for the robust and generalized prediction of the nonlinear cumulative degradation, even under complex usage patterns. The principle presented in this paper can serve as a foundational basis for ultimately realizing a healthy and sustainable battery ecosystem.

Introduction

Lithium-ion batteries (LIBs) are renowned for their high performance and cost-effectiveness, which have resulted in their widespread utilization across a broad spectrum of applications ranging from personal electronic devices and electric vehicles (EVs) to energy storage systems (ESS).^1–3 As their adoption expands among various groups of end-users, even identically manufactured cells experience diverse usage scenarios, which result in numerous degradation pathways.^4–6 In this context, the ability to exactly monitor and predict the degradation processes of batteries operated according to various patterns offers unprecedented opportunities and advantages for both the end-users and suppliers of battery cells. For example, end-users’ trust in the safety of their batteries in use could be enhanced and, by actively adjusting their usage patterns, they could warrant their convenience and lifetime in a balanced fashion.^7,8 Furthermore, suppliers could utilize customer data to further optimize their battery manufacturing processes as well as to more precisely evaluate the residual value of used cells for a healthy and sustainable used-battery ecosystem.^9,10 An accurate understanding of battery degradation and quantification of the residual value under varied usage patterns are expected to play an increasingly critical role as the uptake of LIBs continues to rapidly proliferate in our daily lives and in industry. However, the chemically intricate internal states, stemming from various sequential and parallel reactions, and the associated nonlinear degradation pathways pose significant difficulties for the accurate diagnosis of LIB cells.^11–14

Attempts to address this issue have involved the ongoing advancement of battery management systems (BMSs) by utilizing extensive datasets and sophisticated predictive models based on data accumulated from various studies.^7,15 For instance, public datasets provide a robust foundation for conducting in-depth analyses of battery degradation across diverse operating conditions, chemical compositions, and cell types.^16–18 Likewise, various predictive models developed to forecast capacity trajectories, the cycle life, and the remaining useful life (RUL) aim to enhance the accuracy by utilizing data-driven approaches that minimize the need for feature engineering.^18–20 Despite the remarkable progress, the accurate prediction of the future degradation behavior of batteries under diverse usage scenarios remains a formidable challenge. The majority of studies that have been reported to date have developed predictive models based on cycle data following fixed protocols, which makes it difficult to apply these models to real-world scenarios in which various cycling conditions are dynamically combined.¹⁰ Although some studies have developed predictive models using datasets that consider uncertain future operating conditions,^21–23 the realization of continuous prognostics and the comprehensive reflection of multi-dimensional degradation modes remain in their infancy. Moreover, the prediction of superficial indicators such as the capacity or RUL is insufficient to fully capture the complex, multi-scaled internal degradation of batteries.^24,25 Thus, novel approaches that function on the basis of more in-depth degradation-related indicators are urgently needed. In this regard, precisely designed periodic diagnostic protocols can effectively extract physicochemical degradation information, and enable the degradation behavior to be closely tracked at any specific points in time.^26–28 These approaches aim to maximize the utility of single time-point data and stand in fundamental contrast with data-driven methods that require extensive long-term historical data.²⁹

Many previous studies have clearly demonstrated that battery degradation exhibits path-dependent behavior,^12,30–33 wherein the current state of the battery is determined by its usage history, and that the effects of future operating conditions depend on this current state. Consequently, under dynamic operating scenarios, future degradation is significantly influenced by both the current state and forthcoming usage patterns. Meanwhile, as changes in battery cycle data accumulate over time, many studies have developed time-series models, including statistical, machine learning, and deep learning approaches.^22,34–36 In particular, deep learning models are promising tools due to their ability to learn complex nonlinear relationships and effectively handle high-dimensional data.³⁷ However, there remains considerable room for further improvement as predictions from fixed or randomly varied protocol datasets are made without understanding the underlying sequential degradation mechanisms. Therefore, the combination of degradation path datasets that were collected through periodic diagnostic protocols with time-series deep learning models offers a useful opportunity to predict future degradation paths based on the path dependence of battery degradation under dynamic operating patterns. This methodology enables the fundamental health state of a battery to be precisely reflected, thereby allowing for reliable predictions even under complex usage patterns.

In this work, we developed a framework that leverages an in-depth understanding of the path-dependent degradation of LIBs to predict future degradation pathways in dynamic operating sequences using single time-point diagnostic data. We constructed a dataset by acquiring data from 72 commercial high-nickel lithium nickel manganese cobalt oxide (NMC)/graphite–silicon composite (Gr–SiO_x) cells across 24 dynamic operating sequences. By introducing a periodic diagnostic protocol to quantify the kinetic degradation at various states of charge (SOCs), we systematically tracked and analyzed the extent to which the degradation mechanisms dynamically vary over individual sequences. Our framework achieves a prediction error of 0.76% for future degradation paths at all cycle points, using only information on the single time-point state and future operating conditions. Furthermore, using the predicted future degradation paths, we achieve prediction errors of 0.81% for future capacity trajectories at all cycle points. These results clearly demonstrate the effectiveness of our predictive framework based on the SOC-dependent kinetic features and their path dependence during battery degradation under dynamic usage scenarios.

Results and discussion

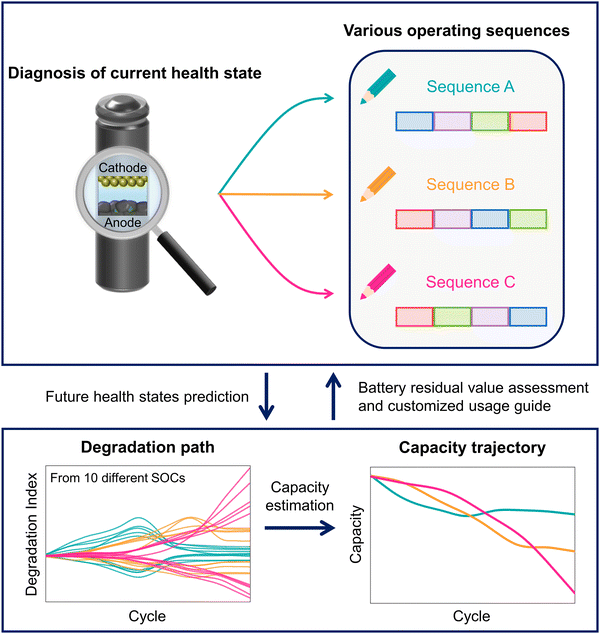
The framework for predicting future degradation paths is schematically depicted in Fig. 1. Each cell exhibits a unique degradation path and corresponding capacity trajectory due to variations in its internal state or operating pattern. The health state of a cell evolves continuously as degradation occurs during use, and this complicates the precise prediction of state changes based on future usage scenarios. However, systematic prediction becomes feasible by considering the path dependence of battery degradation, where future degradation is influenced by the current health state and anticipated usage patterns.

Fig. 1 Schematic of the future degradation path prediction framework under dynamic operating sequences. (upper box) Various possible future operating sequences from the same current health state. (lower box) Dependence of the variation in future degradation paths and capacity trajectories on future operating sequences.

The current health state of the battery can be quantified through an information-rich diagnostic protocol, while future usage patterns can be interpreted as a series of cumulative impacts on the degradation path, which is influenced by each operating condition within the usage sequence. Accordingly, the degradation path can be forecasted by establishing the relationship between internal degradation and future usage plans, with the current health state of the cell serving as a reference. Therefore, future health states can be predicted under dynamic operating sequences via a single time-point diagnosis of the current health state. Furthermore, because the extractable capacity is determined as a result of internal degradation, the capacity trajectory can also be estimated.

This comprehensive framework can utilize insights into the evolution of the degradation for battery life extension and operational optimization in real-world applications such as EVs and ESS. In particular, considering detailed degradation patterns is crucial, as variations in usage habits and seasonal temperature fluctuations can alter the sequence of degradation accumulation.³⁸ Building on this concept, a prediction model based on such path-dependent data can provide customized usage guidelines optimized for the current health state of the cells. In a related line, it enables the accurate assessment of the residual value of a battery in the context of specific usage scenarios.

Design of operating conditions with distinct degradation characteristics

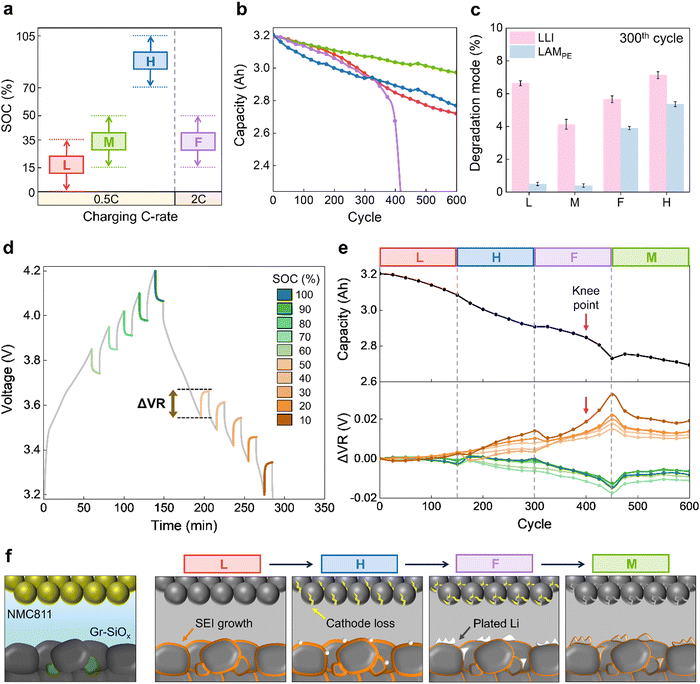
Our objective was to experimentally demonstrate various degradation paths and assess the impact of each condition within the operating sequences on these pathways. To this end, we designed operating conditions commensurate with distinct degradation mechanisms. Previous studies have shown that the predominant degradation mechanisms largely vary according to the SOC ranges and charging C-rates.^6,13,39 Therefore, we cycled commercial NMC811/Gr–SiO_x cells under four distinct operating conditions, as outlined in Fig. 2a. The operating protocols are designed as follows: low SOC (L), medium SOC (M), and high SOC (H) conditions are defined by their respective cycling SOC ranges, all of which were cycled at 0.5C charge. The fast charging (F) condition shares the same cycling SOC range as condition M, but with cycling at 2C charge. Under all conditions, cells were cycled at 2C discharge and a fixed capacity corresponding to an SOC range of 35%. Considering that the operating conditions span partial SOC ranges in each cycle, the capacity was estimated for the full SOC range during the reference performance tests (RPTs) that were conducted every 25 cycles. Hereafter, the points at which RPTs were conducted are referred to as cycle points (Fig. S1, ESI†).

Fig. 2 Designing operating conditions and tracking degradation paths in dynamic operating sequences. (a) Four distinct operating conditions defined by the charging C-rates and SOC ranges. (b) Discharge capacity and (c) results of IC analysis for each operating condition. The data shown are the average values from three cells. (d) Diagnostic protocol for collecting ΔVR data from 10 SOC points, referred to as the degradation index (DI). (e) and (f) An example of a dynamic operating sequence: (e) trends in the discharge capacity and DI. Measurements were taken in intervals of 25 cycles. DI was plotted by adjusting the initial data point of each feature to 0 V. (f) Schematic illustration of the degradation that occurs under each operating condition, with the colored features highlighting the degradation characteristic of each stage.

During the aging test, conducted over 600 cycles for each operating condition, a significant difference in capacity retention was observed (Fig. 2b). The capacity trajectory corresponds to the change in the extractable capacity (determined by the internal state at each cycle point), and underscores that each condition induces distinct primary degradation mechanisms. Specifically, condition M is associated with a gentle linear capacity decay, indicating the mildest degradation at medium SOC.³⁹ Under conditions L and F, a noticeable deviation from condition M was observed with nonlinear decay beginning after 150 cycles. This is attributed to lower extractable capacity due to increased internal resistance. Particularly condition F is characterized by a knee point near the 400th cycle, likely associated with lithium (Li) plating as a result of fast charging.¹⁴ Under condition H, capacity decay occurs more rapidly from the beginning compared to the other conditions, indicating accelerated side reactions and cathode loss at high SOC in the early cycling period.^6,40

Additionally, incremental capacity (IC) curves were obtained every 150 cycles by charging at C/20 during the aging test (Fig. S2, ESI†). The shape of IC curves is known⁴¹ to reflect electrochemical reactions evolving with degradation at both the cathode and anode. Under each condition, the peak shifts and intensity changes in the IC curves progress differently with aging and indicate unique degradation patterns. Analysis of the IC curves enables the degradation mode to be thermodynamically quantified from changes in these curves.^42,43 The degradation modes are broadly divided into three types: loss of Li inventory (LLI), loss of active material in the cathode (LAM_PE), and loss of active material in the anode (LAM_NE).⁴⁴ LLI is associated with the consumption of cyclable lithium, mainly as a result of solid electrolyte interphase (SEI) growth and Li plating, whereas LAM_PE and LAM_NE occur due to the formation of cracks and because the active material undergoes irreversible phase transformations.

The differences in the degradation mechanisms between the four conditions were also analyzed by quantifying the degradation modes of each condition at the 300th cycle by conducting IC analysis (Fig. 2c and Fig. S3, ESI†). The focus was on LLI and LAM_PE, whereas LAM_NE was excluded from the analysis due to the well-known structural stability of the anode.^27,45 It is noteworthy that although the capacities of conditions L, F, and H at the 300th cycle are almost the same, the degradation modes are clearly distinct. Compared to condition M, LLI was more pronounced under conditions L, F, and H, and this is correlated with the extent of by-products generated at the anode interface, each having distinct degradation origins (Fig. S4 and S5, ESI†).

Under condition L, LLI was driven by SEI growth, with the pores being clogged with thickly grown SEI (Fig. S5b, ESI†). This is attributable to continuous SEI formation caused by SEI fracturing resulting from the large volume expansion of the anode in low SOC range cycling.^39,46 The clogged pores increase the resistance and reduce the extractable capacity. Conversely, under condition F, LLI was driven by Li plating, which is characterized by a large overpotential due to kinetically hindered intercalation during fast charging.¹³ Condition H gives rise to the highest LLI, to which both SEI growth and Li plating are significant contributors. This is associated with the promotion of side reactions as the anode voltage approaches 0 V versus Li/Li⁺ in the highly lithiated state.⁴⁰ At the same time, severe cathode loss may occur due to the known structural instability of the high-nickel cathode during fast charging and high SOC cycling.⁴⁷ Accordingly, cracked particles were observed on the cathode, with LAM_PE being more prominent under the F and H conditions compared to the L and M conditions (Fig. S6, ESI†). The electrochemical impedance spectroscopy (EIS) analysis results obtained during the aging tests further confirm distinct degradation behaviors for each condition (Fig. S7, ESI†). To summarize, designing operating conditions with different degradation mechanisms allows for the analysis of the extent to which the degradation pathway changes depending on the sequence of these conditions. Furthermore, it provides a generalized understanding of the degradation progress under dynamic operational patterns, as the resulting aging processes could represent major degradation mechanisms of LIBs.

SOC-wise relaxation voltage as a battery degradation path tracker

We developed a diagnostic protocol to extract the relaxation voltages at various SOCs to assess the current health state and monitor the degradation path by incorporating this into the RPTs (Fig. 2d). The relaxation voltage is the voltage measured while the system reaches electrochemical equilibrium at each rest period. Previous studies have identified the relaxation voltage, typically measured at fully charged or discharged states, as a crucial indicator for diagnosing the degradation.^20,27,48 However, because the response to degradation varies according to the SOC, measurement of the voltage at multiple SOC points provides a more comprehensive understanding of the degradation.^49–51 Therefore, we measured the change in voltage during relaxation (ΔVR) over a 10-minute rest period in the upper SOC range (SOC60–100) during charging and the lower SOC range (SOC10–50) during discharging. Measurements were recorded at 10% SOC intervals. A comparison of ΔVR data with IC curves of the fresh cell revealed an opposite trend across SOC points, confirming that SOC-wise ΔVR characteristics are influenced by the combined phase behaviors of the cathode and anode (Fig. S8, ESI†).

ΔVR is associated with the extent of overvoltage resolved during operation, and serves as an electrochemical indicator of the kinetic degradation of the cell.⁴⁸ Thus, the current health state of the cell can be more thoroughly quantified using ΔVR data from 10 SOC intervals, collectively referred to as the degradation index (DI). In fact, the DI in the aging test revealed distinct primary degradation mechanisms for each condition (Fig. S9 and S10, ESI†). Additionally, each SOC feature exhibited different patterns for the same degradation state. This variation is attributed to differences in the overpotential depending on the SOC for the active material and interfaces,^24,50 which can further be affected by aging characteristics.

The use of these distinct operating conditions and the DI, which reflects the health states of the cell, enabled us to create dynamic operating sequences and monitor the degradation paths. For example, we analyzed the degradation path of an operating sequence in which the L–H–F–M conditions were alternatively used for 150 cycles each (Fig. 2e and f). As the operating conditions change, different degradations accumulate based on the preceding states, thereby resulting in continuous shifts in the capacity and DI trajectories. First, under condition L, an increase in the internal resistance due to rapid SEI growth at the anode interface lowers the capacity and gradually widens the DI. Next, under condition H, the capacity decay is steeper and the SOC features in the DI become more divergent due to continued SEI growth and Li plating seed formation at the anode, along with increased charge transfer resistance resulting from cathode loss.⁵⁰ Then, under condition F, the formation of a thick covering layer as a result of Li plating at the anode, accompanied by intensified cathode loss, results in a nonlinear knee point in the capacity and DI. Lastly, under condition M, mild SEI growth becomes predominant to partly alleviate the overpotential accumulated in previous operations and soften the drastic nonlinear capacity decay. This demonstrates that the DI can serve as a descriptor of the degradation path by offering more detailed information about changes in the internal state than the capacity alone under dynamic operating sequences.

Path-dependent degradation under dynamic operating sequences

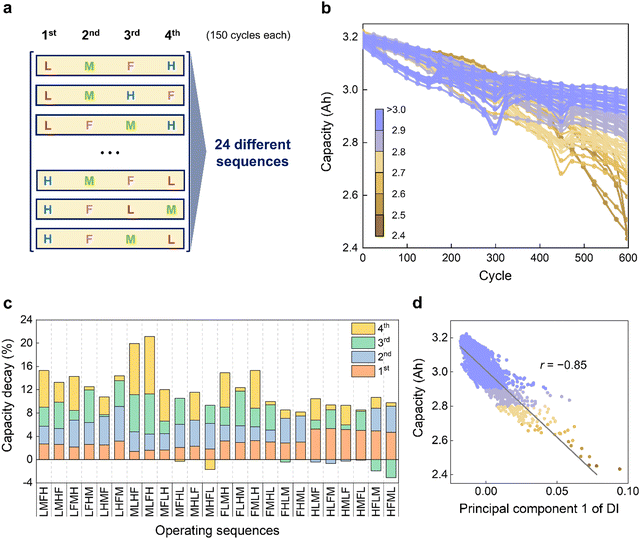
We designed 24 dynamic operating sequences by varying the order in which the four distinct conditions were used (Fig. 3a). Each sequence was used for 600 cycles, divided into four stages of 150 cycles, with different operating conditions assigned to each stage. This approach allowed us to experimentally implement various degradation paths by incorporating every possible instance where each condition appears once in the sequence. Fig. 3b shows the capacity retention of 72 commercial NMC811/Gr–SiO_x cells across all operating sequences. Each sequence includes three cells, with the colors representing the final capacity at 600 cycles. The capacity measurements of each cell are detailed in Table S1 (ESI†). Although each condition was consistently employed once in all the sequences and all the conditions were equally distributed over all the sequences, various capacity trajectories emerged depending on their order, demonstrating that cumulative degradation is influenced by the path dependence of battery degradation.

Fig. 3 Path-dependent degradation determined by operating sequences. (a) 24 different sequences, each consisting of four operating conditions and four stages. Each sequence spans 600 cycles, during which all four operating conditions were used, each lasting 150 cycles. (b) Discharge capacities of 72 NMC811/Gr–SiO_x cells, with three cells per sequence. The color of each curve corresponds to the final capacity at the end of the cycle test. Measurements were taken in intervals of 25 cycles. (c) Capacity loss as a percentage at each stage of every operating sequence. The data shown are the average values from three cells. (d) Correlation between principal component 1 of DI and capacity at all measured cycle points, with a Pearson correlation coefficient of r = −0.85.

The percentage of capacity loss for each stage in all sequences was analyzed (Fig. 3c). The final capacity reduction was more pronounced when the harsh F and H conditions were applied in the later stages compared to the milder L and M conditions. This is because the stress experienced by the battery gradually accelerates as degradation progresses.¹⁴ Moreover, the capacity decay at each stage varied dynamically depending not only on the condition at the given stage but also on all preceding conditions. For instance, a comparison of the sequences HMLF and MHLF revealed that, positioning the M condition in the middle (i.e., as in HMLF) had a mitigating effect such that it slowed the degradation process. In contrast, the consecutive application of stress-inducing conditions, as in the case of MHLF, accelerated degradation more rapidly. IC curves and post-mortem analysis at the end of the cycle test revealed distinct differences in aging mechanisms between the two sequences (Fig. S11, ESI†). Furthermore, instances of negative capacity loss indicate capacity recovery. This phenomenon typically occurred when transitioning from the harsh F and H conditions to the mild L and M conditions and was not observed for the opposite situation (Fig. S12, ESI†). This trend could possibly be explained by the increased uniformity of Li distribution within the electrode and reactivation of trapped Li.⁵² Apart from this, a shift in the SOC from high to low may lead to capacity recovery due to the transfer of Li from the passive area on the electrode (anode overhang) to the active area.⁵³ This implies that the extractable capacity can reversibly increase or decrease depending on the sequence of operating conditions. These findings also indicate the chance of improving battery performance by adjusting operating sequences that regulate degradation accumulation.

Path-dependent degradation was clearly observed not only in terms of the capacity retention but also in the DI trajectory (Fig. S13–S16, ESI†). To verify whether the DI reflects information on the capacity in each state, we examined the correlation between the capacity and DI at all measured cycle points (Fig. 3d). Because the DI consists of 10 features corresponding to the ΔVR measurements across different SOC points, principal component analysis (PCA)⁵⁴ was employed to reduce the dimensionality while preserving the key characteristics. Principal component 1 (PC1) of the DI explained 92.24% of the variance in the data, which allowed the DI to be reduced to one dimension with minimal information loss (Fig. S17 and S18, ESI†). The high linear correlation (Pearson correlation coefficient of −0.85) between the capacity and PC1 of the DI at all cycle points suggests that the DI provides a good indication of the capacity trend during cycling.

Time-series deep learning approach

We developed a framework to predict future degradation paths and capacity trajectories by exploiting the path dependence of battery degradation. Initially, we utilized a sequence-to-sequence (seq2seq) model⁵⁵ to capture the relationship between the current health state, future usage patterns, and the resulting future degradation path of the cell. The seq2seq model, typically used for generating sequence outputs from sequence inputs, was adapted in this case to handle vector inputs by leveraging its inherent flexibility. This model has demonstrated efficacy in domains such as computer science,⁵⁶ robotics,⁵⁷ and chemistry.⁵⁸ For LIBs, the seq2seq model facilitates the prediction of future health states based on a single current health state within time-series cycle data.³⁷

A flowchart of the predictive framework is presented in Fig. 4a. The implemented seq2seq model features an encoder–decoder architecture, with each module processing specific input data (Table S2, ESI†). The encoder converts information about the current health state (capacity and DI) into a fixed-length vector. The decoder generates ordered sequences and is composed of gated recurrent unit (GRU) layers,⁵⁹ a type of recurrent neural network specifically designed to process time-series data. First, the GRU layer was initialized with the vector output received from the encoder. Subsequently, the future operating sequence was input into the decoder and the time-series hidden states were updated to reflect the impact of the operating conditions at each future cycle point. These hidden states were then used to predict the future degradation path that corresponds to the DI trajectory. Moreover, the predicted degradation path allowed for the estimation of the capacity trajectory by taking advantage of the strong correlation between the capacity and DI. For capacity estimation, we employed a random forest regression model⁶⁰ because of its effectiveness in handling high-dimensional data. This framework therefore enables the prediction of future health states in dynamic operating sequences by relying solely on the accurately quantified current health state and future usage plans, without requiring historical data. For a reliable and generalized performance evaluation of the framework, we employed group k-fold cross-validation⁶¹ to ensure that cells with the same operating sequence are included in only one of the training and validation sets at each iteration. The prediction performance was evaluated using the root-mean-squared error (RMSE) and mean absolute percentage error (MAPE) as metrics. Further computational details are provided in the Experimental section.

Fig. 4 Results obtained with the framework for future degradation path and capacity trajectory prediction. (a) Flowchart of the proposed framework. The encoder–decoder network initially predicts the future degradation path using the current health state of the battery and upcoming operating sequence data. This predicted degradation path is then used to forecast the future capacity trajectory. (b) and (c) Observed versus predicted DI of the framework for SOC ranges of (b) 10–50% and (c) 60–100%. (d) Observed versus predicted capacity of the framework. On the diagonal solid line, the predicted values equal the observed values. Insets: Density distribution curves of the residuals between the observed and predicted values.

Performance of the predictive framework

The performance of our framework was assessed to determine whether it could accurately predict the degradation paths from any given point in the cycle to the subsequent point. The framework requires two inputs: diagnostic data about the current health state and the future operating sequence. The use of both of these inputs in combination is referred to as the “full” model. Remarkably, this model consistently achieved high prediction accuracy for all SOC features of the DI, with an RMSE of 0.63 mV and a MAPE of 0.76% (Fig. 4b and c and Table 1). These results demonstrate the superiority of our approach, which leverages the path dependence of the degradation to accurately predict future degradation paths. The proposed model was benchmarked against three alternatives: (1) the “naïve” model, (2) the “sequence-only” model, and (3) the “diagnosis-only” model to distinguish the influence of each input^21–23 (Fig. S19–S21, ESI†). The “naïve” model, which uses the average DI at each cycle point from the training data for predictions, served as the baseline with a MAPE of 4.77%. The average DI herein was acquired by averaging each SOC-specific DI feature separately from the training data. The “sequence-only” model, which relies solely on the future operating sequence without using diagnostic data about the current health state, underperforms compared to the naïve model, with a MAPE of 5.18%. The “diagnosis-only” model, which uses only the diagnostic data pertaining to the current health state without the future operating sequence, outperforms the other benchmark models with a MAPE of 1.41%. This finding suggests that the diagnostic data relating to the current health state significantly contributes to predicting the degradation path of the next cycle point. Moreover, the exceptional performance of the proposed “full” model compared to the benchmark models implies that the synergistic integration of both inputs allows for accurate predictions of the complex degradation path in dynamic operating sequences.

Table 1 Model metrics for degradation path prediction

Model	RMSE (mV)	MAPE (%)
The values refer to the means (standard deviations) of the errors across all iterations of the cross-validation.
Naïve	3.69 (0.62)	4.77 (0.53)
Sequence-only	4.11 (0.60)	5.18 (0.26)
Diagnosis-only	1.34 (0.35)	1.41 (0.17)
Full	0.63 (0.11)	0.76 (0.09)

---

The capacity estimation performance was assessed based on the predicted DI. To this end, we used the actual DI to first construct a random forest regression model that reflected the true relationship between the DI and capacity (Fig. S22, ESI†). The predicted DI was then used as input to this regression model to evaluate its effectiveness for capacity estimation (Fig. 4d and Table 2). The prediction performance of the “full” model is comparable to the actual DI, with an RMSE of 31.78 mAh and a MAPE of 0.81%. In contrast, the benchmark models—the “naïve” model, the “sequence-only” model, and the “diagnosis-only” model—generate higher prediction errors, with MAPEs of 1.72%, 3.14%, and 0.89%, respectively (Fig. S23, ESI†). Although the error of the “diagnosis-only” model is relatively low, the high DI prediction accuracy of the “full” model improves the capacity estimation performance, considering the propagation of errors in the prediction of the degradation path. These results demonstrate the potential of using the predicted degradation paths to estimate various meaningful state variables, including the capacity. The performance comparison of the four models is visualized more clearly in Fig. S24 and S25 (ESI†), in which the results of the degradation path and capacity trajectory prediction for representative cells with various final capacities are plotted.

Table 2 Model metrics for capacity trajectory prediction

Model	RMSE (mA h)	MAPE (%)
The values refer to the means (standard deviations) of the errors across all iterations of the cross-validation.
Naïve	68.83 (3.38)	1.72 (0.06)
Sequence-only	118.70 (4.20)	3.14 (0.15)
Diagnosis-only	35.46 (2.68)	0.89 (0.04)
Full	31.78 (1.19)	0.81 (0.03)

---

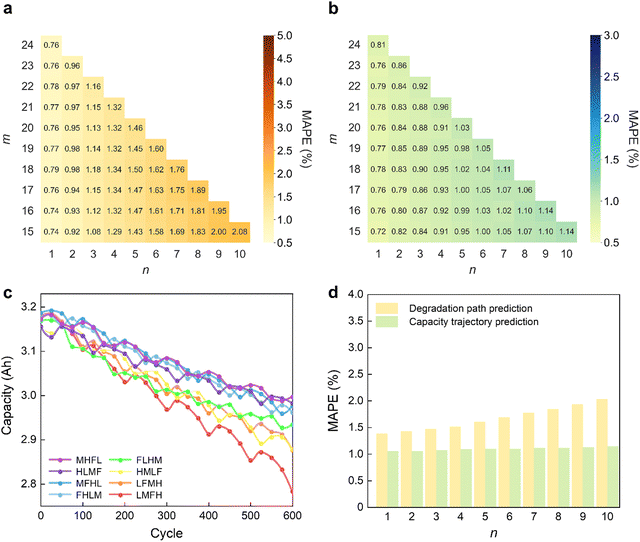
We additionally analyzed the performance of the proposed framework by increasing the number of prediction cycle points. Given that the entire dataset contains data from 600 cycles, which corresponds to 25 cycle points, increasing the number of future cycle points to be predicted reduces the maximum number of available cycle points. Thus, the prediction errors of the degradation path and capacity trajectory of the “full” model are compared for zero-to-m cycle points by varying the forecast length (n) (Fig. 5a and b). As n is extended, the prediction error consistently rises due to the amplified variability in degradation to reach a MAPE of 2.08% for the degradation path and 1.14% for the capacity trajectory at n = 10. Notably, in the case of the “full” model, the small prediction errors across all ranges of m indicate the robustness of the proposed framework to perform stably even with heightened data variability. The results of the benchmark models are summarized in Fig. S26 (ESI†). Overall, the benchmark models gave rise to higher prediction errors as m increased for the same n, indicating low generalizability compared to the “full” model. Unlike the “naïve” model, which consistently produced high prediction errors across all n, the prediction errors of the “sequence-only” model increased less significantly as n became longer. This can be attributed to the growing importance of information about the future operating sequence to predict the long-term degradation. Conversely, the prediction errors of the “diagnosis-only” model increased sharply as n increased because the future degradation significantly deviated from the current health state. As a result, the “naïve” model, the “sequence-only” model, and the “diagnosis-only” model produced high prediction errors with MAPEs of 4.71%, 3.88%, and 3.65%, respectively, in terms of the degradation path prediction for n = 10. In contrast, the proposed “full” model manifested strong robustness and maintained its excellent prediction performance by effectively utilizing both the current health state and the future operating sequence even as n was extended.

Fig. 5 Prediction errors upon varying forecast length and validation with the dataset comprising highly dynamic operating sequences. MAPE for the (a) degradation path and (b) capacity trajectory prediction, for zero-to-m cycle points and varying forecast lengths (n). The units for n and m are the number of cycle points, each representing an interval of 25 cycles from which measurements were taken. (c) Discharge capacities of eight additional NMC811/Gr–SiO_x cells, measured by changing the operating conditions every 25 cycles. The four sets of different operating conditions form a 100-cycle-long block, and repeating this block six times yields a total of 600 cycles. (d) MAPE for predicting the degradation path and capacity trajectory using the dataset consisting of highly dynamic operations for different n values.

Finally, the generalizability of the framework was further validated using additional datasets featuring highly dynamic operating sequences (Fig. 5c and d and Table S3, ESI†). The additional dataset was generated using eight NMC811/Gr–SiO_x cells. The operating conditions were changed every 25 cycles, and the four different sets of operating conditions formed a 100 cycle-long block. Six repetitions of this block yielded a total of 600 cycles. Interestingly, even under these more dynamic operating conditions, the cells exhibited path-dependent degradation behavior that reflected the varying stress conditions with reference to their real-time states. We employed the pre-trained parameters of the “full” model for degradation path prediction to thoroughly assess the ability of our framework to generalize to previously unseen data patterns. Our framework achieved a MAPE of 2.03% for the degradation path and 1.15% for the capacity trajectory at n = 10, thereby highlighting its superior prediction performance by effectively utilizing both the current health state and future operating conditions of the cell (Fig. S27, ESI†). These results clearly demonstrate the applicability and scalability of our framework, and emphasize the importance of considering the path-dependent battery degradation when capturing the complexities of real-world usage scenarios.

Conclusion

In summary, we developed a framework for predicting the future health states of NMC811/Gr–SiO_x commercial cells based on information about their current health state and future usage by utilizing a dataset generated from dynamic operations. The path-dependent degradation across different operating sequences was monitored with the aid of a comprehensive diagnostic protocol. Accordingly, the prediction of future degradation paths from single time-point diagnostic data was accomplished by modeling the path dependence of the battery degradation. The high correlation between the diagnostic features and extractable capacity made possible the subsequent estimation of the capacity trajectories from the projected degradation paths. The integration of time-series deep learning approaches and the path-dependent characteristics of battery degradation enabled the prediction of future dynamic aging pathways with minimal information and small errors. In the broader context, our findings highlight the potential, not only for maintaining LIB cells that are currently in operation, but also for accurately evaluating used LIB cells by leveraging their SOC-dependent degradation characteristics and deep learning approaches that take path-dependent degradation into account.

Data availability

The datasets⁶² developed for this study are available at https://doi.org/10.17632/h2y7mj4kt7.2. The codes for data processing and the predictive framework are also available at the GitHub:⁶³https://doi.org/10.5281/zenodo.13932443.

Author contributions

I. K. and J. W. C. conceived the idea and designed the experiments. I. K. and H. K. conducted the aging experiments and data management. I. K. and S. A. carried out the framework modelling. I. K., H. K., J. O., and M. K. performed the degradation analysis and cell characterization. I. K. and J. W. C. co-wrote the manuscript. J. W. C. supervised the research. All authors discussed the results and commented on the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

J. W. C. acknowledges financial support from the National Research Foundation of Korea grants (RS-2024-00335274 and RS-2024-00429941). J. W. C. also acknowledges support from the Institute of Engineering Research (IOER), the Research Institute of Advanced Materials (RIAM), and the Institute for Battery Research Innovation (IBRI) at Seoul National University. This work was also supported by Hyundai Motor Company. The authors thank Dr Matthieu Dubarry and the University of Hawaii at Mānoa for sharing the Alawa battery emulation toolbox.

References

1. Z. P. Cano, D. Banham, S. Y. Ye, A. Hintennach, J. Lu, M. Fowler and Z. W. Chen, Nat. Energy, 2018, 3, 279–289.
2. M. Li, J. Lu, Z. W. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561.
3. D. M. Davies, M. G. Verde, O. Mnyshenko, Y. R. Chen, R. Rajeev, Y. S. Meng and G. Elliott, Nat. Energy, 2019, 4, 42–50.
4. M. R. Palacín and A. de Guibert, Science, 2016, 351, 1253292.
5. X. S. Hu, L. Xu, X. K. Lin and M. Pecht, Joule, 2020, 4, 310–346.
6. J. S. Edge, S. O'Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. L. Ai, J. Y. Chen, J. Yang, S. Li, M. C. Pang, L. B. Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Z. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221.
7. S. M. Rezvanizaniani, Z. C. Liu, Y. Chen and J. Lee, J. Power Sources, 2014, 256, 110–124.
8. Y. H. Che, X. S. Hu, X. K. Lin, J. Guo and R. Teodorescu, Energy Environ. Sci., 2023, 16, 338–371.
9. G. Harper, R. Sommerville, E. Kendrick, L. Driscoll, P. Slater, R. Stolkin, A. Walton, P. Christensen, O. Heidrich, S. Lambert, A. Abbott, K. Ryder, L. Gaines and P. Anderson, Nature, 2019, 575, 75–86.
10. V. Sulzer, P. Mohtat, A. Aitio, S. Lee, Y. T. Yeh, F. Steinbacher, M. U. Khan, J. W. Lee, J. B. Siegel, A. G. Stefanopoulou and D. A. Howey, Joule, 2021, 5, 1934–1955.
11. S. F. Schuster, T. Bach, E. Fleder, J. Müller, M. Brand, G. Sextl and A. Jossen, J. Energy Storage, 2015, 1, 44–53.
12. T. Raj, A. A. Wang, C. W. Monroe and D. A. Howey, Batteries Supercaps, 2020, 3, 1377–1385.
13. X. B. Han, L. G. Lu, Y. J. Zheng, X. N. Feng, Z. Li, J. Q. Li and M. G. Ouyang, eTransportation, 2019, 1, 100005.
14. P. M. Attia, A. Bills, F. B. Planella, P. Dechent, G. dos Reis, M. Dubarry, P. Gasper, R. Gilchrist, S. Greenbank, D. Howey, O. Liu, E. Khoo, Y. Preger, A. Soni, S. Sripad, A. G. Stefanopoulou and V. Sulzer, J. Electrochem. Soc., 2022, 169, 060517.
15. M.-F. Ng, J. Zhao, Q. Yan, G. J. Conduit and Z. W. Seh, Nat. Mach. Intell., 2020, 2, 161–170.
16. W. He, N. Williard, M. Osterman and M. Pecht, J. Power Sources, 2011, 196, 10314–10321.
17. Y. Preger, H. M. Barkholtz, A. Fresquez, D. L. Campbell, B. W. Juba, J. Romàn-Kustas, S. R. Ferreira and B. Chalamala, J. Electrochem. Soc., 2020, 167, 120532.
18. K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazan, S. J. Harris, W. C. Chueh and R. D. Braatz, Nat. Energy, 2019, 4, 383–391.
19. Y. W. Zhang, Q. C. Tang, Y. Zhang, J. B. Wang, U. Stimming and A. A. Lee, Nat. Commun., 2020, 11, 1706.
20. J. G. Zhu, Y. X. Wang, Y. Huang, R. B. Gopaluni, Y. K. Cao, M. Heere, M. J. Mühlbauer, L. Mereacre, H. F. Dai, X. H. Liu, A. Senyshyn, X. Z. Wei, M. Knapp and H. Ehrenberg, Nat. Commun., 2022, 13, 2261.
21. P. K. Jones, U. Stimming and A. A. Lee, Nat. Commun., 2022, 13, 4806.
22. J. H. Lu, R. Xiong, J. P. Tian, C. X. Wang, C. W. Hsu, N. T. Tsou, F. C. Sun and J. Li, Energy Storage Mater., 2022, 50, 139–151.
23. J. H. Lu, R. Xiong, J. P. Tian, C. X. Wang and F. C. Sun, J. Power Sources, 2023, 581, 233473.
24. A. Weng, P. Mohtat, P. M. Attia, V. Sulzer, S. Lee, G. Less and A. Stefanopoulou, Joule, 2021, 5, 2971–2992.
25. A. Weng, E. Dufek and A. Stefanopoulou, Joule, 2023, 7, 837–842.
26. R. Xiong, Y. Pan, W. X. Shen, H. L. Li and F. C. Sun, Renewable Sustainable Energy Rev., 2020, 131, 110048.
27. B. R. Chen, C. M. Walker, S. Kim, M. R. Kunz, T. R. Tanim and E. J. Dufek, Joule, 2022, 6, 2776–2793.
28. M. Kim, I. Kim, J. Kim and J. W. Choi, ACS Energy Lett., 2023, 8, 2946–2953.
29. Y. Zhang, R. Xiong, H. He and M. G. Pecht, IEEE Trans. Ind. Electron., 2018, 66, 1585–1597.
30. K. L. Gering, S. V. Sazhin, D. K. Jamison, C. J. Michelbacher, B. Y. Liaw, M. Dubarry and M. Cugnet, J. Power Sources, 2011, 196, 3395–3403.
31. Z. Y. Ma, J. C. Jiang, W. Shi, W. G. Zhang and C. C. Mi, J. Power Sources, 2015, 274, 29–40.
32. M. Dubarry, G. Baure and A. Devie, J. Electrochem. Soc., 2018, 165, A773–A783.
33. M. Feinauer, M. Wohlfahrt-Mehrens, M. Hölzle and T. Waldmann, J. Power Sources, 2024, 594, 233948.
34. Y. P. Zhou and M. H. Huang, Microelectron. Reliab., 2016, 65, 265–273.
35. G. J. Ma, S. P. Xu, B. B. Jiang, C. Cheng, X. Yang, Y. Shen, T. Yang, Y. H. Huang, H. Ding and Y. Yuan, Energy Environ. Sci., 2022, 15, 4083–4094.
36. Y. Z. Zhang and M. Y. Zhao, Energy Storage Mater., 2023, 57, 346–359.
37. J. P. Tian, C. Chen, W. X. Shen, F. C. Sun and R. Xiong, Energy Storage Mater., 2023, 61, 102883.
38. Y. Che, Y. Zheng, S. Onori, X. Hu and R. Teodorescu, Cell Rep. Phys. Sci., 2023, 4, 101743.
39. J. G. Zhu, M. Knapp, D. R. Sorensen, M. Heere, M. S. D. Darma, M. Müller, L. Mereacre, H. F. Dai, A. Senyshyn, X. Z. Wei and H. Ehrenberg, J. Power Sources, 2021, 489, 229422.
40. M. G. Ouyang, D. S. Ren, L. G. Lu, J. Q. Li, X. N. Feng, X. B. Han and G. M. Liu, J. Power Sources, 2015, 279, 626–635.
41. M. Dubarry, V. Svoboda, R. Hwu and B. Y. Liaw, Electrochem. Solid-State Lett., 2006, 9, A454–A457.
42. M. Dubarry, C. Truchot and B. Y. Liaw, J. Power Sources, 2012, 219, 204–216.
43. M. Dubarry, N. Costa and D. Matthews, Nat. Commun., 2023, 14, 3138.
44. C. R. Birkl, M. R. Roberts, E. McTurk, P. G. Bruce and D. A. Howey, J. Power Sources, 2017, 341, 373–386.
45. P. P. Paul, V. Thampy, C. Cao, H.-G. Steinrück, T. R. Tanim, A. R. Dunlop, E. J. Dufek, S. E. Trask, A. N. Jansen, M. F. Toney and J. N. Weker, Energy Environ. Sci., 2021, 14, 4979–4988.
46. S. Schweidler, L. de Biasi, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2018, 122, 8829–8835.
47. M. Jiang, D. L. Danilov, R. A. Eichel and P. H. L. Notten, Adv. Energy Mater., 2021, 11, 2103005.
48. G. Fan and X. Zhang, Appl. Energy, 2023, 330, 120308.
49. W. Waag, S. Käbitz and D. U. Sauer, Appl. Energy, 2013, 102, 885–897.
50. V. J. Ovejas and A. Cuadras, J. Power Sources, 2019, 418, 176–185.
51. Y. Che, L. Xu, R. Teodorescu, X. Hu and S. Onori, ACS Energy Lett., 2025, 10, 741–749.
52. B. Epding, B. Rumberg, H. Jahnke, I. Stradtmann and A. Kwade, J. Energy Storage, 2019, 22, 249–256.
53. M. Lewerenz, J. Münnix, J. Schmalstieg, S. Käbitz, M. Knips and D. U. Sauer, J. Power Sources, 2017, 345, 254–263.
54. H. Abdi and L. J. Williams, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 433–459.
55. I. Sutskever, O. Vinyals and Q. Le, Advances in neural information processing systems, 2014, vol. 27, pp. 3104–3112.
56. O. Vinyals, A. Toshev, S. Bengio and D. Erhan, Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2015, 3156–3164.
57. Y. Keneshloo, T. Shi, N. Ramakrishnan and C. K. Reddy, IEEE Trans. Neural Netw. Learn. Syst., 2020, 31, 2469–2489.
58. B. W. Liu, B. Ramsundar, P. Kawthekar, J. D. Shi, J. Gomes, Q. L. Nguyen, S. Ho, J. Sloane, P. Wender and V. Pande, ACS Cent. Sci., 2017, 3, 1103–1113.
59. Y. Yu, X. Si, C. Hu and J. Zhang, Neural Comput., 2019, 31, 1235–1270.
60. Y. Li, C. F. Zou, M. Berecibar, E. Nanini-Maury, J. C. W. Chan, P. van den Bossche, J. Van Mierlo and N. Omar, Appl. Energy, 2018, 232, 197–210.
61. D. Krstajic, L. J. Buturovic, D. E. Leahy and S. Thomas, J. Cheminf., 2014, 6, 1–15.
62. I. Kim and J. W. Choi, Mendeley Data, 2024 DOI:10.17632/h2y7mj4kt7.2.
63. I. Kim and J. W. Choi, GitHub, 2024 DOI:10.5281/zenodo.13932443.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee04787g

---