Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Review of quantitative microbial risk assessments for potable water reuse†
Emily Clements ,
Charlotte van der Nagel,
Katherine Crank
,
Charlotte van der Nagel,
Katherine Crank ,
Deena Hannoun and
Daniel Gerrity*
,
Deena Hannoun and
Daniel Gerrity*
Southern Nevada Water Authority, P.O. Box 99954, Las Vegas, NV 89193, USA. E-mail: daniel.gerrity@snwa.com
First published on 3rd January 2025
Abstract
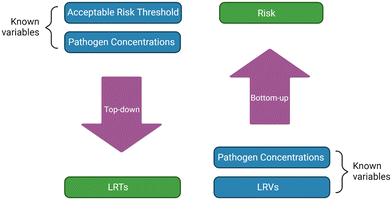
Potable water reuse is becoming more common as communities deal with increased water demands and climate change. Understanding the risks associated with potable reuse is essential to ensuring that public health is protected from waterborne pathogens. This paper provides a review on the studies that have performed quantitative microbial risk assessments (QMRAs) on potable reuse. The 30 articles included here studied direct potable reuse (DPR), indirect potable reuse (IPR), and/or de facto reuse (DFR), and a variety of pathogens, including norovirus, adenovirus, Cryptosporidium, Giardia, Campylobacter, and Salmonella. The QMRAs were either ‘top-down’ or regulations-focused, where log reduction targets (LRTs) were determined based on initial (e.g., raw wastewater) pathogen concentrations and risk goals (e.g., 10−4 annual risk benchmark), or ‘bottom-up’ or risk-estimation-focused, where risks were calculated based on known pathogen concentrations and observed/credited log reduction values (LRVs). Some studies incorporated process failures and pathogen decay, which were often a driving factor for risk, but several studies omitted one or both. Many studies compared multiple treatment trains (e.g., carbon-based advanced treatment (CBAT) vs. reverse-osmosis-based advanced treatment (RBAT)). They found that treatment-based differences were pathogen-dependent because certain processes are better able to inactivate or remove certain pathogens. Many factors influence the risks reported in the various studies, including the assumed ratios of gene copies to infectious units (GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU), assumptions related to ingestion volume and frequency, dynamic vs. static modeling, and Bayesian approaches. The LRTs for the top-down QMRAs varied within and between studies, depending partially on the pathogen concentrations used and whether redundancy was included. The key findings from this review were that while QMRAs often have different goals warranting different assumptions, it is essential that researchers report these assumptions and their justifications so that policymakers and regulators fully understand their implications to avoid overly stringent or nonprotective regulations.
IU), assumptions related to ingestion volume and frequency, dynamic vs. static modeling, and Bayesian approaches. The LRTs for the top-down QMRAs varied within and between studies, depending partially on the pathogen concentrations used and whether redundancy was included. The key findings from this review were that while QMRAs often have different goals warranting different assumptions, it is essential that researchers report these assumptions and their justifications so that policymakers and regulators fully understand their implications to avoid overly stringent or nonprotective regulations.
Water impactWe conducted a comprehensive literature review on quantitative microbial risk assessments (QMRAs) for potable reuse, which will likely become more necessary due to climate change and drought. This review provides timely and critical insights into potable reuse QMRAs to inform future research and policy development for water reuse by identifying gaps, challenges, and best practices in conducting and reporting QMRAs. |
1. Introduction
There has been increased interest in water reuse, particularly in the United States (U.S.), due to population growth, urbanization, climate change, and drought. Recycled water can be utilized for different ends, including non-potable reuse (e.g., industrial applications, toilet flushing, irrigation1) or potable reuse. Indirect potable reuse (IPR) involves the planned discharge of recycled water to an environmental buffer, such as an aquifer, river, or lake, before being treated and used as drinking water.2 For direct potable reuse (DPR), water is treated and added to the drinking water system through raw water augmentation (upstream of the drinking water treatment plant) or treated water augmentation (into the distribution system). DPR through raw water augmentation is sometimes conceptually similar to IPR, specifically when an environmental buffer with a short residence time is used. However, regulatory frameworks may specify the minimum amount of time that recycled water must spend in an environmental buffer to qualify as IPR. Finally, de facto reuse (DFR) occurs when there is unplanned or incidental wastewater influence on a community's drinking water source. DFR is relatively common, with 25% of U.S. drinking water treatment plants (DWTPs) serving more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people having more than 1% treated wastewater in their drinking water source under normal streamflow conditions—and up to 100% at certain DWTPs during drought conditions.3
000 people having more than 1% treated wastewater in their drinking water source under normal streamflow conditions—and up to 100% at certain DWTPs during drought conditions.3
Prior to introducing potable reuse in communities, it is essential to assess the risks associated with waterborne diseases that could be acquired through this process. Quantitative microbial risk assessment (QMRA) is a tool commonly used to assess the likelihood of infection and/or illness resulting from pathogen exposure. The four steps include hazard identification, exposure assessment, dose–response modeling, and risk characterization.4,5 While QMRA has been used extensively to analyze the risk of non-potable reuse including agricultural reuse or other purpose-driven applications,6–11 there have been fewer studies on potable reuse.
As potable reuse regulatory development and project implementation occur, it is essential to understand the microbial risks presented by these systems, including how they can be estimated and ultimately managed. Therefore, the goal of this study was to review the studies that have used QMRA to assess the risks from potable reuse and highlight the implications of various assumptions made during the risk assessment. QMRAs are inherently a product of their assumptions, and if those assumptions are not clear, a QMRA can be misinterpreted. This review will also examine the pathogens driving risks, highlight risk mitigation strategies expected to be most effective, and compare log reduction targets (LRTs) and log reduction value (LRV) assumptions from different studies, as these affect the development of regulations.
2. Materials and methods
A search was performed on the Web of Science on October 28th, 2024. The search term was “ALL = (QMRA OR quantitative microbial risk assessment) AND ALL = (water reuse OR potable reuse OR recycled water OR reclaimed water)”. This resulted in a total of 254 abstracts which were screened to exclude papers that focused on non-potable reuse or did not perform a QMRA. After screening, 28 of these papers were selected for comparison and analysis.During the review of the selected papers, two additional papers were identified that did not use the term quantitative microbial risk assessment, likely because they were published before QMRA was a common term; however, these resources performed a QMRA on potable reuse.12,13 This brought the total number to 30 studies of QMRA for potable reuse.
3. Results and discussion
3.1 Summary of studies
Nappier et al.14 wrote a review summarizing epidemiological studies and QMRAs for potable reuse. The epidemiological studies found no negative health impacts associated with potable reuse,14–16 though data were limited. Since 2018, there have been several more studies published on QMRA for potable reuse, and some have influenced the creation of LRTs for potable reuse treatment trains, such as California's recently drafted DPR regulations.17 Therefore, the goal of this study was to provide an updated critical review on QMRA for potable reuse.Table S1† summarizes the studies which have performed QMRA for potable reuse. It includes the target pathogens for each QMRA, the type of potable reuse project (DPR, IPR, and/or DFR), the associated treatment train(s), and the QMRA approach (i.e., top-down or regulations-focused vs. bottom-up or risk-estimation-focused). Top-down QMRAs aim to identify LRTs based on initial (e.g., raw wastewater) pathogen concentrations and assumed risk goals (e.g., 10−4 annual risk benchmark). Bottom-up QMRAs estimate risk based on known pathogen concentrations and LRVs achieved by or credited to the treatment train, with the conservative practice of LRV crediting generally resulting in greater estimated risks. Those calculated risks are typically compared against a risk benchmark to determine whether the system is adequately protective of public health. These risk benchmarks are often based either on a probability of infection (Pinf), with a typical target of <10−4 infections per person per year (pppy), or a metric that considers health outcomes (e.g., disability adjusted life years (DALYs)), with a typical target of <10−6 DALYs pppy.18
Table S1† also includes other factors that impact the risk calculation, including the volume of water consumed and ingestion frequency. If the pathogen concentrations used in a QMRA are based on molecular methods (i.e., polymerase chain reaction (PCR)), the number of gene copies (GC) often need to be converted to infectious units (IU) for the risk assessment, as dose–response models are often developed based on infectious doses. A conservative GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio of 1.0 assumes every gene copy equates to one infectious pathogen. However, molecular methods often overestimate infectious pathogen exposure because die-off/inactivation generally does not result in a corresponding level of genome damage. Therefore, GC
IU ratio of 1.0 assumes every gene copy equates to one infectious pathogen. However, molecular methods often overestimate infectious pathogen exposure because die-off/inactivation generally does not result in a corresponding level of genome damage. Therefore, GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios can be significantly greater than 1.0 under real-world conditions.19 Some QMRAs incorporate failures, sensitivity analyses, and/or pathogen decay linked to retention time in the environmental buffer. Studies differ based on the dose–response curves used for a given pathogen, although some studies directly compare multiple dose–response models to understand the implications of this assumption on resulting risk estimates. The decisions researchers made in developing their QMRAs and the implications of those decisions are discussed in more detail throughout this paper.
IU ratios can be significantly greater than 1.0 under real-world conditions.19 Some QMRAs incorporate failures, sensitivity analyses, and/or pathogen decay linked to retention time in the environmental buffer. Studies differ based on the dose–response curves used for a given pathogen, although some studies directly compare multiple dose–response models to understand the implications of this assumption on resulting risk estimates. The decisions researchers made in developing their QMRAs and the implications of those decisions are discussed in more detail throughout this paper.
3.2 QMRA type
QMRAs are typically performed top-down, where the pathogen concentrations and risk benchmarks are used to identify LRTs, or bottom-up, where the pathogens concentrations and unit treatment process LRVs are used to estimate risk (Fig. 1). The bottom-up approach was used in a number of studies to determine the risk for a certain scenario or to compare risks across multiple scenarios.12,13,20–37 The top-down approach can be used to identify LRTs for regulatory frameworks and the unit treatment processes that might be necessary to achieve the overall LRT.19,38–43Not every study performed a simple top-down or bottom-up QMRA. Two studies focused on stormwater for potable reuse and performed a blended top-down/bottom-up QMRA.42,43 Since the studies used the same pathogen concentrations and acceptable risk threshold, they both arrived at the same LRTs. However, they then evaluated different treatment trains, specifically by varying the level of aquifer treatment, to determine if the corresponding LRVs would be sufficient to mitigate risk for the different pathogens, albeit without directly calculating risk.
MacNevin and Zornes44 performed a bottom-up QMRA but iterated over different LRVs to determine the minimum required LRV to consistently achieve a 10−4 annual risk of infection, providing a similar result to following a top-down approach. They used the concentrations of Cryptosporidium and Giardia at 20 different water reclamation facilities and started with a LRV of 4. They then increased the LRV by 0.5 at each facility to determine if the annual risk of infection was less than 10−4 every year for 1000 simulations. This resulted in a total of 40 values of minimum LRVs, ranging from 5 to 10, for both Cryptosporidium and Giardia. MacNevin and Zornes44 compared these results in the context of two potential treatment trains: (1) reverse-osmosis-based treatment (RBAT: UF-RO-UVAOP-ESB + Cl2) with LRVs of 12/15/12 and (2) carbon-based advanced treatment (CBAT: O3-BAF-UF-UVAOP-ESB + Cl2) with LRVs of 16/16/11 for viruses, Giardia, and Cryptosporidium, respectively. All facilities would be able to surpass the LRTs with either treatment train.
Soller et al.45 did much of their analysis with the bottom-up approach to determine risks for specific scenarios, but also did a top-down assessment for DPR to determine the LRTs needed to consistently meet the benchmark risk levels. They found a 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log reduction of viruses, with norovirus as the model pathogen, and a 11+ log reduction of Cryptosporidium and Giardia resulted in around 95% of the simulations having annual risk of infection less than 10−4. They demonstrated that 12/10/10 log reductions for viruses, Giardia, and Cryptosporidium, respectively, were insufficient to achieve the 10−4 annual risk benchmark in any of their simulations, which contradicts the findings of MacNevin and Zornes44 for protozoa. This is potentially problematic considering that the “12/10/10” framework has been adopted for IPR in California46,47 and Nevada,48 and now for DPR in Colorado.49 Differences in assumptions between MacNevin and Zornes44 and Soller et al.45 included different starting concentrations of protozoa, with MacNevin and Zornes44 having significantly lower concentrations, the use of point-estimate LRVs associated with treatment processes44 vs. uniform distributions,45 and different dose–response models. A more recent top-down QMRA from Gerrity et al.39 yielded scenarios that generally supported both Soller et al.45 and MacNevin and Zornes,44 depending on whether the pathogen concentrations were assumed to be maximum values or 97.4th percentile values, respectively.
log reduction of viruses, with norovirus as the model pathogen, and a 11+ log reduction of Cryptosporidium and Giardia resulted in around 95% of the simulations having annual risk of infection less than 10−4. They demonstrated that 12/10/10 log reductions for viruses, Giardia, and Cryptosporidium, respectively, were insufficient to achieve the 10−4 annual risk benchmark in any of their simulations, which contradicts the findings of MacNevin and Zornes44 for protozoa. This is potentially problematic considering that the “12/10/10” framework has been adopted for IPR in California46,47 and Nevada,48 and now for DPR in Colorado.49 Differences in assumptions between MacNevin and Zornes44 and Soller et al.45 included different starting concentrations of protozoa, with MacNevin and Zornes44 having significantly lower concentrations, the use of point-estimate LRVs associated with treatment processes44 vs. uniform distributions,45 and different dose–response models. A more recent top-down QMRA from Gerrity et al.39 yielded scenarios that generally supported both Soller et al.45 and MacNevin and Zornes,44 depending on whether the pathogen concentrations were assumed to be maximum values or 97.4th percentile values, respectively.
Church et al.50 used QMRA to develop tentative standards for reuse of dishwashing graywater on military bases for potable use. They followed a top-down approach, but instead of trying to determine LRTs, they determined the final maximum allowable concentrations of norovirus, Salmonella, and E. coli O157:H7 for dishwashing, showering, and drinking, without specifying a certain type of treatment. Church et al.50 found that the maximum allowable concentration for potable reuse was lowest for E. coli O157:H7 (2.7 × 10−6 colony forming units (CFU) per mL). Since E. coli can be monitored with culture-based methods easily and in a cost-effective manner, Church et al.50 suggested converting E. coli O157:H7 to total culturable E. coli with a ratio and applying a 10-fold safety factor. This resulted in a recommended maximum final concentration of E. coli of 1.6 × 10−2 CFU mL−1 when treating recycled dishwashing water for DPR. Overall, top-down QMRAs are useful for identifying LRTs and creating regulations, while bottom-up QMRAs can be used to evaluate the expected performance of an existing treatment train or to determine the inherent safety factor.
3.3 Potable reuse approach (DFR vs. IPR vs. DPR)
Most studies performed their assessment on only DPR19,23,29,32,38,39,44,45,50 or de facto reuse/IPR.12,13,27,28,33–37,41–43 A few studies stated they were doing IPR but neglected the impact of the environmental buffer and pathogen decay, making their analyses consistent with a DPR analysis,26,30 although this is consistent with LRV crediting frameworks that generally omit environmental attenuation.DPR can either utilize raw water augmentation or treated water augmentation (Fig. 2). For raw water augmentation, the treated recycled water can be added back to an environmental buffer (i.e., aquifer, river, or lake) upstream of a drinking water treatment plant or blended directly with the water prior to treatment. This can be distinguished from IPR based on the residence time in the environmental buffer, with some regulatory frameworks requiring minimum storage times for an IPR designation (e.g., a minimum of two months in California46). Bailey et al.23 focused their risk assessment on raw water augmentation, with a retention time of 5 days and a mixing ratio of 20% recycled water and 80% surface water. Treated water augmentation occurs when the recycled water is blended directly into the distribution system. Amoueyan et al.21 studied the risks of both types of DPR. For IPR, the environmental buffer can either be surface water or groundwater, depending on the needs of a particular community. DFR is similar to IPR, but the treated wastewater at the drinking water intake is unplanned or incidental and often lacks additional/advanced treatment.
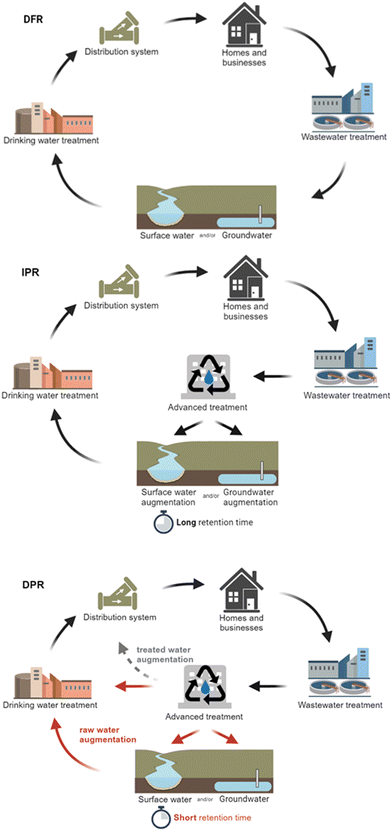 | ||
| Fig. 2 Differences between DFR, IPR, and DPR (raw water augmentation and treated water augmentation). | ||
Both Soller et al.31 and Amoueyan et al.21 compared DFR, IPR, and DPR and found the risks of IPR and DPR to be lower than the risk of DFR if the advanced water treatment (AWT) facilities are operating within design specifications. Amoueyan et al.21,22 found that the lowest risk occurred for DPR with no conventional source water (e.g., surface water or groundwater), and that the risk for IPR was dominated by pathogens assumed to be present in the conventional source water (i.e., not derived from local wastewater), leading to lower risks with greater recycled water contributions (RWCs). Other studies did not account for pathogen concentrations in the traditional source water and therefore found increased risk with higher percentages of recycled water.27 Future assessments of risk in IPR systems should consider pathogen concentrations in the source water, unless there are site-specific data to support their omission, as this would allow for a fair assessment of the relative risk impact of recycled water vs. conventional source water. This could prevent expensive additions to the advanced treatment train on the recycled water side when the driver of risk is actually the conventional source water.
IPR is already implemented in many places, including in the U.S. in states such as California, Virginia, Texas, and Georgia, as well as outside the U.S. in South Africa, Australia, and the United Kingdom.51 However, IPR is not a viable option for all communities, especially communities that lack access to a reservoir or aquifer with an adequate residence time or dilution ratio to sufficiently mitigate risk or meet regulatory requirements. Constructing and maintaining pipelines and pumping the treated water to reservoirs, where the water will be treated again after it is withdrawn, can be barriers for IPR implementation in some communities. Therefore, DPR may be the most sustainable option for certain communities, assuming DPR projects can be permitted. However, DPR greatly reduces the time available for detection and remediation of treatment issues (i.e., the response retention time or RRT).19 Adding an engineered storage buffer (ESB) to a DPR treatment train increases the RRT, allowing for risk reduction through mitigation of off-specification treatment.26 This potentially increases the attractiveness of DPR from the perspective of regulators and other stakeholders.
3.4 Hazard identification: pathogens studied
The first step in QMRA involves hazard identification, which includes choosing the pathogen(s) of greatest relevance for the goals of that study. Most studies analyzed multiple pathogens, although several chose to focus on a single pathogen.13,20,22,25,41 This simplified the analyses and allowed for more focused evaluations, such as equivalency across reuse type (DPR, IPR, and DFR),22 the effect of pathogen ‘spikes’ and hydraulic considerations on risk,25 comparisons of static vs. dynamic modeling and exposure routes,20 or how Bayesian hierarchical modeling influences parameter uncertainty with scarce data.41 Based on the Australian Guidelines for Water Recycling, seven studies used rotavirus or adenovirus, Cryptosporidium, and Campylobacter as their pathogens.28,35–37,40,42,43 Across the other 23 studies, norovirus and Cryptosporidium were the most commonly included pathogens (included in 57% and 70% of studies, respectively), and Giardia was also included in 43% of the studies, though Pecson et al.29 did not include Giardia because Cryptosporidium was assumed to be a conservative surrogate for Giardia. Similarly, adenovirus sometimes required lower LRTs than norovirus and enterovirus, meaning that any LRT approach that was sufficient for controlling norovirus and enterovirus would also be sufficient for adenovirus.19,39 Though some studies included bacteria, such as Salmonella and Campylobacter, many studies included only protozoa and/or viruses. Potable reuse regulations in the U.S. generally omit bacteria because requirements for protozoa and viruses are assumed to be highly protective against bacteria as well.21,32 Potable reuse systems in the U.S. are also required to comply with the Safe Drinking Water Act (SDWA), which includes stipulations for bacteria.There is still hesitance about including norovirus in QMRAs for water reuse because there are not widely used, standardized culture methods to measure norovirus infectivity, and there is uncertainty around how to utilize molecular (e.g., qPCR) norovirus concentrations.26,29 Moreover, there are multiple dose–response models for norovirus that provide different results, and there is no consensus on which is most appropriate. As can be seen in Fig. 3, the same dose of norovirus (100 infectious units) can result in an order of magnitude difference in the probability of infection. At this dose, the dose–response functions without an aggregation parameter predict the following probabilities of infection: the hypergeometric 1F1 model52 predicts 53%, the fractional Poisson53 predicts 72%, and beta-Poisson54 predicts 14%. Meanwhile, the fractional Poisson with an aggregation parameter53,55,56 predicts only 6%. The goal of an aggregation parameter is to prevent overestimation of infection by accounting for incomplete mixing of norovirus with a water body, which was observed in the inoculum used in a human trial.57 The drawback of including an aggregation parameter, however, is the unknown extent of aggregation or disaggregation of norovirus in environmental waters, leading some studies to consider the aggregated models as less conservative (i.e., predict lower probabilities of illness). Chaudhry et al.24 found that using the fractional Poisson aggregated dose–response model for norovirus resulted in three orders of magnitude lower median risk than using the disaggregated model. Soller et al.58 took an approach of modeling norovirus risk within two “bounds”, where the lower bound was set as the aggregated fractional Poisson and the upper bound was set to the hypergeometric 1F1. Lim et al.27 also justified the use of the disaggregated hypergeometric 1F1 as being more conservative; however, in the range simulated in Fig. 3, the fractional Poisson predicts the highest probability of infection at lower doses, indicating that the Messner et al.53 model (not considered in the study) would be a potential better choice for an upper bound or conservative model. A more in-depth discussion and full comparison of norovirus dose–response models was published in Van Abel et al.54 Many of the reviewed QMRAs19,21,22,24,29,31,32,45 included multiple dose–response models for norovirus and Cryptosporidium due to the differences in predicted risks.
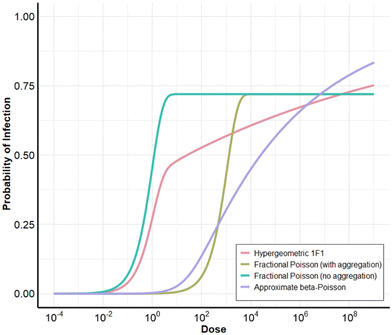 | ||
| Fig. 3 Impact of norovirus dose–response model on risk: hypergeometric 1F1 (no aggregation) from Teunis et al.,52 fractional Poisson with aggregation from Atmar et al.55,56 and Messner et al.,53 fractional Poisson with no aggregation from Messner et al.,53 and approximate beta-Poisson (no aggregation) from Van Abel et al.54 | ||
Drawbacks for norovirus inclusion in QMRAs are not limited to the dose–response model. Norovirus has multiple molecular assays that capture different strains, and some people are resistant to certain strains,39,59 complicating the interpretation of the molecular results. Although it was included in their sampling campaign, Bailey et al.23 chose not to include norovirus in their risk assessment because they did not detect any gene copies in their recycled or surface water samples. Pecson et al.19 found that the uncertainty in the LRTs for norovirus spanned over 10 orders of magnitude and therefore suggested using a hybrid approach of using enterovirus occurrence data, which are culturable and in high concentrations in wastewater, and the rotavirus dose–response model, which is highly infectious, as a measure of gastrointestinal virus in reuse QMRAs.
Soller et al.45 argues that norovirus should be included in risk assessments because it causes approximately 20 million illnesses a year in the U.S.,60 more than half of the illnesses caused by all foodborne pathogens.61 They also argue that newer dose–response models for norovirus can capture uncertainty.58 Soller et al.45 also mentions that though norovirus is not easily culturable, the GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios for other enteric viruses are sometimes low (i.e., molecular data ≈ culture data), recently excreted viruses are likely mostly infectious, and that it is better to use conservative estimates.62 These all support the inclusion of norovirus molecular data in reuse QMRAs, particularly when characterizing influent wastewater concentrations. In contrast, a dynamic QMRA, where community transmission was taken into account, found that waterborne norovirus likely contributes no appreciable risk to public health, because the risk for this specific organism in a community is dominated by secondary infections and foodborne transmission.20
IU ratios for other enteric viruses are sometimes low (i.e., molecular data ≈ culture data), recently excreted viruses are likely mostly infectious, and that it is better to use conservative estimates.62 These all support the inclusion of norovirus molecular data in reuse QMRAs, particularly when characterizing influent wastewater concentrations. In contrast, a dynamic QMRA, where community transmission was taken into account, found that waterborne norovirus likely contributes no appreciable risk to public health, because the risk for this specific organism in a community is dominated by secondary infections and foodborne transmission.20
Three studies have also used a surrogate enteric virus in their QMRA.12,13,25 While Tanaka et al.13 used concentrations from an enteric virus database with 377 samples from unchlorinated secondary effluents, Asano et al.12 used an enteric virus database with 424 secondary effluent samples and 84 tertiary effluent samples. Gerrity et al.25 used SARS-CoV-2 concentrations in wastewater with the hypergeometric dose–response model for norovirus based on the assumption that SARS-CoV-2 concentration dynamics were comparable to norovirus. While their calculated relative risks do not correspond to risk for actual pathogens, Gerrity et al.25 were able to gain insights about how incidental dispersion or engineered mixing could be implemented to attenuate pathogen concentration spikes and ultimately reduce high-end risk estimates. Though Asano et al.12 used the same concentrations for all the enteric viruses, they modeled the risk separately for poliovirus 1, poliovirus 3, and echovirus 12 due to different infectivities.
3.5 Pathogen concentration determination
Determining accurate pathogen concentrations for QMRAs is vital because pathogen concentration has a large impact on risk, but there are many uncertainties around what concentrations should be used. There are seasonal and geographic variations in pathogen concentrations,63 and some studies use point estimates12,39,40 rather than distributions. Different probability distribution functions (PDFs) could be fit to the pathogen data, such as lognormal or triangular. While most studies24,29,31–33,45 used pathogen concentrations from raw wastewater, several used wastewater effluent data,12,13,23,26,27,44 and a few used point estimates of pathogens in urban stormwater.42,43 Many QMRAs assessed the sensitivity of the risk to different concentrations of pathogens in the water, often finding that they were the driving factor in risk.12,13,21–23,33,45 Chaudhry et al.24 and Soller et al.45 independently used the same meta-analysis for pathogen concentrations (i.e., statistical distributions of norovirus concentrations)63 and arrived at similar risk estimates.However, determining accurate and appropriate values can be difficult. Molecular data measures the number of gene copies, rather than the number of infectious pathogens, so the number of gene copies must be converted to infectious units (GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios or harmonization factors). The GC
IU ratios or harmonization factors). The GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio has a large impact on risk,19,25,64 and the numbers can vary widely. As discussed by Gerrity et al.,25 conservative approaches assume a GC
IU ratio has a large impact on risk,19,25,64 and the numbers can vary widely. As discussed by Gerrity et al.,25 conservative approaches assume a GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio of 1.0, where every gene copy is assumed to equate to an infectious pathogen, but the actual number of infectious units might be orders of magnitude lower due to inactivation/degradation.19 Most studies assumed all gene copies were infectious, but Bailey et al.23 had percentages of infectious units for each pathogen. They used point estimates of 38.5% infectious for adenovirus (2.6
IU ratio of 1.0, where every gene copy is assumed to equate to an infectious pathogen, but the actual number of infectious units might be orders of magnitude lower due to inactivation/degradation.19 Most studies assumed all gene copies were infectious, but Bailey et al.23 had percentages of infectious units for each pathogen. They used point estimates of 38.5% infectious for adenovirus (2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GC
1 GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU), 65% for Salmonella (1.5
IU), 65% for Salmonella (1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GC
1 GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU), 25% for Cryptosporidium (4
IU), 25% for Cryptosporidium (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GC
1 GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU), and 13% for Giardia (7.7
IU), and 13% for Giardia (7.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GC
1 GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU). Gerrity et al.39 modeled the GC
IU). Gerrity et al.39 modeled the GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios for norovirus, enterovirus, and adenovirus as log10-uniform distributions from 1
IU ratios for norovirus, enterovirus, and adenovirus as log10-uniform distributions from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 200
1 to 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while Amoueyan et al.21 used a 700
1, while Amoueyan et al.21 used a 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 point estimate GC
1 point estimate GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU for adenovirus. Culture methods, on the other hand, may underestimate the number of infectious viruses present. One proposed option to address this is to assume that only 10% of the viruses present are culturable,65 and this 10-fold correction factor has recently been applied to enterovirus culture data.19,39
IU for adenovirus. Culture methods, on the other hand, may underestimate the number of infectious viruses present. One proposed option to address this is to assume that only 10% of the viruses present are culturable,65 and this 10-fold correction factor has recently been applied to enterovirus culture data.19,39
Low concentrations of pathogens can be difficult to measure, so using larger sample volumes, or more specifically larger equivalent sample volumes (ESVs),66 can provide more data with fewer non-detects. For example, Pecson et al.19 used 1 L samples to identify Cryptosporidium and the detection rate was 98%, compared to 40% with 50 μL samples.67 This would not be of concern for top-down QMRAs if the LRTs are determined from the highest pathogen concentrations, but for bottom-up QMRAs using pathogen concentration distributions, the lowest concentrations would be censored and potentially omitted, resulting in overestimations of risk. The pathogen concentrations in the assessment also depend on the PDFs used to model them. Zhiteneva et al.68 performed a review summarizing assumptions made when selecting the PDFs for source water, treatment steps, and the dose–response models for potable and non-potable reuse. PDFs assume variability in the system and provide a range of final risk estimates. Each dataset needs to be individually fitted to a PDF, and a poorly chosen PDF can over- or underestimate risk.
Historically, QMRAs have relied on limited data. However, the rise of wastewater surveillance for SARS-CoV-2 during the COVID-19 pandemic has caused a substantial increase in wastewater biobanks, with additional reuse-relevant pathogen datasets based on these samples being published. This increase in pathogen data highlights the importance of reviews such as Zhiteneva et al.68 and Darby et al.69 These papers focus on identifying and aggregating high-quality pathogen data, and they provide criteria on fitting data to distributions, guiding future pathogen data collection and selection for QMRAs.
Dispersion/mixing of pathogens in sewer collection systems and wastewater treatment plants (e.g., in clarifiers and aeration basins) results in overall ‘averaging’ of pathogen concentrations over time, effectively attenuating high end concentrations but also elevating low-end concentrations. This may inflate measures of central tendency by increasing risk for most ingestion events, but it will also reduce risks at the upper percentiles that often drive LRT determinations.25 The attenuation effect is particularly apparent for intermittent spikes in influent pathogen concentration (i.e., outlier events).25 Some QMRAs use point estimates based on maximum influent pathogen concentrations, but those data points may be spikes (i.e., outliers) that might actually be attenuated after accounting for dispersion. However, this benefit of dispersion is only realized with intermittent spikes; if high concentrations last for an extended period of time (e.g., during a community outbreak), the effects of dispersion might be negligible. Just as there are stipulations for chemical peak averaging,17 implementing similar guidelines for pathogens could be beneficial, considering the significant impact it could have on pathogen concentrations and resulting LRTs or credited LRVs.
3.6 Environmental buffers: retention time, pathogen decay, and recycled water contribution
Pathogens decay over time, making the inclusion of retention time in the environmental buffer an important consideration. However, many QMRAs and regulatory frameworks do not explicitly consider LRVs during storage or may only account for decay for certain pathogens. In California, for example, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log virus reduction is credited for each month that the water is retained underground for groundwater replenishment.70 If pathogen decay is not considered, any corresponding risk estimates might be artificially inflated, particularly for IPR and DFR scenarios. Similarly, omitting decay from LRV crediting inevitably increases capital and operations and maintenance costs associated with engineered treatment trains, while potentially yielding no appreciable change in public health protection.39
log virus reduction is credited for each month that the water is retained underground for groundwater replenishment.70 If pathogen decay is not considered, any corresponding risk estimates might be artificially inflated, particularly for IPR and DFR scenarios. Similarly, omitting decay from LRV crediting inevitably increases capital and operations and maintenance costs associated with engineered treatment trains, while potentially yielding no appreciable change in public health protection.39
The differences in decay rates for the different pathogens impact the needed retention times for risk reduction. For DFR, Amoueyan et al.22 found that risk associated with wastewater-derived Cryptosporidium exhibited a meaningful increase with fewer than 105 days of storage in the environmental buffer, while Amoueyan et al.20 found that a reservoir storage time of at least 30 days could potentially reduce risk from norovirus in a DFR system below that of DPR, using bacteriophage MS2 decay rates as a surrogate for norovirus.
Even 1% of wastewater effluent in the drinking water source water can have important health risk considerations in reuse.24,31 Soller et al.31 included Cryptosporidium, Giardia, and norovirus in their analysis, and used residence times of 2–360 days for DFR and 30–360 days for IPR. They found that simulations with a retention time less than 180 days exceeded the annual risk benchmark of 10−4, even with an RWC of 1% for DFR. With more than 10% wastewater contribution with DFR, more than 180 days were needed to consistently achieve a probability of annual infection of less than 10−4. Approximately 90 days in the reservoir were required to consistently meet the annual risk benchmark of 10−4 for IPR with surface water augmentation. For DFR, Lim et al.27 also found a negative correlation of risk with the residence time in the lake (between 270 and 360 days), and a positive correlation of risk with RWC, because they assumed the source water was pathogen free. Tanaka et al.13 and Asano et al.12 both assumed a residence time of 6 months in the reservoir, while Zhiteneva et al.33 modeled their residence time between 50 and 120 days. In California, to be considered IPR, instead of DPR with raw water augmentation, the retention time must either be at least 180 days or the project could apply to the State Board for approval for a reduced theoretical retention time, though it can be no less than 60 days.46
Page et al.28 studied the impact of aquifer treatment for urban stormwater in a managed aquifer recharge system. They found that the aquifer alone resulted in LRVs of 1.4, 2.6, and >6.0 for rotavirus, Cryptosporidium, and Campylobacter, respectively, based on diffusion chamber studies. They used different decay rates for the pathogens in the wetlands and the aquifer, with higher average decay rates for rotavirus and Cryptosporidium in the wetland, and a higher decay rate for Campylobacter in the aquifer. The importance of the aquifer as a treatment barrier depended on the pre- and post-treatment processes, but the estimated risk was less than 10−6 DALYs pppy with adequate treatment and retention time.28
Pathogen decay is not always included in QMRAs, even when studying DFR or IPR,24,30 but it can have a large impact on the risk and can vary seasonally. Though Lim et al.27 did not include a temperature component to their decay equations, they highlighted it as a parameter to be incorporated in future models. Bailey et al.23 modeled pathogen decay at different temperatures (4 and 20 °C), but their retention time was only 5 days. Amoueyan et al.21 did include the temperature component, using higher decay coefficients at higher temperatures, potentially allowing for a more accurate assessment of decay. Pathogen decay rates depend on a variety of factors including temperature, sunlight, and salinity, and the experimental decay rates for the same viral types can vary by over an order of magnitude.71–73 However, the exact impact of these factors on decay rates of different pathogens and how they impact each other is still unknown, thus more data are needed. Collecting these data is essential because it can elucidate what LRVs could be credited for different pathogens at various retention times to help reduce reliance on engineered treatment processes by leveraging natural management barriers.
3.7 Treatment processes
Treatment processes have different LRVs for different pathogens (Fig. 4), and the pathogen that drives risk in the final estimates depends on the treatment train in question.24,32 Soller et al.32 and Chaudhry et al.24 found norovirus or Cryptosporidium as the driving factor of risk of infection depending on the treatment processes considered. For example, RBAT (WWTP-MF-RO-UV-ESB + Cl2) led to norovirus having the highest risk, while CBAT (WWTP-O3-BAF-UF-UV-ESB + Cl2) resulted in the risk being dominated by Cryptosporidium, in part because of differing observed or credited LRVs for various treatment process/pathogen combinations (Fig. 4).32,45 In their study, Soller et al.32 used data describing conventional filtration of wastewater to derive LRVs for biologically active filtration (BAF), although LRVs are not currently credited for BAF under some regulatory frameworks (e.g., in California).45 Kimbell et al.34 compared two RBAT trains (TT1: BNR-MBR-RO-UV AOP-Cl2-O3 and TT2: BNR-MF/UF-CF-RO-UV AOP-Cl2-O3) and found that TT1 (14.5/14/12) achieved higher virus LRVs than TT2 (14/15.5/13.5) but lower removal of Giardia and Cryptosporidium. Amoueyan et al.21 also found that whether the annual disease burden was higher for Cryptosporidium or norovirus depended on the treatment train.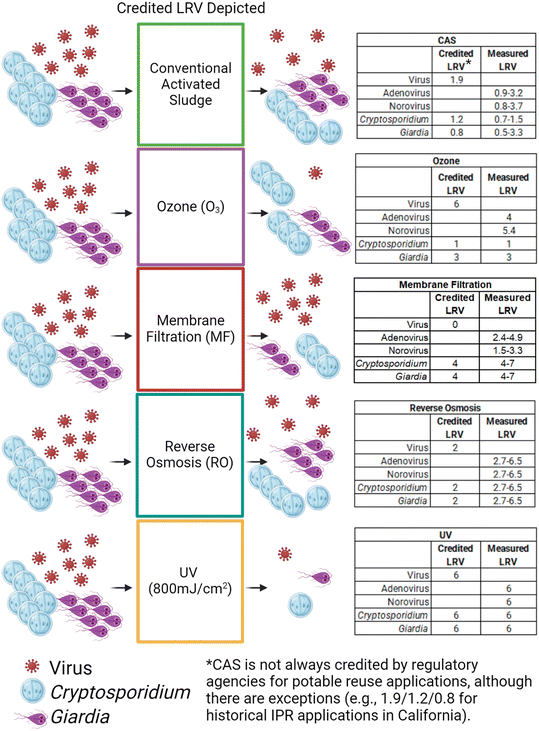 | ||
| Fig. 4 Conceptual diagram of the credited effectiveness of different treatment processes on protozoa and viruses. LRVs from Soller et al.45 Note that observed treatment efficacy may be substantially different from credited treatment efficacy, resulting in an LRV ‘gap’. | ||
As noted earlier, observed LRVs, which are measured experimentally and represent the actual inactivation or removal of microorganisms from the water, are often not the same as the credited or regulatory LRVs. For example, Amoueyan et al.21 incorporated mean observed LRVs for microfiltration (MF) of 4.60, 2.40, and 3.65 for Cryptosporidium, norovirus, and adenovirus, respectively, but noted that the corresponding credited LRVs would likely be 4, 0, and 0 in an actual system. Amoueyan et al.20 estimated risk for norovirus using both LRV approaches and found the risk was orders of magnitude higher using regulatory LRVs—sometimes yielding 95th percentiles exceeding 10−4 pppy. When lower credited LRVs result in overestimated risk to consumers, the outcome may be overdesigned and potentially cost-prohibitive projects.
Chaudhry et al.24 conducted a literature review to incorporate observed LRVs and found membrane processes were the most effective at reducing overall risk, despite UV generally being the most robust from a crediting perspective. Many potable reuse systems will employ UV doses well in excess of 200–300 mJ cm−2 in order to target photolysis of N-nitrosodimethylamine (NDMA) and/or oxidation of recalcitrant compounds such as 1,4-dioxane (i.e., UV AOP), yielding LRV credits of up to 6 for all pathogen groups. In contrast, the mean LRV for UV in Chaudhry et al.24 was 2.2 for Cryptosporidium and 5.0 for norovirus. The Cryptosporidium LRV74 was based on a UV dose of 1.8 mJ cm−2, and the norovirus LRV75 was based on a UV dose of 127 mJ cm−2 (with MS2 as a surrogate). Since the LRV credits were limited by the lower assumed UV doses, Chaudhry et al.24 found that RO—and not UV—resulted in the largest risk reduction when it was employed. When RO was not used, MF and NF reduced risk most in their treatment train. Other studies also describe the significance of UV design dose on the resulting pathogen risk. For example, Soller et al.32,45 found that reducing the UV dose from 800 mJ cm−2 (i.e., UV AOP) to 12 mJ cm−2 (i.e., closer to traditional wastewater treatment) increased the risk of infection by four orders of magnitude, making the low dose UV treatment trains unable to meet the benchmark risk levels.
Annual risks of infection were sometimes lower for CBAT (O3-BAF-UF-ESB + Cl2) vs. RBAT (MF-RO-UV-ESB + Cl2),45 which was consistent with Amoueyan et al.20,21 who also compared CBAT (UF-O3-BAC-UV-ESB + Cl2) vs. RBAT (MF-RO-UV-ESB + Cl2). Although risk may have been lower with CBAT because risk incorporates both pathogen load and treatment, RBAT was sometimes superior from a treatment perspective (i.e., higher overall LRVs), particularly for Cryptosporidium.32,45 Ozone is a robust barrier in terms of bulk organic matter transformation, trace organic compound oxidation, and microbial inactivation,76 yet protozoan pathogens (namely Cryptosporidium) still demonstrate resistance.77 On the other hand, membrane-based treatment can be a challenge in terms of regulatory virus LRV crediting but is generally accepted as a robust barrier for protozoan pathogens from both a regulatory and observed LRV perspective (Fig. 4). Remy et al.30 evaluated a unique treatment train consisting of filtration, reverse electrodialysis, micro-grain activated carbon (μGAC), and UV as advanced tertiary treatment before reservoir augmentation. They found that train consistently yielded higher risks than a more conventional potable reuse train with UF and RO with a 5% bypass. However, both treatment trains were able to meet the 10−6 DALY benchmark for viruses, bacteria, Giardia, and Cryptosporidium.
3.8 Exposure assessment: ingestion volume and frequency
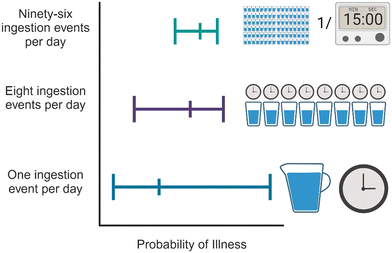
When doing QMRA for drinking water, both the daily ingestion volume and frequency can impact the final risks.26,29 With respect to volume, most studies assumed 2 or 2.5 L per day, but Kobayashi et al.35 assumed 0.75 L d−1, while Church et al.50 assumed 3 L d−1. More frequent ingestion events are more likely to capture rare/short-term but high consequence scenarios. However, calculated risk is somewhat attenuated when the overall daily ingestion volume is spread out over multiple ingestion events (Fig. 5). When California created their draft DPR regulations, they used a daily risk benchmark and 96 ingestion events per day. The modeled failure (assumed to be 15 minutes) would only impact one off-specification ingestion event and would be averaged out by 95 other nominal ingestion events during that day. Similarly with 96 ingestion events, a peak pathogen concentration can also be averaged out. This effectively creates a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log buffer (∼1% of the ingestion events are impacted by failure or a pathogen spike), which would not be the case for QMRAs assuming one ingestion event per day.39 This is also the basis for California requiring only 4
log buffer (∼1% of the ingestion events are impacted by failure or a pathogen spike), which would not be the case for QMRAs assuming one ingestion event per day.39 This is also the basis for California requiring only 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log treatment redundancy to account for a 6
log treatment redundancy to account for a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log treatment process failure lasting 15 minutes.39
log treatment process failure lasting 15 minutes.39
This phenomenon is similar to the dispersion effect discussed in Gerrity et al.25 To further explore the risks with different consumption patterns, Jones et al.26 modeled 1, 8, or 96 ingestion events per day, which captured different pathogen concentrations and different log reductions for each treatment process, based on different possible failure analyses. Only consuming water once per day results in a risk profile that has a larger range than when water is consumed multiple times per day. However, Jones et al.26 also found higher median risks for multiple consumptions a day, again because ‘averaging’ has a disproportionate effect on the lower percentiles of risk.
3.9 Risk characterization
There are different ways to measure risk. Risk endpoints include probabilities of infection and illness, which can be translated into DALYs. Commonly used risk thresholds for probability of infection (Pinf) from drinking water include 10−4 infections per person per year (pppy) or a daily risk of 2.7 × 10−7 (i.e., 10−4 annual risk divided equally across 365 days). The daily risk threshold is potentially more conservative, and potentially more protective of highly susceptible populations, because it does not allow higher risk days to be averaged out, as is the case for the historically common annual risk calculation. Risk of illness requires an additional adjustment to account for the proportion of infections that result in a symptomatic illness. DALYs, on the other hand, are a better representation of the overall health burden of pathogens, as they measure the life years lost or lived with a disability due to pathogen exposure and subsequent infection and illness. The typical guideline is <10−6 DALYs pppy.18 Some studies, instead of directly using a dose–response function, used the dose equivalent to 10−6 DALYs for each pathogen.40,42,43Using one risk endpoint versus another can sometimes lead to opposing conclusions. For example, Lim et al.27 performed a risk assessment for norovirus and Cryptosporidium for DFR and found a higher risk of infection for norovirus (4.4 × 10−2 to 6.4 × 10−1 pppy) than Cryptosporidium (1.2 × 10−4 to 8.8 × 10−3 pppy), but a greater disease burden for Cryptosporidium (7.1 × 10−8 to 5.3 × 10−6 DALYs pppy) than norovirus (6.2 × 10−11 to 3.0 × 10−8 DALYs pppy). This difference is caused by the assumption that Cryptosporidium will have a greater negative health impact (i.e., more severe) than a norovirus infection. When deciding on the preferred risk endpoint, the intended audience is an important consideration. DALYs are potentially more appropriate for communicating and comparing risks outside the U.S., as they are recommended by WHO and used globally (e.g., in Australia).35 However, regulatory development for potable reuse in the U.S. has primarily focused on probability of infection.39
Remy et al.30 and Zhiteneva et al.33 focused on the DALY framework and found risk was driven by Cryptosporidium. Although Remy et al.30 found that Cryptosporidium led to higher DALY estimates than rotavirus, Page et al.28 estimated higher DALYs for rotavirus than Campylobacter and Cryptosporidium. This highlights how disease burden may need to be reevaluated over time, at least in certain regions. The rotavirus vaccine RV5 was introduced in the U.S. in 2006, and the RV1 vaccine was introduced in 2008. Both vaccines are effective in reducing risk and disease burden.78 As new vaccines are developed and dose–response models are created, the pathogens targeted by regulations may need to change to be properly representative. For example, Bailey et al.23 published a QMRA in 2020 and found that adenovirus actually yielded the highest risk when compared to Salmonella, Cryptosporidium, and Giardia. This was due to adenovirus' higher concentrations in recycled water and surface water, presumably due to inadequate disinfection during wastewater treatment that incorporated chloramination and UV. Kimbell et al.34 found that adenovirus also had the highest risk when failures were modeled, compared to a generic enteric virus, Cryptosporidium, and Giardia, though without failures, the generic enteric virus had higher average risks. In either case, viruses dominated the risk calculation because of their higher concentrations.
One study developed a unique alternative to the common risk benchmarks. Church et al.50 chose a target of one illness per 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 exposures (daily probability of illness of 2 × 10−5 per person), meaning that if a city had 50
000 exposures (daily probability of illness of 2 × 10−5 per person), meaning that if a city had 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people drinking once per day, one person per day would get ill on average. This benchmark was chosen because it was two orders of magnitude less than the number of food and water-related illnesses in a military field setting, allowing reuse to contribute up to 1% of the health burden. For reference, this would be much higher (less conservative) than the aforementioned 2.7 × 10−7 daily probability of infection.
000 people drinking once per day, one person per day would get ill on average. This benchmark was chosen because it was two orders of magnitude less than the number of food and water-related illnesses in a military field setting, allowing reuse to contribute up to 1% of the health burden. For reference, this would be much higher (less conservative) than the aforementioned 2.7 × 10−7 daily probability of infection.
3.10 Impact of failures on risk
A single day with a peak pathogen concentration, either due to a pathogen spike or treatment process failure(s), can drive annual risk, so it is important to have reliable online monitoring.32 Failure can be the primary driver of high risk, so it is important to stress test the failure assumptions incorporated into a QMRA.26,33 Amoueyan et al.20–22 included a probability of failure for each treatment process in the train. Amoueyan et al.21 found that while DPR with treated water augmentation typically satisfied public health benchmarks, compound treatment process failures, where multiple processes fail interdependently/simultaneously, resulted in risks as high as 10−2. They also performed a sensitivity analysis on treatment process failures to determine how large of an impact a failure would have on the risk from each pathogen. However, Amoueyan et al.21 noted they may have overestimated the frequency and/or severity of failures (i.e., LRV = 0). They also highlighted that potable reuse systems would likely have failsafe protocols, such as continuous monitoring with diversions when failures occur, and this was not incorporated into their QMRA. Similar to Amoueyan et al.,21 Zhiteneva et al.33 explored the failure of each treatment step by setting each LRV to 0, and they also created a model where the performance of one LRV was correlated with another by 0.5, which could be used to explore process dependency. Kimbell et al.34 included three possible failure scenarios: a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log reduction in treatment for 24 h on 9% of simulated days, a 6
log reduction in treatment for 24 h on 9% of simulated days, a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log reduction in treatment for 24 h on 1% of simulated days, and a compound 9
log reduction in treatment for 24 h on 1% of simulated days, and a compound 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log reduction in treatment for 24 h occurring on 0.09% of simulated days. Without failure, one of their treatment trains had a mean Pinf for adenovirus of 6.65 × 10−9 pppy, but the Pinf reached a maximum of 7.34 × 10−2 with failures. Compound failures resulted in larger 95th or 99th percentile DALY values, depending on their frequency, demonstrating the importance of considering any correlations in process failures.
log reduction in treatment for 24 h occurring on 0.09% of simulated days. Without failure, one of their treatment trains had a mean Pinf for adenovirus of 6.65 × 10−9 pppy, but the Pinf reached a maximum of 7.34 × 10−2 with failures. Compound failures resulted in larger 95th or 99th percentile DALY values, depending on their frequency, demonstrating the importance of considering any correlations in process failures.
Jones et al.26 compared no failure, real failure values from the literature, and total failure. Total failure of UV-AOP (which was simulated to last 15 minutes due to online monitoring and subsequent diversion to an ESB) was the largest driver for increased risk, due to its 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log credit during normal operation. Jones et al.26 found that the hypothetical failure increased the risk for higher percentile annual infection probabilities by up to six orders of magnitude, but the ESB ensured the annual risk of infection still complied with the WHO annual risk limit. Pecson et al.29 assumed a maximum of one critical failure per year per process, where the LRV for that process became 0, which was likely a conservative estimate. They reported median, 95th, and 99th percentile annual risks of infection with and without failures for Cryptosporidium and enterovirus. The median risks of infection without failures were 4.9 × 10−11 and 1.5 × 10−14 for Cryptosporidium and enterovirus, respectively. With failures, the median risks of infection increased to 1.4 × 10−7 for both Cryptosporidium and enterovirus, and the 99th percentiles increased to 1.1 × 10−5 and 2.1 × 10−5 for Cryptosporidium and enterovirus, respectively. Since Jones et al.26 and Pecson et al.29 were not modeling the impact of compound failures, the risks during failure events were lower than those found by Amoueyan et al.21 This highlights the importance of preventing failures and ensuring any treatment train is robust and reliable.
log credit during normal operation. Jones et al.26 found that the hypothetical failure increased the risk for higher percentile annual infection probabilities by up to six orders of magnitude, but the ESB ensured the annual risk of infection still complied with the WHO annual risk limit. Pecson et al.29 assumed a maximum of one critical failure per year per process, where the LRV for that process became 0, which was likely a conservative estimate. They reported median, 95th, and 99th percentile annual risks of infection with and without failures for Cryptosporidium and enterovirus. The median risks of infection without failures were 4.9 × 10−11 and 1.5 × 10−14 for Cryptosporidium and enterovirus, respectively. With failures, the median risks of infection increased to 1.4 × 10−7 for both Cryptosporidium and enterovirus, and the 99th percentiles increased to 1.1 × 10−5 and 2.1 × 10−5 for Cryptosporidium and enterovirus, respectively. Since Jones et al.26 and Pecson et al.29 were not modeling the impact of compound failures, the risks during failure events were lower than those found by Amoueyan et al.21 This highlights the importance of preventing failures and ensuring any treatment train is robust and reliable.
Bailey et al.23 measured pathogen concentrations in recycled water after conventional wastewater treatment and assumed a worst-case scenario for the LRV at the drinking water treatment plant using real-world data from Hijnen and Medema.79 They compared risks from these worst-case scenarios to baseline scenarios, specifically U.S. EPA's LRVs (4/3/2 for virus/Giardia/Crypto) and the WHO's DALY-based LRVs (4/3/3 for virus/Giardia/Crypto) for conventional drinking water treatment. They found that the mean and 95th percentile annual risk for Salmonella, Cryptosporidium, and Giardia for the worst-case scenarios were always within an order of magnitude of the baseline conditions. For adenovirus, the mean and 95th percentile annual risk of infection was between 1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logs higher for the worst-case scenarios. Because Bailey et al.23 used observed data, these worst-case scenarios had less of an impact than some of the modeled failures elsewhere in the literature (e.g., Pecson et al.29).
logs higher for the worst-case scenarios. Because Bailey et al.23 used observed data, these worst-case scenarios had less of an impact than some of the modeled failures elsewhere in the literature (e.g., Pecson et al.29).
Pecson et al.19 suggested incorporating 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log treatment redundancy to protect against undetected failures, for final LRTs of 17/14/14 for viruses/Giardia/Cryptosporidium. Gerrity et al.39 assessed the NWRI Expert Panel recommendations for DPR, which included a recommended 5
log treatment redundancy to protect against undetected failures, for final LRTs of 17/14/14 for viruses/Giardia/Cryptosporidium. Gerrity et al.39 assessed the NWRI Expert Panel recommendations for DPR, which included a recommended 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log redundancy.80 Following the Expert Panel's approach, the top-down QMRA suggested that a 5
log redundancy.80 Following the Expert Panel's approach, the top-down QMRA suggested that a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log redundancy was sufficient to achieve a 2.7 × 10−7 daily risk benchmark at the 99th percentile, except for Giardia with a slightly higher daily risk.39 Rather than incorporating redundancy, Gerrity et al.39 proposed an alternative approach that quantifies a system's LRV tolerance to off-specification conditions. They found that for baseline LRVs of 15/11/11 in a DPR system, off-specification operation with an LRV of 12 for viruses or 8 for Giardia and Cryptosporidium would still satisfy the annual risk benchmark assuming the reduced LRV occurred fewer than 12 days per year for viruses or 3 days per year for the protozoa. This suggests a built-in redundancy of 3
log redundancy was sufficient to achieve a 2.7 × 10−7 daily risk benchmark at the 99th percentile, except for Giardia with a slightly higher daily risk.39 Rather than incorporating redundancy, Gerrity et al.39 proposed an alternative approach that quantifies a system's LRV tolerance to off-specification conditions. They found that for baseline LRVs of 15/11/11 in a DPR system, off-specification operation with an LRV of 12 for viruses or 8 for Giardia and Cryptosporidium would still satisfy the annual risk benchmark assuming the reduced LRV occurred fewer than 12 days per year for viruses or 3 days per year for the protozoa. This suggests a built-in redundancy of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logs for short-term off-specification conditions or failures.
logs for short-term off-specification conditions or failures.
Despite the potentially significant impact of failures, potable reuse treatment trains have been found to be robust and reliable. Pecson et al.81 assessed the mechanical reliability of a DPR treatment train using operator logs of all mechanical issues over a year and found no critical failures, demonstrating the potential reliability of advanced treatment for DPR. Amoueyan et al.22 found that some failures can be inconsequential because of the overall robustness and redundancy of advanced treatment in DPR or the resiliency afforded by the environmental buffer in IPR.
3.11 Computational methods
Most QMRAs are performed with Monte Carlo simulations to account for uncertainty and variability in the input parameters. In Monte Carlo simulations, some or all of the input variables, such as pathogen concentrations, are represented by PDFs. These statistical distributions are randomly sampled for each variable, and the outcome, such as the probability of infection, is calculated. This is repeated many times, creating a distribution of outcomes, to analyze the behavior of the system while accounting for inherent variability and uncertainty.Simpler QMRAs can also be performed, such as by using conservative point estimates instead of distributions for pathogen concentrations. For example, Page et al.40 used the 95th percentile pathogen concentrations to determine the LRTs for Cryptosporidium, Campylobacter, and viruses for urban stormwater reuse, and Gerrity et al.39 used both the maximum point value and the 97.4th percentile point value from pathogen distributions. Percentile is linked to sample size, so the 97.4th percentile was chosen since this percentile within a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 point dataset is statistically equivalent to the maximum value of a 24 point dataset, as can be shown from Blom's equation.82 This might be the required minimum sample size for pathogen monitoring campaigns aimed at developing LRTs. In other words, the maximum value from a 10
000 point dataset is statistically equivalent to the maximum value of a 24 point dataset, as can be shown from Blom's equation.82 This might be the required minimum sample size for pathogen monitoring campaigns aimed at developing LRTs. In other words, the maximum value from a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 point distribution might be considered overly conservative when compared against the maximum from a dataset with only 24 values. Asano et al.12 used four point estimates for pathogen concentrations: the maximum and 90th percentile concentrations of the secondary effluent at the WWTP (assuming an additional LRV of 5 for tertiary treatment), the maximum value detected in the tertiary effluent, and the limit of detection for a tertiary treated wastewater effluent sample. Point estimates with conservative values are useful for creating point estimate regulatory LRTs, while using distributions of concentrations allow the risk distributions and central tendencies to be quantified and more fully characterized.19
000 point distribution might be considered overly conservative when compared against the maximum from a dataset with only 24 values. Asano et al.12 used four point estimates for pathogen concentrations: the maximum and 90th percentile concentrations of the secondary effluent at the WWTP (assuming an additional LRV of 5 for tertiary treatment), the maximum value detected in the tertiary effluent, and the limit of detection for a tertiary treated wastewater effluent sample. Point estimates with conservative values are useful for creating point estimate regulatory LRTs, while using distributions of concentrations allow the risk distributions and central tendencies to be quantified and more fully characterized.19
QMRAs can also be performed dynamically or statically. In static QMRAs, the probability of infection is modeled from a single exposure event without time dependence or system feedback through community spread (Fig. 6). For waterborne diseases, static QMRAs could underestimate overall risk by not including time-dependent secondary transmission, or overestimate the risk by not including the possibility of someone entering an immune state after exposure to the waterborne pathogens.20 While most QMRAs are static, dynamic QMRAs offer time-dependent pathogen loads and the ability to explore the relative contribution of waterborne pathogens to the total number of illnesses. Amoueyan et al.20 used a dynamic QMRA to determine the relative importance of norovirus transmission pathways: foodborne, person-to-person, and person-to-sewage-to-person. They modeled different epidemiological states, such as susceptible, exposed, diseased, carrier, and post-infection (or recovered) using ordinary differential equations, similar to Eisenberg et al.83 Eisenberg et al.83 created a dynamic process model for a Cryptosporidium outbreak that included a 10-state compartmental model of the population, where people could move between susceptible, infected, diseased, or immune states. The number of current infections influenced the infection rate both through person-to-person transmission and through person-to-sewage-to-person transmission. Overall, Amoueyan et al.20 found that waterborne norovirus did not appreciably contribute to the public health risk in their model, because secondary and foodborne transmission dominated the overall risk calculation. Barker et al.38 also included a secondary attack rate, quantifying the percentage of people who would become sick after contact with the infected person. They found that small communities might need additional treatment due to this secondary transmission and the increased contact between members in a small community relative to a large city.
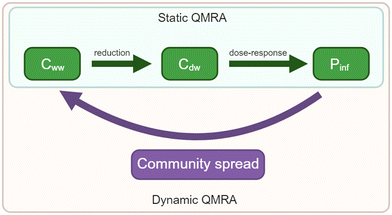 | ||
| Fig. 6 Differences between dynamic and static QMRAs. Cww is the pathogen concentration in wastewater. Cdw is the pathogen concentration in drinking water. Pinf is the probability of infection. | ||
Zhiteneva et al.33 proposed using Bayesian networks as a solution to limited local data availability, where local pathogen data could be combined with pathogen datasets from literature reviews. Bayesian modeling uses Bayes' theorem to update the probabilities of an outcome as more information becomes available.84 Bayesian networks are graphical models that represent a large amount of data using nodes to represent random variables that are connected to each other by their probabilistic dependencies. While Monte Carlo simulations are better suited for prediction because of their continuous distributions, Bayesian networks can be used for forward and backward inference, which could be used to determine how processes perform under certain risk scenarios.33 Bayesian hierarchical modeling (BHM), which is better able to account for variability within and between groups of data, reduces local parameter uncertainty compared to separate modeling, where larger datasets are not taken into account, while still letting local data dominate.41 Seis et al.41 used both local and external pathogen concentrations and compared BHM to separate modeling, where each treatment plant is different and results from one do not influence results from another; complete pooling, where every treatment plant has the same mean and standard deviation; and no pooling, where the treatment plants have different means but a common standard deviation. They included a classical Bayesian hierarchical framework, where a unique mean is estimated for every treatment plant, with the assumption that the local means comes from a common, normal distribution. Seis et al.41 also used extended hierarchical modeling, by letting the individual within-treatment plant variances differ by plant, which added additional hyperparameters in the model. In both cases, the parameters are all estimated on a total data and individual treatment plant level simultaneously, and the information is shared across simulations.41 They found BHM reduced parameter uncertainty, particularly when local data were sparse, while letting local data dominate. Seis et al.41 recommended including external information, such as from meta-analyses of pathogen concentrations, even when local data are available. Widespread use of Bayesian modeling for QMRA could provide more robust analyses, particularly in data-scarce scenarios, by allowing local pathogen concentrations to be supplemented by larger datasets. Bayesian modeling also enables the creation of prediction intervals, quantifying the uncertainty around the predictions. While these could be useful for a greater understanding of risks, the communication of these prediction intervals would be important to prevent unnecessary alarm or unwarranted complacency.
3.12 Regulatory considerations
Top-down QMRAs are the basis for regulations that determine the minimum LRVs for the selected pathogens. In the U.S., viruses, Giardia, and Cryptosporidium are regulated, with these values seen as inclusive for adequate bacterial removal. Table 1 shows the recommended LRTs for the top-down QMRAs on potable reuse. The LRTs varied greatly, both between and within studies. In Barker et al.,38 for example, they compared an outbreak scenario for a small community to a municipal sewage scenario and found the LRT for viruses was 5.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logs higher for an outbreak condition. The three studies with the lowest LRTs all used estimates of stormwater pathogen data.40,42,43 MacNevin and Zornes44 used protozoa concentrations at 20 different WWTPs and found that the LRT for Cryptosporidium differed by as much as 10 depending on the treatment plant in question. Using maximum pathogen concentrations, Gerrity et al.39 found similar LRVs (15/11/11) as Soller et al.45 did when 100% of their simulations had an annual risk less than 10−4, though Soller et al.45 required either 1 more virus LRV (16/11/11) or 2 more LRVs for Cryptosporidium and Giardia (15/13/13). These differences could be due in part to rounding, where Soller et al.45 assessed the percentage of simulations that had Pinf < 10−4, while Gerrity et al.39 calculated the required LRVs and then rounded to the nearest whole number, even if that meant rounding down. For LRVs of 15/11/11, Soller et al.45 found that 99.7% of simulations met the probability of infection benchmark of 10−4.
logs higher for an outbreak condition. The three studies with the lowest LRTs all used estimates of stormwater pathogen data.40,42,43 MacNevin and Zornes44 used protozoa concentrations at 20 different WWTPs and found that the LRT for Cryptosporidium differed by as much as 10 depending on the treatment plant in question. Using maximum pathogen concentrations, Gerrity et al.39 found similar LRVs (15/11/11) as Soller et al.45 did when 100% of their simulations had an annual risk less than 10−4, though Soller et al.45 required either 1 more virus LRV (16/11/11) or 2 more LRVs for Cryptosporidium and Giardia (15/13/13). These differences could be due in part to rounding, where Soller et al.45 assessed the percentage of simulations that had Pinf < 10−4, while Gerrity et al.39 calculated the required LRVs and then rounded to the nearest whole number, even if that meant rounding down. For LRVs of 15/11/11, Soller et al.45 found that 99.7% of simulations met the probability of infection benchmark of 10−4.
| Study | Type | Virus | Giardia | Crypto | Bacteria | Notes |
|---|---|---|---|---|---|---|
| Barker et al. (2013)38 | DPR | 6.9 | 8 | 7.4 | LRTs for municipal sewage scenario | |
| DPR | 12.1 | 10.4 | 12.3 | LRTs for outbreak conditions | ||
| Gerrity et al. (2023)39 | DPR | 13 | 10 | 10 | Used 97.4th percentile pathogen concentrations and included a 10-fold safety factor for viable but nonculturable enterovirus; described tolerance to off-specification conditions rather than redundancy | |
| DPR | 15 | 11 | 11 | Used maximum pathogen concentrations; described tolerance to off-specification conditions rather than redundancy | ||
| MacNevin and Zornes (2020)44 | DPR | 5 | 5 | Minimum LRTs for any WWTP | ||
| DPR | 9.5 | 10 | Maximum LRTs for any WWTP | |||
| Page et al. (2015)40 | General reuse | 5.8 | 4.8 | 4.8 | 5.3 | LRTs based on stormwater |
| Page et al. (2015, 2016)42,43 | IPR | 5.5 | 4.9 | 4.9 | 5.5 | LRTs based on stormwater |
| Pecson et al. (2023)19 | DPR | 17 | 14 | 14 | Included 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log redundancy to protect against failures log redundancy to protect against failures |
|
| Seis et al. (2020)41 | IPR | <12 | Compared different modeling approaches for concentration data: separate point estimate | |||
| IPR | >16 | Compared different modeling approaches for concentration data: separate modeling | ||||
| Soller et al. (2018)45 | DPR | 14 | 12 | 12 | 95% of simulations have cumulative annual risks less than 10−4 | |
| DPR | 15 | 13 | 13 | 100% of simulations have cumulative annual risks less than 10−4 | ||
| DPR | 16 | 11 | 11 | 100% of simulations have cumulative annual risks less than 10−4 | ||
| California Regulations17,46 | DPR | 20 | 14 | 15 | Included 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log redundancy to account for a 6 log redundancy to account for a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log undetected failure and used updated maximum point estimates log undetected failure and used updated maximum point estimates |
|
| IPR | 12 | 10 | 10 | Used maximum point estimates | ||
| Colorado Regulations49 | DPR | 12 | 10 | 10 | Could be as low as 8/6/5.5 (virus/Giardia/Crypto) if justified by pathogen monitoring | |
| Nevada Regulations48 | IPR | 12 | 10 | 10 | ||
| Texas Regulations85 | DPR | 8 | 6 | 5.5 | Minimum LRTs, with actual LRTs potentially higher based on monitoring data; LRV calculation begins after WWTP | |
| Florida Regulations34 | IPR | 14 | 12 | 12 |
Gerrity et al.39 summarized the regulations for IPR and DPR in the United States, in addition to performing bottom-up and top-down DPR QMRAs. For IPR, California requires LRVs of 12/10/10 for viruses, Giardia, and Cryptosporidium, respectively, although additional stipulations are required for surface water augmentation vs. groundwater replenishment. Colorado also implemented the 12/10/10 framework but for DPR,49 and in Texas, where the LRV calculation begins in the treated wastewater effluent, minimum LRTs of 8/6/5.5 are required for DPR.39,46,85 LRTs for DPR in Texas may be higher if warranted by the pathogen monitoring campaign required for each case-by-case DPR permit. For DPR, California targeted a 2.7 × 10−7 daily risk of infection benchmark, rather than an annual risk of 10−4. While this does not impact point estimate QMRAs, it does impact the results for more complicated, Monte Carlo QMRAs by eliminating the aforementioned averaging effect in the annual risk calculation. California found baseline LRVs of 16/10/11 to be adequately protective of public health, and this determination assumed prior point estimate concentrations for Giardia and Cryptosporidium, a peak norovirus concentration reported in the literature,63 and a daily ingestion volume of 2 L spread equally over 96 ingestion events per day.39 However, California set its final LRTs at 20/14/15 to account for a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log treatment failure necessitating a 4
log treatment failure necessitating a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log treatment redundancy.17
log treatment redundancy.17
Regulations are often developed using point estimates based on maximum concentrations, assumed GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios of 1 when using molecular data (e.g., norovirus), and in conjunction with conservative dose–response models. Care should be taken when using maxima, as these peak concentrations are often not comparable across studies. An alternative approach involves using percentiles based on Blom's equation,82 for example, from which 95th or 97.4th percentile concentrations can be determined from individual studies (e.g., a site-specific sampling campaign) or across multiple studies.69 Choosing a single measured point also makes the final risk estimates more susceptible to potentially non-representative site-specific conditions,86 or even error from laboratory analysis. An expert panel from the National Water Research Institute found that California's DPR regulations resulted in inherent conservatism of 9–11
IU ratios of 1 when using molecular data (e.g., norovirus), and in conjunction with conservative dose–response models. Care should be taken when using maxima, as these peak concentrations are often not comparable across studies. An alternative approach involves using percentiles based on Blom's equation,82 for example, from which 95th or 97.4th percentile concentrations can be determined from individual studies (e.g., a site-specific sampling campaign) or across multiple studies.69 Choosing a single measured point also makes the final risk estimates more susceptible to potentially non-representative site-specific conditions,86 or even error from laboratory analysis. An expert panel from the National Water Research Institute found that California's DPR regulations resulted in inherent conservatism of 9–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) logs, which could result in overdesigned and unsustainable potable water reuse systems.39,80 In other words, overly conservative LRTs can increase capital and operations and maintenance costs, while potentially yielding no appreciable improvement in public health protection. These scenarios–and their long-term implications–can be mitigated when using either distributions or percentile point estimates in a QMRA, rather than maximum values.
logs, which could result in overdesigned and unsustainable potable water reuse systems.39,80 In other words, overly conservative LRTs can increase capital and operations and maintenance costs, while potentially yielding no appreciable improvement in public health protection. These scenarios–and their long-term implications–can be mitigated when using either distributions or percentile point estimates in a QMRA, rather than maximum values.
3.13 Other considerations
The results of QMRAs can be community-specific because different communities also have different reuse needs. For example, the QMRA by Church et al.50 focused on reusing dishwashing water and proposed a risk benchmark that was specific to their military scenario. Kimbell et al.34 performed a QMRA for water reuse at Zoo Miami, comparing different treatment trains. Although their exposure assessment was for humans ingesting 2.5 L d−1, the recycled water will be used in the animal exhibits and is not intended for human consumption. They discussed how an interspecies QMRA would need to be done to evaluate the impact of recycled water on the most vulnerable species, which vary in size, habitat, physiology, water consumption, and metabolic rates.Barker et al.38 studied reuse in a small, remote community in Antarctica and compared municipal sewage pathogen loads with estimated loads during a gastroenteritis outbreak. They found that higher LRVs were needed in small communities to meet the benchmark of 10−6 DALYs due to the greater degree of contact between community members in a small population. If regulations are created from the pathogen levels in larger communities and applied to smaller communities with high contact, they might not be protective; conversely, LRTs developed for small communities may be overly stringent for large communities. Therefore, it is important to consider the local context before guidelines from one location are applied to another, highlighting the benefits of allowing tailored LRTs for different communities.
Commonly used risk benchmarks include 10−4 annual probability of infection pppy, as well as 10−6 annual DALYs pppy. However, it is possible to meet one of these benchmarks and not the other, depending on the severity of the disease. Lim et al.27 found that risk from Cryptosporidium and norovirus were both mostly within the acceptable range of the WHO benchmark of 10−6 DALYs but consistently exceeded the 10−4 risk of infection benchmark. This highlights the need to determine what benchmarks are most relevant in a given context to protect public health without being unnecessarily stringent.
The focus of this review is the risk from microbial hazards, but depending on the level of treatment, there are also chemicals that could accumulate in potable reuse systems that could be harmful to public health, including heavy metals, disinfection byproducts, pharmaceuticals, and per- and polyfluoroalkyl substances (PFAS).87,88 Keller et al.89 conducted a review on technological, economic, and environmental considerations of DPR and included a partial list of chemicals of concern after advanced treatment. There could also be problems with public acceptance of potable reuse due to the so-called ‘yuck factor’.90
Remy et al.30 performed a life cycle assessment and a chemical risk assessment alongside their QMRA, which is important for understanding the cumulative health impact of recycled water. They found that while the proposed treatment would meet the 10−6 DALYs pppy target for pathogens, there would be an increase in constituents of emerging concern (CECs) in the IPR reservoir. Germany has health-based precautionary values for iopromide, iomeprol, gabapentin, and EDTA that Remy et al.30 found could be exceeded in the reservoir. The concentrations of glyphosate and AMPA, a degradation product, would exceed the EU guidelines for pesticides (1 μg L−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91), if they were applied to these chemicals.30 Though this may be comparable to current wastewater treatment plants discharging to rivers without tertiary treatment, it highlights the importance of considering both chemical and microbial hazards. Their life cycle assessment found that IPR is competitive in terms of energy consumption and emissions with water importation and seasonal storage and is superior to seawater desalination. Kobayashi et al.35 also performed a life cycle assessment, and highlighted how the local and global impacts of IPR differ. Reducing the local impact from pathogens resulted in a higher global ‘cost’ due to emissions leading to climate change. Page et al.36 included other hazards to humans and the environment in their assessment, including nutrients and chemicals. They found that while the risks from organic chemicals were low, elevated iron levels exceeded potable water guidelines, if post recovery aeration was not employed. Dow et al.92 found that while DPR could significantly reduce energy costs due to reduced pumping requirements from Lake Mead into the Las Vegas Valley, the net present value of DPR ranged from $1.0–4.0 billion, compared to $0.6 billion for the status quo IPR approach. The pairing of a life cycle assessment and chemical risk assessments to potable reuse QMRA would be a beneficial addition to future QMRAs.
91), if they were applied to these chemicals.30 Though this may be comparable to current wastewater treatment plants discharging to rivers without tertiary treatment, it highlights the importance of considering both chemical and microbial hazards. Their life cycle assessment found that IPR is competitive in terms of energy consumption and emissions with water importation and seasonal storage and is superior to seawater desalination. Kobayashi et al.35 also performed a life cycle assessment, and highlighted how the local and global impacts of IPR differ. Reducing the local impact from pathogens resulted in a higher global ‘cost’ due to emissions leading to climate change. Page et al.36 included other hazards to humans and the environment in their assessment, including nutrients and chemicals. They found that while the risks from organic chemicals were low, elevated iron levels exceeded potable water guidelines, if post recovery aeration was not employed. Dow et al.92 found that while DPR could significantly reduce energy costs due to reduced pumping requirements from Lake Mead into the Las Vegas Valley, the net present value of DPR ranged from $1.0–4.0 billion, compared to $0.6 billion for the status quo IPR approach. The pairing of a life cycle assessment and chemical risk assessments to potable reuse QMRA would be a beneficial addition to future QMRAs.
4. Conclusions
This review included 30 publications that performed QMRA for potable reuse, encompassing case studies from Australia, France, Germany, Spain, the U.S., and Antarctica. The studies demonstrated that there are many factors that impact the risks estimated by potable reuse QMRAs, including the assumed ratio of gene copies to infectious units, the assumed volume and frequency of water ingestion, whether the simulation was dynamic or static, and if Bayesian modeling was used. Some decisions are often made for simplicity's sake (such as creating static, non-Bayesian models or assuming one ingestion event per day), but it is important for researchers to understand the basis and implications of these assumptions. Each QMRA is unique and will have different results because each audience/community has its own distinct context and needs. However, QMRAs should consider the impacts that critical assumptions such as ingestion frequency, pathogen concentrations, unit treatment processes, and treatment failures have on risk. The risk benchmarks (probability of infection or DALYs) are also location dependent and should be taken into consideration. This will allow the results to be better understood and contextualized.As regulations are established and potable reuse becomes more widespread, it is crucial to protect human health without imposing excessively stringent requirements that are prohibitively expensive and do not necessarily enhance public health protection. One possible path forward is for regulations to become more flexible, such as was done in Colorado, where LRTs could be reduced if regular sampling provided sufficient evidence that human health would still be protected. By incorporating QMRA for potable reuse, LRTs could be developed for specific contexts, ensuring that health risks are accurately assessed and managed. Continuous monitoring and adaptive management strategies could be implemented to ensure ongoing compliance and safety, providing a dynamic response to emerging data and technological advancements. Due to the rise in wastewater surveillance for public health purposes, more robust and extensive pathogen datasets are expected to be published. Pathogen concentration variability and driving factors will be better characterized, which could reduce potentially unnecessary redundancies which have been built into QMRAs due to uncertainty. Implementing flexible regulations could promote the sustainable and safe expansion of potable reuse systems. Finally, recent publications demonstrate the value and importance of simultaneously evaluating microbial and chemical risks in the context of sustainability and life cycle assessment.
Abbreviations
| DALY | Disability adjusted life year |
| NoV | Norovirus |
| AdV | Adenovirus |
| EnV | Enterovirus |
| Crypto | Cryptosporidium |
| Campy | Campylobacter |
| QMRA | Quantitative microbial risk assessment |
| DPR | Direct potable reuse |
| PCR | Polymerase chain reaction |
| RWC | Recycled water contribution |
| DFR | De facto reuse |
| IPR | Indirect potable reuse |
| SW | Surface water |
| GW | Groundwater |
| LRT | Log reduction target |
| Pinf | Probability of infection |
| LRV | Log reduction value |
| FAT | Full advanced treatment |
| DWTP | Drinking water treatment plant |
| CF | Cartridge filter |
| UV | Ultraviolet |
| MF | Microfiltration |
| UF | Ultrafiltration |
| NF | Nanofiltration |
| ESB | Engineered storage buffer |
| DW | Drinking water |
| pppy | Per person per year |
| TT | Treatment train |
| CBAT | Carbon-based advanced treatment |
| BNR | Biological nutrient removal |
| RO | Reverse osmosis |
| AOP | Advanced oxidation process |
| BAF | Biologically active filtration |
| WWTP | Wastewater treatment plant |
| WW | Wastewater |
| Cl2 | Chlorination |
| GC | Gene copies |
| IU | Infectious units |
| RBAT | Reverse-osmosis-based advanced treatment |
| MBR | Membrane bioreactor |
Data availability
No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.Author contributions
Emily Clements—conceptualization, data curation, formal analysis, methodology, validation, visualization, writing – original draft, writing – reviewing and editing; Charlotte van der Nagel—data curation, formal analysis, writing – reviewing and editing; Katherine Crank—validation, visualization, writing – original draft, writing – reviewing and editing; Deena Hannoun—funding acquisition, supervision, writing – reviewing and editing, Daniel Gerrity—supervision, validation, writing – reviewing and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project was funded in part by the WaterSMART Applied Sciences Program through the United States Bureau of Reclamation (Grant No. R22AP00236). This publication has not been formally reviewed by USBR, so the views expressed here are solely those of the authors.References
- G. Amaris, R. Dawson, J. Gironás, S. Hess and J. de D. Ortúzar, Understanding the preferences for different types of urban greywater uses and the impact of qualitative attributes, Water Res., 2020, 184, 116007 CrossRef CAS PubMed.
- D. Gerrity, B. Pecson, R. S. Trussell and R. R. Trussell, Potable reuse treatment trains throughout the world, J. Water Supply: Res. Technol.--AQUA, 2013, 62, 321–338 CrossRef CAS.
- J. Rice and P. Westerhoff, Spatial and Temporal Variation in De Facto Wastewater Reuse in Drinking Water Systems across the U.S.A., Environ. Sci. Technol., 2015, 49, 982–989 CrossRef CAS PubMed.
- C. N. Haas, J. B. Rose and C. P. Gerba, Quantitative Microbial Risk Assessment, John Wiley & Sons, 2014 Search PubMed.
- A. M. Lammerding and A. Fazil, Hazard identification and exposure assessment for microbial food safety risk assessment, Int. J. Food Microbiol., 2000, 58, 147–157 CrossRef CAS PubMed.
- Y.-J. An, C. G. Yoon, K.-W. Jung and J.-H. Ham, Estimating the microbial risk of E. coli in reclaimed wastewater irrigation on paddy field, Environ. Monit. Assess., 2007, 129, 53–60 CrossRef PubMed.
- M. Benami, O. Gillor and A. Gross, Potential microbial hazards from graywater reuse and associated matrices: A review, Water Res., 2016, 106, 183–195 CrossRef CAS PubMed.
- S. R. Petterson, N. J. Ashbolt and A. Sharma, Microbial risks from wastewater irrigation of salad crops: a screening-level risk assessment, Water Environ. Res., 2001, 73, 667–672 CrossRef CAS PubMed.
- A. Simhon, V. Pileggi, C. A. Flemming, G. Lai and M. Manoharan, Norovirus risk at a golf course irrigated with reclaimed water: Should QMRA doses be adjusted for infectiousness?, Water Res., 2020, 183, 116121 CrossRef CAS PubMed.
- M. L. Partyka and R. F. Bond, Wastewater reuse for irrigation of produce: A review of research, regulations, and risks, Sci. Total Environ., 2022, 828, 154385 CrossRef CAS PubMed.
- L. da Silva Santos, H. H. de Simone Souza, I. D. Amoah, M. E. Magri, C. Nobuyoshi Ide and P. Loureiro Paulo, Treated domestic effluents for non-potable reuse: microbial risk assessment and economic viability, Urban Water J., 2024, 21, 349–363 CrossRef CAS.
- T. Asano, L. Y. C. Leong, M. G. Rigby and R. H. Sakaji, Evaluation of the California Wastewater Reclamation Criteria Using Enteric Virus Monitoring Data, Water Sci. Technol., 1992, 26, 1513–1524 CrossRef.
- H. Tanaka, T. Asano, E. D. Schroeder and G. Tchobanoglous, Estimating the safety of wastewater reclamation and reuse using enteric virus monitoring data, Water Environ. Res., 1998, 70, 39–51 CrossRef CAS.
- S. P. Nappier, J. A. Soller and S. E. Eftim, Potable Water Reuse: What Are the Microbiological Risks?, Curr. Environ. Health Rep., 2018, 5, 283–292 CrossRef PubMed.
- D. F. Metzler, R. L. Culp, H. A. Stoltenberg, R. L. Woodward, G. Walton, S. L. Chang, N. A. Clarke, C. M. Palmer, F. M. Middleton and C. H. Connell, Emergency Use of Reclaimed Water for Potable Supply at Chanute, Kan. [with Discussion], J. - Am. Water Works Assoc., 1958, 50, 1021–1060 CrossRef CAS.
- M. Sinclair, J. O'Toole, A. Forbes, D. Carr and K. Leder, Health status of residents of an urban dual reticulation system, Int. J. Epidemiol., 2010, 39, 1667–1675 CrossRef PubMed.
- Division of Drinking Water, Direct Potable Reuse, California, 2023 Search PubMed.
- World Health Organization, Guidelines for drinking-water quality: fourth edition incorporating the first and second addenda, World Health Organization, 2022 Search PubMed.
- B. Pecson, A. Kaufmann, D. Gerrity, C. N. Haas, E. Seto, N. J. Ashbolt, T. Slifko, E. Darby and A. Olivieri, Science-based pathogen treatment requirements for direct potable reuse, Environ. Sci.: Water Res. Technol., 2023, 9, 3377–3390 RSC.
- E. Amoueyan, S. Ahmad, J. N. S. Eisenberg and D. Gerrity, A dynamic quantitative microbial risk assessment for norovirus in potable reuse systems, Microb. Risk Anal., 2020, 14, 100088 Search PubMed.
- E. Amoueyan, S. Ahmad, J. N. S. Eisenberg and D. Gerrity, Equivalency of indirect and direct potable reuse paradigms based on a quantitative microbial risk assessment framework, Microb. Risk Anal., 2019, 12, 60–75 Search PubMed.
- E. Amoueyan, S. Ahmad, J. N. S. Eisenberg, B. Pecson and D. Gerrity, Quantifying pathogen risks associated with potable reuse: A risk assessment case study for Cryptosporidium, Water Res., 2017, 119, 252–266 CrossRef CAS PubMed.
- E. S. Bailey, L. M. Casanova and M. D. Sobsey, Quantitative microbial risk assessment of North Carolina reclaimed water for potable reuse, AWWA Water Sci., 2020, 2, e1200 CrossRef CAS.
- R. M. Chaudhry, K. A. Hamilton, C. N. Haas and K. L. Nelson, Drivers of Microbial Risk for Direct Potable Reuse and de Facto Reuse Treatment Schemes: The Impacts of Source Water Quality and Blending, Int. J. Environ. Res. Public Health, 2017, 14, 635 CrossRef PubMed.
- D. Gerrity, K. Papp and B. M. Pecson, Pathogen Peak “Averaging” in Potable Reuse Systems: Lessons Learned from Wastewater Surveillance of SARS-CoV-2, ACS ES&T Water, 2022, 2, 1863–1870 Search PubMed.
- C. H. Jones, V. Wylie, H. Ford, J. Fawell, M. Holmer and K. Bell, A robust scenario analysis approach to water recycling quantitative microbial risk assessment, J. Appl. Microbiol., 2023, 134, lxad029 CrossRef PubMed.
- K.-Y. Lim, Y. Wu and S. C. Jiang, Assessment of Cryptosporidium and norovirus risk associated with de facto wastewater reuse in Trinity River, Texas, Microb. Risk Anal., 2017, 5, 15–24 Search PubMed.
- D. Page, P. Dillon, S. Toze and J. P. S. Sidhu, Characterising aquifer treatment for pathogens in managed aquifer recharge, Water Sci. Technol., 2010, 62, 2009–2015 CrossRef CAS PubMed.
- B. M. Pecson, S. C. Triolo, S. Olivieri, E. C. Chen, A. N. Pisarenko, C.-C. Yang, A. Olivieri, C. N. Haas, R. S. Trussell and R. R. Trussell, Reliability of pathogen control in direct potable reuse: Performance evaluation and QMRA of a full-scale 1 MGD advanced treatment train, Water Res., 2017, 122, 258–268 CrossRef CAS PubMed.
- C. Remy, W. Seis, U. Miehe, J. Orsoni and J. Bortoli, Risk management and environmental benefits of a prospective system for indirect potable reuse of municipal wastewater in France, Water Supply, 2019, 19, 1533–1540 CrossRef.
- J. A. Soller, S. E. Eftim and S. P. Nappier, Comparison of Predicted Microbiological Human Health Risks Associated with de Facto, Indirect, and Direct Potable Water Reuse, Environ. Sci. Technol., 2019, 53, 13382–13389 CrossRef PubMed.
- J. A. Soller, S. E. Eftim, I. Warren and S. P. Nappier, Evaluation of microbiological risks associated with direct potable reuse, Microb. Risk Anal., 2017, 5, 3–14 Search PubMed.
- V. Zhiteneva, G. Carvajal, O. Shehata, U. Hübner and J. E. Drewes, Quantitative microbial risk assessment of a non-membrane based indirect potable water reuse system using Bayesian networks, Sci. Total Environ., 2021, 780, 146462 CrossRef CAS PubMed.
- L. K. Kimbell, F. Sabba, G. Hunter and L. Botero, Comparison of treatment trains for indirect potable reuse and use of quantitative microbial risk assessment (QMRA) to evaluate reliability of pathogen removal: Zoo Miami case study, J. Water Process Eng., 2024, 65, 105850 CrossRef.
- Y. Kobayashi, G. M. Peters, N. J. Ashbolt, S. Heimersson, M. Svanström and S. J. Khan, Global and local health burden trade-off through the hybridisation of quantitative microbial risk assessment and life cycle assessment to aid water management, Water Res., 2015, 79, 26–38 CrossRef CAS PubMed.
- D. Page, P. Dillon, J. Vanderzalm, S. Toze, J. Sidhu, K. Barry, K. Levett, S. Kremer and R. Regel, Risk Assessment of Aquifer Storage Transfer and Recovery with Urban Stormwater for Producing Water of a Potable Quality, J. Environ. Qual., 2010, 39, 2029–2039 CrossRef CAS PubMed.
- D. Page, P. Dillon, S. Toze, D. Bixio, B. Genthe, B. E. Jiménez Cisneros and T. Wintgens, Valuing the subsurface pathogen treatment barrier in water recycling via aquifers for drinking supplies, Water Res., 2010, 44, 1841–1852 CrossRef CAS PubMed.
- S. F. Barker, M. Packer, P. J. Scales, S. Gray, I. Snape and A. J. Hamilton, Pathogen reduction requirements for direct potable reuse in Antarctica: evaluating human health risks in small communities, Sci. Total Environ., 2013, 461–462, 723–733 CrossRef CAS PubMed.
- D. Gerrity, K. Crank, E. Steinle-Darling and B. M. Pecson, Establishing pathogen log reduction value targets for direct potable reuse in the United States, AWWA Water Sci., 2023, 5, e1353 CrossRef CAS.
- D. W. Page, K. Barry, D. Gonzalez, A. Keegan and P. Dillon, Reference pathogen numbers in urban stormwater for drinking water risk assessment, J. Water Reuse Desalin., 2015, 6, 30–39 CrossRef.
- W. Seis, P. Rouault and G. Medema, Addressing and reducing parameter uncertainty in quantitative microbial risk assessment by incorporating external information via Bayesian hierarchical modeling, Water Res., 2020, 185, 116202 CrossRef CAS PubMed.
- D. Page, D. Gonzalez, S. Torkzaban, S. Toze, J. Sidhu, K. Miotliński, K. Barry and P. Dillon, Microbiological risks of recycling urban stormwater via aquifers for various uses in Adelaide, Australia, Environ. Earth Sci., 2015, 73, 7733–7737 CrossRef CAS.
- D. Page, D. Gonzalez, J. Sidhu, S. Toze, S. Torkzaban and P. Dillon, Assessment of treatment options of recycling urban stormwater recycling via aquifers to produce drinking water quality, Urban Water J., 2016, 13, 657–662 CrossRef.
- D. MacNevin and G. Zornes, Health risks from protozoa in potable reuse: Implications of Florida's data set, AWWA Water Sci., 2020, 2, e1199 CrossRef CAS.
- J. A. Soller, S. E. Eftim and S. P. Nappier, Direct potable reuse microbial risk assessment methodology: Sensitivity analysis and application to State log credit allocations, Water Res., 2018, 128, 286–292 CrossRef CAS PubMed.
- Division of Drinking Water, Surface Water Augmentation Using Recycled Water, California, 2017 Search PubMed.
- A. W. Olivieri, B. Pecson, J. Crook and R. Hultquist, in Advances in Chemical Pollution, Environmental Management and Protection, ed. P. Verlicchi, Elsevier, 2020, vol. 5, pp. 65–111 Search PubMed.
- O. US EPA, Summary of Nevada's Water Reuse Guideline or Regulation for Potable Water Reuse, https://www.epa.gov/waterreuse/summary-nevadas-water-reuse-guideline-or-regulation-potable-water-reuse, (accessed 20 May 2024).
- Colorado Department of Public Health and Environment, Direct Potable Reuse Policy, 2023 Search PubMed.
- J. Church, M. E. Verbyla, W. H. Lee, A. A. Randall, T. J. Amundsen and D. J. Zastrow, Dishwashing water recycling system and related water quality standards for military use, Sci. Total Environ., 2015, 529, 275–284 CrossRef CAS PubMed.
- World Health Organization, Potable reuse: guidance for producing safe drinking-water, World Health Organization, Geneva, 2017 Search PubMed.
- P. F. M. Teunis, C. L. Moe, P. Liu, S. E. Miller, L. Lindesmith, R. S. Baric, J. Le Pendu and R. L. Calderon, Norwalk virus: How infectious is it?, J. Med. Virol., 2008, 80, 1468–1476 CrossRef PubMed.
- M. J. Messner, P. Berger and S. P. Nappier, Fractional Poisson—A Simple Dose-Response Model for Human Norovirus, Risk Anal., 2014, 34, 1820–1829 CrossRef PubMed.
- N. Van Abel, M. E. Schoen, J. C. Kissel and J. S. Meschke, Comparison of Risk Predicted by Multiple Norovirus Dose-Response Models and Implications for Quantitative Microbial Risk Assessment, Risk Anal., 2017, 37, 245–264 CrossRef PubMed.
- R. L. Atmar, A. R. Opekun, M. A. Gilger, M. K. Estes, S. E. Crawford, F. H. Neill, S. Ramani, H. Hill, J. Ferreira and D. Y. Graham, Determination of the 50% Human Infectious Dose for Norwalk Virus, J. Infect. Dis., 2014, 209, 1016–1022 CrossRef PubMed.
- R. L. Atmar, A. R. Opekun, M. A. Gilger, M. K. Estes, S. E. Crawford, F. H. Neill and D. Y. Graham, Norwalk Virus Shedding after Experimental Human Infection, Emerging Infect. Dis., 2008, 14, 1553–1557 CrossRef PubMed.
- G. McBride, Norovirus dose-response in sewage-related QMRA: The importance of virus aggregation, International Congress on Environmental Modelling and Software.
- J. A. Soller, M. Schoen, J. A. Steele, J. F. Griffith and K. C. Schiff, Incidence of gastrointestinal illness following wet weather recreational exposures: Harmonization of quantitative microbial risk assessment with an epidemiologic investigation of surfers, Water Res., 2017, 121, 280–289 CrossRef CAS PubMed.
- J. Le Pendu, N. Ruvoën-Clouet, E. Kindberg and L. Svensson, Mendelian resistance to human norovirus infections, Semin. Immunol., 2006, 18, 375–386 CrossRef CAS PubMed.
- A. J. Hall, B. A. Lopman, D. C. Payne, M. M. Patel, P. A. Gastañaduy, J. Vinjé and U. D. Parashar, Norovirus Disease in the United States, Emerging Infect. Dis., 2013, 19, 1198–1205 CrossRef PubMed.
- E. Scallan, R. M. Hoekstra, F. J. Angulo, R. V. Tauxe, M.-A. Widdowson, S. L. Roy, J. L. Jones and P. M. Griffin, Foodborne Illness Acquired in the United States—Major Pathogens, Emerging Infect. Dis., 2011, 17, 7–15 CrossRef PubMed.
- C. P. Gerba, W. Q. Betancourt and M. Kitajima, How much reduction of virus is needed for recycled water: A continuous changing need for assessment?, Water Res., 2017, 108, 25–31 CrossRef PubMed.
- S. E. Eftim, T. Hong, J. Soller, A. Boehm, I. Warren, A. Ichida and S. P. Nappier, Occurrence of norovirus in raw sewage – A systematic literature review and meta-analysis, Water Res., 2017, 111, 366–374 CrossRef CAS PubMed.
- C. N. Haas, Quantitative Microbial Risk Assessment and Molecular Biology: Paths to Integration, Environ. Sci. Technol., 2020, 54, 8539–8546 CrossRef CAS PubMed.
- C. P. Gerba and W. Q. Betancourt, Assessing the Occurrence of Waterborne Viruses in Reuse Systems: Analytical Limits and Needs, Pathogens, 2019, 8, 107 CrossRef CAS PubMed.
- K. Crank, K. Papp, C. Barber, P. Wang, A. Bivins and D. Gerrity, Correspondence on “The Environmental Microbiology Minimum Information (EMMI) Guidelines: qPCR and dPCR Quality and Reporting for Environmental Microbiology”, Environ. Sci. Technol., 2023, 57, 20448–20449 CrossRef CAS PubMed.
- L. J. Robertson, L. Hermansen and B. K. Gjerde, Occurrence of Cryptosporidium Oocysts and Giardia Cysts in Sewage in Norway, Appl. Environ. Microbiol., 2006, 72, 5297–5303 CrossRef CAS PubMed.
- V. Zhiteneva, U. Hübner, G. J. Medema and J. E. Drewes, Trends in conducting quantitative microbial risk assessments for water reuse systems: A review, Microb. Risk Anal., 2020, 16, 100132 Search PubMed.
- E. Darby, A. Olivieri, C. Haas, G. D. Giovanni, W. Jakubowski, M. Leddy, K. L. Nelson, C. Rock, T. Slifko and B. M. Pecson, Identifying and aggregating high-quality pathogen data: a new approach for potable reuse regulatory development, Environ. Sci.: Water Res. Technol., 2023, 9, 1646–1653 RSC.
- Division of Drinking Water, Groundwater Replenishment Using Recycled Water, California, 2014 Search PubMed.
- A. B. Boehm, A. I. Silverman, A. Schriewer and K. Goodwin, Systematic review and meta-analysis of decay rates of waterborne mammalian viruses and coliphages in surface waters, Water Res., 2019, 164, 114898 CrossRef CAS PubMed.
- K. Dean and J. Mitchell, Identifying water quality and environmental factors that influence indicator and pathogen decay in natural surface waters, Water Res., 2022, 211, 118051 CrossRef CAS PubMed.
- A. I. Silverman and A. B. Boehm, Systematic Review and Meta-Analysis of the Persistence of Enveloped Viruses in Environmental Waters and Wastewater in the Absence of Disinfectants, Environ. Sci. Technol., 2021, 55, 14480–14493 CrossRef CAS PubMed.
- S. A. Craik, D. Weldon, G. R. Finch, J. R. Bolton and M. Belosevic, Inactivation of cryptosporidium parvum oocysts using medium- and low-pressure ultraviolet radiation, Water Res., 2001, 35, 1387–1398 CrossRef CAS PubMed.
- S. P. Sherchan, S. A. Snyder, C. P. Gerba and I. L. Pepper, Inactivation of MS2 coliphage by UV and hydrogen peroxide: Comparison by cultural and molecular methodologies, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2014, 49, 397–403 CrossRef CAS PubMed.
- D. Gerrity, S. Gamage, J. C. Holady, D. B. Mawhinney, O. Quiñones, R. A. Trenholm and S. A. Snyder, Pilot-scale evaluation of ozone and biological activated carbon for trace organic contaminant mitigation and disinfection, Water Res., 2011, 45, 2155–2165 CrossRef CAS PubMed.
- C. M. Morrison, S. Hogard, R. Pearce, D. Gerrity, U. von Gunten and E. C. Wert, Ozone disinfection of waterborne pathogens and their surrogates: A critical review, Water Res., 2022, 214, 118206 CrossRef CAS PubMed.
- Centers for Disease Control and Prevention, Pinkbook, https://www.cdc.gov/vaccines/pubs/pinkbook/rota.html, (accessed 21 March 2024) Search PubMed.
- W. A. M. Hijnen and G. J. Medema, Elimination of Micro-organisms by Drinking Water Treatment Processes: A Review, IWA Publishing, 2010 Search PubMed.
- National Water Research Institute, DPR Criteria Expert Panel: Preliminary Findings and Recommendations.
- B. M. Pecson, E. C. Chen, S. C. Triolo, A. N. Pisarenko, S. Olivieri, E. Idica, A. Kolakovsky, R. S. Trussell and R. R. Trussell, Mechanical Reliability in Potable Reuse: Evaluation of an Advanced Water Purification Facility, J. AWWA, 2018, 110, E19–E28 Search PubMed.
- G. Blom, Statistical estimates and transformed Beta-variables, John Wiley & Sons, 1958 Search PubMed.
- J. N. S. Eisenberg, E. Y. W. Seto, J. M. Colford, A. Olivieri and R. C. Spear, An Analysis of the Milwaukee Cryptosporidiosis Outbreak Based on a Dynamic Model of the Infection Process, Epidemiology, 1998, 9, 255–263 CrossRef CAS PubMed.
- T. Bayes, LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, F. R. S. communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S, Philos. Trans. R. Soc. London, 1763 DOI:10.1098/rstl.1763.0053.
- Texas Commission on Environmental Quality, Direct Potable Reuse for Public Water Systems, 2022.
- K. Crank, K. Papp, C. Barber, K. Chung, E. Clements, W. Frehner, D. Hannoun, T. Lane, C. Morrison, B. Mull, E. Oh, P. Wang and D. Gerrity, Pathogen and indicator trends in southern Nevada wastewater during and after the COVID-19 pandemic, Environ. Sci.: Water Res. Technol., 2025 10.1039/d4ew00620h.
- C. M. Glover, O. Quiñones and E. R. V. Dickenson, Removal of perfluoroalkyl and polyfluoroalkyl substances in potable reuse systems, Water Res., 2018, 144, 454–461 CrossRef CAS PubMed.
- S. J. Khan, R. Fisher and D. J. Roser, Potable reuse: Which chemicals to be concerned about, Curr. Opin. Environ. Sci. Health., 2019, 7, 76–82 CrossRef.
- A. A. Keller, Y. Su and D. Jassby, Direct Potable Reuse: Are We Ready? A Review of Technological, Economic, and Environmental Considerations, ACS ES&T Eng., 2022, 2, 273–291 Search PubMed.
- J. Rice, A. Wutich, D. D. White and P. Westerhoff, Comparing actual de facto wastewater reuse and its public acceptability: A three city case study, Sustain. Cities Soc., 2016, 27, 467–474 CrossRef.
- European Environment Agency, Pesticides in rivers, lakes and groundwater in Europe, https://www.eea.europa.eu/en/analysis/indicators/pesticides-in-rivers-lakes-and, (accessed 29 May 2024).
- C. Dow, S. Ahmad, K. Stave and D. Gerrity, Evaluating the sustainability of indirect potable reuse and direct potable reuse: a southern Nevada case study, AWWA Water Sci., 2019, 1, e1153 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI includes a table summarizing the 30 studies that conducted quantitative microbial risk assessments for potable reuse. See DOI: https://doi.org/10.1039/d4ew00661e |
| This journal is © The Royal Society of Chemistry 2025 |