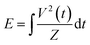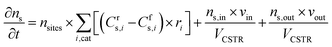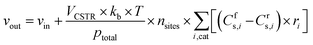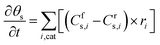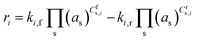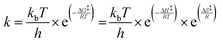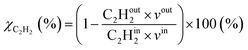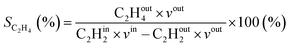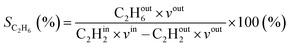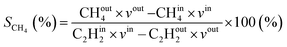Selective catalytic hydrogenation of C₂H₂ from plasma-driven CH₄ coupling without extra heat: mechanistic insights from micro-kinetic modelling and reactor performance

Abstract

We study the selective catalytic hydrogenation of C₂H₂, the main product from non-oxidative CH₄ coupling in gas-phase plasmas, to C₂H₄, a cornerstone of the global chemical industry, by experiments and temperature-dependent micro-kinetic modelling. The model is validated against new experimental data from a nanosecond pulsed plasma reactor integrated with a downstream catalytic bed consisting of Pd/Al₂O₃. We explore the effects of varying Pd loadings (0.1, 0.5, and 1 wt%) on the catalyst activity and the C₂H₄/C₂H₆ product distribution. Consistent with the experimental data, our surface micro-kinetic model shows that while higher Pd loadings lower the catalyst activation temperature for C₂H₂ conversion, they also induce over-hydrogenation to C₂H₆ at lower temperatures and increase oligomerisation in the experiments, which are detrimental to the C₂H₄ yield. The model also elucidates reaction mechanisms and pathways across different temperature regimes, expanding our understanding of the hydrogenation process beyond the experimental range. Besides highlighting the importance of optimising the metal loading to balance C₂H₄ and C₂H₆ selectivity, our findings demonstrate the effective implementation of post-plasma catalysis using a simple catalyst bed heated by hot gas from the plasma region. This study opens possibilities for testing different plasma sources, catalysts, gas flow magnitude and patterns, and catalyst bed-to-plasma distances.

---

Broader context

The direct conversion of methane (CH₄) to ethylene (C₂H₄) is thermodynamically challenging yet critical, given the demand for sustainable methods to synthesise valuable base chemicals, such as ethylene – a core molecule in global industry. The integration of plasma reactors with catalysis offers a promising solution, as it provides an efficient tool for CH₄ coupling into C₂H₂, followed by a pathway to selectively steer the reaction towards C₂H₄. In this study, we demonstrate this synergy by catalytically hydrogenating the C₂H₂ plasma-product into C₂H₄ using Pd catalysts activated by the hot gas stream exiting the plasma reactor, without external heating. Alongside, we developed a temperature-dependent micro-kinetic surface model, providing insights into optimising C₂H₄ selectivity and avoiding C₂H₆ and oligomerisation by-products by balancing catalyst metal loading and reaction temperature. Our results broaden the understanding of coupling plasma to downstream catalysis and open new avenues for developing electrified, scalable and energy-efficient processes for ethylene synthesis and methane valorisation. These findings highlight the potential of plasma and post-plasma catalysis to play a central role in fostering a CO₂-neutral chemical industry and promoting a more sustainable future, as well as providing a framework for further research into energy and environmental (plasma) catalysis.

1. Introduction

The emergence of plasma technologies for converting predominantly inert gases (such as CO₂ and CH₄) marks an important development within the efforts to shift the chemical synthesis of highly valuable light molecules, like C₂H₄ and CH₃OH, from naphtha cracking to electrified processes with a neutral CO₂ loop.^1,2 The transition from traditional routes to plasma-based synthesis has positive techno-economic and environmental impacts, offering a promising solution to alleviate reliance on fossil fuels and greenhouse gas emissions.^1,3–6 Plasma reactors are very flexible in terms of scale and targeted feedstock/products. They are also characterised by ideal coupling to (sometimes intermittent) renewable energy sources such as solar, wind, and hydroelectric power, which become increasingly widespread and cost-effective.^7,8

While plasma-based gas conversion for chemical synthesis has continuously had tangible outcomes in recent years,^9–13 the low product selectivity and purity is one aspect that has challenged plasma technologies in finding large-scale industrial applications. Low selectivity, often regarded as an inherent feature of applying plasma to gas conversion, is generally ascribed to the large temperature gradients observed in plasma reactors and high reactivity of plasmas.¹⁴ The latter results in a wide variety of reactive species (at various distinct energies), which can generate many products. For instance, in pure CH₄ plasmas, the reported products can range from C_(s) to fully saturated C_3,4 olefins, alongside H₂.^15,16 Distinctly, in CH₄ conversion, the product distribution can be promptly correlated to the bulk gas temperature in the reactor, which is in turn determined by the energy density of the plasma source.¹⁶

On the CH₄ pyrolysis front for C_(s) and H₂ production, Fulcheri et al.¹⁷ have been leading tireless plasma research since the 1990s and in their recent work with an arc plasma (T_gas above 2000 °C), they successfully addressed this selectivity problem, attaining >90% conversion and >95% solid carbon selectivity.⁹ The developed process seems robust and has already found industrial implementation with Monolith Materials using a 1 MW pilot plasma plant to co-produce 14 000 tons of carbon black and 4600 tons of hydrogen from CH₄ pyrolysis per year.

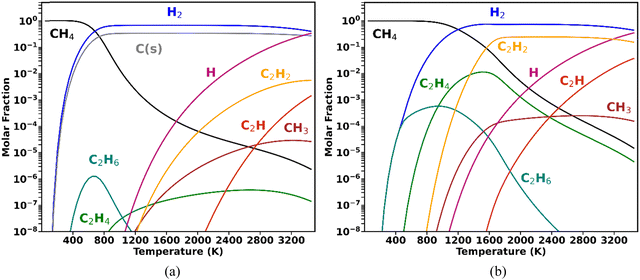
A higher degree of process control is required when CH₄ valorisation is pursued by carbon coupling, such as non-oxidative CH₄ coupling (NOMC), instead of cracking. Selective plasma-based synthesis of C₂H₄ (the most versatile light hydrocarbon, with the highest market value) at high CH₄ conversions has not yet been accomplished. To date, the highest C₂H₄ selectivity from CH₄ coupling in plasma reactors (∼50%) was reported by Delikonstantis et al.,¹⁸ with the utilisation of nanosecond pulsed discharges in a co-axial reactor with an equimolar feed of CH₄ and H₂. However, this level of C₂H₄ selectivity was only achieved at 5 bar, with C₂H₂ remaining the dominant product at lower pressures, as later confirmed by kinetic modelling.¹⁹ In fact, the attainment of high C₂H₄ selectivity at atmospheric pressure is impeded by the thermodynamic equilibrium of gas-phase CH₄ shown in the diagrams in Fig. 1.

Fig. 1 Gas-phase equilibrium composition at 1 bar, initiated with 1 mole of CH₄, under two assumptions: (a) solid carbon is formed in equilibrium with the gas phase, or (b) there is no formation of a solid phase.

The equilibrium compositions clearly demonstrate that when CH₄ is converted under conditions favourable to solid carbon formation (Fig. 1a), the thermodynamically favoured products are C_(s) and H₂ (as in the work by Fulcheri et al.⁹), followed by C₂H₂, with negligible C₂H₄ production. On the other hand, plasma-driven CH₄ pyrolysis can be performed under conditions seeking to inhibit carbon nucleation,²⁰ which is illustrated for the ideal case in Fig. 1b (albeit some C_(s) formation is inevitable in reality). In this case, the dominant products are C₂H₂ and H₂, and although formed in appreciable concentrations, C₂H₄ can never become the major product and its occurrence has a very narrow temperature range.^18,19

These thermodynamic trends allow for the interpretation of common experimental findings in CH₄ plasmas. When a plasma operates under thermal or quasi-thermal conditions, as is the case for DC arc (employed by Monolith), gliding arcs and microwave plasmas, typically the main products observed are H₂, C_(s) and C₂H₂, with relative concentrations that depend on specific reactor configurations. Some examples can be found in ref. 9 and 21–24. Conversely, when a non-thermal plasma (such as a dielectric barrier discharge (DBD) or pulsed corona) is employed, the primary products are C₂H₆ (with some C₂H₄ generation) – mostly with low energy absorption by the gas phase, leading to poor performance in terms of CH₄ conversion and energy efficiencies.^25,26

Undoubtedly, this analysis reveals the essential role of catalytic C₂H₂ hydrogenation in plasma-based CH₄ coupling for selective C₂H₄ synthesis with high conversion and competitive energy efficiency. The coupling of a nanosecond pulsed CH₄/H₂ plasma (with up to 40% C₂H₂ yield at an energy cost of 870 kJ mol⁻¹)^27,28 to post-plasma hydrogenation catalysis using a palladium-coated electrode structure has been performed by Cameli et al.,²⁹ demonstrating a 60% overall C₂H₄ selectivity without external heat or further H₂ addition. The success of this endeavour has highlighted the potential of plasma-catalyst synergy for single-pass NOMC into C₂H₄ in a modular fashion. Further optimisation of the structured catalyst, by employing a bimetallic Pd–Ag material, has increased the C₂H₄ selectivity to 76% C₂H₄, intensifying the process performance by lowering the downstream separation cost.³⁰ Meanwhile, this approach shows great flexibility owing to the independent tuning of the plasma discharge and structured catalyst, which elicits research into different catalyst designs and compositions and alternative (perhaps simpler) catalytic setups, widening the scope of plasma-catalyst utilisation.

In this broader context, we have developed a temperature-dependent surface micro-kinetic model to investigate the selective hydrogenation of C₂H₂, synthesised from NOMC in a plate-to-plate nanosecond pulsed plasma reactor, using a downstream catalyst bed. The latter was packed with three different Pd/Al₂O₃ catalysts, with Pd loadings of 0.1, 0.5 and 1 wt%, which were activated by the heat created in the plasma. The combined (kinetic) modelling and experimental approach aims to explore the mechanisms of post-plasma C₂H₂ hydrogenation in the presence of unreacted CH₄ considering the real thermal conditions in the catalyst bed downstream from the plasma zone. Building upon the current state-of-the-art,^29,30 our objective is to extend the applicability of Cameli's post-plasma catalytic work by demonstrating how a classic catalyst bed can be utilised to harness plasma-generated heat and drive selective C₂H₂ hydrogenation. This strategy may open opportunities for the use of other metal catalysts in this process. Moreover, the new temperature-dependent surface micro-kinetic model aids in interpreting the reactivity results, providing insights into the adsorption/desorption mechanisms and reaction pathways that underlie the observed selectivity trends.

2. Experimental and computational methodology

2.1. Experimental setup

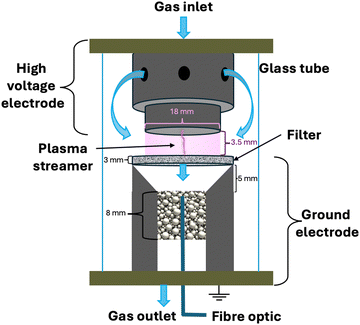
The reactor configuration has been described in detail in our previous work.²⁹ A schematic representation of the experimental setup is reported in Fig. 2. The reactant gas consists of 100 sccm of CH₄ and 100 sccm of H₂ feeds (regulated by two Brooks GF40 mass flow controllers) which enter the reactor from the top of the high voltage electrode. Two parallel electrodes promote electrical breakdown of the recirculating gas. The ground electrode is composed of a 3D-printed body which hosts a stainless-steel sintered filter (AmesPore, porosity 5 μm), to prevent solid carbon deposit from entering the catalytic section downstream. Thus, the catalytic step follows the gas-phase plasma activation sequentially. An NPG-18/100k (Megaimpulse Ltd) power supply is used to ignite and sustain the nanosecond-pulsed discharge (NPD) in the plate-to-plate plasma reactor. Modulation and control of the plasma signal are attained via a waveform generator (Agilent 33220A) and an oscilloscope (Wavesurfer 10, Teledyne Lecroy). The same energy pattern is applied in all experiments, with 3000 pulses per second distributed in three bursts with a frequency of 10 kHz. The applied voltage amplitude is set at 50% of the maximum attainable by the power supply. A visual representation of the energy pattern scheme is reported in the ESI† (Fig. S1). The voltage (V) signal is used to calculate the power (P) dissipated in the discharge via a resistive coupler (RC20, Megaimpulse), which allows assessment of the forward and reflected energy (E) by measuring the voltage across the circuit with a fixed impedance (Z), as per the equation below:

Fig. 2 Schematic of the plate-to-plate plasma reactor with a post-plasma catalytic bed for hydrogenation. Experiments carried out with 100 sccm CH₄ and 100 sccm H₂, with three bursts at 10 kHz, 3000 p s⁻¹, 50% voltage amplitude. The catalytic bed is composed of 200 mg Pd/Al₂O₃ and 800 mg Al₂O₃.

2.2. Catalyst preparation and characterisation

The catalysts used in the post-plasma region were produced via incipient wetness impregnation: a solution of Pd(NO₃)₂ (Alpha Aesar) was used as the catalyst precursor and added to α-Al₂O₃ powder (Alpha Aesar, 99.95% purity, particle size: 0.25–0.45 μm, pores volume: 0.35 mL g⁻¹). Different dilutions of the original solution containing 10 wt% Pd were prepared to attain three metal loadings of 0.1, 0.5, and 1 wt% Pd/Al₂O₃. Overnight drying at 120 °C and calcination at 600 °C for 6 h followed the impregnation step. Metal dispersion was assessed via pulsed H₂ chemisorption (Autochem II 2920, Micromeritics) of the different catalysts. The metal load is determined via ICP-AES (iCAP 6500, Thermo Scientific) as per the ISO 11885 methodology.

2.3. Downstream catalytic C₂H₂ hydrogenation

The post-plasma catalytic hydrogenation step is performed by packing 200 mg of catalyst, diluted in 800 mg of Al₂O₃, into the region downstream from the filter which serves as the ground electrode (Fig. 2). Thereby, the catalyst particles interact with the products formed via the recombination of plasma-generated radicals. Operando temperature monitoring was obtained through a FiSens fibre optic inserted in the catalyst bed. This fibre optic probe can measure multiple temperature points at 5 mm intervals along its axis. However, the length of the catalytic bed (8 mm) was only sufficient for two temperature measurements. The catalyst bed temperature was not independently regulated, as no external heating was applied during the experiments. Instead, the temperature was determined by two heat sources: the gas stream exiting the plasma region (i.e., identical heating in all experiments, given the uniform energy profile applied in the plasma), and the exothermic hydrogenation reactions occurring at the catalyst surface. Since the contribution of hydrogenation reactions to heating varies with catalyst loading, different bed temperatures were observed across the experimental conditions. The outlet stream from the system is analysed via on-line gas chromatography (3000 MicroGC, Inficon), whereby a molesieve column (10 m) with backflush (3 m, Plot U) elutes H₂, N₂, and CH₄, whilst a Plot U column (10 m) with backflush (1 m, Plot Q) elutes C₂ and C₃ species. Internal standard N₂ is fed directly to the GC column, to calculate the total gas volume at the outlet of the reactor, owing to the changing number of moles in the plasma coupling and post-plasma catalytic hydrogenation reactions, as outlined below. This ensures that gas expansion/contraction is properly considered for accurate appraisal of conversion and selectivity.³¹

2CH₄ → C₂H₂ + 3H₂

C₂H₂ + H₂ → C₂H₄ + M

C₂H₄ + H₂ → C₂H₆ + M

The composition of the gas stream entering the catalyst bed was assessed via GC measurements from experiments carried out in the absence of catalyst. In this case, the equations used to evaluate the CH₄ conversion and C₂ product selectivity can be found in ref. 29, where we focus on these plasma-alone experiments. The GC data was used to calculate the concentrations of unreacted CH₄, and formed C₂H_y products, which in turn were taken as a reference to isolate the contributions of plasma and catalysis in the overall conversion and selectivity from the coupled plasma-catalytic process. In this study, the more relevant metrics of C₂H₂ conversion and C₂H₄/C₂H₆ selectivity were calculated using the equations shown in Section 2.4(d) below, both for the experiments (via GC analysis of the outlet gas treated by plasma and catalysis) and the model (using calculated densities). The experimental plasma-alone concentrations were also used as input in the micro-kinetic model (initial partial pressures), as explained below.

2.4. Surface kinetic model

(a) Gas composition, species and reactions included in the model. The initial gas composition used in the model was identical to that measured at the outlet of the plasma reactor. The partial pressures of the gas were calculated and inserted in the model as follows: H₂ = 0.528; CH₄ = 0.300; C₂H₂ = 0.160; C₂H₄ = 0.010 and C₂H₆ = 0.002 (the reference pressure is 1 bar).

The species and reactions considered in the surface kinetic model are outlined in Table 1.

Table 1 Species included in the model (the asterisk, *, denotes an empty surface site, while adsorbed species are followed by *), reaction network with an indication of the initial, transition and final states and respective activation and reaction energies in eV

Gas-phase species		Surface species
H2(g) CH4(g) C2H2(g)		H* C2H2* C2H3* C2H4*
C2H4(g) C2H6(g)		C2H5* CH3* CH2* CH* C*
Reaction	Initial state ⇌ transition state ⇌ final state	Activation energy (eV)	Reaction energy (eV)
r1	H2(g) + 2 * ⇌ *–H–H–* + * ⇌ H* + H*	0.28	−0.83
r2	C2H2(g) + * ⇌ C2H2–* ⇌ C2H2*	0.00	−1.67
r3	C2H4(g) + * ⇌ C2H4–* ⇌ C2H4*	0.00	−0.76
r4	C2H6(g) + 2 * ⇌ *–C2H5–H–* ⇌ C2H5* + H*	1.18	0.18
r5	C2H6(g) + 2 * ⇌ *–CH3–CH3–* ⇌ CH3* + CH3*	2.89	0.60
r6	CH4(g) + 2 * ⇌ *–CH3–H–* ⇌ CH3* + H*	1.29	0.31
r7	C2H2* + H* ⇌ *C2H2–H–* ⇌ C2H3* + *	0.95	0.05
r8	C2H3* + H* ⇌ *C2H3–H–* ⇌ C2H4* + *	0.64	−0.48
r9	C2H4* + H* ⇌ *C2H4–H–* ⇌ C2H5* + *	0.85	0.11
r10	C2H5* + * ⇌ *CH3–CH2–* ⇌ CH3* + CH2*	2.18	0.74
r11	C2H4* + * ⇌ *CH2–CH2–* ⇌ CH2* + CH2*	1.89	1.17
r12	C2H3* + * ⇌ *CH2–CH–* ⇌ CH2* + CH*	1.47	0.34
r13	C2H2* + * ⇌ *CH–CH–* ⇌ CH* + CH*	1.63	0.04
r14	CH3* + * ⇌ *CH2–H–* ⇌ CH2* + H*	1.13	0.32
r15	CH2* + * ⇌ *CH–H* ⇌ CH* + H*	0.79	−0.35
r16	CH* + * ⇌ *C–H* ⇌ C* + H*	1.42	0.38
r17	H2(g) + C2H4* + * ⇌ *–H–C2H5* ⇌ C2H5* + H*	1.44	−0.72

---

Our model is based on this reaction network and the Pd(111) energetics derived from density functional theory (DFT) calculations performed by Nørskov et al.³² These DFT calculations were carried out using Quantum Espresso, with the exchange–correlation contribution to the electronic energy approximated by the BEEF-vdW functional. We refer to the cited study for additional DFT details. The reaction network consists of adsorption and desorption of the gas-phase molecules – reactions r₁–r₆ (with H₂, C₂H₆ and CH₄ dissociating upon adsorption); hydrogenation and de-hydrogenation – reactions r₇–r₉, r₁₄–r₁₆; and surface dissociation and recombination – reactions r₁₀–r₁₃ and r₁₇. In turn, the model provides quantitative information on catalyst activity and selectivity as a function of temperature. The relevant equations and formulas are presented in the following sections.

(b) Numerical details, governing equations and model solution. The micro-kinetic surface model was constructed using the CSTR (continuously stirred tank reactor) approach, which assumes perfect mixing throughout the simulation, with species densities and coverages being considered uniform within the reactor volume. The changes in the number density of gas-phase species (Table 1) as a function of time were calculated using the following balance equation.
where n_s is the number density of species s and t is the simulation time. The first term on the right side is related to the change in n_s due to surface reactions at the catalyst, with C^r_s,i and C^f_s,i being the stoichiometric coefficients of species s in reaction i (reverse, r, and forward, f), and r_i being the reaction rate (expressed in s⁻¹). This term must be multiplied by the total volumetric density of surface sites n_sites (in cm⁻³, with calculation details given in Section S2 in the ESI†) to have the rate involving gas species correctly expressed in cm⁻³ s⁻¹. The approach utilised to calculate the rates will be presented later in this section, following the description of the balance equation for surface species. The second and third terms represent the change in number density due to gas molecules entering and exiting the reactor, respectively. In these, n_s,in is the species density at the inlet and n_s,out at the outlet (note that in a CSTR model, n_s,out equals the species density n_s in the reactor), V_CSTR is the gas volume in the reactor, and v_in and v_out are the volumetric flow rate entering and exiting the reactor, respectively.

The volumetric flow rate of the exiting gas (v_out) used in the equation above is calculated as follows, so that the total pressure (p_total, expressed in Pascal here for unit consistency) in the reactor is maintained constant at ambient pressure in all simulations.

In which k_b is the Boltzmann constant and T is the temperature. In practice, this equates the exiting volumetric flow rate to the incoming flow rate plus the change in volume resulting from catalytic reactions.

Similar to the balance equations above for the gas-phase species, the changes in the surface coverage (θ_s) of surface species s (Table 1) as a function of time t are described using the following balance equation, in which C^f_s,i and C^r_s,i are the stoichiometric coefficients of species s in reaction i, with the forward (f) and reverse (r) reactions, and r_i is the reaction rate of the surface reactions (again expressed in s⁻¹).

The reaction rate (r_i) in the above equations depends on the rate coefficient, species activity and reaction stoichiometry, and is defined as follows.
where k_i,f and k_i,r are the forward and reverse reaction rate coefficients, respectively, and a_s is the activity of species s. The latter may be the partial pressure of gas phase species (p_s, divided by p_total to maintain k_i,f and k_i,r in units of s⁻¹) in surface reactions, or the fractional coverage (θ_s) for surface species. Note that number densities and partial pressures are interconvertible via the ideal gas law. The rate coefficients k_i,f and k_i,r are calculated using transition state theory with the following equation.
In this, h is Planck's constant, R is the universal gas constant, and ΔG^‡, ΔH^‡ and ΔS^‡ are the differences in Gibbs free energy, enthalpy and entropy, respectively, between the initial state and the transition state (see Table 1). The inputs for enthalpy and entropy differences and their respective temperature-dependent thermodynamic corrections are discussed in the following section.

The model is solved using an in-house python code which was written for applications in post-plasma and plasma catalysis. A version of this code is quoted in Section S3 in the ESI.† The input data required to run the code include the reaction network (see Table 1), the formation enthalpies and rotational and vibrational wavenumbers of species in the model (see Table S1 in Section S4 of the ESI†), and the gas-phase species parameters for the Shomate equation (taken from the NIST database).

(c) Assumptions and approximations. This study concerns a pure post-plasma catalysis micro-kinetic model with only stable gaseous molecules present in the gas flow, because plasma-derived radicals rapidly recombine and are thus absent in the catalyst bed. The construction of the model is based on a CSTR approach, which assumes that the densities of the gas species and surface coverages are uniformly distributed over the reactor volume.^33,34 The CSTR choice is intended to achieve a manageable computational complexity, whilst solving the model inexpensively for the three Pd loadings across the wide temperature range investigated in this work. The applicability of this CSTR model (over a PFR model, plug flow reactor) is also corroborated by the relatively large Péclet number (Pe) expected for packed bed systems.³⁵ We believe that the PFR approach could improve the accuracy of the model's predictions by accounting for the changing concentrations across the catalyst bed. However, due to the packing of solids in the reactor utilised in the experiments (i.e., non-trivial gas flow patterns and large Pe), both axial and radial gas mixings are significant, ultimately rendering the PFR approach also approximative. In a PFR configuration, the conversion would likely be higher than in our CSTR model because the latter assumes perfect mixing, thus immediately leading to lower concentrations. In turn, this causes positive order reactions to proceed at a lower rate, which yields a lower conversion for the same residence time as a PFR model.

The temperature of the catalyst bed is also assumed to be uniform throughout the reactor and the model assumes thermal equilibrium between the gas phase and catalyst surface. While temperature gradients will exist in the reactor, their assessment would require a higher-dimensional model incorporating heat transfer mechanisms and gas flow dynamics. Such analysis, though valuable, extends beyond the capabilities of our current 0D framework, which focuses on capturing the chemical kinetic behaviour of the system.

No formation of solid products at the catalyst's surfaces (polymers and carbon black) is considered in the model. Whilst very interesting, such modelling endeavour would rely on DFT data which is presently unavailable and would require a higher dimensional model, which is not within the scope of this study. With respect to the surface reactions, the model calculates rate coefficients based on transition state theory, as explained in the above section, whilst employing DFT-derived activation barriers as input in the rate expressions. While this approach yields more accurate rates than those estimated using sticking coefficients or reaction barriers,³³ it is inherently limited by the availability and quality of DFT data. In this study, all activation energies and frequencies (used to calculate entropies and temperature-dependent corrections) were extracted from the work by Nørskov et al.³² who have described the dehydrogenation of C₂H₆ over many close-packed metal surfaces (see Table S1 in Section S4 of the ESI†).

To account for the activity of the Pd(100) and Pd(211) facets (which may be considerable depending on nanoparticle morphology and particle size),^36,37 we performed a sensitivity analysis by applying the adsorption energies for C₂H₂ and C₂H₄ on Pd(100) and Pd(211) in our micro-kinetic model (see Table S2 in the ESI†). These facets were chosen based on their respective lowest and highest reported activities in the literature.³⁶ Due to the lack of comprehensive DFT data for all reaction species on Pd(100) and Pd(211), we retained our original reaction network developed for Pd(111) and substituted the available adsorption energies for C₂H₂ and C₂H₄. The details of this analysis can be found in Section S5 in the ESI.† The results indicate that Pd(100) is by far the least active facet, with no observable C₂H₂ conversion below ∼600 °C (Fig. S2a, ESI†). Conversely, Pd(211) is an overly active surface, fully hydrogenating C₂H₂ to C₂H₆ at temperatures as low as 90 °C (Fig. S2b, ESI†). These trends, albeit inherently qualitative due to the incomplete DFT datasets, do not align with our experimental results (see Fig. 3 and 4 in Section 3). Thus, we conclude that Pd(111) is the most appropriate facet to model C₂H₂ hydrogenation, for the conditions under study in this work.

Fig. 3 Experimental and modelled C₂H₂ conversion as a function of temperature (average temperature measured in the catalyst bed and assumed to be identical for solid and gas phases) for the three Pd/Al₂O₃ catalysts (see the legend). The number of experimental data points (solid markers) is different for each catalyst.

(d) Conversion and selectivity. For both model and experiments, the overall C₂H₂ conversion (χ_C2H2), and C₂H₄ (S_C2H4) and C₂H₆ (S_C2H6) selectivity, can be derived using the following equations.


where in the experiments, C₂H^out₂ represents the volume fraction of C₂H₂ exiting the reactor (measured by GC in the coupled plasma and catalysis experiments) and v^out is the outlet volumetric flow rate. Likewise, C₂Hⁱⁿ₂ represents the inlet C₂H₂ volume fraction (reference value, measured in the absence of catalyst, as explained above) and vⁱⁿ is the inlet volumetric flow rate. In the model, C₂H^out₂ and v^out are the C₂H₂ density and volumetric flow rate at steady state in the outflow, C₂Hⁱⁿ₂ and vⁱⁿ are the initial C₂H₂ density and volumetric flow rate, respectively. For selectivity, C₂H^out₄ and C₂H^out₆ are GC-derived volume fractions of C₂H₄ and C₂H₆ in the outlet stream in the experiments, respectively; while in the model these are the densities of C₂H₄ and C₂H₆ in steady state, respectively (also corresponding to the outflow).

Additionally, the modelled densities are also used to calculate CH₄ (S_CH4) selectivity using the equation below, with CH^out₄ being the CH₄ density in the steady state (outflow) and CHⁱⁿ₄ being the initial CH₄ density.

The volumetric flow rates at the inlet vⁱⁿ and outlet v^out are explicitly included in these equations to account for the effect of pressure changes due to gas expansion/contraction (as explained above) and temperature increase during the reaction.³⁸

3. Results and discussion

3.1. Plasma reactor for CH₄ coupling – experimental and modelled results

The gas-phase chemistry within the NPD reactor has been thoroughly characterised in our previous studies.^19,27,29 A comprehensive reaction mechanism has revealed that at atmospheric pressure, CH₄ coupling predominantly produces C₂H₂ through the stepwise dehydrogenation of C₂H₆, which itself is formed via the recombination of CH₃ radicals.^19,20,26,39 Unsurprisingly, CH₃ species are the most abundant carbon-based radicals generated from CH₄ dissociation via electron-impact reactions. The principal mechanism for the coupling of electron energy to gas-phase heating involves electron-impact vibrational excitation of CH₄ and H₂ molecules followed by rapid vibrational–translational (VT) relaxation reactions.⁴⁰ The gas temperature within this NPD plasma can reach up to 1500 °C in the vicinity of the discharges, which in turn promotes dehydrogenation of C₂H₆ to C₂H₄ (but also to C₂H₅ and C₂H₃ radicals) and ultimately to C₂H₂.¹⁹

As a result, this plasma configuration achieves a C₂H₂ selectivity of approximately 83% under the specified operating conditions (i.e., three bursts at 10 kHz, 3000 pulses s⁻¹). The conversion of CH₄, co-fed with an equimolar amount of H₂, averages around 46%. The selectivity for C₂H₄ and C₂H₆ is about 5% and 1%, respectively. The remaining percentage is attributed to small quantities of unquantified hydrocarbon products (e.g., C₃ and C₄ species) and solid carbon, which amounts to about 3% of the converted CH₄ in weight.

3.2. Post-plasma catalytic hydrogenation of C₂H₂ to C₂H₄

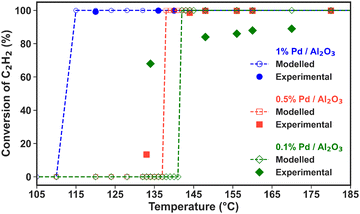
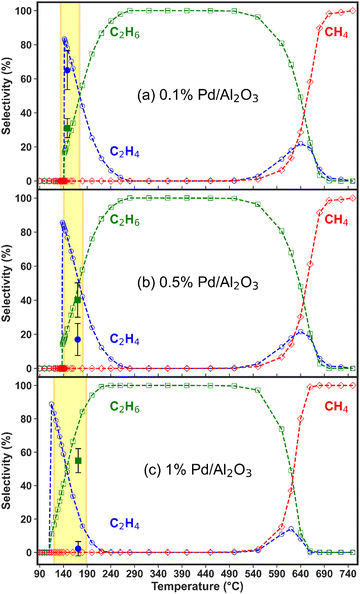
The high C₂H₂ selectivity attained in this NPD reactor enables effective tandem hydrogenation to C₂H₄, which is catalysed by the Pd/Al₂O₃ material placed downstream from the plasma discharge. This strategy allows for the flexible adjustment of the product distribution in a modular fashion, which can be tailored to meet oscillatory market demands. Notably, the catalytic hydrogenation reaction is solely activated by the hot gas flowing from the discharge zone, and it is self-sustained by its exothermic nature (i.e., C₂H₂ + H₂ → C₂H₄, with ΔH⁰ = +175.9 kJ mol⁻¹; and C₂H₂ + 2H₂ → C₂H₆, with ΔH⁰ = +311.5 kJ mol⁻¹). However, the three Pd loadings within the Pd/Al₂O₃ catalyst, along with the dispersion degree of the active metal, promote varying C₂H₂ conversion and C₂H₄/C₂H₆ product distribution trends within different temperature ranges. Consequently, both the reaction temperatures and kinetics may differ with the catalyst used. In the subsequent sections, we discuss the reactivity results for each catalyst within the temperature window measured in the experiments and apply our model to extrapolate the selectivity behaviour at higher and lower temperatures. Whenever possible, we compare the model predictions with our experimental data to reinforce the credibility of these temperature extrapolations.

(a) C₂H₂ conversion. Both experimental and modelled results indicate that the reactivity of the Pd/Al₂O₃ catalysts is influenced by the Pd loading and the dispersion degree of Pd atoms within the material. As seen in Fig. 3, the catalysts with higher Pd loading (and greater metal dispersion) exhibit a lower temperature threshold for activation, i.e., initiation of C₂H₂ hydrogenation. For the 1% Pd catalyst (with a dispersion of 10%), the onset of C₂H₂ conversion occurs between 110 and 120 °C in the experiments. However, this activation temperature range increases to 130–137 °C and 135–144 °C as the Pd loading decreases to 0.5% and 0.1%, with 7% and 33% dispersion, respectively. Note that the dispersion is not determined by the loading, but only related to the preparation method. The lower C₂H₂ conversion onsets observed for the higher Pd loadings can be attributed to the enhanced rates of C₂H₂ and H₂ adsorption due to larger amounts of active sites. In turn, these higher rates give rise to more intense surface heating of the catalysts with higher loading (due to the exothermic nature of C₂H₂ hydrogenation), further accelerating the reaction rates and conversion. These effects are determined by both higher loading and higher metal dispersion, which decrease the activation temperature threshold, explaining the similar activity of the 0.5 and 0.1% loadings.

Fig. 3 also shows that the modelled results align well with the experimental data points in the region where the temperature is exclusively dictated by the plasma discharge and the exothermic heat from the hydrogenation reaction. The lack of control over the experimental temperature does not allow mapping of the catalyst activity across different temperatures in these experiments. However, these results prove that the post-plasma catalytic setup is suitable for C₂H₂ hydrogenation, even at low metal loading, as all catalysts attain C₂H₂ conversion above 90% under the experimental conditions at the steady state. The modelled trends confirm the catalysts’ high activity for C₂H₂ hydrogenation and can give an indication of the behaviour at higher temperatures. The modelled C₂H₂ conversion trends in the 80 to 750 °C temperature range can be found in Fig. S3 in the ESI† (Section S6, ESI†).

Nonetheless, the model underestimates C₂H₂ conversion at lower temperature for the 0.1% Pd/Al₂O₃ and 0.5% Pd/Al₂O₃ catalysts, and it suggests a sharp transition from nil to complete conversion at 137 and 142 °C, whilst experimental data show a more gradual increase. These discrepancies can be ascribed to the temperature input used in the model. The model relies on the gas temperature at the catalyst active sites, while in the experiments, the fibre optic temperature sensor is positioned along the axial axis of the catalytic bed; and it is reasonable to assume that the catalyst surface may be warmer than the surrounding gas due to the exothermic reactions occurring at the active sites. Indeed, it would be very insightful to investigate the heat transfer from the warmer catalyst surface to the gas phase and the temperature gradient in the reactor, as well as the impact of the exothermic chemical reactions, by solving an energy balance equation. However, the current model is unable to capture these effects, as the dynamics of heat transfer and gas flow cannot be accurately considered in this zero-dimensional model. While this is outside the scope of this study, in our future work, we plan the construction and application of a dedicated higher-dimensional computational fluid dynamics and surface kinetics model to explore these aspects as well.

(b) Product selectivity. We have applied the model to calculate the product selectivity from C₂H₂ hydrogenation over a wide range of temperature (up to 750 °C), as depicted in Fig. 4(a)–(c). Within the temperature range registered in the experiments (indicated by the yellow rectangles in Fig. 4), the model predictions agree well with the experimental results (obtained as a single data point for each set of catalytic material) for the 0.1% Pd catalyst (Fig. 4a). This agreement is however less accurate for the other two catalysts. At lower temperatures, the model predicts that C₂H₄ is the main product when the reaction begins, as it is thermodynamically favoured over further hydrogenations to C₂H₆ (a mechanistic analysis is provided in the following section). Over the 0.1% Pd catalyst, the calculated C₂H₄ selectivity peaks at 83% (with 17% C₂H₆ selectivity) at 142 °C, i.e., the onset of the activation temperature, while the experimental values are 65% and 31%, respectively (though with relatively large error bars). Furthermore, the model suggests an inversion in C₂H₄ and C₂H₆ selectivity as the temperature increases, with C₂H₆ becoming dominant due to prompt over-hydrogenation of C₂H₄. However, this could not be validated experimentally because no external catalyst heating was applied in the experiments; hence only one data point is available, corresponding to the temperature reached by plasma heating (and the exothermic hydrogenation reactions).

Fig. 4 Experimental and modelled C₂H₄, C₂H₆ and CH₄ selectivity as a function of temperature (average temperature measured in the catalyst bed and assumed to be identical for solid and gas phases) for the (a) 0.1%, (b) 0.5%, and (c) 1% Pd/Al₂O₃ catalysts. The solid markers correspond to the experimental selectivity measured within the temperature range highlighted by the shaded area (yellow rectangle) on the graph. The dashed lines and hollow markers show the trends predicted by the model.

All catalysts attain near-complete C₂H₂ conversion in the experiments (90% for 0.1% Pd/Al₂O₃ and >99% for 0.5 and 1% Pd/Al₂O₃, see Fig. 3), which is advantageous for downstream separation steps. Thus, under these conditions, the Pd loading is the only independent variable controlling the C₂H₄ selectivity. Notably, the highest C₂H₄ yield (i.e., 12%, at 142 °C) is achieved by 0.1% Pd/Al₂O₃, which favours higher C₂H₄ selectivity despite a slightly lower C₂H₂ conversion.

The C₂H₄ yield is the major metric of successful CH₄ non-oxidative coupling, as it is the most valuable product. Its maximum value is determined by the catalytic C₂H₂ conversion and the corresponding selectivity for C₂H₄, since CH₄ conversion is driven solely by the plasma discharge. While the latter also affects the C₂H₄ yield, it does not vary with the studied Pd loadings, as the amount of C₂H₂ produced in the plasma region remains constant across the different Pd loadings in the post-plasma region. Similarly, the temperature of the gas exiting the plasma zone and entering the catalytic bed is identical in all experiments, as it is purely controlled by the plasma energy (uniform in all experiments). Our reactor configuration, where the catalytic bed is integrated in the post-plasma region without external heating, creates an inherent coupling between reaction temperature and catalyst loading. While the temperature of the gas exiting the plasma zone is constant across all experiments, the bed temperature varies with Pd loading due to the exothermic hydrogenation reactions. Although experiments at lower catalyst loadings could be useful to investigate incomplete conversion regimes, we focus here on conditions achieving full C₂H₂ conversion, which is critical for maximising C₂H₄ yield in industrial applications.

The modelled trend of decreasing C₂H₄ selectivity and increasing C₂H₆ selectivity upon rising temperature is qualitatively consistent for all three catalysts, with the key difference being the temperature at which C₂H₆ becomes the dominant product, see Fig. 4(a)–(c). This shift occurs at lower temperatures with increasing metal loading, indicating higher catalyst activity, and is detrimental for the desired overall C₂H₄ selectivity. Beyond this point, C₂H₆ selectivity becomes 100% due to C₂H₄ over-hydrogenation, until the temperature reaches about 500 °C, where another shift in reactivity occurs, leading to rapidly rising production of CH₄ and a minor region of C₂H₄ formation. The thermodynamic mechanisms driving these observations are discussed in detail in the following section.

However, these higher temperatures exceed the operational range of the catalyst bed, which is limited by the temperature of the gas exiting the discharge region and the exothermic heat of the reaction. The experimental operating window of the catalyst bed (highlighted by the yellow areas in Fig. 4) corresponds to temperatures recorded over the entire hydrogenation experiment and correlate with the gas composition measured at the same acquisition time. The fast reaction kinetics results in a quick temperature rise and onset of steady-state conditions (within 10 min of plasma ignition), which does not allow the GC analysis to capture the transient composition in detail, as shown in Fig. 3. No substantial temperature increase is observed after reaching the steady-state, and all highlighted areas correspond to a relatively narrow temperature range. Given the scale difference between the modelled and experimental temperature ranges, the selectivity data from the experiments would largely overlap. For that reason, we only report one experimental point for the selectivity, as representative of the steady-state conditions.

In the experiments with the 0.1% Pd/Al₂O₃ catalyst, 65% C₂H₄ selectivity was achieved from C₂H₂ hydrogenation, compared to 31% C₂H₆ selectivity, between 140 and 175 °C (Fig. 4a), as also mentioned above. This is consistent with our previous results and other C₂H₂ hydrogenation reports in the literature.^29,41–44 However, this state is reached within 5 min of plasma ignition and changes over longer periods, as the catalyst bed temperature rises to ∼170 °C and oligomerisation products begin to form from C₂H₂ conversion. This is accompanied by a drastic decline in C₂ product detection in the experiments. As previously explained, oligomerisation reactions leading to solid products are not included in the model, which focuses instead on the kinetics of gaseous H₂, C₂H₂, C₂H₄, C₂H₆, and CH₄ (besides the short-lived surface species).

Nonetheless, the formation of oligomerisation by-products is the primary reason for the reduced C₂ selectivity observed experimentally at higher temperatures. On this note, the carbon balance in the system drops from 91% at the start of the hydrogenation processes (at the lower end of the temperature window) to less than 70% after about 50 minutes, when the temperature of the gas-phase is expected to exceed 200 °C. Whilst these solid deposits on the catalyst surface may affect the activity, the time-on-stream data of the product gas composition shows a relatively constant trend over approximately 40 minutes (see Fig. S4 in the ESI†), suggesting that no major catalyst deactivation (via sintering, for instance) occurs.

As observed in Fig. 4(b) and (c), for both higher Pd catalyst loadings, C₂H₆ was detected as the primary product in the experiments, immediately after the reaction began. In fact, practically no C₂H₄ was detected when the 1% Pd/Al₂O₃ catalyst was tested, with C₂H₆ emerging as the sole product at ∼60% selectivity. These results are consistent with model predictions (though only at somewhat higher temperatures for the C₂H₄ selectivity), which suggest that C₂H₄ hydrogenation to C₂H₆ occurs at lower temperatures upon increasing Pd loading. In summary, the temperature range where C₂H₄ is the dominant hydrogenation product shifts to lower temperatures and narrows as the Pd loading is increased. For both catalysts, the experimental and modelled results show close alignment in terms of C₂H₆ selectivity, while the C₂H₄ selectivity is overestimated by the model in the low-temperature regime: below 240 °C for the 0.5% Pd/Al₂O₃ catalyst and below 210 °C for 1% Pd/Al₂O₃.

This discrepancy may be partially related to the difference in temperature considerations – the surface temperature input in the model versus bulk bed temperature measured in experiments, as explained above. However, the most likely factor contributing to selectivity disagreement is the extensive formation of oligomeric carbonaceous deposits (green oil)³⁶ at full C₂H₂ conversion and temperatures above 170 °C, facilitated by the higher Pd loadings. Evidence supporting this mechanism is found in the calculated carbon balance of ∼76% in the experiments with both 0.5% and 1% Pd catalysts, while the hydrogen balance is greater than 91%. This indicates the formation of species with high C/H ratios, typical of oligomerisation compounds, which are not included in our model.

Additionally, an approximative evaluation of the potential impact of carbon deposition in the form of C_(s) was conducted in the model by analysing the CH* + * → C* + H* reaction rate (r₁₆). The results show that the rate of this reaction is relatively negligible across the temperature range investigated in this study (see Fig. S5 in Section S8 of the ESI†). This suggests that deposition of C_(s) particles is very unlikely and cannot cause the observed differences between model predictions and the experimental data in this study. Instead, the analysis indicates that the dominant pathway is the sequential hydrogenation of CH_x surface species (see Section 4), which are converted to CH₄ above 500 °C (rather than dehydrogenated into solid carbon).

Also noteworthy, the formation of Pd carbide during C₂H₂ hydrogenation is closely associated with the deposition of carbonaceous oligomers on the catalyst surface.⁴⁴ While the present model is not able to explicitly account for PdC_x phases, their inclusion could, on the one hand, alter the Pd energetics of the surface reactions, leading to shifts in the model predictions. On the other hand, the model may see accumulation of PdC_x species on the Pd surface, leading to lower C₂H₄ and (especially) C₂H₆ product selectivity and in turn smaller discrepancies between model and experiment. However, a detailed treatment of Pd carbide effects would require dedicated DFT data (which is not available, to the best of our knowledge) and potentially higher-dimensional modelling, beyond the scope of this study, but it represents an important direction for future research. Nevertheless, as discussed, we believe the deposition of high molecular weight oligomerisation solids on the catalyst remains the primary contributor to the disagreement in selectivity.

Finally, the morphology and size of the synthesised particles should be consistent across all tested catalysts (0.1%, 0.5%, and 1% Pd/Al₂O₃), as these were prepared via the same wetness impregnation method. Moreover, identical Al₂O₃ support particles and dilution beads were used in all experiments, further ensuring uniformity. SEM images of the spent catalysts (Fig. S6 in Section S9 of the ESI†) confirm no observable differences in particle size or morphology, indicating that these factors are not the reason for the varying catalytic performances across the three investigated Pd loadings.

Essentially, these results highlight the dual impact of higher Pd loadings: (i) they promote prompt over-hydrogenation to C₂H₆ by lowering the temperature at which sequential surface hydrogenation reactions occur (namely from C₂H₂* to C₂H₃* to C₂H₄* to C₂H₅* and finally C₂H₆; see reactions r₇, r₈, r₉ and reverse of r₄ in Table 1), and (ii) they facilitate oligomerisation reactions at lower temperatures. Therefore, optimisation of the Pd loading in these catalysts is crucial for successful coupling between the plasma and catalysis reactors, as it significantly influences the C₂H₄/C₂H₆ product distribution and the formation of unwanted solid by-products.

(c) Modelled Pd reactivity and reaction pathway analysis. The model was applied to evaluate the forward and reverse rates of the considered reactions as a function of time and temperature, allowing for a mechanistic analysis of the catalyst reactivity. In turn, this provides insights into the reaction pathways that dictate the observed selectivity trends. The results of this analysis are presented in Fig. 5(a)–(d), highlighting the reactivity across the low- and mid-temperature regimes and high-temperature regime, respectively. Additionally, the reaction rates relevant to the following discussions are plotted in Fig. S7–S11 (ESI†) (see Section S10 of the ESI†).

Fig. 5 Reaction pathway diagrams illustrating the reactions between the gaseous reactants (C₂H₂, H₂ and CH₄) and the catalyst surface (a) below 180 °C, (b) between 180 and 480 °C, (c) between 480 and 680 °C and (d) above 680 °C. The resulting adsorbed surface species (marked with *) and their reactions with other surface species are also shown. The eventual desorption of the C₂H₄ (blue), C₂H₆ (green) and CH₄ (red) products (with varying concentrations depending on the temperature) is indicated by the cloud-shaped text boxes. Adsorption reactions are indicated by black arrows, surface hydrogenation reactions by mustard arrows, and surface dissociation reactions by orange arrows. The thickness of the arrows and the size of the blocks are qualitatively representative of the reaction rates and species surface coverage, respectively.

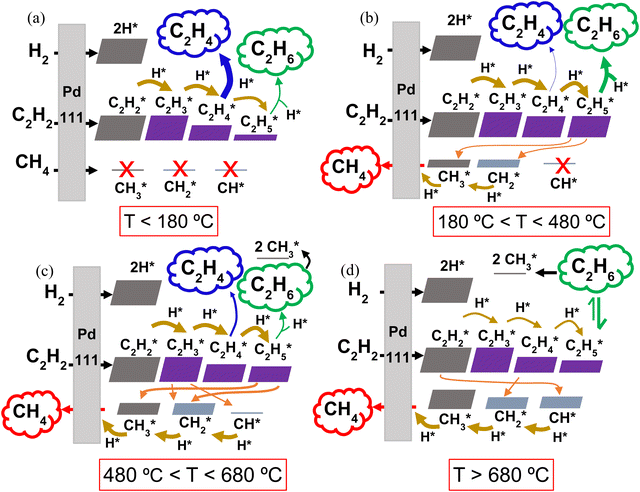
Within the studied temperature range, the adsorption of both H₂ (into 2H*) and C₂H₂ (into C₂H₂*), onto the Pd surface occurs very rapidly, with rates approaching 10²⁵ s⁻¹. Following the formation of C₂H₂* and H*, sequential surface hydrogenation reactions (r₇, r₈ and r₉ in Table 1) proceed, generating C₂H₃*, C₂H₄* and C₂H₅* species – with varying surface coverage, depending on the temperature (as shown in Fig. 5). At temperatures below 180 °C (Fig. 5a), desorption of C₂H₄* (reverse of reaction r₃) is preferred, leading to the evolution of C₂H₄(g) over further hydrogenation to C₂H₅* (r₉). This preference results in the predominance of the desired C₂H₄ product at low temperatures, aligning with the selectivity results observed in our experiments with the 0.1% Pd/Al₂O₃ catalyst. The desorption of C₂H₄* into C₂H₄(g) peaks at 144 °C, coincide with the highest C₂H₄ selectivity. In this temperature range, the coverage of C1 surface species remains negligible, as dissociative desorption of CH₄ (r₆) does not occur.

As the temperature rises, the rate of C₂H₄* desorption decreases, whilst the rates of C₂H₄* hydrogenation to C₂H₅* and subsequent hydrogenation to C₂H₆(g) (r₄) increase significantly (Fig. S7 and Fig. 5b, ESI†). This behaviour was also observed by Wang et al.⁴³ and Shi et al.⁴⁴ for C₂H₂ hydrogenation over Cu and Au-based catalysts. As a result, the C₂H₆ product sees a rise in selectivity and it becomes the main product from ∼180 °C.

As the temperature is further increased, the desorption rate of C₂H₄* falls sharply, dropping to approximately zero around 280 °C. Simultaneously, the hydrogenation reactions to C₂H₅* and C₂H₆(g) accelerate, making C₂H₆ the only product seen by the model between 280 and 450 °C. These rates are plotted in Fig. S8 (ESI†). However, once the temperature reaches 450 °C, the dissociation of C₂H₅* into CH₃* and CH₂* (r₁₀) begins to occur, as shown in Fig. 5b, competing with the hydrogenation to C₂H₆. In turn, this gives rise to the production of CH₄(g), as CH₃* undergoes surface hydrogenation (reverse of the r₆ reaction, as detailed in Fig. S9, ESI†). Thus, at temperatures above 450 °C, CH₄ becomes a product of C₂H₂ hydrogenation over this Pd catalyst, with its selectivity rising rapidly with temperature (cf. Fig. 4 above).

Interestingly, for all three Pd loadings, the model predicts the reappearance of C₂H₄ as a product between ∼500 and 710 °C, depending on the Pd loading (see Fig. 4 above), with a local maximum in C₂H₄ selectivity around 600 °C. This trend is corroborated by our rate analysis, which indicates a second region of C₂H₄* desorption into C₂H₄(g) (reverse of r₃) within this temperature range (see Fig. S10 and Fig. 5c, ESI†). Concurrently, the dissociation rate of C₂H₅* into CH₃* and CH₂* (r₁₀) steadily rises from 500 °C, and C₂H₃* also begins to undergo surface dissociation into CH₂* and CH* (r₁₂) (see Fig. 5c). These dissociation processes explain the sharp decline in C₂H₆ selectivity at elevated temperatures (cf. Fig. 4), as they compete with the hydrogenation steps required to form the C₂H₄ and C₂H₆ products. Indeed, the reaction rates of both C₂H₄* and C₂H₅* + H* (r₉ and r₄) dwindle with increasing temperature (Fig. S10, ESI†). Besides, the observed waning C₂H₆ production can also be ascribed to dissociative adsorption of C₂H₆(g) into 2CH₃* (reverse of r₅) (cf. Fig. 5c), which becomes significant from 600 °C onwards. Collectively, these reactions contribute to enhancing the catalyst surface coverage with CH_x* species, ultimately resulting in the evolution of CH₄(g) – which becomes the dominant product above ∼650 °C.

Beyond 680 °C, additional dissociation reactions begin to take place alongside those discussed above. These are the dissociation of C₂H₂* into 2CH* (r₁₃), C₂H₄* into 2CH₂* (r₁₁) and C₂H₆(g) into C₂H₅* and H* (reverse of r₄), as illustrated in Fig. 5d, with rates shown in Fig. S11 (ESI†). At the same time, all C₂H_y* hydrogenations become slower, while the hydrogenation rates of CH* (reverse of r₁₅) and CH₂* steadily increase (cf. thickness of the arrows in Fig. 5d). As a result, the formation of C₂ hydrocarbons is further weakened, becoming negligible above 700 °C. Meanwhile, the CH₄ production peaks, approaching 100% selectivity at 750 °C and explaining the trend in Fig. 4.

4. Conclusions

In this work, we developed a surface micro-kinetic model that simulates the catalytic C₂H₂ hydrogenation to C₂H₄, following plasma-based non-oxidative CH₄ coupling. We validated the model against experiments using an NPD plasma reactor chemically and thermally integrated with a downstream catalyst bed, employing different Pd/Al₂O₃ materials with Pd loadings of 0.1%, 0.5% and 1%. All three catalysts effectively convert the C₂H₂ present in the exiting gas stream from the plasma discharge without external heating, with conversions above 90%. By applying fixed plasma conditions, we attain a consistent CH₄ conversion around 46%, and C₂H₂ selectivity around 83% for the plasma stage, and thus post-plasma catalytic C₂H₂ hydrogenation into C₂H₄ is the main driver of the final C₂H₄ yield. Our experiments show that only the 0.1% Pd/Al₂O₃ catalyst evolves C₂H₄ as the main hydrogenation product, while at higher Pd loadings, C₂H₆ is predominantly produced. Our model predicts a slightly different trend, with higher C₂H₄ selectivity for all catalysts in the low-temperature regime, though C₂H₆ rapidly becomes predominant above 150–180 °C. The highest C₂H₄ selectivity is obtained at the lowest simulated temperature (i.e., 142 °C, 135 °C and 115 °C for the 0.1%, 0.5% and 1% Pd/Al₂O₃ catalysts, respectively). In the experiments, other oligomerisation by-products are also observed, but they are not included in the model, which might explain the observed discrepancy.

Our results also show that the exothermic nature of the hydrogenation reactions induces a temperature rise within the catalyst bed, which is detrimental to the C₂H₄ selectivity. This is in line with the modelled reaction mechanism, which reveals that by increasing the catalyst temperature, the C₂H₄* desorption rate is lowered, while further hydrogenation is favoured. As this effect is highly undesirable, the deployment of more selective catalysts (e.g., mixed metal alloys)^45,46 able to fine-tune these rates may enhance the process performance.

Other key factors may influence the coupling between the plasma reactor and the catalyst bed. We believe these include the type of catalyst and support (i.e., oxides versus metal-based), the plasma source, reactor geometry, the magnitude and type of gas flow, type of filter, and the distance between the bed and discharge region. Ultimately, these factors directly impact heat transfer, and in turn the catalyst temperature, which, as shown in this work, significantly affects the selective synthesis of C₂H₄. Tailoring these variables allows for fine control over the catalyst bed temperature, thereby maximising C₂H₄ selectivity (and yield) and catalyst performance. This research opens avenues for further exploration of coupling different plasma sources and reactors with simple post-plasma catalytic setups. Potentially, the flexibility in adjusting the catalyst bed temperature through the aforementioned factors may allow for the use of cheaper and more abundant catalysts (such as Cu and Ni), which generally require higher activation temperatures.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge financial support by the Flemish Government through the Moonshot cSBO project “Power-to-Olefins” (P2O; HBC.2020.2620), the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 810182-SCOPE ERC Synergy project), and the Methusalem grant of the University of Antwerp. Fabio Cameli acknowledges the European Union for funding through the HORIZON-WIDERA-2023-TALENTS-02 program, project 101180605.

References

1. I. Amghizar, L. A. Vandewalle, K. M. Van Geem and G. B. Marin, New Trends in Olefin Production, Engineering, 2017, 3, 171–178,  DOI:10.1016/J.ENG.2017.02.006.
2. A. Bogaerts and E. C. Neyts, Plasma Technology: An Emerging Technology for Energy Storage, ACS Energy Lett., 2018, 3, 1013–1027,  DOI:10.1021/acsenergylett.8b00184.
3. R. Snoeckx and A. Bogaerts, Plasma technology-a novel solution for CO₂ conversion?, Chem. Soc. Rev., 2017, 46, 5805–5863,  10.1039/c6cs00066e.
4. E. Delikonstantis, E. Igos, M. Augustinus, E. Benetto and G. D. Stefanidis, Life cycle assessment of plasma-assisted ethylene production from rich-in-methane gas streams, Sustainable Energy Fuels, 2020, 4, 1351–1362,  10.1039/c9se00736a.
5. E. Delikonstantis, F. Cameli, M. Scapinello, V. Rosa, K. M. Van Geem and G. D. Stefanidis, Low-carbon footprint chemical manufacturing using plasma technology, Curr. Opin. Chem. Eng., 2022, 38, 100857,  DOI:10.1016/j.coche.2022.100857.
6. O. Mynko, I. Amghizar, D. J. Brown, L. Chen, G. B. Marin, R. F. de Alvarenga, D. C. Uslu, J. Dewulf and K. M. Van Geem, Reducing CO₂ emissions of existing ethylene plants: evaluation of different revamp strategies to reduce global CO₂ emission by 100 million tonnes, J. Cleaner Prod., 2022, 362, 132127,  DOI:10.1016/j.jclepro.2022.132127.
7. P. Lamichhane, N. Pourali, L. Scott, N. N. Tran, L. Lin, M. E. Gelonch, E. V. Rebrov and V. Hessel, Critical review: ‘Green’ ethylene production through emerging technologies, with a focus on plasma catalysis, Renewable Sustainable Energy Rev., 2024, 189, 114044,  DOI:10.1016/j.rser.2023.114044.
8. T. Nozaki, D. Y. Kim and X. Chen, Plasma-enabled electrification of chemical processes toward decarbonization of society, Jpn. J. Appl. Phys., 2024, 63, 030101,  DOI:10.35848/1347-4065/ad280f.
9. L. Fulcheri, V. J. Rohani, E. Wyse, N. Hardman and E. Dames, An energy-efficient plasma methane pyrolysis process for high yields of carbon black and hydrogen, Int. J. Hydrogen Energy, 2023, 48, 2920–2928,  DOI:10.1016/j.ijhydene.2022.10.144.
10. F. Girard-Sahun, O. Biondo, G. Trenchev, G. van Rooij and A. Bogaerts, Carbon bed post-plasma to enhance the CO₂ conversion and remove O₂ from the product stream, Chem. Eng. J., 2022, 442, 136268,  DOI:10.1016/j.cej.2022.136268.
11. S. Kelly and A. Bogaerts, Nitrogen fixation in an electrode-free microwave plasma, Joule, 2021, 5, 3006–3030,  DOI:10.1016/j.joule.2021.09.009.
12. M. Tatar, V. Vashisth, M. Iqbal, T. Butterworth, G. van Rooij and R. Andersson, Analysis of a plasma reactor performance for direct nitrogen fixation by use of three-dimensional simulations and experiments, Chem. Eng. J., 2024, 497, 154756,  DOI:10.1016/j.cej.2024.154756.
13. M. Scapinello, E. Delikonstantis and G. D. Stefanidis, The panorama of plasma-assisted non-oxidative methane reforming, Chem. Eng. Process. – Process Intensif., 2017, 117, 120–140,  DOI:10.1016/j.cep.2017.03.024.
14. A. Fridman, Plasma chemistry, Cambridge University Press, 2008, 9780521847 DOI:10.1017/CBO9780511546075.
15. S. Heijkers, M. Aghaei and A. Bogaerts, Plasma-Based CH₄ Conversion into Higher Hydrocarbons and H₂: Modeling to Reveal the Reaction Mechanisms of Different Plasma Sources, J. Phys. Chem. C, 2020, 124, 7016–7030,  DOI:10.1021/acs.jpcc.0c00082.
16. M. Wnukowski, Methane Pyrolysis with the Use of Plasma: Review of Plasma Reactors and Process Products, Energies, 2023, 16, 6441,  DOI:10.3390/en16186441.
17. L. Fulcheri and Y. Schwob, From methane to hydrogen, carbon black and water, Int. J. Hydrogen Energy, 1995, 20, 197–202,  DOI:10.1016/0360-3199(94)E0022-Q.
18. M. Scapinello, E. Delikonstantis and G. D. Stefanidis, Direct methane-to-ethylene conversion in a nanosecond pulsed discharge, Fuel, 2018, 222, 705–710,  DOI:10.1016/j.fuel.2018.03.017.
19. E. Morais, E. Delikonstantis, M. Scapinello, G. Smith, G. D. Stefanidis and A. Bogaerts, Methane coupling in nanosecond pulsed plasmas: correlation between temperature and pressure and effects on product selectivity, Chem. Eng. J., 2023, 462, 142227,  DOI:10.1016/j.cej.2023.142227.
20. M. Wnukowski, A. W. van de Steeg, B. Hrycak, M. Jasiński and G. J. van Rooij, Influence of hydrogen addition on methane coupling in a moderate pressure microwave plasma, Fuel, 2021, 288, 119674,  DOI:10.1016/j.fuel.2020.119674.
21. K. Konno, K. Onoe, Y. Takiguchi and T. Yamaguchi, Direct Preparation of Hydrogen and Carbon Nanotubes by Microwave Plasma Decomposition of Methane over Fe/Si Activated by Biased Hydrogen Plasma, Green Sustainable Chem., 2013, 03, 19–25,  DOI:10.4236/gsc.2013.31004.
22. A. Khrabry, I. D. Kaganovich, Y. Barsukov, S. Raman, E. Turkoz and D. Graves, Compact and accurate chemical mechanism for methane pyrolysis with PAH growth, Int. J. Hydrogen Energy, 2024, 56, 1340–1360,  DOI:10.1016/j.ijhydene.2023.12.175.
23. T. Minea, D. C. M. van den Bekerom, F. J. J. Peeters, E. Zoethout, M. F. Graswinckel, M. C. M. van de Sanden, T. Cents, L. Lefferts and G. J. van Rooij, Non-oxidative methane coupling to C₂ hydrocarbons in a microwave plasma reactor, Plasma Process. Polym., 2018, 15, 1–16,  DOI:10.1002/ppap.201800087.
24. J. R. Fincke, R. P. Anderson, T. Hyde, B. A. Detering, R. Wright, R. L. Bewley, D. C. Haggard and W. D. Swank, Plasma Thermal Conversion of Methane to Acetylene, Plasma Chem. Plasma Process., 2002, 22, 105–136,  DOI:10.1023/A:1012944615974.
25. N. García-Moncada, G. van Rooij, T. Cents and L. Lefferts, Catalyst-assisted DBD plasma for coupling of methane: minimizing carbon-deposits by structured reactors, Catal. Today, 2021, 369, 210–220,  DOI:10.1016/J.CATTOD.2020.04.028.
26. P. A. Maitre, M. S. Bieniek and P. N. Kechagiopoulos, Modelling excited species and their role on kinetic pathways in the non-oxidative coupling of methane by dielectric barrier discharge, Chem. Eng. Sci., 2021, 234, 116399,  DOI:10.1016/j.ces.2020.116399.
27. E. Delikonstantis, M. Scapinello, O. Van Geenhoven and G. D. Stefanidis, Nanosecond pulsed discharge-driven non-oxidative methane coupling in a plate-to-plate electrode configuration plasma reactor, Chem. Eng. J., 2020, 380, 122477,  DOI:10.1016/j.cej.2019.122477.
28. E. Delikonstantis, M. Scapinello and G. D. Stefanidis, Low energy cost conversion of methane to ethylene in a hybrid plasma-catalytic reactor system, Fuel Process. Technol., 2018, 176, 33–42,  DOI:10.1016/J.FUPROC.2018.03.011.
29. F. Cameli, M. Scapinello, E. Delikonstantis, F. Sascha Franchi, M. Ambrosetti, L. Castoldi, G. Groppi, E. Tronconi and G. D. Stefanidis, Intensification of plasma-catalytic processes via additive manufacturing. Application to non-oxidative methane coupling to ethylene, Chem. Eng. J., 2024, 482, 148720,  DOI:10.1016/j.cej.2024.148720.
30. F. Cameli, M. Scapinello, E. Delikonstantis and G. D. Stefanidis, Electrified methane upgrading via non-thermal plasma: intensified single-pass ethylene yield through structured bimetallic catalyst, Chem. Eng. Process. – Process Intensif., 2024, 204, 109946,  DOI:10.1016/j.cep.2024.109946.
31. B. Wanten, R. Vertongen, R. De Meyer and A. Bogaerts, Plasma-based CO₂ conversion: How to correctly analyze the performance?, J. Energy Chem., 2023, 86, 180–196,  DOI:10.1016/j.jechem.2023.07.005.
32. M. H. Hansen, J. K. Nørskov and T. Bligaard, First principles micro-kinetic model of catalytic non-oxidative dehydrogenation of ethane over close-packed metallic facets, J. Catal., 2019, 374, 161–170,  DOI:10.1016/j.jcat.2019.03.034.
33. B. Loenders, R. Michiels and A. Bogaerts, Is a catalyst always beneficial in plasma catalysis? Insights from the many physical and chemical interactions, J. Energy Chem., 2023, 85, 501–533,  DOI:10.1016/j.jechem.2023.06.016.
34. H. Ma and W. F. Schneider, Plasma-catalyst modeling for materials selection: challenges and opportunities in nitrogen oxidation, J. Phys. D: Appl. Phys., 2021, 54, 12,  DOI:10.1088/1361-6463/ac1bd1.
35. V. Petrazzuoli, M. Rolland, V. Sassanis, V. Ngu, Y. Schuurman and L. Gamet, Numerical prediction of Péclet number in small-sized fixed bed reactors of spheres, Chem. Eng. Sci., 2021, 240, 116667,  DOI:10.1016/j.ces.2021.116667.
36. B. Yang, R. Burch, C. Hardacre, G. Headdock and P. Hu, Influence of surface structures, subsurface carbon and hydrogen, and surface alloying on the activity and selectivity of acetylene hydrogenation on Pd surfaces: a density functional theory study, J. Catal., 2013, 305, 264–276,  DOI:10.1016/j.jcat.2013.05.027.
37. A. Kordatos, K. Mohammed, R. Vakili, H. Manyar, A. Goguet, E. Gibson, M. Carravetta, P. Wells and C. K. Skylaris, Bridging the size gap between experiment and theory: large-scale DFT calculations on realistic sized Pd particles for acetylene hydrogenation, RSC Adv., 2024, 14, 27799–27808,  10.1039/d4ra03369h.
38. K. Van, T. Veer, F. Reniers and A. Bogaerts, Zero-dimensional modeling of unpacked and packed bed dielectric barrier discharges: the role of vibrational kinetics in ammonia synthesis, Plasma Sources Sci. Technol., 2020, 29, 045020,  DOI:10.1088/1361-6595/ab7a8a.
39. S. Ravasio and C. Cavallotti, Analysis of reactivity and energy efficiency of methane conversion through non thermal plasmas, Chem. Eng. Sci., 2012, 84, 580–590,  DOI:10.1016/j.ces.2012.09.012.
40. E. Morais and A. Bogaerts, Modelling the dynamics of hydrogen synthesis from methane in nanosecond-pulsed plasmas, Plasma Process. Polym., 2023, 1–10,  DOI:10.1002/ppap.202300149.
41. R. Liu, E. Morais, D. Li, P. Liu, Q. Chen, S. Li, L. Wang, X. Gao, A. Bogaerts, H. Guo and Y. Yi, Hybrid plasma catalysis-thermal system for non-oxidative coupling of methane to ethylene and hydrogen, Chem. Eng. J., 2024, 498, 155733,  DOI:10.1016/j.cej.2024.155733.
42. M. Scapinello, E. Delikonstantis and G. D. Stefanidis, A study on the reaction mechanism of non-oxidative methane coupling in a nanosecond pulsed discharge reactor using isotope analysis, Chem. Eng. J., 2019, 360, 64–74,  DOI:10.1016/j.cej.2018.11.161.
43. S. Wang, K. Uwakwe, L. Yu, J. Ye, Y. Zhu, J. Hu, R. Chen, Z. Zhang, Z. Zhou, J. Li, Z. Xie and D. Deng, Highly efficient ethylene production via electrocatalytic hydrogenation of acetylene under mild conditions, Nat. Commun., 2021, 12, 7072,  DOI:10.1038/s41467-021-27372-8.
44. X. Shi, Y. Lin, L. Huang, Z. Sun, Y. Yang, X. Zhou, E. Vovk, X. Liu, X. Huang, M. Sun, S. Wei and J. Lu, Copper Catalysts in Semihydrogenation of Acetylene: From Single Atoms to Nanoparticles, ACS Catal., 2020, 10, 3495–3504,  DOI:10.1021/acscatal.9b05321.
45. M. Jørgensen and H. Grönbeck, Selective Acetylene Hydrogenation over Single-Atom Alloy Nanoparticles by Kinetic Monte Carlo, J. Am. Chem. Soc., 2019, 141, 8541–8549,  DOI:10.1021/jacs.9b02132.
46. Y. Qi, B. Wang, M. Fan, D. Li and R. Zhang, C₂H₂ semi-hydrogenation on the metal M (M = Cu, Ag, Au) alloyed single-atom Pd catalysts: effects of Pd coordination number and environment on the catalytic performance, Chem. Eng. Sci., 2021, 243, 116786,  DOI:10.1016/j.ces.2021.116786.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00203b

‡ Shared first authors.

---