Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Growth rate dependence of the permeability and percolation threshold of young sea ice
Sönke
Maus
 *
*
Department of Civil and Environmental Engineering, NTNU, Trondheim, Norway. E-mail: sonke.maus@ntnu.no; Tel: +47 7359 4707
First published on 2nd January 2025
Abstract
The permeability of sea ice is difficult to observe, and physically based permeability models are lacking so far. Here a model for the permeability of sea ice is presented that combines extensive microstructure observations and modelling with directed percolation theory. The model predicts the dependence of sea ice permeability on brine porosity and growth rate, as well as a percolation transition to impermeable sea ice due to necking of the pores. It is validated by numerical simulations of sea ice permeability on 3D images from X-ray microtomographic imaging and by other existing permeability data. A fundamental model result is that the percolation threshold of sea ice scales as ϕc ∝ a0−1 where a0 is the plate or brine layer spacing. As the plate spacing decreases with growth velocity V, this implies that the percolation threshold increases as ϕc ∝ V1/3, with the cubic root of the growth rate. For growth rates of natural sea ice the percolation threshold is expected to be in the range of 1 to 4 percent volume fraction of brine. While developed for columnar sea ice, a simple modification for granular surface ice also agrees with observations. The model is valid for sea ice during the growth phase, prior to warming and melting. Permeability modelling of spring and summer sea ice, with wider secondary brine channels present, requires 3D pore space observations in warming sea ice that currently are sparse.
1 Introduction
The hydraulic permeability reflects the ability of sea ice to transport fluid through its pore space. It is an important property that controls several sea ice processes and their role in the coupled atmosphere–ice–ocean system. During the melt season, the permeability controls the drainage rate of melt ponds and evolution of its surface properties, like albedo and roughness. During the growth season, permeability controls the salt loss from sea ice and thus is critical for the evolution of sea ice salinity. The latter, in turn, determines many sea ice properties, such as its mechanical, thermal and radiative properties.1 To predict the salinity and desalination of sea ice, models of different complexity have been suggested, of which the most recent approaches involve a parametrisation of the permeability.2–8 The permeability is also important for the biogeochemistry and ecosystem of sea ice,9–11 for air–ice–ocean gas exchange11–14 and for brine transport to the sea ice surface, from where brine freezing and chemistry may create interactions with atmospheric chemistry as far up as the stratosphere.15–18The sea ice permeability is related to its brine volume fraction ϕ. As brine in disconnected inclusions does not contribute to the permeability, knowing the critical brine volume fraction ϕc, at which all brine is disconnected, is important. However, understanding this transition and its dependence on growth conditions and microstructure is a challenging problem. Several authors have proposed percolation theory to address it, and have termed the minimum the percolation threshold of sea ice. The first studies on this problem proposed a threshold brine volume fraction of 5 percent.3,19,20 However, in a recent analysis based on 3D X-ray microtomography of young sea ice, a much lower threshold of 2–3 percent has been found.21 In the present study, I extend the latter21 results by formulating a new model for the percolation threshold and permeability of sea ice that accounts for microstructure and growth conditions. Based on this model, the differences in permeability observations are explained and most earlier work on sea ice permeability is revised.
2 Permeability – definition and previous work
The permeability K (with unit m2) of a porous medium is defined via Darcy’s equation:22,23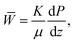 | (1) |
![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) , dynamic viscosity μ and pressure gradient dP/dz. Eqn (1) is valid for flow in one direction, while the permeability in 3D coordinates is a tensor. The present study focuses on the vertical permeability of sea ice, for which dP/dz may be created by meltwater on top of the ice or the upward brine salinity increase. The latter is the primary driver of gravity drainage and desalination of sea ice.
, dynamic viscosity μ and pressure gradient dP/dz. Eqn (1) is valid for flow in one direction, while the permeability in 3D coordinates is a tensor. The present study focuses on the vertical permeability of sea ice, for which dP/dz may be created by meltwater on top of the ice or the upward brine salinity increase. The latter is the primary driver of gravity drainage and desalination of sea ice.
The most widely adopted parametrisation of permeability K of sea ice has been proposed by Freitag,24 on the basis of laboratory experiments. It may be written as:
| K = 2.00 × 10−8ϕ3.1 m2, | (2) |
To address lower brine volume fractions, the permeability of sea ice has been discussed on the basis of percolation theory.3,5,19,20 In these theories, the sea ice permeability becomes zero at some critical brine porosity, for which most studies indicated a threshold of ϕc ≈ 0.05. Maus et al.21 have revisited these studies and concluded that there is little observational basis for a threshold of ϕc ≈ 0.05. Based on numerical simulations on X-ray microtomographic images of young sea ice, they proposed the following equation for the permeability:
| K = 1.49 × 10−8(ϕ − ϕc)2.55 m2, | (3) |
In Fig. 1, the results from ref. 21 and 24 are compared. In view of the wide range of observed permeability in other studies,24–26 they appear surprisingly close. However, both represent young sea ice of similar thickness (20–35 cm) that had grown for a few weeks. The concept to obtain the permeability was also similar in the studies, as both are based on centrifuged sea ice samples. In the first study,24 this provided the basis to measure the permeability in laboratory experiments with decane. In the second study,21 the centrifuged brine provided enough imaging contrast to obtain 3D X-ray microtomographic images for numerical simulations. For other growth conditions, no similar permeability observations are currently available. Also, little data exist at high brine volume fractions above ϕ = 0.20. This includes, for growing sea ice, the skeletal layer near the ice–water interface. In that regime, typically a few centimeters thick, the convective exchange with the ocean is largest. For columnar sea ice, it is characterised by a lamellar structure of vertically oriented plates that are parallel within each grain. For a brine layer of thickness d between the ice lamellae, the permeability is then given by Hele-Shaw flow as d2/12, such that the bulk permeability becomes Kd = ϕ/12d2. With distance from the interface, the ice lamellae thicken due to heat flow and two processes. First, the temperature decreases, and the brine adjusts to a new thermodynamic equilibrium of higher solute concentration. Second, convective exchange with seawater underneath progressively decreases the solute concentration, also increasing the ice solid fraction. Disregarding what exactly happens, this change in brine layer thickness is given as:
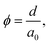 | (4) |
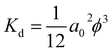 | (5) |
(1) ϕ > ϕ0 – the brine layer regime. In the lamellar regime above ϕ0, the brine layer width is given by the product of brine porosity ϕ and plate spacing a0.
(2) ϕc < ϕ < ϕ0 – the percolation regime. The upper critical porosity ϕ0 marks the transition at which the morphology of sea ice changes from a simple lamellar system of parallel vertical brine layers to a percolation-controlled pore network. In the percolation regime below ϕ0, pores are shrinking and disconnecting.
(3) ϕ < ϕc – the percolation threshold ϕc, below which sea ice is impermeable. In the following, a mathematical model will be formulated that quantifies the transitions and the permeability–porosity relationship in dependence on the growth rate of the ice.
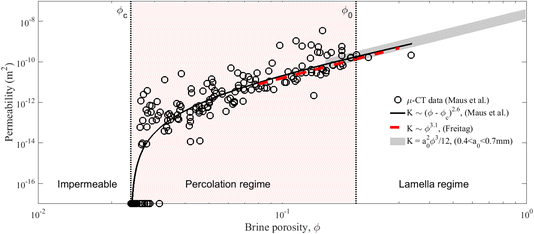 | ||
| Fig. 1 Vertical permeability simulations versus brine porosity with best columnar ice fit from Maus et al.21 compared to the relationship obtained by Freitag24 for young ice (red curve), and the lamella model at high porosity (eqn (5) for a typical range in sea ice plate spacing). The regime boundary for ϕ0 described in the text is chosen tentatively. | ||
3 Fundamental microstructure scales – spacing and thickness of brine layers
Sea ice is henceforth idealized (see eqn (2) above) as an ensemble of parallel vertically oriented plates – ice lamellae. This structure defines the noted plate or brine layer spacing a0, between which brine layers of thickness d are sandwiched (see Fig. 2). While there are deviations from this structure (e.g. at the ice surface), it is a reasonable simplification of columnar sea ice and has been used in many other studies.1 Brine porosity ϕ, plate spacing a0 and brine layer thickness d are simply related as ϕ = d0/a0.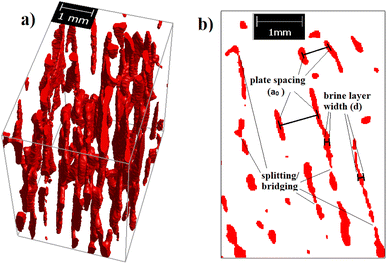 | ||
| Fig. 2 3D (a) and 2D (b) micro-CT-based images of open pores in young sea ice, illustrating the plate (or brine layer) spacing a0, the width d and the locations where the layer has split/bridged. | ||
The key hypothesis proposed here is that there is a transition from a system of parallel brine lamellae to more complex percolating pore networks that takes place when the thickness of brine layers between the plates becomes less than a critical d0. The corresponding critical brine porosity ϕ0 is given as:
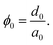 | (6) |
This concept of critical microstructure scales has been applied earlier. The first studies were focusing on changes in mechanical properties that are expected when the sea ice brine layers start to neck.30,31 Other authors3,5,32 later discussed the relevant length scales d0 and a0 in connection with percolation-based permeability models. However, in these earlier studies, detailed observations of 3D pore networks in sea ice were lacking. During recent decades, X-ray computed microtomography (XRT) has emerged as the method of choice to study the 3D microstructure and physics of porous ice and snow media in the environment, including snow,33,34 polar firn and ice cores,35,36 and sea ice.20,21,37–39 In the following, I show that the recent 3D microstructure data from ref. 21 allow for a consistent quantification of the above basic length scales. Fig. 2 illustrates d0 and a0 in 3D and 2D microstructure images from that data.
3.1 Plate spacing versus growth velocity
The fact that most growing sea ice has a lamellar ice–water interface, with concentrated seawater sandwiched between vertical plates, has long been known, with reports of this microstructure dating back up to two centuries.40–42 The first quantitative investigations of this plate spacing ranged from 0.2 to 0.5 mm for thin sea ice,27,30,43via 0.5 to 1 mm for thick Arctic sea ice,44,45 to 1.3–1.5 mm for a very thick ice island,46 suggesting an increasing plate spacing with ice thickness. In later studies, it was shown that the plate spacing decreases with increasing growth velocity.28,47 Other investigators failed to demonstrate the growth velocity dependence in laboratory experiments.48 The present author29,32,49 has studied the problem in detail and proposed a model for the plate spacing based on morphological stability theory developed by W. W. Mullins and R. F. Sekerka.50 In ref. 29, the following relationship between the plate spacing a0 of sea ice and its growth velocity V was derived:| a0 = 0.72V−1/3, | (7) |
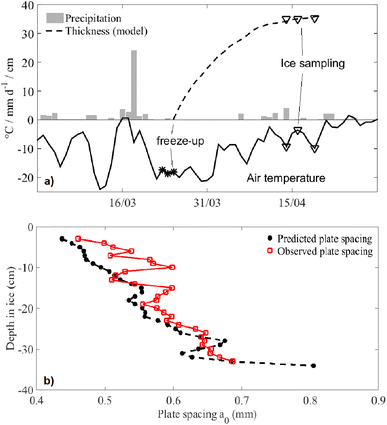
For the present study, I extended the earlier microstructure analysis that accompanied the above permeability measurements21 with plate spacing measurements and an ice growth model. An overview of the field conditions during ice growth is given in Fig. 3, showing air temperature and precipitation from freeze-up in late March to ice core sampling in mid April, when the ice was 3–4 weeks old. The microstructure data analysed in ref. 21 and the present study stem from 15 ice cores of this 35-cm-thick young ice. Each core (of 7.2 cm diameter) was sawed into 3–4-cm-thick segments, which were centrifuged at their in situ temperatures, as well as at lower temperatures. Finally, X-ray microtomographic imaging was performed on samples of 3 cm diameter and thickness, to obtain 3D images with a voxel size of 18 μm. More information was provided in ref. 21.
The plate spacing a0 for the sampled young ice was obtained by model and observation. The modelled plate spacing is based on eqn (7), with growth velocity V obtained with a growth model for young ice.51 Model inputs are (i) the meteorological observations (air temperature, wind velocity, precipitation, cloudiness, humidity) from Longyearbyen airport (5 km from the field site), (ii) a simple approximation of the bulk ice salinity of young ice,52 (iii) starting date and (iv) a guess for the oceanic heat flux. The model than computes the heat budget based on radiative (longwave and shortwave), sensible and latent heat fluxes, the conductive heat flux through the ice and the oceanic heat flux. The model was run with different starting dates and oceanic heat flux within plausible bounds for winter conditions (1 to 10 W m−2). The ice thickness 3–4 weeks later was best matched by the starting date shown in Fig. 3a and an oceanic heat flux of 3 W m−2. The corresponding time series and profile in the growth velocity (not shown) results in the modelled profile of the plate spacing a0 shown as black circles in Fig. 3b. Other parameter pairs (starting date and oceanic heat flux) and model settings are possible. However, that would change the predicted plate spacing only by a few percent, and have little impact on the general results presented below.
Measurements of plate spacings were made on horizontal microtomographic images. This will overestimate the plate spacing, if the brine layers are vertically inclined. A correction factor cos(α) was applied, based on the measured vertical inclination angle α, which implied maximum corrections of 0.04 mm. Second, at low temperatures, the brine layers and pores become, at our spatial resolution, invisible in parts of a sample. Fig. 4 shows this by comparing 3 horizontal slices that are 1 mm apart. To obtain the plate spacing from such imagery, a0 was determined from the images with highest porosity. In addition, non-segmented images were used that often allow for detection of thinner air and brine pores than in segmented images. The measured plate spacing profile are shown in Fig. 3b as red square symbols.
Predicted and observed plate spacings agree reasonably, both in terms of vertical trend and several local extrema. On average, the modelled plate spacing is 0.03 mm smaller than measured, and there appears to be a trend of increasing difference towards the surface. As surface temperatures were lower in the experiment, this difference is likely related to the described pore close-off with decreasing temperature. One may also anticipate an imperfect prediction by eqn (7), an overestimate of ice growth velocities due to uncertainties in the freeze-up date and oceanic heat flux. However, most important is that the average plate spacing for this dataset is consistent for model predictions 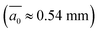 and observations
and observations 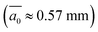 . In the following, a value of
. In the following, a value of 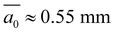 will be used as a reference average for the dataset.
will be used as a reference average for the dataset.
3.2 Critical brine layer thickness d0
The second length scale d0 marks the condition when brine layers bridge. It is more difficult to estimate. The problem has been first discussed in connection with studies of mechanical properties of sea ice. D. L. Anderson and W. Weeks30 proposed, from the analysis of 2D horizontal thin section photographs, that brine layers would split at 0.07 mm thickness (the thinnest layers observed) and, driven by surface energy minimisation, evolve into circular channels with about two times the diameter. As on the samples in question, a plate spacing a0 ≈ 0.46 mm was measured, and these authors proposed a critical brine volume of ϕ0 = d0/a0 = 0.07/0.46 = 0.152, below which many mechanical properties of sea ice should change fundamentally, and presented observations of the elastic modulus to support the idea. Assur44 investigated the idea in connection with a microstructure-based model of the tensile strength of sea ice. However, the value for d0, and the surface energy hypothesis, have not been confirmed by later studies, and the number of measurements obtained by Anderson and Weeks30 were rather limited. Weeks and Assur31 later estimated d0 indirectly on the basis of strength tests on ice with known spacing a0; extrapolating the strength-porosity dependence to zero strength at ϕ0 = d0/a0, they obtained d0 = 0.112 ± 0.01 mm. As this was much larger than d0 = 0.07 mm proposed earlier,30 Weeks and Assur noted that “It is hoped that new measurements of d0…will soon be available”. Microstructure and strength studies performed since then indicate that d0 most likely lies at the higher end of this range.32,53In our recent study of 3D microstructure data,21 the author and his colleagues have obtained a more precise estimate of d0. The relevant data of that study are summarised in Fig. 5. Two length scales were obtained over a wide porosity regime – the median diameter d (or shortest dimension, for non-circular pores) of open brine pores and the throat diameter dt or thinnest part of a pore. For both length scales, a robust power law dependency on the total brine volume ϕ was found, given as:
| dt = 0.389ϕ0.46 mm | (8) |
| d = 0.417ϕ0.34 mm | (9) |
| d0 = d(ϕc = 0.024) ≈ 0.117 ± 0.008 mm. | (10) |
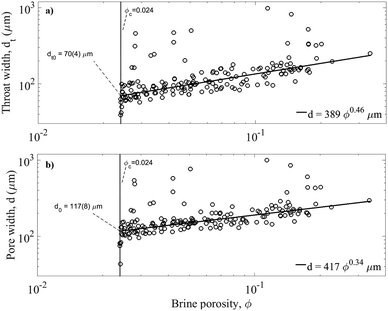 | ||
| Fig. 5 (a) Median throat width dtversus brine volume of young ice from ref. 21; (b) median pore diameter d. The critical dt0 and d0 values are obtained at the intersection of the relationships with the percolation threshold ϕc. | ||
These values, obtained from 3D microstructure imagery, are the first robust results for the critical length scales for ice bridging across brine layers. They improve on earlier, mostly indirect estimates. Interestingly, the thinnest observable thickness of brine layers reported by Anderson and Weeks54 was 0.07 mm, and compares to the characteristic throat diameter dt0 for pore disconnection found by us. The most important scale for the present theory is the average brine layer thickness at that stage, for which d0 = 0.12 mm is considered as the best empirical estimate.
4 Percolation theory – directed versus isotropic
“Percolation” (from latin “percolate” = to filter) refers to the movement of fluids through a porous material like soil, rocks and porous ice media as firn, snow and sea ice. During the past half century “percolation theory”, first described by Broadbent and Hammersley55 has been developed in mathematics and physics. In addition to the structure and properties of pore networks, it deals with broader connectivity problems in other systems, such as forest fires and pandemics.55–57 Key aspects of percolation theory are that it (i) is a probabilistic model of the system connectivity and (ii) exhibits critical behavior at a percolation threshold. The point of criticality is often termed phase transition.The first sea ice studies on this problem concluded that the sea ice pore pace undergoes a percolation phase transition and becomes impermeable at a brine volume fraction of 0.05.3,19,20,26 However, more recent work based on 3D X-ray microtomographic imaging of sea ice has found a threshold of 0.02–0.03 percent for young sea ice.21,58 While the former studies3,5,19,20,26 were based on isotropic percolation, the latter work by the present authors21,58 indicated that directionally growing sea ice should rather be described in terms of directed percolation theory. In directed percolation, fluid is restricted to flow in one spatial direction, and the critical behavior differs from isotropic systems;59,60e.g., the important differences with respect to sea ice are summarised as follows.
4.1 Percolation properties and critical exponents
An essential aspect of percolation theory is that many properties P of a medium, like connectivity and permeability, near the percolation threshold may be described by a power law of the form:| P ∼ (ϕ − ϕc)q, | (11) |
The critical exponents for sea ice shown in Table 1 have been obtained as follows. As described in ref. 21, their approach was to centrifuge brine from young sea ice core segments at different temperatures. The result obtained from centrifuging 15 young ice cores is shown in Fig. 6a. The fitted relationship between centrifuged (effective, connected) porosity ϕeff and total brine porosity ϕ may be written in the form
| ϕeff = cϕ(ϕ − ϕc)β, | (12) |
| σ/σ0 = cσ(ϕ−ϕc)μ, | (13) |
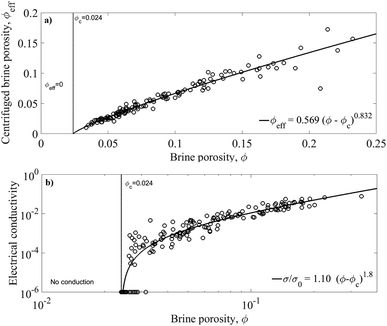 | ||
| Fig. 6 (a) Centrifuged (effective, open) brine porosity of young ice with optimum percolation fit from ref. 21; (b) normalised electrical conductivity with optimum percolation fit against (ϕ − ϕc) (new result). | ||
An essential result in Table 1 is that the deduced critical exponent β = 0.83 ± 0.03 for sea ice is very close to the presently accepted β ≈ 0.82 for 3(+1)D directed percolation,59,60 and far from β ≈ 0.41 in 3D isotropic percolation.56,57 Also for the electrical conductivity the sea ice exponent μ = 1.8 ± 0.1 is slightly closer to the directed percolation exponent of 1.7 from ref. 63, when compared to the isotropic μ = 2.0.56 These results suggest that transport through the pore space of columnar sea ice belongs to the universality class of directed percolation. Note that the critical exponent t for the permeability is not universal, yet depends on the details of the pore space evolution. Its lower bound is the conductivity exponent μ,64,65e.g., the present t = 2.55 should thus be viewed as an empirical value for young sea ice.
Note that there is another important exponent ν that describes the behaviour of the correlation length, which may be understood as the average distance of sites (or pores) in a network.56 In 3D directed percolation it is direction-dependent and has been determined as ν∥ ≈ 1.11 in the percolation direction and ν⊥ ≈ 0.58 normal to it.60 We have omitted this property as the sea ice samples analysed here have been too small to retrieve the correlation length and its critical exponent.
4.2 Percolation and porosity threshold
While the critical exponents μ and β are considered universal and micro-structure independent, this is not the case for the percolation threshold ϕc, at which the connectivity of a network breaks down. As an example one may consider the percolation of a system of thin rods, for which it is known that the critical solid fraction, at which a random assemblage of these rods is interconnected, decreases with increasing aspect ratio. However, there are some interesting general bounds that have been reported for classical lattices. Here the percolation threshold depends on the coordination number Z, and if one defines it in terms of sites or bonds, e.g., on a 3D simple cubic lattice with Z = 6, the site and bond percolation thresholds are ≈0.31 and ≈0.25, respectively, being smaller (≈0.25 and 0.18) for a body-centered cubic lattice with Z = 8 (see Table 2). However, half a century ago, Scher and Zallen68 detected an important aspect for both 2- and 3-dimensional lattices: the higher the coordination number, as well as packing or filling factor F of a lattice, the lower the critical percolation probability Pc, such that their product fc = FPc is approximately constant. The property fc resembles the critical density or filling fraction of a network. For selected 3D lattices a rather constant critical fraction fc in the range 0.15 to 0.16 was found. In Table 2 we compare this result to the corresponding thresholds for directed percolation that have become available during recent years. An interesting fact is that one can make a similar conjecture for directed percolation, where fc ≈ 0.11 appears to be the critical density. Furthermore, it appears that the ratio of isotropic to directed threshold densities is close to 1.5, i.e., that the directed percolation threshold is 2/3 of the isotropic value. This aspect will be important when comparing results for columnar and granular sea ice below.5 Synthesis of a permeability model based on directed percolation
Combining now the general percolation scalings with the sea ice microstructure results from the previous sections one can write| ϕc = fcϕ0 | (14) |
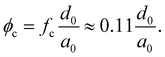 | (15) |
These upper and lower thresholds separate the regimes described in Section 3 that now can be defined in terms of the length scales d0 and a0, as well as fc:
(1) ϕ > ϕ0 – the brine layer regime: the permeability of an ensemble of shrinking brine layers is given by eqn (5) and thus is proportional to a02 and ϕ3. With a0 being related to the ice growth velocity through eqn (7), the permeability equations will be growth-velocity dependent.
(2) ϕc < ϕ < ϕ0 – directed percolation regime: at a critical thickness of d0 ≈ 0.12 mm (and porosity d0/a0) ice bridges form across the brine layers and a more complex network pores with variable diameter forms. With decreasing porosity (due to cooling of the ice) this percolation process continues to close more and more pores. The permeability in this regime is given by eqn (3) as K ≈ (ϕ − ϕc)t, with empirically determined exponent t = 2.55.
(3) ϕc – directed percolation threshold: below ϕc sea ice is vertically impermeable. This happens at a critical pore fraction of fc ≈ 0.11 in the original brine layers, corresponding to the porosity threshold fcd0/a0 given by eqn (14).
The permeability for these porosity regimes is explicitly formulated as a function of a0, d0, fc, and the percolation critical exponent t for the permeability:
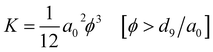 | (16) |
| K = ck(ϕ − fcd0/a0)t [fcd0/a0 < ϕ < d0/a0] | (17) |
| K = 0 [ϕ < fcd0/a0] | (18) |
The parameter ck follows from matching K from eqn (16) and (17) at the upper critical porosity ϕ = d0/a0:
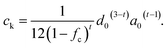 | (19) |
A first test of the consistency of this model with observations is made by comparing ck from eqn (19) to the factor from the numerical simulations, given as 1.48 × 10−8 m2 in eqn (3). Inserting the best estimates of d0 = 0.12 mm, a modelled plate spacing 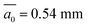 , t = 2.55 and fc = 0.11 into eqn (19) one obtains ck = 1.66 × 10−8 m2, while using the observed
, t = 2.55 and fc = 0.11 into eqn (19) one obtains ck = 1.66 × 10−8 m2, while using the observed 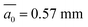 gives ck = 1.81 × 10−8 m2. The standard settings thus give predictions that are 12–22% higher than the permeability simulations. The predicted percolation threshold based on eqn (14) is 0.023 or 0.024, depending if one uses the measured or modelled average plate spacing of
gives ck = 1.81 × 10−8 m2. The standard settings thus give predictions that are 12–22% higher than the permeability simulations. The predicted percolation threshold based on eqn (14) is 0.023 or 0.024, depending if one uses the measured or modelled average plate spacing of 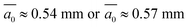 , respectively. This result also agrees remarkably with the value ϕc = 0.024 ± 0.04 from the best centrifuge-based fit (eqn (12)). Hence, the microstructure-based model agrees quantitatively with observations of macroscopic system properties (permeability, connected porosity, percolation threshold), showing the consistency of the macroscopic and microscopic data.
, respectively. This result also agrees remarkably with the value ϕc = 0.024 ± 0.04 from the best centrifuge-based fit (eqn (12)). Hence, the microstructure-based model agrees quantitatively with observations of macroscopic system properties (permeability, connected porosity, percolation threshold), showing the consistency of the macroscopic and microscopic data.
6 Discussion
6.1 Permeability versus growth rate and plate spacing
A central result of the present model is that the percolation threshold (eqn (15)) may be written as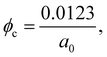 | (20) |
| ϕc ≈ 0.0183V1/3, | (21) |
The model was further tested by sorting the permeability data from Fig. 1 into different groups of plate spacing and growth velocity (according to Fig. 3). The result is presented in Fig. 7 for the modelled plate spacing (being very similar for the measured plate spacing). In the figure three curves are drawn. The black intermediate curve shows the model result (based on eqn (16) to (19)) for an average plate spacing of a0 = 0.55 mm. This curve is almost indistinguishable from the best fit to all data that is also shown as a hatched curve. The two other curves show the model predictions for the upper (5 cm per day) and lower (1 cm per day) bounds during the growth of the ice. For comparison, two subgroups of the data have been selected that correspond to a high (>3.5 cm per day) and low (<1.5 cm per day) regime, and are highlighted with red and green dots. While the scatter is large, the distribution clearly supports the hypothesis of a growth-velocity-dependent permeability. In particular, the low growth-velocity results may be much better understood by a model with a lower permeability threshold (upper red curve). Note that Maus et al.21 did not include these values in the least squares fit of Fig. 1, arguing that they are from a mixed regime of 0.024 < ϕ < 0.031 where both zero and non-zero permeabilities were observed. Fig. 7 now explains this in terms of an ice growth rate difference.
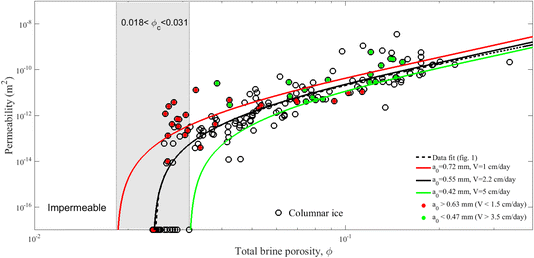 | ||
| Fig. 7 Vertical permeability simulations of columnar ice versus model results (eqn (16) to (19)). The high and low growth rate simulations are depicted with green and red dots, respectively, and compared to the predictions for upper (green curve) and lower (red curve) ice growth rates in the model. The best fit and the model prediction for the average plate spacing are also shown very close to each other. | ||
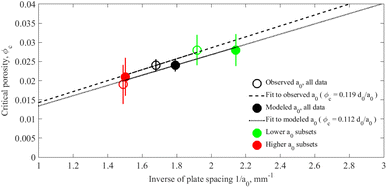
The analysis was extended by another parametric fit. It is seen that each point in Fig. 7 can be interpreted in terms of a unique growth velocity (and/or plate spacing) and percolation threshold. One can thus, based on the model curves, compute ϕc for each simulation point, and compare it with the observed plate spacing a0 to derive the corresponding critical filling fraction fc of the brine layers through eqn (15). This procedure has been performed for the modelled and observed plate spacings from Fig. 3, and by dividing the data into low- and high-growth-velocity subgroups (simply divided by the average plate spacing). The results are shown in Fig. 8, where the inverse of the plate spacing is plotted against the average percolation threshold obtained from the parametric model fit. For the whole dataset, the average fc results are shown as full and open black circles, being 0.112 ± 0.007 for the modelled a0 and 0.119 ± 0.007 for the observed a0. These values are close to fc ≈ 0.11 obtained for directed percolation theory (Table 2). While not surprising, as the estimates of ϕc from theory and observations agreed well, this comparison reconfirms that the model settings and data are consistent.
Fig. 8 also shows the percolation thresholds for the low and high growth velocity subgroups. For perfect agreement these should fall on the stippled and full lines for the observed and modelled plate spacings. Due to the reduced number of data points for the subgroups, the standard deviation is large, and the confidence of these results is not very high. However, the consistence is very reasonable, supporting the hypothesis that the percolation threshold is inversely proportional to the plate spacing a0.
6.2 Granular surface ice
The above data analysis and fitting procedures have focused on columnar sea ice, omitting the results for granular surface ice (not shown so far). In the earlier paper21 it was shown that the results for granular surface ice samples indicate a higher percolation threshold. The database was, however, too limited for a quantitative analysis. According to the present analysis, the dependence of permeability on the growth rate of sea ice might serve as an explanation, as ice is initially growing faster (leading to the low plate spacing shown in Fig. 3).In Fig. 9 only the granular surface ice data (typically the upper 3 centimeters) are compared with the model predictions. The red and green curves span, as shown in Fig. 7 for the columnar ice data, the growth velocity regime of the ice. Although the scatter in this data is large, it is seen that the majority of data points fall below this regime, and that there are also two observations with zero permeability above ϕ ≈ 0.05. As a possible explanation one may consider that the very surface ice is growing faster than in the present ice growth model, e.g., assuming a growth rate of 10 cm per day would raise the percolation threshold to ϕc = 0.04. However, there is another aspect that needs to be considered. Surface sea ice is not only growing faster, it also is very often characterised by a random orientation of crystals, and termed granular. For such ice one would expect that the percolation is isotropic. An ad hoc approach to account for this in the present model involves two steps:
(1) The directed fc ≈ 0.11 is replaced by the isotropic fc ≈ 0.16 (Table 2) in eqn (17) to (19).
(2) As the high porosity state of flow through granular ice, in contrast to the columnar lamella model, is tortuous, a factor T−2 is introduced in the permeability equations (eqn (16) and (17)). Results for the permeability of granular ice and the present samples (not shown) indicate that T−2 ≈ 1/2 is a reasonable value.21,39
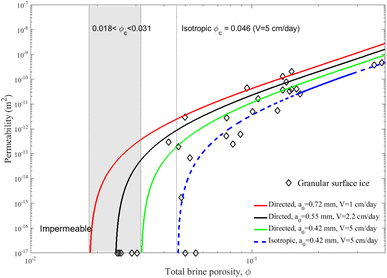 | ||
| Fig. 9 Vertical permeability simulations of granular surface ice versus model results (eqn (16) to (19)) for high and low growth rates as in Fig. 7, plus a modified high-growth-velocity prediction assuming isotropic percolation (blue dashed curve), explained in the text. | ||
The results of such a granular ice modification are shown in Fig. 9 as a blue dashed curve. Assuming the highest growth velocity at the surface, this predicts a percolation threshold of ϕc ≈ 0.046. While the number of permeability simulations is limited, the higher threshold is consistent with the results. More data would be needed for a validation. It also should be noted that the structure of granular ice may differ from the assumed simple plate assemblage with random orientation, and that its critical exponent t may also be different from the columnar value. However, the basic idea introduced here is that granular sea ice has a 50% higher percolation threshold than columnar sea ice. It will be further discussed in connection with previous studies.
6.3 Revisiting previous studies
How do the results compare to earlier studies that had largely agreed on a percolation threshold of ≈0.05?3,19,20,26 In a recent study21 the author and his colleagues qualitatively discussed the following factors as possible reasons: (i) differences in ice growth velocity, (ii) the difference between granular and columnar ice, (iv) aspects of full-thickness permeability and aging of sea ice, (iv) spatial resolution (when analysing CT images20), and (v) limitations in indirect methods, like desalination measurements of sea ice. The present permeability model does now allow a more quantitative assessment of these factors.The third dataset of full depth permeability discussed by Golden et al.19 is the experimental data from Ono and Kasai,74 who measured the upward and downward permeability through 6-cm-thick laboratory grown sea ice at different temperatures. Golden et al.19 also associated these experimental results with their proposed percolation threshold (≈0.05). However, the author and his colleagues21 pointed out that this (very thin) ice must have had a high salinity and, if at all, the data would indicate a percolation transition at a brine volume above 0.1. On the basis of the present model it is now possible to revise the interpretation of these data. Fig. 10 compares the data from Ono and Kasai74 to the present permeability simulations and model predictions. The low- and high-growth-rate model results are again shown with red and green curves, respectively. However, the velocity bounds have been extended with respect to Fig. 7. The lower bound reflects now a plate spacing of 1.0 mm (V ≈ 0.4 cm per day), while the upper bound corresponds to the average growth rate in the experiments from ref. 74, which was V ≈ 8.6 cm per day (giving a0 ≈ 0.35 mm). The green and red curves thus span the typical growth velocity regime from rapidly growing lead ice to thick ice, as well as the observed range in plate spacing.29 It is clear that the experimental results from ref. 74 fall several orders of magnitude below the columnar sea ice model predictions. However, as the experiments from ref. 74 refer to the full-depth permeability, they very likely imply the flow through a granular surface ice regime. To account for this the modifications as described in Section 6.2 were made, and the high-growth-velocity solution was also drawn for this granular ice model, shown as the hatched blue curve denoted as ‘isotropic’. This curve now shows much better agreement with the upward permeability tests from ref. 74. The modelled (granular) percolation threshold in that case is ϕc ≈ 0.055. One may further argue that the very surface ice likely has grown faster than the average of V ≈ 8.6 cm per day reported by Ono and Kasai;74e.g., for a 50% larger growth rate (≈13 cm per day) the model would closely fit the upward permeability data, with a porosity threshold ϕc ≈ 0.055 (not shown).
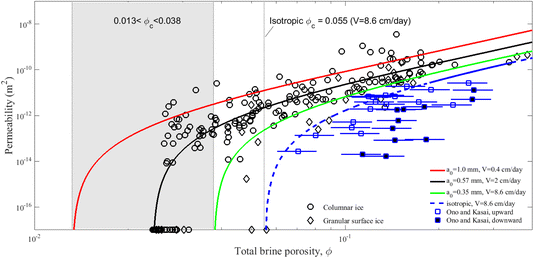 | ||
| Fig. 10 Vertical permeability simulations versus model results (eqn (16) to (19)). Compared to Fig. 7 the model bounds for high and low growth rate are chosen somewhat higher and lower, to resemble the range in naturally growing sea ice (with percolation threshold range 0.013 < ϕc < 0.038). The upper growth rate is set to V = 8.6 cm per day for comparison to Ono and Kasai’s74 experiments (blue symbols). A modified high-growth-rate prediction, assuming isotropic percolation, is shown as blue dashed curve, and the corresponding ϕc = 0.055 is also highlighted. | ||
Note that Golden et al.19 only showed the much smaller downward permeability observations from ref. 74, and that their hypothesis of a percolation threshold of 0.05 for these data implies a salinity of ≈5. The data points in Fig. 10 are based on a two-times higher salinity that appears much more likely for this thin, young ice.21 The comparison to the present model indicates that the downward permeability rather reflects a porosity threshold of 0.1 or higher. It is not clear why the downward permeability should be so much smaller than the upward permeability (and the threshold so large). The author and his colleagues21 suggested that, if the downward experiments were performed after the upward experiments, the ice salinity could have been reduced (which would shift the data points to lower porosity to the left). Another explanation could be that pouring cold brine on the surface, as done by Ono and Kasai74 in downward tests, led to additional crystal growth affecting the permeability.
In summary, when modifying the present model for granular surface ice (using an isotropic instead of directed percolation approach), one would expect a 50% higher percolation threshold than for columnar sea ice. For an initial growth rate of 5 to 10 cm per day for surface ice, this implies a percolation threshold in the range 0.04 < ϕc < 0.06. A review of permeability measurements involving flow through the ice surface appears to be consistent with such a hypothesis.
Among the few other micro-CT studies, Salomon et al.66 reported, for a voxel size of 25 μm, vertical connectivity down to a porosity of 0.05, yet the number of samples below that value was limited (at 0.03 two were permeable, one not). The authors of ref.39 have analysed granular and columnar Arctic sea ice samples with the same spatial resolution as in ref. 20, a voxel size of 41.5 μm, and reported a percolation threshold of ϕc ≈ 0.08 for columnar ice. As this ice was from intermediate depths (0.3–1 m) of 1.4-m-thick sea ice, this is a large value compared to the present predictions. Other factors like raw data quality, noise and filtering, as well as aspects of centrifuging and sample dimensions (see above) may have influenced the results. In that context another study of young sea ice76 is interesting: here the voxel size was 11.8 μm and the percolation threshold of columnar samples appeared to be close to 0.05. However, in that study considerable amounts of brine could not be centrifuged out, which was likely due to a low (10×g) centrifuge acceleration.
6.4 Relevance for sea ice modelling
The essential results of the present work for sea ice modelling summarised in Fig. 10 are highlighted as follows:(1) The percolation threshold of columnar sea ice depends on its growth rate and can be expected to vary in the range 0.01 < ϕc < 0.04 for typical natural growth conditions.
(2) The corresponding permeability, when corrected for brine porosity, may vary by almost 2 orders of magnitude.
(3) The permeability can be parametrised in terms of brine volume and ice growth velocity alone.
(4) The estimate of a 50% larger percolation threshold for granular surface ice (compared to columnar ice grown at the same rate) is another important conjecture supported by observations.
The present work provides the relationship of permeability and brine volume ϕ for different growth conditions. The brine volume dependence on ice temperature and salinity is approximately ϕ ≈ cmSi/Ti, where Ti is given in °C and cm is typically in the range −0.05 to −0.07 °C/ppt for natural sea ice conditions (for more exact formulations see ref. 44 and 79). The sea ice salinity Si is thus of particular importance to obtain the permeability. Starting with the work by Cox and Weeks2 there have been considerable efforts to numerically predict the sea ice salinity evolution based on ‘mushy layer’ theories of gravity-driven brine drainage.5–8,80,81 All these models require as input a permeability–porosity function that in most cases has been taken from the discussed study by Freitag.24 The present model improves this considerably and makes it possible to account for microstructure and growth rate effects, as well as physically consistent percolation thresholds. However, some caution is in order: the mentioned large-scale models have so far only used the vertical permeability in their model frameworks, while horizontal permeability and percolation thresholds are likely to play a role. Hence one needs more observations and modelling effort on the anisotropy of permeability to properly predict salinity. The present author is currently working on a salinity prediction model based on the microstructure scales d0 and a0, in line with the present work and some earlier approaches.5,32,82
The permeability equations (eqn (16) to (18)) may, using the relationship in eqn (7) between a0 and growth velocity V, be written as:
| K = 0.0432V−2/3ϕ3 [ϕV−1/3 > 0.167], | (22) |
| K = ck(ϕ−0.0183V1/3)2.55 [0.0183 < ϕV−1/3 < 0.167], | (23) |
| K = 0 [ϕV−1/3 < 0.0183], | (24) |
| ck = 2.60 × 10−8V(−1.55/3) m2 | (25) |
6.5 Ocean–ice–atmosphere fluxes of gas and matter
The vertical permeability of sea ice is also essential for understanding sea ice biogeochemistry and air–ice gas fluxes.11–14 Sea ice plays a different role than open water or cracks in the ice. Due to its low temperature it contains solutes and chemical species at higher concentration, and also allows for bio-geochemical processes in its pore space that would not take place in the oceanic surface layer. This implies interactions between sea ice and atmospheric chemistry, for which the sea ice permeability is important.An example for the effect of sea ice permeability and chemistry on gas exchange with the ocean and the atmosphere is the CO2 budget.84,85 During wintertime and sea ice growth it is the near bottom permeability of sea ice that controls gravity-driven brine convection, and a transport of CO2 to deeper ocean layers.86 When the ice melts, the surface is undersaturated with CO2, leading to enhanced CO2 uptake by the ocean. This process is complicated by the carbonate chemistry and thermodynamics of cooling sea ice, where calcium may precipitate as calcite or as ikaite. This implies differences in the alkalinity and buffering capacity of brine, and in the temperature (and permeability) of calcium precipitation. While brine convection transfers the CO2 to deeper ocean layers, the carbonate precipitates may then remain in the ice, with consequences for the carbon budget.17,18,85 The permeability may play a critical role in this puzzle.
A related impact on atmospheric chemistry is the enhanced bromine release by a reduced buffering capacity of sea ice brine due to calcite precipitation,16 with bromine acting as a catalyst for the destruction of stratospheric ozone.15,87 The process depends on the ability of liquid brine to migrate to the surface, and hence on ice microstructure and permeability. Others88 have discussed sea ice as the source of iodine in the atmosphere, with production by micro-algae in the ice linked to brine transport to the surface. Also this process will depend on the detailed permeability and connectivity of the sea ice pore space, and the details of sea ice thermodynamics and growth conditions.
The ocean–ice–atmosphere exchange of dimethyl sulfide (DMS), as a major source of polar atmospheric aerosols, was recently studied by Gourdal et al.89 The fluxes were linked to algae growth (during spring and summer) and DMS production at the sea ice bottom in connection with brine circulation and gas diffusion in the ice (molecular diffusion of gas dissolved in brine as well as upward movement of gas bubbles). Also the exchange of methane between sea ice and the atmosphere during the winter season has been studied.90 In these and many other studies on gas fluxes (ref. 11 and 13, for example), the permeability has been suggested as an important property. However, most investigators have interpreted their results relying on a constant percolation threshold of ϕc ≈ 0.05 and the permeability equation (eqn (2)) from Freitag.13,89,90 The present model for the permeability and its threshold provides the basis for a revised analysis of such studies.
Two processes are of particular relevance for the noted air–ice gas fluxes. One is the transport of brine to the sea ice surface and the overlying snow layer, triggering air–ice exchange processes as mentioned for the halogen chemistry.15,87,88 This transport is still poorly understood. During wintertime it may relate to internal freezing and upward expulsion of brine towards the surface. While the colder the ice, the more brine will be expelled, colder ice will also approach the permeability threshold, which in turn depends on growth conditions. This interaction may lead to complex bounds in the brine fluxes. However, what role the micro-scales d0 and a0 play at the ice surface, and how permeability evolves there, needs to be further studied. Not only is the initial ice growth not columnar, but the microstructure is also affected by other factors like large temperature fluctuations, drainage processes in the freeboard, interaction with snow and weathering. The second is the transport of gas by rising gas bubbles that form in warming ice during the melt season.14,90 For such bubble movement in old ice, the percolation thresholds may differ from those of thin brine layer networks during ice growth.
6.6 Relevance for directed percolation in general
Directed percolation has been used to theoretically describe a wide range of processes in statistical physics:59,60 catalytic reactions, epidemics, calcium dynamics, forest fires, directed polymers, porous media, and even turbulence. However, only very few experimental realisations have been reported.59,60 While gravity-driven directed percolation of natural porous media had already been discussed by Broadbent and Hammersley,55 so far it has not been realised experimentally. To understand why sea ice may exhibit directed percolation behavior, the following brief overview is given following ref. 59.Directed percolation may be described as a spreading process restricted to a given direction, where activity may either spread over the entire lattice or die out. The inactive state is called absorbing, as it can be reached and not left again, and directed percolation is thus a non-equilibrium process. When interpreting the direction as time, it may be viewed as a dynamic reaction–diffusion process in d + 1 dimensions, governed by the following operations of active (A) and inactive (I) sites:
(i) Diffusion: I + A → A + I
(ii) Self-destruction: A → I
(iii) Offspring production: A → A + A
(iv) Coagulation: A + A → A
Depending on the ratio between (ii) self destruction and (iii) offspring production, the spreading may remain active or reach the absorbing state from where it cannot escape.
The pore space evolution of sea ice may be interpreted as such a reaction–diffusion process. The direction is given by heat flow and gravity resulting in a columnar anisotropic microstructure and pore networks. The non-conservative character is related to thermo- and fluid dynamics: cooling leads to decreasing porosity but also to vertical movement of brine, while gravity drainage exchanges fluid vertically with the ocean underneath. As the ocean salinity is less than that of brine inside pores, this process also decreases (increases) the pore size and volume for upflow (downflow). The change in brine porosity, pore sizes and pore connectivity thus spreads vertically. The redistribution of solute and brine corresponds to diffusion (i), the porosity decrease due to thermodynamics and upward flow corresponds to self destruction (ii), the downward flow and brine transport may create (iii) offsprings and coagulating channels (iv). Sea ice reaches an inactive state below the percolation limit, once salt fluxes between ice and ocean, in concert with thermodynamic transitions, have locked the pore space. It cannot escape from this new absorbing state before it warms again. While the absorbing state is not strictly met in sea ice, which intermittently warms and cools, one expects a fluctuation between active and inactive states. Whereas the present study (as well as ref. 21) cannot be considered as a proof that DP manifests itself in sea ice, the above considerations and the present data analysis support the hypothesis.
6.7 Limitations and future needs
The present study helps to better understand the scatter in observations and simulations of permeability, Fig. 7 and 9 relating it to differences in ice type and growth velocity. How large are the expected uncertainties in the model results and observations? As discussed in Section 5, the equations based on the standard settings for d0, fc and t predict a permeability that is only slightly higher (12–22%) than the best fit to simulations. The underestimate of permeability by simulation and experiment, related to finite sample sizes and pore inclination/tortuosity, has a similar magnitude (Section 6.3.2). In granular ice with higher tortuosity the underestimate will be larger. Such underestimates may be reduced by simulations on samples with larger diameter. To keep the spatial resolution this requires micro-CT optics with more pixels.The model results depend mainly on parametrisations for the plate spacing a0, the value of d0, and the critical exponent t. The question if d0 is indeed constant, and the mechanism that leads to bridging at d0, needs to be investigated. The growth rate dependence of a0 is reasonably understood,29 and taking the plate spacing error as 10% results in a 20% permeability error. The effect of t increases with decreasing porosity, e.g., varying t within its confidence range 2.55 ± 0.25 at ϕ = 0.07 and a0 = 0.55 mm changes the permeability by up to 50%. More data, and also here simulations on larger samples, would improve the confidence of t. However, t is not a true universal exponent, yet is expected to vary with pore size distribution, and progress may be made by studies that constrain t based on certain pore space metrics.64,65 There is another refinement that one may introduce in the model: the formulation of the columnar permeability model assumed no initial (at ϕ0) tortuosity. However, as discussed above, typical brine layer inclination angles in young ice are 10–20°. The corresponding permeability reduction, given as cos(α)2, is 3–12%.
To model the permeability of granular ice the same critical exponent t as obtained empirically for the columnar ice data has been used. This ad hoc approach was necessary as there is insufficient data for granular surface ice. As the pore space evolution with porosity may be different for granular compared to columnar ice, and as granular ice may be better described by isotropic percolation (due to which argument a 50% higher ϕc was proposed), a different exponent t could expected. Also adopting the plate spacing and bridging concept for granular ice may need some modification. However, the simple approach reasonably explains the difference in percolation threshold of granular and columnar ice as indicated by simulations and observations.
Older ice has often experienced severe temperature fluctuations that will change the microstructure from their initial scales (d0 and a0) to coarser brine channels. The permeability may then reach values one to two orders of magnitude above the range of young ice.24 Important questions are: Is this transition smooth and does the permeability evolution remain related to the original growth conditions? Or does the permeability of old summer ice become independent of the young ice permeability during its formation, and thus the growth conditions? Some information on pore size evolution during warming and aging of sea ice is available but limited,38,39,66,91 and more detailed studies are needed.
It should also be noted that percolation theory based on critical exponents is strictly valid only close to the percolation threshold ϕc. In practice it often holds at higher porosity, where the effect of ϕc due to the (ϕ − ϕc)q dependence is weak. With more exact fits closer to ϕc, however, the simplicity of the present model would be lost. Also, the constant fc approach from ref. 68 is semi-empirical and does not work for all isotropic lattices.92 The agreement we find for sea ice might be coincidence and deserves further studies.
7 Conclusions
In this study I have derived equations that predict the permeability of sea ice, and its percolation threshold, in dependence on the growth rate of ice. While eqn (16) to (19) appear rather simple, their derivation is the result of half a century of studies by many investigators, starting with an approach to relate the mechanical behavior of sea ice to its microstructure and a critical porosity ϕ0 ≈ d0/a0.30,44 A value of ϕ0 ≈ 0.2 has since then been discussed in many investigations of the mechanical properties of sea ice mechanics.31,53,93,94 Studies on sea ice thermodynamics and desalination then indicated another critical porosity of about ϕc ≈ 0.052, and in later years this transition was interpreted in terms of permeability and percolation theory.3,19,20,26 Only recently, X-ray microtomographic imaging has provided sufficient data to study these microstructure details, derive a more accurate ϕc, and draw conclusions about the relevant (directed) percolation model.21 The present study has extended that work by a model for the percolation threshold and permeability that is supported by most observations. It puts the above critical porosities into a unified form ϕc = fcϕ0 = fcd0/a0, where fc is based on directed percolation theory, d0 is the critical brine layer width, and the plate spacing a0 is related to the growth rate of ice.29It is anticipated that d0 and a0 are relevant for other sea ice properties and processes, some of which were briefly discussed in the present paper. Increasing availability and quality of 3D sea ice microstructure data in recent years21,38,39,66,91,95 imply an increasing potential to study the relationships of physical properties, microstructure and growth conditions. Such studies are, in the author’s opinion, inevitable for obtaining a good understanding of the role of sea ice in the environment.
Data availability
The microCT data (170 GB) are available online.21Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was partly funded through the Research Council of Norway (RCN) programme PETROMAKS2, grant no. 308786.References
-
W. F. Weeks, On Sea Ice, Univ. of Alaska Press, 2010, p. 600 Search PubMed
.
- G. F. N. Cox and W. F. Weeks, J. Geophys. Res., 1988, 93, 12449–12460 CrossRef
.
- C. Petrich, P. J. Langhorne and Z. F. Sun, Cold Reg. Sci. Technol., 2006, 44, 131–144 CrossRef
.
- M. Vancoppenolle, C. M. Bitz and T. Fichefet, J. Geophys. Res.:Oceans, 2007, 112, C04022 CrossRef
.
-
S. Maus, Report Series of Geophysics, University of Helsinki, 2008, pp. 99–112 Search PubMed
.
- P. J. Griewank and D. Notz, J. Geophys. Res.:Oceans, 2013, 118, 3370–3386 CrossRef
.
- A. K. Turner and E. C. Hunke, J. Geophys. Res.:Oceans, 2015, 120, 1253–1275 CrossRef
.
- D. Rees Jones and M. Grae Worster, J. Geophys. Res.:Oceans, 2014, 119, 5599–5621 CrossRef
.
- I. Melnikov, J. Geophys. Res.:Oceans, 1995, 100, 4673–4680 CrossRef
.
-
D. Thomas and G. S. Dieckmann, Sea Ice: an Introduction to its Physics, Chemistry, Biology and Geology, Blackwell, 2003 Search PubMed
.
- M. Vancoppenolle,
et al.
, Quat. Sci. Rev., 2013, 79, 207–230 CrossRef
.
- I. Semiletov, A. Makshtas, S. Akasofu and E. L. Andreas, Geophys. Res. Lett., 2004, 31, L05121 CrossRef
.
- M. Angelopoulos,
et al.
, Front. Earth Sci., 2022, 10, 864523 CrossRef
.
- N. Geilfus, B. Delille, J. Tison, M. Lemes and S. Rysgaard, Elem. Sci. Anth., 2023, 11, 00056 CrossRef
.
- T. Koop, A. Kapilashrami, L. T. Molina and M. J. Molina, J. Geophys. Res., 2000, 105, 26393–26402 CrossRef CAS
.
- R. Sander, J. Burrows and L. Kaleschke, Atmos. Chem. Phys., 2006, 6, 4653–4658 CrossRef CAS
.
- G. S. Dieckmann, G. Nehrke, S. Papadimitriou, J. Göttlicher, R. Steininger, H. Kennedy, D. Wolf-Gladrow and D. N. Thomas, Geophys. Res. Lett., 2008, 35, L08501 CrossRef
.
- S. Morin, G. M. Marion, R. von Glasow, D. Voisin, J. Bouchez and J. Savarino, Atmos. Chem. Phys., 2008, 8, 7317–7324 CrossRef CAS
.
- K. M. Golden, S. F. Ackley and V. I. Lytle, Science, 1998, 282, 2238–2241 CrossRef CAS PubMed
.
- D. J. Pringle, J. E. Miner, H. Eicken and K. M. Golden, J. Geophys. Res., 2009, 114, C12017 Search PubMed
.
- S. Maus, M. Schneebeli and A. Wiegmann, The Cryosphere, 2021, 15, 4047–4072 CrossRef
.
-
F. A. L. Dullien, Porous Media: Fluid Transport and Pore Structure, Academic Press, 2nd edn, 1991 Search PubMed
.
-
D. A. Nield and A. Bejan, Convection in Porous Media, Springer, 2nd edn, 1999 Search PubMed
.
-
J. Freitag, PhD thesis, Universität Bremen, 1999
.
- T. Maksym and M. O. Jeffries, J. Geophys. Res., 2000, 105, 26313–26331 CrossRef
.
- K. M. Golden, H. E. A. Heaton, J. Miner, D. J. Pringle and J. Zhu, Geophys. Res. Lett., 2007, 34, L16501 CrossRef
.
- W. F. Weeks and W. L. Hamilton, Am. Mineral., 1962, 47, 945–961 CAS
.
- M. Nakawo and N. K. Sinha, Atmos.-Ocean, 1984, 22, 193–206 CrossRef
.
- S. Maus, Ann. Glaciol., 2020, 61, 408–425 Search PubMed
.
- D. L. Anderson and W. F. Weeks, Trans., Am. Geophys. Union, 1958, 39, 632–640 CrossRef
.
-
W. F. Weeks and A. Assur, Ice and Snow, 1963, pp. 258–276 Search PubMed
.
-
S. Maus, On Brine Entrapment in Sea Ice: Morphological Stability, Microstructure and Convection, Logos, Berlin, 2007 Search PubMed
.
- F. Flin, J. B. Brzoska, B. Lesaffre, C. Coleou and R. A. Pieritz, Ann. Glaciol., 2004, 38, 39–44 CrossRef
.
- M. Schneebeli and S. A. Sokratov, Hydrol. Processes, 2004, 18, 3655–3665 CrossRef
.
- J. Freitag, F. Wilhelms and S. Kipfstuhl, J. Glaciol., 2004, 50, 243–259 CrossRef
.
- M. W. Hörhold, M. R. Albert and J. Freitag, J. Glaciol., 2009, 55, 625–630 CrossRef
.
- R. Obbard, G. Trodermann and I. Baker, J. Glaciol. 2009, 55, 1113–1115 Search PubMed.
-
S. Maus, J. Becker, S. Leisinger, M. Matzl, M. Schneebeli and A. Wiegmann, 23rd Proc. Port and Ocean Engineering under Arctic Conditions, Trondheim, Norway, 2015, https://www.poac.com Search PubMed
.
- M. Oggier and H. Eicken, J. Glaciol., 2022, 68, 833–848 Search PubMed
.
- W. Scoresby, Mem. Wernerian Soc., 1815,(2), 328–336 Search PubMed
.
- D. Walker, Proc. R. Soc. London, 1859, 9, 609–611 CrossRef
.
- F. Ruedorff, Ann. Phys., 1861, 190, 63–81 CrossRef
.
- T. Fukutomi, M. Saito and Y. Kudo, Low Temp. Sci., 1952, 9, 113–123 Search PubMed
.
-
A. Assur, Arctic Sea Ice, 1958, pp. 106–138 Search PubMed
.
- W. Schwarzacher, J. Geophys. Res., 1959, 64, 2357–2367 CrossRef
.
- N. V. Cherepanov, Tr. Arkt. Antarkt. Nauchno-Issled. Inst., 1964, 267, 13–18 Search PubMed
.
- N. K. Sinha and C. Zhan, J. Mater. Sci. Lett., 1996, 15, 2118–2121 CrossRef CAS
.
-
W. F. Weeks and G. Lofgren, Physics of Snow and Ice, Sapporo, Japan, 1967, pp. 579–597 Search PubMed
.
-
S. Maus, in Physics and Chemistry of Ice, ed. W. F. Kuhs, Royal Society of Chemistry, 2007, pp. 371–382 Search PubMed
.
- W. W. Mullins and R. F. Sekerka, J. Appl. Phys., 1964, 35, 444–451 CrossRef
.
- G. A. Maykut, J. Geophys. Res., 1978, 83, 3646–3658 CrossRef
.
- G. F. N. Cox and W. F. Weeks, J. Glaciol., 1974, 13, 109–120 CrossRef
.
-
S. Maus, Proceedings - 27th Conference on Port and Ocean Engineering under Arctic Conditions, Glasgow, Scotland, 2023, p. 41, https://www.poac.com Search PubMed
.
- W. F. Weeks and D. L. Anderson, Trans., Am. Geophys. Union, 1958, 39, 641–647 CrossRef
.
- S. R. Broadbent and J. M. Hammersley, Math. Proc. Cambridge Philos. Soc., 1957, 53, 629–641 CrossRef CAS
.
-
D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor & Francis, 2nd edn, 1992 Search PubMed
.
- M. Sahimi, Rev. Mod. Phys., 1993, 65, 1393–1534 CrossRef
.
- S. Maus, S. Bahafid, M. Hendriks, S. Jacobsen and M. Geiker, Cold Reg. Sci. Technol., 2023, 208, 103780 CrossRef
.
- H. Hinrichsen, Adv. Phys., 2000, 49, 815–958 CrossRef CAS
.
-
M. Henkel, H. Hinrichsen and S. Lübeck, Non-equilibrium Phase Transitions. Volume I: Absorbing Phase Transitions, Springer, 2008 Search PubMed
.
- A. Sur, J. Lebowitz, J. Marro, M. Kalos and S. Kirkpatrick, J. Stat. Phys., 1976, 15, 345–353 CrossRef
.
- H. Janssen and U. Täuber, Ann. Phys., 2005, 315, 147–192 CAS
.
- H. Janssen and O. Stenull, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2001, 63, 025103(R) CrossRef PubMed
.
- A. J. Katz and A. H. Thompson, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 34, 8179–8181 CrossRef CAS PubMed
.
- P. Le Doussal, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 39, 4816–4819 CrossRef CAS PubMed
.
- M. Salomon, S. Maus and C. Pertrich, J. Glaciol., 2022, 68, 571–590 CrossRef
.
- GeoDict, Geometric material Models and Computational PreDictions of Material Properties, 2012–2024, https://www.geodict.com.
- H. Scher and R. Zallen, J. Chem. Phys., 1970, 53, 3759–3761 CrossRef CAS
.
- D. S. Gaunt and M. F. Sykes, J. Phys. A: Math. Gen., 1983, 16, 783–799 CrossRef
.
- S. Lübeck and R. Willmann, J. Stat. Phys., 2004, 115, 1231–1250 CrossRef
.
- P. Grassberger, J. Stat. Mech.:Theory Exp., 2009, 2009, P08021 Search PubMed
.
- J. Wang, Z. Zhou, Q. Liu, T. Garoni and Y. Deng, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042102 CrossRef PubMed
.
-
M. Shokr and N. Sinha, Sea Ice Physics and Remote Sensing, John Wiley and Sons, 2015 Search PubMed
.
- N. Ono and T. Kasai, Ann. Glaciol., 1985, 6, 298–299 CrossRef
.
- T. Kawamura, Contrib. Inst. Low Temp. Sci., Hokkaido Univ., Ser. A, 1988, 3120, 1–29 Search PubMed
.
-
J. Buettner, MSc thesis, University Bergen, 2011
.
- R. Morey, A. Kovacs and G. F. N. Cox, Cold Reg. Sci. Technol., 1984, 9, 53–75 CrossRef CAS
.
- K. Jones, M. Ingham and H. Eicken, J. Geophys. Res., 2012, 117, C02005 Search PubMed
.
- G. F. N. Cox and W. F. Weeks, J. Glaciol., 1986, 32, 371–375 CrossRef CAS
.
- N. Jeffery, E. Hunke and S. Elliott, J. Geophys. Res., 2011, 116, C07020 CrossRef
.
- J. R. Urrego-Blanco, N. Urban, E. C. Hunke, A. Turner and N. Jeffery, J. Geophys. Res.:Oceans, 2016, 121, 2709–2732 CrossRef
.
- V. L. Tsurikov, Okeanologiia, 1965, 5, 463–472 CAS
.
- C. Renshaw, O. Marchenko, E. Schulson and E. Karulin, J. Glaciol., 2018, 64, 443–449 CrossRef
.
- E. P. Jones and A. R. Coote, J. Geophys. Res., 1981, 86, 11041–11043 CrossRef CAS
.
- S. Rysgaard, R. N. Glud, M. K. Sejr, J. Bendtsen and P. B. Christensen, J. Geophys. Res., 2007, 112, C03016 CrossRef
.
- L. G. Anderson, E. Falck, E. P. Jones, S. Jutterström and J. H. Swift, J. Geophys. Res., 2004, 109, C06004 Search PubMed
.
- W. R. Simpson, R. von Glasow and K. Riedel,
et. al.
, Atmos. Chem. Phys., 2007, 7, 4375–4418 CrossRef CAS
.
- A. Saiz-Lopez., C. S. Blaszczak-Boxe and L. Carpenter, Atmos. Chem. Phys., 2015, 15, 9731–9746 CrossRef CAS
.
- M. Gourdal, O. Crabeck, M. Lizotte, V. Galindo, M. Gosselin, M. Babin, M. Scarratt and M. Levasseur, Elem. Sci. Anth., 2019, 7, 33 CrossRef
.
- E. Damm, S. Thoms, M. Aneloppulos, L. von Albedyll, A. Rinke and C. Haas, Front. Earth Sci., 2019, 12, 1338246 CrossRef
.
- C. M. Frantz, B. Light, S. Farley, S. Carpenter, R. Lieblappen, Z. Courville, M. V. Orellana and K. Junge, The Cryosphere, 2019, 13, 775–793 CrossRef
.
- I. Balberg and N. Binenbaum, Phys. Rev. B:Condens. Matter Mater. Phys., 1987, 35, 8749–8752 CrossRef CAS PubMed
.
-
B. Michel, Ice Mechanics, Les Presses De L’Université Laval, Québec, 1978 Search PubMed
.
- J. A. Richter-Menge and K. F. Jones, J. Glaciol., 1993, 39, 609–618 CrossRef
.
- R. Lieb-Lappen, E. Golden and R. Obbard, Cold Reg. Sci. Technol., 2017, 138, 24–35 CrossRef
.
| This journal is © The Royal Society of Chemistry 2025 |