Fiber formation seen through the high-resolution computational microscope

Abstract

Supramolecular fibers draw widespread attention due to their role in biological systems and ability to form complex materials exhibiting rich and dynamic behavior. Although the information about the supramolecular structure is encoded in their molecular blocks, a complete understanding of how this information translates into the final structure requires detailed insights into the energy landscape of the process and the possible routes across this landscape. Here, we study the formation of 1,3,5-cyclohexanetricarboxamide fibers by a Markov state model of molecular dynamics simulations with the polarizable CHARMM Drude force-field. We provide insights into all stages of supramolecular fiber formation up to microsecond timescales, starting from primary nucleation, through fiber elongation and secondary nucleation, and finally, the assembly of single fibers into bundles. Our results show that nucleation involves a rapid collapse of dissolved monomers into disordered assemblies, which gradually transform into nuclei and then grow into elongated fibers. Moreover, elongation and secondary nucleation appeared to be competing processes, depending on the density of the monomers adsorbed at the fiber–liquid interface. Finally, bundling involves the initial association of fibers by interactions between surface-exposed groups, followed by stabilization of the bundle by surface reorganization, which allows for favorable interactions between aromatic groups.

---

Introduction

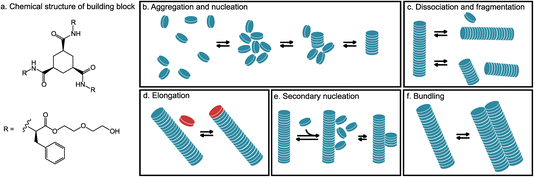
Supramolecular fiber networks exhibit rich and dynamic behavior, not present in conventional covalently bonded polymers. They hold promising applications in electronics,¹ biomedicine,^2–4 and material science⁵ and are an integral part of cellular life.⁶ The early stages of supramolecular network formation are extensively studied due to their influence on the final structure.^7,8 Unfortunately, detailed insights, especially on a short timescale and molecular length scale, such as how a nucleus is formed or what processes follow after a stable nucleus is established, are scarce because of the experimental limitations associated with the transient nature of the processes.^9–11 Therefore, many computational studies have recently been devoted to these systems.^9,12,13 Most of these studies focus only on the first step of formation, the self-assembly of a single fiber, and use coarse-grained molecular dynamics (CG-MD) in which intermolecular interactions are modeled at a resolution that groups several atoms into one interaction site.^14–19 While providing important insights, these studies are limited in scope and accuracy.

This work aims to give insights into a number of key processes that take place during the self-assembly of supramolecular networks, including primary and secondary nucleation, dissociation, fragmentation, elongation, and bundling at a high resolution of intermolecular interaction. Here, we study an atomistic, polarizable model of 1,3,5-cyclohexanetricarboxamide (CTA; Fig. 1a) molecules in water, which create columnar stacks via trifold hydrogen bonding between neighboring molecules.²⁰ Self-assembly of fibers with trifold hydrogen bonding has recently been a subject of many experimental^21–23 and computational studies.^{14,15,24–27} In our previous work,²⁸ we observed that self-assembly simulations with standard atomistic force-fields, such as CGenFF or GROMOS, lead to very stable but unordered aggregates. The more expensive CHARMM Drude force field,²⁹ which explicitly models atom polarizability, showed a stable fiber structure and exhibited more dynamic behavior, which held the promise that self-assembly of stable fibers and potentially of a bundle consisting of several fibers could be achieved. However, studying these processes requires simulations on a large spatial and temporal scale and, therefore, seems not to be feasible for standard (polarizable) atomistic molecular dynamics simulations. To decrease the size of the studied system, we have separated the fiber formation process into several smaller elementary processes, and to address the long timescale, we have used a conformational resampling approach.

Fig. 1 (a) Chemical structure of 1,3,5-cyclohexanetricarboxamide (CTA). (b–f) Schemes summarizing processes studied in this work: (b) aggregation and nucleation, (c) dissociation and fragmentation, (d) elongation, (e) secondary nucleation, and (f) bundling.

To decrease the size of the system, we have separated the self-assembly process into several distinct phases, which were inspired by studies of protein fiber aggregation.^6,30 In general, the formation of protein aggregates follows a complex pathway consisting of many different transitions occurring simultaneously.³¹ However, the elementary processes making up the pathway to fibers are established (Fig. 1b–f). Here, we briefly summarize the results of protein fiber formation.^6,30,31 The self-assembly starts with the creation of a nucleus. A nucleus grows mainly by elongation, in which new molecules arrive at the end of the fiber by diffusion. In rare cases, it can grow by head-to-tail fiber–fiber association. Reverse processes, dissociation and fragmentation, are possible, but due to strong interactions are negligible for proteins.³¹ Fragmentation is typically induced by thermal or mechanical forces. Additionally, new nuclei can be formed by nucleation catalyzed by the existing surface of the fiber, here called secondary nucleation, which leads to the formation of a bundle of fibers.³¹ In addition, bundles can be created by the aggregation of fibers leading to different shapes and organizations.³²

Since the formation of nuclei when using a model at atomistic resolution happens on a timescale beyond that of standard computational techniques, we use conformational resampling and Markov state modeling (MSM) to model the process. MSM can give insights into processes beyond the timescales of conventional molecular dynamics.^33–35 It has also been used to study self-assembly.^36,37 Using this method, we were able to give insights not only into the early stages of self-assembly but also into later stages, such as elongation and secondary nucleation. Moreover, we confirm the view on the nature of the CTA assembly obtained from the simulations by cryo-TEM measurements of assembled fibers and bundles.

Methods

Molecular dynamics

All simulations were performed with a tailored GROMACS^38,39 version using the CHARMM Drude force-field²⁹ at 298.15 K (Section S1†). Systems consisted of CTA molecules and water (SWM4-NDP model⁴⁰). Due to the high computational cost of this method, we could simulate only small systems with high concentrations (∼0.3 M). For example, we simulated 8 CTA molecules with 1539 water molecules for primary nucleation, which is equivalent to 0.29 M, much higher than the critical gelation concentration of 0.36 mM.²⁰ We justify such high concentration by assuming that molecules end up in a small volume at one point in time, creating a locally highly concentrated system. An overview of the simulations performed is given in Table S1 of the ESI.† Equilibration was done in NPT ensemble, but the production simulations were run in the NVT ensemble due to the lack of an efficient barostat implementation in GROMACS for the CHARMM Drude force-field. Details of the model and parameters, including set-up files and topologies, are available in the ESI.†

Rare-event sampling

To simulate processes occurring on a long timescale (e.g., nucleation), we implemented a conformational resampling method,⁴¹ which is based on favoring the least visited states (Section S1.b†). In principle, in this method, we run many parallel simulations starting from the least visited state, which allows us to explore less-visited parts of the energy landscape. Starting at the edges of the already explored landscape, eventually, new states will be visited. By repeating this procedure many times, we hope to sample the complete available conformational space. To define and distinguish different states in the conformational landscape of interest, we measured the size of the largest ordered stack of molecules (Section S2†). Such a measure was applied to study crystal formation using metadynamics.⁴² We implemented this collective variable using MDAnalysis.⁴³ As a result, we obtained an ensemble of simulations consisting of all possible states and transitions between them. Most importantly, the ensemble also includes a completed fiber consisting of all molecules organized in an ordered array.

Markov state model (MSM)

The combination of all trajectories allows us to study the pathways of the self-assembly by Markov State Modeling (MSM) using pyEMMA (Section S3†).³⁴ Although for the resampling method, the number of ordered molecules has been sufficient as a collective variable to sample formation of the fiber, it turned out to be insufficient to fulfil the Markov assumption (Fig. S5†). Therefore, for MSM, we used a more detailed measure: a vector containing eight elements v=(a₁, …, a₈), whose i-th element describes the number of the ordered neighbors of molecule i, that is , where 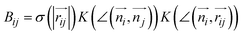and σ and K are smooth cut-off functions for distance and angle, respectively. As a result, B_ij represents a continuous value ranging from 0 to 1 that reflects the extent to which the i-th molecule and the j-th molecule form a neighbor pair based on their distance and orientation (Section S2†). Consequently, each a_i value ranges from 0 to 2, representing the number of ordered neighbors of the i-th molecule (due to the spatial arrangement of molecules in linear stacks, it is not possible for a molecule to have more than two ordered neighbors). The vector v is made invariant under numbering by ordering the elements of the vector from smallest to largest (Fig. S6†).^44,45

We discretize conformational space by assigning states to clusters with centers w = (b₁, …, b₈), where b_i is an integer 0, 1 or 2 (unlike in vector v where a_i are real numbers). As a result, trajectories were discretized into 35 active states. Discretized trajectories were used to estimate Bayesian MSM⁴⁶ using a lag-time of 87 frames. We test the Markovianity of the model by performing the Chapman–Kolmogorov test (Fig. S7†).⁴⁷ The model is coarse-grained using the hidden Markov model.⁴⁸ To investigate the fiber formation mechanism, we analyzed the model using transition path theory (TPT),⁴⁹ which gives insight into the pathways between specific states. In particular, we analyzed pathways leading to self-assembled fiber from randomly distributed molecules.

Cryo-TEM

High-resolution cryo-TEM images were obtained with a JEOL JEM3200-FSC microscope. For details, see Section S7.†

Results and discussion

A. Primary nucleation

We simulated the formation of small CTA stacks from randomly distributed molecules in water at 298.15 K with a total simulation time of 6.7 μs using conformational resampling and analyzed the trajectories by Markov State Modeling (MSM). The initial conditions model a system of solubilized CTA molecules at high temperature, which is instantaneously cooled to 298.15 K. For the analysis, we excluded all trajectories that led to the formation of an infinite fiber (i.e., a fiber that crosses the periodic boundary conditions connecting to itself), which on the timescale of the simulations performed here is irreversible (we did not observe disassembly of such an infinite fiber). The analysis showed thirteen slow processes, and the results are summarized in Fig. 2a–c. Initially, molecules aggregate into a cluster, where every molecule is in direct contact with four to five neighbors on average (Fig. 2b). Molecules in the aggregate are unordered, as can be seen from the low dipole moment and the low number of hydrogen bonds present (Fig. S9†), which suggests that molecules interact mostly by non-directional interactions. Thus, van der Waals and hydrophobic interactions drive the first part of the formation process. Although most molecules stay in the aggregate throughout the majority of the simulations, they still have the flexibility to rearrange within it. Such rearrangements occasionally lead to a small ordered stack, whose lifetime depends on the length of the stack (see section B). The coarse-grained Markov model was analyzed using transition path theory (TPT). Pathway decomposition showed that the main pathway (38.6%) follows a stepwise mechanism, i.e., monomers form dimers, a dimer and a monomer form a trimer, etc. (see the green dotted line in Fig. 2a). Other pathways also follow a stepwise mechanism except for one step, in which n-mers associate with a dimer (see orange and yellow dotted lines in Fig. 2a, and a complete set in Table S2†). Therefore, the mechanism can be described as stepwise with sporadic dimer association to the growing stack. It is worth noting that it was shown that the mechanism of formation of a similar type of fiber, based on benzene 1,3,5-tricarboxamide derivative, depends on concentration.⁵⁰ Therefore, the pathways we observe here could be the result of a high concentration of molecules. As the ordered stack grows, the dipole moment and the number of CTA–CTA amide hydrogen bonds steadily grow, whereas the number of molecules in direct contact decreases, reaching two for the largest ordered fiber that can be reached in the simulation. See ESI† for a video of the fastest observed process of formation.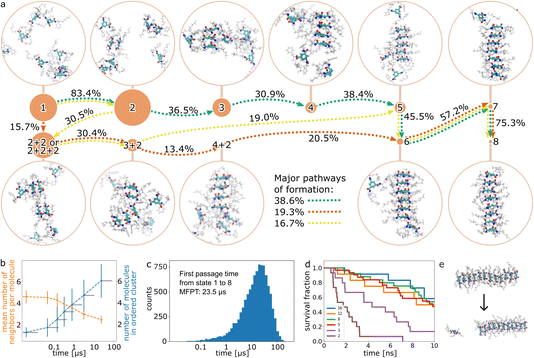

Fig. 2 Primary nucleation. (a) Mechanism of formation of ordered CTA fiber from randomly distributed molecules using MSM and TPT. The filled circles represent states with size proportional to the equilibrium population and numeral(s) indicating the number of molecules in the ordered stack (Table S1†). The arrows represent the net flux with a percentage indicating the relative flux of the path and are only shown for three major pathways (green, orange, and yellow; Table S3 and Fig. S7†). For each state, a representative snapshot is shown. For clarity the trisamidocyclohexane core is shown in thick lines, side chains are semi-transparent, and water is not shown at all. (b) Progress of the size of the ordered cluster (blue) and of the average number of neighbors of a CTA molecule (orange) along the main pathway (dotted green line in (a)). The grey horizontal lines represent the 0.95 confidence intervals of the first passage time to the state. (c) Histogram of expected simulation time for reaching eight molecules in an ordered stack, starting from randomly distributed molecules. (d) Survival analysis of a series of simulations starting from ordered stacks of 2, 3, 5, 8, 12, and 16 molecules. (e) Example snapshots of a single molecule dissociation from an ordered stack (size 12).

TPT shows that the mean first passage time (MFPT) from unordered agglomerate to eight-mer fiber is 23.5 μs, which shows that the process is slow on the MD time scale. We used the transition matrix of the coarse-grained Markov process to generate ten thousand discrete trajectories starting from the randomly distributed molecules and ending when they reached the ordered stack (Fig. 2c). The probability that in 100 ns of conventional MD simulation we observe a process of formation of an eight-molecule fiber is 0.0034, i.e., from 100 ns simulations, on average only 1 out of 294 is expected to yield an eight-molecule fiber.

B. Dissociation and fragmentation

To further study the stability and critical size of formed nuclei, we performed a series of simulations of small ordered stacks of 2, 3, 5, 8, 12, and 16 molecules in water. For every stack size, we run a series of 10 ns simulations (Section S5†) and measure the time of dissociation of a molecule from the stack. Using the Kaplan–Meier estimator, we calculate the survival rate;⁵¹ results are presented in Fig. 2d. All dimers and most trimers dissociated within the 10 ns of simulation. In more than half the simulations of ordered stacks with five and more molecules, these stayed intact during this time, and the survival fraction for them is similar, showing that the cooperativity effect reaches a maximum for such sizes.²⁸ Therefore, we can anticipate the smallest stable nucleus (i.e., critical nucleation size) is around four to five molecules. In most simulations, if dissociation takes place, it occurs at the end of the fiber (for example, as shown in Fig. 2e). However, we once observed the fragmentation of a fiber into two small fibers (Fig. S10†). Fragmentation is probably unlikely because the cooperative binding is strongest in the middle of the fiber. Although fragmentation is rare (one event was observed in a total of 115 simulations of stacks with more than 5 molecules), it is also a way to generate new nuclei (Fig. 1c).

C. Elongation

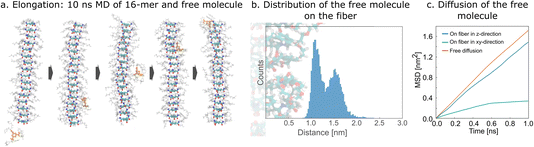
In a sense, the growth of the ordered stack is observed in the MSM with eight molecules. However, an unambiguous elongation process is difficult to define and to distinguish from forming a stable nucleus. Therefore, we performed 21 × 10 ns simulations of 16-mer fiber with two free ends together with one free molecule placed randomly in the simulation box, anticipating that we would observe elongation of the fiber (Fig. 3a). However, the free molecule does not reach the vicinity of the fiber end in most of these simulations. We observed only one elongation event of the added molecule on one of the ends of the fiber. Interestingly, in most simulations, the added molecule adsorbs to the side of the fiber and tends to laterally diffuse along it (Fig. 3a). To quantify this diffusional process, we ran 10 × 15 ns simulations of an infinite fiber and one free molecule. In all cases, the initially free molecule adsorbs on the surface of the fiber within 6 ns (Fig. 3b). In seven simulations, the absorbed molecule stayed in the vicinity of the surface until the end of the simulation, while we also observed three events of desorption (Section S6(i)†).

Fig. 3 Elongation. (a) Representative snapshots of simulations of a 16-mer and a free molecule; the molecule adsorbs on the fiber and moves on its surface, eventually reaching one of the ends of the fiber. (b) Distribution of the distance of the center of the single molecule to the center of the infinite fiber (analyzed over the final 2.5 ns of 15 ns simulations). (c) First 1 ns of mean squared displacement (MSD) for a molecule in the proximity of fiber along the main axis of the fiber (blue), in the plane of the fiber (green), and for free molecule (orange). The curves are scaled for dimensionality (i.e. free diffusion by factor of 3, diffusion in xy-plane by factor of 2, and diffusion in z-direction by factor of 1).

We also found that the binding on the surface of the fiber is not strong enough to immobilize the adsorbed molecule. Analysis of the diffusion showed that a molecule on the fiber covers a similar distance in the mean-squared sense in the direction parallel to the main axis of the fiber as a free molecule in solution (Fig. 3c). The mean-squared displacement in the direction perpendicular to the fiber levels off, reflecting the fact that the molecule remains bound to the surface, and movement resembles diffusion in confinement. We anticipate that the elongation progresses as follows: free molecules randomly diffuse in solution and eventually encounter a fiber on which they absorb. Then, they diffuse along the surface of the fiber, and if they do not desorb, they eventually reach the end of the fiber, where they can adsorb to a free end. Adsorption anywhere on the fiber, followed by diffusion along the fiber, is a reasonable proposition to explain the formation of fibers on the experimental timescales observed. The alternative, in which monomers diffuse freely in the solution until they find a free end of a fiber and adsorb there, would take a very long time especially in the later stages of gelation when few free molecules are left. The quantitative comparison of these two models can be found in Section S6(ii).† Probably the diffusion along the fiber is crucial for gelators with low critical gelation concentration to form and stabilize in a reasonable time (such that an existing fiber does not dissolve before the new molecule arrives). It is noteworthy that movement along the fiber consisting of large oligopeptides was also observed in the experiment and simulation reported by Maity et al.⁵²

D. Secondary nucleation

If molecules tend to adsorb on the surface of the fiber and diffuse along the fiber axis, they can also interact with each other on the surface, and possibly create a nucleus that grows on the side of an existing fiber. To see if such a process is feasible, we performed similar sampling simulations as for primary nucleation, however, this time the simulation is of eight molecules in the presence of an infinite fiber consisting of eight molecules. We performed TPT analysis of MSM of many short simulations (cumulative time 1.95 μs), which is presented in Fig. 4a (see ESI† for video of the fastest observed trajectory). Due to the shorter cumulative time of simulations, some transitions are not sampled well, and the Markovianity assumption is not fulfilled for them (Fig. S8†). Therefore, we discuss the results only qualitatively.

Fig. 4 Secondary nucleation. (a) Mechanism of formation of ordered fiber from randomly distributed molecules (indicated by cyan color) on the side of an existing fiber (indicated by orange color). The mechanism is obtained by analysis of coarse-grained MSM using TPT. Representation of states, populations, transitions, major pathways and molecules is analogous to Fig. 2. (b) Cryo-TEM image of the self-assembled bundle of fibers. (c) Histogram of widths of single fibers in bundles gathered from eight cryo-TEM images (ESI S7†).

We observed that initially, molecules adsorb on the surface of the fiber. In contrast to the aggregates formed in the absence of a fiber, molecules adsorbed on the fiber interact not only with each other in an unordered cluster but also with the molecules forming the fiber, which leads to more dispersed and smaller aggregates on the surface of the fiber. Ordered stacks can form within the aggregates, and grow by further rearrangement or by new molecules joining. Similar to primary nucleation, the process follows a stepwise mechanism with a sporadic dimer association.

We experimentally confirmed the existence of bundles of fibers of CTA by performing cryo-TEM imaging (Fig. 4b, S12–S16†). From these images, it can be seen that fibers create very well-ordered bundles with a consistent structure within the bundles: most of the time, they have a Gaussian distribution of the fiber width within one image. However, when all histograms are merged into one (Fig. 4c), the width is scattered, which is indicative of a complex arrangement of fibers within the bundles. Although such bundles may arise from different mechanisms than secondary nucleation, such as bundling (Section E), or can be artifacts of sample preparation,⁵³ this observation supports that the final arrangement of two parallel fibers observed in secondary nucleation is realistic.

E. Bundling

Bundles can be formed by secondary nucleation but also by individual fibers interacting with each other. Intertwining interactions are crucial for network formation and, therefore, gelation.⁵⁴ During simulations, we did not observe branching of the single stack. Therefore, one way these single-stack fibers can create a network could be by strongly interacting with each other. To check that, we performed 20 × 10 ns simulations of two infinite fibers (Fig. 5a–c), and in all of them, the two fibers merged and, in this form, stayed until the end of simulations (the histogram of the distance between the centers of fibers is presented in Fig. S18†). Fibers randomly diffuse through the simulation box until they come close to each other and interact. Initially, when the hydroxyl side chains are in contact (and the distance between centers is larger than 1.9 nm), they can still dissociate. However, after some time, the hydroxyl groups of side chains move aside to the edges of the interface between the fibers (the distribution of the hydroxyl groups in the final bundle is presented in Fig. 5d), making the phenyl rings of the neighboring fibers accessible for interaction. The fibers in the bundle interact with each other strongly by hydrophobic interaction (Fig. 5c) and the complex does not dissociate on the timescales of the simulations. We did not notice a difference between the bundling of parallel and antiparallel oriented fibers (Section S8†), suggesting that the interactions between the macrodipoles of the fibers are not a crucial factor in their bundling. If we add one more fiber to the two-fiber bundle, we observe that fiber becomes part of the bundle. The angle between the three fibers shows a multimodal distribution around 70°, 110°, and 180°, which could explain why we observe such a variety of structures in cryo-TEM pictures.

Fig. 5 Bundling. (a–c) Snapshots of selected simulation of bundling of two fibers, red beads indicate the benzene rings and blue the end hydroxyl groups. Fibers merge upon the strong interaction of phenyl rings with each other. (d) 2D histogram of terminal hydroxyl groups (–OH) in the final structure; it can be seen that hydroxyl groups mainly stay on the edge of the fiber interface, making a space for hydrophobic interactions of phenyl groups between fibers. (e) Histogram of the angle created by three fibers.

F. Summary and discussion of the mechanism of supramolecular self-assembly

In this work, we study the mechanism of fiber and bundle formation of CTA. Our results not only align with existing research but also give unique insights. We study the mechanism by investigating several distinct phases schematically summarized in Fig. 1. Firstly, molecules aggregate into an unordered cluster by non-directional hydrophobic interactions. Then, they rearrange within the aggregate and create a small ordered stack by hydrogen bonding. When the stack consists of more than 4–5 molecules, its stability no longer increases, reaching a limiting value; such stacks may be seen as the critical nuclei. Nuclei grow into fibers by further rearrangement within smaller aggregates. We show that longer fibers are most likely to grow by new molecules adsorbing on their surface and diffusing along the surface until reaching one of the ends, where it can then lead to elongation. Given the large surface of the fiber, adsorption on and diffusion along an existing fiber is more likely than a new molecule encountering one of the ends straight from the solution. We speculate that the balance of interactions that allows both adsorption on (high enough affinity) and diffusion along (not too strong binding) the fiber could be the decisive property that distinguishes gelators with low critical gel concentration from non-gelators. If sufficient molecules are adsorbed on the surface of a fiber, they can also interact with each other and result in the creation of a new nucleus on the side of the fiber, rather than diffuse to the ends and lead to elongation. Therefore, elongation and secondary nucleation are competitive processes. Although not studied here, we could imagine that a high concentration of molecules promotes secondary nucleation: high concentration could lead to many molecules being present on the surface of existing fibers, easily exceeding the critical nucleus size. On the other hand, low concentration could lead to a small number of molecules on the side of the existing fiber, such that locally, the nucleation size is not exceeded, leading only to the elongation of the existing fiber. However, very low concentrations could lead to the main fiber slowly dissolving. We observed that fragmentation of a somewhat longer fiber into two fragments should be feasible. At very low concentration, the fragmentation can continue, but at higher concentration, the two fragments can subsequently act as separate nuclei speeding up assembly. Moreover, fibers can interact with each other by hydrophobic interactions of phenyl groups in the CTA side chains. This results in the creation of bundles of fibers, which we observed experimentally. Such interaction could also happen between parts of long fibers resulting in their crosslinking, which if happening multiple times could result in the creation of a gel network.

We would like to highlight that our results in many places align with existing reports in this research area. Molecules forming trifold hydrogen bonding stacks similar to those of CTA, especially derivatives of 1,3,5-benzenetricarboxamide (BTA), have recently become the focus of many experimental^21–23 and computational studies.^{14,15,24–27} Both types of studies showed that the BTA supramolecular polymer is formed in a cooperative fashion via a nucleation and growth mechanism. Similar to the computational work of Pavan and co-workers,^14,15 on BTA molecules in CG MD simulations, we observed that the fast creation of an unordered cluster precedes slow formation of an ordered fiber. We also found an increase of stability when an ordered stack consists of 4–5 molecules. It seems that there is no significant difference between the interaction of antiparallel and parallel-oriented fibers, which is in line with the observations of Pereira Oliveira et al.⁵⁵ We found many similarities to research on protein fiber formation. Although protein fibers consist of molecules that are much larger than the molecules studied here and the nature of their interactions is different (mostly they interact by local interactions, without the cooperative effect coming from electronic changes), similar steps have been distinguished: nucleation, elongation, dissociation, secondary nucleation and fragmentation.^6,30 Probably the biggest difference between these systems lies in the interaction strengths between molecular blocks, which in case of proteins is almost irreversible, allowing the neglect of dissociation in a model.

Conclusions

Overall, we show a detailed mechanism of supramolecular fiber formation with an atomistic resolution, by distinguishing and studying several different processes occurring: aggregation and nucleation, elongation, secondary nucleation and bundling, schematically shown in Fig. 1, showing the complexity of the network created by different processes involved in the self-assembly. Our results show that nucleation involves a fast collapse of dissolved monomers into disordered assemblies, which gradually transform into nuclei consisting of ordered stacks of 4–5 monomers, and then grow to elongated fibers. Moreover, elongation and secondary nucleation appeared to be competing processes, depending on the density of monomers adsorbed at the fiber–liquid interface. Finally, bundling involves the initial association of fibers by interactions between surface-exposed groups, followed by stabilization of the bundle involving surface reorganization to allow for interactions with non-solvent exposed groups. The timescale and fidelity of these processes depend strongly on the nature and strength of mutual interactions between monomers, solvent, and fibers, thereby emphasizing the necessity to consider all these factors in future supramolecular designs. The subtlety and strong interdependence of these interactions, together with the role of conformational freedom and the existence of several competing processes, make a successful design not feasible by qualitative considerations alone but require the development of high-level computational approaches capable of modeling a complete supramolecular assembly process.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

T. K. P., A. H. V., and J. v. E. conceptualized the study. T. K. P. performed the computations. V. L. performed experimental measurements. T. K. P. and A. H. V. wrote the original draft. A. H. V. and J. v. E. supervised the project. All authors approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge W. Evers for help with the cryo-TEM experiments. T. K. P. thanks S. J. Marrink, P. Frederix and S. Zhan for the discussions. T. K. P. acknowledges the financial support by the EC 7th Framework Programme Marie Curie Actions via the European Initial Training Network SMARTNET. V.L acknowledges financial support by Program 7A of NanoNextNL. NanoNextNL is a Dutch consortium of 130 companies, universities, knowledge institutes and university medical centers, aimed at research into micro and nanotechnology.

Notes and references

1. H. A. M. Ardona and J. D. Tovar, Bioconjugate Chem., 2015, 26, 2290–2302.
2. L. R. Hart, J. L. Harries, B. W. Greenland, H. M. Colquhoun and W. Hayes, Polym. Chem., 2013, 4, 4860–4870.
3. J. Boekhoven and S. I. Stupp, Adv. Mater., 2014, 26, 1642–1659.
4. R. Dong, Y. Zhou, X. Huang, X. Zhu, Y. Lu and J. Shen, Adv. Mater., 2015, 27, 498–526.
5. T. Aida, E. W. Meijer and S. I. Stupp, Science, 2012, 335, 813–817.
6. G. Wei, Z. Su, N. P. Reynolds, P. Arosio, I. W. Hamley, E. Gazit and R. Mezzenga, Chem. Soc. Rev., 2017, 46, 4661–4708.
7. W. H. Binder, Macromol. Rapid Commun., 2019, 40, 1800610.
8. P. Dastidar, Chem. Soc. Rev., 2008, 37, 2699–2715.
9. P. W. J. M. Frederix, I. Patmanidis and S. J. Marrink, Chem. Soc. Rev., 2018, 47, 3470–3489.
10. Y. Li, B. C. Abberton, M. Kröger and W. K. Liu, Polymers, 2013, 5, 751–832.
11. P. A. Korevaar, S. J. George, A. J. Markvoort, M. M. J. Smulders, P. A. J. Hilbers, A. P. H. J. Schenning, T. F. A. De Greef and E. W. Meijer, Nature, 2012, 481, 492–496.
12. D. Bochicchio and G. M. Pavan, Adv. Phys.:X, 2018, 3, 316–338.
13. T. K. Piskorz, L. Perez-Chirinos, B. Qiao and I. R. Sasselli, ACS Omega, 2024, 9, 31254–31273.
14. M. Garzoni, M. B. Baker, C. M. A. Leenders, I. K. Voets, L. Albertazzi, A. R. A. Palmans, E. W. Meijer and G. M. Pavan, J. Am. Chem. Soc., 2016, 138, 13985–13995.
15. D. Bochicchio and G. M. Pavan, ACS Nano, 2017, 11, 1000–1011.
16. O. S. Lee, V. Cho and G. C. Schatz, Nano Lett., 2012, 12, 4907–4913.
17. K. K. Bejagam and S. Balasubramanian, J. Phys. Chem. B, 2015, 119, 5738–5746.
18. Y. S. Velichko, S. I. Stupp and M. O. De La Cruz, J. Phys. Chem. B, 2008, 112, 2326–2334.
19. T. Yu and G. C. Schatz, J. Phys. Chem. B, 2013, 117, 14059–14064.
20. K. J. C. van Bommel, C. van der Pol, I. Muizebelt, A. Friggeri, A. Heeres, A. Meetsma, B. L. Feringa and J. van Esch, Angew. Chem., Int. Ed., 2004, 43, 1663–1667.
21. S. Cantekin, T. F. A. de Greef and A. R. A. Palmans, Chem. Soc. Rev., 2012, 41, 6125–6137.
22. J. Boekhoven, J. M. Poolman, C. Maity, F. Li, L. van der Mee, C. B. Minkenberg, E. Mendes, J. H. van Esch and R. Eelkema, Nat. Chem., 2013, 5, 433–437.
23. J. M. Poolman, C. Maity, J. Boekhoven, L. Van Der Mee, V. A. A. Sage, G. J. M. Groenewold, S. I. Van Kasteren, F. Versluis, J. H. Van Esch and R. Eelkema, J. Mater. Chem. B, 2016, 4, 852–858.
24. D. Bochicchio, M. Salvalaglio and G. M. Pavan, Nat. Commun., 2017, 8, 147.
25. M. B. Baker, L. Albertazzi, I. K. Voets, C. M. A. Leenders, A. R. A. Palmans, G. M. Pavan and E. W. Meijer, Nat. Commun., 2015, 6, 6234.
26. L. Albertazzi, D. van der Zwaag, C. M. a Leenders, R. Fitzner, R. W. van der Hofstad and E. W. Meijer, Science, 2014, 344, 491–495.
27. R. Q. Albuquerque, A. Timme, R. Kress, J. Senker and H. W. Schmidt, Chem.–Eur. J., 2013, 19, 1647–1657.
28. T. K. Piskorz, A. H. De Vries and J. H. Van Esch, J. Chem. Theory Comput., 2022, 18, 431–440.
29. J. A. Lemkul, B. Roux, D. Van Der Spoel and A. D. Mackerell, J. Comput. Chem., 2015, 36, 1473–1479.
30. S. I. A. Cohen, M. Vendruscolo, M. E. Welland, C. M. Dobson, E. M. Terentjev and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065105.
31. S. I. A. Cohen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, J. Mol. Biol., 2012, 421, 160–171.
32. A. Aggeli, I. A. Nyrkova, M. Bell, R. Harding, L. Carrick, T. C. B. McLeish, A. N. Semenov and N. Boden, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11857–11862.
33. S. Doerr, M. J. Harvey, F. Noé and G. De Fabritiis, J. Chem. Theory Comput., 2016, 12, 1845–1852.
34. M. K. Scherer, B. Trendelkamp-Schroer, F. Paul, G. Perez-Hernandez, M. Hoffmann, N. Plattner, C. Wehmeyer, J. H. Prinz and F. Noe, J. Chem. Theory Comput., 2015, 11, 5525–5542.
35. B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396.
36. M. R. Perkett and M. F. Hagana, J. Chem. Phys., 2014, 140, 214101.
37. N. W. Kelley, V. Vishal, G. A. Krafft and V. S. Pande, J. Chem. Phys., 2008, 129, 214707.
38. M. J. Abraham, T. Murtola, R. Schulz, S. Pall, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25.
39. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
40. W. Yu, P. E. M. Lopes, B. Roux and A. D. MacKerell, J. Chem. Phys., 2013, 138, 034508.
41. R. Harada, T. Nakamura, Y. Takano and Y. Shigeta, J. Comput. Chem., 2015, 36, 97–102.
42. G. A. Tribello, F. Giberti, G. C. Sosso, M. Salvalaglio and M. Parrinello, J. Chem. Theory Comput., 2017, 13, 1317–1327.
43. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
44. E. Hong, K. Lee and W. Wenzel, Int. J. Biol. Biomed. Eng., 2007, 1, 50–52.
45. U. Sengupta, M. Carballo-Pacheco and B. Strodel, J. Chem. Phys., 2019, 150, 115101.
46. B. Trendelkamp-Schroer, H. Wu, F. Paul and F. Noé, J. Chem. Phys., 2015, 143, 174101.
47. J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105.
48. F. Noé, H. Wu, J. H. Prinz and N. Plattner, J. Chem. Phys., 2013, 139, 184114.
49. F. Noé, C. Schütte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19011–19016.
50. D. Bochicchio and G. M. Pavan, J. Phys. Chem. Lett., 2017, 8, 3813–3819.
51. E. L. Kaplan and P. Meier, J. Am. Stat. Assoc., 1958, 53, 457–481.
52. S. Maity, J. Ottelé, G. M. Santiago, P. W. J. M. Frederix, P. Kroon, O. Markovitch, M. C. A. Stuart, S. J. Marrink, S. Otto and W. H. Roos, J. Am. Chem. Soc., 2020, 142, 13709–13717.
53. D. J. Adams, J. Am. Chem. Soc., 2022, 144, 11047–11053.
54. K. Hanabusa, M. Yamada, M. Kimura and H. Shirai, Angew. Chem., Int. Ed., 1996, 35, 1949–1951.
55. M. Pereira Oliveira, H. W. Schmidt and R. Queiroz Albuquerque, Chem.–Eur. J., 2018, 24, 2609–2617.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00188e

---