Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the non-universality of distance metrics in laser-induced breakdown spectroscopy†
J. Vrábel *ab,
E. Képešab,
P. Nedělníka,
A. Záděrac,
P. Pořízka*ab and
J. Kaiserab
*ab,
E. Képešab,
P. Nedělníka,
A. Záděrac,
P. Pořízka*ab and
J. Kaiserab
aCEITEC, Brno University of Technology, Purkyňova 123, 612 00 Brno, Czech Republic. E-mail: pavel.porizka@ceitec.vutbr.cz; jakub.vrabel@ceitec.vutbr.cz
bInstitute of Physical Engineering, Brno University of Technology, Technická 2, 61669 Brno, Czech Republic
cInstitute of Manufacturing Technology, Brno University of Technology, Technická 2, 61669 Brno, Czech Republic
First published on 22nd May 2025
Abstract
The ability to measure similarity between high-dimensional spectra is crucial for numerous data processing tasks in spectroscopy. Many popular machine learning algorithms depend on, or directly implement, a form of similarity or distance metric. Despite its profound influence on algorithm performance and sensitivity to signal fluctuations, the selection of an appropriate metric remains often neglected within the spectroscopic community. This work aims to shed light on the metric selection process in Laser-Induced Breakdown Spectroscopy (LIBS) and study consequences for data analysis and analytical performance in selected applications. We studied six relevant distance metrics: Euclidean, Manhattan, cosine, Siamese, fractional, and mutual information. We assessed their response to changes in sample composition, additive noise, and signal intensity. Our results show specific vulnerabilities of commonly used metrics, such as the Euclidean metric's high sensitivity to additive noise and the cosine metric's sensitivity to spectral shifts. The Siamese metric stood out in the majority of studied cases and outperformed others in a direct comparison within the spectra classification task. This work provides basic guidelines for selecting metrics in various contexts. The methodology is general and can be directly extended to other spectroscopic techniques that possess comparable data properties.
1. Introduction
Laser-Induced Breakdown Spectroscopy (LIBS)1 is an analytical technique based on optical emission spectroscopy, capable of rapid and inexpensive elemental analysis. It uses a high-power, pulsed laser source focused on the target to ablate the material and produce radiative plasma. The plasma emission is collected and guided to the spectrometer, where the spectra are recorded using a camera.2,3 LIBS found broad applicability ranging from industry,4,5 biology,6,7 geology,8–10 and space exploration,11 among others. The key features of LIBS are a high repetition rate (up to kHz (ref. 12)), the possibility of remote analysis, and minimal requirements for sample preparation.The rapid advancement in instrumentation and growing demands for the analytical capabilities of spectroscopic techniques necessitated the broad adoption of machine learning (ML) techniques,13,14 especially artificial neural networks (ANNs). This is particularly evident in LIBS, where large datasets (∼millions of measurements) containing spectra with a strongly non-linear signal response are common. Examples of prominent ML techniques successfully implemented in LIBS include PCA,15,16 SOM,9,17 SVM,18,19 ANNs,20–23 CNNs,24,25 SIMCA,26 ICA,27 and PLS-DA.28,29 An equally substantial focus on ML is present in complementary spectroscopic techniques; e.g., for Raman, some impactful studies are reported in ref. 30–32 and for IR spectroscopies, ref. 33–35.
Generally, a considerable portion of ML models use a form of similarity‡ computation. In supervised learning, we may need to compute the distance between unknown spectra and labeled representatives to determine class correspondence. In unsupervised learning, for example, a reconstruction error can be considered (in autoencoders36 or RBM37,38). Prior to computing the distance (or more generally, the similarity), a metric must be selected.39 It is crucial to recognize that no single distance metric is universally optimal for all types of data or analysis objectives. Despite the widespread use of Euclidean distance in spectroscopic applications, it often proves inadequate for high-dimensional, sparse datasets, where alternative metrics may better capture domain-specific structures. Selecting the right metric can markedly influence a model's behavior and lead to substantial performance gains, underscoring the need to tailor distance measures to the characteristics of each problem.
The authors of ref. 40 proved that for high-dimensional spaces and arbitrarily distributed data, the concept of proximity between two points becomes less meaningful (when using traditional distance metrics such as Euclidean or Manhattan). This phenomenon is one of the aspects of the curse of dimensionality (COD), which indicates that high-dimensional spaces are inherently sparse.§ As a result, the contrast diminishes because the ratio of distances between the nearest and farthest points to a given reference tends to approach one. In spectroscopy, the effects of the COD are further amplified by the feature sparsity of the data, where only a fraction of the whole spectra usually contains unique information.38,41
Furthermore, from a spectroscopic perspective, the concept of similarity between two distinct spectra is poorly defined or entirely absent in the literature. It is worth questioning whether a slight change in total spectral intensity or the removal of a single spectral line makes two spectra more dissimilar. The answer to such questions depends on the specific task being addressed, which motivated us to study the behavior of selected similarity metrics across various case scenarios that allowed us to isolate individual effects on the metrics. Ultimately, we introduce a novel similarity metric (in the context of LIBS), based on Siamese networks, that outperforms other metrics in the majority of studied tasks.
We use LIBS as a representative spectroscopic technique due to its ability to measure large datasets in a very short time and the rich information contained in its spectra. However, the presented methodology can be generalized to other spectroscopic techniques (e.g., Raman and FTIR), provided that the data exhibit the relevant properties studied in our prior work,13 such as high dimensionality, sparsity, and redundancy. The range of applicability is not strictly defined, but as a rule of thumb, we consider spectra with dimensions larger than about 1000 channels to be sufficiently high-dimensional. This heuristic is based on our preliminary experiments, which show consistent behavior at 1024 channels, a common configuration in single-channel Czerny–Turner spectrometers. Determining an exact threshold is beyond the scope of this work. In this study, we focus on broadband echelle spectra with dimensions far exceeding the threshold.
The number of spectroscopically relevant features (spectral lines) is just a fraction of the total wavelength variables, which represents the sparsity. The redundancy property has two forms; value redundancy, where a selected line is represented by many mutually correlated wavelengths (variables), and line redundancy, which stands for the possibility of having multiple spectral lines representing the same physical property (e.g., the presence of a chemical element).
1.1. Related work
To the best of our knowledge, there are no existing studies within the LIBS literature that explicitly address the impact of distance metric selection. Several alternative distance metrics were successfully applied in the context of LIBS data processing, e.g., cosine distance for database matching,42 or Mahalanobis distance.43,44 Literature in other spectroscopic techniques covers this topic more extensively.Some of the most common metrics in spectroscopy include Euclidean distance, Manhattan distance, Spectral Angle Mapper (SAM, equivalent to cosine similarity), Mahalanobis Distance (MD), and the information-theoretic Spectral Information Divergence (SID). In vis-NIR spectroscopy, the work reported in ref. 45 compares Euclidean, MD, SAM, SID, and Principal Component (PC)-based alternatives for soil spectra, with the aim to relate the distance response to sample composition. This study found MD to be the least effective, while PC-based methods outperformed the rest. More recently, a similar study46 (also in vis-NIR) utilized Euclidean, MD, SAM, and PC-based alternatives, leading to Euclidean, SAM, and PC-MD selected as almost-optimal. However, these results are not directly transferable to LIBS due to the substantially different nature of studied NIR spectra, which contained only a fraction of spectroscopic features/lines in comparison to LIBS spectra (with hundreds of spectral lines). Furthermore, a PC-based transformation preserves the Euclidean distance and angles in the original spectral space, unless too many higher components are omitted. For LIBS spectra, keeping just 10 principal components usually captures ∼99% of the dataset's variance.15 Because of this, the Euclidean distance is unaffected by such transformation.
A comprehensive review of the similarity metrics relevant to hyperspectral imaging was done in ref. 47. This included Euclidean, Manhattan, fractional, cosine, and several more exotic metrics with limited practical use cases. Similar to our approach, they used both synthetic data (consisting of Gaussians) and real and measured reflectance spectra of pigment patches. Despite the amount of studied details and effects (e.g., peak translation and peak intensity change) the study is inconclusive for LIBS data due to the considerably lower complexity of utilized spectra and missing quantitative comparisons.
Siamese networks were recently used in mass spectrometry,48 but traditional metrics such as cosine similarity (referred to by a different term in the original paper) were shown to outperform them. We extend the Siamese network architecture by using the triplet loss and demonstrate that it can significantly outperform all standard metrics in most of the studied scenarios. Unlike previous work, we directly compare selected metrics in a classification task. Furthermore, we introduce a novel LIBS distance dataset specifically designed to study metric sensitivity to changes in sample composition, marking a unique contribution to the field.
2. Methods and data
2.1. Distance metric
Let us consider each spectrum in the dataset as a point in m-dimensional space. The number of dimensions is determined by the spectrometer's resolution, which corresponds to the number of discrete wavelengths (or other spectral variables) at which measurements are performed. The coordinate along each dimension is given by the intensity measured at the corresponding wavelength. A metric space is a structure that contains an ordered pair of a set X and a non-negative real function d(x, y), where x and y are elements of the set, i.e. points. The function d(x, y), called a metric, must fulfill three basic conditions:(a) d(x, y) = 0 if and only if x = y.
(b) Symmetry d(x, y) = d(y, x).
(c) Triangle inequality d(x, y) + d(y, z) ≥ d(x, z) (in certain cases, a more general condition, such as the Schwarz inequality, needs to be used37).
On any set X containing at least two elements, we can define an arbitrary number of distance functions. Therefore, it is essential to specify which metric is used when discussing the distance between two points. Examples of metrics defined on Rm, the m-dimensional real space, include:
(a) Minkowski metric is a broad class of metrics defined as:
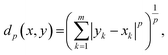 | (1) |
(b) Manhattan metric is a special case of eqn (1), where p = 1:
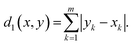 | (2) |
(c) Euclidean metric is a special case of eqn (1), where p = 2:
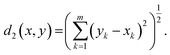 | (3) |
The Euclidean metric represents the natural distance, which corresponds to the shortest straight line between two points. This is a consequence of the fact that in the classical limit, we live in a 3-dimensional Euclidean space. An important lemma for the Euclidean distance is that it is invariant to rotations of the m-dimensional space.
In many applications, it is advantageous to relax one or more of the metric conditions (e.g., the triangle inequality) and utilize a pseudo-metric. Examples of pseudo-metrics are fractional metrics (i.e., Minkowski with p ∈ (0,1)) or the cosine similarity.
(d) Cosine similarity is a pseudo-metric, which relies on the dot product of two vectors. When considering a spectrum as a point in n-dimensional space, connecting this point to the origin yields a vector. Then a normalized dot product of two vectors is
 | (4) |
Note that this is equivalent to a cosine of the angle between the two vectors; therefore, dCS(x, y) = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. A complementary quantity, the cosine distance is often defined as 1 − dCS(x, y).
θ. A complementary quantity, the cosine distance is often defined as 1 − dCS(x, y).
In the spectroscopic literature, several metrics equivalent to cosine similarity (such as SAM, normalized correlation, etc.) are commonly used, with no qualitative difference in performance.45,46 A distinct property of the cosine similarity is its invariance to a total spectral intensity change. This is exceptionally useful for dealing with laser energy fluctuations in LIBS.
(e) Mutual information (MI) quantifies the amount of information that one distribution provides about another.49 The formal definition of MI for discrete random variables is
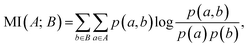 | (5) |
MI is closely related to the Shannon entropy. While the entropy quantifies the uncertainty within a single variable, MI measures how the entropy of one variable is reduced by knowing the other variable. If the variables are independent, their shared information content is zero. In contrast, if they are highly dependent, knowing one variable significantly reduces the uncertainty about the other.
We use a simplified approach to calculate MI based on an image registration algorithm.50 In the first step, a joint histogram of both spectra and two individual histograms are computed and normalized. Then, these are used as joint and marginal probability distributions, respectively. Note that the binning parameter in the histogram computation significantly affects the result and should be optimized for a given task (we use 100 bins). MI is then directly computed using these quantities and provided definitions.
(f) Siamese neural networks (SNNs) are versatile ANN-based models designed for similarity comparison.51,52 SNNs consist of two or more identical subnetworks that share parameters. These subnetworks are trained to create an embedding that minimizes the difference between similar inputs and maximizes the difference between dissimilar inputs. To enhance the possibility of discriminating between similar and dissimilar examples we used the triplet loss:
 | (6) |
The triplet loss consists of embeddings f(·), where a is an anchor, p a positive example (similar input to the anchor), and n a negative example (dissimilar to the anchor). By minimizing the triplet loss, the model learns to embed the positive example closer to the anchor than the negative example, within a specified margin α. Details of how the Siamese network was trained are provided below.
2.2. LIBS spectral modeling
For simplicity, we assumed the Local Thermodynamic Equilibrium (LTE) condition to be valid and therefore the intensity of spectral lines can be described by Boltzmann statistics.53,54 Synthetic spectra were generated for selected elements, temperature, and electron density. This required a database with spectral lines and corresponding parameters (energy levels, degeneracy factors, Einstein coefficients, and partition functions). We used the NIST database and NIST LIBS tool to generate spectra.55 The following parameters were used for spectral generation: kBT = 1 eV; ne = 1 × 1017 cm−3 (Boltzmann constant, temperature, and electron density, respectively).2.3. Samples
(a) Fe–Co certified distance set. The set contains 11 samples, with compositions ranging from pure iron (Fe) to pure cobalt (Co) in 10% incremental changes (see Fig. 1). Possible deviations from the exact 10% increment are only negligible in the context of this study (less than 0.5 wt%). Some minor elements, such as manganese (Mn) and lead (Pb), may be present in concentrations below 0.2 wt%. The exact composition and further details are provided in ref. 56.(b) Fe & Al standards: nine samples from three different manufacturers were used: SPL LABMAT (CZ), Bundesanstalt für Materialforschung und prüfung (BAM, DE), and ERM Certified Reference Materials (BE). Among these, six samples were steel standards with varying compositions of minor elements and three samples were aluminum alloys. The samples and their compositions are listed in Table 1. We specifically selected Fe and Al-dominated matrices due to their distinct differences in spectral signals.
| Producer | ID | Alloy | Fe | Al | C | Cr | Co | Mn | Mo | Ni | Si |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SPL | 19/6 | Steel | 81.02 | 0.01 | 0.03 | 13.08 | 0.02 | 0.66 | 0.44 | 3.91 | 0.6 |
| SPL | 20/6 | Steel | 70.95 | — | 0.04 | 18.26 | 0.15 | 1.43 | 0.27 | 7.93 | 0.38 |
| SPL | 21/6 | Steel | 96.99 | 0.02 | 0.36 | 0.08 | — | 1.21 | 0.01 | 0.02 | 1.26 |
| ERM | EB313 | Al | 0.39 | 94.73 | — | 0.12 | — | 0.5 | 0 | — | 0.36 |
| ERM | EB316 | Al | 0.11 | 87.39 | — | 0.01 | — | 0.2 | — | 0.02 | 11.98 |
| BAM | 310 | Al | 0.07 | 98.81 | — | 0 | — | 0 | — | 0 | 0.08 |
| BAM | C2 | Steel | 78.06 | — | 0.01 | 14.72 | — | 0.69 | 0.01 | 6.12 | 0.37 |
| BAM | C3 | Steel | 74.01 | — | 0.03 | 11.89 | — | 0.72 | 0.03 | 12.85 | 0.46 |
| BAM | C8 | Steel | 69.87 | — | 0.14 | 17.96 | 0.02 | 1.7 | — | 8.9 | 1.41 |
2.4. LIBS experiment
For both sample sets, the LIBS Discovery instrument, developed at the Central European Institute of Technology, Brno University of Technology (Czech Republic), was used. A laser source, Q-switched Nd:YAG laser Quantel CFR Ultra (532 nm, 10 ns, 20 Hz), was focused on the sample surface using a VIS-graded triplet lens with a focal length of 24.5 mm forming a spot size of 100 microns. The emission of the plasma was collected using wide-angle optics (45 degrees) and guided using an optical fiber to an echelle spectrometer (EMU-65, Catalina Scientific). Plasma emission was detected using a gated EMCCD camera. Samples were analyzed in an air atmosphere. The result of such a measurement was a spectrum with 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 values, representing intensity at a corresponding wavelength starting at 200 nm with an equidistant step of 0.02 nm. The system parameters were chosen according to prior experience with LIBS experiments; the gate delay of the camera was 1 μs and the gate width was 50 μs (minimum for the camera used). 20 mJ ablation energy was used for the Fe–Co sample set and three energies (10, 20, and 30 mJ) for Fe & Al standards.
002 values, representing intensity at a corresponding wavelength starting at 200 nm with an equidistant step of 0.02 nm. The system parameters were chosen according to prior experience with LIBS experiments; the gate delay of the camera was 1 μs and the gate width was 50 μs (minimum for the camera used). 20 mJ ablation energy was used for the Fe–Co sample set and three energies (10, 20, and 30 mJ) for Fe & Al standards.
2.5. Data
(a) The Fe–Co measured dataset (available at ref. 56) contains 11 samples with 50 spectra per sample. Spectra were measured from the certified standards (see Section 2.3).(b) The Fe–Co generated dataset contains simulated spectra replicating the composition of their measured counterparts. The raw spectra were then modified by adding noise drawn from normal distributions N(0,0.012), N(0,0.022), and N(0,0.052). We use the notation N(μ,σ2), where μ is mean σ2 variance, and σ standard deviation. The standard deviations are scaled relative to the maximum value in the corresponding dataset.
(c) The Fe & Al dataset consists of 27 sub-categories, each defined by a combination of sample and experimental setup. These sub-categories can be distinguished either by class, based on the predominant composition (e.g., steel, and Al alloy), or by experimental conditions (such as the three laser energy levels). Each sample/setup includes 50 available spectra. It is important to note that Fe and Al matrices were chosen due to their fundamental differences in the number of spectral lines: Fe spectra are characterized by a large number of lines, whereas Al spectra have relatively few. The signal intensity is influenced by the laser energy.
(d) An LIBS benchmark classification dataset (available at ref. 57) was originally designed for the challenging out-of-sample classification of LIBS spectra. The dataset contains spectra from 138 soil samples (500 spectra per sample for training and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra for test in total), which are grouped into 12 distinct classes. The dataset was introduced for the EMSLIBS 2019 contest and serves as a benchmark for comparing classification algorithms in the LIBS community. Elemental compositions of samples are provided in metadata.
000 spectra for test in total), which are grouped into 12 distinct classes. The dataset was introduced for the EMSLIBS 2019 contest and serves as a benchmark for comparing classification algorithms in the LIBS community. Elemental compositions of samples are provided in metadata.
2.6. Siamese network training
We trained the Siamese network using the training subset of the LIBS benchmark classification dataset, consisting of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 labeled spectra (100 per sample). Spectra were normalized by the total emissivity of the plasma, estimated by summing all intensity values in the spectra. Triplets were constructed based on class correspondence, with positive examples from the same class and negatives from randomly selected distinct classes. The model was selected through heuristic pseudo-optimization, informed by prior experience with ANN-based models in spectroscopy. The input size of the model is 40
000 labeled spectra (100 per sample). Spectra were normalized by the total emissivity of the plasma, estimated by summing all intensity values in the spectra. Triplets were constructed based on class correspondence, with positive examples from the same class and negatives from randomly selected distinct classes. The model was selected through heuristic pseudo-optimization, informed by prior experience with ANN-based models in spectroscopy. The input size of the model is 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. It has two convolutional layers with kernel sizes of 50 and 10, strides of 2 and 2, and paddings of 1, each producing 50 output channels. After the first convolutional layer, a max-pooling layer with a kernel size 7 and stride 3 is applied. Each convolutional layer is followed by a ReLU activation function. The output is flattened and processed using a fully connected layer with 256 hidden units, followed by an output with 10 units. The model is trained for 50 epochs with a batch size of 128 and a learning rate of 1 × 10−4. The predictions of the model (embeddings) are compared using the L2 norm.
000. It has two convolutional layers with kernel sizes of 50 and 10, strides of 2 and 2, and paddings of 1, each producing 50 output channels. After the first convolutional layer, a max-pooling layer with a kernel size 7 and stride 3 is applied. Each convolutional layer is followed by a ReLU activation function. The output is flattened and processed using a fully connected layer with 256 hidden units, followed by an output with 10 units. The model is trained for 50 epochs with a batch size of 128 and a learning rate of 1 × 10−4. The predictions of the model (embeddings) are compared using the L2 norm.
The models were trained using cloud GPU services (Azure and Google Colab), while predictions, which require considerably less computational power, were performed locally on a CPU. It is important to note that simulated spectra were resampled to match the model's input resolution before applying the Siamese metric.
2.7. Data visualization and processing
The dependence of the signal on composition is evident in Fig. 2. The intensity of relevant lines evolves non-linearly in response to changes in composition. The number of relevant features (i.e., spectral lines) is comparable for both matrices. | ||
| Fig. 2 Example spectra from the Fe–Co measured dataset (right). Details of a selected spectral range. The measured signal exhibits a monotonic but nonlinear dependence on composition. | ||
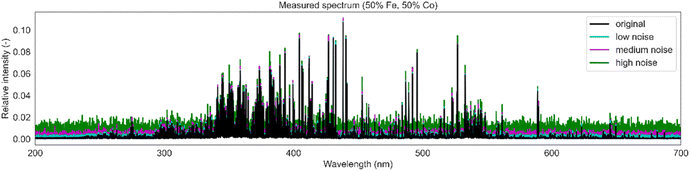
The magnitude of additive noise in measured spectra is depicted in Fig. 3. For low and medium noise, the majority of relevant lines remain detectable, either by a trained expert or an appropriate algorithm. For high noise, a substantial number of lines become indistinguishable from noise. A similar phenomenon is visible in Fig. 4, for simulated spectra. The discrepancies between simulated and measured spectra originate from multiple factors (non-ideal model, non-complete database of transitions, atmospheric conditions, calibration of the spectrometer, etc.).
Unless indicated otherwise, spectra were normalized by the total emissivity prior to distance computations. For measured spectra, no intensity calibration or background subtraction was performed, apart from dark image subtraction. The simulated spectra were multiplied by an efficiency function to suppress intensity in the UV region. This was done to better match the measured spectra, as UV wavelengths are strongly absorbed by the atmosphere. In the classification task, spectra were normalized by their maximal value.
3. Results and discussion
This section presents our findings on the behavior of different distance metrics in spectroscopically relevant scenarios. We begin by analyzing how metrics respond to continuous changes in sample composition, followed by the effects of varying noise levels. Next, we study the impact of changes in total signal intensity, and finally, we compare the classification performance of K-Nearest Neighbors (KNNs) using various distance metrics.3.1. Distance vs. composition
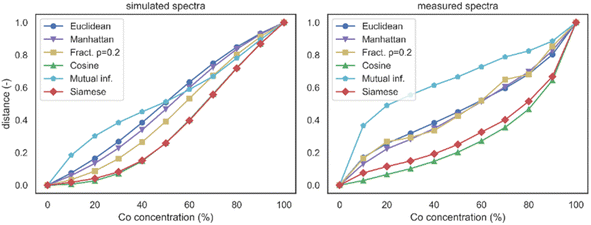
First, we show how distance metrics evolve in response to changes in sample composition, utilizing Fe–Co datasets 2.5.1 and 2.5.2 (measured and simulated). Distances between spectra from all composition combinations were computed and visualized as distance heatmaps. For measured spectra (Fig. 5), the mean of 50 spectra was taken for each sample. The Euclidean distance exhibited an almost linear response w.r.t. sample composition change. Other metrics from the Minkowski metrics family (Manhattan and fractional) behaved similarly to the Euclidean metric in a qualitative manner and varied only in absolute values. The cosine distance exhibited a gradual increase with changes in composition, in contrast to the mutual information distance, which showed the opposite behavior. While all metrics had a broken symmetry about the secondary diagonal, the effect was particularly evident for the Siamese metric. This property could be explained by the variations in the information content within the selected reference spectrum.For generated spectra, only a single spectrum per composition was used. Distance matrices are presented in Fig. 6. Despite the simplicity of the employed spectrum generation algorithm, the results from simulated data are qualitatively comparable to those from measured data. Discrepancies could be attributed to the absence of noise in the simulated spectra. Simulated spectra enabled a more controlled study of similarity, as they omitted signal contributions from minor elements (that are always present in measurements) and experimental noise. This fact was subsequently used to isolate the effect of the additive noise.
To examine finer details, a reference spectrum (pure Fe) was selected and used to calculate pairwise distances between the reference and all remaining compositions in the Fe–Co dataset (Fig. 7). This essentially is a line plot of the first column in each heatmap. The analysis further supports the claim that the Euclidean metric exhibits an almost linear response to composition changes. While Manhattan and fractional distances showed slight deviations from linearity in the case of simulated spectra, they closely aligned with the Euclidean metric for measured spectra. The non-smoothness of the fractional distance can be attributed to experimental noise and numerical errors stemming from the algorithm instability. Both the cosine and Siamese distances exhibited similar trends and, for simulated data, resembled a sigmoid function. In contrast, mutual information showed a sharp increase toward higher dissimilarity, followed by an almost linear progression. This behavior is likely due to the additional entropy introduced by new spectral lines from mixed composition samples, which were absent in the pure Fe spectrum. These trends in metric behavior are crucial for the discussion on classification performance in the following sections. While the Euclidean metric is the most human-interpretable metric (due to correlation with compositional change), it may not necessarily be optimal for a classification algorithm. In contrast, for classification tasks, it is advantageous to overlook minor compositional changes corresponding to intra-class spectral variability.
3.2. Noise sensitivity
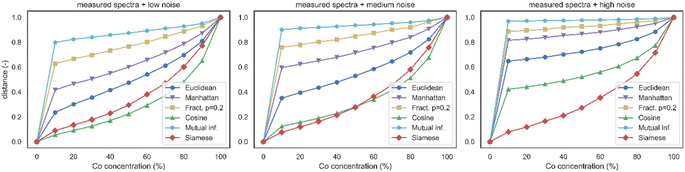
Analogically to the previous case, we studied measured and simulated spectra from Fe–Co datasets 2.5.1 and 2.5.2 that were altered by additive noise. Noisy spectra of pure Fe were selected as the reference for distance calculations. The noise was normally distributed around zero mean μ with a specified variance σ2, or standard deviation σ, and was taken in the absolute value to prevent unphysical negative intensity values. Three noise levels were considered: low N(0,0.012), medium N(0,0.022), and high N(0,0.052). Standard deviations were related to the maximal intensity observed in spectra.In measured spectra (see Fig. 8), the mutual information metric was significantly compromised even by low noise. This is attributable to the employed algorithm for mutual information estimation, which relies on histograms. Given that the noise distribution remained consistent in all spectra, a considerable fraction of the information was washed out. The remaining lines of higher intensity were not sufficient to provide the necessary contrast. Minkowski metrics with lower p parameters were more prone to the noise-related performance decrease. While the Manhattan metric was still usable for low-noise setup, its effectiveness decreased for medium noise. The Euclidean metric lost the majority of its contrast in the high noise setups. The cosine metric demonstrated resilience to small and medium noises but started to fail for high noise. The Siamese metric proved resilient to all tested noise levels. This remarkable property was most likely a consequence of the utilized architecture of the Siamese neural network, where the dimensionality reduction at the output layer served as a denoising function.
For simulated spectra (see Fig. 9), the majority of results were analogical to measured spectra, except the Siamese metric. The response curve of the Siamese metric was non-smooth and discontinuous at certain concentrations. This is a consequence of the fundamental differences in simulated and measured data, as the Siamese network model was trained solely on measured data. To enable the use of the Siamese metric, the simulated spectra were resampled to match the dimensionality and resolution of the measured spectra, which consist of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 points spanning from 200 nm in 0.02 nm increments. Such resampling cannot correct for differences in spectral intensities or the vastly different number of spectroscopic features present in real measurements. This limiting factor of the Siamese metric can be potentially treated either by fine-tuning the model on the target task or by more advanced spectra transfer approaches that can correct signal discrepancies (see 58,59).
002 points spanning from 200 nm in 0.02 nm increments. Such resampling cannot correct for differences in spectral intensities or the vastly different number of spectroscopic features present in real measurements. This limiting factor of the Siamese metric can be potentially treated either by fine-tuning the model on the target task or by more advanced spectra transfer approaches that can correct signal discrepancies (see 58,59).
The noise sensitivity study revealed that Minkowski family metrics are highly susceptible to noise. Therefore, we dropped them from further studies and kept only Euclidean as the best-performing representative. Note that we also provide additional distance heatmaps for noisy spectra in the ESI.†
3.3. Signal intensity dependence
The total emissivity of LIBS plasma is indirectly influenced by the energy of the incident laser (since higher-energy pulses ablate more material, producing a hotter, denser plasma and increasing overall emission), leading to variations in intensities of measured spectra. Here, we used the Fe & Al dataset, measured on three distinct energies, to demonstrate the effect of total intensity change. The first spectrum in the dataset (steel sample, laser energy 10 mJ) was selected as a reference point. The simplicity of the dataset (consisting of only two matrices with significantly different spectra) allows us to clearly demonstrate the non-universality of the Euclidean metric.Distances between the reference spectrum and each of the remaining spectra were computed individually using the selected metrics. For brevity, we present only the Euclidean, cosine, mutual information, and Siamese metrics; the remaining Minkowski-family metrics performed worse than Euclidean, as detailed in the ESI.†
Fig. 10 schematically shows how these pairwise distances were computed: the reference spectrum is compared to subsequent spectra from three samples, each measured at three energies, yielding 50 spectra per sample-energy combination. Error bars in the following figures represent standard deviations across repeated acquisitions for each condition.
Computed distances based on the diagram (Fig. 10) for the Euclidean metric are shown in Fig. 11. The outcome is counter-intuitive, as demonstrated by marked distances in Fig. 11 (red dashed ellipses). The Euclidean distance between the reference spectrum (steel sample, laser energy 10 mJ) and certain other steel spectra (measured at higher laser energies) was greater than the distance between the reference and marked Al alloy spectra. This could potentially lead to misclassification in a distance-based classification algorithm. While this behavior can be mitigated through proper spectral normalization (as detailed in the ESI†), preserving the original shape of spectra is sometimes necessary for specific applications (e.g., imaging) to retain spatial information.
Distances obtained from the cosine metric are shown in Fig. 12. In contrast to the Euclidean metric, spectra from the steel matrix were clearly separable from those of the Al alloys. Moreover, this separation was not affected by changes in laser energy and the corresponding changes in intensity. This is a consequence of the intrinsic data normalization in the cosine metric (as discussed in Section 2.1).
 | ||
| Fig. 12 Cosine distances between the reference spectrum (steel sample, laser energy 10 mJ) and corresponding spectra from the Fe & Al dataset. | ||
The mutual information-based metric was capable of separating matrices without normalizing the data, owing to its scaling invariance (see Fig. 13). However, the contrast between steel and Al alloy matrices was lower than that for the cosine metric. Note that the mutual information is natively a similarity metric, so the distance was computed as 1 − MI. The advantage of MI is its capability to compare spectra with non-matching resolution or intensity levels (as it depends only on histograms). A considerably higher error bar of the first bin was caused by the presence of the reference spectrum in the spectrum batch corresponding to the first sample/energy bin. The presence of an identical spectrum maximized the MI, which biased the mean and standard deviation values of the bin.
 | ||
| Fig. 13 MI distances between the reference spectrum (steel sample, laser energy 10 mJ) and corresponding spectra from the Fe & Al dataset. | ||
The highest contrast was achieved using the Siamese metric (Fig. 14). This result underlined the validity of utilizing alternative metrics. Note that the employed Siamese network model was trained on a different dataset (originally designed for the classification of soil spectra) but performed well on metal spectra.
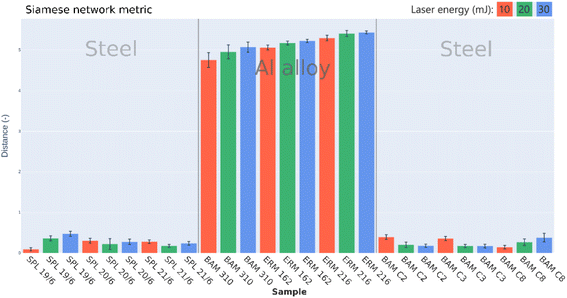 | ||
| Fig. 14 Siamese distances between the reference spectrum (steel sample, laser energy 10 mJ) and corresponding spectra from the Fe & Al dataset. | ||
3.4. Classification performance
To move beyond qualitative metric comparisons and case studies, we provide a direct quantitative evaluation in the form of classification accuracy performance. We employed KNNs as a straightforward and interpretable distance-based classifier to isolate the effect of different metrics. This classification task was based on the EMSLIBS 2019 contest21 and the LIBS benchmark classification dataset.57 In the contest, the winning team achieved classification accuracy exceeding 90%. This result was made possible through the use of more complex data processing algorithms, including a human-in-the-loop strategy. Standalone classification algorithms (e.g., ANNs, SVM, KNNs, etc.) typically achieved accuracy below 70%. The primary objective was not to surpass baseline or state-of-the-art algorithms for the benchmark dataset, but rather to study the effect of distance metrics.The KNN model was trained on the training data subset (50 spectra per sample, 5000 in total) and was later used to predict the test data (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra). Optimal values for the k parameter were determined on the validation data from values (2, 5, 10, 15, 20, 30,…, 90, 100, 150, 200, 250, and 300) for each metric. In Table 2, we compared validation and test performances for selected metrics. Note that we omitted the Manhattan and fractional metrics as they achieved significantly worse performance during the preliminary validation evaluation. The mutual information metric was also excluded due to the extremely high computational cost of calculating the Gram matrix for KNNs and because it was outperformed by other metrics during validation. The Siamese metric performed best, particularly when a higher number of neighbors k was considered, compared to lower k values for standard metrics. Notably, for the Siamese metric, comparable test performance was achieved across a range of k values (up to k = 200), though we report only the lowest k value. This raises new questions to be explored in future research.
000 spectra). Optimal values for the k parameter were determined on the validation data from values (2, 5, 10, 15, 20, 30,…, 90, 100, 150, 200, 250, and 300) for each metric. In Table 2, we compared validation and test performances for selected metrics. Note that we omitted the Manhattan and fractional metrics as they achieved significantly worse performance during the preliminary validation evaluation. The mutual information metric was also excluded due to the extremely high computational cost of calculating the Gram matrix for KNNs and because it was outperformed by other metrics during validation. The Siamese metric performed best, particularly when a higher number of neighbors k was considered, compared to lower k values for standard metrics. Notably, for the Siamese metric, comparable test performance was achieved across a range of k values (up to k = 200), though we report only the lowest k value. This raises new questions to be explored in future research.
| Metric | Euclidean | Cosine | Siamese | Eucl. + shift | Cos. + shift | Siam. + shift |
|---|---|---|---|---|---|---|
| Validation acc. (%) | 83.6 | 86.9 | 95.4 | 70.1 | 71.9 | 72.0 |
| Test acc. (%) | 59.2 | 61.0 | 64.7 | 53.8 | 53.3 | 54.0 |
| Best k valid | 5 | 5 | 7 | — | — | — |
| Best k test | 9 | 10 | 40 | — | — | — |
To study the impact of spectral shifts, validation, and test spectra were randomly shifted by s pixels within the range of −3 to 3. The drop in classification performance due to these shifts was less pronounced in the test data, likely due to the inherent complexity of the (out-of-distribution) classification task. While the Siamese metric still outperformed other metrics, the gap was significantly smaller for shifted spectra. The largest performance drop due to the shift was observed for the Siamese metric, followed by the cosine metric. It is worth noting that the Siamese network architecture used in this study was not optimized to handle spectral shifts. This limitation could potentially be mitigated by incorporating additional convolutional and max-pooling layers, which will be explored in future work.
4. Conclusion
We studied the importance of distance metric selection for various tasks in spectroscopic data processing. Our extensive analysis underlines the absence of a universal distance metric for (LIBS) spectroscopic data across all tasks of interest. The selection of an appropriate metric depends on three critical factors: human interpretability, computational cost, and task-dependent performance. Metrics such as Euclidean and Manhattan, despite their simplicity and ease of interpretation, fall short in robustness across varying noise levels and laser energies. The cosine metric is a more robust alternative when data normalization is critical but is sensitive to spectral shifts. The computationally expensive mutual information offers scale invariance but struggles with additive noise. The Siamese network-based metric stands out for its all-round performance and resilience to noise and intensity changes but requires substantial computational resources and data to build the model. Its effectiveness is also determined by the specific architecture of the neural network, suggesting the possibility of task-specific tuning for optimal results.Future research could address the task optimization of metrics based on Siamese networks or the development of a more advanced, task-universal metric based on a foundation model.
Data availability
Fe–Co measured dataset: this dataset contains spectra from 11 samples with 50 spectra per sample, measured from certified standards. It is available at https://doi.org/10.6084/m9.figshare.21984989.v1. Fe–Co generated data: the parameters to generate these data are described in the main text and the code will be available upon request. LIBS benchmark classification dataset: this dataset comprises spectra from 138 soil samples grouped into 12 distinct classes, originally designed for out-of-sample classification challenges in LIBS spectra. Available at Figshare: https://doi.org/10.6084/m9.figshare.c.4768790.Conflicts of interest
There are no conflicts to declare.Acknowledgements
JV is grateful for the financial support received under the projects CEITEC VUT-J-23-8332 and CEITEC-K-21-6978. JV, EK, and PP gratefully acknowledge the funding by the Czech Science Foundation (GACR 23-05186K). JK acknowledges the funding by the Faculty of Mechanical Engineering at Brno University of Technology (FSI-S-23-8389).References
- A. W. Miziolek, V. Palleschi, I. Schecheter, A. W. Miziolek, V. Palleschi and I. Schechter, et al., Laser-Induced Breakdown Spectroscopy (LIBS), Igarss, 2014, vol. 2006, p. 620 Search PubMed.
- W. D. Hahn and N. Omenetto, Laser-Induced Breakdown Spectroscopy (LIBS), Part I: Review of Basic Diagnostics and Plasma Particle Interactions: Still-Challenging Issues Within the Analytical Plasma Community, Appl. Spectrosc., 2010, 64, 335–366 CrossRef PubMed , https://opg.optica.org/as/abstract.cfm?URI=as-64-12-335ACnC:/Vasili/Laboratory/Articles/studyplasma.Data/PDF//2010.Omenettoreview-3017268501/2010.Omenettoreview.pdf.
- D. W. Hahn and N. Omenetto, Laser-induced breakdown spectroscopy (LIBS), part II: review of instrumental and methodological approaches to material analysis and applications to different fields, Appl. Spectrosc., 2012, 66(4), 347–419 CrossRef CAS.
- R. Noll, C. Fricke-Begemann, M. Brunk, S. Connemann, C. Meinhardt and M. Scharun, et al., Laser-induced breakdown spectroscopy expands into industrial applications, Spectrochim. Acta, Part B, 2014, 93, 41–51, DOI:10.1016/j.sab.2014.02.001.
- R. Noll, V. Sturm, U. Aydin, D. Eilers, C. Gehlen and M. Hohne, et al., Laser-induced breakdown spectroscopy-From research to industry, new frontiers for process control, Spectrochim. Acta, Part B, 2008, 63(10), 1159–1166, DOI:10.1016/j.sab.2008.08.011.
- L. Sancey, V. Motto-Ros, B. Busser, S. Kotb, J. M. Benoit and A. Piednoir, et al., Laser spectrometry for multi-elemental imaging of biological tissues, Sci. Rep., 2014, 4(1), 6065, DOI:10.1038/srep06065.
- B. Busser, S. Moncayo, J. L. Coll, L. Sancey and V. Motto-Ros, Elemental imaging using laser-induced breakdown spectroscopy: a new and promising approach for biological and medical applications, Coord. Chem. Rev., 2018, 358, 70–79 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S0010854517305167.
- J. O. Cáceres, F. Pelascini, V. Motto-Ros, S. Moncayo, F. Trichard and G. Panczer, et al., Megapixel multi-elemental imaging by Laser-Induced Breakdown Spectroscopy, a technology with considerable potential for paleoclimate studies, Sci. Rep., 2017, 7(1), 5080, DOI:10.1038/s41598-017-05437-3.
- J. Klus, P. Pořízka, D. Prochazka, P. Mikysek, J. Novotný and K. Novotný, et al., Application of self-organizing maps to the study of U-Zr-Ti-Nb distribution in sandstone-hosted uranium ores, Spectrochim. Acta, Part B, 2017, 131, 66–73 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S0584854716303718.
- D. Prochazka, T. Zikmund, P. Pořízka, A. Břínek, J. Klus and J. Šalplachta, et al., Joint utilization of double-pulse laser-induced breakdown spectroscopy and X-ray computed tomography for volumetric information of geological samples, J. Anal. At. Spectrom., 2018, 33(11), 1993–1999, 10.1039/c8ja00232k.
- R. C. Wiens, S. Maurice, B. Barraclough, M. Saccoccio, W. C. Barkley and J. F. Bell, et al., The ChemCam Instrument Suite on the Mars Science Laboratory (MSL) Rover: Body Unit and Combined System Tests, Space Sci. Rev., 2012, 170(1), 167–227, DOI:10.1007/s11214-012-9902-4.
- H. Bette and R. Noll, High speed laser-induced breakdown spectrometry for scanning microanalysis, J. Phys. D Appl. Phys., 2004, 37(8), 1281–1288, DOI:10.1088/0022-3727/37/8/018.
- J. El Haddad, A. Harhira, E. Képeš, J. Vrábel, J. Kaiser and P. Pořízka, Chemometric Processing of LIBS Data, in Laser Induced Breakdown Spectroscopy (LIBS), John Wiley & Sons, Ltd, 2023, pp. , pp. 241–275, available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781119758396.ch12 Search PubMed.
- E. Képeš, J. Vrábel, J. E. Haddad, A. Harhira, P. Pořízka and J. Kaiser, Machine Learning in the Context of Laser-Induced Breakdown Spectroscopy, in Laser Induced Breakdown Spectroscopy (LIBS), John Wiley & Sons, Ltd, 2023, pp. , pp. 305–330, available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781119758396.ch15 Search PubMed.
- P. Pořízka, J. Klus, E. Képeš, D. Prochazka, D. W. Hahn and J. Kaiser, On the utilization of Principal Component Analysis in Laser-Induced Breakdown Spectroscopy data analysis, a review, Spectrochim. Acta, Part B, 2018, 148, 65–82 CrossRef.
- P. Pořízka, J. Klus, A. Hrdlička, J. Vrábel, P. Škarková and D. Prochazka, et al., Impact of Laser-Induced Breakdown Spectroscopy data normalization on multivariate classification accuracy, J. Anal. At. Spectrom., 2017, 32(2), 277–288 RSC.
- S. Pagnotta, E. Grifoni, S. Legnaioli, M. Lezzerini, G. Lorenzetti and V. Palleschi, Comparison of brass alloys composition by laser-induced breakdown spectroscopy and self-organizing maps, Spectrochim. Acta, Part B, 2015, 103–104, 70–75 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S0584854714003139.
- J. Cisewski, E. Snyder, J. Hannig and L. Oudejans, Support vector machine classification of suspect powders using laser-induced breakdown spectroscopy (LIBS) spectral data, J. Chemom., 2012, 26(5), 143–149, DOI:10.1002/cem.2422.
- J. Vrábel, P. Pořízka, J. Klus, D. Prochazka, J. Novotný and D. Koutný, et al., Classification of materials for selective laser melting by laser-induced breakdown spectroscopy, Chem. Pap., 2019, 73(12), 2897–2905, DOI:10.1007/s11696-018-0609-1.
- J. Moros, J. Serrano, F. J. Gallego, J. Macías and J. J. Laserna, Recognition of explosives fingerprints on objects for courier services using machine learning methods and laser-induced breakdown spectroscopy, Talanta, 2013, 110, 108–117 CrossRef CAS PubMed , http://www.sciencedirect.com/science/article/pii/S0039914013000994.
- J. Vrábel, E. Képeš, L. Duponchel, V. Motto-Ros, C. Fabre and S. Connemann, et al., Classification of challenging Laser-Induced Breakdown Spectroscopy soil sample data – EMSLIBS contest, Spectrochim. Acta, Part B, 2020, 169, 105872 CrossRef , http://www.sciencedirect.com/science/article/pii/S0584854720300422.
- A. Koujelev, M. Sabsabi, V. Motto-Ros, S. Laville and S. L. Lui, Laser-induced breakdown spectroscopy with artificial neural network processing for material identification, Planet. Space Sci., 2010, 58(4), 682–690 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S003206330900186X.
- J. Vrábel, E. Képeš, P. Pořízka and J. Kaiser, Artificial Neural Networks for Classification, in Chemometrics and Numerical Methods in LIBS, John Wiley & Sons, Ltd, 2022, pp. , pp. 213–240, available from: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781119759614.ch9 Search PubMed.
- J. Chen, J. Pisonero, S. Chen, X. Wang, Q. Fan and Y. Duan, Convolutional neural network as a novel classification approach for laser-induced breakdown spectroscopy applications in lithological recognition, Spectrochim. Acta, Part B, 2020, 166, 105801 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S0584854719306317.
- E. Képeš, J. Vrábel, T. Brázdil, P. Holub, P. Pořízka and J. Kaiser, Interpreting convolutional neural network classifiers applied to laser-induced breakdown optical emission spectra, Talanta, 2024, 266, 124946 CrossRef PubMed , https://www.sciencedirect.com/science/article/pii/S0039914023006975.
- J. B. Sirven, B. Sallé, P. Mauchien, J. L. Lacour, S. Maurice and G. Manhès, Feasibility study of rock identification at the surface of Mars by remote laser-induced breakdown spectroscopy and three chemometric methods, J. Anal. At. Spectrom., 2007, 22(12), 1471–1480, 10.1039/b704868h.
- O. Forni, S. Maurice, O. Gasnault, R. C. Wiens, A. Cousin and S. M. Clegg, et al., Independent component analysis classification of laser induced breakdown spectroscopy spectra, Spectrochim. Acta, Part B, 2013, 86, 31–41 CrossRef CAS , https://www.sciencedirect.com/science/article/pii/S0584854713001067.
- X. Zhu, T. Xu, Q. Lin, L. Liang, G. Niu and H. Lai, et al., Advanced statistical analysis of laser-induced breakdown spectroscopy data to discriminate sedimentary rocks based on Czerny–Turner and Echelle spectrometers, Spectrochim. Acta, Part B, 2014, 93, 8–13 CrossRef CAS , http://www.sciencedirect.com/science/article/pii/S0584854714000020.
- J. L. Gottfried, F. C. De Lucia, C. A. Munson and A. W. Miziolek, Laser-induced breakdown spectroscopy for detection of explosives residues: A review of recent advances, challenges, and future prospects, Anal. Bioanal. Chem., 2009, 395(2), 283–300 CrossRef CAS PubMed.
- F. Lussier, V. Thibault, B. Charron, G. Q. Wallace and J. F. Masson, Deep learning and artificial intelligence methods for Raman and surface-enhanced Raman scattering, TrAC, Trends Anal. Chem., 2020, 124, 115796 CrossRef CAS , https://www.sciencedirect.com/science/article/pii/S0165993619305783.
- J. Liu, M. Osadchy, L. Ashton, M. Foster, C. J. Solomon and S. J. Gibson, Deep convolutional neural networks for Raman spectrum recognition: a unified solution, Analyst, 2017, 142(21), 4067–4074, 10.1039/c7an01371j.
- A. Cui, K. Jiang, M. Jiang, L. Shang, L. Zhu and Z. Hu, et al., Decoding Phases of Matter by Machine-Learning Raman Spectroscopy, Phys. Rev. Appl., 2019, 12(5), 54049 CrossRef CAS , https://link.aps.org/doi/10.1103/PhysRevApplied.12.054049.
- J. L. Lansford and D. G. Vlachos, Infrared spectroscopy data- and physics-driven machine learning for characterizing surface microstructure of complex materials, Nat. Commun., 2020, 11(1), 1513, DOI:10.1038/s41467-020-15340-7.
- W. Fu and W. S. Hopkins, Applying Machine Learning to Vibrational Spectroscopy, J. Phys. Chem. A, 2018, 122(1), 167–171, DOI:10.1021/acs.jpca.7b10303.
- X. F. Cadet, O. Lo-Thong, S. Bureau, R. Dehak and M. Bessafi, Use of Machine Learning and Infrared Spectra for Rheological Characterization and Application to the Apricot, Sci. Rep., 2019, 9(1), 19197, DOI:10.1038/s41598-019-55543-7.
- D. Rumelhart, G. E. Hinton and R. J. Williams, in Learning internal representations by error propagation, 1986 Search PubMed.
- G. E. Hinton and R. R. Salakhutdinov, Reducing the Dimensionality of Data with Neural Networks, Science, 1979, 313(5786), 504–507 CrossRef PubMed , http://science.sciencemag.org/content/313/5786/504.abstract.
- J. Vrábel, P. Pořízka and J. Kaiser, Restricted Boltzmann Machine method for dimensionality reduction of large spectroscopic data, Spectrochim. Acta, Part B, 2020, 167, 105849 CrossRef , http://www.sciencedirect.com/science/article/pii/S0584854720300410.
- A. N. Kolmogorov and S. V. Fomin, Elements of the Theory of Functions and Functional Analysis, Dover Pub, Mineola, N.Y, 1999 Search PubMed.
- C. C. Aggarwal, A. Hinneburg and D. A Keim, On the Surprising Behavior of Distance Metrics in High Dimensional Space, in Database Theory — ICDT 2001, ed. J. Van den Bussche, V. Vianu, Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 2001, vol. 1973, DOI:10.1007/3-540-44503-X_27.
- E. Kepes, J. Vrabel, P. Pořízka and J. Kaiser, Addressing the Sparsity of Laser-Induced Breakdown Spectroscopy Data with Randomized Sparse Principal Component Analysis, J. Anal. At. Spectrom., 2021 10.1039/d1ja00067e.
- P. Jahoda, I. Drozdovskiy, S. J. Payler, L. Turchi, L. Bessone and F. Sauro, Machine learning for recognizing minerals from multispectral data, Analyst, 2021, 146(1), 184–195, 10.1039/d0an01483d.
- O. Samek, H. H. Telle and D. C. S. Beddows, Laser-induced breakdown spectroscopy: a tool for real-time, in vitro and in vivo identification of carious teeth, BMC Oral Health, 2001, 1(1), 1, DOI:10.1186/1472-6831-1-1.
- D. Diaz, M. Alejandro and D. W. Hahn, Laser-Induced Breakdown Spectroscopy and Principal Component Analysis for the Classification of Spectra from Gold-Bearing Ores, Appl. Spectrosc., 2019, 74(1), 42–54, DOI:10.1177/0003702819881444.
- L. Ramirez-Lopez, T. Behrens, K. Schmidt, R. A. V. Rossel, J. A. M. Demattê and T. Scholten, Distance and similarity-search metrics for use with soil vis-NIR spectra, Geoderma, 2013, 199, 43–53 CrossRef CAS , https://www.sciencedirect.com/science/article/pii/S0016706112003308.
- R. Zeng, D. G. Rossiter, Y. G. Zhao, D. C. Li, F. Liu and G. H. Zheng, et al., The choice of spectral similarity algorithms influences suspected soil sample provenance, Forensic Sci. Int., 2023, 347, 111688 CrossRef CAS PubMed , https://www.sciencedirect.com/science/article/pii/S037907382300138X.
- H. Deborah, N. Richard and J. Y. Hardeberg, A Comprehensive Evaluation of Spectral Distance Functions and Metrics for Hyperspectral Image Processing, IEEE J. Sel. Top. Appl. Earth Obs. Rem. Sens., 2015, 8(6), 3224–3234 Search PubMed.
- C. Qin, X. Luo, C. Deng, K. Shu, W. Zhu and J. Griss, et al., Deep learning embedder method and tool for mass spectra similarity search, J. Proteonomics, 2021, 232, 104070 CrossRef CAS PubMed , https://www.sciencedirect.com/science/article/pii/S1874391920304383.
- C. E. Shannon, A Mathematical Theory of Communication, Bell Syst. Tech. J., 1948, 27(3), 379–423 CrossRef.
- F. Maes, D. Loeckx, D. Vandermeulen and P. Suetens, Image Registration Using Mutual Information BT, in Handbook of Biomedical Imaging: Methodologies and Clinical Research, ed. Paragios N., Duncan J. and Ayache N., Springer US, Boston, MA, 2015, pp. 295–308, DOI:10.1007/978-0-387-09749-7_16.
- J. Bromley, I. Guyon, Y. LeCun, E. Säckinger and R. Shah, Signature Verification using a “Siamese” Time Delay Neural Network, in Advances in Neural Information Processing Systems, ed. Cowan J., Tesauro G. and Alspector J., Morgan-Kaufmann; 1993, available from: https://proceedings.neurips.cc/paper_files/paper/1993/file/288cc0ff022877bd3df94bc9360b9c5d-Paper.pdf Search PubMed.
- S. J. Wetzel, R. G. Melko, J. Scott, M. Panju and V. Ganesh, Discovering symmetry invariants and conserved quantities by interpreting siamese neural networks, Phys. Rev. Res., 2020, 2(3), 33499 CrossRef CAS , https://link.aps.org/doi/10.1103/PhysRevResearch.2.033499.
- A. Ciucci, M. Corsi, V. Palleschi, S. Rastelli, A. Salvetti and E. Tognoni, New Procedure for Quantitative Elemental Analysis by Laser-Induced Plasma Spectroscopy, Appl. Spectrosc., 1999, 53(8), 960–964, DOI:10.1366/0003702991947612.
- E. Tognoni, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti and M. Mueller, et al., A numerical study of expected accuracy and precision in Calibration-Free Laser-Induced Breakdown Spectroscopy in the assumption of ideal analytical plasma, Spectrochim. Acta, Part B, 2007, 62(12), 1287–1302 CrossRef , http://www.sciencedirect.com/science/article/pii/S0584854707003187.
- A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Ver. 5.2), National Institute of Standards and Technology, Gaithersburg, MD, 2013 Search PubMed.
- J. Vrabel, LIBS spectra: Fe–Co certified sample set, 2023, available from: https://figshare.com/articles/dataset/LIBS_spectra_Fe-Co_certified_sample_set/21984989.
- E. Képeš, J. Vrábel, S. Střítežská, P. Pořízka and J. Kaiser, Benchmark classification dataset for laser-induced breakdown spectroscopy, Sci. Data, 2020, 7(1), 53, DOI:10.1038/s41597-020-0396-8.
- E. Képeš, J. Vrábel, P. Pořízka and J. Kaiser, Improving laser-induced breakdown spectroscopy regression models via transfer learning, J. Anal. At. Spectrom., 2022, 37(9), 1883–1893, 10.1039/d2ja00180b.
- J. Vrábel, E. Képeš, P. Nedělník, J. Buday, J. Cempírek and P. Pořízka, et al., Spectral library transfer between distinct laser-induced breakdown spectroscopy systems trained on simultaneous measurements, J. Anal. At. Spectrom., 2023, 38(4), 841–853, 10.1039/d2ja00406b.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00377b |
| ‡ For purposes of this work, we use terms distance and (dis-)similarity interchangeably but we mention formal requirements for a proper distance metric in Section 2. |
| § By sparse in this context, we mean that data occupy only a tiny fraction of the space, with most of it being effectively empty. |
| This journal is © The Royal Society of Chemistry 2025 |