Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Depth profiling of noble gases in ilmenite and olivine substrates†
Yuta Otsuki *a,
Ken-ichi Bajoa,
Tomoya Obaseab and
Hisayoshi Yurimotoa
*a,
Ken-ichi Bajoa,
Tomoya Obaseab and
Hisayoshi Yurimotoa
aDepartment of Natural History Sciences, Faculty of Science, Hokkaido University, Sapporo, Hokkaido 060-0810, Japan. E-mail: yotsuki@ep.sci.hokudai.ac.jp; Tel: +81-11-706-9174
bDepartment of Earth and Planetary Sciences, Institute of Science Tokyo, Meguro-ku, Tokyo, 152-8551, Japan
First published on 18th April 2025
Abstract
Solar wind noble gases in extraterrestrial materials provide important insights into past solar activity and space weathering processes. These noble gases are concentrated within the uppermost 100 nm of material surfaces, requiring in situ analysis with high depth and lateral resolution. Additionally, the multi-isotope analysis of noble gases is useful in evaluating the degassing of materials. To address these requirements, we developed a depth profiling method for multi-noble gas isotopes by time-of-flight secondary neutral mass spectrometry. We prepared ilmenite and olivine substrates co-implanted with 4He, 20Ne, 22Ne, 36Ar, and 40Ar as standards for solar wind-irradiated materials and surveyed the optimal analytical conditions to improve the substrate detection limits. As a result, we achieved 4He, 20Ne, 22Ne, 36Ar, and 40Ar detection limits of 7 × 1016, 3 × 1016, 9 × 1015, 2 × 1016, and 5 × 1016 cm−3 for ilmenite and 2 × 1017, 4 × 1016, 2 × 1016, 2 × 1016, and 9 × 1017 cm−3 for olivine, respectively. The reproducibility for the concentration and elemental/isotope ratio measurements ranged from 5% to 31%. This method allowed for the visualization of nano-scale solar wind noble gas distributions on extraterrestrial material surfaces, providing insights into the solar wind activities and space weathering of celestial bodies.
Introduction
Solar wind noble gases in extraterrestrial materials serve as a useful proxy for analyzing solar wind irradiation to reveal past solar activities or space weathering processes.1,2 The typical energy of a solar wind particle is approximately 1 keV per nucleon, and the implanted particles are concentrated within the top 100 nm of the material surface on airless bodies.3 Previous studies have anticipated the actual measurements of noble gas profiles in lunar samples,4 but conventional noble gas mass spectrometers lacked the spatial resolution necessary to reveal the precise distribution of implanted noble gases.In the 1970s, combining ion beam sputtering and electron ionization, gas ion probes (beam diameter, 200 μm; depth resolution, ∼10 nm) were successfully used for the 4He depth profiling of lunar samples.3,5–8 However, other noble gas isotopes such as 20Ne and 36Ar were difficult to measure in natural samples due to their high background. In addition, all sputtered particles will be ionized from the crater bottom and crater edge, which in principle limits the depth resolution. Recent developments in secondary ion mass spectrometry have led to improvements in the detection limits of the depth profiling of helium and argon implanted into semiconductors and metals in engineering applications. However, the rastering areas of these measurements have been limited to several tens of μm.9,10 In cosmochemical studies, the depth distribution of noble gases in extraterrestrial materials has been measured by the Closed System Stepwise Etching (CSSE) method, in which a sample is etched stepwise in a vacuum and the noble gases extracted from the sample surface are measured with a noble gas mass spectrometer.11,12 However, the CSSE method cannot determine the absolute depth of etching.
In recent years, time-of-flight secondary neutral mass spectrometry (TOF-SNMS) has been performed using a laser ionization mass nanoscope (LIMAS).13–21 The LIMAS uses Ga ion beam sputtering and post-ionization with a femtosecond (fs) laser for high-resolution 4He analysis, reaching a 4He detection limit of 2 × 1017 cm−3 with a ∼2 μm primary beam spot size.14 Note that a unit cm−3 used here is atoms per cm3, of which unit corresponds to approximately 3.7 × 10−20 ρ−1 cm3 STP g−1, where ρ is the density (g cm−3) of the host material.
Bajo et al.18 conducted 4He depth profiling in the diamond-like carbon target of NASA/Genesis22 using a LIMAS to obtain the 4He depth profile. The depth profile was consistent with that of ion implantation simulations performed using the Stopping and Range of Ions in Matter (SRIM) software23 under the solar wind speed distribution observed by a spacecraft.24 They proposed that the 4He depth profiling of extraterrestrial materials could reveal the energy distribution of solar wind. Conventional analyses of noble gases in extraterrestrial materials suggest that light noble gases (i.e., He and Ne) are partially degassed to a certain degree during or after solar wind irradiation.1,25,26 Therefore, the simultaneous analysis of Ne and Ar isotopes in addition to 4He to evaluate noble gas retention at each measurement point is of high interest.
In this study, we developed a depth profiling technique for Ne, Ar, and He in minerals. Ilmenite and olivine samples implanted with 4He, 20Ne, 22Ne, 36Ar, and 40Ar were prepared as analogues of solar wind-implanted lunar and asteroidal samples to understand past solar activity using in situ depth profiling. In addition to the 4He analysis, we performed the multi-isotope depth profiling of 4He, 20Ne, 22Ne, 36Ar, and 40Ar using LIMAS, achieving low detection limits for the noble gas isotopes.
Materials and methods
Materials for analysis
Ion-implanted substrates were prepared for the noble gases to develop depth profiles of their concentrations and isotopic ratios. Polished substrates of an ilmenite crystal ((Fe0.7Mg0.3)TiO3) from Monastery mine, South Africa, and an olivine crystal ((Mg0.9Fe0.1)2SiO4) from San Carlos, USA, were prepared as representative lunar and asteroidal materials for ion implantation. The ion implantations of 4He, 20Ne, 22Ne, 36Ar, and 40Ar were carried out using an ion implanter (ULVAC IMX-3500RS) at the Toray Research Center, Inc. The irradiation energies and doses for each noble gas are summarized in Table 1. Ion implantation was performed at room temperature, and the angle of incidence was set to 0°. Ilmenite and olivine were fixed on a p-type silicon wafer, and ion implantation was carried out simultaneously to produce samples hereafter referred to as HNA-IL and HNA-OL, respectively. The silicon wafer was used for mass assignment because the TOF spectra were much simpler than those of ilmenite and olivine, which was referred to as HNA-Si. The ion implantation doses were certified to ±5% accuracy.| Isotope | Energy/keV | Dose/cm−2 |
|---|---|---|
| a Implantation experiment was conducted at room temperature. | ||
| 4He | 20 | 2.00 × 1015 |
| 20Ne | 60 | 1.00 × 1014 |
| 22Ne | 60 | 1.00 × 1013 |
| 36Ar | 110 | 1.00 × 1013 |
| 40Ar | 110 | 1.00 × 1014 |
We used polished substrates of Monastery ilmenite and San Carlos olivine without ion implantation, i.e., blank-IL and blank-OL, respectively, to evaluate the backgrounds of the noble gas isotopes. The ilmenite and olivine substrates were coated with ∼10 nm of gold before noble gas measurements to reduce electrostatic charge-up due to primary beam irradiation during depth profiling.
Depth profiling by LIMAS
Depth profiling was performed using a JEOL LIMAS15 at Hokkaido University. A pulsed 69Ga ion beam (30 keV, ∼30 nA) was targeted on the sample surface with a focused ion beam system. A primary ion pulse of 400 ns width was focused on a ∼2 μm spot and rastered to an area of ∼18 × 25 μm2 (30 × 30 pixels). Sputtered neutral particles were post-ionized using an fs laser (Astrella, Coherent) with an energy of 6 mJ, a pulse width of 35 fs, and a wavelength of 795 nm. Post-ionized ions were injected into a multi-turn TOF mass spectrometer (MULTUM II)27 with an acceleration voltage of −5 kV. Ions not of interest were removed from the ion trajectory by adjusting the timing of the ion injection and the ion gate in the MULTUM II system. Flight times of several hundred microseconds separated the ions of interest from other interfering ions. The ions of interest were then detected using a high-speed ion detection system using two-stage microchannel plates (MCP; F1217-011, Hamamatsu Photonics). This single sequence from sputtering to ion detection is referred to as a mass scan, and the signal intensity is given in the unit of ion counts per mass scan (cpms). The repetition rate of the mass scan was set to 1 kHz and synchronized with the fs laser system. The timing control and data acquisition systems were based on the description by Bajo et al.16,17During depth profiling, 100 mass scans (taking 0.1 s) were collected for one pixel to obtain a TOF spectrum, and all TOF spectra for each pixel were recorded. The rastering of 30 × 30 pixels was repeated for more than several hundred measurement layers (90 s per layer) until the noble gas decreased to a constant intensity, which was considered the background of the noble gas isotope signals. The depth profile was obtained using data from the inner 10 × 10 pixel area to reduce the crater edge effect. After depth profiling, residual gas was measured without primary beam irradiation and referred to as blank iM (iM: 4He, 20Ne, 22Ne, 36Ar, and 40Ar ions). To compare the backgrounds of the noble gas signals, blank-IL and blank-OL were analyzed under the same analytical conditions as those for HNA-IL and HNA-OL.
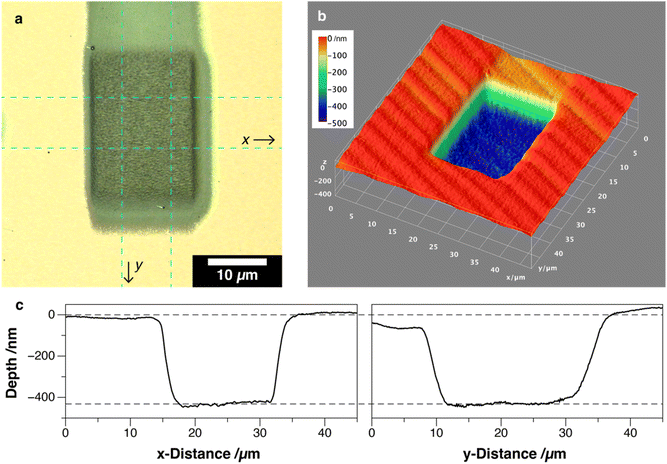
After depth profiling, the depth of the sputtering crater was measured using a three-dimensional (3D) confocal laser microscope (VK-X200, Keyence). A typical sputtering crater is shown in Fig. 1. The sputtering rate was calculated by dividing the crater depth by the total number of measurement layers. The precision of the crater depth measurement was ±5% (Fig. S1†).
Calibration for isotope concentrations and isotope ratios of noble gases
Isotope concentrations for noble gas iM at depth layer k (CiM,k) can be calculated using the relative sensitivity factors (RSFs) as follows:
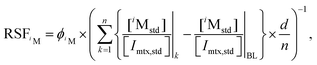 | (1) |
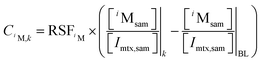 | (2) |
The ion intensity ratios of noble gas ions in depth layer k can be converted to elemental or isotopic ratios with RSFs and calculated as follows:
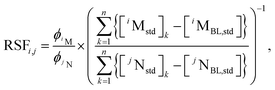 | (3) |
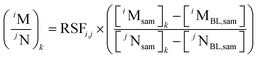 | (4) |
Identification of target ion species
To simultaneously measure 4He, 20Ne, 22Ne, 36Ar, 40Ar, and major elements as matrix ions, we optimized the appropriate analytical conditions for mass spectrometry, in which each ion signal of interest was separated from isobaric ions and other signals that can overlap due to overtaking ions with smaller m/z. The TOF T for each ion was calculated using eqn (5):
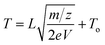 | (5) |
The values of T for multiple ions were calculated using eqn (5) by adjusting the valence and isotopes to find TOF conditions where all noble gases and major elements of olivine and ilmenite (i.e., O, Mg, Si, Ti, and Fe) did not overlap. The noble gas ions were measured at a shorter TOF than the major element ions, as the tails of the intense peaks interfered with the smaller peaks of the noble gas isotopes. As a result, we found TOF windows for measuring m/z 4 (4He+), 8 (16O2+), 9 (36Ar4+), 10 (20Ne2+, 30Si3+, and 40Ar4+), 11 (22Ne2+), 12 (24Mg2+ and 48Ti4+), and 20 (20Ne+ and 40Ar2+) along with either 18 (36Ar2+) or 28 (28Si+ and 56Fe2+) at a TOF of 455–461 μs using the activation of the ion gate. The calculated TOF spectra of these m/z are shown in Fig. S2.† Under the conditions optimized for measuring other noble gas ions, m/z 18 and 28 overlapped. These ions can be selected by controlling the ion gates of MULTUM II. As we found that using 36Ar4+ was a better approach as mentioned later, we measured m/z 28 peaks.
In the analysis of natural samples, many other ion peaks from minor and trace elements were detected in addition to the target ions in the TOF spectra. The ion peaks of major elements and implanted noble gases can be first assigned by comparing with calculations and respectively checking the depth profiles, which showed constant intensity during analysis, and peak depth profiles. In addition, the ions of residual gases such as O, N, and Ar can be assigned through blank analysis. The exact m/z values of unknown peaks, such as minor and trace element ions, can be calculated from the TOF difference ΔT between the unknown and the known ion peak if the lap number is the same. The following equation was used for the calculations:
 | (6) |
Ion implantation simulation
We simulated the depth profile of the noble gases in the substrates using the Transport of Ions in Matter (TRIM) in the SRIM program.23 The simulation parameters for ilmenite and olivine are (Fe0.7Mg0.3)TiO3 and (Mg0.9Fe0.1)2SiO4 for stoichiometry and 4.47 and 3.35 g cm−3 for density, respectively. The implantation energy was set as the same as that of HNA-IL and HNA-OL as listed in Table 1. The numbers of simulated ions were 106 for 4He and 20Ne, 5 × 105 for 40Ar, and 105 for 22Ne and 36Ar, respectively. The depth profiles were binned in 5 nm bins and calculated for the doses (Table 1) of each noble gas (Fig. S3†).Results and discussion
Time-of-flight spectra of standard samples
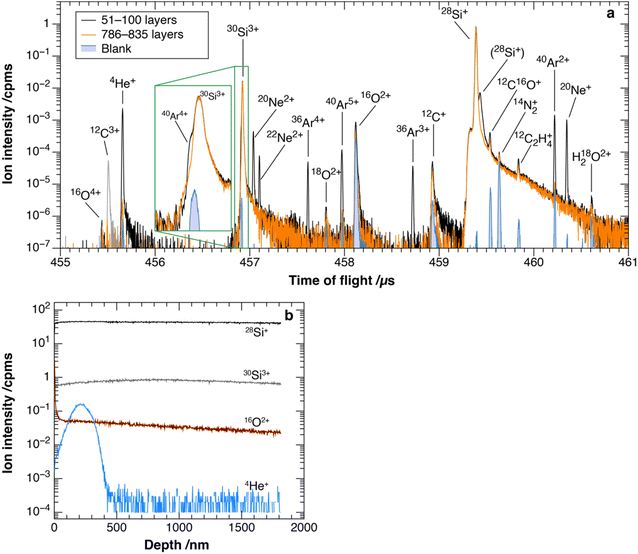
Fig. 2a shows the TOF spectrum obtained from HNA-Si. The full width at half maximum (FWHM) of the peak at 455.656 μs (assigned later as 4He+) was 9 ns, where m/Δm is ∼25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. We defined the ion intensity by integrating the ion at ±9 ns from the peak TOF, which covered 99.05% of the peak at 455.656 μs. This range was set based on the FWHM of the peak for each analysis.
000. We defined the ion intensity by integrating the ion at ±9 ns from the peak TOF, which covered 99.05% of the peak at 455.656 μs. This range was set based on the FWHM of the peak for each analysis.
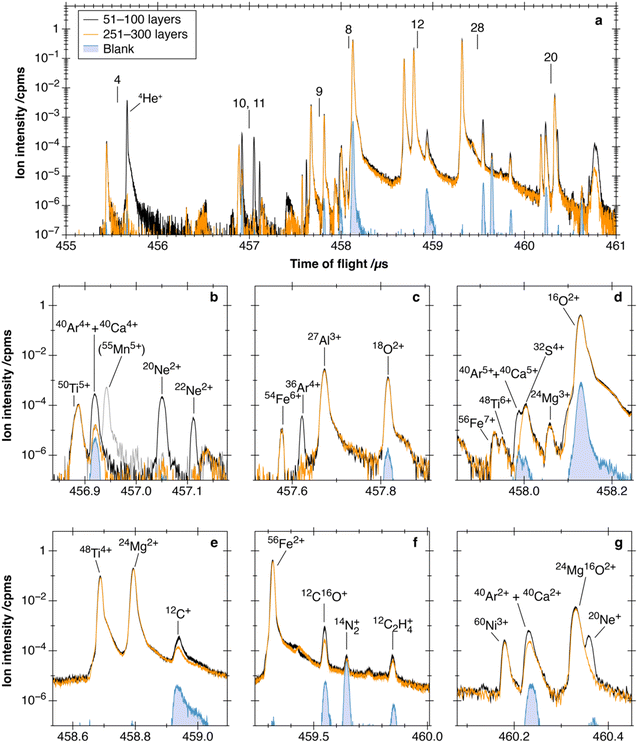
The peak assignments were applied by the procedure described in the Identification of target ion species section (Fig. 2a). The two high-intensity peaks at 456.923 and 459.389 μs remained constant throughout the analysis (Fig. 2b) and were respectively assigned to 30Si3+ and 28Si+. A long tail was observed after the 30Si3+ and 28Si+ peaks, which was a signal in the MCP induced by a large number of ions striking the channels of MCP (hereafter referred to as dark currents).15 The peak profile of 4He+, 20Ne2+, 22Ne2+, 36Ar4+, 40Ar5+, 36Ar3+, 40Ar2+, and 20Ne+ derived from ion implantations is shown in Fig. 2a. The peak at 458.119 μs representing adsorbed 16O2+ was intense at the beginning of the depth profile and decreased rapidly (Fig. 2b). Five peaks were observed in the TOF window of m/z 28. Based on the TOF of the 28Si+ peak (459.389 μs) and eqn (6), the peaks at 459.537, 459.633, and 459.839 μs were assigned as 12C16O+, 14N2+, and 12C2H4+, respectively (Fig. 2a). The peak at 459.432 μs was assigned to the secondary ion of 28Si because this peak was also detected with the primary beam on and without the fs laser. The 12C3+ peak, which interfered with the 4He+ peak, was removed using the ion gate in the ion trajectory (Fig. 2a). The peaks of the target ions from the HNA-IL and HNA-OL samples were assigned using the same assignment procedure (Fig. 3 and 4).
For HNA-IL, 4He+ did not show interference from other peaks (Fig. 3a). The right-hand side slope of the 24Mg16O2+ peak overlapped with the 20Ne+ peak (Fig. 3g). 20Ne2+ was not interfered with by other ion peaks, while 22Ne2+ was not fully resolved from an unknown peak (Fig. 3b). 36Ar4+ was interfered with by the left-hand side slope of the 27Al3+ peak (Fig. 3c). However, it was less interfered with by other peaks, as 36Ar2+ and 36Ar3+ were not fully resolved from 54Fe3+ and (24Mg2+ + 48Ti4+), respectively (Fig. S4† and potentially seen in Fig. 3e but not observed). The TOF spectra of 40Ar2+, 40Ar4+, and 40Ar5+ showed overlap by 40Ca ions due to the insufficient mass resolution of the analytical conditions (Fig. 3b, d and g). The mass resolution using the FWHM of the 40Ar2+ peak in the HNA-Si spectrum was ∼27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Fig. 2a), but the m/Δm of 40Ar and 40Ca was 190
000 (Fig. 2a), but the m/Δm of 40Ar and 40Ca was 190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. We mainly used 40Ar4+ to match the valence with 36Ar4+ and also analyzed 40Ar2+ for comparison. The 55Mn5+ peak was located at 456.940 μs between the 40Ar4+ and 20Ne2+ peaks (Fig. 3b). The 55Mn5+ peak was removed using the ion gate during noble gas measurements. Ion gate operation did not affect the 40Ar4+ peak, as it was operated when the ion packets at m/z 10 and 11 were well separated before the TOF of 456.9 μs.
000. We mainly used 40Ar4+ to match the valence with 36Ar4+ and also analyzed 40Ar2+ for comparison. The 55Mn5+ peak was located at 456.940 μs between the 40Ar4+ and 20Ne2+ peaks (Fig. 3b). The 55Mn5+ peak was removed using the ion gate during noble gas measurements. Ion gate operation did not affect the 40Ar4+ peak, as it was operated when the ion packets at m/z 10 and 11 were well separated before the TOF of 456.9 μs.
For HNA-OL, 4He+ did not show interference from other peaks (Fig. 4a). 20Ne+ had interference from the 24Mg16O2+ peak for the same reason as that for the HNA-IL measurement (Fig. 4g). The tail from the 30Si3+ peak, produced by the dark currents, slightly overlapped with both 20Ne2+ and 22Ne2+ peaks (Fig. 4b). 36Ar4+ did not show interference from other peaks (Fig. 4c). Fig. 4g, b and d show the TOF spectra of 40Ar2+, 40Ar4+, and 40Ar5+, respectively, where 40Ca ions overlap with 40Ar ions similar to that in the HNA-IL measurements.
Depth profile of noble gases in minerals
Blank-IL and blank-OL were measured under the same analytical conditions and the depth profiles are shown in Fig. S5.† The backgrounds of noble gas ions for blank-IL and blank-OL are listed in Table 2 with blank iMs (ion intensities of each residual noble gas in the sample chamber) measured continuously throughout each analysis. The noble gas background was defined as the average of 106 mass scans after sputtering to ∼100 nm depth to avoid contamination on the sample surface. The error was defined as the standard deviation (1SD) of five data points obtained by binning the data into 2 × 105 mass scans. Similarly, blank iM was defined as the average of 106 mass scans, with the error determined as the 1SD of five data points by binning into 2 × 105 mass scans.| 4He+ | 20Ne2+ | 22Ne2+ | 36Ar4+ | 40Ar4+ | |
|---|---|---|---|---|---|
| a Units are cpms. n.d.: not detected (<10−6 cpms). | |||||
| Blank-IL | (4.6 ± 1.2) × 10−5 | (8.0 ± 11.5) × 10−6 | (2.0 ± 2.7) × 10−6 | (2.6 ± 1.2) × 10−5 | (1.0 ± 0.1) × 10−3 |
| Blank iM | (3.9 ± 1.8) × 10−5 | (5.0 ± 5.0) × 10−6 | (1.0 ± 2.2) × 10−6 | (1.0 ± 2.2) × 10−6 | (3.2 ± 0.5) × 10−4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Blank-OL | (9.6 ± 1.7) × 10−5 | (5.6 ± 1.6) × 10−5 | (2.3 ± 1.2) × 10−5 | (4.0 ± 6.5) × 10−6 | (2.8 ± 0.2) × 10−3 |
| Blank iM | (4.9 ± 1.0) × 10−5 | (9.0 ± 8.2) × 10−6 | (1.0 ± 2.2) × 10−6 | (1.0 ± 2.2) × 10−6 | (4.5 ± 0.4) × 10−4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| HNA-IL | (1.1 ± 0.1) × 10−4 | (2.9 ± 1.6) × 10−5 | (5.0 ± 6.1) × 10−6 | (4.6 ± 1.0) × 10−5 | (6.6 ± 0.4) × 10−4 |
| Blank iM | (1.6 ± 0.8) × 10−5 | (6.0 ± 5.5) × 10−6 | (1.0 ± 2.2) × 10−6 | n.d. | (1.5 ± 0.2) × 10−4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| HNA-OL | (1.1 ± 0.3) × 10−4 | (3.1 ± 0.7) × 10−5 | (4.0 ± 4.2) × 10−6 | (6.0 ± 4.2) × 10−6 | (8.1 ± 0.3) × 10−3 |
| Blank iM | (3.0 ± 1.0) × 10−5 | (5.0 ± 5.0) × 10−6 | n.d. | n.d. | (1.4 ± 0.2) × 10−4 |
The blank-IL and blank-OL backgrounds were in agreement with the blank iMs within the standard deviation (Table 2) for ions with less interference from other peaks (i.e., 4He+, 20Ne2+, and 22Ne2+ for blank-IL and 36Ar4+ for blank-OL). Therefore, the influence of noble gases originally contained in the minerals was smaller than that of residual gases in the sample chamber. For 4He+ in blank-OL, the background was twice as high as that in blank 4He+. Similar results were observed by Bajo et al.,14 who mentioned the possible sputtering of 4He adsorbed onto the sputtered surface from residual gas in the sample chamber. Therefore, the degree of adsorption may vary between materials. For other ions, the higher backgrounds for blank-OL and blank-IL compared with blank iMs were due to the interference mentioned in the previous section.
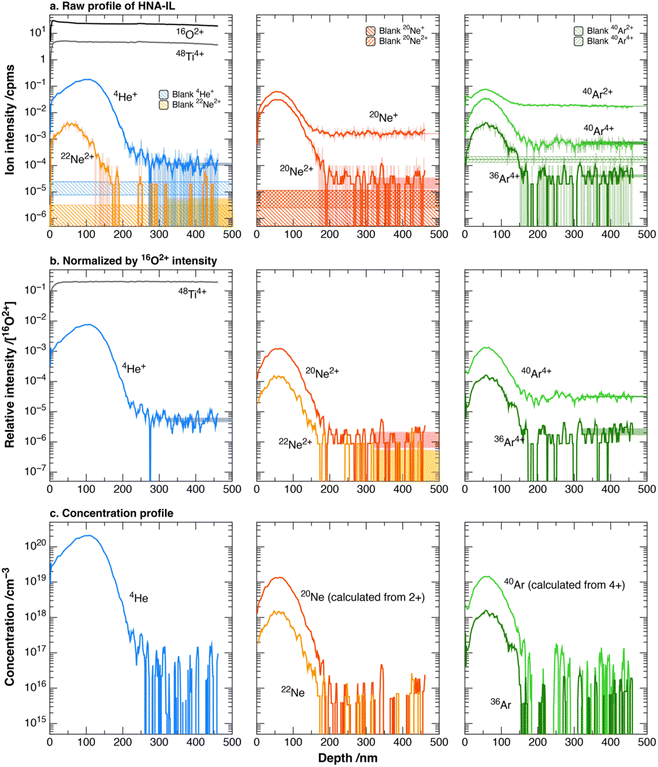
The depth profiles of noble gases and selected major ions of HNA-IL and HNA-OL are shown in Fig. 5 and 6. For both samples, all noble gas ions showed a peak at a depth of several tens to ∼100 nm, which decreased to a background intensity deeper than 300 nm. The measured depth profiles were slightly distributed at shallower depths than the simulated profiles (Fig. S3†), which are broadly consistent by considering some electrostatic charge-up of the substrates during ion implantation experiments. The background is defined as the average of the last 106 mass scans for each noble gas isotope (Fig. 5a and 6a). We evaluated the error of the background by binning these data into 5 data points and calculating the standard deviation (2 × 105 mass scans per point). The backgrounds and blank iMs are summarized in Table 2.
 | ||
| Fig. 5 Noble gas depth profiles of HNA-IL. (a) Raw profile of the noble gas and major element ions (Table S1†). The raw data are shown as a light-colored line with the moving average as a dark solid line. The moving average was calculated over an interval of 5 data points. Blank iMs and backgrounds for each ion are shown as a colored range corresponding with the average ± 1SD (Table 2). (b) Ion intensities normalized by the 16O2+ intensity. The moving average with an interval of 5 data points is shown. 20Ne+ and 40Ar2+ were omitted to simplify the figure. The colored range is the baseline with 1SD for each ion. The mean value was calculated using the last 106 mass scans, and the standard deviation was calculated by binning data points into 5 points, the same as that for the backgrounds. (c) The baseline was subtracted from the normalized profile corrected to concentration using eqn (1) and (2). The moving average with an interval of 5 data points is shown. | ||
 | ||
| Fig. 6 Noble gas depth profiles of HNA-OL. (a) Raw profile of noble gas and major element ions (Table S2†). The three graphs were obtained in a single measurement but separated to simplify the figure. The raw data are shown as a light-colored line with the moving average as a dark solid line. The moving average was calculated over an interval of 5 data points. Blank iMs and backgrounds for each ion are shown as a colored range corresponding to the average ± 1SD (Table 2). (b) Ion intensities normalized by 16O2+ intensity. The moving average with an interval of 5 data points is shown. 20Ne+ and 40Ar2+ were omitted to simplify the figure. The colored range is the baseline with 1SD for each ion. The mean value was calculated using the last 106 mass scans, and the standard deviation was calculated by binning data points into 5 points, the same as that for the backgrounds. (c) Baseline-subtracted normalized profile corrected for concentration using eqn (1) and (2). The moving average with an interval of 5 data points is shown. | ||
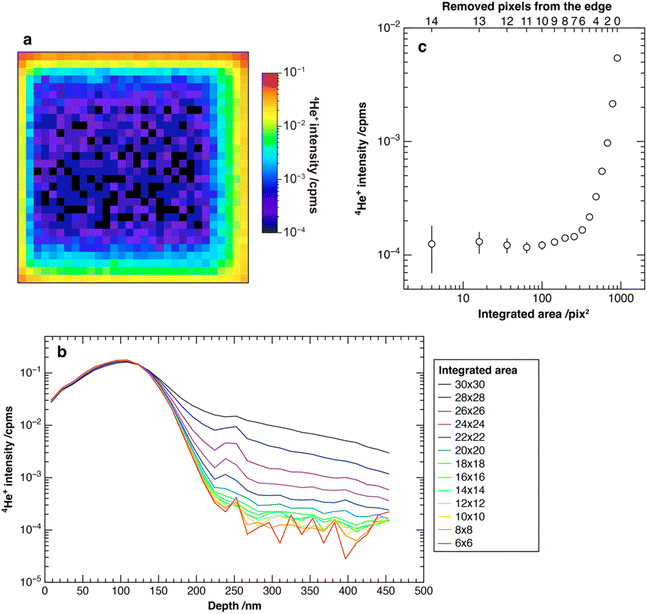
The backgrounds of 4He+ for HNA-IL and HNA-OL were higher than those of blank-IL and blank-OL, respectively (Table 2), which may be ascribed to the crater-edge effect. The image of 4He+ accumulated for the last 100 layers of HNA-IL is shown in Fig. 7a. The 4He+ intensity of the outer few pixels was significantly higher than that of the central area, broadening the depth profile shown in Fig. 7b from the crater-edge effect. The averaged intensity of the last 100 layers with changing data integration area is shown in Fig. 7c. The intensity was nearly constant after removing the outer 7 pixels. The depth profiles shown in Fig. 5 removed the outer 10 pixels, sufficiently reducing the crater-edge effect. The higher backgrounds than those of blank-IL and blank-OL may have been caused by the weak halo of the primary beam. Nagata et al.19 reported that a very weak halo spreads out from the center of the primary beam in the LIMAS. The weak halo consistently sputtered the high-concentration layer exposed on the crater edge, interfering with the signals from the crater bottom. We refer to this phenomenon as the weak halo effect. Both 4He+ and 20Ne2+ in HNA-IL and HNA-OL exhibited background intensities approximately three orders of magnitude lower than their peak intensities (Fig. 5a and 6a), supporting the idea of a common cause for the higher background.
The backgrounds of other ions of HNA-IL and HNA-OL were similar to those of blank-IL and blank-OL due to the respective interfering ions. The backgrounds of 20Ne2+ and 40Ar4+ were respectively lower than those of 20Ne+ and 40Ar2+. The 20Ne+ peak showed interference from the 24Mg16O2+ peak. However, the interference of 24Mg16O4+ with 20Ne2+ was not detected. 40Ca4+ was much less ionized than 40Ca2+. Thus, we used 20Ne2+ and 40Ar4+ peaks for the 20Ne and 40Ar measurements, respectively.
Detection limits of noble gases
The ion intensity profiles of HNA-IL and HNA-OL were normalized with the 16O2+ profile to calculate RSFiM using eqn (1) (Fig. 5b and 6b). The baseline was calculated using the last 106 mass scans. We subtracted the baseline from the relative intensity and calculated the concentration profile using eqn (2) (Fig. 5c and 6c). We defined the detection limits by multiplying RSFiM by 3SD of the baseline. The standard deviation was calculated by binning the last 106 mass scans within 2 × 105 mass scans. The detection limits for each noble gas ranged from 9 × 1015 to 9 × 1017 cm−3 depending on each interference and standard deviation of base lines. Detection limits of all noble gases are summarized in Table 3. The detection limit of 40Ar was different between two samples. This is due to the differences in calcium abundance in Monastery ilmenite and San Carlos olivine. In addition, detection limits of 4He and 22Ne also differed between the two samples, which could be due to slight differences in the weak halo effect.| Isotopes | HNA-IL | HNA-OL | ||||
|---|---|---|---|---|---|---|
| Measured ions | Detection limits/cm−3 | Major interference | Measured ions | Detection limits/cm−3 | Major interference | |
| a WHE: weak halo effect | ||||||
| 4He | 4He+ | 7 × 1016 | WHE or residual gas | 4He+ | 2 × 1017 | WHE or residual gas |
| 20Ne | 20Ne2+ | 3 × 1016 | WHE or residual gas | 20Ne2+ | 4 × 1016 | 30Si3+ tail |
| 22Ne | 22Ne2+ | 9 × 1015 | WHE or residual gas | 22Ne2+ | 2 × 1016 | 30Si3+ tail |
| 36Ar | 36Ar4+ | 2 × 1016 | 27Al3+ + residual gas | 36Ar4+ | 2 × 1016 | WHE or residual gas |
| 40Ar | 40Ar4+ | 5 × 1016 | 40Ca4+ + residual gas | 40Ar4+ | 9 × 1017 | 40Ca4+ + 30Si3+ |
Solar wind noble gases are concentrated on the very surface of extraterrestrial materials. Based on the single-grain analyses of lunar ilmenites,28 the concentrations of 4He, 20Ne, 22Ne, and 36Ar were estimated to be approximately 1021, 1019, 1018, and 1018 cm−3, respectively, assuming that all noble gases were concentrated to the top 100 nm of the spherical grain. The detection limits we achieved were approximately more than two orders of magnitude lower than the concentrations in lunar soils, allowing for the depth profiling of 4He, 20Ne, 22Ne, and 36Ar from the grain surface with extremely high spatial resolution.
Reproducibility of noble gas analysis by LIMAS
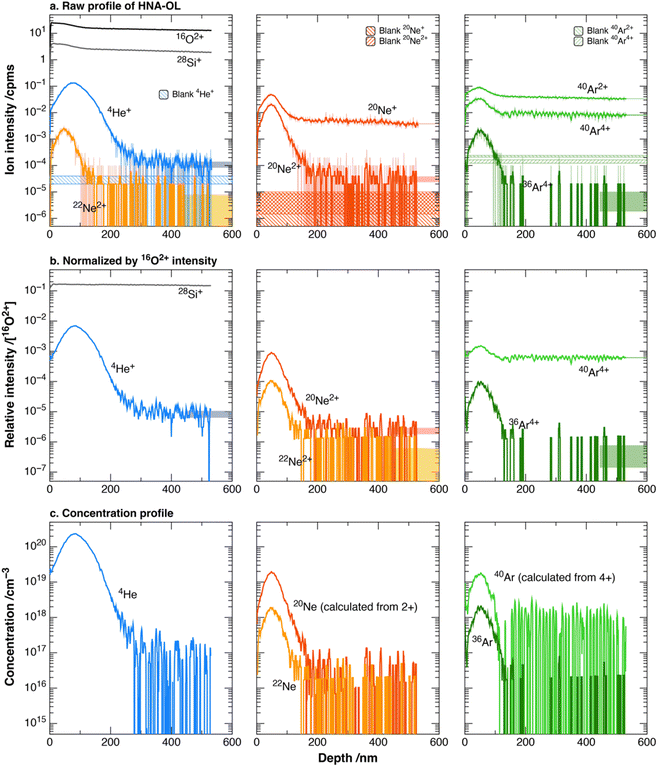
We conducted eleven measurements on HNA-IL to calculate the RSFs for concentrations of each noble gas isotope and at selected elemental and isotopic ratios (Fig. 8 and Table S3†). Each measurement run took about 12 h, and the eleven measurements were conducted over a period of 6 months. The standard deviations by counting statistics for each run were less than 5%. The reproducibility of RSFs including RSFi,j and RSFiM showed a variation of 11–31%, which was much larger than the statistical errors (Fig. 8). | ||
| Fig. 8 Reproducibility of RSFs in 11 HNA-IL measurements. Error bars denote the counting errors in 1SD, with most being smaller than the symbol. The mean values and 1SD are described for each RSFs and shown as solid lines and gray regions, respectively. The numbers noted below the mean values are lap numbers of each ion in MULTUM II. Data are listed in Table S3.† | ||
The instrumental mass fractionation in the LIMAS arises primarily from two factors: (a) change of laser post-ionization efficiency due to the differences in ionization efficiencies between isotopes or between elements and between independent measurements and (b) the differences in ion transmittance into MULTUM II and within MULTUM II between different lap numbers20 for ions and between independent measurements. 20Ne2+ and 40Ar4+ are both measured after 107 laps in the MULTUM II, and thus, RSF20,40 is only affected by factor (a). Its standard deviation is 5%, which is the highest reproducibility, and this indicates that relative ionization efficiencies between Ne2+ and Ar4+ were stable. On the other hand, RSF20,22 is affected solely by factor (b) because isotopes would have similar ionization efficiency to each other, and the standard deviation was 12%. This is due to the change of relative ion transmittance between ions with 102–107 laps in the MULTUM II between independent measurements. The standard deviations of RSF20,36 and RSF4,20 are 11% and 31%, respectively. The former reflects the propagation of the reproducibility of factors (a) and (b), with factor (b) being the dominant contributor. The latter shows the worst reproducibility because the flight path length of 4He+ is ∼1.5 times longer than those of Ne and Ar ions measured here, and this would be more sensitive to factor (b). In addition, ionization efficiency of He+ may also vary relative to Ne2+ and Ar4+ because of the extremely high ionization energy. The standard deviations of RSFiM are in the range of 19–26% (1SD). Both factors (a) and (b) affect here. In addition, the calculation of the RSFiM uses the sputtering rate (d/n in eqn (1)), which includes the measurement errors of the laser microscope of ∼5% (Fig. S1†).
Fig. 9 shows the simulated and measured 20Ne/22Ne depth profiles. The simulation suggests that the 20Ne/22Ne ratio of HNA-IL in the 0–100 nm range was maintained at 10. We binned the measured 20Ne and 22Ne data to make the counting error for 20Ne/22Ne less than 10%. As a result, 13 data points were obtained within the 0–100 nm range. The mean value of these 13 points was 10.1 ± 0.9 (1SD), with 1SD comparable to the counting error of each data point. This indicated that the isotope ratios during the single depth profiling were sufficiently uniform within the error. The ratio could be measured at a depth resolution of ∼10 nm with a precision of 10%.
The single-grain analyses of lunar ilmenites showed that the concentrations of 4He, 20Ne, and 36Ar varied by two to three orders of magnitude among individual grains.28 Consequently, the reproducibility of RSFiM (∼20% for all isotopes) was sufficient for the concentration analysis. 4He/20Ne and 20Ne/36Ar ratios provide insights into the degassing of light noble gases from lunar soils. The single-grain analyses of lunar ilmenites revealed 4He/20Ne and 20Ne/36Ar ratios of 34–495 and 6–40, respectively, which are minimum and maximum values of ilmenite grains separated from lunar soil 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 reported by Nichols et al. (1994).28 Thus, the reproducibility of RSF4,20 and RSF20,36 (31% and 11%) was sufficient to estimate the bulk 4He/20Ne and 20Ne/36Ar ratios in lunar ilmenites. The 20Ne/22Ne ratio of materials irradiated by solar wind indicated depth-dependent mass fractionation during solar wind implantation.11 Closed system stepwise etching indicated that the 20Ne/22Ne ratio of lunar ilmenite was ∼14 at the surface and ∼11 in the subsurface region.12 The reproducibility of RSF20,22 (∼12%) and the 20Ne/22Ne depth profile obtained using the LIMAS suggested that the fractionation of Ne isotopes could be visualized with actual depth, allowing for the more precise characterization of the implantation profile of solar wind noble gases.
501 reported by Nichols et al. (1994).28 Thus, the reproducibility of RSF4,20 and RSF20,36 (31% and 11%) was sufficient to estimate the bulk 4He/20Ne and 20Ne/36Ar ratios in lunar ilmenites. The 20Ne/22Ne ratio of materials irradiated by solar wind indicated depth-dependent mass fractionation during solar wind implantation.11 Closed system stepwise etching indicated that the 20Ne/22Ne ratio of lunar ilmenite was ∼14 at the surface and ∼11 in the subsurface region.12 The reproducibility of RSF20,22 (∼12%) and the 20Ne/22Ne depth profile obtained using the LIMAS suggested that the fractionation of Ne isotopes could be visualized with actual depth, allowing for the more precise characterization of the implantation profile of solar wind noble gases.
Applicability to other extraterrestrial samples
This study demonstrates a measurement technique optimized for ilmenite and olivine, because we focus on measurements of lunar and asteroidal regolith samples. The results indicate that one critical factor for the optimization is to consider the sample composition, which influences detection limits due to interfering ions. For example, in materials with higher aluminum or silicon content, interferents such as 27Al3+ to 36Ar4+ or 30Si3+ and 40Ca4+ overlapping with 20Ne2+ and 40Ar4+ may become significant. In such cases, the TOF conditions and selected ions to be measured optimized in this study may not be ideal, necessitating modifications to measurement parameters according to the discussion in this study. Preparation of ion-implanted reference samples is also necessary in such cases.A possible application of this method is for noble gases trapped in presolar grains or interplanetary dust particles, whose sample sizes are much smaller than typical lunar or asteroidal sample sizes. To ensure high depth resolution for the depth profiling, a large smooth surface relative to the primary beam diameter is required. Therefore, a smaller primary beam diameter is needed. In order to achieve it, the primary beam current must be reduced. However, reducing the beam current leads to lower ion intensities per mass scan, which, in turn, raises the detection limit for noble gases.
Despite these challenges, the method presented here represents a novel approach to obtaining depth profiles of He, Ne, and Ar isotopes and their compositions based on an absolute depth scale, which has not been previously achieved.
Conclusions
4He, 20Ne, 22Ne, 36Ar, and 40Ar co-implanted ilmenite and olivine standards were prepared herein. We optimized the analytical conditions of the LIMAS for the multi-isotope depth profiling of 4He, 20Ne, 22Ne, 36Ar, 40Ar, and major elements of ilmenite and olivine. All target ions except for 40Ar were separated from the interference ions and determined using the ion assignment procedures for ilmenite and olivine standards.The depth profiles of 4He, 20Ne, 22Ne, 36Ar, and 40Ar were obtained by sputtering an area of ∼6 × 8 μm2, and the detection limits for 4He, 20Ne, 22Ne, 36Ar, and 40Ar were respectively 7 × 1016, 3 × 1016, 9 × 1015, 2 × 1016, and 5 × 1016 cm−3 for ilmenite and 2 × 1017, 4 × 1016, 2 × 1016, 2 × 1016, and 9 × 1017 cm−3 for olivine. We evaluated the reproducibility of RSFs to calculate the noble gas compositions and concentrations. The reproducibility of the RSFs between independent measurement runs was in the 5–31% range (1SD). The stability of the 20Ne/22Ne ratios during depth profiling was restricted by counting errors. Therefore, this analytical method can be used to analyze solar wind noble gases in extraterrestrial materials. Based on the depth profiling of noble gases, this approach can reveal past solar activity and the underlying mechanisms of solar wind implantation and degassing processes.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Y. O., K. B., and H. Y. designed the study. Y. O., K. B., and T. O. carried out the LIMAS analysis. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Go Kinoda and Shingo Ogawa of the TORAY Research Center, Inc. for preparing the ion-implanted samples. We sincerely thank the two anonymous reviewers for their valuable comments, which have helped improve our manuscript. We acknowledge editorial handling by Dr Derya Kara Fisher. We also thank Charlesworth Author Services for their professional English editing services. This work was supported by grants from the Japan Society for the Promotion of Science (JSPS) KAKENHI and the Japan Science and Technology Agency (JST) to YO, KB, and HY.References
- R. Wieler, Do lunar and meteoritic archives record temporal variations in the composition of solar wind noble gases and nitrogen? A reassessment in the light of Genesis data, Geochemistry, 2016, 76, 463–480 CrossRef CAS.
- C. M. Pieters and S. K. Noble, Space weathering on airless bodies, J. Geophys. Res.:Planets, 2016, 121, 1865–1884 CrossRef PubMed.
- T. Kirsten, Rare gages implanted in lunar fines, Philos. Trans. R. Soc., A, 1977, 285, 391–395 CrossRef CAS.
- J. Kerridge, A reevaluation of the solar-wind sputtering rate on the lunar surface, Lunar and Planetary Science Conference Proceedings, 1991, vol. 21, pp. 301–306 Search PubMed.
- J. Kiko, H. W. Müller, K. Büchler, S. Kalbitzer, T. Kirsten and M. Warhaut, The gas ion probe: a novel instrument for analyzing concentration proeiles of gases in solids, Int. J. Mass Spectrom. Ion Phys., 1979, 29, 87–100 CrossRef CAS.
- J. Kiko, K. Büchler, J. Jordan, S. Kalbitzer, T. Kirsten, H. W. Müller, T. Plieninger and M. Warhaut, A comparison of rare gas concentration profiles in lunar and artificially implanted ilmenites measured with the gas ion probe, Meteoritics, 1976, 11, 309–311 Search PubMed.
- M. Warhaut, J. Kiko and T. Kirsten, Microdistribution patterns of implanted rare gases in a large number of individual lunar soil particles, Lunar and Planetary Science Conference Proceedings, 1979, vol. 10, pp. 1531–1546 Search PubMed.
- H. W. Müller, J. Kiko and T. Kirsten, He-depth profiles with high resolution (∼100 Å) by the rare gas ion probe technique, Meteoritics, 1975, 10, 459 Search PubMed.
- M. A. Ray, J. E. Baker, C. M. Loxton and J. E. Greene, Quantitative analysis and depth profiling of rare gases in solids by secondary-ion mass spectrometry: detection of (CsR)+ molecular ions (R = rare gas), J. Vac. Sci. Technol., A, 1988, 6, 44–50 CrossRef CAS.
- H. Yamazaki, Quantitative depth profiling of argon in tungsten films by secondary ion mass spectrometry, Anal. Sci., 2001, 17, 407–410 CrossRef CAS PubMed.
- A. Grimberg, H. Baur, P. Bochsler, F. Bühler, D. S. Burnett, C. C. Hays, V. S. Heber, A. J. G. Jurewicz and R. Wieler, Solar wind neon from Genesis: implications for the lunar noble gas record, Science, 2006, 314, 1133–1135 CrossRef CAS PubMed.
- J.-P. Benkert, H. Baur, P. Signer and R. Wieler, He, Ne, and Ar from the solar wind and solar energetic particles in lunar ilmenites and pyroxenes, J. Geophys. Res., 1993, 98, 13147 CrossRef CAS.
- S. Ebata, M. Ishihara, K. Uchino, S. Itose, M. Matsuya, M. Kudo, K. Bajo and H. Yurimoto, Development of laser ionization mass nanoscope (LIMAS), Surf. Interface Anal., 2012, 44, 635–640 CrossRef CAS.
- K. Bajo, N. Kawasaki, I. Sakaguchi, T. T. Suzuki, S. Itose, M. Matsuya, M. Ishihara, K. Uchino and H. Yurimoto, Anal. Chem., 2024, 96, 5143–5149 CrossRef CAS PubMed.
- K. Bajo and H. Yurimoto, Nanoscale analysis of noble gas in solids, J. Anal. Sci. Technol., 2024, 15, 1–9 CrossRef.
- K. Bajo, O. Fujioka, S. Itose, M. Ishihara, K. Uchino and H. Yurimoto, Electronic data acquisition and operational control system for time-of-flight sputtered neutral mass spectrometer, Surf. Interface Anal., 2019, 51, 35–39 CrossRef CAS.
- K. Bajo, S. Itose, M. Matsuya, M. Ishihara, K. Uchino, M. Kudo, I. Sakaguchi and H. Yurimoto, High spatial resolution imaging of helium isotope by TOF-SNMS, Surf. Interface Anal., 2016, 48, 1190–1193 CrossRef CAS.
- K. Bajo, C. T. Olinger, A. J. G. Jurewicz, D. S. Burnett, I. Sakaguchi, T. Suzuki, S. Itose, M. Ishihara, K. Uchino, R. Wieler and H. Yurimoto, Depth profiling analysis of solar wind helium collected in diamond-like carbon film from Genesis, Geochem. J., 2015, 49, 559–566 CrossRef CAS.
- K. Nagata, K. Bajo, S. Itose, M. Matsuya, M. Ishihara, K. Uchino and H. Yurimoto, Aberration-corrected focused ion beam for time-of-flight secondary neutral mass spectrometry, Appl. Phys. Express, 2019, 12, 085005 CrossRef CAS.
- A. Tonotani, K. Bajo, S. Itose, M. Ishihara, K. Uchino and H. Yurimoto, Evaluation of multi-turn time-of-flight mass spectrum of laser ionization mass nanoscope, Surf. Interface Anal., 2016, 48, 1122–1126 CrossRef CAS.
- H. Yurimoto, K. Bajo, I. Sakaguchi, T. T. Suzuki, A. J. G. Jurewicz, S. Itose, K. Uchino and M. Ishihara, Quantitative analysis of helium by post-ionization method using femtosecond laser technique, Surf. Interface Anal., 2016, 48, 1181–1184 CrossRef CAS.
- D. S. Burnett, B. L. Barraclough, R. Bennett, M. Neugebauer, L. P. Oldham, C. N. Sasaki, D. Sevilla, N. Smith, E. Stansbery, D. Sweetnam and R. C. Wiens, The Genesis Discovery Mission: Return of Solar Matter to Earth, in The Genesis Mission, 2003, pp. 1–26 Search PubMed.
- J. F. Ziegler, M. D. Ziegler and J. P. Biersack, SRIM – The stopping and range of ions in matter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823 CrossRef CAS.
- D. B. Reisenfeld, R. C. Wiens, B. L. Barraclough, J. T. Steinberg, M. Neugebauer, J. Raines and T. H. Zurbuchen, Solar Wind Conditions and Composition During the Genesis Mission as Measured by in situ Spacecraft, Space Sci. Rev., 2013, 175, 125–164 CrossRef.
- P. Signer, H. Baur, U. Derksen, P. Etique, H. Funk, P. Horn and R. Wieler, Helium, neon, and argon records of lunar soil evolution, Lunar and Planetary Science Conference Proceedings, 1977, vol. 3, pp. 3657–3683 Search PubMed.
- K. Nagao, R. Okazaki, T. Nakamura, Y. N. Miura, T. Osawa, K. Bajo, S. Matsuda, M. Ebihara, T. R. Ireland, F. Kitajima, H. Naraoka, T. Noguchi, A. Tsuchiyama, H. Yurimoto, M. E. Zolensky, M. Uesugi, K. Shirai, M. Abe, T. Yada, Y. Ishibashi, A. Fujimura, T. Mukai, M. Ueno, T. Okada, M. Yoshikawa and J. Kawaguchi, Irradiation history of Itokawa regolith material deduced from noble gases in the Hayabusa samples, Science, 2011, 333, 1128–1131 CrossRef CAS PubMed.
- D. Okumura, M. Toyoda, M. Ishihara and I. Katakuse, A compact sector-type multi-turn time-of-flight mass spectrometer ‘MULTUM II’, Nucl. Instrum. Methods Phys. Res., Sect. A, 2004, 519, 331–337 CrossRef CAS.
- R. H. Nichols, C. M. Hohenberg and C. T. Olinger, Implanted solar helium, neon, and argon in individual lunar ilmenite grains: surface effects and a temporal variation in the solar wind composition, Geochim. Cosmochim. Acta, 1994, 58, 1031–1042 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00430b |
| This journal is © The Royal Society of Chemistry 2025 |