Particle signal considerations for isotope ratio analysis with single particle multi-collector inductively coupled plasma mass spectrometry

Abstract

Particle analysis has benefitted from the advent of single particle inductively coupled plasma-mass spectrometry (spICP-MS) due to its robustness, sensitivity, and high-throughput nature. Previous methods of spICP-MS have typically utilized quadrupole or time-of-flight mass analyzers and therefore employ electron multiplier-based detectors (such as secondary electron multipliers or microchannel plates). However, to obtain precise measurements on elemental or isotopic ratios within individual particles, multi-collector ICP-MS (MC-ICP-MS) can be used. Here, we investigate Ce isotope ratios, specifically ¹⁴²Ce/¹⁴⁰Ce, by spMC-ICP-MS using an all-Faraday cup collector array. Using 1 μm (diameter) cerium dioxide particles, integration times of the Faraday cup detectors were varied from 50–500 ms. The signal from the cerium isotopes in the particles was used to determine isotope ratios, which closely matched the expected natural isotopic abundances. Due to the signal decay response from the Faraday cups, the signal from particles lasts much longer than the expected 1–2 ms (up to 100 s of ms). To explore this effect on isotope ratio analysis, multiple ratio analysis methods were used to determine how to obtain optimal precision and accuracy. Relative differences were around 2% for methods that calculated isotope ratios from summing the total signal of an individual particle before calculating the ratio (rather than using every data point individually). It was found that summing all data points per particle, or integrating under the signal peak, yielded both accurate and precise isotope ratios within the particle population. Particles were also sampled off a solid substrate via microextraction, and isotope ratios were determined with relative differences of 0.13% to 9%. This demonstrates the ability to use spMC-ICP-MS to obtain isotope ratios on particles, with little to no relative difference in comparison to the expected ratio, even when operating Faraday detectors at fast 50 ms integration times.

---

Sarah E. Szakas

Currently, Dr Sarah Szakas is a Postdoctoral Researcher at Oak Ridge National Laboratory, in the Chemical and Isotopic Mass Spectrometry group (Chemical Sciences Division). She graduated with her B.S. in Forensic and Toxicological Chemistry from West Chester University of Pennsylvania in 2017 and worked for a healthcare compliance laboratory immediately after. She quickly realized she was eager to dive deeper into research which led her to pursue graduate studies in Analytical Chemistry from Iowa State University, where she earned her doctorate in 2024 under Dr Alexander Gundlach-Graham. Her current research focuses on developing and advancing single particle and single cell inductively coupled plasma mass spectrometry (sp-ICP-MS) for both time-of-flight and multi-collector-based platforms. Her work also explores coupling laser ablation-based techniques for bioimaging. Beyond the lab, Sarah serves as the Outreach Chair for the ORNL Postdoc Association and works to create a supportive environment for fellow researchers. When not pipetting particle suspensions, Sarah enjoys traveling, reading a good book, and hiking in the Great Smokey Mountains!

Introduction

An emerging area of research in the past decade has been the detection and identification of particulate matter (PM), especially in the micro-particle (at least one dimension from 1–1000 μm) and nanoparticle (one dimension less than 100 nm) size regimes. Many areas of research have focused on environmental particles, especially with the detection of plastics and other anthropogenic inputs. The “gold standard” typically used to characterize PM is microscopy, specifically scanning electron microscopy-energy dispersive X-ray spectroscopy (SEM-EDS) with automated particle analysis (APA). This method allows for the determination of PM morphology and elemental composition. While this type of analysis provides critical information without being destructive to the sample, it can take multiple hours per sample. With these time and sensitivity constraints, SEM-EDS-APA is analytically ‘capped’ at a specified number of particles, which may bias results towards both larger particles, and particles whose X-rays are more readily detected. If isotopic information is warranted, then single particle aerosol mass spectrometry (SPAMS), fission track (FT) thermal ionization mass spectrometry (TIMS), secondary ion mass spectrometry (SIMS), or large geometry secondary ion mass spectrometry (LG-SIMS) can be used.^1–4 High precision and accuracy is achieved through these mass spectral measurements, but like microscopy-based techniques, they are often limited in throughput.⁵

A newer method of PM detection, that provides significantly higher throughput, is single-particle inductively coupled plasma-mass spectrometry (spICP-MS). In spICP-MS, a dilute suspension of particles is introduced to the ICP source, and each particle generates a discrete cloud of ions that are subsequently detected, typically with a signal duration lasting about 500 μs. Detecting ions from unique particles requires fast detection, since long dwell or integration times decrease the signal-to-noise ratio (SNR) until a signal is no longer distinguishable from the background. In routine quadrupole-based spICP-MS, dwell times usually range from 10–50 ms while typical time-of-flight (TOF)-based spICP-MS uses integration times of 1 or 2 ms (but both have the capability to acquire data at acquisition rates in the 10 s of μs).^6–10 Benefits of using spICP-MS methods for detection of inorganic particles include high sensitivity (down to 10⁻¹⁸ g – or attograms – of specific nuclides per particle), high transport efficiencies (up to ∼80% of particles with specific nebulizers/spray chambers), and high-throughput measurements (e.g., particle number concentrations (PNCs) of thousands of particles per mL or per minute).¹¹

Isotopic analysis via spICP-MS requires consideration for the type of mass analyzer selected. Generally, when using quadrupole-based MS platforms, isotopic precisions cannot be reported for single particles, as the settling time needed when changing voltages does not allow for monitoring more than one nuclide per dwell time. A TOF-based MS platform can detect all nuclides of interest at every integration time due to the nature of the fast ion-counters used, such as microchannel plates. The ability to determine isotope ratios is controlled by Poisson statistics and is therefore dependent on particle size (signal intensity) and sensitivity (ability to detect each isotope of interest).^12,13 It has been estimated that a best-case scenario isotopic precision, or relative standard deviation (RSD), for particle populations obtained by spICP-TOFMS is ∼1%.^13,14

MC-ICP-MS yields the greatest precision in isotope ratios among these techniques, with the ability to obtain RSDs lower than 0.001% in bulk digestion-based approaches.¹⁵ Integration times used in MC-ICP-MS are usually ≥50 ms and can even be on the order of seconds to minutes, with integration time selection depending on a number of factors including acceptable detector noise levels, the volume of sample available, and the desired level of precision. However, when considering the analysis of particles using MC-ICP-MS, selection of integration time must be made with regard to the short signal durations.

Particle signal durations using Faraday detectors depend on both the particle size (signal intensity) and the detector decay constant (or time constant), inherent to the amplifier.^16,17 This causes intense, transient particle signals to show temporal spread that can span a few hundred ms. With consideration to this spread in particle signal, particle suspensions must be at proper dilutions, and may be readily analyzed at integration times of tens to hundreds of ms.^18,19 Previous studies have explored using spMC-ICP-MS for Ag, Pt, Er, and Nd nanoparticles (spherical diameters ranging from 40–400 nm).^20–23 For example, it was found that isotope ratios within Nd nanoparticles showed lower relative differences obtained via spMC-ICP-MS than with spICP-TOFMS.²³

An important application of single particle analysis is isotopic ratio determination within particles for reference materials. Particle standards are common for select elements, such as gold, due to their use in calibration for methods such as flow cytometry and microscopy. However, there are limited particulate standards with differing chemical compositions that are also well-characterized regarding particle size distribution, particle number concentration, and isotopic ratio. Current analysis techniques include microscopy, TIMS, MC-ICP-MS, SIMS, and LG-SIMS.²⁴ As previously mentioned, many of these measurement techniques are limited by throughput, making it impractical to carry out measurements on a statistically significant number of particles. Isotopic analysis can be carried out by traditional MC-ICP-MS analysis, either on the solution used to synthesize the particles, or on a solution of digested particles. Doing so eliminates information on individual particles, as well as minimizes the ability to compare compositional homogeneity across the particle population(s). This is especially important in the field of nuclear forensics and safeguards, where particle standards are used for instrument calibration and quality control (QC) for FT-TIMS and LG-SIMS measurements. Examples of these include particulate test materials that are created with lanthanide elements, as well as uranium.²⁵ Isotopic ratios, and their precisions, need to be characterized in a high-throughput approach for batches of reference particles to provide statistically significant information regarding the particle population. This is motivation to explore validation of spMC-ICP-MS for these types of analyses.

The goal of this study is to investigate the use of spMC-ICP-MS, with an all-Faraday cup collection array, for isotope ratio analysis using 1 μm cerium dioxide (CeO₂) particles. While not directly compared to SIMS or TIMS in this study, previous research into the precisions of uranium particles (of multiple sizes of U particles ≥1 μm diameter) by LG-SIMS were shown to be <1% for ²³⁵U/²³⁸U while for LA-MC-ICP-MS the (2σ) precision ranged from 1.8–6%.^26,27 Therefore, we would expect precision of ratios obtained via solution-based spMC-ICP-MS to be similar (without consideration of the total number of particles analyzed or integration time of the instrument).

This study considers both instrumental parameters and data treatment methods that affect sensitivity, precision, and sample throughput. Previous work has reported that Faraday detectors have an inherently slow response to sudden changes in signal intensity.²⁸ However, this is the first report to investigate the effect of signal integration time on isotope ratio precision for particles when using an all-Faraday detector array. Results herein show that longer signal integration times may improve isotopic ratio precision at the cost of sensitivity and sample throughput. Furthermore, seven different data analysis methods were explored, with an emphasis on how post-measurement treatment of data relates to the precision of the ratios, here obtained for ¹³⁶Ce, ¹³⁸Ce, and¹⁴²Ce relative to ¹⁴⁰Ce.^29,30 Finally, we demonstrate how microextraction (ME) sampling can be coupled to spMC-ICP-MS (spME-MC-ICP-MS) for particle extraction.^31–34 ME has been previously shown to extract particles directly off substrates and deliver them to the ICP at dilutions that allow for particles to enter the plasma one at a time.³⁴ This demonstrates the potential for spME-MC-ICP-MS to be used directly with solid-sampling, such as on environmental swipes which are used frequently in nuclear forensics and safeguards to detect isotopic ratios of interest within individual particles, or from surfaces on which particle reference materials are deposited.

Methods and materials

CeO₂ particle synthesis

Ceria (CeO₂) microparticles were synthesized using a Savannah River National Laboratory-designed aerosol-based droplet-to-particle via in-line calcination production method.³⁵ This method has been utilized and described in detail previously to make uranium-based and cerium-based microparticles.^25,36–38 Briefly, feedstocks of 1.686 mM of cerium(III) nitrate were flowed through a flow-focusing monodisperse aerosol generator (FMAG, Model 1520, TSI Inc.) using filtered air to produce aerosolized droplets. These droplets were flowed through a diffusion drier (Model 3062, TSI, Inc.), at a flow rate of 10.0 ± 0.1 L min⁻¹, into a three-zone tube furnace set to 350 °C, 450 °C, and 600 °C, at the inlet, middle, and outlet, respectively. The dried and calcined particles were then either diverted to an aerodynamic particle sizer (APS, Model 3321, TSI, Inc.) to obtain in situ aerodynamic particle size distributions, or to a custom electrostatic precipitator mini-ACE for particle collection.³⁹

Ceria particle characterization

The ceria microparticles were characterized with a Hitachi SU5000 scanning electron microscope (SEM) to analyze particle size and morphology. Images were acquired using electron backscatter mode with an accelerating voltage of 10 kV in variable pressure mode to prevent excess charging. The SEM sample was prepared by depositing the particles onto carbon tape. The size distribution was obtained by manual sizing of ∼300 particles using ImageJ.⁴⁰ SEM images and the measured particle size distribution of this sample population are shown in Fig. 1, demonstrating a mean equivalent circular diameter (ECD) of 1.09 ± 0.10 μm. The APS measured an aerodynamic particle size distribution, which assumed spherical particles with a density of 1 g mL⁻¹. The true particle density was estimated to be 2.7 g mL⁻¹ (Fig. 1c), by reconciling the APS data with SEM-measured size distributions. This particle density is lower than that of commercial powder CeO₂. A closer examination of the particle SEM images reveals that these particles are porous, explaining the low density.

Fig. 1 SEM images of prepared cerium dioxide particles are shown in (a) and (b). Particle diameters were estimated to be 1.09 ± 0.10 μm. In (c), the density of these particles, found using an aerodynamic particle sizer, was measured at 2.7 g mL⁻¹.

Single particle MC-ICP-MS

A stock suspension of CeO₂ particles was prepared by weighing 3.2 mg of the 1.09 μm CeO₂ particles and suspending in 2 mL of water (type I ultrapure 18.2 MΩ-cm water); this stock suspension had a particle number concentration (PNC) of ∼1.0 × 10⁹ particles mL⁻¹. A subsequent dilution of this stock was made to avoid double events and to be more suitable for single particle analysis. The PNC of this suspension was ∼3.8 × 10⁵ particles per mL, which was screened via spICP-TOFMS (icpTOF R, TOFWERK AG, Thun, Switzerland) to confirm PNC would be low enough for the longer integration times used with Faraday cup detectors.

The instrument used for all isotope ratio experiments was the Thermo Fisher Scientific Neoma MC-ICP-MS (Bremen, Germany). The sample was introduced via the CytoSpray chamber (Elemental Scientific Instruments, Omaha, NE, USA) with a self-aspirating perfluoroalkoxy alkane (PFA) nebulizer at a flow rate of 50 μL min⁻¹. Isotopes of interest were detected via five Faraday cups equipped with 10¹¹ Ω resistance amplifiers. The center cup measured ¹⁴⁰Ce and the other cups monitored ¹³⁶Ce, ¹³⁸Ce, and ¹³⁹La and ¹⁴²Ce (shown in Table 1). Integration times, or collection time per data point, were varied: 50, 100, 250, or 500 ms. Further instrument operational details can be found in Table 1.

Table 1 Instrument parameters

	Traditional liquid intro			Microextraction intro
Neb Ar gas flow (L min^−1)	0.20			0.20
Additional Ar gas flow (L min^−1)	0.84			0.60
Cooling Ar gas flow (L min^−1)	14
Auxiliary Ar gas flow (L min^−1)	0.80
Solution uptake rate (μL min^−1)	50
RF power	1199
Cones	H sampler and Ni skimmer (elemental scientific Inc.)
Analysis time (s)	100			45 (per extraction)
Detector setup
Cup configuration	L3	L2	L1	Center	H1
Amplifier resistor (Ω)	10^11	10^11	10^11	10^11	10^11
Isotope of interest	^136Ce	^138Ce	^139La	^140Ce	^142Ce

---

Microextraction with spMC-ICP-MS

The experimental setup for the microextraction system has been described previously.³⁴ Briefly, a modified Advion Plate Express (Advion, Ithaca, NY), fitted with a ProScan Motorized XY Stage (Prior Scientific, Rockland, MA), was used to extract particles off a polytetrafluoroethylene (PTFE) surface and deliver them to the nebulizer. A 500 nL aliquot of a 300× dilution of the stock particle suspension was deposited on the PTFE surface (∼1.7 × 10³ particles). The extraction head was lowered onto the PTFE surface, with a force of 300 N, forming a seal (2 mm × 4 mm). Next, a 6-port valve directed a solution of 5% HNO₃ (with a flow rate of 100 μL min⁻¹) through the probe head and to the ICP-MS, mobilizing, particles and delivering them to the MC-ICP-MS. It has been shown that extracted particles tend to concentrate at the front of the extraction volume.³⁴ Typically ∼70% of the extracted particles were observed in a 3 s window at the front end of the extraction period. However, the employment of a CytoSpray chamber and PFA nebulizer used for particle suspensions was found to be compatible with the microextraction workflow and dramatically increased the temporal spacing of particles during extraction (shown in Fig. S1†). The duration of particle extraction was set to 30 s, and extractions (n = 20) were conducted for each dwell time (50, 100, 250, and 500 ms).

Particle digestion and analysis

Bulk digestion was completed for verification of the isotope ratios of the analyzed particles. Here, 1 mL of particle stock suspension, 1 mL of optima grade concentrated HNO₃, and 1 mL of 30% H₂O₂ were added to a pre-weighed Savillex vial. The vials were capped tightly and heated overnight at 120 °C on a hotplate, then allowed to cool to room temperature. The resultant solution was diluted by a factor of ∼2000× with 2% HNO₃ and run on the same instrument used for single particle analysis to obtain the isotopic ratios of ¹³⁶Ce, ¹³⁸Ce, and¹⁴²Ce relative to ¹⁴⁰Ce. This solution was also used for cup peak-centering and tuning before single particle analysis, as well as in between sample runs when switching the integration times.

Data analysis

Mass spectral signals were analyzed using in-house code written in Python. Particle data was sorted by using an iterative 3σ approach.^41,42 Briefly, the average intensity from all data points in a mass spectrum are used and a threshold is set at 3σ. Data points above this threshold were determined to be derived from particle signals and set aside. A new average was calculated with the remaining data and this process iteratively continued until no further data points were labeled as particle derived. After finding particle signals, isotope ratio analysis was carried out using various methods (see Fig. S2†). The differences in these methods will be discussed in detail in the Results and discussion.

Results and discussion

Faraday cup detector response to single particles

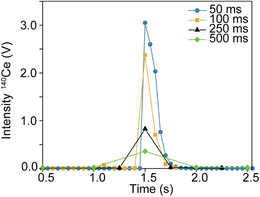
The first focus of this study was to explore different integration times and their effects on isotope ratio measurements within single particles. Fig. 2 shows time traces obtained from integration times of 50, 100, 250, and 500 ms. Note, the y-axis (voltage detected) is not the same in each sample. Individual particle signals are represented as ‘spikes’ due to the sudden flux in the number of ions hitting the detector from a particle event. As the time used to collect ion signal increases up to 500 ms, particle signal becomes less discernible from the background. In Fig. 3, the transient signal from ¹⁴⁰Ce in a representative particle from each integration time is compared. The loss in sensitivity from 50 ms to 500 ms is ∼88% (from peak maximums).

Fig. 2 Time traces for the cerium dioxide particles measured using (a) 50 ms, (b) 100 ms, (c) 250 ms, and (d) 500 ms integration times for the Faraday cup detectors. Only ¹⁴⁰Ce and ¹⁴²Ce are shown. As the integration time increases, the average intensity per particle decreases, and less particles are detected.

Fig. 3 One representative particle from each integration time is overlayed. Increasing the time of data collection on the Faraday cup (to 500 ms) decreases sensitivity (per particle). Shorter integration times tend to show a pattern of exponential decay after the initial ‘spike’, which is caused by detector decay from the particle signal input.

An important observation for data treatment for isotope ratios is the number of data points acquired for each particle. In ‘typical’ spICP-MS, transients lasting ∼500 μs should span 1 or 2 data points, even with acquisition rates of 1 ms. For spMC-ICP-MS, however, there is a large spread of signal due to detector decay which has previously been reported.¹⁹Fig. 4 shows histograms of the number of data points detected per particle for each integration time. The average number of data points per particle (rounded to the nearest integer) was 5, 2, 1, and 1 from shortest to longest integration time.

Fig. 4 The average number of data points per particle (rounded to the nearest integer) for the (a) 50 ms, (b) 100 ms, (c) 250 ms, and (d) 500 ms samples were 4, 2, 1, and 1, respectively. As integration time decreases, the number of data points obtained per particle decreased.

The observed spread in signal is due to the detector (Faraday cup) used for these measurements. Faraday cups provide low to no gain as the signal relies on post-ion strike current amplification while typical single-particle methods assume fast ion-counting detector types (electron multipliers). As shown in previous publications, the spread in signal is inherent to using Faraday cups with a current amplifier.^16,43 To confirm this, the same particle suspension was run with a secondary electron multiplier (EM) detector with integration times ranging from 5 to 50 ms. The time trace for ¹³⁶Ce signal with a 50 ms integration time (which were the longest used for the EM detectors) is shown in Fig. 5. A zoomed-in time trace for ¹³⁶Ce collected with the Faraday cups is shown in Fig. S3† for comparison. This integration time was chosen to directly compare the number of data points per particle with the Faraday detectors. Using an ion-counting detector, particle signals are clearly seen as characteristic ‘spikes’. The average number of data points per particle detected with the secondary EM detector was 1, rounded to the nearest integer (1.1 ± 0.3 out of n = 185 particles detected).

Fig. 5 Cerium dioxide particles detected with a secondary EM detector with a 50 ms integration time are shown in (a). The yellow band in (a) is a three second selection, shown in (b). The signal from these particles is the expected ‘spike’ composed of one or two data points, typical for ion-counter detector types used in traditional spICP-MS.

Furthermore, it is known that precision in ratio analysis is limited by the electrical noise from the resistor in the amplifier loop.⁴⁴ Slow response time of high-ohmic resistors (i.e., 10¹³ Ω) is typically accounted for by a tau correction – a mathematical correction where the signal decay is essentially used to correct ratio bias as a function of the signal gradient specific to an individual Faraday detector.^45,46 These high-ohmic resistors allow for greater precision due to increased sensitivity of low signal ions from greater signal to noise. They have successfully been shown to work on non-stable ion beams such as from laser ablation MC-ICP-MS techniques.^47,48 Higher ohmic resistors yield greater sensitivity, but due to their slower response time, 10¹¹ Ω resistors were used in this study. There are also voltage limitations (∼0.5 V) on the 10¹³ amplifiers, precluding their use for the relatively strong ion beams observed from particles. Consideration for electrical noise in correcting for ratio bias due to varying arrival and decay times of ion signal in the Faraday cup detectors has never been studied for signal particle analysis, to the author's knowledge. Signals arriving rapidly with sudden decreases are affected by this amplifier response. Therefore, isotope ratios both among and within particles show some variation; relative enhancement or suppression of certain isotopes changes the ratio at the specified data point. For single particle analysis, both the quick ion onset and the short signal duration must be considered to account for the temporal signal spread. Both factors must also be considered for data analysis when determining how to identify particle signal from background and determine isotopic ratios within particles.

Isotopic ratios via bulk-digestion MC-ICP-MS

Particles were digested and measured on the MC-ICP-MS both for cup centering and precise ratio determinations before and in between particle samples. The average cerium isotope ratios obtained for each selected integration time (50, 100, 250, and 500 ms) can be found in Table 2. To determine if the particles isotopically matched the Ce isotopic composition from the particle digest, a ‘true’ ratio was determined by measuring the particle digest sample with a 4 s integration time. The ratio obtained from this digested solution closely matched natural Ce ratios; the percent difference in the isotope ratios obtained for ¹³⁶Ce/¹⁴⁰Ce, ¹³⁸Ce/¹⁴⁰Ce, and ¹⁴²Ce/¹⁴⁰Ce from the control (Ce single element standard, High Purity Standards, SC, USA) and the digested particle solution were 0.03, 0.27, and 0.01%, respectively. A simplified direct mass bias factor was determined from the digested samples and applied to the particle ratio data obtained.⁴⁹ The average ratios obtained from the 4 s integration of the digested particle standard were used as the ‘true’ ratio. To calculate a mass bias factor for each integration time, each average background-subtracted cerium isotope signal was used to obtain each isotope ratio (¹³⁶Ce/¹⁴⁰Ce, ¹³⁸Ce/¹⁴⁰Ce, and ¹⁴²Ce/¹⁴⁰Ce). Then, the ‘true’ ratio was divided by this ratio, resulting in a mass bias factor unique to each integration time. This factor was applied to all ratios obtained for particles vs. spMC-ICP-MS analysis. Factors can be found in Table 2. It was expected for the mass bias to be less drastic at the 500 ms time regime (compared to the 50 ms) due to longer integration times typically yielding higher precisions; however, this is not seen in the minor isotope mass bias factors. This may indicate a higher concentration of the digest solution may need to be used to calculate these factors, which would also better mimic the intensity of particle signals. The relative percent differences between the mass bias factors for 50 ms and 500 ms (for all isotopes) were considered insignificant (all <0.11%), but future work should investigate appropriate considerations for mass bias factors for spMC-ICP-MS.

Table 2 Isotope ratios and mass bias factors for each integration time for MC-ICP-MS measurements on the bulk particle digestion

Integration time (ms)	^136Ce/^140Ce (SD)	Mass bias factor	^138Ce/^140Ce (SD)	Mass bias factor	^142Ce/^140Ce (SD)	Mass bias factor
4 s ‘True’	0.00210367 (56)		0.0028456 (58)		0.1256362 (16)
50	0.002006 (27)	1.0486	0.002790 (26)	1.0197	0.12951 (30)	0.9700
100	0.002005(20)	1.0492	0.002789(19)	1.0203	0.12959 (19)	0.9695
250	0.002005 (13)	1.0492	0.002788 (12)	1.0206	0.12960 (10)	0.9694
500	0.0020058 (83)	1.0488	0.0027887 (87)	1.0206	0.129568 (75)	0.9696

---

Isotopic ratio analysis within individual particles

Particle-derived signal, as previously described in the experimental section, was determined using an iterative 3σ approach.^50,51 Background for isotopes of interest were determined to be negligible. Once particle signals were determined, these packets of signal were analyzed in three ways. The first method used every data point detected per particle transient. If both isotopes of interest were detected concurrently, the data point was treated as unique and used for ratio analysis. The second method used the major isotope, ¹⁴⁰Ce, to determine the maximum signal detected within a particle packet. The corresponding signal for the minor isotopes (¹³⁸Ce, ¹³⁶Ce, ¹⁴²Ce) at the maximum ¹⁴⁰Ce data point were then used to determine isotope ratios (referred to as MAX). In the third method, signal for each particle packet was summed (analogous to split event correction) into a singular point which was then used to determine ratios (referred to as SEC).

The isotope ratio within individual particles is based solely on the intensity detected, but the sample population ratio was determined in four ways: average global linear regression slope analysis (LRS_global), particle event-by-event linear regression slope analysis (LRS_event), particle event-by-event area ratio analysis (AR), and global averaging (AVG_global). LRS_global, LRS_event, and AR methods have been used previously for LA-MC-ICP-MS isotope ratio determinations, of uranium particles using integration times of 100 and 200 ms.³⁰ These methods were slightly modified for our data sets, and using MAX and SEC methods to select or bin data are novel to our approach.

Particle signals solely consisting of a single data point (maximum signal and split event corrected signal) were only analyzed by LRS (LRS_MAX and LRS_SEC) and by taking the average ratio of all particle events (AVG_MAX and AVG_SEC). While linear regression returns a calculated slope (and standard error of the slope) based on fitting the data to a line, all other ratio analysis methods are obtained via averaging. For LRS_event, a slope is fit from the data points within an individual particle, and then the average of the slopes from all particles is recorded. Overviews of each of these analysis models are depicted in Fig. S2.†

To investigate these methods, only ¹⁴⁰Ce and ¹⁴²Ce will be considered, as they are the most abundant Ce isotopes. The population ratios of ¹⁴²Ce/¹⁴⁰Ce obtained by each method (with mass bias correction applied) are shown in Table 3. The ratios for particles where all four Ce isotopes (¹³⁶Ce, ¹³⁸Ce, ¹⁴⁰Ce, and ¹⁴²Ce) were detected can be found Tables S1–S4.†Fig. 6a shows the percent difference of the ratios obtained from all analysis methods, from the digested ‘true’ ratio. In Fig. 6a, LRS_global, LRS_event, LRS_MAX, and AVG_MAX ratio analysis show declining percent difference as integration time increases. The ratios trend closer to the expected value when the full particle signal is detected in one data point. However, AR, LRS_SEC, and AVG_SEC displayed relatively accurate ratios for almost all integration times used. The maximum relative difference from the expected ratio from these three analysis methods was ∼2%. Further ANOVA testing for statistical significance between ratio analysis techniques for methods determined via a mean ratio (LRS_event, AR, AVG_max, and AVG_sec) between different integration times can be found in Fig. S4.†

Table 3 Mass-bias corrected isotope ratio obtained for each integration time with each method. Deviation is reported for each result and is based on the standard error of slope for LRS, SEC LRS, and MAX LRS, and standard deviation for all the other methods. For reference, the ‘true’ ¹⁴²Ce/¹⁴⁰Ce ratio was previously reported to be 0.1256362(16)

	Individual data points			Maximum only		Split event correction only		n
	LRSglobal	LRSevent	AR	LRSMAX	AVGMAX	LRSSEC	AVGSEC
50 ms	0.13445 (23)	0.1359 (22)	0.1242 (27)	0.13525 (45)	0.1326 (51)	0.12557 (12)	0.1243 (78)	211
100 ms	0.13131 (30)	0.1336 (61)	0.1245 (30)	0.13055 (65)	0.1299 (39)	0.1252 (39)	0.1254 (15)	182
250 ms	0.12805 (35)	0.1298 (80)	0.1261 (13)	0.12643 (45)	0.1278 (39)	0.12704 (27)	0.1258 (25)	167
500 ms	0.12366 (18)	0.129 (27)	0.12603 (17)	0.1241 (16)	0.1269 (19)	0.12512 (73)	0.1269 (16)	22

---

Fig. 6 The absolute percent differences of the isotopic ratio (obtained by all ratio methods) of ¹⁴²Ce/¹⁴⁰Ce within particles versus the ratio obtained via digested particle standard are shown in (a). The highest percent difference is about 8% from the LRS_event method. The relative standard deviation of the isotope ratios obtained from each method in (b) are below 5% (with one exception), and LRS_global, LRS_MAX, LRS_SEC, and AVG_SEC are below 2% for every integration time used.

Evaluation of the ratio methods also involves determining their precision, or RSD. The RSDs, shown in Fig. 6b, were calculated by dividing the reported standard deviation by the reported ratio in Table 3. Interestingly, RSDs increased as integration times increased for all methods using linear regression slope analysis; LRS_global RSD increased from 0.17% to 1.5%, LRS_event increased from 1.6% up to 21%, LRS_MAX increased from 0.33% to 1.29%, LRS_SEC increased from 0.10% to 0.59% when comparing the ratios from the 50 ms and 500 ms samples. These methods yielded the lowest RSDs of all methods at the lowest integration times, but increasing integration time increases the RSDs of particle isotope ratios. On the other hand, RSDs for the AVG_MAX and AVG_SEC samples either trend downward as integration time increases or remain relatively constant. Overall, all RSDs (besides LRS_event) are below 5%.

To determine the most accurate and precise isotope ratios within particles via spMC-ICP-MS, both the integration times and method for ratio analysis should be considered. There are both benefits and drawbacks to using shorter integration times (e.g., 50 ms). If particle sizes are smaller than 1 μm, or unknown, a shorter integration time would ensure particle signals detected are from single particle events. While this may cause higher percent difference with some methods such as LRS, low integration times can be paired with AR or LRS_SEC methods which provide high accuracy and precision. Both methods utilize more of the peak shape of the transient signal (rather than just the intensity at a single data point) when determining isotope ratios. LRS_SEC and AVG_SEC methods first combine all counts of the isotope of interest (detected at each data point) into a single data point before determine isotope ratios. Similarly, the AR method integrates under the particle signal curve, and the whole area is used to determine the ratio of each isotope. Both AR and LRS_SEC methods remained within ∼1% relative difference to the expected ratio, and their RSDs were ∼0.1% and 2%, respectively.

Using a longer integration time, such as 500 ms, gave the best RSDs for all methods (besides LRS_event). However, when moving to higher integration times, there is a risk to not detect particles due to loss in sensitivity, or to detect more than one particle within a data collection time bin (aka double event). This limits the number of particles detected, for example, only 22 particles were detected in the 500 ms sample (vs. 211 detected in the same suspension using 50 ms integration). Perhaps thresholding values may need to be altered based on integration times, but they were not altered here. To leverage sensitivity and limit detector noise, 100 ms may be a suggested compromise. Furthermore, the AR and LRS_SEC methods yielded the most accurate ratios and most consistent results across various integration times and are thus recommended. When using these methods, error of the determined ratio may outweigh the error introduced due to the integration time and detector decay. This should be further explored with the EM detectors, especially if a detector array uses both detector types for major and minor isotopes of interest.

Solid-surface sampling of particles via micro-extraction

To show the applicability to determine high-precision, accurate ratios within individual particles sampled off solid substrates, micro-extraction (ME) was also coupled to the MC-ICP-MS. The same Ce-particles were deposited, extracted, and delivered to the MC-ICP-MS. The particle signals were like those obtained from the particle suspension, with the time traces of 50, 100, 250, and 500 ms integration times shown in Fig. 7 (with each cluster of particles originating from one extraction). Time traces for all extractions run for each integration are shown in Fig. S5.† One aspect of ME sample introduction that must be considered carefully is that particles picked up off a surface may not be temporally resolved from each other. ME parameters were optimized to control the introduction of single particles to the instrument; however, with each extraction, the dissolved background shows an increase with subsequent decay back to the baseline throughout the run. This background at the beginning of the run is significant enough to be considered particle signal from the thresholding used for these experiments. Because of this, the ratios may be calculated with data points that should be considered background. Only ¹⁴²Ce to ¹⁴⁰Ce is reported for these samples. The methods previously identified as the most accurate with the least RSD were used; ratios from these particle extractions were obtained using LRS_global, LRS_SEC, AVG_SEC, and AR methods (Table 4). For all ratios, the mass bias correction factors found from the digested solutions were applied.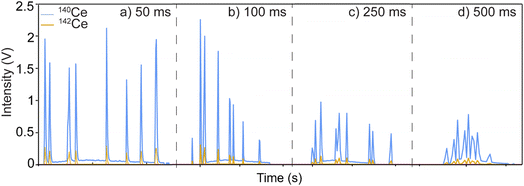

Fig. 7 Representative extraction profile (time trace) for one extraction at each integration time used: (a) 50 ms, (b)100 ms, (c) 250 ms, (d) 500 ms.

Table 4 ¹⁴²Ce/¹⁴⁰Ce ratios determined by LRS_global, AR, LRS_SEC and AVG_SEC for spME-MC-ICP-MS

	LRSglobal	AR	LRSSEC	AVGSEC
50 ms	0.13057 (11)	0.1260 (28)	0.125467 (68)	0.115 (24)
100 ms	0.12928 (14)	0.1243 (29)	0.12462 (10)	0.125 (15)
250 ms	0.12657 (13)	0.12545 (78)	0.125448 (47)	0.1251 (15)
500 ms	0.12622 (13)	0.12524 (56)	0.125349 (58)	0.1254 (14)

---

Because backgrounds were elevated, the ratio determination of individual particles for many of the extractions unintendedly returns the isotopic ratio of the data points both within particles and the ionic background. However, when comparing these ratios to the liquid suspensions, a majority of the RSDs and percent differences are comparable but are ratio-analysis-method dependent. For example, at a 500 ms integration, the LRS_global ratio from the ME sample shows a lower RSD and a lower relative percent difference than the liquid sample introduction: RSD of 0.11% vs. 1.45% and percent difference of 0.47% vs. 1.58%, respectively. This is most likely an attribute of having more data points per particle in the ME data. However, when using the AR method that integrates under the total particle signal, ME-particle ratios have ∼6× higher RSDs at the 500 ms integration than ratios obtained via ‘normal’ sample introduction. The RSDs and percent differences of the ME-particle ratios are provided in Table S5.† Future work should focus on the subtraction of drifting or unstable backgrounds (which was not attempted here). The highest accuracy was found using LRS_SEC, which concurred with the previous findings.

Conclusion

We successfully demonstrated the use of spICP-MS on a MC-ICP-MS platform with monodispersed 1 μm ceria particles. This study emphasizes the considerations needed for data collection and treatment when performing high precision isotopic ratio analysis on individual particles and particle populations. Single particle analysis via MC-ICP-MS is possible, even when limited through electronic noise, apparent through elongated particle signal response times, inherent to Faraday cup detection. While precision is limited due to the transient nature of single particles, using fast integration times, as low as 50 ms, may be enough to obtain low RSDs and low percent differences. This is dependent on the method used to determine isotope ratios, in which summing all the particle signal intensity into a single data point and/or integrating under the particle signal curve yield the best results (LRS_SEC and AR).

Single particle MC-ICP-MS seems especially useful to gain insight on important isotopic determinations, especially for particles in the 1 μm size regime. It has shown to be useful for both rapid screening of particle standards and has possible applications to environmental and/or nuclear forensics and safeguard analysis, especially when combined with microextraction. Future work on spMC-ICP-MS should focus on the gain statistics and signal delay intrinsic to the detector to better correct particle ratios. Mass bias correction within particle signals should also be further explored. The use of multiple detectors for different isotopes should also be considered, for example, using a traditional set up to measure major isotopes while using an EM to concurrently detect minors. The ratios obtained with these measurements would need to be evaluated for this multi-modal detection of particle signal.

Data availability

The authors are happy to provide data upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Oak Ridge National Laboratory, managed by UT-Battelle for the Department of Energy under contract DE-AC05-000R22725. This work was funded by the United States National Nuclear Security Administration's (NNSA) Office of Defense Nuclear Nonproliferation Research & Development. The authors would like to acknowledge Jacquelyn DeMink at ORNL for assistance with graphic design. We would like to thank Spencer Scott and Rachel Bergin at Savannah River National Laboratory for their support in production of the ceria test particles and Lax Saraf and Kelliann Koehler at the Clemson Electron Microscopy Facility for their help in acquiring the SEM data.

References

1. G. Tamborini, M. Betti, V. Forcina, T. Hiernaut, B. Giovannone and L. Koch, Spectrochim. Acta, Part B, 1998, 53, 1289–1302.
2. M. Kraiem, S. Richter, H. Kühn and Y. Aregbe, Anal. Chim. Acta, 2011, 688, 1–7.
3. P. Peres, P. M. L. Hedberg, S. Walton, N. Montgomery, J. B. Cliff, F. Rabemananjara and M. Schuhmacher, Surf. Interface Anal., 2013, 45, 561–565.
4. Y. Ye, N. Aizezi, J. Feng, B. Han, X. Li, Z. Su, L. Li and Y. Liu, Anal. Chem., 2025, 97, 5554–5562.
5. S. Boulyga, S. Konegger-Kappel, S. Richter and L. Sangély, J. Anal. At. Spectrom., 2015, 30, 1469–1489.
6. J. Liu, X. Wei, C. Wu, L. Zheng, M. Wang, M. Chen and J. Wang, Anal. Chim. Acta, 2023, 1254, 341114.
7. I. Abad-Álvaro, E. Peña-Vázquez, E. Bolea, P. Bermejo-Barrera, J. R. Castillo and F. Laborda, Anal. Bioanal. Chem., 2016, 408, 5089–5097.
8. M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346.
9. I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016, 31, 135–144.
10. S. Harycki and A. Gundlach-Graham, J. Anal. At. Spectrom., 2023, 38, 111–120.
11. P. Menero-Valdés, M. I. Chronakis, B. Fernández, C. D. Quarles Jr, H. González-Iglesias, B. Meermann and R. Pereiro, Anal. Chem., 2023, 95, 13322–13329.
12. A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855.
13. S. E. Szakas and A. Gundlach-Graham, J. Anal. At. Spectrom., 2024, 39, 1874–1884.
14. L. Hendriks, R. Brünjes, S. Taskula, J. Kocic, B. Hattendorf, G. Bland, G. Lowry, E. Bolea-Fernandez, F. Vanhaecke, J. Wang, M. Baalousha, M. von der Au, B. Meermann, T. R. Holbrook, S. Wagner, S. Harycki, A. Gundlach-Graham and F. von der Kammer, Nanoscale, 2023, 15, 11268–11279.
15. F. Vanhaecke, L. Balcaen and D. Malinovsky, J. Anal. At. Spectrom., 2009, 24, 863–886.
16. T. Pettke, F. Oberli, A. Audétat, U. Wiechert, C. R. Harris and C. A. Heinrich, J. Anal. At. Spectrom., 2011, 26, 475–492.
17. A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, Rapid Commun. Mass Spectrom., 2015, 29, 1617–1622.
18. G. Craig, M. S. A. Horstwood, H. J. Reid and B. L. Sharp, J. Anal. At. Spectrom., 2020, 35, 1011–1021.
19. S. Yamashita, K. Yamamoto, H. Takahashi and T. Hirata, J. Anal. At. Spectrom., 2022, 37, 178–184.
20. S. Yongyang, W. Wei, L. Zhiming, D. Hu, Z. Guoqing, X. Jiang and R. Xiangjun, J. Anal. At. Spectrom., 2015, 30, 1184–1190.
21. S. Yamashita, M. Ishida, T. Suzuki, M. Nakazato and T. Hirata, Spectrochim. Acta, Part B, 2020, 169, 105881.
22. X. Tian, H. Jiang, M. Wang, W. Cui, Y. Guo, L. Zheng, L. Hu, G. Qu, Y. Yin, Y. Cai and G. Jiang, Anal. Chim. Acta, 2023, 1240, 340756.
23. B. T. Manard, V. C. Bradley, L. Hendriks, D. R. Dunlap, N. A. Zirakparvar, B. W. Ticknor, M. Toro-Gonzalez and H. B. Andrews, Talanta, 2025, 127516.
24. S. Richter, J. Truyens, C. Venchiarutti, Y. Aregbe, R. Middendorp, S. Neumeier, P. Kegler, M. Klinkenberg, M. Zoriy, G. Stadelmann, Z. Macsik, A. Koepf, M. Sturm, S. Konegger-Kappel, A. Venzin, L. Sangely and T. Tanpraphan, J. Radioanal. Nucl. Chem., 2023, 332, 2815.
25. B. E. Naes, S. Scott, A. Waldron, S. Lawson, M. G. Bronikowski, L. I. Gleaton, R. J. Smith, K. N. Wurth, T. J. Tenner and M. Wellons, Analyst, 2023, 148, 3226–3238.
26. J. Wimpenny, K. M. Samperton, P. Sotorrio, M. S. Wellons, S. M. Scott, D. Willingham and K. Knight, J. Anal. At. Spectrom., 2023, 38, 827–840.
27. E. E. Groopman, T. L. Williamson and D. S. Simons, J. Anal. At. Spectrom., 2022, 37, 2089–2102.
28. A. Gourgiotis, G. Manhès, P. Louvat, J. Moureau and J. Gaillardet, J. Anal. At. Spectrom., 2015, 30, 1582–1589.
29. Q. Yang, H. Gong, X. Wang, M. Duan, Y. Xiao and W. Sun, J. Anal. At. Spectrom., 2022, 37, 1000–1009.
30. S. Kappel, S. F. Boulyga, L. Dorta, D. Günther, B. Hattendorf, D. Koffler, G. Laaha, F. Leisch and T. Prohaska, Anal. Bioanal. Chem., 2013, 405, 2943–2955.
31. H. W. Paing, B. T. Manard, B. W. Ticknor, J. R. Bills, K. A. Hall, D. A. Bostick, P. Cable-Dunlap and R. K. Marcus, Anal. Chem., 2020, 92, 8591–8598.
32. B. T. Manard, K. T. Rogers, B. W. Ticknor, S. C. Metzger, N. A. Zirakparvar, B. D. Roach, D. A. Bostick and C. R. Hexel, Anal. Chem., 2021, 93, 11133–11139.
33. V. C. Bradley, T. L. Spano, S. C. Metzger, B. W. Ticknor, D. R. Dunlap, N. A. Zirakparvar, B. D. Roach, C. R. Hexel and B. T. Manard, Anal. Chim. Acta, 2022, 1209, 339836.
34. J. S. Stanberry, H. B. Andrews, C. V. Thompson, B. W. Ticknor and B. T. Manard, Anal. Chem., 2025, 97(3), 1688–1694.
35. M. S. Wellons, I. M. A. Devore and W. W. Kuhne, US Pat., 11594349-B2, 2023.
36. D. Piedmont, M. Topsakal, A. Kiss, S. Tazik, R. Bergin, L. Shultz-Johnson, M. Wellons, S. Scott, C. Barrett and S. K. Gill, Advantages of Synchrotron for High Sensitivity Single Particle Analysis in Nuclear Forensics, Institute of Nuclear Materials Management, 2024.
37. S. Scott, et al., New particle working standards for NWAL particle laboratory calibration and quality control-operational engineering for an aerosol-based production platform for the synthesis of plutonium-containing reference particulate materials, Conference: 2023 INMM & ESARDA joint annual meeting, Austria Center in Vienna, Austria, 2023, vol. 22(26).
38. S. M. Scott, A. T. Baldwin, M. G. Bronikowski, M. A. DeVore II, L. A. Inabinet, W. W. Kuhne, B. E. Naes, R. J. Smith, E. Villa-Aleman, T. J. Tenner, K. N. Wurth and M. S. Wellons, Scale-up and Production of Uranium-bearing QC Reference Particulates By An Aerosol Synthesis Method, 2021.
39. D. C. Carlson, J. J. Degange and P. Cable-Dunlap, US Pat., 6964189, 2005.
40. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
41. C. Degueldre, P. Y. Favarger and S. Wold, Anal. Chim. Acta, 2006, 555, 263–268.
42. F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2013, 28, 1220–1232.
43. T. Hirata, S. Yamashita, M. Ishida and T. Suzuki, Mass Spectrom., 2020, 9, A0085.
44. J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, Anal. Chim. Acta, 2014, 819, 49–55.
45. A. Pramann and O. Rienitz, J. Anal. At. Spectrom., 2024, 39, 1540–1550.
46. T. Hirata, S. Niki, S. Yamashita, H. Asanuma and H. Iwano, J. Anal. At. Spectrom., 2021, 36, 70–74.
47. N. A. Zirakparvar, B. Manard, C. Hexel, D. Dunlap, S. Metzger, D. Bostick, V. Bradley and B. Ticknor, Int. J. Mass Spectrom., 2023, 492, 117114.
48. B. T. Manard, C. D. Quarles Jr, V. C. Bradley, T. L. Spano, N. A. Zirakparvar, B. W. Ticknor, D. R. Dunlap, P. Cable-Dunlap, C. R. Hexel and H. B. Andrews, J. Am. Chem. Soc., 2024, 146, 14856–14863.
49. K. J. Mathew, G. O'Connor, A. Hasozbek and M. Kraiem, J. Anal. At. Spectrom., 2013, 28, 866–876.
50. H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369.
51. A. Gundlach-Graham and R. Lancaster, Anal. Chem., 2023, 95, 5618–5626.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ja00107b

‡ This manuscript has been authored in part by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).

§ Both authors contributed equally and should be considered first author.

---