Open Access Article
Open Access ArticleDesign and simulation of biomimetic microfluidic designs to achieve uniform flow and DNA capture for high-throughput multiplexing†
Enas
Osman
a,
Jonathan
L'Heureux-Hache
b,
Phoebe
Li
b and
Leyla
Soleymani
 *abcd
*abcd
aSchool of Biomedical Engineering, McMaster University, Hamilton L8S 4L8, Ontario, Canada. E-mail: soleyml@mcmaster.ca
bDepartment of Engineering Physics, McMaster University, Hamilton L8S 4L8, Ontario, Canada
cMichael G. DeGroote Institute for Infectious Disease Research, McMaster University, Hamilton L8S 4L8, Ontario, Canada
dDepartment of Biochemistry and Biomedical Sciences, McMaster University, Hamilton L8S 4L8, Ontario, Canada
First published on 5th February 2025
Abstract
High-throughput multi-analyte point-of-care detection is often constrained by the limited number of analytes that can be effectively monitored. This study introduces bio-inspired microfluidic designs optimized for multi-analyte detection using 38–42 biosensors. Drawing inspiration from the human spinal cord and leaf vein networks, these perfusion-oriented designs ensure uniform flow velocity and consistent molecular capture while maintaining spatial separation to prevent cross-talk. In silico optimizations achieved velocity profile uniformity with coefficients of variance of 0.89% and 0.86% for the spine- and leaf-inspired designs, respectively. However, simulations revealed that velocity uniformity alone is insufficient for accurate molecular capture prediction without consistent reaction site channel dimensions. The bio-inspired designs demonstrated superior performance, stabilizing—coefficient of variance below 20%—in DNA capture within 10 minutes, compared to 68 minutes for a simple branched design. This work underscores the potential of bio-inspired microfluidics to enable scalable, uniform, and high-performance systems for multi-analyte detection.
Introduction
Multiplexing, which refers to either generating multiple signals for a single analyte1 or detecting multiple analytes simultaneously, plays a critical role in advancing diagnostics across various fields.2 In health monitoring and disease diagnostics, the continuous multiplexed measurement of biomarkers such as glucose,3 lactate,3 urea,4 citrate,5 metal ions,6 and small proteins such as enzymes, hormones, and cytokines provides invaluable information about physiological health.7 Similarly, profiling microRNA (miRNA) biomarkers has gained prominence for diagnosing, assessing prognosis, and monitoring diseases, including cancer, neurodegenerative disorders, and cardiovascular conditions.8,9 Thousands of miRNAs are screened to obtain accurate profiles of pathogenic expressions, with focused panels typically requiring 20–42 analytes for precise diagnosis.8 In environmental and food safety monitoring, multiplexing is required for the detection of well over 100 pathogens (e.g. bacteria10 and viruses11), contaminants, and harmful chemicals10 in a single sample. Identification of different species, as well as determination of antibiotic resistance can inform effective treatment strategies and reduce response times, potentially saving lives.12 These diverse biomarkers can be detected by immobilizing biorecognition elements such as aptamers,13 oligonucleotides, enzymes, antibodies, and peptides14 onto sensing surfaces designed to selectively bind to their targets.15 Integrating a large number of biosensors, often rely on the amalgamation of biorecognition elements into a single device which presents significant technical challenges, requiring multiple readout labels, cross-contamination, and signal interference.16Conventional diagnostic methods that have been designed for operation at centralized laboratories are not suitable for rapid clinical decision making at or near the patient, which adds delays in diagnosis, especially for those in remote and resource-poor areas.17,18 This has fueled the development of portable, simple, rapid, and multiplexed point-of-care (POC) diagnostics.19
Microfluidic systems offer several advantages for the development of fully-integrated biosensors for POC diagnostics and health monitoring.7 These include reducing sample and reagent volumes,20 increasing local analyte concentrations,21 enabling multiplexing,22 and providing reproducible reaction conditions at the detection zones,23 all of which are essential for optimizing sensor performance. Electrochemical transduction, in particular, has been widely adopted within microfluidic platforms due to its compatibility with miniaturization while maintaining sensitivity and reliability.24–27 However, current electrochemical microfluidic systems are typically limited to detecting 2–4 analytes simultaneously,28 falling short of the demands for modern diagnostics. The primary challenge lies in integrating the detection of multiple analytes within a single device.
A key challenge in multi-analyte detection within passive flow channel designs—especially without the use of valves—is maintaining consistent biochemical environments and ensuring uniform interaction times across the channels. This is particularly critical in multiplexed affinity-based biosensors. Achieving consistent target capture efficiency across multiple biosensors integrated into a single system, while ensuring distinct signal readout without interference from neighboring electrodes, often demands precise assay29,30 and channel16 designs. Surface treatments between electrodes are commonly employed in electrochemical arrays within a single channel to isolate adjacent electrodes.31 However, in the absence of such advanced assay designs and surface treatments, these systems are prone to issues such as cross-contamination during immobilization and capture,31 signal interference from adjacent electrodes, and cross-talk caused by lateral movement of electroactive species between electrodes.16 To address challenges that compromise high-fidelity performance, spatial separation techniques employing separate detection zones either by mechanical seperators32 or air pockets (hydrophobic areas),33 parallel channels,34 or bifurcating designs14 have been proposed. These approaches promote uniformity by maintaining consistent channel resistance and equal distances from the sample introduction point. Despite their advantages, majority of these designs are typically limited to detecting 2–4 analytes,14,28,34 due to the increased complexity of scaling for high-throughput multiplexing.
Scaling up microfluidic designs while maintaining spatial separation poses significant challenges due to the need for uniform flow velocity, analyte distribution, and target capture efficiency. Improper channel design can result in stagnation or dead zones, areas with little to no flow, that are particularly prevalent in branched systems.35 Similarly, suboptimal channel configurations can result in flow deformation, where uneven flow distributions and secondary flow patterns can disrupt efficient analyte transport.36 While such effects can be exploited for particle separation and entrapment,37 unintended use may contribute to significant non-uniformity across different channels or outlets. Additionally, neglecting pressure drops at junctions can worsen energy losses and result in unwanted flow patterns, reducing channel consistency.38,39 These limitations can be mitigated by biomimetic designs and the use of computational approaches such as finite element analysis that are well-suited for predicting and optimizing the performance metrics of multiplexed microfluidic systems.40In silico methods enable the development of multiplexed biosensors with uniform flow velocities and consistent chemical reaction conditions, thereby reducing reliance on experimental trial and error.40 Recent studies have explored novel designs in silico including manifold and biomimetic designs to address flow velocity uniformity while maintaining spatial separation. Biomimetic structures are particularly interesting because of their high functionality in flow velocity and distribution profiles.41 A manifold channel network inspired by the human circulatory system was optimized to achieve a flow velocity uniformity with 2.5% standard deviation across four channels, though experimental validation using microparticle image velocimetry indicated an approximately 10% standard deviation.42 While promising for velocity profile uniformity, this design lacked capture efficiency modeling and was limited in the number of reaction sites. In another study, a tentacles-like device inspired by many invertebrates demonstrated flow velocity uniformity in silico in simultaneous multi-analyte detection.43 This design successfully addressed velocity uniformity and cross-talk prevention by employing spatial separation across six detection zones. Similarly, a rhombus tree-like device with a series of bifurcations achieved a uniform velocity profile, culminating in a chamber with a 10% standard deviation through in silico optimization; however, the design is prone to signal interference due to the lack of spatial separation.40
As demonstrated in previous studies, most multi-analyte microfluidic designs are constrained by the limited number of analytes they can effectively detect. To overcome this limitation, we developed biomimetic microfluidic systems inspired by the spinal cord and staghorn plant leaf vein networks, incorporating 38–42 biosensors into a single microfluidic system. These bio-inspired designs were optimized in silico to achieve uniform flow velocity and consistent analyte capture across different channels while maintaining spatial separation to prevent cross-talk between reaction sites. The performance of these designs was further validated through direct comparison with a simpler branched microfluidic design.
Methods
Theory
We simulated the fluid dynamics within the microfluidic channels using COMSOL Multiphysics® software (version 6.2, COMSOL AB, Stockholm, Sweden). To apply the computational finite element analysis from the hydrodynamic equations module, we assumed laminar flow of an incompressible fluid, governed by the Navier–Stokes eqn (1). This equation governs the motion of fluids, representing the conservation of momentum, where u is the velocity of fluid, ρ is the density of fluid, p is pressure, K is the viscous stress tensor, and F denotes the external force applied to the fluid. For incompressible flow, where the density remains constant, the continuity eqn (2) converges to zero. This assumption is valid based on the properties of the fluid and the scale of the microfluidic channels.44| ρ(u·∇u) = ∇·[−pI + K] + F | (1) |
| ρ∇·u = 0 | (2) |
To study DNA–DNA hybridization in the reaction sites, we used the transport of diluted species module in COMSOL 6.2, which models the diffusion and convection of diluted species in a liquid, as described by Fick's law, when flow is present.45
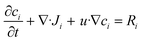 | (3) |
| Ji = −Di∇ci | (4) |
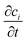 represents the rate of change of the concentration of species i over time, ∇·Ji is the divergence of the flux accounting for the net rate of species i entering or leaving the volume due to diffusion, u·∇ci term represents convection, which is the transport of species i due to the bulk movement of the fluid at velocity u, and Ri is the reaction term of the rate of production or consumption of species i due to the chemical reaction. By substituting the flux term with Fick's law of diffusion (4), the flux of species i is proportional to the gradient of its concentration and moves from high to low concentration, governed by the diffusion constant Di.45
represents the rate of change of the concentration of species i over time, ∇·Ji is the divergence of the flux accounting for the net rate of species i entering or leaving the volume due to diffusion, u·∇ci term represents convection, which is the transport of species i due to the bulk movement of the fluid at velocity u, and Ri is the reaction term of the rate of production or consumption of species i due to the chemical reaction. By substituting the flux term with Fick's law of diffusion (4), the flux of species i is proportional to the gradient of its concentration and moves from high to low concentration, governed by the diffusion constant Di.45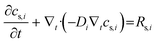 | (5) |
| Ns,i = −Di∇tcs,i | (6) |
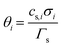 | (7) |
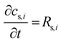 | (8) |
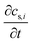 term represents the rate of change of surface concentration, ∇t·(−Di∇tcs,i) represents surface diffusion of species i, and Rs,i is the surface transport term representing the rate of production or consumption of species i on the surface. The surface coverage fractional occupancy is represented by (7), where θi is fractional occupancy, Γs is the total surface site density, and σi is the molecular surface area of species i.
term represents the rate of change of surface concentration, ∇t·(−Di∇tcs,i) represents surface diffusion of species i, and Rs,i is the surface transport term representing the rate of production or consumption of species i on the surface. The surface coverage fractional occupancy is represented by (7), where θi is fractional occupancy, Γs is the total surface site density, and σi is the molecular surface area of species i.
Approach to simulations
The microfluidic designs were created using AutoCAD (version 2024, Autodesk Inc., San Rafael, CA, USA), and subsequently imported into COMSOL Multiphysics. The designs were then used to model and analyze the fluid dynamics within the microchannels under various conditions. The simulations employed the Navier–Stokes equations to model laminar flow, providing insights into the velocity and pressure profiles within the microchannels. The boundary conditions included a no-slip condition at the walls, representing the adherence of fluid to the channel surfaces. At the outlet, a zero-pressure boundary condition suppressing backflow was used to simulate an open-ended flow, allowing fluid to exit the microchannels without resistance. At the inlet, a fully developed flow profile was applied with flow rate set at 100 μL min−1 unless otherwise stated, which assumes that the fluid entering the channel had a uniform velocity distribution characteristic of steady-state flow. The initial conditions defined the starting state of the fluid, ensuring consistency in the velocity and pressure fields before simulation steps began. Solver settings included a time-dependent solver for transient analysis with a range of 0–600 s with 10 s increments.Additionally, the model was used to study the transport of diluted species and surface reactions to simulate and understand the DNA–DNA hybridization on the surface of reaction sites. The conditions for the transport of diluted species contained a boundary condition set with an initial concentration of zero, followed by a gradual inflow of different target concentrations using a step function from 0 to 1 and a diffusion coefficient of small molecules in water defined as 1 × 10−9 m2 s−1 (ref. 45) (Table S1†). A general inward flux was modeled as (R = Kon × concentration), coupled with a surface reaction rate defined by R. The Kon (0.96 × 106 M−1 min−1) and Koff (0.09 min−1) values are extracted from our previous work.46 Furthermore, we introduced Multiphysics coupling of laminar flow and transport of diluted species models to consider how the flow velocity affects DNA transport and hybridization, reflecting realistic behavior in a microfluidic system. Surface reactions parameters were set at zero initial concentration and site occupancy, with a surface probe density of 4.55 × 1012 molecules per cm2, and surface reaction rate of R. Solver conditions were set at stationary for laminar flow and time-dependent with a range from 1–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s with 800 s increments and physics-controlled tolerance.
000 s with 800 s increments and physics-controlled tolerance.
The meshing strategy for 2D simulation were adjusted to ensure accurate results while maintaining computational efficiency. Normal, fine, and extremely fine meshes were tested using the staghorn sumac leaf inspired design to demonstrate mesh independency (Fig. S1†). Fine and extremely fine meshing showed identical flow velocity uniformity (coefficient of variance 0.86%), while normal demonstrate slightly higher variability (coefficient of variance 2.4%). Therefore, the meshing strategy for laminar flow used the default fine mesh option. Additionally, we tested the chosen fine mesh under varies flow rates (10–1000 μL min−1), demonstrating no difference in the coefficient of variance measurement (Fig. S2†). In the 3D simulation, the meshing strategy was designed to achieve accurate results while maintaining computational efficiency. We employed a combination of physics-defined and user-defined approaches, utilizing a fine mesh for the reaction sites, a fine mesh for the boundaries, and a coarse mesh for the remaining geometry. Further increase of mesh refinement showed no improvement in capture kinetics.
The fraction of free sites was obtained by using boundary probes that are assigned to measure the fractions of free sites at each of the reaction sites. The fractions are then converted into capture efficiency using eqn (9):
| Capture efficiency (%) = 100% × (1 − fraction of free sites) | (9) |
Results and discussion
Design of bio-inspired microfluidic systems
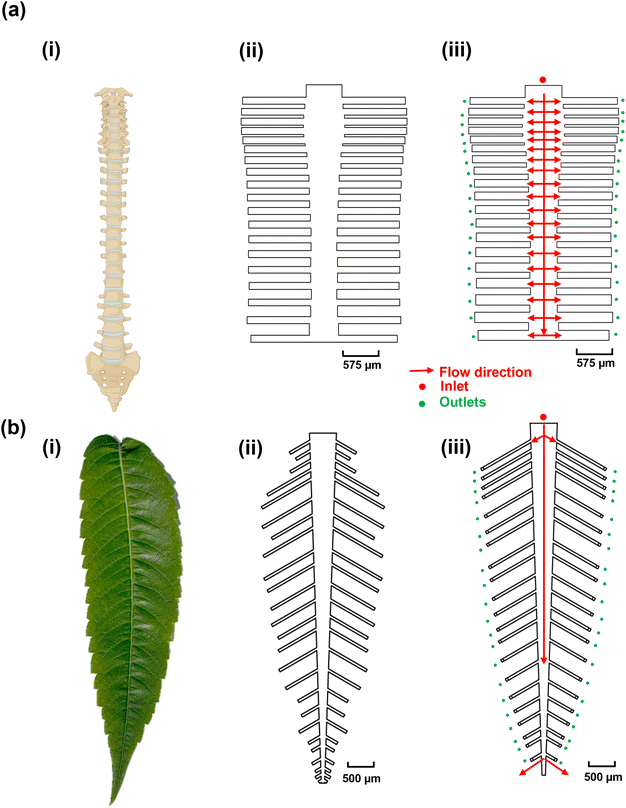
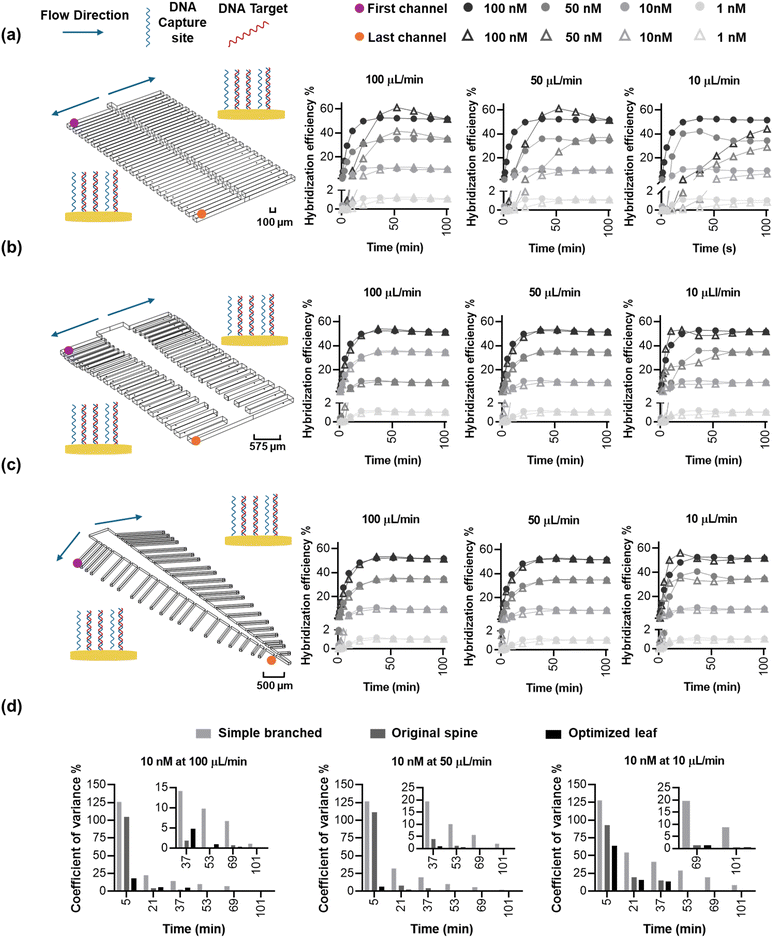
The objective of this study was to create bio-inspired designs (Fig. 1) that enable uniform flow distribution, target availability, and uniform target/probe interaction times to ensure consistent target capture efficiency across multiple reaction sites. This is crucial because biosensor signals are directly correlated with the number of available targets.46 We explored the structural designs of the human spine and leaves, both of which feature multi-channel networks, as templates for creating multiplexed microfluidic systems. We hypothesized that the human spine (Fig. 1a-i), which serves as the primary conduit for afferent and efferent signals between the brain and the body,47 could provide a template for ensuring uniform DNA hybridization and capture across different channels. To test this hypothesis, the dimensions of the spine-inspired design were scaled down by 1000 times from the real-life dimensions of a healthy human spine47 (Fig. 1a-ii and iii; Table S2†). Similarly, leaves were selected for their role in distributing nutrients for growth and photosynthesis through an intricate network of veins (Fig. 1b-i). The dimensions of a real staghorn sumac leaf were measured and scaled down by 1000 times (Fig. 1b-ii and iii) as well to guide the development of a multiplexed, biomimetic microfluidic system (Table S3†).Optimization of the spine-inspired microfluidics design
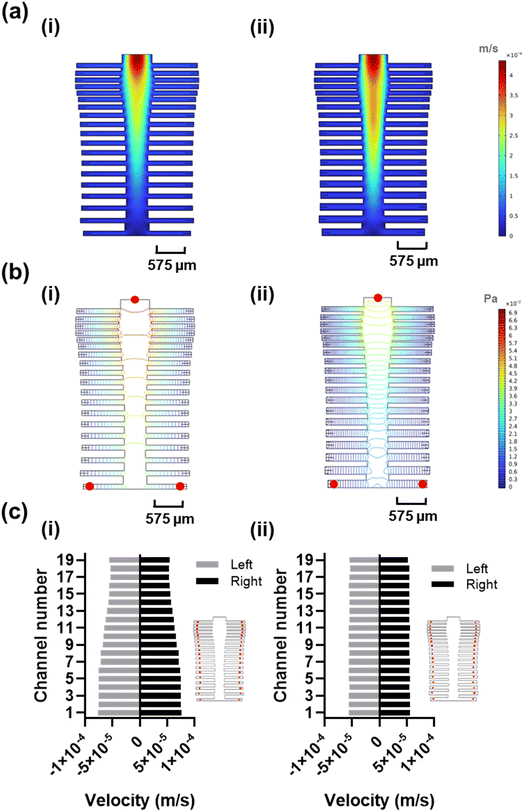
The spine-inspired design dimensions were adapted from the spinal measurements of the healthy individuals cadavers.47 The human spine consists of 33 vertebrae; however, for this design, the lower lumbar spine L4–L5, sacral, and coccygeal spine were not considered. These vertebrae were excluded as their fusion would not allow for channel separation, adding unnecessary fabrication complexity. As a result, the number of subchannels in the design was set at 38. The original dimensions of a human spinal vertebrae were scaled from the millimeter to the micrometer range to create the microfluidic channels (Table S2†), achieving a Reynold's number of 18.6 and a range of 14.3–18.6 (due to width variability) in the original and optimized designs, respectively. Both original and optimized designs ensure laminar flow (Re < 2000).48 The bio-inspired designs were optimized using a moderate flow rate of 100 μL min−1 shown to improve capture efficiency and sample delivery in similar systems.49,50 The original dimensions resulted in good velocity uniformity (Fig. 2a-i) and pressure distribution (Fig. 2b-i), consistent with the inherit neural networking functions,51 with a coefficient of variance of 14.68% (Fig. 2c-i) in the velocity profile at the reaction sites (positioned at an equal distance from the outlets (Fig. 2c-i, red circles). We manually fine-tuned the original design by varying the subchannel widths within the 95.5–153.5 μm range while observing the velocity profile of the system, to create an improved velocity profile (Fig. 2a-ii), along with lower pressure drop across the inlet and the furthest reaction sites from the inlet (Fig. 2b-ii, red circles) compared to the original design (Fig. 2b-i). As a result, the redesign shows a reduced coefficient of variance of 0.89% (Fig. 2c-ii) in the velocity vector at the reaction sites (Fig. S3†).Optimization of the leaf-inspired microfluidics design
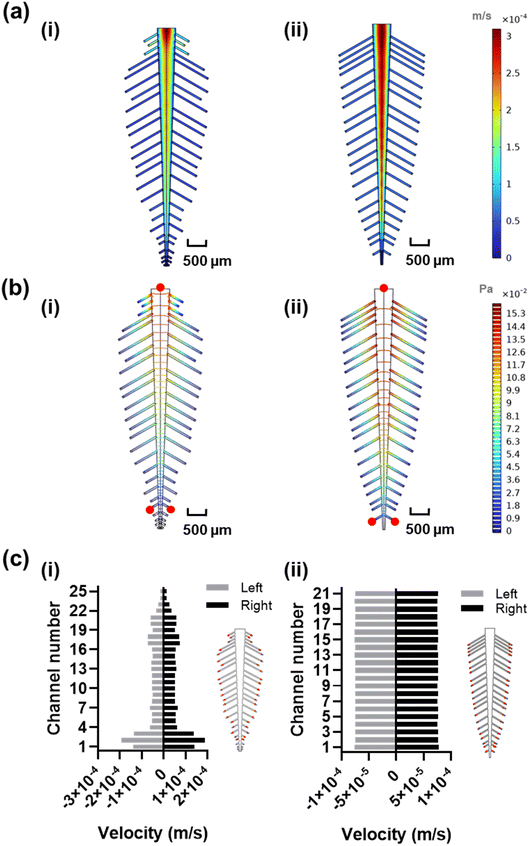
In order to estimate the length and width of each leaf vein, we measured and scaled a real staghorn sumac leaf from the millimeter to the micrometer range to achieve a low Reynolds number of 20.8 at 100 μL min−1, ensuring a laminar flow regime (Re < 2000) in the leaf-inspired original and optimized microchannels design. The original dimensions resulted in poor uniformity in velocity profile (Fig. 3a-i), and pressure (Fig. 3b-i), which may be due to the functional trade-offs inherent in the natural design of veins and leaves,52 as well as the exclusion of the shorter peripheral channels and additional sub-veins in the inspired design. The redesign, with 42 subchannels, demonstrated an improved velocity profile (Fig. 3a-ii), along with a lower pressure drop across the inlet and the furthest reaction sites from the inlet, indicating a smoother flow (Fig. 3b-ii, red circles). The velocity profile variability across the reaction sites (positioned at an equal distance from all the outlets, Fig. 3c-i red circles) in the original design shows a coefficient of variance of 59.81% (Fig. 3c-i and S3†) which is above the acceptable range for analyte detection.53 To address this high variability, the design was manually fine-tuned by reducing the resistance in the side veins/channels and adjusting the length of each channel within the 380–1700 μm range, while observing the velocity profile of the system, ultimately achieving a coefficient of variance of 0.86% in the velocity vector across all the reaction sites (Fig. 3c-ii and S3†).DNA–DNA hybridization uniformity in the bio-inspired designs
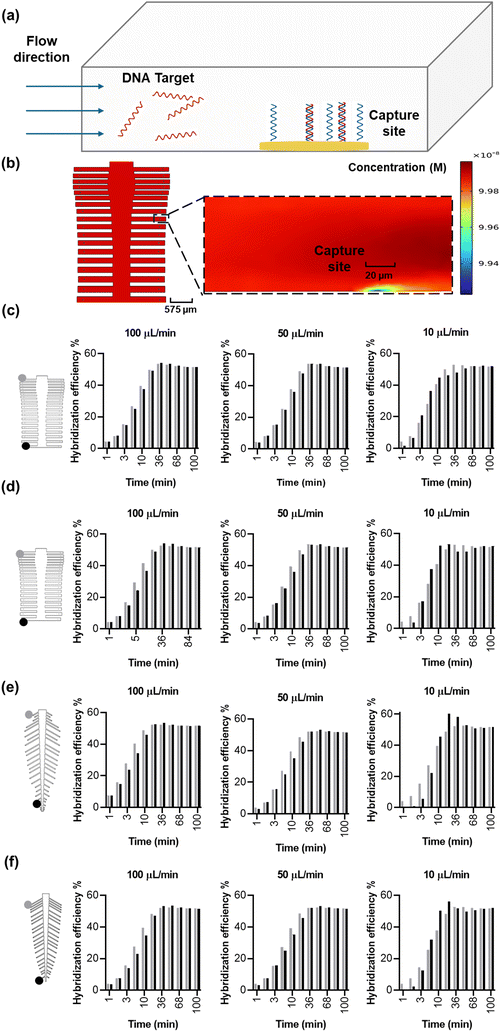
We sought to answer whether the optimized designs are in fact superior in DNA hybridization uniformity over the original designs, evaluated by calculating the variance in capture coefficient across the various reaction sites. In order to accurately simulate capture, a probe density of 4.55 × 1012 molecules per cm2, Kon of 0.96 × 106 M−1 min−1, and Koff of 0.09 min−1 were extracted from previous work in a similar system,46 resulting in a Kd of 94 nM. We then simulated the system (Fig. 4a) at a fully developed flow to mitigate initial operational effects (e.g. pump initial variability) with a gradual concentration increase from 0 nM to a homogenous target concentration of 100 nM—positioned at the middle of the log-linear dynamic range of the biosensor—to understand and verify the uniformity of the binding kinetics on the spine and leaf inspired systems. Circular electrodes were positioned at an equal distance from all the subchannel outlets, and they were modeled as reaction sites to capture the flowing target at flow rates of 10, 50 and 100 μL min−1. As the concentration of target is higher in the bulk solution than the reaction sites, molecules diffuse from the bulk to the reaction sites through the diffusion layer54 (Fig. 4b). We expect the capture efficiency of the reaction sites within different subchannels to be the same because of the reduced coefficient of variance of the velocity vector at the reaction sites (Fig. 2c-ii and 3c-ii), which ensures uniform convection and target transport. However, coupling convection, diffusion, and surface reactions in the simulation of capture efficiency will achieve a more accurate prediction than convection alone of the performance of the bio-inspired designs for biosensing.The original and optimized spine-inspired designs show the same capture efficiency over time in all the 38 capture reaction sites and minimal drop in hybridization efficiency between the reaction sites in the first and last channels (Fig. 4c and d), with a coefficient of variance of 0.43% and 0.59% at 100 μL min−1, 1.14% and 1.49% at 50 μL min−1, and 3.20% and 3.61% at 10 μL min−1 for the original and optimized spine-inspired designs at 20 minutes, respectively (Fig. S4a†). While both original and optimized spine-inspired designs demonstrate uniform capture across all 38 subchannels, it is interesting to observe that the original spine-inspired design has marginally lower coefficient of variance in all the tested flow rates (10, 50, 100 μL min−1) (Fig. S4a†). We hypothesize that the optimized spine-inspired design is more variable due to variable widths (ranging from 98.5–153.5 μm) of the subchannels, creating variable amount of target diffused DNA within each subchannel.55 While in the original spine-inspired design with uniform subchannels widths (100 μm), the distance between the centerline of the flow and the reaction sites (diffusion path) is equal, allowing target DNA to reach the reaction site uniformly through sideways (lateral) diffusion.54 Furthermore, as flow rate increases, convection becomes more dominant, reducing the effect of diffusion, resulting in less difference between the original and optimized spine-inspired systems (Fig. S4a†). At flow rates of 10, 50, and 100 μL min−1, the average Peclet numbers for the original design are 0.62, 3.09, and 6.19, compared to 0.53, 2.63, and 5.26 for the optimized design, confirming the dominance of diffusion at lower flow rates.
The original and optimized leaf-inspired designs demonstrate uniform capture efficiency over time with the optimized design being less time variable and demonstrating a smaller drop in hybridization efficiency between the reaction sites in the first and last channels (Fig. 4e and f). These designs exhibit coefficient of variance of 1.5% and 0.79% at 100 μL min−1, 1.74% and 1.74% at 50 μL min−1, and 8.33% and 5.49% at 10 μL min−1, for the original and optimized leaf-inspired designs at 20 minutes, respectively (Fig. S4b†). The improved variability in the optimized leaf-design is expected due to the uniform widths (80 μm) of all the subchannels in both leaf-inspired designs. A clear trend is observed in all the original and optimized designs (Fig. 4c–f), demonstrating initial high variability due to analyte concentration gradient across the microchannels. As the transport of analytes and reactions progress, moderate variability arises as convection–diffusion redistributes analytes downstream, eventually reaching a plateau as the system equilibrates. At lower flow rates (10 μL min−1), diffusion dominates, causing slower equilibration (68 minutes). In contrast, higher flow rates (50–100 μL min−1) enhance convection, reducing variability and allowing faster equilibrium (36 minutes).
Leveraging velocity profile geometry and surface reactions modeling is an effective approach for enhancing DNA–DNA hybridization uniformity in biosensor designs. Based on the uniformity of DNA–DNA hybridization, we selected the original spine-inspired design and the optimized leaf-inspired design for further kinetic analysis.
To understand whether a bio-inspired branched design is indeed needed for multiplexed biosensing, we compared the performance of the spine- and leaf-based designs to a simple branched channel with the same main and subchannels width (100 μm) containing a similar number (40 electrodes) of reaction sites (Fig. 5a). The simple branched design demonstrated a velocity coefficient of variance of 210.98% at the 40 reaction sites (Fig. S5†). Our simulation of DNA–DNA kinetics – simulated with a surface coverage 4.55 × 1012 molecules per cm2, range of target concentration (1, 10, 50, and 100 nM), and under variable flow rates (10, 50, 100 μL min−1), resulted in a large drop of hybridization efficiency between the first and last channel reaction sites in the simple branched compared to the spine and leaf inspired designs (Fig. 5a–c). Additionally, the systems demonstrate a trend of high (>35%) at 36 minutes for the simple branched and 5 minutes for the bio-inspired designs, moderate (10–35%) at 84 and 36 minutes for the simple branched and bio-inspired designs, respectively, and low (<10%) coefficient of variance overtime for both designs across all target concentration and flow rate parameters (Fig. 5c, Tables S4–S6†). The highest variability demonstrated by all three designs is at target 10 nM under 10 μL min−1 showing a coefficient of variance of 127.81%, 92.58%, and 63.64% at 5 minutes, 54.14%, 19.24%, and 16.05% at 20 minutes, 29.23%, 5.48%, and 5.79% at 52 minutes, and 8.68%, 0.49%, and 0.52% at 100 minutes for the simple branched, spine-inspired, and leaf-inspired designs, respectively. Less variability at later timepoints is reported in literature when surface reaction and mass transport models are taken into account.56 Interestingly, the DNA capture coefficient of variance decreases with the increase of flow rate from 10 to 100 μL min−1 (Fig. 5d), respectively, which could be attributed to the dominance of convection over diffusion at higher flow rates, ensuring more uniform delivery of target DNA molecules to the reaction sites.57 While a simple branched design may be appropriate in specific cases where a capture gradient is beneficial,58 its significant variability in molecular capture across reaction sites, extending up to 68 minutes, makes it unsuitable for applications requiring rapid and uniform multi-analyte detection.
The bio-inspired designs were further evaluated under different surface probe densities (low: 4.55 × 1011, high: 4.55 × 1013 molecules per cm2) at a target concentration of 100 nM under 100 μL min−1 flow rate. Although higher probe densities resulted in slightly increased variability in the leaf-inspired design, both spine- and leaf-inspired designs maintained a coefficient of variance below 5% across all time points (1–164 minutes, Fig. S6, Table S7†). Furthermore, the bio-inspired designs were tested using various fluids characterizing different specimens used in clinical biosensing (plasma, whole blood, and saliva) using a moderate probe density of 4.55 × 1012 molecules per cm2 and a target concentration of 100 nM under a flow rate of 100 μL min−1. The experiments resulted in a more pronounced effect than varying the probe density, with saliva showing the highest variability, followed by blood and plasma, corresponding directly to their viscosities from high to low (Table S1†). Higher viscosity reduces the diffusion coefficient, slowing the random motion of molecules and increasing the time needed for them to reach the reaction sites.59 As a result, dilution may be necessary for whole blood and saliva, particularly when using short incubation times (<10 minutes in the original spine-inspired design and <20 minutes in the optimized leaf-inspired design). In all complex media the original spine-inspired design achieved variability below 10% within 1 minute, while the optimized leaf design required 20 minutes to reach similar variability levels (Fig. S7, Table S8†). This highlights the superior performance of bio-inspired designs in challenging media, where uniformity and rapid response are critical.
Conclusion
There is a growing need for multiplexed biosensors that ensure uniform flow velocity, analyte distribution, and target capture for high-throughput multi-analyte detection. To address this, we adapted the designs of the spinal cord and leaf vein networks into microfluidic platforms, leveraging their inherent self-regulation and optimized resource distribution. These bio-inspired structures aim to achieve uniform flow and DNA–DNA hybridization, providing a robust foundation for multiplexed detection systems.To evaluate the efficacy of these designs, we first analyzed the velocity and pressure profiles in the original designs, followed by optimizing their dimensions to improve flow uniformity at the reaction sites through computational simulations. We then compared the original and optimized designs in terms of molecular capture at a target concentration of 100 nM, under varying flow rates (10, 50, and 100 μL min−1). Notably, the original spine-inspired design exhibited less variability than the optimized design, suggesting that a combined approach—optimizing flow dynamics, mass transport, and surface reaction modeling—better predicts DNA capture uniformity than flow dynamics alone.
In further validation, we compared a simple branched design with the bio-inspired designs to assess the variability in target capture in the different reaction sites. The capture kinetics in both designs initially exhibited high variability more than 35% at 36 minutes for the simple branched and 5 minutes for the bio-inspired designs, transitioning to moderate variability between 10% and 35% at 84 and 36 minutes for the simple branched and bio-inspired designs respectively, then eventually both designs stabilizing with less than 10% variability as adsorption–desorption and mass transport reached steady-state. Notably, the bio-inspired designs demonstrated significantly lower variability compared to the simple branched design, achieving stabilization (coefficient of variance <20%) within 10 minutes, compared to up to 68 minutes for the simple branched design under varying flow rates and target concentrations. Furthermore, the bio-inspired systems were tested using various probe densities and complex media (plasma, whole blood, and saliva), demonstrating low variability across all conditions, highlighting the benefits of bio-inspired designs for biosensing.
The findings underscore the advantages of bio-inspired methodologies in the creation of multiplexed and multi-analyte sensing devices. We anticipate that these designs will find practical applications in areas requiring multiplexing, such as organ-on-a-chip platforms, monitoring food and water for various contaminants, and diagnostic panels. Future research will concentrate on refining these designs through experimental validation to develop optimized multiplexed systems for the aforementioned applications.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
E. O. designed the study, conducted the simulation, data analysis, and manuscript writing. J. L. H. contributed to the surface reactions simulations and manuscript writing. P. L. contributed to design optimizations and manuscript editing. L. S. contributed to the design and conceptualization of the study and manuscript writing. All authors have approved the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the financial support of the Government of Canada through Natural Sciences and Engineering Research Council (NSERC) and Canada Research Chair program.References
- K. Sato, M. Yamanaka, H. Takahashi, M. Tokeshi, H. Kimura and T. Kitamori, Electrophoresis, 2002, 23, 734–739 CrossRef.
- E. P. Kartalov, J. F. Zhong, A. Scherer, S. R. Quake, C. R. Taylor and W. French Anderson, BioTechniques, 2006, 40, 85–90 CrossRef.
- F. Bakhshandeh, H. Zheng, N. G. Barra, S. Sadeghzadeh, I. Ausri, P. Sen, F. Keyvani, F. Rahman, J. Quadrilatero, J. Liu, J. D. Schertzer, L. Soleymani and M. Poudineh, Adv. Mater., 2024, 36, 2313743 CrossRef CAS PubMed.
- M. A. Yokus, T. Songkakul, V. A. Pozdin, A. Bozkurt and M. A. Daniele, Biosens. Bioelectron., 2020, 153, 112038 CrossRef CAS PubMed.
- L. Gu, Y. Zhang, D. Wang and J. Liu, Adv. Sens. Res., 2024, 3, 2300167 CrossRef CAS.
- X. Zheng, W. Cheng, C. Ji, J. Zhang and M. Yin, Rev. Anal. Chem., 2020, 39, 231–246 CrossRef CAS.
- M. K. Araz, A. M. Tentori and A. E. Herr, SLAS Technol, 2013, 18, 350–366 CrossRef CAS.
- G. A. Ganepola, World J. Gastrointest. Oncol., 2014, 6, 22 CrossRef.
- T. Jet, G. Gines, Y. Rondelez and V. Taly, Chem. Soc. Rev., 2021, 50, 4141–4161 RSC.
- B. Ma, J. Li, K. Chen, X. Yu, C. Sun and M. Zhang, Foods, 2020, 9, 278 CrossRef PubMed.
- A. Bosch, G. Sánchez, M. Abbaszadegan, A. Carducci, S. Guix, F. S. Le Guyader, R. Netshikweta, R. M. Pintó, W. H. M. Van Der Poel, S. Rutjes, D. Sano, M. B. Taylor, W. B. Van Zyl, D. Rodríguez-Lázaro, K. Kovač and J. Sellwood, Food Anal. Methods, 2011, 4, 4–12 CrossRef.
- A. Kling, C. Chatelle, L. Armbrecht, E. Qelibari, J. Kieninger, C. Dincer, W. Weber and G. Urban, Anal. Chem., 2016, 88, 10036–10043 CrossRef PubMed.
- E. M. McConnell, J. Nguyen and Y. Li, Front. Chem., 2020, 8, 2296–2646 Search PubMed.
- J.-H. Han, D. Lee, C. H. C. Chew, T. Kim and J. J. Pak, Sens. Actuators, B, 2016, 228, 36–42 CrossRef.
- P. Khashayar, S. Al-Madhagi, M. Azimzadeh, V. Scognamiglio and F. Arduini, TrAC, Trends Anal. Chem., 2022, 156, 116706 CrossRef.
- Z. Liao, J. Wang, P. Zhang, Y. Zhang, Y. Miao, S. Gao, Y. Deng and L. Geng, Biosens. Bioelectron., 2018, 121, 272–280 CrossRef PubMed.
- P. Yager, G. J. Domingo and J. Gerdes, Annu. Rev. Biomed. Eng., 2008, 10, 107–144 CrossRef.
- Y. Zhang and N. Zhou, Electroanalysis, 2022, 34, 168–183 CrossRef.
- J. R. Mejía-Salazar, K. Rodrigues Cruz, E. M. Materón Vásques and O. Novais De Oliveira Jr, Sensors, 2020, 20, 1951 CrossRef.
- M. I. Hajam and M. M. Khan, Biomater. Sci., 2024, 12, 218–251 RSC.
- C. Zhao, Z. Ge and C. Yang, Micromachines, 2017, 8, 28 CrossRef.
- A. Nagy, E. L. Tóth, K. Iván and A. Gáspár, Microchem. J., 2015, 123, 125–130 CrossRef.
- Y. Liu and X. Jiang, Lab Chip, 2017, 17, 3960–3978 Search PubMed.
- A. Fragoso, D. Latta, N. Laboria, F. Von Germar, T. E. Hansen-Hagge, W. Kemmner, C. Gärtner, R. Klemm, K. S. Drese and C. K. O'Sullivan, Lab Chip, 2011, 11, 625–631 Search PubMed.
- H. Adam, S. C. B. Gopinath, M. K. Md Arshad, T. Adam, U. Hashim, Z. Sauli, M. A. Fakhri, S. Subramaniam, Y. Chen, S. Sasidharan and Y. S. Wu, J. Taiwan Inst. Chem. Eng., 2023, 146, 104814 CrossRef.
- J. M. Mohan, K. Amreen, A. Javed, S. K. Dubey and S. Goel, Curr. Opin. Electrochem., 2022, 33, 100930 Search PubMed.
- A. A. Akhlaghi, H. Kaur, B. R. Adhikari and L. Soleymani, ECS Sens. Plus, 2024, 3, 011601 Search PubMed.
- K. R. Mitchell, J. E. Esene and A. T. Woolley, Anal. Bioanal. Chem., 2022, 414, 167–180 CrossRef PubMed.
- Z. Song, R. Yuan, Y. Chai, Y. Zhuo, W. Jiang, H. Su, X. Che and J. Li, Chem. Commun., 2010, 46, 6750 RSC.
- R. Polsky, J. C. Harper, D. R. Wheeler and S. M. Brozik, Electroanalysis, 2008, 20, 671–679 Search PubMed.
- C. K. Tang, A. Vaze, M. Shen and J. F. Rusling, ACS Sens., 2016, 1, 1036–1043 CrossRef.
- J. P. Pursey, Y. Chen, E. Stulz, M. K. Park and P. Kongsuphol, Sens. Actuators, B, 2017, 251, 34–39 CrossRef.
- R. Bruch, M. Johnston, A. Kling, T. Mattmüller, J. Baaske, S. Partel, S. Madlener, W. Weber, G. A. Urban and C. Dincer, Biosens. Bioelectron., 2021, 177, 112887 CrossRef PubMed.
- R. Vinoth, T. Nakagawa, J. Mathiyarasu and A. M. V. Mohan, ACS Sens., 2021, 6, 1174–1186 CrossRef PubMed.
- J. Zilberman-Rudenko, J. L. Sylman, H. H. S. Lakshmanan, O. J. T. McCarty and J. Maddala, Cell. Mol. Bioeng., 2017, 10, 16–29 CrossRef.
- D. Di Carlo, Lab Chip, 2009, 9, 3038 RSC.
- A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2019, 144, 87–113 RSC.
- Y. Lin, D. He, Z. Wu, Y. Yao, Z. Zhang, Y. Qiu, S. Wei, G. Shang, X. Lei, P. Wu, W. Ding and L. He, Bio-Des. Manuf., 2023, 6, 38–50 Search PubMed.
- M. Sayed Razavi and E. Shirani, J. Biomech., 2013, 46, 2303–2309 Search PubMed.
- L. Saias, J. Autebert, L. Malaquin and J. L. Viovy, Lab Chip, 2011, 11, 822–832 Search PubMed.
- V. Sharma, R. Balaji and V. Krishnan, Biomimetics, 2018, 3, 7 CrossRef PubMed.
- S. A. Solovitz, J. Zhao, W. Xue and J. Xu, J. Fluids Eng., 2013, 135, 021101 CrossRef.
- P. Gharpure, S. Veeralingam and S. Badhulika, Microfluid. Nanofluid., 2021, 25, 1–15 CrossRef.
- A. Günther and K. F. Jensen, Lab Chip, 2006, 6, 1487–1503 RSC.
- COMSOL Multiphysics® v. 6.2, COMSOL AB, Stockholm, Sweden Search PubMed.
- E. Osman, S. Sakib, R. Maclachlan, S. Saxena, A. A. Akhlaghi, B. R. Adhikari, Z. Zhang, Y. Li and L. Soleymani, ACS Sens., 2024, 9(9), 4599–4607 CrossRef.
- A. Frostell, R. Hakim, E. P. Thelin, P. Mattsson and M. Svensson, Front. Neurol., 2016, 7, 1664–2295 Search PubMed.
- Q. Zhao, D. Yuan, J. Zhang and W. Li, Micromachines, 2020, 11, 461 CrossRef PubMed.
- A. Laribi, S. Allegra, M. Souiri, R. Mzoughi, A. Othmane and F. Girardot, Talanta, 2020, 215, 120904 CrossRef PubMed.
- J. Chou, L. E. Li, E. Kulla, N. Christodoulides, P. N. Floriano and J. T. McDevitt, Lab Chip, 2012, 12, 5249 RSC.
- P. A. Guertin, Front. Neurol., 2013, 3, 1664–2295 Search PubMed.
- I. S. Matos, M. Boakye, I. Niewiadomski, M. Antonio, S. Carlos, B. C. Johnson, A. Chu, A. Echevarria, A. Fontao, L. Garcia, D. Kalantar, S. Madhavan, J. Mann, S. McDonough, J. Rohde, M. Scudder, S. Sharma, J. To, C. Tomaka, B. Vu, N. Yokota, H. Forbes, M. Fricker and B. W. Blonder, New Phytol., 2024, 244(2), 407–425 CrossRef PubMed.
- G. F. Reed, F. Lynn and B. D. Meade, Clin. Vaccine Immunol., 2002, 9, 1235–1239 CrossRef.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Nat. Biotechnol., 2008, 26, 417–426 CrossRef.
- N. Xiao, B. Wang and J. J. Huang, Chem. Eng. Sci., 2021, 235, 116505 CrossRef.
- I. Jokić, Z. Djurić, K. Radulović, M. Frantlović, G. V. Milovanović and P. M. Krstajić, Biosensors, 2021, 11, 194 CrossRef PubMed.
- I. Pereiro, A. Fomitcheva-Khartchenko and G. V. Kaigala, Anal. Chem., 2020, 92, 10187–10195 CrossRef CAS.
- J. Wang, P. Brisk and W. H. Grover, Lab Chip, 2016, 16, 4212–4219 RSC.
- E. Osman, S. Sakib, R. Maclachlan, S. Saxena, A. A. Akhlaghi, B. R. Adhikari, Z. Zhang, Y. Li and L. Soleymani, ACS Sens., 2024, 9, 4599–4607 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc01023j |
| This journal is © The Royal Society of Chemistry 2025 |