Leveraging dielectrophoresis in inertial flow for versatile manipulation of micro and nanoparticles†
Haotian
Cha
a,
Lingxi
Ouyang
a,
Xiangxun
Chen
 ab,
Yuao
Wu
ab,
Yuao
Wu
 a,
Xiaoyue
Kang
c,
Hongjie
An
a,
Xiaoyue
Kang
c,
Hongjie
An
 ad,
Weihua
Li
ad,
Weihua
Li
 e,
Nam-Trung
Nguyen
e,
Nam-Trung
Nguyen
 *a and
Jun
Zhang
*a and
Jun
Zhang
 *af
*af
aQueensland Micro- and Nanotechnology Centre, Griffith University, Nathan, Queensland 4111, Australia. E-mail: nam-trung.nguyen@griffith.edu.au
bBioscience Discipline, School of Environment and Science, Griffith University, Nathan, Queensland 4111, Australia
cSchool of Mechanical and Mining Engineering, The University of Queensland, Brisbane, QLD 4072, Australia
dSchool of Environment Science, Griffith University, 170 Kessel Road, Nathan, QLD 4111, Australia
eSchool of Mechanical, Materials, Mechatronic and Biomedical Engineering, University of Wollongong, Wollongong, 2522 Australia
fSchool of Engineering and Built Environment, Griffith University, Brisbane, QLD 4111, Australia. E-mail: jun.zhang@griffith.edu.au
First published on 25th March 2025
Abstract
The manipulation of micro and nanoparticles has extensive applications in biomedical research, clinical diagnostics, environmental monitoring, drug discovery, and the mining industry. Dielectrophoresis (DEP) utilises nonuniform electric fields to manipulate particles, offering a label-free, high-precision, and non-invasive method for both natural and synthetic particles. DEP manipulation has been well studied in the Stokes flow region with ultra-low Reynolds numbers (Re ≪ 1), where viscous effects dominate. However, its application in the inertial flow regime remains largely unexplored. This study aims to bridge the gap by coupling DEP and inertial flow for the manipulation of particles across micro and nano scales. First, we theoretically analysed the physical coupling of DEP and inertial lift forces along the vertical direction in microchannels, utilising symmetrical interdigitated electrode (IDE) arrays patterned on the top and bottom channel surfaces. We then experimentally investigated how the vertical coupling of DEP and inertial lift forces affects particle lateral focusing properties. The effects of DEP along the vertical direction were leveraged and amplified by the inertial effects along the lateral direction. Finally, we applied DEP in the inertial flow regime for size-based and dielectric property-based separation of particles and cells, as well as nanoparticle focusing and filtration. We believe that leveraging DEP in inertial flow will advance the field by providing a versatile and powerful method for the manipulation of micro and nanoparticles.
1 Introduction
Manipulation of micro- and nanoparticles is critical for biomedical research,1,2 clinical diagnosis,3,4 environment monitoring,5 drug discovery,6 the mining industry,7 the food industry,8,9 material synthesis,10etc. Microfluidics, the science of controlling fluid flow at the microscale,11 has become a powerful tool for precisely manipulating tiny particles, droplets and cells.12–14 Microfluidic manipulation makes use of active electric,15,16 magnetic,17,18 acoustic,19,20 optical,21,22 and thermal23,24 force fields, passive hydrodynamic forces25–31 and physical geometries of microchannels.32–34Dielectrophoresis (DEP) is a prominent technique that manipulates particles using electric fields. DEP induces forces on particles by the interaction of field-induced electric polarisation and a nonuniform electric field.35,36 DEP can manipulate particles based on their intrinsic dielectric properties without requiring them to be electrically charged or magnetically labelled. DEP offers label-free operation, high precision, and real-time controllability, making it suitable for trapping, concentrating and isolating deoxyribonucleic acid (DNA) molecules,37 circulating tumour cells (CTCs),38 blood cells,39 viruses,40 extracellular vesicles,41 bacteria,42 synthetic nanoparticles,43etc.
DEP manipulation has been extensively studied in the linear Stokes flow regime with extremely low Reynolds numbers (Re = ρUDh/μ ≪ 1, where ρ is the fluid density, U is the average flow velocity, μ is the dynamic viscosity, and Dh is the channel hydraulic diameter), where viscous forces dominate fluid flow.44–49 This regime simplifies the governing equations, facilitating accurate modelling of particle dynamics within DEP force fields. Besides, the slow flow allows for ample time to transport particles and cells to target positions. However, low flow speed results in low processing throughput, which may be partially mitigated through multiplexing and parallelisation. Moreover, prolonged exposure to electric fields and associated Joule heating effects can impact cellular functionality and viability.50–52
In contrast, high-speed fluid flow with finite inertia opens new opportunities for high-throughput particle manipulation.28 In a moderately high Reynolds number range (∼1 < Re ≲ 100) between Stokes and turbulent flow regimes, both fluid inertia and viscosity are significant. The inertial effects bring about other effects, such as inertial lift forces and secondary flow, which can significantly alter particle dynamics compared to the Stokes flow regime.53 To date, DEP manipulation in the inertial flow region has been rarely explored,54–56 leaving a significant knowledge gap in effectively coupling DEP with inertial flow. The nonlinearity of inertial flow complicates DEP manipulation, rendering conventional device designs for the Stokes flow region ineffective, particularly those based on lateral deflection of particles, as high flow speeds reduce the particles' residence time in the DEP zone.57
The present work explores the coupling of DEP with inertial flow for efficient particle manipulation. Unlike conventional DEP devices that primarily employ lateral deflection, we utilise the counterbalance between DEP and inertial forces to precisely control vertical equilibrium positions. Lateral inertial effects, such as secondary flow, further modulate and amplify particle lateral migration. The combination of vertical and lateral migration controls particle focusing positions in three-dimensional (3D) space. In this paper, we pattern interdigitated electrodes (IDEs) on top and bottom channel surfaces to generate symmetrical DEP forces. The DEP forces are then coupled with inertial lift forces to adjust the vertical equilibrium positions of particles. We first analyse the physical coupling of DEP and inertial lift forces along the vertical direction. Next, we examine how vertical displacement affects particle lateral migration in straight, spiral and serpentine channels. After that, we demonstrate the use of this coupling scheme for size-based and dielectric property-based separation of particles and cells, as well as nanoparticle focusing and filtration, respectively. We believe that coupling DEP with inertial flow will advance the field by offering an accurate, high-speed, and versatile strategy for manipulation and separation of micro and nanoparticles.
2 Materials and methods
2.1 Design and fabrication of DEP–inertial microfluidic devices
The proposed hybrid DEP–inertial microfluidic devices consisted of two symmetric interdigitated electrode (IDE) layers on the top and bottom and a middle fluidic channel layer with straight, serpentine or spiral microchannels, respectively, Fig. 1A. The straight channel had a width (W) of 300 μm, a height (H) of 50 μm and a length (L) of 34 mm. The serpentine channel comprised 19 zigzag periods, with the length and width of each U-turn being 750 μm and 300 μm, respectively. The height of the serpentine channel was 50 μm. For the spiral channel, the width and height were 150 μm and 30 μm, respectively. The initial spiral radius was 3.5 mm, and the space between adjacent loops was fixed at 1 mm. | ||
| Fig. 1 The coupling of DEP and inertial lift forces along the vertical direction. (A) The device consists of symmetric interdigitated electrode (IDE) layers on the top and bottom and a middle fluidic layer. (B) The electric field and n-DEP force distribution in a longitudinal section. Arrow vectors indicate the magnitude and direction of the n-DEP force. The background colour map illustrates the electric field distribution and corresponds to the right colour bar. (C) Longitudinal distribution of the vertical n-DEP force (FDEPz) at different heights. z/H represents the dimensionless distance to the channel bottom surface. The forces are symmetric along z/H = 0.5 with the same magnitude but in opposite directions. (D) Vertical n-DEP force (FDEPz) at different heights (z). (E) The distribution of average n-DEP force with different electric voltages. In the simulation, the particle size is 10 μm. Re[K(ω)] is approximated to be −0.5, based on polystyrene particles in DI water at an electric frequency of 1 MHz, as shown in ESI† Appendix Fig. S4. (F and G) Coupling of negative DEP (n-DEP) with inertial lift forces along the vertical direction. Particles at inertial equilibrium positions are repelled away from the electrodes and eventually migrate to the vertical channel centre when the n-DEP force exceeds the inertial lift force. (H and I) Coupling of positive DEP (p-DEP) and inertial lift forces along the vertical direction. The particles are attracted toward the top and bottom channel surfaces and eventually trapped on them if the p-DEP force dominates over the inertial lift force. | ||
The fluidic channel layer was made of double-sided polyethene terephthalate (PET) tape (3 M, 8000 series). A femtosecond laser cutting machine (A Series, Oxford Lasers, UK) cut through the double-sided tape to form microchannels. For the electrode layers, aluminium (300 nm thickness) was sputtered on glass substrates (Sail Brand) and then selectively etched using aluminium etchants, where the protective layer was formed by spin coating of a positive photoresist and maskless lithography (MLA150, Heidelberg, Germany). The width and spacing of the IDEs were both 20 μm. The inlet and outlets on the top layer were formed by drilling holes through the electrode layer using a hand drill. The two IDE layers and the middle fluidic channel layer were bonded after treating glass substrates with a 3-aminopropyl triethoxysilane (APTES, No. 919-30-2, Aldrich) solution. The device fabrication process is described in ESI† Appendix Fig. S1.
2.2 Particle preparation
Spherical polystyrene beads with diameters of 20 μm (1020 KB, Phosphorex), 15 μm (1015 KB, Phosphorex), 10 μm (G1000, Thermo Fisher Scientific), 8 μm (129, Phosphorex), 5 μm (G0500, Thermo Fisher Scientific), 1.1 μm (B0100, Thermo Fisher Scientific), 0.5 μm (G500, Thermo Fisher Scientific), 0.2 μm (R200, Thermo Fisher Scientific), and 0.1 μm (R100, Thermo Fisher Scientific) were suspended in deionised (DI) water, respectively. The particle-weight ratio in the suspension was from 0.01% to 0.05%. Tween 20 (P9416, Sigma-Aldrich) at a weight ratio of 0.1% was added as a surfactant to prevent particle aggregation. To characterise the separation performance of the devices, binary particle mixtures (8 μm & 10 μm, 0.2 μm & 1.1 μm) were prepared in DI water. The concentrations of 8 μm and 10 μm particles were 8.78 × 105 and 4.63 × 105 counts per mL, respectively. For nanoparticle separation, the concentrations of 0.2 μm and 1.1 μm particles were 1.14 × 109 and 0.7 × 107 counts per mL, respectively.2.3 DEP buffer preparation
The DEP buffer consisted of 8% sucrose (SA030, Chem-supply), 0.3% anhydrous D-glucose (GA018, Chem-Supply) and around 1% DPBS solution (14200-075, Gibcp) by volume in Milli Q water (pH = 7, Milli-Q® Direct 8, France). To inhibit Joule heating and electrode electrolysis, the conductivity of the DEP buffer was around 100 μs cm−1. The conductivity of the DEP medium was measured using a conductivity meter (HI5521, Hanna, USA). The solution density was around 1.06–1.09 g cm−3 to prevent the cells from settling.2.4 Cell preparation
The Chinese hamster ovary (CHO) cell line, attained from the American Type Culture Collection (ATCC), was cultured with Dulbecco's modified Eagle medium (DMEM, No. 11885-084, Gibco) supplemented with 10% fetal bovine serum (FBS, 10099-141, Gibco) and 1% penicillin–streptomycin (15140-122, Gibco). The culture was kept in an incubator (Forma 381, Thermo Scientific, USA) at 37 °C, containing 5% (v/v) CO2. CHO cells were detached by 5 min treatment of trypsin–EDTA (0.25%, 25200056, Gibco) and re-dispersed in the DEP buffer when the cell confluence reached approximately 85%. Live cell controls were prepared by resuspending CHO cells in 2 mL of culture medium, whereas dead cell controls were generated by incubating CHO cells in 2 mL of 70% v/v methanol (UN 1230, Chem-Supply) for 15 minutes. After centrifugation at 130g for 5 minutes, the cell pellet was collected and washed with 2 ml DEP buffer twice. Finally, cells were resuspended in 2 ml of DEP buffer for the experiments. The measured size of live CHO cells was 13–16 μm, while the dead cells ranged from 14–17 μm. The dielectric spectra of live and dead cells in the DEP buffer were measured using a 3DEP analyser (DEPTech, Uckfield, UK).For the experiments of separation of CHO cells based on dielectric properties, equal quantities of viable and nonviable CHO cells were mixed and suspended in the DEP buffer. The concentration of live and dead cells was 8 × 104 and 6.5 × 104 cells per mL, respectively. After processing through the DEP–inertial device, the cells from two outlets were collected and counted using a hemocytometer (718620, Neubauer Pattern, BLAUBRAND, Germany). The collected cells were also seeded into a 96-well plate at different dilution ratios with a culture medium (undiluted, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 1
4, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8). Brightfield images of cells were taken using an Olympus CKX53 microscope with a DP74 camera after 4 and 24 hours of seeding the cells. Subsequently, cells were treated with a PrestoBlue® cell viability kit (A13262, Invitrogen) for 30 minutes to quantify the proliferation of live CHO cells. The fluorescence intensity was measured using a microplate reader (CLARIOstar, BMG LABTECH, Germany), where the emission and excitation wavelengths were 590 and 560 nm, respectively, following the manufacturer protocol. The fluorescence intensity of undiluted live cells was used as the reference for the comparative analyses.
8). Brightfield images of cells were taken using an Olympus CKX53 microscope with a DP74 camera after 4 and 24 hours of seeding the cells. Subsequently, cells were treated with a PrestoBlue® cell viability kit (A13262, Invitrogen) for 30 minutes to quantify the proliferation of live CHO cells. The fluorescence intensity was measured using a microplate reader (CLARIOstar, BMG LABTECH, Germany), where the emission and excitation wavelengths were 590 and 560 nm, respectively, following the manufacturer protocol. The fluorescence intensity of undiluted live cells was used as the reference for the comparative analyses.
2.5 Experiment setup and data analysis
The microfluidic device was placed on an inverted microscope (IX73, Olympus, Japan). The particle/cell samples were infused into the device using a syringe pump (ISPLab02, DK Infusetek, China). A high-speed camera (VEO, Photron, USA) was mounted on the microscope to capture the brightfield images of the trajectory for microparticles. For nanoparticles, a high-sensitive camera (PCO.EDGE 3.1, USB sCMOS, PCO, Germany) was used to capture the fluorescence trajectories of these fluorescent particles. The open-source software ImageJ (National Institutes of Health) was used to process and analyse the high-speed videos and fluorescence trajectories of particles. A sinusoidal electrical signal, produced by a function generator (AFG3102C, Tektronix, USA) and amplified by an RF amplifier (TVA-R5-13A+, Mini-Circuits, USA), was connected to the top and bottom IDE pads using two BNC crocodile clips. An oscilloscope (TBS 1062, Tektronix, USA) was utilised to measure the waveform of the imported electrical signal.To quantify the separation performance on microparticles and CHO cells, the particle/cell suspensions were collected from different outlets, and the particle/cell concentration was measured using a hemocytometer. To distinguish the viable and nonviable cells, a trypan blue (15250-061, Gibco) was used (1 part cell suspension, 4 parts trypan blue). Furthermore, we calculated the separation purity and recovery, defined as follows:
Purity (P) is the ratio of the target particle number ([Ntarget]outlet/inlet) to the total number of particles ([Ntotal]outlet/inlet) at the same outlet/inlet.
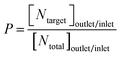 | (1) |
The recovery (RE) is defined as the ratio of the number of target particles at the specific outlet ([Ntarget]target outlet) to the total number of target particles at the inlet([Ntarget]inlet).
 | (2) |
For characterisation of filtration performance for nanoparticles, we used dynamic light scattering (DLS) (LiteSizer 500, Anton Paar, Austria) to measure the size distribution before and after the filtration process. In addition, a nanoparticle tracking analysis (NTA) system (Nanosight NS300, Malvern Panalytical, UK) was also utilised to measure the particle concentration and size distribution. It should be noted that the NTA can only analyse particles with the size below 1 μm.
3 Results
3.1 Coupling of vertical DEP and inertial lift forces
To effectively couple the symmetrical inertial lift forces in a rectangular channel, we designed symmetric interdigitated electrode (IDE) arrays patterned on the top and bottom substrates to generate symmetric DEP forces, Fig. 1A. The particles can be attracted to or repulsed from the electrode layers according to the different polarizabilities between particles and the surrounding medium,45Fig. 1B. Since there is no difference in the distribution of force fields between positive DEP (p-DEP) and negative DEP (n-DEP) forces, but the only difference is the force direction, we will only examine the characteristics of n-DEP force distribution.Electric fields and induced DEP forces are symmetric along the vertical centerline of the microchannel, Fig. 1B. This symmetry remains for the pairing electrodes at the top and bottom with inverse electrical phases in ESI† Appendix Fig. S2 and S3. Therefore, we only study the bottom half of the channel due to the symmetry of DEP forces. Without explicit notice, the DEP force implies the vertical component (FDEPz) throughout the discussion in this paper. The strength and oscillation of DEP forces are highly related to the distance to the electrodes, Fig. 1B and C. The maximum DEP force is close to the electrodes, but the magnitude of the DEP force oscillates significantly along the longitudinal (x) direction. The peak value of DEP force occurs near the electrode edges (x = 20, 40, 60 μm), whereas the trough points are in the middle of gaps between electrodes, Fig. 1C and D. Besides, both the strength of DEP force and its oscillational magnitude drop sharply when particles drift away from the electrode layers (0.2H ≤ z ≤ 0.5H), Fig. 1C and D. Furthermore, raising the electric voltage on the IDEs will enhance the magnitude of DEP force, Fig. 1E. In the inertial flow regime, particles suspended in the medium will follow the fluid flow at high speeds (U ∼ 0.6 m s−1). The net effect of the fluctuating DEP force on the particles is determined by its average magnitude.
In the inertial flow regime, DEP forces counterbalance inertial lift forces, modifying the equilibrium positions of particles along the vertical direction. Without DEP forces, inertial lift forces (blue curve in Fig. 1F–I) result in two symmetric equilibrium positions, about 0.2H away from the top and bottom channel walls.54 If an n-DEP force (green curve in Fig. 1F and G) is applied, the original symmetrical equilibrium positions near the bottom and top will be repelled further away from the channel walls according to the net force (red dashed curve), Fig. 1F. Increasing the electric voltage, particles are levitated closer to the vertical centre. Upon a certain electric voltage threshold, the n-DEP force exceeds the inertial lift force, and the net force is consistently directed to the vertical channel centre, Fig. 1G. This means that the particles will migrate vertically and stabilise at the channel's vertical centreline. In contrast, if a p-DEP force is applied, the particles will be attracted to the electrode regions, where the net force curve is expanded (red dashed curve in Fig. 1H). If the electric voltage is large enough, the p-DEP force can dominate over the inertial lift force, and the particles will be trapped on the channel surface, Fig. 1I. A theoretical analysis on the coupling of DEP forces and inertial lift forces along the vertical direction is in ESI† Appendix Information S1.
In summary, IDEs symmetrically patterned on the bottom and top channel surfaces can generate a symmetric DEP force field on particles. Coupling symmetric DEP and inertial lift forces can precisely control the vertical equilibrium positions of particles. Horizontal components of inertial effects (i.e., lateral inertial lift force and secondary flow) are not uniform along the vertical direction. For example, the no-slip boundary causes the fluid velocity to peak at the channel centre. This promises the modification of particle positions in the horizontal direction. In the following section, we will investigate the lateral migration of particles through the coupling of vertical DEP and inertial lift forces.
3.2 Modulation of particle lateral focusing through the coupling of vertical DEP and inertial lift forces
In this section, we experimentally investigated the modification of lateral particle focusing by coupling DEP forces and inertial lift forces within the three typical channel geometries—straight, serpentine, and spiral. The experimental setup is schematically shown in Fig. 2A. | ||
| Fig. 2 Modulation of particle lateral migration by coupling vertical DEP and inertial lift forces. (A) A schematic experimental setup and a photo of the fabricated microfluidic device. (B) Inertial focusing of particles in a low-aspect-ratio (H/W = 1/6) straight channel. The symmetric equilibrium positions of particles near the top and bottom channel walls are due to the counterbalance of two inertial lift forces (i.e., shear lift force Fs and wall lift force Fw).28 (C) The particle focusing positions before (i) and after (ii) applying n-DEP forces in the straight channel. Particles disperse more broadly after applying n-DEP forces on particles. (D and E) Secondary flow in serpentine and spiral microchannels, respectively. The arrow represents the fluid velocity. The colour legend indicates the magnitude of the secondary flow velocity. (F) Particle focusing positions (i) before and (ii) after applying n-DEP forces in a serpentine channel. After n-DEP forces are applied to levitate particles off the electrodes, the particles migrate laterally from sidewalls toward the channel centre. (G) Particle focusing positions (i) before and (ii) after applying n-DEP forces in a spiral channel. When n-DEP forces repel particles off the electrodes, particles migrate laterally toward the outer wall. The particle size is 10 μm, and the flow rate is 500 μL min−1 (Re = 47). The applied electric voltage is 40 V, and the electric frequency is 1 MHz. The scale bar is 100 μm. | ||
For straight channels, coupling vertical DEP and inertial lift forces cannot significantly modify the lateral position of particles. Without DEP, particles migrate to the symmetric equilibrium positions near the top and bottom channel walls due to the pure inertial lift forces,58Fig. 2B and C(i). Besides, particles distribute broadly near the channel central region along the lateral direction because of a blunted lateral velocity profile in a low-aspect-ratio (H/W = 1/6) channel.59,60 After applying a vertical n-DEP force on the particles, they disperse more widely because of repulsion from the electrode layers and levitation toward the channel vertical centre. Some particles even stay near the channel sidewalls, Fig. 2C(ii). This is because the longitudinal velocity of particles becomes too fast when levitating toward the channel's vertical centre, and the duration of particles in the microchannel becomes too short. Therefore, the lateral migration due to inertial lift forces is not significant.
For curved channels, coupling vertical DEP and inertial lift forces can significantly modify the lateral focusing of particles, Fig. 2D–G. In both spiral and serpentine channels, the curvature-induced secondary flow, a minor flow perpendicular to the primary flow, acts on the particles and alters their initial equilibrium positions due to inertial lift forces.53 In a serpentine channel, the alternating channel curvature induces oscillating secondary flows, Fig. 2D. Particles focus on four symmetrical equilibrium positions along the channel centreline, which are represented as two focusing streaks near the sidewalls from the top-down view, Fig. 2F(i). When n-DEP forces are applied and levitate particles vertically, particles migrate laterally toward the channel centre, Fig. 2F(ii). Two-sided focusing streaks can even combine as a single one at the channel middle when the electric voltage is above a threshold, ESI† Appendix Fig. S5.
In contrast, in a spiral channel, the channel curvature direction is consistent, as well as the secondary flow, Fig. 2E. The counterbalance of secondary flow and inertial lift forces results in two symmetrical equilibrium positions along the vertical centre, shown as one focusing position of particles from the top view,28,61Fig. 2G(i). Upon applying an n-DEP force to push particles away from the electrode layers, particles migrate laterally toward the outer wall. This is because the secondary flow near the vertical central region is directed to the outer wall, and its strength is much stronger than others. This process results in a unilateral focusing streak near the outer wall, Fig. 2G(ii). The particle-focusing positions in a spiral channel under various electric voltages are shown in ESI† Appendix Fig. S6.
In summary, particle vertical displacement by coupling vertical DEP and inertial forces can modulate particle lateral focusing positions in curved channels. Compared with straight channels, the curvature-induced secondary flow in spiral and serpentine channels can significantly modify the inertial focusing positions through the coupling scheme. By coupling DEP forces with inertial flow, particle inertial focusing positions can be precisely regulated by adjusting the electric field. This new mechanism provides more flexibility to precisely manipulate and separate particles and cells at high speed and by multiple modes, which will be demonstrated as follows.
3.3 Size-based particle separation by coupling n-DEP force with inertial flow
We applied the proposed coupling scheme for the size-based separation of particles. We first investigated the effects of particle size on the focusing patterns in the hybrid microfluidic device consisting of a sandwiched serpentine channel and IDE layers, Fig. 3A. Particle sizes ranged from 5 to 20 μm. The applied electric voltage (Vpp) was varied from 0 V to 40 V with a 2 V interval, and the frequency was constant at 1 MHz. The colour-coded map was used to quantitatively illustrate particle distribution in the microchannel, with each colour indicating the normalised frequency of particles at specific lateral positions.62 We could observe that two-sided particle focusing streaks shift toward the channel centre with increasing electric voltage, Fig. 3B. In addition, they can combine and merge as a single focusing band at the channel centre when the applied electric voltage is above a critical value. This critical voltage depends on particle size, indicating the possibility of size-based particle separation. For example, when Vpp was in the range from 32 to 36 V, 10 μm particles could focus as a single streak at the channel centre, while 8 μm particles remained near the two sidewalls. Thus, size-based particle separation of this binary mixture could be achieved. Moreover, the effective electric voltage for the separation of particle mixtures depends on the flow rate, Fig. 3C. The higher the flow rate is, the higher the electric voltage should be.Furthermore, we achieved the separation of the 8 μm and 10 μm particle mixture and evaluated the separation performance using the hybrid DEP–inertial microfluidic device, Fig. 3D. The particle mixture was infused into the device at 500 μL min−1 (Re = 47). When Vpp was 0 V, both particles were focused near the two sidewalls, Fig. 3D(i)–(iii). When Vpp was 35 V, 10 μm particles migrated to the channel centre and merged as a single focusing streak, while 8 μm particles still remained near the two sidewalls as two focusing streaks, although they experienced a slight lateral displacement, Fig. 3D(iv)–(vi) and ESI† Appendix Movie S1. Thus, they can be separated by the differential lateral positions. Furthermore, we collected separated particles from the middle and side outlets and quantitatively evaluated the separation performance. Fig. 3E shows the brightfield and fluorescence microscopy images of particles. Following a single processing step, the purity of 10 μm and 8 μm particles was enhanced from 35% to 98.2% and from 65% to 93.78%, respectively, Fig. 3F. Concurrently, the recovery of 10 μm and 8 μm particles was as high as 90.92% and 99.45%, respectively, Fig. 3G. This indicates the high separation resolution (particle size gap of 2 μm) and efficiency (>90%) using this coupling scheme.
3.4 Dielectric property-based particle separation by coupling p-DEP and n-DEP forces with inertial flow
This section explores the physical coupling of positive and negative DEP forces with inertial flow for dielectric property-based particle separation. Particles/cells can experience n-DEP or p-DEP forces based on the dielectric properties of particles and the electric frequency.45 As discussed in section 2.1, particles will be attracted to the electrode layers if a p-DEP force is applied along the vertical direction, Fig. 1H and I. Given the opposing vertical migration direction as compared to n-DEP forces, the lateral migration of particles is expected to be opposite, and particles will migrate towards the two sidewalls, Fig. 4A. The opposite lateral migration direction of particles under p-DEP and n-DEP forces indicates the potential of particle separation based on their dielectric properties.To verify the above hypothesis, we first investigated the focusing behaviour of cells with different dielectric properties in the hybrid DEP–inertial microfluidic device. Chinese hamster ovary (CHO) cells, a commonly used cell line in in vitro studies, were used as a model cell type due to their wide application in biopharmaceutical research and toxicology.63 Live CHO cells were suspended in the DEP medium, while dead CHO cells were obtained after treatment with methanol. We measured the dielectric spectra (i.e., Clausius–Mossotti (CM) factor) of both live and dead CHO cells using 3DEP equipment,64Fig. 4B. At 1 MHz, the CM factor of live and dead CHO cells is 0.7 and −0.25, resulting in p-DEP and n-DEP forces, respectively, Fig. 4B. Live CHO cells experienced p-DEP forces and migrated laterally closer to the nearby sidewalls, Fig. 4C. In contrast, dead CHO cells shifted toward the channel centre since n-DEP forces were exerted, Fig. 4D. The opposite lateral migration direction of live and dead CHO cells promises the separation of cells based on distinct dielectric properties using our coupling scheme.
Furthermore, we demonstrated and evaluated the separation of dead and live CHO cells by coupling p-DEP and n-DEP forces with inertial flow, Fig. 4E. We mixed live and dead cells with a ratio of around 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and delivered the mixture at 600 μL min−1 (Re = 56). The applied electric voltage was 35 V. Without DEP forces (Vpp = 0 V), live and dead cells were broadly dispersed and overlapped largely with each other, Fig. 4E(i), which is challenging for effective separation. When the electric field was applied, live and dead cells migrated to distinct lateral positions, exiting from side and middle outlets, respectively, Fig. 4E(ii). This approach enabled the continuous and efficient separation of live and dead CHO cells based on their distinct dielectric properties, ESI† Appendix Movie S2. Furthermore, we quantitatively characterised the separation performance, Fig. 4F. The live and dead CHO cells were purified significantly, from both around 50% in the original mixture to 87.26% and 93.85% after a single processing step, respectively. The concentration of both cells was enriched almost four times from the original mixture.
1 and delivered the mixture at 600 μL min−1 (Re = 56). The applied electric voltage was 35 V. Without DEP forces (Vpp = 0 V), live and dead cells were broadly dispersed and overlapped largely with each other, Fig. 4E(i), which is challenging for effective separation. When the electric field was applied, live and dead cells migrated to distinct lateral positions, exiting from side and middle outlets, respectively, Fig. 4E(ii). This approach enabled the continuous and efficient separation of live and dead CHO cells based on their distinct dielectric properties, ESI† Appendix Movie S2. Furthermore, we quantitatively characterised the separation performance, Fig. 4F. The live and dead CHO cells were purified significantly, from both around 50% in the original mixture to 87.26% and 93.85% after a single processing step, respectively. The concentration of both cells was enriched almost four times from the original mixture.
In addition, the hybrid DEP–inertial microfluidic device demonstrated good biocompatibility with CHO cells. After processing, CHO cells were collected from the outlets after processing and seeded into a 96-well plate at different dilutions (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 1
4, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) for subsequent cell culture. The dilution was applied to avoid excessive or insufficient cell concentration, ensuring optimal conditions for cell growth. Cell images were captured at 4 and 24 hours post-seeding, Fig. 4G. The full-scale images of culture wells are in ESI† Appendix Fig. S7. Live CHO cells adhered to the culture plate and exhibited normal proliferation within 24 hours. Furthermore, a PrestoBlue® cell viability kit was used to quantify the proliferation of CHO cells. Fluorescence intensity was measured using a microplate reader, as shown in Fig. 4H. The fluorescence intensity in the side outlets (SOs) was significantly higher than in the middle outlet (MO), demonstrating both the effective separation of cells based on dielectric properties and the good biocompatibility of the separation process.
8) for subsequent cell culture. The dilution was applied to avoid excessive or insufficient cell concentration, ensuring optimal conditions for cell growth. Cell images were captured at 4 and 24 hours post-seeding, Fig. 4G. The full-scale images of culture wells are in ESI† Appendix Fig. S7. Live CHO cells adhered to the culture plate and exhibited normal proliferation within 24 hours. Furthermore, a PrestoBlue® cell viability kit was used to quantify the proliferation of CHO cells. Fluorescence intensity was measured using a microplate reader, as shown in Fig. 4H. The fluorescence intensity in the side outlets (SOs) was significantly higher than in the middle outlet (MO), demonstrating both the effective separation of cells based on dielectric properties and the good biocompatibility of the separation process.
3.5 Manipulation and separation of nanoparticles by coupling n-DEP force with inertial flow
Leveraging DEP forces with inertial flow in spiral channels can extend the manipulation of particles from the micro to nanoscale. We designed and fabricated a DEP–spiral microfluidic device by stacking a spiral channel with the top and bottom IDE layers, where the microelectrodes were curled perpendicular to the spiral channel, Fig. 5A–C. The symmetric n-DEP forces from the top and bottom surfaces pinch particles toward the vertical middle region, where the secondary flow is directed to the outer wall and drags particles toward the outer wall consistently, Fig. 5B. For example, 1.1 μm particles were randomly distributed at 100 μL min (Re = 18) when there was no DEP force (Vpp = 0 V), Fig. 5D. Applying an electric field, an n-DEP force was induced on the particles, and particles migrated toward the outer wall and remained in the region. By increasing the electric voltage, particles migrated closer to the outer wall and focused within a narrower region. A similar trend was also observed for 500 nm particles, ESI† Appendix Fig. S8.Additionally, the flow speed also affects the lateral migration of particles in the DEP–spiral microfluidic device, Fig. 5E. Increasing the flow rate shortens the residence time of particles in the channel, subsequently suppressing the lateral migration of particles. In this case, enhancing electric voltage can levitate particles further to the middle region, where the secondary flow velocity is stronger so that particles can be equivalently focused at a higher flow rate, ESI† Appendix Fig. S9. In addition, the smaller the particle size, the more challenging it is to focus them tightly, Fig. 5F. This is because the DEP force is proportional to the third power of particle size, eqn (S6),† and DEP forces on smaller particles are too weak to sufficiently push particles vertically to the effective secondary flow region, ESI† Appendix Fig. S10.
Furthermore, we demonstrated the effective separation of the nanoparticle mixture based on the particles' size-dependent focusing property in the hybrid microfluidic device, Fig. 5G. In the absence of an electric field and at 100 μL min−1 (Re = 18), both 1.1 μm and 200 nm particles randomly dispersed and completely overlapped each other, Fig. 5H(i). By applying a Vpp of 38 V on the IDEs, the larger (1.1 μm) particles focused near the outer wall, while the smaller (200 nm) particles occupied the whole channel as multiple focusing streaks, Fig. 5H(ii) and ESI† Appendix Movie S3. Therefore, 1.1 μm and 200 nm particles could be separated.
The particle samples were collected and visualized using a fluorescence microscope, Fig. 5I. The fluorescence images clearly indicated that 200 nm particles were purified from the mixture. A single peak at around 200 nm from the dynamic light scattering (DLS) analysis of the samples further validated the finding, Fig. 5J. The nanoparticle tracking analysis (NTA) of the samples proved that 200 nm particles were enriched after processing, Fig. 5K. It should be noted that some of the 200 nm particles were lost and collected from the outer outlet. This may be solved by recirculating the samples through the same device to further enhance the recovery of 200 nm particles. Meanwhile, 1.1 μm particles from the outer outlet can be further purified using the same method.
4 Discussion and conclusions
This work explored the coupling of DEP with inertial flow for particle manipulation. We proposed an innovative coupling scheme by counterbalancing symmetric DEP forces and inertial lift forces along the vertical direction, which can subsequently control particles' trajectory in three dimensions (3D). Three different channel geometries were studied. Curved (i.e., serpentine and spiral) channels were the most effective geometries for the coupling scheme. This is because the curvature induces significant cross-sectional secondary flow, which effectively promote lateral migration of particles. Levitating particles' vertical positions can control the strength of secondary flow drag on particles because the non-slip wall boundary causes a minimum fluid velocity near the channel walls and a maximum fluid velocity near the channel centre. Subsequently, the lateral migration of particles can be manipulated. This coupling scheme offers more flexible and precise control of particles in three dimensions. Compared to conventional inertial microfluidics, where the equilibrium positions of particle focusing are predominantly determined by the channel geometries and flow rate,27,65,66 combining DEP and inertial forces offers more flexibility in adjusting particle positions in 3D. This approach enhances manipulation capabilities by enabling real-time control through electrical signals.This multiphysics coupling scheme also introduces more selection parameters for cell separation. Physically coupling DEP forces and inertial effects can distinguish cells based on their size and dielectric properties. This overcomes the shortcoming of conventional inertial microfluidics in separating cell groups of similar size.53,67 Here, we demonstrated the efficient separation of live and dead CHO cells with similar sizes based on differences in dielectric properties. In comparison with conventional techniques such as density gradient centrifugation and flow cytometry, our microfluidic chip enables fast, precise separation while maintaining normal cell proliferation. Furthermore, this feature could expand separation capabilities when dealing with complex cell samples, e.g., circulating tumour cells (CTCs). The partial size overlapping between CTCs and blood cells prohibits efficient isolation of CTCs. Combining double selection criteria using the coupling scheme will be a promising strategy since cancer cells possess different dielectric properties than blood cells.68 Similarly, the same scheme may also be applied for isolating inflammation-related cells, like neutrophils or monocytes. Activated neutrophils, common in inflammatory responses, exhibit altered dielectric properties compared to their inactivated counterparts.69 The high-speed feature of the inertial flow allows for a high processing throughput and short duration of cells within electric fields, minimising the negative impact of the electric field on cells. Besides, it is possible to label cells with specific particles to modify their dielectric properties, enabling a more specific separation. These have not been demonstrated here due to the scope of this work, but indicate many possible applications of the proposed coupling scheme and future development.
Furthermore, the coupling scheme can extend the applicable particle size range from the microscale to the nanoscale. In this work, we chose a spiral channel to manipulate submicron particles because the secondary flow in the spiral channel is unidirectional and more stable for focusing small particles. We observed effective lateral deflection of particles as small as 200 nm. The challenge in manipulating such small particles lies in effectively enhancing DEP forces to levitate them into the middle region where the secondary flow can operate. Expanding the manipulation scale of particles enables potential applications in the separation, detection, and analysis of smaller particles, such as bacteria, extracellular vesicles, viruses, and synthetic nanoparticles.
In conclusion, this work introduces an innovative coupling scheme of DEP and inertial flow for real-time microparticle focusing, multi-criteria cell separation, and nanoparticle filtration. Leveraging DEP in inertial flow advances multiphysics microfluidics, offering fast, flexible, and versatile manipulation functions for particles and cells from the microscale to the nanoscale.
Data availability
All data supporting the findings of this study are available within the paper and ESI,† or upon reasonable request from the corresponding authors.Author contributions
JZ conceived the idea, designed and supervised the project, and revised and edited the manuscript; NTN designed and supervised the project and revised and edited the manuscript; HTC fabricated the microfluidic devices, prepared the particle samples, performed the experiments, analysed the experimental data for visualisation and wrote the manuscript draft; LXOY and HJA contributed to the experimental tests and fabrication of the microfluidic devices; YAW and XXC contributed to the biological cell preparation and experiments; XYK and WHL contributed to the data analysis. All authors provided critical feedback and reviewed and approved the manuscript.Conflicts of interest
The authors have declared no conflicts of interest.Acknowledgements
NTN and JZ acknowledge the support from the Australian Research Council (ARC) Australian Laureate Fellowship (Grant No. FL230100023) and ARC DECRA fellowship (Grant No. DE210100692). This work was partly performed at the Queensland node-Griffith of the Australian National Fabrication Facility, a company established under the National Collaborative Research Infrastructure Strategy to provide nano and microfabrication facilities for Australian researchers.References
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef PubMed
.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef PubMed
.
- S. Nagrath, L. V. Sequist, S. Maheswaran, D. W. Bell, D. Irimia, L. Ulkus, M. R. Smith, E. L. Kwak, S. Digumarthy and A. Muzikansky, Nature, 2007, 450, 1235–1239 CrossRef
.
- S. L. Stott, C.-H. Hsu, D. I. Tsukrov, M. Yu, D. T. Miyamoto, B. A. Waltman, S. M. Rothenberg, A. M. Shah, M. E. Smas and G. K. Korir, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18392–18397 Search PubMed
.
- P. Aryal, C. Hefner, B. Martinez and C. S. Henry, Lab Chip, 2024, 24, 1175–1206 RSC
.
- P. Neužil, S. Giselbrecht, K. Länge, T. J. Huang and A. Manz, Nat. Rev. Drug Discovery, 2012, 11, 620–632 Search PubMed
.
- Y. Geng, S. Ling, J. Huang and J. Xu, Small, 2020, 16, 1906357 CrossRef PubMed
.
- X. Li, B. You, H. C. Shum and C.-H. Chen, Biomaterials, 2022, 287, 121631 Search PubMed
.
- S. Neethirajan, I. Kobayashi, M. Nakajima, D. Wu, S. Nandagopal and F. Lin, Lab Chip, 2011, 11, 1574–1586 Search PubMed
.
- S. Marre and K. F. Jensen, Chem. Soc. Rev., 2010, 39, 1183–1202 RSC
.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef PubMed
.
- M. Joanicot and A. Ajdari, Science, 2005, 309, 887–888 CrossRef PubMed
.
- X. Mu, W. Zheng, J. Sun, W. Zhang and X. Jiang, Small, 2013, 9, 9–21 CrossRef CAS PubMed
.
- C. W. Shields Iv, C. D. Reyes and G. P. López, Lab Chip, 2015, 15, 1230–1249 RSC
.
- A. Ramachandran, D. A. Huyke, E. Sharma, M. K. Sahoo, C. Huang, N. Banaei, B. A. Pinsky and J. G. Santiago, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 29518–29525 CrossRef CAS
.
- F. Paratore, V. Bacheva, G. V. Kaigala and M. Bercovici, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 10258–10263 CrossRef CAS PubMed
.
- H. Lin, W. Yu, K. A. Sabet, M. Bogumil, Y. Zhao, J. Hambalek, S. Lin, S. Chandrasekaran, O. Garner and D. Di Carlo, Nature, 2022, 611, 570–577 CrossRef CAS
.
- A. Mishra, T. D. Dubash, J. F. Edd, M. K. Jewett, S. G. Garre, N. M. Karabacak, D. C. Rabe, B. R. Mutlu, J. R. Walsh and R. Kapur, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 16839–16847 CrossRef CAS PubMed
.
- M. Wu, Y. Ouyang, Z. Wang, R. Zhang, P.-H. Huang, C. Chen, H. Li, P. Li, D. Quinn and M. Dao, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10584–10589 CrossRef
.
- S. P. Zhang, J. Lata, C. Chen, J. Mai, F. Guo, Z. Tian, L. Ren, Z. Mao, P.-H. Huang and P. Li, Nat. Commun., 2018, 9, 2928 Search PubMed
.
- B. Ciraulo, J. Garcia-Guirado, I. de Miguel, J. Ortega Arroyo and R. Quidant, Nat. Commun., 2021, 12, 2001 Search PubMed
.
- B. Hamza, S. R. Ng, S. M. Prakadan, F. F. Delgado, C. R. Chin, E. M. King, L. F. Yang, S. M. Davidson, K. L. DeGouveia and N. Cermak, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2232–2236 Search PubMed
.
- E. L. Talbot, J. Kotar, L. Parolini, L. Di Michele and P. Cicuta, Nat. Commun., 2017, 8, 15351 Search PubMed
.
- S. Xu, A. J. Hutchinson, M. Taheri, B. Corry and J. F. Torres, Nat. Commun., 2024, 15, 2996 CrossRef PubMed
.
- S. Wang, Q. Xu, Z. Zhang, S. Chen, Y. Jiang, Z. Feng, D. Wang and X. Jiang, Lab Chip, 2023, 23, 4324–4333 Search PubMed
.
- T. Hamacher, J. T. Berendsen, J. E. van Dongen, R. M. van der Hee, J. Cornelissen, M. L. Broekhuijse and L. I. Segerink, Lab Chip, 2021, 21, 4477–4486 Search PubMed
.
- S. S. Kuntaegowdanahalli, A. A. S. Bhagat, G. Kumar and I. Papautsky, Lab Chip, 2009, 9, 2973–2980 Search PubMed
.
- D. Di Carlo, Lab Chip, 2009, 9, 3038–3046 Search PubMed
.
- B. Zhang, P. Leishangthem, Y. Ding and X. Xu, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2100145118 Search PubMed
.
- B. R. Mutlu, J. F. Edd and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7682–7687 Search PubMed
.
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CrossRef
.
- R. Yuan, J. Lee, H.-W. Su, E. Levy, T. Khudiyev, J. Voldman and Y. Fink, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10830–E10838 CrossRef
.
- W. Xi, F. Kong, J. C. Yeo, L. Yu, S. Sonam, M. Dao, X. Gong and C. T. Lim, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10590–10595 CrossRef PubMed
.
- S. Grebenyuk, A. R. Abdel Fattah, M. Kumar, B. Toprakhisar, G. Rustandi, A. Vananroye, I. Salmon, C. Verfaillie, M. Grillo and A. Ranga, Nat. Commun., 2023, 14, 193 CrossRef PubMed
.
- B. Çetin and D. Li, Electrophoresis, 2011, 32, 2410–2427 CrossRef PubMed
.
- J. Voldman, Annu. Rev. Biomed. Eng., 2006, 8, 425–454 CrossRef PubMed
.
- A. Barik, Y. Zhang, R. Grassi, B. P. Nadappuram, J. B. Edel, T. Low, S. J. Koester and S.-H. Oh, Nat. Commun., 2017, 8, 1867 Search PubMed
.
- M. Li and R. K. Anand, J. Am. Chem. Soc., 2017, 139, 8950–8959 Search PubMed
.
- S.-I. Han, S.-M. Lee, Y.-D. Joo and K.-H. Han, Lab Chip, 2011, 11, 3864–3872 Search PubMed
.
- E. Iswardy, T.-C. Tsai, I.-F. Cheng, T.-C. Ho, G. C. Perng and H.-C. Chang, Biosens. Bioelectron., 2017, 95, 174–180 CrossRef PubMed
.
- J. M. Lewis, A. D. Vyas, Y. Qiu, K. S. Messer, R. White and M. J. Heller, ACS Nano, 2018, 12, 3311–3320 Search PubMed
.
- L. D'Amico, N. Ajami, J. Adachi, P. Gascoyne and J. Petrosino, Lab Chip, 2017, 17, 1340–1348 Search PubMed
.
- S.-H. Jung, C. Chen, S.-H. Cha, B. Yeom, J. H. Bahng, S. Srivastava, J. Zhu, M. Yang, S. Liu and N. A. Kotov, J. Am. Chem. Soc., 2011, 133, 10688–10691 Search PubMed
.
- K. Zhao, Larasati, B. P. Duncker and D. Li, Anal. Chem., 2019, 91, 6304–6314 CrossRef PubMed
.
- D. Kim, M. Sonker and A. Ros, Anal. Chem., 2018, 91, 277–295 CrossRef PubMed
.
- E.-S. Yu, H. Lee, S.-M. Lee, J. Kim, T. Kim, J. Lee, C. Kim, M. Seo, J. H. Kim and Y. T. Byun, Nat. Commun., 2020, 11, 2804 CrossRef PubMed
.
- K. Khoshmanesh, S. Nahavandi, S. Baratchi, A. Mitchell and K. Kalantar-zadeh, Biosens. Bioelectron., 2011, 26, 1800–1814 CrossRef PubMed
.
- J. Zhou, Y. Tao, R. Xue and Y. Ren, Adv. Mater., 2023, 35, 2207093 CrossRef
.
- Y. C. Kung, K. W. Huang, W. Chong and P. Y. Chiou, Small, 2016, 12, 4343–4348 CrossRef PubMed
.
- M. Radisic, H. Park, H. Shing, T. Consi, F. J. Schoen, R. Langer, L. E. Freed and G. Vunjak-Novakovic, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 18129–18134 Search PubMed
.
- T. Taghian, D. Narmoneva and A. Kogan, J. R. Soc. Interface, 2015, 12, 20150153 CrossRef PubMed
.
- A. LaLonde, M. F. Romero-Creel and B. H. Lapizco-Encinas, Electrophoresis, 2015, 36, 1479–1484 CrossRef PubMed
.
- J. Zhang, S. Yan, D. Yuan, G. Alici, N.-T. Nguyen, M. Ebrahimi Warkiani and W. Li, Lab Chip, 2016, 16, 10–34 Search PubMed
.
- J. Zhang, S. Yan, G. Alici, N.-T. Nguyen, D. Di Carlo and W. Li, RSC Adv., 2014, 4, 62076–62085 Search PubMed
.
- J. Zhang, D. Yuan, Q. Zhao, S. Yan, S.-Y. Tang, S. H. Tan, J. Guo, H. Xia, N.-T. Nguyen and W. Li, Sens. Actuators, B, 2018, 267, 14–25 Search PubMed
.
- M. Khan and X. Chen, Electrophoresis, 2022, 43, 879–891 Search PubMed
.
- H. Cha, H. Fallahi, Y. Dai, D. Yuan, H. An, N.-T. Nguyen and J. Zhang, Lab Chip, 2021, 22, 423–444 Search PubMed
.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 Search PubMed
.
- A. J. Chung, D. R. Gossett and D. Di Carlo, Small, 2013, 9, 685–690 CrossRef PubMed
.
- J. Zhang, S. Yan, W. Li, G. Alici and N.-T. Nguyen, RSC Adv., 2014, 4, 33149–33159 RSC
.
- N. Xiang, H. Yi, K. Chen, D. Sun, D. Jiang, Q. Dai and Z. Ni, Biomicrofluidics, 2013, 7, 044116 CrossRef PubMed
.
- H. Cha, H. Fallahi, Y. Dai, S. Yadav, S. Hettiarachchi, A. McNamee, H. An, N. Xiang, N.-T. Nguyen and J. Zhang, Lab Chip, 2022, 22, 2789–2800 Search PubMed
.
- I. Tzani, M. Castro-Rivadeneyra, P. Kelly, L. Strasser, L. Zhang, M. Clynes, B. L. Karger, N. Barron, J. Bones and C. Clarke, Nat. Commun., 2024, 15, 8605 CrossRef PubMed
.
- K. F. Hoettges, E. A. Henslee, R. M. Torcal Serrano, R. I. Jabr, R. G. Abdallat, A. D. Beale, A. Waheed, P. Camelliti, C. H. Fry and D. R. Van Der Veen, Sci. Rep., 2019, 9, 19153 Search PubMed
.
- J. Zhang, S. Yan, R. Sluyter, W. Li, G. Alici and N.-T. Nguyen, Sci. Rep., 2014, 4, 4527 CrossRef PubMed
.
- M. G. Lee, S. Choi and J.-K. Park, J. Chromatogr. A, 2011, 1218, 4138–4143 Search PubMed
.
- N. Xiang and Z. Ni, Lab Chip, 2022, 22, 4792–4804 Search PubMed
.
- S. Shim, K. Stemke-Hale, J. Noshari, F. F. Becker and P. R. Gascoyne, Biomicrofluidics, 2013, 7, 011808 Search PubMed
.
- H.-W. Su, J. L. Prieto and J. Voldman, Lab Chip, 2013, 13, 4109–4117 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc01037j |
| This journal is © The Royal Society of Chemistry 2025 |





