Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A review of microfluidic approaches for carbon capture and storage research
Abhishek Ratanparaa,
Yaofa Lib and
Myeongsub Kim *a
*a
aDepartment of Ocean and Mechanical Engineering, Florida Atlantic University, 777 Glades Road, Boca Raton, FL 33431, USA. E-mail: kimm@fau.edu
bMechanical Engineering Department, University of California, Riverside, 900 University Ave., Riverside, CA 92521, USA
First published on 30th April 2025
Abstract
The reliance on fossil fuels for the increasing global energy demand necessitates the advancement of carbon capture and storage technologies to mitigate anthropogenic CO2 emissions. However, conventional experimental platforms have reached their practical limitations, stagnating further advancements in optimizing carbon capture and storage (CCS) processes. Microfluidic technologies have emerged as promising tools for investigating and optimizing CCS processes at the microscale, offering precise control over gas–liquid interactions, reaction kinetics, and multiphase flow dynamics, which would be very challenging with conventional macroscale platforms. This review uniquely consolidates carbon capture and storage advancements, providing a structured approach that starts from fundamental mechanisms and systematically progresses to advanced microfluidic-assisted CCS strategies. Unlike prior reports, this review demonstrates how microfluidics complements conventional macroscale approaches and outperforms in certain aspects for studying CO2 capture and storage through specific experimental examples. The carbon capture section explores microfluidic approaches for physical absorption, chemical absorption, and adsorption, highlighting their advantages over conventional methods. The discussion extends to key mass transfer models, microchannel geometries, and flow regimes that dictate CO2 dissolution rates and interfacial transport phenomena. The carbon storage section examines microfluidic investigations into carbon mineralization and geological sequestration, providing insights into pore-scale trapping mechanisms, mineralization kinetics, and enhanced storage efficiency. The integration of real-time analytical techniques has further facilitated high-resolution quantification of CO2 transport and reaction dynamics. Despite significant progress, challenges remain in scaling microfluidic findings to field applications, accurately mimicking reservoir conditions, and developing reactive microfluidic platforms for in situ mineralization studies. This review aims to show the pivotal role of microfluidics in accelerating CCS innovation.
1. Introduction
Addressing global warming is among the most critical challenges faced by the scientific community today. With technological advancements driving a steady increase in global energy demand, projected to rise by 28% by 2040, fossil fuels are expected to remain a primary energy source for the foreseeable future.1 This reliance on fossil fuels results in the emission of substantial greenhouse gases, particularly carbon dioxide (CO2), which intensifies climate change by contributing to severe environmental consequences such as rising sea levels and increasingly extreme weather events. According to the 2022 International Energy Agency (IEA) report, global anthropogenic CO2 emissions reached an alarming 36.8 gigatons (Gt), highlighting the urgent need for emission mitigation and carbon removal solutions.2In recent decades, researchers have increasingly focused on preventing further CO2 emissions to the atmosphere. Carbon capture and storage (CCS) technologies have been developed to capture emissions from industries such as coal-based thermal power plants, cement production plants, and steel manufacturing plants, storing the captured CO2 in stable geological formations to prevent atmospheric release. CCS has made significant strides since the 1970s, with early efforts rooted in amine scrubbing – a chemical absorption process that remains foundational in industrial CO2 capture due to its high capture efficiency and reliability.3 Another landmark project, the Sleipner Project in Norway, initiated in 1996, demonstrated the feasibility of large-scale CO2 storage by successfully storing over 1 million tons of CO2 annually in an underground sandstone formation, setting a precedent for modern geological storage initiatives.4 Building on these foundational technologies, the field of CCS has been expanded to somewhat contemporary methods such as oxy-fuel combustion, membrane separation, metal–organic frameworks (MOFs), and the use of ionic liquids and nanofluids.5–9 Additionally, storage technologies of captured carbon, such as CO2-based enhanced oil recovery (EOR) and carbon storage in saline aquifers, have parallelly been developed.10 EOR is a dual-purpose approach, where injected CO2 boosts oil production while facilitating long-term underground CO2 sequestration. Each technique offers unique advantages and challenges, but all share a common goal of reducing atmospheric CO2 levels. These methods have been comprehensively documented and are being improved constantly. Most researchers in these fields have raised concerns about some drawbacks despite their advancements.
In the field of carbon capture, most of the solvents or chemicals are corrosive, non-selective, and require large amounts of energy to regenerate the captured carbon.11 Conventional macroscale experimental methods in CCS research would be impractical in resolving these issues as they would require comprehensive parametric studies for characterization using an extensive number of resources and labor work. Additionally, the conventional macroscale experimental methods face challenging analytical issues like uncertainties in the characterization of the CO2 capture process due to the indistinct gas–liquid interface, inconvenient or impossible measurements of physical dissolution, and chemical reactions of CO2 in solvent due to complex kinetic and thermodynamic properties. Similarly, in the carbon storage field, the existing methods face the challenges of slow reaction kinetics in carbon mineralization, the uncertainty of long-term safe CO2 storage stability due to the risk of leakage, and huge capital and monitoring costs.12–14 Conventional research methods like core tests, field pilot studies, computation studies, and batch reactor experiments are not fully qualified to work on these challenges because these methods would require extensive parametric studies, substantial resources, and intensive labor for characterization. Additionally, they would face analytical difficulties in accurately monitoring the CO2 trapping mechanism due to complex multiphase flow dynamics, indistinct fluid–rock interactions, and the inability to capture real-time pore-scale dissolution and mineralization processes in geological formations. These limitations highlight the urgent need to adopt advanced technological research methods like microfluidics to overcome existing challenges and move towards a more sustainable and effective solution for carbon capture and storage.
Adopting microfluidic technology improves research efficiency in both carbon capture and storage. For carbon capture, microfluidics enables a well-defined gas–liquid interface at the microscale, allowing precise analysis of CO2 absorption and desorption.15 It facilitates rapid solvent screening and optimization with minimal material usage, significantly reducing time and resource requirements compared to conventional methods. For carbon storage, microfluidic platforms replicate a wide range of complex geological structures, enabling the study of key mechanisms such as mineralization, capillary trapping, and dissolution under controlled conditions. These systems provide real-time monitoring of multiphase flow and reactive transport, offering insights that are difficult to achieve with traditional experimental methods. Overall, microfluidics accelerates CCS research by enhancing control, significantly reducing time and cost, and improving experimental observation techniques. Acknowledging these advantages over conventional methods, researchers are increasingly shifting toward microfluidic platforms for CCS-based research.
This increasing interest in microfluidic-based CCS research is reflected in the growing number of publications over the past decade. According to our trend search from Scopus, the number of research articles on microfluidic approaches for CCS has steadily increased from 2017 to 2024, as shown in Fig. 1. This trend highlights the growing recognition of microfluidics as a valuable tool for advancing carbon capture and storage technologies. Given the growing amount of literature in this field, there is a need to consolidate this work and provide a comprehensive understanding of microfluidic contributions to CCS research. Several recent review articles have addressed various aspects of CCS technology-based microfluidic research. For example, Abolhasani et al. explored early applications of segmented flow microfluidics in CO2 dissolution studies, especially focused on chemical absorption processes, CO2 utilization in materials science, and supercritical CO2 as a solvent.16 Cheng et al. provided an in-depth review of microfluidic-based chemical absorption technology for CO2 capture, discussing mass transfer dynamics, gas–liquid flow patterns, and the optimization of absorber design for improved performance.17 Liu et al. highlighted the application of high-throughput droplet microfluidics in producing monodisperse microcapsules for carbon capture, focusing on fabrication techniques and the scalability of microfluidic approaches for large-scale CO2 mitigation.18 Pan et al. reviewed the advancement in micro and nano scale studies for CCS applications, summarizing the potential of in situ visualization and understanding of gas–liquid interactions in confined domains using microfluidics, which is crucial for optimizing CO2 capture and storage processes.19 While these reviews provide valuable insights into specific aspects of microfluidic technology, a well-balanced study consolidating the primary advancements is needed to present a comprehensive perspective on how microfluidic technology outperforms conventional methods across all key aspects of CCS research. This review aims to consolidate the overall microfluidic research in both fields of carbon capture and carbon storage research. Unlike prior studies that solely focused on solvent selection, gas–liquid interaction, microfluidic fabrication, flow dynamics, or comprehensive collection of experimental research on microfluidics, our review integrates these aspects with experimental examples, directly comparing microfluidic approaches to conventional macroscale platforms. By systematically evaluating the advantages of microfluidics, we provide a clear framework for its benefits over traditional methods. Additionally, we incorporate qualitative analyses of key studies demonstrating how advancements in solvent optimization, surface wettability manipulation, and real-time reaction monitoring have driven significant breakthroughs in CCS research. This work not only contextualizes existing research but also identifies emerging challenges for future innovations.
In this review, we have presented a structured approach, starting from the fundamental mechanism of CCS and progressing systematically to the advanced methodologies of microfluidic platform applications, which ensures an accessible resource to most of the researchers in these fields. We divide this review into two parts: microfluidics-assisted carbon capture and microfluidics-assisted carbon storage research. Section 2 discusses the mechanisms of carbon capture elucidated by microfluidic approaches. After introducing specific examples and strategies for capturing CO2, such as physical absorption, chemical absorption, and adsorption, the review transitions into detailed discussions of mass transport theories, channel designs, and measurement techniques that influence gas–liquid interaction efficiency. These subsections provide practical guidance for selecting appropriate theoretical models (e.g., Fickian diffusion, two-film theory) and interpreting experimental observations based on microchannel geometry and flow behavior. These insights not only clarify how microfluidics can be optimized for carbon capture but also serve as a bridge to section 3, where the same tools and principles are adapted to study CO2 behavior in porous media and geological environments. Section 3 focuses on carbon storage research using microfluidic platforms, covering different CO2 storage approaches like carbon mineralization, storage in saline aquifers, and enhanced oil recovery. In this section, we demonstrate how the core ideas developed in section 2, such as interfacial transport analysis, flow visualization techniques, and channel design, are extended to evaluate mineralization kinetics, pore-scale trapping, and flow behavior in realistic subsurface analogs. Furthermore, we review various microfluidic models used in these studies, along with their flow dynamics and measurement techniques. Lastly, we provide a comprehensive summary, highlighting challenges and future directions for microfluidic applications in CCS research.
2. Role of microfluidics in carbon capture
2.1. Carbon capture mechanisms
Many carbon separation methods include chemical absorption, physical absorption, adsorption, membrane separation, chemical-looping combustion, and biological and cryogenics.20 However, carbon capture mechanisms can be primarily categorized into three types: physical absorption, chemical absorption, and adsorption.21 Each operates on distinct principles to retain CO2 molecules in a capturing medium and has advantages and limitations. Advancing research in these mechanisms to address their limitations using macroscale platforms presents major challenges, such as high solvent consumption, inefficient control over mass transfer dynamics, and difficulty in precisely monitoring reaction kinetics. These constraints hinder the development of optimized or novel capture materials and techniques. Given these limitations, microfluidic technology has been increasingly adopted to advance carbon capture research. It offers several advantages, including precise control over fluid dynamics, high surface-area-to-volume ratios, well-defined gas–liquid interfaces for effective interaction studies, efficient material usage, and improved accessibility for analyzing reaction kinetics. To provide a strong foundation for understanding the role of microfluidics in carbon capture, it is essential to first discuss the primary CO2 capture mechanisms and their associated research limitations, as well as how microfluidic technology offers solutions to these challenges. This section presents a detailed explanation of these mechanisms and examines how conventional macroscale research is adapted to microfluidic-based approaches to overcome existing constraints.For example, Lefortier et al. conducted a study to screen the CO2 solubility and diffusivity in various ionic solvents such as poly(ethylene glycol)dimethyl ether (Depeg), 1-octanol, 1-methyl-2-pyrrolidinone (NMP), propylene carbonate (PC) and 1-methyl-3-butylimidazolium bis(trifluoromethylsulfonyl)imide.29 As shown in Fig. 2, they used a segmented flow-based microchannel with a T-junction to generate monodisperse CO2 bubbles in proposed solvents; they achieved rapid determination of CO2 solubility and diffusivity in each solvent. By adopting a microfluidic platform, they reduced the experimental time to 5 minutes per sample, which typically takes hours per solvent batch with macroscale platforms. Moreover, the microfluidic experimental measurements were found to be accurate compared with the literature values for pure solvents. This research demonstrates the superiority of microfluidic techniques with respect to time and volume requirements to conduct such studies.
 | ||
| Fig. 2 Schematic representation of the experimental setup with the field of view. In the field of view, the top lane shows bubble shrinkage due to absorption; the lower lanes show slow expansion due to pressure drop.29 | ||
With a similar microfluidic experimental technique, Voicu et al. explored a novel approach to CO2 capture using frustrated Lewis pairs (FLPs) within a microfluidic system.30 FLP theory involves a Lewis acid and a Lewis base that are too bulky to bond, so they stay “frustrated” and reactive. This reactivity allows them to capture and activate small molecules like CO2. In this microfluidic study, Voicu et al. demonstrated an efficient, low-energy CO2 capture by enhancing control over various reaction conditions. FLPs provide a promising route for CO2 capture from direct emissions and for direct air capture (DAC), where the CO2 concentrations are significantly low. To have an efficient FPL system for different acids and bases, the conventional methods would take days, along with bulk solvents, to produce a similar outcome.
Similarly, Zhao et al. conducted a rigorous experimental study on DES solvents with the enzyme carbonic anhydrase to increase the reaction rate (Fig. 3).31 They developed a microfluidic encapsulation platform to produce microcapsules of DES solvents with precisely controlled amounts of carbonic anhydrase. They found that the homogenous distribution of enzymes is key to gaining higher mass transfer efficacy with the DES solvent. Previously, similar attempts were made to use enzymes like carbonic anhydrase in DES using a macroscale. However, due to the heterogeneous distortion of enzymes in DES solvent in a macroscale setup, poor reaction rates for carbon capture were yielded. The microcapsules showed a 253-fold increase in CO2 absorption rate and a 74-fold increase in absorption capacity compared to neat DES.
 | ||
| Fig. 3 [Left] Schematic diagram of the flow-focusing microchannel, encapsulating DES and CA. IF – inner fluid; MF – middle fluid; OF – outer fluid. [Right] Effect of the flow rates on the microcapsule size and shell thickness in a 3D glass-capillary microfluidic device (in the graph, “d” as a function of QO/(QI + QM) – flow rate of inner fluid; QM – flow rate of middle fluid; QO – flow rate of outer fluid: figures (a)–(c) show actual experimental images of microcapsules with varying sizes and shell thicknesses).31 | ||
For instance, Hallenbeck et al. used a glass microfluidic reactor to compare the CO2 absorption capacity and absorption rate of several amino acid salt-based solvents like lysinate (LYS), glycinate (GLY), taurine (TAU), and prolinate (PRO). Using a tailored CO2 microbubble flow in solvent (Fig. 2), each solution was tested and compared with MEA for its CO2 absorption capacity. They found that potassium lysinate (LYS) exhibited a 50% higher CO2 absorption capacity than MEA, with a maximum CO2 loading of 1.32 mol CO2 per mol lysine versus 0.68 mol for MEA. Additionally, the time to reach 90% of maximum CO2 loading was the shortest for MEA (0.30 seconds), followed closely by GLY and PRO (0.34 seconds), while LYS took longer (0.47 seconds) but showed superior long-term absorption stability. With a simple microfluidic platform, this time-dependent study can be done, which otherwise would require a very complex macroscale setup to analyze such a minute time-dependent analysis.
Several studies have demonstrated the substantial benefits of microfluidic platforms for enhancing CO2 capture on adsorption-based mechanisms. Jin et al. conducted a study in which a microfluidic channel was used to synthesize N-doped microporous carbon spheres for CO2 capture.44 N-doping (nitrogen doping) introduces nitrogen atoms into the carbon framework, enhancing the material's CO2 capture capacity by creating basic sites that interact strongly with acidic CO2 molecules. This modification not only improves CO2 selectivity but also enhances the thermal stability of the adsorbent. To obtain it, they used nanodroplet templating, where tiny oil droplets acted as templates for creating a network of uniform micropores (Fig. 4). After synthesis and carbonization, the oil droplets were removed, leaving behind highly porous structures that increased the surface area and active sites for CO2 adsorption. In conventional macroscale systems, such as batch reactors, synthesizing porous carbon typically results in particles with inconsistent sizes and pore structures. This inconsistency reduces adsorption efficiency and leads to non-uniform gas–solid interactions. Furthermore, macroscale processes often require chemical activation and additional post-synthesis steps, which are time-consuming and environmentally harmful. In contrast, Jin et al. produced highly uniform carbon spheres with a Brunauer–Emmett–Teller (BET) surface area of 576 m2 g−1 and a microporous volume of 0.22 cm3 g−1, significantly improving the adsorption capacity from 0.42 mmol g−1 (untreated carbon spheres) to 1.20 mmol g−1, a nearly 200% improvement (Fig. 4).44 Additionally, the microfluidic process enabled continuous production with real-time control over the synthesis, making it more scalable and sustainable.
 | ||
| Fig. 4 [Left] Illustrative image of the fabrication of microporous carbon spheres. [Right] (a) Experimental images showing the controllable formation of emulsions at varying flow rates (values in each photo indicate the outer-to-inner phase ratio), (b) optical micrographs of solidified 2% FS with an inset displaying the particle size distribution, (c) formation of double emulsions, (d) optical micrographs of nanodroplets dispersed in water, and (e) optical micrographs of solidified 2% FS with 10% oil phase, with insets showing the corresponding particle size distributions. Scale bars: 1000 μm.44 | ||
Similarly, Xie et al. advanced the concept by incorporating a self-templated synthesis of N-doped hierarchical porous carbon spheres (in a self-templated synthesis, the precursor decomposes or transforms into carbon, creating multiple types of pores).45 This process used ZIF-8 (a type of metal–organic framework) as a sacrificial template, enabling in situ nitrogen doping during pyrolysis (Fig. 5). The resulting carbon spheres exhibited a hierarchical pore structure with a specific surface area (SBET) of 886.9 m2 g−1 and superior CO2 adsorption capacity of 1.29 mmol g−1 at 30 °C and 1 bar.45 Compared to macroscale synthesis, which often yields particles with a wide size distribution and high diffusion resistance, the microfluidic system ensured monodisperse particles with optimized mesoporous structures (Fig. 5), enhancing selective CO2 adsorption in mixed gas streams.
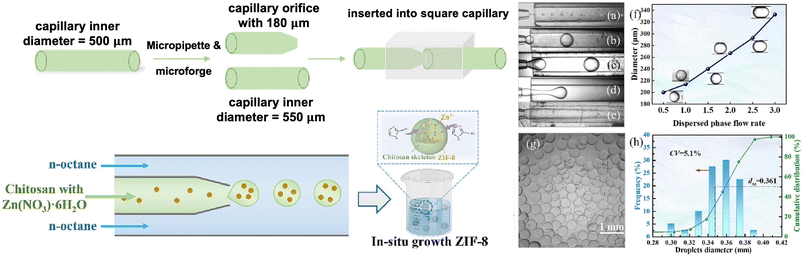 | ||
| Fig. 5 [Left] Fabrication of chitosan-based microparticles using a capillary microfluidic device and the formation of chitosan/ZIF-8 composites. [Right] The influence of different dispersed phase flow rates on droplet formation, with optical images shown for (a) 0.2 mL h−1, (b) 1 mL h−1, (c) 2 mL h−1, (d) 4 mL h−1, and (e) 6 mL h−1. (f) The effect of the continuous and dispersed phase flow rate ratio on droplet diameter (continuous phase flow rate = 10 mL h−1). (g) Optical micrograph and (h) particle size distribution of chitosan microdroplets.45 | ||
Another innovative example is the work published by Kurlov et al., who developed CaO-based CO2 sorbents with a hierarchical porous structure using microfluidic droplet templating.46 In calcium looping processes commonly used for industrial CO2 capture, the sintering and attrition of CaO particles reduce their long-term stability and adsorption capacity. By employing microfluidic emulsification to create monodisperse oil droplets as templates, they synthesized a sorbent with a stable hierarchical structure, which enhanced mass transfer and improved cyclic stability. The CO2 uptake capacity of the microfluidic-fabricated sorbent was 140% higher than that of conventional limestone-based sorbents, making it highly suitable for large-scale applications.46 Similarly, Yu et al. presented a novel in-capsule synthesis of MOFs for CO2 capture using a double-capillary microfluidic assembly (Fig. 6).47 In conventional systems, deploying MOFs as loose particles leads to operational challenges, such as high-pressure drops and particle aggregation. The microfluidic approach allowed MOFs to be synthesized directly inside gas-permeable microcapsules, preserving their high surface area while providing protection from moisture and preventing particle agglomeration. This configuration significantly improved CO2 adsorption efficiency and operational stability, addressing the limitations of traditional MOF-based systems.47
 | ||
| Fig. 6 [Top] Schematic representation of the microfluidic system used for the in situ encapsulated synthesis of MOFs, where the shell material TEGO Rad 2650 is structurally similar to TEGO Rad 2100 and TEGO Rad 2500. [Bottom left] Microscopy images of encapsulated HKUST-1 crystals: (a) microcapsules containing precursor solutions of copper(II) nitrate trihydrate (Cu(NO3)2·3H2O) and 1,3,5-benzenetricarboxylic acid (H3BTC) dissolved in N,N-dimethylformamide (DMF) before heating, (b) sequential stages of HKUST-1 crystal formation during the in situ thermal reaction within the microcapsules over a reaction time of 1–15 minutes, and (c) HKUST-1 crystals synthesized via the conventional solvothermal method in bulk solution for comparison. [Bottom right] three-dimensional X-ray microtomography of encapsulated HKUST-1 within a glass tube: (a) microcapsules containing HKUST-1 and residual DMF solvent, and (b) dried microcapsules after solvent removal.47 | ||
| Mechanism | Microfluidic strategy | Microfluidic purpose and outcomes | Functional category | |
|---|---|---|---|---|
| Physical absorption | Segmented flow microchannel (T-junction) with CO2 bubbles in ILs and PC | CO2 solubility and diffusivity determined in less than 5 min per sample. The measurements were validated against literature values. CO2 loading findings were from 0.8–1.3 mmol g−1 in different solutions | Mass transfer enhancement and solvent selection | 29 |
| Bubble dissolution analysis in oil-filled microchannels | Dissolution patterns were used to derive interfacial mass transfer rates. The modeled interfacial transfer rate was approximately 10−4 m s−1 | 48 | ||
| Reservoir-specific diffusivity studies using microfluidic chips | CO2 diffusivity was quantified in brine and oil systems using in situ visualization. Diffusivity values were found to be 1.5 × 10−9 m2 s−1 in brine and 3.2 × 10−10 m2 s−1 in oil | 49 | ||
| Microbubble visualization in DES and PEGDME solvents | KLa values were compared across five solvents. Deep eutectic solvents (DES) showed a 1.5× improvement in transfer rate. The KLa of the DES system was 0.0031 s−1, with visualization completed in 90 seconds | 24 | ||
| Model-based IL flow simulation in pressure-tunable microchannels | A trade-off between CO2 solubility and energy efficiency was analyzed under pre-combustion conditions. The estimated energy cost for absorption using pressurized ionic liquids was 32 MJ kg−1 of CO2 | 25 | ||
| Chemical absorption | Microencapsulation of carbonic anhydrase in DES via glass microfluidics | Microfluidic encapsulation of carbonic anhydrase in DES led to a 253-fold increase in CO2 absorption rate. The enzyme was uniformly distributed, and the CO2 loading reached 2.8 mmol g−1 | Reaction kinetics of solvent and CO2 | 31 |
| Frustrated Lewis pairs tested under segmented microdroplet flow | Low-energy CO2 activation was demonstrated at approximately 0.1 bar using frustrated Lewis pairs under segmented droplet flow in a microfluidic setup | 30 | ||
| SpectIR-fluidic reactor for FTIR absorption tracking | Real-time monitoring of CO2 bond conversion kinetics was performed using FTIR within a microfluidic reactor. Bond changes were observed within 5 seconds, and the reaction yield was tracked spectroscopically | 38 | ||
| Functionalized ILs in microchannels with CO2 gas flow | Thermodynamic performance of functionalized ionic liquids was evaluated in microchannels. The reaction enthalpy was −35 kJ mol−1, and the viscosity was measured at 79 cP at 25 °C | 35 | ||
| SH-amine testing under microfluidic flow | Sterically hindered amines achieved faster CO2 uptake than MEA, completing absorption within 3 seconds. The solvents also showed reduced degradation and reached a CO2 capture of 1.5 mol mol−1 | 36 | ||
| Real-time spectroscopy in glass–PDMS reactor | Absorption curves for test solvents were plotted in under 10 seconds using real-time spectroscopy. The feedback loop resolved dynamic changes with an accuracy of ±3% | 37 | ||
| Adsorption | Nanodroplet-templated synthesis of N-doped microporous carbon | N-doped carbon produced via droplet templating achieved a BET surface area of 576 m2 g−1. CO2 uptake increased threefold compared to unmodified carbon, reaching 1.2 mmol g−1 | Material synthesis with pore/morphology control | 44 |
| Self-templated porous carbon spheres in flow-focusing chip | Self-templated porous carbon spheres generated in a flow-focusing device achieved a surface area of 886.9 m2 g−1. CO2 adsorption was measured at 1.29 mmol g−1 at 30 °C | 45 | ||
| Hierarchical CaO sorbents via monodisperse emulsion templates | Hierarchical CaO sorbents created using monodisperse emulsion templates showed a 140% increase in CO2 capacity compared to conventional CaO and remained stable for 25 operational cycles | 46 | ||
| In-capsule MOF synthesis via a capillary double emulsion device | MOFs synthesized within capillary double-emulsion droplets retained 95% of their surface area and showed a twofold improvement in humidity resistance compared to bulk materials | 47 | ||
| MOF-coated fibers synthesized in microreactors | MOF-coated fibers fabricated in microreactors achieved a surface area of 1745 m2 g−1 and demonstrated CO2 uptake of 2.1 mmol g−1 at 298 K | 42 | ||
| Double-emulsion capsule with internal MOF synthesis | Microcapsules with internally synthesized MOFs retained 95% porosity after five humid cycles and exhibited CO2 uptake up to 1.9 mmol g−1 under ambient conditions | 47 |
2.2. Mass transfer models
With an understanding of various carbon capture methods and the adoption of microfluidics for research advancement, we now discuss specific aspects of the microfluidic approach, such as mass transfer models to analyze CO2 dissolution, flow patterns, microfluidic channel design, and measurement techniques for CO2 dissolution. Selecting the appropriate transport model is critical for accurately quantifying dissolution rates, as different models account for varying transport mechanisms, including diffusion, convection, and interfacial dynamics. Improper model selection can lead to significant deviations in mass transfer predictions, affecting the optimization of microfluidic devices for CO2 capture. Various models have been developed to describe CO2 transport in microfluidic systems, each addressing different aspects of mass transfer varying from a basic diffusion process to complex interactions at the gas–liquid interface. This section presents key models used in CO2 microfluidic capture, along with experimental research examples demonstrating their applications. This section aims to help researchers determine the most suitable model for their specific system parameters and experimental conditions in the microfluidic approach.
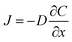 | (1) |
 | (2) |
 | ||
| Fig. 7 [Left] Visualization and analysis of CO2 diffusion into water. Time-lapse images showing fluorescence quenching as CO2 diffuses into water, leading to solution acidification. Diffusion coefficients were obtained at a pressure of 5 bar. A diffusion coefficient is determined for each frame captured during the experiment, with each data point spaced 2 s apart. The error bars account for uncertainties in measurements (e.g., initial pH, temperature) and their effect on the calculated diffusion coefficient (D). [Right] The overall diffusion coefficient at this pressure is determined as D = 1.74 × 10−9 m2 s−1, obtained by averaging individual D values.49 | ||
 | ||
| Fig. 8 [Left] (a) Schematic representation and analysis of CO2 bubble dynamics in microfluidic systems with volume reconstruction where (i) and (ii) represent two random sections illustrating the roundness of the reconstructed CO2 bubble, (b) comparison between the local gas flow rate, determined from in situ measurements, and the inlet gas flow rate, showing discrepancies at high viscosities where small flow rates are calibrated using the local measurement. (c) The ratio of rear cap curvature to front cap curvature as a function of the capillary number, highlighting the transition from capillary-dominated to viscous-dominated regimes, is modeled by κR/κF = (1 + Ca/Cac)−1 with Cac = 5 × 10−2. [Right] Representation of the diffusive mass flux of CO2 bubbles in silicone oils under varying viscosity and pressure conditions. (a) Temporal evolution of the diffusive mass flow rate and interfacial area for a viscosity of 103 cS, showing an initial linear phase followed by a drop as saturation occurs. (b) Mass diffusion flux at different viscosities, demonstrating that higher viscosity fluids exhibit a more significant decline in flux due to increased diffusion resistance. (c) Early mass flux J0 as a function of gas pressure, following the relation J0 = kD(PG − Patm), indicating that higher pressures enhance CO2 transfer rates. (d) Dissolution coefficient kD as a function of oil molecular weight, showing an inverse relationship modeled by kD = 3 × 104 M−1, where higher molecular weight oils impose greater resistance to CO2 diffusion.48 | ||
 | (3) |
Frost et al. chose the convective diffusion model to analyze a bilayer microfluidic device with a porous membrane because of its ability to capture molecular transport influenced by simultaneous flow (Fig. 9).52 This model allowed for a detailed analysis of how the flow rate and membrane porosity affected concentration distributions. The study found that at higher flow rates, convection dominated, minimizing diffusion effects, while at lower flow rates, diffusion significantly influenced transport. This balance was critical for optimizing CO2 permeation efficiency in diffusion–convective environments.52
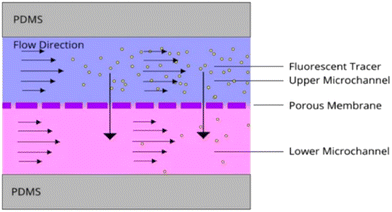 | ||
| Fig. 9 Schematic representation of convection–diffusion mass transport in a microfluidic device. Molecules from the high-concentration stream (purple) diffuse into the low-concentration stream (pink) while convecting downstream, illustrating the simultaneous influence of advection and diffusion on mass transfer within the microchannel.52 | ||
| NA = kG(CA,G − CA,i) = kL(CA,i − CA,L) | (4) |
 | (5) |
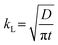 | (6) |
 | ||
| Fig. 11 [Left] Experimental image of gas–liquid flow at different flow rates (from a to i). [Right] The calculated volumetric mass transfer coefficient (kLa) for different flow rates.58 | ||
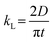 | (7) |
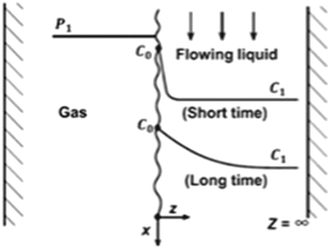 | ||
| Fig. 12 Illustrative image showing gas–liquid interaction representing penetration mass transfer theory.62 | ||
2.3. Microchannel geometries and flow patterns
Similar to the transport model, selecting the appropriate microchannel geometry and flow pattern is essential for ensuring flow stability and reproducibility in microfluidic CO2 capture studies. The microchannel geometry directly impacts the mass transfer efficiency, gas–liquid interfacial area, and overall experimental precision. Improper design selection can lead to significant errors and poor reproducibility. This subsection aims to provide the reviewers with overall knowledge of different geometries and flow patterns, highlighting their impact on experimental outcomes and helping researchers select optimal designs for improved performance.Common cross-sectional shapes of microchannels include rectangular, circular, square, triangular, trapezoidal, and elliptical (Fig. 13). Each geometry offers distinct advantages, influencing the liquid film thickness, bubble formation, and overall gas–liquid interaction. Among these, rectangular channels are the most widely used due to their high surface-to-volume ratio and the ability to generate thin, stable liquid films that improve mass transfer. Al-Rawashdeh et al. showed that rectangular channels produced a spatially uniform liquid film caused by the corner capillary effect, which stabilized the flow pattern and enhanced Taylor bubble formation, ensuring uniform CO2 absorption.63 Quantitative studies further highlight the role of microchannel dimensions in optimizing performance. Reducing the hydraulic diameter (dh) from 762 μm to 254 μm resulted in a 2.6-times increase in the volumetric mass transfer coefficient (kLa), confirming that smaller channels significantly boost mass transfer efficiency.64
 | ||
| Fig. 13 Illustration of different cross sections of microchannels, different junctions in microchannel geometries, and their wireframe views. | ||
In contrast, circular channels are preferred for Taylor flow systems, offering symmetrical flow profiles and consistent bubble generation. Their design reduces pressure drops and ensures steady flow, making them ideal for gas–liquid contact applications. However, circular channels often require specialized molds or capillary assembly for fabrication, which can be more challenging than rectangular channels. Square cross-sections balance rectangular and circular geometries, ensuring moderate mass transfer efficiency and flow stability.65 Triangular and trapezoidal channels are less common but serve specific purposes where higher velocity gradients and enhanced mixing are required, particularly in low Reynolds number flows.66 Trapezoidal cross-sections provide smoother flow transitions, reducing flow disturbances and improving selectivity in chemical absorption processes. Meanwhile, elliptical channels offer reduced shear stress and smooth flow profiles, making them suitable for gentle flow applications, such as enzymatic CO2 conversion or biological reactions. The hydraulic diameter (dh) of microchannels used for CO2 absorption generally ranges between 200 μm and 1000 μm, while the channel length (Lc) in laboratory experiments is usually limited to 400 mm for easier visualization and flow control.17 Channel size directly affects energy dissipation and mass transfer, with smaller channels promoting slug flow patterns in broader gas velocity ranges and significantly enhancing mass transfer performance.67–69
In addition to the channel cross-section, the junction types and their configurations significantly affect gas–liquid interaction and bubble formation (Fig. 13). Common microfluidic CO2 capture system junctions include T-junctions, Y-junctions, and cross-junctions. Among these, T-junctions are the most frequently used due to their reliable blocking–squeezing mechanism, which generates stable Taylor bubbles at low liquid flow rates.70,71 This mechanism ensures consistent bubble formation and improved mass transfer performance. Tan et al. demonstrated that T-junctions achieve a superior mass transfer rate due to comparatively high shear forces. It was found that the slug formation stage was responsible for 30–40% of the total mass transfer.72 Y-junctions are preferred for their smoother bubble generation, particularly at higher flow rates, while cross-junctions facilitate intensive mixing between gas and liquid phases but are associated with higher pressure drops.73,74
Flow patterns in microchannels significantly affect the mass transfer dynamics and efficiency of CO2 absorption. These patterns depend on the gas and liquid flow rates, channel geometry, and physical properties of the fluids (Fig. 14). The most common flow patterns observed in gas–liquid systems are bubble flow, slug (Taylor) flow, annular flow, stratified flow, and churn flow, each with distinct characteristics. In bubble flow, small, dispersed gas bubbles are randomly distributed within a continuous liquid phase.75 Typically, the bubble shape is spherical in bubble flow, whereas slug flow, also known as Taylor flow, consists of elongated bubbles (plugs or slugs) with a comparable diameter to the channel or tube in the liquid phase.76 This flow type is the most desirable for CO2 absorption experiments due to its high mass transfer efficiency. While bubble flow has a greater surface area-to-volume ratio, which may intuitively suggest a higher mass transfer, the stagnate layer surrounded by the bubble only limits the diffusion mass transfer, whereas, in Tylor flow, the thin liquid layer between gas and surface walls provides faster diffusion rate by preventing any stagnate layer buildup. Studies have shown that slug flow provides up to 50% higher mass transfer rates than bubble flow, particularly in rectangular channels where uniform bubble size and stability are maintained.77,78 Bubble flow is observed at low gas flow rates and is characterized by dispersed bubbles in the continuous liquid phase. It is commonly used in systems that require gentle flow conditions to prevent shear-sensitive reactions. Annular flow occurs at high gas flow rates, where the gas forms a core surrounded by a thin liquid film along the channel walls. This pattern offers good gas–liquid contact but comes with increased pressure drop and reduced stability. Stratified flow, where gas and liquid form separate layers, is more common in horizontal large-diameter channels than in microchannels.79 Churn flow represents an unstable transition between slug and annular flow, with highly irregular gas–liquid interactions, making it less suitable for controlled CO2 capture processes. The choice of flow patterns directly impacts the volumetric mass transfer coefficient. These findings demonstrate the importance of optimizing channel size and flow pattern to maximize CO2 absorption efficiency. Additionally, spiral and serpentine channels have been known to intensify CO2 absorption by promoting radial mixing and extending the gas–liquid interface.80,81 These designs reduce residence time while maintaining high mass transfer coefficients, offering continuous and efficient CO2 absorption in high-throughput systems (Fig. 15).
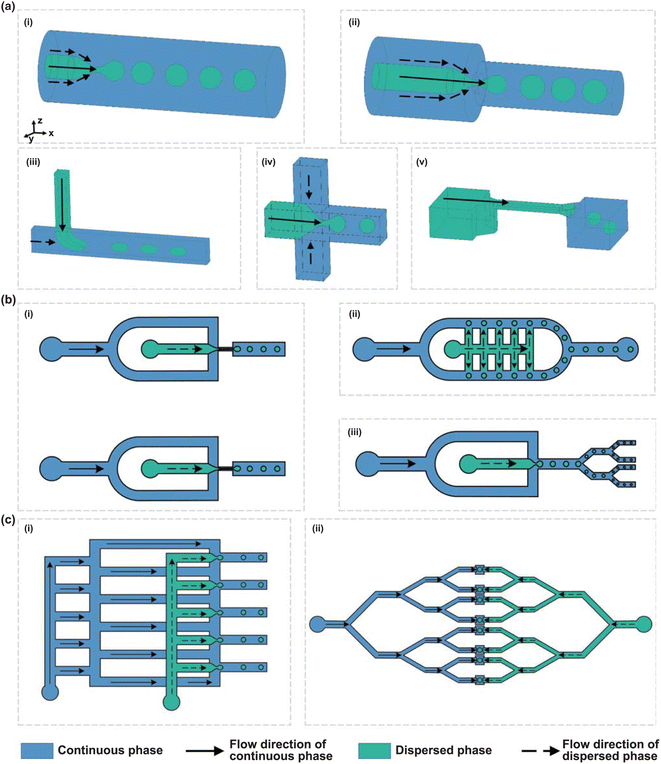 | ||
| Fig. 14 Schematic illustration of microchannel characteristics. (a) Flow behaviors in different droplet generators: (i) co-flow, (ii) flow-focusing, (iii) T-junction, (iv) cross-junction, and (v) step emulsification, demonstrating various methods for generating emulsions in microfluidic systems. (b) The scale-up strategies for microfluidic processes: (i) parallel numbering-up of both dispersed and continuous phase nozzles, (ii) parallel numbering-up of dispersed phase nozzles only, and (iii) splitting of emulsion droplets to achieve higher throughput. (c) The fluid distribution network in two common layouts: (i) ladder network and (ii) tree network, illustrating different methods for ensuring uniform flow distribution across multiple microchannels.18 | ||
 | ||
| Fig. 15 [Top] Schematic of the microfluidic approaches for evaluating CO2 absorption. The top panel illustrates two designs. (a) Microreactor operating under limited mixing conditions, along with sequential images showing changes in CO2 microbubble size. (b) A long serpentine microchannel under high mixing conditions, with images of CO2 microbubbles at two different locations. The scale bar represents 100 μm.81 [Bottom] Actual photograph of the spiral channel and meandering channel geometries.80 | ||
For large-scale CO2 capture, multi-channel integration and high-throughput systems are essential to achieve scalable performance. Conventional single-channel systems have limitations in throughput, but recent advancements in parallel microchannel reactors and tree-like manifolds have enabled high-throughput absorption while maintaining uniform flow.82 Li et al. developed a 16-parallel-channel reactor, which achieved volumetric mass transfer coefficients (kL) ranging from 1.59 to 90 s−1, ensuring stable slug flow across all channels (Fig. 16).83 Tree-like structures and fractal designs are commonly employed to reduce flow resistance and ensure uniform distribution across multiple channels, further enhancing performance in multi-channel systems.
 | ||
| Fig. 16 [Top left] Schematic of parallelization of a flow-focusing device. [Top right] Droplets formed in four integrated flow-focusing devices, demonstrating the simultaneous generation of emulsions in multiple channels.82 A channel consists of 16 flow-focusing junctions.83 [Bottom] A schematic of a microfluidic geometry where 128 cross junctions are integrated together and its magnified view.84 | ||
2.4. Measurement techniques of CO2 capture in microfluidics
Along with the mass transfer models, microfluidic channel geometry and flow pattern selection play a crucial role in microfluidic CO2 capture studies, and the ability to accurately measure CO2 dissolution and transport dynamics is equally essential. Accurate and reliable measurement of CO2 capture efficiency in microfluidic systems is critical for optimizing system performance, validating mass transfer models, and scaling for real-world applications. Advanced measurement techniques combined with microfluidic platforms enable real-time monitoring of key parameters such as localized gas concentration, pH profiles across the interface, and ionic composition, which are often impractical or highly challenging in conventional systems. This section outlines key methods for quantifying CO2 capture in microfluidics, including optical methods, electrochemical sensors, gas chromatography, and Raman spectroscopy, along with details on accuracy, time scales, and applications.Optical methods are widely used in microfluidic systems due to their non-invasive nature and ability to provide real-time measurements of CO2 concentration and dissolution behavior. Among the optical techniques, brightfield microscopy and fluorescence microscopy are the most used for visualizing gas–liquid interfaces and tracking CO2 dissolution in microchannels. Brightfield microscopy offers a simple and direct imaging approach, ideal for observing bubble dynamics and flow patterns. In contrast, fluorescence microscopy is used for more quantitative analysis, such as changes in pH, temperature, and phase concentration. A recent study by Mohaddes et al. developed a fluorescence-based microfluidic method for measuring the minimum miscibility pressure (MMP) of CO2 in crude oil (Fig. 17).85 This method leverages the inherent fluorescence of crude oils and achieves precise, operator-independent measurements. Compared to conventional techniques, such as the rising bubble apparatus, which can take days, this microfluidic method provides quantitative MMP values in under 30 minutes with an accuracy difference of less than 0.5 MPa. Such advancements highlight the potential of fluorescence-based approaches for rapid, real-time CO2 measurement in microfluidic CO2 capture systems, offering a significant improvement in both speed and accuracy over traditional methods.85
 | ||
| Fig. 17 Fluorescence-based microfluidic measurement of MMP for CO2 in crude oils. [Left] (a) Fluorescence images of CO2 bubbles at different pressures: below MMP (5.9 MPa), at MMP (6.1 MPa), and above MMP (6.2 MPa), showing the transition from distinct CO2 bubbles to complete mixing. (b) Correlation between microfluidic MMP measurements and rising bubble apparatus (RBA) MMP values showing strong agreement. (c) Temperature dependence of MMP for synthetic oil mixtures of varying API gravities, demonstrating a linear increase in MMP with temperature. [Right] Operator-independent fluorescence measurements showing intensity fluctuations at (a) 4.83 MPa and (b) 6.07 MPa. Red-circled data points correspond to selected images. (c) Average intensity within the detection region over time at various pressures. (d) Logarithmic variance of the intensity derivative reveals the steepest change.85 | ||
Infrared absorption spectroscopy is a popular approach for measuring CO2 concentration by detecting the absorption of infrared light at specific wavelengths. For instance, Tavernier et al. developed an inline microfluidic system for measuring CO2 concentration using infrared absorption at 4.24 μm (Fig. 18).86 The system operated under pressures ranging from 0 to 70 bars, offering precise real-time measurements, even in challenging environments such as oil fields.86
 | ||
| Fig. 18 [Left] Microfluidic gas–liquid phase separation for CO2 measurement. Schematic of the microchannel design, featuring deep and thin regions for controlled phase separation. [Right] Experimental images showing sequential air and water flow, demonstrating effective gas isolation for inline CO2 analysis with infrared absorption spectroscopy.86 | ||
Gas chromatography (GC) has been utilized in analyzing the composition of CO2 and its reaction by-products in microfluidic systems. While less suitable for real-time monitoring, it provides high-resolution and quantitative analysis of gas-phase products. Rudyk et al. used GC to characterize CO2 reduction products during EOR experiments, demonstrating its importance in identifying and quantifying multiple gas species.87
Raman spectroscopy is increasingly used for real-time monitoring of CO2 absorption and isotopic analysis. One significant application of Raman spectroscopy is in measuring δ13C values—a ratio representing the relative abundance of the heavier isotope 13C compared to 12C in CO2. This value is commonly used in geochemical studies to trace the source of CO2 or analyze carbon cycling processes. Li et al. used micro-laser Raman spectroscopy to quantitatively determine δ13C values in natural CO2 gas samples. The method showed relative errors ranging from 0.076% to 1.154%, with results that matched those from Isotope Ratio Mass Spectrometry (IRMS).88 Unlike IRMS, however, Raman spectroscopy offered faster results within minutes and required less sample preparation. In another study, Wells et al. used Raman spectroscopy to monitor CO2 hydrate formation in high-pressure microfluidic devices. Their findings revealed that hydrate conversion reached 47% within 1 hour, compared to days or weeks required for similar results in bulk systems.89 These analytical methods collectively contribute to advancing microfluidic CO2 capture research. Optical techniques provide rapid and non-invasive measurement capabilities; electrochemical sensors enable direct chemical monitoring, and gas chromatography is a reliable validation tool. Combining these approaches ensures a comprehensive evaluation of CO2 absorption processes, guiding the development of efficient carbon capture technologies.
3. Role of microfluidics in carbon storage
3.1. CO2 storage approaches
Successful carbon capture must be followed and combined with suitable carbon storage and/or sequestration technologies to prevent the captured CO2 from returning to the atmosphere. According to the definition by Scott et al., carbon sequestration generally refers to the permanent locking of carbon with a lifetime of greater than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years, whereas carbon storage often refers to the temporary containment of CO2 with a lifetime of 1000 years or less, with the later maintaining the possibility of re-accessing the stored CO2 for future utilization purposes.90,91 Nevertheless, the two terms, storage and sequestration, are frequently used interchangeably in the literature, and no distinction will be made between them in this review, as both timescales are hardly meaningful in lab-scale experiments using microfluidics.
000 years, whereas carbon storage often refers to the temporary containment of CO2 with a lifetime of 1000 years or less, with the later maintaining the possibility of re-accessing the stored CO2 for future utilization purposes.90,91 Nevertheless, the two terms, storage and sequestration, are frequently used interchangeably in the literature, and no distinction will be made between them in this review, as both timescales are hardly meaningful in lab-scale experiments using microfluidics.
The National Academies of Sciences, Engineering, and Medicine, in their report published in 2019, laid out six major technical approaches to CO2 removal and storage, including (i) coastal blue carbon, (ii) terrestrial carbon removal and sequestration, (iii) bioenergy with carbon capture and sequestration (BECCS), (iv) DAC, (v) carbon mineralization, and (vi) geologic CO2 sequestration.92 Coastal blue carbon aims to take advantage of improved land use and management practices that increase the carbon stored in living plants or sediments in mangroves, tidal marshlands, seagrass beds, and other tidal or salt-water wetlands, whereas terrestrial carbon removal and sequestration aims to enhance soil carbon storage through afforestation/reforestation, changes in forest management, or changes in agricultural practices. BECCS typically refers to the integration of trees and crops that extract CO2 from the atmosphere as they grow, the use of this biomass in power plants, and the application of carbon capture and sequestration via CO2 injection into geological formations. Similarly, DAC aims to capture CO2 from ambient air and concentrate it so that it can be injected into a storage reservoir. Finally, carbon mineralization aims to take the CO2 captured through BECCS or DAC and bond it with reactive minerals such as peridotite and basaltic lava for permanent sequestration, whereas geological sequestration looks to inject captured CO2 into geological formations such as saline aquifers. In addition to these six pathways, CO2 conversion technologies, such as electrochemical, photocatalytic, thermocatalytic, and biological processes, also contribute to carbon sequestration.93–95 These methods serve as post-capture pathways that transform CO2 into valuable products like fuels, chemicals, and solid materials. Although these pathways have been identified for carbon storage, most of them are merely combinations of carbon storage with various carbon capture technologies. For “pure” carbon storage, there are essentially only two approaches, namely carbon mineralization and geological sequestration, which, along with their overlap with microfluidics, will be our particular focus in this review.91 The readers are referred to the work by Kazemifar and the National Academies of Science, Engineering, and Medicine, and the review articles on CO2 conversion for more generic reviews of technologies for carbon sequestration, utilization, and their technological readiness.91,92,96,97
| CaSiO3 (wollastonite) + CO2 → CaCO3 | (8) |
| Mg2SiO4 (olivine) + 2CO2 → 2MgCO3 + SiO2 | (9) |
| CaMgSi2O6 (pyroxenes) + 2CO2 → CaMg(CO3)2 + 2SiO2 | (10) |
| Mg3Si2O5(OH)4 (serpentine polytypes) + 3CO2 → 3MgCO3 + 2SiO2 + 2H2O | (11) |
| Mg(OH)2 (brucite) + CO2 → 3MgCO3 + H2O | (12) |
Depending on the location where carbon mineralization is performed, two approaches have been proposed and exercised: ex situ carbon mineralization and in situ carbon mineralization. In the former, CO2-bearing air and surface waters are brought to react with crushed and/or ground mine tailings, alkaline industrial wastes, or sedimentary formations above the earth's surface, whereas in the latter, CO2-bearing fluids are injected and circulated through subsurface porosity in geological formations, and reactions occur in situ in the subsurface environment. While both methods potentially offer giant storage capacities at similar costs, in situ carbon mineralization has attracted more scientific interest, as it involves uncertain feedback between permeability, reactive surface area, and reaction rate, providing a fascinating topic for fundamental research.103
So far, most experiments investigating carbon mineralization processes are based on core samples.104–110 Microfluidic studies of mineralization are challenging because, in carbon mineralization, CO2 directly reacts with solids, meaning that the microfluidic devices would have to be fabricated or functionalized with reactive minerals, which causes significant challenges in fabrication and pore-scale quantification. Nevertheless, one recent study by Neil et al. attempted to identify key processes for carbon mineralization in fractured mafic and ultramafic rocks using microfluidic experiments. They employed a reactive microfluidic system to observe coupled reactions and flow in a simple fracture network containing both dead ends and a primary flow pathway for natural rock samples (Fig. 19).111 The microfluidic device allowed for the direct observation of transport and chemistry for realistic mineralization systems, comparison of reaction vs. transport, and measurement of how reaction affects flow and can potentially lead to clogging. As shown in Fig. 19, rectangular chips of crystalline gypsum were cut, and a comb-like flow path was defined by a laser cut. A Teflon sheet is sandwiched between acrylic sheets and held together by epoxy (Loctite metal/concrete). Their results depict a visible difference in mineralization within the main channel at different flow rates, with calcites more dominant at higher flow rates. Channel clogging was not observed, presumably because the reaction of gypsum to calcite and vaterite is a volume-reduction reaction. A noticeable difference was observed in the amount and type of precipitation found in the dead-end channels of the flow path, where the faster flow rate resulted in more mineralization within the dead ends and a greater abundance of calcite. The experiments, however, cannot reveal whether the calcite forms as a result of vaterite transformation or direct precipitation, calling for further studies in that regard.
 | ||
| Fig. 19 [Left] The schematic of carbon mineralization occurring in different zones of a fractured mafic/ultramafic rock. [Right] The schematic showing a microfluidic model system used to investigate carbon mineralization in a fracture.111 | ||
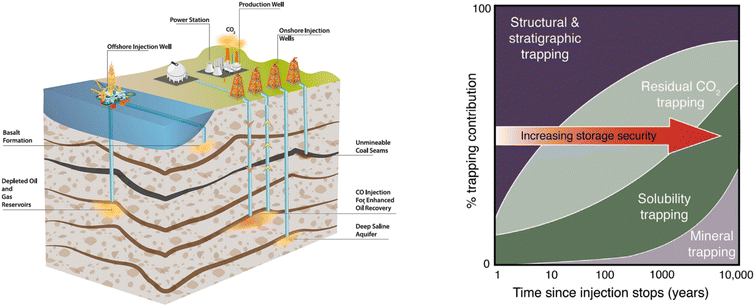 | ||
| Fig. 20 [Left] Options for storing CO2 in deep underground geological formations.112 [Right] A general representation of the evolution of trapping mechanisms over time.114 | ||
The safety and security of geological CO2 sequestration are enabled by effective trapping mechanisms, including structural trapping, residual trapping, solubility trapping, and mineral trapping. Under typical reservoir conditions, compressed and supercritical CO2 is less dense than the resident fluids and thus tends to rise through the formations driven by buoyancy forces. Therefore, as part of the requirement for site selection, a low-permeability rock, typically called a reservoir seal or a caprock, is needed to structurally contain the rising CO2. This mechanism is referred to as structural trapping, which plays a crucial role in the initial stage of CO2 injection, as shown in Fig. 20.122 However, structuring trapping doesn't eliminate the risk of CO2 leakage, as any pre-existing faults or cracks in the caprock can cause catastrophic leakage, rendering all the efforts in vain. Therefore, secondary trapping mechanisms such as residual trapping, solubility trapping, and mineral trapping have been explored. Residual trapping, also known as capillary trapping, relies on capillary pressure and surface tension between the injected CO2 and the resident brine to immobilize the CO2.123 Solubility trapping is due to the dissolution of CO2 into the pore brine, which results in a denser CO2-bearing brine fluid that tends to sink rather than rise. Mineral trapping occurs when dissolved CO2 reacts with minerals in the geologic formation, promoting precipitation of carbonate minerals.124 Fig. 20 shows the contribution of each trapping mechanism depending on the formation characteristics and injection stage.
Given the long-term implications of CO2 injections, developing a holistic understanding and predictive models capable of providing accurate and reliable predictions of large-scale CO2 migration through the reservoir is considered a prerequisite for site selections and post-injection operations. One big challenge in this regard is the extensive range of spatial (from km to sub-micrometer) and temporal scales (from milliseconds to years) involved in these geophysical and geochemical processes.122,125 Evidence shows that the nature of the large-scale mobility of the fluids (i.e., flow displacement patterns) is linked to pore-scale physics and interfacial instabilities. It is also increasingly accepted that developing subgrid-scale models capable of accurately representing pore-scale processes is critical for improving the accuracy of reservoir-scale simulations.126–128 In this regard, extensive microfluidic studies have been conducted to probe, observe, quantify, and understand various pore-scale mechanisms at the microscopic scale. These studies have been pivotal to advancing our understanding of multiphase flow in porous media, miscible and immiscible displacement processes, flow regimes, interfacial instabilities, Haines jumps, capillary pressure and hysteresis, and wettability effects.97,122–160 As mentioned previously, one significant advantage, among others, of microfluidics is the valuable optical access it offers, which allows for direct observation and quantification of pore-scale mechanisms enabled by advanced optical flow diagnostics such as epi-fluorescent microscopy, multi-color microscopy, high-speed imaging, and particle imaging velocimetry (PIV).129–133,136,138 Microfluidic experiments combined with those imaging techniques have characterized microscopic processes with great temporal and spatial resolutions, which would not have been possible in core sample experiments and field observations.161 These microfluidic studies and findings are reviewed in detail in section 3.3.
3.2. Microfluidic models for CO2 storage studies
A microfluidic porous model system, so-called micromodel, is typically defined as an artificial representation of a porous medium made of a transparent material. Such a device must: (i) bear a flow network, (ii) contain features of micrometers to sub-millimeters in size, and (iii) offer a certain level of optical access. The flow network consists of connected throats and pores through which fluids of one or more phases and/or components flow. Since the advent of microfluidic devices, arguably by Chatenever et al. and later by Lenormand et al., numerous micromodels have been developed and constructed to study the physical, chemical, and biological processes during carbon storage in porous media.162,163 This section provides a brief description of the different types of microfluidic devices used in carbon storage studies, with a focus on a few unconventional devices that have been reported just recently. For a comprehensive knowledge of micromodels and the relevant fabrication and imaging techniques, the readers are referred to several reviews by Karadimitriou et al., Gerami et al., and Jahanbakhsh et al.132,133,164 This review is to update and complement them from a microfluidics perspective.Silicon is another common material used to fabricate micromodels. As silicon is not transparent in the visible spectrum, an etched silicon wafer that carries the flow network is usually anodically bonded with a glass wafer, through which the internal flow can be observed optically.143,146,166,167 The etching of silicon using DRIE is highly directional, enabling close to 90° side walls in etched microchannels, which is crucial to producing 2D micromodels. Additionally, PDMS and PMMA have been extensively used to fabricate 2D micromodels for their ease of fabrication and cost-effectiveness, with a possible fabrication of 3D micromodels.168 However, PDMS and PMMA are mechanically weak compared to silicon and glass and incompatible with many chemicals and common organic solvents, rendering them unsuitable for high-pressure and high-temperature experiments.169,170 Other materials that have been successfully used to fabricate micromodels include UV-sensitive polymers and geomaterials such as calcite and rock slices.171–173 Several studies reported the fabrication and use of high-pressure micromodels, which allowed direct measurement of multiphase flow at reservoir-relevant pressures.174–176 The readers are referred to the review by Jahanbakhsh et al. (2020) for common materials as well as their advantages and disadvantages for micromodel fabrication.133
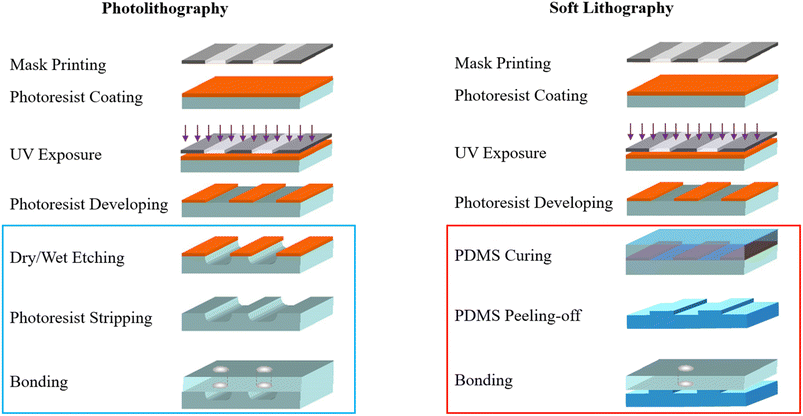
The fabrication method of a micromodel depends on the material selected. The two most common techniques include photolithography, which is used to process glass and silicon, and soft lithography, which is used to process PDMS and many other polymers. These methods are further complemented by different techniques, including micromachining, direct laser writing, mineral coating and deposition, and, more recently, 3D printing, as summarized in Gerami et al. and Jahanbakhsh et al.132,133 As illustrated in Fig. 21, a standard photolithography process involves mask making, photoresist spin coating, UV exposing, and developing, which is followed by etching, cleaning, and bonding. On the other hand, soft lithography, which is also initiated with mask-making and photoresist processing, finishes with PDMS molding.
 | ||
| Fig. 22 [Left] Fabrication steps of a 2.5D micromodel.165 [Right] Fabrication steps of a dual-porosity dual-depth micromodel.179 | ||
While these non-reactive micromodels have been serving as excellent platforms to investigate physical processes, they are not suitable for real carbon storage studies where erosive reactions are expected. For such cases, it is critical to fabricate micromodels using chemically reactive materials that are geologically representative of the subsurface environment. Several studies have explored “bottom-up” or “top-down” approaches to creating micromodels with reactive minerals such as calcite.171,172,180,181 Bottom-up approaches have grown reactive minerals (e.g., CaCO3) in situ within a traditional non-reactive micromodel (Fig. 23). Lee et al. developed a technique to selectively grow CaCO3 in a glass microchannel to form a porous section.182 The method is enabled by a UV-curable precursor solution, which creates preferential sites for CaCO3 growth. Upon delicate controls of the rinsing and precipitating flows, CaCO3 posts were successfully grown with pre-defined geometry, as shown in Fig. 23. This approach, while novel and precise, requires sophisticated control of various parameters and has a low throughput. Wang et al., Song et al., and Alzahid et al. took a similar approach by fabricating a standard micromodel in glass, silicon, and PDMS, respectively, and grew a thin layer or grains of CaCO3 crystals within.180,181,183 The approach is relatively straightforward to implement, but the major drawback is that the original surfaces (i.e., glass, silicon, or PDMS) of the micromodels are either not fully covered with CaCO3 or only by a thin layer of CaCO3 of O (1 μm) thick, making them unsuitable for studies of the dissolution rate or prolonged fluid–mineral interactions.
 | ||
| Fig. 23 A few representative micromodels that are chemically reactive. [Top left] Hybrid calcite–glass micromodel employing glass etching and in situ growth of calcium carbonate nanocrystals.183 [Middle left] A calcite micromodel fabricated using the site-selective in situ grown calcium carbonate approach.182 [Bottom left] A calcite micromodel created from a thin slice of calcite employing a laser cutter and wet etching.172 [Right] Pure calcite micromodel fabricated with photolithography and wet etching.184 | ||
Top-down strategies often employ traditional micro-milling and etching combined with laser cutting and patterning for better precision.172,184 The work by Song et al. is among the first studies to successfully fabricate a calcite-based micromodel using laser cutting and wet etching (Fig. 23).172 The process started with thin sectioning a large block of natural calcite crystal, following which a porous pattern was generated with the aid of a layer of beeswax and a laser cutter. The micromodel was completed by wet etching in hydrochloric acid, drilling, and bonding to another piece of glass. While this approach is innovative, its precision is relatively limited, with a minimum feature size of approximately 140 μm. Soulaine et al. and Rembert et al. adopted a similar idea of using a thin calcite slice that is pre-machined, and the thin calcite of a pre-defined shape was then directly embedded in a straight PDMS microchannel.185,186 However, the entire micromodel consisted of only one calcite post, hardly justified as a simulation of geologic media. To take one step further, Singh et al. embedded a real rock slice 500 μm thick into a PDMS channel.171 Thanks to the use of real rock slices, this micro model is faithfully representative of real geometry and geochemistry, thus being ideal when quantifying global quantities such as reaction rates and pressure drops. However, the use of such natural material makes each micromodel different and unique in terms of physical, geological, and chemical properties, hindering the necessary repeatability test at the pore scale as well as the possibility of parametric studies of pore flow using control variables. Moreover, the opaqueness of the rock sample renders the optical-based measurement challenging and sub-optimal. Most recently, Rahman et al. reported an innovative microfluidic approach that includes novel 2D reactive porous media and advanced pore flow diagnostics for studying pore-scale dissolution in porous media with unprecedented details (Fig. 23).184 The 2D micromodels were fabricated in calcite by combining photolithography and wet etching directly on the calcite sample, which facilitates unobstructed optical access to the pore flow, improving over previous methods. Additionally, by molding the microchannel with UV glue, the authors could eliminate unwanted reactions outside the porous section, thus achieving more controlled flow and reactions. Their results revealed the crucial roles of reactive transport and local concentration gradients in mineral dissolution in porous media and called for reconsidering many assumptions (Fig. 24).
 | ||
| Fig. 24 [Left] A schematic diagram illustrating the on-chip pressure sensor enabled by astigmatic particle tracking.187 [Middle] Micromodel with integrated fiber-optical pressure sensors.188 [Right] 3D sketch of the microfluidic chip with integrated SIP sensors and sample results of calcite dissolution.186 | ||
In addition, several recent developments attempted to integrate on-chip sensors into the porous section to enable in situ measurement of pore-scale quantities, such as pore pressure. Zarikos et al. reported the manufacturing procedure of a micromodel with integrated fiber optic pressure sensors with a circular measurement window of 260 μm in diameter, which measures pressure at the pore scale.188 The integrated micromodel was tested for both single- and two-phase flows, which led to valuable insights into the link between fast pressure changes and pore-scale events. More recently, Raventhiran et al. reported the design and fabrication of an on-chip sensor that quantifies pressure in microfluidic devices based on a novel technique called astigmatic particle tracking.187 With this technique, thin membranes that sense pressure variations in the fluid flow can be characterized conveniently by imaging the shapes of the particles embedded in the membranes. This innovative design only relies on the reflected light from the back of the microchannel, rendering the sensor separate and noninvasive to the flow of interest. This sensor was then applied to characterize the pressure drop in single-phase flows with an accuracy of ∼70 Pa. Rembert et al. developed a complex electrical conductivity acquisition using the spectral-induced polarization (SIP) method on a microfluidic chip equipped with electrodes. Enabled by high-speed microscopy, the micromodel provides direct observation and monitoring of microscopic reactive transport processes in porous media, highlighting the strong correlation between SIP response and dissolution.186
3.3. Flow dynamics in CO2 storage within microfluidics
Micromodels are well-suited to identify, observe, and characterize pore-scale processes when combined with advanced optical diagnostic techniques such as epi-fluorescence microscopy and micro-PIV.137,140,147,163,166,189–192 In fact, the application of micromodels and microfluidics has directly contributed to the discovery of numerous pore-scale mechanisms in carbon storage, which is the primary focus of this section. , where μn and μw are the dynamic viscosities of the nonwetting and wetting phases, respectively, and the capillary number
, where μn and μw are the dynamic viscosities of the nonwetting and wetting phases, respectively, and the capillary number  , where σ is the surface tension between the two fluids, θ is the contact angle between the fluids and the solid surfaces, and U is the bulk flow velocity. Here, U = Q/(Aϕ), where Q is the volumetric flow rate, A is the cross-sectional area of the flow domain, and ϕ is the porosity of the porous media. Depending on the balance of viscous and capillary forces, three distinct flow regimes exist: (1) stable displacement, (2) viscous fingering, and (3) capillary fingering. For the specific case of CO2 injection into deep saline aquifers, the flow falls into either the viscous fingering or capillary fingering regime, depending on the injection rate, the distance from the injection well, and the stage of the injection process (Fig. 25).
, where σ is the surface tension between the two fluids, θ is the contact angle between the fluids and the solid surfaces, and U is the bulk flow velocity. Here, U = Q/(Aϕ), where Q is the volumetric flow rate, A is the cross-sectional area of the flow domain, and ϕ is the porosity of the porous media. Depending on the balance of viscous and capillary forces, three distinct flow regimes exist: (1) stable displacement, (2) viscous fingering, and (3) capillary fingering. For the specific case of CO2 injection into deep saline aquifers, the flow falls into either the viscous fingering or capillary fingering regime, depending on the injection rate, the distance from the injection well, and the stage of the injection process (Fig. 25).
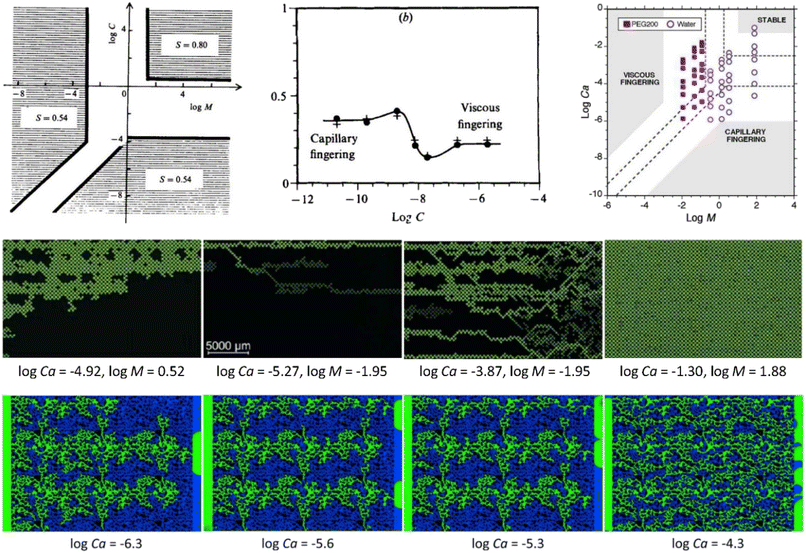 | ||
| Fig. 25 [Top left] The original phase diagram achieved by Lenormand et al., demonstrating the existence of capillary fingering, viscous fingering, stable displacement regimes, and the crossover between them.137 [Top middle] Plot of the invading fluid at breakthrough, showing a decrease of the nonwetting phase saturation at the crossover between capillary and viscous fingering.137 [Top right] An updated phase diagram obtained by Zhang et al.189 [Middle row] Representative displacement patterns for capillary fingering, crossover, viscous fingering, and stable displacement, respectively, captured in homogeneous micromodels.189 [Bottom row] Representative displacement patterns going from capillary fingering to crossover, and finally to viscous fingering as the capillary number increases in 2D heterogeneous micromodels.166 | ||
Lenormand et al. are among the first ones to investigate the flow regimes or so-called “phase diagram” of multiphase flow in porous media using a series of experiments in a homogeneous micromodel (i.e., featuring a regularly arranged porous structure) for a large parameter space, which essentially laid the foundation of the current understanding of pore-scale multiphase flow in porous media.137 Their experiments clearly showed the existence of the three basic domains (i.e., capillary fingering, viscous fingering, and stable displacement), as shown in Fig. 25, within which the patterns remain unchanged.137 Cottin et al. illustrated the role of the viscous forces in the invasion process and their competition with the capillary force heterogeneities.141 Later, Zhang et al. conducted displacement experiments in a water-wet pore network micromodel with microfabricated pore structures.189 Using seven wetting–non-wetting fluid pairs, they explored viscosity ratios (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M = −1.95 to 1.88) and capillary numbers (log
M = −1.95 to 1.88) and capillary numbers (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca = −5.88 to −1.02) across four orders of magnitude. In the experiments with PEG200 as the resident phase (M < 1), unstable displacement was observed by viscous fingering over all capillary numbers. For the experiments with water as the resident phase, unstable displacement occurred by capillary fingering at low capillary number, whereas crossover into stable displacement was observed for the fluid pairs with M > 1 when the viscous forces were increased by increasing the injection rate.137
Ca = −5.88 to −1.02) across four orders of magnitude. In the experiments with PEG200 as the resident phase (M < 1), unstable displacement was observed by viscous fingering over all capillary numbers. For the experiments with water as the resident phase, unstable displacement occurred by capillary fingering at low capillary number, whereas crossover into stable displacement was observed for the fluid pairs with M > 1 when the viscous forces were increased by increasing the injection rate.137
Wang et al. continued the work by Zhang et al. with two sets of experiments: discontinuous-rate injection, where the micromodel was saturated with water before each injection rate was imposed, and continuous-rate injection, where the rate was increased after quasi-steady conditions were reached.189,193 For the discontinuous-rate experiments, capillary fingering and viscous fingering are the dominant mechanisms for low (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ≤ −6.61) and high injection rates (log
Ca ≤ −6.61) and high injection rates (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ≥ −5.21), respectively. However, crossover from capillary to viscous fingering was observed for log
Ca ≥ −5.21), respectively. However, crossover from capillary to viscous fingering was observed for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ranging from −5.91 to −5.21, resulting in a large decrease in CO2 saturation, in agreement with the numerical predictions by Lenormand et al.137 Recently, Li et al. studied the pore-scale flow of CO2 and water in 2D heterogeneous porous micromodels over a Ca range of nearly three orders of magnitude.143 It was reported that under conditions relevant to CO2 sequestration, final CO2 saturation first decreases and then increases logarithmically with Ca within the capillary and viscous-fingering regimes, respectively, with a minimum occurring during the crossover regime. A recent study by Rabbani et al. demonstrated with microfluidic experiments that gradual and monotonic variation of pore sizes along the front path suppresses viscous fingering during immiscible displacement, which not only provides insights into ways for suppressing unwanted interfacial instabilities in porous media but also opens the door to a new way to understand flow instability in porous media.194
Ca ranging from −5.91 to −5.21, resulting in a large decrease in CO2 saturation, in agreement with the numerical predictions by Lenormand et al.137 Recently, Li et al. studied the pore-scale flow of CO2 and water in 2D heterogeneous porous micromodels over a Ca range of nearly three orders of magnitude.143 It was reported that under conditions relevant to CO2 sequestration, final CO2 saturation first decreases and then increases logarithmically with Ca within the capillary and viscous-fingering regimes, respectively, with a minimum occurring during the crossover regime. A recent study by Rabbani et al. demonstrated with microfluidic experiments that gradual and monotonic variation of pore sizes along the front path suppresses viscous fingering during immiscible displacement, which not only provides insights into ways for suppressing unwanted interfacial instabilities in porous media but also opens the door to a new way to understand flow instability in porous media.194
While a tentative consensus has been achieved regarding the flow regimes during drainage, conflicting findings have been reported in the literature regarding the relationship between the final saturation of the invading phase and Ca at different M. Some recent studies reported a monotonically increasing relation, whereas others indicated either a decreasing saturation or nonmonotonic behavior.135,141,189 For a fluid pair with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M = −4.7, Lenormand et al. found that the saturation decreases during the crossover, with two high-saturation plateaus for low and high Ca corresponding to capillary and viscous fingering, respectively.137 Wang et al. noted a substantial decrease in CO2 saturation between log
M = −4.7, Lenormand et al. found that the saturation decreases during the crossover, with two high-saturation plateaus for low and high Ca corresponding to capillary and viscous fingering, respectively.137 Wang et al. noted a substantial decrease in CO2 saturation between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca = −5.91 and −5.21, which is consistent with the findings of Lenormand et al.137,193 Chen et al. investigated the crossover during water displacing oil (log
Ca = −5.91 and −5.21, which is consistent with the findings of Lenormand et al.137,193 Chen et al. investigated the crossover during water displacing oil (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M = −3, −2.7, −2, −1.7) in a hydrophobic rough fracture for −7.07 ≤ log
M = −3, −2.7, −2, −1.7) in a hydrophobic rough fracture for −7.07 ≤ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ≤ −3.07 and observed that the saturation of the invading fluid first decreases and then increases with increasing Ca, with the minimum value occurring at log
Ca ≤ −3.07 and observed that the saturation of the invading fluid first decreases and then increases with increasing Ca, with the minimum value occurring at log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca = −4.07 or log
Ca = −4.07 or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca = −5.07, depending on M.139 This agrees with the study in a 2D heterogeneous micromodel by Li et al., where again a minimum CO2 saturation was observed during the crossover from capillary fingering to viscous fingering.143 The existence of a minimum value was attributed to the fact that both fingering propagation toward the outlet and void filling in the transverse/backward directions were suppressed during the crossover. The inconsistent findings certainly call for additional endeavors for more insights and deterministic measurements.
Ca = −5.07, depending on M.139 This agrees with the study in a 2D heterogeneous micromodel by Li et al., where again a minimum CO2 saturation was observed during the crossover from capillary fingering to viscous fingering.143 The existence of a minimum value was attributed to the fact that both fingering propagation toward the outlet and void filling in the transverse/backward directions were suppressed during the crossover. The inconsistent findings certainly call for additional endeavors for more insights and deterministic measurements.
Moebius and Or studied the rapid interfacial dynamics during drainage, showing interfacial velocities exceeding 50 times the mean front velocity.148 Armstrong and Berg imaged pore drainage events in a glass micromodel system and analyzed the dependency of interfacial velocity on the bulk flow rate and spatial fluid configurations, as shown in Fig. 26.196 Their results indicated that pore drainage events are cooperative, revealing that capillary pressure differences over multiple pores affect fluid topology and menisci dynamics, which highlight the inertial effect. Additionally, it was discovered that the velocity of a pore drainage is controlled by its intrinsic dynamics and is, therefore, independent of the bulk flow rate. Kazemifar et al. quantified the flow dynamics associated with water displacement by CO2 in a 2D homogeneous porous micromodel.146 Employing dual-color fluorescent microscopy and micro-PIV techniques, they were able to capture the pore-scale burst events (Haines jumps) with sufficient time resolution, which showed that velocity jumps 20–25 times larger in magnitude than the bulk velocity and that these bursts of water flow occurred both in-line with and against the bulk flow direction. With the velocity data captured with micro-PIV, they calculated that the maximum local Reynolds number Re for CO2 reaches as high as 25, which is well beyond the limit of Re = 10 for the validity of Darcy's law, highlighting the effects of inertia. Li et al. extended the study to a 2D heterogeneous micromodel whose porous structures were inspired by sandstone CO2 storage reservoirs. They measured a local Re of 21 in the CO2 phase.166 Furthermore, these drainage events were observed to be cooperative, extending beyond tens of pores, confirming that Haines jumps are non-local phenomena.167 Some representative velocity fields captured during the occurrences of Haines jumps are shown in Fig. 26. Informed by these microfluidic studies, several numerical studies attempted to incorporate an inertial effect in the model and noted that the capillary number is not sufficient to characterize the two-phase flow, as suggested by Lenormand et al.137,140,198–200 Instead, the Ohnesorge number, which gives the relative importance of viscous forces over inertial and capillary forces, is required to fully describe the fluid flow, along with the viscosity ratio.137
Micromodels are well suited for characterizing interfacial areas thanks to their excellent optical access and the availability of various optical flow diagnostic tools. In 2D micromodels, the interfacial area reduces to interfacial length due to the 2D nature of the flow, assuming the depth of the micromodel is constant. Tsakiroglou et al. performed unsteady displacement experiments in a glass-etched pore network to examine the impact of the capillary number on relative permeability and capillary pressure.154 They found that these properties are sensitive to the transient displacement pattern, which changes from the invasion percolation to frontal drive as the capillary number increases, highlighting the influence of the fluid configuration and interfacial area on capillary pressure. Cheng et al. studied interfacial areas in the Pc–Sw relation during quasi-static drainage and found that the specific interfacial area lifts the hysteresis in the capillary pressure and saturation relationship in porous media.207 Their work provided the first experimental validation of theoretical predictions, showing that the capillary-dominated subset plays a role like a state variable and that the interfacial area is essential for describing multiphase flow properties, as well as capillary pressure and fluid saturation.201 Karadimitriou et al. studied interface movement under transient conditions using a 2D PDMS micromodel.151 While their results produced a unique Pc–Sw–awn surface for both drainage and imbibition, different relationships were obtained under steady state and transient conditions. This suggests that one interfacial area surface cannot sufficiently describe two-phase flow under transient and quasi-static conditions. This mismatch was attributed to the disconnection of the non-wetting phase, and the interfacial areas between the solid and the two fluid phases were not included in the capillarity theory, which warrants further research.
Zhang et al. calculated the total interfacial length in 2D micromodels at different flow stages and found a linear relationship between specific interfacial length and non-wetting fluid saturation.177 In a dual-permeability micromodel, Zhang et al. reported that while the linearity between interfacial length and nonwetting fluid saturation is preserved for both low and high flow rates, the slope for high flow rates was much larger than that for low flow rates. This behavior was attributed to a geometrical effect: the smaller pores, which are invaded only at high flow rates, are associated with higher interfacial length.177 Liu et al. confirmed this linear relationship for both homogeneous and heterogeneous pore networks using LBM simulations and observed a higher slope for higher flow rates.152 It was conjectured that the higher slope results from viscous fingering in which some fingers are stretched very thinly and even broken into smaller ganglia, resulting in a higher interfacial length than in capillary fingering and stable displacement. To that end, Li et al. performed high-speed measurements in 2D heterogeneous micromodels and confirmed that the total specific interfacial length scales linearly with CO2 saturation, which is in agreement with what was previously reported in the literature.143 Higher slopes were noted for high Ca cases, likely because CO2 fingers stretch or even break into ganglia in the viscous-fingering regime. They also noted the critical role of inertia in creating significant numbers of isolated CO2 ganglia via snap-off events at high Ca, which in turn increases total capillary-associated interfaces and reduces film-associated interfaces. The reduction and potential elimination of capillary hysteresis through developing new functional relationships that include a more complete set of variables is highly desirable. Future research is needed to enable more accurate determination of the interfacial area and other functional variables (e.g., interfacial curvature and Euler characteristics) and direct measurement of pore-scale pressure using on-chip microscale pressure sensors.187,188
From a pore scale perspective, wettability governs the capillary force and directly impacts the interface stability and displacement efficiency. Most previous studies on the wettability effects on flow behavior in porous media reported that increasing the contact angle of the resident wetting phase (i.e., making the wetting phase less wetting) stabilizes the displacement interface under various flow conditions, leading to more compact displacement patterns and thus increasing the displacement efficiency.153,209 Herein, we provide an overview of several representative microfluidic studies. Trojer et al. experimentally studied the wettability impacts on fluid–fluid-displacement patterns in granular media using a thin bed of glass beads.209 They varied the glass surface contact angle from 5° (drainage) to 120° (imbibition) through a combination of cleaning and salinization procedures. Holtzman conducted micromodel experiments in a plastic micromodel to understand the role of pore-scale heterogeneity and wettability in fluid displacement.157 Their results show that increasing the contact angle suppresses both trapping and fingering, hence reducing the sensitivity of the displacement to the underlying geometry disorder. Jung et al. studied the wettability effects in microfluidic Hele-Shaw cells where the contact angle was varied from 0° to 134°.213 The results indicated a consistent crossover between stable interfacial displacement at contact angles greater than 100° and capillary fingering at low contact angles less than 60°. Hu et al. used a high-pressure micromodel-microscopy system to study supercritical CO2 invasion into brine-saturated water-wet and intermediate-wet micromodels and observed a smaller number of fingers with larger finger width under intermediate-wet conditions.208,214 Zhao et al. performed a more comprehensive investigation of wettability effects by systematically varying the wettability of the porous flow cell over a wide range of contact angles.173 They found that increasing the solid matrix affinity to the invading fluid results in a more efficient displacement of the resident fluid up to a critical wetting transition, beyond which the trend is reversed (Fig. 27). This behavior was attributed to two pore-scale mechanisms: cooperative pore filling (increasing displacement efficiency) and corner flow (decreasing displacement efficiency). This work suggests that wettability is a necessary dimension, in addition to the capillary number, Ca, and viscosity ratio, M, to fully describe two-phase flow in porous media.
 | ||
| Fig. 27 [Top left] Schematic showing the micromodel used for the study of wettability effects by Zhao et al. (2016). [Top right] The micromodel was made of a photocurable polymer (NOA81) patterned with circular posts. [Bottom] displacement patterns for various wettability conditions (left to right: θ = 150°, 120°, 90°, 60°, 7°) and capillary numbers (bottom to top: Ca = 2.9 × 10−3, 2.9 × 10−2, 2.9 × 10−1); note the contact angles were defined with reference to the invading fluid (θ > 90° and θ < 90° correspond to drainage and imbibition, respectively).173 | ||
Li et al. investigated the pore-scale flow dynamics of liquid CO2 and water in 2D micromodels with different wetting properties using high-speed micro-PIV under reservoir-relevant conditions for drainage and imbibition scenarios.167 They noted that when CO2 displaces water in a hydrophilic micromodel (i.e., drainage), unstable capillary fingering occurs, and the pore flow is dominated by successive pore-scale burst events (i.e., Haines jumps). However, when the same experiment was repeated in a nearly neutral wetting micromodel (i.e., weak imbibition where capillary forces are minimized), flow instability and fluctuations were virtually eliminated, leading to a more compact displacement pattern. Enabled by high-speed microscopy, their measurements further revealed a significant alteration of the pore-filling mechanisms during drainage and imbibition, as shown in Fig. 28. While the former typically featured burst events, which often occur only at one of the several throats connecting a pore, the latter is typically dominated by a cooperative filling mechanism involving simultaneous invasion of a pore from multiple throats. This cooperative filling mechanism leads to the merging of two interfaces and releases surface energy, causing instantaneous high-speed events that are similar yet fundamentally different from burst events.
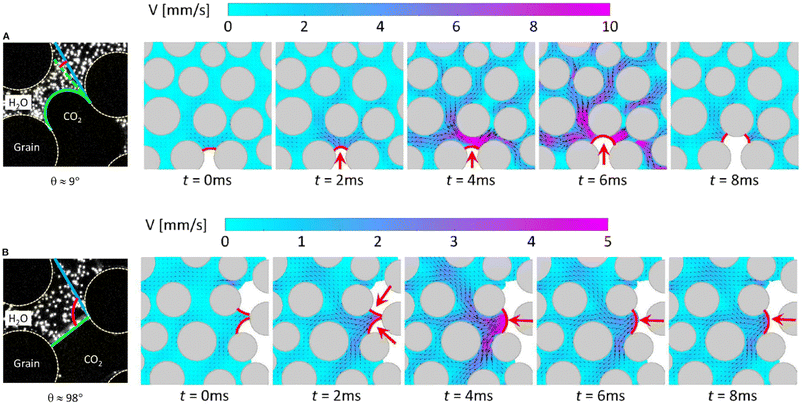 | ||
| Fig. 28 [Top] Evolution of velocity fields during a Haines jump event in drainage. [Bottom] Evolution of velocity fields during a cooperative filling event in weak imbibition.167 | ||
Chang et al. performed supercritical CO2 injection into heterogeneous micromodels while considering three different wetting conditions: uniformly water-wet, uniformly intermediate-wet, and mostly water-wet with intermediate-wet patches.156 High storage efficiency and wide interconnections of CO2 flow paths were observed in reservoirs containing more and uniformly distributed intermediate-wet and water-wet patches, whereas hindered storage efficiency and channelized CO2 flow paths were observed in reservoirs containing heterogeneously distributed intermediate-wet patches. Most recently, Irannezhad et al. studied the displacement of silicone oil by water in a mostly oil-wet porous medium patterned with discrete water-wet clusters that have precisely controlled wettability.215 It was observed that the macroscopic displacement pattern varies dramatically depending on the details of wettability alteration. The invading water preferentially fills strongly water-wet clusters but encircles weakly water-wet clusters instead, resulting in significant trapping of the defending oil. The experimental observation was explained with pore-scale simulations, which revealed that the fluid–fluid interfaces at mixed-wet pores resemble an S-shaped saddle with mean curvatures close to zero. The studies reviewed above have demonstrated the complex nature of wettability and its effects on multiphase flow in porous media. While numerical simulation still faces challenges in accurately modeling wettability effects, microfluidic experiments are expected to continue to play a key role in the identification of new physics as well as the development and validation of new models.216
Salt precipitation due to drying of brine is a physical process where the injected CO2, which is often low in the water component, extracts water molecules from the resident brine, causing the dissolved solutes to saturate, crystallize, separate from the brine, and eventually deposit in pore spaces. Kim et al. conducted a pore-scale experiment on salt precipitation using micromodels (Fig. 29).169 Their results indicate that the porosity decreases by ∼20% due to salt precipitation and that the salt precipitation front moves at a constant velocity, which is 2% of the superficial CO2 flow speed. Two different types of salt formation were observed, with large bulk crystals on the same order of the pore size (20–50 μm) forming during the early stage of the drying process and polycrystalline aggregated structures ranging over broad length scales forming in late stages of the drying process and aggregating from the CO2–brine interface. Rufai & Crawshaw studied the evaporation of brine in 2.5D silicon micromodels and noted that the evaporation rate of brine is strongly impacted by salt precipitation, which was attributed to salt deposition at the matrix surface progressively impeding hydraulic connectivity to the evaporating surface.222 Nooraiepour et al. investigated the precipitation of salt crystals in a microfluidic vessel under various reservoir-relevant pressure and temperature conditions.223 They showed that the magnitude, distribution, and precipitation patterns of salt accumulations are influenced by the phase of the injected CO2 (i.e., gaseous, liquid, or supercritical), presumably due to the differences in CO2 density and the solubility of water in CO2 for different CO2 phases. Injection of gaseous CO2 resulted in higher salt precipitation than liquid and supercritical CO2, and micrometer-sized halite crystals are thought to have the potential to partially or entirely clog fracture apertures. Ho & Tsai conducted experiments using a microfluidic device and noted the two types of crystal patterns, bulk crystal and polycrystalline aggregate, which are in agreement with the results by Kim et al.169,224 He et al. studied the morphology and distribution of salt precipitation in porous structures and the effects of wettability and CO2 flow rate using silica micromodels.225,226 It was found that for hydrophilic and neutral porous surfaces, ex situ precipitation occurs, which completely blocks the throats and pore bodies and results in a significant reduction in permeability. However, for a hydrophobic porous surface, in situ precipitation occurs and occupies a much smaller pore volume, which only causes a mild reduction in permeability compared to the hydrophilic case at the same injection rate, highlighting the important role played by surface wettability in salt precipitation.
 | ||
| Fig. 29 [Left] Experiments of salt precipitation in the regular grid-like microfluidic network in PMMA.169 [Right] Evolution of the calcite grains over time, subject to dissolution by HCl. The dissolution rate is shown to be strongly dependent on the pore flow and the presence of gas bubbles.184 | ||
Mineral precipitation in porous media can be more complicated, as it further involves complex mixing and reactive transport behaviors, in addition to the challenges observed in drying. The relative importance of reaction, diffusive transfer, and advective transport is often characterized by two dimensionless parameters, the Péclet number (Pe) and the Damköhler number (Da), defined as Pe = Vl/D and DaI = kl/V, respectively.227 Here, V is the fluid velocity, l is the characteristic length scale (e.g., pore diameter), D is the diffusion coefficient, and k is the reaction rate constant. Physically, Pe defines the ratio of advective to diffusive transport rates, and DaI defines the ratio of the overall chemical reaction rate to the advective mass transport rate. When, however, the transport is dominated by diffusion, the second Damköhler number, DaII, which compares the chemical reaction rate to the diffusive mass transfer rate, is defined as DaII = DaI·Pe = kl2/D.227 The definitions of Pe and Da provide a convenient basis for characterizing reactive transport and predicting local reaction potentials in porous media.
Several studies investigated reactive transport and mineral precipitation processes in 2D micromodels. For example, Zhang et al. studied mineral precipitation in a 2D micromodel to observe how a porous structure affects the mixing processes between CaCl2 and Na2CO3.217 They considered four different saturation states and revealed that in certain conditions, pore spaces were occluded by CaCO3 precipitates along the transverse mixing zone, thus substantially modifying pore connectivity and mixing patterns. Fanizza et al. evaluated the abiotic precipitation of uranium (U(VI)) in a microfluidic pore network and suggested that uranium precipitation can block pores, alter fluid flow paths, and potentially limit mixing, thus slowing further precipitation.228 Willingham et al. investigated the effects of porous media structure on mixing-controlled reactions using micromodel experiments.229 Their results indicated that grain orientation significantly affects mixing and the extent of reaction at the pore scale and that the interfacial contact area between reactive species plumes is a controlling factor for mixing and the extent of chemical reaction.
Several other studies conducted very similar micromodel experiments focusing on various effects, such as the combined effects of evaporation and reaction, and the effects of Mg2+ concentration on the morphology and polymorphs of CaCO3 and calcite nucleation and growth.230 For more information on the geochemical reactions in carbon sequestration, the readers are referred to several previous reviews.231–234 More recently, several studies have been conducted specifically to support the development of pore-scale modeling.219,234–237 Their experiments, where a barium chloride solution was injected into PDMS micromodels, leading to the dissolution of celestine and growth of barite, marked 4 stages of the process: the induction period, the crystal growth, the clogging, which prevented the mixing of the reactant solutions, and finally the dissolution of celestine crystals. Additionally, they showed that the evolution of the porosity–diffusivity relationship in response to precipitation reactions displays a behavior deviating from Archie's law. Although applying an extended power law improves the description of the evolving porosity–diffusivity, the model still neglects post-clogging features, calling for further studies. It is also worth noting that many microfluidic studies have been devoted to the understanding of microbially induced calcite precipitation (MICP) in porous media, which unfortunately cannot be covered in this review due to space constraints. The readers are referred to the following references for the recent advances in MICP research.192,221,238–240
Several other studies focused on dissolution to understand the pore-scale mechanisms that lead to pore structure changes due to dissolution.241 In this scenario, it is often required that the micromodels be fabricated out of reactive/dissolvable materials, such as calcite, which is reactive with acids, and gypsum, which slowly dissolves in water.220,242,243 Song et al. and Soulaine et al. studied the dissolution of calcite reservoirs by weak acids using calcite-based micromodels.181,244 Their results illustrate highly flow-directed dissolution and associated positive feedback wherein acid preferentially invades high conductivity flow paths, resulting in higher dissolution rates, called “wormholing”. Song et al. later reported a new microscale mechanism that dictates the overall behavior of the reactive dissolution, where the reaction product, CO2, due to carbonate rock dissolution, forms a separate, protective phase that engulfs the carbonate rock grain and reduces further dissolution.181 Agrawal et al. conducted experiments by flowing an acidic solution through a microscopic capillary channel in a calcite crystal at two different flow rates.245 Two key stages in pore shape evolution were observed: a transient phase and a quasi-steady-state phase. Their results also showed that the common assumption of constant pore shape in pore network modeling (i.e., ignoring dissolution) may lead to an overestimation of pore conductance by up to 80%. Jiménez-Martínez et al. used a combination of pore-scale experiments and numerical simulation to study the effects of single and multiphase flow on dissolution and precipitation in a geomaterial-based micromodel.218 They found that the presence of CO2 bubbles significantly changes the flow dynamics and the resulting reaction patterns from a single-phase system, spatially homogenizing the rock dissolution. Additionally, bubbles redirect oversaturated fluid into low-velocity regions, thereby enhancing carbonate precipitation therein. Xu et al. studied reaction-infiltration instability, specifically the dissolution finger growth in radial geometries, using gypsum-based microfluidic devices.243 In their experiments, pure water was injected to dissolve circular gypsum samples, which showed a few features consistent with theoretical and numerical predictions on the finger growth dynamics, such as screening and selection between the fingers. More recently, Rahman et al. conducted dissolution experiments using a 2D micromodel fabricated out of a pure calcite crystal and noted that the dissolution rate strongly depends on the local pore flow and the presence of gas bubbles that are either initially trapped or generated in situ (Fig. 29).184 Combined, mineral dissolution in porous media is allured by the coupled process of reaction, solute transport, and pore flow, which is further complicated by instability and multiphase flow. Although microfluidics has enabled the discovery and characterization of numerous pore-scale mechanisms, direct modeling and predicting mineral dissolution in porous media is still challenging, even in single-phase flow. Additionally, mineral dissolution coupled with multiphase flow remains minimally explored, providing vast research opportunities for microfluidics to contribute.244
4. Challenges and future directions in microfluidic-based carbon capture and storage
Even with significant advancements in microfluidic research for carbon capture and storage (CCS), there is still much to be done to bridge the gap between laboratory-scale innovations and real-world deployment. While microfluidic platforms have demonstrated excellent application benefits over conventional macroscale methods, several challenges remain that must be addressed to fully leverage their potential. Therefore, in this section, we have discussed key obstacles in microfluidic CCS research, which presents the scope of future research.• Microfluidic platforms offer highly controlled environments and precise analysis of gas–liquid interactions and reaction kinetics. However, their small scale presents a significant challenge for handling large CO2 outputs in industrial applications. Some studies suggest that multi-channel parallelization and hybrid modeling, which integrates microfluidic insights with large-scale CCS simulations, could enable microfluidics to contribute to large-scale carbon capture. However, concerns remain regarding high-pressure drops and the practicality of large-scale fabrication, which could limit their feasibility. Addressing these challenges presents a promising research direction for advancing microfluidic-based CCS technologies.
• A literature review reveals that most microfluidic studies operate at ambient pressure and temperature, with limited variations to simulate real-world conditions. However, key CCS processes often occur under extreme conditions. For instance, CO2 capture via chemical absorption, such as amine scrubbing, typically operates at around 70 °C, while CO2 sequestration in deep geological formations takes place under high-pressure (≥100 bar) and high-temperature (≥50 °C) environments. This disparity between experimental and real-world conditions limits the direct applicability of microfluidic findings to large-scale implementation. Recent advancements in high-pressure, high-temperature microfluidic systems, including developing pressure-resistant materials and thermally stable microchannels, offer promising solutions. Implementing these innovations in CCS research could enable more accurate assessments of CO2 dissolution, trapping mechanisms, and mineralization reactions, ensuring that microfluidic insights are more relevant for industrial applications.
• This review presents studies that have incorporated reservoir-mimicking surfaces in microfluidic CO2 storage experiments. However, most research still relies on PDMS or glass-based microfluidic platforms, limiting the understanding of reactive transport behavior, long-term mineralization, and multiphase interactions such as capillary trapping. To address these gaps, more rigorous studies using reservoir-relevant materials are needed. Additionally, advancements in microfabrication techniques, such as 3D printing and laser lithography, could enable more accurate replication of fracture networks and permeability variations observed in natural reservoirs.
• Furthermore, our review highlights a significant gap in understanding mineral precipitation and its effects on pore clogging and flow diversion during CO2 sequestration. While carbon capture mechanisms are well studied, the long-term stability of CO2 storage remains poorly characterized. More comprehensive research incorporating reactive substrates and in situ imaging techniques could provide valuable insights into these processes, improving predictions of CO2 retention and migration in geological formations.
• Most microfluidic devices used for CCS bear a quasi-2D nature, i.e., the depth is usually much smaller than the other two dimensions, causing deviations from realistic 3D porous media. It is still a topic of scientific debate regarding how much of the knowledge that has been learned from those 2D systems can be directly applicable to realistic 3D systems.242 Therefore, more research is needed to ensure a faithful translation of the understanding obtained in 2D micromodels to realistic 3D processes.
• The unique advantages of microfluidic platforms discussed throughout this review, such as precise control of flow, tunable environmental conditions, high-resolution imaging, and material adaptability, can also be extended to a wide range of CO2 utilization strategies that were not covered in this review. In particular, while CO2 conversion was not a primary focus here, processes such as electrochemical reduction, photocatalytic transformation, and biological fixation stand to benefit significantly from microfluidic integration, enabling improved control over reaction conditions, deeper mechanistic understanding, and more efficient catalyst screening for compact and scalable CO2 utilization systems.
• Finally, proper upscaling from microscales to large scales has remained a big challenge.243–247 As described in section 2.3, recent progress in multi-channel and high-throughput microfluidic designs is a few examples toward large-scale implementation. However, there is a lack of extensive work in this field, and future work should aim to bridge this gap. Additionally, new approaches are needed to ensure the proper incorporation of pore-scale physics in large-scale modeling and predictions by developing novel constitutive relations.
5. Conclusion
Microfluidic technologies have emerged as a revolutionary tool for advancing CCS research, offering precise control over gas–liquid interactions, real-time in situ monitoring, and enhanced analytical capabilities while significantly reducing resource requirements. This review provides a comprehensive understanding of how microfluidic platforms have redefined experimental approaches in CCS research, replacing traditional macroscale setups and driving innovation in both carbon capture and storage. The first section focuses on microfluidic-based carbon capture, beginning with fundamental CO2 capture mechanisms and detailing how microfluidic advancements address current challenges in solvent-based absorption, adsorption, and gas–liquid reaction kinetics. Additionally, mass transport theories are explored in relation to different microfluidic models, providing insights into their applicability across various capture processes supported by relevant experimental studies. The influence of flow patterns and microchannel geometries on CO2 dissolution, reaction kinetics, and mass transport efficiency is examined, along with advanced measurement techniques such as micro-PIV, fluorescence imaging, and spectroscopy, which enhance gas–liquid interaction analysis. The second section, dedicated to microfluidic-based carbon storage research, explores recent advancements in various storage methods, particularly mineralization and geological sequestration. It covers pore-scale trapping mechanisms, mineralization kinetics, and permeability evolution, highlighting the role of microfluidics in understanding multiphase flow dynamics and reactive transport. However, fabricating microfluidic devices for carbon storage presents greater challenges than carbon capture micromodels, as it requires precise surface modifications to mimic the complex heterogeneity of geological formations. This review addresses conventional and emerging fabrication techniques, discussing their applicability and limitations with contextual examples. Lastly, we have provided challenges like replicating geological conditions, scaling issues with microfluidics to handle large amounts of carbon, and a limited pressure and temperature range compared to micromodels. We also discussed some future scopes with possible solutions for these challenges.Data availability
The data analyzed in this review were obtained from publicly available sources, including PubMed, Web of Science, and various journal databases. All relevant data can be accessed through the provided citations within the review. Where data was not readily available, attempts were made to contact the original researchers for further information.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AR and MK acknowledge the National Science Foundation for support of this work under award number 2207642. YL acknowledges the partial support by the NSF Career Award under award number 2144802 with Dr. Fangyu Cao as the program officer. Acknowledgement is also made by YL to the donors of the American Chemical Society Petroleum Research Fund for partial support of this research under Doctoral New Investigator Grant 62687-DNI9.References
- U.S. Energy Information Administration, EIA projects 28% increase in world energy use by 2040, 2017, Sep 14 [cited 2025 Apr 24], available from: https://www.eia.gov/todayinenergy/detail.php?id=32912 Search PubMed.
- International Energy Agency, CO2 emissions in 2022 – Analysis, 2023 [cited 2025 Apr 24], available from: https://www.iea.org/reports/co2-emissions-in-2022 Search PubMed.
- G. T. Rochelle, Amine scrubbing for CO2 capture, Science, 2009, 325(5948), 1652–1654, DOI:10.1126/science.1176731.
- H. Kongsjorden, O. Karstad and T. A. Torp, Saline aquifer storage of carbon dioxide in the Sleipner project, Waste Manage., 1998, 17(5–6), 303–308, DOI:10.1016/S0956-053X(97)10037-X.
- S. Yadav and S. S. Mondal, A review on the progress and prospects of oxy-fuel carbon capture and sequestration (CCS) technology, Fuel, 2022, 308, 122057, DOI:10.1016/j.fuel.2021.122057.
- M. Kárászová, B. Zach, Z. Petrusová, V. Červenka, M. Bobák and M. Šyc, et al., Post-combustion carbon capture by membrane separation: Review, Sep. Purif. Technol., 2020, 238, 116448, DOI:10.1016/j.seppur.2019.116448.
- R. Aniruddha, I. Sreedhar and B. M. Reddy, MOFs in carbon capture—Past, present, and future, J. CO2 Util., 2020, 42, 101297, DOI:10.1016/j.jcou.2020.101297.
- N. McQueen, K. V. Gomes, C. McCormick, K. Blumanthal, M. Pisciotta and J. Wilcox, A review of direct air capture (DAC): Scaling up commercial technologies and innovating for the future, Prog. Energy, 2021, 3(3), 032001, DOI:10.1088/2516-1083/abf1ce.
- H. A. Salih, J. Pokhrel, D. Reinalda, I. AlNashf, M. Khaleel and L. F. Vega, et al., Hybrid Slurry/Nanofluid systems as alternative to conventional chemical absorption for carbon dioxide capture: A review, Int. J. Greenhouse Gas Control, 2021, 110, 103415, DOI:10.1016/j.ijggc.2021.103415.
- A. Bashir, M. Ali, S. Patil, M. S. Aljawad, M. Mahmoud and D. Al-Shehri, et al., Comprehensive review of CO2 geological storage: Exploring principles, mechanisms, and prospects, Earth Sci. Rev., 2024, 249, 104672, DOI:10.1016/j.earscirev.2023.104672.
- U. Khan, C. C. Ogbaga, O. A. O. Abiodun, A. A. Adeleke, P. P. Ikubanni and P. U. Okoye, et al., Assessing absorption-based CO2 capture: Research progress and techno-economic assessment overview, Carbon Capture Sci. Technol., 2023, 8, 100125, DOI:10.1016/j.ccst.2023.100125.
- A. Busch, P. Bertier, Y. Gensterblum, G. Rother, C. J. Spiers and M. Zhang, et al., On sorption and swelling of CO2 in clays, Geomech. Geophys. Geo Energy Ge Resour., 2016, 2(2), 111–130, DOI:10.1007/s40948-016-0024-4.
- M. S. Blondes, M. D. Merrill, S. T. Anderson and C. A. DeVera, Carbon dioxide mineralization feasibility in the United States, Sci. Invest. Rep., 2018, 5079, 1–29, DOI:10.3133/sir20185079.
- A. Sanna, M. Uibu, G. Caramanna, R. Kuusik and M. M. Maroto-Valer, A review of mineral carbonation technologies to sequester CO2, Chem. Soc. Rev., 2014, 43, 8049, 10.1039/c4cs00035h.
- T. Fu, Microfluidics in CO2 capture, sequestration, and applications, in: Advances in Microfluidics - New Applications in Biology, Energy, and Materials Sciences, 2016, DOI:10.5772/64284.
- M. Abolhasani, A. Günther and E. Kumacheva, Microfluidic studies of carbon dioxide, Angew. Chem., Int. Ed., 2014, 53(31), 7992–8002, DOI:10.1002/anie.201403719.
- H. Cheng, Y. Fan, D. Tarlet, L. Luo and Z. Fan, Microfluidic-based chemical absorption technology for CO2 capture: Mass transfer dynamics, operating factors, and performance intensification, Renewable Sustainable Energy Rev., 2023, 181, 113357, DOI:10.1016/j.rser.2023.113357.
- X. Liu, W. Gao, Y. Lu, L. Wu and Y. Chen, High-throughput microfluidic production of carbon capture microcapsules: Fundamentals, applications, and perspectives, Int. J. Extreme Manuf., 2024, 6(3), 032010, DOI:10.1088/2631-7990/ad339c.
- X. Pan, L. Sun, X. Huo, C. Feng and Z. Zhang, Research progress on CO2 capture, utilization, and storage (CCUS) based on micro-nano fluidics technology, Energies, 2023, 16(23) DOI:10.3390/en16237846.
- S. D. Kenarsari, D. Yang, G. Jiang, S. Zhang, J. Wang and A. G. Russell, Review of recent advances in carbon dioxide separation and capture, RSC Adv., 2013, 3(45), 22739–22773, 10.1039/c3ra43965h.
- E. Graham, S Gopinath., E. Forte, G. Jackson, A. Galindo and C. S. Adjiman. The development of a molecular systems engineering approach to the design of carbon-capture solvents, in: Process Systems and Materials for CO2 Capture, 2017, pp. 1–41, DOI:10.1002/9781119106418.ch1.
- R. Ben-Mansour, M. A. Habib, O. E. Bamidele, M. Basha, N. A. A. Qasem and A. Peedikakkal, et al., Carbon capture by physical adsorption: Materials, experimental investigations and numerical modeling and simulations – A review, Appl. Energy, 2016, 161, 225–255, DOI:10.1016/j.apenergy.2015.10.011.
- US Department of Commerce, National Oceanic and Atmospheric Administration, What is ocean acidification?. [cited 2025 Apr 24], available from: https://oceanacidification.noaa.gov Search PubMed.
- Z. H. Ban, L. K. Keong and A. M. Shariff, Physical absorption of CO2 capture: A review, Adv. Mater. Res., 2014, 917, 134–143, DOI:10.4028/www.scientific.net/amr.917.134.
- H. Zhai and E. S. Rubin, Systems analysis of physical absorption of CO2 in ionic liquids for pre-combustion carbon capture, Environ. Sci. Technol., 2018, 52(8), 4996–5004, DOI:10.1021/acs.est.8b00411.
- S. Yang, L. Zhang and D. Song, Conceptual design, optimization and thermodynamic analysis of a CO2 capture process based on Rectisol, Energy, 2022, 244, 122566, DOI:10.1016/j.energy.2021.122566.
- A. A. Manafpour, F. Feyzi and M. Rezaee, An environmentally friendly deep eutectic solvent for CO2 capture, Sci. Rep., 2024, 14(1), 1–15, DOI:10.1038/s41598-024-70761-4.
- J. Salimi and F. Salimi, CO2 capture by water-based Al2O3 and Al2O3-SiO2 mixture nanofluids in an absorption packed column, Rev. Mex. Ing. Quim., 2016, 15(1), 185–192 CAS.
- S. G. R. Lefortier, P. J. Hamersma, A. Bardow and M. T. Kreutzer, Rapid microfluidic screening of CO2 solubility and diffusion in pure and mixed solvents, Lab Chip, 2012, 12(18), 3387–3391, 10.1039/c2lc40260b.
- D. Voicu, M. Abolhasani, R. Choueiri, G. Lestari, C. Seiler and G. Menard, et al., Microfluidic studies of CO2 sequestration by frustrated Lewis pairs, J. Am. Chem. Soc., 2014, 136(10), 3875–3880, DOI:10.1021/ja411601a/suppl_file/ja411601a_si_001.pdf.
- B. Zhao, K. Zhao, Y. Cheng, S. Huang, J. Xu, Y. Xu, K. He, D. Huang, H. Qian and W. Chen, Encapsulated deep eutectic solvent and carbonic anhydrase jointly by microfluidics for high capture performance of carbon dioxide, Sep. Purif. Technol., 2023, 315, 123701, DOI:10.1016/J.SEPPUR.2023.123701.
- M. Wang, A. Lawal, P. Stephenson, J. Sidders and C. Ramshaw, Post-combustion CO2 capture with chemical absorption: A state-of-the-art review, Chem. Eng. Res. Des., 2011, 89(9), 1609–1624, DOI:10.1016/J.CHERD.2010.11.005.
- X. Wang and C. Song, Carbon capture from flue gas and the atmosphere: A perspective, Front. Energy Res., 2020, 8, 560849, DOI:10.3389/FENRG.2020.560849/PDF.
- Y. Gohshi, H. Müller and E. A. G. Zagatto, Selectivity in analytical chemistry (IUPAC recommendations 2001), Pure Appl. Chem., 2001, 73(8), 1998–1999 Search PubMed.
- F. Zareiekordshouli, A. Lashani-Zadehgan and P. Darvishi, Thermophysical properties and CO2 absorption studies of the amine functionalized [Amim][Tf2N] and the non-functionalized counterpart [Bmim][Tf2N] ionic liquids, Int. J. Greenhouse Gas Control, 2016, 53, 328–337, DOI:10.1016/J.IJGGC.2016.08.022.
- S. Murai, Y. Maezawa, D. Muraoka, T. Muramatsu and S. Saito, Development of new sterically hindered amine for PCC, Energy Procedia, 2017, 114, 1904–1909, DOI:10.1016/J.EGYPRO.2017.03.1321.
- A. H. Casey and G. E. Triplett, Microfluidic reaction design for real-time chemical reactions monitoring, Proc. SPIE, 2021, 11662, 22–30, DOI:10.1117/12.2575995.
- N. Jia, L. Torres de Oliveira, A. Bégin-Drolet and J. Greener, A SpectIR-fluidic reactor for monitoring fast chemical reaction kinetics with on-chip attenuated total reflection Fourier transform infrared spectroscopy, Anal. Methods, 2023, 15(39), 5129–5138, 10.1039/D3AY00842H.
- H. Rashid and A. Rafey, Solid adsorbents for carbon dioxide capture: A review, Chem. Ecol., 2023, 39(7), 775–791, DOI:10.1080/02757540.2023.2227622.
- R. Ben-Mansour, O. E. Bamidele and M. A. Habib, Evaluation of Mg-MOF-74 for post-combustion carbon dioxide capture through pressure swing adsorption, Int. J. Energy Res., 2015, 39(15), 1994–2007, DOI:10.1002/ER.3428.
- R. M. Siqueira, G. R. Freitas, H. R. Peixoto, J. F. D. Nascimento, A. P. S. Musse and A. E. B. Torres, et al., Carbon dioxide capture by pressure swing adsorption, Energy Procedia, 2017, 114, 2182–2192, DOI:10.1016/j.egypro.2017.03.1355.
- K. Ma, Y. Wang, Z. Chen, T. Islamoglu, C. Lai and X. Wang, et al., Facile and scalable coating of metal-organic frameworks on fibrous substrates by a coordination replication method at room temperature, ACS Appl. Mater. Interfaces, 2019, 11(25), 22714–22721, DOI:10.1021/acsami.9b04780/suppl_file/am9b04780_si_001.pdf.
- M. M. Sabzehmeidani and M. Kazemzad, Recent advances in surface-mounted metal-organic framework thin film coatings for biomaterials and medical applications: A review, Biomater. Res., 2023, 27(1), 1–31, DOI:10.1186/s40824-023-00454-y.
- Z. Jin, X. Jiang, Z. Dai, L. Xie, W. Wang and L. Shen, Continuous synthesis of nanodroplet-templated, N-doped microporous carbon spheres in microfluidic system for CO2 capture, ACS Appl. Mater. Interfaces, 2020, 12(47), 52571–52580, DOI:10.1021/acsami.0c14044/suppl_file/am0c14044_si_001.pdf.
- L. Xie, Z. Jin, Z. Dai, T. Zhou, X. Zhang and Y. Chang, et al., Fabricating self-templated and N-doped hierarchical porous carbon spheres via microfluidic strategy for enhanced CO2 capture, Sep. Purif. Technol., 2023, 322, 124267, DOI:10.1016/j.seppur.2023.124267.
- A. Kurlov, A. Armutlulu, F. Donat, A. R. Studart and C. R. Müller, CaO-based CO2 sorbents with a hierarchical porous structure made via microfluidic droplet templating, Ind. Eng. Chem. Res., 2020, 59(15), 7182–7188, DOI:10.1021/acs.iecr.9b05996/suppl_file/ie9b05996_si_001.pdf.
- W. Yu, M. Gao, G. Rim, T. G. Feric, M. L. Rivers and A. Alahmed, et al., Novel in-capsule synthesis of metal-organic framework for innovative carbon dioxide capture system, Green Energy Environ., 2023, 8(3), 767–774, DOI:10.1016/j.gee.2021.08.002.
- M. Sauzade and T. Cubaud, Initial microfluidic dissolution regime of CO2 bubbles in viscous oils, Phys. Rev. E, 2013, 88(5), 051001, DOI:10.1103/PhysRevE.88.051001.
- A. Sell, H. Fadaei, M. Kim and D. Sinton, Measurement of CO2 diffusivity for carbon sequestration: A microfluidic approach for reservoir-specific analysis, Environ. Sci. Technol., 2013, 47(1), 71–78, DOI:10.1021/es303319q.
- A. Paul, T. Laurila, V. Vuorinen and S. V. Divinski. Fick's laws of diffusion, in Thermodynamics, diffusion and the Kirkendall effect in solids, Springer, 2014, pp. 115–139, DOI:10.1007/978-3-319-07461-0_3.
- J. R. Fanchi, Fluid flow equations, in Shared earth modeling, Gulf Professional Publishing, 2002, pp. 150–169, DOI:10.1016/B978-075067522-2/50009-4.
- T. S. Frost, V. Estrada, L. Jiang and Y. Zohar, Convection–diffusion molecular transport in a microfluidic bilayer device with a porous membrane, Microfluid. Nanofluid., 2019, 23(10), 1–13, DOI:10.1007/s10404-019-2283-1.
- M. N. Kashid, A. Renken and L. Kiwi-Minsker, Gas–liquid and liquid–liquid mass transfer in microstructured reactors, Chem. Eng. Sci., 2011, 66(17), 3876–3897, DOI:10.1016/j.ces.2011.05.015.
- Z. Pang, C. Zhu, Y. Ma and T. Fu, CO2 absorption by liquid films under Taylor flow in serpentine minichannels, Ind. Eng. Chem. Res., 2020, 59(26), 12250–12261, DOI:10.1021/acs.iecr.0c02217.
- N. Afraz, A. Adi and K. Hecht, The effect of diffusion on mass transfer in a laminar falling film: Observation versus theory, Chem. Eng. Sci., 2021, 232, 116363, DOI:10.1016/j.ces.2020.116363.
- O. A. Ibrahim, M. Navarro-Segarra, P. Sadeghi, N. Sabaté, J. P. Esquivel and E. Kjeang, Microfluidics for electrochemical energy conversion, Chem. Rev., 2022, 122(7), 7236–7266, DOI:10.1021/acs.chemrev.1c00499.
- L. Han, J. Fu, M. Li, S. Gong, N. Gao and C. Zhang, et al., A theoretical unsteady-state model for K_L of bubbles based on the framework of wide energy spectrum, AIChE J., 2016, 62(4), 1007–1022, DOI:10.1002/aic.15092.
- C. Li, C. Zhu, Y. Ma, D. Liu and X. Gao, Experimental study on volumetric mass transfer coefficient of CO2 absorption into MEA aqueous solution in a rectangular microchannel reactor, Int. J. Heat Mass Transfer, 2014, 78, 1055–1059, DOI:10.1016/j.ijheatmasstransfer.2014.07.071.
- E. P. van Elk, M. C. Knaap and G. F. Versteeg, Application of the penetration theory for gas–liquid mass transfer without liquid bulk: Differences with systems with a bulk, Chem. Eng. Res. Des., 2007, 85(4), 516–524, DOI:10.1205/cherd06066.
- T. Sherwood, R. Pigford and C. Wilke, Mass transfer, McGraw-Hill, New York, 1975 Search PubMed.
- T. H. M. Ho, J. Yang and P. A. Tsai, Microfluidic mass transfer of CO2 at elevated pressures: Implications for carbon storage in deep saline aquifers, Lab Chip, 2021, 21(20), 3942–3951, 10.1039/D1LC00106J.
- T. Deleau, M. H. H. Fechter, J. J. Letourneau, S. Camy, J. Aubin and A. S. Braeuer, et al., Determination of mass transfer coefficients in high-pressure two-phase flows in capillaries using Raman spectroscopy, Chem. Eng. Sci., 2020, 228, 115960, DOI:10.1016/j.ces.2020.115960.
- M. Al-Rawashdeh, A. Cantu-Perez, D. Ziegenbalg, P. Löb, A. Gavriilidis and V. Hessel, et al., Microstructure-based intensification of a falling film microreactor through optimal film setting with realistic profiles and in-channel induced mixing, Chem. Eng. J., 2012, 179, 318–329, DOI:10.1016/j.cej.2011.11.014.
- H. Ganapathy, A. Shooshtari, S. Dessiatoun, M. M. Ohadi and M. Alshehhi, Hydrodynamics and mass transfer performance of a microreactor for enhanced gas separation processes, Chem. Eng. J., 2015, 266, 258–270, DOI:10.1016/j.cej.2014.12.028.
- K. Keniar and S. Garimella, Analytical modeling of laminar annular flow condensation in an arbitrarily shaped microchannel, Int. J. Heat Mass Transfer, 2020, 162, 120334, DOI:10.1016/j.ijheatmasstransfer.2020.120334.
- S. Mehdizadeh, N. Pourmahmoud and A. Akbari, A numerical simulation of the hydrothermal characteristics of a microchannel using cavities, ribs, and secondary channels, Chem. Eng. Process., 2024, 201, 109787, DOI:10.1016/j.cep.2024.109787.
- A. Kawahara, P. Y. Chung and M. Kawaji, Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel, Int. J. Multiphase Flow, 2002, 28(9), 1411–1435, DOI:10.1016/S0301-9322(02)00037-X.
- J. El Hajal, J. R. Thome and A. Cavallini, Condensation in horizontal tubes, Part 1: Two-phase flow pattern map, Int. J. Heat Mass Transfer, 2003, 46(18), 3349–3363, DOI:10.1016/S0017-9310(03)00139-X.
- R. Kong, S. Kim, S. Bajorek, K. Tien and C. Hoxie, Effects of pipe size on horizontal two-phase flow: Flow regimes, pressure drop, two-phase flow parameters, and drift-flux analysis, Exp. Therm. Fluid Sci., 2018, 96, 75–89, DOI:10.1016/j.expthermflusci.2018.02.030.
- M. Nekouei and S. A. Vanapalli, Volume-of-fluid simulations in microfluidic T-junction devices: Influence of viscosity ratio on droplet size, Phys. Fluids, 2017, 29(3), 032007, DOI:10.1063/1.4978801.
- W. Khan, A. K. Chandra, K. Kishor, S. Sachan and M. S. Alam, Slug formation mechanism for air–water system in T-junction microchannel: A numerical investigation, Chem. Pap., 2018, 72(11), 2921–2932, DOI:10.1007/s11696-018-0522-7.
- J. Tan, Y. C. Lu, J. H. Xu and G. S. Luo, Mass transfer characteristic in the formation stage of gas–liquid segmented flow in microchannel, Chem. Eng. J., 2012, 185–186, 314–320, DOI:10.1016/j.cej.2012.01.054.
- M. M. L. Diouf and O. J. Romero, Numerical study of droplet formation in a Y-junction microchannel, J. Mec. Theor. Appl., 2017, 55(1), 317–330, DOI:10.15632/jtam-pl.55.1.317.
- J. Y. Qian, X. J. Li, Z. X. Gao and Z. J. Jin, Mixing efficiency analysis on droplet formation process in microchannels by numerical methods, Processes, 2019, 7(1), 33, DOI:10.3390/pr7010033.
- S. Takagi and Y. Matsumoto, Surfactant effects on bubble motion and bubbly flows, Annu. Rev. Fluid Mech., 2011, 43, 615–636, DOI:10.1146/annurev-fluid-122109-160756.
- Y. Taitel and D. Barnea, Two-phase slug flow, Adv. Heat Transfer, 1990, 20, 83–132, DOI:10.1016/S0065-2717(08)70026-1.
- C. Butler, B. Lalanne, K. Sandmann, E. Cid and A. M. Billet, Mass transfer in Taylor flow: Transfer rate modelling from measurements at the slug and film scale, Int. J. Multiphase Flow, 2018, 105, 185–201, DOI:10.1016/j.ijmultiphaseflow.2018.04.005.
- Y. Liu, J. Yue, C. Xu, S. Zhao, C. Yao and G. Chen, Hydrodynamics and local mass transfer characterization under gas–liquid–liquid slug flow in a rectangular microchannel, AIChE J., 2020, 66(2), e16805, DOI:10.1002/aic.16805.
- L. Shui, J. C. T. Eijkel and A. van den Berg, Multiphase flow in microfluidic systems – Control and applications of droplets and interfaces, Adv. Colloid Interface Sci., 2007, 133(1), 35–49, DOI:10.1016/j.cis.2007.03.001.
- S. Kuhn and K. F. Jensen, A pH-sensitive laser-induced fluorescence technique to monitor mass transfer in multiphase flows in microfluidic devices, Ind. Eng. Chem. Res., 2012, 51(26), 8999–9006, DOI:10.1021/ie300978n.
- S. Seo, B. Lages and M. Kim, Catalytic CO2 absorption in an amine solvent using nickel nanoparticles for post-combustion carbon capture, J. CO2 Util., 2020, 36, 244–252, DOI:10.1016/j.jcou.2019.11.011.
- W. Li, E. W. K. Young, M. Seo, Z. Nie, P. Garstecki and C. A. Simmons, et al., Simultaneous generation of droplets with different dimensions in parallel integrated microfluidic droplet generators, Soft Matter, 2008, 4(2), 258–262, 10.1039/b712917c.
- W. Li, J. Greener, D. Voicu and E. Kumacheva, Multiple modular microfluidic (M3) reactors for the synthesis of polymer particles, Lab Chip, 2009, 9(18), 2715–2721, 10.1039/b906626h.
- T. Nisisako and T. Torii, Microfluidic large-scale integration on a chip for mass production of monodisperse droplets and particles, Lab Chip, 2008, 8(2), 287–293, 10.1039/b713141k.
- P. Nguyen, D. Mohaddes, J. Riordon, H. Fadaei, P. Lele and D. Sinton, Fast fluorescence-based microfluidic method for measuring minimum miscibility pressure of CO2 in crude oils, Anal. Chem., 2015, 87(6), 3160–3164, DOI:10.1021/ac5047856.
- E. Tavernier, J. Sellier, F. Marty, P. Tabeling and T. Bourouina, Microsystem with fluidic and optical interface for inline measurement of CO2 in oil fields, IEEE Sens. J., 2008, 8(5), 430–434, DOI:10.1109/jsen.2008.918170.
- S. Rudyk, P. Spirov and E. Søgaard, Application of GC–MS chromatography for the analysis of the oil fractions extracted by supercritical CO2 at high pressure, Fuel, 2013, 106, 139–146, DOI:10.1016/j.fuel.2012.12.004.
- J. Li, R. Li, B. Zhao, H. Guo, S. Zhang and J. Cheng, et al., Quantitative measurement of carbon isotopic composition in CO2 gas reservoir by micro-laser Raman spectroscopy, Spectrochim. Acta, Part A, 2018, 195, 191–198, DOI:10.1016/j.saa.2018.01.082.
- J. D. Wells, W. Chen, R. L. Hartman and C. A. Koh, Carbon dioxide hydrate in a microfluidic device: Phase boundary and crystallization kinetics measurements with micro-Raman spectroscopy, J. Chem. Phys., 2021, 154(11), 110901, DOI:10.1063/5.0039533.
- V. Scott, R. S. Haszeldine, S. F. B. Tett and A. Oschlies, Fossil fuels in a trillion tonne world, Nat. Clim. Change, 2015, 5(5), 419–423, DOI:10.1038/nclimate2578.
- F. Kazemifar, A review of technologies for carbon capture, sequestration, and utilization: Cost, capacity, and technology readiness, Greenhouse Gases: Sci. Technol., 2021, 12(1), 200–230, DOI:10.1002/ghg.2131.
- National Academies of Sciences, Medicine, Division on Earth Life Studies, Ocean Studies Board, Board on Chemical Energy, Environmental Systems and Board on Atmospheric Sciences, Negative emissions technologies and reliable sequestration: A research agenda, National Academies Press, Washington, (DC), 2019, DOI:10.17226/25259.
- B. Kumar, B. Muchharla, M. Dikshit, S. Dongare, K. Kumar and B. Gurkan, et al., Electrochemical CO2 conversion commercialization pathways: A concise review on experimental frontiers and technoeconomic analysis, Environ. Sci. Technol. Lett., 2024, 11(11), 1161–1174, DOI:10.1021/acs.estlett.4c00564.
- O. Emmanuel and T. C. Ezeji, Advances in carbon dioxide capture and conversion technologies: Industrial integration for sustainable chemical production, Next Sustain., 2025, 6, 100108, DOI:10.1016/j.nxsust.2025.100108.
- A. Saravanan, D. V. N. Vo, S. Jeevanantham, V. Bhuvaneswari, V. A. Narayanan and P. R. Yaashikaa, et al., A comprehensive review on different approaches for CO2 utilization and conversion pathways, Chem. Eng. Sci., 2021, 236, 116515, DOI:10.1016/j.ces.2021.116515.
- G. Yergaziyeva, Z. Kuspanov, M. Mambetova, N. Khudaibergenov, N. Makayeva and C. Daulbayev, Advancements in catalytic, photocatalytic, and electrocatalytic CO2 conversion processes: Current trends and future outlook, J. CO2 Util., 2024, 80, 102682, DOI:10.1016/j.jcou.2024.102682.
- L. Cheng, X. Li, G. Rong and C. Zhou, The effect of surface wettability and wall roughness on the residual saturation for the drainage process in sinusoidal channels, Transp. Porous Media, 2019, 129(1), 203–229, DOI:10.1007/s11242-019-01284-0.
- K. S. Lackner, C. H. Wendt, D. P. Butt, E. L. Joyce and D. H. Sharp, Carbon dioxide disposal in carbonate minerals, Energy, 1995, 20(11), 1153–1170, DOI:10.1016/0360-5442(95)00071-N.
- W. Seifritz, CO2 disposal by means of silicates, Nature, 1990, 345, 486, DOI:10.1038/345486b0.
- P. Kelemen, S. M. Benson, H. Pilorgé, P. Psarras and J. Wilcox, An overview of the status and challenges of CO2 storage in minerals and geological formations, Front. Clim., 2019, 1, 1–20, DOI:10.3389/fclim.2019.00009.
- S. Zhang and D. J. DePaolo, Rates of CO2 mineralization in geological carbon storage, Acc. Chem. Res., 2017, 50(9), 2075–2084, DOI:10.1021/acs.accounts.7b00334.
- S. Snæbjörnsdóttir, B. Sigfússon, C. Marieni, D. Goldberg, S. R. Gislason and E. H. Oelkers, Carbon dioxide storage through mineral carbonation, Nat. Rev. Earth Environ., 2020, 1(2), 90–102, DOI:10.1038/s43017-019-0011-8.
- P. B. Kelemen, N. McQueen, J. Wilcox, P. Renforth, G. Dipple and A. P. Vankeuren, Engineered carbon mineralization in ultramafic rocks for CO2 removal from air: Review and new insights, Chem. Geol., 2020, 550, 119628, DOI:10.1016/j.chemgeo.2020.119628.
- P. B. Kelemen and G. Hirth, Reaction-driven cracking during retrograde metamorphism: Olivine hydration and carbonation, Earth Planet. Sci. Lett., 2012, 345–348, 81–89, DOI:10.1016/j.epsl.2012.06.018.
- K. Yoshida, A. Okamoto, H. Shimizu and R. Oyanagi, Fluid infiltration through oceanic lower crust in response to reaction-induced fracturing: Insights from serpentinized troctolite and numerical models, J. Geophys. Res.: Solid Earth, 2020, 125, e2020JB020268, DOI:10.1029/2020JB020268.
- W. Zhu, F. Fusseis, H. Lisabeth, T. Xing, X. Xiao and V. De Andrade, et al., Experimental evidence of reaction-induced fracturing during olivine carbonation, Geophys. Res. Lett., 2016, 43(18), 9535–9543, DOI:10.1002/2016GL070834.
- F. Renard, Reaction-induced fracturing: When chemistry breaks rocks, J. Geophys. Res.: Solid Earth, 2021, 126(2), e2020JB021451, DOI:10.1029/2020JB021451.
- P. B. Kelemen and J. Matter, In situ carbonation of peridotite for CO2 storage, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(45), 17295–17300, DOI:10.1073/pnas.0805794105.
- O. I. Ulven, B. Jamtveit and A. Malthe-Sørenssen, Reaction-driven fracturing of porous rock, J. Geophys. Res.: Solid Earth, 2014, 119(10), 7473–7486, DOI:10.1002/2014JB011102.
- L. Monasterio-Guillot, A. Fernandez-Martinez, E. Ruiz-Agudo and C. Rodriguez-Navarro, Carbonation of calcium-magnesium pyroxenes: Physical-chemical controls and effects of reaction-driven fracturing, Geochim. Cosmochim. Acta, 2021, 304, 258–280, DOI:10.1016/j.gca.2021.02.016.
- C. W. Neil, Y. Yang, H. Nisbet, U. C. Iyare, L. Boampong, W. Li, Q. Kang, J. Hyman and H. Vishwanathan, An integrated experimental modeling approach to identify key processes for carbon mineralization in fractured mafic and ultramafic rocks, PNAS Nexus, 2024, 3(9), 388, DOI:10.1093/pnasnexus/pgae388.
- A. Bashir, M. Ali, S. Patil, M. S. Aljawad, M. Mahmoud and D. Al-Shehri, et al., Comprehensive review of CO2 geological storage: Exploring principles, mechanisms, and prospects, Earth Sci. Rev., 2024, 249, 104672, DOI:10.1016/j.earscirev.2023.104672.
- A. K. Furre, O. Eiken, H. Alnes, J. N. Vevatne and A. F. Kiær, 20 years of monitoring CO2 injection at Sleipner, Energy Procedia, 2017, 114, 3916–3926, DOI:10.1016/j.egypro.2017.03.1523.
- International Energy Agency (IEA), 20 years of carbon capture and storage, OECD Publishing, Paris, 2016. DOI:10.1787/9789264267800-en.
- L. H. Spangler, L. M. Dobeck, K. S. Repasky, A. R. Nehrir, S. D. Humphries and J. L. Barr, et al., A shallow subsurface controlled release facility in Bozeman, Montana, USA, for testing near-surface CO2 detection techniques and transport models, Environ. Earth Sci., 2010, 60(2), 227–239, DOI:10.1007/s12665-009-0400-2.
- S. Mito, Z. Xue and T. Ohsumi, Case study of geochemical reactions at the Nagaoka CO2 injection site, Japan, Int. J. Greenhouse Gas Control, 2008, 2(3), 309–318, DOI:10.1016/j.ijggc.2008.04.007.
- C. Jenkins, A. Chadwick and S. D. Hovorka, The state of the art in monitoring and verification - ten years on, Int. J. Greenhouse Gas Control, 2015, 40, 312–349, DOI:10.1016/j.ijggc.2015.05.009.
- M. Ivandic, C. Juhlin, S. Lüth, P. Bergmann, A. Kashubin and D. Sopher, et al., Geophysical monitoring at the Ketzin pilot site for CO2 storage: New insights into the plume evolution, Int. J. Greenhouse Gas Control, 2015, 32, 90–105, DOI:10.1016/j.ijggc.2014.10.015.
- S. E. Greenberg, R. Bauer, R. Will, R. Locke, M. Carney and H. Leetaru, et al., Geologic carbon storage at a one-million-tonne demonstration project: Lessons learned from the Illinois Basin - Decatur project, Energy Procedia, 2017, 114, 5529–5539, DOI:10.1016/j.egypro.2017.03.1913.
- J. Q. Shi, C. Imrie, C. Sinayuc, S. Durucan, A. Korre and O. Eiken, Snøhvit CO2 storage project: Assessment of CO2 injection performance through history matching of the injection well pressure over a 32-month period, Energy Procedia, 2013, 37, 3267–3274, DOI:10.1016/j.egypro.2013.06.214.
- O. Eiken, P. Ringrose, C. Hermanrud, B. Nazarian, T. A. Torp and L. Høier, Lessons learned from 14 years of CCS operations: Sleipner, In Salah and Snøhvit, Energy Procedia, 2011, 4, 5541–5548, DOI:10.1016/j.egypro.2011.02.541.
- S. M. Benson and D. R. Cole, CO2 sequestration in deep sedimentary formations, Elements, 2008, 4(5), 325–331, DOI:10.2113/gselements.4.5.325.
- M. A. Hesse, F. M. Orr and H. A. Tchelepi, Gravity currents with residual trapping, Energy Procedia, 2009, 1(1), 3275–3281, DOI:10.1016/j.egypro.2009.02.113.
- E. H. Oelkers, S. R. Gislason and J. Matter, Mineral carbonation of CO2, Elements, 2008, 4(5), 333–337, DOI:10.2113/gselements.4.5.333.
- S. Bachu, D. Bonijoly, J. Bradshaw, R. Burruss, S. Holloway and N. Peter, et al., CO2 storage capacity estimation: Methodology and gaps, Int. J. Greenhouse Gas Control, 2007, 1, 430–443, DOI:10.1016/S1750-5836(07)00086-2.
- H. E. Huppert and J. A. Neufeld, The fluid mechanics of carbon dioxide sequestration, Annu. Rev. Fluid Mech., 2014, 46, 255–272, DOI:10.1146/annurev-fluid-011212-140627.
- C. A. Buckner, R. M. Lafrenie, J. A. Dénommée, J. M. Caswell, D. A. Want and G. G. Gan et al., in Microfluidics in CO2 capture, sequestration, and applications, IntechOpen, 2016, vol. 11(Tourism), p. 13 Search PubMed.
- L. K. Abidoye, K. J. Khudaida and D. B. Das, Geological carbon sequestration in the context of two-phase flow in porous media: A review, Crit. Rev. Environ. Sci. Technol., 2015, 45(11), 1105–1147, DOI:10.1080/10643389.2014.924184.
- N. K. Karadimitriou and S. M. Hassanizadeh, A review of micromodels and their use in two-phase flow studies, Vadose Zone J., 2012, 11(3), vzj2011.0072, DOI:10.2136/vzj2011.0072.
- H. Singh and R. S. Myong, Critical review of fluid flow physics at micro- to nano-scale porous media applications in the energy sector, Adv. Mater. Sci. Eng., 2018, 2018, 1–31, DOI:10.1155/2018/9565240.
- A. Anbari, H. Chien, S. S. Datta, W. Deng, D. A. Weitz and J. Fan, Microfluidic model porous media: Fabrication and applications, Small, 2018, 14(18), 1–15, DOI:10.1002/smll.201703575.
- A. Gerami, Y. Alzahid, P. Mostaghimi, N. Kashaninejad, F. Kazemifar and T. Amirian, et al., Microfluidics for porous systems: Fabrication, microscopy and applications, Transp. Porous Media, 2019, 130(1), 277–304, DOI:10.1007/s11242-018-1202-3.
- A. Jahanbakhsh, K. L. Wlodarczyk, D. P. Hand, R. R. J. Maier and M. M. Maroto-Valer, Review of microfluidic devices and imaging techniques for fluid flow study in porous geomaterials, Sensors, 2020, 20(14), 4030, DOI:10.3390/s20144030.
- K. Singh, H. Scholl, M. Brinkmann, M. Di Michiel, M. Scheel and S. Herminghaus, et al., The role of local instabilities in fluid invasion into permeable media, Sci. Rep., 2017, 7(1), 1–11, DOI:10.1038/s41598-017-00191-y.
- S. C. Cao, S. Dai, J. Jung and S. Cindy, Supercritical CO2 and brine displacement in geological carbon sequestration: Micromodel and pore network simulation studies, Int. J. Greenhouse Gas Control, 2016, 44, 104–114, DOI:10.1016/j.ijggc.2015.11.026.
- Y. Song, C. Zhao, M. Chen, Y. Chi, Y. Zhang and J. Zhao, Pore-scale visualization study on CO2 displacement of brine in micromodels with circular and square cross sections, Int. J. Greenhouse Gas Control, 2020, 95, 102958, DOI:10.1016/j.ijggc.2020.102958.
- R. Lenormand, E. Touboul and C. Zarcone, Numerical models and experiments on immiscible displacements in porous media, J. Fluid Mech., 1988, 189(1), 165–187, DOI:10.1017/S0022112088000953.
- Y. Guo, F. Liu, J. Qiu, Z. Xu and B. Bao, Microscopic transport and phase behaviors of CO2 injection in heterogeneous formations using microfluidics, Energy, 2022, 256, 124524, DOI:10.1016/j.energy.2022.124524.
- Y. Y. F. Chen, S. Fang, D. D. S. Wu and R. Hu, Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture, Water Resour. Res., 2017, 53(9), 7756–7772, DOI:10.1002/2017WR021051.
- Y. Chen, D. Wu, S. Fang and R. Hu, Experimental study on two-phase flow in rough fracture: Phase diagram and localized flow channel, Int. J. Heat Mass Transfer, 2018, 122, 1298–1307, DOI:10.1016/j.ijheatmasstransfer.2018.02.031.
- C. Cottin, H. Bodiguel and A. Colin, Drainage in two-dimensional porous media: From capillary fingering to viscous flow, Phys. Rev. E, 2010, 82, 046315, DOI:10.1103/PhysRevE.82.046315.
- F. Guo and S. A. Aryana, An experimental investigation of flow regimes in imbibition and drainage using a microfluidic platform, Energies, 2019, 12(7), 1390, DOI:10.3390/en12071390.
- Y. Li, G. Blois, F. Kazemifar and K. T. Christensen, High-speed quantification of pore-scale multiphase flow of water and supercritical CO2 in 2-D heterogeneous porous micromodels: Flow regimes and interface dynamics, Water Resour. Res., 2019, 55(5), 3758–3779, DOI:10.1029/2018WR024635.
- G. Blois, J. M. Barros and K. T. Christensen, A microscopic particle image velocimetry method for studying the dynamics of immiscible liquid–liquid interactions in a porous micromodel, Microfluid. Nanofluid., 2015, 18(5–6), 1391–1406, DOI:10.1007/s10404-014-1537-1.
- Y. Chen, Y. Li, A. J. Valocchi and K. T. Christensen, Lattice Boltzmann simulations of liquid CO2 displacing water in a 2D heterogeneous micromodel at reservoir pressure conditions, J. Contam. Hydrol., 2018, 212, 14–27, DOI:10.1016/j.jconhyd.2017.09.005.
- F. Kazemifar, G. Blois, D. C. Kyritsis and K. T. Christensen, Quantifying the flow dynamics of supercritical CO2–water displacement in a 2D porous micromodel using fluorescent microscopy and microscopic PIV, Adv. Water Resour., 2016, 95, 352–368, DOI:10.1016/j.advwatres.2015.05.011.
- F. Kazemifar, G. Blois, D. C. Kyritsis and K. T. Christensen, A methodology for velocity field measurement in multiphase high-pressure flow of CO2 and water in micromodels, Water Resour. Res., 2015, 51(4), 3017–3029, DOI:10.1002/2014WR016787.
- F. Moebius and D. Or, Interfacial jumps and pressure bursts during fluid displacement in interacting irregular capillaries, J. Colloid Interface Sci., 2012, 377(1), 406–415, DOI:10.1016/j.jcis.2012.03.070.
- L. C. Chang, H. H. Chen, H. Y. Shan and J. P. Tsai, Effect of connectivity and wettability on the relative permeability of NAPLs, Environ. Geol., 2009, 56(7), 1437–1447, DOI:10.1007/s00254-008-1238-8.
- D. Chen, L. J. Pyrak-Nolte, J. Griffin and N. J. Giordano, Measurement of interfacial area per volume for drainage and imbibition, Water Resour. Res., 2007, 43(12), 1–6, DOI:10.1029/2007WR006021.
- N. K. Karadimitriou, S. M. Hassanizadeh, V. Joekar-Niasar and P. J. Kleingeld, Micromodel study of two-phase flow under transient conditions: Quantifying effects of specific interfacial area, Water Resour. Res., 2014, 50(10), 8125–8140, DOI:10.1002/2014WR015388.
- Y. Liu, D. D. Nolte and L. J. Pyrak-Nolte, Hysteresis and interfacial energies in smooth-walled microfluidic channels, Water Resour. Res., 2011, 47(1), 1–9, DOI:10.1029/2010WR009541.
- L. J. Pyrak-Nolte, D. D. Nolte, D. Chen and N. J. Giordano, Relating capillary pressure to interfacial areas, Water Resour. Res., 2008, 44(6), 1–14, DOI:10.1029/2007WR006434.
- C. D. Tsakiroglou, M. A. Theodoropoulou and V. Karoutsos, Nonequilibrium capillary pressure and relative permeability curves of porous media, AIChE J., 2003, 49(10), 2472–2486, DOI:10.1002/aic.690491004.
- J. Avendaño, N. Lima, A. Quevedo and M. Carvalho, Effect of surface wettability on immiscible displacement in a microfluidic porous media, Energies, 2019, 12(4), 664, DOI:10.3390/en12040664.
- C. Chang, T. J. Kneafsey, J. Wan, T. K. Tokunaga and S. Nakagawa, Impacts of mixed-wettability on brine drainage and supercritical CO2 storage efficiency in a 2.5-D heterogeneous micromodel, Water Resour. Res., 2020, 56(7), e2019WR026789, DOI:10.1029/2019WR026789.
- R. Holtzman, Effects of pore-scale disorder on fluid displacement in partially-wettable porous media, Sci. Rep., 2016, 6(1), 1–10, DOI:10.1038/srep36221.
- R. Holtzman and E. Segre, Wettability stabilizes fluid invasion into porous media via nonlocal, cooperative pore filling, Phys. Rev. Lett., 2015, 115(16), 164501, DOI:10.1103/PhysRevLett.115.164501.
- S. S. Datta, H. Chiang, T. S. Ramakrishnan and D. A. Weitz, Spatial fluctuations of fluid velocities in flow through a three-dimensional porous medium, Phys. Rev. Lett., 2013, 111, 064501, DOI:10.1103/PhysRevLett.111.064501.
- S. Roman, C. Soulaine, M. A. AlSaud, A. Kovscek and H. Tchelepi, Particle velocimetry analysis of immiscible two-phase flow in micromodels, Adv. Water Resour., 2016, 95, 199–211, DOI:10.1016/j.advwatres.2015.08.015.
- J. C. Perrin, M. Krause, C. W. Kuo, L. Miljkovic, E. Charoba and S. M. Benson, Core-scale experimental study of relative permeability properties of CO2 and brine in reservoir rocks, Energy Procedia, 2009, 1(1), 3515–3522, DOI:10.1016/j.egypro.2009.02.144.
- A. Chatenever and J. C. Calhoun, Visual examinations of fluid behavior in porous media - Part I, JPT, J. Pet. Technol., 1952, 4(06), 149–156, DOI:10.2118/135-g.
- R. Lenormand, C. Zarcone and A. Sarr, Mechanisms of the displacement of one fluid by another in a network of capillary ducts, J. Fluid Mech., 1983, 135, 337–353, DOI:10.1017/S0022112083003110.
- N. K. Karadimitriou, V. Joekar-Niasar, S. M. Hassanizadeh, P. J. Kleingeld and L. J. Pyrak-Nolte, A novel deep reactive ion etched (DRIE) glass micro-model for two-phase flow experiments, Lab Chip, 2012, 12(18), 3413–3418, 10.1039/c2lc40530j.
- K. Xu, T. Liang, P. Zhu, P. Qi, J. Lu and C. Huh, et al., A 2.5-D glass micromodel for investigation of multi-phase flow in porous media, Lab Chip, 2017, 17(4), 640–646, 10.1039/c6lc01476c.
- Y. Li, F. Kazemifar, G. Blois and K. T. Christensen, Micro-PIV measurements of multiphase flow of water and liquid CO2 in 2-D heterogeneous porous micromodels, Water Resour. Res., 2017, 53(7), 6178–6196, DOI:10.1002/2017WR020850.
- Y. Li, G. Blois, F. Kazemifar and R. S. Molla, Pore-scale dynamics of liquid CO2–water displacement in 2D axisymmetric porous micromodels under strong drainage and weak imbibition conditions: High-speed μPIV measurements, Front. Water, 2021, 3, 710370, DOI:10.3389/frwa.2021.710370.
- M. Zhang, J. Wu, L. Wang, K. Xiao and W. Wen, A simple method for fabricating multi-layer PDMS structures for 3D microfluidic chips, Lab Chip, 2010, 10(9), 1199–1203, 10.1039/b923101c.
- M. Kim, B. U. Moon and C. H. Hidrovo, Enhancement of the thermo-mechanical properties of PDMS molds for the hot embossing of PMMA microfluidic devices, J. Micromech. Microeng., 2013, 23(9), 095024, DOI:10.1088/0960-1317/23/9/095024.
- B. S. Hardy, K. Uechi, J. Zhen and H. P. Kavehpour, The deformation of flexible PDMS microchannels under a pressure-driven flow, Lab Chip, 2009, 9(7), 935–938, 10.1039/B813061B.
- R. Singh, M. Sivaguru, G. A. Fried, B. W. Fouke, R. A. Sanford and M. Carrera, et al., Real rock-microfluidic flow cell: A test bed for real-time in situ analysis of flow, transport, and reaction in a subsurface reactive transport environment, J. Contam. Hydrol., 2017, 204, 28–39, DOI:10.1016/j.jconhyd.2017.08.001.
- W. Song, T. W. de Haas, H. Fadaei and D. Sinton, Chip-off-the-old-rock: The study of reservoir-relevant geological processes with real-rock micromodels, Lab Chip, 2014, 14(22), 4382–4390, 10.1039/C4LC00608A.
- B. Zhao, C. W. MacMinn and R. Juanes, Wettability control on multiphase flow in patterned microfluidics, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(37), 10251–10256, DOI:10.1073/pnas.1603387113.
- S. J. Cox, A. Davarpanah and W. R. Rossen, Interface shapes in microfluidic porous media: Conditions allowing steady, simultaneous two-phase flow, Transp. Porous Media, 2023, 147(1), 197–216, DOI:10.1007/s11242-023-01905-9.
- S. Morais, N. Liu, A. Diouf, D. Bernard, C. Lecoutre and Y. Garrabos, et al., Monitoring CO2 invasion processes at the pore scale using geological labs on chip, Lab Chip, 2016, 16(18), 3493–3502, 10.1039/c6lc00830e.
- S. Morais, A. Cario, N. Liu, D. Bernard, C. Lecoutre and Y. Garrabos, et al., Studying key processes related to CO2 underground storage at the pore scale using high-pressure micromodels, React. Chem. Eng., 2020, 5(7), 1156–1185, 10.1039/d0re00023j.
- C. Zhang, M. Oostrom, J. W. Grate, T. W. Wietsma and M. G. Warner, Liquid CO2 displacement of water in a dual-permeability pore network micromodel, Environ. Sci. Technol., 2011, 45(17), 7581–7588, DOI:10.1021/es200983n.
- M. Buchgraber, M. Al-Dossary, C. M. Ross and A. R. Kovscek, Creation of a dual-porosity micromodel for pore-level visualization of multiphase flow, J. Pet. Sci. Eng., 2012, 86–87, 27–38, DOI:10.1016/j.petrol.2012.03.012.
- W. Yun, C. M. Ross, S. Roman and A. R. Kovscek, Creation of a dual-porosity and dual-depth micromodel for the study of multiphase flow in complex porous media, Lab Chip, 2017, 17(8), 1462–1474 RSC.
- Y. A. Alzahid, P. Mostaghimi, A. Gerami, A. Singh, K. Privat and T. Amirian, et al., Functionalisation of polydimethylsiloxane (PDMS) microfluidic devices coated with rock minerals, Sci. Rep., 2018, 8(1), 1–15, DOI:10.1038/s41598-018-33495-8.
- W. Song, F. Ogunbanwo, M. Steinsbø, M. A. Fernø and A. R. Kovscek, Mechanisms of multiphase reactive flow using biogenically calcite-functionalized micromodels, Lab Chip, 2018, 18(24), 3881–3891, 10.1039/C8LC00793D.
- S. G. Lee, H. Lee, A. Gupta, S. Chang and P. S. Doyle, Site-selective in situ grown calcium carbonate micromodels with tunable geometry, porosity, and wettability, Adv. Funct. Mater., 2016, 26(27), 4896–4905, DOI:10.1002/adfm.201600573.
- W. Wang, S. Chang and A. Gizzatov, Toward reservoir-on-a-chip: Fabricating reservoir micromodels by in situ growing calcium carbonate nanocrystals in microfluidic channels, ACS Appl. Mater. Interfaces, 2017, 9(34), 29380–29386, DOI:10.1021/acsami.7b10746.
- R. M. Rahman, E. Niemur, G. Blois, F. Kazemifar, M. Kim and Y. Li, A novel microfluidic approach to quantify pore-scale mineral dissolution in porous media, Sci. Rep., 2025, 15(1), 6342, DOI:10.1038/s41598-025-90429-x.
- C. Soulaine, S. Roman, A. Kovscek and H. A. Tchelepi, Mineral dissolution and wormholing from a pore-scale perspective, J. Fluid Mech., 2017, 827, 457–483, DOI:10.1017/jfm.2017.499.
- F. Rembert, A. Stolz and C. Soulaine, A microfluidic chip for geoelectrical monitoring of critical zone processes, Lab Chip, 2023, 23(15), 3433–3442, 10.1039/D3LC00377A.
- N. Raventhiran, R. S. Molla, K. Nandishwara, E. Johnson and Y. Li, Design and fabrication of a novel on-chip pressure sensor for microchannels, Lab Chip, 2022, 22(22), 4306–4316, 10.1039/d2lc00648k.
- I. M. Zarikos, S. M. Hassanizadeh, L. M. van Oosterhout and W. van Oordt, Manufacturing a micro-model with integrated fibre optic pressure sensors, Transp. Porous Media, 2018, 122(1), 221–234, DOI:10.1007/s11242-018-1000-y.
- C. Zhang, M. Oostrom, T. W. Wietsma, J. W. Grate and M. G. Warner, Influence of viscous and capillary forces on immiscible fluid displacement: Pore-scale experimental study in a water-wet micromodel demonstrating viscous and capillary fingering, Energy Fuels, 2011, 25(8), 3493–3505, DOI:10.1021/ef101732k.
- M. Kim, A. Sell and D. Sinton, Aquifer-on-a-chip: Understanding pore-scale salt precipitation dynamics during CO2 sequestration, Lab Chip, 2013, 13(13), 2508, 10.1039/c3lc00031a.
- L. Zuo, C. Zhang, R. W. Falta and S. M. Benson, Micromodel investigations of CO2 exsolution from carbonated water in sedimentary rocks, Adv. Water Resour., 2013, 53, 188–197, DOI:10.1016/j.advwatres.2012.11.004.
- Y. Xiao, X. He, G. Ma, C. Zhao, J. Chu and H. Liu, Biomineralization and mineralization using microfluidics: A comparison study, J. Rock Mech. Geotech. Eng., 2024, 16(2), 661–669, DOI:10.1016/j.jrmge.2023.03.019.
- Y. Wang, C. Zhang, N. Wei, M. Oostrom, T. W. Wietsma and X. Li, et al., Experimental study of crossover from capillary to viscous fingering for supercritical CO2–water displacement in a homogeneous pore network, Environ. Sci. Technol., 2013, 47(1), 212–218, DOI:10.1021/es3014503.
- H. S. Rabbani, D. Or, Y. Liu, C. Y. Lai, N. B. Lu and S. S. Datta, et al., Suppressing viscous fingering in structured porous media, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(19), 4833–4838, DOI:10.1073/pnas.1800729115.
- W. B. Haines, Studies in the physical properties of soils, J. Agric. Sci., 1925, 15, 529–535 CrossRef CAS.
- R. T. Armstrong and S. Berg, Interfacial velocities and capillary pressure gradients during Haines jumps, Phys. Rev. E, 2013, 88(4), 043010, DOI:10.1103/PhysRevE.88.043010.
- A. Ferrari, J. Jimenez-Martinez, T. Le Borgne, Y. Méheust and I. Lunati, Challenges in modeling unstable two-phase flow experiments in porous micromodels, Water Resour. Res., 2015, 51(3), 1381–1400, DOI:10.1002/2014WR016384.
- A. Fakhari, Y. Li, D. Bolster and K. T. Christensen, A phase-field lattice Boltzmann model for simulating multiphase flows in porous media: Application and comparison to experiments of CO2 sequestration at pore scale, Adv. Water Resour., 2018, 114, 36–46, DOI:10.1016/j.advwatres.2018.02.005.
- I. Zacharoudiou, E. M. Chapman, E. S. Boek and J. P. Crawshaw, Pore-filling events in single junction micro-models with corresponding lattice Boltzmann simulations, J. Fluid Mech., 2017, 824, 550–573, DOI:10.1017/jfm.2017.363.
- Y. Chen, A. J. Valocchi, Q. Kang and H. S. Viswanathan, Inertial effects during the process of supercritical CO2 displacing brine in a sandstone: Lattice Boltzmann simulations based on the continuum-surface-force and geometrical wetting models, Water Resour. Res., 2019, 55(12), 11144–11165, DOI:10.1029/2019WR025746.
- S. M. Hassanizadeh and W. G. Gray, Thermodynamic basis of capillary pressure in porous media, Water Resour. Res., 1993, 29(10), 3389–3405, DOI:10.1029/93WR01495.
- S. M. Hassanizadeh and W. G. Gray, Mechanics and thermodynamics of multiphase flow in porous media including interphase boundaries, Adv. Water Resour., 1990, 13(4), 169–186, DOI:10.1016/0309-1708(90)90040-B.
- S. M. Hassanizadeh and W. G. Gray, Toward an improved description of the physics of two-phase flow, Adv. Water Resour., 1993, 16(1), 53–67, DOI:10.1016/0309-1708(93)90029-F.
- W. G. Gray, K. Bruning and C. T. Miller, Non-hysteretic functional form of capillary pressure in porous media, J. Hydraul. Res., 2019, 57(6), 747–759, DOI:10.1080/00221686.2019.1671520.
- J. E. McClure, R. T. Armstrong, M. A. Berrill, S. Schlüter, S. Berg and W. G. Gray, et al., Geometric state function for two-fluid flow in porous media, Phys. Rev. Fluids, 2018, 3(8), 084306, DOI:10.1103/PhysRevFluids.3.084306.
- C. T. Miller, K. Bruning, C. L. Talbot, J. E. McClure and W. G. Gray, Nonhysteretic capillary pressure in two-fluid porous medium systems: Definition, evaluation, validation, and dynamics, Water Resour. Res., 2019, 55(8), 6825–6849, DOI:10.1029/2018WR024586.
- J. T. Cheng, L. J. Pyrak-Nolte, D. D. Nolte and N. J. Giordano, Linking pressure and saturation through interfacial areas in porous media, Geophys. Res. Lett., 2004, 31(8), 1–4, DOI:10.1029/2003GL019282.
- R. Hu, J. Wan, Y. Kim and T. K. Tokunaga, Wettability impact on supercritical CO2 capillary trapping: Pore-scale visualization and quantification, Water Resour. Res., 2017, 53(8), 6377–6394, DOI:10.1002/2017WR020721.
- M. Trojer, M. L. Szulczewski and R. Juanes, Stabilizing fluid-fluid displacements in porous media through wettability alteration, Phys. Rev. Appl., 2015, 3(5), 054008, DOI:10.1103/PhysRevApplied.3.054008.
- R. A. Salathiel, Oil recovery by surface film drainage in mixed-wettability rocks, JPT, J. Pet. Technol., 1973, 25(10), 1216–1224, DOI:10.2118/4104-PA.
- W. G. Anderson, Wettability literature survey-Part 6: The effects of wettability on waterflooding, JPT, J. Pet. Technol., 1987, 39(12), 1605–1622, DOI:10.2118/16471-PA.
- S. Iglauer, M. A. Fernø, P. Shearing and M. J. Blunt, Comparison of residual oil cluster size distribution, morphology and saturation in oil-wet and water-wet sandstone, J. Colloid Interface Sci., 2012, 375(1), 187–192, DOI:10.1016/j.jcis.2012.02.025.
- M. Jung, M. Brinkmann, R. Seemann, T. Hiller, M. Sanchez De La Lama and S. Herminghaus, Wettability controls slow immiscible displacement through local interfacial instabilities, Phys. Rev. Fluids, 2016, 1(7), 074202, DOI:10.1103/PhysRevFluids.1.074202.
- R. Hu, J. Wan, Y. Kim and T. K. Tokunaga, Wettability effects on supercritical CO2–brine immiscible displacement during drainage: Pore-scale observation and 3D simulation, Int. J. Greenhouse Gas Control, 2017, 60, 129–139, DOI:10.1016/j.ijggc.2017.03.011.
- A. Irannezhad, B. K. Primkulov, R. Juanes and B. Zhao, Fluid-fluid displacement in mixed-wet porous media, Phys. Rev. Fluids, 2023, 8(1), L012301, DOI:10.1103/PhysRevFluids.8.L012301.
- A. Irannezhad, B. K. Primkulov, R. Juanes and B. Zhao, Characteristics of fluid-fluid displacement in model mixed-wet porous media: Patterns, pressures, and scalings, J. Fluid Mech., 2023, 967, 1–20, DOI:10.1017/jfm.2023.500.
- C. Zhang, K. Dehoff, N. Hess, M. Oostrom, T. W. Wietsma and A. J. Valocchi, et al., Pore-scale study of transverse mixing induced CaCO3 precipitation and permeability reduction in a model subsurface sedimentary system, Environ. Sci. Technol., 2010, 44(20), 7833–7838, DOI:10.1021/es1019788.
- J. Jiménez-Martínez, J. D. Hyman, Y. Chen, J. W. Carey, M. L. Porter and Q. Kang, et al., Homogenization of dissolution and enhanced precipitation induced by bubbles in multiphase flow systems, Geophys. Res. Lett., 2020, 47(7), e2020GL087163, DOI:10.1029/2020GL087163.
- J. Poonoosamy, C. Westerwalbesloh, G. Deissmann, M. Mahrous, E. Curti and S. V. Churakov, et al., A microfluidic experiment and pore scale modelling diagnostics for assessing mineral precipitation and dissolution in confined spaces, Chem. Geol., 2019, 528, 119264, DOI:10.1016/j.chemgeo.2019.07.039.
- L. Xu, P. Szymczak, R. Toussaint, E. G. Flekkøy and K. J. Måløy, Dissolution phase diagram in radial geometry, Front. Phys., 2020, 8, 1–12, DOI:10.3389/fphy.2020.00369.
- S. Xia and W. Song, Controls on microbially-induced carbonate precipitation in geologic porous media, Sci. Total Environ., 2024, 957, 177647, DOI:10.1016/j.scitotenv.2024.177647.
- A. Rufai and J. Crawshaw, Micromodel observations of evaporative drying and salt deposition in porous media, Phys. Fluids, 2017, 29(12), 1–12, DOI:10.1063/1.5004246.
- M. Nooraiepour, H. Fazeli, R. Miri and H. Hellevang, Effect of CO2 phase states and flow rate on salt precipitation in shale caprocks - A microfluidic study, Environ. Sci. Technol., 2018, 52(10), 6050–6060, DOI:10.1021/acs.est.8b00251.
- T. H. M. Ho and P. A. Tsai, Microfluidic salt precipitation: Implications for geological CO2 storage, Lab Chip, 2020, 20(20), 3806–3814, 10.1039/d0lc00238k.
- D. He, R. Xu, T. Ji and P. Jiang, Experimental investigation of the mechanism of salt precipitation in the fracture during CO2 geological sequestration, Int. J. Greenhouse Gas Control, 2022, 118, 103693, DOI:10.1016/j.ijggc.2022.103693.
- D. He, P. Jiang and R. Xu, Pore-scale experimental investigation of the effect of supercritical CO2 injection rate and surface wettability on salt precipitation, Environ. Sci. Technol., 2019, 53(24), 14744–14751, DOI:10.1021/acs.est.9b03323.
- A. M. Tartakovsky, G. Redden, P. C. Lichtner, T. D. Scheibe and P. Meakin, Mixing-induced precipitation: Experimental study and multiscale numerical analysis, Water Resour. Res., 2008, 44(6), 1–19, DOI:10.1029/2006WR005725.
- M. F. Fanizza, H. Yoon, C. Zhang, M. Oostrom, T. W. Wietsma and N. J. Hess, et al., Pore-scale evaluation of uranyl phosphate precipitation in a model groundwater system, Water Resour. Res., 2013, 49(2), 874–890, DOI:10.1002/wrcr.20088.
- T. W. Willingham, C. J. Werth and A. J. Valocchi, Evaluation of the effects of porous media structure on mixing-controlled reactions using pore-scale modeling and micromodel experiments, Environ. Sci. Technol., 2008, 42(9), 3185–3193, DOI:10.1021/es7022835.
- A. L. Harrison, G. M. Dipple, W. Song, I. M. Power, K. U. Mayer and A. Beinlich, et al., Changes in mineral reactivity driven by pore fluid mobility in partially wetted porous media, Chem. Geol., 2017, 463, 1–11, DOI:10.1016/j.chemgeo.2017.05.003.
- V. Boyd, H. Yoon, C. Zhang, M. Oostrom, N. Hess and B. Fouke, et al., Influence of Mg2+ on CaCO3 precipitation during subsurface reactive transport in a homogeneous silicon-etched pore network, Geochim. Cosmochim. Acta, 2014, 135, 321–335, DOI:10.1016/j.gca.2014.03.018.
- L. Li, J. R. Sanchez, F. Kohler, A. Røyne and D. K. Dysthe, Microfluidic control of nucleation and growth of CaCO3, Cryst. Growth Des., 2018, 18(8), 4426–4434, DOI:10.1021/acs.cgd.8b00508.
- R. Chang, S. Kim, S. Lee, S. Choi, M. Kim and Y. Park, Calcium carbonate precipitation for CO2 storage and utilization: A review of the carbonate crystallization and polymorphism, Front. Energy Res., 2017, 5, 17, DOI:10.3389/fenrg.2017.00017.
- Y. S. Jun, D. E. Giammar and C. J. Werth, Impacts of geochemical reactions on geologic carbon sequestration, Environ. Sci. Technol., 2013, 47(1), 3–8, DOI:10.1021/es3027133.
- J. Poonoosamy, C. Soulaine, A. Burmeister, G. Deissmann, D. Bosbach and S. Roman, Microfluidic flow-through reactor and 3D Raman imaging for in situ assessment of mineral reactivity in porous and fractured porous media, Lab Chip, 2020, 20(14), 2562–2571, 10.1039/d0lc00360c.
- J. Poonoosamy, R. Lu, M. I. Lönartz, G. Deissmann, D. Bosbach and Y. Yang, A lab-on-a-chip experiment for upscaling diffusivity of evolving porous media, Energies, 2022, 15(6), 2160, DOI:10.3390/en15062160.
- M. I. Lönartz, Y. Yang, G. Deissmann, D. Bosbach and J. Poonoosamy, Capturing the dynamic processes of porosity clogging, Water Resour. Res., 2023, 59(11), 1–14, DOI:10.1029/2023WR034722.
- R. Singh, H. Yoon, R. A. Sanford, L. Katz, B. W. Fouke and C. J. Werth, Metabolism-induced CaCO3 biomineralization during reactive transport in a micromodel: Implications for porosity alteration, Environ. Sci. Technol., 2015, 49(20), 12094–12104, DOI:10.1021/acs.est.5b00152.
- C. Wu, J. Chu, S. Wu, L. Cheng and L. A. van Paassen, Microbially induced calcite precipitation along a circular flow channel under a constant flow condition, Acta Geotech., 2019, 14(3), 673–683, DOI:10.1007/s11440-018-0747-1.
- Y. Wang, K. Soga, J. T. DeJong and A. J. Kabla, A microfluidic chip and its use in characterizing the particle-scale behavior of microbial-induced calcium carbonate precipitation (MICP), Geotechnique., 2019, 69(12), 1086–1094, DOI:10.1680/jgeot.18.P.031.
- K. E. Eide, CO2 sequestration: The effect of carbonate dissolution on reservoir rock integrity, Master's thesis, Norwegian University of Science and Technology (NTNU), 2012, https://hdl.handle.net/11250/239780 Search PubMed.
- C. X. Zhou, R. Hu, H. W. Li, Z. Yang and Y. F. Chen, Pore-scale visualization and quantification of dissolution in microfluidic rough channels, Water Resour. Res., 2022, 58(11), e2022WR032255, DOI:10.1029/2022WR032255.
- L. Xu, P. Szymczak, R. Toussaint, E. G. Flekkøy and K. J. Måløy, Experimental observation of dissolution finger growth in radial geometry, Front. Phys., 2019, 7, 1–10, DOI:10.3389/fphy.2019.00096.
- C. Soulaine, S. Roman, A. Kovscek and H. A. Tchelepi, Pore-scale modelling of multiphase reactive flow: Application to mineral dissolution, J. Fluid Mech., 2018, 855, 616–645, DOI:10.1017/jfm.2018.655.
- P. Agrawal, A. Raoof, O. Iliev and M. Wolthers, Evolution of pore-shape and its impact on pore conductivity during CO2 injection in calcite: Single pore simulations and microfluidic experiments, Adv. Water Resour., 2020, 136, 103480, DOI:10.1016/j.advwatres.2019.103480.
- E. Marafini, M. La Rocca, A. Fiori, I. Battiato and P. Prestininzi, Suitability of 2D modelling to evaluate flow properties in 3D porous media, Transp. Porous Media, 2020, 134, 315–329 CrossRef.
- A. R. Kovscek, J. M. Nordbotten and M. A. Fernø, Scaling up FluidFlower results for carbon dioxide storage in geological media, Transp. Porous Media, 2024, 151(5), 975–1002 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |