Open Access Article
Open Access ArticleComputational insights into hydrogen interaction with the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/h2_char_0031_0304.gif) 1) and Ru (10
1) and Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/h2_char_0031_0304.gif) 0) surfaces: implications for alkane and polyolefin hydrogenolysis†
0) surfaces: implications for alkane and polyolefin hydrogenolysis†
Fabio Colasuonno ,
Sohaib Umer
,
Sohaib Umer and
Martina Lessio
and
Martina Lessio *
*
School of Chemistry, The University of New South Wales, Sydney, NSW 2052, Australia. E-mail: martina.lessio@unsw.edu.au
First published on 9th April 2025
Abstract
Hydrogen interaction with transition metal surfaces such as those exposed by ruthenium (Ru) nanoparticles is critical in applications like hydrogen storage and catalytic processes such as Fischer–Tropsch, Haber–Bosch, and plastic waste hydrogenolysis. While the Ru(0001) surface is well-studied, hydrogen interaction with the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and Ru (10
1) and Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) facets remains mostly underexplored. In this contribution, we use density functional theory calculations to investigate hydrogen adsorption and dissociation and provide insights into the adsorbed hydrogen role in catalytic polyolefin plastic hydrogenolysis. We start our investigation by exploring all the unique surface and subsurface sites for hydrogen adsorption and dissociation and identify hcp and higher hollow as the most favorable atomic hydrogens adsorption sites on the Ru (10
0) facets remains mostly underexplored. In this contribution, we use density functional theory calculations to investigate hydrogen adsorption and dissociation and provide insights into the adsorbed hydrogen role in catalytic polyolefin plastic hydrogenolysis. We start our investigation by exploring all the unique surface and subsurface sites for hydrogen adsorption and dissociation and identify hcp and higher hollow as the most favorable atomic hydrogens adsorption sites on the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and Ru (10
1) and Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, respectively. We find that atomic hydrogen can easily migrate on these surfaces to achieve the most stable arrangement at different coverages. We then combine these findings with ab initio thermodynamics and microkinetic modeling to build surface phase diagrams, which show that both surfaces are fully hydrogenated under typical catalytic conditions. We then study how the presence of a full hydrogen coverage affects the adsorption and dehydrogenation of butane as a proxy for polyethylene, as these are the initial steps in the catalytic hydrogenolysis of polyolefin plastic waste. We find that the adsorption energy of butane decreases when the two surfaces are fully hydrogenated but adsorption remains favorable. We then investigate two possible mechanisms for the dehydrogenation step. The most favorable dehydrogenation mechanism involves the reaction of a surface hydrogen with an alkane hydrogen to produce H2 gas and an adsorbed alkyl radical. However, both mechanisms have positive reaction free energies suggesting that polyolefin dehydrogenation will be slow on these surfaces.
0) surfaces, respectively. We find that atomic hydrogen can easily migrate on these surfaces to achieve the most stable arrangement at different coverages. We then combine these findings with ab initio thermodynamics and microkinetic modeling to build surface phase diagrams, which show that both surfaces are fully hydrogenated under typical catalytic conditions. We then study how the presence of a full hydrogen coverage affects the adsorption and dehydrogenation of butane as a proxy for polyethylene, as these are the initial steps in the catalytic hydrogenolysis of polyolefin plastic waste. We find that the adsorption energy of butane decreases when the two surfaces are fully hydrogenated but adsorption remains favorable. We then investigate two possible mechanisms for the dehydrogenation step. The most favorable dehydrogenation mechanism involves the reaction of a surface hydrogen with an alkane hydrogen to produce H2 gas and an adsorbed alkyl radical. However, both mechanisms have positive reaction free energies suggesting that polyolefin dehydrogenation will be slow on these surfaces.
Introduction
The investigation of the interactions between hydrogen and metal surfaces is an important and growing research field due to its multiple possible applications, spanning from hydrogen storage to catalysis. Specifically, in the field of catalysis, Ru nanoparticles have demonstrated outstanding performances in multiple reactions that use hydrogen gas such as the Haber–Bosch process, the Fischer–Tropsch process, and, in the last decade, the chemical conversion of plastic waste to fuels via hydrogenolysis.1–8 Nanoparticles typically expose a plethora of facets, some more prominent than others depending on their surface energy; however, specific facets can be selectively grown by engineering the synthetic process and tune the reactivity of the nanoparticle.9–13 In fact, different facets can have very different chemistry and catalytic capability. Thus, in the context of catalytic reactions using hydrogen, an understanding of the interactions of these surfaces with H2 and their hydrogen coverage under operating conditions is needed. The hydrogen coverage can alter the surface chemistry and consequently the catalytic ability of the surface.The most exposed surface for hcp Ru nanoparticles is the (0001) which is the most stable one and it is always exposed, for this reason it has been widely investigated experimentally and computationally.14–17 In a recent study by our group, we used ab initio thermodynamics and kinetics to investigate the hydrogen coverage of this surface under different conditions of H2 pressure and temperature, ranging from STM conditions to catalytic conditions relevant to polyolefin plastic waste hydrogenolysis.18 The (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and the (10
1) and the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) facets are also always exposed, despite to a lesser extent, as they constitute the edges of Ru nanoparticles as demonstrated by the calculated Wulff shape for Ru.19 Furthermore, their exposure can be enhanced via specific synthetic protocols and this has been shown to lead to higher catalytic activity towards reactions such as the hydrogen evolution reaction and the oxygen evolution reaction.9,20–23
0) facets are also always exposed, despite to a lesser extent, as they constitute the edges of Ru nanoparticles as demonstrated by the calculated Wulff shape for Ru.19 Furthermore, their exposure can be enhanced via specific synthetic protocols and this has been shown to lead to higher catalytic activity towards reactions such as the hydrogen evolution reaction and the oxygen evolution reaction.9,20–23
In this work, we aim to study the hydrogen coverage on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and the (10
1) and the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces of Ru under typical catalytic conditions for polyolefin plastic waste hydrogenolysis, a relatively new application of supported Ru nanoparticles. During hydrogenolysis, the large H2 pressures lead to the formation of atomic surface hydrogens that react with the plastic polymer breaking down the polymeric chain. In order to study these processes, we start our investigation focusing on the interaction between hydrogen and the investigated surfaces. Specifically, we analyze all the possible adsorption surface sites for both atomic and molecular hydrogen to identify the most stable ones; as part of this analysis, we also investigate the occupation of subsurface sites by atomic hydrogen. In addition, we characterize the energetics for atomic hydrogen to hop in between the most stable sites and diffuse on the surface. We then study the effect of the atomic hydrogen coverage on the dissociation energy of molecular hydrogen to establish whether the buildup of atomic hydrogen can prevent further H2 dissociation leading to submonolayer coverage. Finally, we use ab initio thermodynamics and microkinetic modeling to compute atomic hydrogen surface coverage phase diagrams that allow us to identify the most stable atomic hydrogen coverage under different conditions of H2 pressure and temperature. We find that the investigated surfaces are both characterized by a full atomic hydrogen surface coverages under catalytic conditions. We thus explore the effect of these surface conditions on the polyolefin hydrogenolysis mechanism initial steps that ultimately lead to C–C cleavage, specifically adsorption and dehydrogenation; to this end, we use butane as a proxy for polyethylene.
0) surfaces of Ru under typical catalytic conditions for polyolefin plastic waste hydrogenolysis, a relatively new application of supported Ru nanoparticles. During hydrogenolysis, the large H2 pressures lead to the formation of atomic surface hydrogens that react with the plastic polymer breaking down the polymeric chain. In order to study these processes, we start our investigation focusing on the interaction between hydrogen and the investigated surfaces. Specifically, we analyze all the possible adsorption surface sites for both atomic and molecular hydrogen to identify the most stable ones; as part of this analysis, we also investigate the occupation of subsurface sites by atomic hydrogen. In addition, we characterize the energetics for atomic hydrogen to hop in between the most stable sites and diffuse on the surface. We then study the effect of the atomic hydrogen coverage on the dissociation energy of molecular hydrogen to establish whether the buildup of atomic hydrogen can prevent further H2 dissociation leading to submonolayer coverage. Finally, we use ab initio thermodynamics and microkinetic modeling to compute atomic hydrogen surface coverage phase diagrams that allow us to identify the most stable atomic hydrogen coverage under different conditions of H2 pressure and temperature. We find that the investigated surfaces are both characterized by a full atomic hydrogen surface coverages under catalytic conditions. We thus explore the effect of these surface conditions on the polyolefin hydrogenolysis mechanism initial steps that ultimately lead to C–C cleavage, specifically adsorption and dehydrogenation; to this end, we use butane as a proxy for polyethylene.
Methods
Computational approach
All calculations were performed using the periodic Vienna Ab initio Simulation Package (VASP) 6.3.2.24–26 The Perdew–Burke–Ernzerhof (PBE) functional27 with the D3BJ dispersion scheme28,29 has been adopted throughout all the calculations. Nuclei and frozen core electrons were modeled using the projector augmented wave (PAW) scheme from VASP30 while valence electrons were modeled with plane waves with a 400 eV energy cut-off. A 4 × 4 × 1 Γ-centered Methfessel–Paxton grid was selected for k-points sampling for all the surface calculations, while for butane and hydrogen molecules only the Γ point was sampled. We selected a first-order Methfessel–Paxton smearing method with a smearing width of 0.2 eV for all the geometries involving the surface; for butane and hydrogen molecules a gaussian smearing method was used with a small smearing width of 0.001 eV in order to simulate the sharp difference between the occupied and unoccupied energy levels in molecules. All the structures were optimized until the maximum force on each atom was less than 0.03 eV Å−1. To verify that the optimized geometries represent actual minimum points on the potential energy surface, frequency calculations were carried out for all atoms belonging to the adsorbates as well as the first layer of the slab as this strategy represents a good balance between computational cost and accuracy as shown in section S1 of the ESI.† Thermochemistry corrections to the electronic energies (E) were derived from the frequency calculations and used to compute free energies (G) as shown in eqn (1):| G = E + ZPE + H(T) − T × S(T) | (1) |
The climbing-image nudged elastic band (CI-NEB) algorithm as implemented in the Vienna Transition State Tools (VTST) package for VASP was utilized for transition state (TS) searches.31 Furthermore, we refined and checked the TS structures derived with the CI-NEB method utilizing the dimer algorithm from the same package.32 A stricter force convergence criteria than the one for the optimization was selected for the TS optimization and set to 0.01 eV Å−1 for both the CI-NEB and dimer methods. All TS structures were confirmed to be an actual saddle point on the potential energy surface by performing a frequency analysis and ensuring that only one imaginary frequency was found. These results were also used to calculate G of the TS structures (according to eqn (1)) and derive the corresponding activation free energies.
Surfaces were modeled using a 4 × 4 supercell (a = 10.93 Å and b = 9.85 Å) for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface and a 3 × 2 supercell (a = 8.04 Å and b = 8.49 Å) for the (10
1) surface and a 3 × 2 supercell (a = 8.04 Å and b = 8.49 Å) for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) to be able to simulate a variety of hydrogen coverages. The slab thickness was set to three layers based on convergence tests (see section S1 of the ESI†) and the bottom layer was kept frozen for computational efficiency. In order to avoid self-interaction between slabs, we added 15 Å of vacuum space above the surface. Asymmetric unit cells were adopted for both surfaces, with adsorbates simulated only on the side of the slab allowed to relax. Therefore, we added dipole corrections in the direction orthogonal to the surface. To benchmark our surface models, we compared our calculated surface energy values (as shown in section S2 in the ESI†) with previously computed data available in the literature. Our methodology confirms the trend observed in the literature with the differences being imputable to the different choice of computational method.
0) to be able to simulate a variety of hydrogen coverages. The slab thickness was set to three layers based on convergence tests (see section S1 of the ESI†) and the bottom layer was kept frozen for computational efficiency. In order to avoid self-interaction between slabs, we added 15 Å of vacuum space above the surface. Asymmetric unit cells were adopted for both surfaces, with adsorbates simulated only on the side of the slab allowed to relax. Therefore, we added dipole corrections in the direction orthogonal to the surface. To benchmark our surface models, we compared our calculated surface energy values (as shown in section S2 in the ESI†) with previously computed data available in the literature. Our methodology confirms the trend observed in the literature with the differences being imputable to the different choice of computational method.
Ab initio thermodynamics
Similarly to our previous work on the Ru (0001) surface,18 we utilize ab initio thermodynamics to compute surface phase diagrams that depict the most thermodynamically stable atomic hydrogen coverage resulting from the direct dissociation of H2, defined as in eqn (2), on the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and the Ru (10
1) and the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces under various conditions of temperature and H2 pressure.
0) surfaces under various conditions of temperature and H2 pressure.| H2(g) + 2* → 2H* | (2) |
In order to obtain the aforementioned phase diagrams, we need to calculate the formation free energies for each coverage resulting from different numbers of H2 molecules directly dissociating on the bare surface from gas phase (ΔGf), as described by eqn (3):
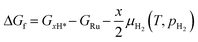 | (3) |
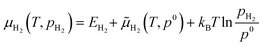 | (4) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) H2(T, p0) have been derived from the JANAF-NIST thermochemistry tables adopting the methodology described by Sholl.33 The
H2(T, p0) have been derived from the JANAF-NIST thermochemistry tables adopting the methodology described by Sholl.33 The  term is included to account for the H2 pressure (pH2) contribution, with p0 being a reference H2 pressure, for simplicity assumed to be standard pressure (i.e., 1 bar).
term is included to account for the H2 pressure (pH2) contribution, with p0 being a reference H2 pressure, for simplicity assumed to be standard pressure (i.e., 1 bar).
By creating plots of ΔGf vs. μH2 − μH2(T, pH2), with μH2 being μH2(T, pH2) evaluated at 0 K and 1 bar, the data needed to generate the surface phase diagrams were obtained. Specifically, in each of these plots, the H2 pressure was fixed and the temperature was varied across a range (refer to Fig. S1 of the ESI†) to determine the most stable coverage, defined as the one with the most negative ΔGf under the given conditions. This process has been explained in detail in our previous work.18
In addition to the cumulative direct dissociation energy ΔGf, we calculated the stepwise direct dissociation free energy (ΔGDiss) to assess the effect of H* coverage on the H2 dissociation favorability. ΔGDiss is calculated as follows:
 | (5) |
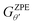 is the ZPE corrected free energy of a Ru surface at θ′H* coverage (which is the starting hydrogen coverage plotted in Fig. 1) with θ = θ′ + 2H*, and
is the ZPE corrected free energy of a Ru surface at θ′H* coverage (which is the starting hydrogen coverage plotted in Fig. 1) with θ = θ′ + 2H*, and  is the ZPE corrected free energy of a gas phase hydrogen molecule.
is the ZPE corrected free energy of a gas phase hydrogen molecule.
Microkinetic modeling
The thermodynamic study is completed with a microkinetic analysis in which rate constants for each step are used to calculate the rate of the overall process, and by solving the associated differential equations the concentration of each species is obtained at different temperatures and H2 pressures. For this purpose we followed the procedure used by López et al. to study the hydrogen coverage on MXene materials.34 Specifically, the barrierless Hertz–Knudsen equation is used to determine H2 gas dissociative adsorption rate constant (kads) as shown in eqn (6):
 | (6) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, and 12 on the (10
1) surface, and 12 on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface), S is the sticking coefficient for which we adopted a value of 0.001 in order to describe the observed high sticking probability,35,36 and m is the mass of H2. On the other hand, the rate constant for H* associative desorption to give H2 gas (kdes) has been computed by means of the Hertz–Knudsen equation for activated processes as shown in eqn (7):
0) surface), S is the sticking coefficient for which we adopted a value of 0.001 in order to describe the observed high sticking probability,35,36 and m is the mass of H2. On the other hand, the rate constant for H* associative desorption to give H2 gas (kdes) has been computed by means of the Hertz–Knudsen equation for activated processes as shown in eqn (7):
 | (7) |
| Gdes = GH2 + G2* − 2GH* | (8) |
Results and discussion
Surface hydrogen coverage under experimental catalytic conditions
We started our study by investigating the most stable surface sites for H2 and atomic hydrogen adsorption. Surface site definitions are provided in Fig. S3† and adsorption energy results are summarized in Tables S7 and S8 of the ESI.† For both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, the only stable site for H2 adsorption is the higher top; all the other explored sites led to spontaneous dissociation upon optimization. On the (10
0) surfaces, the only stable site for H2 adsorption is the higher top; all the other explored sites led to spontaneous dissociation upon optimization. On the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, the most stable site for H* is the hcp site, followed by the fcc site, and then the fourfold hollow site. On the (10
1) surface, the most stable site for H* is the hcp site, followed by the fcc site, and then the fourfold hollow site. On the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, atomic hydrogen prefers to adsorb on the higher hollow site, closely followed by the higher bridge (less then 0.01 eV difference in adsorption energy), meaning that both sites are likely to be occupied.
0) surface, atomic hydrogen prefers to adsorb on the higher hollow site, closely followed by the higher bridge (less then 0.01 eV difference in adsorption energy), meaning that both sites are likely to be occupied.
In addition to the surface sites, we also investigated subsurface sites occupation inspired by findings widely reported for Pd and its alloys as hydrogen storage materials.38 In particular, we tested the octahedral site for both surfaces given that it has been reported to be the most stable subsurface site for Ru;39 this site is located underneath the highly stable hcp and fcc sites on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface and higher hollow and higher bridge sites on the (10
1) surface and higher hollow and higher bridge sites on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (Fig. S4 in the ESI†). For the (10
0) surface (Fig. S4 in the ESI†). For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, we also tested the tetragon pyramidal one, which is located underneath the highly stable fourfold hollow sites. All the investigated cases have either a positive reaction energy for the migration of H* from a surface to the subsurface site located underneath or the subsurface H* spontaneously migrates to the surface upon optimization. Specifically, for the octahedral site we found that the subsurface H* spontaneously migrates to the surface on the bare (10
1) surface, we also tested the tetragon pyramidal one, which is located underneath the highly stable fourfold hollow sites. All the investigated cases have either a positive reaction energy for the migration of H* from a surface to the subsurface site located underneath or the subsurface H* spontaneously migrates to the surface upon optimization. Specifically, for the octahedral site we found that the subsurface H* spontaneously migrates to the surface on the bare (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, while the reaction energy for the surface → subsurface migration is 0.96 eV on the bare (10
1) surface, while the reaction energy for the surface → subsurface migration is 0.96 eV on the bare (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. The (10
0) surface. The (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) tetragon pyramidal site was also found to be unstable upon optimization. Previous studies have shown that a higher hydrogen surface coverage can increase the favorability of subsurface migration on the Ru (0001) surface.39–41 Therefore, we calculated the surface → subsurface migration reaction energy starting from a surface fully covered in H* and moving one H* from a surface site to the one directly underneath it. On the (10
1) tetragon pyramidal site was also found to be unstable upon optimization. Previous studies have shown that a higher hydrogen surface coverage can increase the favorability of subsurface migration on the Ru (0001) surface.39–41 Therefore, we calculated the surface → subsurface migration reaction energy starting from a surface fully covered in H* and moving one H* from a surface site to the one directly underneath it. On the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, the subsurface H* occupying an octahedral site no longer spontaneously migrates to the corresponding surface site but the subsurface site occupation remains non-favorable with a surface → subsurface migration reaction energy of 0.18 eV; for the tetragon pyramidal site, the subsurface H* spontaneously migrates to the corresponding surface fourfold hollow site while displacing the H* nearby to a bridge site. For the fully covered (10
1) surface, the subsurface H* occupying an octahedral site no longer spontaneously migrates to the corresponding surface site but the subsurface site occupation remains non-favorable with a surface → subsurface migration reaction energy of 0.18 eV; for the tetragon pyramidal site, the subsurface H* spontaneously migrates to the corresponding surface fourfold hollow site while displacing the H* nearby to a bridge site. For the fully covered (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, the surface → subsurface migration reaction energy towards an octahedral site is slightly more favorable than on the bare surface, with a reaction energy of 0.77 eV. Overall, based on these results, we concluded that subsurface site occupation of hydrogen atoms does not need to be considered for the (10
0) surface, the surface → subsurface migration reaction energy towards an octahedral site is slightly more favorable than on the bare surface, with a reaction energy of 0.77 eV. Overall, based on these results, we concluded that subsurface site occupation of hydrogen atoms does not need to be considered for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces of Ru.
0) surfaces of Ru.
We then proceeded to study the energetics for H2 dissociation at the surfaces and how it is affected by H* coverage based on our findings for the (0001) surface showing a strong effect of H* coverage on the H2 adsorption and dissociation energetics. To this end, we first generated different H* coverages spanning from 0 ML to 1 ML, and for each coverage we established the most favorable arrangement of atoms as reported in Fig. S5 and S6 in the ESI.† We modeled the dissociation of H2 as direct dissociation from gas phase (see eqn (2)) rather than a two-step process with H2 adsorption followed by dissociation like we did in our previous work on the (0001) surface. This is based on our findings showing that H2 molecular adsorption can only occur on the higher top sites while dissociation on all the remaining surface sites is not only spontaneous upon optimization but also significantly more favorable (at least 0.4 eV, see Tables S7 and S8 in the ESI†).
The H2 direct dissociation energy (ΔGDiss, defined in eqn (5)) shows an overall increasing trend as a function of H* coverage on both the investigated surfaces (Fig. 1, raw data reported in Tables S9 and S10 in the ESI†). More specifically, ΔGDiss has a flat trend up to 0.375 ML for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface and 0.333 ML (10
1) surface and 0.333 ML (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface with a subsequent increase of 0.29 eV and 0.37 eV, respectively. These results can be explained based on different sites being occupied at different coverages. For the (10
0) surface with a subsequent increase of 0.29 eV and 0.37 eV, respectively. These results can be explained based on different sites being occupied at different coverages. For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, H* exclusively occupies hcp sites for starting coverages up to 0.375 ML. Once the coverage reaches 0.5 ML, there are no more hcp sites available and the fcc sites are in too close proximity to be occupied, causing the fourfold hollow sites to be occupied. Since the fourfold hollow sites are less stable than the hcp we observe a sharp increase in the dissociation energy. For the (10
1) surface, H* exclusively occupies hcp sites for starting coverages up to 0.375 ML. Once the coverage reaches 0.5 ML, there are no more hcp sites available and the fcc sites are in too close proximity to be occupied, causing the fourfold hollow sites to be occupied. Since the fourfold hollow sites are less stable than the hcp we observe a sharp increase in the dissociation energy. For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, H* occupies the higher bridge sites for starting coverages up to 0.334 ML and the direct dissociation energy shows a slight decrease as a function of coverage, indicating attractive lateral H–H interactions. When the starting coverage reaches 0.5 ML, all the newly adsorbed hydrogen atoms occupy higher hollow sites progressively displacing the H* previously sitting on the nearby higher bridge sites to higher hollow sites due to the strong lateral repulsion occurring between H* on close sites; at 1 ML coverage all H* occupy higher hollow sites. When comparing results across the two surfaces, we observe that H2 dissociation is consistently more favorable on the (10
0) surface, H* occupies the higher bridge sites for starting coverages up to 0.334 ML and the direct dissociation energy shows a slight decrease as a function of coverage, indicating attractive lateral H–H interactions. When the starting coverage reaches 0.5 ML, all the newly adsorbed hydrogen atoms occupy higher hollow sites progressively displacing the H* previously sitting on the nearby higher bridge sites to higher hollow sites due to the strong lateral repulsion occurring between H* on close sites; at 1 ML coverage all H* occupy higher hollow sites. When comparing results across the two surfaces, we observe that H2 dissociation is consistently more favorable on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface than on the (10
1) surface than on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. This difference can be promptly explained with a comparison of the average H* coordination number (CN) across its adsorption sites at 1 ML of H* coverage on the two surfaces: the average H* CN on the (10
0) surface. This difference can be promptly explained with a comparison of the average H* coordination number (CN) across its adsorption sites at 1 ML of H* coverage on the two surfaces: the average H* CN on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (4.66) is lower than on the (10
1) surface (4.66) is lower than on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (5.5), indicating a stronger driving force for the (10
0) surface (5.5), indicating a stronger driving force for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) H* adsorption sites to be saturated by hydrogen.
1) H* adsorption sites to be saturated by hydrogen.
Overall, we found that for both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and the (10
1) and the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface ΔGDiss depends on H* coverage and it becomes less favorable for coverages >0.5 ML due to different sites being occupied. However, a large driving force for H2 dissociation is consistently observed for all coverages, with dissociation spontaneously occurring upon optimization. This behavior is very different from what we observed on the (0001) surface in our previous work, for which H2 adsorption cannot occur once the H* coverage reaches 0.875 ML meaning that a full monolayer of atomic hydrogen cannot be achieved on this surface.18 Given how favorable H2 dissociation is on the (10
0) surface ΔGDiss depends on H* coverage and it becomes less favorable for coverages >0.5 ML due to different sites being occupied. However, a large driving force for H2 dissociation is consistently observed for all coverages, with dissociation spontaneously occurring upon optimization. This behavior is very different from what we observed on the (0001) surface in our previous work, for which H2 adsorption cannot occur once the H* coverage reaches 0.875 ML meaning that a full monolayer of atomic hydrogen cannot be achieved on this surface.18 Given how favorable H2 dissociation is on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, we checked the stability of coverages above 1 ML. For both surfaces, dissociation does not occur spontaneously upon optimization at 1 ML; however, it is still energetically favorable over the Ru (10
0) surfaces, we checked the stability of coverages above 1 ML. For both surfaces, dissociation does not occur spontaneously upon optimization at 1 ML; however, it is still energetically favorable over the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (ΔGDiss = −0.56 eV) while it is not favorable for the (10
1) surface (ΔGDiss = −0.56 eV) while it is not favorable for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (ΔGDiss = 0.27 eV).
0) surface (ΔGDiss = 0.27 eV).
Once H2 dissociates on a surface, the resulting H* may need to diffuse over the surface to reach the most stable configuration. We therefore studied the energetics of H* diffusion between the most stable surface sites identified earlier in this study. In particular, for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, we identified two migration pathways for H* atoms to diffuse between hcp sites: hcp site → fcc site → hcp site and hcp site → fourfold hollow site → fcc site → hcp site (Fig. 2a). We therefore calculated the activation energies for hcp site → fcc site, hcp site → fourfold hollow site, and fourfold hollow → fcc site diffusion at different H* coverages (Table 1). Backward activation energies were also calculated as H* might first adsorb at fcc and fourfold hollow sites and then migrate to hcp given the similar stability of these sites (Table S7†). The hcp → fcc activation energy shows negligible dependence on H* coverage for coverages from 0.062 ML to 0.5 ML. At higher coverages, the hcp → fcc migration could not be simulated due to lateral repulsion from neighboring H* atoms forcing the fcc H* to spontaneously migrate back to the hcp site upon optimization. For the hcp → fourfold hollow activation energy dependence on H* coverage is also mostly negligible. Overall, all activation energies are sufficiently low that we can expect diffusion to occur at all coverages investigated for both pathways. At H* coverage >0.5 ML, fourfold hollow sites start being occupied; hence we have investigated migration in between these sites, which are sufficiently close for H* to diffuse directly from one to the other (Fig. 2a). The corresponding activation energy has been calculated at 0.875 ML since these sites can be occupied only at high H* coverages and resulted to be 0.09 eV.
1) surface, we identified two migration pathways for H* atoms to diffuse between hcp sites: hcp site → fcc site → hcp site and hcp site → fourfold hollow site → fcc site → hcp site (Fig. 2a). We therefore calculated the activation energies for hcp site → fcc site, hcp site → fourfold hollow site, and fourfold hollow → fcc site diffusion at different H* coverages (Table 1). Backward activation energies were also calculated as H* might first adsorb at fcc and fourfold hollow sites and then migrate to hcp given the similar stability of these sites (Table S7†). The hcp → fcc activation energy shows negligible dependence on H* coverage for coverages from 0.062 ML to 0.5 ML. At higher coverages, the hcp → fcc migration could not be simulated due to lateral repulsion from neighboring H* atoms forcing the fcc H* to spontaneously migrate back to the hcp site upon optimization. For the hcp → fourfold hollow activation energy dependence on H* coverage is also mostly negligible. Overall, all activation energies are sufficiently low that we can expect diffusion to occur at all coverages investigated for both pathways. At H* coverage >0.5 ML, fourfold hollow sites start being occupied; hence we have investigated migration in between these sites, which are sufficiently close for H* to diffuse directly from one to the other (Fig. 2a). The corresponding activation energy has been calculated at 0.875 ML since these sites can be occupied only at high H* coverages and resulted to be 0.09 eV.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface as a function of hydrogen coverage. Values for the backward process are reported in brackets. Energies are reported at 0 K with ZPE corrections
1) surface as a function of hydrogen coverage. Values for the backward process are reported in brackets. Energies are reported at 0 K with ZPE corrections
| Atomic hydrogen coverage [ML] | hcp → fcc activation energy [eV] | hcp → fourfold hollow activation energy [eV] | Fourfold hollow → fcc activation energy [eV] |
|---|---|---|---|
| 0.062 | 0.14 (0.16) | 0.16 (0.22) | 0.21 (0.17) |
| 0.125 | 0.15 (0.17) | 0.16 (0.22) | 0.22 (0.18) |
| 0.500 | 0.13 (0.15) | 0.11 (0.18) | 0.11 (0.06) |
| 0.875 | — | 0.09 (0.16) | — |
For the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface we do not explore the migration pathway linking the most stable higher bridge sites, because H2 dissociation was found to spontaneously lead to the most stable arrangement of H*. We instead focused on two other migration pathways and calculated the associated barriers (Table 2): higher bridge site → higher hollow site and higher hollow site → lower hollow site → higher hollow site (Fig. 2b). The first pathway is important because up to 0.5 ML H* coverage only higher bridge sites are occupied but beyond this coverage a newly added H* adsorbs on a higher hollow site and forces a neighboring higher bridge H* to move to a higher hollow site. The second pathway is important as the migration between neighboring higher hollow sites can only occur via a lower hollow site. The higher bridge → higher hollow pathway was found to be essentially barrierless while the higher hollow → lower hollow pathway presents a more significant activation barrier for H* migration. That said, they are sufficiently small at all investigated H* coverages that a fast diffusion process should occur on this surface as well. Thus, overall, the most favorable arrangement of hydrogen atoms can be achieved on both the (10
0) surface we do not explore the migration pathway linking the most stable higher bridge sites, because H2 dissociation was found to spontaneously lead to the most stable arrangement of H*. We instead focused on two other migration pathways and calculated the associated barriers (Table 2): higher bridge site → higher hollow site and higher hollow site → lower hollow site → higher hollow site (Fig. 2b). The first pathway is important because up to 0.5 ML H* coverage only higher bridge sites are occupied but beyond this coverage a newly added H* adsorbs on a higher hollow site and forces a neighboring higher bridge H* to move to a higher hollow site. The second pathway is important as the migration between neighboring higher hollow sites can only occur via a lower hollow site. The higher bridge → higher hollow pathway was found to be essentially barrierless while the higher hollow → lower hollow pathway presents a more significant activation barrier for H* migration. That said, they are sufficiently small at all investigated H* coverages that a fast diffusion process should occur on this surface as well. Thus, overall, the most favorable arrangement of hydrogen atoms can be achieved on both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and the (10
1) and the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface upon H2 dissociation. Our results reporting a small effect of the H* coverage on the migration activation energy compare well with previously reported data for the Ru (0001) surface.39
0) surface upon H2 dissociation. Our results reporting a small effect of the H* coverage on the migration activation energy compare well with previously reported data for the Ru (0001) surface.39
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface as a function of hydrogen coverage. Values for the backward process are reported in brackets. Energies are reported at 0 K with ZPE corrections
0) surface as a function of hydrogen coverage. Values for the backward process are reported in brackets. Energies are reported at 0 K with ZPE corrections
| Atomic hydrogen coverage [ML] | Higher bridge → higher hollow activation energy [eV] | Higher hollow → lower hollow activation energy [eV] |
|---|---|---|
| 0.083 | 0.00 (0.01) | 0.14 (0.21) |
| 0.250 | 0.01 (0.02) | 0.19 (0.25) |
| 0.583 | 0.06 (0.08) | — |
In order to determine the expected H* coverage under different temperature and H2 pressure conditions, we built a surface phase diagram according to ab initio thermodynamics (Methods section) for both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (Fig. 3a) and the (10
1) surface (Fig. 3a) and the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (Fig. 3b); the phases displayed in these diagrams represent the most stable H* coverage at the given conditions. Both surfaces show that coverages lower than 1 ML are only stable at temperatures higher than 500 K under all H2 pressures investigated (0.1 bar to 100 bar). This suggests that under catalytic conditions the two investigated surfaces are fully covered in H*. Given our finding that for the (10
0) surface (Fig. 3b); the phases displayed in these diagrams represent the most stable H* coverage at the given conditions. Both surfaces show that coverages lower than 1 ML are only stable at temperatures higher than 500 K under all H2 pressures investigated (0.1 bar to 100 bar). This suggests that under catalytic conditions the two investigated surfaces are fully covered in H*. Given our finding that for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface H2 dissociation is favorable even at H* coverage >1 ML, we also checked the stability of H* coverages exceeding 1 ML on this surface. Interestingly we observe that different coverages show different stability ranges. The (10
1) surface H2 dissociation is favorable even at H* coverage >1 ML, we also checked the stability of H* coverages exceeding 1 ML on this surface. Interestingly we observe that different coverages show different stability ranges. The (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) thermodynamic surface phase diagram (Fig. 3a) shows that all coverages investigated are stable under certain temperature and H2 pressure conditions but the 0.5 ML, and the 1 ML ones have the largest stability range. On the other hand, coverages between 0.083 and 0.334 ML are not stable under any condition on the (10
1) thermodynamic surface phase diagram (Fig. 3a) shows that all coverages investigated are stable under certain temperature and H2 pressure conditions but the 0.5 ML, and the 1 ML ones have the largest stability range. On the other hand, coverages between 0.083 and 0.334 ML are not stable under any condition on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, hence they are not observed in the phase diagram (Fig. 3b). We can explain these different stability ranges based on the trend of ΔGDiss in Fig. 1. Indeed, when ΔGDiss becomes significantly less favorable as the starting coverage increases (e.g., from 0.334 ML to 0.5 ML for the (10
0) surface, hence they are not observed in the phase diagram (Fig. 3b). We can explain these different stability ranges based on the trend of ΔGDiss in Fig. 1. Indeed, when ΔGDiss becomes significantly less favorable as the starting coverage increases (e.g., from 0.334 ML to 0.5 ML for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, Fig. 1) we observe a widening of the temperature stability range of the coverage formed by dissociating H2 molecules up to the abrupt increase in ΔGDiss. On the other hand, if no significant changes are observed in ΔGDiss as the starting coverage increases, (e.g., downhill from 0 ML to 0.167 ML on the (10
0) surface, Fig. 1) we observe a widening of the temperature stability range of the coverage formed by dissociating H2 molecules up to the abrupt increase in ΔGDiss. On the other hand, if no significant changes are observed in ΔGDiss as the starting coverage increases, (e.g., downhill from 0 ML to 0.167 ML on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, or almost flat from 0.250 ML to 0.375 ML on the (10
0) surface, or almost flat from 0.250 ML to 0.375 ML on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface) the formed coverages are either not present or their temperature stability ranges are extremely narrow in the phase diagram.
1) surface) the formed coverages are either not present or their temperature stability ranges are extremely narrow in the phase diagram.
In order to provide a complete analysis of the H* coverage stability on the investigated surfaces, we also accounted for the direct dissociation kinetics by creating kinetic phase diagrams (Fig. 3c and d). Because the method used for the generation of these phase diagrams (Methods section) calculates the continuous variation of coverage with temperature rather than discrete coverages, we cannot report exact phase transitions between individual coverages; we instead report transitions between ranges of coverages. The kinetic phase diagrams show an increased stability of high coverages (0.8–1.0 ML) relative to the thermodynamic ones, with transitions to lower coverages only occurring at around 880 K for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (Fig. 3c) and 780 K for the (10
1) surface (Fig. 3c) and 780 K for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (Fig. 3d). The increased stability of high coverages when including kinetic effects can be explained by the high affinity of the investigated surfaces towards atomic hydrogen, as reported by significantly lower reaction rates for associative desorption compared to the dissociative adsorption process (Tables S5 and S6 in the ESI†). Overall, the kinetic phase diagrams also confirm that under catalytic conditions the two investigated surfaces will be fully covered in H*.
0) surface (Fig. 3d). The increased stability of high coverages when including kinetic effects can be explained by the high affinity of the investigated surfaces towards atomic hydrogen, as reported by significantly lower reaction rates for associative desorption compared to the dissociative adsorption process (Tables S5 and S6 in the ESI†). Overall, the kinetic phase diagrams also confirm that under catalytic conditions the two investigated surfaces will be fully covered in H*.
Effect of hydrogen coverage on adsorption and dehydrogenation of butane
Ru nanoparticles have been used successfully for the catalytic hydrogenolysis of polyethylene. In order for the polymer chain to break down, the polymer must interact with the hydrogenated Ru surface. Therefore, to assess whether such interactions are favorable on the two Ru surfaces under study in this work, we investigated the adsorption of butane at catalytically relevant H* coverages. The interaction of polymeric chains with surfaces is known to occur via a train–loop–tail adsorption mode, meaning that only a small portion of the polymeric chain (i.e., the so called “train”) directly interacts with the surface.42 Recent molecular dynamics simulations have confirmed this behavior for Ru nanoparticles of the typical size used in hydrogenolysis experiments (1–3 nm)2,3,15,43 and have shown that the train length distribution is centered around five carbon atoms.44 This suggests that butane is a reasonable model of the adsorbed portion of the polymer that will undergo hydrogenolysis on small nanoparticles. Moreover, given the relatively small size of butane, we are able to use a smaller unit cell and maintain a reasonable computational cost. In typical hydrogenolysis experiments the catalyst is first reduced using hydrogen and then the polymer or alkane is introduced, eventually followed by more hydrogen to carry out the reaction.45 Given the significant exposure to elevated H2 pressure (above 10 bar) and temperatures (above 450 K) and based on our computed phase diagrams for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces (Fig. 3), we expect both surfaces to be fully covered by H* when the polymer reacts at the surface. Thus, butane adsorption energy was evaluated on the fully H* covered surfaces, with butane positioned on top of the H* layer (Fig. S7 and S8†), as well as on the bare surface as reference.
0) surfaces (Fig. 3), we expect both surfaces to be fully covered by H* when the polymer reacts at the surface. Thus, butane adsorption energy was evaluated on the fully H* covered surfaces, with butane positioned on top of the H* layer (Fig. S7 and S8†), as well as on the bare surface as reference.
At 0 ML of H* coverage, butane favorably adsorbs on both surfaces as indicated by the negative adsorption energies (Table 3). At 1 ML the adsorption energy remains negative meaning that interaction with the surface is still favorable, but it increases by about 0.4 eV on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface and 0.3 eV on the (10
1) surface and 0.3 eV on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. To explain these changes in adsorption energy as a result of surface hydrogenation, we calculated the d-band centers of the bare and hydrogenated surfaces. We found that the d-band center shifts to more negative values for the hydrogenated surfaces (Table S11†), which is a known effect of species chemisorbed at a surface.46 As a result of this shift, the surface d-states are less available to interact with the butane adsorbate, thus leading to the observed decrease in adsorption energy. On both surfaces we tested a few different initial configurations of butane for each coverage. While at 0 ML there is a more pronounced difference in stability between different configurations (about 0.05 eV), at 1 ML all configurations tested are essentially isoenergetic (maximum difference <0.02 eV). This suggests that while the hydrogenated surface is still attractive, there are no specific chemical interactions but general dispersion interaction. A potentially more favorable adsorption route for butane on the fully covered surface may involve H* atoms recombining and desorbing as H2 to leave empty surface sites for the polymer train to interact directly with the surface, similarly to what was proposed for the hydrogen mediated ammonia decomposition.46 However, this is unlikely to happen given that the dissociation energy of a single H2 molecule even at H* coverage nearing 1 ML (Fig. 1) is similar to the adsorption energy of butane on the bare surface; this indicates that there is no thermodynamic driving force for multiple H* atoms to desorb to allow butane to adsorb on empty surface sites.
0) surface. To explain these changes in adsorption energy as a result of surface hydrogenation, we calculated the d-band centers of the bare and hydrogenated surfaces. We found that the d-band center shifts to more negative values for the hydrogenated surfaces (Table S11†), which is a known effect of species chemisorbed at a surface.46 As a result of this shift, the surface d-states are less available to interact with the butane adsorbate, thus leading to the observed decrease in adsorption energy. On both surfaces we tested a few different initial configurations of butane for each coverage. While at 0 ML there is a more pronounced difference in stability between different configurations (about 0.05 eV), at 1 ML all configurations tested are essentially isoenergetic (maximum difference <0.02 eV). This suggests that while the hydrogenated surface is still attractive, there are no specific chemical interactions but general dispersion interaction. A potentially more favorable adsorption route for butane on the fully covered surface may involve H* atoms recombining and desorbing as H2 to leave empty surface sites for the polymer train to interact directly with the surface, similarly to what was proposed for the hydrogen mediated ammonia decomposition.46 However, this is unlikely to happen given that the dissociation energy of a single H2 molecule even at H* coverage nearing 1 ML (Fig. 1) is similar to the adsorption energy of butane on the bare surface; this indicates that there is no thermodynamic driving force for multiple H* atoms to desorb to allow butane to adsorb on empty surface sites.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) Ru surfaces. Energies are reported at 0 K with ZPE corrections
0) Ru surfaces. Energies are reported at 0 K with ZPE corrections
| Surface | Butane adsorption energy at 0 ML H* coverage [eV] | Butane adsorption energy at 1 ML H* coverage [eV] |
|---|---|---|
(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) 1) |
−0.98 | −0.56 |
(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) 0) |
−1.07 | −0.74 |
Comparing results across the two surfaces, we notice that the adsorption energies on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface are consistently more favorable than on the (10
0) surface are consistently more favorable than on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface. This result can be explained on the bare surface by the higher surface energies calculated for the (10
1) surface. This result can be explained on the bare surface by the higher surface energies calculated for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (Table S4 in the ESI†) indicating lower stability and stronger driving force to interact with adsorbates. On the fully H* covered surfaces, the trend can be explained based on the alignment of the surface H*, which carry a partial negative charge (−0.17 |e| average for the H* on the (10
0) surface (Table S4 in the ESI†) indicating lower stability and stronger driving force to interact with adsorbates. On the fully H* covered surfaces, the trend can be explained based on the alignment of the surface H*, which carry a partial negative charge (−0.17 |e| average for the H* on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface, and −0.20 |e| average for the H* on the (10
0) surface, and −0.20 |e| average for the H* on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface), with the hydrogens belonging to the adsorbed butane molecule, which carry a partial positive charge (0.03 |e| averaged across all the butane hydrogens on both surfaces). On the (10
1) surface), with the hydrogens belonging to the adsorbed butane molecule, which carry a partial positive charge (0.03 |e| averaged across all the butane hydrogens on both surfaces). On the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface only two C–H bonds directly align with two H* (Fig. S7†) while on the (10
1) surface only two C–H bonds directly align with two H* (Fig. S7†) while on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface four C–H bonds pointing downwards are aligned with four H* (Fig. S8†).
0) surface four C–H bonds pointing downwards are aligned with four H* (Fig. S8†).
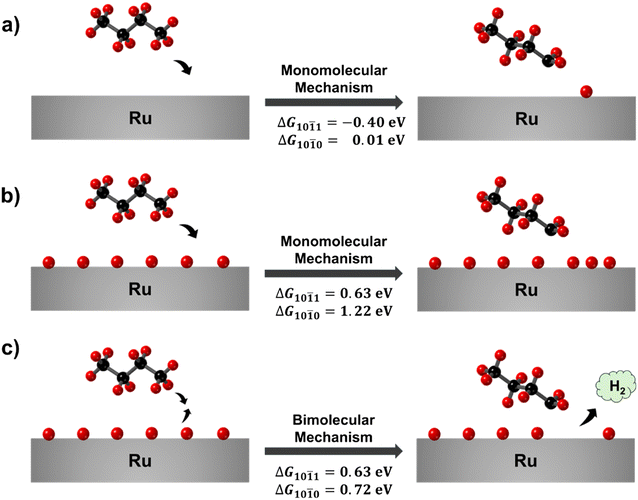
Having established that butane favorably interacts with both surfaces even at 1 ML of H* coverage, expected under experimental conditions, we move on to analyze the effect of the H* coverage on the dehydrogenation process, which is the first step in the hydrogenolysis mechanism and it is followed by the C–C cleavage.47 Either a terminal or central C–C cleavage can occur for butane (and polyethylene); here we focus on the dehydrogenation leading to a terminal cleavage given that it is associated with the production of the unwanted product methane. The main mechanism for metal catalyzed alkane dehydrogenation proposed in the literature is a monomolecular (MM) mechanism (Fig. 4a), in which one C–H bond breaks by interacting with bare Ru surface atoms.15,48,49 This is a reasonable mechanism for these studies in which only the bare surface was modeled. Given our finding that these surfaces will be fully covered by hydrogen, we propose an alternative mechanism in which a H* combines with the H from the butane C–H bond being cleaved thus forming H2 and freeing surface area for the alkyl radical adsorption (Fig. 4c); we refer to this mechanism as the bimolecular (BM) mechanism.
We start our analysis with the more established MM mechanism. Although both the surfaces will be fully covered by hydrogen under experimental conditions, we still calculated the dehydrogenation reaction energy at 0 ML of H* coverage as a point of reference. We found that the reaction is thermodynamically favored on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (ΔG = −0.40 eV) and thermoneutral on the (10
1) surface (ΔG = −0.40 eV) and thermoneutral on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) (ΔG = −0.01 eV). Given that this reaction results in the formation of one H*, the more favorable reaction energy on the (10
0) (ΔG = −0.01 eV). Given that this reaction results in the formation of one H*, the more favorable reaction energy on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface can be simply explained by the stronger H* adsorption energy (Tables S7 and S8†) and more favorable H2 dissociation (Fig. 1) with respect to the (10
1) surface can be simply explained by the stronger H* adsorption energy (Tables S7 and S8†) and more favorable H2 dissociation (Fig. 1) with respect to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. In addition, we observed an attractive interaction between the adsorbed butyl radical and the H* on the (10
0) surface. In addition, we observed an attractive interaction between the adsorbed butyl radical and the H* on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (Table S12 of the ESI†), which could further contribute to the more favorable reaction energy on this surface.
1) surface (Table S12 of the ESI†), which could further contribute to the more favorable reaction energy on this surface.
When the surfaces are fully covered, the H* and the radical resulting from the C–H cleavage in the MM mechanism (Fig. 4b) have to adsorb on less stable vacant sites: namely the higher top sites for the butyl radical on both surfaces, and an interstitial position between a bridge and a higher hollow site for H* on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and a bridge site on the (10
0) and a bridge site on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1). These sites will be fully surrounded by preadsorbed H*, thus possibly leading to large lateral repulsion. Not surprisingly, we find the dehydrogenation energies to be significantly higher relative to the 0 ML case. Once again, we observe that the reaction energies for the (10
1). These sites will be fully surrounded by preadsorbed H*, thus possibly leading to large lateral repulsion. Not surprisingly, we find the dehydrogenation energies to be significantly higher relative to the 0 ML case. Once again, we observe that the reaction energies for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface are more favorable (although still positive) relative to the (10
1) surface are more favorable (although still positive) relative to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. In addition to the attractive interaction between the butyl radical and the H* on the (10
0) surface. In addition to the attractive interaction between the butyl radical and the H* on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface discussed above, this can be explained based on our finding previously presented that H2 dissociation at 1 ML is not favorable on the (10
1) surface discussed above, this can be explained based on our finding previously presented that H2 dissociation at 1 ML is not favorable on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface while it is still favorable on the (10
0) surface while it is still favorable on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface. As an alternative to the butyl radical and H* having to adsorb on the fully hydrogenated surfaces, one could hypothesize that multiple H* atoms might recombine and desorb to leave space for the radical. However, this is highly unlikely given that the dissociation energy of just one H2 molecule at high coverage is significantly more favorable than the MM dehydrogenation reaction energy even at 0 ML, indicating no thermodynamic driving force for H* atoms to desorb to allow this reaction to happen. We thus conclude that H* is poisoning the surface by blocking the available adsorption sites for the alkyl radicals. Similar poisoning effects have been reported for other reactions involving hydrogen and Ru nanoparticles.46,50
1) surface. As an alternative to the butyl radical and H* having to adsorb on the fully hydrogenated surfaces, one could hypothesize that multiple H* atoms might recombine and desorb to leave space for the radical. However, this is highly unlikely given that the dissociation energy of just one H2 molecule at high coverage is significantly more favorable than the MM dehydrogenation reaction energy even at 0 ML, indicating no thermodynamic driving force for H* atoms to desorb to allow this reaction to happen. We thus conclude that H* is poisoning the surface by blocking the available adsorption sites for the alkyl radicals. Similar poisoning effects have been reported for other reactions involving hydrogen and Ru nanoparticles.46,50
The computed reaction free energies for the BM mechanism at 1 ML of H* coverage (Fig. 4c) are positive for both the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces. In particular, the reaction free energy for the (10
0) surfaces. In particular, the reaction free energy for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface (0.63 eV) is the same as the one computed for the MM mechanism at 1 ML of H* coverage, suggesting that the two dehydrogenation mechanisms will compete on this surface. On the other hand, the BM mechanism for the fully hydrogenated (10
1) surface (0.63 eV) is the same as the one computed for the MM mechanism at 1 ML of H* coverage, suggesting that the two dehydrogenation mechanisms will compete on this surface. On the other hand, the BM mechanism for the fully hydrogenated (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface is significantly more favorable than the MM mechanism (0.5 eV lower free energy), meaning that the BM mechanism will be the main dehydrogenation route on this surface. The preference for the BM mechanism for the (10
0) surface is significantly more favorable than the MM mechanism (0.5 eV lower free energy), meaning that the BM mechanism will be the main dehydrogenation route on this surface. The preference for the BM mechanism for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface can be explained by the fact that the desorption of only one H* from the surface, though energetically unfavorable, is compensated by the decrease in co-adsorbing H* lateral interactions as well as by the gain of rotational and translational mode of the desorbed H2 molecule. While the latter is a common effect for both surfaces, the decrease in lateral interactions is more pronounced on the (10
0) surface can be explained by the fact that the desorption of only one H* from the surface, though energetically unfavorable, is compensated by the decrease in co-adsorbing H* lateral interactions as well as by the gain of rotational and translational mode of the desorbed H2 molecule. While the latter is a common effect for both surfaces, the decrease in lateral interactions is more pronounced on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface because the adjacent higher hollow H* adsorption sites are 0.5 Å closer to each other than any adjacent site pair on the (10
0) surface because the adjacent higher hollow H* adsorption sites are 0.5 Å closer to each other than any adjacent site pair on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface. Overall, we expect that butane dehydrogenation via the BM mechanism would compete with the MM mechanism on the (10
1) surface. Overall, we expect that butane dehydrogenation via the BM mechanism would compete with the MM mechanism on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface while it will dominate the reactivity of butane dehydrogenation on the (10
1) surface while it will dominate the reactivity of butane dehydrogenation on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. More generally, both mechanisms have positive reaction energies suggesting that the dehydrogenation step will be slow on these fully hydrogenated surfaces and the observed reactivity of Ru nanoparticles is mainly due to the significant exposure of the (0001) surface.
0) surface. More generally, both mechanisms have positive reaction energies suggesting that the dehydrogenation step will be slow on these fully hydrogenated surfaces and the observed reactivity of Ru nanoparticles is mainly due to the significant exposure of the (0001) surface.
Conclusions
In this study, we employed periodic DFT calculations to investigate the interaction of molecular and atomic hydrogens with the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and Ru (10
1) and Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces, a limited area of research thus far. The promising activities of these Ru surfaces in various catalytic processes encouraged us to explore their potential role in plastic hydrogenolysis, a process that uses large hydrogen pressures and moderate temperatures to cleave polymeric chains and convert polyolefin plastic waste into useful chemicals. Understanding how hydrogen interacts with the surface and affects its reactivity towards the plastic chains is crucial for ultimately unraveling the reaction mechanism, predicting the product distribution, and designing improved catalyst.
0) surfaces, a limited area of research thus far. The promising activities of these Ru surfaces in various catalytic processes encouraged us to explore their potential role in plastic hydrogenolysis, a process that uses large hydrogen pressures and moderate temperatures to cleave polymeric chains and convert polyolefin plastic waste into useful chemicals. Understanding how hydrogen interacts with the surface and affects its reactivity towards the plastic chains is crucial for ultimately unraveling the reaction mechanism, predicting the product distribution, and designing improved catalyst.
We started our investigation by identifying the most favorable sites for atomic hydrogen adsorption on the two Ru surfaces, namely hcp and fcc sites on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, and higher hollow and higher bridge sites on the (10
1) surface, and higher hollow and higher bridge sites on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. We found that H2 spontaneously dissociates on all the investigated sites except for the higher top sites on both surfaces. This behavior is very different from the most stable surface of Ru, the (0001), on which H2 was found to molecularly adsorb in a previous work. Furthermore, our results show that atomic hydrogen can easily migrate on the surface to achieve the most stable arrangement at different coverages. Using ab initio thermodynamics and microkinetic modelling, we then developed phase diagrams to predict the atomic hydrogen coverage in a wide range of temperature (200 K to 1500 K) and H2 pressure (0.1 bar to 100 bar). The phase diagrams indicate that the investigated Ru surfaces will be fully covered with hydrogen under the typical catalytic conditions (473–523 K, and 10–90 bar of H2 pressure). Having established the level of hydrogenation of these surfaces under experimental conditions, we moved on to explore how this aspect affects the polymer hydrogenolysis. To this end, we used butane to model the portion of the polyethylene chain directly interacting with the surface. In particular, we studied the adsorption and dehydrogenation of butane, the two steps needed for C–C cleavage to occur. We found that, despite being less favorable, the adsorption can occur on both surfaces even when fully hydrogenated. We then explored the energetics of two possible mechanisms for butane dehydrogenation, namely the monomolecular and the bimolecular mechanism. In the former, one butane C–H bond breaks by interacting with the surface, leading to the formation of co-adsorbed butyl radical and atomic hydrogen. In the bimolecular one, an adsorbed hydrogen mediates the interaction between the butane C–H bond and the surface, leading to the formation of an adsorbed butyl radical and an H2 molecule. Our computed reaction free energies suggest that the monomolecular mechanism is favorable on the bare surface but the bimolecular one is preferred on the fully hydrogenated surfaces, especially for the (10
0) surface. We found that H2 spontaneously dissociates on all the investigated sites except for the higher top sites on both surfaces. This behavior is very different from the most stable surface of Ru, the (0001), on which H2 was found to molecularly adsorb in a previous work. Furthermore, our results show that atomic hydrogen can easily migrate on the surface to achieve the most stable arrangement at different coverages. Using ab initio thermodynamics and microkinetic modelling, we then developed phase diagrams to predict the atomic hydrogen coverage in a wide range of temperature (200 K to 1500 K) and H2 pressure (0.1 bar to 100 bar). The phase diagrams indicate that the investigated Ru surfaces will be fully covered with hydrogen under the typical catalytic conditions (473–523 K, and 10–90 bar of H2 pressure). Having established the level of hydrogenation of these surfaces under experimental conditions, we moved on to explore how this aspect affects the polymer hydrogenolysis. To this end, we used butane to model the portion of the polyethylene chain directly interacting with the surface. In particular, we studied the adsorption and dehydrogenation of butane, the two steps needed for C–C cleavage to occur. We found that, despite being less favorable, the adsorption can occur on both surfaces even when fully hydrogenated. We then explored the energetics of two possible mechanisms for butane dehydrogenation, namely the monomolecular and the bimolecular mechanism. In the former, one butane C–H bond breaks by interacting with the surface, leading to the formation of co-adsorbed butyl radical and atomic hydrogen. In the bimolecular one, an adsorbed hydrogen mediates the interaction between the butane C–H bond and the surface, leading to the formation of an adsorbed butyl radical and an H2 molecule. Our computed reaction free energies suggest that the monomolecular mechanism is favorable on the bare surface but the bimolecular one is preferred on the fully hydrogenated surfaces, especially for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. However, the reaction free energies are positive, indicating that the dehydrogenation process will be slow.
0) surface. However, the reaction free energies are positive, indicating that the dehydrogenation process will be slow.
Overall, our investigation suggests that the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces are unlikely to be particularly active towards polyolefin hydrogenolysis trains but they are very effective for H2 splitting. Thus, we hypothesize that, in a typical nanoparticle exposing multiple low-index facets along with the most stable (0001) facet, the Ru (10
0) surfaces are unlikely to be particularly active towards polyolefin hydrogenolysis trains but they are very effective for H2 splitting. Thus, we hypothesize that, in a typical nanoparticle exposing multiple low-index facets along with the most stable (0001) facet, the Ru (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and (10
1) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces will split H2 and store atomic hydrogen. This stored hydrogen can then diffuse to other exposed surfaces, where the polyolefin cleavage is occurring, as needed; migration of atomic hydrogen across facets is a well-known phenomenon for Ru.51 However, more work is needed to elucidate the polyethylene hydrogenolysis mechanism on less hydrogenated facet exposed in typical nanoparticles, such as the most stable (0001) facet. Work is currently underway in our group to investigate these aspects.
0) surfaces will split H2 and store atomic hydrogen. This stored hydrogen can then diffuse to other exposed surfaces, where the polyolefin cleavage is occurring, as needed; migration of atomic hydrogen across facets is a well-known phenomenon for Ru.51 However, more work is needed to elucidate the polyethylene hydrogenolysis mechanism on less hydrogenated facet exposed in typical nanoparticles, such as the most stable (0001) facet. Work is currently underway in our group to investigate these aspects.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
F. C.: conceptualization; data curation; formal analysis; methodology; investigation; writing – original draft; writing – review and editing; S. U.: conceptualization; data curation; formal analysis; methodology; investigation; writing – original draft; M. L.: conceptualization; funding acquisition; project administration; resources; supervision; methodology; writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research by F. C. is supported by a University International Postgraduate Award (UIPA) scholarship from UNSW Sydney. This work was supported by the Australian Research Council Discovery Project DP230100596. We are grateful for the computational resources and services from the National Computational Infrastructure (NCI), provided by the Australian Government under the National Computational Merit Allocation Scheme and the computational cluster Katana supported by the Research Technology Services at UNSW Sydney. Prof Richard Tilley, Prof Justin Gooding, Prof Julie Rorrer, Michele Pettini, and Marzia Cavallo are acknowledged for their helpful suggestions during this project.References
- J. Humphreys, R. Lan and S. Tao, Development and Recent Progress on Ammonia Synthesis Catalysts for Haber–Bosch Process, Adv. Energy Sustainability Res., 2021, 2(1), 2000043 CrossRef CAS.
- G. Celik, R. M. Kennedy, R. A. Hackler, M. Ferrandon, A. Tennakoon, S. Patnaik, A. M. Lapointe, S. C. Ammal, A. Heyden, F. A. Perras, M. Pruski, S. L. Scott, K. R. Poeppelmeier, A. D. Sadow and M. Delferro, Upcycling Single-Use Polyethylene into High-Quality Liquid Products, ACS Cent. Sci., 2019, 5(11), 1795–1803 CrossRef CAS PubMed.
- J. E. Rorrer, C. Troyano-Valls, G. T. Beckham and Y. Román-Leshkov, Hydrogenolysis of Polypropylene and Mixed Polyolefin Plastic Waste over Ru/C to Produce Liquid Alkanes, ACS Sustainable Chem. Eng., 2021, 9(35), 11661–11666 CrossRef CAS.
- J. E. Rorrer, A. M. Ebrahim, Y. Questell-Santiago, J. Zhu, C. Troyano-Valls, A. S. Asundi, A. E. Brenner, S. R. Bare, C. J. Tassone, G. T. Beckham and Y. Román-Leshkov, Role of Bifunctional Ru/Acid Catalysts in the Selective Hydrocracking of Polyethylene and Polypropylene Waste to Liquid Hydrocarbons, ACS Catal., 2022, 12(22), 13969–13979 CrossRef CAS.
- Y. Nakagawa, S. I. Oya, D. Kanno, Y. Nakaji, M. Tamura and K. Tomishige, Regioselectivity and Reaction Mechanism of Ru-Catalyzed Hydrogenolysis of Squalane and Model Alkanes, ChemSusChem, 2017, 10(1), 189–198 CrossRef CAS PubMed.
- M. Tamura, S. Miyaoka, Y. Nakaji, M. Tanji, S. Kumagai, Y. Nakagawa, T. Yoshioka and K. Tomishige, Structure-Activity Relationship in Hydrogenolysis of Polyolefins over Ru/Support Catalysts, Appl. Catal., B, 2022, 318, 121870 CrossRef CAS.
- L. Chen, Y. Zhu, L. C. Meyer, L. V. Hale, T. T. Le, A. Karkamkar, J. A. Lercher, O. Y. Gutiérrez and J. Szanyi, Effect of Reaction Conditions on the Hydrogenolysis of Polypropylene and Polyethylene into Gas and Liquid Alkanes, React. Chem. Eng., 2022, 7, 844–854 RSC.
- C. Wang, T. Xie, P. A. Kots, B. C. Vance, K. Yu, P. Kumar, J. Fu, S. Liu, G. Tsilomelekis, E. A. Stach, W. Zheng and D. G. Vlachos, Polyethylene Hydrogenolysis at Mild Conditions over Ruthenium on Tungstated Zirconia, JACS Au, 2021, 1(9), 1422–1434 CrossRef CAS PubMed.
- A. R. Poerwoprajitno, L. Gloag, J. Watt, S. Cheong, X. Tan, H. Lei, H. A. Tahini, A. Henson, B. Subhash, N. M. Bedford, B. K. Miller, P. B. O'Mara, T. M. Benedetti, D. L. Huber, W. Zhang, S. C. Smith, J. J. Gooding, W. Schuhmann and R. D. Tilley, A Single-Pt-Atom-on-Ru-Nanoparticle Electrocatalyst for CO-Resilient Methanol Oxidation, Nat. Catal., 2022, 5(3), 231–237 CrossRef CAS.
- A. R. Poerwoprajitno, L. Gloag, T. M. Benedetti, S. Cheong, J. Watt, D. L. Huber, J. J. Gooding and R. D. Tilley, Formation of Branched Ruthenium Nanoparticles for Improved Electrocatalysis of Oxygen Evolution Reaction, Small, 2019, 15(17), 1804577 CrossRef PubMed.
- F. Wang, C. Li, X. Zhang, M. Wei, D. G. Evans and X. Duan, Catalytic Behavior of Supported Ru Nanoparticles on the {1 0 0}, {1 1 0}, and {1 1 1} Facet of CeO2, J. Catal., 2015, 329, 177–186 CrossRef CAS.
- X. Cui, Z. Li, H. Jang, M. G. Kim, S. Liu, L. Hou and X. Liu, Anomalous Dominated (100) Index Facet Endows Ruthenium Nanoparticles with Accelerated Alkaline Hydrogen Evolution, Inorg. Chem. Front., 2024, 11(5), 1552–1560 RSC.
- X. Du, Y. Lang, K. Cao, J. Yang, J. Cai, B. Shan and R. Chen, Bifunctionally Faceted Pt/Ru Nanoparticles for Preferential Oxidation of CO in H2, J. Catal., 2021, 396, 148–156 CrossRef CAS.
- Y. Nanba, T. Ishimoto and M. Koyama, Structural Stability of Ruthenium Nanoparticles: A Density Functional Theory Study, J. Phys. Chem. C, 2017, 121(49), 27445–27452 CrossRef CAS.
- T. Xie, G. R. Wittreich and D. G. Vlachos, Multiscale Modeling of Hydrogenolysis of Ethane and Propane on Ru(0001): Implications for Plastics Recycling, Appl. Catal., B, 2022, 316, 121597 CrossRef CAS.
- M. Zhao and Y. Xia, Crystal-Phase and Surface-Structure Engineering of Ruthenium Nanocrystals, Nat. Rev. Mater., 2020, 5(6), 440–459 CrossRef CAS.
- L. Li, F. Tian, L. Qiu, F. Wu, W. Yang and Y. Yu, Recent Progress on Ruthenium-Based Electrocatalysts towards the Hydrogen Evolution Reaction, Catalysts, 2023, 13(12), 1497 CrossRef CAS.
- F. Colasuonno and M. Lessio, Thermodynamic and Kinetic Insights into Hydrogen Adsorption and Dissociation on the Ru (0001) Surface under STM and Catalytic Conditions, J. Phys. Chem. C, 2023, 127(49), 23645–23653 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Surface Energies of Elemental Crystals, Sci. Data, 2016, 3(1), 160080 CrossRef CAS PubMed.
- L.-L. Wang, Z.-Y. Yu and T.-B. Lu, Recent Advances of Ruthenium-Based Materials for Acidic Oxygen Evolution Reaction: From Catalyst Design to Proton Exchange Membrane Water Electrolysers, J. Mater. Chem. A, 2024, 12(35), 23297–23314 RSC.
- L. Chen, Y. Li and X. Liang, Ar/H2/O2-Controlled Growth Thermodynamics and Kinetics to Create Zero-, One-, and Two-Dimensional Ruthenium Nanocrystals towards Acidic Overall Water Splitting, Adv. Funct. Mater., 2021, 31(11), 2007344 CrossRef CAS.
- J. Watt, C. Yu, S. L. Y. Chang, S. Cheong and R. D. Tilley, Shape Control from Thermodynamic Growth Conditions: The Case of Hcp Ruthenium Hourglass Nanocrystals, J. Am. Chem. Soc., 2013, 135(2), 606–609 CrossRef CAS PubMed.
- R. Manabe, H. Nakatsubo, A. Gondo, K. Murakami, S. Ogo, H. Tsuneki, M. Ikeda, A. Ishikawa, H. Nakai and Y. Sekine, Electrocatalytic Synthesis of Ammonia by Surface Proton Hopping, Chem. Sci., 2017, 8(8), 5434–5439 RSC.
- G. Kresse and J. A. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, A Dimer Method for Finding Saddle Points on High Dimensional Potential Surfaces Using Only First Derivatives, J. Chem. Phys., 1999, 111(15), 7010–7022 CrossRef CAS.
- D. S. Sholl and J. A. Steckel, Equilibrium Phase Diagrams From Ab Initio Thermodynamics, in Density Functional Theory, John Wiley & Sons, Inc., 2009, pp. 163–177 Search PubMed.
- M. López, Á. Morales-García, F. Viñes and F. Illas, Thermodynamics and Kinetics of Molecular Hydrogen Adsorption and Dissociation on MXenes: Relevance to Heterogeneously Catalyzed Hydrogenation Reactions, ACS Catal., 2021, 11(21), 12850–12857 CrossRef.
- M. Johansson, O. Lytken and I. Chorkendorff, The Sticking Probability for H2 on Some Transition Metals at a Hydrogen Pressure of 1bar, J. Chem. Phys., 2008, 128(3), 034706 CrossRef CAS PubMed.
- P. Feulner and D. Menzel, The Adsorption of Hydrogen on Ruthenium (001): Adsorption States, Dipole Moments and Kinetics of Adsorption and Desorption, Surf. Sci., 1985, 154(2–3), 465–488 CrossRef CAS.
- I. A. W. Filot, Introduction to Microkinetic Modeling, Technische Universiteit Eindhoven, 2018 Search PubMed.
- S. K. Konda and A. Chen, Palladium Based Nanomaterials for Enhanced Hydrogen Spillover and Storage, Mater. Today, 2016, 19(2), 100–108 CrossRef CAS.
- J. Greeley and M. Mavrikakis, Surface and Subsurface Hydrogen: Adsorption Properties on Transition Metals and near-Surface Alloys, J. Phys. Chem. B, 2005, 109(8), 3460–3471 CrossRef CAS PubMed.
- M. Y. Chou and J. R. Chelikowsky, First-Principles Study of Hydrogen Adsorption on Ru(0001): Possible Occupation of Subsurface Sites, Phys. Rev. Lett., 1987, 59(15), 1737–1740 CrossRef CAS PubMed.
- K. L. Kostov, W. Widdra and D. Menzel, Hydrogen on Ru(0 0 1) Revisited: Vibrational Structure, Adsorption States, and Lateral Coupling, Surf. Sci., 2004, 560(1–3), 130–144 CrossRef CAS.
- J. M. H. M. Scheutjens and G. J. Fleer, Statistical Theory of the Adsorption of Interacting Chain Molecules. 2. Train, Loop, and Tail Size Distribution, J. Phys. Chem., 1980, 84(2), 178–190 CrossRef CAS.
- J. E. Rorrer, G. T. Beckham and Y. Román-Leshkov, Conversion of Polyolefin Waste to Liquid Alkanes with Ru-Based Catalysts under Mild Conditions, JACS Au, 2020, 1, 8–12 CrossRef PubMed.
- M. Zare, P. A. Kots, Z. R. Hinton, T. H. Epps, L. T. J. Korley, S. Caratzoulas and D. G. Vlachos, Effect of Reaction Media on Hydrogenolysis of Polyethylene Plastic Waste: Polymer-Surface Interactions in Small Alkane/Polymer Blends, Appl. Catal., B, 2024, 351, 123969 CrossRef CAS.
- A. Musa, E. A. Jaseer, S. Barman and N. Garcia, Review on Catalytic Depolymerization of Polyolefin Waste by Hydrogenolysis: State-of-the-Art and Outlook, Energy Fuels, 2024, 38(3), 1676–1691 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Electronic Factors Determining the Reactivity of Metal Surfaces, Surf. Sci., 1995, 343(3), 211–220 CrossRef CAS.
- A. Beck, J. Marlowe, M. J. Gordon and P. Christopher, Is There a Discernible Photochemical Effect Beyond Heating for Visible Photon-Mediated NH 3 Decomposition over Ru/Al2O3?, J. Phys. Chem. C, 2024, 128(21), 8590–8600 CrossRef CAS.
- J. H. Sinfelt, Catalytic Hydrogenolysis on Metals, Catal. Lett., 1991, 9(3–4), 159–171 CrossRef CAS.
- D. D. Hibbitts, D. W. Flaherty and E. Iglesia, Effects of Chain Length on the Mechanism and Rates of Metal-Catalyzed Hydrogenolysis of n-Alkanes, J. Phys. Chem. C, 2016, 120(15), 8125–8138 CrossRef CAS.
- M. M. Islam, C. R. A. Catlow and A. Roldan, Mechanistic Pathways for the Dehydrogenation of Alkanes on Pt(111) and Ru(0001) Surfaces, ChemCatChem, 2024, 16(11), e202301386 CrossRef CAS.
- M. V. Arena, E. D. Westre, D. E. Brown, J. Kutzner and S. M. George, Surface Diffusion of Hydrogen on a Stepped Ru(001) Surface, Surf. Sci., 1995, 325(1–2), 151–162 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lf00002e |
| This journal is © The Royal Society of Chemistry 2025 |